Reflection on modern methods: trial emulation in the presence of immortal-time bias. Assessing the benefit of major surgery for elderly lung cancer patients using observational data

Abstract

Acquiring real-world evidence is crucial to support health policy, but observational studies are prone to serious biases. An approach was recently proposed to overcome confounding and immortal-time biases within the emulated trial framework. This tutorial provides a step-by-step description of the design and analysis of emulated trials, as well as R and Stata code, to facilitate its use in practice. The steps consist in: (i) specifying the target trial and inclusion criteria; (ii) cloning patients; (iii) defining censoring and survival times; (iv) estimating the weights to account for informative censoring introduced by design; and (v) analysing these data. These steps are illustrated with observational data to assess the benefit of surgery among 70–89-year-old patients diagnosed with early-stage lung cancer. Because of the severe unbalance of the patient characteristics between treatment arms (surgery yes/no), a naïve Kaplan-Meier survival analysis of the initial cohort severely overestimated the benefit of surgery on 1-year survival (22% difference), as did a survival analysis of the cloned dataset when informative censoring was ignored (17% difference). By contrast, the estimated weights adequately removed the covariate imbalance. The weighted analysis still showed evidence of a benefit, though smaller (11% difference), of surgery among older lung cancer patients on 1-year survival. Complementing the CERBOT tool, this tutorial explains how to proceed to conduct emulated trials using observational data in the presence of immortal-time bias. The strength of this approach is its transparency and its principles that are easily understandable by non-specialists.

Key Messages

• In observational data, when the start of follow-up and treatment initiation do not coincide, confounding and immortal-time biases are a concern for the estimation of causal treatment effects.

• These biases can be controlled using a cloning technique, proposed within the framework of emulated trials.

• Informative censoring triggered by cloning patients must be accounted for using inverse-probability-of-censoring weighting.

• We offer a step-by-step tutorial detailing how to use the method in practice, alongside an application evaluating the causal effect of surgery among elderly lung cancer patients.

Introduction

Randomised controlled trials (RCTs) are the gold-standard to evaluate the efficacy of an intervention. However, the external validity of RCTs is often limited. In particular, the trial population rarely reflects the diversity of patients in practice. Older patients, or patients with comorbidities, are often not eligible for RCTs,¹ leading to a lack of randomised evidence in these populations. For instance in England, the median age at non-small cell lung cancer (NSCLC) diagnosis is 73.5 years,² but in randomised trials more than half of included patients were diagnosed at an age less than 60:³ a pattern that is common to many cancers in an ageing population.⁴

In the absence of available RCTs (or in complement), observational data represent a valuable source of information to estimate real-world causal effects. However, the nature of such data poses several challenges. A first challenge is the presence of confounding due to the absence of randomisation. For instance, when using routinely collected data to estimate the effect of a treatment, the patients’ characteristics are likely to differ between treatment groups since clinicians adapt treatment prescriptions according to these characteristics. If these unbalanced measured characteristics are also prognostic variables for the outcome of interest, not accounting for them leads to confounding bias. A second challenge, often overlooked in practice, is the issue of immortal-time bias: non-pharmacological treatments, such as surgery, are unlikely to be received on the day of diagnosis and treatment is more likely to be received among patients with longer survival.⁵ Immortal-time bias usually arises when the start of follow-up and treatment initiation do not coincide. For instance in observational data, surgery is observed only for patients who have survived up to the date of planned surgery. This artificially contributes to an inflated beneficial effect of surgery if control and treatment groups were defined at time zero while using the surgery status observed later in time.^6,7

When these two caveats are ignored, the estimated treatment effect is usually biased. Traditionally, both issues have been addressed using multivariable regression models in which treatment is modelled as a time-updated covariate to estimate conditional effects.⁸ A more recent suggestion to control for these biases has been proposed by Hernàn^9,10 within the framework of emulated trials, for the estimation of marginal effects. This method consists of mimicking a target trial by using a formal process for selecting patients and defining the exposure, outcome and causal estimand. To address measured confounding at baseline and immortal-time bias, Hernàn^9,10 proposed a strategy of analysis based on participant cloning. Two exact copies (clones) of each patient’s record are created: one clone is allocated to the intervention arm of the emulated trial, the other clone is allocated to the control arm. As such, the study arms are identical at baseline. Then, a clone is censored when the treatment actually received is no longer compatible with the treatment strategy of the arm they entered. This induces informative censoring (i.e. selection bias over time), as described by Hernàn,¹⁰ since treatment received typically depends on individual characteristics. This informative censoring can be addressed using inverse-probability-of-censoring weights in the analysis, in which uncensored observations are up-weighted to represent censored observations with similar characteristics and thus to allow unbiased estimation of the causal effect of interest.¹¹

Details on the implementation of this approach are scarce in the literature, limiting its use in practice. To date, the two papers introducing the concept of trial emulation have been cited over 160 times, but to our knowledge, only two articles reported the use of the cloning approach.^12,13 This tutorial provides a step-by-step description of the design, methodology and statistical analysis of emulated trials when immortal-time bias is a concern. This is illustrated using population-based cancer registrations, used to investigate the benefits of surgical treatment for older NSCLC patients. We provide the corresponding R and Stata code along with a toy dataset, for an easier implementation of the method.

Motivating example

NSCLC is the most common type of lung cancer and is the leading cause of cancer death in the UK. When diagnosed at an early stage, surgery is the first-line treatment with curative intent.¹⁴ In England, evidence suggests that elderly patients experience reduced access to surgery.² RCT evidence of the benefits of the surgery in older patients is scarce in the literature. Older patients have a higher prevalence of comorbidities and frailty and poorer health status than younger patients, thus confounding the effect of surgery on survival in observational data.

We aim to estimate the causal effect of surgery received within 6 months of diagnosis on 1-year survival and 1-year restricted mean survival time (RMST).¹⁵ To answer this question, we used data on cancer patients recorded in the National Cancer Registry in England and linked to secondary care administrative records.

In this example, the risk of immortal-time bias is an issue since study entry (diagnosis) and treatment initiation (surgery) occur at different times. Indeed, median delay to surgery is 29 days (from 0 to 176 days) and 6.7% (n = 156 patients) of patients, for whom clinical intention to surgery is unknown, died within 6 months after diagnosis (Figure 1). This motivates our use of Hernàn’s emulated trial strategy with cloning.¹⁰

Figure 1.

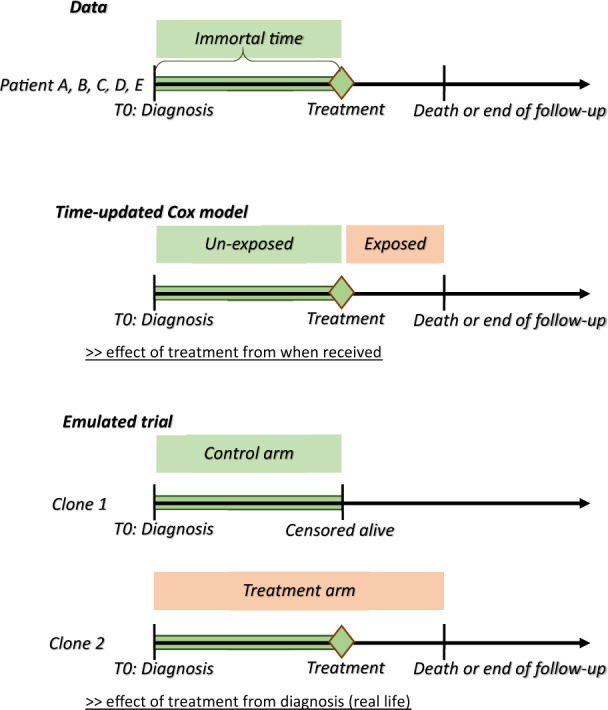
Graphic description of immortal-time bias and possible corrections. Patients A, B, C, D, E with survival patterns and treatment status as defined in Figure 2.

Methods

The framework of emulated trials allows the conduct of transparent studies using observational data, which helps the assessment of how reliable the results are. In particular, it ensures that the research question is aligned with the aim of the study, and makes it clear how the study was designed and analysed, with the identification of the primary outcome and exposure of interest, which will contribute to a more reproducible research using observational data. The general principle is to mimic a target trial, which is the randomised trial we would ideally conduct to address the causal research question. Several steps are required to emulate a trial using this methodology: (i) specification of the target trial and inclusion criteria; (ii) cloning; (iii) definition of survival time and vital status for each clone according to its arm; (iv) estimation of the censoring weights; and (v) estimation of the causal contrast. Step (i) is the design stage of the emulated trial, steps (ii)–(iv) are the practical implementation of this design, step (v) is the statistical analysis.

Step i: specification of the target trial and inclusion criteria

This step involves a detailed specification of the design (e.g. parallel arm trial, cross-over), aim (e.g. effectiveness, safety), eligibility and exclusion criteria, treatment strategies (clear description of the intervention and comparator), assignment and implementation (e.g. recruitment method, timing for treatment initiation), outcome and follow-up time, vital status at end of follow-up, adjustment variables, causal contrast (e.g. difference in means, risk ratio) and estimand (e.g. per protocol, intention-to-treat) of the target trial and its real-world counterpart. See Table S1 (available as Supplementary data at IJE online) for a description of each component in our illustrative example. A precise definition of the elements of the target trial makes the design of the observational study more straightforward and suitable for the estimation of the causal estimands. The CERBOT tool (Comparative Effectiveness Research Based on Observational data to emulate a Target trial) is a useful tool to guide researchers in this process.¹⁶ We also recommend the use of the CONSORT style flow diagram to report on patient selection.¹⁷ Most items are standard to clinical trials but, when there is a delay between the start of follow-up and treatment initiation, the definitions of the treatment implementation and causal contrast are more complex. A grace period—during which treatment initiation can happen—must be defined. The grace period length is chosen to reflect clinical practice, e.g. when patients are allowed time to complete clinical tests before treatment initiation, or when there are hospital delays before surgery. The grace period is needed to avoid ill-defined interventions that are problematic for causal inference.¹⁰ This is particularly important when the timing of the intervention is likely to affect the outcome. Two causal contrasts are common in clinical trials: intention-to-treat (ITT) and per protocol (PP) estimates. They correspond to the distinction between effectiveness and efficacy, respectively. Using observational data, no information is available on the planned treatment, therefore the targeted causal contrast is the per protocol effect.

Table S1 presents the definition of the target and emulated trials for our illustrative example. We included patients with a stage I or II NSCLC diagnosis, aged 70–89 years at diagnosis, a good performance status (levels 0–2) and a Charlson’s comorbidity index lower than 2. Assessment of eligibility was performed at diagnosis. The primary outcome of interest was all-cause death within a year following diagnosis. The per-protocol effect of surgery within 6 months of diagnosis on survival was quantified by the differences between the study arms in: (i) 1-year survival probabilities; and (ii) restricted mean survival times (survival time difference over a 1-year window).^15,18 Further information on data and participants are provided in Supplementary File S1, available as Supplementary data at IJE online.

Step ii: cloning

Cloning patients allows us to assign patients to both arms for the duration for which treatment allocation is unknown. At baseline, in our illustration, we assumed that all patients were equally likely to be offered surgery or not. As such, all patients entered both arms of the trial, independently of their subsequent surgery status. Thus, we created two clones of each patient with one clone allocated to each study arm, hence doubling the size of our dataset. The study arms are therefore identical with respect to demographics and clinical characteristics at the time of diagnosis. This removes confounding bias, at baseline only.

Step iii (a): defining censoring and time to censoring

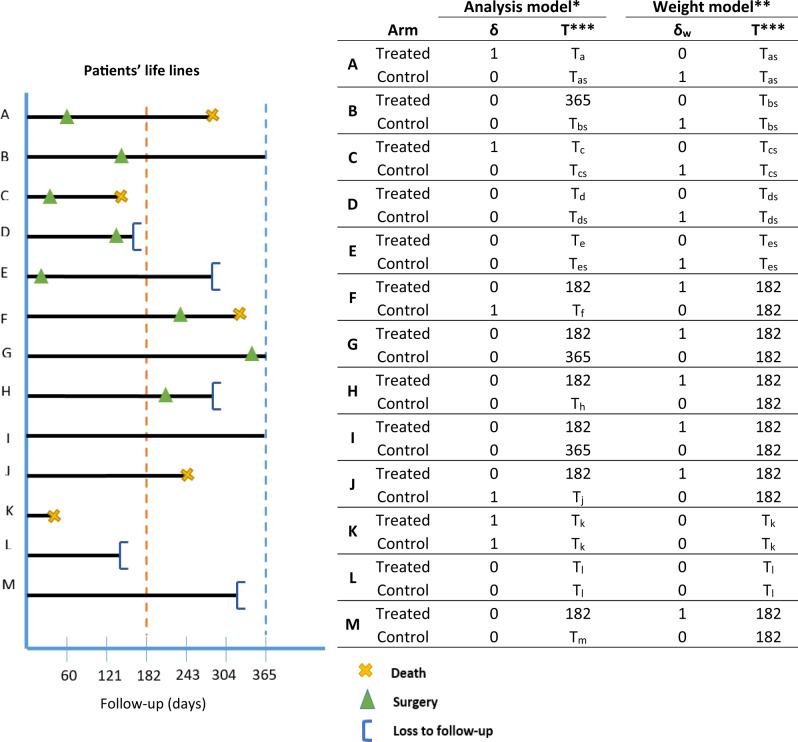
In each arm, patient follow-up times are censored when their treatment is no longer compatible with the treatment strategy for the arm, that is, when there is a deviation from the planned protocol. In our example, this means that: (i) patients who received surgery within 6 months were censored at their time of surgery in the no surgery (control) arm; and (ii) patients who did not receive surgery within 6 months were censored at 6 months in the treated arm (including patients who received major surgery beyond 6 months). This artificial censoring—introduced by design—could occur at any time between diagnosis and 6 months in the no surgery arm, but only at 6 months in the surgery arm. Figure 2 illustrates all possible censoring mechanisms in this emulated trial setting, with 13 types of patient records that could be seen in the cancer registry data. Censoring indicators and the time to censoring contribute to the weight model in step iv.

Figure 2.

Definition of the outcome and survival time for each patient in each arm, for both the weight and the analysis models. Patients A–E have records of surgery within the grace period and contribute to the weight models until their time of surgery, with censoring indicators equal to 1 in the control arm as they deviate from the protocol, and equal to 0 in the treated arm as they cannot deviate from the protocol after their record of surgery. For the analysis model in the control arm, these patients are censored at their time of surgery. Patients F–J comply with the control arm’s definition, and as such contribute the full grace period length (180 days, 6 months) to the weight models, with censoring indicators equal to 0 in the control arm as they do not deviate from the protocol, and equal to 1 in the treated arm as they deviate from the protocol. For the analysis model in the treated arm, these patients are censored at 6 months (180 days). Patients K and L contribute to both arms (analysis and weight models) equally as they do not deviate from any of the protocols since their survival times are censored or correspond to the event of interest before we could have assessed their receipt of surgery. Patient M complies with the control arm’s definition and as such contributed the full grace period length (6 months) to the weight models, with event indicators equal to 0 in the control arm as they do not deviate from the protocol, and equal to 1 in the treated arm as they deviate from the protocol. For the analysis model in the treated arm, this patient is censored at 6 months. *Event of interest: death (δ = 1); **event of interest: deviation from protocol (δ_w= 1); ***time in days used as follow-up time in the analysis or weight model; T_X: time to death or time to censoring for patient X; T_XS: time to surgery for patient X.

Step iii (b): defining outcome and survival time

For each patient, their event (if any) only contributes to the arm in which the patient is still uncensored at the time of event, i.e. the arm the patient is compliant with. The survival time of patients who die within the grace period without having received surgery (patient K, Figure 2) and the survival time pre-treatment (patients A, B, C, D, E, Figure 2) or the full length of the grace period (patients F, G, H, I, J, Figure 2), contribute to both arms, thus controlling for immortal-time bias. These outcomes and survival times contribute to the analysis model in step v. Model-based standard errors are underestimated because of an artificial increase in the number of events. Non-parametric bootstrap should be used instead, for steps ii to v.

Step iv: accounting for informative censoring due to artificial censoring

Although cloning (step ii) allows us to account for confounding at baseline, the artificial censoring introduced (step iii) is usually informative. If the decision to perform surgery was completely random or made based on patients’ characteristics that were not associated with the outcome, the artificial censoring done in step iii would be ignorable, and would not bias the results. However, in most observational studies, treatment decision is based on characteristics also associated with the outcome, i.e. the confounders. In our example, the decision to perform surgery is associated with age, performance status and comorbidity index, which are also associated with survival. In such situations, the artificial censoring introduces selection bias.¹⁰ Indeed, in the illustration, censored patients in the control arm (i.e. receiving surgery in the grace period) are different from patients who remained in the risk set for that arm.

The proposed approach to address this problem is to use inverse-probability-of-censoring weighting (IPCW).^11,19 The purpose of the weights is to up-weight patients remaining in the risk set so that they represent censored patients, and as such, maintain the comparability of the study arms throughout the grace period. In the absence of time-varying variables, a standard approach to estimate the weights is to predict the individual probabilities of remaining uncensored at each time of event, using a Cox regression model. This requires working with a dataset split at each time of event. The model includes variables predictive of the censoring mechanism, selected a priori based on clinical knowledge, and is arm-specific to capture potential interactions between covariates and treatment. The weights are the inverse of these probabilities. Since several computing steps are involved, we provide both R and Stata codes, along with a toy dataset R_data.R, data.csv, and results (Supplementary File S2, available as Supplementary data at IJE online).

When using IPCW to correct for informative censoring, the following assumptions are required to obtain an unbiased estimate of the causal effect of surgery:

1. no unmeasured confounders: all covariates associated with both the treatment assignment and deviation from the protocol are measured;

2. correct model specification: the Cox models used to derive the weights are correctly specified (e.g. functional forms for continuous variables, interactions included as necessary, proportional hazards assumption met);

3. positivity: the probability of deviating from the protocol is non-zero at all follow-up times of the grace period and for each patient;

4. consistency: the observed survival outcome under a treatment strategy is identical to what would have been observed had we assigned patients to this treatment strategy (the potential outcome).

In addition, before conducting the primary analysis, we need to ensure the weights can remove imbalance between arms. This can be done using standardized differences defined for each main prognosis factor as the weighted mean (or proportion) difference between groups divided by the weighted pooled standard deviation. A variable with a standardised difference below 10% is usually considered balanced. Remaining imbalances on one variable or more might suggest a mis-specification of the weight model. In such instance, adding interactions in the weight model and higher order terms for continuous variables might improve the balancing ability of the weights. If the imbalance is relatively small, these variables might be adjusted for in the weighted analysis model for double robustness.²⁰

In our example, for the weight models we adjusted for the effects of all covariates presented in Table S1 in a multivariable Cox model for the control group and in a multivariable logistic regression model for the surgery group, given that there is only one time at which patients can deviate from the protocol (6 months). Therefore, the corresponding times-to-event were the times of surgery in the no surgery arm if surgery happened in the grace period (time-varying weights), and 6 months in the surgery arm if surgery did not happen in the grace period (time-fixed weights) (Figure 2). All available prognostic factors were included in the models. We predicted the individual probabilities to experience an event, at each time of event. The weights are the inverse of such probabilities. An example of the calculation of such weights is provided for three patients of the no surgery arm in Table 1. Patient G remains in the risk set of the control arm, and their weights are updated at all times other patients are censored (receiving surgery, such as K) in that arm.

Table 1.

Toy example for the computation of weights in the control arm (patients A, G and K from Figure 2)

Patient ID	Arm	T-start	T-stop	Surgery	T-surgery	δ	δw	Weight
K	Control	0	40	0		1	0	1.00
A	Control	0	40	1	61	0	0	1.00
A	Control	40	61	1	61	0	1	1.00
G	Control	0	40	0		0	0	1.23
G	Control	40	61	0		0	0	1.35
G	Control	61	182	0		0	0	1.52

Data are split at each time of event (i.e. surgery and death). T-start and T-stop represent the beginning and end of the time intervals between two events (in the cohort); Surgery is the surgery status indicator; T-surgery is the time of surgery; δ and δ_w are the event status for the analysis and weight models, respectively. 40: time of death of patient K; 61: time of treatment of patient A; 182: end of grace period (∼6 months).

Step v: primary analysis

Once weights are estimated and adequately remove imbalance, a weighted analysis model must be used to estimate the per-protocol effect, accounting for informative censoring. An issue is the variance estimation for the treatment effect, accounting for both the uncertainty in weight estimation and the inflation of the sample size. One solution is to use the non-parametric bootstrap on steps (ii)-(v) to obtain valid 95% confidence intervals.

In our example, survival curves were estimated in each arm using a weighted non-parametric Kaplan-Meier estimator.¹⁹ The 95% confidence intervals for the difference in 1-year survival and difference in RMSTs were obtained using non-parametric bootstrap with 1000 replicates. We do not recommend using a simple Cox proportional hazards model to analyse the data. Indeed, the proportional hazard assumption is violated, given the design of the emulated trial with the cloning step and the similarities between arms in the grace period. Most importantly, hazard ratios are not recommended for causal inference.²¹ Alternatively, more flexible multivariable time-dependent models can be considered.²²

All analyses were conducted in both Stata version 15 and R version 3.5, for reproducibility.

Other multivariable approaches can account for both confounding and immortal-time biases, such as regression models with time-updated treatment indicator and delayed entry models.⁸ We contrast the results of the emulated trial to the results obtained using a multivariable Cox model with time-updated treatment. For comparability with the emulated trial approach, we predicted survival probabilities for the whole cohort as if they all had been treated at time zero and as if they had not. The difference between these two probabilities gives a marginal estimate of the treatment effect.

Results

Patient characteristics

Selection criteria led to the inclusion of 2309 patients (Supplementary Figure S1, available as Supplementary data at IJE online) We excluded 71 patients with a surgery recorded prior to their diagnosis. Supplementary Table S2, available as Supplementary data at IJE online, presents the characteristics of the patients by group defined by the observed exposure status, before cloning; 1241 patients received surgery within 6 months, 144 of whom died within a year (11.6%, representing 123.2 per 1000 person-years), with a median survival time of 185 days [interquartile range (IQR): 97–283 days]. Among 1068 patients who did not receive surgery, 362 (33.9%, representing 402.5 per 1000-person-years) died within a year, with a median survival time of 205 days (IQR: 122–283 days).

As shown in Table S2, all variables except sex were unbalanced between treatment groups as standardized differences were larger than 10%, suggesting confounding at baseline. Patients without a record of surgery tended to be older and a larger proportion of them were diagnosed as emergency, at stage II, with higher CCI and lower performance status than patients who received surgery.

Primary analysis

We benchmarked the results of the emulated trial with a naïve approach using a Kaplan-Meier estimation of the 1-year survival by surgery status on the original (non-cloned) dataset, and an unweighted Kaplan-Meier estimation on the cloned dataset. We also compared the results with those obtained from a multivariable Cox model with a time-updated treatment indicator.

Naïve approach

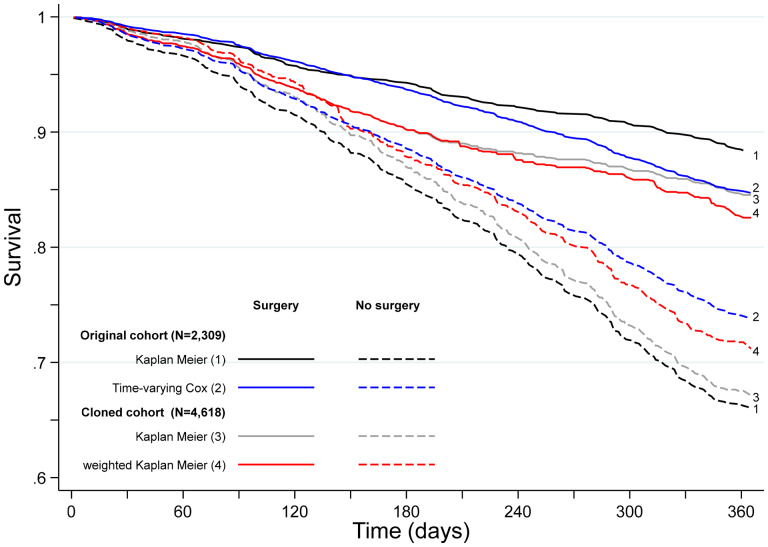
When confounding and immortal-time biases are ignored, the Kaplan-Meier estimates of 1-year survival were 88.4% [95% confidence interval (CI): 86.0–90.6%] and 66.0% (95% CI: 62.1–69.7%) for treated and untreated patients, respectively. This corresponds to a difference of 22.4% (95% CI: 18.1–26.9%) in 1-year survival and of 33 days (95% CI: 14–48) in RMST (Table 2). Interestingly, the survival differences between groups were evident from diagnosis, which reflects the impact of pre-treatment deaths (Figure 3).

Table 2.

1-year survival estimates and restricted mean survival time at 1 year, with 95% confidence intervals

	One-year survival (%)	95% CI a		RMST (days)	95% CI a
Original cohort
Kaplan-Meier
Treated
Yes	88.4	86.0	90.6	340	320	343
No	66.0	62.1	69.7	307	290	312
Differencesb	22.4	18.1	26.9	33	14	48
Time-updated Cox model
Treated
Yes	84.7	82.2	87.1	337	332	342
No	73.8	71.3	76.6	318	313	323
Differencesd	10.9	6.6	14.7	19	12	26
Emulated cohort
Kaplan-Meier
Surgery arm	84.5	83.0	86.3	333	329	336
No surgery arm	67.2	64.4	69.7	312	307	318
Differencesc	17.3	14.6	20.1	21	17	25
Weighted Kaplan-Meier
Surgery arm	82.6	80.4	84.8	331	327	335
No surgery arm	71.2	67.9	74.5	318	312	325
Differencesd	11.4	7.9	15.3	13	8	20

RMST, Restricted Mean Survival Time, measured at 1 year.

^aThe 95% CI were calculated using 1000 bootstrap replicates.

^bThese differences are prone to both confounding and immortal-time biases.

^cThese differences are prone to informative censoring.

^dThese differences account for all types of biases, under the assumptions detailed in method.

Figure 3.

Contrasting one-year survival curves from different estimation methods.

Multivariable Cox model with time-updated treatment indicator

Confounding and immortal-time biases are accounted for with this type of analysis. The models are adjusted for all measured potential confounders. The 1-year survival estimates for treated and untreated patients were 84.7% (95% CI: 82.2–87.1%) and 73.8% (95% CI: 71.3–76.6%) respectively. The difference between these survival probabilities is the causal effect of surgery from the time it is performed on 1-year survival from diagnosis.

Un-weighted analyses after cloning

All 2309 patients were cloned so that each clone entered the surgery and no surgery arms. Thus, at baseline, the characteristics of both arms of the emulated trial were perfectly balanced. However, there were imbalances between arms at 6 months (Supplementary Figure S2, available as Supplementary data at IJE online). This is because treatment assignment is affected by variables also associated with the outcome (mortality).

One year after diagnosis, the survival difference was 17.3% (95% CI: 14.6–20.1%) between patients in the surgery arm (84.5%, 95% CI: 83.0–86.3%) vs. the no surgery arm (67.2%, 95% CI: 64.4–69.7%, Table 2). Unlike in the naïve analysis, early deaths contributed to both arms, reducing the survival gap soon after diagnosis (Figure 3). However in this analysis informative censoring was ignored.

Weighted analyses after cloning

The weights showed a good ability to remove covariate imbalance at 6 months: weighted standardized differences are all within 10% (Supplementary Figure S2, available as Supplementary data at IJE online).

The weighted difference in 1-year survival decreased to 11.4% (95% CI: 7.9–15.3%), still showing evidence of a benefit of surgery in older NSCLC patients. Surgery within 6 months of diagnosis explains a gain of 13 days (95% CI: 8–20 days) of life expectancy, in the first year. This is the causal effect of surgery as done in practice (including waiting times) on 1-year survival from diagnosis.

Discussion

In this tutorial, we described the different steps required to emulate a target trial using observational data. When the start of follow-up and the time of treatment initiation do not coincide i.e. when the exposure (or treatment) status is not defined at the inclusion within the study, immortal-time bias is a concern if the study groups are defined based on the observed treatment allocation. Indeed, treatment receipt at a given time t is conditional on having survived up to time t, and consequently, treatment receipt is more likely to be observed among patients with longer survival. We illustrated how cloning patients at the start of follow-up, carefully defining the survival time and vital status for each clone, and choosing the length of the grace period, as proposed by Hernàn et al.,^9,10 can address both confounding and immortal-time biases. However, by cloning and censoring the patients to account for confounding at baseline and immortal-time bias, we introduce an informative censoring, which does not exist in the original dataset. This artificial censoring can be adjusted for by inverse-probability weights in the statistical analysis, which is the main complexity of this approach. It is important to note that this informative censoring is not the same as censoring due to loss to follow-up or administrative censoring. It is instead a consequence of the methodology used and reflects confounding over time. Nevertheless, if censoring due to loss of follow-up occurs in the data at hand, it is possible to estimate a second set of weights that will be multiplied to the weights we describe in this paper.

The analytical strategy we present in this paper has been proposed in 2016,^9,10 but there is currently no tutorial explaining how to proceed to conduct such studies, which might explain why its use is still scarce in practice. By providing a step-by-step procedure, along with Stata and R code, and example data, we help researchers implement this type of design to remove immortal-time bias. Our illustrative example reinforces the impact of this bias and the importance of properly accounting for it.

Alternative statistical techniques, such as Cox regression with a time-updated treatment or delayed entry models, can handle confounding and immortal-time biases. These two methods focus on the same target estimand, but the delayed entry method makes fewer assumption about interactions between the treatment and the covariates. However, both lead to the estimation of the treatment effect once treated and does not capture the effect of the time lag between diagnosis and treatment receipt. On the contrary, in an emulated trial, the waiting time to treatment is considered as part of the intervention, as it happens in practice. This estimate is therefore more relevant for real-world evidence.

In our lung cancer data, although differences in 1-year survival are similar when estimated via an emulated trial or a Cox regression with time-updated treatment, survival is lower for both groups in the emulated trial results. This can be explained by: (i) early death contributing to both arms in the emulated trial; (ii) possible interactions between treatment and covariates not included in the Cox regression with time-updated treatment; and (iii) different target estimands.

Simulation studies are needed to empirically compare the performance of these different approaches in a wide range of scenarios. Karim et al.²³ compared emulated sequential trials with marginal structural models in the presence of time-updated confounders, but they did not look at methods to handle immortal-time bias.

A major non-statistical advantage of the proposed approach is that its general principle is easily understandable by researchers and clinicians working in clinical trials. Although the inverse-probability-weighting is a complex concept, many clinicians and epidemiologists are familiar with the closely related propensity-score weighting approach. In addition, the similarity of the structure of the design steps with the design of RCTs makes this approach more appealing to clinicians. Moreover, the framework of emulated trials is transparent, emphasizing the importance of defining precisely the research question, inclusion criteria, causal contrast of interests, exposures etc., which is common practice in clinical trials but less commonly reported in epidemiological research. The CERBOT tool has been developed to help researchers in this process and provides recommendations for the statistical analysis.¹⁶ In the analysis phase, the use of censoring weights allows the assessment of balance over time between the study arms, thus ensuring internal validity. Reporting can also be more transparent with the use of the CONSORT checklist for randomized trials, including the CONSORT flow chart for patient selection.¹⁷

In our illustration, we showed evidence of a benefit of surgical treatment among elderly lung cancer patients, as already suggested in the literature.²⁴ Controlling for the biases introduced by confounding and immortal time, we showed a reduction of the effect size. However, for real policy impact, this simplified illustration would need to address a few additional challenges. First, we performed a complete-case analysis, which limits the generalizability of our findings. We excluded 10.8% and 13.5% of patients with missing information on stage at diagnosis or performance status, respectively (Supplementary Figure S1). We did not account for missing data in our illustrative example, in order to focus on the issue inherent to trial emulation only. However, complete-case analysis is rarely appropriate for the estimation of marginal effects. In practice, if one can assume a missing at random mechanism for the missing data, multiple imputation is proposed as an efficient way to address partially observed covariates when using inverse-probability weighting.²⁵ However, multiple imputation combined with bootstrap, which is required when patients are cloned, can be challenging and very computationally intensive. Alternatively, a weighted approach for missing data can be used with two sets of weights that are estimated and multiplied together (missingness weights and censoring weights), as proposed in other time-varying settings.¹¹ Although unbiased under a missing at random mechanism, this approach is usually inefficient for moderate sample sizes, and therefore we decided not to implement it in our example. Second, we estimated censoring weights using Cox proportional hazards regression models, which allowed us to estimate weights achieving balance over time, but more flexible modelling approaches (such as flexible hazard-based regression models) could be considered.²² Third, we considered simple Kaplan-Meier estimation of the survival curve up to 1 year after diagnosis. The analyses could have been done using multivariable flexible models of time-to-event data. It is important to note that hazards are likely not to be proportional due to the design and cloning. Hence a Cox model proportional hazards model would not be appropriate for analysing the data. More importantly, the hazard ratio (HR) cannot have a causal interpretation, as it is an average of conditional time-specific effects from a cohort changing over time.²¹

In this tutorial, we recommend the use of the non-parametric bootstrap to obtain confidence intervals. However, this can be computationally intensive for large datasets. If one wants to estimate model-based standard errors, a current limitation is the presence of an artificial inflation of the number of events due to patients dying during the grace period and before being exposed (before receiving surgery in our example, 6.7% of patients, 156 deaths). Further methodological investigation is needed to develop an appropriate variance estimator in this context.

Finally, it is important to emphasize the importance of assessing the plausibility of the assumptions made, before causally interpreting the results. The positivity assumption usually holds if the inclusion criteria are defined appropriately. In our example, we restricted our study to older NSCLC patients who were still potentially eligible for surgery given their individual characteristics, so we believe all the included patients had a non-null probability to either receive surgery or not. The consistency assumption requires the treatment to be well defined to be valid. Surgical procedures for NSCLC are usually well standardized. Finally, by design, the exchangeability assumption holds at baseline since the two arms are identical due to cloning. However, over time the informative censoring introduces confounding, which can be addressed using censoring weights only if all the confounders are measured: this is difficult to assess in practice. In our example, several unmeasured factors such as social support and postoperative care may have confounded the relationship between surgery and survival. Nevertheless, the proposed approach allowed us to control for measured confounders and immortal-time bias, and our results are consistent with the literature.

In conclusion, this tutorial presents the step-by-step details of the design and analysis of an emulated target trial from observational data when immortal-time bias is an additional issue. Through an example whose aim was to estimate the causal effect of early surgery for older NSCLC patients, we illustrated how the framework for trial emulation contributes to the improvement of the reproducibility and transparency of epidemiological studies using non-randomized data.

Supplementary data

Supplementary data are available at IJE online.

Funding

This work was supported by Cancer Research UK (grant number C7923/A18525).