Hydrodynamic Simulations of the Performance Landscape for Suction-Feeding Fishes Reveal Multiple Peaks for Different Prey Types

Abstract

The complex interplay between form and function forms the basis for generating and maintaining organismal diversity. Fishes that rely on suction-feeding for prey capture exhibit remarkable phenotypic and trophic diversity. Yet the relationships between fish phenotypes and feeding performance on different prey types are unclear, partly because the morphological, biomechanical, and hydrodynamic mechanisms that underlie suction-feeding are complex. Here we demonstrate a general framework to investigate the mapping of multiple phenotypic traits to performance by mapping kinematic variables to suction-feeding capacity. Using a mechanistic model of suction-feeding that is based on core physical principles, we predict prey capture performance across a broad range of phenotypic trait values, for three general prey types: mollusk-like prey, copepod-like prey, and fish-like prey. Mollusk-like prey attach to surfaces, copepod-like prey attempt to escape upon detecting the hydrodynamic disturbance produced by the predator, and fish-like prey attempt to escape when the predator comes within a threshold distance. This approach allowed us to evaluate suction-feeding performance for any combination of six key kinematic traits, irrespective of whether these trait combinations were observed in an extant species, and to generate a multivariate mapping of phenotype to performance. We used gradient ascent methods to explore the complex topography of the performance landscape for each prey type, and found evidence for multiple peaks. Characterization of phenotypes associated with performance peaks indicates that the optimal kinematic parameter range for suction-feeding on different prey types are narrow and distinct from each other, suggesting different functional constraints for the three prey types. These performance landscapes can be used to generate hypotheses regarding the distribution of extant species in trait space and their evolutionary trajectories toward adaptive peaks on macroevolutionary fitness landscapes.

Introduction

The complex interplay between form and function forms the basis for the generation and maintenance of organismal diversity. This diversity may be understood in terms of the myriad ways organisms are able to exploit resources in the environment (Wainwright 2009; Pigot et al. 2016). Although selection targets the fitness of the organism, it does so by affecting the distribution of phenotypic traits that influence the capacity of the organism to accomplish the tasks that enable it to meet the essential challenges of growth, survival, and reproduction (Kingsolver and Pfennig 2007). Consequently, understanding how complex functions evolve is contingent upon the ability to predict how interactions between these traits affect performance (Benkman 2003; Oufiero et al. 2012).

In this paper, we define performance as the ability of an organism to carry out fitness-determining tasks. Because performance is the product of the interplay between phenotypic traits, it is possible to map each combination of traits to its respective performance, to produce a “performance landscape.” Although these high-dimensional performance spaces can only be visualized as two-dimensional (2D) or 3D constructs, a performance landscape is the complex multivariate relationship between phenotypic traits and performance (Arnold 1983). In the case of morphological traits, this is often referred to as the morphospace. However, in addition to morphology, traits that underlie performance also include behavioral or kinematic traits. We therefore refer to this space as a “trait space,” and the set of all possible combinations of measured traits represents the potential phenotypic diversity contained within the trait space. Notably the potential and realized diversity of trait combinations differ, because the realized diversity is limited by adaptive, developmental, and biomechanical constraints.

Performance landscapes are conceptually related to adaptive landscapes, except that performance landscapes capture a specific behavior, which might have limited effects on fitness. Conversely, the adaptive landscape summarizes all performances affected by the measured phenotypic traits. Because the slope of the adaptive surface corresponds to the selection gradient and the curvature to the expected trait variation in a population (Lande and Arnold 1983; Arnold 2003), the adaptive landscape could link functional and evolutionary biology (Arnold 1983). The topography may signal the existence of constraints or drivers of evolution, in the form of positive or negative slopes, allowing the adaptive landscape to be used to examine potential evolutionary trajectories. While the adaptive landscape was originally conceived of in terms of genotype frequencies in a population (Haldane 1927, 1954; Wright 1932), the concept was subsequently extended to encompass morphological traits (Simpson 1953; Lande 1976, 1979).

The adaptive landscape does not address performance per se, but selection on phenotypic traits is often inferred in terms of their influence on performance (Arnold 1983, 2003; Kingsolver and Huey 2003). For example, adaptive peaks for the morphology of the legs, tail, and body of Caribbean anoles are associated with different microhabitats and are interpreted as adaptations for locomotion in each specific microhabitat (Mahler et al. 2013). Similarly, variation in bill morphology of Galapagos finches (Boag and Grant 1984; Grant 1986) or the craniofacial morphology of Cyprinodon pupfishes (Martin and Wainwright 2013) corresponds to diet specialization and are inferred as adaptations for different trophic niches. Clearly, using Caribbean anoles for the mapping of leg and body morphology to climbing or running performance or Cyprinodon fishes for the mapping of jaw morphology to bite force, it is possible to generate performance landscapes for these organisms. Such performance landscapes would only estimate one component of fitness, a single task such as capturing food items, and cannot be used to estimate selection gradients or expected trait variation in the population. However, they can elucidate the regions of trait space where trait combinations result in higher performance and identify regions where performance in one task trades-off with performance at another. Furthermore, a comparison of the realized trait space and the performance landscape can be used to generate hypotheses regarding the evolutionary processes that affect the distribution of extant species, i.e., what role has performance (at a specific task) played in shaping extant phenotypic distributions of species? For example, if the realized trait space overlaps regions of high performance, this supports the hypothesis that selection on this combination of traits is affected by selection on the associated performance task. Conversely, if the realized trait space overlaps regions of low performance, selection on this combination of traits may be primarily driven by selection for other performance tasks, these traits may be shaped by indirect selection on other traits, or the phenotypic response to selection is hampered by developmental, biomechanical, or other constraints.

Here we describe our process for modeling the performance landscape for suction-feeding in all fishes. In the first step, we detail the theoretical principles behind the performance landscape and how kinematics governs feeding success for during suction-feeding. We discuss how this can inform a description of the landscape with respect to key morphological and kinematic traits. We then describe a method that allows us to evaluate the topography of the landscape and, importantly, to identify and characterize its peaks. Finally, we characterize regions of kinematic trait space during suction-feeding that are associated with high performance and compare these regions among prey types.

Adaptive landscapes and performance

The action of natural selection on populations drives the evolution of phenotypes, and ultimately that of organismal diversity. One approach to understanding the macroevolutionary trajectories leading to extant organismal diversity is to infer the mode of trait evolution using the distribution of trait variation across extant, closely-related species. Such evolutionary models are frequently implemented by fitting continuous trait data to an Ornstein–Uhlenbeck type model, which attempts to model the change in trait values through time as the result of selection and drift. The effect of drift is modeled as a Brownian motion process operating on the trait, whereas selection is modeled as the function of the selection strength and the distance of a trait from the optimum value of the trait. Thus, the model estimates three parameters: the rate of Brownian motion $\sigma$, selection strength $\alpha$, and the optimum value $\theta$ (Felsenstein 1985; Martins 1994; Butler and King 2004). It is possible to construct and compare multiple models of increasing complexity, each with an increasing number of peaks. Thus, a model with no peaks can be compared with a one- or two-peaks model, comparing scenarios that trait evolution is dominated by drift, or by attraction to one or two adaptive peaks. The model is parameterized using a combination of morphological and possibly behavioral or ecological descriptions, and a phylogenetic hypothesis pertaining to the clade’s history. These methods can be fitted either with (Price et al. 2011; Konow et al. 2017) or without (Ingram and Mahler 2013) reference to an a priori hypotheses specifying which lineages correspond to particular peaks. Note that implementations of these models do not assume an a priori location of the adaptive peaks or selection regimes, and also eschew quantification of fitness or fitness-related functions (Ingram and Mahler 2013; Mahler et al. 2013; Pfaender et al. 2016; Rossoni et al. 2019).

These types of models have yielded considerable success, but also possess limitations. With the underlying assumption of these models being that populations evolve toward adaptive peaks, the models can only infer peaks from the data and are severely limited in their ability to locate peaks in unoccupied regions of trait space (e.g., Stayton 2019). When models rely on user-provided reference to an a priori hypotheses specifying which lineages correspond to particular peaks (e.g., by coding ecological and/or trophic niches using SIMMAP mapping; Collar et al. 2009; Price et al. 2011), the OU model cannot account for the possibility of multiple peaks for the same coded niche, and could infer a peak that represents an intermediate value between the real peaks. Furthermore, they are limited to the location of peaks and are unable to identify valleys which may constrain evolution. Other limitations of the OU models include the unrealistic modeling of the OU “regime” as an infinite basin of attraction with a Gaussian distribution, and the fact that they are often limited to univariate data, although some generalizations exist (Ingram and Mahler 2013; Clavel et al. 2015; Khabbazian et al. 2016).

We can narrow these gaps in our understanding of the proximate source of trait space occupation by quantifying the relationship between morphology and performance by creating a performance landscape. While adaptive landscapes illustrate how population fitness varies across trait space, performance landscapes illustrate how the performance of individuals (at specific tasks) varies across trait space. Notably, performance landscapes do not indicate the importance of these tasks to population fitness (Arnold 2003). Since the same traits are likely to affect the performance of multiple tasks, and possibly in different ways, assessing the selection on phenotype may entail quantifying the effect of performance on a range of related tasks (Dickson and Pierce 2019; Stayton 2019).

Yet performance landscapes can provide useful information regarding features of the adaptive landscape. For example, they may reveal the presence of multiple performance peaks, i.e., a many-to-one relationship between form and function. Many-to-one mapping is an inherent aspect of complex functions when the outcome depends on more than two parameters, such that multiple solutions can yield the same result (Wainwright et al. 2005; Wainwright 2009; Muñoz 2019). Many-to-one mapping has been demonstrated in the case of tree seedlings (Marks and Lechowicz 2006), frog legs (Moen 2019), and squirrel jaws (Zelditch et al. 2017), and can be a driver of morphological diversity (Alfaro et al. 2004, 2005). As explained above, OU models cannot account for multiple peaks for the coded niche, i.e., many-to-one solutions. Furthermore, performance landscapes can be employed not just to examine performance gradients (i.e., quantify the change in performance given a change in the underlying phenotype), but also to identify and quantify constraints such as conflict and trade-offs between performance at different tasks (Brodie and Ridenhour 2003; Ghalambor et al. 2003), changes in the magnitude of trade-offs due to environmentally dependent reaction norms (Giebelhausen and Lampert 2001), and the presence of performance valleys (Martin 2016).

A straight-forward way to estimate a performance landscape is to collect empirical data from multiple organisms that vary in their phenotypic traits. However, the resulting performance landscape will be confined to the vicinity of the phenotypes occupied by observed data points, as extrapolation of form–function relationships to phenotypes distant from those observed would be unreliable (Phillips and Arnold 1989; Arnold et al. 2001; Arnold 2003). Further, examining the limits of the occupied region of trait space is not necessarily sufficient to explain why other regions are unoccupied. However, extending the boundaries of analysis is possible if form can be related mechanistically to function. Such mechanistic links have been successfully applied to explain the morphology of labrid jaws (Alfaro et al. 2004, 2005), bacterial shape (Schuech et al. 2019), and the shape of turtle shells and humeri (Polly et al. 2016; Dickson and Pierce 2019; Stayton 2019). Here, we take advantage of the knowledge of core physical principles that underlie suction-feeding behavior to describe the performance landscape for suction-feeding fish, examine and characterize its surfaces, and identify the performance peaks and troughs.

Suction-feeding in fishes

Suction-feeding represents a ubiquitous, evolutionary conserved mode of feeding among aquatic vertebrates (Ferry-Graham and Lauder 2001) and describes a mode of prey capture in which the rapid expansion and concomitant lowering of pressure inside the mouth cavity generates a flow that overcomes the escape response of the prey to draw it into the mouth (Alexander 1970; Wainwright and Day 2007; Day et al. 2015). Functionally, suction is accomplished by a complex and coordinated combination of cranial rotation, depression of the hyoid and the lower jaw, and abduction of the suspensorium and the opercular and branchiostegal membranes (reviewed in Day et al. 2015). These movements result in a wave of dorsal–ventral expansion from the mouth to the opercular slits (Day et al. 2005; Bishop et al. 2008) such that a unidirectional flow of water passes from the mouth, through the buccal cavity to exit at the gills (Day et al. 2005, 2015; Holzman et al. 2008a; Jacobs and Holzman 2018). Peak flow occurs at or near the time of peak mouth opening (Bishop et al. 2008; Jacobs and Holzman 2018), which is thought to reduce the possibility of prey escaping (Muller et al. 1982).

The hydrodynamics of suction-feeding are generally well understood. Computational models (Van Wassenbergh and Aerts 2009; Yaniv et al. 2014; Van Wassenbergh 2015) and empirical measurements (Day et al. 2005, 2015; Jacobs and Holzman 2018) show that the suction flow in front of the fish’s mouth is unsteady and characterized by steep temporal and spatial gradients, but only affects a volume of approximately one gape diameter away from the mouth. In front of the fish and external to the mouth, the flow serves to draw the prey into the mouth, provided that the escape force exerted by the prey is insufficient to overcome the opposing force exerted by the suction flows (Holzman et al. 2007; Wainwright and Day 2007; Van Wassenbergh et al. 2010). The three hydrodynamic forces exerted on the prey by the suction flows are drag force, acceleration reaction force, and the pressure-gradient force across the prey (Wainwright and Day 2007). Drag force results from the differential in speed between the prey and the flow around it, acceleration–reaction force from the acceleration of water around the prey, and the pressure-gradient force from the spatial and temporal gradients (i.e., the acceleration) of the speed of the flow (Holzman et al. 2007, 2012; Wainwright and Day 2007; Day et al. 2015). The relative importance of each force to prey capture depends on characteristics of both the predator and the prey, but acceleration-based forces often dominate in moving prey toward the mouth, and the capacity for a fish to generate such forces relies on faster mouth expansion and is often aided by small mouth size and timing to maximize the force on the prey (Holzman et al. 2008a, 2012; Day et al. 2015). Moving the jaws forward moves the force field extending from the mouth closer to the prey, and the forward acceleration of the mouth may provide an additional source of acceleration to the forces being exerted on the prey (Holzman et al. 2008b, 2008c, 2012).

Mouth kinematics can be adapted to increase the force exerted on the prey, but they cannot overcome the rapid dissipation of those forces, and prey may employ counterstrategies to detect predators and move away from the force field to avoid capture. For example, prey can attach to a surface or conduct an evasive maneuver by exerting a force of its own, directed away from the predator (Lenz and Hartline 1999; Buskey et al. 2002). Suction-feeding fish may use rapid forward motion to close the distance to the prey, but this motion generates a hydrodynamic disturbance ahead of the moving body (White 2011). Many zooplanktonic animals possess sensory mechanisms to detect such hydrodynamic disturbances. For example, copepods possess hairs on their antennae that bend in response to flows and trigger an escape reflex (Yen et al. 1992; Fields and Yen 1997; Kiørboe and Visser 1999; Woodson et al. 2005). Prey with well-developed eyesight may take the looming presence of a predator as a cue and seek to escape when the approach rate of the predator is too fast (Batty 1989; Domenici 2002; Paglianti and Domenici 2006). Consequently, the kinematics, morphology, and the behavior of both the predator and the prey will influence the capture strategy of suction-feeding fish and the results of the predator–prey interaction.

Modeling the performance landscape for suction-feeding fishes

We employed a two-step process to model the performance landscape: (1) we generated a large set (>25,000) of phenotypic combinations by randomly sampling from phenotypic ranges reported in literature and used a mechanistic model to predict feeding performance for three types of prey (mollusk-like, copepod-like, and fish-like) and (2) we modeled the relationship between feeding performance and phenotype across trait space by fitting general additive models (GAMs). We employed this two-step process for two reasons. First, our mechanistic model is computationally slow, and thus generating the entire landscape at desirable resolution, or adding new points to the landscape (e.g., for applying the gradient accent method; see below), would be very time-consuming. Second, the model takes as input vectors of the kind produced from digitization of high-resolution filmed feeding strikes (e.g., gape diameter at each point in time), while data in literature are typically in the form of variables (e.g., peak gape diameter and time to peak gape [TTPG]). While it is possible to cross-translate the two input methods, we feel that the variable-based input would facilitate broader use and comparisons with other studies. All scripts and simulations generated during this study may be found in the Open Science Framework repository (https://osf.io/9uc3y/).

Model inputs

In our analysis, we focused on six kinematic variables known to be important to suction-feeding performance (Holzman et al. 2007, 2012, 2008c; Day et al. 2015; China et al. 2017): (1) peak gape as the diameter of the gape when it is 95% open, (2) TTPG the time taken to open the gape from 20% of maximum gape to 95% of maximum gape, (3) peak jaw protrusion as 95% of the maximal jaw protrusion, (4) time to peak jaw protrusion (TTPJP) as the time taken for the jaws to protrude from 20% to 95% of their maximal jaw protrusion, (5) ram speed as the forward motion of the fish, and (6) strike distance calculated to allow the mouth of the predator to be at the initial location of the prey at the time of peak gape, given ram speed and jaw protrusion. We conducted a literature survey to obtain plausible ranges of kinematic data measured for prey strikes in 16 species of suction-feeding centrarchids (Holzman et al. 2012), 33 species of serranids (Oufiero et al. 2012), 25 species of cichlids (Hulsey et al. 2010), as well as our unpublished data on Pomacentrids (four species), serranids (three additional species), and cichlids (four additional species). The observed ranges for peak gape were 0.9–35.3 mm, TTPG 0.002–0.039 s, peak jaw protrusion 0.54–14.9 mm, TTPJP 0.002–0.038 s, ram speed 0.66–2155 m/s, and strike distance 0.00017–0.048 m. As we only use the source data to obtain plausible parameter ranges, the number of species in each group does not affect the outcome. However, this selection imposes some limits on the scope of the landscapes examined here; for example, they are not representative of either small cryptic species or large pelagics, of fish that rely on biting, or of larval fish. It should be noted that the chosen families encompass a large number of species for which suction-feeding has been studied in detail.

Prey type

We estimated the performance landscape for suction-feeding on three types of prey: prey which attach to the surface by clinging to a holdfast, prey which detect the hydrodynamic disturbance generated by the forward motion of a predator and use this to trigger an escape reaction, and visually oriented prey which try to escape when the predator is within a critical distance. We term these prey types mollusk-like, copepod-like, and fish-like prey, but note that these represent generalized hydrodynamic groups of prey targeted by suction-feeding fish, rather than specific or exclusive categories. For example, attaching to the surface is a common defense strategy in shelled gastropods, which may also use chemical or behavioral defenses (Feder 1963; Pohnert 2004; Wainwright and Day 2007). Prey fish typically rely on vision to spot an approaching predator, but may also be able to detect hydrodynamic disturbances via the lateral line system (Weihs and Webb 1984; Paglianti and Domenici 2006; McHenry et al. 2009; Nair et al. 2017). Finally, while copepods can register hydrodynamic disturbance via sensitive mechanoreceptors on their antennae, chemical cues may also play a role, along with behavioral strategies like diurnal vertical migration (Kiørboe and Visser 1999; Jamieson 2005; Buskey et al. 2012). We further defined the characteristics for each prey along with the performance metric associated with prey capture. Mollusk-like prey was modeled to respond to the strike by attaching to a holdfast, i.e., maintaining position. Accordingly, feeding performance for mollusk-like prey was defined as the maximum force the predator is able to exert on the prey, such that a greater maximum force is able to dislodge more strongly attached prey. Copepod-like prey was defined as an evasive prey that starts an escape maneuver in response to a threshold strain rate (i.e., threshold hydrodynamic disturbance), equivalent to most zooplankton. To calculate the hydrodynamic disturbance generated by the moving fish, we modeled the fish as a sphere moving in an ideal fluid and calculated strain as the second order tensor of the velocity field. We then calculated the strain rate magnitude at the location of the prey as the Euclidian norm of the deformation tensor (derivation in the Supplementary Material). Feeding performance against copepod-like prey was determined to be the lowest strain rate threshold, i.e., the most sensitive prey the predator is able to capture. The escape reaction of copepod-like prey was modeled as being directed away from the predator with a maximum escape force of 2×10⁻⁴ N and a reaction time of 1 ms, which is in line with observations on escaping zooplankton (Lenz and Hartline 1999; Buskey et al. 2002). Fish-like prey was defined as an evasive prey that starts an escape maneuver in response to the approach of the predator. Feeding performance against fish-like prey was determined as the greatest escape force the predator can overcome. Similar to copepod-like prey, the escape reaction of fish-like prey was modeled as being directed away from the predator with a reaction time of 1 ms, while a threshold escape distance was set to 0.75× maximum gape, which is within the volume affected by the suction flow of fish (Jacobs and Holzman 2018). For all the above-mentioned cases, we defined the prey as a neutrally buoyant ellipsoid with a maximum diameter of 0.1 mm and a maximum length of 2 mm.

We estimated feeding performance using the suction-induced force field model (SIFF; Holzman et al. 2012), a mechanistic model that uses a suite of parameters characterizing the shape and behavior of the prey and the kinematics of the predator to predict whether the prey is captured or escapes. By using this mechanistic modeling approach, we can extend our analysis to any region of trait space, irrespective of whether such trait values or trait combinations exist in the wild. SIFF is described in detail in Holzman et al. (2007, 2012) and Wainwright and Day (2007). Briefly, SIFF uses the time-dependent gape size, jaw protrusion, ram speed, and strike distance during the feeding strike to estimate the flow speed at the location of the prey. SIFF then utilizes the estimated flow, and its spatial and temporal derivatives, to calculate the total force exerted on the prey as the sum of drag forces, acceleration reaction forces, and pressure-gradient forces. Gravitational forces are ignored because prey are assumed to be neutrally buoyant. Summing the forces exerted by the suction flow on the prey and the forces applied by the prey, either to cling to a holdfast or substrate (attached prey) or swim away from the predator (evasive prey), allows SIFF to predict the motion of the prey relative to the predator and determine whether it ultimately entered the mouth of the predator (i.e., captured).

Because SIFF takes as input vectors such as would be obtained from digitizing high-speed recordings of suction-feeding strikes, we sampled randomly from the phenotypic trait ranges, under a uniform distribution, and used Equation (11) from Muller et al. (1982) to generate the vectors that describe the time-dependent opening of the gape, the protrusion of the jaw, and the forward motion of the fish. We predicted the maximum flow speed using the relationship between peak gape, TTPG, and the normalized TTPJP, and maximum flow speed from Jacobs and Holzman (2018), and generated a time-dependent vector of flow speed, with flow starting at 20% of mouth opening and peaking at the time of peak gape. We defined the strike distance of the predator, i.e., the distance from which the strike is launched, such that the mouth of the predator would be at the initial location of the prey at the time of peak gape given ram speed and jaw protrusion.

For each trait combination, we ran SIFF to simulate the outcome of the strike, i.e., success or failure. To determine the feeding performance against mollusk-like prey, we extracted the maximum force exerted on the prey during the strike. To determine the feeding performance for copepod-like and fish-like prey, we estimated the threshold in which prey capture switched from failure to success using an iterative binary search algorithm. The search started with two points that yielded failure and success, and then narrowed the search range until the flip point from failure to success could be identified with a precision of 0.0001 s⁻¹ and 0.00001 N, respectively. We calculated performance for N = 29,537 individual combinations of kinematic variables for attached prey, N = 29,068 for copepod-like prey and N = 26,982 for fish-like prey.

Generating the performance landscape

The trait variables do not have a simple, additive impact on a complex function like prey capture; rather the contribution of any one variable is non-linear and dependent on the values of the other variables (Holzman et al. 2012). However, SIFF and the associated binary search algorithm are computationally demanding, which limits our ability to estimate performance throughout the landscape. We therefore used GAMs to predict performance at each point in parameter space for the three prey types. We used the function BAM (mgcv package, Wood 2017) to describe the relationship between performance and phenotypic traits, using a penalized cubic regression splines and shrinkage smoothing to reduce the estimated effect of parameters that provide little explanatory power (Wood 2017). The distributions of suction performance for the three prey types deviated from normality and were log-transformed prior to model fitting. We specified the GAMs with only smooths and tensor smooths. Tensor smooths are often useful for covariates measured in different (Wood 2017), units, and evaluation of the fitted models revealed that all tensor smooths were significant. We examined the fitted models for over-smoothing by examining the basis dimension, i.e., the dimension for the set of basis functions of the spline, roughly corresponding to the degrees of freedom allowed for each smooth term in the model, and for concurvity, a condition where a smooth term can be approximated by one or more of the other smooth terms, to improve the stability of the estimate and model interpretation (Wood 2017). All parameters were significant except for peak gape for copepod-like prey, with the fitted models described >95% of variance in the predicted capture rates simulated using SIFF (mollusk-like prey: r²=0.916, copepod-like prey: r² = 0.951, fish-like prey: r² = 0.954; Supplementary Table S1).

We further tested the predictive ability of the model by randomly dividing it into training/tests data sets (training data set containing 90% original data and the tests data set 10%) and reconstructed the landscape from the data in the training set. We then used the reconstructed landscape model to predict performance for the test set and performed a linear regression of the SIFF-obtained performance versus GAM-predicted performance. We repeated this procedure 100 times and calculated the confidence intervals around the intercept and the slope. If the landscape offers an unbiased prediction of performance, we would expect a regression slope of 1 and an intercept of 0. For mollusk-like prey, the 95% confidence interval (CI) about the intercept was (−0.00369, 0.00344) and about the slope (0.99705, 1.00116), for copepod-like prey, corresponding 95% CI were intercept (−0.00004, 0.00321) and slope (0.99895, 1.00045) and for fish-like prey intercept (−0.01387, 0.00202) and slope (0.99764, 1.00033). This allowed us to conclude that our models accurately predict the feeding performance for all three types of prey.

Finally, we assessed data saturation (Faulkner and Trotter 2017) by sub-sampling the data set to obtain subsets of smaller sample size. For each subset, we fitted the same model and carried out a linear regression of fitted against observed values. We then plotted mean-squared error (MSE) of the linear regression against sample size. When sampling across the performance volume is sufficient to capture most of the ruggedness of the landscape, the variance of the MSE should decrease as MSE converges on the error variance. We found that for our models, a data set with ∼25,000 points produced a saturated model (Supplementary Fig. S1).

Evaluating landscape topography

Because the topography of the landscapes may be rugged, we require a method for finding not just the point of maximum performance, but points associated with local performance peaks as well.

In cases where the performance landscapes can be formulated as a closed mathematical function, peaks may be located by analytical means, but in other cases the rugosity of the landscape surface must be examined using less systematic methods. For bivariate landscape, even a complex (i.e., “ill-behaved”) surface can often be conveniently represented graphically (e.g., Schuech et al. 2019) either as a contour landscape or as a 3D surface, where it is usually straightforward to identify peaks, valleys, and saddles and the slope of the surface represents the performance gradient. Indeed, 2D projections of the three landscapes reveal these features, as well as several flat, uniform projections (Supplementary Figs. S2–S4). However, since our landscapes are defined by six parameters, such projections can be misleading if they fail to capture the full effect of parameter interactions. This is illustrated in Fig. 1, in which a hypothetical performance landscape is characterized by the three traits A, B, and C. In this example, the interaction between A and B (Fig. 1a) implies that the value chosen for trait A (Fig. 1b) drastically changes the contours of the projection (i.e., 2D plot) of the performance landscape on traits B and C (Fig. 1c, d). In this hypothetical case, projecting the landscape for lower value of trait A results in a peak at a high value of B and moderately-high values of C, whereas projecting the landscape for a higher value of trait A results in a peak at low values of B and C. We therefore employed a more general approach to finding the local maxima by modifying the gradient descent method (Cauchy 1847). For simplicity we will describe the principle of the method in the 2D case, and then extend it to our 6D landscapes.

Fig. 1.

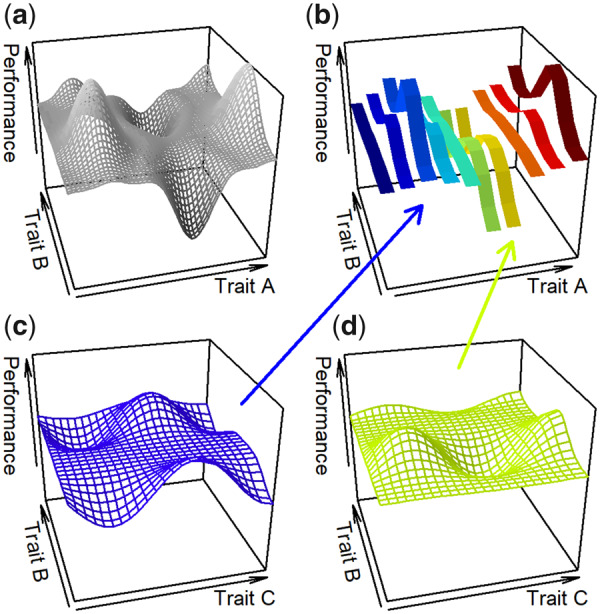
Conceptual illustration of how 2D projections of a performance landscape described by the three traits A, B, and C may be misleading. (a) The projection of the landscape on traits A and B, for a value of C. To illustrate the impact of C on performance, a value is chosen for A (b). Due to the interaction between A and B, the value chosen for trait A affects the 2D projection of the landscape on B and C (c, d).

In the gradient descent method, the local minimum is found by traveling along the path described by the most negative gradient, i.e., the steepest descent, but this is equivalent to finding a local maximum by traveling along the path described by the most positive gradient (Fig. 2a). A point on the landscape is chosen at random and the associated performance is evaluated. Each parameter may remain constant, increase or decrease by a small amount, which for two parameters creates 3²=9 possible combinations and thus eight points surrounding the center (starting) point. The performance at these eight points describes the landscape immediately surrounding the center point, and the performance gradients in the eight directions are calculated by evaluating the performance for each point and dividing the performance difference by the Euclidian distance to the center point. The direction is determined by the steepest positive gradient. A local peak is found when all gradients are negative. Repeating this procedure for various starting points and comparing the end points will reveal the existence of the number of local peaks, if they exist (Voran and Catellier 2009). We illustrate this procedure using start point/end point plots, where each plot represents a parameter with the start point on the horizontal axis and the end point on the vertical axis (Fig. 2b). Because a horizontal “band” of points represents identical end points, the number of horizontal bands reflects the number of local peaks. Furthermore, if the start points result in end points above the 1:1 diagonal line, this indicates that the slope is overall positive, i.e., higher trait values are associated with higher performance whereas if a horizontal band is formed from start point along the range, this indicates that the peak has a larger “basin of attraction.” Gradient ascent analysis is a versatile approach that enables stepwise exploration of the landscape and is thus suitable for examining the direction and endpoint of incremental trait evolution, and is easily expanded to multivariate landscapes, with the local peaks represented in a start point/end point matrix with one plot for each parameter. The method is not exhaustive and computationally slow, but the greater challenge is to ensure that the outcome is not subject to step length. At one extreme, if the landscape is locally rough, the method may find numerous local peaks that do not represent an actual topography, whereas if the landscape is spiky, too great a step may overshoot a peak altogether. We performed multiple trials with variable strep length and compared the results to ensure consistency.

Fig. 2.

Conceptual illustration of the gradient ascent method. (a) A bivariate performance landscape is shown, with traits A and B on the horizontal axes and performance on the vertical axis. The surface contours are shown on a plane below. The gradient ascent paths are shown for three random starting points (red circle, green square, and blue diamond) and tracked across the landscape, in the direction of the steepest gradient. A local peak has been located when the gradients in all directions are negative. (b) The start points and the end points for each path and trait are plotted. The path of the red circle starts at a point in the middle of the range of trait A and close to the lower end of trait B. After following the path of steepest ascent, it ends on a peak located in the low-A, medium-B region of the landscape. This is also the local peak that the path of the green square ends up on, while the path of the blue diamond finishes on a peak located at the edge of the landscape (maximum value of A), but the same value for B. Thus, the gradient ascent method run for three starting points resulted in the identification of two local maxima, which is reflected in the two sets (red circle and green square, vs. blue diamond) of end values in (b). Since two different local peaks must differ in either one or both coordinates, the number of horizontal lines will indicate the number of peaks in the landscape (although if many more paths are tracked across the landscape, a visual analysis may not be possible). Comparing the location of start points and end points will furthermore indicate the overall shape of the landscape informed by individual parameters: if end points mostly are above the diagonal, this implies an overall positive slope, whereas if end points are produced from start points from across the range, the basin of attraction of a peak is large.

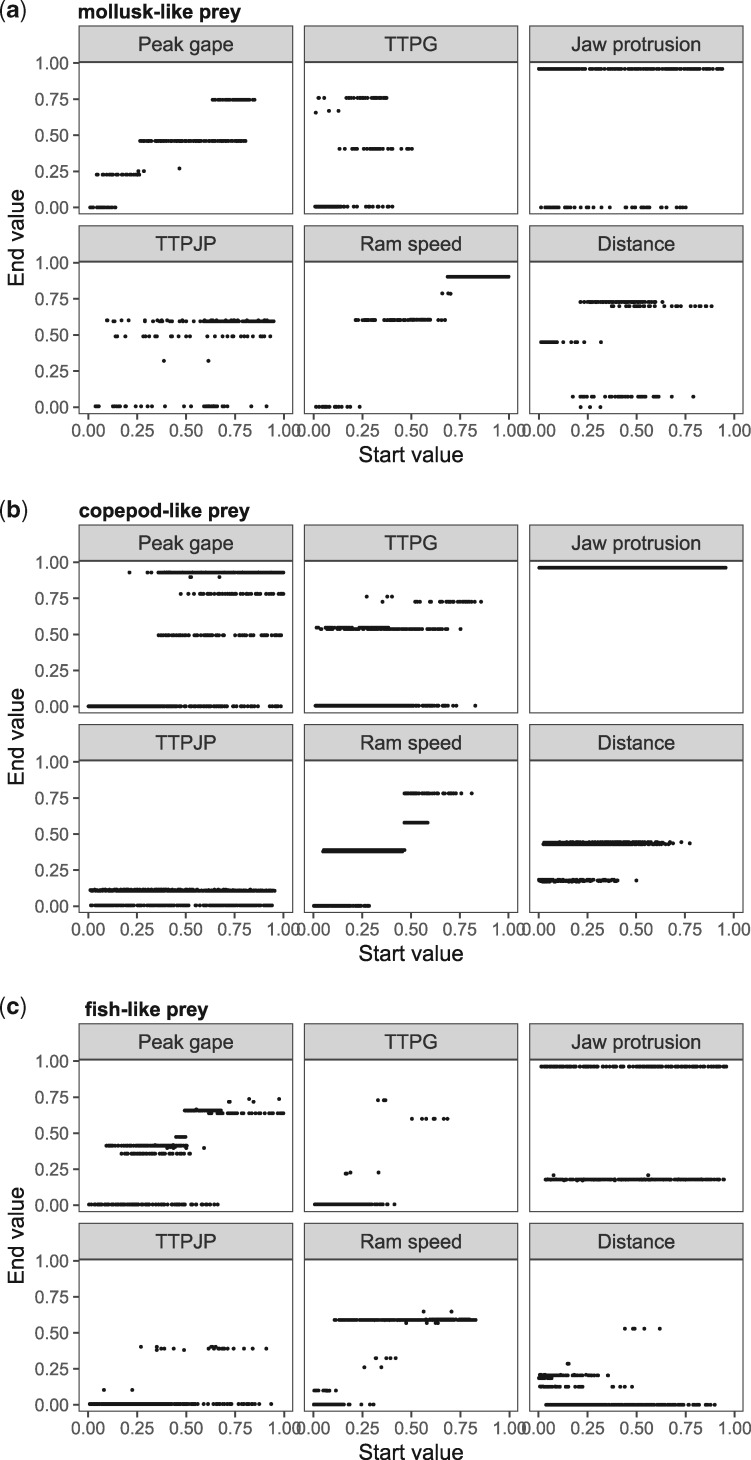
We performed the gradient ascent method for each prey landscape, for a parameter step length of 1% but where the value of each parameter was capped to the observed maximum and minimum values. To improve the sensitivity in finding the location of the peak, we allowed the algorithm to run until a point had been found where all performance gradients were negative. Here, the algorithm backtracked one step and retracked the steepest gradient path but with a parameter step length of 0.01%. The resulting start point/end point matrix plots revealed the existence of multiple peaks in all three prey landscapes, indicating rugged topographies, but also an edge effect which manifested itself in the form of pronounced horizontal bands at the minimum and maximum of the range of each parameter (Fig. 3). Because we lack information of the landscape beyond the modeled range, we considered the peaks located at the maximum of the variable range unreliable. However, none of our trait variables can be less than 0, and performance at different tasks may improve with lower values for some of the parameters. For example, fish swimming very slowly will produce weaker hydrodynamic disturbance which could improve feeding performance on copepod-like prey. We therefore retained the peaks located at the minimum of the variable range. In the case of jaw protrusion, the method found few local peaks that were described by intermediate values; rather, most peaks were characterized by values at either extreme of the range. As we were unable to judge the impact of edge effects, we removed jaw protrusion from further analyses.

Fig. 3.

Gradient ascent analysis for the performance landscape for suction feeding on (a) mollusk-like prey, (b) copepod-like prey, and (c) fish-like prey with the parameters scaled to the [0,1]-interval. Start and end points for the six variables that describe the landscapes are plotted on the x- and the y-axes, respectively. As described in Fig. 1, the number of local peaks is reflected in the number of horizontal lines. Note that the three prey types here are not “real” prey but refer to prey which respond to an approaching predator in a way typical for mollusks, copepods, and fish (i.e., clinging to a holdfast, attempting escape hydrodynamic strain is detected, or attempting escape when a predator is within a certain distance).

Characterizing performance landscape peaks

In view of the considerable rugosity revealed by the gradient ascent analysis (Figs. 2 and 3) we examined the trait space occupied by the peaks using a cluster analyses, preceded by a principal component analysis for only the points located on the peaks, repeated separately for each prey type. Prior to conducting the PCA, we rescaled performances and trait values to span the range 0–1, according to the following equation:

$$\mathrm{recsaled}\mathrm{ }\mathrm{value}=1-\frac{\left(\mathrm{original}\mathrm{ }\mathrm{value}-\mathrm{maximum}\mathrm{ }\mathrm{value}\right)}{\left(\mathrm{minimum}\mathrm{ }\mathrm{value}-\mathrm{maximum}\mathrm{ }\mathrm{value}\right)}$$ (1)

except in the case of performance for copepod-like prey, for which lower performance values indicate ability to capture more sensitive prey, for which the formula was edited to

$$\mathrm{recsaled}\mathrm{ }\mathrm{value}=1-\frac{\left(\mathrm{original}\mathrm{ }\mathrm{value}-\mathrm{minimum}\mathrm{ }\mathrm{value}\right)}{\left(\mathrm{maximum}\mathrm{ }\mathrm{value}-\mathrm{minimum}\mathrm{ }\mathrm{value}\right)}$$ (2)

such that superior performance is represented by higher values for all prey types. The first two dimensions of the PCAs explained >75% of the variance in the traits that characterize the local peaks for all three prey types (Supplementary Table S2), and we confined our analyses to these. For mollusk-like prey, the first dimension explained 68.0% of the variance with strong positive loadings on TTPJP and strike distance and negative on TTPG, while the second dimension explained 27.5% and loaded strongly on peak gape, and ram. For copepod-like prey, the first dimension explained 68.1% of the variance with strong positive loading primarily on peak gape. The second dimension explained 29.2% with strong positive loadings on ram speed. For fish-like prey, the first component explained 65.6% of the variance and loaded strongly positive on peak gape and ram speed, while the second dimension explained 21.8% and loaded strongly on peak gape.

We employed two further approaches to examine the pattern described by the peaks in trait space. First, to describe the regions of the local peaks in terms of their associated feeding performance and kinematic trait profiles, we performed cluster analyses on the results of the PCAs. This resulted in “peak clusters” that are similar in their kinematic profiles. Second, to characterize the basin of attraction in trait space associated with each “peak cluster,” we performed a kernel density estimation for the density of start points that reached each peak cluster. The local peaks in the performance landscape for mollusk-like prey could be broadly categorized into four peak clusters (Fig. 4a and SupplementaryFig. S5). Feeding performance differed considerably between these clusters with cluster 1 outperforming the other three, and an examination of the trait profiles revealed the existence of contrasting strategies. Peak cluster 1 described strikes with short strike distance, while the remaining three were associated with longer strike distance but varied in terms of speed of mouth and jaw movements. Four peak clusters could be identified in the landscape for copepod-like prey, with slightly differing performance levels (Fig. 4b and SupplementaryFig. S6). All peak clusters were described by maximal jaw protrusion, and the two highest performing peak clusters were also associated with slow TTPG, fast TTPJP, and slow ram speed. The remaining strategies were all associated with fast TTPG, fast ram speed, slower TTPJP, and larger strike distance. For fish-like prey, four clusters could be identified, of which two had considerably higher and more consistent performance than the other two, as well as narrower trait ranges (Fig. 4c and SupplementaryFig. S7). The highest performing peak clusters in this landscape are characterized by fast mouth and jaw movements and either large jaw protrusion and slower ram speed or vice versa. The other clusters show a broader range of parameter values for both TTPJP, ram speed and strike distance. Regardless of the relative heights of the peak clusters, all exceeded the average performance of points on the landscape (Fig. 4 and Supplementary Figs. S5–S7).

Fig. 4.

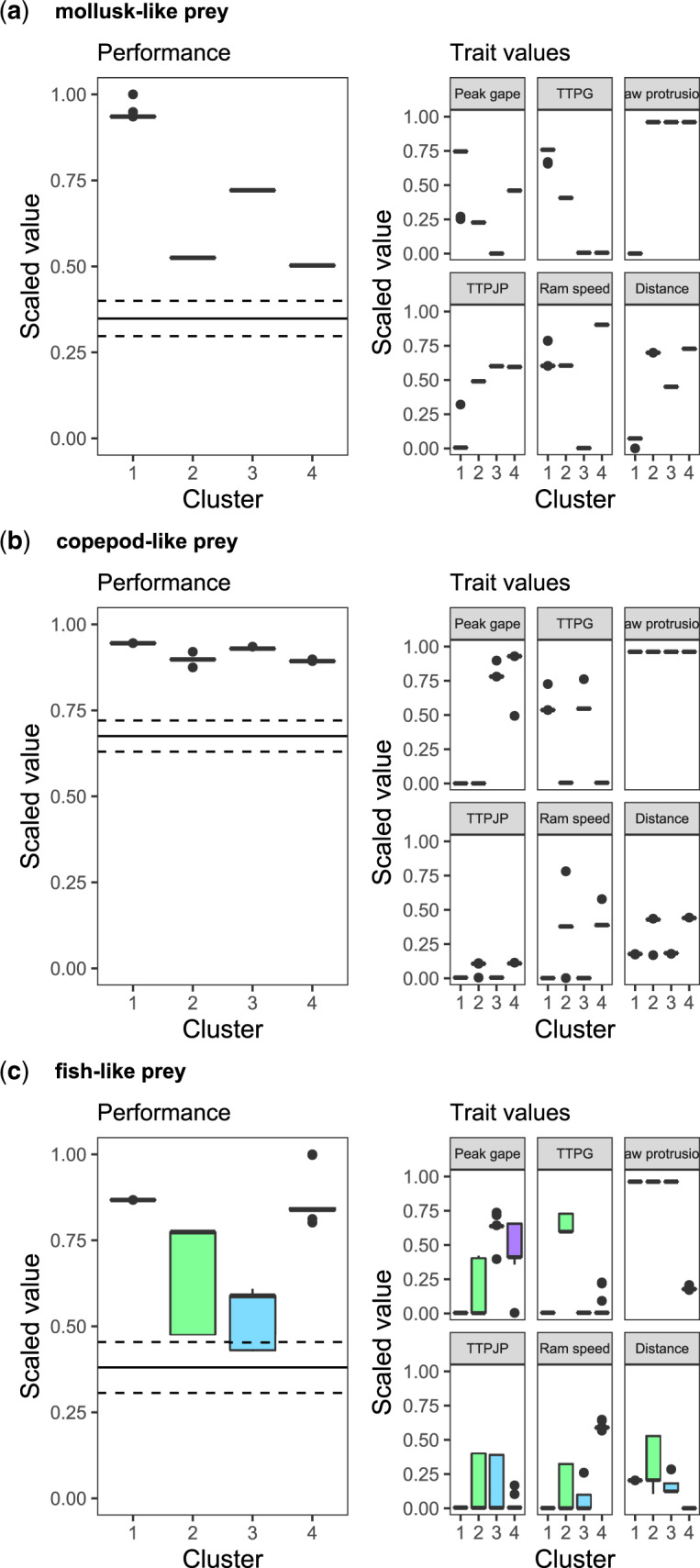
Many to one mapping of kinematics to performance yields multiple peak clusters of unequal height. Boxplots show the performance associated with each peak cluster (left panels) and the range of trait values (right panels) associated with each peak cluster. Data are for (a) mollusk-like prey, (b) copepod-like prey, and (c) fish-like prey. Horizontal lines in the right panels show mean performance in the landscape (solid line)±s.e. (dashed lines) and whiskers indicate 1.5* inter-quartile range. For each prey type, four peak clusters could be identified, associated with different performance levels (left panels). For all prey types, peak cluster 1 outperforms the rest, but the margin is much greater for mollusk-like prey (top panel). The trait profiles of each peak cluster (right panels) generally indicate a narrow range of traits for each peak cluster, with the exception of cluster 2 and 3 for fish-like prey (lower panels). Again, note that these are not “real” prey but prey which respond to a predator in a manner typical for that of mollusks, copepods, and fish.

To identify the basin of attraction in trait space for each of the performance peak clusters, we used a kernel density analysis. For mollusk-like prey, the basins of attraction were of roughly equal size and partly overlapping (in the 2D projection), especially those of clusters 2, 3, and 4 (Fig. 5a). For copepod-like prey, peak clusters 2 and 4 attracted roughly equal proportion of start points, resulting in two larger basins of attraction, associated with clusters 2 and 4 and two slightly smaller ones associated with clusters 1 and 3 (all of which overlapped to some extent in the 2D projection; Fig. 5b). For fish-like prey, peak cluster 4 attracted most start points, and the basins of attraction were generally somewhat smaller and denser than in the other landscapes, with those of peak clusters 1 and 2 almost completely overlapping in the 2D projection (Fig. 4c).

Fig. 5.

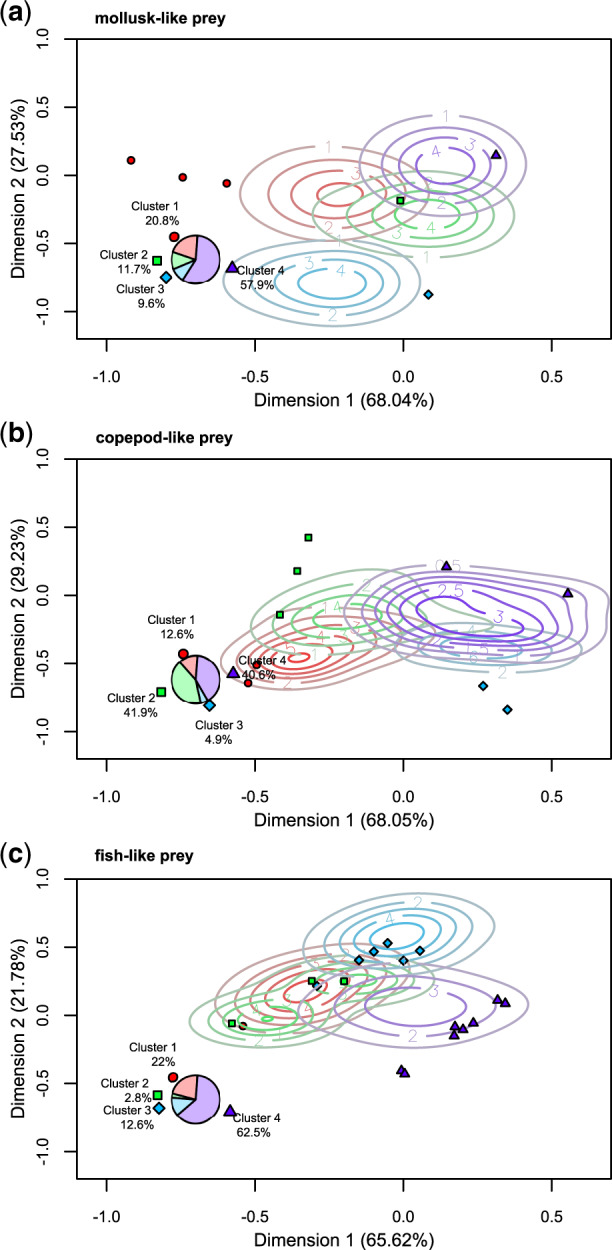
Different peaks have different “basins of attraction.” Kernel density estimate contours of the location of the start points associated with each peak cluster (as identified by color and point shape), projected onto the first two dimensions of the PCA performed on the local peaks. The local peaks defining the clusters are denoted by solid points in the associated color and shape, and the fraction of points belonging to each cluster is shown in the inset pie chart. Top panel shows the clusters of the landscape for mollusk-like prey, middle panel the landscape for copepod-like prey, and lower panel the landscape for fish-like prey. The full color version is available in the electronic version, but is not necessary for interpretation of the figures.

Discussion

The analyses show that the suction-feeding performance landscapes for all three prey types are complicated, having a rugged topography, with multiple local performance peaks scattered across the trait space. We also show that the performance landscapes for the different types of prey differ from each other, with respect to the location of the peaks, the uniformity of the height of the peaks, and the profile of the phenotypes associated with peaks. For each prey type, the identified performance peaks could be classified into four clusters. These peak clusters differed from each other both in terms of their kinematic trait profiles as well as performance levels, but in all cases, performance exceeded that of the average landscape. Feeding performance is thus highly dependent on the specific kinematic phenotype of the predator, but predators that target similar prey may still exhibit different kinematic strategies.

Implications for trophic specialization

Models of the evolution of specialized feeding strategies, such as piscivory or other evasive prey specialists, commonly feature a generalized ancestor (Sibbing et al. 1998; de Graaf et al. 2008; Gajdzik et al. 2019). Although it would therefore be reasonable to hypothesize that increased trophic specialization is accompanied by concomitant morphological specialization or functional diversity, this is often not the case (Bellwood et al. 2006; Cooper and Westneat 2009; Borstein et al. 2019), such that generalists are not universally more morphologically or functionally diverse than other feeding guilds. While specialists are generally considered more constrained by trade-offs, expected performance trade-offs between feeding specialists and between prey types often fail to materialize (Van Wassenbergh et al. 2007; Oufiero et al. 2012; Walker and Caddigan 2015). Comparing the three performance landscapes, we find that the performance peaks for all three prey types are generally associated with narrowly defined phenotypes, and might therefore indicate that capture of evasive prey is not a more specialized feeding strategy than capture of prey that attaches to a holdfast. However, this analysis does not account for performance trade-offs for predators switching between prey, or opportunistically feeding on alternative prey. Importantly, the prediction based on the performance landscape does not depend on performance in extant species, which could be biased due to other selective processes such as bottlenecks and historic constraints but is based on core physical principles used to generate the landscape.

Many-to-one mapping is considered a mechanism that helps explain the morphological diversity observed in suction-feeding fish (Alfaro et al. 2004, 2005; Wainwright et al. 2005). Examination of the traits associated with performance peaks showed that different peaks were associated with different trait clusters, indicating that similar feeding performance can be attained with disparate kinematic strategies (Fig. 3). This is in line with the notion that suction-feeding is characterized by many-to-one relationships (Holzman et al. 2011, 2012), consistent with its multivariate and complex nature (Wainwright et al. 2005; Wainwright 2009). Notably, our analyses show that many-to-one mapping can be manifested either by the existence of multiple local peaks or when a cluster encompasses a broad range of trait values: in mollusk-like and copepod-like prey, given the narrowly defined trait ranges for each cluster, the many-to-one mapping is largely associated with between-cluster differences, while in fish-like prey many-to-one mapping is also to a smaller extent present within clusters.

Implication for the location of extant species

While performance landscapes cannot predict the selection pressures exerted on the different traits, they can be used to generate testable hypotheses regarding the evolutionary processes shaping the extant functional diversity. For example, on the landscape for copepod-like prey, peak cluster #1 is associated with the highest performance (Fig. 4b) and has one of the largest basins of attraction as indicated by the kernel density analysis (Fig. 5b and inset). Together, these parameters should bias the evolution of zooplanktivore specialists to preferentially occupy this peak cluster. Conversely, peak clusters #2 and #3 have the lowest performance peaks on the landscape for fish-like prey (Fig. 4c) and are also associated with smaller basins of attraction (Fig. 5c and inset), generating the prediction that the evasive specialists (i.e., piscivores) should rarely occupy this peak cluster. Clearly, other evolutionary processes as well as developmental, biomechanical, and ecological constraints can operate to bias the evolution of these feeding guilds. However, contrasting adaptive and performance landscapes can inform about the importance (or lack thereof) of performance at a particular task in the selection on its underlying traits.

Even when performance is identified as an important driver of trait evolution, the relationships between the location of the peak and the distribution of the extant species is subject to interpretation. One view holds that species are expected to be found at or close to an adaptive peak, broadly overlapping regions of high performance in trait space (Grant 1986; Collar et al. 2009; Martin and Wainwright 2013). This view often informs the interpretation of models that support an OU-like trait evolution. Conversely, species can be constrained within a pareto front that is delimited by the trade-offs between different functions (Sheftel et al. 2013; Shoval et al. 2013; Hart et al. 2015). The vertices of the pareto front correspond to performance specialists, but often this inference is made based on location in trait space, rather than based on measured relative performance (Kavanagh et al. 2007, 2013; but see, e.g., Dickson and Pierce 2019; Schuech et al. 2019; Stayton 2019). Our performance landscapes now provide the tools for testing these competing hypotheses regarding the location of extant species in suction-feeding fish. Combining kinematic data from observations of feeding strikes with diet data could allow us to test the “pareto front” prediction that specialists are found at the vertices of the Pareto fronts and generalists in-between. Alternatively, an OU process could align the evolution of phenotypic traits toward adaptive peaks that should correspond to regions of high performance (i.e., one or more peaks). Lastly, it could be that the evolution of the traits we measured is unrelated to the performance landscape, indicating that biomechanical or developmental constraints govern the evolution of suction-feeding kinematics in fish.

In summary, we have shown that the performance landscapes for suction-feeding fish are rugged, indicative of many-to-one relationship between phenotype and performance optima. Closer examination of the peak clusters in our landscapes further suggests that prey type affect both ruggedness, in terms of the number of peak clusters in each landscape, as well as the range of phenotypic diversity associated with each peak cluster. The former is consistent with many-to-one relationships between phenotype and performance, as expected for complex functions like suction-feeding. The latter is indicative of differing degrees of phenotypic specialization associated with feeding on different prey types, with evasive prey requiring a more specialized phenotype than mollusk-like prey. This generates testable hypotheses with respect to the location of extant species. Because we can distinguish between performance peaks, both in terms of their relative height in the performance landscape and the size of their respective basins of attraction, for multiple landscapes, we can generate predictions about where in trait space we are likely to find the highest density of feeding specialists and test these using data collected on multiple species.

Funding

This work was supported by U.S.-Israel Binational Science Foundation (BSF) grant 2016136 to C.H.M and R.H.; and IUI post-doc scholarship to K.H.O.

Supplementary data

Supplementary data are available at ICB online.

 

From the symposium “Melding Modeling and Morphology: integrating approaches to understand the evolution of form and function” presented at the annual meeting of the Society for Integrative and Comparative Biology January 3–7, 2020 at Austin, Texas.