Predictive study of tuberculosis incidence by time series method and Elman neural network in Kashgar, China

Abstract

Objectives

Kashgar, located in Xinjiang, China has a high incidence of tuberculosis (TB) making prevention and control extremely difficult. In addition, there have been very few prediction studies on TB incidence here. We; therefore, considered it a high priority to do prediction analysis of TB incidence in Kashgar, and so provide a scientific reference for eventual prevention and control.

Design

Time series study.

Setting Kashgar, China

Kashgar, China.

Methods

We used a single Box-Jenkins method and a Box-Jenkins and Elman neural network (ElmanNN) hybrid method to do prediction analysis of TB incidence in Kashgar. Root mean square error (RMSE), mean absolute error (MAE) and mean absolute percentage error (MAPE) were used to measure the prediction accuracy.

Results

After careful analysis, the single autoregression (AR) (1, 2, 8) model and the AR (1, 2, 8)-ElmanNN (AR-Elman) hybrid model were established, and the optimal neurons value of the AR-Elman hybrid model is 6. In the fitting dataset, the RMSE, MAE and MAPE were 6.15, 4.33 and 0.2858, respectively, for the AR (1, 2, 8) model, and 3.78, 3.38 and 0.1837, respectively, for the AR-Elman hybrid model. In the forecasting dataset, the RMSE, MAE and MAPE were 10.88, 8.75 and 0.2029, respectively, for the AR (1, 2, 8) model, and 8.86, 7.29 and 0.2006, respectively, for the AR-Elman hybrid model.

Conclusions

Both the single AR (1, 2, 8) model and the AR-Elman model could be used to predict the TB incidence in Kashgar, but the modelling and validation scale-dependent measures (RMSE, MAE and MAPE) in the AR (1, 2, 8) model were inferior to those in the AR-Elman hybrid model, which indicated that the AR-Elman hybrid model was better than the AR (1, 2, 8) model. The Box-Jenkins and ElmanNN hybrid method therefore can be highlighted in predicting the temporal trends of TB incidence in Kashgar, which may act as the potential for far-reaching implications for prevention and control of TB.

Strengths and limitations of this study.

• The Box-Jenkins method has good prediction performance and high prediction accuracy.

• Elman neural network can capture the non-linear information of time series well.

• A hybrid model often improves the prediction accuracy of a single model.

• The long-term prediction accuracy of AR-Elman hybrid model will decline.

Introduction

Tuberculosis (TB) is still a major global public health problem and the ninth leading cause of death in the world.^1–3 TB accounts for a large loss to society and for a significant reduction in the labour force, because (1) TB is contagious, (2) patient resistance is low, and (3) treatment time is long. All countries recognise this and are working hard to fight TB. In 2018, the number of new reported TB cases was about 10 million; this figure has remained relatively stable in recent years. The latest treatment results show that the global TB treatment success rate is 83%. WHO has set targets for the ‘stop TB’ strategy. The targets mention that by 2030, on the basis of the work in 2015, TB deaths should be reduced by 90%, and annual new TB cases should be reduced 80%.⁴ In order to achieve these goals, TB prevention and control services must be provided in the broad context of universal health coverage, joint action must be taken to address the social and economic consequences of TB, and technological breakthroughs should be achieved by 2025 in order to make the TB incidence decline faster than that at any time in history. According to the global TB report 2019,⁴ China has the second highest number of TB cases in the world.⁴ The TB incidence in western China was much higher than that in eastern and central China. The province with the highest TB incidence in the west is Xinjiang province. In 2016 and 2017, the annual TB incidence per 100 000 people in Xinjiang was 185.66 and 202.58, respectfully, nearly three times higher in Xinjiang than that national level in the same years.

There are 14 Prefectural-Level cities in Xinjiang, China, among which Kashgar has a very high TB incidence rate. In 2016 and 2017, the annual TB incidences per 100 000 people in Kashgar were 427.44 and 465.33, respectively, nearly seven times higher than the national level. Doing a good job in the prevention and control of TB in Kashgar is, therefore, an important link to reduce the TB incidence in Xinjiang and China.

Mastering changing law of the incidence of infectious diseases, using the existing surveillance data to analyse, then, to predict possible epidemic trend and provide reference data for the prevention, can better help to control occurrence and epidemic of infectious diseases. Prediction of infectious diseases is to predict occurrence, development and epidemic trend of infectious diseases according to the occurrence, development law and related factors of infectious diseases.

There are many forecasting methods for infectious diseases: the grey prediction method,⁵ the exponential smoothing prediction method,^{6 7} the dynamic model prediction method,⁸ the Box-Jenkins method,⁹ the neural network method,¹⁰ with the deepening of prediction research, more and more scholars like to use the Box-Jenkins method,^11–21 there are many different models in this method, and if appropriate models are chosen according to the characteristics of time series, high prediction ability often can be obtained. The Neural network has a strong nonlinear mapping ability, in which Elman neural network is composed of input layer, hidden layer, connection layer and output layer. The Elman network has a dynamic memory function, and it is very suitable for time series prediction. At present, the Elman network is widely used in various fields, and has achieved notable successful prediction results.^22–26 Sometimes, the prediction effect of a single model is not ideal, in order to further improve the prediction accuracy, many studies adopt the combined model prediction method,^27–29 the combined model can absorb the advantages of two or more methods so as to achieve a higher prediction accuracy.

The TB incidence in Kashgar is very high, and it is urgent to do a good job in the prevention and control of TB in this area. Accurate prediction of TB incidence is a prerequisite for prevention and control, which can help advance in resource planning and policy formulation. In this study, the popular Box-Jenkins time series method was used to build a model for predicting the TB incidence in Kashgar, and in order to improve the prediction accuracy, the Elman neural network with its strong ability to capture nonlinear information was used to construct the combined model for prediction analysis.

Materials and methods

Study area and data sources

We selected Kashgar as the study site (see figure 1). This area is located in the south of Xinjiang province in China and has an area of approximately 16.2 000 km² and a permanent population of 4.64 million in 2018. TB case data from January 2005 to December 2017 were obtained from the Center for Disease Control and Prevention (CDC) of Xinjiang Uygur Autonomous Region, all TB cases in Xinjiang must be reported to the CDC through the infectious disease surveillance system within 24 hours. The TB cases datasets used need permission of the CDC. Population data were obtained from the website of Xinjiang Bureau of Statistics (http://tjj.xinjiang.gov.cn/tjj/tjfw/list_tjfw.shtml). Based on the population data and TB case data, we calculated the incidence data of TB.

Figure 1.

The red part of this picture is the location of Kashgar in Xinjiang, China. Kashgar is located in the South of Xinjiang, and it has a very high incidence of tuberculosis.

Patient and public involvement

Patients were not involved in the design of this study as it involved only observational analysis of an anonymised, pre-existing, routinely collected dataset.

Autoregressive moving average model

The autoregressive moving average (ARMA) model³⁰ is an important time series analysis and prediction model in Box-Jenkins method, also known as an auto-regression moving average model. The ARMA (p, q) model is a model with autocorrelation order p and moving average order q, the p and q are judged by the autocorrelation function (ACF) and partial ACF (PACF) diagram of stationary data. If the original data are stable, the autocorrelation coefficients are trailing, and the partial correlation coefficients are p-order truncated, then q=0, the ARMA (p, q) model is written as AR (p), and its expression is as follows:

X_t=c+ϕ₁X_t-1+ϕ₂X_t-2+ … +ϕ_pX_t-p+ε_t,

where, X_t is the observed value at t, ϕ₁,…,ϕ_p are model parameters, c is a constant, if only ϕ₁, ϕ₂, ϕ_p are not zeros, then, The AR (p) model becomes a sparse model, which can be written as AR ((1, 2, p)).

If the original data are stable, the autocorrelation coefficients are q-order truncated and the partial correlation coefficients are trailing, then p=0 and the ARMA (p, q) model becomes MA (q), its expression is as follows:

X_t=μ+ε_t+θ₁ε_t-1+θ₂ε_t-2+…+θ_qε_t-q

where,μ is the expected value of X_t. θ₁,…,θ _p are model parameters.

If the original data are stable, the autocorrelation coefficients are trailing, and the partial correlation coefficients are also trailing, then the expression of the ARMA (p, q) model is as follows:

X_t=c+ϕ₁X_t-1+ϕ2X_t-2+…+ϕ_pX_t-p+ε_t-θ₁ε_t-1-θ₂ε_t-2 -… -θ_qε_t-q.

There are four main steps in ARMA modelling:

First step. The prerequisite for ARMA modelling is the stationary of time series. Check whether the data are stable by the Augmented Dickey-Fuller (ADF) unit root test. In this study, the significant level probability (p value) is 0.05, and if the p value is less than 0.05, then, the data are considered stable. By observing the ACF and the PACF of the stable data, we can determine the possible values of p and q and establish the possible ARMA (p, q) model.

Second step. The parameters of ARMA(p, q) model are estimated by the maximum likelihood estimation or the least square estimation, and the model parameters are tested. If p value is less than 0.05, the parameters have statistical significance. The best model is determined according to the value of the Akaike information criterion (AIC), the Schwarz criterion (SC) and the Goodness of Fit (R²) of model. The smaller AIC and SC are, the larger the R² is, and the better the model is.

Third step. To determine whether the established ARMA (p, q) model is suitable. The residual sequence of a suitable model shall be the white noise process, and its ACF and PACF coefficients should be within twice the SD range, otherwise, it is considered that the extraction of information in the established model is not sufficient, and it is necessary to consider improving the accuracy of the model.

Fourth step. Using the established model to do prediction and analysis.

Elman neural network model

The E1man neural network (see figure 2) was proposed by E1man in 1990.³¹ The model is generally divided into four layers: input layer, hidden layer, receiving layer and output layer. The characteristic of the E1man network is that the output of the hidden layer is connected to the input of the hidden layer through the delay and storage of the receiving layer, which makes it sensitive to the data of the historical state. The addition of the internal feedback network increases the ability of the network itself to deal with dynamic information, thus achieving the purpose of dynamic modelling.

Figure 2.

The structure diagram of Elman neural network. w¹, w² and w³ are the connection weight matrixes. x_c(k) and x(k) represent the output of the contact unit and the hidden layer unit, respectively, y(k) represents the output of the output unit, u(k-1) represents the input of the input unit.

The mathematical structure of the Elman neural network is as follows:

x(k)=f(w¹x_c(k)+ w²u(k-1))

x_c(k)=α x_c(k-1)+x(k-1)

y(k)=g(w³x(k))

Where, w¹ is the connection weight matrix between the contact unit and the hidden layer unit, w² is the connection weight matrix between the input unit and the hidden layer unit, w³ is the connection weight matrix between the hidden layer unit and the output unit. x_c(k) and x(k) represent the output of the contact unit and the hidden layer unit, respectively, y(k) represents the output of the output unit,α is a self-connected feedback gain factor, 0≤α＜1, f(x) often takes the sigmoid function.

There are four main steps in Elman neural network modelling:

First step. Data standardisation processing. Data standardisation is scaling the data to a small specific interval. In order to remove the unit limit of the data and convert it into dimensionless pure value, it is convenient for the index of different units or order of magnitude to be compared and weighted. In our study, we used function package mapminmax() to standardise the data, standardised data were in the range (−1 to 1).

Second step. Determine the input layer, the output layer. Generally, the input and output layer are determined according to the characteristics of data and the needs of the analysis.

Third step. Set the parameters of the Elman model, such as training epochs and goals. In our study, training epochs and goals of the Elman neural network were set to 2000 and 0.00001, respectively. Determine the number of neurons in the hidden layer, so that the error of the established Elman model is minimised. At present, there is no ideal analytical expression for the number of neurons in the hidden layer. The number of neurons has a great influence on the performance of the network. When the number of neurons is too large, it will lead to that the network learning time being too long, poor generalisation performances and even failure to converge, but when the number of neurons is too small, the fault-tolerant ability of the network is poor. In general, the number of neurons does not exceed 20.³² In this study, matlab cyclic structure was used to find the optimal number of neurons by comparing the root mean square error (RMSE) values of Elman networks with neurons 1–20.

Fourth step. According to the optimal number of neurons in the hidden layer, the Elman model is constructed, and then the prediction and analysis can be made.

Model comparison measures

Three performance indexes, RMSE, mean absolute error (MAE) and mean absolute percentage error (MAPE) were used to assess the fitting and forecasting accuracy of two models. The smaller these three values are, the better the model is. Their expressions are as follows¹⁰:

RMSE= ${\displaystyle \sqrt{\frac{\sum _{t=1}^n(X_t-{\hat{X}}_t{)}^2}{n}}}$,

MAE= ${\displaystyle \frac{\sum _{t=1}^n|X_t-{\hat{X}}_t|}{n}}$,

MAPE=${\displaystyle \frac{\sum _{t=1}^n\frac{|X_t-{\hat{X}}_t|}{X_t}\times 100}{n},}$

where, ${\displaystyle {\hat{X}}_t}$ is the simulating and forecasting values, X_t is the actual values and n is the number of observations.

Statistical software

All data analyses were conducted using Eviews7, matlab2015b, ArcMap V.10.1.

Results

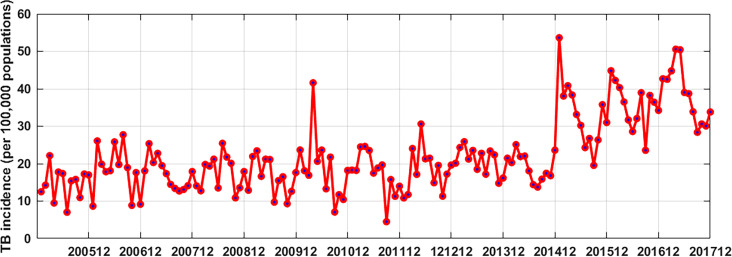
From January 2005 to December 2017, the number of reported TB cases was 141 984 in Kashgar, Xinjiang, the average annual TB cases were 7888 and the average annual incidence was 191.18 per 100 000 population. Figure 3 shows the time series graph of the TB incidence. It can be seen from the figure 3 that the curve of TB incidence has strong non-linear characteristics from 2005 to 2014, and the TB incidence from 2015 to 2017 was significantly higher than that of previous years.

Figure 3.

Graph of the tuberculosis (TB) incidence in Kashgar from January 2005 to December 2017. The curve of TB incidence shows strong non-linear characteristics from 2005 to 2014, and the TB incidence increases significantly from 2015 to 2017.

The data of TB incidence from January 2005 to December 2017 were divided into two parts. The data from January 2005 to December 2016 were used to build model and the data from January 2017 to December 2017 were used to test the model.

Establishment of the ARMA Model

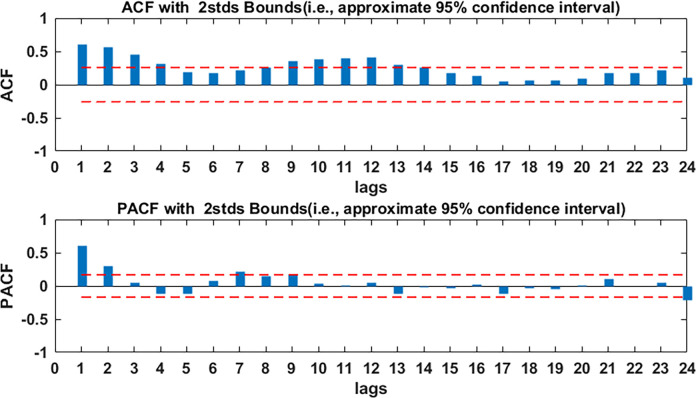
The ARMA modelling requires data stability, so, first of all, the stability of the modelling part of the data was verified by the ADF test. The results of the ADF test showed that p value was less than 0.05 (see table 1), which indicated that the data were stable and could be directly used to build the model. Second, the ACF and the PACF graphs of the modelling data were plotted (see figure 4), it was obvious from figure 4 that the autocorrelation coefficients are trailing distribution and the partial correlation coefficients are almost a second-order truncated distribution, only at the lag 7, 8 and 9, the correlation coefficients are a little large. Based on this situation, we considered establishing four models: AR (2) model, AR ((1, 2, 7)) model, AR ((1, 2, 8)) model and AR ((1, 2, 9)) model. The least square method was used to test the parameters of the four models. The results of the test were shown in table 2; we can see that, of the four models, only the AR (2) model and the AR ((1, 2, 8)) model passed the parameter test. Comparing the two models, it was found that the AR ((1, 2, 8)) model had smaller AIC and SC values, and the R² value of the AR ((1, 2, 8)) model was larger than the R² value of the AR (2), so the AR (2) model was abandoned. Then, the residual analysis of the AR ((1, 2, 8)) model was carried out, the autocorrelation and partial correlation coefficient of the residuals were almost all within two times SD, and only in the lag 5, 6, 12, they were beyond the range of two times standard deviation (see figure 5), which indicated that the AR ((1, 2, 8)) model could be used to roughly predict the TB incidence in Kashgar. We used the AR ((1, 2, 8)) model to fit the TB incidence from September 2005 to December 2016, the fitting RMSE, MAE and MAPE were 6.15, 4.33 and 0.2858, respectively; we used the AR ((1, 2, 8)) model to predict the TB incidence from January 2017 to December 2017, the prediction RMSE, MAE and MAPE were 10.88, 8.75 and 0.2029, respectively.

Table 1.

The augmented Dickey-Fuller (ADF) test of the training data

t-Statistics			P value
ADF test statistic		−3.47	0.01
Test critical values	1% level	−3.48
	5% level	−2.88
	10% level	−2.58

Figure 4.

Autocorrelation function (ACF) and partial ACF (PACF) graphs of modelling data. As the delay of the lag order, the autocorrelation coefficients are trailing and the partial correlation coefficients are truncated, so it was deemed suitable to use the AR model. AR, autoregressive.

Table 2.

Parameter estimates of the tentative models with their Akaike information criterion (AIC) and Schwarz criterion (SC) values

Models	Variables	Coefficients	SE	T	P values	AIC	SC
AR (2)	C	21.42	2.17	9.86	<0.01
	AR (1)	0.42	0.08	5.20	<0.01	6.55	6.62
	AR (2)	0.34	0.08	4.17	<0.01
AR ((1, 2, 7))	C	22.93	3.73	6.14	<0.00
	AR (1)	0.41	0.08	5.10	<0.00	6.53	6.62
	AR (2)	0.32	0.08	3.88	<0.00
	AR (7)	0.12	0.007	1.74	0.08
AR ((1, 2, 8))	C	23.53	4.56	5.16	<0.01
	AR (1)	0.40	0.08	4.84	<0.01	6.53	6.61
	AR (2)	0.32	0.08	3.96	<0.01
	AR (8)	0.15	0.07	2.17	0.03
AR ((1, 2, 9))	C	29.07	15.53	1.87	0.06
	AR (1)	0.37	0.08	4.64	<0.01	6.46	6.55
	AR (2)	0.31	0.08	3.93	<0.01
	AR (9)	0.26	0.07	3.80	<0.01

AR, autoregressive.

Figure 5.

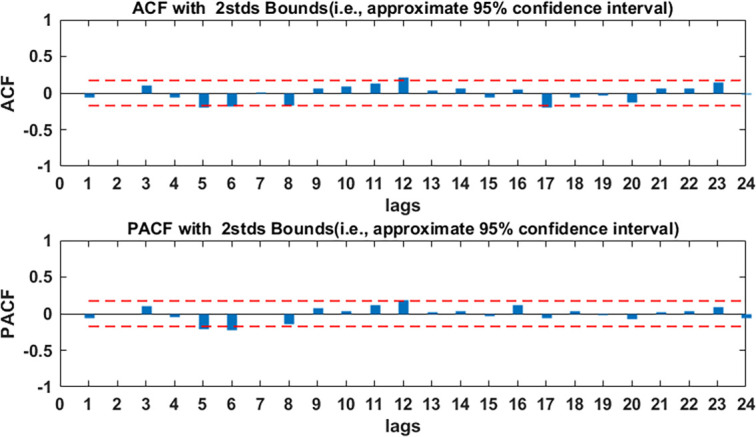
Autocorrelation function (ACF) and partial ACF (PACF) graphs of residuals of AR ((1, 2, 8)) model. Autocorrelation coefficients and partial correlation coefficients are almost in 95% CI, so AR ((1, 2, 8)) model can extract the information of original data well. AR, autoregressive.

Establishment of the AR-Elman model

In order to improve the prediction accuracy of the AR ((1, 2, 8)) model, we tried to establish an AR ((1, 2, 8))-Elman hybrid model. The fitting sequence of the AR ((1, 2, 8)) model was used as input variable, and the actual TB incidence was used as output variable. Due to a little similarity of the annual trend of TB incidence in Kashgar (see figure 3), therefore, we created 12 time-lagged variables as input features. Supposing that x_t represented the TB incidence at time t, and then the input matrix and the output matrix of modelling data set used in this study were designed as follows (N=12)

input matrix= ${\displaystyle \begin{array}{cc}{x}_1& x_2\dots x_i\\ x_2& x_3\dots x_{i+1}\\ x_N& x_{N+1}\dots \dots \end{array}}$, output matrix=[x_N+1x_N+2… x_N+i ]

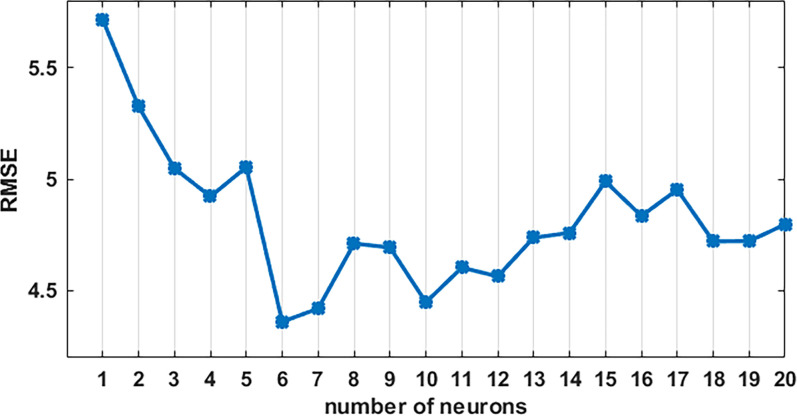
We selected 12 as the number of input layers of AR-Elman network and one as the number of output layers representing the forecast value. By the matlab cyclic structure, we selected the optimal number of neurons between 1 and 20, and finally, we found when the number of neurons was 6 (see figure 6), the RMSE was the smallest, and the AR-Elman was optimal. We used the AR-Elman model to fit the training data, RMSE was 3.78, MAE was 3.38, MAPE was 0.1837, and the R² of the model was 0.83; we used the AR-Elman model to predict the TB incidence from January 2017 to December 2017, RMSE was 8.86, MAE was 7.29, and MAPE was 0.2006. The fitting curves of the AR ((1, 2, 8)) model and the AR-Elman model, and the prediction curve of the AR-Elman model are shown in figure 7. Comparison results of the AR ((1, 2, 8)) model and the AR-Elman model are shown in table 3, both the fitting RMSE, MAE and MAPE and the predicting RMSE, MAE and MAPE of the AR-Elman model are smaller than those of the single AR ((1, 2, 8)) model, which indicated that the AR-Elman combined model established in this study was more suitable for predicting the TB incidence in Kashgar.

Figure 6.

The numbers of neurons in AR-Elman model and the corresponding root mean square error (RMSE). When the number of neuron is 6, the RMSE was the smallest, and the AR-Elman model fitting ability is the best. AR, autoregressive.

Figure 7.

The fitting curves of the AR ((1, 2, 8)) model and the AR-Elman model, and the prediction curve of the AR-Elman model. The red line stands for the original tuberculosis incidence curve, the green line stands for AR ((1, 2, 8)) model fitting curve, and the blue line stands for AR-Elman model fitting curve. The blue dotted line stands for prediction curve of the AR-Elman model, the black dotted line stands for predicted curve of CIs. The fitting ability of AR-Elman hybrid model was slightly better than that of the single AR ((1, 2, 8)). AR, autoregressive.

Table 3.

Comparison results of in-sample fitting and out-of-sample forecasting performance for the AR ((1, 2, 8)) model and the AR-Elman model

Models	Fitted efficacy			Models	Forecasted efficacy
	RMSE	MAE	MAPE		RMSE	MAE	MAPE
AR ((1, 2, 8))	6.15	4.33	0.2585	AR ((1, 2, 8))	10.88	8.75	0.2029
AR-Elman	3.78	3.38	0.1837	AR-Elman	8.86	7.29	0.2006

AR, autoregressive; MAE, mean absolute error; MAPE, mean absolute percentage error; RMSE, root mean square error.

Discussion

According to the WHO 2019 Global TB report,⁴ around the world, TB mortality was down about 3% every year, the incidence was down about 2% every year, 16% of TB patients died of the disease.⁴ But the rate of decline has not reached the pace of the ‘stop TB Strategy Plan’. Therefore, it is necessary to strengthen the prevention and control of TB. In order to significantly narrow these gaps, greater progress must be made in a group of countries with a high burden of TB. The burden of TB in China ranks second in the world, and Xinjiang is the province with high incidence of TB in China, and Kashgar is the area with the high TB incidence in Xinjiang. Therefore, it was considered a high priority urgent to do a good job in the prevention and control of TB in Kashgar.

The prediction and early warning of infectious diseases is an important link in the prevention and control of infectious diseases.^32–34 Therefore, this study carried out research from the point of view of prediction to explore an accurate prediction model and do the prediction analysis of TB incidence in Kashgar, so as to provide scientific reference for the prevention and control of the disease in this area. The Box-Jenkins method is a popular time series prediction method, this method has good prediction performance and high prediction accuracy; Elman Neural network can capture nonlinear information of time series data very well. In this study, the two methods were combined to study the prediction model of TB incidence in Kashgar.

Many studies have found that Box-Jenkins method has a good ability of fitting and forecasting. For stationary time series that do not contain seasonality, it is more suitable to use the ARMA model of the Box-Jenkins method to do prediction analysis,³⁵ for non-stationary time series of infectious diseases with obvious seasonality, it is more suitable to use the seasonal autoregressive integrated moving average (SARIMA) model of the Box-Jenkins method for prediction analysis.^9–12 In our study, from figure 3, we could see that the seasonality of the TB incidence in Kashgar from 2005 to 2014 was not obvious, there was only a certain seasonality from 2015 to 2017, and we found that the time series of TB incidence was stable by the ADF unit root test, and the autocorrelation and partial correlation coefficients of modelling data at lag 12, 24 were not obviously large, therefore, for our research data, we used the ARMA model to do forecast analysis, and finally, we established the AR ((1, 2, 8)) model of the Box-Jenkins method with its good performance in fitting and predicting the TB incidence of Kashgar in Xinjiang. In figure 3, we can also see that the time series of TB incidence has strong non-linear, Since the AR ((1, 2, 8)) model we settled on mainly extracted the linear information of data, and knowing that the neural network can capture the non-linear information of data well, we used the AR ((1, 2, 8)) model and Elman neural network model to establish the AR-Elman hybrid model and improve the prediction accuracy of TB incidence rate in Kashgar. Many studies have found that the combination model can improve the accuracy of prediction: Wang et al²⁸ found that SARIMA-non-linear autoregressive network (NAR) hybrid model has an outstanding ability to improve the prediction accuracy relative to SARIMA model and NAR model when they were used to predict pertussis incidence in China. Li et al²⁷ found ARIMA-GRNN hybrid model was shown to be superior to the single ARIMA model in predicting the short-term TB incidence in the Chinese population. Our research was consistent with these literatures that our AR-Elman hybrid model was more accurate than the single AR ((1, 2, 8)) model.

In the past few years, Xinjiang’s economic development was relatively backward, medical resources were scarce, diagnosis and treatment were delayed, the continuous spread of TB has become a difficult problem in Xinjiang. In recent years, Xinjiang has introduced many new policies to increase investment in TB prevention and control, and the relevant departments of disease prevention and control in Xinjiang have also done a lot of effective work, which has helped to control the rapid increase of the TB incidence in Xinjiang. In order to do a good job in the prevention and control of TB in Xinjiang, many departments need to make joint efforts. Our research was mainly to build a high-precision prediction model to help early warning and prediction analysis of TB in Kashgar. Finally, we established the AR-Elman hybrid model, which had high fitting and prediction accuracy of TB incidence in Kashgar, Xinjiang.

Our study found that Box-Jenkins and Elman neural network hybrid method is an effective method for predicting the incidence of TB in Kashgar, it can provide a scientific reference for prediction analysis of TB incidence. However, our study also has some limitations: our method is only suitable for short-term prediction, long-term prediction performance will decline, for two main reasons: first, our model was based on historical data characteristics; second, climatic factors, environmental factors, demographic factors and political issues may have certain impacts on the rate of change of TB incidence. Therefore, if the established model becomes old and researchers want to obtain more accurate prediction results, the model parameters will need to be adjusted, the model updated based on the new modelling sample data, and then the prediction analysis redone.

Conclusions

Kashgar has a very high TB incidence, in order to provide some help for the prevention and control of this disease, the prediction problem of the TB incidence was studied. First, a single AR ((1, 2, 8)) prediction model was established by using Box-Jenkins method, with good fitting and prediction performance. Second, in order to improve the prediction accuracy of the single AR ((1, 2, 8)) model, we used the single AR ((1, 2, 8)) and the Elman neural network with its strong ability to capture nonlinear information to establish AR-Elman hybrid model. The fitting and prediction accuracy of the hybrid model was higher than that of the single AR ((1, 2, 8)) model. The AR-Elman hybrid model can provide a scientific reference for predicting and warning of the TB incidence in Kashgar, Xinjiang.