SUMMARY
Converging evidence suggests that the brain encodes time through dynamically changing patterns of neural activity, including neural sequences, ramping activity, and complex spatiotemporal dynamics. However, the potential computational significance and advantage of these different regimes have remained unaddressed. We combined large-scale recordings and modeling to compare population dynamics between premotor cortex and striatum in mice performing a two-interval timing task. Conventional decoders revealed that the dynamics within each area encoded time equally well, however, the dynamics in striatum exhibited a higher degree of sequentiality. Analysis of premotor and striatal dynamics, together with a large set of simulated prototypical dynamical regimes, revealed that regimes with higher sequentiality allowed a biologically-constrained artificial downstream network to better read out time. These results suggest that although different strategies exist for encoding time in the brain, neural sequences represent an optimal and flexible dynamical regime for enabling downstream areas to read out this information.
eTOC
By recording in the striatum and premotor cortex during a two-interval timing task Zhou et al. show that while both areas encode time, the dynamics in the striatum is more sequential. These striatal neural sequences provide an ideal code for downstream areas to read out time in biologically plausible manner.
INTRODUCTION
Tracking the passage of time on the subsecond to second scale is critical for motor control and many forms of learning and cognition, including the ability to anticipate future events (Ivry and Spencer, 2004; Merchant et al., 2013a). While the neural mechanisms underlying timing remain poorly understood, there is growing evidence that time is represented via population-level spatiotemporal patterns of neural activity, and that these dynamical regimes are distributed across multiple areas (Paton and Buonomano, 2018; Wang et al., 2018). To date, numerous different dynamical regimes have been implicated in timing, including neural sequences, ramping, and complex mixed and multi-peaked patterns (Leon and Shadlen, 2003; Hasselmo, 2008; Pastalkova et al., 2008; Long et al., 2010; MacDonald et al., 2011; van der Meer and Redish, 2011; Kraus et al., 2013; Stokes et al., 2013; Crowe et al., 2014; Carnevale et al., 2015; Kraus et al., 2015; Emmons et al., 2017; Heys and Dombeck, 2018; Tsao et al., 2018; Liu et al., 2019). However, the potential computational significance of these different regimes remains unclear. In particular, what is the potential computational tradeoff of encoding time through the progressive activation of neurons (a neural sequence), approximately linear changes in firing rate, or complex neural trajectories in which any given neuron can exhibit multiple peaks in activity? Answering this question has been hampered by challenges in rigorously quantifying and comparing different dynamical regimes across different brain areas. For example, while it is often the case that neural trajectories appear sequence-like when sorted appropriately, the degree of sequentiality is rarely quantified—e.g., the overlap of the temporal fields of consecutively active neurons (related to the temporal sparsity), or the presence of additional secondary peaks, is often not taken into account.
Some of the brain areas that have consistently been implicated in timing exhibit fundamentally different circuit motifs; for example, while premotor areas are characterized by the presence of robust recurrent excitation, striatal circuits lack recurrent excitation (Shepherd, 1998). The functional and computational consequences of these different circuit motifs for the encoding of time remain unexplored. Here we explicitly contrasted the dynamics of dorsolateral striatum (DLS) and secondary motor cortex (M2) during a two-interval timing task. We developed novel measures to quantify the sequentiality of the dynamics, and whether neural activity undergoes temporal scaling from the short to long intervals. We found that the DLS exhibits more sequential dynamics, which provide a more flexible regime for downstream areas to read out time in a biologically plausible manner. These findings suggest a previously unknown computational role for the striatum in timing, and provide general insights into which type of dynamical regimes are optimal for reading out temporal information in downstream brain areas.
RESULTS
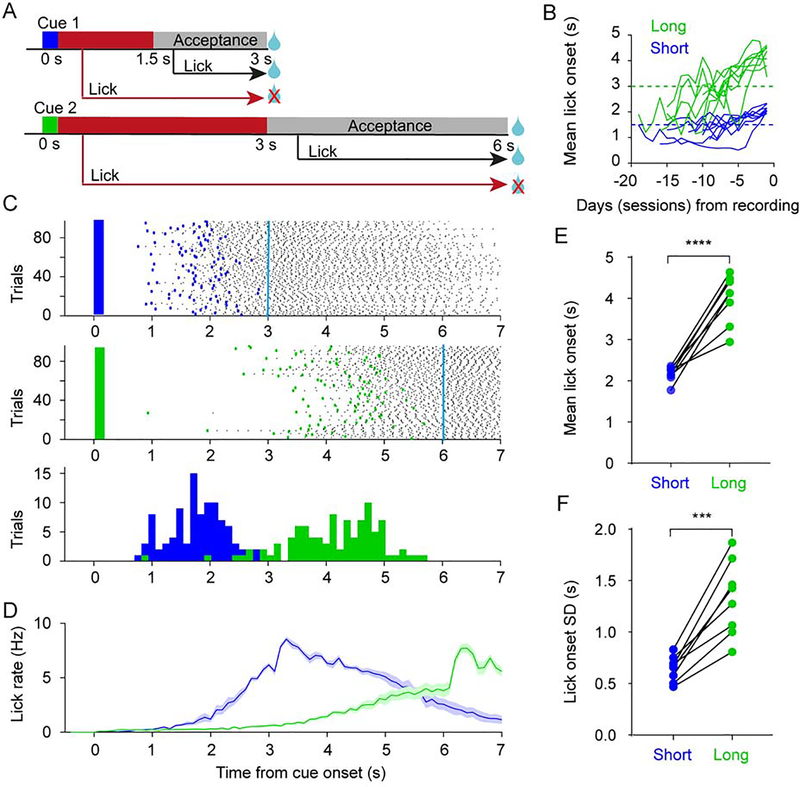
We compared simultaneously recorded neural dynamics in M2 and DLS, as head-fixed mice performed a two-interval timing task (n = 8). Animals were randomly presented with one of two olfactory cues for 0.2 s. A reward was delivered with a 3 s (cue 1, short interval) or 6 s delay (cue 2, long interval) if mice withheld licking for the first 1.5 s after cue 1 onset, or 3 s after cue 2 onset (Figure 1A). Mice learned to differentially time the onset of their anticipatory licking in response to the cues (Figures 1B–D). The mean and standard deviation of the lick onset time were both significantly higher for the long interval cue (Figures 1E–F).
Figure 1. Two-interval timing task in mice.
(A) Task schematic. In each trial mice were presented with one of two olfactory cues for 0.2 s, and rewarded if they withheld licking during the time period indicated in red. Mice were rewarded irrespective of whether they licked or not during the acceptance period shown in grey. Cue 1: short interval, Cue 2: long interval.
(B) Learning curve of mean lick onset time for all 8 mice up to the day before recording day (1 session per day). The dashed horizontal lines denote the start of the lick acceptance period for short (blue) and long interval (green) trials.
(C) Lick raster plot on short (top) and long (middle) interval trials for one animal on the recording day. Only trials with anticipatory licking are shown (Cyan lines denote the time of reward). Bottom: distribution of the same animal’s lick onset times on short (blue) and long (green) interval trials.
(D) Average lick rate on short (blue) and long (green) interval trials across all mice (n = 8). Shaded area represents SEM. Cyan lines denote the time of reward.
(E) The mean lick onset time was significantly higher for the long interval (n = 8 mice; two-sided paired t-test, t7 = 8.296, P < 0.0001).
(F) The standard deviation of the lick onset time was significantly higher for the long interval (n = 8 mice; two-sided paired t-test, t7 = 6.728, P = 0.0003).
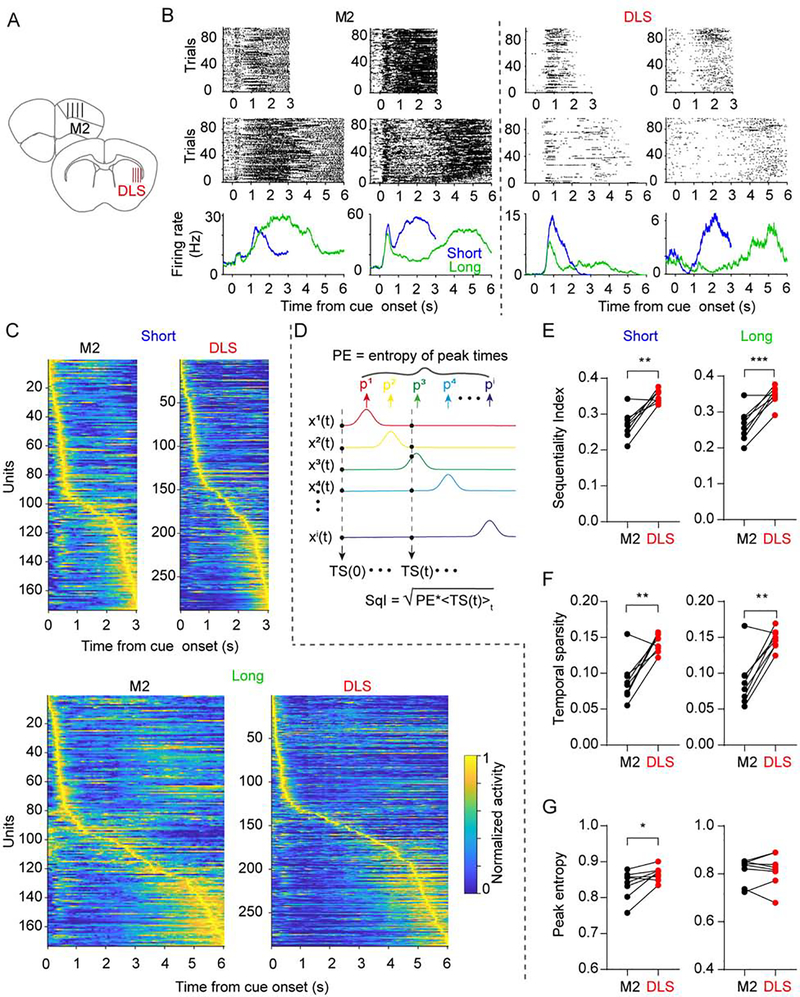
We next used silicon microprobes to simultaneously record spiking activity from neurons in M2 and DLS, as well-trained mice performed the task (range of isolated units: 81 – 263 in M2, 157– 288 in DLS, Figure 2A–B). To confirm that, if as reported previously, population dynamics in M2 and DLS encode elapsed time, we decoded time from the population activity on a trial-by-trial basis using a supervised decoder (see Methods). For both short and long interval trials, we found a similar decoding performance between M2 and DLS (Figure S1A–C). Furthermore, since these areas are also associated with motor performance, we confirmed that the animals’ lick onset time could be decoded with similar accuracy from each area (Figures S1D–E). These results demonstrate that the neural dynamics in both areas can encode two different temporal intervals, but do not address whether both areas use similar encoding schemes. To attempt to rigorously quantify the potential differences in dynamics in both areas we introduced a novel sequentiality index (SqI) bounded between 0 and 1 (see Methods). Two aspects of neural dynamics were factored into computing SqI (Figure 2C–G). First, the entropy of the distribution of peak firing times across the population—which captures whether the entire interval is homogeneously “tiled” by the peak firing times of neurons. Second, a measure of temporal sparsity—which captures how much of the activity at each point in time can be attributed to a single neuron. Interestingly, for both delay intervals, SqI was significantly higher in DLS relative to M2 (Figure 2E). This difference appeared to be primarily due to a higher temporal sparsity of DLS dynamics (Figures 2F–G).
Figure 2. Higher sequentiality indices in DLS compared to M2.
(A) Illustration of the silicon microprobe recording site locations in M2 and DLS.
(B) Spiking raster plot for two example units for short (top) and long (middle) intervals with corresponding average firing rate (bottom) in M2 (left) and DLS (right).
(C) Simultaneously recorded population activity from one animal in M2 and the DLS for the short (top) and long (bottom) interval. Each row represents the firing rate of one unit normalized by its maximum rate. Units were ordered by their latency to maximum firing rate in each area independently (See also Figure S1). Temporal sparsity is reflected in the off-diagonal regions.
(D) The sequentiality index (SqI) was calculated from the entropy of the peak response times (PE) across all units multiplied by the temporal sparsity (TS).
(E) The SqI in DLS was significantly higher than in M2 for both time intervals (n = 8 mice; two-sided paired t-test, t7 = 5.157, P = 0.001 and t7 = 5.855, P = 0.0006 for the short and long intervals, respectively).
(F) The temporal sparsity in DLS was significantly higher than that in M2 for both time intervals (n = 8 mice; two-sided paired t test, t7 = 4.486, P = 0.003 and t7 = 5.299, P = 0.001 for the short and long interval, respectively).
(G) The peak entropy in DLS was slightly higher than that in M2 for the short interval but not significant different for the long interval.(n = 8 mice; two-sided paired t test, t7 = 2.780, P = 0.027 and t7 = 0.107, P = 0.918 for the short and long interval, respectively).
Given that both areas encoded time but exhibited significant differences in neural dynamics, a critical question is how the neural dynamics observed during the short and long delay trials are related. Specifically, whether the response profile scaled from the short to the long delay trials, or if neurons had the same absolute temporal profile in response to both cues (Murakami et al., 2014; Mello et al., 2015; Wang et al., 2018). To address this question we first examined how well a decoder trained on the short trials, could predict either absolute time (from 0 to 3 s) or scaled (normalized) time during long trials. While cross-performance was significantly worse under both conditions, the scaled condition was significantly better than the absolute (Figure S1C). Furthermore, cross-sorted neurograms suggested significant spatial differences during short and long delays, albeit with some shared early sensory and late motor responses (Figure S1F–G). We next developed an absolute-scaling index (ASI; Figure S2) to quantify if each unit’s activity during both cues is more consistent with an absolute (ASI = 1) or scaling (ASI = 0) property. While a sizable population of cells scaled their responses within the cue-reward interval, other units exhibited a similar temporal profile in response to both cues. The mean ASI, however, was not significantly different between M2 and DLS, suggesting a comparable mixture of temporally scaled and non-scaled response types in both areas.
DLS dynamics provides a better code to read out time
Experimental and computational studies have suggested that sequential dynamics observed in numerous brain areas underlies timing (Hahnloser et al., 2002; Buonomano, 2005; Long and Fee, 2008; Pastalkova et al., 2008; Kraus et al., 2013; Rajan et al., 2016; Murray and Escola, 2017). However, the potential computational benefit of using neural sequences over other dynamical regimes to encode time has not been addressed. We hypothesized that neural sequences provide a flexible dynamical regime that can be easily read out by downstream areas utilizing biologically plausible learning rules. First, in contrast to the sophisticated machine learning approaches that can perform optimal decoding, biological networks likely rely on simple associative learning rules such as STDP and LTP to decode time. Second, since the projecting neurons of any given area are generally all excitatory or inhibitory, any set of first-order downstream units should at first pass decode time using a complement of positive (or negative) weights.
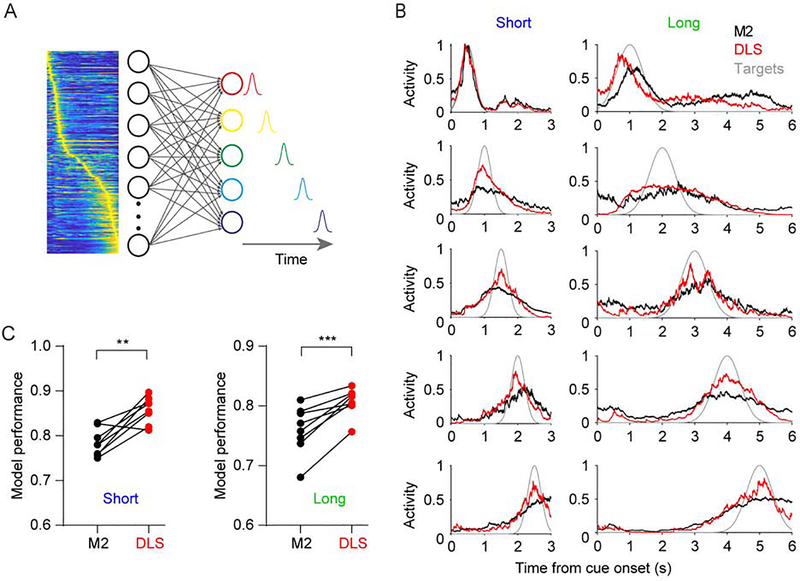
To test this hypothesis we first examined the ability of hypothetical downstream units to read out time from the experimentally observed dynamics of M2 and DLS. Based on the dynamics in M2 and DLS five output units were trained to produce five delays, while only allowing non-negative weights onto the output units (Figure 3A). Consistent with the higher SqI in DLS, outputs trained on DLS dynamics during both the short and long intervals were significantly better at producing the target delays, with performance quantified as the correlation coefficient between the generated and target trajectories. (Figures 3B and 3C). These regional differences were robust to a range of upper weight values and target trajectory numbers used in the model (Figure S3). Importantly, the enhanced DLS performance was not due to higher activity in this area, and these findings remained unchanged when the analysis was confined to significantly responsive cells (Figure S4).
Figure 3. DLS dynamics with higher sequentiality are better at generating timed responses.
(A) Illustration of the model used to quantify how well downstream networks can read out time from different dynamical regimes. The five outputs units were trained to generate responses at five different evenly spaced time intervals using a non-negative weight constrained least square model.
(B) Responses of the five output units trained to decode the experimentally observed dynamics in M2 (black) or DLS (red). The model was run separately for the short (left) and long (right) interval. Target functions are shown in grey.
(C) Performance of the artificial downstream network as measured by the average correlation coefficient between the generated and target trajectories was significantly higher in DLS for both time intervals (n = 8 mice; two-sided paired t test, t7 = 4.565, P = 0.0026 and t7 = 6.027, P = 0.0005 for the short and long interval, respectively) (See also Figures S2–S4).
Neural sequences provide a set of near orthogonal basis functions to read out time
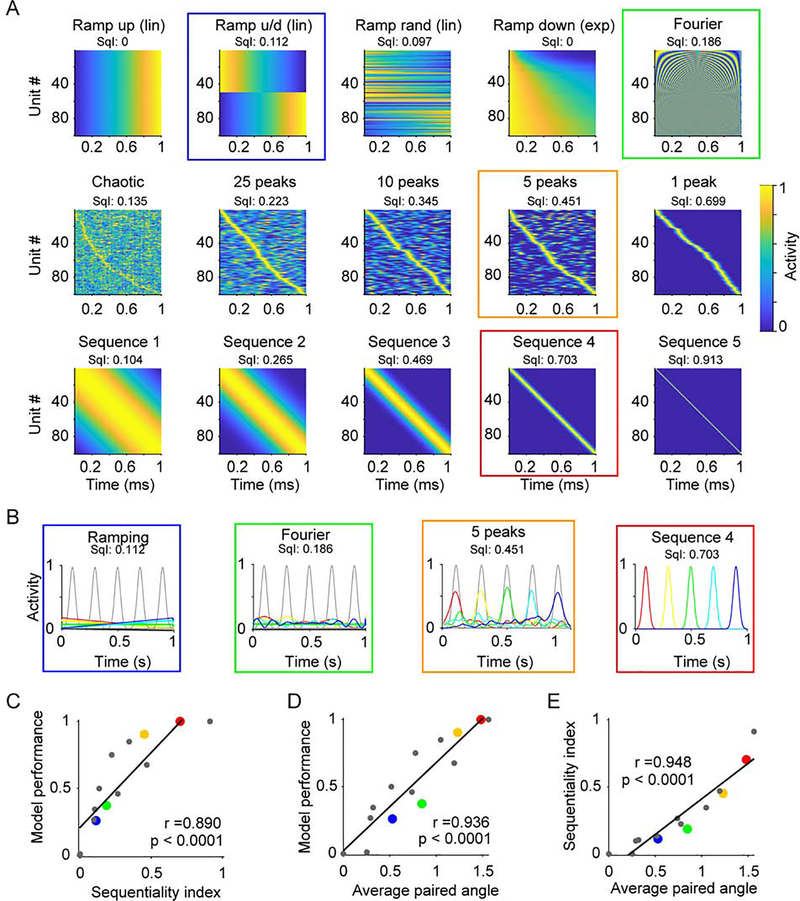
To further understand why dynamics with higher sequentiality (i.e., DLS compared to M2) provided the downstream units a better regime to read out time, we contrasted a wide range of prototypical experimentally observed regimes, includes families of neural sequences (Hahnloser et al., 2002; Pastalkova et al., 2008; Kraus et al., 2013), ramps (Leon and Shadlen, 2003), exponential decaying activity (Shankar and Howard, 2012; Liu et al., 2019), and complex spatiotemporal dynamics (Carnevale et al., 2015; Bakhurin et al., 2017), as well as a high-dimensional periodic basis function. Together, these prototypical regimes exhibited a wide spectrum of sequentiality as measured by their SqI (Figure 4A). Each regime was used as the input to a set of downstream units that were trained to produce five delays using the same constraints as those in Figure 3. Compared to other patterns, e.g., ramping, periodic, or complex (multi-peaked) patterns, sequential trajectories provided the best performance (Figure 4B). Quantification of this effect revealed a positive correlation of performance with the SqI of different regimes (Figure 4C). This result can be understood in terms of the set of basis functions that each dynamical regime provides for downstream neurons to extract temporal information through a weighted linear combination of each unit. In the extreme, neural sequences offer a quasi-orthogonal set of basis functions to read out time. And importantly, in contrast to other near orthogonal basis sets, sequences can be read out using only non-negative weights. Orthogonal bases provide a larger domain from which to generate a target vector. Indeed, the model performance and SqI positively correlated with the average paired angle between all the units in a given dynamical regime (Figure 4D,E).
Figure 4. Neural sequences provide a set of near orthogonal basis functions to read out time.
(A) Prototypical examples of different dynamical regimes that can encode time. Examples are based on a number of experimentally observed dynamical regimes, e.g. linear (lin) or exponential (exp) ramping, and a high-dimensional periodic regime (“Fourier”). The corresponding sequentiality index (SqI) is displayed on top. Colored squares emphasize the dynamics used in panels B and corresponding dots in panel C, D and E.
(B) The trajectories (color coded as in Figure 3A) generated by 4 activity patterns from (A) denoted by the corresponding color coded square, and the target functions (grey).
(C) The SqI is significantly correlated with the performance of the output units (n = 15 simulated data sets, Pearson correlation coefficient r = 0.890, P < 0.0001). Black line represents the best linear fit.
(D) Average of the angles between all xi pairs correlates with model performance (correlation coefficient r = 0.936, P < 0.0001). Note that for the sequence 4 dynamics outlined in red (corresponding to the red dots in panels C, and E) the average angle is 1.47 in radians, corresponding to a near orthogonal 84 degrees.
DISCUSSION
Previous studies have reported neural codes for elapsed time in both M2 and DLS (Merchant et al., 2013b; Crowe et al., 2014; Carnevale et al., 2015; Gouvea et al., 2015; Mello et al., 2015; Emmons et al., 2017). Consistent with these previous results we observed a distributed code for elapsed time in both areas during a two-interval timing task. Specifically, using traditional decoders elapsed time was decoded equally well in M2 and DLS on a trial-by-trial basis. Interestingly however, dynamical regimes in DLS and M2 exhibited different signatures: the dynamics in DLS was more sequential, and provided a better set of basis functions for downstream areas to read out time in a biologically plausible manner. Importantly, M2 sends a strong excitatory projection to the DLS which plays a role in driving striatal activity during reward-conditioned behavior (Lee et al., 2019), raising the possibility that the mutually inhibitory circuit motifs of the striatum are optimizing cortical dynamics for downstream areas to read out time (Burke et al., 2017).
We propose that neural sequences can provide a quasi-orthogonal set of basis functions for downstream areas to read out time in a biologically plausible manner. The biological constraints include the fact that the projecting neurons in a given area are either excitatory (e.g., cortex) or inhibitory (e.g., striatum), thus first-order downstream neurons generally receive only excitatory or inhibitory weights from a given area. Additionally, in contrast to the machine learning and Bayesian decoder methods often used to demonstrate the encoding of elapsed time, downstream biological networks are likely to rely on simple associative forms of synaptic plasticity. These constraints can severely limit the ability of downstream neurons to effectively read out time. Here we showed that when biological constraints are taken into account, neural sequences provide a superior dynamical regime to encode time, compared to ramps and complex spatiotemporal patterns. But we stress, that many of the dynamic regimes considered (Figure 4), including linear and exponential ramping, can drive complex temporal patterns when using more sophisticated decoding schemes, or by allowing positive and negative weights (Shankar and Howard, 2012; Liu et al., 2019). More generally, however, the quasi-orthogonality of neural sequences is advantageous because in the extreme it resembles the coordinate system of neuron space (e.g., neuron’s activity vector over time is composed of 0s and a single 1). And this standard coordinate system provides the only set of orthogonal basis functions that does not require negative values. Indeed, the advantage of sparse neural sequences has been previously noted in a bird song model showing that increased temporal sparsity decreases learning time (Fiete et al., 2004).
These results help clarify a large body of diverse experimental data regarding temporal processing, and raise the hypothesis that some of the local computations performed by different areas might be best understood not simply as encoding time, but optimizing the code. Specifically, a large body of data has suggested a pivotal role for the striatum in timing in the range of seconds, and that time is encoded in dynamically changing spatiotemporal patterns of neural activity (Buhusi and Meck, 2005; Merchant et al., 2013a; Paton and Buonomano, 2018). Yet it remains unknown whether the striatum should be considered a timer per se—in the sense that it actively generates the appropriate dynamics, or is simply “propagating” the spatiotemporal patterns of input it receives. Our results are consistent with the suggestion that while the DLS might not generate the neural dynamics that underlies timing, it may optimize the dynamics by creating neural sequences that are ideally suited for downstream areas to generate timed patterns.
STAR METHODS:
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Dean V. Buonomano (dbuono@ucla.edu).
Materials Availability
This study did not generate new unique reagents.
Data and Code Availability
The pre-processed data and codes to analyze the pre-processed data are available at http://dx.doi.org/10.17632/mz357z8pwx.1. Codes for the ASI and SqI measure used in this study can also be found at: https://github.com/ShanglinZhou/M2_DLS_2Intervals. The raw data are available on reasonable request.
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Male C57Bl/6J mice (n = 8, 14 – 20 weeks old at the time of recording (The Jackson Laboratory #000664) were used in this study. Animals were kept on a 12-h light cycle, and group housed until the first stereotaxic surgery. All procedures were approved by the University of California, Los Angeles Chancellor’s Animal Research Committee.
METHOD DETAILS
Surgical procedures.
Animals underwent an initial head bar implantation surgery under isoflurane anesthesia in a stereotaxic apparatus (model 1900; Kopf Instruments) to fix stainless steel head restraint bars bilaterally on the skull with dental cement. Animals recovered for at least one week before starting behavioral training. Animals underwent a second surgery under isoflurane anesthesia on the day prior to recording, to make craniotomies for silicon microprobe insertion in M2 and DLS. An additional craniotomy was made over the posterior cerebellum for placement of an electrical reference wire. Animals were individually housed after surgery. All behavioral training and recording sessions were performed in awake, head-restrained animals.
Two-interval timing task.
Mice were food restricted to maintain their weight at approximately 90% of their baseline level and given water ad libitum. During daily training sessions, animals were mounted on the head bar restraint bracket and stood on a fixed polystyrene ball. Mice were initially habituated to head fixation and trained to consume a liquid reward (5 μL, 10% sweetened condensed milk). The reward was delivered from a tube positioned between an infrared lick meter (Island Motion) by actuation of an audible solenoid valve (Neptune Research). In these habituation sessions, animals were given a total of 80 reward stimuli with intertrial interval (ITI) randomly sampled from a uniform distribution of 20 – 30 s, and were exposed to a constant stream of pure air through a tube positioned in front of the nose (2 L/min air flow). When animals reached a criterion of consuming at least 90% of the delivered rewards for two consecutive days, they were presented with olfactory cues (isoamyl acetate or citral corresponding to short or long intervals in a counterbalanced manner). Olfactory cues with a duration of 0.2 s were made by bubbling air (0.15 L/min) through aromatic liquids diluted 1:10 in mineral oil (Sigma-Aldrich), and merging this product with the 2 L/min stream of pure air. Initially, cues were followed by reward delivery after 3 s or 6 s for short or long interval irrespective of the animal’s licking response. The short and long interval trials were presented in random order (80 – 100 trials per interval, with ITIs randomly sampled from a uniform distribution of 20 – 30 s). After training animals on both time intervals using unconditional reward delivery for at least one week (one session per day), we introduced the final stage of training, which included acceptance windows to further differentiate their licking responses. These windows were defined as 1.5 – 3 s and 3 – 6 s after cue onset for the short and long intervals, respectively. Reward was omitted if mice licked before these time windows; otherwise, reward was delivered regardless of whether or not they licked. When the mean anticipatory lick onset times exceeded 1.5 s for the short interval and 3 s for the long interval for at least two consecutive days, animals underwent a surgical procedure in preparation for recording on the following day. On average animals went through 13.25 ± 1.25 days of training with two cues before recording. On the recording session, animals received 100 – 240 trials per interval in random order with ITIs randomly sampled from a uniform distribution of 20 – 30 s. Analysis of neural activity only used trials containing anticipatory licking (both rewarded and unrewarded trials). Furthermore, to minimize potential confounds from spontaneous licking, we excluded trials in which licking occurred within a one second period before cue onset.
Electrophysiological recordings.
Simultaneous recordings were performed on the right hemisphere in M2 (2.5 mm anterior, 0.55 to 1.75 mm lateral, 0.5 mm ventral relative to bregma) and DLS (1 mm anterior, 1.9 to 2.5 mm lateral, 3.5 mm ventral relative to bregma), using silicon microprobes containing 256 electrodes targeting each area (type 256A in M2 and 256ANS in DLS) (Yang et al., 2020). The placement of the silicon microprobes was confirmed histologically at the end of each experiment by coating the prongs with a fluorescent dye (Di-D; Thermo Fisher) before implantation. Spike sorting was carried out using Kilosort software (Pachitariu et al., 2016). If not specified, all units were included in the analysis. Each unit’s firing rate per trial was estimated by convolving the spike train with a decaying exponential kernel (time constant = 0.1 s). Firing rates were then normalized to the range of 0 and 1. To determine whether a cell was significantly responsive to a particular interval, the firing rate was binned in steps of 0.1 s from the time of cue onset until the end of the interval (3 s for short, and 6 s for long). A unit was classified as being responsive to a given interval, if there were at least two consecutive bins showing a significant difference relative to baseline (two sample unpaired t test, P < 0.05).
Absolute scaling index.
We developed an absolute scaling index (ASI) to quantify whether the temporal profiles of the neuronal firing rates dilate from the short to long interval (temporal scaling), or remain unchanged (absolute timing). As illustrated in Figure S2A, this index searches for the best transformation to match the response profile of the long interval (y(t)) to the short interval (x(t)), by concatenating an absolute portion of the long response (yabs(t)) with a temporally scaled portion of the long response (yscale(t’)). More specifically, we searched for a breakpoint τ to divide y(t) into an absolute and scaled segment, that best matches x(t), as measured by the Euclidean distance (Dist(τ)). In the case of absolute timing the best match will be when the entire short response is matched with the unscaled early part of the long response with τ = tmax, resulting in an ASI = 1—i.e. the first half of the long interval matches the entire short interval. In contrast, an ASI = 0, would correspond to a τ = 0, and the response profile of a neuron during the short and long interval match when plotted in normalized time. ASI is calculated through the following steps.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
τ spans all possible breakpoints from 0 to tmax (for the short interval). The segment before τ denotes the absolute period and the period after τ denotes the segment scaled by α = (2*tmax - τ)/(tmax - τ) for the long response. τmin corresponds to the breakpoint with the minimal Euclidian distance Dist(τ). In steps 3 and 4 the absolute and scaling weights are calculated between dynamics for short interval and time-warped dynamics for the long interval with Na:b being the number of time points between a and b, and absolute ratio AbsR(τmin) at τmin were calculated. The absolute temporal factor corresponds to τmin/tmax, and ASI was defined as the average of the absolute temporal factor and the AbsR(τmin). Only cells responsive to both the short and long intervals were used for the ASI analysis.
Decoding of elapsed time and lick onset.
To test how well the dynamics in M2 and DLS could decode the time elapsed from cue onset to the scheduled time of reward, we used a standard supervised decoder, specifically, a support vector machine (SVM) decoder as described in a previous study (Bakhurin et al., 2017). Specifically, decoding was performed with a one-to-one multiclass support vector machine (SVM) with a radial-basis function (RBF) kernel, and implemented using the LIBSVM library (Chang and Lin, 2011). Decoding was performed on a trial-by-trial basis. For each trial the average firing rate of each neuron was binned to widths of 0.1 s and 0.2 s for the short and long intervals, respectively, leading to a total of 30 bins for both intervals. Elapsed time was decoded from the population firing rates in each trial by requiring a classifier to label each rate vector at a given bin in the trial as coming from one of the 30 time bins. Leave-one-trial-out cross validation was used. By testing a given bin the corresponding predicted time bin was defined as the bin that produced the highest score of all 30 readout units. Performance was defined as the correlation coefficient between the correct and predicted time bin across all trials tested. To compare the performance for M2 and DLS, we equalized the number of units in each area by using the minimum number of units (M) of the two areas, and randomly selected M units from the area with larger population to train the SVM, and repeated this process 10 times. Final performance was defined as the average correlation coefficient across these 10 repetitions.
Lick onset time in each trial was also decoded as described previously (Figures S2C and S2D) (Bakhurin et al., 2017). Dynamics between 0.4 s before cue onset and 0.4 s after the maximum lick onset in a session was binned with steps of 0.1 s for both the short and long interval. The labels of each binned population rate vectors at the time, immediately before, and immediately after lick onset were assigned the value of 1; all other vectors were labeled as 0. The SVM’s output was represented by a single readout that scores how closely each population vector in the test population trajectory predicts lick onset. The predicted lick onset bin was the one in which the readout was at its highest value. Testing was performed with a leave-one-trial-out strategy, and the performance was defined as the root mean square error (RMSE) between the correct lick onset and the predicted onsets across all tested trials. The number of units was again controlled between M2 and DLS.
Sequentiality Index.
To quantify the degree to which different dynamical regimes could be described as a sequence we developed a novel measure of sequentiality index (SqI). Our SqI was inspired by a previously described measure (Orhan and Ma, 2019), but relies on temporal sparsity rather than the ridge-to-background ratio, and is bounded between 0 and 1 (Figures 2 and 4). As illustrated in Figure 2D, this normalized sequentiality index was calculated as:
where PE (peak entropy) captures the entropy of the distribution of peak times across the entire population. M is the number of bins for estimating the peak time distribution (30 and 60 for neural dynamics in the short and long intervals in Figure 2, and 10 for the simulated dynamics in Figure 4), and pj is the number of units that peak in time bin j divided by the total number of units. TS (temporal sparsity) provides a measure of entropy of the distribution of normalized activity in any given moment. TS is maximum when only one unit accounts for all the activity in each time bin t. represents the activity of unit i in time bin t, normalized by the sum of the activity of all neurons at time t; <>t denotes the time average; and N is the number of units. The SqI approaches 1 when the peak times of each neuron homogeneously tile the entire duration and one neuron is active at every moment in time with the temporal fields being non-overlapping. Note that SqI is sensitive to the width of the temporal fields of the neurons, and this is an important feature because the extreme sequences with very broad temporal field converge towards a regime with a fixed-point attractor. We stress that because sequentiality represents a fairly complex feature of dynamics, that no single measure of sequentiality is perfect. The measure defined here seems effective at capturing the biological dynamical regimes studied here. However, it is important to note that this measure can break down under some artificial manipulations (e.g., if one were to shuffle the time bins of a sequential neural trajectory).
Non-negative weight constrained least square fitting model.
Average dynamics in M2 and DLS, and prototypical dynamical regimes, were used as inputs to five output units (Figures 3 and 4).The five target intervals were represented as Gaussian functions with evenly spaced means over a total duration T of 3 or 6 s, representing the short and long intervals for the M2 and DLS analyses respectively and 1 s for prototypical dynamical regimes. To account for Weber’s law the width (w) of the Gaussian functions was 0.2 s and 0.4 s for the short and long intervals for the M2 and DLS analyses, and 0.025 s for the prototypical dynamics.
To “train” the output units, and ensure that all output weights were non-negative, we used a least square fitting function lsqcurvefit from MATLAB (MathWorks) with weight constrained between 0 and 10 (unless otherwise specified).
Generation of artificial dynamics.
To study the relationship between sequentiality index and the performance of non-negative weight constrained least square fitting model, we artificially generated various prototypical dynamics regimes composed of 100 units (Figure 4). In these prototypical regimes time spanned 0 to 1 s with steps dt of 0.001 s.
Ramp up (linear).
The activity of unit i xi(t) was defined as:
where U(0,1) was a value sampled from a uniform distribution between 0 and 1 and max (yi(t)) was the maximum value of the yi. In effect all units ramped from 0 to 1 with the same slope with a small amount of noise.
Ramp up/down (linear).
As above, but 50 units ramped up and 50 units ramped down linearly.
Ramp random.
Ramping dynamics of each unit started and ended at a random level chosen between 0 and 1:
where a and b were randomly sampled from a uniform distribution U(0,1).
Exponential ramping down.
The activity of unit i xi(t) was defined as:
with τi randomly sampled from a uniform distribution U(0.1, 2) and U(0,1) being a uniform distribution between 0 and 1.
Fourier-like.
A Series of sine waves with progressively increasing frequencies was defined as follows (note all values are positive):
Chaotic.
Dynamics for each unit received independent Gaussian noise, which was described as:
where σ (0, 1) is a random number sampled from a Gaussian distribution with 0 mean and 1 standard variance, and time constant τ = 0.02 s.
Sequences with different temporal sparsity.
Sequential dynamics with different temporal sparsity were defined as follows:
where w took the values of 0.005, 0.025, 0.1, 0.25, or 0.5 s.
Multiple peaks.
Complex multipeaked dynamics was generated similarly to prototypical sequence dynamics, but instead of a single Gaussian each unit was defined as the sum of p Gaussian functions (p = 1, 5, 10 and 25 respectively), each with a mean chosen from a uniform distribution U(0,1) and a width of 0.025 s.
QUANTIFICATION AND STATISTICAL ANALYSIS
Statistical analyses were carried out with standard functions in MATLAB (MathWorks) and Prism (GraphPad Software). Data collection and analysis were not performed with blinding to the conditions of the experiments. The sample size, type of test and P values are indicated in the figure legends. Data distribution was assumed to be normal, but this was not formally tested. The P value of Pearson correlations was calculated with the MATLAB corrcoef function. All data and error bars represent the mean and SEM. In all figures, the convention is *: P < 0.05, **: P < 0.01, ***: P < 0.0001, ****: P < 0.0001.
Supplementary Material
KEY RESOURCES TABLE.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited Data | ||
| Preprocessed data | This paper | http://dx.doi.org/10.17632/mz357z8pwx.1 |
| Experimental Models: Organisms/Strains | ||
| Mouse: C57BL/6J | https://www.jax.org/strain/000664 | RRID:IMSR_JAX:000664 |
| Software and Algorithms | ||
| MATLAB | MathWorks | N/A |
| Prism | GraphPad Software | N/A |
| Kilosort | Pachitariu et al. (2016) | N/A |
| LIBSVM | Chang and Lin (2011) | https://www.csie.ntu.edu.tw/~cjlin/libsvm/ |
| Study specific analysis code | This paper | https://github.com/ShanglinZhou/M2_DLS_2Intervals |
HIGHLIGHTS.
Timing is critical to the brain’s ability to predict and prepare for future events.
During a two-interval task time was encoded in both premotor cortex and striatum.
Dynamics in the striatum, however, was more sequential.
Striatal sequences provide an ideal set of basis functions to read out time.
ACKNOWLEDGEMENTS
We thank Konstantin Bakhurin, Kwang Lee, and Vishwa Goudar for technical assistance and helpful discussions. D.V.B. and S.C.M. were supported by NIH grant NS100050. S.C.M. was supported by NIH grants NS096994, DA042739, DA005010, and NSF NeuroNex Award 1707408. S.Z. was supported by a Marion Bowen Postdoctoral Grant.
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Bakhurin KI, Goudar V, Shobe JL, Claar LD, Buonomano DV, and Masmanidis SC (2017). Differential Encoding of Time by Prefrontal and Striatal Network Dynamics. The Journal of Neuroscience 37, 854–870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buhusi CV, and Meck WH (2005). What makes us tick? Functional and neural mechanisms of interval timing. Nat Rev Neurosci 6, 755–765. [DOI] [PubMed] [Google Scholar]
- Buonomano DV (2005). A learning rule for the emergence of stable dynamics and timing in recurrent networks. J Neurophysiol 94, 2275–2283. [DOI] [PubMed] [Google Scholar]
- Burke DA, Rotstein HG, and Alvarez VA (2017). Striatal Local Circuitry: A New Framework for Lateral Inhibition. Neuron 96, 267–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carnevale F, de Lafuente V, Romo R, Barak O, and Parga N (2015). Dynamic Control of Response Criterion in Premotor Cortex during Perceptual Detection under Temporal Uncertainty. Neuron 86, 1067–1077. [DOI] [PubMed] [Google Scholar]
- Chang CC, and Lin CJ (2011). LIBSVM: A Library for Support Vector Machines. Acm T Intel Syst Tec 2. [Google Scholar]
- Crowe DA, Zarco W, Bartolo R, and Merchant H (2014). Dynamic Representation of the Temporal and Sequential Structure of Rhythmic Movements in the Primate Medial Premotor Cortex. The Journal of Neuroscience 34, 11972–11983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emmons EB, De Corte BJ, Kim Y, Parker KL, Matell MS, and Narayanan NS (2017). Rodent Medial Frontal Control of Temporal Processing in the Dorsomedial Striatum. The Journal of Neuroscience 37, 8718–8733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiete IR, Hahnloser RHR, Fee MS, and Seung HS (2004). Temporal Sparseness of the Premotor Drive Is Important for Rapid Learning in a Neural Network Model of Birdsong. Journal of Neurophysiology 92, 2274–2282. [DOI] [PubMed] [Google Scholar]
- Gouvea TS, Monteiro T, Motiwala A, Soares S, Machens C, and Paton JJ (2015). Striatal dynamics explain duration judgments. Elife 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hahnloser RHR, Kozhevnikov AA, and Fee MS (2002). An ultra-sparse code underlies the generation of neural sequence in a songbird. Nature 419, 65–70. [DOI] [PubMed] [Google Scholar]
- Hasselmo ME (2008). Grid cell mechanisms and function: Contributions of entorhinal persistent spiking and phase resetting. Hippocampus 18, 1213–1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heys JG, and Dombeck DA (2018). Evidence for a subcircuit in medial entorhinal cortex representing elapsed time during immobility. Nature Neuroscience 21, 1574–1582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivry RB, and Spencer RMC (2004). The neural representation of time. Curr Opinion Neurobiol 14, 225–232. [DOI] [PubMed] [Google Scholar]
- Kraus BJ, Brandon MP, Robinson RJ 2nd, Connerney MA, Hasselmo ME, and Eichenbaum H (2015). During Running in Place, Grid Cells Integrate Elapsed Time and Distance Run. Neuron 88, 578–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraus BJ, Robinson RJ, White JA, Eichenbaum H, and Hasselmo ME (2013). Hippocampal “Time Cells”: Time versus Path Integration. Neuron 78, 1090–1101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K, Bakhurin KI, Claar LD, Holley SM, Chong NC, Cepeda C, Levine MS, and Masmanidis SC (2019). Gain Modulation by Corticostriatal and Thalamostriatal Input Signals during Reward-Conditioned Behavior. Cell reports 29, 2438–2449 e2434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leon MI, and Shadlen MN (2003). Representation of time by neurons in the posterior parietal cortex of the macaque. Neuron 38, 317–327. [DOI] [PubMed] [Google Scholar]
- Liu Y, Tiganj Z, Hasselmo ME, and Howard MW (2019). A neural microcircuit model for a scalable scale-invariant representation of time. Hippocampus 29, 260–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long MA, and Fee MS (2008). Using temperature to analyse temporal dynamics in the songbird motor pathway. Nature 456, 189–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long MA, Jin DZ, and Fee MS (2010). Support for a synaptic chain model of neuronal sequence generation. Nature 468, 394–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacDonald Christopher J., Lepage Kyle Q., Eden Uri T., and Eichenbaum H (2011). Hippocampal “Time Cells” Bridge the Gap in Memory for Discontiguous Events. Neuron 71, 737–749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mello GBM, Soares S, and Paton JJ (2015). A scalable population code for time in the striatum. Curr Biol 9, 1113–1122. [DOI] [PubMed] [Google Scholar]
- Merchant H, Harrington DL, and Meck WH (2013a). Neural Basis of the Perception and Estimation of Time. Annual Review of Neuroscience 36, 313–336. [DOI] [PubMed] [Google Scholar]
- Merchant H, Pérez O, Zarco W, and Gámez J (2013b). Interval Tuning in the Primate Medial Premotor Cortex as a General Timing Mechanism. The Journal of Neuroscience 33, 9082–9096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murakami M, Vicente MI, Costa GM, and Mainen ZF (2014). Neural antecedents of self-initiated actions in secondary motor cortex. Nat Neurosci 17, 1574–1582. [DOI] [PubMed] [Google Scholar]
- Murray JM, and Escola GS (2017). Learning multiple variable-speed sequences in striatum via cortical tutoring. Elife 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orhan AE, and Ma WJ (2019). A diverse range of factors affect the nature of neural representations underlying short-term memory. Nature Neuroscience 22, 275–283. [DOI] [PubMed] [Google Scholar]
- Pachitariu M, Steinmetz N, Kadir S, Carandini M, and Kenneth D. H (2016). Kilosort: realtime spike-sorting for extracellular electrophysiology with hundreds of channels. bioRxiv. [Google Scholar]
- Pastalkova E, Itskov V, Amarasingham A, and Buzsaki G (2008). Internally Generated Cell Assembly Sequences in the Rat Hippocampus. Science 321, 1322–1327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paton JJ, and Buonomano DV (2018). The Neural Basis of Timing: Distributed Mechanisms for Diverse Functions. Neuron 98, 687–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajan K, Harvey Christopher D., and Tank David W. (2016). Recurrent Network Models of Sequence Generation and Memory. Neuron. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shankar KH, and Howard MW (2012). A Scale-Invariant Internal Representation of Time. Neural Computation 24, 134–193. [DOI] [PubMed] [Google Scholar]
- Shepherd GM (1998). The synaptic organization of the brain., Vol Fourth Edition (New York: Oxford University; ). [Google Scholar]
- Stokes MG, Kusunoki M, Sigala N, Nili H, Gaffan D, and Duncan J (2013). Dynamic Coding for Cognitive Control in Prefrontal Cortex. Neuron 78, 364–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsao A, Sugar J, Lu L, Wang C, Knierim JJ, Moser M-B, and Moser EI (2018). Integrating time from experience in the lateral entorhinal cortex. Nature. [DOI] [PubMed] [Google Scholar]
- van der Meer MA, and Redish AD (2011). Theta phase precession in rat ventral striatum links place and reward information. J Neurosci 31, 2843–2854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Narain D, Hosseini EA, and Jazayeri M (2018). Flexible timing by temporal scaling of cortical responses. Nat Neurosci 21, 102–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang L, Lee K, Villagracia J, and Masmanidis SC (2020). Open source silicon microprobes for high throughput neural recording. J Neural Eng 17, 016036. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The pre-processed data and codes to analyze the pre-processed data are available at http://dx.doi.org/10.17632/mz357z8pwx.1. Codes for the ASI and SqI measure used in this study can also be found at: https://github.com/ShanglinZhou/M2_DLS_2Intervals. The raw data are available on reasonable request.