A model for COVID-19 with isolation, quarantine and testing as control measures

Abstract

In this article we propose a compartmental model for the dynamics of Coronavirus Disease 2019 (COVID-19). We take into account the presence of asymptomatic infections and the main policies that have been adopted so far to contain the epidemic: social distancing, isolation of a portion of the population, quarantine for confirmed cases and testing. We refer to quarantine as strict isolation, and it is applied to confirmed infected cases.

In the proposed model, the proportion of people in isolation, the level of contact reduction and the testing rate are control parameters that can vary in time, representing policies that evolve in different stages. We obtain an explicit expression for the basic reproduction number ${\mathcal{R}}_0$ in terms of the parameters of the disease and of the control policies. In this way we can quantify the effect that isolation and testing have in the evolution of the epidemic. We present a series of simulations to illustrate different realistic scenarios. From the expression of ${\mathcal{R}}_0$ and the simulations we conclude that isolation (social distancing) and testing among asymptomatic cases are fundamental actions to control the epidemic, and the stricter these measures are and the sooner they are implemented, the more effective they are in flattening the curve of infections. Additionally, we show that people that remain in isolation significantly reduce their probability of contagion, so risk groups should be recommended to maintain a low contact rate during the course of the epidemic.

1. Introduction

1.1. Historical overview

In late December 2019, several cases of an unknown pneumonia were identified in the city of Wuhan, Hubei province, China (The 2019-nCoV Outbreak Joint Field Epidemiology Investigation Team and Li, 2020). Doctors at first conjectured that they could be severe acute respiratory syndrome (SARS) cases (BBC News, 2020), mostly related to the Huanan Seafood Wholesale Market. In the beginning of January 2020 Chinese officials ruled out the hypothesis that the cases were of SARS (Al Jazeera, 2020), and a few days later the cause was identified to be a new coronavirus that was named SARS-CoV-2. The name given to the infectious disease caused by SARS-CoV-2 is COVID-19.

The first death due to COVID-19 was reported on 9 January and it was a 61-year-old man in Wuhan (The New York Times, 2020). On January 22 the Chinese authorities announced the quarantine of greater Wuhan. Starting from mid January, infected cases were reported in Thailand, Japan, Republic of Korea, and other provinces in China (The 2019-nCoV Outbreak Joint Field Epidemiology Investigation Team and Li, 2020), and from that moment the virus rapidly spreads across many Asian countries, reached Europe and North America. On February 28, with more than 80.000 confirmed cases and nearly 3.000 deaths globally, WHO increased the assessment of the risk of spread and risk of impact of COVID-19 to very high at the global level (World Health Organization, 2020a). Following a steep increase in the number of cases and deaths, in March several nations across the five continents closed their borders, declared forced isolation for the whole population except for essential workers and/or imposed strict measures of social distancing (World Health Organization, 2020b). Detailed information on the actions taken by each country can be found in the report (Hale et al., 2020). In the meantime, on March 11, WHO declared that COVID-19 was characterized as a pandemic (World Health Organization, 2020c). At that time WHO recommended, apart from social distancing measures, that it was essential to test intensively (World Health Organization, 2020e). The indications were to test every suspected case, to isolate till recovery any positive individual, and to track and test all contacts in the past two days of new confirmed cases.

The most common symptoms of COVID-19 are fever, cough and shortness of breath. Most of the cases result in mild or no symptoms, but others progress to viral pneumonia and multi-organ failure. It is yet difficult to estimate the mortality of this virus, since on one side it depends on early detection and appropriate treatment, and on the other it can only be calculated if the real number of infected people is known. However, there is enough evidence to assure that a significant portion of the infections is asymptomatic (Lavezzo et al., 2020, Mizumoto et al., 2020, Nishiura et al., 2020), which makes it difficult to detect them. As of March 2020, WHO estimated a death rate of 3,4% worldwide (World Health Organization, 2020f), but this rate has decayed in the course of the pandemic reaching the global value of 2,2% up to December 2020 (Worldometer, 2020b), and other larger or smaller values depending on the country (John Hopkins University & Medicine, 2020).

1.2. Mathematical modeling

In this article we propose a compartmental model for the dynamics of COVID-19. We take into account the presence of asymptomatic infections, and also the main policies that have been adopted by several countries in the past months to fight this disease, these being: isolation, quarantine and testing. We model isolation by separating the population in two groups: one composed by key-workers that keep working during the pandemic, and the other group consisting of people that are enforced/recommended to stay at home. Certainly, in the group of people that maintain a higher contact rate one can also include people that do not respect social distancing restrictions, that has lately shown to be significant in some countries. We refer to quarantine as strict isolation, and it is applied to confirmed infected cases. Testing is supposed to be applied to all symptomatic cases, and to a portion of the population selected using some of the criteria adopted by health organizations (see e.g. Public Health England, 2020, Centers for Disease Control and Prevention, 2020a). The idea to analyze the quantitative effects of non-pharmaceutical interventions, such as isolation and social distancing, on the evolution of the epidemic was inspired by the work (Ferguson et al., 2020).

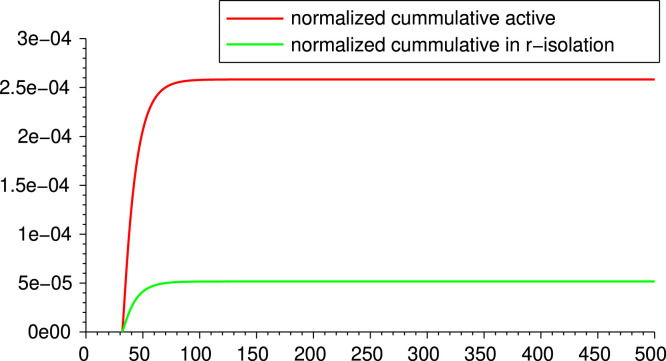
For the proposed model, we obtain an expression for the basic reproduction number ${\mathcal{R}}_0$ in terms of the parameters of the disease and of the control parameters. In this way we can quantify the effects that isolation and testing have on the epidemic. We exhibit a series of simulations to illustrate different realistic situations. We compare, in particular, different levels of isolation and testing. From the expression of ${\mathcal{R}}_0$ and the simulations, we conclude that isolation (social distancing) and testing among asymptomatic cases are fundamental actions to control the epidemic, and the stricter these measures are and the sooner they are implemented, the more effective they are in flattening the curve of infections. Additionally, we show that people that remain in isolation significantly reduce their probability of contagion (see Fig. 4 below), so risk groups should be recommended to maintain a low contact rate during the course of the epidemic.

Fig. 4.

Comparison of infections for active population and population in $r$-isolation from lockdown.

Several mathematical models for COVID-19 have been appearing since the beginning of the pandemic. At the time being, the flux of publications is very high, so it is difficult to keep track of everything that is being published. We next mention and describe some selected models that have common features with ours. Casella (2021) considered a simple model, with infected and reported infected compartments, and they assume that the transmission rate $\beta$ is a function of a control u, this is $\beta =\beta \left(u\right)$. They analyze feedback control strategies, where the control depends on the number of reported cases. Djidjou-Demasse et al. (2020) treated mild and severe cases, the latter having a reduced transmission rate since they are assumed to be in isolation. They use a time-dependent control $c$ for modeling the reduction of contacts for the whole population, and optimize with respect to this control. Also related to our model, Giordano et al. (2020) developed the SIDARTHE model that discriminates infected individuals depending on whether they were diagnosed and on the severity of their symptoms, putting isolation the diagnosed ones. Other models sharing some characteristic with ours have been developed in e.g. (Sarkar et al., 2020, Shi et al., 2020, Liu et al., 2020).

Previous works, preceding COVID-19 pandemic, had already considered quarantine, unreported cases and other features of the kind. For instance, (Feng et al., 2007) introduced a model with quarantined and hospitalized compartments, and Chowell et al. (2003) analyzed the effect of diagnosing and contact reduction. Other references in this direction are e.g. (Lipsitch et al., 2003, Castillo-Chavez et al., 2003). In contrast to the mentioned models, ours combines asymptomatic compartment, diagnose rate, quarantine and contact reduction.

The article is organized as follows. In Section 2 we introduce the model, and we discuss its structure. In Section 3 we show an expression of the basic reproduction number ${\mathcal{R}}_0$ in terms of the parameters and we propose an equivalent threshold. Estimation of realistic parameters and numerical simulations are given in Section 4, while Section 5 is devoted to the conclusions and a description of possible continuations of this research. Finally, in the Appendix we include the analytical computations of the expression of ${\mathcal{R}}_0$ and a sensitivity analysis with respect to the involved parameters.

2. The model description

We set up a model to describe the spread of the virus SARS-CoV-2 through a susceptible population. We build upon a SEIR model to obtain a more structured dynamics which also conveys the effects of the non-pharmaceutical intervention policies being adopted by several countries to face its outbreak.

First of all, we normalize to $1$ the total population of $N$ individuals, so that all the compartments (and their sub-compartments) introduced below represent the proportion of individuals of the total population in such compartment. We will assume the population remains constant over time, i.e., we neglect the natural birth and death rates. We start by splitting the population in the compartments listed in Table 1.

Table 1.

List of aggregated compartments.

Compartment	Description
$S$	Susceptible
$E$	Exposed
$I$	Infectious
$A$	Asymptomatic and infectious
$Q$	Infected in quarantine (including hospitalized)
$R$	Recovered

More specifically, the compartment $S$ collects all the individuals that are susceptible to the virus. Once an individual from $S$ gets exposed to the virus, moves to the compartment $E$. Let us point out that individuals in $E$, though already exposed to the virus, are not contagious yet. After a given latent time, an individual in $E$ becomes infectious, and thus is allocated to the compartment $I$. At this stage, after a suitable time, the individual may either remain infectious but asymptomatic (or with mild symptoms), in which case moves to the compartment $A$, or may show acute symptoms, thus being assigned to the compartment $Q$, after being tested and then quarantined. Finally, individuals in $A$ and $Q$ will eventually be removed from those compartments and will end up either in the compartment $R$ after a recovery time or dead.

We will assume that the fraction of asymptomatic individuals among all infected is given by a certain probability $\alpha \in (0,1)$. It is intuitive that the presence of a relevant portion of asymptomatic infectious individuals plays a major role in the spread of the epidemic, as observed in the current outbreak (Mizumoto et al., 2020, Nishiura et al., 2020). Indeed, an asymptomatic individual will maintain a high contact rate, and thus might infect more susceptible individuals with respect to an infectious individual with symptoms that is in quarantine. Additionally, it is worth mentioning that $\alpha$ also accounts for the fraction of under-reported cases.

In our model, we refer to $\beta$ as the effective contact rate and it is given by the product between the transmissibility $\nu$ (i.e., probability of infection given contact between a susceptible and infected individual), and the average rate of contact $c$ between susceptible and infected individuals. In Table 2, Table 3 we list all the parameters of the model and their description.

Table 2.

Parameters of COVID-19.

Par.	Description
$\tau$	Inverse of the latent time from exposure to infectiousness onset
$\sigma$	Inverse of the time from infectiousness onset to possible symptoms onset
$\theta$	Inverse of mean incubation time (i.e. ${\theta }^{-1}={\tau }^{-1}+{\sigma }^{-1}$)
$\alpha$	Proportion of asymptomatic (undetected) infections
${\gamma }_1$	Recovery rate for asymptomatic or mild symptomatic cases
${\gamma }_2$	Recovery rate for severe and critical cases
$\mu$	Mortality rate among confirmed cases
$\delta$	Probability of detection by testing in compartment $E$

Table 3.

Parameters of Public Policies interventions.

Par.	Description
$\beta \left(t\right)$	Transmission rate at time $t$ (proportional to contact rate)
$r\left(t\right)$	Reduction coefficient of transmission rate for people in isolation at time $t$
$\rho \left(t\right)$	Testing rate of people with mild or no symptoms at time $t$
$p\left(t\right)$	Proportion of the population in $r$-isolation

The model as described so far takes into account several characteristics of the pathogen and its spread in a susceptible population. We now want to add further structural features to the model in order to include the non-pharmaceutical interventions adopted by public policies to contain the epidemic. In particular, we assume the following conditions.

• (i)A part $p$ of the population is in isolation (either voluntarily, or as a result of public safety policies). The remaining $1-p$ of the population instead gathers all those so-called “key workers” (such as physicians and paramedicals, workers in logistics and distribution, food production, security, and others), that must continue with a regular activity, thus maintaining a large contact rate and being exposed to a higher risk of infection. We will generically refer to such $1-p$ part of population as the active population, as opposed to the population in isolation. In this group we can also include people that simply do not respect social distancing, and thus maintain a high contact rate. A situation like this has been observed in countries were monitoring was not strict and a significant percentage of the population did not respect isolation.
• (ii)The fraction $1-p$ of active population has an effective contact rate $\beta$, whereas the part $p$ of population in isolation has a contact rate reduced by a factor $r$, thus its compound transmission rate is $r\beta$. We will therefore refer to such portion of the population as in $r$-isolation. The factor $r$ takes into account the reduction in the contact rate of a person in isolation, this is, the considerably smaller cluster of contacts of a person in isolation compared to someone in the fraction $1-p$ of active population.
• (iii)A centralized controller (such as the national health system) may intervene on the system by testing a portion of the population to check for the infectious pathogen. We assume the testing kit to be reliable, that is, we neglect the possibility of false positive/negative (see Remark 2.3. 4. related to this matter). As a rule, then, an individual from the compartment $S$ will always test negative, an individual from $I$ or $A$ always positive, while an individual from $E$ will result positive with a probability $\delta \in [0,1]$. In this way, even though the individuals in $E$ are not contagious, we account for the possibility that they might result positive to the test, depending on the stage of development of the pathogen in that specific individual and to the efficacy of the testing kit.

Let us notice that, in general, the effective contact rate $\beta$ depends on a variety of factors, including the density of population in a given country/region (see Section 4.1 for further considerations). However, during a pandemic, even the effective contact rate of the individuals not in isolation may be reduced by increased awareness (for example, maintaining the social distancing), or by respecting stricter safety protocols and by availability of proper Personal Protection Equipment (PPE), including face shields, masks, gloves, soap, and so on.

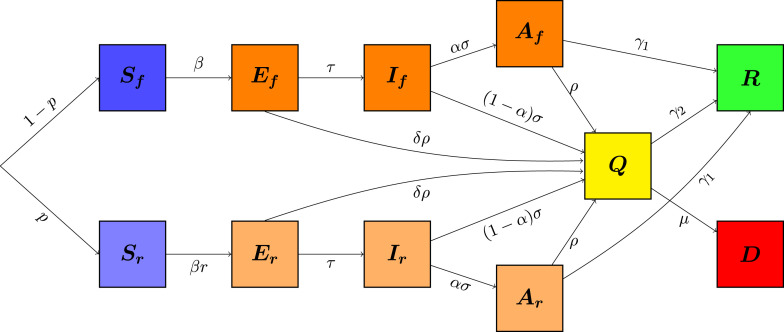
According to the above description, each compartment $S$, $E$, $I$ and $A$ is partitioned as follows: $S=S_f\cup S_r$, where $S_f$ are susceptible and active, while $S_r$ are susceptible and in $r$-isolation; $E=E_f\cup E_r$, where $E_f$ are exposed and active, while $E_r$ are exposed and in $r$-isolation; $I=I_f\cup I_r$, where $I_f$ are infectious and active, $I_r$ are infectious and in $r$-isolation; $A=A_f\cup A_r$, where $A_f$ are asymptomatic infectious and active, $A_r$ are asymptomatic infectious and in $r$-isolation. The compartment $Q$ collects all the infected individuals who have been tested positive, either after onset of severe symptoms, or because of a sample test among the population, according to the procedure described in (iii) of the above list. Let us stress that, among these compartments, only the individuals in $Q$ are aware of being infected, and thus contagious, hence they are either hospitalized or at home, but in both cases they follow strict procedures to reduce their contact rate to $0$. Finally, we will use the compartments $R$ for the recovered and immune individuals, and $D$ for the disease-induced deaths. Both these last compartments will be removed from the dynamics and will end up in the counter system (2). Moreover, we point out that the portion $p$ of the population in $r$-isolation is predetermined at the initial time of the evolution, reflecting the public policy in place in that specific period of time. Of course, such fraction $p$ may be updated at a later time, accordingly to newer (stricter or looser) public policies.

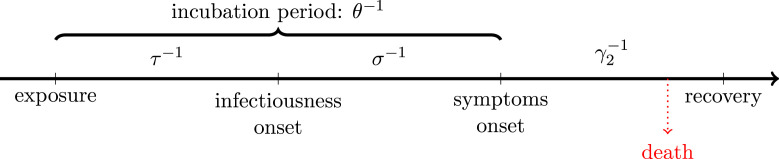
The first set of constants, related to the pathogen itself (assuming no mutation occurs in the time of epidemic, or if so, the mutation does not affect such parameters of the virus) and its induced disease, are collected in Table 2. A graphical representation of the course of the disease for symptomatic carriers can be seen in Fig. 1.

Fig. 1.

Disease timeline for symptomatic cases.

The second set of parameters is related to public policies, and consists of the parameters in Table 3. Let us recall at this point that $\beta$ varies in each territory, depending mainly on population density and behavior. These constants may be used as control parameters, via the tuned lockdown as decided by the public policies (reflecting on $p$ and partially on $r$), the awareness of the population in respecting the social distancing among individuals and in the widespread use of personal protection equipment (expressed by $\beta$ and partially by $r$), the availability of testing kits, that results in a higher or lower value of $\rho$.

The extended state variable of the system thus becomes

$$\tilde{X}=(E_f,E_r,I_f,I_r,A_f,A_r,Q,S_f,S_r,R,D),$$

where the description of the compartments is given in Table 4.

Table 4.

List of extended compartments.

Compartment	Description
$E_f$	Exposed, not in isolation, not contagious
$E_r$	Exposed, in $r$-isolation, not contagious
$I_f$	Infected and contagious, not in isolation
$I_r$	Infected and contagious, in $r$-isolation
$A_f$	Asymptomatic and contagious, not in isolation
$A_r$	Asymptomatic and contagious, in $r$-isolation
$Q$	Infected and tested positive, in enforced quarantine
$S_f$	Susceptible not in isolation
$S_r$	Susceptible in $r$-isolation
$R$	Recovered and immune
$D$	Dead

We focus in particular on the evolution of the variable

$$X=(E_f,E_r,I_f,I_r,A_f,A_r,Q,S_f,S_r),$$

that follows the model

$$\begin{array}{c}{Ė}_f=\beta \left(t\right)S_f\left[I_f+A_f+r\left(t\right)(I_r+A_r)\right]-\rho \left(t\right)\delta E_f-\tau E_f\hfill \\ {Ė}_r=r\left(t\right)\beta \left(t\right)S_r\left[I_f+A_f+r\left(t\right)(I_r+A_r)\right]-\rho \left(t\right)\delta E_r-\tau E_r\hfill \\ {İ}_f=\tau E_f-\sigma I_f-\rho \left(t\right)I_f\hfill \\ {İ}_r=\tau E_r-\sigma I_r-\rho \left(t\right)I_r\hfill \\ {Ȧ}_f=\sigma \alpha I_f-\rho \left(t\right)A_f-{\gamma }_1{A}_f\hfill \\ {Ȧ}_r=\sigma \alpha I_r-\rho \left(t\right)A_r-{\gamma }_1{A}_r\hfill \\ \dot{Q}=\sigma (1-\alpha )(I_f+I_r)+\rho \left(t\right)\left[\delta (E_f+E_r)+I_f+I_r+A_f+A_r\right]\hfill \\ -{\gamma }_{2}Q-\mu Q\hfill \\ {Ṡ}_f=-\beta \left(t\right)S_f[I_f+A_f+r\left(t\right)(I_r+A_r)]\hfill \\ {Ṡ}_r=-r\left(t\right)\beta \left(t\right)S_r[I_f+A_f+r\left(t\right)(I_r+A_r)]\hfill \end{array}$$ (1)

while the dynamics

$$\left(\begin{array}{c}Ṙ={\gamma }_1(A_f+A_r)+{\gamma }_{2}Q\hfill \\ Ḋ=\mu Q\hfill \end{array}\right)$$ (2)

only provides counters for the proportion (over the total population) $R$ of recovered and $D$ of dead individuals. See the compartmental diagram associated to this model in Fig. 2.

Fig. 2.

Model diagram.

Remark 2.1 About the Testing Rate $\rho$ —

The parameter $\rho$ indicates the proportion of the population presenting either mild or no symptoms that is tested daily. It can also be thought as the inverse of the mean duration that an infected person in compartments $A$ passes without being tested. For instance, if the system manages to detect, each day, 5% of the asymptomatic infections, then $\rho =0.05$. If we are in an ideal “trace and test” situation (see e.g. South Korea The Guardian, 2020), in which for each confirmed infection, their recent contacts are rapidly and efficiently traced and tested, then $\rho$ will be greater and this will have an impact in the basic reproduction number (see Section 3).

Recalling that testing is supposed to be applied, at least, to all acute symptomatic cases, we add a counter for the positive tests $T\left(t\right)$ until time $t$, which evolves according to the equation

$$\dot{T}=\sigma (1-\alpha )(I_f+I_r)+\rho \left(t\right)\left(\delta (E_f+E_r)+I_f+I_r+A_f+A_r\right).$$

Having this quantity, one can estimate the total number of tests in each territory using the testing positive rate of that location, which is the ratio between reported cases and tests done (World Health Organization, 2020d, Worldometer, 2020a).

Remark 2.2 About Symptoms, Testing and Quarantine —

In our framework, we assume that all cases with severe symptoms are (tested and) quarantined, and we set the parameter $\alpha \in (0,1)$ to be the fraction of asymptomatic (or under-reported) cases, including the cases with mild symptoms. But we can adapt our model to a scenario in which even severe symptoms are not tested until critical. In this case, with a very large value for $\alpha$, only a small portion among the symptomatic individuals enters directly to $Q$, while the others need to be tested (according to the sampling test rate $\rho$ among the population) to be quarantined.

System (1) is endowed with the set of initial conditions given by the vector

$$X_0=(E_{f,0},E_{r,0},I_{f,0},I_{r,0},A_{f,0},A_{r,0},Q_0,S_{f,0},S_{r,0})$$ (3)

with components in the interval $[0,1]$. Setting

$${\mathcal{C}}_1≔\left\{X={\left(x_i\right)}_{i=1,\dots ,9}\in {\mathbb{R}}^9:x_i\in [0,1],\text{ for }i=1,\dots 9,\sum _{i=1}^9{x}_i\le 1\right\},$$

it is easy to check that ${\mathcal{C}}_1$ is invariant under the flow of system (1), that is, given an initial condition $X_0\in {\mathcal{C}}_1$, the solution $X\left(t\right)$ to (1)–(3) remains in ${\mathcal{C}}_1$ for all $t>0$.

Remark 2.3 Possible Extensions of the Model —

We collect here some variations of model (1) that can be formulated in the same framework considered in this paper.

• 1.
  (Potential contagion from quarantined individuals) One might consider a small but not negligible contact rate between susceptible individuals and people in the compartment $Q$, accounting for infections (mainly of medicals and paramedicals) occurred during hospitalization of an infected individual, or for individuals tested positive in enforced quarantine at home, which do not strictly comply with the isolation procedures and end up infecting relatives or other contacts. In this case, the equations for the evolution of the susceptible compartments shall be completed with additional terms involving $\epsilon$ in the following way:

  $$\begin{array}{c}{Ṡ}_f=-\beta \left(t\right)S_f[I_f+A_f+r\left(t\right)(I_r+A_r)+\epsilon Q],\hfill \\ {Ṡ}_r=-r\left(t\right)\beta \left(t\right)S_r[I_f+A_f+r\left(t\right)(I_r+A_r)+\epsilon Q],\hfill \end{array}$$

  and the same terms with opposite sign shall appear in the equation corresponding to $\dot{Q}$.
• 2.(Possible reinfection or reactivation) At the current stage, it is still not clear how long the immunity of a recovered individual lasts, with a number of findings tending towards a rather long duration (An et al., 2020, Time, 2020, Wajnberg et al., 2020). For this reason, in (1) we assume that a recovered individual will remain immune over the time framework considered in the different scenarios. However, the model can easily describe the case of recovered individuals becoming susceptible again, by adding a transfer term from the compartment $R$ to $S_f$ and $S_r$, with a coefficient depending on the inverse of the average period of immunity. Similarly, the model can include the case of reactivation of the virus in an individual previously declared recovered (and not newly exposed to the virus), by inserting a transfer term from the compartment $R$ into $I_f$ and $I_r$, with appropriate coefficients depending on the probability of the reactivation of the virus and on the inverse of the average time of reactivation. However, up to now, even if reinfection cases have been reported, they remain rare (Centers for Disease Control and Prevention, 2020b).
• 3.
  (ICU occupation) A crucial issue while coping with the outbreak of the epidemic, which leads to the so-called urge of flattening the curve, is whether the number of critical cases in need of intensive care (IC) treatment (due to respiratory failure, shock, and multiple organ dysfunction or failure) would saturate the number of available intensive care units (ICUs). This parameter can be directly estimated from model (1), by considering for each country the number of available ICUs and the percentage of positive confirmed cases requiring IC treatment. For example, this percentage has been estimated to be about 6% for China (WHO China, 2020), and up to 12% for Italy (Grasselli et al., 2020, Remuzzi and Remuzzi, 2020). As an alternative, it would be possible to insert a further compartment $C$ in model (1) counting the number of the individuals needing ICU treatment, by modifying the equations corresponding to the compartments $Q$ and $D$ as follows:

  $$\dot{Q}=\sigma (1-\alpha )I+\rho \left(t\right)\left[\delta E+I+A\right]-{\gamma }_{2}Q-{\tau }_{c}Q$$

  $$\dot{C}={\tau }_{c}Q-{\mu }_{c}C-{\gamma }_{c}C$$

  $$\dot{D}={\mu }_{c}C$$

  with suitable coefficients ${\tau }_c$, ${\mu }_c$ and ${\gamma }_c$ denoting the inverse of the time from symptoms onset to critical symptoms, the mortality of critical cases, and the recovery rate for critical cases, respectively.
• 4.(Test sensitivity) One should note that with the presence of the parameter $\delta$ we are taking into account the possibility of not detecting the virus at the beginning of the infection. We can further include the possibility of having false negative tests in the course of pre-symptomatic, asymptomatic or mild symptomatic infections, by multiplying the rate $\rho$ by a parameter ${\gamma }_{\mathrm{sens}}\in (0,1)$, this being such that $1-{\gamma }_{\mathrm{sens}}$ is the probability of a false negative. This would not yield a complication in the analysis that follows, but we choose to disregard this feature for a sake of simplicity of presentation.
• 5.(Adding birth and natural mortality rate) In this paper we have considered the whole population as a fixed number of individuals during the time period of the evolution. It is of course possible to consider the case of an evolving total population, by including in the model (1) birth and natural mortality rate. In particular, newborns of susceptible individuals shall enter the corresponding susceptible compartment. Regarding descendants of infected mothers, there is still not enough evidence neither to confirm the possibility nor to estimate the probability of trans-placental transmission (Facchetti et al., 2020, Fenizia et al., 2020). On the other hand, the natural mortality rate shall act on each compartment of system (1), as well as on $R$ in system (2).

3. The basic reproduction number for model (1)

We are interested in determining the basic reproduction number ${\mathcal{R}}_0$ associated with system (1). To do this, we assume to fix a time interval $[t_0,t_1]$ such that the coefficients $\beta \left(t\right)$, $r\left(t\right)$ and $\rho \left(t\right)$ are constant over $[t_0,t_1]$. This is coherent with the setting of the scenarios simulated in Section 4.2 below, where we set such coefficients to be piecewise constant functions, sharing the same switching times, that represent different phases of restrictions and policies. Thus, according to the calculations given in Appendix A.1 and the parameters in Table 2, Table 3, we obtain that the value of ${\mathcal{R}}_0$ for each time interval between two consecutive switching times is given by

$${\mathcal{R}}_0=\frac{1}{2}\left(\phi +\sqrt{{\phi }^2+\frac{4\sigma \alpha }{\rho +{\gamma }_1}\phi }\right),$$ (4)

with

$$\phi =\frac{\beta \tau [1-(1-r^2)p]}{(\rho \delta +\tau )(\sigma +\rho )}.$$ (5)

From this explicit formula for the reproduction number ${\mathcal{R}}_0$, we can highlight the following qualitative dependence of ${\mathcal{R}}_0$ on each parameter of the system.

• –If the effective contact rate $\beta$ increases, then ${\mathcal{R}}_0$ increases.
• –
  Focusing on the coefficient $1-(1-r^2)p$, we realize the following:

  • (i)
    with fixed $r$, the closer $p$ is to $1$, that is, as larger is the portion of population in $r$-isolation, the lower ${\mathcal{R}}_0$ becomes. In particular, in the extreme case $p=1$, we realize that ${\mathcal{R}}_0$ depends quadratically on $r$, as also noted in Appendix A.3;
  • (ii)
    with $p$ fixed, the smaller $r$ is, that is, as lower the reduction factor in the contact rate of each individual in $r$-isolation is, the more ${\mathcal{R}}_0$ decreases.
• –The larger $\alpha$ is, that is, in case of a higher rate of asymptomatic infections or a higher proportion of under-reported cases, then the higher ${\mathcal{R}}_0$ is.
• –If $\sigma$ increases, corresponding to shorter onset time, then ${\mathcal{R}}_0$ decreases.
• –If either $\rho$ or ${\gamma }_1$ increase, i.e., if either the control action by testing is strengthened, for example through an improved tracing and tracking system, or the recovery rate improves, for example, because of new and more effective treatments, then ${\mathcal{R}}_0$ decreases.
• –If $\delta$ increases, for example, as a result of improved testing kits able to detect the infection at an earlier stage, then ${\mathcal{R}}_0$ decreases.

Moreover, we can characterize the crucial condition ${\mathcal{R}}_0\le 1$ by means of a simpler expression than (4), as described in the next result.

Proposition 3.1 Alternative Threshold —

Set

$${\mathcal{T}}_0≔\frac{\beta \tau [1-(1-r^2)p]}{(\rho \delta +\tau )(\sigma +\rho )}\left(1+\frac{\sigma \alpha }{\rho +{\gamma }_1}\right).$$

Then ${\mathcal{R}}_0$ is smaller than (respectively, equal to or greater than) 1 if and only if the same relation holds for ${\mathcal{T}}_0$ . In particular, if $\phi >1$ (see (5) ), then ${\mathcal{R}}_0>1$ and ${\mathcal{T}}_0>1$ .

We postpone the proof of Proposition 3.1 to Appendix A.2. A more quantitative analysis of the dependence of the threshold ${\mathcal{T}}_0$ on the parameters of the model is developed in Appendix A.3.

Remark 3.2 About No Testing Among Asymptomatic Carriers —

If we consider the case when $\rho =0$, that is, the situation without sample testing among the asymptomatic population, then the basic reproduction number ${\mathcal{R}}_0$ is independent of the latent time $\tau$. In particular, ${\mathcal{T}}_0$ becomes

$$\frac{\beta [1-(1-r^2)p]}{\sigma }\left(1+\frac{\sigma \alpha }{{\gamma }_1}\right).$$

 

Remark 3.3 On the Time-Dependent Reproduction Number —

Relation (4) gives an expression of ${\mathcal{R}}_0$, that is the reproduction number in a totally susceptible population. As the epidemic evolves, a portion of the population becomes immune to the disease, and this makes the reproduction number decrease. More precisely, when $p=0$ and all the population has the same contact rate, the time-dependent reproduction number is given by $\mathcal{R}\left(t\right)=S\left(t\right){\mathcal{R}}_0$, where $S\left(t\right)$ is the susceptible portion of the population. In our model, since the groups of active individuals and in $r$-isolation evolve differently (see Scenario A${}_4$ and Fig. 4 below), the time-dependent reproduction number $\mathcal{R}\left(t\right)$ is given by the formula (4) where $\phi$ in (5) is

$$\frac{\beta \tau [S_f\left(t\right)+r^2{S}_r\left(t\right)]}{(\rho \delta +\tau )(\sigma +\rho )}.$$

In the tables of Section 4 showing the outcomes of the numerical simulations, we exhibit the value of ${\mathcal{R}}_0$ at the beginning of each phase, where $S\left(t\right)$ is still close to 1.

In Remark 4.1 we make an analysis relating the evolution of ${\mathcal{R}}_t$ and the time-to-peak.

Remark 3.4 On Herd Immunity —

Herd immunity is defined as the proportion of the population that needs to be immunized in order to naturally slow down the spread of the disease. It depends on the value of the basic reproduction number in the following way: herd immunity level equals $1-\frac{1}{{\mathcal{R}}_0}$. So the bigger ${\mathcal{R}}_0$, the higher the herd immunity. In connection with the previous Remark 3.3, we highlight that herd immunity is achieved at the time $t$ when $\mathcal{R}\left(t\right)$ equals 1.

4. Numerical simulations

4.1. Retrieving parameters

In Table 5 we collect some parameter values estimated in the literature, in order to do realistic simulations. Recall the description of the parameters given in Table 2, Table 3.

Table 5.

Realistic range of parameters values.

Par.	Value–Range	Reference	Remark
$\beta$	[0.62,2]	Alimohamadi et al., 2020, Bastos and Cajueiro, 2020, Flaxman et al., 2020, Shen et al., 2020	1.
${\tau }^{-1}$	${\tau }^{-1}={\theta }^{-1}\text{–}{\sigma }^{-1}$	Liang and Yuan (2020)	2.
${\sigma }^{-1}$	1–3 days	Read et al., 2020, Zhang et al., 2020, Zhou et al., 2020, Prete et al., 2020	4.
${\theta }^{-1}$	5.1–6.4 days	Backer et al., 2020, Lauer et al., 2020, Liang and Yuan, 2020	5.
${\gamma }_1$	7.5–12 days	WHO China, 2020, Hu et al., 2020	6.
${\gamma }_2$	15–22 days	WHO China, 2020, Zhou et al., 2020	7.
$\mu$	[0.009/14,0.094/14]	World Health Organization, 2020f, Wang et al., 2020, John Hopkins University & Medicine, 2020	8.
$\alpha$	[0.265, 0.765]	Wikipedia contributors, 2020, Lavezzo et al., 2020, Petersen and Phillips, 2020	3.
$p$	$[0,1]$	Hale et al. (2020)	9.
$r$	$[0,1]$	Hale et al. (2020)	9.
$\rho$	[0,0.5]	Worldometer (2020a)	10.
$\delta$	1	Harvard Health Publishing (2020)	11.

Several remarks regarding the parameter values in Table 5 follow.

• 1.It is difficult to find estimates for the transmission rate $\beta$, since its meaning significantly varies with each model choice. Additionally, note that $\beta$ strongly depends on the population behavior and public policies, so it has a rather large range of realistic values. Alternatively, to obtain the exhibited interval, we use ${\mathcal{R}}_0$ pooled estimations to retrieve values of $\beta$ as a function of ${\mathcal{R}}_0$ and other parameters. For the numerical simulations, we choose the estimate by Shen et al. (2020), where they calibrated an SEIR model with isolation and estimated the transmission rate $\beta$, before lockdown.
• 2.The mean duration of the latent period can be computed using the estimates for the incubation period (i.e. from exposure to symptom onset) and the time from infectiousness onset to symptom onset, so it is reasonable to take ${\tau }^{-1}$ between 2 and 4 days. More precisely, in Liang and Yuan (2020) they fitted an SEIQR model to the data from Wuhan and estimated a latent period of duration 2.92 days with a 95% CI of $(1.09,5.28)$.
• 3.In Wikipedia contributors (2020) they show the testing results on Diamond Princess passengers, a cruise ship that was quarantined in February–March 2020, at the beginning of the epidemic. Almost all passengers and crew members were tested, resulting in 410 asymptomatic infections among 696 positive-tested persons, which yields an asymptotic rate of 0.589. In Lavezzo et al. (2020), they studied the infection in the municipality of Vo’, Italy. They estimated a median of asymptomatic cases of 44.8% with a 95% CI of (26.5,64.3). Other estimates were given in Day, 2020, Mizumoto et al., 2020, Nishiura et al., 2020. Let us observe that $\alpha$ can also be regarded as the proportion of under-reported cases, and in that case its value mainly depends on the number of tests.
• 4.In Zhou et al. (2020), they measured time from infectiousness onset to appearance of symptoms. It resulted in approximate 1 day for fever and 1–3 days for cough. Furthermore, it has been observed in clinical cases studied in Woelfel et al. (2020) that the contagious period may start before the appearance of symptoms, and outlast the symptoms’ end.
• 5.The Ref. Backer et al. (2020) estimates $\theta$ to be 6.4 days based on travelers returning from Wuhan. In Lauer et al. (2020) it was estimated to be 5.1 days. Other estimates were given in Liang and Yuan (2020).
• 6.The estimate of ${\gamma }_1$ is difficult, since for asymptomatic cases is hard to observe and track the time from exposure to recovery. Hu et al. (2020) estimated 9.5 days for asymptomatic cases, while (WHO China, 2020) estimated 14 days for mild cases. So it is reasonable to assume ${\gamma }_1$ in the range 7.5–12, considering around 2 days between infectiousness onset and symptoms onset.
• 7.In Zhou et al. (2020) they measured viral shedding duration, and estimated a median of 20 days, with an interquartile range of $(17,24)$. Removing the approximately 2-day period from infectiousness onset to symptoms onset, we get an IQR for ${\gamma }_2^{-1}$ of $(15,22)$. These values approximate the duration of quarantine recommended to positive-tested cases.
• 8.The rate $\mu$ strongly depends on the percentage of infections that have been detected, since it is proportional to the ratio between confirmed cases and deaths. Based on the WHO Director-General’s opening remarks at the media briefing of 3 March 2020 (World Health Organization, 2020f), we consider a global death rate of 3.4% among confirmed cases, although countries with a low number of tests tends to have a higher death rate $\mu$ (Worldometer, 2020b, John Hopkins University & Medicine, 2020).
• 9.The values of $p$ and $r$ vary in each country/territory depending on the public policies and the population’s compliance to these measures. A detailed and real-time survey on the percentage of people under lockdown in each country can be found in Hale et al. (2020).
• 10.As already mentioned in Remark 2.1, $\rho$ represents the proportion of the infected asymptomatic population that is tested daily. In a realistic scenario, it would not be reasonable to set a too high value of $\rho$, let us say, over 0.5, because it would account for detecting more than 50% of the infected asymptomatic population daily.
• 11.It is not yet know “at what point during the course of illness a test becomes positive” (see Harvard Health Publishing (2020)). For the simulations we set $\delta$ equal to 1/2. As supported by the sensitivity analysis in the Appendix A.3, different values for $\delta$ do not affect significantly the evolution of the epidemic. We have observed this fact numerically.

4.2. Simulations for different scenarios

In this subsection we consider several scenarios and show their outcomes. Many of the graphics are in logarithmic scale, given that the values represent portions of the population, and then they can assume very small values. In Table 6 we list the parameters’ values that are fixed for all numerical simulations. The simulations were done with Python and all the codes are in the GitHub repository github.com/lucasmoschen/covid-19-model.

Table 6.

Chosen COVID-19 parameters for the numerical simulations.

Par.	Value
$\beta$	0.7676
$\tau$	1/3.2
$\sigma$	1/2
$\theta$	1/5.2
${\gamma }_1$	1/8
${\gamma }_2$	1/16
$\alpha$	0.4

4.2.1. Scenarios A: the impact of testing among asymptomatic individuals

We consider the four different scenarios with the following characteristics:

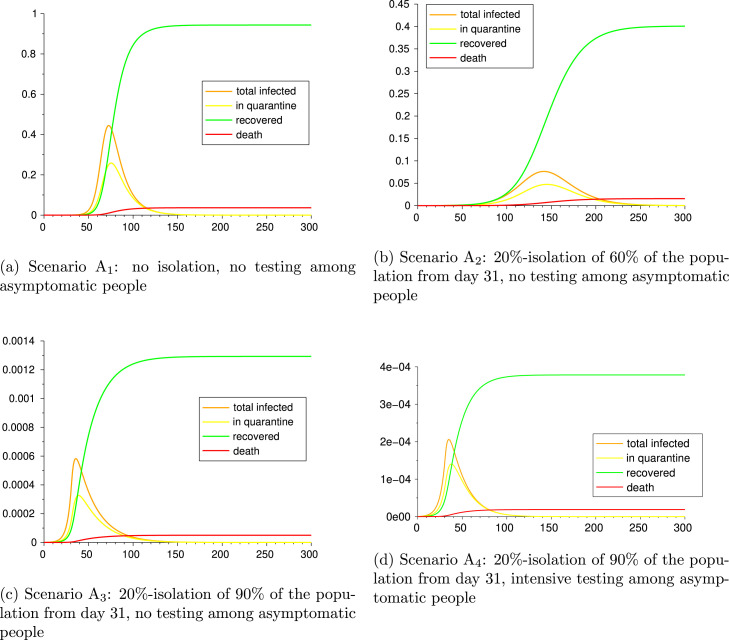
Scenario A${}_1$: no isolation, no testing among asymptomatic people

Scenario A${}_2$: 20%-isolation of 60% of the population from day 31, no testing among asymptomatic people

Scenario A${}_3$: 20%-isolation of 90% of the population from day 31, no testing among asymptomatic people

Scenario A${}_4$: 20%-isolation of 90% of the population from day 31, intensive testing among asymptomatic people

These Scenarios A can be seen as: no action, mild lockdown, strict lockdown and strict lockdown with track/trace/test in place. As initial condition we take, in all the scenarios, one exposed case per million inhabitant, this is:

$$E_f\left(0\right)+E_r\left(0\right)=1\times 10^{-6},S_f\left(0\right)+S_r\left(0\right)=1-1\times 10^{-6}.$$

The remainder of the compartments start with value 0. Results and parameters for Scenario A are given in Table 7 and graphics in Fig. 3. We can observe the effect of the lockdown on the epidemic. The mild lockdown of A${}_2$ reduces more than half of the infections w.r.t. the no action situation A${}_1$, while the strict lockdowns A${}_3$ and A${}_4$ induce a reduction of the order of 10⁻³ in total recovered, deaths and positive tests. In particular, comparing A${}_3$ and A${}_4$ we can see that testing and consequent quarantine for positive-tested asymptomatic cases not only reduces the infections and deaths more than 66%, but also the duration of the epidemic.

Table 7.

Scenarios A${}_1$, A${}_2$, $A_3$ and A${}_4$. Parameters and epidemics outputs.

Par.	A${}_1$	A${}_2$	A${}_3$	A${}_4$
$p$	0	0 if $t\le 31$ 0.6 if $t>31$	0 if $t\le 31$ 0.9 if $t>31$
$r$	1	1 if $t\le 31$ 0.2 if $t>31$
$\rho$	0			0.05
$\delta$	1/2
$\mu$	0.058/14
${\mathcal{R}}_0$	2.51	2.51 if $t\le 31$ 1.4 if $t>31$	2.51 if $t\le 31$ 0.69 if $t>31$	$2.02$ if $t\le 31$ $0.54$ of $t>31$
Peak day (for $Q$)	75	146	40	39
Peak size (maximum of $Q$)	$2.59\times 10^{-1}$	$4.74\times 10^{-2}$	$3.27\times 10^{-4}$	$1.4\times 10^{-4}$
Recovered	$9.43\times 10^{-1}$	$4.01\times 10^{-1}$	$1.29\times 10^{-3}$	$3.78\times 10^{-4}$
Deaths	$3.66\times 10^{-2}$	$1.56\times 10^{-2}$	$5.01\times 10^{-5}$	$1.87\times 10^{-5}$
Positive tests	$5.88\times 10^{-1}$	$2.5\times 10^{-1}$	$8.06\times 10^{-4}$	$3.02\times 10^{-4}$
Ending day ($Q\le 10^{-9}$)	376	$>$500	314	232

Fig. 3.

Scenarios A${}_1$, A${}_2$, $A_3$ and A${}_4$.

For Scenario A${}_4$ we make a comparison between the infection rate in two different groups: the one of active individuals (with contact rate $\beta$) and the other one of individuals in $r$-isolation (with contact rate $r\beta$). For each group, we compute the percentage of the group population that gets infected. By comparing the new infections’ curves and the cumulative infections, we can give an estimate on the lower chance that people in $r$-isolation have to get exposed to the virus. Fig. 4 shows for the scenario A${}_4$ the curves of cumulative new infections for each group, normalized by the proportions $1-p$ and $p$, as determined by the initial setting. We deduce that, in this particular scenario, an individual that remain active have nearly 5 times more chance to get infected than one that chooses $r$-isolation.

4.2.2. Scenarios B: different restriction level of lockdown

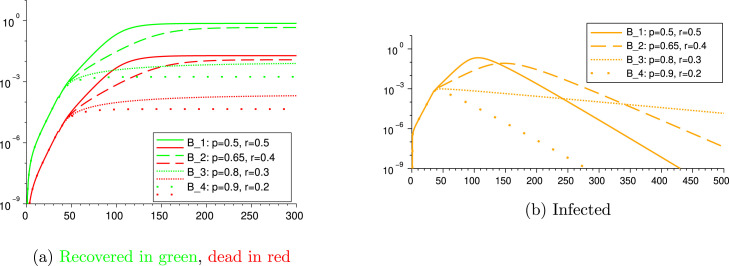
We next consider the following four scenarios in which we vary the values of the portion $p$ of people under lockdown and their level $r$ of restriction of social contacts.

Scenario B${}_1$: 50%-isolation of 50% of the population from day 35

Scenario B${}_2$: 40%-isolation of 65% of the population from day 35

Scenario B${}_3$: 30%-isolation of 80% of the population from day 35

Scenario B${}_4$: 20%-isolation of 90% of the population from day 35

We measure the outcomes. The parameters and results are given in Table 8, and graphics in Fig. 5. The parameters that are not specified in Table 8, are repeated from Table 6, Table 7.

Fig. 5.

Scenarios B${}_1$, B${}_2$, B${}_3$ and B${}_4$.

Scenarios B${}_1$ and B${}_2$ show cases in which the restrictions are not strong enough. Indeed, in both cases the basic reproduction number ${\mathcal{R}}_0$ remains above 1 also after the lockdown intervention (see Table 8), and the infection reaches 71.6% and 43.6% of the population, causing the death of 1.89% and 1.15% of the population, respectively, which is a catastrophic outcome. Comparing these four scenarios, we shall deduce that, in order to be effective in containing the outbreak, the lockdown shall address at least 80% of the population reducing their contact rate to about 30% of their usual contacts. Indeed, in the scenario B${}_3$, the basic reproduction number becomes 0.93 after day 35, meaning that loosening the restrictions of this scenario (while keeping all other parameters unchanged) might turn the ${\mathcal{R}}_0$ above 1.

Table 8.

Scenarios B${}_1$, B${}_2$, B${}_3$ and B${}_4$. Parameters and epidemic outputs.

Par.	B${}_1$	B${}_2$	B${}_3$	B${}_4$
$\delta$	1/2
$\mu$	0.034/14
$p$	0 if $t\le 35$ 0.5 if $t>35$	0 if $t\le 35$ 0.65 if $t>35$	0 if $t\le 35$ 0.8 if $t>35$	0 if $t\le 35$ 0.9 if $t>35$
$r$	1 if $t\le 35$ 0.5 if $t>35$	1 if $t\le 35$ 0.4 if $t>35$	1 if $t\le 35$ 0.3 if $t>35$	1 if $t\le 35$ 0.2 if $t>35$
$\rho$	0.02
${\mathcal{R}}_0$	2.29 if $t\le 35$ 1.64 if $t>35$	2.29 if $t\le 35$ 1.33 if $t>35$	2.29 if $t\le 35$ 0.95 if $t>35$	2.29 if $t\le 35$ 0.62 if $t>35$
Peak day (for $Q$)	109	151	54	44
Peak size (maximum of $Q$)	$1.46\times 10^{-1}$	$5.74\times 10^{-2}$	$6.62\times 10^{-4}$	$5.34\times 10^{-4}$
Recovered	7.32 $\times 10^{-1}$	4.61 $\times 10^{-1}$	8.47 $\times 10^{-3}$	1.74 $\times 10^{-3}$
Deaths	1.91 $\times 10^{-2}$	1.2 $\times 10^{-2}$	2.21 $\times 10^{-4}$	4.53 $\times 10^{-5}$
Positive tests	5.1 $\times 10^{-1}$	3.21 $\times 10^{-1}$	5.91 $\times 10^{-3}$	1.21 $\times 10^{-3}$
Ending day	431	$>$500	$>$500	280

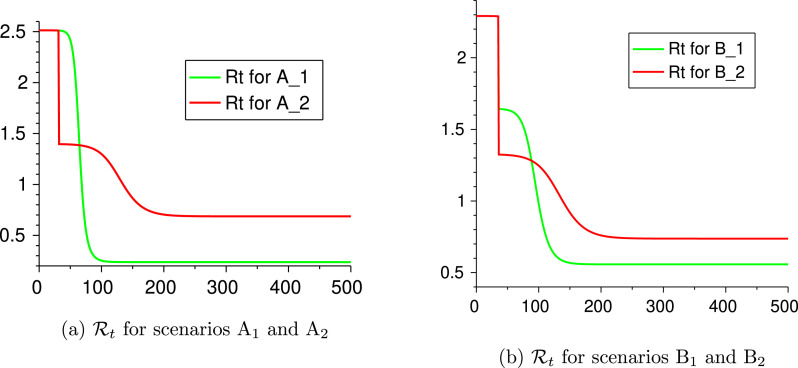
Remark 4.1 On the Time-to-Peak —

From Table 7, Table 8 one can see that Scenarios A${}_2$ and B${}_2$ have a much longer time-to-peak. This behavior is due to the value of the time-dependent reproduction number ${\mathcal{R}}_t$ (see Remark 3.3). More precisely, in Scenario A${}_2$, one has ${\mathcal{R}}_0=1.4$ after day 31, and 40% of the population infected along the wave, hence ${\mathcal{R}}_t$ assumes values close to 1 for a quite long time and this makes the growth of the infections slower. This phenomenon does not occur for the other scenarios A. See Fig. 6(a) where we compare the evolution of ${\mathcal{R}}_t$ for scenarios A${}_1$ and A${}_2$. A similar situation occurs for Scenario B${}_2$. See Fig. 6(b).

Fig. 6.

Evolution of the reproduction number for some scenarios.

4.2.3. Scenarios C: early vs. late lockdown

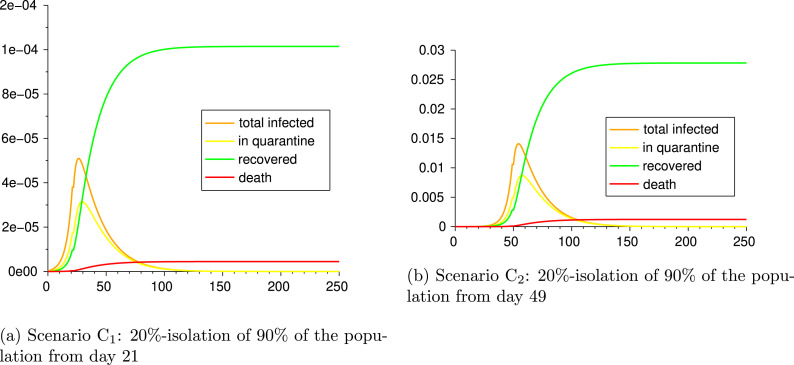
We now compare two situations, one in which lockdown starts just 21 days after the first confirmed cases, and the other for which lockdown starts four weeks later. More precisely, we consider the following two scenarios and measure the different outputs:

Scenario C${}_1$: 20%-isolation of 90% of the population from day 21

Scenario C${}_2$: 20%-isolation of 90% of the population from day 49

The parameters and outputs are given in Table 9 and Fig. 7. It is evident the impact of delaying the beginning of lockdown on the final outcome: the numbers of recovered and deaths in the Scenario C${}_2$ are of the order of $10^3$ times those of the Scenario C${}_1$. As an example, from Table 9 we notice that, at the end of the epidemic, the Scenario C${}_1$ counts 4.2 deaths per million inhabitants, while the Scenario C${}_2$ faces 1020 deaths per million. Moreover, the epidemic in Scenario $C_2$ lasts about 110 days more than in Scenario $C_1$, thus also undergoes worst economic consequences of the lockdown.

Table 9.

Scenarios C${}_1$ and C${}_2$: early lockdown vs. late lockdown. Parameters and epidemic outputs.

Par.	C${}_1$	C${}_2$
$\delta$	1/2
$\mu$	0.058/14
$p$	0 if $t\le 21$ 0.9 if $t>21$	0 if $t\le 49$ 0.9 if $t>49$
$r$	1 if $t\le 21$ 0.2 if $t>21$	1 if $t\le 49$ 0.2 if $t>49$
$\rho$	0.02
${\mathcal{R}}_0$	2.29 if $t\le 21$ 0.62 if $t>21$	2.29 if $t\le 49$ 0.62 if $t>49$
Peak day	29	57
Peak size (maximum of $Q$)	$3.14\times 10^{-5}$	$8.69\times 10^{-3}$
Recovered	1.01 $\times 10^{-4}$	2.78 $\times 10^{-2}$
Deaths	4.47 $\times 10^{-6}$	1.23 $\times 10^{-3}$
Positive tests	7.19 $\times 10^{-5}$	1.97 $\times 10^{-2}$
Ending day	217	330

Fig. 7.

Scenarios C${}_1$ and C${}_2$.

4.2.4. Scenarios D: early testing vs. late testing

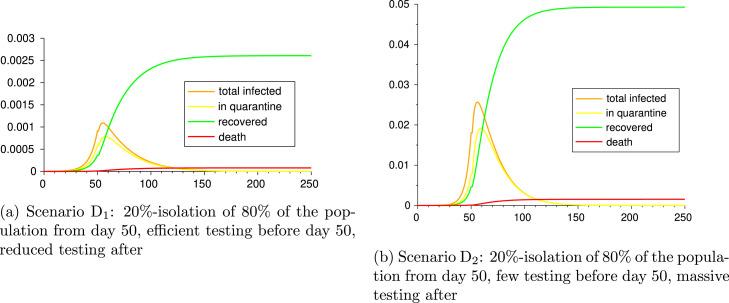
Now we want to assess the impact of testing time. For this, we consider the following two scenarios and measure the different outputs:

Scenario D${}_1$: 20%-isolation of 80% of the population from day 50, efficient testing before day 50, reduced testing after

Scenario D${}_2$: 20%-isolation of 80% of the population from day 50, few testing before day 50, massive testing after

The parameter values and outcomes of the epidemic in Scenarios D${}_1$ and D${}_2$ are given in Table 10 and figures in Fig. 8. It can be seen the cost in infection and lives it has to start testing late. It is worth noticing that, in spite of a higher total number of tests carried out in the Scenario D${}_2$, the strategy adopted in the Scenario D${}_1$ attains a considerably better outcome: indeed, the infections and deaths of Scenario D${}_2$ are of the order of 10${}^2$ w.r.t. the ones in Scenario D${}_1$, and the only difference was doing efficient testing at the beginning of the epidemic.

Table 10.

Scenarios D${}_1$ and D${}_2$: early efficient testing vs. late massive testing. Parameters and epidemic outputs.

Par.	D${}_1$	D${}_2$
$\delta$	1/2
$\mu$	0.034/14
$p$	0 if $t\le 50$ 0.8 if $t>50$
$r$	1 if $t\le 50$ 0.2 if $t>50$
$\rho$	0.1 if $t\le 50$ 0.05 if $t>50$	0.01 if $t\le 50$ 0.1 if $t>50$
${\mathcal{R}}_0$	1.68 if $t\le 50$ 0.75 if $t>50$	2.4 if $t\le 50$ 0.62 if $t>50$
Peak day	58	59
Peak size (maximum of $Q$)	$7.82\times 10^{-4}$	$1.92\times 10^{-2}$
Recovered	2.61 $\times 10^{-3}$	4.93 $\times 10^{-2}$
Deaths	7.89 $\times 10^{-5}$	1.52 $\times 10^{-3}$
Positive tests	2.11 $\times 10^{-3}$	4.07 $\times 10^{-2}$
Ending day	352	332

Fig. 8.

Scenarios D${}_1$ and D${}_2$.

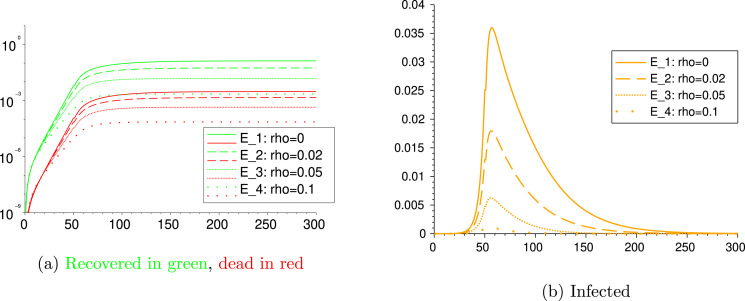
4.3. Scenarios E: different testing rates

Now we fix the parameters $\beta ,\mu ,p,r$ as in Table 10 and we vary only $\rho$ to take the four different values 0, 0.02, 0.05 and 0.1 over the whole time period. We get the outcome of Fig. 9. From the comparison among these four scenarios, we realize that a high value of $\rho$, as the result of an efficient tracing and testing strategy, may reduce the number of cumulative infected individuals and deaths of an order of $10^2$.

Fig. 9.

Scenarios E${}_1$, E${}_2$, E${}_3$ and E${}_4$.

5. Conclusions

In this paper we present an SEIR model with Asymptomatic and Quarantined compartments to describe the recent and ongoing COVID-19 outbreak. Our model is intended to highlight the strength of three different non-pharmaceutical interventions imposed by public policies in containing the outbreak and the total number of disease-induced infections and deaths:

• –reduction of contact rate for a given portion of the population;
• –enforced quarantine for confirmed infectious individuals;
• –Track/trace/test strategy to search for the virus among potentially asymptomatic individuals.

We show that, as expected, each of these interventions has a beneficial impact on flattening the curve of the outbreak. However, the comparison among different scenarios shows the remarkable efficacy of early massive testing, when the limited number of infected individuals makes contact tracing easier and more effective, as in Scenario D${}_1$, and of a timely lockdown, starting with few confirmed infected cases, as in Scenario C${}_1$. In both situations, the timing of the intervention plays a crucial role on the incisiveness of the public safety policy. This key remark is under-appreciated in the current literature and in the public address, and it shall be taken under consideration in those countries facing a second or subsequent outbreak of the epidemic.

In addition, we give an explicit representation of the basic reproduction number in terms of the several parameters of the model, which allows to describe its dependence on the features of the virus and on the implemented non-pharmaceutical interventions.

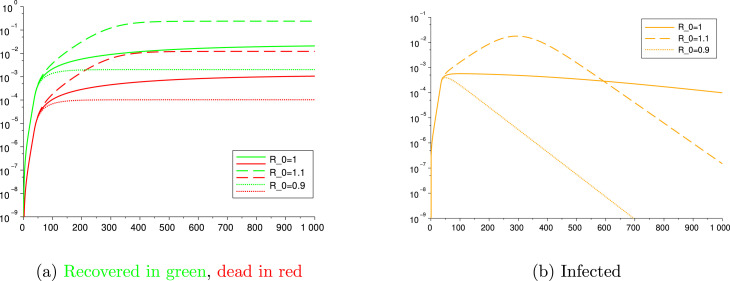
This description makes available a valuable tool to tune the public policies in order to control the outbreak of the epidemic, forcing ${\mathcal{R}}_0$ below the threshold $1$. However, considering the major effects of an enduring lockdown on the economy of the country that applies it, it is desirable to loosen the lockdown measures after the containment of the outbreak. Nevertheless, the decision makers and each individual shall be aware that a value of ${\mathcal{R}}_0$ only barely greater than $1$ would lead to an increase in the number of infected and dead by an order $2$ of magnitude, thus provoking the collapse of the relative national health system. This is better explained by the following scenarios: consider a situation with constant testing $\rho =0.05$ and no lockdown where, after the first 35 days of outbreak with a high ${\mathcal{R}}_0$ ($\approx 2$), the population gains awareness of the risk and manage to reduce its contact rate so as to steer ${\mathcal{R}}_0$ to either 0.9, $1$ or 1.1. Fig. 10 illustrates the large deviations among the outcome of these three different situations.

Fig. 10.

The impact of small variations on ${\mathcal{R}}_0$.

In order to allow the population to circulate with no restrictions, it is necessary that herd immunity (see Remark 3.4) is achieved. The value that matters to compute this threshold is the basic reproduction number under no social distancing, which has been estimated in this article and in many others as being, in general, greater than 2.5. So achieving herd immunity would imply to infect at least 60% of the population, which would lead, with the current mortality rates, to 1%–5% of the population dying, which is, obviously, a catastrophic unwanted situation. Hence, reinforcing what was said in the above paragraph, until a vaccine or treatment is not found, it is necessary to maintain the value of ${\mathcal{R}}_0$ below 1 by a combination of isolation and effective tracing and testing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix.

A.1. Computing ${\mathcal{R}}_0$

Recalling the model (1), we are able to give an analytic expression of the basic reproduction number ${\mathcal{R}}_0$ associated to the system.

In order to do so, we assume to fix a time interval $[t_0,t_1]$ such that the coefficients $\beta \left(t\right)$, $r\left(t\right)$ and $\rho \left(t\right)$ are constant over $[t_0,t_1]$. This is coherent with the setting of Section 4, where we assume such coefficients to be piecewise constant functions, sharing the same switching times. Thus, the following procedure allows to evaluate the value of ${\mathcal{R}}_0$ for each time interval between two consecutive switching times.

It is well known that the reproduction number ${\mathcal{R}}_0$ is the crucial parameter to establish whether Disease Free Equilibria (DFE) are stable or not (Diekmann et al., 1990, van den Driessche and Watmough, 2002). We denote by ${\mathcal{X}}_s$ the set of DFE, which is given by

$${\mathcal{X}}_s=\left\{X\in {\mathcal{C}}_1:E_f=E_r=I_f=I_r=A_f=A_r=Q=0\right\}.$$

We can recast system (1) in the compact form

$$Ẋ\left(t\right)=f\left(X\left(t\right)\right)$$ (6)

by introducing

$$f\left(X\right)=\left(\begin{array}{c}\beta S_f\left[I_f+A_f+r(I_r+A_r)\right]-\rho \delta E_f-\tau E_f\\ r\beta S_r\left[I_f+A_f+r(I_r+A_r)\right]-\rho \delta E_r-\tau E_r\\ \tau E_f-\sigma I_f-\rho I_f\\ \tau E_r-\sigma I_r-\rho I_r\\ \sigma \alpha I_f-\rho A_f-{\gamma }_1{A}_f\\ \sigma \alpha I_r-\rho A_r-{\gamma }_1{A}_r\\ \sigma (1-\alpha )[I_f+I_r]+\rho \left(\delta (E_f+E_r)+I_f+I_r+A_f+A_r\right)-{\gamma }_{2}Q-\mu Q\\ -\beta S_f[I_f+A_f+r(I_r+A_r)]\\ -r\beta S_r[I_f+A_f+r(I_r+A_r)]\end{array}\right).$$

The stability of (6) around a DFE $X^{\ast }$ is related to the spectral properties of the linearized system around $X^{\ast }$, whose dynamics is ruled by the Jacobian $Df={(\partial f_i∕\partial x_j)}_{i,j=1,\dots ,9}$ of $f$. However, the high dimensionality of $Df\left(X\right)$ makes it difficult to develop an analytical analysis of its spectrum and its stability properties. We will therefore follow a different approach, deducing the value of ${\mathcal{R}}_0$ from the result in van den Driessche and Watmough (2002), which ensures that ${\mathcal{R}}_0$ is given by the formula ${\mathcal{R}}_0=\rho \left(F{V}^{-1}\right)$, where $\rho \left(A\right)$ denotes the spectral radius of the matrix $A$. A comment on the applicability of the results in van den Driessche and Watmough (2002) is given in Remark A.1 below.

Since $X^{\ast }$ is a DFE, we may assume that $X^{\ast }=(0,0,0,0,0,0,0,1-p,p)$, for some $p\in [0,1]$ representing the portion of population that is initially in the compartment $S_r$, while the remaining $1-p$ fraction of the population is in $S_f$. Thus, in our setting, the matrices $F$ and $V$ related to the dynamics (6) are given by

$$F=\left(\begin{array}{ccccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill \beta (1-p)\hfill & \hfill r\beta (1-p)\hfill & \hfill \beta (1-p)\hfill & \hfill r\beta (1-p)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill r\beta p\hfill & \hfill r^2\beta p\hfill & \hfill r\beta p\hfill & \hfill r^2\beta p\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \sigma \alpha \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \sigma \alpha \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \sigma (1-\alpha )+\rho \hfill & \hfill \sigma (1-\alpha )+\rho \hfill & \hfill \rho \hfill & \hfill \rho \hfill & \hfill 0\hfill \end{array}\right),$$

$$V=\left(\begin{array}{ccccccc}\hfill \rho \delta +\tau \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \rho \delta +\tau \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\tau \hfill & \hfill 0\hfill & \hfill \sigma +\rho \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\tau \hfill & \hfill 0\hfill & \hfill \sigma +\rho \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \rho +{\gamma }_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \rho +{\gamma }_1\hfill & \hfill 0\hfill \\ \hfill -\rho \delta \hfill & \hfill -\rho \delta \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\gamma }_2+\mu \hfill \end{array}\right).$$

Since $V$ is non-singular, we compute

$$V^{-1}=\left(\begin{array}{ccccccc}{(\rho \delta +\tau )}^{-1}& 0& 0& 0& 0& 0& 0\\ 0& {(\rho \delta +\tau )}^{-1}& 0& 0& 0& 0& 0\\ \frac{\tau }{(\sigma +\rho )(\rho \delta +\tau )}& 0& {(\sigma +\rho )}^{-1}& 0& 0& 0& 0\\ 0& \frac{\tau }{(\sigma +\rho )(\rho \delta +\tau )}& 0& {(\sigma +\rho )}^{-1}& 0& 0& 0\\ 0& 0& 0& 0& {(\rho +{\gamma }_1)}^{-1}& 0& 0\\ 0& 0& 0& 0& 0& {(\rho +{\gamma }_1)}^{-1}& 0\\ \frac{\rho \delta }{({\gamma }_2+\mu )(\rho \delta +\tau )}& \frac{\rho \delta }{({\gamma }_2+\mu )(\rho \delta +\tau )}& 0& 0& 0& 0& {({\gamma }_2+\mu )}^{-1}\end{array}\right).$$

Thus, one can easily compute the matrix $F{V}^{-1}$ and check that its characteristic polynomial is given by

$$p\left(\lambda \right)=-{\lambda }^5{P}_2\left(\lambda \right),$$

where $P_2\left(\lambda \right)$ is a second order polynomial of the form

$$P_2\left(\lambda \right)={\lambda }^2-\frac{\beta \tau (1-p+r^{2}p)}{(\rho \delta +\tau )(\sigma +\rho )}\lambda -\frac{\sigma \alpha \tau \beta (1-p+r^{2}p)}{(\rho +\sigma )(\rho \delta +\tau )(\rho +{\gamma }_1)}.$$

$P_2\left(\lambda \right)$ has one positive and one negative root, given by

$${\lambda }_{1∕2}=\frac{1}{2}\left(\frac{\beta \tau (1-p+r^{2}p)}{(\rho \delta +\tau )(\sigma +\rho )}\pm \sqrt{\Delta }\right),$$

with

$$\Delta ={\left(\frac{\beta \tau (1-p+r^{2}p)}{(\rho \delta +\tau )(\sigma +\rho )}\right)}^2+\frac{4\sigma \alpha \tau \beta (1-p+r^{2}p)}{(\rho +\sigma )(\rho \delta +\tau )(\rho +{\gamma }_1)}>0.$$

Since the term $\frac{\beta \tau (1-p+r^{2}p)}{(\rho \delta +\tau )(\sigma +\rho )}$ is positive, the value of ${\mathcal{R}}_0$ coincides with ${\lambda }_1$, i.e., 

$${\mathcal{R}}_0={\lambda }_1=\frac{1}{2}\left(\frac{\beta \tau (1-p+r^{2}p)}{(\rho \delta +\tau )(\sigma +\rho )}+\sqrt{\Delta }\right).$$ (7)

This is an analytic expression of ${\mathcal{R}}_0$, which shows its explicit dependence on the different parameters of model (1). Proposition 3.1 gives a convenient equivalent condition to ensure the stability of DFE.

Remark A.1

In order to directly apply the results in van den Driessche and Watmough (2002), it is required that the eigenvalues of $Df\left(X^{\ast }\right)$ have negative values and, under this assumption, the asymptotic stability of the DFE is established. In our case, the matrix $Df\left(X^{\ast }\right)$ has zero as an eigenvalue of double multiplicity, with associated eigenvectors in the directions of the last two variables, these being $S_f$ and $S_r$. It is not hard to see that the results in van den Driessche and Watmough (2002) hold for our system by simply modifying asymptotic stability to stability in the directions of the susceptible compartments, which has no consequence in the meaning of the threshold ${\mathcal{R}}_0$. Alternatively, a way to force the system to comply all the technical assumptions from (van den Driessche and Watmough, 2002) is adding birth and natural mortality to our model, which has no relevant impact in the results we showed (since the natural daily birth/death rates are of the order of 10⁻⁵, hence negligible w.r.t. the other parameters).

A.2. Proof of Proposition 3.1

We remind that Proposition 3.1 claims the following: for

$$\phi =\frac{\beta \tau [1-(1-r^2)p]}{(\rho \delta +\tau )(\sigma +\rho )}\text{ and }{\mathcal{T}}_0=\phi \left(1+\frac{\sigma \alpha }{\rho +{\gamma }_1}\right),$$

${\mathcal{R}}_0$ is smaller than (respectively, equal to or greater than) 1 if and only if the same relation holds for ${\mathcal{T}}_0$. Indeed, by a straightforward computation we realize that

$${\mathcal{R}}_0\le 1⟺\phi +\sqrt{{\phi }^2+\frac{4\sigma \alpha }{\rho +{\gamma }_1}\phi }\le 2⟺\left(0<\right)\sqrt{{\phi }^2+\frac{4\sigma \alpha }{\rho +{\gamma }_1}\phi }\le 2-\phi \stackrel{\ast }{⟺}{\phi }^2+\frac{4\sigma \alpha }{\rho +{\gamma }_1}\phi \le {\left(2-\phi \right)}^2⟺\frac{4\sigma \alpha }{\rho +{\gamma }_1}\phi \le 4-4\phi ⟺\phi \left(1+\frac{\sigma \alpha }{\rho +{\gamma }_1}\right)\le 1⟺{\mathcal{T}}_0\le 1.$$

Observe that the implication $⟸$ in the equivalence $\stackrel{\ast }{⟺}$ holds true because

$${\mathcal{T}}_0\le 1⟹\phi \le \frac{\rho +{\gamma }_1}{\rho +{\gamma }_1+\sigma \alpha }\le 1,$$

thus $|2-\phi |=2-\phi$. In particular, the same chain of relations holds with the equal sign. Finally, since ${\mathcal{R}}_0\le 1$ is equivalent to ${\mathcal{T}}_0\le 1$, then also ${\mathcal{R}}_0>1$ is equivalent to ${\mathcal{T}}_0>1$.

In addition, let us notice that, if $\phi >1$, then both ${\mathcal{R}}_0>1$ and ${\mathcal{T}}_0>1$. Indeed, from the definition of ${\mathcal{T}}_0$, since $\frac{\sigma \alpha }{\rho +{\gamma }_1}\ge 0$, we have that ${\mathcal{T}}_0\ge \phi >1$, and thus also ${\mathcal{R}}_0>1$.

A.3. Sensitivity analysis of the threshold ${\mathcal{T}}_0$

The explicit representation (7) of the basic reproduction number ${\mathcal{R}}_0$ allows to study the sensitivity of ${\mathcal{R}}_0$ with respect to the several parameters of the model (1). Moreover, thanks to Proposition 3.1, we know that the threshold

$${\mathcal{T}}_0=\frac{\beta \tau [1-(1-r^2)p]}{(\rho \delta +\tau )(\sigma +\rho )}\left(1+\frac{\sigma \alpha }{\rho +{\gamma }_1}\right)$$

can be used for an equivalent characterization of the condition ${\mathcal{R}}_0<1$. For this reason, it is handier to develop the sensitivity of ${\mathcal{T}}_0$ with respect to the parameters of the model, and deduce its dependence on perturbations of the parameters. We thus compute the normalized sensitivity index $S_x$ corresponding to the $x$ parameter, given by

$$S_x≔\frac{x}{{\mathcal{T}}_0}\frac{\partial {\mathcal{T}}_0}{\partial x},$$

and we get that

$$S_{\beta }=1>0,$$

$$S_{\tau }=\frac{\rho \delta }{\rho \delta +\tau }>0,$$

$$S_p=-\frac{(1-r^2)p}{1-(1-r^2)p}<0,$$

$$S_r=\frac{2r^{2}p}{1-(1-r^2)p}>0,$$

$$S_{\delta }=-\frac{\rho \delta }{\rho \delta +\tau }<0,$$

$$S_{\alpha }=\frac{\sigma \alpha }{\rho +{\gamma }_1+\sigma \alpha }>0,$$

$$S_{{\gamma }_1}=-\frac{\sigma \alpha {\gamma }_1}{(\rho +{\gamma }_1)(\rho +{\gamma }_1+\sigma \alpha )}<0,$$

$$S_{\sigma }=-\frac{\sigma [{\gamma }_1+(1-\alpha )\rho ]}{(\sigma +\rho )(\rho +{\gamma }_1+\sigma \alpha )}<0,$$

$$S_{\rho }=-\frac{\rho }{\rho +{\gamma }_1+\sigma \alpha }\left[\frac{[\delta (\sigma +2\rho )+\tau ](\rho +{\gamma }_1+\sigma \alpha )}{(\rho \delta +\tau )(\sigma +\rho )}+\frac{\sigma \alpha }{\rho +{\gamma }_1}\right]<0.$$

We thus notice the same qualitative dependence on the parameters already observed in Section 3. In particular, if we increase $k$ times the parameter $\beta$, then ${\mathcal{T}}_0$ increases $k$ times as well. Similar deductions can be made on the other parameters, with the corresponding coefficients obtained by inserting the values of the parameters from Table 5. Moreover, from the expression of $S_{\tau }$ we realize that, if either $\rho$ or $\delta$ equal zero, then ${\mathcal{T}}_0$ does not depend on $\tau$ (as it happens for ${\mathcal{R}}_0$ as well, as noticed in Remark 3.2). Similarly, if $\rho =0$, then $S_{\delta }=0$, thus ${\mathcal{T}}_0$ does not depend on $\delta$. Regarding the parameters $p$ and $r$, their dependence is mutually related as follows: if $p=0$, then ${\mathcal{T}}_0$ does not depend on $r$ (since $S_r=0$), whereas if $r=1$ then ${\mathcal{T}}_0$ does not depend on $p$.