Mathematical modeling of COVID-19 infection dynamics in Ghana: Impact evaluation of integrated government and individual level interventions

Abstract

The raging COVID-19 pandemic is arguably the most important threat to global health presently. Although there Although there is currently a a a vaccine, preventive measures have been proposed to reduce the spread of infection but the efficacy of these interventions, and their likely impact on the number of COVID-19 infections is unknown. In this study, we proposed the SEIQHRS model (susceptible-exposed-infectious-quarantine-hospitalized-recovered-susceptible) model that predicts the trajectory of the epidemic to help plan an effective control strategy for COVID-19 in Ghana. We provided a short-term forecast of the early phase of the epidemic trajectory in Ghana using the generalized growth model. We estimated the effective basic Reproductive number Re in real-time using three different estimation procedures and simulated worse case epidemic scenarios and the impact of integrated individual and government interventions on the epidemic in the long term using compartmental models. The maximum likelihood estimates of Re and the corresponding 95% confidence interval was 2.04 [95% CI: 1.82–2.27; 12th March-7th April 2020]. The Re estimate using the exponential growth method was 2.11 [95% CI: 2.00–2.24] within the same period. The Re estimate using time-dependent (TD) method showed a gradual decline of the Effective Reproductive Number since March 12, 2020 when the first 2 index cases were recorded but the rate of transmission remains high (TD: Re = 2.52; 95% CI: [1.87–3.49]). The current estimate of Re based on the TD method is 1.74 [95% CI: 1.41–2.10; (13th May 2020)] but with comprehensive integrated government and individual level interventions, the Re could reduce to 0.5 which is an indication of the epidemic dying out in the general population. Our results showed that enhanced government and individual-level interventions and the intensity of media coverage could have a substantial effect on suppressing transmission of new COVID-19 cases and reduced death rates in Ghana until such a time that a potent vaccine or drug is discovered.

1. Introduction

COVID-19 pandemic remains a major public health concern globally as the number of new cases and case fatalities keep increasing every day. As of May 16, 2020 at 16.13GMT, there were 4,628,879 cases and 308,655 deaths with 1,759,729 recoveries confirmed worldwide (Worldometer, 2020). The global spread has been rapid, with 213 Countries and Territories around the world now having reported at least one case (Worldometer, 2020). In Ghana, the first two index cases were recorded on the March 12, 2020 and by 13th May of 2020, the total number of cases was 4120 including 320 recoveries and 18 deaths.1

National governments have instituted measures in response to the pandemic. Such measures included lockdowns (partial or full) and enhanced safety protocols to control transmission. As part of an integrated intervention, the Government of Ghana adapted a partial lockdown in the two most affected cities, Greater Accra and Greater Kumasi for two weeks, which was extended for a further one week. This was concurrence with individual control measures (social distancing, enhanced contact tracing, handwashing and the use of hand sanitizers, and intensive media education), and government interventions (closure of schools, provision of personal protective equipment (PPE) to health workers, quarantine, self-isolation, hospitalization, and treatment). All the aforementioned interventions have been implemented in Ghana with the aim to prevent the spread of COVID-19 but no studies to date have evaluated its long term impact on the expected number of cases and deaths to inform policy decision.

The global nature of this pandemic with countries at difference levels of the epidemic curves, suggests that the crisis could be long. Clearly, economies cannot immediately return to how things were prior to the pandemic. But it is equally clear that the lockdown cannot persist indefinitely, because of its damaging impact on the economy and social life. We need to adapt and minimise the harm it can do, and continue to suppress the spread of the virus while ensuring that children are educated, that businesses can reopen, and that society can function. This will require continuous monitoring of transmission so that remedial measures can be re-instituted should there be a resurgence.

Measurement of transmission intensity is important to describe the intensity of the disease outbreak, to assess the impact of public health measures on transmission, to understand epidemiological patterns, and for planning intervention studies. The single most important measure of transmission intensity is the basic Reproductive number, R0. The R0 describes the number of cases, on average, an infected person will cause during their infectious period. To contain the virus, the R0 must be kept below 1, and this means minimising the risk of spreading the virus at every turn. When R0 is greater than 1, the virus will spread. It is equally important to bring down the number of new cases per day. Lowering the number of new cases per day as much as possible, together with an R0 below 1, will mean fewer cases and reduced harm.

The R0 for COVID-19 was recently estimated in the South Korea (Choi, Ki, & Health, 2020), China (Kucharski et al., 2020) and other countries, but limited evidence supports the applicability of R0 outside the region for which the value was estimated (Ridenhour, Kowalik, & Shay, 2018). Since Ro is a function of effective contact rate, any factor having the potential to influence the contact rate, including individual behavioral changes, other human social behavior, and organization, including population density (e.g., rural vs. urban), social organization (e.g., integrated vs. segregated), as well as the innate biological characteristics of particular pathogens, and seasonality (e.g., wet vs. rainy season for vector-borne infections), will ultimately affect Ro (Delamater, Street, Leslie, Yang, & Jacobsen, 2019).

In this study, we described the epidermic dynamics and estimated the R0 for COVID-19 in an entirely susceptible Ghanaian population using a mathematical model. We provided estimates of the initial basic Reproductive number (at the beginning of the outbreak) and the time-dependent Reproductive number at any time during the outbreak using four different estimation procedures: next-generation matrix (Odo Diekmann, Heesterbeek, & Roberts, 2010), exponential growth method (Wallinga & Lipsitch, 2007), maximum likelihood (White et al., 2009), and time-dependent Reproductive number method (Wallinga and Teunis (2004)). We also assessed the effects of individual and government level integrated interventions on cumulative incidence and new cases per day in Ghana.

2. Methods

2.1. Model data

The outbreak data for Ghana were cumulative numbers of confirmed cases and deaths obtained from the Ghana Health Service (GHS). The data from the GHS is a daily time series data of reported COVID-19 cases. These dataset do not include individual patient-level information, but aggregate number of total suspected and confirmed cases tested at the two main laboratory facilities at the University of Ghana (UG), and the Kwame Nkrumah University of Science and Technology (KNUST). At UG, the test is conducted at the Noguchi Memorial Institute of Medical Research, and at KNUST, the test is conducted at Kumasi Center for Collaborative Research in Tropical Medicine. COVID-19 testing was performed using real-time polymerase chain reaction (RT-PCR) with the DaAn RT-PCR SARS-CoV-2 detection kit (DaAn Gene Co. Ltd, Guangdong, China). The kit uses a one-step RT-PCR technique that selectively amplifies the ORF1ab and N genes of the SARS-CoV-2 and includes an endogenous internal control for quality control purposes thus, ensuing false negatives are reduced.

2.2. Model formulation

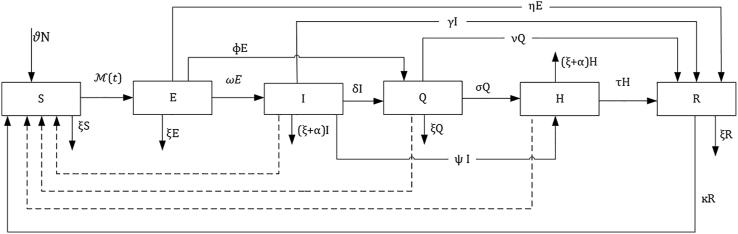
Although researchers do not fully understand the transmission dynamics of COVID-19, we formulated the SEIQHRS model (Fig. 1) based on the available information and the basic understanding of the biological mechanism through which infection spreads in the population. We partitioned the Ghanaian population into five distinct classes (S = susceptible, E = Exposed, I=Infectious, Q = Self-isolation/Quarantined, H=Hospitalized, R = Recovery). We defined susceptible populations as all uninfected individuals at time t but there is the likelihood there may be infected at time t+τ where τ is the incremental continuous-time point. We included newborn babies from all compartments into the susceptible class since there is not enough evidence on vertical transmission of the virus from the pregnant woman to the unborn baby. After successful transmission of COVID, the susceptible individuals S enter the exposed class $E$ where they are infected but not yet infectious to others. They stay in the exposed class before they become infectious and move to the infectious class $I$ or identified through contact tracing and quarantined at class $Q$. The hospitalized class $H$ is the proportion of the population who have been infected but have been identified through contact tracing or self-report to health facilities and hospitalized. We specified three modes of recovery based on the current understanding of the transmission dynamics. First, a fraction of the population who are exposed may recover from the infection without necessarily infecting others and therefore do not transit through the infectious category but enter directly into the recovery class $R$ because of boosted immunity. Second, those who become infectious may also recover and move to the recovery class (R) or die from COVID-19. Finally, those in the quarantine-based hospitals and those in self-isolation may also recover and join the recovery class. Individuals who live in Ghana and those arriving from other countries (Ghanaian citizens and non-citizens) who have not yet contracted COVID-19 were classified as susceptible. Thus, the total population size, $N$, is $N=S+E+I+Q+H+R$ .

Fig. 1.

Schematic representation of the flow of the SEIQHRS model. The dashed arrow indicates the need for interaction with the infectious, quarantine, or hospitalized compartments for disease transition to individuals in the susceptible class. $\mathcal{M}\left(\mathit{t}\right)=(\mathit{p}{\mathit{\beta }}_{\mathit{I}}\mathit{I}+{\mathit{\epsilon }}_{\mathit{Q}}{\mathit{\beta }}_{\mathit{Q}}\mathit{Q}+{\mathit{\epsilon }}_{\mathit{H}}{\mathit{\beta }}_{\mathit{H}}\mathit{H})$.

The experience we gather from the contact tracing being carried out by the Government of Ghana and commentary from some infectious disease experts globally showed that some individuals have come into contact with SARS- CoV-2 positive patients but were tested negative for SARS-CoV-2. We therefore assume that although people might have the infection, they may not instantaneously be infectious to others. As such we have specified and distinguished the exposed or the latent individuals from those who are infectious to others based on the traditional definition of an exposed person in infectious disease modeling. We agreed that there may be some exposed individuals capable of transmitting the infection but their overall impact of the dynamics of infection is assumed to be negligible in this study. Furthermore, studies have shown that individuals who recover from viral diseases usually would have either long-life immunity, short term immunity, or in some cases there may be no immunity at all (Keeling & Rohani, 2011). Since enough is not known about COVID-19, this study assumed that individuals who recover from COVID-19 may have short term immunity but once the immunity wanes; these individuals will become susceptible to the same or a different viral strain of COVID-19 (Lan et al., 2020). For the purpose of assessing government intervention, we define the quarantine-based hospitalized class to consists of all exposed and infectious individuals who were identified through contact tracing, isolation, and hospitalization. We further assumed that individuals leave the hospitalize class only after they have fully recovered from COVID-19 or when they suffer from COVID-19 disease-induced death or die naturally.

2.3. Parameterization of the SEIQHRS model

To provide a detailed understanding of the transmission of COVID-19 and the control strategies required to mitigate its spread and relative impact on the Ghanaian population and examine the epidemiology of the infection, we detailed the parameterization of the SEIQHRS model from which useful public health guidance can be generated (Table 1). Our SEIQHRS model has eleven parameters: the birth rate ($\vartheta$), natural death rate ($\xi )$, rate of transmission from being exposed to becoming infectious within the infectious community (${\beta }_I$). The rate of transmission from the quarantine class is ${\beta }_Q$ and that of transmission from the hospitalized class is denoted by ${\beta }_H$. $\rho \left(t\right)=e^{-(r\times \epsilon \times t)}$ is the time-dependent integrated individual-level intervention and the intensity of media coverage which is parameterized by two non-negative rates $r$ and $\epsilon =\frac{(E+I+Q+H+D)}{(S+E+I+Q+H+D)}$. $\epsilon$ is the proportion of COVID-19 positive cases and deaths in the population. $r$ is the rate of intensity of adherence to prevention guidelines by the individual and media coverage, We assume that the transmission rate also decreases with time as suggested by Chowell, Hengartner, Castillo-Chavez, Fenimore, and Hyman (2004), and this assumption also seems plausible because of the integrated interventions put out by the Government of Ghana. This assumption is similar to what was reported during the SARS epidemic of 2002–2003 where many people began to wear face masks to try to prevent disease spread through contact with airborne particles (Riley et al., 2003).

Table 1.

Epidemiological parameter estimates for the SEIQHRS compartmental model that fit the cumulative number of cases in Ghana.

Parameters	Biological meaning	Estimate	Scenario 1	Scenario 2	Scenario 3	Scenario 4	Scenario 5	Reference
N	The size of the total population in Ghana	30985230	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	a
$\xi$	The rate at which the individual in the susceptible, exposed, infectious, and recover classes suffer natural death. In this study, $\xi$ also represents the population crude birth rate.	$\frac{\frac{Deaths}{Person}}{Day}=\frac{\frac{7.218}{1000}}{365}=1.978\times {10}^{-5}da{y}^{-1}$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	b
$\vartheta$	Birth rate	$1.978\times {10}^{-5}da{y}^{-1}$	†	†	†	†	†	Assume to be same as the death rate
$r$	The intensity of individual-level intervention	$0\le r\le 1$	$\times$	$\times$	$\times$	$\times$	0.00001	Random selection for the purpose of assessing individual-level integrated intervention
${\beta }_I,$	Community transmission rate: The rate at which susceptible individuals become infected through contact with an infectious individual in the general population (${\beta }_I)$	0.168 $da{y}^{-1}$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	Estimated
${\beta }_H$	Hospital Transmission Rate: The rate at which susceptible individuals become infected through contact with a hospitalized person	$\frac{1}{5}\times 0.168=.0336$$da{y}^{-1}$	$\times$	$\surd$	$\surd$	$\surd$	$\surd$	Assumed
${\epsilon }_H$	Measures put in place to reduce the average contact rate at health facilities example use of PPEs	$0\le {\epsilon }_H<1$	1	1	0.95	$\surd$	$\surd$	Corresponding to 5% reduction
${\beta }_Q$	Quarantine/Self Isolation Transmission Rate: The rate at which susceptible individuals become infected through contact with self-isolated or quarantine person	$\frac{1}{5}\times 0.168=.0336$$da{y}^{-1}$	$\times$	$\surd$	$\surd$	$\surd$	$\surd$	Assumed
${\epsilon }_Q$	Measures put in place to reduce the average contact rate at quarantine centers eg example use of PPEs	$0\le {\epsilon }_Q\le 1$	1	1	0.95	$\surd$	$\surd$	Corresponding to 5% reduction
$\omega$	The rate at which an exposed person becomes infectious. $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\omega $}\right.$ represents the average duration of the exposed or latent period (that is the average amount of time spent in the $E$ class).	$\frac{1}{4.6}da{y}^{-1}$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$
$\gamma$	The rate of recovery of an infectious person who lives in the community. $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\gamma $}\right.$ is the average infectious period or time from Infection to recovery without hospitalization	$\frac{1}{14}$$da{y}^{-1}$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	Chen, Xiong, Bao, and Shi (2020)
$\mathit{\alpha }$	COVID-19 induced death rate	$\frac{1}{50}$$da{y}^{-1}$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	Narrative from the Ghana Health Service
$\mathit{\kappa }$	Rate of COVID-19 waning immunity. The rate at which those who recover from the disease become susceptible again over time	$\frac{1}{60}da{y}^{-1}$	†	†	†	†	†	Approximated value in Ghana
$\mathit{\tau }$	The rate at which those who are hospitalized recovers. That is, the time of hospitalization to recovery $\frac{1}{\tau }$	$\frac{1}{120}da{y}^{-1}$	$\times$	$\times$	$\times$	$\surd$	$\surd$	Extreme case scenario
$\mathit{\nu }$	The rate at which quarantine or self-isolated person recovers	$\frac{1}{120}da{y}^{-1}$	$\times$	$\times$	$\times$	$\surd$	$\surd$	Assumed extreme case scenario
$\mathit{\delta }$	The rate at which an infectious person is quarantined	$\frac{1}{120}da{y}^{-1}$	$\times$	$\surd$	$\surd$	$\surd$	$\surd$	Assumed extreme case scenario
$\mathit{\sigma }$	The rate at which quarantine or self-isolated person is hospitalized	$\frac{1}{10}da{y}^{-1}$	$\times$	$\surd$	$\surd$	$\surd$	$\surd$	Assumed extreme case scenario
$\mathit{\psi }$	The rate at which infectious individuals are identified through contact tracing and hospitalized	$\frac{1}{120}da{y}^{-1}$	$\times$	$\surd$	$\surd$	$\surd$	$\surd$	Assumed extreme case scenario
$\phi$	The rate at which an exposed person is quarantined	$\frac{1}{120}da{y}^{-1}$	$\times$	$\surd$	$\surd$	$\surd$	$\surd$
$\mathit{\eta }$	The rate at which an exposed person recovers without necessarily becoming infectious or being quarantined-that is the rate of self-recovery from COVID-19 without recover without medical intervention-Self immunity boosting	$\frac{1}{14}da{y}^{-1}$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	General knowledge on COVID-19

√: Parameter used in the projection; × ∶ Parameter set to zero; †: Not used.

^ahttps://worldpopulationreview.com/countries/ghana-population/: Based on projections of the latest United Nations data as at May 13, 2020.

^bhttps://www.macrotrends.net/countries/GHA/ghana/death-rate.

The parameter, $\rho \in [0,1]$ basically models the impact of behavioral change on reducing the effective reproduction number, cumulative number of cases and deaths similar to previous studies that model the impact of behavioral change as a result of intensive media education and increased rate social distancing based on the change in the daily cumulated number of cases and deaths (Shen, Xiao, & Rong, 2015; Tuncer, Mohanakumar, Swanson, & Martcheva, 2018). $\rho =0$ indicates perfect adherence to COVID-19 prevention protocols (positive behavioral change) and $\gamma$ represents the rate of recovery among the infectious class, $\alpha$ is COVID-19 induced death rate, and $\kappa$ is the rate of COVID-19 waning immunity (rate of moving from recovered class to the susceptible class). The rate at which an exposed individual recovers without necessarily becoming infectious to others is denoted by $\eta$. The rate at which infectious and exposed individuals are removed from the exposed and infectious classes respectively and quarantine is $\delta$ and $\phi$ respectively. The community infectious and quarantine classes are hospitalized at a rate of $\psi$ and $\sigma$ respectively. The quarantined and hospitalized individuals recover at a rate of $\nu$ and $\tau$ respectively.

Furthermore, in determining the effective contact rate and the duration of infectiousness, this study assumed homogenous population mixing and contact patterns where all population members are equally likely to come into contact with one another because of the typical Ghanaian culture, social attributes, and settings. Admittedly, heterogeneous mixing, where there is possible variation in contact patterns among age subgroups, social class, religious affiliations, or geographic regions would have been appropriate but data available to estimate the parameter of interest for these different subgroups of the population would have been near impossible. Furthermore, we assumed that the rate at which susceptible individuals are quarantined is the same as the rate at which susceptible individuals will return to the susceptible class after laboratory results have proved negative. We assumed unstructured populations, that is, we did not account for age or sex structure and therefore assumed a fixed value for the transmission rate using available data from the cumulative number of cases. However, our model can be adopted to include difference sociodemographic/economic classes, which would require splitting each variable of the model into specific classes if data are available.

The following system of differential equations (1.1), (1.6) describes the transmission dynamics of COVID-19 in Ghana. This system of ODEs was solved numerically via the standard Runge–Kutta method using the function ode from the package deSolve (Soetaert, Petzoldt, & Setzer, 2010). $\rho$ in equation (1.1), (1.2a), (1.2b) with the was substituted with the exponential term $e^{-(r\times t\times \left(\frac{E+I+Q+H+D}{S+E+I+Q+H+D}\right)}$ before solving the systems of differential equation.

$$\frac{dS}{dt}=\vartheta N+\kappa R-\xi S-\frac{\left(p{\beta }_{I}I+{\epsilon }_Q{\beta }_{Q}Q+{\epsilon }_H{\beta }_{H}H\right)}{N}S$$ (1.1)

$$\frac{dE}{dt}=\frac{\left(p{\beta }_{I}I+{\epsilon }_Q{\beta }_{Q}Q+{\epsilon }_H{\beta }_{H}H\right)}{N}S-\left(\omega +\eta +\xi +\phi \right)E$$ (1.2a)

$$\frac{dI}{dt}=\omega E-\left(\delta +\gamma +\xi +\alpha +\psi \right)I$$ (1.3a)

$$\frac{dQ}{dt}=\phi E+\delta I-\left(\xi +\nu +\sigma \right)Q$$ (1.4a)

$$\frac{dH}{dt}=\sigma Q+\psi I-(\tau +\xi +\alpha )H$$ (1.5a)

$$\frac{dR}{dt}=\eta E+\gamma I+\tau H+\nu Q-(\kappa +\xi )R$$ (1.6)

With $N=S+E+I+Q+H+R$, this dynamic system has four infected states; E, I, $Q$ and $H$ and two uninfected states $S$ and $R$. For assessing the impact of the intervention, we kept track of the number of cumulative deaths and cases at time $t$. Thus $\frac{dC}{dt}=\left(\omega +\eta +\xi +\phi \right)E$ is the total number of cumulative cases at time $t$ and let $\frac{dD}{dt}=\alpha \left(I+H\right)$ represent the cumulative number of COVID-19 induced deaths at time $t$. The effect of importation of COVID-19 infections was explored numerically through simulations. The study only considered constant-valued parameters with the exception of the proportion of the population adhering to the integrated government interventions.

2.4. Estimation of model parameters

Limited data and lack of clear understanding of the etiology of the disease spread place severe restrictions on the attempt to model the dynamics of COVID-19. Nonetheless, this study relied on previous studies and the ongoing discussions from experts at the Ghana Health Service and around the world to initialize the model parameters. The transmission rate ${\beta }_I$ in the community was estimated from the observed number of cases using the non-linear least square estimation via Levenberg-Marquardt algorithm that minimizes the sum of squared error between the observed cumulative number of cases and predicted cumulative cases. Other parameters were carefully chosen to fit our definition of worst-case scenario. The systems of differential equations were analysed using the “desolve” package in R (Soetaert et al., 2010) and the estimation of $Re$ using the method of maximum likelihood, time-dependent procedure and the exponential growth methods were done using the “$R_0$” package in $R$ (Obadia, Haneef, Boëlle, & making, 2012). The $R_0$ estimate using the exponential growth and the maximum likelihood methods is dependent on the choice of generation time and therefore sensitivity analysis was conducted to determine the how $R_0$ changes with generation time for exponential growth and the maximum likelihood methods.

2.5. Estimation of the basic reproductive number

2.5.1. The next generation matrix

We derived the effective basic Reproductive from our dynamic system in model 1.1–1.6. We used the next-generation matrix $K$ proposed by Diekmann, Heesterbeek, and Metz (1990); (Diekmann et al., 2010) to estimate the basic reproductive number which is the dominant eigenvalue of $K$. To compute $R_0$, we created a sub-model that only considers the ‘disease’ compartments, a subset of the equations in the SEIQHRS model. The disease compartments are those that include individuals that are in any stage of infection which, for the SEIQHRS model, includes both the exposed, infectious, and quarantine individuals. We only used the latent class as our transmission state of our dynamic models as that was the only state that described the production of new COVID-19 infections and used both the latent, infectious, quarantine and hospitalized classes to represent the transition states; that is changes in the state among infected individuals. The linearized infection subsystem with four infected states is as follows:

$$E^1=\frac{\left(p{\beta }_{I}I+{\epsilon }_Q{\beta }_{Q}Q+{\epsilon }_H{\beta }_{H}H\right)}{N}S-\left(\omega +\eta +\xi +\phi \right)E$$ (1.2b)

$$I^1=\omega E-\left(\delta +\gamma +\xi +\alpha +\psi \right)I$$ (1.3b)

$$Q^1=\phi E+\delta I-\left(\xi +\nu +\sigma \right)Q$$ (1.4b)

$$H^1=\sigma Q+\psi I-(\tau +\xi +\alpha )H$$ (1.5b)

The NGM is composed of two key components: The transmission $F$ and the transition $V^{-1}$.

$F=\left[\frac{\partial F_i\left(x_0\right)}{\partial x_j}\right]$ are the new infections while the $V=\left[\frac{\partial V_i\left(x_0\right)}{\partial x_j}\right]$ transfer of infections from one compartment to another. $x_0$ is the disease-free equilibrium state.

From these two equations, the Jacobian matrix at the DFE gives the characteristic equation.

$$F_1=\frac{\left(p{\beta }_{I}I+{\epsilon }_Q{\beta }_{Q}Q+{\epsilon }_H{\beta }_{H}H\right)}{N}S$$

$F_2=F_3=F_4=0$ because no new infections enter the $I$, $Q,$ and $H$ compartments but, rather they transition from the $E$ compartment into the $I,Q,$ and $H$ compartments.

$$F=\left[\begin{array}{l}{F}_1\hfill \\ F_2\hfill \\ \begin{array}{l}{F}_3\hfill \\ F_4\hfill \end{array}\hfill \end{array}\right]=\left[\begin{array}{l}\frac{\left(p{\beta }_{I}I+{\epsilon }_Q{\beta }_{Q}Q+{\epsilon }_H{\beta }_{H}H\right)S}{N}\hfill \\ 0\hfill \\ \begin{array}{l}0\hfill \\ 0\hfill \end{array}\hfill \end{array}\right],V=\left[\begin{array}{l}{V}_1\hfill \\ V_2\hfill \\ \begin{array}{l}{V}_3\hfill \\ V_4\hfill \end{array}\hfill \end{array}\right]=\left[\begin{array}{l}-\left(\omega +\eta +\xi +\phi \right)E\hfill \\ \omega E-\left(\delta +\gamma +\xi +\alpha +\psi \right)I\hfill \\ \begin{array}{l}\phi E+\delta I-\left(\xi +\nu +\sigma \right)Q\hfill \\ \sigma Q+\psi I-(\tau +\xi +\alpha )H\hfill \end{array}\hfill \end{array}\right]$$

$$F=\left[\begin{array}{lll}\begin{array}{l}\frac{\partial F_1}{\partial E}\hfill \\ \frac{\partial F_2}{\partial E}\hfill \end{array}\hfill & \begin{array}{l}\frac{\partial F_1}{\partial I}\hfill \\ \frac{\partial F_2}{\partial I}\hfill \end{array}\hfill & \begin{array}{l}\begin{array}{ll}\frac{\partial F_1}{\partial Q}\hfill & \frac{\partial F_1}{\partial H}\hfill \end{array}\hfill \\ \begin{array}{ll}\frac{\partial F_2}{\partial Q}\hfill & \frac{\partial F_2}{\partial H}\hfill \end{array}\hfill \end{array}\hfill \\ \frac{\partial F_3}{\partial E}\hfill & \frac{\partial F_3}{\partial I}\hfill & \begin{array}{ll}\frac{\partial F_3}{\partial Q}\hfill & \frac{\partial F_3}{\partial H}\hfill \end{array}\hfill \\ \frac{\partial F_4}{\partial E}\hfill & \frac{\partial F_4}{\partial I}\hfill & \begin{array}{ll}\frac{\partial F_4}{\partial Q}\hfill & \frac{\partial F_4}{\partial H}\hfill \end{array}\hfill \end{array}\right]\Rightarrow F\left(x\right)=\left(\begin{array}{lll}\begin{array}{l}0\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{l}\frac{p{\beta }_{I}S}{N}\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{l}\begin{array}{ll}\frac{{\epsilon }_Q{\beta }_{Q}S}{N}\hfill & \frac{{\epsilon }_H{\beta }_{H}S}{N}\hfill \end{array}\hfill \\ \begin{array}{ll}0\hfill & 0\hfill \end{array}\hfill \end{array}\hfill \\ 0\hfill & 0\hfill & \begin{array}{ll}0\hfill & 0\hfill \end{array}\hfill \\ 0\hfill & 0\hfill & \begin{array}{ll}0\hfill & 0\hfill \end{array}\hfill \end{array}\right)$$

At DFE, $S=N$ and we have

$$F\left(x\right)=\left(\begin{array}{lll}\begin{array}{l}0\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{l}p{\beta }_I\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{l}\begin{array}{ll}{\epsilon }_Q{\beta }_Q\hfill & {\epsilon }_H{\beta }_H\hfill \end{array}\hfill \\ \begin{array}{ll}0\hfill & 0\hfill \end{array}\hfill \end{array}\hfill \\ 0\hfill & 0\hfill & \begin{array}{ll}0\hfill & 0\hfill \end{array}\hfill \\ 0\hfill & 0\hfill & \begin{array}{ll}0\hfill & 0\hfill \end{array}\hfill \end{array}\right)$$

$$V\left(x\right)=\left[\begin{array}{lll}\begin{array}{l}\frac{\partial V_1}{\partial E}\hfill \\ \frac{\partial V_2}{\partial E}\hfill \end{array}\hfill & \begin{array}{l}\frac{\partial V_1}{\partial I}\hfill \\ \frac{\partial V_2}{\partial I}\hfill \end{array}\hfill & \begin{array}{l}\begin{array}{ll}\frac{\partial V_1}{\partial Q}\hfill & \frac{\partial V_1}{\partial H}\hfill \end{array}\hfill \\ \begin{array}{ll}\frac{\partial V_2}{\partial Q}\hfill & \frac{\partial V_2}{\partial H}\hfill \end{array}\hfill \end{array}\hfill \\ \frac{\partial V_3}{\partial E}\hfill & \frac{\partial V_3}{\partial I}\hfill & \begin{array}{ll}\frac{\partial V_3}{\partial Q}\hfill & \frac{\partial V_3}{\partial H}\hfill \end{array}\hfill \\ \frac{\partial V_4}{\partial E}\hfill & \frac{\partial V_4}{\partial I}\hfill & \begin{array}{ll}\frac{\partial V_4}{\partial Q}\hfill & \frac{\partial V_4}{\partial H}\hfill \end{array}\hfill \end{array}\right]$$

$$\Rightarrow \mathit{V}\left(\mathit{x}\right)=\left(\begin{array}{lll}-\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }+\phi \right)\mathit{\omega }\hfill & 0-\left(\mathit{\delta }+\mathit{\gamma }+\mathit{\xi }+\mathit{\alpha }+\mathit{\psi }\right)\hfill & \begin{array}{l}\begin{array}{ll}0\hfill & 0\hfill \end{array}\hfill \\ \begin{array}{ll}0\hfill & 0\hfill \end{array}\hfill \end{array}\hfill \\ \phi \hfill & \mathit{\delta }\hfill & \begin{array}{ll}-\left(\mathit{\xi }+\mathit{\nu }+\mathit{\sigma }\right)\hfill & 0\hfill \end{array}\hfill \\ 0\hfill & \mathit{\psi }\hfill & \begin{array}{ll}\mathit{\sigma }\hfill & -(\mathit{\tau }+\mathit{\xi }+\mathit{\alpha })\hfill \end{array}\hfill \end{array}\right)$$

$${\mathit{V}}^{-1}\left(\mathit{x}\right)=\left[\begin{array}{lll}\begin{array}{l}\frac{-1}{\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }+\phi \right)}\hfill \\ \frac{-\mathit{\omega }}{\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }+\phi \right)\left(\mathit{\delta }+\mathit{\gamma }+\mathit{\xi }+\mathit{\alpha }+\mathit{\psi }\right)}\hfill \end{array}\hfill & \begin{array}{l}0\hfill \\ \frac{-1}{\left(\mathit{\delta }+\mathit{\gamma }+\mathit{\xi }+\mathit{\alpha }+\mathit{\psi }\right)}\hfill \end{array}\hfill & \begin{array}{ll}\begin{array}{l}0\hfill \\ 0\hfill \end{array}\hfill & \begin{array}{l}0\hfill \\ 0\hfill \end{array}\hfill \end{array}\hfill \\ \frac{-(\mathit{\alpha }\phi +\mathit{\delta }\mathit{\omega }+\mathit{\delta }\phi +\mathit{\gamma }\phi +\phi \mathit{\psi }+\phi \mathit{\xi })}{\left(\mathit{\xi }+\mathit{\nu }+\mathit{\sigma }\right)\left(\mathit{\delta }+\mathit{\gamma }+\mathit{\xi }+\mathit{\alpha }+\mathit{\psi }\right)\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }+\phi \right)}\hfill & \frac{-\mathit{\delta }}{\left(\mathit{\xi }+\mathit{\nu }+\mathit{\sigma }\right)\left(\mathit{\delta }+\mathit{\gamma }+\mathit{\xi }+\mathit{\alpha }+\mathit{\psi }\right)}\hfill & \begin{array}{ll}\frac{-1}{\left(\mathit{\xi }+\mathit{\nu }+\mathit{\sigma }\right)}\hfill & 0\hfill \end{array}\hfill \\ \frac{-(\mathit{\alpha }\phi \mathit{\sigma }+\mathit{\omega }\mathit{\nu }\mathit{\psi }+\mathit{\delta }\mathit{\omega }\mathit{\sigma }+\mathit{\delta }\phi \mathit{\sigma }+\mathit{\gamma }\phi \mathit{\sigma }+\mathit{\omega }\mathit{\psi }\mathit{\sigma }+\phi \mathit{\psi }\mathit{\sigma }+\mathit{\xi }\mathit{\omega }\mathit{\psi }+\mathit{\xi }\phi \mathit{\sigma })}{(\mathit{\tau }+\mathit{\xi }+\mathit{\alpha })\left(\mathit{\xi }+\mathit{\nu }+\mathit{\sigma }\right)\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }+\phi \right)\left(\mathit{\delta }+\mathit{\gamma }+\mathit{\xi }+\mathit{\alpha }+\mathit{\psi }\right)}\hfill & \frac{-(\mathit{\nu }\mathit{\psi }+\mathit{\delta }\mathit{\sigma }+\mathit{\psi }\mathit{\sigma }+\mathit{\xi }\mathit{\psi })}{(\mathit{\tau }+\mathit{\xi }+\mathit{\alpha })\left(\mathit{\xi }+\mathit{\nu }+\mathit{\sigma }\right)\left(\mathit{\delta }+\mathit{\gamma }+\mathit{\xi }+\mathit{\alpha }+\mathit{\psi }\right)}\hfill & \begin{array}{ll}\frac{-\mathit{\sigma }}{(\mathit{\tau }+\mathit{\xi }+\mathit{\alpha })\left(\mathit{\xi }+\mathit{\nu }+\mathit{\sigma }\right)}\hfill & \frac{-1}{(\mathit{\tau }+\mathit{\xi }+\mathit{\alpha })}\hfill \end{array}\hfill \end{array}\right]$$

The dominant eigenvalue of the Next Generation Matrix $K=-F{V}^{-1}$ is equal to $R_0$ which we obtained by solving $R_0=\rho \left(\text{Κ}\right).$ $\rho$ is the spectral radius (i.e the eigenvalue with the largest magnitude) of $\text{Κ}$. We solved $\left|K-\lambda I\right|=0$ to derive the basic reproductive number. The effective reproductive number $R_e$ is given by

$$R_e=\frac{\mathit{\omega }\mathit{p}{\mathit{\beta }}_{\mathit{I}}}{\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }+\phi \right)\left(\mathit{\delta }+\mathit{\gamma }+\mathit{\xi }+\mathit{\alpha }+\mathit{\psi }\right)}+\frac{(\mathit{\alpha }\phi +\mathit{\delta }\mathit{\omega }+\mathit{\delta }\phi +\mathit{\gamma }\phi +\phi \mathit{\psi }+\phi \mathit{\xi }){\mathit{\epsilon }}_{\mathit{Q}}{\mathit{\beta }}_{\mathit{Q}}}{\left(\mathit{\xi }+\mathit{\nu }+\mathit{\sigma }\right)\left(\delta +\gamma +\xi +\alpha +\psi \right)\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }+\phi \right)}+\frac{(\mathit{\alpha }\phi \mathit{\sigma }+\mathit{\omega }\mathit{\nu }\mathit{\psi }+\mathit{\delta }\mathit{\omega }\mathit{\sigma }+\mathit{\delta }\phi \mathit{\sigma }+\mathit{\gamma }\phi \mathit{\sigma }+\mathit{\omega }\mathit{\psi }\mathit{\sigma }+\phi \mathit{\psi }\mathit{\sigma }+\mathit{\xi }\mathit{\omega }\mathit{\psi }+\mathit{\xi }\phi \mathit{\sigma }){\mathit{\epsilon }}_{\mathit{H}}{\mathit{\beta }}_{\mathit{H}}}{(\mathit{\tau }+\mathit{\xi }+\mathit{\alpha })\left(\mathit{\xi }+\mathit{\nu }+\mathit{\sigma }\right)\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }+\phi \right)\left(\mathit{\delta }+\mathit{\gamma }+\mathit{\xi }+\mathit{\alpha }+\mathit{\psi }\right)}$$

Simplified to:

$$R_e=\frac{\mathit{\omega }\mathit{p}{\mathit{\beta }}_{\mathit{I}}}{\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }+\phi \right)\left(\mathit{\delta }+\mathit{\gamma }+\mathit{\xi }+\mathit{\alpha }+\mathit{\psi }\right)}+{\mathit{\epsilon }}_{\mathit{Q}}{\mathit{\beta }}_{\mathit{Q}}\left[\frac{\phi }{\left(\mathit{\xi }+\mathit{\nu }+\mathit{\sigma }\right)\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }+\phi \right)}+\frac{\mathit{\delta }\mathit{\omega }}{\left(\mathit{\xi }+\mathit{\nu }+\mathit{\sigma }\right)\left(\delta +\gamma +\xi +\alpha +\psi \right)\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }+\phi \right)}\right]+{\mathit{\epsilon }}_{\mathit{H}}{\mathit{\beta }}_{\mathit{H}}\left[\frac{\phi \mathit{\sigma }}{(\mathit{\tau }+\mathit{\xi }+\mathit{\alpha })\left(\mathit{\xi }+\mathit{\nu }+\mathit{\sigma }\right)\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }+\phi \right)}+\frac{\mathit{\omega }\mathit{\psi }}{(\mathit{\tau }+\mathit{\xi }+\mathit{\alpha })\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }+\phi \right)\left(\mathit{\delta }+\mathit{\gamma }+\mathit{\xi }+\mathit{\alpha }+\mathit{\psi }\right)}+\frac{\mathit{\delta }\mathit{\omega }\mathit{\sigma }}{(\mathit{\tau }+\mathit{\xi }+\mathit{\alpha })\left(\mathit{\xi }+\mathit{\nu }+\mathit{\sigma }\right)\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }+\phi \right)\left(\mathit{\delta }+\mathit{\gamma }+\mathit{\xi }+\mathit{\alpha }+\mathit{\psi }\right)}\right]$$

${\mathit{R}}_{\mathit{e}}={\mathit{R}}_{\mathit{eI}}+{\mathit{R}}_{\mathit{eQ}}+{\mathit{R}}_{\mathit{eH}}$ is the contribution of infectious individuals in the general population, quarantine class, and hospital infectives to the overall $R_e$.

$R_e$ is defined as the number of secondary infections caused by a single infectious individual introduced into a completely susceptible population in the presence of control measures (individual and government interventions) in place. Assuming there is no intervention (quarantine, isolation, hospitalization, and treatment), then $\phi =\mathit{\psi }=\mathit{\tau }=\mathit{\sigma }=\mathit{\nu }=\mathit{\delta }=0$, and $\mathit{p}=1,$ the basic reproductive number $R_0$ estimated before the implementation of all interventions is given by

$${\mathit{R}}_0=\frac{\mathit{\omega }{\mathit{\beta }}_{\mathit{I}}}{\left(\mathit{\omega }+\mathit{\eta }+\mathit{\xi }\right)\left(\mathit{\gamma }+\mathit{\xi }+\mathit{\alpha }\right)}\dots \dots .\left(1.8\right)$$

2.5.2. The maximum likelihood estimates

We also estimated the effective basic reproductive number $R_{e,}$ and the generation time using the maximum likelihood-based method proposed by Forsberg White and Pagano (2008). The generation time is the time lag between infection in a primary case and a secondary case. The estimates were based on readily available daily reported case data. The estimation of ${\text{R}}_{0,}$ and the generation time for COVID-19 based on the maximum likelihood is important since the estimate can be obtained in real-time to quantify the impact of government intervention and inform an appropriate public health response to the COVID-19. The generation time was assumed to follow a gamma distribution with mean 6.5 days (N. M. Ferguson, Laydon, Nedjati Gilani, et al., 2020) and a standard deviation of 2 days. The number of new cases recorded per day was assumed to follow the Poisson distribution. The maximum likelihood for $R_{0,}$ in terms of the generation, time is given by$\mathcal{L}\left({\text{R}}_{0,}\text{p}\right)=\prod _{\text{t}=1}^{\text{T}}\frac{{\text{e}}^{-{\mathrm{\mu }}_{\text{t}}}{{\mathrm{\mu }}_{\text{t}}}^{{\text{N}}_{\text{t}}}}{{\text{N}}_{\text{t}}!},$ where ${\mathrm{\mu }}_{\text{t}}={\text{R}}_0\sum _{\text{j}=1}^{\text{min}(\text{k},\text{t})}{\text{N}}_{\text{t}-\text{j}}{\text{p}}_{\text{j}}$, ${\text{N}}_{\text{t}}$ represent the incident data, ${\text{p}}_{\text{j}}$ is the generation time with $\text{j}=1,\dots ,\text{k}$, $T$ is the most recent time point of observation in the early epidemic growth stage of the disease (Forsberg White & Pagano, 2008). We imputed unobserved cases at the beginning of the epidemic to correct for missing data.

2.5.3. Exponential growth estimate

This study employed the exponential growth method proposed by Wallinga and Lipsitch (2007) to estimate the initial basic Reproductive number within the first 30 days of the epidemic in Ghana. The exponential growth rate, denoted by $r$, is defined by the per capita change in the number of new cases per unit of time. Since incidence data are typical count data and follows the Poisson distribution, Poisson regression model was used to estimate $r.$ Wallinga and Lipsitch (2007) showed that the basic reproductive number $R_0=\frac{1}{\mathcal{M}(-r)}$ where $\mathcal{M}$ is the moment generating function of the (discretized) generation time distribution. To determine a period in the epidemic curve over which growth is exponential, we employed a deviance based $R$-squared statistic proposed by Obadia, Haneef, and Boëlle (2012).

2.5.4. Time-dependent estimate

The study also estimated time-varying basic reproductive numbers for COVID-19 using the technique proposed by Wallinga and Teunis (2004). The time-dependent Ro computes the basic Reproductive numbers by averaging over all transmission networks compatible with observations. The effective reproductive number for case $j$ is given by $R_j=\sum i{p}_{ij}$ where $p_{ij}=\frac{N_{i}w(t_i-t_k)}{{\sum }_{i\ne j}{N}_{i}w(t_i-t_k)}$ is the probability that case $i$ with onset at time $t_i$ was infected by case $j$ with onset at time $t_j$. These are averaged as $R_t=\frac{1}{N_t}\sum _{\left\{t_j=t\right\}}{R}_j$.

2.6. Forecasting early epidemic dynamics in Ghana

We employed a two-parameter generalized-growth model (GGM) (Viboud, Simonsen, & Chowell, 2016) to characterize COVID-19 epidemic growth in Ghana. The change in the number of new cases per unit time is given by $\frac{dC\left(t\right)}{dt}=rC{\left(t\right)}^p$ where $r$ is the intrinsic growth rate and $p\in \left[\mathrm{0,1}\right]$ is the deceleration growth parameter. The solution to the differential equation $\frac{dC\left(t\right)}{dt}$ is$C\left(t\right)$, that is, the cumulative number of cases per unit time (days). We estimated both $r$ and $p$using the non-linear least square estimation procedure in Stata 16 (StataCorp, College Station, TX, USA). This was achieved by fitting the model to cumulative time series data between March 12, 2020 to April 7, 2020. The estimated parameters of the model were then used to forecast the early growth of the epidemic in Ghana.

2.7. Interventions

This study developed and utilized a mathematical model that incorporates intervention strategies for COVID-19. Although there is no vaccine yet for COVID-19, the Government of Ghana and other countries have initiated several interventions to reduce new infections. Our study simulated two modes of interventions. The first is the individual level integrated intervention which includes social distancing, use of face mask, use of hand sanitizers, self-confinement, and use of running water with soap to wash hands. The integrated government interventions include the provision of personal protective equipment, contact tracing, self-isolation based on contact tracing of an index positive case, quarantining, and the intensity of media coverage in selected areas. Key among these interventions in Ghana was partial lockdown placed within the Greater Accra and the Greater Kumasi in the Ashanti Region, but we do not study its impact since it was lifted in less than three weeks and also we do not foresee the government re-introducing the lockdown to other parts of the country as it is perceived to be highly unsustainable in the country .2 The individual and government integrated interventions work instantaneously although the process is complex, capital and labor-intensive, and requires a great deal of commitment. Almost all the interventions focus on the susceptible population and the population of infectives as the interaction between the two subclasses would likely lead to onward transmission of the virus to the larger population. Studies have shown that isolation is effective against any infectious disease even when the etiology of the disease is largely unknown (Keeling & Rohani, 2011). We model five scenarios of the intervention to examine their likely impact on the dynamics of the epidemic. Specifically, by studying the different scenarios we examine the likely impact of government and individual-level interventions on the worse-case scenario of COVID-19 in Ghana.

Scenario 1: First, we modeled the worse-case scenario where we assume that there is no government or individual level interventions and that the individual can only recover from COVID-19 through pure natural process (immune system boosting). We defined this scenario as the normal-life situation.

Scenario 2: Second, we modeled the impact of enhanced contact tracing on worst-case scenario 1 and further assume that isolation and treatment centers can transmit the infection to the general public and medical staff at a rate that is one-five of the community transmission rate.

Scenario 3: Third, we assessed the impact of enhanced contact tracing on worst-case scenario 1 and further assume that the rate at which isolation and treatment centers will transmit the infection to the general public and medical staff will be reduced by at most 10% (5% reduction from the isolation centers and 5% reduction from hospitals). This is achieved by providing personal protective equipment to frontline line health workers and enforcing strict adherence to isolation protocols to prevent transmission of infection at the centers.

Scenario 4: We modeled scenario 3 in addition to effective case management. That is, we introduced a gradual increase in the rate of recovery among the quarantine and hospitalized classes.

Scenario 5: We modeled scenario 4 in addition to improved individual level interventions-social distancing, use of hand sanitizers, use of face mask, washing hands with running water with soap, and avoidance of social gathering and intensive media coverage.

3. Results

3.1. Distribution of COVID-19 cases

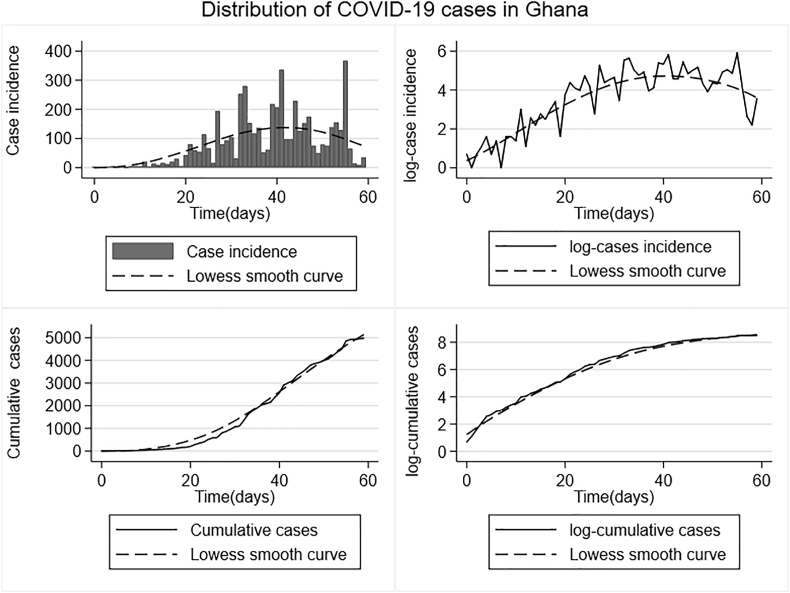
As of May 13th, 2020, Ghana had a total of 5530 confirmed cases of COVID-19 with 674 recoveries and a total of 24 COVID-19 related deaths resulting in a case fatality rate of 0.43%. The Greater Accra region is currently the epicenter with 4204 confirmed cases. The highest daily number of new cases recorded is 367 (Fig. 2). The Regional distribution of cases can be found at the official Ghana Health Service website (https://ghanahealthservice.org/covid19/).

Fig. 2.

The distribution of COVID-19 cases in Ghana.

3.2. Forecast of early epidemic in Ghana

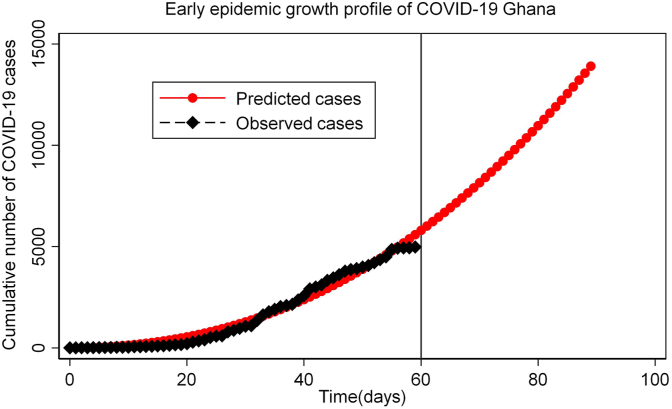
The generalized growth model (GGM) (Chowell, Sattenspiel, Bansal, & Viboud, 2016) which is characterized by the initial growth rate $r,$the deceleration parameter $p$ were jointly estimated using nonlinear least square estimation procedure ($R^2=99.3,RMSE=70.52$). The results of the GGM showed that the epidemic profile follows sub-exponential growth in the cumulative number of cases with an average growth rate of 1.66 [95% CI: 1.32–1.99] and deceleration growth parameter of 0.56 [95%: 0.52–0.59] within the first 60 days of epidemic assuming that Ghana recorded 2 index cases at the start of the epidemic. The expected number of cases is projected to rise within the first 90 days of the epidemic with total case count of 13907 (9733–18079). The distribution of cases and the projection of a 90-day epidemic profile can be found in Fig. 3.

Fig. 3.

Early forecast of epidemic growth using the generalized growth model with a growth rate of 1.66 and deceleration of growth parameter 0.56 and the initialize at $\mathit{y}\left(0\right)=2$. Left part of the vertical line represents observed data set used in fitting the model. Right part of the vertical line is the projections based on the model.

3.3. Estimation of the effective reproductive number

The $R_e$ estimates from all the three methods (exponential growth, time dependent and maximum likelihood) exceeded the threshold figure of 1 indicating the possibility of a higher transmission potential of the infection in the communities if the Government does not significantly improve the currently integrated intervention. The time dependent Ro rapidly declined from 10.3 (95% CI: 8.3, 12.4) in the first disease generation to 2.2 (95% CI: 1.9, 2.8) in the second disease generation, assuming a gamma-distributed generation interval with the mean of 6.5 days and standard deviation of 2 days. The current estimate of $R_e$ based on the time dependent method is 1.74 [95% CI: 1.41–2.10; (13th May 2020)]. The estimated $R_e$ from the four different methods can be found in Table 2 below.

Table 2.

Estimation of the initial Reproductive number by three different methods.

Method	Point estimate; ${\mathit{R}}_0$ [95% CI
Maximum Likelihood	2.02 [1.84–2.20]
Maximum Likelihood with missing value bias corrected	1.97 [1.80–2.15]
Exponential Growth	2.11 [2.00–2.24]
Time dependent	2.52 [1.87–3.49]

Note: For the TD method, daily estimates were averaged over the first 38 days and confidence interval was obtained using 1000 bootstrap simulations. The Bias corrected Maximum Likelihood (ML) method corrects the bias in the Reproductive number estimate occurring in method ML when the epidemic curve is not observed from the first case on (Obadia et al., 2012). The confidence limit of the next generation matrix was obtained using Markov Chain Monte Carlo.

3.4. Sensitivity analysis of ${\mathit{R}}_{\mathit{e}}$estimates

This study varied the generation time between 4 and 14 days with a standard deviation of 1 day. The graph of the basic Reproductive number versus mean generation time in days showed that the Ro estimates increases with increasing mean generation time for both ML and EG as expected (Nishiura, Castillo-Chavez, Safan, & Chowell, 2009) (Fig. 4). To obtain a correct estimate of the average generation time and to make data-driven policy decisions, there is the urgent need for more data on generation time (Peak et al., 2020).

Fig. 4.

Sensitivity analysis according to choice of generation time for Maximum Likelihood (ML) and Exponential Growth Methods (EG).

3.5. Effects of integrated government interventions on cumulative incidence, deaths and effective reproductive number

3.5.1. Simulation results-SEIQHRS model

Five different scenarios were studied to understand the trajectory of the epidemic. We forecast a range of possible future scenarios by assessing the impact of various individual and integrated government interventions. This section presents the results of the different intervention scenarios and the expected impact on COVID-19 deaths and total cumulative cases.

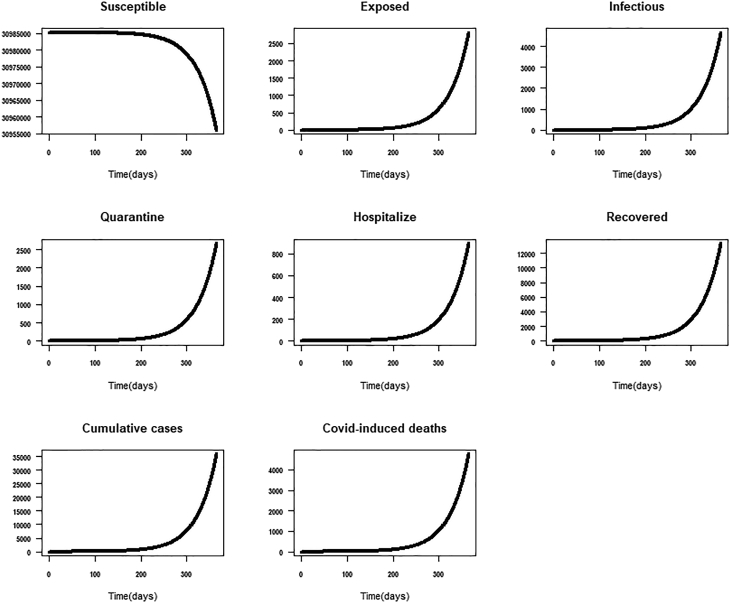
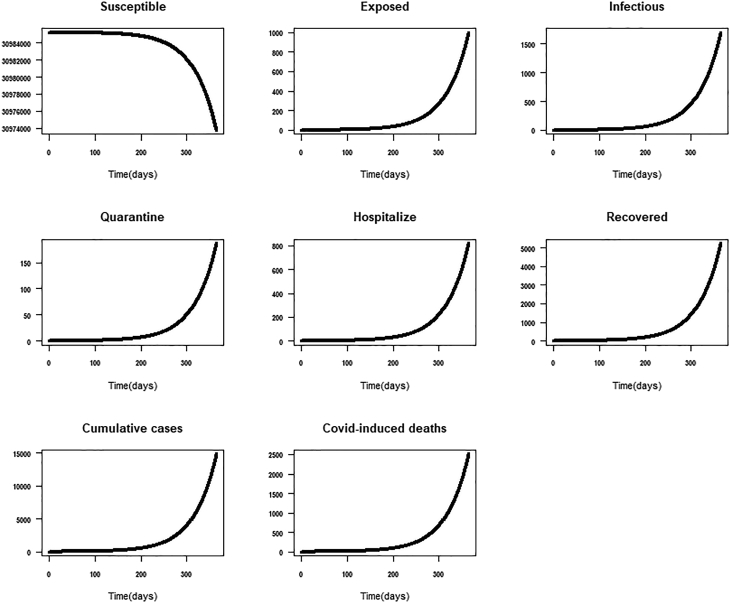
Scenario 1: It represents the worse case scenario. We defined the worst-case scenario as the social-cultural and political life of the individual and the country at large before the first two index cases of COVID-19 were reported in Ghana. That is before the March 12, 2020, there were no government and individual-level interventions to address COVID-19. Had the situation remained the same, we explore what would have been the total number of expected cases and deaths assuming that the epidemic lasted a year-long (March 12, 2021). The worse case scenario assumes that because of the immune system, some individuals could have recovered from COVID-19 without being quarantined or hospitalized for special care. The expected total cumulative number of cases, deaths and $R_0$ assuming a worst-case scenario was 81009 [64002-98017], 10484 [8284–12685], 1.4 respectively (Table 3; Fig. 5).

Table 3.

Effects of integrated government interventions on cumulative incidence, deaths and basic reproductive number.

Scenario	No. cumulative cases	No. deaths	$R_0,R_e$
1: Worse-case scenario. No government or individual level interventions but assuming individual can recover when exposed with their normal immune system: normal-life situation	81009 [64002-98017]	10484 [8284–12685]	$R_0=$1.4
2: Impact of enhanced contact tracing on worst-case scenario 1 and further assume that isolation and treatment centers could transmit the infection to the general public and medical staff but at a rate that is one-fifth of the community transmission rate.	35959 [28236-43682]	4776 [3751–5801]	$R_e=1.4$
3. Impact of enhanced contact tracing on worst-case scenario 1 and further assume that the rate at which isolation and treatment centers will transmit the infection to the general public and medical staff will be reduced by 10% (5% reduction from the isolation centers and 5% reduction from hospitals). This is achieved by providing PPEs to frontline line health workers and enforcing strict adherence to isolation protocols to prevent transmission of infection at the centers.	14834 [11489-18179]	2513 [1946–3080]	$R_e=1.4$
4. Scenario 3 plus effective case management. That is we introduced a gradual increase in the rate of recovery among the quarantine and hospitalized classes.	9941 [7650–12232]	1605 [1234–1976]	$R_e=1.3$
5. Scenario 4 plus improved individual level interventions-Social distancing, use of hand sanitizers, use of face mask, washing hands with running water with soap, and avoidance of social gathering and intensive media coverage	282 [178–386]	64 [40–88]	$R_e=0.5$

The results in Table 3 were obtained from using parameter estimates from Table 1.

Fig. 5.

Worst-case scenario: no government or individual interventions-red colour represents observed cases.

Scenario 2: We assessed the impact of contact tracing assuming that individuals who are quarantine or hospitalize can also transmit the infection to the general community. Enhanced contact tracing alone could reduce the expected number of cases to 35959 [28236-43628] and the total expected death toll could reduce to 4776 [3751–5801] independent of the fact that these centers could transmit infection. The effective reproduction number did not change from the worse-case scenario (Table 3, Fig. 6).

Fig. 6.

Impact of enhanced contact tracing by the Government.

Scenario 3: This scenario includes all the intervention in scenario 2 but also considers the possibility of the Government providing personal protective equipment to frontline workers and ensuring that people who are self-isolated or quarantine adhere strictly to prevention guidelines to reduce transmission from these centers. Under these conditions, expected cumulative cases and deaths would reduce to 14834 [11489-18179] and 2513 [1946–3080], respectively. The effective reproduction number did not change from the worse-case scenario (Table 3, Fig. 7).

Fig. 7.

Impact of Government intervention: provision of personal protective equipments and adherence to strict prevention guidelines at quarantine and treatment centers.

Scenario 4: This includes all the proposed interventions in scenario 3 but with improved case management at the quarantine and treatment centers. We measured case management by increasing the rate of recovery at the quarantine and treatment centers. This reduces the cumulative number of cases to 9941 [7650–12232] and 1605 [1234–1976], respectively. The effective reproductive number dropped marginally from 1.4 to 1.3 (Table 3, Fig. 8).

Fig. 8.

Impact of improved case management.

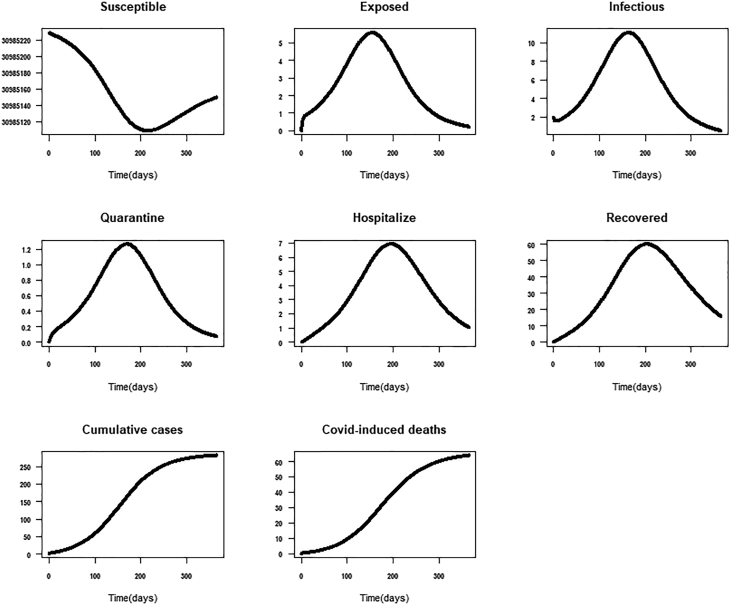
Scenario 5: In addition to scenario 4, we assessed the impact of integrated individual-level intervention such as social distancing, use of face mask, using soap with running water to wash hands, the intensity of media education measured by a media person’s willingness to constantly broadcast new cases and educate the general public on COVID-19. If all these prevention guidelines are adhered to, the expected total cumulative cases and deaths may reduce to 282 [178–386] and 64 [40–88], respectively. The effective reproductive number dropped to 0.5 (Table 3, Fig. 9).

Fig. 9.

Impact of integrated Government and individual-level interventions.

4. Discussions

The main focus of the study is to understand the dynamics of COVID-19 infection in Ghana using mathematical models that incorporate waning immunity to COVID-19, natural birth and death rates, integrated individual and government interventions and the fact that an exposed person may recover without necessarily been infectious to other due to boosted immunity. The proposed model allow for possible transmission of infection from quarantine, isolation and treatment centers similar to what was reported by Giordano et al. (2020). Our model further assume that individuals who recovered from COVID-19 may become susceptible again which is in sharp contrast to (Giordano et al., 2020). We provide short and long epidemic trajectory of COVID-19 infections in Ghana and simultaneously quantify the impact of integrated government and individual-level interventions in the presence of individual level-boosted immunity. We provide an estimate of the effective basic reproductive number using four different methods to comprehensively assess the variations in the estimates associated with the different methods. The addition of birth and deaths making it more applicable to project future scenarios assuming that COVID-19 extends beyond one-year. Incorporating self-boosted immunity represents a more natural setting of the dynamics of COVID-19 infection on what we know so far.

Previous studies have used mathematical models to study the dynamics of COVID-19 (Giordano et al., 2020; Lin et al., 2020; Munayco et al., 2020; Roosa et al., 2020) and the impact of individual and government interventions in the short term. Contact tracing and isolation of cases is among the common government interventions for controlling COVID-19 disease outbreaks and most studies have shown that they are effective (Giordano et al., 2020). However, most of these studies ignore the fact that quarantine, isolation and treatment centers could possibly transmit the infection to the general public and medical staff. The possibility of having high number of incident case infections because of increased transmission rate from the quarantine and treatment centers should not be ignored. These parameters makes our model different from other models reported in the medical literature to understand the dynamics of COVID-19 infections (Davies, Kucharski, Eggo, Gimma, & Edmunds, 2020; Prem et al., 2020).

The basic reproductive number from the three different approaches ranges from 1.4 to 3.5 which is similar to what have been reported in Li et al. (2020); Riou & Althaus (2020). The time-dependent basic Reproductive number showed that the intensity of the infection has declined since the very early phase of the epidemic in Ghana as expected and this could be explained by the early intervention put in place by the Government and increase in the level of individual awareness on ways of preventing infection through extensive media coverage. That notwithstanding, the overall time-dependent mean $R_e$ estimate remains greater than 1, suggesting the need to intensify integrated Government and individual-level interventions towards bringing it below 1. The time-dependent basic reproductive number is sensitive to the choice of generation time of the infection and therefore, our estimate is subject to change on condition that the generation time for infected individuals is different from what was reported in ( Ferguson, Laydon, Nedjati Gilani, et al., 2020). Therefore, caution must be applied when one wants to duly rely on estimates of $R_e$from the early phase of the epidemic.

The $R_e$ estimates derived from the Next Generation Matrix in the presence of intervention showed that collaborated efforts from the individual, media and integrated Government interventions were the only way to reduce the effective Reproductive number to a figure below 1 to eradicate COVID-19 in Ghana. Although the number of cumulative cases and deaths reduced with respect to each intervention introduced, none of the isolated interventions could significantly reduce the $R_e$ to a figure below 1. This could partly be explained by the fact that we chose an extreme rate of contact tracing and quarantining to depict a worse-case scenario. That notwithstanding, the model emphasized the need for a well-coordinated multiple interventions to reduce the intensity of the spread of COVID-19 in Ghana. The projections showed that different interventions could play a key role in reducing the expected number of cumulative cases and deaths in the next 365 days. Effective and enhanced contact tracing, provision of PPEs, improved case management, social distancing, use of face mask, intensive media coverage, personal hygiene, and immunity-boosting could all play a critical role in reducing the spread of infection in Ghana. The effectiveness of these integrated interventions as found in this study have been reported elsewhere (Prem et al., 2020). We have shown in this study that separate interventions could reduce the burden of COVID-19 but it was evident that we need both the government and the individual level interventions to reduce the impact of COVID-19 to the barest minimum.

Although the model improved our basic understanding of the infectiousness and the intensity of the COVID-19 spread in Ghana in terms of the projections and the effectiveness of individual and government interventions, our results should be interpreted with caution. This study has some limitations. Ideally, parameter estimates for all projections should originate from the country data but limited data prevented us from accurately estimating all parameters for the model. As with all modeling studies, our predictions are based on reasonable assumptions which may not represent what happens in reality. Several unmeasured factors could influence the dynamics of COVID-19 in Ghana and therefore caution should be taken when relying on mathematical models to inform policy decision. Ideally, sensitivity analysis could have been carried out focusing on the parameters that are policy related but this study did carry out such analysis as the focus was basically on worse case scenario and how varying degree of government and individual level interventions could impact on the spread.

Nonetheless, evidence from this study can be used to inform policy decisions about the need for the government to continue the enhance contact tracing, provision of personal protective equipment to frontline health workers and improved case management. Such Government interventions could play a major role in reducing the intensity of infection. Similarly, individual-level interventions such as social distancing, use of alcohol-based hand-sanitizers, wearing of face mask and intensive media education are critical to reducing the rate of infection. The effectiveness of these government interventions depends on how well we prevent infections that originate from quarantine, treatment and isolation centers. We emphasized the need to effectively integrate both individual and government level interventions to reduce the spread of infection. Our findings show that the over-reliance of government interventions alone may not reduce the spread of infection. Individuals must adhere to the prevention protocols and the media must intensify its daily report on COVID-19 cases to improve behavioral change, which have beneficial impact on the incidence cases.

Author contributions

Duah Dwomoh; Julius Fobil, Bright Adu: Conceptualization, Duah Dwomoh, Samuel Iddi, Samuel Bosomprah, Justice Moses Aheto: Methodology, Kojo Mensah Sedzro, Justice Moses Aheto: Data curation; Duah Dwomoh: Writing- Original draft preparation; Julius Fobil, Bright Adu: Visualization, Investigation.: Supervision.: Julius Fobil; All authors: Writing- Reviewing and Editing. All authors read and approved the final manuscript.

Declaration of competing interest

Authors declare no conflict of interest.

Handling editor: Dr. J Wu