Insights into the evaporation characteristics of saliva droplets and aerosols: Levitation experiments and numerical modeling

Abstract

Understanding the transmission phenomena of SARS-CoV-2 by virus-laden droplets and aerosols is of paramount importance for controlling the current COVID-19 pandemic. Detailed information about the lifetime and kinematics of airborne droplets of different size is relevant in order to evaluate hygiene measures like wearing masks but also social distancing and ventilation concepts for indoor environments. However, the evaporation process of expiratory droplets and aerosols is not fully understood. Consequently, the main objective of this study is to present evaporation characteristics of saliva droplets. An acoustic levitator is utilized in conjunction with microscopic imaging for recording the temporal evolution of the evaporation of saliva droplets under well-defined ambient conditions. Following the evaporation of the water content, a saliva droplet reaches a final size, which remains stable in the timescale of hours. By investigating numerous droplets of different size, it was found that the final droplet diameter correlates well to 20 % of the initial diameter. This correlation is independent of the ambient conditions for a temperature range from 20  °C to 29  °C and a relative humidity from 6 % to up to 65 %. The experimentally obtained evaporation characteristics are implemented into a numerical model, which is based on one-dimensional droplet kinematics and a rapid mixing evaporation model. By taking into account the evaporation-falling curve as presented by Wells, the significance of the experimental results for predicting the lifetime of saliva droplets and aerosols is demonstrated. The numerical predictions may be used to determine the impact of the droplet size and the ambient conditions on the transmission risks of infectious diseases like COVID-19.

Nomenclature

Latin Letters

$B_{\mathrm{H}}$

Spalding heat transfer number

$B_{\mathrm{M}}$

Spalding mass transfer number

$\mathit{Bi}$

Biot number

$c_{\mathrm{D}}$

Drag coefficient

$D$

Diameter

$D_{12}$

Binary diffusion coefficient

$g$

Gravitational acceleration

$\dot{m}$

Mass flow

$\mathit{Nu}$

Nusselt number

$\mathit{Pe}$

Peclet number

$\mathit{Pr}$

Prandtl number

$\dot{Q}$

Heat flux

$R^2$

Coefficient of determination

$\mathit{Re}$

Reynolds number

$\mathrm{RH}$

Relative humidity

$\mathit{Sc}$

Schmidt number

$\mathit{Sh}$

Sherwood number

$T$

Temperature

$t$

Time

$u$

Vertical velocity

$Y$

Mass fraction

Greek Letters

$\alpha$

Convective heat transfer coefficient

$\lambda$

Heat conductivity

$\nu$

Kinematic viscosity

$\rho$

Density

$\Phi$

Reduction coefficient

Subscripts

$\mathrm{0}$

Initial

$\mathrm{d}$

Droplet

$\mathrm{eq}$

Equilibrium

$\mathrm{g}$

Gas

$\mathrm{pre}$

Precipitated

$\mathrm{s}$

Surface

$\mathrm{vap}$

Evaporating

1. Introduction

The Coronavirus Disease 2019 (COVID-19) is caused by the Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2), which has been classified and named by Gorbalenya et al. (2020). Since the outbreak of the disease in December 2019 (Huang et al., 2020, Zhu et al., 2020), COVID-19 has become a pandemic with more than 53 million confirmed cases and 1.3 million deaths worldwide as reported by the World Health Organization on November 13, 2020 (WHO, 2020). Understanding the dominating transmission phenomena of SARS-CoV-2 is the key for controlling the pandemic until an effective vaccination or specific anti-infective treatments are available.

Besides direct human contact or indirect contact through an intermediate object, airborne transmission by means of droplets and aerosols plays a major role for the spread of infectious diseases (Morawska, 2006). Any person generates a considerable amount of droplets during different respiratory activities like breathing, talking, coughing, or sneezing. In order to determine the probability of infecting others by getting in touch or inhaling these droplets, two main questions have to be assessed:

• 1.How long does the virus survive within saliva droplets and aerosols?
• 2.How long do saliva droplets and aerosols stay airborne?

The study by van Doremalen et al. (2020) provides insights for discussing the first question. The authors investigated the lifetime of SARS-CoV-2 within aerosols experimentally. One major result is that the virus remained viable for the complete observation time of 3 h with a half-life of 1.1 h to 1.2 h. Based on such long survival times, a detailed answer to the second question may provide the decisive timescale for a clearer understanding of airborne transmission phenomena of the ongoing COVID-19 pandemic.

The droplet size was identified by Duguid, 1945, Duguid, 1946 and Loudon and Roberts (1967) as the most important parameter determining the time for which saliva droplets may remain airborne. However, the characterization of the spectrum of different droplet sizes as generated during respiratory activities is a challenging task, in particular since a wide range of droplet diameters from the sub-micrometer to the millimeter scale needs to be covered by experimental techniques. Hence, the size distribution and the sites of origin of droplets generated during different expiratory activities were the focus of more recent research studies by Papineni and Rosenthal (1997), Morawska et al. (2009), Xie et al. (2009), and Johnson et al. (2011). The results of these studies differ considerably. Nevertheless, it can be stated that the droplet concentration, the size distribution, and the initial velocities mainly depend on the respiratory activity itself. For instance, higher droplet concentrations and initial velocities are reported for coughing and sneezing as compared to breathing and talking.

Assuming a breathing and talking person in an indoor environment without sufficient ventilation, the lifetime of droplets of different size can be estimated by the well-known evaporation-falling curve introduced by Wells (1934). This methodology was refined using a state of the art modeling approach by Xie et al. (2007). The main conclusion is that large droplets are quickly accelerated downwards by gravitation and hit the ground, whereas small droplets will evaporate before they can move far away, as schematically illustrated in Fig. 1(a). Using this approach, a distinctive size of droplets surviving longest in the air can be identified as a function of the ambient temperature and humidity. Moreover, the evaporation-falling model can be used to define a safe distance from a potentially infected person with a low probability of virus transmission by droplets and aerosols. It is important to note that droplets can travel much greater distances in the case of coughing and sneezing as reviewed in the work of Jayaweera et al. (2020).

Fig. 1.

Schematic illustration of a breathing and talking person in an indoor environment without sufficient ventilation considering (a) simplified water and (b) actual saliva droplets.

In addition to the droplet size, the composition of expiratory droplets must be considered for predicting the droplet lifetime. According to Xu et al. (2020), saliva is in particular important for the transmission and diagnosis of COVID-19. In the studies by Wells (1934) and Xie et al. (2007), pure water droplets are investigated. This is a reasonable assumption, since human saliva mainly consists of water. However, saliva droplets also comprise a mixture of ions and proteins, which do not evaporate under typical ambient conditions. Hence, a complete evaporation of expiratory droplets, as illustrated in Fig. 1(a), is not possible. Instead, the droplets reach an equilibrium diameter as soon as the water content has evaporated. This knowledge is used in the example of a breathing and talking individual in an indoor environment as discussed in Fig. 1(b). The fate of large droplets does not change, since they fall to the ground before the water content has evaporated. However, the residues of smaller droplets, usually described as droplet nuclei, are characterized by a considerably longer residence time in comparison to pure water and can linger in the air for extended periods (Jayaweera et al., 2020, Morawska, 2006).

Specifying the risk of transmission of COVID-19 to a susceptible person via these aerosols is an ongoing discussion (Allen and Marr, 2020, Asadi et al., 2020, Fennelly, 2020, Meselson, 2020, Morawska and Cao, 2020, Shiu et al., 2019, Stadnytskyi et al., 2020). In fact, most authors claim that the airborne transmission route through aerosols is significant and has to be considered in order to control the current pandemic. This thesis is supported by documented outbreaks associated with the spread of the disease in indoor environments, for instance by Wang and Du (2020), Ong et al. (2020), and Lu et al. (2020). A vital parameter for modeling the airborne transmission through droplets and aerosols is the equilibrium diameter after evaporation of the water content, since the size of the residual droplets determines how long they remain suspended in the air. However, the evaporation characteristics of actual expiratory fluids are poorly understood. As a consequence, the ratio of equilibrium and initial diameter reported in the literature varies considerably.

A substantial amount of numerical studies neglect the protein content and use saline solution as a surrogate for expiratory fluids (Chao et al., 2009, Chaudhuri et al., 2020, Feng et al., 2020, Parienta et al., 2011). Based on this assumption, Liu et al. (2016) predicted the dried droplet nuclei size to be 32 % of the initial diameter. Nicas et al. (2005) take also the proteins into account and estimate the equilibrium diameter to be 50 % of the initial diameter based on a theoretical analysis of the droplet composition. Marr et al. (2019) use an advanced modeling approach by Mikhailov et al. (2004) and demonstrate that the assumed amount of proteins is a major source of uncertainty. The authors determine an equilibrium diameter of 19 % to 41 % depending on the assumed protein content. In view of the wide range of numerical results, experimental data is indispensable for validation of the modeling approaches.

However, experimental results from actual expiratory fluids are scarce. Duguid (1946) investigated the evaporation characteristics of six saliva droplets, which were suspended by a fine glass fiber. The equilibrium diameter after evaporation of the water content is reported to be in the range of 20 % to 33 % of the initial diameter with an average result of 25 %. It is important to note that Duguid (1946) mixed the saliva with a red dye, and the author mentions that the actual equilibrium diameter may be smaller. Liu et al. (2016) investigate the evaporation of saliva droplets on a flat Teflon surface. The evolution of the droplet mass is recorded using an analytical balance. Based on this experiment, the authors determine an equilibrium diameter of approximately one third of the initial diameter at a relative humidity of 84 %. The results of two droplets suspended in an acoustic levitator are presented by Chaudhuri et al. (2020). The authors use a saline solution as a surrogate for expiratory fluids and observe crystallization after complete evaporation of the water content. In a similar study by Basu et al. (2020) is concluded that the size of the final crystallite is 20 % to 30 % of the initial diameter for different droplet sizes and ambient conditions. Whether the results of saline droplets can be directly applied to actual respiratory fluids is not clear. Moreover, information on the accuracy of the diagnostics used to determine the droplet size is insufficiently documented.

The important conclusion of the literature review is that statistically significant data for validation of expiratory droplet evaporation is not available. Consequently, the prediction of airborne transmission phenomena by droplets and aerosols is subject to considerable uncertainty. In particular, the differences between expiratory and pure water droplets, as illustrated in Fig. 1, are inconclusive. This issue is emphasized by the vast range of size ratios between equilibrium and initial diameter found in the literature.

In order to improve this situation, experimental investigations of saliva droplets are performed in the present study. An acoustic levitator is used in conjunction with suitable diagnostics for recording evaporation characteristics under well-defined ambient conditions in detail. The main objective of the levitation experiments is to determine the equilibrium droplet diameter with sufficient accuracy. The influence of the relative humidity on the equilibrium diameter is highlighted in many studies (Liu et al., 2016, Marr et al., 2019, Nicas et al., 2005, Yang and Marr, 2011). Hence, the relative humidity in the proximity of the evaporating droplet is varied over a wide range from 6 % to up to 70 %. Furthermore, the experimentally obtained evaporation characteristics are implemented into a numerical model in order to predict the time saliva droplets may stay airborne. This is done by recalculating the evaporation-falling curve by Wells (1934) for non-completely evaporating saliva droplets.

2. Experimental setup and diagnostics

The experimental setup is based on an acoustic levitator with a resonance frequency of 100 kHz, which is well suited for the contact-free investigation of droplets with a diameter in the range of approximately 10 µm to 1000 µm. The largest droplets that can be investigated with the present experimental setup are limited by the manual injection of a droplet using a syringe, whereas the smallest droplet limit is due to destabilization effects. We are well aware that acoustic streaming does affect the evaporation rate of droplets suspended in an acoustic levitator (Yarin et al., 1999). In the present study, experimental conditions are sought, which minimize the influence of acoustic streaming on the evaporation process. This is mainly realized by the comparatively high resonance frequency of 100 kHz, a low amplitude of the acoustic actuator and the focus on small droplets. Additionally, a preliminary study was performed with the objective to compare the effect of acoustic streaming to forced convection flow. This approach has been established by Zaitone and Tropea (2011). Using Particle Image Velocimetry, it was found that the increase of the evaporation rate due to acoustic streaming corresponds to that of forced convection at a relative velocity of approximately 0.1 m s⁻¹. Hence, the impact of acoustic streaming is assumed to be negligible compared to the variation of ambient conditions. This judgment is supported by a comparison of experimental and model results in Section 4.1.

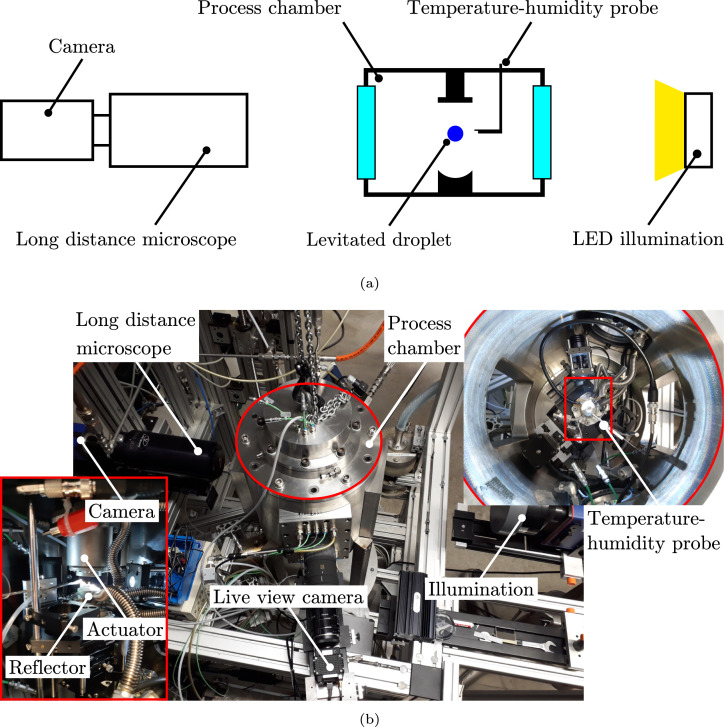
The acoustic levitator is installed in a process chamber. A miniaturized combined temperature–humidity probe is placed in the vicinity of the levitated droplet, as illustrated in Fig. 2. In this way, well-defined ambient conditions around the levitated droplet are ensured during the experiments. The temperature–humidity probe is positioned sufficiently far outside of the acoustic field in order to avoid disturbances, which may compromise the acoustic levitation of the droplet.

Fig. 2.

Schematic (a) and real (b) illustration of the experimental setup.

Saliva probes were taken from the mouth of two healthy men and injected into the acoustic levitator using a syringe. The actual injection process is based on the careful atomization of some saliva at the edge of the acoustic actuator. By doing so, several saliva droplets are generated, which will quickly accumulate at the pressure nodes of the acoustic field. This process is not accessible with the rather slow camera used for the detailed analysis of the evaporation process, since the frame rate is set to 1 Hz for all experiments of the present study. Nevertheless, a similar injection process of a water droplet was recorded with a frame rate of 4000 Hz using a high speed camera as part of a preliminary study with focus on different injection strategies. The resulting video is provided as supplementary material. In this paper, the key result is that the duration of the complete video is about 0.3 s, whereas the evaporation process of the droplets covers one to several minutes. For this reason, the portion of water that evaporates during the injection process is assumed to be negligible. This assumption is supported by the discussion of numerical results in Section 4.1.

Following successful injection of a droplet, the evaporation process of the suspended droplet was recorded using microscopic imaging. A shadowgraphy configuration was chosen for determining the temporal evolution of the droplet diameter (see Fig. 2). Exemplary microscopic images taken immediately after injecting a saliva droplet into the acoustic levitator are shown in Fig. 3. The contour of the levitated droplet is well recognizable, which is of major importance for determining the evolution of the droplet diameter during the evaporation process. However, two considerably smaller droplets are also observable in all three consecutive images. These droplets are remnants from the injection process, which have not coalesced to the actual droplet under investigation. From some experiments, it has been found that these remnants may hover around the large droplet for extended periods in a manner similar to moons. This phenomenon does not have a considerable impact on the experiment unless the contour of the droplet under investigation and the contour of smaller droplets overlap (see Fig. 3). In this case, the droplet diameter is measured too large by the automatic post-processing routine. The working principle of this routine will be elucidated in the last paragraphs of this section. It should be noted that the bias of moon like droplets was only corrected manually for determining the ratio between equilibrium and initial diameter.

Fig. 3.

Exemplary microscopic images taken immediately after injecting a saliva droplet into the acoustic levitator.

In addition, a distinct bright spot in the center of the levitated droplet can be observed in Fig. 3. This optical effect is caused by the first order refracted light from the main illumination source. In other words, the droplet is acting as a lens in the optical path of the measurement setup. This is evident as the shape of the rectangular light source can be recognized and is actually imaged more sharply for smaller droplets (cf. Fig. 6). Even the small droplets shown in Fig. 3 are characterized by a rectangular bright spot, which will be referred to as the glare point in the following. This glare point is relevant for the discussion of precipitation phenomena of evaporating saliva droplets, since it relies on the highly transparent nature of saliva. In particular, the glare point will not appear for opaque objects (Blaisot and Yon, 2005, Hovenac, 1986). Hence, the glare point can be utilized to distinguish between optically transparent and opaque droplets, which was realized for detecting the crystallization of urea-water droplets by Kontin et al. (2010). Furthermore, the vanishing of the glare point can also be observed in studies using a saline solution as a surrogate for respiratory fluid (Basu et al., 2020, Chaudhuri et al., 2020). Finally, the glare point should not be confused with a small bright spot on the left side of the droplet images shown in Fig. 3. This bright spot results from the direct reflection of a circular illumination source used for the live view camera depicted in Fig. 2.

Fig. 6.

Shadow images of the initial and equilibrium droplets of four exemplary levitation experiments.

The post-processing of the recorded droplet images is based on a robust threshold algorithm, which has been developed in previous studies (Gepperth et al., 2012, Lieber et al., 2019, Müller et al., 2006). Basically, the routine separates the droplet from the white background using a dynamic threshold, which is set to 80 % of the median intensity of the image under investigation. By separating the droplets from the background, the outer contour of each droplet is identified and the diameter is determined based on the enclosed area. However, a calibration is necessary since the determination of the droplet size is dependent on the selected threshold level, the droplet position relative to the focal plane, and the droplet size itself (Kashdan et al., 2003). In order to address this issue, a depth of field calibration is performed, which has been discussed previously in detail by Lieber et al. (2020). Briefly speaking, a glass plate with numerous opaque dots is installed in the test section at the same optical setting like for the levitation experiments. In this study, opaque dots with a diameter between 20 µm and 1000 µm are recorded during the calibration procedure. It is important to note that the dots are generated by an etching process with an absolute accuracy of 0.1 µm.

The depth of field calibration is achieved by moving the calibration plate in the direction perpendicular to the image plane. This is necessary to obtain quantitative data from slightly blurred droplets, which are located outside the focal plane. In the calibration procedure, this situation can be simulated by blurred dots on the calibration plate. Following this procedure, the measured diameter of one droplet is corrected based on the known diameter from the calibration plate and the average intensity gradient at the outer contour of the droplet. The accuracy of the diagnostics for determining the droplet diameter is verified by applying the calibration procedure to the data of the recorded dots from the calibration plate. In the present study, the maximum deviation was 2.5 µm within a defined distance from the focal plane of 200 µm. The main characteristics of the measurement technique as defined by the optical setup and the calibration procedure are summarized in Table 1.

Table 1.

Essential characteristics of the microscopic imaging diagnostics.

Parameter	Unit	Value
Measurement volume	mm3	1.6$\times$1.2$\times$0.4
Field of view	mm2	1.6$\times$1.2
Resolution	µm/pixel	1
Detectable diameters	µm	20–1000
Numerical aperture		$\simeq$0.1
Exposure time	ms	$\simeq$10

3. Experimental results

The first results to be presented will focus on a general discussion about the evaporation process of saliva droplets. This includes the comparison to the evaporation of a pure water droplet and the definition of the most important qualitative and quantitative evaporation characteristics. Subsequently, the equilibrium diameter is determined for a total of 75 saliva droplets. The acquired data is used to investigate the impact of the initial droplet diameter as well as the ambient temperature and humidity. Moreover, the measurement accuracy is discussed and a correlation between initial and equilibrium diameter is derived.

3.1. Evaporation characteristics of single saliva droplets

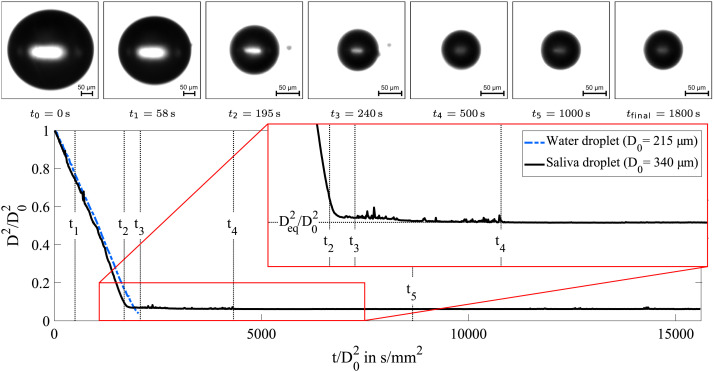
The evaporation process of a levitated saliva droplet at an ambient temperature of 23  $°$C and a 50 % relative humidity is shown in Fig. 4. In the first minutes of the droplet lifetime, an approximately linear evolution of the normalized surface $D^2∕D_0^2$ is observed. This behavior is known as the classical $D^2$-law. Hence, this phase of the evaporation process can be described by a constant reduction rate of the droplet surface. The time axis shown in Fig. 4 is normalized by the squared initial diameter of the droplet $D_0^2$. The resulting unit corresponds to the reciprocal unit of the reduction rate of the droplet surface. This normalization is suitable for a direct comparison of droplets with different initial diameters.

Fig. 4.

Temporal evolution of the normalized surface of a saliva and a water droplet ($T_{\mathrm{g}}=\text{23}°\text{C}$, $\mathrm{RH}=\text{50}\text{\%}$). The evaporation process of the saliva droplet is illustrated by means of microscopic images at specific times after start of the levitation experiment. In addition, a video of this levitation experiment is provided as supplementary material.

In addition, a pure water droplet is investigated under the same ambient conditions as the saliva droplet. The initial evaporation rate of both droplets is nearly identical (see Fig. 4). Hence, the first stage of the evaporation process of saliva droplets can be represented by the evaporation of pure water. A complete evaporation of the water droplet is expected. However, the presented evolution of the normalized surface does not reach zero. The reason for this behavior is that very small droplets with a diameter of the order of 10 µm become unstable and consequently move out of the pressure node of the acoustic field. This phenomenon limits the investigation of smaller droplets in the acoustic levitator as addressed in Section 2.

In contrast to the evaporation of the water droplet, the evaporation of the saliva droplet is characterized by a sudden stop of the linear decrease of the droplet surface at approximately 200 s after the start of the evaporation process. From this point on, the measured droplet size remains constant over the entire observation time of half an hour. This phenomenon can be explained by the presence of salts and proteins contained in saliva droplets. These compounds do not decompose under typical ambient conditions and therefore prevent the complete evaporation of the saliva droplet.

For a discussion of precipitation effects, the transition from a linear decrease of the droplet surface to a constant diameter is of particular interest. During this transition phase, a decrease of the evaporation rate is determined as illustrated by a zoom-in view in Fig. 4. This slow evaporation rate may be an indication for the formation of a precipitate. A more detailed discussion about the transition phase will be presented in Section 4.1. Furthermore, conspicuous peaks of the normalized surface are observed. However, these peaks may be attributed to small droplets, which did stabilize after the injection process around the droplet under investigation as addressed in Section 2. This thesis is confirmed by a video of the levitation experiment provided as supplementary material.

In order to perform a qualitative analysis of the evaporation characteristics, several shadow images of the evaporating saliva droplet at specific time steps are additionally shown in Fig. 4. An important indication can be derived from the bright spot located at the center of the droplet image called glare point. The vanishing of this optical effect can be utilized to detect the onset of crystallization as discussed in Section 2. During the transition phase, the glare point of the droplet becomes blurred. No further changes of the droplet image are observed within the remaining observation time. Therefore, this state is expected to be stable in the time frame of hours and the final droplet size will be named the equilibrium diameter $D_{\mathrm{eq}}$. However, the glare point is still slightly visible and the spherical shape of the droplet is preserved. Hence, it can be concluded that no complete crystallization did occur in the present levitation experiment. Instead, the equilibrium droplet is found to be partially translucent. This outcome may be caused by a sol–gel transformation of the saliva droplet, which was also speculated by Vejerano and Marr (2018). Moreover, Richards et al. (2020) showed that gel transitions can occur in levitated droplets containing similar compounds as respiratory droplets. In conjunction with the literature cited above, the experimental observations of the present study indicate that a gel transition can indeed occur in respiratory droplets. Further discussion of the precipitation behavior of saliva droplet will be given based on numerical results in Section 4.1.

In summary, the evaporation process of saliva droplets can be subdivided into two main stages. The first stage can be represented by the evaporation of pure water, while the second stage is mainly characterized by a constant equilibrium diameter. This final droplet size remains stable in the time frame of hours and is therefore a decisive criterion for determining the time saliva droplets may stay airborne. Moreover, the results highlight the difference between water and saliva droplets, which must be taken into account for predicting the airborne transmission of infectious diseases. This applies in particular to closed rooms, as previously discussed by means of Fig. 1. In this context, the size of the equilibrium diameter is of major importance. In order to address this issue, 75 levitation experiments with saliva droplets were conducted and evaluated for determining the effect of the initial droplet size and the ambient conditions. The corresponding results will be elucidated in the following subsections.

3.2. Effect of the initial droplet size

A first set of 39 levitation experiments is conducted under typical indoor thermodynamic conditions at a temperature between 22  $°\text{C}$ and 29  $°\text{C}$ and a relative humidity from 41 % to 53 %. The main objective is to determine the equilibrium diameter after evaporation of the water content. Furthermore, the impact of the initial droplet size is assessed. This is of interest, since a wide range of droplet sizes are generated during any respiratory activities. Eventually, the equilibrium diameter could be determined for a range of initial droplet diameters between approximately 150 µm and 700 µm.

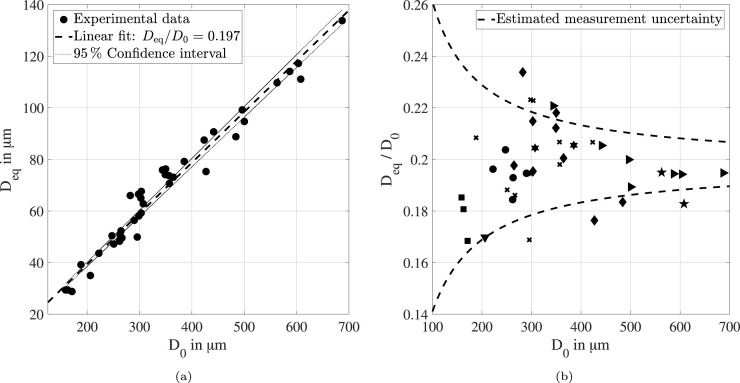
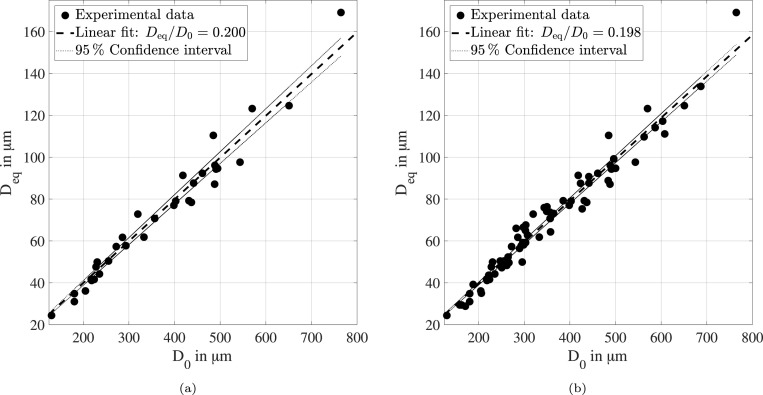
Care was taken that the droplets were already recorded during the injection process in order to capture the actual initial diameter of each droplet. The decrease of the droplet diameter was then recorded until the droplet reached a constant size. To ensure that this was the case, at least additional 60 seconds were recorded from the time a constant drop diameter was visually observed the first time. The resulting equilibrium diameter $D_{\mathrm{eq}}$ of all droplets is presented as a function of the initial droplet diameter $D_0$ in Fig. 5(a). Obviously, the equilibrium diameter correlates well with a value of 20 % of the initial droplet size. This result is confirmed by the high linear regression coefficient of $R^2=\text{0.967}$.

Fig. 5.

Correlation between equilibrium diameter $D_{\mathrm{eq}}$ and initial droplet diameter $D_0$ under typical indoor thermodynamic conditions (a), and illustration of the experimental uncertainty of the diagnostics and the saliva samples (b).

In addition, four exemplary levitation experiments are illustrated by means of shadow images of the initial and equilibrium droplets in Fig. 6. Obviously, not all droplets maintain a perfectly spherical shape. Moreover, some images show a blurred droplet contour, which may be caused by small oscillations of the droplet exposed to the acoustic field. These phenomena are of great importance to the discussion of the measurement accuracy. Using the calibration procedure, a maximum deviation of the droplet diameter of 2.5 µm was derived. However, non-spherical droplets and small oscillations must also be considered. Hence, the absolute measurement accuracy of the microscopic imaging diagnostics is estimated to be 5 µm.

The impact of the estimated accuracy on the determined ratio between equilibrium and initial diameter is illustrated in Fig. 5(b). The resulting measurement uncertainty increases considerably towards the smallest initial droplets of this study. The experimental data is also shown by means of different markers. The markers indicate different saliva samples, which were taken from different persons at an ambient temperature of about 25 $°\text{C}$ and at different times from early morning to late evening. In this way, it can be studied whether the concentration of salts and proteins changes depending on the taken saliva sample. However, no clear correlation is observed. Instead, most experimental data points are almost uniformly distributed within the estimated uncertainty band. Hence, it is assumed that the main uncertainty of the experimental investigation is caused by the limitation of the accuracy of the diagnostics. This implies that a statistically significant amount of experimental data is required to determine the equilibrium diameter of saliva droplets with sufficient accuracy. Therefore, more levitation experiments are performed, which will be elucidated in the following section.

3.3. Effect of the ambient temperature and humidity

During all levitation experiments, the temperature and humidity were monitored in the proximity of the droplets in order to assess the impact of the ambient conditions on the evaporation process of saliva droplets. The influence of the humidity is of particular interest, since many studies report a strong dependency (Liu et al., 2016, Marr et al., 2019, Nicas et al., 2005, Yang and Marr, 2011). Therefore, 33 additional levitation experiments were performed at significantly lower humidities of 6 % to 21 % relative humidity. The experimental setup is not very well suited to achieve higher humidity conditions than those of typical indoor environments, as reported in the previous section. Nevertheless, results of three droplets at a relative humidity between 65 % to 70 % could be obtained.

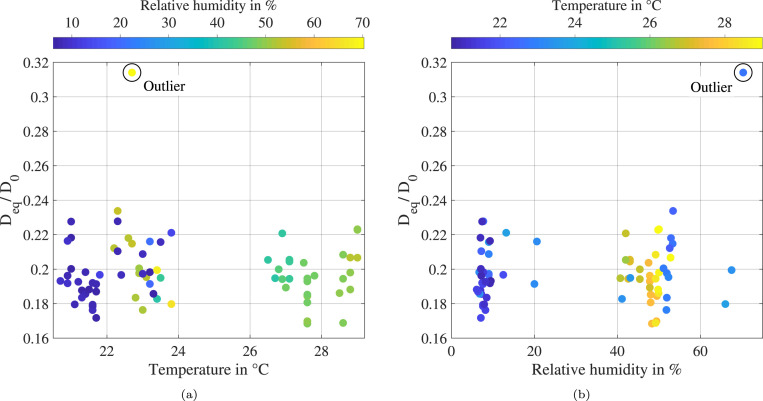
The impact of the ambient temperature on the ratio between equilibrium and initial diameter is illustrated in Fig. 7(a) for the complete set of 75 levitation experiments. It was found that no correlation can be derived, since the results are randomly distributed within the uncertainty band of the measurement technique (cf. Fig. 5(b)). However, one droplet at a temperature of 22.7  $°\text{C}$ features a considerably higher ratio between equilibrium and initial diameter over 0.3.

Fig. 7.

Impact of ambient temperature (a) and humidity (b) on the ratio between equilibrium diameter $D_{\mathrm{eq}}$ and initial diameter $D_0$.(For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

This outlier may be explained by the dependency of the equilibrium diameter on the humidity, which is presented in Fig. 7(b). The outlier corresponds to the highest relative humidity of approximately 70 %, which could be achieved by the present measurement setup. At the same time, no distinct impact of the relative humidity is visible in the complete range between 6 % and 65 %. These experimental results reflect well the numerical predictions by Marr et al. (2019) assuming a protein concentration of 3 mg ml⁻¹. The authors report a constant ratio between equilibrium and initial diameter of 19 % for a relative humidity lower than 64 %. Furthermore, an exponential increase of the equilibrium diameter is predicted for a higher humidity. Nevertheless, it should be noted that more experimental data is required to validate the behavior at high humidity conditions.

The complete data set of 75 levitation experiments is presented in the two graphs shown in Fig. 7. For this reason, a color coding is applied to resolve effects of the ambient conditions that may otherwise be lost. However, no further correlations on the ambient temperature and humidity are resolved using the color coding. Most importantly, the impact of the ambient conditions can obviously be neglected in the temperature range from 20  $°\text{C}$ to 29  $°\text{C}$ and the relative humidity range from 6 % to 65 %. For these conditions, the ratio between equilibrium and initial diameter is found to be independent of the initial droplet size. This statement is confirmed by the correlation at low humidity conditions shown in Fig. 8(a) as well as for the complete humidity range shown in Fig. 8(b). Both linear regressions are characterized by a high correlation coefficient $R^2=\text{0.963}$.

Fig. 8.

Correlation between equilibrium diameter $D_{\mathrm{eq}}$ and initial droplet diameter $D_0$ at low humidity conditions from 6 % to 21 % (a) and for the range between 6 % to 65 % (b).

The experimentally obtained correlation between initial and equilibrium droplet diameter is in good agreement with the general evaporation theory for an aqueous solution with a specific amount of non-volatile components. Hence, an extrapolation of the correlation to smaller droplets, which were not accessible by the presented experimental methodology, seems to be feasible. Only the Kelvin effect is expected to affect the equilibrium droplet diameter considerably for droplets smaller than 0.1 µm. However, such small droplets are in the same size range as the virus. Hence, a constant equilibrium diameter of 20 % of the initial diameter may be assumed when predicting the evaporation process of virus-laden saliva droplets. The experimentally determined equilibrium diameter may be utilized to predict the time saliva droplets will stay airborne, which will be directly demonstrated in the next section.

4. Numerical analysis of saliva droplets and aerosols

The experimentally obtained evaporation characteristics are used in a numerical scheme for predicting the airborne lifetime of saliva droplets and aerosols. First, the modeling approach will be discussed in detail and compared to experimental findings. Subsequently, breathing and talking individuals are assumed in an indoor scenario without any ventilation as illustrated in Fig. 1. Hence, freely falling droplets, which evaporate simultaneously, can be utilized to estimate the lifetime of respiratory droplets with sufficient accuracy. This methodology was first proposed by Wells (1934) and later refined using a state of the art modeling approach by Xie et al. (2007). However, pure water droplets are assumed in both studies. In the present numerical investigation, the so-called evaporation-falling curve established by Wells (1934) is extended to actual saliva droplets.

4.1. Modeling of saliva droplets and aerosols

The numerical model is based on one-dimensional droplet kinematics, which is coupled to an evaporation model. It is applied to predict the airborne lifetime of saliva droplets of different size. The evaporation model relies on the hydrodynamic approach by Abramzon and Sirignano (1989). The two main equations represent the evaporating mass flow

$${\dot{m}}_{\text{vap}}=\pi D_{\text{d}}{\rho }_{\text{g}}{D}_{\mathrm{12,g}}ln(1+B_{\text{M}}){\mathit{Sh}}^{\ast }\Phi ,$$ (1)

and the heat flux, which is imposed on the droplet surface

$${\dot{Q}}_{\text{s}}=\pi D_{\text{d}}{\lambda }_{\text{g}}(T_{\text{g}}-T_{\text{d}})\frac{ln(1+B_{\text{H}})}{B_{\text{H}}}{\mathit{Nu}}^{\ast }.$$ (2)

It should be taken into account that these heat and mass transfer equations are mainly coupled by the temperature dependence of the vapor pressure and the cooling enthalpy of the evaporating water. In addition, the fluid properties of the droplet and the surrounding gas phase depend on the temperature and the composition of the fluid. The influence of the convective heat and mass transfer is considered by the correlations of Frössling (1938) for calculating the Sherwood number

$${\mathit{Sh}}_0=2+\text{0.552}{\mathit{Re}}_{\mathrm{d}}^{1∕2}{\mathit{Sc}}^{1∕3},$$ (3)

and the Nusselt number

$${\mathit{Nu}}_0=2+\text{0.552}{\mathit{Re}}_{\mathrm{d}}^{1∕2}{\mathit{Pr}}^{1∕3}.$$ (4)

Furthermore, the correction of the impact of the evaporating mass flow on the velocity field around the droplet is taken into account (Abramzon & Sirignano, 1989):

$${\mathit{Sh}}^{\ast }=2+\frac{{\mathit{Sh}}_0-2}{{(1+B_{\mathrm{M}})}^{0.7}\frac{ln(1+B_{\mathrm{M}})}{B_{\mathrm{M}}}},$$ (5)

$${\mathit{Nu}}^{\ast }=2+\frac{{\mathit{Nu}}_0-2}{{(1+B_{\mathrm{H}})}^{0.7}\frac{ln(1+B_{\mathrm{H}})}{B_{\mathrm{H}}}}.$$ (6)

More detailed information about the fundamentals of the evaporation model can be found in textbooks, for example by Sirignano (2009) or Sazhin (2014).

In general, saliva consists of a variety of salts and proteins, which are relevant for the physicochemical properties of the fluid (Sarkar et al., 2019). However, only the water content will evaporate under typical ambient conditions. Hence, the complex composition of saliva is simplified as a binary mixture of water with a certain proportion of non-volatile components in the present study. A negligibly low vapor pressure is considered for the mixture of salts and proteins in saliva droplets in order to prevent any evaporation of these components. This is reflected by the experimental findings of this study (cf. Fig. 4). Additionally, Raoult’s law is used for calculating the vapor pressure of the aqueous solution. For reasons of simplicity and lack of data in the literature, it is assumed that all other thermophysical properties of the non-evaporating components correspond to those of water. By doing so, the difference between water and saliva is exclusively focused on the equilibrium droplet diameter, which has been determined by the levitation experiments. A mass concentration of salts and proteins of 0.8 % is assumed for the saliva droplets, which results in a ratio between equilibrium and initial diameter of 20 %.

The present evaporation model employs the rapid mixing approach with respect to droplet-internal heat and mass transfer. Hence, infinitely fast transport inside the droplet is assumed, resulting in spatially uniform temperature, concentration, and fluid properties within the droplet. Concerning heat transfer, this statement can be verified by means of the Biot number $\mathit{Bi}$, which relates the heat transfer between the droplet and the gas phase to the heat conduction inside the droplet. As a matter of fact, the assumption

$$\mathit{Bi}=\frac{\alpha D_{\mathrm{d}}}{2{\lambda }_{\mathrm{d}}}\ll 1,$$ (7)

is valid over a wide range of thermodynamic conditions for saliva droplets in air. In contrast, the concentration of non-volatile components within the droplet may develop considerable spatial gradients. Despite this, it is not mandatory to employ a computationally expensive evaporation model with a spatial discretization of the droplet, since only one component of saliva will evaporate. In this context, a computationally efficient model is advantageous for use in detailed numerical simulations to evaluate ventilation concepts for indoor scenarios.

Nevertheless, spatial concentration gradients inside of the droplet may become important, when the droplet size approaches the equilibrium diameter. At this point of the evaporation process, most of the water content of the saliva droplet is consumed by evaporation. Hence, precipitation effects of the non-volatile components are to be expected. One indication for such effects is the reduction of the evaporation rate, which has been observed during the levitation experiment presented in Fig. 4. Other studies speculate that a crystallization (Basu et al., 2020, Chaudhuri et al., 2020) or a sol–gel transformation (Vejerano & Marr, 2018) occurs for respiratory droplets. The underlying processes, however, have not been determined for actual saliva droplets. In order to provide new insights into this evaporation characteristic, exemplary model results of single droplets are discussed and compared to the experimental results.

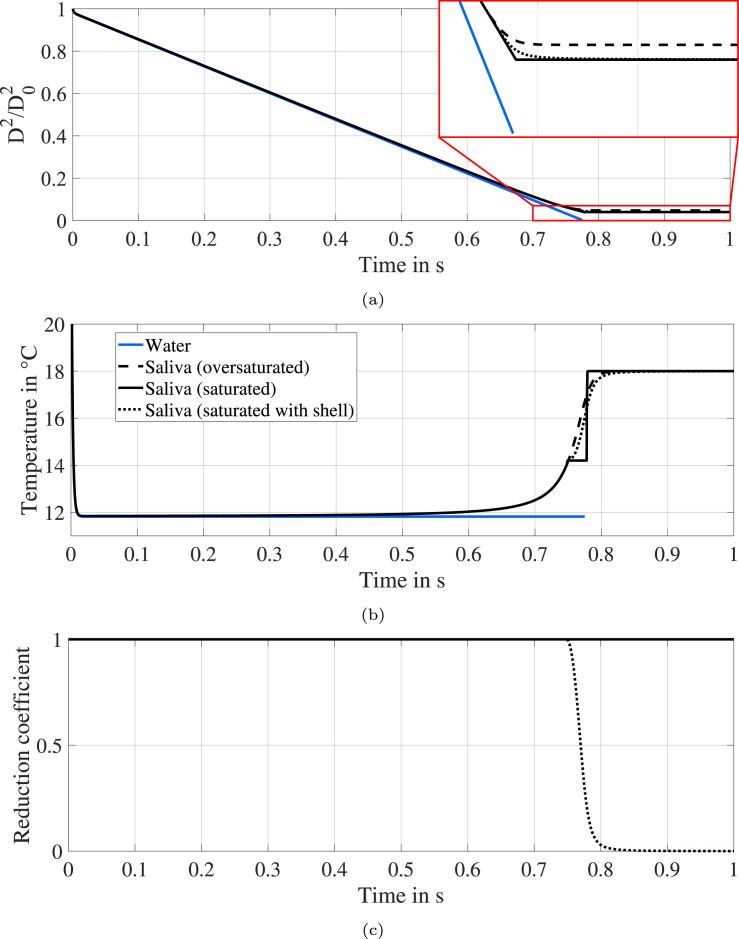
The modeled evaporation process of a water and a saliva droplet is illustrated by means of the evolution of the normalized surface and the temperature in Fig. 9. To simulate an expiratory droplet expelled by a human in a typical indoor scenario, the initial droplet temperature is set to 33  $°\text{C}$ and the ambient conditions are defined by a temperature of 18  $°\text{C}$, a relative humidity of 50 % and a relative velocity of 0 m s⁻¹. The first phase of the evaporation process is characterized by rapid cooling of the droplet, until an equilibrium temperature is established. The associated drop of the temperature causes increased fluid density and, consequently, an additional reduction of the droplet surface. However, even for the strong temperature drop of over 20  $°\text{C}$, the droplet surface shrinks only by 2 % of the initial surface due to cooling and enhanced evaporation during this phase (see Fig. 9(a)).

Fig. 9.

Normalized surface area (a), temperature (b) and reduction coefficient (c) of an evaporating droplet with an initial diameter of 20 µm and an initial temperature of 33 $°\text{C}$ at an ambient temperature of 18 $°\text{C}$, a relative humidity of 50 % and a relative velocity of 0 m s⁻¹.

Moreover, the timescale of this effect is extremely short and with approximately 1 % of the overall evaporation time comparable to the timescale of the injection process used in the levitation experiments as discussed in Section 2. This provides an estimate of the bias involved in determining the initial diameter, which is caused by the timeframe of the injection process. The estimated bias accounts for 1 % of the actual initial droplet diameter and is negligible. It should be noted that this estimation was verified for droplets with an initial diameter between 5 µm and 500 µm.

The second characteristic phase of the evaporation process starts, after the droplet reaches its equilibrium temperature. This phase can be described by the well-known $D^2$-behavior, which was also observed in the experimental investigation of this study (cf. Fig. 4). No apparent differences between water and saliva are detected, until the impact of the non-volatile components comes into play. In the numerical model, the increasing amount of non-volatile components causes a decrease of the vapor pressure according to Raoult’s law and, consequently, a decrease of the evaporation rate. This effect is partly compensated by a simultaneous increase of the droplet temperature (see Fig. 9(b)). During this final phase of the evaporation process, precipitation phenomena are relevant. In the case when no saturation of the aqueous solution is considered, the mass fraction of salts and proteins continues to increase until an equilibrium droplet diameter is obtained. Apart from the amount of salts and proteins contained in saliva, this equilibrium droplet size is mainly dependent on the ambient conditions, in particular the relative humidity. Even more important, a considerable amount of water will not evaporate from the saliva droplet.

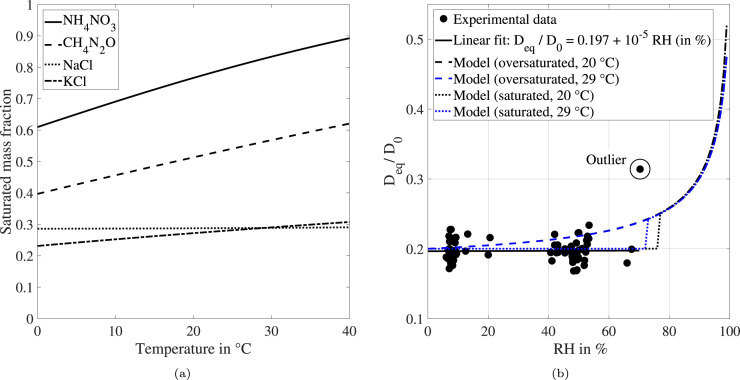
However, a supersaturated solution is not a physically sound assumption. In order to consider precipitation effects, information about the saturated mass fraction of the salts and proteins contained in saliva is needed. In view of the vast range of components contained in actual saliva, this represents a major challenge for the implementation in the numerical model. The formulation of a widely used surrogate for saliva is discussed by Sarkar et al. (2019). The saturated mass fraction of some main components of this surrogate are presented as a function of the droplet temperature in Fig. 10(a). The correlations for ammonium nitrate (${\mathrm{NH}}_4{\mathrm{NO}}_3$), sodium chloride ($\mathrm{NaCl}$) and potassium chloride ($\mathrm{KCl}$) can be found in the work by Seinfeld and Pandis (2016) and the one for urea (${\mathrm{CH}}_4{\mathrm{N}}_2\mathrm{O}$) in the datasheet of BASF (2006). To stay within the scope of the present study, the saturation behavior of saliva is simplified by that of a single component. Urea is chosen for this purpose as it represents an intermediate solubility of the components shown in Fig. 10(a). The heat of solution of aqueous urea solution is taken from the study by Egan Jr. and Luff (1966).

Fig. 10.

Saturated mass fraction as a function of the droplet temperature for several components of a well-known model saliva formulation (a) and impact of RH on $D_{\mathrm{eq}}∕D_0$ for experimental and model results (b).

The impact of taking saturation into account is illustrated in Fig. 9. For a first comparison, it is assumed that the precipitate does not affect the evaporation process. By doing so, the only significant difference from a supersaturated solution is that the mass fraction of non-volatile components is limited. A second equilibrium droplet temperature is established after the saturation condition is fulfilled, since also the effect of Raoult’s law is limited. At the end of the evaporation process, the entire water content is consumed by evaporation. Consequently, the equilibrium diameter depends solely on the amount of salts and proteins contained in saliva. However, the saturated case in Fig. 9 is characterized by a sudden stop of the evaporation process, which does not agree with the experimentally observed behavior (cf. Fig. 4).

In order to address this issue, the numerical approach is extended by taking into account an inhibiting effect of precipitation on the evaporation rate. In contrast to the assumption of rapid mixing, spatial concentration gradients can develop inside of the droplet due to a limited internal diffusion. Therefore, the most likely scenario is the formation of precipitates on the droplet surface, which may induce the generation of a permeable shell around the evaporating saliva droplet. A similar scenario for respiratory droplets was also speculated by Vejerano and Marr (2018). In the present study, the effect of precipitation on the evaporation rate is modeled as a resistance on the evaporating mass transfer by introducing the reduction coefficient

$$\Phi =1-Y_{\mathrm{pre}}^2(3-2Y_{\mathrm{pre}})$$ (8)

as a multiplier in Eq. (1). The precipitated mass fraction is denoted by $Y_{\mathrm{pre}}$. An additional resistance of the permeable shell on heat transfer is not considered. This approach for modeling the precipitation behavior of multi-component droplets is based on the work of Reinhold (2001) and was also used by Kontin et al. (2010) for urea-water droplets. Model results considering a permeable shell are additionally shown in Fig. 9. By taking into account the reduction coefficient from Eq. (8), the evolution of the normalized surface is characterized by a continuous reduction of the evaporation rate as the droplet size approaches the equilibrium diameter. Otherwise, the behavior is very similar to the purely saturated case. In particular, the equilibrium diameter converges to the same magnitude and only a negligibly small amount of water remains within the droplet.

For a further in-depth analysis, the results of the model are compared to experimentally obtained evaporation characteristics. In Fig. 10(b), the ratio between equilibrium and initial diameter ($D_{\mathrm{eq}}∕D_0$) is illustrated as a function of the relative humidity (RH). The experimental data was already discussed using Fig. 7(b). Apart from the outlier at $\mathrm{RH}\approx \text{70}\text{\%}$, no impact of RH on $D_{\mathrm{eq}}∕D_0$ is detected. This statement is supported by a linear fit of the experimental data showing an increase of $D_{\mathrm{eq}}∕D_0$ of less than $\text{0.1}\text{\%}$ over the range $\text{6}\text{\%}<\mathrm{RH}<\text{65}\text{\%}$. Model results are presented considering two precipitation scenarios as well as the ambient temperature range of the experimental investigation. The initial droplet temperature is set equal to the ambient temperature and the relative velocity is 0 m s⁻¹. If saturation is not taken into account, a continuous increase in $D_{\mathrm{eq}}∕D_0$ is predicted with increasing RH. The reason for this behavior is the growing impact of Raoult’s law with increasing RH. The influence of the ambient temperature is negligible as it is only noticeable for extremely high humidity conditions. However, the continuous increase of $D_{\mathrm{eq}}∕D_0$ for the supersaturated case does not match the experimental data.

By taking saturation into account, a better agreement to the experimental data is obtained (see Fig. 10(b)). This is caused by the fact that saturation sets in before any further reduction of the droplet size is limited by Raoult’s law. Nevertheless, a distinct jump of $D_{\mathrm{eq}}∕D_0$ is predicted for a humidity of approximately 70 % to 75 %. For situations where the relative humidity is higher, the saturated mass fraction is not reached. Hence, $D_{\mathrm{eq}}∕D_0$ is determined by the influence of Raoult’s law and the results are consistent with the supersaturated case. Moreover, the discriminating humidity between a constant equilibrium diameter and an exponential increase of $D_{\mathrm{eq}}∕D_0$ depends on the ambient temperature. This behavior can be explained by the fact that the saturated mass fraction is modeled as a function of the droplet temperature (see Fig. 10(a)). The outlier at $\mathrm{RH}\approx \text{70}\text{\%}$ is an experimental indication that the numerically predicted jump of the equilibrium diameter might actually occur. However, this data point should not be used for further evaluation, since it was not possible to establish a sufficiently stable relative humidity for this levitation experiment. In this context, it should be emphasized that more experimental data is necessary for the validation of the numerical model at high humidity conditions. For this purpose, a detailed variation of the relative humidity for different temperature levels must be performed.

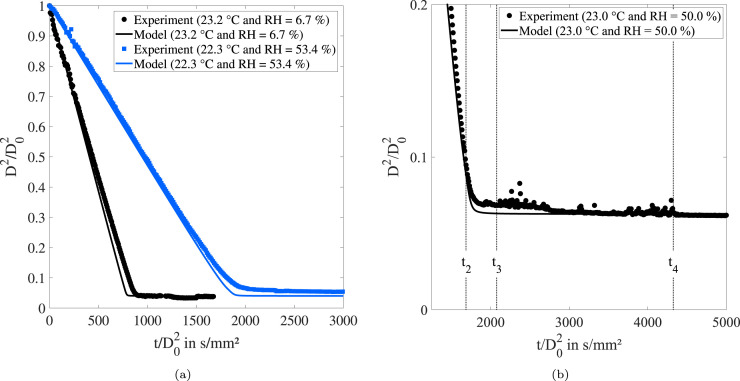
For a more detailed validation of the modeling approach at lower humidity conditions, numerical results are compared to exemplary data of levitation experiments in Fig. 11. The precipitation behavior is modeled by taking into account saturation and the build-up of a permeable shell. In order to enable a direct comparison to the experimental results, the initial droplet temperature is set to the equilibrium temperature during the phase of water evaporation and the relative velocity is 0 m s⁻¹. In Fig. 11(a), experimental and numerical results are depicted for two cases, which cover a wide range of ambient humidity conditions, and consequently feature considerably different evaporation rates. The reduction of the normalized surface is approximately twice as fast at $\mathrm{RH}\approx \text{7}\text{\%}$ compared to $\mathrm{RH}\approx \text{53}\text{\%}$. Even more important, the evaporation rate during the phase of water evaporation and the time scale of the precipitation dynamics are in good agreement with the experimental data.

Fig. 11.

Comparison between the experimental and numerical results for two droplets with considerably different evaporation rates (a) and the long-term experiment presented in Fig. 4(b).

In addition, the long-term experiment, which has been presented and discussed in Section 3.1, is compared to model results using a zoom-in view in Fig. 11(b). Here, the transition phase from the $D^2$-behavior to the formation of the equilibrium diameter is the focus of the analysis. It is important to mention that the recording of this experiment was started with a significant time delay after successful injection of the droplet, since it was the first levitation experiment performed in the present study. Hence, the resulting equilibrium diameter is with 25 % of the initial diameter too large and was not used for any further evaluation. In order to enable a direct comparison to the numerical approach, the model results are scaled up to fit the experimentally determined equilibrium diameter. By doing so, the precipitation dynamics can be studied in detail. The evaporation rate and the time scale of the precipitation dynamics are predicted fairly well. However, the experimental results deviate earlier from the $D^2$-behavior and reach the equilibrium diameter later. Similar trends can also be deduced from the data shown in Fig. 11(a). One reason for this characteristic is that the saturation of salts and proteins is modeled as a single component. Consequently, a better adaption of the model results may be achieved by taking into account several non-volatile components with different saturated mass fractions.

In summary, it could be demonstrated that precipitation dynamics have to be taken into account for predicting the evaporation process and the equilibrium diameter of saliva droplets. The best fit to experimental results was achieved by assuming a formation of a permeable shell around the droplet. Moreover, optical diagnostics suggest a sol–gel transition rather than complete crystallization of the droplet as discussed in Section 3.1. Therefore, the experimental and numerical results provide new insights into the environment the virus is exposed to within the droplet, which may be relevant for predicting the virus lifetime. Nevertheless, more experimental evidence is needed for further validation of the precipitation dynamics. The most important finding of the present study, however, is that the evolution of the droplet diameter $D_{\mathrm{d}}$ can be predicted with sufficient accuracy by the evaporation model. This is relevant to modeling of the droplet kinematics. A one-dimensional approach is chosen, which is based on the equation of motion for a single droplet

$$\frac{\mathrm{d}{u}_{\text{d}}}{\mathrm{d}t}=-\frac{3}{4}\frac{{\rho }_{\mathrm{g}}{c}_{\mathrm{D}}}{{\rho }_{\mathrm{d}}{D}_{\mathrm{d}}}|u_{\text{g}}-u_{\text{d}}|(u_{\text{g}}-u_{\text{d}})+(1-\frac{{\rho }_{\mathrm{g}}}{{\rho }_{\mathrm{d}}})g.$$ (9)

In Eq. (9), the effects of inertia, drag, gravity, and buoyancy are taken into account. The correlation established by Ihme et al. (1972) is used for the drag coefficient

$$c_{\mathrm{D}}=0.36+5.48{\mathit{Re}}_{\mathrm{d}}^{-0.573}+\frac{24}{{\mathit{Re}}_{\mathrm{d}}}.$$ (10)

It should be noted that the correlation is only valid for perfect spheres, which is justified by the low aerodynamic forces acting on the freely falling droplets.

4.2. Applicability of the results to smaller droplets respectively aerosols

The majority of expiratory droplets are smaller than those accessible by the experimental technique. Hence, a direct validation of the numerical model for such small droplets respectively aerosols cannot be performed. From a theoretical point of view, however, the evaporation process of droplets with different initial diameter scales very well if the square of the initial droplet diameter is used for normalization. For instance, the model results presented in Fig. 11 are completely independent of the initial droplet diameter. One exception is the influence of the convective heat and mass transfer, which is considered by correlations for ${\mathit{Sh}}_0$ and ${\mathit{Nu}}_0$ in Eqs. (3), (4). The dependency of ${\mathit{Sh}}_0$ and ${\mathit{Nu}}_0$ on the droplet diameter $D_{\mathrm{d}}$ is taken into account using the droplet Reynolds number

$${\mathit{Re}}_{\mathrm{d}}=\frac{D_{\mathrm{d}}|u_{\text{g}}-u_{\text{d}}|}{{\nu }_{\text{g}}},$$ (11)

which is defined by the relative velocity between a droplet and the gas phase $u_{\text{g}}-u_{\text{d}}$ and the kinematic viscosity of air ${\nu }_{\text{g}}$. According to Eq. (11), the evaporation rate increases with increasing droplet diameter if a significant relative velocity between the droplet and the gas phase prevails. However, small droplets respectively aerosols follow the air flow almost perfectly and are therefore characterized by a negligible relative velocity. Hence, the effect of forced convection is presumably negligible.

Furthermore, it is interesting to study if an impact on the precipitation behavior is to be expected for smaller droplets respectively aerosols. For this purpose, the droplet Peclet number

$${\mathit{Pe}}_{\mathrm{d}}=\frac{{\dot{m}}_{\mathrm{vap}}}{2\pi D_{\mathrm{d}}{\rho }_{\mathrm{d}}{D}_{\mathrm{12,d}}}=\frac{{\mathit{Sh}}^{\ast }}{2}\frac{D_{\mathrm{12,g}}}{D_{\mathrm{12,d}}}\frac{{\rho }_{\mathrm{g}}}{{\rho }_{\mathrm{d}}}ln(1+B_{\mathrm{M}}),$$ (12)

as introduced by Makino and Law (1988), can be used. Similar to the Biot number for heat transfer, ${\mathit{Pe}}_{\mathrm{d}}$ relates the mass transfer between the droplet and the gas phase to the diffusion inside the droplet. In other words, the influence of diffusive resistance in multi-component droplets on the evaporation process is quantified by ${\mathit{Pe}}_{\mathrm{d}}$ (Burger et al., 2003). Hence, a higher concentration gradient inside the droplet is expected for a higher ${\mathit{Pe}}_{\mathrm{d}}$. The dependency of ${\mathit{Pe}}_{\mathrm{d}}$ on the droplet diameter becomes apparent by inserting Eq. (1) into Eq. (12). By doing so, ${\mathit{Pe}}_{\mathrm{d}}$ mainly depends on the binary diffusion coefficient of the gas phase $D_{\mathrm{12,g}}$ and the droplet $D_{\mathrm{12,d}}$. In addition, the density ratio $\frac{{\rho }_{\mathrm{g}}}{{\rho }_{\mathrm{d}}}$ and the Spalding number for mass transfer $B_{\mathrm{M}}$ account for the concentration jump at the phase interface. Consequently, the only dependence on the droplet size is due to forced convection, which was found to be negligible previously. In conclusion, the scaling of the precipitation dynamics to smaller droplets and aerosols is straightforward assuming a negligible relative velocity. For a constant relative velocity, lower concentration gradients inside of the droplet are expected, which leads to less pronounced precipitation dynamics.

4.3. Simulation results and discussion

For verification of the numerical model, the evaporation-falling curve by Wells (1934) is recalculated for water droplets and compared to the results found by Xie et al. (2007). The ambient temperature is set to 18  $°\text{C}$, and a variation of the relative humidity between 0 % and 90 % is studied. Moreover, quiescent ambient conditions with $u_{\text{g}}$ = 0 m s⁻¹ are assumed, which corresponds to the indoor scenario without any ventilation flow. The initial droplet temperature is assumed to be 33  $°\text{C}$, and the initial height above the ground is set to 2 m.

A variation of the initial droplet diameter from 5 µm to 200 µm is performed in steps of 2.5 µm. The airborne lifetime of each droplet is set either when the droplet hits the ground or when it is completely evaporated. The results of the numerical model are illustrated in Fig. 12(a). Obviously, large droplets are accelerated quickly by gravitation and fall to the ground, whereas small droplets evaporate quickly and will not move large distances away (cf. Fig. 1(a)). A distinctive droplet size can be identified dependent on the ambient humidity, which will survive the longest in the air. Even more important, the quantitative results are in very good agreement with the ones found by Xie et al. (2007). In addition, some experimental support for the numerical results is provided in the study by Davies et al. (2013). The authors present the evaporation process of a pure water droplet with an initial diameter of approximately 46 µm at 80 % relative humidity. The evaporation time of about 7 s is quite consistent with the model results shown in Fig. 12(a).

Fig. 12.

Results of recalculating the evaporation-falling curve by Wells (1934) for (a) water droplets, and (b) saliva droplets using the ratio between equilibrium and initial diameter as determined in the present study.

Following the successful verification of the numerical model, the airborne lifetime of saliva droplets is predicted for ambient and initial conditions identical to those of the water droplets. As indicated in Section 3.1, the evaporation of large saliva droplets is identical to that of pure water (see Fig. 12(b)). However, complete evaporation of saliva droplets does not occur. Instead, smaller droplets continue to fall even after their water content is consumed by evaporation. Finally, the residual droplets will reach their final velocity, which is mainly dependent on their equilibrium diameter. Consequently, the airborne lifetime increases drastically in comparison to that of pure water droplets, as shown in Fig. 12(b).

For a further in-depth analysis, the airborne lifetime of the entire range of initial droplet sizes is shown in Fig. 13. Results at a relative humidity of 90 % are excluded, since appropriate experimental data is necessary to validate the numerical model for such high humidity conditions. This new illustration of the numerical results offers the possibility to subdivide the droplet size range into three regimes with different dominating effects:

Fig. 13.

Predicted airborne lifetime of saliva droplets for the entire range of initial droplet sizes. The virus lifetime is estimated based on the results found by van Doremalen et al. (2020).

• •Regime III: For droplets with an initial diameter larger than 150 µm, the airborne lifetime is mainly determined by the initial droplet size. The studied variation of the relative humidity affects the airborne lifetime by less than one second. Hence, droplet evaporation may be neglected with sufficient accuracy. It should be mentioned that during normal respiration, such large droplets are barely generated.
• •Regime II: For droplets between 50 µm and 150 µm, the droplet lifetime is dominated by the evaporation process. Hence, the impact of the ambient conditions is significant and the airborne lifetime increases with lower relative humidity and higher temperature. In addition, the equilibrium droplet size is becoming increasingly important to smaller initial droplet diameters. The combination of both effects may extend the airborne droplet lifetime of saliva droplets by up to two orders of magnitude compared to water droplets.
• •Regime I: For droplets with an initial diameter that is smaller than 50 µm, the airborne lifetime is mainly determined by the equilibrium droplet size. The evaporation time of the water content accounts for less than 1 % of the total airborne lifetime.

The difference between pure water and saliva can be evaluated in Regimes I and II. For this range of initial droplet sizes, the airborne lifetime may increase from seconds for water to minutes and hours for saliva droplets. Hence, the experimentally determined equilibrium diameter is of great importance to predicting the time saliva droplets stay in the air. It should be noted that similar one-dimensional predictions were performed in a recent study by Vuorinen et al. (2020). However, a higher concentration of non-volatile components was assumed, which leads to considerably shorter airborne lifetimes in Regimes I and II.

The half-life of SARS-CoV-2, as determined by van Doremalen et al. (2020), is additionally indicated in Fig. 13 in order to relate the predicted airborne lifetime of saliva droplets to the lifetime of the virus. Moreover, the corresponding times for a viable virus content of 90 % and 1 % are estimated assuming exponential decay. This offers the possibility to come back to the two questions raised in Section 1, which are vital for assessing the probability of infecting other persons by getting in touch or inhaling airborne droplets. Over a wide range of initial droplet sizes, the time saliva droplets will stay in the air is the decisive timescale for predicting the airborne transmission risk of COVID-19. Nevertheless, the virus lifetime must be considered for the droplet size range of Regime I, since the viable virus content decreases significantly from 90 % after approximately 10 min to 1 % after approximately 8 h in the air. The half-life of 1.1 h to 1.2 h corresponds to the airborne lifetime of a droplet with an initial diameter of 20 µm and a corresponding equilibrium diameter of 4 µm.

One main conclusion is that a safe distance cannot be defined for an indoor scenario without sufficient ventilation (cf. Fig. 1(b)). Medium-size droplets, which correspond to an airborne lifetime of minutes are particularly dangerous, since these droplets still contain a high viable amount of the virus. Face masks, however, can remove most droplets of this size range and additionally will reduce the number of smaller droplets. A detailed description of the protective mechanisms of face masks can be found in the studies by Long et al. (2020), Dbouk and Drikakis (2020b), and Kähler and Hain (2020). Furthermore, ventilation concepts are of utmost importance to removing aerosols consisting of very small droplets, which follow small air currents almost perfectly. Consequently, the accumulation of very small droplets with an airborne lifetime in the order of hours can be effectively prevented (Morawska et al., 2020).

5. Outlook

The merits of the numerical model used in the present study are its simplicity and the low computational effort for investigating the airborne lifetime of saliva droplets. In particular, the difference between pure water and actual saliva droplets can be assessed, and the dominating parameters for predicting the airborne transmission risk can be identified. However, the present model includes certain assumptions, which are restricted to the scenario of breathing and talking persons in an indoor environment without ventilation. For a more general investigation of the airborne transmission risk, the interaction of the droplets and the ambient air flow has to be taken into account. In this context, it should be noted that even in an unventilated environment, human respiration can cause small air currents, which may affect the airborne lifetime of small droplets. Furthermore, the initial droplet velocity must be considered for coughing or sneezing events (Xie et al., 2007). In order to assess the impact of these additional effects under realistic initial and boundary conditions, numerical simulations are necessary, as shown by the recent studies by Feng et al. (2020), Dbouk and Drikakis (2020a), Vuorinen et al. (2020), Peng et al. (2020), and Shao et al. (2021).

The droplet evaporation models of these numerical studies can be validated using the experimentally determined evaporation characteristics presented in this study. By doing so, the uncertainty of predicting the airborne transmission risk of COVID-19 may be reduced significantly. However, more experimental data is required covering a wider range of ambient conditions, especially situations where humidity is higher than 65 %. An additional research objective is the identification of the ambient temperature at which saliva droplets decompose completely as well as the rate of decomposition. This information may be of interest for the development of effective indoor air cleaning devices. Moreover, the simultaneous experimental investigation of the droplet and the virus lifetime is conceivable. In summary, the methodology of the present study may serve as a basis for future experimental work on the evaporation characteristics of saliva droplets.

6. Conclusion

The main objective of the present study was to extend the understanding of the evaporation characteristics of saliva droplets and aerosols. For this purpose, an experiment was set up for investigation of single saliva droplets positioned in an acoustic levitator under well-defined ambient and initial conditions. Microscopic imaging was used as diagnostics for recording the temporal evolution of the droplet size during the evaporation process. By an established post-processing and calibration routine, the droplet diameter was determined with high accuracy. Experimental data with known measurement uncertainty was obtained from 75 levitated saliva droplets. These experimental results have been used to determine the impact of the initial diameter as well as the ambient temperature and humidity. The main outcome is that a saliva droplet reaches an equilibrium size after evaporation of the water content, which correlates well to 20 % of the initial diameter for a relative humidity between 6 % and 65 %.

This correlation was implemented into a numerical model, which is based on one-dimensional droplet kinematics and a rapid mixing evaporation model. From simulation runs, the airborne lifetime of saliva droplets and aerosols was predicted as a function of the initial droplet size and the ambient humidity. The numerical results have been used to discriminate three regimes of the initial droplet diameter, which highlight the relevant effects. While the largest expiratory droplets quickly hit the ground, the airborne lifetime of droplets smaller than approximately 150 µm is mainly defined by their evaporation characteristics. The airborne lifetime of droplets with an initial diameter of less than 50 µm is mainly determined by their equilibrium size. Most importantly, these small droplets may stay airborne for more than one hour. It could be demonstrated that the experimentally determined ratio between initial and equilibrium diameter may affect the airborne droplet lifetime considerably. Consequently, the experimental results can serve for validating similar evaporation models, which are of great importance to numerical predictions of the airborne transmission risk of infectious diseases like COVID-19.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary material related to this article.

Video S1

Long-term levitation experiment at RH=50 % and T=23 °C.

Video S2

Exemplary demonstration of the droplet injection principle.