Abstract
Each individual's skin has its own features, such as strength, elasticity, or permeability to drugs, which limits the effectiveness of one-size-fits-all approaches typically found in medical treatments. Therefore, understanding the transport mechanisms of substances across the skin is instrumental for the development of novel minimal invasive transdermal therapies. However, the large difference between transport timescales and length scales of disparate molecules needed for medical therapies makes it difficult to address fundamental questions. Thus, this lack of fundamental knowledge has limited the efficacy of bioengineering equipment and medical treatments. In this article, we provide an overview of the most important microfluidics-related transport phenomena through the skin and versatile tools to study them. Moreover, we provide a summary of challenges and opportunities faced by advanced transdermal delivery methods, such as needle-free jet injectors, microneedles, and tattooing, which could pave the way to the implementation of better therapies and new methods.
I. INTRODUCTION
Our skin interacts continuously with a wide variety of substances. Some are unwanted, such as environmental contamination, or other hazardous components due to accidental exposure. In contrast, the dermal application of lotions, creams, cosmetics, and other personal care products,1,2 as well as the use of therapeutic drugs, constitute a daily routine for millions of people and for veterinary use.3 Most of these products, whether meant to have therapeutic or cosmetic effects, contain agents that act locally at its surface (topical)4 or deeper in the skin.5 Fortunately for our evolutionary adaptation to different environmental conditions, our skin is a formidable barrier that protects us from unwanted attacks, but it also limits the transport of desired substances.6 Therefore, studies of skin permeability and ways to increase the efficiency of the penetration processes are crucial for the development of drug delivery systems, particularly for transdermal and injectable administration routes.
Transport phenomena related to skin penetration have been extensively studied, modeled, and reviewed in previous works.7,8 The combination of experiments with novel imaging methods9,10 and in silico investigations and numerical modeling11,12 have contributed to strengthening this enormous field of study. For example, machine learning procedures enable the development of complex methods to build new, more predictable models for skin permeability13 (machine learning is an application of artificial intelligence that provides the systems the ability to automatically learn by themselves from data, without being explicitly programmed).
To expand on previously published work, in this article, we frame current theoretical, experimental, and in silico approaches in the context of transdermal methods for drug delivery. In doing so, we provide a wide overview of the current challenges faced by biomicrofluidics technology in this field. Ongoing efforts focused on developing and optimizing models for skin transport are of great relevance from a scientific perspective but also for its faster deployment into society in the form of new medical devices and minimally invasive therapies. On the other side, we have observed a wider adoption of wearable medical technologies during the last few years. Wearable devices integrated with electronic and optical biosensors provide data in real time about patient status. Tattoo-like films and patches placed over skin have been used to monitor physiological variables, such as temperature.14–16 Although there has been a large amount of studies about transdermal penetration, most of them have addressed the problems of skin permeation from standard samples.
The delivery of drugs has followed a one-size-fits-all approach for decades, which helped improve the quality of life of millions of humans and eradicate many diseases. However, in recent years, we have observed a change in paradigm toward a personalized and preventive medicine.14 The challenges to perform transdermal delivery then become evident because each skin region has different components and properties and greatly varies between individuals.
In Table I, we present commonly used terms related to skin transport found in the literature, which we also use in this work.
TABLE I.
Terminology related to skin permeation processes.
| Concept | Definition |
|---|---|
| Skin permeation/transdermal transport | The mass transport of substances from the skin surface to the general circulation. It includes permeation through the stratum corneum, diffusion through each skin layer and final uptake by the capillary network in the dermis, thus enabling the transportation to target tissues. Permeation routes are illustrated in Fig. 2.17 |
| Vehicle | The inert medium in which the therapeutic agent is formulated.18 |
| Passive diffusion | Mechanism through which the permeation process in human or animal skin takes place. Permeation is attributed to the passive diffusion of the drug from a vehicle on the skin surface to systemic circulation. Passive diffusion is affected by physicochemical factors (e.g., drug-vehicle interaction) and skin conditions (e.g., hydration, pathological issues).17 |
| Active diffusion | It involves the use of external energy to act as a driving force and to reduce the barrier nature of stratum corneum. Mechanical methods such as needles, microneedles, jet injectors (described in Sec. V) constitute active systems for drug diffusion.19 |
| Permeation enhancer | Physical or chemical agents that alter the passive diffusion by favoring skin permeability; they are properly described in Sec. V. When permeation enhancers are used the diffusion becomes active.20 |
| Transdermal drug delivery | Drug diffusion through the various layers of the skin and into the systemic circulation for a therapeutic effect to be exerted.19 |
| Dermal drug delivery | Topical delivery to pathological sites within the skin (minimal systemic absorption).19 |
| Partition coefficient (K)) | It represents the ratio of concentrations of a compound in a mixture of two immiscible media. |
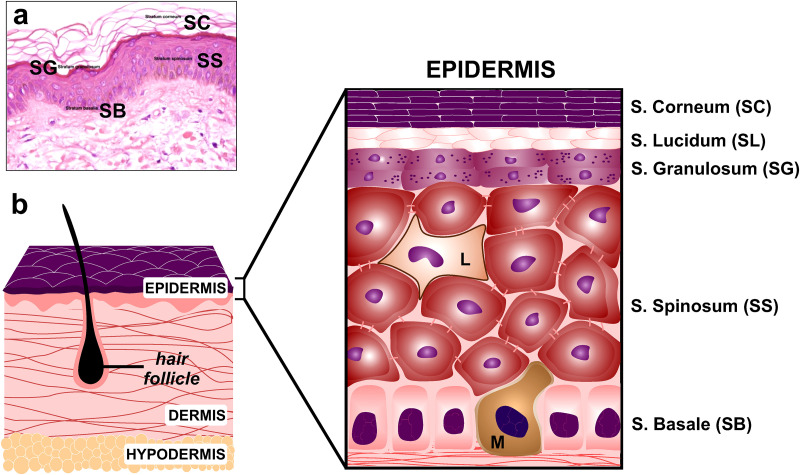
Skin is the first defense barrier against external assaults (pathogens, xenobiotics, UV irradiation) and prevents the loss of water and solutes. Notably, it is constituted by complex mechanical, chemical, and immunological barriers. Furthermore, skin architecture is mechanically complex as evidenced by the numerous studies to determine its properties with experiments or advanced models.21–23 Skin is composed of different types of cells and layers, as follows:24–26
-
•
Epidermis: Its outermost hydrophobic layer is the Stratum Corneum (SC), which is constituted by dead, keratinized, corneocytes (cells), embedded in a lipid matrix composed of cholesterol, ceramides, and fatty acids. The Stratum Lucidum (SL) and Stratum Granulosum (SG) layers are found under the SC. The Stratum Spinosum (SS) houses the Langerhans cells, which are cells from the immune system. The Stratum Basale (SB) is the deepest epidermal layer below which lie the layers of the dermis. The cells from the epidermal layers are connected to each other by intercellular protein connections (e.g., tight junctions, TJ).
-
•
Dermis: It is composed of a strong connective tissue (1.5–3 mm) and provides elasticity and stability. The papillary region with capillary loops and nerve terminations on top contains thin collagen and fine elastin fibers, while the reticular region is mainly formed by dense collagen fibers interlaced in a net-like manner. The sebaceous sweat glands, hair follicles, sensors for touch, and blood vessels are present also in the dermis. Fibroblasts are the predominating cell in the dermis and secrete extracellular matrix connective tissue.
-
•
Hypodermis: Also known as subcutaneous fat layer, it is mainly made of cells containing large fat droplets and provides a mechanical cushion, thermal insulation, and energy storage. It also connects the skin (epidermis + dermis) with the muscle. This layer is the most variable in depth (from 3 to more than 10 mm), depending on the specific location in the body, age, gender, and body mass.
The epidermis layers can be seen in Fig. 1(a), as observed with optical microscopy. A corresponding scheme in Fig. 1(b) illustrates the structure of the skin and its constitutive layers.
FIG. 1.
(a) Overview of the human epidermis (optical microscopy image, ×200). (b) Scheme of the skin architecture (not to scale). Stratum Corneum (SC), Stratum Lucidum (SL), Stratum Granulosum (SG), Stratum Spinosum (SS), and Stratum Basale (SB) constitute the epidermis, directly connected to the dermis layer. Hair follicles and the fibers network are also represented in the scheme. Hypodermis is the subcutaneous layer formed by adipose cells. L: Langerhans cell, M: Melanocyte. Figure 1(a): Adapted from B. R. Smoller and M. Hiatt Kim, Dermatopathology: The Basics (Springer Nature, New York, 2009). Copyright 2009 Springer Nature.26
The biological complexity of skin architecture denotes the difficulty to investigate fluid transport processes across the largest organ of the human body. In particular, the SC is of particular interest for drug delivery, because it plays a major role in skin absorption for transdermal drug delivery systems.27 Nowadays, it is well established that permeation routes are limited by the epidermis structure28 and the lipid composition of the SC.29,30 In fact, the lipid matrix of this layer is the target of the chemical penetration enhancers (agents that favor skin permeability; they are described in Sec. V).31 Also, passive diffusion across the SC is restricted to lipophilic chemical compounds with less than 500 Da (Dalton) molecular weight (1 Da =1 g/mol).19,30 Thus, any molecule must cross multiple chemical and physical barriers during its interaction with the skin structure. Accordingly, the passage through each barrier is determined by disparate timescales and length scales, which have hindered the establishment of a comprehensive skin model encompassing all relevant transport parameters. Therefore, accurate approaches to address skin permeability, theoretical and experimentally, are crucial.
Typically, a porous medium is defined as a solid material that contains empty spaces called pores.32 Interestingly, although skin does not have actual pores like other materials, such as sedimentary rocks, paper. or soil, it is considered as the outermost porous medium of the human body.33,34 This assumption is based on the presence of interstitial fluid and vascular channels between the skin cells. To the best of our knowledge, there are unanswered challenging questions concerning the in situ and real time fluid dynamics across the skin conceived as a porous medium. Depending on our ability to answer these questions and the development of new measurement methods, we will be able to pave the way to novel applications that will improve the quality of life through advanced medical treatments or cosmetics.
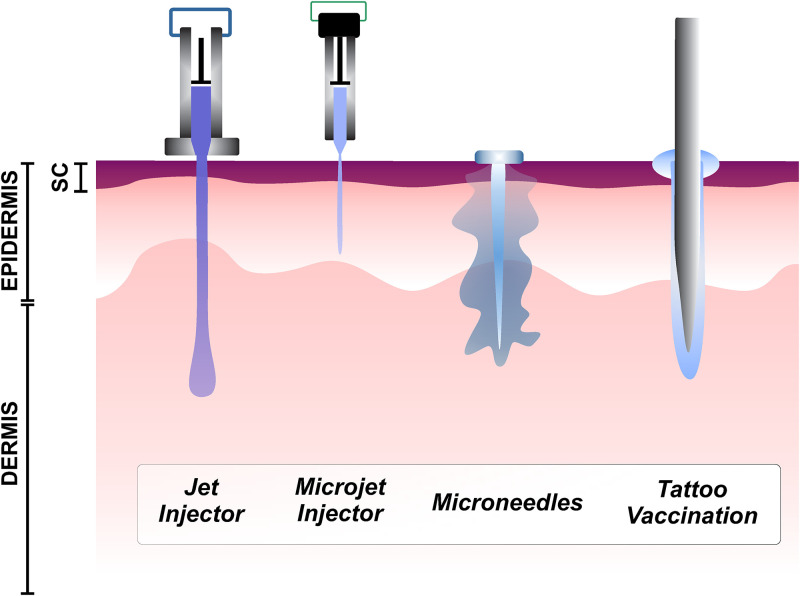
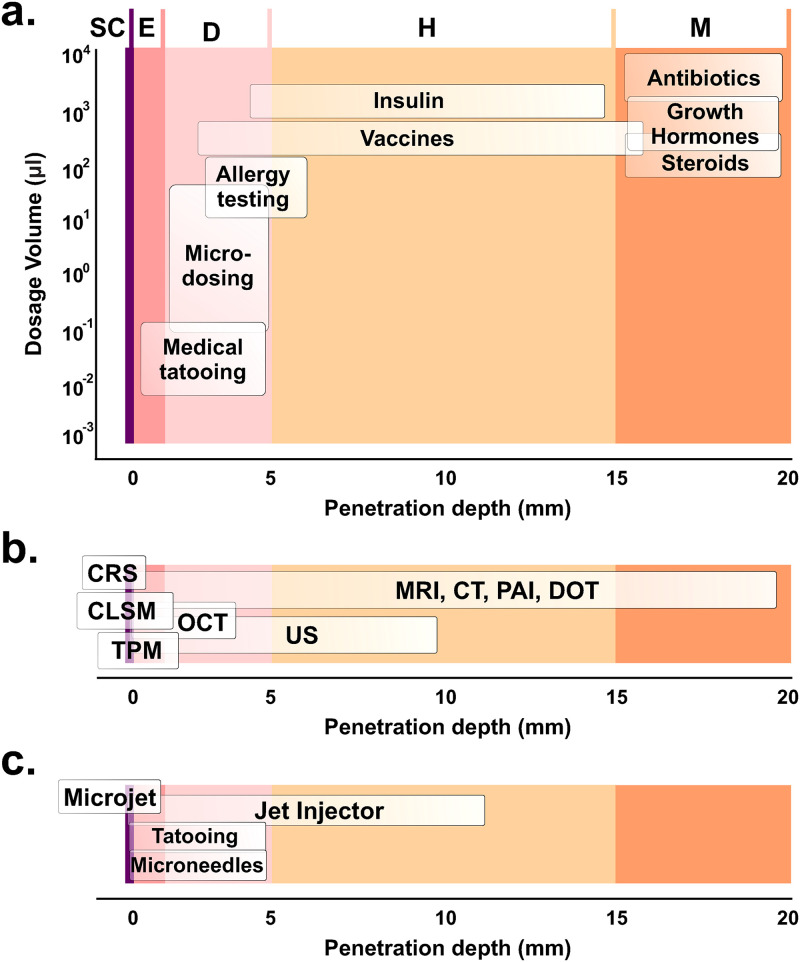
In this work, we discuss the current challenges when performing permeability studies on the skin, in relation to biomicrofluidics. The article is organized as follows: Sec. II gives a brief chronology of the different theoretical approaches to assess skin permeation. Section III describes the most used experimental imaging methodologies to study the transport processes across the skin. In Section IV, we describe the transport phenomena from in silico approaches. Last, in Sec. V, we discuss the most relevant challenges faced by modern medicine methods aimed at delivering novel formulations of drugs and vaccines. We focus on three delivery methods, needle-free jet injectors, microneedles, and tattooing, with comparable injecting “object” length scales, ∼10 μm. These scales are larger than other methods such as sonophoresis and lipid nanoparticles, and consequently less invasive. Moreover, from the selected methods, jet injectors and tattooing have received little attention compared to other delivery techniques.
Our ambition is to give a broad perspective on the studies of skin permeation processes in the frame of technological advances in drug administration strategies, and current trends in personalized medicine.
II. PENETRATION PROCESS ACROSS SKIN: POROUS MEDIUM APPROACH
To characterize exhaustively skin penetration processes, it is necessary to have accurate data of the molecules to be delivered and the vehicle used for the transport.18 These data include, e.g., molecular weight, solubility, lipophilicity, the ratio hydrophobicity/hydrophilicity, diffusion , and partition coefficients (the partition coefficient represents the ratio of concentrations of a compound in a mixture of two immiscible media). Other skin properties such as thickness and the chemical and cellular composition of its layers must be known, particularly the SC architecture, which dominates transdermal absorption. The values of skin properties found in the literature vary greatly, not only due to its heterogeneous nature but also by the large number of methods used in determining the specific property of interest.35–37 For example, the fracture of skin depends on parameters such as relative humidity, temperature, age, etc. As a result, skin critical stress values, G, can be found with a wide range of 500 kPa–20 MPa.38–40
All these requirements make the characterization of penetration processes a challenge, given the complexity of the skin structure and the wide variety of methodologies to assess the problem. Hence, theoretical approaches can help in describing or predicting real-life scenarios, which will be described further in this section (Subsection II A).
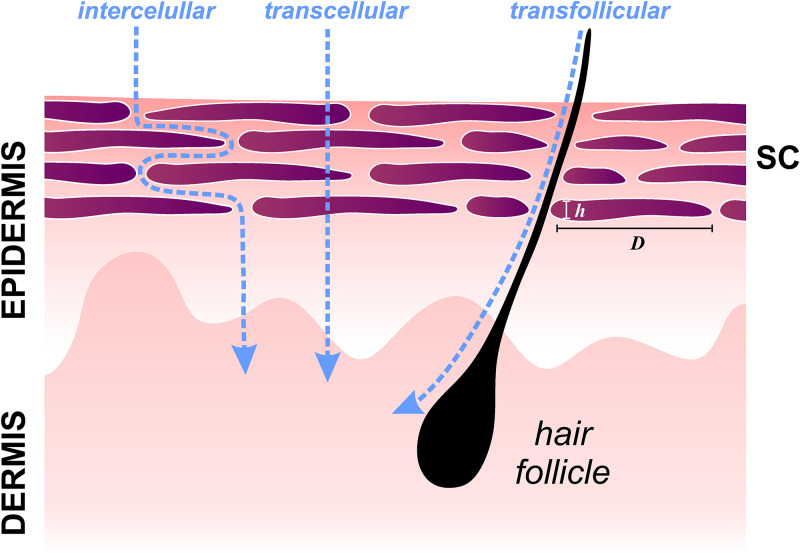
Drug penetration efficiency can be described by Fick's law, arguably the most intuitive model to quantify the flux permeation across a barrier. First, Fick's law relates the diffusive flux to the concentration gradient; second, Fick's law predicts how diffusion affects the change in concentration with respect to time. Considering the skin as a membrane exposed to a solute on one side, the amount of solute that crosses the barrier per unit of time can be estimated after reaching a steady state.7 However, this macroscopic approach assumes skin as a homogeneous medium, excluding active diffusion mechanisms and complex pathways and barriers that solutes meet during diffusion. Basically, SC provides three pathways: through the corneocytes, between corneocytes (intercellular spaces),41,42 and along appendages, such as glands or hair follicles (transfollicular route) (Fig. 2). The SC is 10–50 μm thick, and it is composed of 15–20 layers of corneocytes, dead, and keratinized epidermal cells.43 Typically, a corneocyte is 0.8 μm thick with a diameter of ∼40 μm.
FIG. 2.
Schematic representation of the most common permeation routes through the Stratum Corneum (SC): intercellular, transcellular, and transfollicular routes (not to scale).
A. Theoretical models to study skin permeation
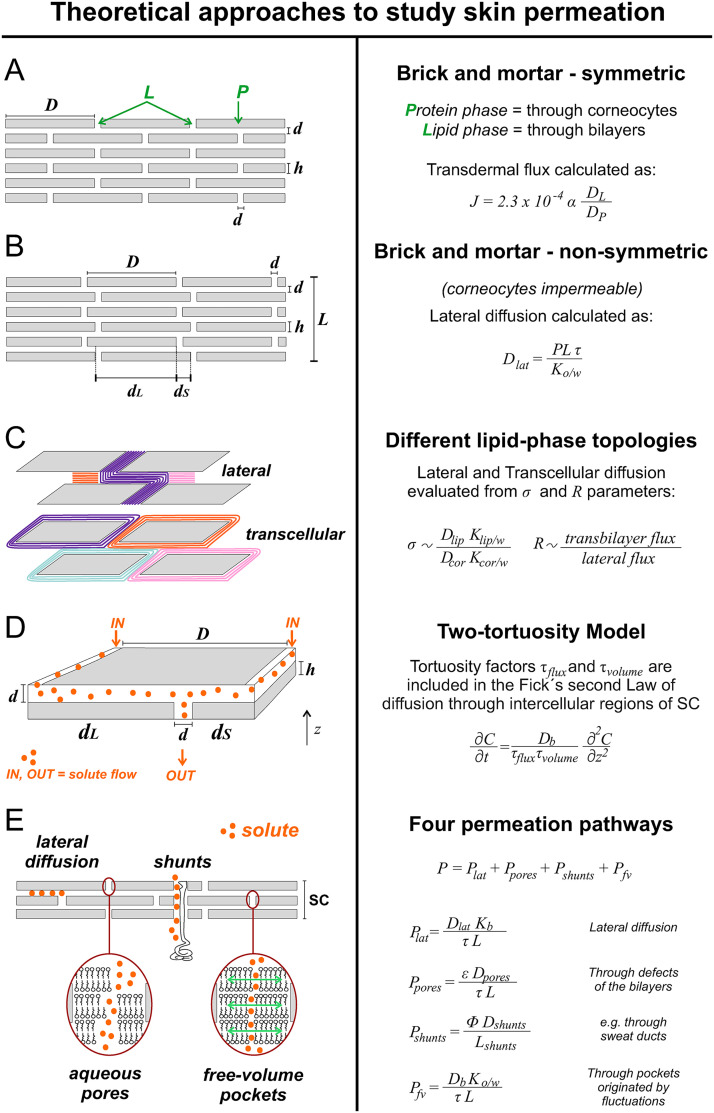
As mentioned before, the SC controls transdermal penetration; thus, most of the theoretical models we present in this section will be based on the SC structure. The topography of SC and the keratinized cells on the surface are shown in Fig. 3,44,45 revealing stacked corneocytes layers and the lipid sheets between them. The SC architecture has been described as a brick and mortar structure, where corneocytes represent the bricks, and lipid sheets are the mortar-filled spaces between cells. The lipid-filled space is permeable to hydrophobic molecules, while the corneocytes, in general, are highly impermeable to most solutes. Several theoretical models described in this section will provide a more comprehensive understanding about the permeability of corneocytes. This SC architecture gives a porous representation, since the permeable lipid sheets would represent voids (i.e., pores) in a medium composed of interconnected cells. The evolution of this representation has been updated and adapted throughout the years by different researchers (the details are summarized in Fig. 4).
FIG. 3.
(a) SEM micrograph of epidermis excised from the thigh region of human cadaver. Scale bar: 10 μm. (b) TEM image showing the corneocytes layers. Scale bar: 2 μm. (c) TEM micrograph where lipid layers can be observed between the corneocytes (white arrow). Scale bar: 200 nm. (b) and (c) correspond to human skin from cosmetic surgery. Figure 3(a): Reprinted with permission from Manda et al., J. Pharm. Sci. 103(6), 1638–1642 (2014). Copyright 2014 Elsevier.45 Figures 3(b) and 3(c): Reprinted with permission from Pilgram et al., J. Invest. Dermatol. 113(3), 403–409 (1999). Copyright 1999 Elsevier.44
FIG. 4.
Schematic representation of the most relevant theoretical approaches to assess permeation through SC and its most significant equations. (a) The symmetric structure of the SC presented for the first time in 1975. (b) Non-symmetric description of lateral diffusive paths along lipid bilayer of SC. (c) Two different lipid-phase topology: top scheme: lateral diffusion through an uninterrupted lipid pathway; bottom scheme: each corneocyte surrounded by intact lipid bilayers. (d) The two-tortuosity model and the tortuosity factors included in the Fick's second law. (e) Four permeation pathways considered to assess the transport of molecules through the skin; based on Refs. 29, 43, 47, 53–56, 59, and 60. Figure 4(a): Reprinted with permission from Michaels et al., AIChE J. 21, 985 (1975). Copyright 1975 John Wiley & Sons Inc.46 Figure 4(b): Adapted with permission from Johnson et al., J. Pharm. Sci. 86(10), 1162–1172 (1997). Copyright 1997 Elsevier.47 Figure 4(c): Adapted with permission from Wang et al., J. Pharm. Sci. 96(3), 620–648 (2006). Copyright 2006 Elsevier.48 Figure 4(d): Adapted with permission from Kushner et al., J. Pharm. Sci. 96(12), 3226–3251 (2007). Copyright 2007 Elsevier.49
The first brick-mortar concept was introduced in 1975,46 with a symmetric structure representation of the SC layer, where the interstitial horizontal lengths between cells and the vertical spaces , are all of the same length, ∼75 nm [Fig. 4(a)]. This mathematical model comprises a heterogeneous SC, composed by a lipid phase (L) in the intercellular region and a protein phase (P) within the corneocytes, and predicts the transdermal flux as follows [Eq. (1)]:
| (1) |
where and are the partition and diffusion coefficients of each phase. The model was correlated with empirical skin permeation fluxes in cadaveric skin samples with ten different radiolabeled drugs. It explained and predicted the penetration rate of these substances. A wide range of variation between maximum and minimum transport rate values for different drugs was found: six orders of magnitude between the ephedrine (300 μg/cm2 h) and digitoxin (1.3 × 10−4 μg/cm2 h). Since the mineral oil/water partition coefficient of ephedrine is 70 times higher than the one for digitoxin, it was evidenced that the hydrophobic nature of the substance plays a crucial role enhancing the skin penetration process. This pioneering work has influenced more than 600 investigations since 1975, reaching more than 100 citations in the last five years (Scopus data).
Another model expressing the relationship between macroscopic permeability measurements of the skin, and geometric characteristics of the SC, was built as a non-symmetric description of lateral diffusive paths along lipid bilayers, where and represent the long and short lateral diffusion pathways, respectively [Fig. 4(b)].47 The steady state diffusive flux along a given bilayer was described by Fick's first law, allowing the estimation of the lateral diffusion coefficient for more than 120 compounds from the following equation [Eq. (2)]:
| (2) |
where P and L are permeability and the thickness of SC, respectively; represents tortuosity and is the octanol–water partition coefficient. The lateral diffusion coefficients exhibited a strong molecular weight dependence for low-molecular weight solutes (<300 Da). For instance, diffusion values for methanol (32 Da) and testosterone (288 Da) were ∼10−6 and ∼10−9 cm2/s, respectively, confirming that small solutes diffuse faster than the larger ones. It was found that the diffusive resistance associated with lateral diffusion is sufficient to explain the overall resistance of solute permeation through the SC, indicating that corneocytes are an impermeable barrier.
More recently, the diffusion through the corneocytes was modeled considering two different lipid-phase topologies.48 The first considers lateral diffusion through an uninterrupted lipid pathway [Fig. 4(c), top], while the second considers each corneocyte surrounded by intact lipid bilayers, and molecule hopping from one layer of corneocytes to the next, i.e., transcellular diffusion [Fig. 4(c), bottom]. This is a more realistic representation of the SC microstructure that uses a trapezoidal geometry to represent the corneocytes shape. Quantifications of the flux of solutes in the SC as well as permeability studies were done with the parameter which correlates with the ratio of lipid to-corneocytes phase permeabilities [Eq. (3)],
| (3) |
where and (cm2/s) represent the diffusion coefficient in each phase, while and (dimensionless) are the partition coefficients for lipid and corneocyte phases, respectively, relative to an aqueous solution . The limiting cases are when corneocytes are highly impermeable or highly permeable . The latter represents the situation where the lipid phase controls the SC permeability. Also, the model defines a ( = 500 or = 1200 depending on the experimental condition) to establish if most of the solute travels by lateral diffusion through the lipid bilayer or by transcellular diffusion through the corneocytes . A dimensionless parameter R was defined as the ratio of transbilayer (i.e., transcellular) flux to lateral flux within a lipid bilayer [Eq. (4)],
| (4) |
The models described until here helped determine the and R values for all the tested molecules: water, ethanol, nicotinamide, and testosterone. The SC permeability of each component was obtained from published experimental data as well as the partition and diffusion coefficients. Ethanol (eth) and nicotinamide (nic) exhibited the same hydrophilicity and for both molecules (i.e., corneocytes are permeable). Particularly, = 0.022 > = 0.0035, which means that corneocyte permeability plays a major role for nicotinamide transport. Due to its smaller size, the diffusivity of ethanol in both lipid ( = 8.5 × 10−7 cm2/s) and corneocyte ( = 1.2 × 10−5 cm2/s) phases is larger than that of nicotinamide ( = 9.2 × 10−8 and = 7.4 × 10−6 cm2/s). Moreover, higher R values were found for ethanol than nicotinamide, since transbilayer flux decreases monotonically with an increase in solute molecular weight. All tested molecules exhibited and , indicating that corneocytes are highly permeable for the molecules studied, concluding that the lipid phase controls their permeation process.
Another model, the two-tortuosity model, deals with the empirical determination of key parameters, lipid bilayer diffusion , and vehicle bilayer partition coefficients to assess transdermal transport in a more simple way [Fig. 4(d)]. Usually, permeation measurements require previous experiments (e.g., measurements of the solute release from SC) to determine these coefficients in the lipid bilayers of SC. The two-tortuosity model was validated using finite element simulations and offers a simplified alternative for obtaining and for hydrophobic solutes directly from permeation measurements.49 This model describes the diffusion of hydrophobic solutes assuming that transport is restricted to the intercellular domains of SC, and contains two tortuosity factors in the equations: (i) the total amount of lipids in SC and (ii) the impact of lateral diffusion through the SC . Then, Fick's second law for the intercellular region of SC with tortuosity factors included is derived as [Eq. (5)]
| (5) |
where C is the concentration of solute and z is the thickness of SC. From the solution of the equation of the model and considering the known values of the structural parameters of the SC (number of corneocytes, length of corneocytes, height of the cells, etc.), and are directly evaluated from a regression analysis of SC permeation experiments. Experimental results with naphthol and testosterone in Franz diffusion cells (see Sec. III for more details of this experimental method) were combined with numerical diffusion values from finite element Method simulations. The regression analysis from mass delivered vs time curves provided values of and within an error of 2%–3% for native human SC structures, in agreement with the expected values according to Fluorescence Recovery After Photobleaching (FRAP) experiments.50 For example, the testosterone value deduced from the two-tortuosity model was 1.9 × 10−8 cm2/s, compared to 2.0 × 10−8 cm2/s previously obtained from a work combining two sets of experiments: one to assess SC permeability and other to measure the solute release from the SC.51
Other studies have explored permeation routes for different molecules. Pioneering work from more than half a century ago considered hair follicles and sweat ducts as permeation routes.52 More recently, the skin permeability was modeled for hydrophobic and hydrophilic solutes with four penetration routes in the SC [Fig. 4(e)]:53 (i) lateral diffusion along bilayers , (ii) diffusion through aqueous pores created by imperfections in the lipid layer (mostly responsible for the transport of hydrophilic solutes, ), (iii) diffusion through shunts (e.g., sweat ducts, ), and (iv) free-volume diffusion through lipid bilayers . The latter refers to fluctuations of the bilayer lipids as a pathway through “free pockets” for small hydrophobic solutes. Thus, skin permeability to a solute is given by the contribution of the different pathways [Eq. (6)],
| (6) |
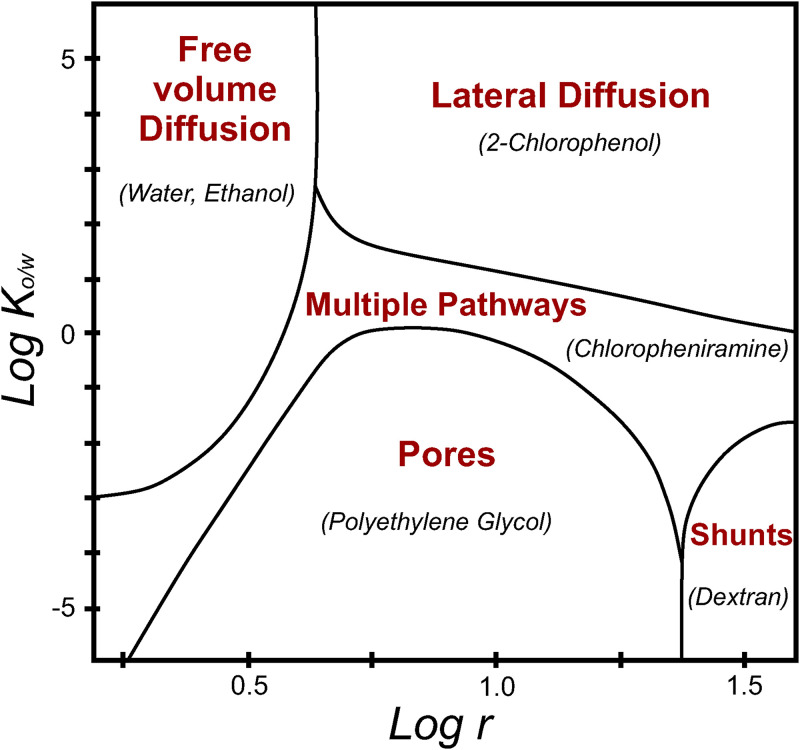
The relative role played by these contributions is mainly determined by a combination of molecular radius and hydrophobicity of the molecule of interest. Figure 5 shows the relative contribution of each penetration route depending on and molecule radius . This model found that: (a) lateral diffusion plays a dominant role for large lipophilic solutes, (b) aqueous pores are important for small and hydrophilic drugs, (c) diffusion through shunts are the dominant pathway for large hydrophilic solutes, and (d) free-volume diffusion plays an important role for low-molecular weight hydrophobic and low-molecular weight moderately hydrophilic solutes.
FIG. 5.
Relative contribution of lateral diffusion, diffusion through pores, diffusion through shunts, and free-volume diffusion, for various octanol/water partition coefficients and molecule radii . An example is given (between brackets) for each penetration route. Redrawn from Ref. 53. A schematic representation of each permeation route can be found in Fig. 4(e). Adapted from S. Mitragotri, J. Controlled Release 86(1), 69–92 (2003). Copyright 2003 Elsevier.
In what follows, we list the equations describing the contribution of each permeation route:
-
•Lateral diffusion is the most studied and modeled pathway for large hydrophobic solutes in lipid membranes.54–56 The permeability due to this phenomenon is given by [Eq. (7)]
where and are diffusion and partition coefficients in the lipid bilayer; is the tortuosity, and L the SC thickness. Previous works29,47 determined and = 3.6.(7) -
•For small hydrophilic solutes, aqueous pore-membrane models have been proposed to describe the transport through water-filled spaces within lipid bilayers. This approach is based on the hypothesis that nm-sized voids inside the SC result from defects of the lipid bilayers (e.g., lattice vacancies, missing lipids). The voids are imagined as uniform cylindrical tortuous pores traversing the barrier layer, describing the SC as a porous membrane.43 The area fraction occupied by pores is low, about 2 × 10−5.53 Permeability through aqueous pores is given by Eq. (8),53
where is the porosity and is the diffusion coefficient.(8) Interestingly, in other non-biological systems, a proton mobility has been observed in the extended nanospace (101–103 nm scale),57,58 which is a transitional phase from single molecules to normal liquids in the microspace. The ion mobility of protons in nm-sized confined spaces can be affected by both proton hopping and by Stokes–Einstein diffusion. The proton diffusion coefficient varies almost a magnitude order between nanochannel sizes in the range of 180 and 1580 nm.58 We suggest that this interesting phenomenon could be explored in nm-sized spaces in the skin structure, such as in the aforementioned pores in the lipid membrane or the spaces between corneocytes.
-
•For large hydrophilic solutes (>100 000 Da), transdermal transport occurs by shunts (i.e., appendages). The area fraction occupied by follicles and sweat glands is about 10−3 and 10−4, respectively. Permeability through this route can be written as [Eq. (9)],
where is the length of a sweat duct, typically of the order of 500 μm; and is the fraction covered by hair follicles and sweat ducts.(9) -
•An analysis based on the scaled particle theory was developed for small and hydrophobic solutes (<400 Da).59 This theory describes the energy required to open free pockets (cavities) caused by density fluctuations in the lipid bilayer. The time-scale associated with solute jumps between free-volume pockets are nanoseconds, while fluctuations of the bilayers occur in microseconds. Thus, solute jumps can be modeled in a stationary lipid structure. The equation to predict skin permeability through these cavities is given by Eq. (10),60
where and are diffusion and partition coefficients in the lipid bilayer, respectively. This equation was reformulated with experimental work leading to Eq. (11),(10)
where r is the solute molecular radius (Å). The model predictions were compared with experimental data47 yielding a mean error value of 5%.(11) This model was later adapted to study properties such as porosity, tortuosity, and the hindrance factor of the skin aqueous pore channels. Experiments with four hydrophilic substances in human cadaver skin were done while perturbing the skin by changing its electrical resistance with ultrasound, and then comparing the permeation values with different solutes.61 For instance, porosity increases as the extent of skin perturbation increases. This behavior has been observed independently of the solute size, so porosity may be considered as an intrinsic property of the skin membrane rather than solute size-dependent. Conversely, changes on hindrance factor and tortuosity after skin perturbation were significantly dependent on the radius of the solute.
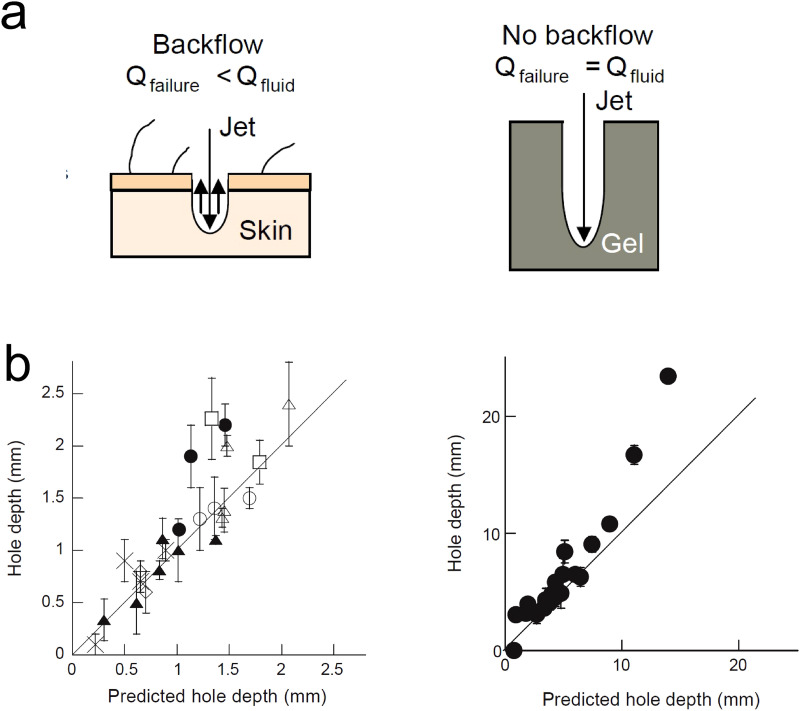
The analysis and theoretical approaches described so far consider the passive diffusion of solutes. However, some transdermal methods of drug delivery involve the action of external forces to penetrate the skin. In Sec. V, we describe those that we consider most relevant for future medical applications, such as jet injectors devices. Experimental studies and predictive models have been developed to describe the mechanisms of interaction between liquid jets and the skin. For instance, a theoretical model was developed to predict the hole depth as a function of jet and skin properties.40 The formation of a hole is a critical step in needle-free liquid jet injections and its depth determines the fluid penetration. An experimental setup using Franz cells (previously validated to represent in vivo jet injections) was used to quantify the dispersion of solutes through polyacrylamide gels and human and porcine skin and derive a theoretical model to predict the hole depth . Using high-speed imaging, the authors determined the flow during the injection (Qfailure) and compared the value with the experimental flow rate (Qfluid). They found that there exists a backflow of the jet during the injection in the skin that is not evidenced in polyacrylamide gels [Fig. 6(a)]. Therefore, two separate models were developed. Equations (12) and (13) predict the hole depth in polyacrylamide and skin samples, respectively,
| (12) |
where is the jet velocity, is the nozzle diameter, is the density of the jet fluid, is the length of the initial region before the jet enters the polyacrylamide gel (standoff distance), and is the critical stress for the failure due to jet puncture (for example, 0.065 MPa for 10% acrylamide gels). The length of the initial region is defined as the length traveled by the fluid at . The jet core velocity is defined as the velocity of the jet in the center of the orifice used to create the jet,
| (13) |
where H is the hole diameter and is the fitted parameter. The main drawback of this model is that cannot be predicted as a function of the standoff distance (i.e., distance between the device and the skin). However, the authors experimentally observed that the hole depth decreases as the standoff distance increases.
FIG. 6.
Prediction of the penetration depth in jet injectors. (a) Schematic representation of the fluid dynamics during the hole formation in skin (left) and polyacrylamide gel (right), showing the backflow phenomenon in skin samples. (b) Hole depth (mm) vs predicted hole depth (mm) in skin (left) and polyacrylamide (right) samples, where □ and △ are human skin and X, ◇, ○, and ▴ porcine skin. Each symbol corresponds to different experimental conditions. Reprinted with permission from J. Baxter and S. Mitragotri, J. Controlled Release 106, 361–373 (2005). Copyright 2005 Elsevier.40
Predicted hole depths in polyacrylamide gels [Fig. 6(b), left] and skin [Fig. 6(b), right] correlate well with the experimental values (r = 0.94 for the gel, r = 0.88 for human skin). The range of hole depths in Fig. 6 was created by varying nozzle diameter from 76 to 304.8 μm and jet exit velocity from 110 to 200 m/s.
Penetration dynamics of microjets in skin and soft tissues was also studied in a more recent work,62 where the dependence between penetration depth and jet velocity is given by Eq. (14),
| (14) |
where is the critical velocity the jet exceeds to penetrate and is the fitting parameter.
Recently, other work focused on estimating the depth of a light source embedded in a scattering medium.63 The method consists on optical fibers coupled with photodiodes for high-speed acquisition of reflectance profiles. The authors used an empirical inverse model for estimating source depth at high speed. Additionally, Monte Carlo simulations were used to generate a dataset of reflectance profiles to which a polynomial model was fitted. The polynomial model generated depth estimations within 2 mm of the true depth, up to a source depth of 15 mm. These results confirm that this system is suitable for non-invasive monitoring of Needle-Free Injections (NFIs) in the scattered medium of skin samples. In Sec. III, we will describe other methods and imaging techniques that allow skin visualization and quantification of penetration depth.
III. SKIN PERMEATION PROCESSES STUDIED THROUGH IMAGING TECHNIQUES
Typically, in vitro skin permeation studies are performed in Franz diffusion cells. These devices were developed in 1970 and consist of a cell that holds a chamber with the solute of interest, a membrane through which the solute will diffuse (skin in our case) and an acceptor chamber from which samples are further investigated.64 Franz tests allow the studies of skin permeation in full-thickness skin models.65,66 The permeation across dermatome human skin explants (an area of skin that is innervated by a single spinal nerve) is considered as the gold standard for assessing the delivery of drugs from a transdermal system.67 However, as we will discuss in Sec. V, ethical and economics reasons promote the developing of more reliable alternatives. In addition, permeation experiments done in Franz cells analyze the final state of the diffusive process, thus impeding the studies in real time. Conversely, other methodologies such as imaging techniques have the potential to allow the quantification of solutes throughout the whole diffusive process.
Imaging methods to study skin-related phenomena can be divided as invasive and non-invasive. Non-invasive imaging methods are of great importance in medical diagnostics, because the skin is available for dermatological inspection needed to identify suspicious lesions, such as structural pathological changes in the skin due to cancer.68 Additionally, non-invasive techniques enable the in vivo examination of samples for histometric studies. Histometric measurements are a quantitative approach to investigating skin changes that cannot be described properly by qualitative histological parameters. The main parameters determined during histometric analysis are nucleus diameter, glandular volumes, and cell perimeters.25 Studies on transdermal permeation processes require, for example, the determination of thicknesses of the skin and their layers. Compared to traditional sectioning where the invasive and destructive methodology of tissue processing contributes to distortion of the histological sections, one advantage of in vivo histometry is the lack of artifacts due to the excision of the skin.69
Imaging methods can also be characterized according to their spatial and temporal resolution. Spatial resolution refers to the smallest size of a given feature that can be detected by the technique. Temporal resolution represents the ability of the technique to distinguish between instantaneous events (i.e., from the beginning of one frame to the next). This ability to resolve fast-moving objects is comparable to the shutter speed for a camera. Typically, a mechanical or electronic shutter controls the exposure time to the light source, which must be sufficiently short as the time difference between one frame and the next.70 The human eye can detect a frequency of 10 Hz (i.e., takes an image every 0.1 s)71 and distinguish objects that are separated by 0.1 mm or larger.72 For research purposes, it is important to capture the smallest details in both temporal and spatial resolution. Therefore, if we want to see microscopic changes that occur at frequencies higher than the human eye can detect, we will need additional equipment, namely, high-speed cameras for improving resolution. Certainly, the specific problem of the research will dictate how the high-speed imaging needs to be done. For taking high-speed images, illumination and trigger signal (i.e., how to take the events at the right moment) are key factors. For example, the need for short exposure times (∼μs) reduces the signal level; thus, illumination must be increased up to four orders of magnitude to achieve high contrast and distinguish the details on the image.70
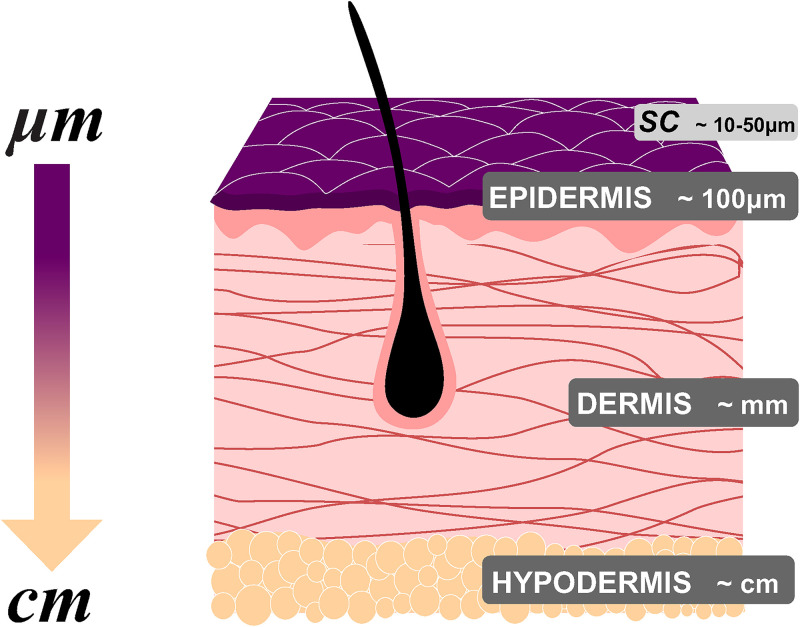
The main challenge to address transport phenomena in situ and in real time is the opaque nature of the skin, which makes it difficult to monitor the permeation process with conventional imaging techniques. Besides, the critical dimensions for transdermal transport can range from centimeters (hypodermis) down to tens of micrometers (SC) (Fig. 7).
FIG. 7.
Simplified schematic representation of the skin, indicating the typical order of magnitude of each layer thicknesses (not to scale). Epidermis ∼100 μm, dermis ∼mm, and hypodermis ∼cm. SC thickness. The outermost layer of epidermis is about 10–50 μm.
In what follows, we list the most used non-invasive imaging techniques with their main characteristics. Since skin is a complex tissue, not all techniques are capable of capturing the wide time and length scales at which transdermal phenomena occur. The complementarity between different tools is related to technical constraints such as the penetration depth and lateral resolution provided, as well as the physical dimensions of skin layers and their components.
A. Ultrasound (US)
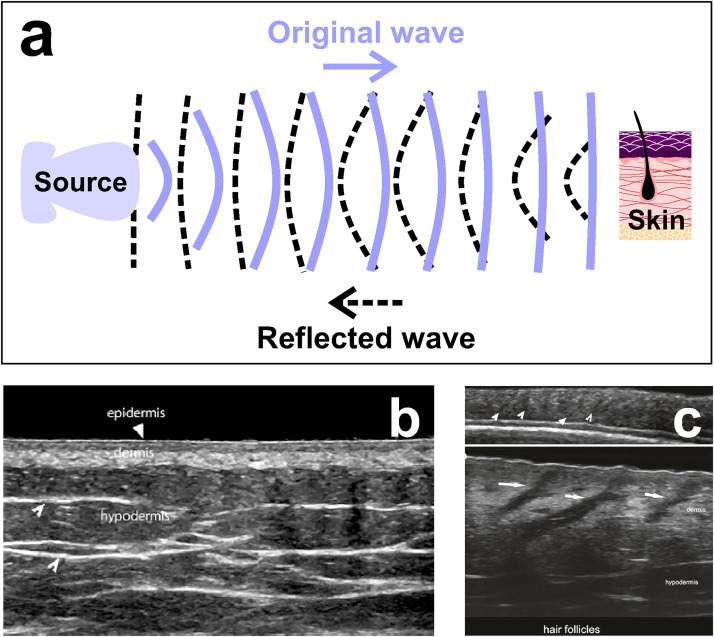
It is arguably the most popularly known technique due to its wide use in medical diagnosis (e.g., pregnancy) and therapy. It utilizes sound waves at frequencies over 20 kHz and enables in situ quantitative measurements of native and engineered tissues (i.e., biomaterials used as tissue mimics), as well as tissue stiffness and viscoelastic properties.73,74 For clinical practices, frequencies of 1–15 MHz are used to image biological tissues (Fig. 8). This low-cost technique allows monitoring of tissue development over time, and it is ideal for preclinical and clinical applications, reaching an imaging depth up to 10 mm with a spatial resolution of 20–100 μm.75 There is a tradeoff between imaging depth and spatial resolution. For example, imaging at low frequencies (1 MHz) allows deeper penetration (∼3 cm) but reduces spatial resolution to a few hundreds of micrometers. In general, US poses a much lower resolution than other techniques, like magnetic resonance imaging (MRI). Recently, a super-resolution ultrasound imaging method was developed for experimental use.76 This method has high temporal accuracy and generated 10 super-resolution images using 3000 acquired frames that can be collected within 6 s. Figure 8 shows the fundamental working principle of the US method [Fig. 8(a)] and representative US images of non-pathological skin [Figs. 8(b) and 8(c)].77
FIG. 8.
Ultrasound. (a) Schematic representation of the method. The source transmits sound waves to the skin; then, the reflected waves are collected by the machine and processed as images. (b) US image reveals epidermis, dermis, and hypodermis layers in a non-pathological human skin. (c) US images show the anatomy of the hair follicles (white arrows) at 18 MHz (top) and at 70 MHz (bottom). Figures 8(b) and 8(c): Reprinted with permission from X. Wortsman, Atlas of Dermatologic Ultrasound (Springer Nature, Cham, 2018). Copyright 2018 Springer Nature.77
B. Optical coherence tomography (OCT)
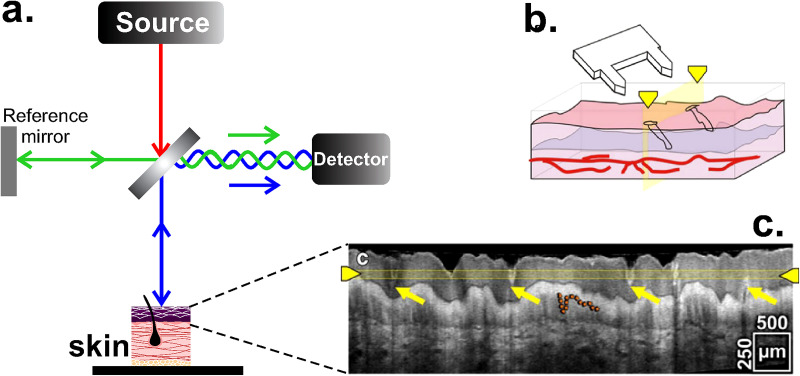
It is a technique that has been exploited since the 1990s and allows three-dimensional (3D) visualization of the in vivo tissue structure through the measurement of interference and coherence between signals reflected from the object and reference signals [Fig. 9(a)].78,79 OCT can be used from near IR (NIR, 700–2000 nm) to visible light (400–700 nm)80,81 and provide anatomical information until 3 mm penetration depth with a lateral resolution of 1–15 μm.9 The highly light scattering nature of skin and its many inhomogeneities are the main cause of difficulties to obtain good quality images. However, OCT enables the determination of the thickness of SC and epidermis,82 as well as cell migration and location in tissue engineering.83 OCT does not inherently offer the ability to track molecular species.81 Thus, in order to assess the biochemical distribution of certain molecules, spectroscopic OCT approaches have been developed to detect the absorption of indocyanine green and near-infrared dyes.84 OCT also enables the in situ and in vivo imaging of the skin. For example, Figs. 9(b) and 9(c) show the OCT image of the microneedle-treated area of human skin (hands) during the insertion of a microneedle array85 (this method of transdermal delivery is described in Sec. V), allowing the characterization of the insertion process and the tissue disruption. About the temporal resolution of the technique, a recent study shows that a temporal resolution of 1.5 ms can be achieved for estimating red blood cell flux.86
FIG. 9.
OCT. (a) Schematic representation of the interferometric method, where the interference between the light source and the sample is detected. (b) Illustration of the microneedle array insertion in the skin. (c) Cross-sectional view of the microneedle-treated area. Yellow arrows indicate the disruption on the tissue after the insertion and the orange dashed line highlights the border between epidermis and dermis. The experiment was done with an OCT system operating at 800 nm (Ti:sapphire as light source) and an effective axial resolution less than 3 μm. Figures 9(b) and 9(c): Reprinted by permission from Coulman et al., Pharm. Res. 28, 66 (2011). Copyright 2010 Springer Nature.85
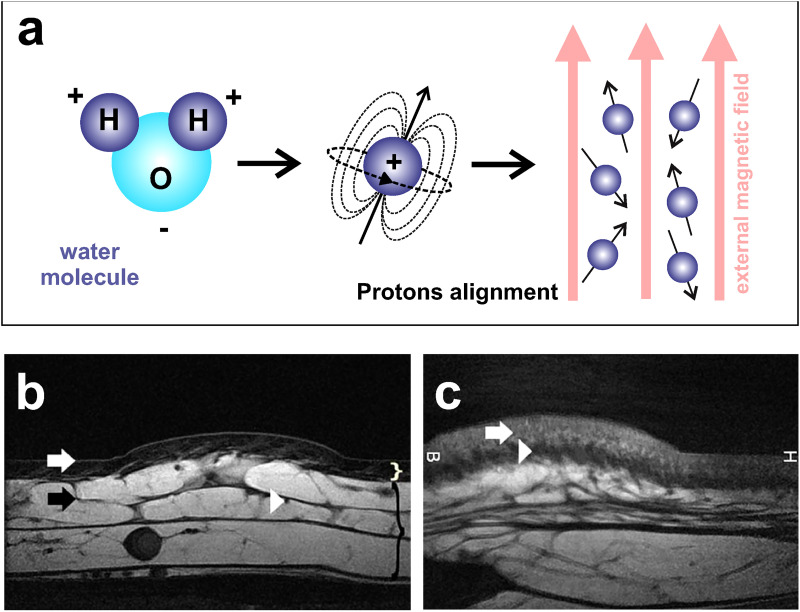
C. Magnetic resonance imaging (MRI)
It is based on the detection of protons in the water molecules present in the body [Fig. 10(a)]. In our skin, the percentage of water is approximately 64%.87 MRI offers many advantages, given its spatial resolution (under 100 μm) and excellent penetration depth capable to image the whole body.88 MRI enables us to distinguish among the skin layers: epidermis, dermis, and hypodermis and their different components.89–91 For instance, Figs. 10(b) and 10(c) show MRI images of the posterior side of the calf and temporal region of the face of healthy volunteers. Skin layers are clearly distinguished in both images.92 In clinical practice, MRI allows the follow-up of cutaneous lesions, enabling physicians to monitor the progress of a therapy. The technique is expensive and images always contain some random noise due to the movement of charged particles and electrical resistance of the electronic components of the system, which reduces the quality of the images (with grains or irregular patterns). MRI requires a relatively long acquisition time. A temporal resolution of 30–50 ms is routinely used in conventional cardiac MRI,93 but an in-house method with modern hardware allowed obtaining a temporal resolution of 6 ms for similar studies.94
FIG. 10.
MRI. (a) Schematic representation of the method. When a magnetic field is applied, protons align with that field. Then, the introduced radiofrequency pulses force the realignment of the protons according to their spin frequency. (b) MRI image of the calf. Epidermis (white arrow), dermis (white curly bracket), hypodermis (black curly bracket), an interlobular septum (black arrow), and a septal vessel (white arrowhead) are visible. (c) MRI image at the face. Superficial (white arrow) and deep dermis (white arrowhead) are well observable. Figures 10(b) and 10(c): Reprinted with permission from Aubry et al., Eur. Radiol. 19, 1595 (2009). Copyright 2009 Springer Nature.92
D. Confocal laser scanning microscopy (CLSM)
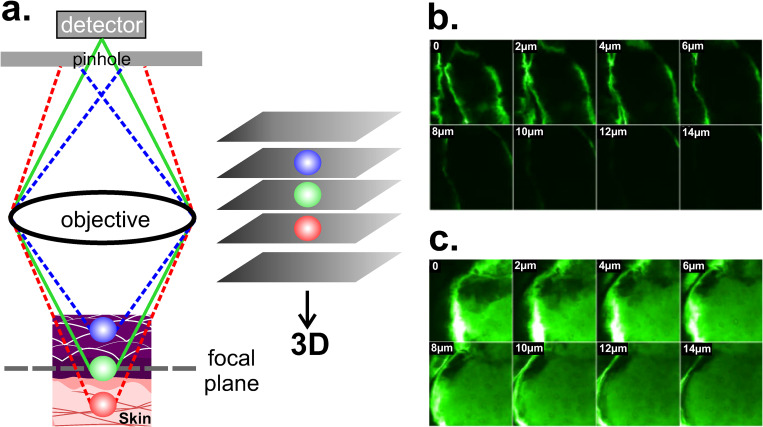
CLSM is one of the most widely used techniques in the field of cellular biology. It enables high resolution 3D images (∼140 nm lateral resolution) from biological samples, both in vivo and in vitro conditions.73,95,96 CLSM light source ranges from UV (200–400 nm) to NIR (700–2000 nm) and it can operate in reflectance or fluorescence mode. Because reflectance mode does not require staining of the sample, it can easily be used for in vivo imaging of skin surfaces. In reflectance mode, samples can be scanned at multiple depths to create a 3D volumetric image, up to 350 μm depth in human skin,97 enough to reach the whole epidermis and part of the dermis. On the other hand, using a combination of fluorescent dyes for different target structures, the fluorescent mode allows staining and parallel visualization of cells or their components within an intact three-dimensional environment.96 A pinhole just before the detector spatially rejects all the fluorescence except that originating from the focus [Fig. 11(a)]. For example, CLSM in fluorescence mode allowed the study of skin permeation in full-thickness skin from porcine ears under the effect of ultrasound as a permeation enhancer. Confocal images reveal the effectiveness of ultrasound for enhancing the diffusion process in samples treated at 20 KHz for 2 h [Fig. 11(c)], when compared to samples without treatment [Fig. 11(b)].98 In Sec. V, we discuss physical and chemical agents that favor permeability processes. One of the main disadvantages of CLSM is that high intensity lasers (up to 250 mW) from the light source can damage the sample (photodamage) and be destructive for the fluorophore itself, causing a photobleaching effect (loss of fluorescence intensity).95 For fluorescence microscopy, temporal resolution is limited by the recycle time of the fluorescent molecule between ground and excited state and by the detector efficiency. A method for increasing the temporal resolution of a CLSM from 44 ms to 2 ms was recently developed.99
FIG. 11.
CLSM. (a) Schematic representation of the working principle in fluorescent mode, where the pinhole rejects all the fluorescent except that originating from the focal plane (green). Images are taken at different penetration depths thus allowing the tridimensional reconstruction. (b) and (c) Confocal images obtained from the surface (0 μm) to a depth of 14 μm showing the diffusion of calcein (fluorescent dye). Images from (c) were obtained after an ultrasound treatment (20 KHz, 2 h). The increase in fluorescence intensity confirms both the enhancement of the diffusion at the same depth and the higher penetration depth. Excitation and emission wavelengths for calcein were 488 nm and 543 nm, respectively. Figures 11(b) and 11(c): Reprinted with permission from Alvarez-Román et al., Microsc. Microanal. 92(6), 1138–1146 (2003). Copyright 2003 Elsevier.98
E. Confocal Raman spectroscopy (CRS)
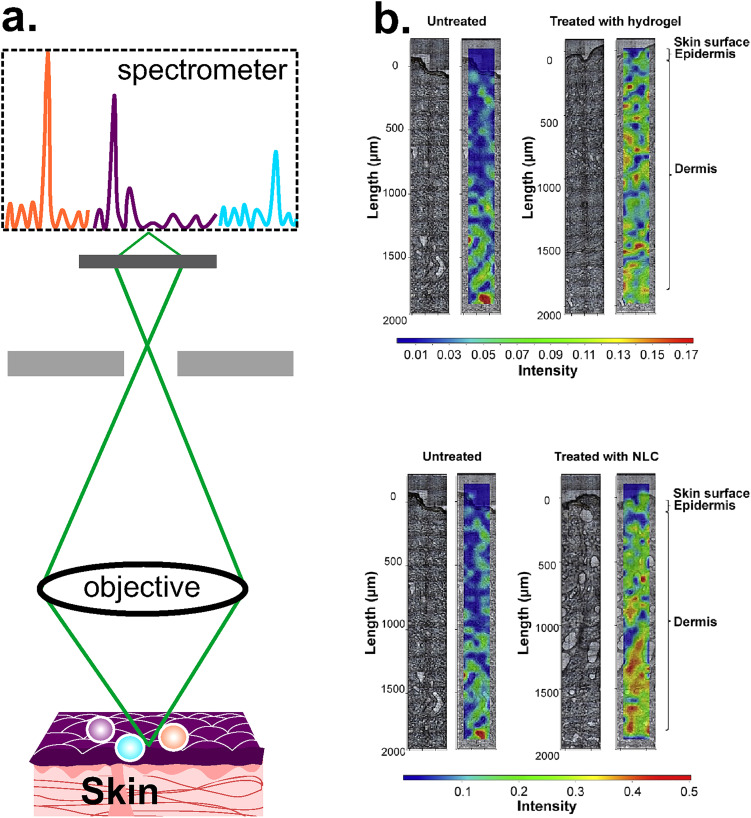
Raman scattering was discovered in 1928 and provides a way to measure molecular composition through inelastic scattering, a process where the molecule exchanges its energy with that of the incident light. The energy difference between the initial and final states represents the specific vibrational frequency of the molecule of interest (Raman shift).100 Raman Spectroscopy (RS) is a non-invasive powerful technique to identify the molecular composition of materials and has been used in biological systems to measure concentrations of analytes in blood, such as glucose, and sweat constituents in the skin (lactate, urea).101 Raman shifts are independent of the excitation wavelength and thus offer flexibility in the choice of the wavelength range.100 Although RS allows detecting molecular composition, no information about skin morphology and permeation routes can be obtained. The CRS is an improved system that couples a microscope with a Raman spectrometer and provides information about depth profiles in tridimensional structures, allowing the mapping of the chemical composition of the sample [Fig. 12(a)]. For example, a recent study reported a Raman spectroscopic mapping made in cryosections of the human skin (10 μm thick) with the aim to study new vehicles for lidocaine. The permeation of lidocaine with Nanostructured Lipid Carriers (NLCs) was compared against lidocaine with hydrogel, one of the conventional vehicles. The study showed high intensity values of the drug in epidermis and dermis when the new tested vehicle was used [Fig. 12(b)].102 The spatial resolution of CRS is of the order of 0.5–1 μm, depending on the laser type and magnification of the objective lens,103 though a recent work reported a lateral resolution of 250 nm.104 CRS has also been used to study the hydration level in human skin in vivo, reaching a depth of up to 40 μm.105 Besides, CRS enabled the study of changes in SC thickness due to the effect of moisturizers,106 and short-term effect of hands washing.107 Despite the versatility of RS, turbidity in biological tissues is high, which produces a significant spectrum overlap.
FIG. 12.
CRS. (a) Schematic representation of the CRS system, where the spectrometer is coupled with a microscope to analyze the chemical composition of the sample. (b) Qualitative Raman maps of lidocaine with hydrogel distribution (top) and lidocaine with NCL (bottom), where the intensity scale is: red > green > blue. Raman maps are from Ref. 102 and were done in a skin area of 2000 μm (perpendicular to SC) × 200 μm (parallel to SC). Untreated skin samples were used as control. Figure 12(b): Reprinted with permission from Bakonyi et al., J. Pharm. Biomed. Anal. 154, 1–6 (2018). Copyright 2018 Elsevier.
F. Two-photon microscopy (TPM)
This non-invasive technique provides an excellent alternative for biological systems because no photon excitation occurs out of the focus, thus photobleaching and photodamage are restricted to the focal plane [Fig. 13(a)]. This highly localized excitation is one of the main advantages of TMP. Also, the excitation light from TPM (NIR) generally scatters less than the excitation light commonly used in CLSM (blue-green).108 In the range of 700–1200 nm, absorption and scattering coefficients of the skin components are low compared to UV-visible spectrum. Therefore, high NIR intensities can be applied to image thick samples at high penetration depths. TPM was used in relatively low scattering biological materials, such as neuronal tissue, allowing a penetration depth of 1 mm.109 For denser samples, TPM provided images by autofluorescence from epithelial tissue of a healthy human tongue down to 360 μm [Figs. 13(b) and 13(c)].110 TPM does not provide an improvement on spatial resolution, due to the use of longer wavelength for excitation (approximately twice that for one photon excitation). Since the resolution scales inversely with the wavelength, it results in approximately half of the resolution when compared to CLSM.111 Another drawback is local heating at the sample surface when powerful lasers are applied (peak power in a hundred gigawatts).108,112 Regarding temporal resolution, it has been reported a system of Multifocal Multi-Photon Microscopy (MPM) that shows the contraction of cardiac myocites at a fast rate of 640 Hz.113
FIG. 13.
TPM. (a) Working principle of two-photon (2P) microscopy in comparison with 1-photon (1P). In TPM photobleaching and photodamage are restricted to the focal plane because no photon excitation occurs out of focus. (b) Two-photon autofluorescence images of a healthy human tongue, ranging from a depth of 40 μm to 360 μm. The field of view in these lateral images is 170 μm. (c) Three-dimensional rendering of a sequence of 200 lateral images. Figures 13(b) and 13(c): Reprinted with permission from N. J. Durr et al., J. Biomed. Opt. 16, 026008 (2011). Copyright 2011 SPIE.110
G. Computed tomography (CT)
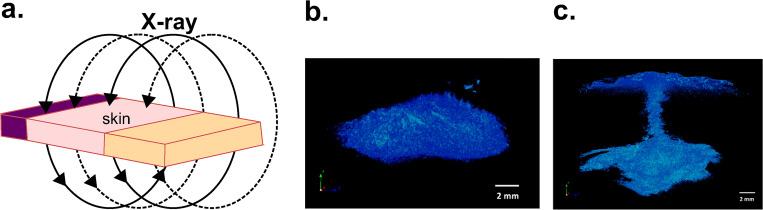
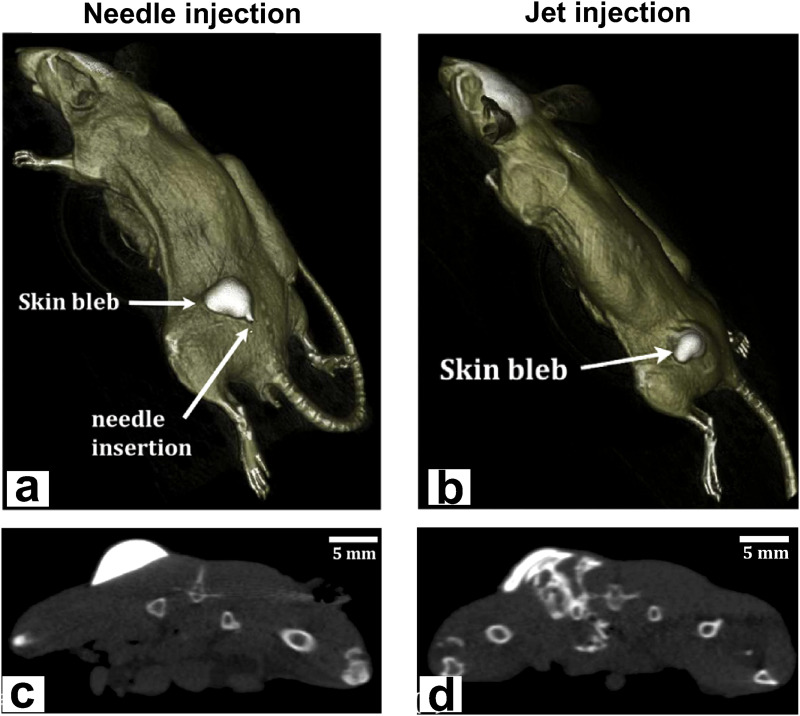
It is widely used for non-invasive imaging of the anatomy of the human body. CT imaging generates a 3D reconstruction of the sample by collecting transmitted x-ray at different angles [Fig. 14(a)].75 For non-medical applications, the method is, therefore, termed “industrial CT” or “micro-CT” if the resolution is in the micrometer range. The lateral resolution of industrial CT scanners is often higher than that of medical scanners (5–150 μm vs 70 μm, respectively). In medical CTs, the x-ray source and detector move around a stationary sample. In industrial CTs, they are fixed and the sample rotates, thus allowing better image resolution adjustments. Guidelines establish that the best resolution for a sample is 1000 times smaller than the width of the sample.114 Micro-CT has been used to characterize intradermal jet injection efficiency in mouse cadavers, reaching a penetration depth of ∼10 mm (more details about jet injection can be found in Sec. V).115 It also served to study the injectate dispersion patterns in porcine cadaver skin up to 10 mm.38 Micro-CT images in Fig. 14 show an elliptical pattern (b) and a perpendicular pattern followed by elliptical dispersion (c). The study allowed the determination of the average percentage of injectate delivered by needle-assisted jet injection to different layers: dermis: 1%–5%, subcutaneous fat: 64%–77%, and muscle: 18%–33%. This tool is medium cost9 and portable CT scanners for medical use are available.116 The main drawbacks are the radiation exposure and the lack of sensitivity to visualize the contrast between different soft tissues; therefore, contrast agents such as nanoparticles117 or cationic compounds118 are needed. For most medical purposes, the temporal resolution of CT scanners is of little importance because the structures imaged have minimal or no motion, with a typical resolution between 83 and 135 ms. However, it is very relevant for cardiac CT to image the whole cardiac cycle, where multisegment image reconstruction is often used to increase temporal resolution at higher heart rates.119
FIG. 14.
CT. (a) Schematic representation of a CT scan: CT imaging generates a 3D reconstruction of the sample by collecting transmitted x-ray at different angles. (b) The micro-CT image shows the elliptic pattern presented by most of the needle-assisted jet injections (10 out of 15) within subcutaneous fat of porcine cadaver skin. (c) A 6 mm-perpendicular pattern followed by elliptical dispersion. Injected solution was a mixture of iodine-based contrast solution with de-ionized water and food coloring. Figures 14(b) and 14(c): Reprinted with permission from Li et al., J. Controlled Release 243, 195–203 (2016). Copyright 2016 Elsevier.38
H. Photoacoustic imaging (PAI)
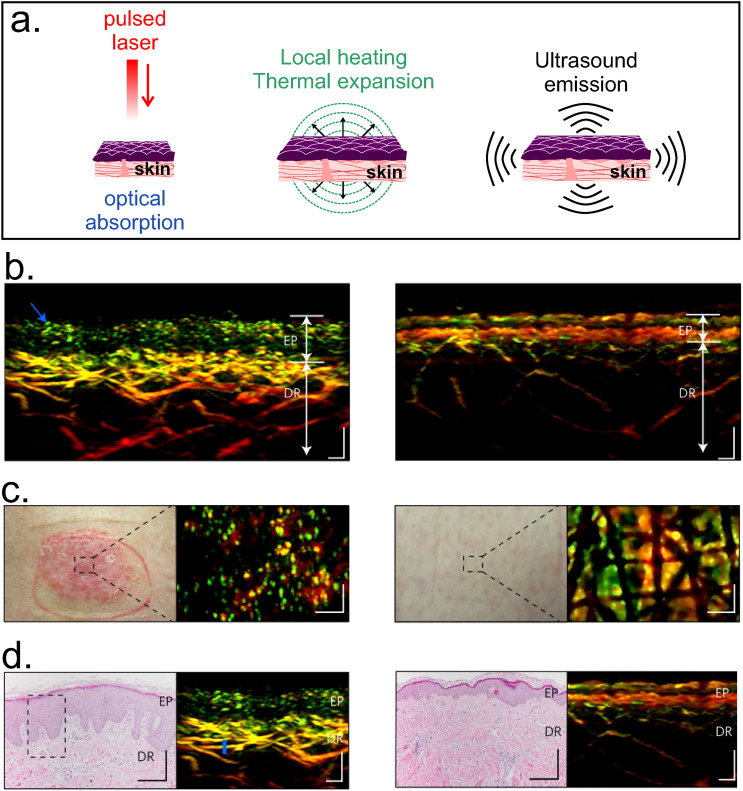
This method combines the advantages of ultrasonic and optical imaging, using the conversion from optical (nanosecond laser pulsed irradiation) to ultrasonic energy (acoustic waves). The photon energy is absorbed by the sample and thermal expansion occurs due to the increase in temperature of the tissue, emitting ultrasonic waves in the MHz range, which are detected and processed as images [Fig. 15(a)].9,75 Spatial resolution and imaging depth are scalable with the detected ultrasonic bandwidth. For instance, signals with 1 MHz can provide ∼1 mm spatial resolution, but if the bandwidth is 10 MHz, a 0.1 mm resolution can be achieved.120 The detection hardware can be acoustic based or optical based. One of the main challenges of PAI technique is the proper integration of the imaging detection hardware and the software for real-time assessments. Generally, PAI systems can be grouped into three configurations depending on the optical illumination methods and acoustic detection methods: tomography (PAT), microscopy (PAM), and mesoscopy or raster-scanning optoacoustic mesoscopy (RSOM). PAT systems are able to visualize vascular structures at centimeters depth, while PAM configurations allow a penetration depth of 3 mm and a lateral resolution of ∼45 μm (higher resolution of ∼5 μm can be achieved by restricting the penetration depth to 100 μm). RSOM achieves a lateral resolution of 15–40 μm and a depth of 2 mm.121 This system has been useful to characterize lesions in the skin of psoriasis patients: elongated capillary loops near the skin surface, widened epidermal structures (EP), and dilated and dense vascularization in the dermis (DR)122 [Fig. 15(b)]. The typical Optical-Resolution-PAI systems based on mechanical scanning have a cross-sectional scanning rate of 1 Hz/mm. However, a custom-made scanning system with a scan rate of 500 Hz has been recently reported.123 The technique is inexpensive and has been used for monitoring drug delivery.124 For instance, PAI imaging was used to monitor the delivery of doxorubicin loaded in gold nanoparticles for anti-tumor therapy in cancer cell lines.125 Although the technique does not involve ionizing radiation,126 human exposure to electromagnetic radiation must be limited for safety reasons. Maximum Permissible Exposure (MEP) levels are determined as a function of the wavelength of the light source, exposure time, and time repetition. The American National Standard ANSI Z136.3-2018 provides guidance for lasers in health care, and it is applicable to lasers that operate at wavelengths between 180 nm and 1000 μm on the UV, visible, and IR regions of the electromagnetic spectrum. Commonly excitation sources (e.g., Ti:Sapphire laser) are expensive and require water cooling and regular maintenance. These practical limitations hinder the translation of PAI from laboratory to clinical environment. Thus, novel sources have emerged such as light emitting diodes (LEDs). They are compact, robust, relatively cheap, do not require regular maintenance, and are available over a wide range of wavelengths.127 Recently, a linear transducer array for photoacoustic-ultrasound imaging with LED-based excitation was used to obtain in vivo tomographic images of human finger joint and images from mouse knee ex vivo. The low power of LED illumination limits the penetration depth; therefore, 576 elements were needed for this application.128
FIG. 15.
PAI. (a) Schematic representation of the photoacoustic method: the sample absorbs the optical energy from the laser source and is thermally expanded due to local heating, thus enabling the generation of ultrasonic sound waves that can be detected and processed as images. The bottom panel exhibits: (b) RSOM cross-sectional, (c) clinical, and (d) histological images of psoriatic (left) and healthy (right) human skin. Elongated capillary, thicker epidermis (EP) and increased vascularization in the dermis (DR) are detected by PAI in psoriatic skin and validated with histological images from skin punch biopsies. Scale bars: RSOM and histological images: 200 μm; clinical images: 300 μm. Figures 15(b)–14(d): Reprinted with permission from Aguirre et al., Nat. Biomed. Eng. 1, 0068 (2017). Copyright 2017 Springer Nature.122
I. Diffuse optical tomography (DOT)
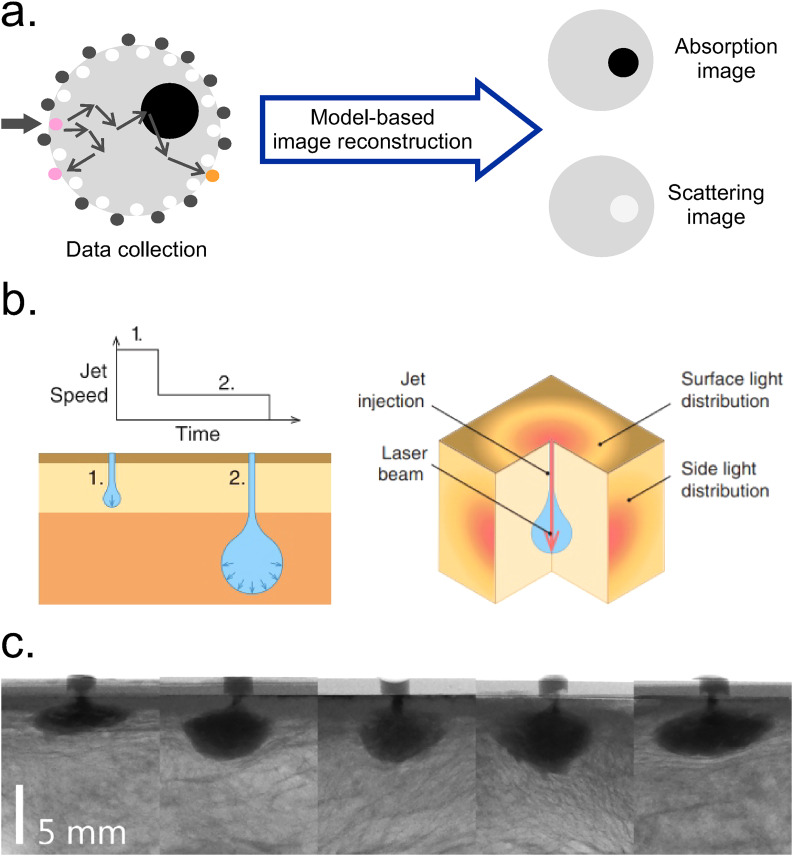
Diffuse Optical Imaging (DOI) techniques for characterizing biological tissues have been explored in numerous studies to identify absorbing or light-emitting features in a reconstructed, tridimensional tissue volume. Particularly, when DOI used to create 3D models is called Diffuse Optical Tomography (DOT). This method involves an array of optic fibers typically arranged along a circular path and attached to the surface of the tissue. Then, the light beam from the source is delivered to one point of the surface. Since in biological tissues scattering is dominant over absorption, light is multiply scattered due to different cellular structures. Part of the light is absorbed by chromophores (hemoglobin, water molecules, etc.) and the scattered photons are received by optic fibers detectors. The data collection is complete when the light beam is delivered to all of the preselected points along the tissue. This input is finally reconstructed using algorithms to produce a spatial distribution of tissue absorption and scattering coefficients [Fig. 16(a)].129 The accuracy of diffuse optical imaging is related to the accuracy of image reconstruction. Hence, efficient algorithms are needed for precise reconstruction.130 DOT uses a light source in the NIR range (650–950 nm) to minimize tissue absorption, which results in a penetration depth of 6 cm in the breast and 2–3 cm in the brain and joints.129 Depending on the type of laser source [continuous-wave (CW), pulsed, amplitude-modulated sinusoidal wave], DOT can work in different modes of operation. For the CW mode, the sampling rate (time resolution) varies between 2 and 250 Hz in different commercially available near infrared imaging (NIRI) devices.131 Spatial resolution is <10 mm for all the operations modes.132 Due to its capability to infer scattering and absorption from NIR light, the technique is also known as a Near Infrared Spectroscopy (NIRS) method.133 DOT can be made portable, is of low cost, and uses non-ionization radiation. This tool also enables the early detection and monitoring of progressive diseases (cancer, osteoarthritis, etc.).129 Spatially resolved diffuse imaging (SRDI) is a variation of DOI that involves recovering the optical parameters from the surface light profile produced by a single source in the tissue. This technique allowed the estimation of the penetration depth of high-speed jet injections in ex vivo porcine skin134 (more details about the jet injection method can be found in Sec. V). The strategy consisted of coupling the light beam into the fluid jet during penetration allowing the light to travel progressively deeper into the tissue as the jet penetrates [Fig. 16(b)]. Images were acquired using a micro-CT system [Fig. 16(c)].
FIG. 16.
DOT. (a) Schematic representation of DOT technique, which involves multiple diffuse light measurements with the sample illuminated from various locations. After the data collection, the input is reconstructed using algorithms to produce a spatial distribution of tissue absorption and scattering coefficients. Redrawn from Ref. 129. (b) Left: Illustration of the concept of jet injection control, where the initial jet causes the penetration into the skin and the next slower jet induces dispersion. Right: Schematic representation of the coupling method between the light beam and the fluid jet. (c) Representative micro-CT images taken during the jet penetration in the subcutaneous layer. Injections were performed at 80–95 ns−1 using glycerol and an x-ray contrast agent. The volume ejected was 200 μl. High-speed videography (5000 fps) was used to record the diffuse light emitted from the side and surface of the tissue. Figures 16(b) and 16(c): Reprinted with permission from Brennan et al., J. Biophotonics 12, e201900205 (2019). Copyright 2019 John Wiley & Sons Inc.134
Table II summarizes the main characteristics of the aforementioned techniques to assess transport phenomena through the skin.
TABLE II.
Imaging techniques to assess skin permeation. Source, temporal resolution (ms), maximum penetration depth (mm), lateral resolution (μm) and main models of study are considered for each method.
| Imaging techniques/acronym | Source | Temporal resolution (ms) |
z: Maximum Penetration Depth (mm) x, y: Lateral resolution (μm) |
Model/ samples |
Refs. |
|---|---|---|---|---|---|
| Ultrasound/US | Sound waves | 2 | z: 1–10 x, y: 20–100 |
In vivo In vitro |
73–77 |
| Optical coherence tomography/OCT | NIR to visible | 1.5–4.5 | z: 1–3 x, y: 1–15 |
In vivo Ex vivo |
9, 78–86 |
| Magnetic resonance imaging/MRI | Magnetic field | 30–50 | z: No limits for the whole body x, y: <100 |
In vivo In vitro |
87–94 |
| Confocal laser scanning microscopy/CLSM | UV to NIR | 2–40 | z: <0.350 x, y: 0.14–0.20 |
In vivo ex vivo In vitro |
73, 95–99 |
| Confocal Raman spectroscopy/CRS | UV to IR | Given by the microscopy system | z: 0.040. x, y: 0.50–1 |
In vivo In vitro |
100–107 |
| Two-photon microscopy/TPM | NIR | 1.5 (Multifocal MPM) |
z: 0.360–1. x, y: 0.40 |
In vivo Ex vivo In vitro |
108–113 |
| Computed tomography/CT | X-ray | 83–135 | z: No limits for the whole body x, y: 5–150 |
In vivo Ex vivo |
9, 38, 75, 114–119 |
| Photoacoustic imaging/PAI | IR and sound waves | 2 | z: ∼10–20 (PAT) x, y: 15–40 (RSOM) |
In vivo In vitro |
9, 75, 120–128 |
| Diffuse optical tomography/DOT | NIR | 4–500 | z: ∼60 x, y: <104 |
Ex vivo In vitro |
129–134 |
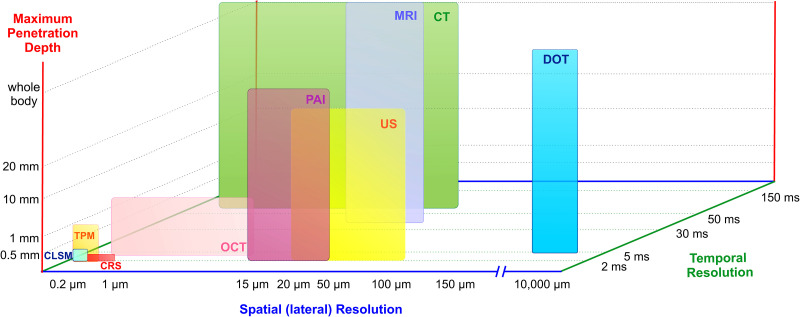
Figure 17 compares the spatial and temporal resolution of each technique, as well as the maximum penetration depth.
FIG. 17.
Schematic comparison of different imaging techniques including temporal resolution (ms), lateral resolution (μm), and maximum penetration depth (mm).
In the last few decades, imaging strategies to track cells for tissue engineering and the study of novel biomaterials have been extensively applied.9,75,83 However, no current investigations address the complex issue of tracking molecules through the skin with high resolution in space and time. As can be seen in Fig. 17, techniques with high spatial and temporal resolution (e.g., CLSM, TPM) are not able to reach high penetration depth. Conversely, the most penetrating techniques (e.g., MRI) lack high spatial and temporal resolution. In particular, for drug delivery purposes, tracking the location of the drugs across skin layers is essential. Imaging techniques capable to reach at least some millimeters of penetration depth are needed for therapeutic agents tailored for dermal injection. Moreover, if the study needs to address complex processes through SC, the imaging technique must offer a suitable spatial resolution in the order of tens of micrometers to analyze the transport phenomena between the corneocytes.
The temporal resolution also deserves special attention. For example, a needle-free method for transdermal delivery based on pulsed microjets can reach jet velocities ∼100 m/s135 (more details about this technology can be found in Sec. V). To study this method, a time-scale resolution of 1–2 μs is needed to follow the permeation process through the epidermis (∼100–150 μm thick) in real time. Recent studies have imaged the process of microjets injections at lower velocities using high-speed cameras coupled with a microscope system.136,137 In one case, 50 nl microjets ejected at 20–40 m/s to puncture agarose gel, a transparent substrate used to mimic the porous medium of the skin. In other case, fluorescent molecules injected by microjets at 5–47 m/s were imaged in porcine ex vivo skin samples. On the other hand, experiments in human skin in vitro with pulsed microjets (∼10–15 nl) ejected at ∼150 m/s were also conducted,135 but the assessment of penetration depth was destructive and done after the injection and not in real time.
Arguably, none of the available techniques can capture the whole transdermal delivery phenomenon dynamics with sufficient temporal and spatial resolution. Therefore, the great challenge of emerging applications for drug delivery and studies on skin permeation relies on finding complementary techniques to those already in use.
IV. IN SILICO APPROACHES
Computational modeling of biological soft tissues requires tackling complex multiphasic structures at various length scales. These models can be predictive or descriptive, depending on the details they provide. Since this article is aimed at providing a better insight into the underlying processes of molecules delivery into the skin, we briefly introduce in silico methods for skin biophysics studies. Undoubtedly, biophysics studies such as skin mechanical properties are relevant for more representative studies of skin permeability.138,139 We have separated in silico approaches into two main categories: (a) skin biophysics and (b) skin permeability, as follows:
-
(a)
Skin biophysics
Computational models can be classified as phenomenological, structural, and structurally based phenomenological models.11 Phenomenological models analyze the overall macroscopic behavior of the tissue without considering interactions between elemental units (e.g., stress–strain relation in a deformation). Structural models address the tissue as a composite material constituted by microstructural elements (e.g., collagen fibers) and deal with geometrical characteristics and spatial arrangement of the components. Structurally based phenomenological models combine the previous two to address a continuum approach, where a given component is not strictly modeled but its contributions (e.g., mechanical) are accounted for the general behavior of the composite. These approaches can be used to develop image-based computational models through the processing of different imaging modalities (MRI, CLSM, CT, etc.), leading to more realistic and accurate geometrical description of the tissue. For instance, this latter methodology was used for cardiac tissue140,141 as well as to assess the mechanical role of the SC by combining strategies of image processing, histological techniques, and Finite Element Methods (FEMs).142,143
Biomechanical properties of the skin (e.g., elasticity, viscoelasticity) have been extensively studied through different mechanical constitutive models.144–147 These works demonstrate that the macroscopic mechanical behavior of the skin is intrinsically related to its tissue microstructure. However, mechanical properties vary with individual-specific characteristics and location in the body, the surrounding environment, as well as with the tools and operation modes used, which usually adds complexity to the investigations.148,149
-
(b)
Skin permeability
Measuring skin permeability is a time-consuming task due to its structural inhomogeneity and mechanical anisotropy. Moreover, result variability between different subjects and within different skin parts of the same specimen is notoriously known to experts in the field.38 Besides ethical issues that need to be strictly followed, the high-cost of reliable imaging methodologies renders investigations on transdermal transport a difficult task. Computational models are complementary tools for predicting skin permeability, because they offer the possibility to quantify physical parameters required for specific applications, such as predictions of the penetration depth after drug injection. Modeling can also reduce the costs in the early stages of the investigations by exploring scenarios hard to replicate in research laboratories. For example, the main challenge in modeling skin permeability is tracking molecules in heterogeneous media where diffusion and partition coefficients take different values in each sub-region or layer. The most widely used in silico approaches for skin permeability since 1992 can be found elsewhere.12 The main finding of that study was that QSPR (quantitative structure−property relationship) models are still widely used to predict skin permeability. In the field of skin permeation studies, QSPR models provide algorithms to calculate the skin permeability coefficient in different conditions. Here, is defined as the steady state flux of molecules across the skin membrane (i.e., the path length, ). The model assumes that structural and physicochemical characteristics of a chemical compound are related to the property of interest (e.g., permeability coefficient, ), through a mathematical equation [Eq. (15)],
| (15) |
The QSPR model predicted partition coefficients of hydrophobic and hydrophilic solutes in the SC lipoid layers and thus helped us to extend the available database of partition and binding properties of the SC. Studies to measure the SC partition and binding coefficients showed that solute partition to the SC lipid and protein phase can be calculated as and 4.2 , respectively.150 The main limitation of QSPR models is that they cannot be used to predict skin permeability in complex contexts, such as in the presence of penetration enhancers. Also, these models cannot be used when the barrier properties of the skin are altered by formulation components or when skin hydration is modified.7,151
Computational mechanics is a powerful tool to tackle continuum and discontinuum problems from different disciplines. Continuum problems involve constitutive laws and boundary or initial conditions, while discontinuum problems deal with the shape and size of individual particles and the interaction laws between them.152 Although millions of particles are simulated, the length of the whole system is too small and cannot be considered as a macroscopic system. Thus, numerical simulations of discontinuum problems (also called “microscopic”) can be used to derive the macroscopic constitutive relations required to describe the phenomenon in the framework of the macroscopic continuum theory.153 In other words, the goal is to find the constitutive relations from these discontinuum methods for the micro–macro transition toward a continuum theory. Therefore, macroscopic quantities like the velocity-field of a circulating liquid can be obtained from microscopic quantities like contact-forces between the particles of the liquid.154
Discontinuum methods are the so-called particle-based approaches, such as Molecular Dynamics (MD) and Discrete Element Methods (DEMs). They are appropriate tools that consider the fine-structure of the elemental units and model the interaction between a large number of particles (atoms, molecules) within a system. DEMs have been useful to study granular systems while MD was used for atomistic and molecular systems.153 Contrarily, Finite Element Methods (FEMs) are based on the discretization of a continuous domain of interest (skin in our case) into discrete subdomains to calculate the relevant parameters in a macroscopic approach.155
The inhomogeneous structure of the skin makes it difficult to treat the problem of solutes transport with continuum methods, which typically assume homogeneity. In the framework of living tissues, cells can be modeled as interactive particles using particle-based methods.156 However, the skin has also been treated as a continuum medium to solve certain problems where its structure could be described from average materials properties, which are continuous (e.g., diffusion coefficient in the lipoid layer). In what follows, we will present some examples to illustrate how both approaches are useful to assess the problem of skin permeation.
MD simulations have been used to calculate permeability coefficients of several molecules such as water, ethanol, urea, dimethylsulfoxide (DMSO), among others. For hydrophilic molecules, the obtained permeability using MD was a few orders of magnitude higher than experimental values previously reported. For example, water and ethanol exhibited a difference of two orders of magnitude ( ∼10−7 cm/s vs ∼10−5 cm/s in both cases).157 Interpretation of the results may critically depend on the lipid model used (an equimolar mixture of ceramide, cholesterol, and free fatty acid in this study) and the experimental conditions of the experiments chosen to compare (e.g., hydration of the skin membrane). A recent work proposed a new skin barrier model with different molecular composition (ceramides, cholesterol, free fatty acids, acyl ceramides, and water) validated by cryo-electron microscopy.151 Although the relative values of permeability reflected those obtained from in vitro experiments, discrepancies were found between the absolute values of calculated by MD and experimental data. For example, water presented = − 2.9 and = − 4.5. The authors suggest that the lower calculated permeability (i.e., more negative) is due to the overestimation of experimental values because of a skin membrane excessively hydrated, which led to higher permeability measurements.
FEM simulations were extensively used to model partition coefficients in SC158 and diffusivity in the presence of enhancers (i.e., active diffusion).159 Also, a finite element model to simulate the water diffusion through SC has demonstrated that both intercellular and transcellular routes are important during the permeation process of water.160 In particular, for topical treatments and skin toxicity assessment, it is important to quantify the accumulation of solutes in the epidermis and the dermis. Many mathematical models are based in the assumption that clearance of solutes starts at the bottom of the epidermis. Recently, a novel three-dimensional model to simulate the concentration of solutes in dermis and epidermis was developed. Here, the authors used FEM to incorporate capillary loops within the dermis, which allowed them to determine a more accurate and realistic depth of sink, varying between 100 and 180 μm, depending on the experimental conditions. Moreover, they found that assuming a clearance at the bottom of epidermis underestimates the effective depth of the sink by 50%.161 Certainly, this study will lead to a more precise analysis of therapeutic or toxic effects by the accumulation of solutes.
FEMs allow modeling phenomena related to mechanical methods for drug diffusion, such as needle-free injector (NFI) devices (see Sec. V for more details). A finite element simulation using ANSYS Fluent was used to study the impact of different geometric parameters on the propelled microjet in an air-powered needle-free injector to establish the optimal conditions for achieving the maximum peak of stagnation pressure.162 The total stagnation pressure of a microjet determines its penetration capabilities. The model predicts an optimum nozzle diameter in the range of 200–250 μm for the maximum penetration depth in the experimental system used. For the investigated nozzle geometry, a better design was found at around 10° (nozzle entry angle). These studies contribute valuable data for clinical applications since the nozzle diameter can be varied according to desired penetration depths.
Particle-based and continuum approaches complement each other; thus, it is common to use them in multiscale simulation experiments. As an example, transdermal drug delivery was modeled using MD to obtain the microscopic diffusion coefficient in the lipoid layers of the SC. After a homogenization procedure, the resulting effective diffusion parameters were used in FEM simulations to study the macroscopic process. The average lateral diffusivity of fentanyl obtained by numerical simulation was 1.2 × 10−7 cm2/s, in good agreement with experimental data in the order of ∼10−8–10−7 cm2/s.163 A similar strategy was also employed to quantify the diffusivity of caffeine and naphthol, but modeling a more realistic SC constituted of ceramides, cholesterol, and free fatty acids.164
The advances in modeling the skin permeation have steadily grown in the last few decades. However, the processes of transport through the skin still constitute a computationally demanding problem for several reasons. They require a high resolution in different length and time scales and adequate tools to analyze the large amount of data from experimental measurements made with modern imaging techniques. This leads to enormous computational resources and the need to combine strategies to resolve the problem in reasonable computing times. Parallel computing allows the execution of many calculations simultaneously and it is often used to address big and complex problems in terms of computational demands.165 The problem of skin permeation has been parallelized in a preliminary setup to resolve the brick and mortar configuration, where the challenge comprises the anisotropic geometries and different coefficients (one for each layer: lipids and cells).166 The applicability of the algorithm to the brick and mortar problem resulted in a quick convergence but inducing a potential imbalance in the workload (i.e., issues with the distribution of work between the processors).
V. DISCUSSION
Despite the progress made by the scientific community to understand skin penetration processes, several experimental limitations and incomplete models stand in the way of the advent of novel drug delivery systems. The broad range of advanced strategies for controlled drug release, such as microneedles arrays and modular reservoirs for drug storage, demonstrates the ongoing efforts to improve the traditional methodologies or developing new reliable alternatives.167,168 Novel transdermal methods for drug delivery and vaccination devices such as Needle-Free Injectors (NFIs), microneedles, gene guns, tattoo devices, etc., overcome some traditional delivery methods in several aspects. They provide a higher immunological response, drug dose sparing, and reduction in pain, which improves patient compliance.169,170 In Subsections V A–V D, we briefly describe what we consider the most reliable alternatives that face traditional techniques. These new methods are schematized in Fig. 18.
FIG. 18.
Some of the existing methods for transdermal drug delivery: jet injector, microjet injector, microneedles and tattoo vaccination. They are briefly described in Subsections V A–V D. Figure 18: Adapted/Redrawn with permission from Y.-C. Kim, in Percutaneous Penetration Enhancers Physical Methods in Penetration Enhancement, edited by H. Dragicevic and N. I. Maibach (Springer, Berlin, 2017), pp. 485–499. Copyright 2017 Springer Nature.170
Commonly injected drugs include antibiotics, hormones (e.g., steroids, growth hormone), vaccines, insulin, among others. Characteristic dosage volumes are relatively large, ranging from 0.1 to 1 ml. These volumes are typically injected at different penetration depths, ranging from hundreds of micrometers to tens of millimeters (Fig. 19).
FIG. 19.
(a) Typical dosage volume (μl) and penetration depth (mm) of commonly used medicines. Adapted from Ref. 182. (b) Maximum penetration depth (mm) of the imaging techniques described in Sec. III (References can be found in Table II). (c) Penetration depth (mm) of the transdermal drug delivery systems summarized in Subsections V A–V D: jet injector,39,115,177–185 microjet,39,135,137,170 microneedles,186–194 and tattooing.170,195–197 SC: Stratum corneum, E: Epidermis, D: Dermis, H: Hypodermis (i.e., subcutaneous), M: Muscle tissue. Figure 19: Reprinted with permission from C. Berrospe Rodriguez et al., J. Biomed. Opt. 22, 105003 (2017). Copyright 2017 SPIE.
There is mounting evidence that intradermal delivery (ID) of vaccines increases the effectiveness of these procedures, which traditionally are done either intramuscular (IM) or subcutaneous (subC).171 ID immunization favors two main pathways: antigen migration through lymph ducts and activation, and migration of dendritic cells (antigen-presenting cells) leading to the activation of T-cells.171 Clinical trials with vaccines against influenza and hepatitis B viruses are clear examples where ID administration resulted more effective than IM. For instance, it has been demonstrated that immunogenicity of one fifth of a dose of influenza vaccine by ID route is comparable to the IM standard dose in healthy children.172 Similarly, unresponsive patients to hepatitis B vaccination received 80 μg ID dose or 160 μg of the typical IM dose of the vaccine. The seroconversion rate was 94.1% in the first group and 50% in the IM group.173 Apart from vaccines, the injection of insulin for diabetes management is another example. For decades, insulin has been tailored to be delivered at the subcutaneous fat due to consistent perfusion. However, a clinical trial using microneedles has demonstrated that the uptake is optimal in ID administration.174
Epidermal (ED) immunization has also demonstrated successful results when compared to traditional administration routes. The epidermis has unique characteristics that made it suitable for vaccines targeting. It houses immunologically active cells, Langerhans cells, and lacks blood vessels or sensory nerves, which is important for pain-free delivery.175 However, the epidermis is too thin (∼100–150 μm) for needle injection; thus, other alternatives have arisen to overcome this issue, such as the Epidermal Powder Immunization (EPI). In fact, the topical delivery of powder vaccine against influenza in mice showed a higher antibody response of 300% and 700% when compared to IM or subC vaccination, respectively.176
A. Jet injector
Jet injectors have been used for 75 years to vaccinate millions of people. The large-scale use of these devices was in the 1940s for hepatitis B immunization.177 Although it is currently available for clinical procedures, the adoption of Jet injector technology has been limited by inadequate control of penetration depth, occasional pain, and bruising at the site of entry, possibly due to unintended deeper penetration depths (up to subcutaneous layer).39 However, novel versatile jet injectors have been designed to overcome these difficulties by introducing adjustable parameters (e.g., driving pressure, volume ejected).177 Jet injectors are NFI devices based on the ejection of a liquid drug (typically ∼100 μl) through a nozzle at high-pressure, thus generating a high-velocity jet (from ∼100 m/s178 to ∼850 m/s179) to puncture the skin surface and ideally deliver drugs to the required depth.180 Penetration of a liquid jet into the skin depends on the jet diameter and the jet velocity.181,182 A wide nozzle diameter (0.1–0.2 mm) increases penetration depth but is more painful.177 The driving mechanisms for the injection are varied (chemical, mechanical, optical, etc.) and jet injectors are able to deliver macromolecules (vaccines, insulin, growth hormone, etc.) and small molecules (lidocaine, ketamine, etc.).183 These devices have demonstrated better humoral and cellular immune responses in pigs when compared to IM vaccination against swine influenza virus.184 Also, a recent study in patients with type 2 diabetes mellitus has shown that the use of a NFI can significantly lower the dosage of insulin required to achieve good glycemic control and reduce topical adverse reactions when compared to the subC administration using the well-known Lantus pen.185 In Fig. 20, micro-CT images compare the needle injection and jet injection in mice. After the needle injection, the total injected volume remains ID and the bleb is larger. After the NFI procedure, the bleb in the site of injection is smaller and half of the injected solution (contrast agent) remains in intradermal and subcutaneous tissue.115
FIG. 20.
Jet injector. Comparison of needle-based and Jet injection from micro-CT images. (a) and (b) show the whole-body images of the mice and the blebs formed in the sites of injection. (c) and (d) are axial planes showing the distribution of the injected solution (0.1 ml of Optiprep, a contrast agent). Figure 20: Reprinted with permission from J. O. Marston and C. M. R. Lacerda, J. Controlled Release 305, 101–109 (2019). Copyright 2019 Elsevier.115
B. Microjet injector
This emerging NFI strategy is based on pulsed microjets and consists of the injection of liquid jets of small diameter (50–100 μm) and low volume (∼nl) that can deliver vaccines into the epidermis region (up to 400 μm) at ∼100 m/s, thus promoting an effective immune response.135 The lower penetration depth and smaller volumes in comparison with conventional jet injectors would reduce pain and allow a more precise control of the delivered molecules.170 Recent studies on porcine skin samples showed that microjet injection (jet velocities of up to ∼50 m/s) has a faster injection and higher dispersion rate when compared to traditional methods (tattooing needle injections and topical application). Moreover, no tissue damage was observed and SCs remain intact after six repetitive injections.137 The main disadvantage of this method, which is still in the early development phase, is that penetration is limited to the epidermal layer.39 Figure 21(a) displays the bright field and fluorescence images obtained after an ex vivo experiment using a microject injector to puncture porcine skin with an aqueous solution of Rhodamine B. For comparison, Fig. 21(b) shows the tissue damage after solid needle injection (tattoo needle).
FIG. 21.
Microjet injector. (a) Bright field (i) and fluorescence images (ii–iv) of a porcine skin sample exposed to a three repetitive microjet injections (25 m/s) of Rhodamine B solution. There was no visible entry point or other damage effects to the skin. (b) Bright field (i), fluorescence image (ii), and post-processing image (iii) of a porcine skin sample after solid needle injection. Skin damage can be clearly observed. Reprinted with permission from K. Cu et al., Ann. Biomed. Eng. 48, 2028 (2020). Copyright 2020 Author(s), licensed under a Creative Commons 4.0 Attribution License.137
C. Microneedles
Microneedles are micrometer-sized (smaller than 1 mm) needles, which can be grouped in four types depending on their microfabrication technology: solid, hollow, coated with drugs, and dissolving. These different types of microneedles were extensively described in recent works, where biomedical applications and the current status of clinical research are also discussed.186–189 Due to their length and superficial penetration, microneedles are minimally invasive and potentially pain-free. Microneedles have been used with low-molecular weight drugs (lidocaine, naltrexone, etc.), therapeutic agents based on protein and peptides (insulin, parathyroid hormone, etc.) and vaccines (hepatitis B, HPV, etc.).190 A recent example shows that vaccination in mice using microneedles patches coated with the vaccine against influenza-virus like particle (VLP) induced protection similar or better than IM immunization. The study also showed an improved efficacy of protection after 14 months of vaccination.191 The microneedle fabrication and scaling process for commercial use is complex since it involves a compromise between chosen materials, the thickness of the target area, and the optimization of the dimensions to reduce pain during the insertion.192,193 Figure 21(a) shows a dissolving microneedle made of carboxy-methylcellulose. An array of these microneedles was used to inject sulphorhodamine B in porcine cadaver skin [Fig. 22(b)]. The penetration through the SC was assessed using a fluorescence microscope [Fig. 22(d)].194
FIG. 22.
Dissolving microneedles for transdermal drug delivery. (a) Carboxy-methylcellulose microneedles. (b) Porcine cadaver skin showing sulforhodamine delivery after the insertion of the microneedles. (c) Bright field and (d) fluorescence microscopic images showing a histological cross section after the penetration of two adjacent microneedles. Reprinted with permission from Lee et al., Biomaterials 29(13), 2113–2124. Copyright 2008 Elsevier.194
D. Tattoo vaccination
Tattooing is a method for depositing pigments in the skin with cosmetic and medical purposes. Tattoo machines have also been adapted for intradermal injection of drugs, which is done by puncturing the skin with high-frequency oscillating needles that deliver the effective dose in smaller portions.195 It was demonstrated that intradermal delivery by tattooing promotes specific cellular and humoral immune responses by stimulating antigen-presenting cells.170 For example, a higher peptide-specific immune response was elicited with a tattoo device when compared to subC administration of a peptide-based vaccine against HPV. Moreover, the addition of synthetic immunostimulatory molecules enhanced the immune response after subC injection to comparable levels to those reached after tattoo delivery.196 The multiple insertions of needles may cause pain and local trauma at the site of application, which makes this device less acceptable for human usage. However, this cutaneous trauma (necrosis, inflammation) triggers the healing process in the skin, thus attracting leukocytes and pro-inflammatory cytokines and favoring the immunological impact of the tattooing procedure (Fig. 23).197
FIG. 23.
Transdermal delivery by tattooing. Eosin-hematoxylin staining of: (a) untreated mice skin (E: Epidermis, DL: Dermal Layer) and tattooed skin at day 0.5 (b), 1 (c), and 14 (d). Tattooing produces necrosis (N), dermal hemorrhage (DH), epidermal hyperplasia (EH), and dermal pigmentation (P). It also triggers the immune response by attracting neutrophils (Neu) to the site of injection. Reprinted with permission from Gopee et al., Toxicol. Appl. Pharmacol. 209(2), 145–158 (2005). Copyright 2005 Elsevier.197
E. Future perspectives
Conventional systems based on hypodermic needles and syringes are not suited for injecting high-viscosity vaccines,198 nor do they perform properly under the complexity of fractional doses vaccination (i.e., smaller dose or microdosing), which demand narrow target delivery into the intradermal region.171 However, a recent innovative system was developed, where the viscous fluid to be injected is surrounded with a lubricating fluid, lowering the injection force and easing the fluid's flow through the needle.199 In this context, we see a great opportunity niche for novel drug delivery systems to manage these new advances in vaccination, which will also imply more studies associated with the performance of these new technologies. Accompanying the previous observation, we believe that there is a need to have a comprehensive study covering factors affecting drug permeation with focus on the actual physicochemical properties of the drugs, and corresponding vehicles, combined with specific physiological factors.
The main challenges ahead for transdermal drug delivery investigation are related to imaging technologies, theoretical modeling of skin permeation, and molecular tracking. As discussed before, microjet injection is perhaps the method that entails more efforts due to the limitations of traditional techniques to quantify in real time and in vivo the permeation processes in the skin, since the desired high spatiotemporal resolution is ∼10 μm (jet diameter is ∼25 μm) and ∼1–2 μs, respectively. Therefore, efforts to better understand fluid dynamics in the context of NFI technology would provide promising scientific advances for biomedical applications and fundamental mechanisms of fluid transport in soft tissues, other than skin.
We also believe that the lack of standardized methodologies capable to address entirely the skin penetration process is a motivation for the development of new opportunities based on complementary techniques. Multimodal imaging holds promises to overcome the limitations of imaging methods, utilizing a combination of them to obtain higher spatial resolution and molecular information.200 Current platforms of multimodal imaging require contrast agents to provide detectability, thus enabling a more comprehensive visualization at different levels. For example, a triple modality MRI, PAI, and Raman imaging with nanoparticles as contrast agents were used to obtain more accurate brain tumor imaging in mice.201 Along this line, a system combining US and PAI modalities was developed, integrating an ultrasound transducer and a pulsed laser diode. The compact handheld probe allowed in vivo measurements of a human finger joint. Images revealed the skin, blood vessels, and the underlying bone. Phantom experiments showed a possible imaging depth of 10–15 mm for a frame rate of 0.5 Hz and a lateral resolution of 400 μm, which degrades to 600 μm with depth.202
Chemical enhancers and physical methods to increase skin permeability have been used to circumvent the limitations of transdermal delivery methods.203 For instance, heat and ultrasound are used as physical enhancers. Ultrasound generates a high stress condition under which aqueous pores pathways are formed in the lipoid layers of the SC, favoring the drug permeation.204 Mechanisms by which ultrasound enhances skin permeability are varied, including acoustic cavitation, thermal effects, radiation forces, and convection.205 Cavitation is considered the main mechanism and this process occurs when gas bubbles are formed in response to pressure variation due to the movement of sound waves.206 Ultrasound can be applied simultaneously with the drug or as a pre-treatment and can be classified in high-frequency (>3 MHz), therapeutic (0.7–3 MHz), and low-frequency (20–100 kHz).205 For example, a 6-hour permeation study on rat skin showed a threefold enhanced ketorolac penetration after the continuous application of ultrasound waves during 30 min (1 MHz frequency, 3 W/cm2 intensity) when compared to passive diffusion without enhancing treatment.207
In addition, thermal-based approaches for enhancing skin permeation are based on the selective removal of SC by localized microsecond heat pulses. Thermal ablation is the process by which lasers create transient microchannels in the skin of ∼50–100 μm in diameter, allowing a precise control on the ablated skin depth. Many laser types have been tested, including CO2 laser, Ti:sapphire, Nd:YAG, among others. This technology is used for a large variety of molecules, such as antibodies, DNA and RNA, and hydrophilic macromolecules.208 For example, transdermal transport of fluorescent labeled insulin was assessed in vitro using full-thickness skin samples from pigs. The study showed that the cumulative amount of insulin after 12 h (∼14 nmol/cm2) was higher after a Er:YAG laser treatment, when compared to the negligible fluorescence signal obtained without the enhancing method.209
The main drawback of physical methods is that they require additional equipment to excite the acting mechanisms, such as laser sources for thermal-based approaches and industrial or miniaturized transducers for ultrasound-mediated drug delivery.
On the other hand, the acting mechanisms of chemical enhancers are varied;20,210 they can act when put directly (topic) on the skin (e.g., modifying the structure of the SC by causing an increase in hydration)211 or can be included in the formulation phase as vehicles. Propylene glycol (PG) is commonly used as a solvent for lipophilic drugs and it is a well-established chemical enhancer. Moreover, its action is more potent in combination with other chemical compounds.212 Therefore, understanding the mechanisms of penetration enhancing activity is also a fundamental task at the interface between skin structure and skin permeation studies.
Understanding the transport scenarios of a given molecule or mix of substances can also contribute to the preparation of new medicine formulations. For example, for a given vaccine or drug to be delivered via needle-free injections, mixing the active therapeutic compound with a lubricating additive can be beneficial.199 Delivering biopharmaceuticals (recombinant proteins, monoclonal antibodies, etc.) is especially difficult due to the large sizes of the molecules, susceptibility to degradation, and loss of activity in pernicious environmental conditions.213 Although several chemical agents (small sugars, polysaccharides, surfactants, etc.) have been developed to overcome some of these limitations and increase the stability of biological drugs,214 their use requires special attention in terms of increased risk of toxicity and side effects. Also, the addition of these substances leads to high-viscosity formulations, affecting the delivery via a needle injection,215 the most common procedure in modern medicine. We consider that future investigations should focus on developing new technologies for drug delivery and bespoke formulations to reduce the viscosity.
Since skin permeability can widely vary in different studies, reproducibility is hard to achieve. Therefore, the scientific community should reconsider the way that databases or published data related to transdermal delivery and transport are consulted. It is now accepted by most experts that, despite its popularity in the past, studies on transport mechanisms of skin made with different species (human, pig, etc.) provide a very limited comparison, and consequently any model to validate such experiments should be reevaluated. Moreover, the availability of human skin is limited and expensive, which lengthens experimental work. Furthermore, the request by the general public and scientific community to stop or at least diminish the use of laboratory animals is paired with more evidence that animal models have many limitations, and extrapolation of results is not straightforward.216 As a result of these limitations and global trends, alternative methods that rely on artificial membranes and 3D cultures as skin surrogates have increased.67 For example, human skin equivalents (HSEs) are bioengineering substitutes of human skin that can be used as in vitro models.217 However, despite the possibility to perform investigations using these alternatives under standardized protocols, there are still persistent problems in recreating the actual mechanical and biological environment of the skin, including metabolism and signal pathways. This led to further developments of artificial systems based on organ-on-a-chip technology, artificial membranes, and microdevices.218 It should be noted that these studies require special infrastructure and knowledge hard to replicate in many research institutions.
To conclude, given the fact that each individual has a unique skin at any given moment, we propose as the ultimate goal of the community studying transdermal transport phenomena to join efforts with other research field specialists and to design and build non-invasive equipment that operates in real time, which in turn can help validate newly developed models.
ACKNOWLEDGMENTS
M.M. acknowledges the Comisión Nacional de Energía Atómica from Argentina. D.F.R. acknowledges the funding from the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Programme (Grant Agreement No. 851630). We are thankful for the insightful discussions with M.Sc. D. van der Ven, Professor W. Steenbergen, Professor R. Verdaasdonk, and Professor S. Mitragotri.
DATA AVAILABILITY
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
REFERENCES
- 1.Hettwer S., Besic Gyenge E., and Obermayer B., Int. J. Cosmet. Sci. 42, 313 (2020). 10.1111/ics.12623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nohynek G. J., Lademann J., Ribaud C., and Roberts M. S., Crit. Rev. Toxicol. 37, 251 (2007). 10.1080/10408440601177780 [DOI] [PubMed] [Google Scholar]
- 3.Jorge S. and Dellagostin O. A., Biotechnol. Res. Innov. 1, 6 (2017). 10.1016/j.biori.2017.10.001 [DOI] [Google Scholar]
- 4.Sharadha M., Gowda D. V., Vishal Gupta N., and Akhila A. R., Int. J. Res. Pharm. Sci. 11, 368 (2020). 10.26452/ijrps.v11i1.1831 [DOI] [Google Scholar]
- 5.Harb A. C., Tarabay R., Diab B., Ballout R. A., Khamassi S., and Akl E. A., BMC Nurs. 14, 1 (2015). 10.1186/s12912-014-0053-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Münch S., Wohlrab J., and Neubert R. H. H., Eur. J. Pharm. Biopharm. 119, 235 (2017). 10.1016/j.ejpb.2017.06.019 [DOI] [PubMed] [Google Scholar]
- 7.Mitragotri S., Anissimov Y. G., Bunge A. L., Frasch H. F., Guy R. H., Hadgraft J., Kasting G. B., Lane M. E., and Roberts M. S., Int. J. Pharm. 418, 115 (2011). 10.1016/j.ijpharm.2011.02.023 [DOI] [PubMed] [Google Scholar]
- 8.Naegel A., Heisig M., and Wittum G., Adv. Drug Deliv. Rev. 65, 191 (2013). 10.1016/j.addr.2012.10.009 [DOI] [PubMed] [Google Scholar]
- 9.Nam S. Y., Ricles L. M., Suggs L. J., and Emelianov S. Y., Tissue Eng. Part B Rev. 21, 88 (2015). 10.1089/ten.teb.2014.0180 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Guggenheim E. J., Lynch I., and Rappoport J. Z., Int. J. Biochem. Cell Biol. 83, 65 (2017). 10.1016/j.biocel.2016.12.008 [DOI] [PubMed] [Google Scholar]
- 11.Limbert G., Proc. R. Soc. A 473, 20170257 (2017). 10.1098/rspa.2017.0257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pecoraro B., Tutone M., Hoffman E., Hutter V., Almerico A. M., and Traynor M., J. Chem. Inf. Model. 59, 1759 (2019). 10.1021/acs.jcim.8b00934 [DOI] [PubMed] [Google Scholar]
- 13.Ashrafi P., Sun Y., Davey N., Wilkinson S. C., and Moss G. P., J. Pharm. Pharmacol. 72, 197 (2020). 10.1111/jphp.13203 [DOI] [PubMed] [Google Scholar]
- 14.Tricoli A., Nasiri N., and De S., Adv. Funct. Mater. 27, 1 (2017). 10.1002/adfm.201605271 [DOI] [Google Scholar]
- 15.Bandodkar A. J., Jeerapan I., and Wang J., ACS Sens. 1, 464 (2016). 10.1021/acssensors.6b00250 [DOI] [Google Scholar]
- 16.Yetisen A. K., Martinez-Hurtado J. L., Ünal B., Khademhosseini A., and Butt H., Adv. Mater. 30, 1706910 (2018). 10.1002/adma.201706910 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Singh S. and Singh J., Med. Res. Rev. 13, 569 (1993). 10.1002/med.2610130504 [DOI] [PubMed] [Google Scholar]
- 18.Karadzovska D., Brooks J. D., Monteiro-Riviere N. A., and Riviere J. E., Adv. Drug Deliv. Rev. 65, 265 (2013). 10.1016/j.addr.2012.01.019 [DOI] [PubMed] [Google Scholar]
- 19.Brown M. B., Martin G. P., Jones S. A., and Akomeah F. K., Drug Deliv. J. 13, 175 (2006). 10.1080/10717540500455975 [DOI] [PubMed] [Google Scholar]
- 20.Williams A. C. and Barry B. W., Adv. Drug Deliv. Rev. 64, 128 (2012). 10.1016/j.addr.2012.09.032 [DOI] [Google Scholar]
- 21.Dąbrowska A., Rotaru G. M., Spano F., Affolter C., Fortunato G., Lehmann S., Derler S., Spencer N. D., and Rossi R. M., Tribol. Int. 113, 316 (2017). 10.1016/j.triboint.2017.01.027 [DOI] [Google Scholar]
- 22.Graham H. K., McConnell J. C., Limbert G., and Sherratt M. J., Exp. Dermatol. 28, 4 (2019). 10.1111/exd.13826 [DOI] [PubMed] [Google Scholar]
- 23.Dagdeviren C., Shi Y., Joe P., Ghaffari R., Balooch G., Usgaonkar K., Gur O., Tran P. L., Crosby J. R., Meyer M., Su Y., Webb R. C., Tedesco A. S., Slepian M. J., Huang Y., and Rogers J. A., Nat. Mater. 14, 728 (2015). 10.1038/nmat4289 [DOI] [PubMed] [Google Scholar]
- 24.Derrickson B. H. and Tortora G. J., Principles of Anatomy and Physiology (John Wiley & Sons, Inc., 2008). [Google Scholar]
- 25.Humbert A. P., Fanian F., and Maibach H., Agachés Measuring the Skin, 2nd ed. (Springer, Cham, 2017). [Google Scholar]
- 26.Smoller B. R. and Hiatt Kim M., Dermatopathology: The Basics (Springer Nature, New York, 2009). [Google Scholar]
- 27.Trommer H. and Neubert R. H. H., Skin Pharmacol. Physiol. 19, 106 (2006). 10.1159/000091978 [DOI] [PubMed] [Google Scholar]
- 28.Andrews S. N., Jeong E., and Prausnitz M. R., Pharm. Res. 30, 1099 (2013). 10.1007/s11095-012-0946-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Potts R. H., Russell O., and Guy H., Pharm. Res. 9, 663 (1992). 10.1023/A:1015810312465 [DOI] [PubMed] [Google Scholar]
- 30.Bos J. D. and Meinardi M. M. H. M., Exp. Dermatol. 9, 165 (2000). 10.1034/j.1600-0625.2000.009003165.x [DOI] [PubMed] [Google Scholar]
- 31.Marjukka Suhonen T., Bouwstra J. A., and Urtti A., J. Controlled Release 59, 149 (1999). 10.1016/S0168-3659(98)00187-4 [DOI] [PubMed] [Google Scholar]
- 32.Ishizaki K., Nanko M., and Komameni S., Porous Materials: Process Technology and Applications (Springer-Science + Business Media, B.V, Dordrecht, 1998). [Google Scholar]
- 33.Vafai K., Porous Media: Applications in Biological Systems and Biotechnology (CRC Press, 2011). [Google Scholar]
- 34.Kitson N. and Thewalt J. L., Acta Derm. Venereol. 208, 12–15 (2000). 10.1080/000155500750042808 [DOI] [PubMed] [Google Scholar]
- 35.Zhao F., Wu D., Yao D., Guo R., Wang W., Dong A., Kong D., and Zhang J., Acta Biomater. 64, 334 (2017). 10.1016/j.actbio.2017.09.044 [DOI] [PubMed] [Google Scholar]
- 36.Castle J. R., DeVries J. H., and Kovatchev B., Diabetes Technol. Ther. 19, S67 (2017). 10.1089/dia.2017.0012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zelikin A. N., Ehrhardt C., and Healy A. M., Nat. Chem. 8, 997 (2016). 10.1038/nchem.2629 [DOI] [PubMed] [Google Scholar]
- 38.Li X., Ruddy B., and Taberner A., J. Controlled Release 243, 195 (2016). 10.1016/j.jconrel.2016.10.010 [DOI] [PubMed] [Google Scholar]
- 39.Hogan N. C., Taberner A. J., Jones L. A., and Hunter I. W., Expert Opin. Drug Delivery 12, 1637 (2015). 10.1517/17425247.2015.1049531 [DOI] [PubMed] [Google Scholar]
- 40.Baxter J. and Mitragotri S., J. Controlled Release 106, 361 (2005). 10.1016/j.jconrel.2005.05.023 [DOI] [PubMed] [Google Scholar]
- 41.Chen X., Grégoire S., Formanek F., Galey J. B., and Rigneault H., J. Controlled Release 200, 78 (2015). 10.1016/j.jconrel.2014.12.033 [DOI] [PubMed] [Google Scholar]
- 42.Moser K., Kriwet K., Naik A., Kalia Y. N., and Guy R. H., Eur. J. Pharm. Biopharm. 52, 103 (2001). 10.1016/S0939-6411(01)00166-7 [DOI] [PubMed] [Google Scholar]
- 43.Becker A. V. and Kuznetsov S. M., in Porous Media: Applications in Biological Systems and Biotechnology, edited by Vafai K. (CRC Press, 2011), pp. 331–364. [Google Scholar]
- 44.Pilgram G. S. K., Engelsma-Van Pelt A. M., Bouwstra J. A., and Koerten H. K., J. Invest. Dermatol. 113, 403 (1999). 10.1046/j.1523-1747.1999.00706.x [DOI] [PubMed] [Google Scholar]
- 45.Manda P., Angamuthu M., Hiremath S. R., Raman V., and Narasimha Murthy S., J. Pharm. Sci. 103, 1638 (2014). 10.1002/jps.23946 [DOI] [PubMed] [Google Scholar]
- 46.Michaels A. S., Chandrasekaran S. K., and Shaw J. E., AIChE J. 21, 985 (1975). 10.1002/aic.690210522 [DOI] [Google Scholar]
- 47.Johnson M. E., Blankschtein D., and Langer R., J. Pharm. Sci. 86, 1162 (1997). 10.1021/js960198e [DOI] [PubMed] [Google Scholar]
- 48.Wang T.-F., Kasting G. B., and Nitsche J. M., J. Pharm. Sci. 95, 620 (2006). 10.1002/jps.20509 [DOI] [PubMed] [Google Scholar]
- 49.Kushner J., Deen W., Blankschtein D., and Langer R., J. Pharm. Sci. 96, 3236 (2007). 10.1002/jps.20896 [DOI] [PubMed] [Google Scholar]
- 50.Johnson M. E., Berk D. A., Blankschtein D., Golan D. E., Jain R. K., and Langer R. S., Biophys. J. 71, 2656 (1996). 10.1016/S0006-3495(96)79457-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mitragotri S., Pharm. Res. 17, 1026 (2000). 10.1023/A:1007547809430 [DOI] [PubMed] [Google Scholar]
- 52.Scheuplein R. J., J. Invest. Dermatol. 48, 79 (1967). 10.1038/jid.1967.11 [DOI] [PubMed] [Google Scholar]
- 53.Mitragotri S., J. Controlled Release 86, 69 (2003). 10.1016/S0168-3659(02)00321-8 [DOI] [PubMed] [Google Scholar]
- 54.Oshima A., Nakashima H., and Sumitomo K., Langmuir 35, 11725 (2019). 10.1021/acs.langmuir.9b01595 [DOI] [PubMed] [Google Scholar]
- 55.Tocanne J. F., Dupou-Cézanne L., and Lopez A., Prog. Lipid Res. 33, 203 (1994). 10.1016/0163-7827(94)90027-2 [DOI] [PubMed] [Google Scholar]
- 56.Jacobson R., Ishihara K., and Imman A., Annu. Rev. Physiol. 49, 163 (1987). 10.1146/annurev.ph.49.030187.001115 [DOI] [PubMed] [Google Scholar]
- 57.Kazoe Y., Mawatari K., and Kitamori T., Anal. Chem. 87, 4087 (2015). 10.1021/acs.analchem.5b00485 [DOI] [PubMed] [Google Scholar]
- 58.Chinen H., Mawatari K., Pihosh Y., Morikawa K., Kazoe Y., Tsukahara T., and Kitamori T., Angew. Chem. Int. Ed. 51, 3573 (2012). 10.1002/anie.201104883 [DOI] [PubMed] [Google Scholar]
- 59.Reiss H., Advances in Chemical Physics, edited by Prigogine I. (Interscience Publishers, New York, 1964), pp. 1–83. [Google Scholar]
- 60.Mitragotri S., J. Pharm. Sci. 91, 744 (2002). 10.1002/jps.10048 [DOI] [PubMed] [Google Scholar]
- 61.Kushner J., Blankschtein D., and Langer R., J. Pharm. Sci. 96, 3263 (2007). 10.1002/jps.20955 [DOI] [PubMed] [Google Scholar]
- 62.Tagawa Y., Oudalov N., El Ghalbzouri A., Sun C., and Lohse D., Lab Chip 13, 1357 (2013). 10.1039/c2lc41204g [DOI] [PubMed] [Google Scholar]
- 63.Brennan K. A., Kulasingham D. A. N., Nielsen P. M. F., Taberner A. J., and Ruddy B. P., J. Opt. 21, 15604 (2019). 10.1088/2040-8986/aaf4db [DOI] [Google Scholar]
- 64.Zsikó S., Csányi E., Kovács A., Budai-Szűcs M., Gácsi A., and Berkó S., Sci. Pharm. 87, 19 (2019). 10.3390/scipharm87030019 [DOI] [Google Scholar]
- 65.Lee J. D., Young Kim J., Jang H. J., Lee B. M., and Kim K. B., Regul. Toxicol. Pharmacol. 103, 56 (2019). 10.1016/j.yrtph.2019.01.002 [DOI] [PubMed] [Google Scholar]
- 66.Rajitha P., Shammika P., Aiswarya S., Gopikrishnan A., Jayakumar R., and Sabitha M., J. Drug Delivery Sci. Technol. 49, 463 (2019). 10.1016/j.jddst.2018.12.020 [DOI] [Google Scholar]
- 67.Neupane R., Boddu S. H. S., Renukuntla J., Babu R. J., and Tiwari A. K., Pharmaceutics 12, 152 (2020). 10.3390/pharmaceutics12020152 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Jerjes W., Hamdoon Z., and Hopper C., Skin Res. Technol. 26, 153 (2020). 10.1111/srt.12791 [DOI] [PubMed] [Google Scholar]
- 69.Sauermann K. and Jaspers S., in Bioengineering of the Skin: Skin Imaging and Analysis, edited by Wilhelm K.-P., Elsner P., Berardesca E., and Maibach H. I., 2nd ed (CRC Press, 2007), pp. 165–175. [Google Scholar]
- 70.Versluis M., Exp. Fluids 54, 1458 (2013). 10.1007/s00348-013-1458-x [DOI] [Google Scholar]
- 71.Tsuji K., The Micro-World Observed by Ultrahigh-Speed Cameras (Springer Nature, Cham, 2018). [Google Scholar]
- 72.Yanoff M. and Duker J. S., Ophtalmology (Elsevier, 2009). [Google Scholar]
- 73.Nouveau-Richard S., Monot M., Bastien P., and de Lacharrière O., Skin Res. Technol. 10, 136 (2004). 10.1111/j.1600-0846.2004.00067.x [DOI] [PubMed] [Google Scholar]
- 74.Deng C. X., Hong X., and Stegemann J. P., Tissue Eng. Part B Rev. 22, 311 (2016). 10.1089/ten.teb.2015.0453 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Gil C. J., Tomov M. L., Theus A. S., Cetnar A., Mahmoudi M., and Serpooshan V., Micromachines 10, 474 (2019). 10.3390/mi10070474 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Yu J., Lavery L., and Kim K., Sci. Rep. 8, 13918 (2018). 10.1038/s41598-018-32235-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Wortsman X., Atlas of Dermatologic Ultrasound (Springer Nature, Cham, 2018). [Google Scholar]
- 78.Neerken S., Lucassen G. W., Bisschop M. A., Lenderink E., and Nuijs T. A. M., J. Biomed. Opt. 9, 274 (2004). 10.1117/1.1645795 [DOI] [PubMed] [Google Scholar]
- 79.Fercher A. F., Z. Med. Phys. 20, 251 (2010). 10.1016/j.zemedi.2009.11.002 [DOI] [PubMed] [Google Scholar]
- 80.Shu X., Beckmann L., and Zhang H. F., J. Biomed. Opt. 22, 121707 (2017). 10.1117/1.JBO.22.12.121707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Kim J., Brown W., Maher J. R., Levinson H., and Wax A., Phys. Med. Biol. 60, R211 (2015). 10.1088/0031-9155/60/10/R211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Welzel J., in Bioengineering of the Skin: Skin Imaging and Analysis, edited by Wilhelm K.-P., Elsner P., Berardesca E., and Maibach H. I., 2nd ed (CRC Press, 2007), pp. 127–136. [Google Scholar]
- 83.Appel A. A., Anastasio M. A., Larson J. C., and Brey E. M., Biomaterials 34, 6615 (2013). 10.1016/j.biomaterials.2013.05.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Xu C., Ye J., Marks D. L., and Boppart S. A., Opt. Lett. 29, 1647 (2004). 10.1364/OL.29.001647 [DOI] [PubMed] [Google Scholar]
- 85.Coulman S. A., Birchall J. C., Alex A., Pearton M., Hofer B., O’Mahony C., Drexler W., and Považay B., Pharm. Res. 28, 66 (2011). 10.1007/s11095-010-0167-x [DOI] [PubMed] [Google Scholar]
- 86.Li B., Wang H., Fu B., Wang R., Sakadžic S., and Boas D. A., J. Biomed. Opt. 22, 016014 (2017). 10.1117/1.JBO.22.1.016014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Mitchell H. W., Hamilton H. H., Steggerda T. S., and Bean F. R., J. Biol. Chem. 158, 625 (1945). 10.1016/S0021-9258(19)51339-4 [DOI] [Google Scholar]
- 88.Kechidi R. and Aubry S., in Agaches’s Measuring the Skin, edited by Humbert A. P., Fanian F., and Maibach H. (Springer, Cham, 2017), pp. 477–486. [Google Scholar]
- 89.Stefanowska J., Zakowiecki D., and Cal K., J. Eur. Acad. Dermatol. Venereol. 24, 875 (2010). 10.1111/j.1468-3083.2010.03588.x [DOI] [PubMed] [Google Scholar]
- 90.Denis A., Loustau O., Vial J., De Ribes C. L. C., Railhac J. J., and Sans N., J. Radiol. 89, 873 (2008). 10.1016/S0221-0363(08)73875-7 [DOI] [PubMed] [Google Scholar]
- 91.Bittoun J., Saint-Jalmes H., Querleux B. G., Darrasse L., Jolivet O., Idy-Peretti I., Wartski M., Richard S. B., and Leveque J. L., Radiology 176, 457 (1990). 10.1148/radiology.176.2.2367660 [DOI] [PubMed] [Google Scholar]
- 92.Aubry S., Casile C., Humbert P., Jehl J., Vidal C., and Kastler B., Eur. Radiol. 19, 1595 (2009). 10.1007/s00330-009-1348-z [DOI] [PubMed] [Google Scholar]
- 93.Xue H., Kellman P., Larocca G., Arai A. E., and Hansen M. S., J. Cardiovasc. Magn. Reson. 15, 1 (2013). 10.1186/1532-429X-15-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Krishnamurthy R., Pednekar A., Cheong B., and Muthupillai R., J. Magn. Reson. Imaging 31, 872 (2010). 10.1002/jmri.22123 [DOI] [PubMed] [Google Scholar]
- 95.Naik A., Kalia Y. N., Fessi H., and Guy R. H., J. Pharm. Biopharm. 58, 301 (2004). 10.1016/j.ejpb.2004.03.027 [DOI] [PubMed] [Google Scholar]
- 96.Biel S. S., Wepf R., and Wessel S., in Bioengineering of the Skin: Skin Imaging and Analysis, edited by Wilhelm K.-P., Elsner P., Berardesca E., and Maibach H. I. (CRC Press, 2007), pp. 149–164. [Google Scholar]
- 97.Boustany N. N., Boppart S. A., and Backman V., Annu. Rev. Biomed. Eng. 12, 285 (2010). 10.1146/annurev-bioeng-061008-124811 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Alvarez-Román R., Merino G., Kalia Y. N., Naik A., and Guy R. H., J. Pharm. Sci. 92, 1138 (2003). 10.1002/jps.10370 [DOI] [PubMed] [Google Scholar]
- 99.Arkhipov A. Y., Khaziev E. F., Skorinkin A. I., Bukharaeva E. A., and Samigullin D. V., Microsc. Microanal. 26, 204 (2020). 10.1017/S1431927620000148 [DOI] [PubMed] [Google Scholar]
- 100.Shih W.-C., Bechtel K. L., and Feld M. S., in Handbook of Optical Sensing of Glucose in Biological Fluids and Tissues, edited by Tuchin V. V. (CRC Press, 2008), pp. 353–385. [Google Scholar]
- 101.Caspers P. J., Lucassen G. W., Carter E. A., Bruining H. A., and Puppels G. J., J. Invest. Dermatol. 116, 434 (2001). 10.1046/j.1523-1747.2001.01258.x [DOI] [PubMed] [Google Scholar]
- 102.Bakonyi M., Gácsi A., Kovács A., Szűcs M. B., Berkó S., and Csányi E., J. Pharm. Biomed. Anal. 154, 1 (2018). 10.1016/j.jpba.2018.02.056 [DOI] [PubMed] [Google Scholar]
- 103.Giridhar G., Manepalli R. R. K. N., and Apparao G., in Spectroscopic Methods for Nanomaterials Characterization, edited by Thomas S., Thomas R., Zachariah A. K., and Mishra R. (Elsevier Inc, 2017), pp. 141–161. [Google Scholar]
- 104.Park J., Kim J., and Kwon H., Bull. Korean Chem. Soc. 41, 34 (2020). 10.1002/bkcs.11914 [DOI] [Google Scholar]
- 105.Dąbrowska A. K., Adlhart C., Spano F., Rotaru G.-M., Derler S., Zhai L., Spencer N. D., and Rossi R. M., Biointerphases 11, 031015 (2016). 10.1116/1.4962547 [DOI] [PubMed] [Google Scholar]
- 106.Crowther J. M., Sieg A., Blenkiron P., Marcott C., Matts P. J., Kaczvinsky J. R., and Rawlings A. V., Br. J. Dermatol. 159, 567 (2008). 10.1111/j.1365-2133.2008.08703.x [DOI] [PubMed] [Google Scholar]
- 107.Davies M. A., Skin Res. Technol. 26, 30 (2020). 10.1111/srt.12760 [DOI] [PubMed] [Google Scholar]
- 108.Benninger R. K. P. and Piston D. W., Curr. Protoc. Cell Biol. Chap. 4, Unit 4.11.24 (2013). 10.1002/0471143030.cb0411s59 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Theer P., Hasan M. T., and Denk W., Opt. Lett. 28, 1022 (2003). 10.1364/OL.28.001022 [DOI] [PubMed] [Google Scholar]
- 110.Durr N. J., Weisspfennig C. T., Holfeld B. A., and Ben-Yakar A., J. Biomed. Opt. 16, 026008 (2011). 10.1117/1.3548646 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.So P. T. C., Encycl. Life Sci. 1, 1–5 (2002). [Google Scholar]
- 112.Mondal P. P., Front. Mol. Biosci. 1, 1 (2014). 10.3389/fmolb.2014.00011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Bahlmann K., So P. T., Kirber M., Reich R., Kosicki B., McGonagle W., and Bellve K., Opt. Express 15, 10991 (2007). 10.1364/OE.15.010991 [DOI] [PubMed] [Google Scholar]
- 114.du Plessis A., Broeckhoven C., Guelpa A., and le Roux S. G., Gigascience 6, gix027 (2017). 10.1093/gigascience/gix027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Marston J. O. and Lacerda C. M. R., J. Controlled Release 305, 101 (2019). 10.1016/j.jconrel.2019.05.023 [DOI] [PubMed] [Google Scholar]
- 116.Rumboldt Z., Huda W., and All J. W., Am. J. Neuroradiol. 30, 1630 (2009). 10.3174/ajnr.A1603 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Kim J., Chhour P., Hsu J., Litt H. I., Ferrari V. A., Popovtzer R., and Cormode D. P., Bioconjugate Chem. 28, 1581 (2017). 10.1021/acs.bioconjchem.7b00194 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Lakin B. A., Patel H., Holland C., Freedman J. D., Shelofsky J. S., Snyder B. D., Stok K. S., and Grinstaff M. W., J. Orthop. Res. 34, 1130 (2016). 10.1002/jor.23141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Lin E. and Alessio A., J. Cardiovasc. Comput. Tomogr. 3, 403 (2009). 10.1016/j.jcct.2009.07.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Xu M. and Wang L. V., Rev. Sci. Instrum. 77, 041101 (2006). 10.1063/1.2195024 [DOI] [Google Scholar]
- 121.Attia A. B. E., Balasundaram G., Moothanchery M., Dinish U. S., Bi R., Ntziachristos V., and Olivo M., Photoacoustics 16, 100144 (2019). 10.1016/j.pacs.2019.100144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Aguirre J., Schwarz M., Garzorz N., Omar M., Buehler A., Eyerich K., and Ntziachristos V., Nat. Biomed. Eng. 1, 0068 (2017). 10.1038/s41551-017-0068 [DOI] [Google Scholar]
- 123.Kim J., Kim J. Y., Jeon S., Baik J. W., Cho S. H., and Kim C., Light Sci. Appl. 8, 1 (2019). 10.1038/s41377-018-0109-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Moore C. and Jokerst J. V., Theranostics 9, 1550 (2019). 10.7150/thno.32362 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Manivasagan P., Bharathiraja S., Bui N. Q., Jang B., Oh Y. O., Lim I. G., and Oh J., Int. J. Biol. Macromol. 91, 578 (2016). 10.1016/j.ijbiomac.2016.06.007 [DOI] [PubMed] [Google Scholar]
- 126.Pysz M. A., Gambhir S. S., and Willmann J. K., Clin. Radiol. 65, 500 (2010). 10.1016/j.crad.2010.03.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Allen T. J., in LED-Based Photoacoustic Imaging, edited by Singh M. K. A. (Springer Nature Singapore, Singapore, 2020), pp. 23–43. [Google Scholar]
- 128.Francis K. J., Boink Y. E., Dantuma M., Singh M. K. A., Manohar S., and Steenbergen W., Biomed. Opt. Express 11, 2152 (2020). 10.1364/BOE.384548 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Jiang H., Diffuse Optical Tomography: Principles and Applications (CRC Press, 2011). [Google Scholar]
- 130.Ansari M. A., Erfanzadeh M., Hosseini Z., and Mohajerani E., J. Lasers Med. Sci. 5, 13 (2014). 10.22037/2010.V5I1.4569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Scholkmann F., Kleiser S., Metz A. J., Zimmermann R., Mata Pavia J., Wolf U., and Wolf M., Neuroimage 85, 6 (2014). 10.1016/j.neuroimage.2013.05.004 [DOI] [PubMed] [Google Scholar]
- 132.Ferrari M. and Quaresima V., Neuroimage 63, 921 (2012). 10.1016/j.neuroimage.2012.03.049 [DOI] [PubMed] [Google Scholar]
- 133.Durduran A. G., Choe T., Baker R., and Yodh W. B., Rep. Prog. Phys. 73, 076701 (2010). 10.1088/0034-4885/73/7/076701 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Brennan K. A., Ruddy B. P., Nielsen P. M. F., and Taberner A. J., J. Biophotonics 12, e201900205 (2019). 10.1002/jbio.201900205 [DOI] [PubMed] [Google Scholar]
- 135.Arora A., Hakim I., Baxter J., Rathnasingham R., Srinivasan R., Fletcher D. A., and Mitragotri S., Proc. Natl. Acad. Sci. U.S.A. 104, 4255 (2007). 10.1073/pnas.0700182104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Oyarte Gálvez L., Brió Pérez M., and Fernández Rivas D., J. Appl. Phys. 125, 144504 (2019). 10.1063/1.5074176 [DOI] [Google Scholar]
- 137.Cu K., Bansal R., Mitragotri S., and Rivas D. F., Ann. Biomed. Eng. 48, 2028 (2020). 10.1007/s10439-019-02383-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Joodaki H. and Panzer M. B., Proc. Inst. Mech. Eng. Part H 232, 323 (2018). 10.1177/0954411918759801 [DOI] [PubMed] [Google Scholar]
- 139.Crichton M. L., Chen X., Huang H., and Kendall M. A. F., Biomaterials 34, 2087 (2013). 10.1016/j.biomaterials.2012.11.035 [DOI] [PubMed] [Google Scholar]
- 140.Steinman D. A., Ann. Biomed. Eng. 30, 483 (2002). 10.1114/1.1467679 [DOI] [PubMed] [Google Scholar]
- 141.Burton B. M., Aras K. K., Good W. W., Tate J. D., Zenger B., and MacLeod R. S., Ann. Biomed. Eng. 46, 1325 (2018). 10.1007/s10439-018-2048-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Leyva-Mendivil M. F., Page A., Bressloff N. W., and Limbert G., J. Mech. Behav. Biomed. Mater. 49, 197 (2015). 10.1016/j.jmbbm.2015.05.010 [DOI] [PubMed] [Google Scholar]
- 143.Evans S. L. and Holt C. A., J. Strain Anal. Eng. Des. 44, 337 (2009). 10.1243/03093247JSA488 [DOI] [Google Scholar]
- 144.Humphrey J. D., Proc. R. Soc. London Ser. A 459, 3 (2003). 10.1098/rspa.2002.1060 [DOI] [Google Scholar]
- 145.Jor J. W. Y., Parker M. D., Taberner A. J., Nash M. P., and Nielsen P. M. F., Wiley Interdiscip. Rev. Syst. Biol. Med. 5, 539 (2013). 10.1002/wsbm.1228 [DOI] [PubMed] [Google Scholar]
- 146.Li W., Biomed. Eng. Lett. 5, 241 (2015). 10.1007/s13534-015-0201-3 [DOI] [Google Scholar]
- 147.Lanir Y., J. Elast. 129, 7 (2017). 10.1007/s10659-016-9607-0 [DOI] [Google Scholar]
- 148.Kalra A. and Lowe A., J. Aging Sci. 4, 156 (2016). 10.4172/2329-8847.1000156 [DOI] [Google Scholar]
- 149.Rahrovan S., Fanian F., Mehryan P., Humbert P., and Firooz A., Int. J. Women’s Dermatol. 4, 122 (2018). 10.1016/j.ijwd.2018.03.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150.Wang L., Chen L., Lian G., and Han L., Int. J. Pharm. 398, 114 (2010). 10.1016/j.ijpharm.2010.07.035 [DOI] [PubMed] [Google Scholar]
- 151.Lundborg M., Wennberg C. L., Narangifard A., Lindahl E., and Norlén L., J. Controlled Release 283, 269 (2018). 10.1016/j.jconrel.2018.05.026 [DOI] [PubMed] [Google Scholar]
- 152.Munjiza A. A., The Combined Finite-Discrete Element Method (John Wiley & Sons, Ltd, London, 2004). [Google Scholar]
- 153.Luding S., in Advanced Computational Methods in Science and Engineering: Lecture Notes in Computational Science and Engineering, edited by Koren B. and Vuik K. (Springer, Berlin, 2009), Vol. 71, pp. 453–492. [Google Scholar]
- 154.Luding S., Lätzel M., Volk W., Diebels S., and Herrmann H. J., Comput. Method. Appl. Mech. Eng. 191, 21 (2001). 10.1016/S0045-7825(01)00242-0 [DOI] [Google Scholar]
- 155.Larson F. and Bengzon M. G., The Finite Element Method: Theory, Implementation and Applications (Springer-Verlag, Berlin, 2013). [Google Scholar]
- 156.Van Liedekerke P., Tijskens E., Ramon H., Ghysels P., Samaey G., and Roose D., Phys. Rev. E 81, 061906 (2010). 10.1103/PhysRevE.81.061906 [DOI] [PubMed] [Google Scholar]
- 157.Gupta R., Sridhar D. B., and Rai B., J. Phys. Chem. B 120, 8987 (2016). 10.1021/acs.jpcb.6b05451 [DOI] [PubMed] [Google Scholar]
- 158.Barbero A. M. and Frasch H. F., Ann. Biomed. Eng. 33, 1281 (2005). 10.1007/s10439-005-5591-4 [DOI] [PubMed] [Google Scholar]
- 159.Rim J. E., Pinsky P. M., and Van Osdol W. W., Ann. Biomed. Eng. 33, 1422 (2005). 10.1007/s10439-005-5788-6 [DOI] [PubMed] [Google Scholar]
- 160.Xiao P. and Imhof R. E., Int. J. Pharm. 435, 88 (2012). 10.1016/j.ijpharm.2012.01.047 [DOI] [PubMed] [Google Scholar]
- 161.Calcutt J. J. and Anissimov Y. G., Int. J. Pharm. 569, 11857 (2019). 10.1016/j.ijpharm.2019.118547 [DOI] [PubMed] [Google Scholar]
- 162.Mohizin A. and Kim J. K., Comput. Biol. Med. 118, 103642 (2020). 10.1016/j.compbiomed.2020.103642 [DOI] [PubMed] [Google Scholar]
- 163.Rim J. E., Pinsky P. M., and Van Osdol W. W., Ann. Biomed. Eng. 37, 1217 (2009). 10.1007/s10439-009-9678-1 [DOI] [PubMed] [Google Scholar]
- 164.Gajula K., Gupta R., Sridhar D. B., and Rai B., J. Chem. Inf. Model. 57, 2027 (2017). 10.1021/acs.jcim.7b00224 [DOI] [PubMed] [Google Scholar]
- 165.Moulic J. R. and Kumar M., Comput. Syst. Eng. 3, 1 (1992). 10.1016/0956-0521(92)90088-Z [DOI] [Google Scholar]
- 166.Kreienbuehl A., Naegel A., Ruprecht D., Speck R., Wittum G., and Krause R., Comput. Visualization Sci. 17, 99 (2015). 10.1007/s00791-015-0246-y [DOI] [Google Scholar]
- 167.Villarruel Mendoza L. A., Scilletta N. A., Bellino M. G., Desimone M. F., and Catalano P. N., Front. Bioeng. Biotechnol. 8, 1 (2020). 10.3389/fbioe.2020.00827 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Delcassian D., Patel A. K., Cortinas A. B., and Langer R., J. Drug Targeting 27, 229 (2019). 10.1080/1061186X.2018.1438440 [DOI] [PubMed] [Google Scholar]
- 169.Gupta J., Park S. S., Bondy B., Felner E. I., and Prausnitz M. R., Biomaterials 32, 6823 (2011). 10.1016/j.biomaterials.2011.05.061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170.Kim Y.-C., in Percutaneous Penetration Enhancers Physical Methods in Penetration Enhancement, edited by Dragicevic H. and Maibach N. I. (Springer, Berlin, 2017), pp. 485–499. [Google Scholar]
- 171.Nicolas J. F. and Guy B., Expert Rev. Vaccines 7, 1201 (2008). 10.1586/14760584.7.8.1201 [DOI] [PubMed] [Google Scholar]
- 172.Chiu S. S., Peiris J. S. M., Chan K. H., Wong W. H. S., and Yu L. L., Pediatrics 119, 1076 (2007). 10.1542/peds.2006-3176 [DOI] [PubMed] [Google Scholar]
- 173.Micozkadioglu H., Zumrutdal A., Torun D., Sezer S., Ozdemir F. N., and Haberal M., Renal Failure 29, 285 (2007). 10.1080/08860220601166263 [DOI] [PubMed] [Google Scholar]
- 174.Rini C. J., McVey E., Sutter D., Keith S., Kurth H. J., Nosek L., Kapitza C., Rebrin K., Hirsch L., and Pettis R. J., Drug Delivery Transl. Res. 5, 332 (2015). 10.1007/s13346-015-0239-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175.Kendall M. A. F., in Drug Delivery (Handbook of Experimental Pharmacology), edited by Schäfer-Korting M. (Springer, Berlin, 2010), Vol. 197, pp. 193–219. [Google Scholar]
- 176.Chen D., Endres R. L., Erickson C. A., Weis K. F., McGregor M. W., Kawaoka Y., and Payne L. G., Nat. Med. 6, 1187 (2000). 10.1038/80538 [DOI] [PubMed] [Google Scholar]
- 177.Barolet D. and Benohanian A., Clin. Cosmet. Investig. Dermatol. 11, 231 (2018). 10.2147/CCID.S162724 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 178.Krizek J., De Goumoëns F., Delrot P., and Moser C., Lab Chip 20, 3784–3791 (2020). 10.1039/D0LC00646G [DOI] [PubMed] [Google Scholar]
- 179.Tagawa Y., Oudalov N., Visser C. W., Peters I. R., van der Meer D., Sun C., Prosperetti A., and Lohse D., Phys. Rev. X 2, 031002 (2012). 10.1103/PhysRevX.2.031002 [DOI] [Google Scholar]
- 180.Mohizin A. and Kim J. K., J. Mech. Sci. Technol. 32, 5737 (2018). 10.1007/s12206-018-1121-9 [DOI] [Google Scholar]
- 181.Schramm J. and Mitragotri S., Pharm. Res. 19, 1673 (2002). 10.1023/A:1020753329492 [DOI] [PubMed] [Google Scholar]
- 182.Berrospe-Rodriguez C., Visser C. W., Schlautmann S., Rivas D. F., and Ramos-Garcia R., J. Biomed. Opt. 22, 105003 (2017). 10.1117/1.JBO.22.10.105003 [DOI] [PubMed] [Google Scholar]
- 183.Mitragotri S., Nat. Rev. Drug Discovery 5, 543 (2006). 10.1038/nrd2076 [DOI] [PubMed] [Google Scholar]
- 184.Gorres J. P., Lager K. M., Kong W. P., Royals M., Todd J. P., Vincent A. L., Wei C. J., Loving C. L., Zanella E. L., Janke B., Kehrli M. E., Nabel G. J., and Rao S. S., Clin. Vaccine Immunol. 18, 1987 (2011). 10.1128/CVI.05171-11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185.Xing Y., Xie X., Xu J., Liu J., He Q., Yang W., Zhang N., Li X., Wang L., Fu J., Zhou J., Gao B., Ming J., Liu X., Lai J., Liu T., Shi M., and Ji Q., Expert Opin. Drug Delivery 16, 995 (2019). 10.1080/17425247.2019.1649251 [DOI] [PubMed] [Google Scholar]
- 186.Yang J., Liu X., Fu Y., and Song Y., Acta Pharm. Sin. B 9, 469 (2019). 10.1016/j.apsb.2019.03.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 187.Waghule T., Singhvi G., Kumar S., and Monohar M., Biomed. Pharmacother. 109, 1249 (2019). 10.1016/j.biopha.2018.10.078 [DOI] [PubMed] [Google Scholar]
- 188.Jeong S., Park J., Lee Y., Kim Y., Park J., and Kim S., Pharmaceutics 12, 1113 (2020). 10.3390/pharmaceutics12111113 [DOI] [Google Scholar]
- 189.Hadžiabdi J., Micromachines 11, 961 (2020). 10.3390/mi11110961 [DOI] [Google Scholar]
- 190.Kim Y.-C., Park J.-H., and Prausnitz M. R., Adv. Drug Deliv. Rev. 64, 1547 (2012). 10.1016/j.addr.2012.04.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 191.Quan F. S., Kim Y. C., Song J. M., Hwang H. S., Compans R. W., Prausnitz M. R., and Kang S. M., Clin. Vaccine Immunol. 20, 1433 (2013). 10.1128/CVI.00251-13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 192.Al-Qallaf B. and Das D. B., Ann. N. Y. Acad. Sci. 1161, 83 (2009). 10.1111/j.1749-6632.2009.04083.x [DOI] [PubMed] [Google Scholar]
- 193.Chen S., Wu D., Liu Y., Huang Y., Xu H., Gao W., Zhang J., Sun J., and Zhuang J., J. Drug Delivery Sci. Technol. 56, 101547 (2020). 10.1016/j.jddst.2020.101547 [DOI] [Google Scholar]
- 194.Lee J. W., Park J. H., and Prausnitz M. R., Biomaterials 29, 2113 (2008). 10.1016/j.biomaterials.2007.12.048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 195.Kim Y. C. and Prausnitz M. R., Drug Delivery Transl. Res. 1, 7 (2011). 10.1007/s13346-010-0005-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 196.Pokorná D., Poláková I., Kindlová M., Dušková M., Ludvíková V., Gabriel P., Kutinová L., Müller M., and Šmahel M., Vaccine 27, 3519 (2009). 10.1016/j.vaccine.2009.03.073 [DOI] [PubMed] [Google Scholar]
- 197.Gopee N. V., Cui Y., Olson G., Warbritton A. R., Miller B. J., Couch L. H., Wamer W. G., and Howard P. C., Toxicol. Appl. Pharmacol. 209, 145 (2005). 10.1016/j.taap.2005.04.003 [DOI] [PubMed] [Google Scholar]
- 198.Hasson S. S. A. A., Al-Busaidi J. K. Z., and Sallam T. A., Asian Pac. J. Trop. Biomed. 5, 344 (2015). 10.1016/S2221-1691(15)30366-X [DOI] [Google Scholar]
- 199.Jayaprakash V., Costalonga M., Dhulipala S., and Varanasi K. K., Adv. Healthcare Mater. 9, 2001022 (2020). 10.1002/adhm.202001022 [DOI] [PubMed] [Google Scholar]
- 200.Rieffel J., Chitgupi U., and Lovell J. F., Small 11, 4445 (2015). 10.1002/smll.201500735 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 201.Kircher M. F., De La Zerda A., Jokerst J. V., Zavaleta C. L., Kempen P. J., Mittra E., Pitter K., Huang R., Campos C., Habte F., Sinclair R., Brennan C. W., Mellinghoff I. K., Holland E. C., and Gambhir S. S., Nat. Med. 18, 829 (2012). 10.1038/nm.2721 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 202.Daoudi K., van den Berg P. J., Rabot O., Kohl A., Tisserand S., Brands P., and Steenbergen W., Opt. Express 22, 26365 (2014). 10.1364/OE.22.026365 [DOI] [PubMed] [Google Scholar]
- 203.Benson H., Curr. Drug Delivery 2, 23 (2005). 10.2174/1567201052772915 [DOI] [PubMed] [Google Scholar]
- 204.Elias P. M., Holleran W. M., Feingold K. R., Tsai J., and Menon G. K., J. Invest. Dermatol. Symp. Proc. 7, 79 (2002). 10.1046/j.1523-1747.2002.19632.x [DOI] [PubMed] [Google Scholar]
- 205.Oberli M. A., Schoellhammer C. M., Langer R., and Blankschtein D., Ther. Delivery 5, 843 (2014). 10.4155/tde.14.32 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 206.Petrilli R. and Lopez R. F. V., Braz. J. Pharm. Sci. 54, e01008 (2018). 10.1590/s2175-97902018000001008 [DOI] [Google Scholar]
- 207.Tiwari S. B., Pai R. M., and Udupa N., Drug Deliv. 11, 47 (2004). 10.1080/10717540490265261 [DOI] [PubMed] [Google Scholar]
- 208.Szunerits S. and Boukherroub R., Front. Bioeng. Biotechnol. 6, 1 (2018). 10.3389/fbioe.2018.00015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 209.Fang J. Y., Lee W. R., Shen S. C., Wang H. Y., Fang C. L., and Hu C. H., J. Controlled Release 100, 75 (2004). 10.1016/j.jconrel.2004.08.009 [DOI] [PubMed] [Google Scholar]
- 210.Gupta R., Dwadasi B. S., Rai B., and Mitragotri S., Sci. Rep. 9, 1 (2019). 10.1038/s41598-018-37186-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 211.Pham Q. D., Björklund S., Engblom J., Topgaard D., and Sparr E., J. Controlled Release 232, 175 (2016). 10.1016/j.jconrel.2016.04.030 [DOI] [PubMed] [Google Scholar]
- 212.Haque T. and Talukder M. M. U., Adv. Pharm. Bull. 8, 169 (2018). 10.15171/apb.2018.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 213.Mitragotri S., Burke P. A., and Langer R., Nat. Rev. Drug Discovery 13, 655 (2014). 10.1038/nrd4363 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 214.Daugherty A. L. and Mrsny R. J., Adv. Drug Delivery Rev. 58, 686 (2006). 10.1016/j.addr.2006.03.011 [DOI] [PubMed] [Google Scholar]
- 215.Zhang Q., Fassihi M. A., and Fassihi R., AAPS PharmSciTech 19, 1520 (2018). 10.1208/s12249-018-0963-x [DOI] [PubMed] [Google Scholar]
- 216.Robinson N. B., Krieger K., Khan F., Huffman W., Chang M., Naik A., Yongle R., Hameed I., Krieger K., Girardi L. N., and Gaudino M., Int. J. Surg. 72, 9 (2019). 10.1016/j.ijsu.2019.10.015 [DOI] [PubMed] [Google Scholar]
- 217.Kazem S., Linssen E. C., and Gibbs S., Drug Discovery Today 24, 1899 (2019). 10.1016/j.drudis.2019.06.002 [DOI] [PubMed] [Google Scholar]
- 218.Orive G., Taebnia N., and Dolatshahi-Pirouz A., Adv. Healthcare Mater. 9, 1901023 (2020). 10.1002/adhm.201901023 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.