Topological metals and finite-momentum superconductors

Significance

Our work uncovers an interesting connection between topological band theory and superconductivity. While BCS superconductivity at zero magnetic field is largely insensitive to electron wavefunction, in this work we reveal a rich phase diagram of finite-momentum superconductivity in the presence of spin–orbit splitting and Zeeman fields, where electron pairing depends closely on the topology of spin texture on the Fermi surface.

Abstract

We show that the Zeeman field can induce a topological transition in two-dimensional spin–orbit-coupled metals and, concomitantly, a first-order phase transition in the superconducting state involving a discontinuous change of Cooper pair momentum. Depending on the spin–orbit coupling strength, we find different phase diagrams of two-dimensional (2D) superconductors under in-plane magnetic field.

A fundamental concept in the theory of metals is Fermi surface, the locus of gapless electronic Bloch states in momentum space. While Bloch states in conventional metals are spin degenerate, the degeneracy is lifted by a magnetic field via a Zeeman effect and in noncentrosymmetric crystals by spin–orbit coupling (SOC). In both scenarios, the Fermi surface becomes spin split. When attractive interaction is present at low energy, pairing instability of the Fermi surface turns a metal into a superconductor. The interplay between spin–orbit and Zeeman splitting has interesting consequences for superconductivity, as shown in many previous works (1–18). Recent discovery of superconductivity in a variety of two-dimensional spin–orbit-coupled materials, including transition metal dichalcogenides (19) and strontium titanate films (20), adds additional venues for further investigation of this important problem.

In this paper, we take a fresh look at spin–orbit-coupled metals and superconductors through the lens of wavefunction topology. We characterize the topology of electron wavefunctions on spin-split Fermi surfaces and establish a correspondence between topological metals in two dimensions and topological crystalline insulators in three dimensions. Applying an in-plane magnetic field to spin–orbit-coupled two-dimensional (2D) metals can induce a topological phase transition, characterized by a change of spin texture on the Fermi surface and $\pi$ phase shift in quantum oscillation. When the metal becomes superconducting at low temperature, the field-induced topological transition of Fermi surface is found to strongly impact electron pairing. We present phase diagrams of 2D superconductors under in-plane magnetic fields for various SOC strengths.

This work is organized as follows. We start with a case study of 2D Rashba systems under an in-plane magnetic field, which induces a topology change of spin texture on the Fermi surface. We then define a general set of topological invariants for 2D metals having any space–time parity symmetry in terms of quantized $\pi$ Berry phase on spin-nondegenerate Fermi surface. Finally, we examine the impact of Fermi surface spin splitting on superconductivity and show that the field-induced topological transition of the Fermi surface can cause a change in pairing from intrapocket to interpocket, leading to a first-order phase transition in the finite-momentum superconducting state at finite field. Importantly, the intrapocket pairing state evolves smoothly from the zero-momentum Bardeen–Cooper–Schrieffer (BCS) state at zero field, while the interpocket pairing state evolves smoothly from the finite-momentum Fulde–Ferrell–Larkin–Ovchinnikov (FFLO) state at field beyond the Pauli limit. By combining microscopic calculation, symmetry analysis, Ginzburg–Landau theory, and physical argument, we obtain a global phase diagram of spin–orbit-coupled superconductors under Zeeman field.

Rashba Systems

We consider a single-component 2D electron gas with SOC under magnetic field

$$H\left(\mathit{k}\right)=\frac{k^2}{2m}-\mu +\mathit{g}\left(\mathit{k}\right)\cdot \mathit{\sigma }+\mathit{\sigma }\cdot \mathit{B},$$ [1]

where $\mathit{k}=\left(k_x,k_y\right)$ is the 2D momentum, $m$ is effective mass, $\mu$ is chemical potential, $\mathit{g}\left(\mathit{k}\right)$ is the SOC vector, $\mathit{B}$ is the Zeeman energy due to the in-plane magnetic field, and Pauli matrices $\mathit{\sigma }=\left({\sigma }_x,{\sigma }_y,{\sigma }_z\right)$ denote spin.

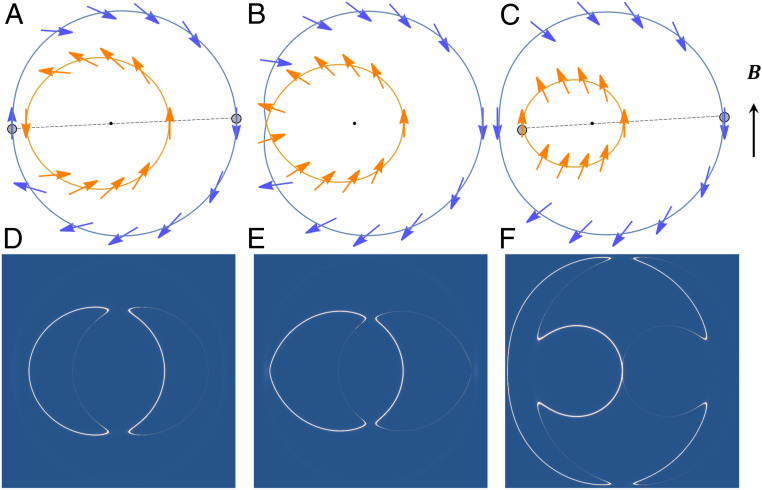
As a concrete example, we consider Rashba SOC $\mathit{g}={\alpha }_{\mathrm{R}}\mathit{k}\times \widehat{\mathit{z}}$ with Rashba coefficient ${\alpha }_{\mathrm{R}}$. At $\mathit{B}=\mathbf{0}$, in the energy eigenstate the electron’s spin is tied with its momentum due to Rashba SOC. As a result, two concentric Fermi circles are present, with helical spin textures of the same chirality. The shape and spin configuration of both Fermi surfaces evolve with the in-plane magnetic field. As $\mathit{B}$ increases, the two pockets approach each other and deform into ovals known as Cartesian ovals (Fig. 1A). The electron’s spin lies within the $xy$ plane and winds by $2\pi$ around both inner and outer Fermi surfaces. At a critical field $B={\alpha }_{\mathrm{R}}{k}_{\mathrm{F}}\equiv {\mathrm{\Delta }}_{so}$ with $k_{\mathrm{F}}=\sqrt{2m\mu }$, the two ovals touch each other at a point ${\mathit{k}}_{\mathrm{P}}\equiv k_{\mathrm{F}}\widehat{\mathit{z}}\times \widehat{\mathit{B}}$, where a twofold spin degeneracy arises. The resulting Fermi surface is a single self-intersecting curve known as a limaçon of Pascal (Fig. 1B). As the field increases further, these two ovals disconnect again and move away from each other (Fig. 1C). Now, the spin winding number on each Fermi surface is 0, and the spin configuration resembles more the Zeeman-dominated case. The inner Fermi surface shrinks further and eventually disappears at sufficiently high fields.

Fig. 1.

(A–C) Fermi surfaces in normal phase. Yellow and blue colors denote inner and outer Fermi surfaces, respectively, and arrows denote electron spins. Shaded small disks in A and C denote paired electrons in corresponding superconducting phases. (D–F) Bogouliubov Fermi segments in corresponding superconducting phase, represented by maxima of zero-energy electronic density of states (DOS) $\rho =-\frac{1}{\pi }\mathrm{I}\mathrm{m}\left[\mathrm{t}\mathrm{r}\left(G{\tau }_e\right)\right]$, where $G$ is Gor’kov Green’s function, and ${\tau }_e=\text{diag}\left(\mathrm{1,0}\right)$ acts in the particle-hole space. We choose parameters $m=1,\mu =10,{\alpha }_{\mathrm{R}}=1,\mathrm{\Delta }=1$, broadening $\eta =0.01$, and magnetic field (A and D) $B=3$, (B and E) $B={\mathrm{\Delta }}_{so}=\sqrt{20}$, and (C and F) $B=7$.

The merging of two pockets and the change of spin winding number at $B={\mathrm{\Delta }}_{so}$ mark another type of Fermi surface topological transition. It is fundamentally different from Lifshitz transitions that reconnect Fermi contours through a saddle point in the energy dispersion. Here instead, the original Dirac point at $\mathit{k}=0$ moves to ${\mathit{k}}_{\mathrm{P}}$ at the Fermi level and results in Fermi surface touching at $B={\mathrm{\Delta }}_{so}$. The dispersion around ${\mathit{k}}_{\mathrm{P}}$ takes the form of an overtitled and anisotropic Dirac cone,

$$H\left({\mathit{k}}_{\mathrm{P}}+\mathit{p}\right)=-v_{\mathrm{F}}{p}_x+{\alpha }_{\mathrm{R}}\left(p_x{\sigma }_y-p_y{\sigma }_x\right),$$ [2]

where $v_{\mathrm{F}}=\sqrt{2\mu /m}$ is the Fermi velocity. Moreover, the topology of Fermi surface in momentum space is unchanged before and after the transition, and the DOS remains finite throughout, unlike the van Hove singularity resulting from saddle points.

Topology of Metals

Unlike Lifshitz transition associated with Fermi surface geometry, what we uncovered in Rashba systems involves the topology of quantum wavefunction on a spin nondegenerate Fermi surface. To characterize the wavefunction topology, we introduce a general topological invariant for 2D systems having any parity symmetry, i.e., invariant under any transformation that reverses the orientation of the space–time manifold, including time-reversal $\mathcal{T}$, reflection $M$ ($x\to -x$), and the combined operation of twofold rotation ($x\to -x,y\to -y$) and time-reversal $C_2\mathcal{T}$. We define the Berry phase $\phi ={\oint }_{E_{\mathit{k}}=\mu }{\mathit{A}}_{\mathit{k}}\cdot d\mathit{k}$ as the topological invariant of a Fermi surface, where ${\mathit{A}}_{\mathit{k}}=-i{\psi }_{\mathit{k}}^{†}{\nabla }_{\mathit{k}}{\psi }_{\mathit{k}}$ is the Berry connection and ${\psi }_{\mathit{k}}$ is the wavefunction with energy $E_{\mathit{k}}$. One can transform the Berry phase $\phi$ into an integral of Berry curvature ${\mathrm{\Omega }}_{\mathit{k}}={\left({\nabla }_{\mathit{k}}\times {\mathit{A}}_{\mathit{k}}\right)}_z$ on the $\mathit{k}$-space section enclosed by the Fermi contour; namely, $\phi ={\int }_{E_{\mathit{k}}<\mu }{\mathrm{\Omega }}_{\mathit{k}}{d}^2\mathit{k}$. Under the parity symmetry, we find energy dispersion is even $E_{\mathit{k}}=E_{P\mathit{k}}$ while Berry curvature is odd ${\mathrm{\Omega }}_{\mathit{k}}=-{\mathrm{\Omega }}_{P\mathit{k}}$, where $P$ can be $\mathcal{T},M$ or $C_2\mathcal{T}$. As a result, $\phi =-\phi$ (mod $2\pi$), and the Berry phase would be either zero or quantized to $\pi$, if inside the enclosed section there are even or odd numbers of Dirac points, respectively. At a Dirac point, two bands cross and the Berry curvature becomes singular. Due to the parity symmetry, Dirac points are restricted to be at time-reversal-invariant points ($P=\mathcal{T}$) or on the reflection-invariant lines ($P=M$) or anywhere in the momentum space ($P=C_2\mathcal{T}$).

This quantized Berry phase therefore serves as a $Z_2$ topological invariant. Generally speaking, Zeeman splitting of Fermi surface results in 0 Berry phase, while spin–orbit splitting results in $\pi$ Berry phase on each Fermi surface enclosing a time-reversal-invariant momentum. In the 2D Rashba model, the $Z_2$ topological distinction continues to hold in the presence of a Zeeman field, which preserves reflection and $C_2\mathcal{T}$. We can also include higher-order SOC such as hexagonal warping (21) to break $C_2\mathcal{T}$ symmetry while preserving reflection $M\left(x\to -x\right)$, so that the SOC vector reads $\mathit{g}={\alpha }_{\mathrm{R}}\mathit{k}\times \widehat{\mathit{z}}+w\left(k_{+}^3+k_{-}^3\right)\widehat{\mathit{z}}$, where $k_{\pm }=k_x\pm i{k}_y$. In this case, the Dirac point is on the $k_x=0$ line as restricted by $M$, and only magnetic field $\mathit{B}\parallel x$ can drive a topological transition of Fermi surfaces.

We refer to Fermi surfaces having quantized Berry phase $\pi$ and 0 as topological and trivial, respectively. It is interesting to note that Fermi surfaces with quantized $\pi$ Berry phase are the hallmark of surface states in 3D topological (crystalline) insulators protected by parity symmetry—$\mathcal{T}$, $M$, or $C_2\mathcal{T}$ (22–26). While these topological surface states are known as “half” of 2D metals, we now turn this viewpoint the other way. The 2D topological metals, defined as having spin-nondegenerate Fermi surfaces with $\pi$ Berry phase, can be viewed as a “sum” of topological surfaces. Thus follows a correspondence between 2D topological metals and 3D dimensional topological (crystalline) insulators.

Since the sum of Berry phases over all Fermi surfaces must be zero in any 2D metal with parity symmetry, topological metals have an even number of spin-nondegenerate Fermi surfaces with $\pi$ Berry phase. A transition from a topological metal to a trivial one generally involves the touching of two Fermi surfaces at a band degeneracy point to enable the change of Berry phase from $\pi$ to 0 on each Fermi surface. We thus conclude that an in-plane magnetic field generally induces a topological phase transition in spin–orbit-coupled 2D metals, provided that parity symmetry (e.g., $C_2\mathcal{T}$ or $M$) is present.

The presence of a spin–orbit-split Fermi surface leads to beatings in quantum oscillation phenomena, as observed in semiconductor heterostructures and noncentrosymmetric metals. The Berry phase change from $\pi$ to 0 across the topological transition can be further detected by analyzing the phase shift of quantum oscillation as a function of in-plane magnetic field (27, 28). We also note recent works on topological characterization of 3D metals under Zeeman fields using Chern numbers on Fermi surfaces (27, 29).

When attractive interaction is present, metals with spin-split Fermi surfaces may become unstable to pairing at low temperature. The competition between spin–orbit and Zeeman splitting, which drives the topological transition in the normal state, also significantly impacts the superconducting state, which we now turn to.

Finite-Momentum Superconductivity

We consider clean superconductors with a local attraction and an energy gap that is small compared to Fermi energy. In this case, superconductivity at zero field is the conventional BCS type. Increasing temperature $T$ and/or in-plane magnetic field $\mathit{B}$ drives superconducting to normal transition. The superconducting order parameter near the transition is determined by the pair susceptibility (9, 10, 17)

$$\chi \left(\mathit{q},\mathit{B},T\right)=N_0\log \frac{{\omega }_D}{T}-\sum _{s=\pm }\delta {\chi }_s\left(\mathit{q},\mathit{B},T\right),$$ [3]

where $\mathit{q}$ is Cooper pair momentum. The first term is the $\mathit{q}=0$ pair susceptibility in BCS theory, where $N_0$ is the total DOS of Fermi surfaces and ${\omega }_D$ is the Debye frequency. The second term is the correction due to Fermi surface spin splitting and finite Cooper pair momentum:

$$\delta {\chi }_s={\oint }_{{\mathrm{F}\mathrm{S}}_s}\frac{dk}{\left|\mathit{v}\right|}\left\{\varphi \left(\frac{Q+s{\mathcal{E}}_{+}}{2\pi T}\right){\cos }^2\frac{\theta }{2}+\varphi \left(\frac{Q+s{\mathcal{E}}_{-}}{2\pi T}\right){\sin }^2\frac{\theta }{2}\right\}$$ [4]

is contribution from inner ($s=+$) or outer ($s=-$) Fermi surface, $\varphi \left(x\right)=\mathrm{R}\mathrm{e}\psi \left(\frac{1+ix}{2}\right)-\psi \left(\frac{1}{2}\right)$, $\psi$ is the digamma function, $\mathit{v}$ is electron velocity, $Q=\mathit{v}\cdot \mathit{q}$ is the depairing energy of finite-momentum pairing, ${\mathcal{E}}_{\pm }=\left|{\mathit{h}}_{+}\right|\pm \left|{\mathit{h}}_{-}\right|$ is the Zeeman depairing energy of inter- ($+$) or intrapocket ($-$) Cooper pairs, $\theta =⟨{\mathit{h}}_{+},{\mathit{h}}_{-}⟩$ is the angle between ${\mathit{h}}_{\pm }=\mathit{B}+\mathit{g}\left(\frac{1}{2}\mathit{q}\pm \mathit{k}\right)$, and $\mathit{g}\left(\mathit{k}\right)$ is the SOC vector.

In the presence of Rashba SOC, the inner $\left(s=+\right)$ and outer $\left(s=-\right)$ Fermi surfaces at $B=0$ have different DOS given by $N_s=\frac{1}{2}{N}_0\left(1-\frac{1}{2}s\lambda \right)$ with $\lambda ={\mathrm{\Delta }}_{so}/\mu$, respectively. As shown in refs. 1 and 2, when ${\mathrm{\Delta }}_{so}\gg {\mathrm{\Delta }}_0$, this DOS asymmetry (often neglected) is important in determining Cooper pair momentum and critical fields at low temperatures. In this work, we always take into account DOS asymmetry $N_{+}\ne N_{-}$ when SOC is present.

From pair susceptibility, the in-plane critical field $B_c\left(T\right)$ is given by $v{\chi }_{max}=1$, where $v$ is the attractive interaction strength in $s$-wave channel and ${\chi }_{max}$ is the maximum of $\chi \left(\mathit{q}\right)$ among all $\mathit{q}$. In this way we also determine the Cooper pair momentum $\mathit{q}$ near $B_c$.

Depending on the magnetic field $B$ and Rashba coupling energy ${\mathrm{\Delta }}_{so}$ in comparison to the BCS gap ${\mathrm{\Delta }}_0=2{\omega }_D{e}^{-1/N_{0}v}$, we find three phases at $T=0$ near the upper critical field: the normal phase (N) and finite-momentum superconducting phases whose Cooper pairs are dominantly interpocket (I) and intrapocket (II), respectively. In the limit of vanishing SOC ${\mathrm{\Delta }}_{so}=0$, phase I reduces to the well-known FFLO state, which occurs at magnetic field above the Pauli limit $B_P\equiv {\mathrm{\Delta }}_0/\sqrt{2}$ (30, 31). Here the Zeeman splitting of the Fermi surface favors interpocket pairing between majority and minority spin states. In the opposite limit of large SOC ${\mathrm{\Delta }}_{so}\gg {\mathrm{\Delta }}_0$, the helical spin texture of the spin–orbit-split Fermi surface favors intrapocket pairing (II). This phase can survive magnetic fields much larger than the Pauli limit and is destroyed only when Zeeman energy becomes comparable to SOC and distorts the Fermi surface significantly (1, 2).

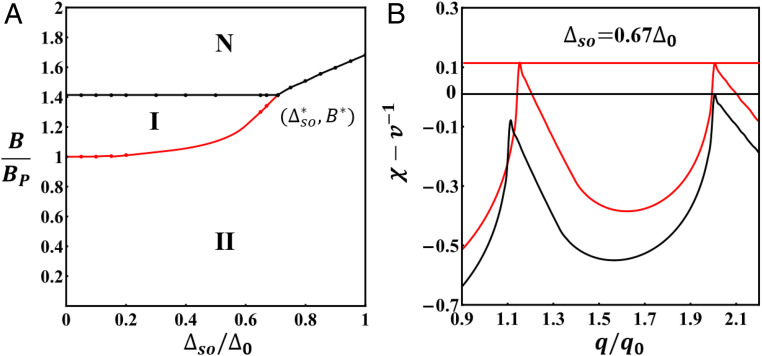
By calculating $\chi \left(\mathit{q},\mathit{B},T=0\right)$, we obtain the phase diagram shown in Fig. 2A. Phases I and II are both finite-momentum superconductors indistinguishable by symmetry. They are separated by a first-order quantum phase transition, where the Cooper pair momentum changes abruptly mainly due to the change of pairing from interpocket to intrapocket. As shown in Fig. 1A, the topological metal $\left(B<{\mathrm{\Delta }}_{so}\right)$ has helical spin configuration of Fermi surfaces and hence electrons from the same Fermi surface can have opposite spins, which results in the intrapocket pairing (II) of Fig. 1D. On the contrary, the trivial metal $\left(B>{\mathrm{\Delta }}_{so}\right)$ as shown in Fig. 1C has Zeeman spin configuration where two Fermi surfaces are spin polarized along opposite directions, and hence electrons from different Fermi surfaces can have opposite spins, leading to interpocket pairing (I) in Fig. 1F. Here our argument is based on Fermi surface spin configuration controlled by magnetic field. In the superconducting phase, the Cooper pair momentum can also alter Fermi surface spin configuration. Quantitative calculations taking into account both effects show that the exact phase boundary between I and II at $T=0$ is at ${\mathrm{\Delta }}_{so}/B\approx 0.7$. The first-order phase boundary between I and II ends at a tricritical point $\left({\mathrm{\Delta }}_{so}^{*},B^{*}\right)$ with ${\mathrm{\Delta }}_{so}^{*}\approx 0.7{\mathrm{\Delta }}_0,B^{*}\approx {\mathrm{\Delta }}_0$, where three phases (I, II, N) meet. Remarkably, near $\left({\mathrm{\Delta }}_{so}^{*},B^{*}\right)$ the phase boundary between superconducting phases I and II is a straight line ${\mathrm{\Delta }}_{so}/B\approx 0.7$ and closely follows the one between topological and trivial metal in the absence of superconductivity. This finding demonstrates the direct impact of topology on finite-momentum pairing in spin–orbit-coupled metals.

Fig. 2.

(A) Phase diagram in the ${\mathrm{\Delta }}_{so}$-$B$ plane at zero temperature, where N is the normal phase and I and II denote superconducting phases whose Cooper pairs are mainly inter- and intrapocket, respectively. Black (red) lines denote second- (first-)order phase transitions. (B) Pair susceptibility at the first-order (red) and second-order (black) phase transitions when ${\mathrm{\Delta }}_{so}=0.67{\mathrm{\Delta }}_0$, where $q_0={\mathrm{\Delta }}_0/v_{\mathrm{F}}$. Dots are from numerical calculations and lines are from interpolation of dots. We set $\mu =50T_c$ to include DOS asymmetry.

We further consider low-energy Bogouliubov quasiparticles of the superconducting phase under a magnetic field. As the field strength increases, the energy gap closes and zero-energy quasiparticles form a Fermi surface that is marked different from the normal-state Fermi surface. At $B<{\mathrm{\Delta }}_{so}$ (Fig. 1D), two Bogouliubov–Fermi segments are formed by the inner pocket, while the outer pocket is fully gapped. At $B>{\mathrm{\Delta }}_{so}$ (Fig. 1F), four Bogouliubov–Fermi segments are formed by both inner and outer Fermi surfaces. Such Bogouliubov–Fermi segments as shown in Fig. 1 D–F can be measured experimentally via scanning tunneling microscope spectroscopy (32) or quasiparticle interference. In terms of topology, we find Berry phases along zero-energy contours of Bogouliubov quasiparticles are zero, and Bogouliubov–Fermi surfaces are trivial in our model. As a result, within the superconducting phase, topological transitions cannot be realized, and there are either first-order phase transitions (${\mathrm{\Delta }}_{so}<{\mathrm{\Delta }}_{so}^{*}$) or no phase transitions (${\mathrm{\Delta }}_{so}>{\mathrm{\Delta }}_{so}^{*}$), as shown in the phase diagram Fig. 2A.

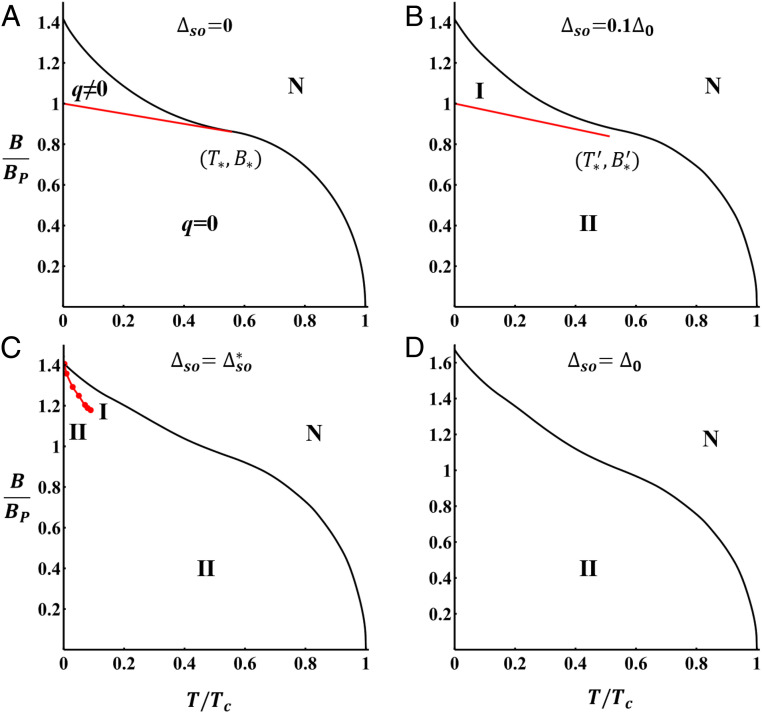
Our results on finite-momentum superconductivity at $T=0$ have important implications for the global phase diagram as a function of temperature and magnetic field, which is plotted in Fig. 3 for different SOC strengths. Without SOC, phases I (FFLO) and II (BCS) are separated by a first-order phase transition line in the $T$-$B$ plane, which starts at $\left(T=0,B=B_P\right)$ and ends at a finite-temperature tricritical point $\left(T_{*}=0.56T_c,B_{*}=0.6{\mathrm{\Delta }}_0\right)$ where phases I, II, and N meet (33, 34) (Fig. 3A).

Fig. 3.

Phase diagram in the $T$-$B$ plane with different SOC strengths. Black (red) lines denote second- (first-)order phase transitions. We set (B) $\mu =10T_c$ and (C and D) $\mu =50T_c$ to include DOS asymmetry, which drives the tricritical point $\left(T_{*},B_{*}\right)$ in A to a critical point $\left(T_{*}^{\prime },B_{*}^{\prime }\right)$ in B.

In the presence of SOC, a small field $B\ll {\mathrm{\Delta }}_{so}$ displaces the centers of inner and outer Fermi pockets to opposite momenta $\pm {\mathit{k}}_0\propto \pm \mathit{B}$. Then, pairing within the inner (outer) Fermi pocket would lead to Cooper pair momentum $\pm \mathit{q}\equiv \pm 2{\mathit{k}}_0$, respectively. Importantly, due to the difference in DOS on the two pockets, the pairing susceptibilities $\chi \left(\mathit{q}\right)$ and $\chi \left(-\mathit{q}\right)$ are generally unequal. The larger of the two sets the Cooper pair momentum near the superconducting transition temperature. This argument shows that the Cooper pair momentum $\mathit{q}$ is linearly proportional to $\mathit{B}$ in the weak-field regime. The resulting finite-momentum superconductor is characterized by intrapocket pairing and evolves smoothly out of the BCS state at $B=0$ and hence is different from the conventional FFLO phase at $B>B_P$.

The linear coupling between Cooper pair momentum and in-plane magnetic field can be also deduced at a formal level from the Ginzburg–Landau free energy in terms of the real-space order parameter $\psi \left(\mathit{r}\right)$, $F=\int d\mathit{r}f$ with

$$f={\psi }^{*}\alpha \psi +\beta |\psi {|}^4.$$ [5]

The coefficient of the quadratic term $\alpha$ can be expanded in powers of the wavevector $\mathit{q}$. Up to fourth order, it takes the following form dictated by symmetry,

$$\alpha =a_0+a_1{q}^2+a_2{q}^4-\left(b_0+b_1{q}^2\right)\mathit{q}\cdot {\mathbf{\Lambda }}_{\mathit{B}},$$ [6]

where ${\mathbf{\Lambda }}_{\mathit{B}}$ is an odd-in-$\mathit{B}$ vector. Here, in addition to even-order terms $a_0,a_1,a_2$, odd terms $b_0,b_1$ may be allowed in spin–orbit-coupled systems, which are invariant under joint rotation of Cooper pair momentum and the Zeeman field. At weak field, ${\mathbf{\Lambda }}_{\mathit{B}}\propto \mathit{B}$. By minimizing $\alpha$, we find the induced Cooper pair momentum $\mathit{q}$ near normal-superconducting transition is proportional to $\mathit{B}$:

$$\mathit{q}=\frac{b_0}{2a_1}{\mathbf{\Lambda }}_{\mathit{B}}\propto \mathit{B}.$$ [7]

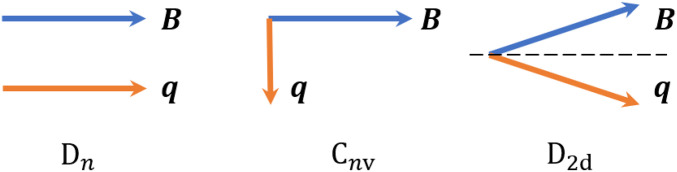
Since the new terms are odd under inversion $I:\mathit{q}\to -\mathit{q},\mathit{B}\to \mathit{B}$ or reflection $M_z:\mathit{q}\to \mathit{q},\mathit{B}\to -\mathit{B}$, they exist in systems with broken $I$ and $M_z$ or equivalently in the following 15 point groups: ${\mathrm{D}}_n,{\mathrm{C}}_{n\mathrm{v}},{\mathrm{C}}_n,{\mathrm{D}}_{2\mathrm{d}},{\mathrm{S}}_4,{\mathrm{C}}_1\hspace{0.17em}\left(n=\mathrm{2,3,4,6}\right)$. The direction of ${\mathbf{\Lambda }}_{\mathit{B}}$ and hence the induced Cooper pair momentum depend on the point group symmetry. Fig. 4 shows the direction of $\mathit{q}$ for point groups ${\mathrm{D}}_n,{\mathrm{C}}_{n\mathrm{v}}$, and ${\mathrm{D}}_{2\mathrm{d}}$, respectively. For 2D Rashba systems, the induced Cooper pair momentum at weak field can be obtained by calculating $a_1$ and $b_0$ using BCS theory: $\mathit{q}=2{\alpha }_{\mathrm{R}}\mathit{B}\times \widehat{\mathit{z}}/v_{\mathrm{F}}^2$ (4). Note that the DOS asymmetry must be included to obtain a nonzero $\mathit{q}$.

Fig. 4.

Cooper pair momentum $\mathit{q}$ is determined by magnetic field $\mathit{B}$ under different point groups. In ${\mathrm{D}}_{2\mathrm{d}}$, directions of $\mathit{q},\mathit{B}$ form a mirror pair with respect to the mirror plane denoted by a dashed line.

By numerically calculating the susceptibility $\chi \left(\mathit{q}\right)$ as a function of $B$, we locate the normal-superconducting phase boundary, i.e., the upper critical field curve $B_c\left(T\right)$. Without SOC ($b_0=b_1=0$), the $B_c\left(T\right)$ curve is divided into two parts by a tricritical point $\left(T_{*},B_{*}\right)$, which corresponds to $a_0=a_1=0$ and $a_2>0$. The Cooper pair momentum at the onset of superconductivity changes from $q=0$ at $B<B_{*}$ to $q=\sqrt{\left|a_1\right|/2a_2}$ at $B>B_{*}$.

When SOC is present, due to $b_0,b_1\ne 0$ the Cooper pair momentum is already nonzero at weak field. Our microscopic calculation shows that for both small and large Rashba couplings, the Cooper pair momentum at $T_c$ changes smoothly with the field. In other words, there is no tricritical point on the $B_c\left(T\right)$ curve. On the other hand, a perturbatively small SOC strength cannot eliminate the strong first-order transition between BCS and FFLO states at low temperature. Therefore, for small SOC strength, we expect the phase diagram shown in Fig. 3B. Since at $B\ne 0$ the superconducting phases I and II both have finite-momentum Cooper pairs and share the same symmetry, the first-order transition between them starts at $\left(T=0,B\gtrsim B_P\right)$ (Fig. 2A) and ends at a critical point $\left(T_{*}^{\prime },B_{*}^{\prime }\right)$, which is located inside the superconducting phase and away from the $B_c\left(T\right)$ curve (Fig. 3B).

As SOC strength increases, the critical point $\left(T_{*}^{\prime },B_{*}^{\prime }\right)$ moves to a higher field and lower temperature. At certain SOC strength ${\mathrm{\Delta }}_{so}={\mathrm{\Delta }}_{so}^{*}$, a zero-temperature tricritical point $\left(0,B^{*}\right)$ arises (Fig. 3C), a direct result of the topological transition of the normal-state Fermi surface. Near the zero-temperature tricritical point $\left(0,B^{*}\right)$, Eq. 6 also applies. In a small range of SOC strength ${\mathrm{\Delta }}_{so}^{*}⩽{\mathrm{\Delta }}_{so}⩽{\mathrm{\Delta }}_{so}^{**}\approx 1.1{\mathrm{\Delta }}_{so}^{*}$, only phase II exists at zero temperature, while a short first-order line between phases I and II remains at finite temperature. Finally, for ${\mathrm{\Delta }}_{so}>{\mathrm{\Delta }}_{so}^{**}$, the entire superconducting region is phase II with interpocket pairing (1–9) as shown in Fig. 3D. Putting all these results together, we arrive at a global phase diagram of 2D superconductors under an in-plane magnetic field, for different SOC strengths.

Conclusion

To conclude, we show that the interplay between SOC and Zeeman effect leads to additional normal and superconducting phases in metals. The Fermi surface transition in normal phase is of topological origin and drives a first-order phase transition within the finite-momentum superconducting state. Depending on the SOC strength, we find different phase diagrams of 2D superconductors under an in-plane magnetic field.

Data Availability.

All study data are included in this article.