Foraging trade-offs, flagellar arrangements, and flow architecture of planktonic protists

Significance

Flagellated unicellular protists play a key role in the biogeochemistry of the ocean. The composition and function of their communities are shaped by fundamental trade-offs between resource acquisition and predation risk. The flagellates gather resources by creating feeding currents by means of beating flagella, but the resulting fluid disturbance attracts flow-sensing predators, thus giving rise to a trade-off. Here we quantify this trade-off by visualizing the fluid flow that the foraging activity generates. We show that the flow architecture relates to the arrangement and beat kinematics of their flagella in characteristic ways that can be predicted qualitatively from simple fluid mechanical models.

Abstract

Unicellular flagellated protists are a key element in aquatic microbial food webs. They all use flagella to swim and to generate feeding currents to encounter prey and enhance nutrient uptake. At the same time, the beating flagella create flow disturbances that attract flow-sensing predators. Protists have highly diverse flagellar arrangements in terms of number of flagella and their position, beat pattern, and kinematics, but it is unclear how the various arrangements optimize the fundamental trade-off between resource acquisition and predation risk. Here we describe the near-cell flow fields produced by 15 species and demonstrate consistent relationships between flagellar arrangement and swimming speed and between flagellar arrangement and flow architecture, and a trade-off between resource acquisition and predation risk. The flow fields fall in categories that are qualitatively described by simple point force models that include the drag force of the moving cell body and the propulsive forces of the flagella. The trade-off between resource acquisition and predation risk varies characteristically between flow architectures: Flagellates with multiple flagella have higher predation risk relative to their clearance rate compared to species with only one active flagellum, with the exception of the highly successful dinoflagellates that have simultaneously achieved high clearance rates and stealth behavior due to a unique flagellar arrangement. Microbial communities are shaped by trade-offs and environmental constraints, and a mechanistic explanation of foraging trade-offs is a vital part of understanding the eukaryotic communities that form the basis of pelagic food webs.

Unicellular flagellated protists play a key role in the biogeochemical cycles of the global ocean. Their photosynthetic activity and grazing on microbes are major processes in the microbial food web, and they may control the populations of bacteria and cyanobacteria (1). By being grazed, they transfer primary production to higher trophic levels (2–4). Thus, flagellates are both consumers and prey, but we do not understand how their resource acquisition trades off against predation mortality, or how this trade-off shapes their foraging behavior.

In the low Reynolds number (Re) world of protists, viscosity impedes predator-prey contact. The physical mechanisms that nevertheless allow flagellates to daily clear a volume of water for prey that corresponds to approximately 10⁶ times their own cell volume (5, 6) are not well understood. Many marine flagellates are mixotrophic and can acquire resources both through photosynthesis and by eating other organisms (7). Their demand for inorganic mineral nutrients is also constrained by viscosity that retards the advective enhancement of diffusive uptake (8).

To encounter prey and enhance advective transport of nutrients, protists may swim or create a feeding current through the beating of one or several flagella (9, 10). However, the beating of flagella produces fluid disturbances that exposes the flagellate to its rheotactic (flow-sensing) predators (11). Small flagellates are grazed by microzooplankton, many of which perceive their prey from the fluid disturbance that the prey generates (12, 13). Thus, there are fundamental foraging trade-offs. Such trade-offs are largely unexplored among the eukaryotic microbes that form the basis of aquatic food webs. This is crucial, because the diversity of microbial communities is determined by such trade-offs in concert with environmental constraints (14–17). Microbial diversity in turn governs the functionality and “services” of microbial communities, and hence also their role in ocean biogeochemistry (18, 19).

Here we explore the trade-off between resource acquisition and predation risk in marine nanoflagellates and microflagellates by describing the flow fields produced by the action of their flagella. The quantification of near-cell feeding currents has been reported in only a few species of free-swimming protists (10, 20). The kinematics, wave patterns, and arrangement and number of flagella are highly diverse among flagellated protists (Fig. 1). Theoretical models suggest that the feeding currents and fluid signal generated by a swimming cell depends on the arrangement of the flagella (11, 13, 21, 22). We use microparticle image velocimetry (µPIV) to visualize and quantify the flow fields generated by free-swimming planktonic protists with diverse flagellar arrangements and beat patterns. We show how the different modes of swimming produce very different flow architectures and demonstrate a trade-off between resource acquisition and predation risk in flagellated protists.

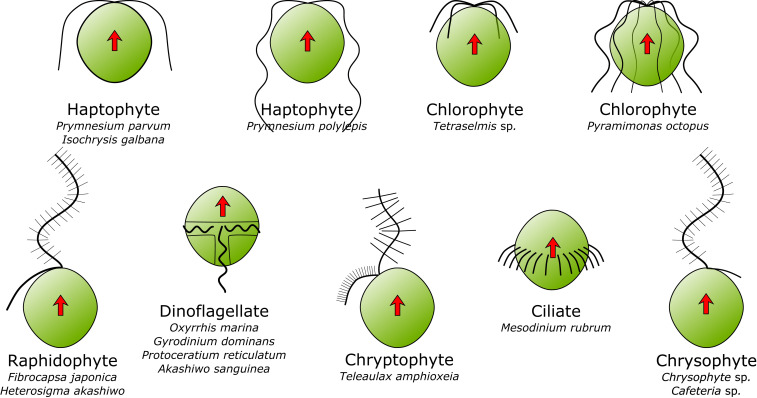
Fig. 1.

Schematic overview of the diverse flagellar arrangements and beat patterns represented in this study. Latin names below each taxonomic group indicate the species (or other taxonomic unit) examined. Flagellar hairs are drawn when feasible, but some flagellar morphologies (e.g., the dinoflagellates) are deliberately simplified (25, 63). Redrawn from several sources; not to scale.

Results

Flagellar Arrangements, Beat Patterns, Kinematics, and Swimming Speeds.

We observed 15 species of free-swimming protists using a high-speed, high-resolution camera and microscope system (Fig. 1 and SI Appendix, Table S1 and Movies S1–S4). Some species were also observed when attached to the microscope slide. In species with a single flagellum producing the feeding current, the flagellum can either push or pull the cell, depending on whether or not the flagellum has hairs (23); this study included only pullers with a hairy flagellum. Some species have an additional flagellum that is used in conjunction with prey handling (raphidophytes and chrysophytes). In species with more than one active flagellum, the flagella are arrayed in multiples of two (2, 4, 8), and the two opposing flagella are synchronized and in antiphase with the alternating flagella (24) (e.g., Movie S4, Tetraselmis sp. and Pyramimonas octopus). The dinoflagellates are very different; they also have two flagella, a trailing one and a transverse one, both contained in a groove-like structure. The transverse flagellum is embedded in a “sock” such that the beating flagellum drives an undulating membrane, which is further equipped with hairs (25). The length of the transverse flagellum is difficult to measure, but it is long, at least 10 times the cell diameter.

In most species, the beat pattern is of the sinusoidal type, that is, a continuously produced wave directed away from the cell. In three species—Prymnesium parvum, Isochrysis galbana, and Tetraselmis sp.—the beat is of the ciliary type, that is, with a clear difference between power and return stroke, which results in a more jagged forward swimming motion (Movie S4). Finally, the ciliate Mesodinium rubrum has a girdle of long cilia around the equator of the cell that beat sequentially to produce a fast gliding motion during the short swimming bursts (26).

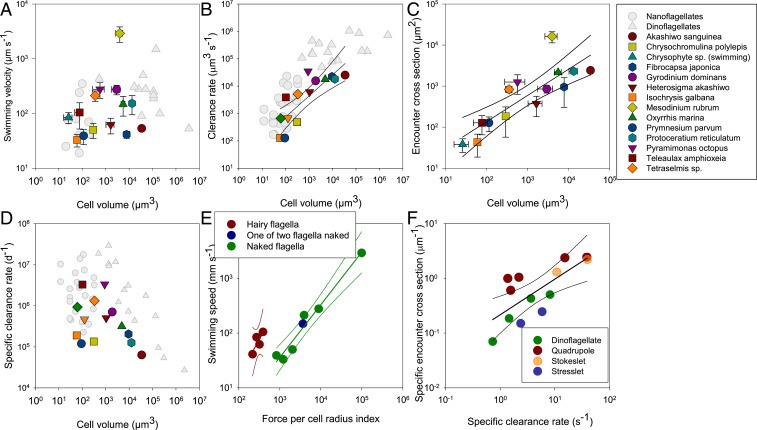
The swimming velocities of the protists that we studied ranged over two orders of magnitude, from 33 to nearly 3,000 µm s⁻¹. These velocities correspond to velocities observed by others (27) and are not related to cell size (Fig. 2A). Rather, swimming speed depends on flagellar characteristics. At low Re, the swimming speed (v), to first order, varies in proportion to the propulsive force (F) and inversely with the cell radius (r): v ~ F/r (28). The propulsive force in turn is roughly proportional to the flagellum length (L), the number of active flagella (n) and their beat frequency (f) and beat amplitude (A): F ~ L × n × f × A. Despite all other differences, observed swimming speeds indeed vary largely in proportion to this index of propulsive force divided by cell radius, with the highest proportionality factor (i.e., greater force) seen for the hairy flagella (Fig. 2E). The dinoflagellates and ciliate could not be included in this analysis due to a lack of estimates of length and number of flagella, respectively.

Fig. 2.

Key traits of the investigated flagellate species. (A) Swimming velocity as a function of cell volume (R² = 0.06; P = 0.4). (B) Potential clearance rate derived from flow fields as a function of cell volume (LogClearance = 1.33 + 0.77 × LogVolume; R² = 0.68). (C) Encounter-cross section for U* = 50 μm s⁻¹ as a function of cell volume (LogCross- section = 0.85 + 0.64 × LogVolume; R² = 0.70). (D) Specific clearance rate as a function of cell volume. (E) Swimming speed as a function of the force per cell radius index (F/r) for species with naked (R² = 0.97) and hairy (R² = 0.69) flagella. F/r = L × n × f × A/r, where L is flagellum length, n is the number of active flagella, f is their beat frequency, A is the beat amplitude, and r is the cell radius. (F) Specific encounter cross-section against specific clearance rate: LogSpecific cross-section = −0.66 + 0.65 × LogSpecific clearance; R² = 0.54) Error bars in A and C are SDs. Regression lines are shown with 95% confidence limits. Gray symbols in A, B, and D are literature values compiled by Kiørboe (27).

Flow Fields.

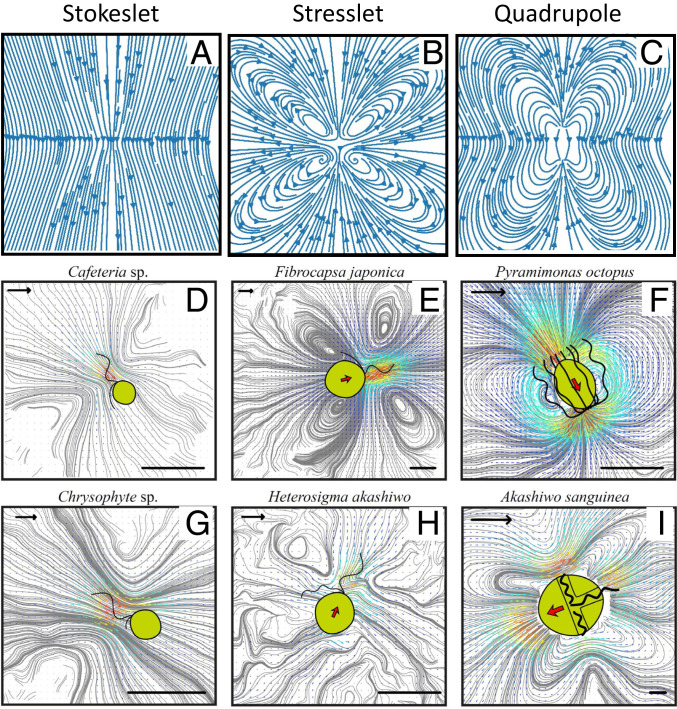
The different flagellar arrangements produce highly diverse flow fields (Fig. 3, Movies S5–S8, and SI Appendix, Fig. S1). The time-averaged flow fields can be grouped into three categories based on the number and position of active flagella and on the similarities of the flow architectures and their resemblance to flow fields produced by highly idealized point force models (see below). The first category is attached specimens with one flagellum that produces a flow field resembling that of a stokeslet (i.e., the flow generated by a single point force in a fluid), corresponding to the beating flagellum (Cafeteria sp. and Chrysophyte sp.) (Fig. 3 A, D, and G). The second category is free-swimming “pullers” that produce flow fields resembling that of a stresslet, that is, two opposing point forces of equal magnitude (Fibrocapsa japonica and Heterosigma akashiwo) (Fig. 3 B, E, and H). These forces correspond to the force generated by the beating flagellum and the opposing drag force of the cell body. The third category is free swimmers with the flagella acting mostly equatorially to generate flow fields resembling those produced by three-stokeslet quadrupole models (M. rubrum, Prymnesium polylepis, P. parvum, P. octopus, Tetraselmis sp., and the dinoflagellates) (Fig. 3 C, F, and I). The three point forces here represent the two forces due to the two (or more) beating flagella positioned or acting laterally to the cell body and the opposing drag force of the moving cell body of a magnitude equal to the sum of the propulsive forces. The dinoflagellates are included in this group but are somewhat different due to the trailing flagellum.

Fig. 3.

Streamlines of three types of point force models (A–C) and time-averaged flow fields around six flagellate species (laboratory frame) (D–I). In D and G, the cells are sessile, and the flow fields resemble a stokeslet (A). In E and H, the cells are free-swimming “pullers,” with the flagellar forces primarily at the front, and the flow fields resemble a stresslet (B). In F and I, the cells are free-swimming and have the forces in a mostly equatorial position. These produce flow fields that resemble various forms of quadrupoles (C). (Length scale bars: 10 μm; flow scale bars [arrows in upper left corner]: 100 μm s⁻¹.)

Qualitatively, the flow fields for these three groups compare well with flow fields predicted from idealized point force models that include the forces due to the beating flagella and the drag force of the cell body. Each force is constant in time and acts on a point in the fluid, thus ignoring the presence of the cell body, the extension of flagella, and the temporal variation in forces during a beat cycle. These highly idealized models have previously been used to describe observed flows generated by self-propelled microorganisms (20, 29), but here we show that they can describe the flows generated by a large range of micro swimmers.

Clearance Rate and Fluid Disturbances.

The observed flow fields allow rough estimates of the potential clearance rates of the flagellates, as well as quantification of the extension of the fluid disturbance that they produce and hence an assessment of predation risk (Materials and Methods). Estimated clearance rates increase with cell size and scale with cell volume to power ∼3/4, similar to the scaling of experimentally measured clearance rates reported in the literature for a different set of species (5) (Fig. 2B).

Rheotactic predators perceive their prey from fluid disturbances, and the relevant property of the fluid disturbance for detection is flow speed (30). Critical flow speed, U*, for prey detection is ∼20 to 100 µm s⁻¹ for microbial predators and is independent of predator size (27). We used the time-averaged flow fields to compute the area within which the imposed flow speed exceeds U* = 50 µm s⁻¹. The resulting area of course depends on the chosen threshold, but the pattern is robust to the choice of threshold (SI Appendix, Fig. S2). This area is a measure of the predator encounter cross-section and thus serves as a proxy for predation risk. The encounter cross-section scales with cell volume to power ∼2/3, not significantly different from the clearance rate scaling above (Fig. 2C).

The volumetric encounter rate (i.e., the encounter cross-section multiplied by the velocity difference between predator and prey) may be a better estimate of predation risk. This predator clearance rate can be computed for stationary (ambush) predators from the flagellate swimming speeds and shows a similar scaling with flagellate cell size as the encounter cross-section (SI Appendix, Fig. S3A). We do not have the necessary information to compute the volumetric encounter rate for motile predators. Here the predator velocity dominates the velocity difference, and the aforementioned simpler index may be more representative for motile predators.

Foraging-Survival Trade-Off.

Volume-specific clearance rates, whether estimated from flow fields or measured in incubation experiments, are of order 10⁶ d⁻¹ but vary by two orders of magnitude, with no apparent correlation with size (Fig. 2D). However, a significant fraction of this variation is accounted for by variation in the fluid disturbance cross-sectional area normalized by cell volume, thus demonstrating a trade-off (Fig. 2F and SI Appendix, Fig. S2): high clearance rates lead to high mortality risk from rheotactic predators. The trade-off is even more pronounced if the volumetric encounter rate is used as a risk proxy (SI Appendix, Fig. S3B). This relationship applies across all the species examined, as well as for each of the flow types defined above, but is offset among the different types (Fig. 2F). This offset implies characteristic risk-to-gain ratios for each type: quadrupole types have the highest predation risk relative to the clearance gain and the stresslet types the lowest, with the other types in between.

Discussion

The fluid dynamics of flagellated protists has previously been explored mainly in the context of propulsion (31, 32). However, feeding and predator avoidance are probably more significant components of the fitness of an organism, and both are directly dependent on the flow generated by the activity of the flagella. While swimming may bring organisms to regions of greater food availability and increase predator encounter rates, the energetic costs of swimming are often considered negligible (31), and the selection pressure to optimize swimming efficiency by altering the arrangement of the flagella is probably of secondary importance. Below we discuss how resource acquisition and predation risk relate to the flow fields generated by the flagella.

Clearance Rate Magnitudes.

Flow architecture plays a major role in resource acquisition. A flagellate may increase its prey encounter rate by pulling streamlines close to the cell body (33). This is also true for the advective enhancement of diffusive uptake of dissolved nutrients (9, 10, 21, 34). Thus, flow architecture has similar implications as particle feeding and acquisition of dissolved nutrients, consistent with the observation that pure phototrophic and pure heterotrophic species can be found with the same flagellar arrangements (35, 36).

Simple point force and other simple analytical models of the flow generated by self-propelled micro swimmers underestimate clearance rates by several orders of magnitude (22, 37–40). While these simple models may properly describe the flow at some distance from the cell body (see below), they might not accurately account for the cell body–flagellum interactions in the very near field where prey encounters happen (41). For this, either detailed CFD models or, as here, directly observed flow fields in the immediate vicinity of swimming organisms are needed. The potential clearance rates estimated here from near-cell flow fields are roughly similar to but up to an order of magnitude lower than those measured experimentally in particle feeding flagellates. Our estimates assume a conservative generic prey:predator size ratio of 1:10 and passive interception of prey particles on the cell surface. Many flagellates are known to feed on prey particles larger than one-tenth their own size (42), and many also use other prey capture mechanisms besides simple interception (43). Both of these factors would contribute to higher clearance rates. In addition, the predator:prey size ratio varies among flagellate species, which may account for some of the size-independent variability in estimated clearance rates.

Despite the limitations of simple analytical models, it has long been hypothesized that a feeding current produced by a tethered microorganism (described by a stokeslet) yields a higher clearance rate than that obtained by a free-swimming one (described by a stresslet) (44–47). The argument is that the former produces higher local flow rates close to the cell body. This prediction has been supported experimentally for particle-feeding flagellates (47), ciliates (48), and ciliated invertebrate larvae (49) and is consistent with our observations (Fig. 2F). However, CFD computations for a tethered flagellate do not support it (50). Moreover, models have suggested that species with the flagella acting in front of the cell (pullers) have streamlines that come closer to the cell body than those with equatorially arranged flagella and therefore have significantly higher clearance rates (22). This is not consistent with our prediction from observed flow fields (Fig. 2F).

Stealth.

The production of feeding and swimming currents increases the conspicuousness of protists to their rheotactic predators, and the “hydrodynamic size” (area) of a foraging flagellate is typically one to two orders of magnitude larger than its physical size (Fig. 2C). However, there are major differences in predation risk between behaviors, since the spatial extension of the fluid disturbance, normalized with cell volume, varies by more than one order of magnitude among species (Fig. 2F). Similar magnitudes of behavior-dependent predation risk have been demonstrated in larger zooplankton, both from fluid dynamic considerations and experimentally (11, 51). Two factors determine the spatial extension of the flow field: the intensity (force) of the disturbance—roughly proportional to the swimming speed and the size of the cell (28)—and the spatial attenuation of the flow, both of which are functions of the flagellar arrangement in characteristic ways. A force index, estimated simply as the radius times the speed of the cell, is a major predictor of fluid disturbance (SI Appendix, Fig. S4). Relative to size, the flagellates that produce quadrupole and stokeslet-type flow fields are the “noisier,” while the dinoflagellates and those that produce a stresslet-type flow field are “quieter.”

Can we rationalize these differences? The simple point force models may properly describe the imposed flow in the far field, and they predict very different spatial attenuation of the flow velocity (SI Appendix, SI Text) (31). Thus, the flow due to a stokeslet attenuates inversely with distance, and that due to a stresslet attenuates with the inverse of distance squared. This is consistent with the differences in the spatial extensions of the observed flow fields for flagellates with one active flagellum. The flow due to a quadrupole attenuates with distance to the power of 3 if the forces are placed equatorially or to the power of 2 if the forces are offset, and the stresslet component dominates (29). Thus, an equatorial or breast stroke arrangement of the propulsive forces appears to be optimal for stealth, as also suggested by previous models (11, 13, 29). If the forces are offset from one another, the stresslet component dominates, and the flow attenuates with the inverse of distance squared. The dinoflagellates with an equatorial and a pushing flagellum are included with the stresslet types in terms of noisiness, largely consistent with expectations. However, the quadrupole breast stroke swimming types are more, not less, noisy relative to their size and force intensity compared with the other types (Fig. 2F and SI Appendix, Fig. S4). We must conclude that the simple point force models provide only a partial explanation of the “noisiness” estimated from our observations for flagellates with multiple active flagella.

Trade-Offs.

Each of the four types of swimming gaits that we have identified based on flagellar arrangement and flow architecture, show the same trade-off between resource acquisition and predation risk. However, there are consistent differences between flagellar arrangements (Fig. 2F) that largely follow from the above. Quadrupole types run a higher risk relative to their clearance rate than the stresslet type, with the other types being intermediate. The different gain-to-risk ratios for the different swimming gaits suggests that there are other trade-offs related to flow architecture than the simple foraging trade-off considered here. With the exception of the special dinoflagellates, cells with multiple active flagella all have the force acting laterally to the cell, not in front, and consequently all produce the quadrupole-type flow field. Multiple flagella generate faster swimming speeds that trade-off against higher predation risk. Higher swimming speeds yield potential fitness advantages, such as the ability to rapidly find ephemeral resource patches. The ocean is highly heterogeneous on the microscale (52), and both autotrophic and heterotrophic protists have been demonstrated to accumulate in such patches, allowing them to increase their resource uptake manifold (53–56). The encounter rate with patches increases with the square of the swimming speed for the diffusive type of motility that is characteristic of microorganisms, as does the rate at which chemotactic behavior allows the cells to climb concentration gradients leading to such patches. Thus, the higher predation risk of the quadrupole types may be warranted by increased access to resources.

Trait-based models of microbial communities are currently being developed by many groups to quantify the role of microbes in ocean biogeochemistry (57–60). Mechanistically underpinned trade-offs are key components of such models (61). The trade-off between resource acquisition and predation risk is a fundamental one that applies across all life forms (62). Our quantification of this trade-off for pelagic protists and demonstration that it varies in a consistent way across planktonic flagellated protists may help further the development of such models.

Materials and Methods

Cultures.

All cultures were grown nonaxenically at 18 °C and 100 µmol photos m⁻² s⁻¹ (PAR) on a 12-h:12- h light:dark cycle. We used B1 medium at a salinity of 32. The purely heterotrophic dinoflagellates Gyrodinium dominans and Oxyrrhis marina were offered Rhodomonas salina as prey twice weekly at a 5:1 prey:predator cell number ratio. Cultures were kept in exponential growth for at least 1 wk before experiments. Cultures of bacterivorous flagellates (Crysophyte sp. and Cafeteria sp.) had an autoclaved, organically grown rice grain added at each cell culture transfer to serve as bacterial substrate.

Videography and Particle Image Velocimetry (PIV).

The observational setup was an Olympus IX71 inverted microscope equipped with a UPLSAPO60XO/1.35 oil-immersion objective and a Phantom v210 high-speed digital camera with a resolution of 1,280 × 800 pixels, which provided 5 pixels µm⁻¹. We added 0.3 µm neutrally buoyant, polystyrene tracer particles (final concentration of <1%) to subsamples of each culture. Particles were pretreated with bovine serum albumin and sonicated to minimize aggregation. A drop of the sample was placed on a microscope slide, and a small chamber at least 300 µm high was built by stacking coverslips on either side of the sample and resting a coverslip on the top. The coverslips were adhered with silicone. The objective was focused in the middle of the sample, ensuring at least 150 µm to the nearest surface. Short video sequences of free-swimming individuals were recorded at 250 to 2,000 fps.

PIV analysis was performed using DaVis 8.0.6 software (LaVision). In our µPIV setup, the several µm focal depth of the microscope objective defined the depth of field. All videos were reduced to 250 fps before PIV analysis. We used a multipass analysis protocol with a final interrogation window size of 32 × 32 pixels with 75% overlap. The flow speed resolution limit due to Brownian motion of the seeding particles is ∼10 µm s⁻¹, but slow advective flows made speed measurements <30 to 50 µm s⁻¹ noisy. Frame-by-frame PIV results are provided in Movies S5–S8.

We produced flow fields averaged over one or several beat cycle by first tracking the cell frame by frame using the Manual Tracking plugin for ImageJ (v. 1.51; https://imagej.nih.gov/ij). We then relocated each frame of the flow field relative to the cell and obtained a time average for each interrogation window using R (v. 3.3.3; https://www.r-project.org).

Flow-Based Clearance Rate Estimates.

To quantify potential clearance rates, we constructed the time-averaged flow field relative to the organism by subtracting the velocity vector of the swimming cell. We assumed that all prey sitting on streamlines that pass within one prey radius from the cell are captured. We further assumed a generic 1:10 prey:predator size ratio and then followed the flow lines upstream (in front of the cell) to where fluid velocities were the highest. Here we quantified the flux through the disk-shaped area set by the flow lines that passed within one prey radius of the flagellate cell (assuming a radially symmetric flow field). We note that several of the studied species do not catch prey, and thus the clearance rate estimates should be considered potential rates.

Fluid Disturbance Quantification.

We quantified the predation risk as the cross-sectional area, A_U*, within which the flow induced by the flagellate exceeds a critical value, U* = 50 µm s⁻¹. We exported flow fields from the DaVis software and used R to quantify A_U* While the absolute value of A_U* obviously decreases with increasing values of U*, the comparison between species is robust to the specific choice of U*.

Data Availability.

All study data are included in the main text and supporting information.