Statistical fundamentals on cancer research for clinicians: Working with your statisticians

Highlights

• •Different trial types require different sample size calculation and interpretation.
• •Statistical modeling may help to minimize confounding effects and bias.
• •Statistical pitfalls can be avoided by following correct statistical guidance.

Abstract

Purpose

To facilitate understanding statistical principles and methods for clinicians involved in cancer research.

Methods

An overview of study design is provided on cancer research for both observational and clinical trials addressing study objectives and endpoints, superiority tests, non-inferiority and equivalence design, and sample size calculation. The principles of statistical models and tests including contemporary standard methods of analysis and evaluation are discussed. Finally, some statistical pitfalls frequently evident in clinical and translational studies in cancer are discussed.

Results

We emphasize the practical aspects of study design (superiority vs non-inferiority vs equivalence study) and assumptions underpinning power calculations and sample size estimation. The differences between relative risk, odds ratio, and hazard ratio, understanding outcome endpoints, purposes of interim analysis, and statistical modeling to minimize confounding effects and bias are also discussed.

Conclusion

Proper design and correctly constructed statistical models are critical for the success of cancer research studies. Most statistical inaccuracies can be minimized by following essential statistical principles and guidelines to improve quality in research studies.

1. Introduction

Cancer research is the soundest tool to generate new knowledge to advance oncology practice. Broadly, there are two types of clinical studies: experimental and observational. Observational studies are undertaken without a specific intervention and can be prospective or retrospective [1]. Experimental studies involve an intervention and studying its subsequent effects, often tested in phase I/II/III/IV clinical trials [2], [3], [4]. While carefully designed and well-conducted randomized controlled trials (RCTs) provide the highest quality evidence regarding efficacy and safety of a particular intervention, they also have limitations, often related to practical or ethical considerations, that represent the tension between “ideal” trial settings and the “real world” environment [5]. Although with important caveats, observational and non-randomized comparative studies could provide a cost-saving and practical alternative.

An important research principle should be reproducibility with high validity, applicability to the target population of interest, and transferability to clinical practice. While preliminary concept envisioning is expected, it is desirable for a clinician to quickly engage experienced biostatistician colleagues to minimize bias, improve statistical power, and provide robust estimations of effect size and other model parameters [6]. An optimal design, especially for RCTs, should address: (1) relevant primary/secondary/exploratory objectives, (2) clinical endpoints and hypothesis testing, (3) a target study population with inclusion/exclusion criteria, (4) rigorous procedures, including randomization, monitoring and quality control, and plans for possible extension or premature termination, (5) a statistical analysis plan (SAP) with model selection and justification, and (6) planned sensitivity analysis for relevant subgroups.

This paper provides practical insights for clinicians about fundamental statistical concepts and methodologies used in oncology research, especially for phase III trials. Some examples from the head and neck cancer (HNC) perspective are provided, generally in the curative setting. However, the principles are equally applicable to other oncology domains. Other types of trials (e.g., phase I/II trials and umbrella protocols) or emerging methods (e.g., machine learning) are not addressed due to the intended scope of this paper. Also, while not addressed further, we encourage caution at the design phase of trials addressing radiotherapy combined with novel agents since there may be unique toxicities including temporal occurrence and character that may not be anticipated [7]. Interested readers should research this important area separately [8], [9].

2. Study design

2.1. Superior, non-inferiority and equivalence trials

Most oncology studies focus on superiority to evaluate whether an intervention is “better” (e.g. higher efficacy, lower toxicity) compared to a control group, using the null hypothesis (H0) that the interventional and control groups are equally effective with an alternative hypothesis (H1, i.e. the clinical “hypothesis”) that they are not equal (i.e. the experimental arm can be either more or less effective than the control arm, which is commonly referred to as “two-sided”) [10]. A nonsignificant result implies insufficient evidence to reject H0. It is critical for H1 to be based on sound clinical judgement and updated knowledge, otherwise it risks exposing patients to unnecessary and/or inferior treatment. For example, the H1 for the recently published ARTSCAN III trial [11] posited a 10% higher 5-year OS for cetuximab versus cisplatin which was based on one trial of cetuximab compared to radiotherapy-alone [12] without considering the effect from concurrent chemotherapy (CCRT) [13]. However, after the trial initiation, the authors responded to emerging evidence showing inferior outcome of cetuximab-radiation versus chemoradiation [14], prompting an unplanned interim analysis that resulted in early trial termination due to inferior outcomes in the intervention (cetuximab-radiotherapy) arm.

In recent years, non-inferiority studies, such as treatment de-intensification trials in HPV-positive (HPV + ) oropharyngeal cancer (OPC) [15], or withholding neck surgery following favorable response to radiotherapy [16], have gained popularity. In contrast to superiority studies addressing effectiveness, non-inferiority studies evaluate whether a less intensive or less costly intervention is not unacceptably less efficacious compared to standard-of-care (SOC) [17]. The H0 is that SOC is better than the experimental intervention, and the H1 is that the experimental intervention is at least as effective as SOC. A non-inferiority study is always one-sided, thus addressing the chance of observing a difference as large as, and in the same direction, as that observed. The margin to be detected is usually also smaller (e.g., 5% in 5-year overall survival [OS] in the recent RTOG-1016 trial) and, therefore, a larger sample size is usually required [18], [19]. Another example of a non-inferiority trial is NRG HN-002 (NCT02254278) which hypothesized that two treatment arms (reduced dose IMRT with or without weekly cisplatin) were non-inferior to the SOC of high-dose CCRT in low-risk minimal smoking HPV + OPC, where effectiveness was defined as 2-year progression-free survival (PFS) of ≥ 85% with a margin of 6% compared to SOC (assuming 2-year PFS for SOC is 91%), and without unacceptable swallowing toxicity at 1-year. Notably, there was no SOC arm and the comparator PFS value is based on recent historical data with the understanding that the winning arm would be taken forward to compare against SOC in phase III.

Another design to prove absence of a significant difference between treatment interventions is an equivalence study. “Noninferiority” and “equivalence” are often used interchangeably to test whether a new treatment is as effective as the SOC. However, there are subtle difference. To prove clinical equivalence, a margin (Δ) is chosen by identifying the clinically acceptable difference in the justification for equivalence [20], which is “two-sided”: addressing the chance of seeing a difference in either direction. If two treatments are equivalent to each other (i.e., the difference is within a pre-defined acceptable margin), the 95% confidence interval (CI) of the parameter that assesses the treatment effect must lie within this margin [21], [22]. For example, the trial by Garrel et al. [23] is an equivalence trial, which compared “equal” effectiveness of sentinel node biopsy versus neck dissection (SOC) with a delta of 10% in operable T1-T2N0 oral and oropharyngeal cancer.

In summary, superiority, non-inferiority, and equivalence studies are three study types with different assumptions about treatment effects [24] [Table 1]. They require different sample size calculations and interpretation. When a superiority study shows a non-significant p value, it is also important not to conclude that the two arms are similar (i.e., non-inferiority or equivalence).

Table 1.

Null Hypothesis and Alternative Hypothesis of Superiority, Equivalent and Non-inferiority Studies.

Type of study	Null hypothesis	Alternative hypothesis	Type of test
Superiority Study	The experimental arm has the same performance as the control arm	The experimental arm has different performance compared to the control arm	Two-sided* or one-sided**
Non-Inferiority Study	The experimental arm is inferior to the control arm	The experimental arm is at least as effective as the control arm	One-sided**
Equivalence Study	The experimental arm has different performance compared to the control arm	The experimental arm is equivalent to the control arm	Two-sided*

* Two-sided test means bi-directional (either better or worse effect) on the performance of the primary endpoint.

** One-sided test means uni-directional (i.e., better effect) on the performance of the primary endpoint.

Traditional trials often employ frequentist approaches which require an H0 and use “fixed” input (e.g., effect size, toxicity reduction) at the design phase. However, this may be challenging when data are sparse, especially for novel technologies (e.g., protons). Bayesian adaptive trial design is exploring this uncertain domain, which can allocate more patients with updated information to the more beneficial treatment arm if a difference is observed during a trial as recently used when evaluating protons in lung cancer [25], [26]. However, it is not being used in four ongoing Phase III proton trials in HNC (NCT04607694, NCT01893307, NCT02923570, TORPEdO trial-ISRCTN16424014). Nonetheless, a similar philosophy to streamline eligibility to only include patients who may benefit from protons by pre-screening using NTCP modelling is a component of one trial (DAHANCA 35, NCT04607694), which has been validated to be feasible [27].

2.2. Study population, sample size calculations and power analysis

Attention to the study population is critical, including how patients will be selected and informed, who will be excluded, and when following diagnosis will they enter the study. Careful attention to case assembly will reduce variability and maintain power to detect differences. However, selection criteria must not be overly narrow to ensure the generalizability of the results. The case assembly should consider important prognostic factors (e.g., disease stage or important biological factors) that influence disease behaviour/response/tolerance to treatment. Recently, the HNC population is considered as two broad groups: tobacco/alcohol-related and HPV-related cancers. HPV + HNC patients have more favorable prognosis and their inclusion in trials may perturb sample size calculations due to dramatically different event rates for many outcomes (See examples later).

For a prospective study, the number of subjects (sample size) needed to address the primary end-point and detect meaningful potential differences requires estimation. The sample should be sufficient to minimize the risk of random errors, unbalanced case inclusion, and bias relating to any intervention (typically addressed by randomization). For a retrospective study with fixed sample size, power analysis can estimate the possibility of identifying statistically significant differences (termed the “power”). A pre-requisite is to specify the H0/H1 and then calculate the sample size to ensure sufficient statistical power to differentiate between these hypotheses, while controlling the probability of incorrectly rejecting the H0.

While mostly applicable to RCTs, the principles of sample size estimation are also important in other studies. There should be a credible judgement about the likely rate for the primary end-point (e.g., OS) in the control group, followed by a similar appreciation of the conceivable medically important impact of the experimental intervention on the end-point. Researchers should avoid overly optimistic effect differences that could result in early trial closure [11]; alternatively, it may undermine study power as occurred in another study with an ambitious assumption of 15% absolute difference [28], and may impact ability to detect smaller differences. The likelihood of a false-positive result is normally expressed as the Type I error (or α, typically set at ≤ 0.05), and the false negative rate as the Type II error (or β). By convention “1-β” is referred to as the “statistical power”, e.g., value of 0.8, derived from a β level of ≤ 0.20. The time for trial entry/accrual should be sufficiently short to retain relevance, maintain sensitivity to avoid distracting the research environments from addressing other relevant questions that may emerge over time, and mitigate confounding arising from evolution of treatment/management in such areas as quality or implementation arising during the study accrual period. “Five years” is generally considered an upper limit of desirable accrual duration [29]. Finally, the time period for events to manifest following completion of patient entry influences the design and ultimate trial logistics.

The parameters required for the sample size calculation include significance level (α), statistical power (1-β), and effect size [Δ] [e.g., Cohen’s effect size, odd ratio (OR) or hazard ratio (HR)], and the variation or “spread” of distribution (often using standard deviation) of the study endpoint(s) [Table 2]. Although fixed values of these parameters are often used for sample size determination, they have been criticized for oversimplification by overlooking inherent uncertainties about the assumptions [30]. Different suppositions about parameters are recommended to provide a more comprehensive evaluation of their influence on sample size determination. For early phase clinical trials and pilot observation studies, the significance levels can be less stringent (e.g. α = 0.15 or 0.20 for Phase II trials) [31], while in some Phase III trials, power is often more stringent (e.g. 0.90) [32]. The estimated effect size is the minimal clinical meaningful difference, ordinarily chosen by interpreting prior research findings. For example, to calculate the impact of CCRT on locally advanced HNC, a strategy might be to choose an effect size based on a robust dataset such as the Meta-Analysis of Chemotherapy in Head and Neck Cancer (MACH-NC) [33].

Table 2.

Variables Required for Sample Size Calculation.

Key Parameters	Definition	Conventional Value	Relationship to Sample Size
Significance Level (α)	The chance of false positive result	0.05 or 0.10, one-sided or two-sided; Need to conduct multiplicity adjustment when deal with multiple tests	α ↓ ⇒ samples ↑
Statistical Power (1-β)	The chance of true positive result	0.80 or 0.90	power ↑ ⇒ samples ↑
Effect Size (θ)	Minimal Clinical Meaningful Difference	Continuous Outcome: mean difference; Binary Outcome: odd ratio (OR); Time to Event Outcome: hazard ratio (HR)	effect size ↑ ⇒ samples ↓
Variance (standard deviation, STD)	The variability of the continuous outcome measure	Only used for continuous outcomes	STD ↓ ⇒ samples ↓
Example - Changes in Sample Size Due to Change of Assumption (CCTG HN.6 Trial [NCT00820248])
Assumptions			Estimated Sample Size
Assumption 1: Effect size (HR 0.7), 2-year PFS 45% for control arm, alpha 0.05, beta 0.2, recruitment 3.2 years, additional follow up 3 years			320 (final sample size estimation)
Assumption 2: Larger effect size (HR 0.65), no change in other assumptions (larger difference in hazard rates between treatment arms, which translated into larger difference in actuarial rate of event manifestation)			224 (smaller samples)
Assumption 3: Longer recruitment (5 years), no change in other assumptions (more events manifest within the total length of the trial)			304 (smaller samples)
Assumption 4: Longer follow-up (5 years), no change in other assumptions (more events manifest within the total length of the trial)			282 (smaller samples)
Assumption 5: Larger statistical power (0.9), no change in other assumptions (less chance of false negative)			430 (larger samples)
Assumption 6: Lower PFS for both control arm (2-year PFS 60%) and treatment arm with the same hazard ratio, no change in other assumptions (i.e. lower hazard rates for both treatment and control arms)			400 (larger samples)

Abbreviation; PFS: progression free survival.

As an example, the CCTG HN.6 trial (NCT00820248) [34] required 320 patients over 3.2 years to observe a total of 246 events (any relapse or death) assuming the following: alpha 0.05 with 80% power; 2-year PFS of 45% for the control group, and a HR (discussed later) of 0.7 (representing a 30% reduction of the likelihood of an event, corresponding to a 12.2% absolute difference in 2-year PFS); an enrollment of 100 patients/year; and all patients followed for an additional 3 years to ensure the emergence of enough PFS events. If the assumption for any aforementioned parameters changes, the estimated sample size would also change accordingly (Table 2).

Changes in biologic characteristics of disease could also alter the sample size calculation due to changes in assumptions regarding the risk of events. Recent trials in locally advanced HNC [28], [35] showed dramatically diminished power due to unanticipated emergence of HPV + OPC which changed event rates significantly rendering the original trials, designed before appreciating this phenomenon, virtually obsolete. A lower-than-expected event rate due to unanticipated confounding by the emerging HPV population, e.g., RTOG 0129 [27], cannot be addressed by longer follow-up. Investigators should be aware of this problem when designing trials to ensure adequate sample size. Planned interim analysis could identify the need to augment sample size. For example, RTOG 1016 (NCT01302834) [15] required sample size expansion from the original 706 to a final accrual of 987 due to a lower-than-estimated event rate.

Planned sample size is also critical in studies on precision/molecular radiotherapy research. Studies with limited numbers of patients can be used for exploratory or pilot analysis and hypothesis generation. Multicenter collaborations and integrative analysis on such trials are encouraged for further confirmation/validation.

2.3. Randomization, stratification and intention-to-treat

Randomization is a fundamental pillar of prospective trials because it provides the opportunity to balance the distribution of all baseline covariates (observed and unobserved) across treatment groups. The date of randomization also provides a useful initiation date for cohort analysis to minimize potential lead-time bias due to potential differences in duration of treatments under comparison (e.g., surgery vs non-surgical treatment).

Stratification should improve the efficiency of a RCT by reducing the variation of the treatment effect. Stratified randomization can be conducted by assigning patients with certain characteristics equally to each treatment arm. The study randomization list should be generated by an independent biostatistician, and distributed/monitored by an independent administration center.

An intention-to-treat analysis is an additional important principle to reduce confounding by analyzing patients according to their original randomization assignment, regardless of the treatment they actually received.

3. Data analysis and reporting

3.1. Understanding study endpoints

The most commonly used oncological endpoints in studies include: OS, PFS/disease-free survival (DFS), and cause-specific survival (CSS) [36] (Table 3). The advantage of OS is its objective definition (alive or dead) and consequent less susceptibility to misreporting. However, it does not distinguish index-cancer death from competing mortality. Alternatively, CSS restricts events to index-cancer death and therefore addresses ablative or tumoricidal effects of a treatment, but the accuracy of cause of death attribution remains a concern. PFS/DFS has become more popular in clinical trials recently because both treatment failure and death are considered “events”, which garners more incidents resulting in greater power and reduced study sample size. However, the terms “disease-free” or “progression-free” can both be misleading because death from other cause, such as cardiac event/suicide/car accident, are also counted as “events” although unrelated to “the cancer-of-interest”. OS and PFS/DFS all suffer from other consequences such as the detrimental effect of smoking on cancer survival. While the effect on OS is consistent and rational in HPV + OPC patients, the effect on disease control is not consistent [37], [38]. It is possible that the lower DFS or OS in heavy smokers results from death due to competing risk, and does not necessarily indicate that smoking has induced a more aggressive tumor phenotype. In turn, it does not indicate that smokers would uniformly benefit from intensified treatment. Furthermore, in a landmark initial study addressing this hypothesis, the occurrence of a second primary cancer was included as an event, together with survival and disease recurrence, in attempting to unravel the impact of smoking on outcome of these patients [39]. A subsequent publication from the same group did not observe worse cancer specific outcomes in smokers [38].

Table 3.

Definition of Commonly Used Oncologic Outcome Endpoint and Analytic Procedure.

Study endpoint	Endpoint definition
Overall survival (OS)	From date of diagnosis (or date of treatment or date of randomization for RCTs) to date of death from any cause or last follow-up. The event is death due to any cause
Cause specific survival (CSS)	From date of diagnosis (or date of treatment or date of randomization for RCTs) to date of death due to index cancer or last follow-up. The event is death due to index cancer. Death due to other causes can be treated as competing risk events.
Relapse free survival (RFS)	From date of diagnosis (or date of treatment or date of randomization for RCTs) to date of first relapse or date of death or last follow-up. The event is first recurrence. Usually, death without any recurrence can be treated as a competing risk event.
Progression/Disease free survival (PFS/DFS)	From date of treatment to date of first recurrence (relapse) or date of death or last follow-up. The event is first recurrence or death.
Local failure (LF) Regional failure (RF) Distance failure (DF)	From date of treatment to date of local or regional or distant failure or date of death or last follow-up. The event is local or regional or distant failure. Usually, death without failure can be treated as a competing risk event.
Definition of Event, Censor, and Competing Risk
First Event	OS	CSS	RFS	PFS/DFS	LC	RC	DC
None (alive, no disease)	Censor	Censor	Censor	Censor	Censor	Censor	Censor
Local (primary site) failure	N/A	N/A	Event	Event	Event	N/A	Competing risk
Regional (lymph node) failure	N/A	N/A	Event	Event	N/A	Event	Competing risk
Distant (remote sites) metastasis	N/A	N/A	Event	Event	N/A	N/A	Event
Death due to index cancer	Event	Event	Competing risk	Event	Competing risk	Competing risk	Competing risk
Death due to other causes	Event	Competing risk	Competing risk	Event	Competing risk	Competing risk	Competing risk

Abbreviation: N/A: not applicable; OS: overall survival; CSS: cause-specific survival; RFS: recurrence-free survival; PFS: progression-free survival; DFS: disease-free survival; LC: local control; RC: regional control; DC: distant control.

Oncologic outcomes are often time-to-event endpoints and their analysis differs from simple calculations of frequencies. The event may not be observable for all subjects due to attrition of cases from the sample or termination of follow-up, which are considered as censored data. For time-to-event endpoints, the uniformly agreed analysis is the Kaplan-Meier method with log-rank test for comparison [40]. It provides an estimate of event-free probability at any time point during the follow-up period, and permits censoring and varying lengths of follow-up. However, it does not take into account death due to competing-risk and could overestimate the event-of-interest when calculating a disease-specific endpoint (e.g. local/regional/distant failure), since a competing-risk event can preclude the event-of-interest from occurring [41], exemplified in Fig. 1. For these endpoints, the competing-risk model is more appropriate. This is especially important for vulnerable populations, including the elderly, susceptible to competing mortality. While many HNC patients are heavy tobacco users, additional alcohol use contributes further to their inherent risk of non-cancer mortality. Table 3 summarises commonly accepted terms and analytic procedures (“censoring”, and “competing risk calculations”) for various oncologic endpoints.

Fig. 1.

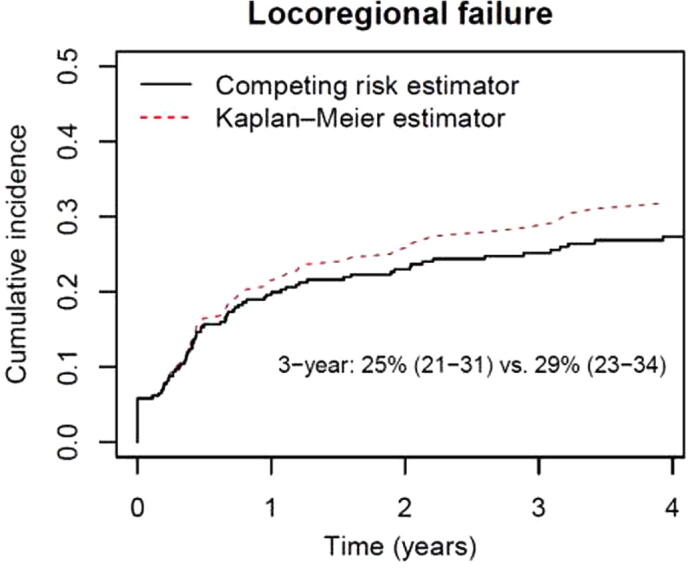
Actuarial Rate of Locoregional Failure Estimated by Kaplan-Meier Method vs Competing Risk Method in HPV-negative OPC Patients Treated at Princess Margaret Cancer Centre, Toronto, Canada.

3.2. Median follow-up and actuarial estimation

The purpose of reporting median follow-up in survival analysis studies is to describe the maturity of data. It is generally calculated on surviving patients only, which ideally should be specifically stated since it is important to appreciate if sufficient time has elapsed to permit most events to occur. Survival estimates become less accurate when they extend beyond the median follow-up time due to insufficient numbers at risk. Thus, it is unrealistic to estimate 5-year OS in a study with only 3 years of median follow-up time.

Survival rates are often derived by Kaplan-Meier analysis which uses median time-to-event as an estimation. However, median time can also be unstable and susceptible to outliers, such as patients who die shortly after treatment or those with long survival. This is relevant when comparing long-term outcomes beyond the traditional 5-year period when two arms could exhibit significantly different median follow-up. Restricted mean survival time (RMST) calculates mean survival time over a pre-specified, clinically important time point. It is equivalent to the area-under-the-Kaplan-Meier-curve from the beginning of a study through that pre-specified time points (e.g., 2-year or 3-year) [42], [43]. It is complimentary to Kaplan-Meier analysis, and may augment time-dependent data analyses in clinical trials and meta-analyses [44]. A case study of individual patient data (IPD) network meta-analysis (NMA) on nasopharyngeal cancer has shown different results using both methods [45]. RMST difference is valid and interpretable even if the proportional hazards assumption is violated [45].

Ideally, clinical trials should also have sufficient follow-up to appreciate late toxicity, which might alter the conclusion of the trial [46], [47]. For example, the RTOG 91–11 trial initially reported superior 5-year laryngeal preservation and locoregional control with similar OS using CCRT compared to induction chemotherapy, while radiotherapy-alone fared the worst [47]. However, long-term results [46] showed a trend for better OS with induction chemotherapy compared to CCRT, leading to speculation that unexplained death might be attributed to greater long -term toxicity (e.g., silent aspiration) with the latter approach.

3.3. Interim analysis

Interim analysis is important and should preferably be pre-planned and undertaken in a controlled manner, generally under the auspices of a data monitoring committee that includes experts who are not investigators on the trial. The focus is often directed at the safety of patients (a principal reason) in the event that a trial needs to be paused or terminated for several reasons: 1). Excessive toxicity mandating immediate closure, as occurred in an altered fractionation radiotherapy trial in locally advanced HNC where only 82 of 226 planned cases were eventually accrued [48], 2). Clear superiority of one treatment compared to another may be grounds for closure for ethical reasons, especially when the primary question may have been addressed and there is no further rationale to continue expending resources, and further patients could continue receiving a proven inferior approach: this was seen with the experimental treatment in the highly influential trial of chemoradiotherapy in nasopharyngeal carcinoma that changed practice globally [49], 3). Unexpected significantly worse performance of an experimental arm also warrants immediate closure as was evident in the DAHANCA 10 trial using darbepoetin alfa to improve anemia in HNC (HR for OS: 1.30) or the ARTSCAN III trial (NCT01969877) [11] comparing cetuximab versus cisplatin-chemoradiotherapy (HR for OS: 1.63), 4). Other reasons for premature closure include futility, relating to inadequate power consequent on slow accrual. Examples include the rare trial that compared chemo-radiotherapy versus definitive surgery in HNC [50], [51] and the PARADIGM induction chemotherapy trial [52]. Unplanned interim analysis may occasionally be useful if the investigators respond to new evidence from other studies during the course of the trial [11], and may result in amendments or premature closure.

Alternatively, multiple interim analyses may inflate false positive findings. This multiplicity problem dictates the need for methodologies developed for statistical adjustment on stopping rules. Group sequential design is a commonly used procedure which defines p-values for considering trial stoppage at an interim analysis while preserving the overall type I error [53], [54].

Rather than focussing only on trial closure, an important alternative consideration for the data safety monitoring committee, may be the observation during the trial that borderline differences exist justifying the addition of either more patients or an extended duration [55].

Finally, an important factor for the broader research landscape concerns the impact of stopping comparative effectiveness trials which may still contribute useful information by enhancing the power of subsequent meta-analyses addressing important questions or may identify value to treatments in later follow-up if they are less invasive, or less expensive/inconvenient [56].

4. Addressing confounding variables

4.1. Observational studies and propensity score matching

Observational, often retrospective, studies are often considered less impactful than prospective trials because of compromised ability to address case eligibility and biases, the temptation to apply risks and assessments from post treatment outcomes to the baseline prognostic framework, and generally have less rigor to evaluate endpoints that may not be predefined, and a higher likelihood of imbalanced baseline characteristics compared to clinical trials. Propensity score matching may help to address this [57], [58] by creating matched groups of untreated and treated cases with the same likelihood of clinical behaviour or treatment response for a given a set of observed covariates. Ideally propensity score matching requires large samples with a reasonable spread of baseline variables across the population and substantial overlap between the comparison groups. The process generally includes: (1) choosing variables to be included in the propensity score, (2) choosing matching and weighting strategies to balance covariates across treatment groups, (3) balancing covariates after matching or weighting the sample, and (4) interpreting treatment effect estimates [59]. The covariates used in propensity score matching are identified from variables predictive of the outcomes-of-interest [60].

Two types of propensity score matching designs predominate: the most common identifies propensity score matched samples [61]; the other creates propensity scores, and conducts outcome analysis using all samples adjusting for the subsequent propensity scores [62]. One-to-one or one-to-two matching are commonly used. Since propensity score matching can only control for observable covariates, hidden bias may remain due to unobserved variables after matching [63].

4.2. Univariable vs multivariable analysis

Univariable analysis (UVA) is commonly used to assess association between a single predictor or risk factor and the study endpoint. However, biased inference may be derived from UVA due to pre-existing confounding effects [64]. Multivariable analysis (MVA) is a statistical method to adjust for observed confounding factors to correct for and enable accurate inference.

For MVA model construction, four selection procedures are typical: forward, backward, stepwise, and best subset selection. All choose candidate variables for inclusion in the MVA, usually identified from significant variables in UVA, or important risk factors related to the study endpoint, or frequent confounders such as age and treatment. The forward selection algorithm starts by adding candidate variables sequentially; attributes with the lowest p-value below the selection criteria (e.g., 0.05), are chosen iteratively until no new variables can be added. Backward selection starts by including all candidate variables followed by sequential iterative removal according to highest p-value exceeding the selection criteria, until no variables can be removed. Stepwise algorithm uses a combination of backward and forward selection. Best subset selection assesses combinations of variables (“subset of variables”) and identifies the most optimal model using model evaluation criteria, such as the Akaike Information Criterion (AIC), the Bayes Information Criterion (BIC) [65], [66], adjusted R-square, residual sum of squares, Mallow’s Cp Statistic, and concordance index (C-index). C-Index (ranges from 0 to 1) is the standard performance measure for survival model assessment, and a higher value indicates a higher predictability in a survival model.

To construct a reliable and robust multivariable model, the minimal number of “samples” (referring to “events” in time-to-event outcome) per variable is important for model performance and estimation. Generally, the minimum number of “samples”/“event” per variable lies between 5 and 20 [67], [68]. In survival analysis, ten “events” per variable is often the minimum required sample size for linear regression models to ensure accurate prediction in subsequent subjects [69], [70], [71].

4.3. Difference between multivariate analysis and multivariable analysis

Although often used interchangeably, the terms “multivariable analysis” and “multivariate analysis” are distinct. A multivariable model is an analysis with a single endpoint but multiple independent variables, whereas a multivariate analysis describes multiple study outcome endpoints, i.e., different adverse events with multiple independent variables [72], [73], [74], using a single model and provides unbiased and precise parameter estimation and potentially increased statistical power.

5. Statistical modeling

5.1. Risk classifications and prediction

Evaluation of clinical factors includes both association studies and predictive studies. Association studies identify prognostic factors associated with study outcomes. Predictive studies address multiple predictors with combined effects on response to treatment and outcome prediction.

The development of a clinical prediction model involves three components: model building, validation, and implementation. Both model building and validation are guided by model prediction performance evaluations. The first step is to select candidate risk factors, including clinical factors or biomarkers with strong preliminary data suggesting prognostic impact, and previously established clinical factors or biomarkers that could be confounders or effect modifiers [75].

The second step is model construction where the decision about the most important variables to predict outcome is usually conducted through multivariable regression modeling based on model selection algorithms such as stepwise or backward selection. Another aspect of model specification is the interactive effects of risk factors. After predictive model construction, patients can be classified into high-risk vs low-risk groups.

Finally, either external validation or internal validation should be conducted to verify the developed predictive model. Cross-validation is one of the common techniques for internal validation [76], [77]. More stringent validation is achieved by addressing external validity, using a different, independent dataset from a similar patient population. Nomograms or web applications are commonly used implementation tools underpinned by outputs derived from prediction models [74].

5.2. Estimates of comparative risk association

When comparing two treatments, both the magnitude of the treatment effect between both treatments and its direction (i.e., an improved or a detrimental result) are important. Several measures of comparative risk association, including relative risk (RR) and odds ratio (OR), can be used to assess differential effects according to the interventions at static time points [78] using binary measures (e.g., toxicity vs no toxicity, response vs no response). However, the most frequently used method for contemporary clinical studies is the HR which applies to time-to-event outcomes. HRs are estimated for an event (e.g., death) over the entire trial duration between two treatments and are a convenient measure of the treatment effect in efficacy studies, although the number of events in either arm is not shown directly. Simplistically, a HR is calculated by the ratio of hazard rates of experimental divided by that of control arm.

Using the CCTG HN.6 trial [34] as an example again, the 2-year PFS was assumed to be 45% with the corresponding hazard rate of 0.40 [−log(0.45)/2 years] for the control arm. With 12.2% absolute difference, the 2-year PFS would be 57.2% for the experimental arm, corresponding to a hazard rate 0.28 [−log(0.572)/2 years], and a HR of 0.7 [0.28/0.40]. When the results are analyzed, if the HR is 1.0, the treatments are considered equivalent, while values < 1.0 indicate superiority and values > 1.0 indicate that the experimental arm is worse. In the example shown, a HR of 0.7 means that the experimental arm has a 30% decrease in hazard of death compared to the control. Correspondingly, if the HR is 1.3, the experimental treatment would have a 30% higher hazard of death compared to the control. It is also usual to indicate 95% confidence intervals (CI) of the HR. It should not overlap unity (1.0) if the effect between the two arms is statistically significant at the level of p < 0.05. This is important for the reader, since it is possible to see comparative survival curves, including when significant differences exist, displayed with only HRs and CIs, but without the p-values. Finally, HRs can be adjusted for covariates within the multivariable Cox regression model that generated the hazard rates.

6. Addressing data heterogeneity

6.1. Sensitivity analysis and subgroup analysis

The goal for personalized medicine is often to identify best treatment for subsets of patients based on demographic, clinical and genetic characteristics. Understanding heterogeneity of treatment response is complex due to the intricate oncology environment. In clinical trials, subgroup analysis should be pre-planned and specified in the trial protocol and readers should be extremely wary when attempting to implement management derived from results of unplanned analyses. However, subset analysis is often useful to understand results of a trial and for hypothesis generation when designing future trials.

Besides subgroup analysis, sensitivity analysis is also important to assess the robustness of a statistical model to its assumptions. It is often used to evaluate consistency in results and conclusions given different parameters of a particular model, including comparison of models using differing clinical covariates, with and without interactive effects. Various statistical models can be applied to the same study to evaluate the estimation of association and outcome prediction. The same analysis methods can be applied to different sample cohorts such as intention-to-treat, per-protocol cohorts, and safety cohorts (randomized patients who received at least a component of the treatment) to evaluate the robustness of parameter estimation and statistical inference.

6.2. Multiple comparison adjustment

When multiple models or statistical tests are conducted on a single study, especially in biomarker research, one of the important issues is multiple comparison adjustments or multiplicity. Due to the large number of potential hypotheses and the discovery-based nature of such studies, investigators may be overwhelmed by the large number of potential analyses possible or become distracted by signals that may inflate false-positives. The multiplicity issues arising within cancer studies are classic problems in drug evaluation and have been heavily studied by regulatory agencies, pharmaceutical/biotech industries, and research institutes [79]. Statistical algorithms, such as the Bonferroni correction, and Hochberg procedure [80], referred to as multiplicity adjustment procedures (MAPs), have been developed based on the logic that multiplicity can be adjusted by applying more stringent criteria on type I error control.

7. Meta-analysis

Meta-analysis studies are a synthesis of pooled information from existing studies to draw statistics inference. Several types of meta-analyses exist: literature-based, IPD-based, and NMA. Many meta-analyses are derived from published literature, but these are vulnerable to publication bias, “file drawer” effect (i.e., never see the light of day), and variation in quality of separate studies related to methodology (including eligibility) and outcome assessment. In contrast, IPD is considered the gold standard which contains the data of each individual patient, but may not always be available due to confidential policy or data transfer issues, or logistical/operational costs. Finally, NMA summarizes relative treatment effects from independent trials which infers indirect treatment comparisons. However, indirect evidence should be interpreted with caution since it may be more susceptible to imbalanced stratification [81]. Notably, an important caveat when interpreting results for any meta-analyses is that historical migration (demographics, staging, and treatment techniques/systemic agents, etc.) may occur if trials are conducted over different eras.

8. Common statistical pitfalls

Common pitfalls are seen in the oncology literature including incomplete/inappropriate study design, mis-specified statistical models and tests, incomprehensible scientific reports, and tables and figures using incorrect formats. Additional drawbacks include unadjusted analysis of treatment effects without multivariable analysis, insufficient adjustment for baseline measurements, the use of covariates measured after the start of treatment, and composite response measures (Table 4). For longitudinal studies with repeated measurement over time, researchers should take into account all measurements instead of limiting analyses to baseline measures [82].

Table 4.

Common pitfalls in study design, analysis, and report.

Stage of the study	Type of pitfall	Consequence	Correction
Study design	Study population with exclusions and exclusions not described, initiation time of intervention not specified or consistent across the trial	Introduce bias into comparison and analysis	Clearly define study cohort and be mindful of potential lead time bias
	No sample size calculation and power analysis	Too few samples, or too low statistical power, or waste of resource	Conduct sample size calculation and power analysis before data collection
	No multiplicity adjustment	Sample size underestimated, or inflation of Type I error	Conduct multiple comparison adjustment using more stringent Type I error control
	No control group or inappropriate control group	Introduces bias into comparison and analysis	Identify matched control group
	No detailed statistical analysis plan in study design	Introduces bias or incorrect statistical test is used	Develop comprehensive statistical analysis plan
Statistical Modeling and Analysis	Incorrect statistical models and tests on study endpoints	Introduces bias, misleading results and incorrect conclusions	Carefully identify correct statistical models in statistical analysis plan
	No model assumption checking and model diagnosis	Inappropriate statistical models and tests are conducted	Carefully check model assumption and conduct model diagnosis
	Treating observations within the same patient as independent samples	Underestimate or overestimate within- subject variation, provide misleading results	Use appropriate statistical models to incorporate both within subject and between subject variations
	Use association tests (e.g., chi square test or linear regression) to evaluate agreement	Provide incorrect conclusion on agreement test	Conduct appropriate test on agreement such as kappa coefficient or correlation coefficient
	Use logistic regression on time-to-event outcomes	Ignores follow up time, provides misleading results and conclusions	Conduct survival analysis models on time to event outcomes
Statistical Report and Manuscript	Use categorization on continuous factor without discussion of cut-off selection	Provide incomplete information on study evaluation	Conduct exploratory analysis on different cut- offs, explore both continuous and categorized variable
	Use standard error to describe variability in a population	Standard error refers to the variability of parameter, but not for population	Provide standard deviation to describe variability in a population
	Use approximate p-values such as P < 0.05 or P > 0.05	Incomplete information	Provide exact p-values in the report
	Provide p-values without corresponding confidence interval	Incomplete information	Provide both p-value and corresponding confidence interval
	Provide odds ratio or hazard ratio without specifying reference category	Provide incomplete information and potential wrong association direction	Specify the reference group for both the comparison variable and outcome
	Indistinction between statistical significance and clinical significance	Draw conclusion only based on statistical significance	Draw conclusion based on both statistical and clinical significance
	Failure to report all the analyses that have been conducted and/or undertaking unplanned subset analysis	Potential misleading conclusions due to selection bias or fishing	Provide all the analysis results that have been conducted for the study including subgroup and sensitivity analysis
	“No-significance” refers to “no association” or “no effect”	Potential misleading conclusion due to small study or limited sample size	Report both p-values and parameter estimations, provide useful information for future meta-analysis
	Inappropriate use of graphs and tables	Provide misleading information and conclusion	Use appropriate graphs and tables to illustrate the analysis results
	Claiming superiority based on unplanned subgroup and interaction analysis	Over-interpretation and drawing conclusions based on exploratory analysis results Potential false positive inflation due to multiple comparisons	Restrict unplanned subgroup analysis to hypothesis generating Report interaction analysis results with ratio of HR

9. Conclusions

This paper provides an overview of statistical principles for clinical and translational research studies and demonstrates how proper study design and correctly specified statistical models are important for the success of cancer research studies. We emphasize the practical aspects of study design, and assumptions underpinning power calculations and sample size estimation. The differences between RR, OR, and HR, understanding outcome endpoints, and statistical modeling to minimize confounding effects and bias are also discussed. Finally, we describe commonly encountered statistical pitfalls that can be avoided by following correct statistical principles and guidance to improve the quality of research studies.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.