Abstract
Background
Optical coherence tomography (OCT) imaging is inherently susceptible to distortion artifacts due to the natural curvature of the eye. This study proposes a novel model for widefield OCT angiography (OCTA) distortion correction and analyzes the effects of this correction on quantification metrics.
Methods
Widefield OCTA images were obtained on normal subjects at five fixation spatial positions. Radial and field distortion correction were applied and images stitched together to form a corrected widefield montage image. Vessel area density (VAD), vessel complexity index (VCI), and flow impairment area were quantified on the original and corrected montage images.
Results
This model allows for distortion correction and montaging of widefield images. There were either statistically insignificant or small magnitude changes in vessel density and vessel complexity between uncorrected and corrected widefield images. There was a significant and large difference in flow impairment area, both in the macular (+8.2%, P=0.049) and peripheral areas (+17.2%, P=0.011), following correction. The relationship between pre- and post-correction flow impairment area was non-linear.
Conclusions
Distortion correction of widefield OCTA images can result in clinically and statistically significant differences in important quantification metrics. This effect appears to be most pronounced in the periphery.
Keywords: Optical coherence tomography angiography (OCTA), widefield imaging, montage, distortion correction, quantification metrics
Introduction
Optical coherence tomography (OCT) angiography (OCTA) has recently emerged as a means of acquiring rapid, non-invasive, depth-resolved images of the posterior segment vasculature (1,2). OCTA holds numerous advantages over traditional retinal visualization methods, such as fundus photography and fluorescein angiography (FA). One of the promises of OCTA is its ability to provide visualization and eventually quantification of the microvasculature. However, currently available OCTA technology also has several important limitations that prevent OCTA from fully assuming the diagnostic role of other imaging techniques. Chief among these limitations is the fact that, at present, OCTA cube images are restricted to at most 12×12 mm in size. Moreover, the 12×12 mm scan protocol is currently not widely available (3). For a larger field of view that approximates the images provided by fundus photography or FA, a montage technique can be used (4,5). In montage imaging, multiple images are taken with varying fixation targets. These individual images are then stitched together, using common overlapping features among them, to produce a final widefield image. In a previous case series, montage images were found to be comparable or superior to FA in detecting vascular abnormalities across a variety of pathologies (6).
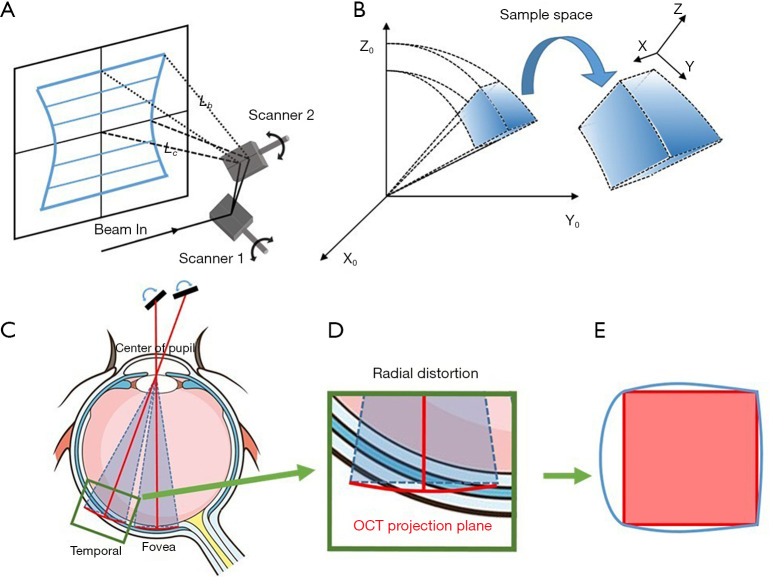
In general, a typical OCT system suffers from two types of distortion: field distortion and optical distortion (7). During OCT scanning, a pair of orthogonally arranged galvo-mirror scan at constant angular speeds that provide a two-way raster scan, so that the backscattering light from retinal tissue with the same optical path length as the reference optical length is recorded as a flat surface using a Cartesian coordinate system (Figure 1A). This introduces the fan-shape field distortion in 3D space (Figure 1B), the correction of which is well-described in the literature (8). However, when imaging the retina, another distortion will be created by the geometry of the eyeball; the curvature of the eye introduces the radial distortion when generating the en-face projection. The extent of radial distortion is determined by the distance from the scan (the pivotal point at the pupil plane) to the fovea and the axial length of the eye, as illustrated in Figure 1C. As the light spot moves from the fovea to the far peripheral region, the distortion increases due to the curvature of retina, as shown in Figure 1D (9). The radial arc length of the retina is longer than the length that is projected on the projection plane; therefore, the en-face images produced by the distorted 3D volumetric data result in 2D images with more significant distortion around the border (Figure 1E).
Figure 1.
Schematic of image acquisition in OCT system. (A) Setup of two-way OCT galvo-scanner, that provides a raster scan pattern of the OCT probe beam at the fundus. The scanner 1 facilitates the fast B-scan with a fixed maximum scanning angle (that determines the B-scan size), and the scanner 2 is driven to steer OCT beam moving in the orthogonal direction to the Scanner 1, providing 3D scan. The distance from center of the region to the scanner (Lc) is shorter than the distance from the border of the region to the scanner (Lb), thus the lengths of corresponding B-scans are not equal at each B-scan locations within the field of view, as shown by the blue lines; (B) the fan shape region in sample space (x0,y0,z0) is scanned by OCT system which is mapped to a data cube in a new Cartesian coordinate system (x,y,z) during data recording. This effect squeezes the pixels in deep retinal layers and stretches the pixels at the superficial retinal layer; (C) illustration shows that two OCT 3D scans are obtained in the foveal and peripheral regions that suffer from radial distortion. The effects of distortion depend on the radial location of the scans; (D) zoomed-in region of at the peripheral region shown in (C), the actual retina and OCT projection plane are not coincident; (E) the area inside the blue circle is the actual retina region scanned by the OCT, and the red area is the corresponding region recorded in the data cube. Note the illustrations are not to the scale. OCT, optical coherence tomography.
While these distortions may not be pronounced on small images, such as 3×3 or 6×6 mm scans, they become more relevant in scans that are larger than 12×12 mm. Radial distortion—a consequence of the en-face projection method that is widely used in ophthalmology—is particularly marked when imaging the far peripheral region of the retina, impacting the image quality and the morphology of the vascular networks. Montaged OCTA images are thus especially susceptible to these distortions as they are composed of multiple 12×12 mm scans, many of which are obtained from the periphery of the eye.
Moreover, the creation of montaged images requires registration of images, which depends on the overlapped regions between adjacent scans to ensure common information. Image distortion can compound difficulties in image registration, and different registration methods can in turn introduce additional image distortion. Correcting image distortion prior to registration may mitigate the effects of further distortion introduced by registration.
In clinical practice and for research purposes, image distortion introduces difficulties in quantification of images. With quantitative metrics from OCTA images increasingly finding clinical application (10), it is important to recognize and try to correct possible factors that can introduce variability into these measurements. Several distortion correction methods have been developed previous mainly based on Fermat’s principle, Podoleanu et al. used ray tracing method to correct the distortion on cross sectional OCT images (11). Ortiz et al. developed a numerical approach to correct the distortion on 3D anterior segments OCT (7). However, these methods required prior knowledge of the system and samples. Other methods have also been introduced that require calibration (8,12), which is generally not feasible for clinical applications. Thus, we propose a novel methodology which uses 12×12 mm OCTA en-face images to montage and then generate an extended field-of-view retinal image that incorporates correction of both field and radial distortion with minimum parameters.
Methods
This prospective study conformed to the Declaration of Helsinki and the Health Insurance Privacy and Portability Act and was approved by the Institutional Review Board at Tufts Medical Center.
Imaging protocol
Sixteen eyes from nine healthy participants (two females, seven males) were imaged. The mean age was 28.2 years. Participants had no to moderate myopia (0 to –7 D) with otherwise no ocular pathology. Axial length was measured in all participant eyes using a Carl Zeiss IOLMaster (Carl Zeiss Meditec AG, Jena, Germany). Five measurements were taken in each eye and then averaged to obtain a final axial length measurement.
Thirty minutes prior to imaging, all eyes were dilated using Tropicamide 0.5% ophthalmic solution. OCTA imaging was performed on the Carl Zeiss PLEX Elite 9000 swept-source OCTA prototype (Carl Zeiss Meditec, Dublin, CA, USA). The system is powered by a swept-source tunable laser that has a center wavelength of 1,060 nm, operating at 100,000 A-scans per second with an A-scan depth of 3.0 mm. The 12×12 mm OCTA scans were performed using the following nine fixation points, which were in-built into the device’s software: superonasal, superior, superotemporal, nasal, central (foveal), temporal, inferonasal, inferior, and inferotemporal. FastTrack motion correction software was used during image acquisition. Each 12×12 mm scan consisted of 500 A-scans per B-scan with two-time repeats before moving to the next sequential B-scan location, which results in a homogenous sampling grid with an A-scan and B-scan separation of 24 µm. Five 12×12 mm images were taken in each eye. Un-montaged images were exported individually for analysis.
Radial distortion correction
All image correction and analysis steps were performed using Matlab 2017b (Mathworks, Natick, MA, USA). To compensate for radial distortion, the approximate relative location of each single OCT scan and its angular scan range was first estimated by rough image stitching. The algorithm first calculated the Kaze features (i.e., identified by multiscale 2D feature detection and described in nonlinear scale spaces) on two images and then paired the common features between the scans in order to roughly stitch them together (13). The locations of the fovea and optic disc were then used as a reference to approximate the scanning angle for radial distortion correction. The compensation was based on the estimated distance from the off-axis angle to the fovea and the local curvature of eyeball.
The shape of the eyeball is approximated as a sphere and with the pivotal point of the scanning OCT beam at the center of the pupil (Figure 1C). The distortion correction model is described in Figure 2 in more detail, where the axial length of the eyeball is assumed to be 2R and the arbitrary scanning angle is θ, which is within the range of the field of view represented by Φ. The scanning interval between adjacent A-scans in the fast axis is dθ.
Figure 2.
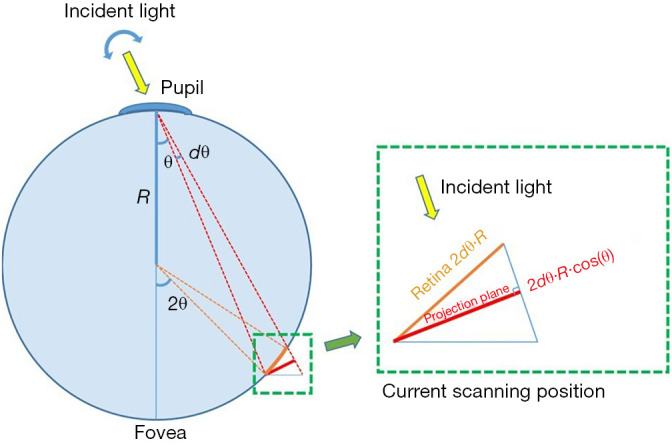
Geometric model for radial distortion correction. The axial length of eye ball is assumed to be 2R. At each scanning position θ, each small step of the scanning angle is dθ. At the scanning position (region inside the green dash line), the retina plane on the sphere (orange line) is projected to the plane that is perpendicular to the incident light (red line) for recording. Therefore, the actual length of the retina is not correctly represented in the data cube. The accumulation of this error causes the radial distortion. Note drawings are not to the scale.
The correction ratio, Ld(λ), for every pixel from the center of the fovea to the current angular scanning location λ can be integrated by:
| [1] |
For stitching the final widefield image, the calculated correction ratio Ld for each pixel was used to re-map that pixel into its original location in 3D. The numerator represents the real arc length from the fovea to the current scanning location and the denominator is the length on the projection plane. After this procedure was completed for all the pixels, the en-face 2D image was then obtained by projection to minimize the distortion for better visualization. We modified the concept of the azimuthal equidistant projection on a sphere to ensure that all points on the corrected image are at the correct azimuth from the fovea, and that the distances from the fovea represented correctly (14).
Field distortion correction
To correct the field distortion, the working distance, scanning angle and the axial length of eye were recorded and then used to calculate the transformation matrix, as described previously (8). Briefly, we first built a 3D matrix based on the size of the image and the estimated parameters above. Then, each pixel in the 2D image was re-sampled and transformed to a sphere surface in the 3D matrix. The coordinates in the 3D matrix were then transferred to the original physical space as the fan shape volume in Figure 1B. Finally, the fan shape images were projected to a natural space to minimize the field distortion.
Image stitching
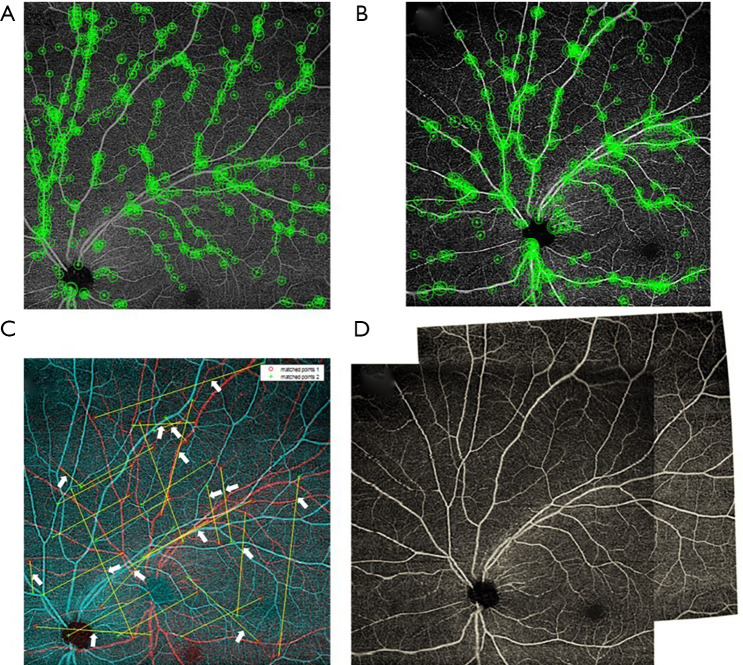
After compensating for distortion, all individual images were stitched together using a feature-based image stitching method. The algorithm starts with a two-image pair with relatively larger overlapping areas. The overall signal strength is calculated on each image to compensate and normalize the inhomogeneous illuminance of the vessel. The scale, corner, and the invariant features are calculated on the images (Figure 3A,B) and are further paired by the random sample consensus (RANSAC) method (Figure 3C) (15). The affine and B-spline transformation are calculated by the paired feature points. After transformation, the overlapping areas are blended between the two images (Figure 3D). We perform the two-image registration process iteratively until the five images were registered together as a single widefield image.
Figure 3.
Image registration and montaging procedure. (A,B) The KAZE feature points on two individual images are identified, represented by green circle cross symbols; (C) feature points on the two images (displayed in red and cyan colors respectively) are paired, represented by connected lines. Then RANSAC algorithm is used to reject the outlier of matched pairs, e.g., those pointed by the white arrows. The spatial transformation matrix is calculated by the remaining paired and matched points; (D) the final images are finally registered and stitched together to form a montage image. RANSAC, random sample consensus.
Quantitative analysis
To quantitatively analyze the influence of distortion, we applied our previously-described MATLAB-based algorithm to calculate quantification metrics (16-19). The vessel area density (VAD), flow impairment area, and vessel complexity index (VCI) were calculated on the corrected and uncorrected widefield en-face OCTA images. VAD describes the percentage of the image occupied by flow information, i.e., the percentage of the vessel area in the entirety of binarized image. Flow impairment area is calculated from vessel skeleton map as the non-perfusion area between vessels. Finally, VCI describes the degree of branching in vessels.
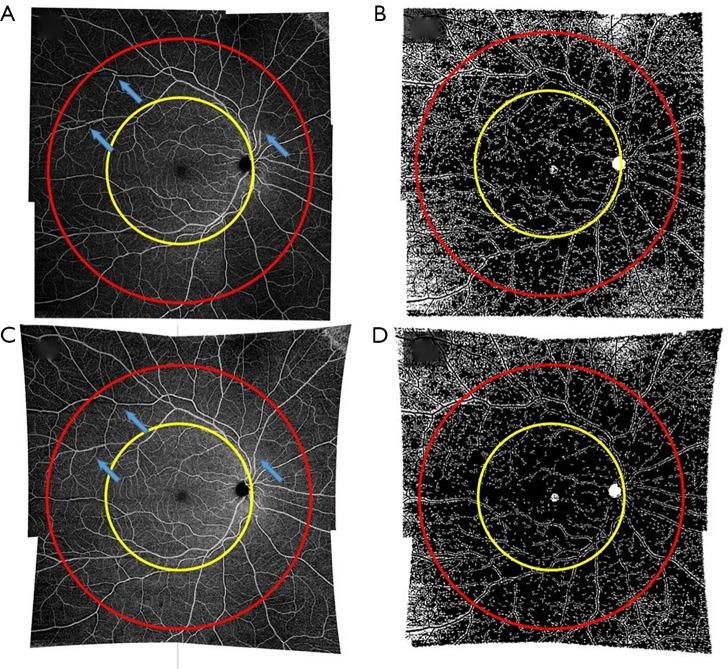
The images (Figure 4) were divided into a macular and peripheral region (Figure 4A,C), and the corresponding flow impairment areas are extracted (Figure 4B,D). The macular region was defined by a circle with a radius r equivalent to the distance between the central macula and the optic disc. The peripheral region was defined by a concentric circle with a radius of 1.8r. Image areas outside of the circle were excluded from further quantification due to low image quality caused by vignetting, focusing issue and aberrations.
Figure 4.
Example of quantitative analyses on macular and peripheral regions. Five 12×12 mm images were acquired with the following fixation points: central, superonasal, superotemporal, inferonasal, and inferotemporal, which were used for montaging to form a wide field of view composite image. (A) The montaged image of the uncorrected images. Blue arrows show the registration error due to the distortion; (B) the flow impairment map of (A); (C) the montaged image of corrected images. Blue arrows show better connection of vessels; (D) the flow impairment map of (C). The macular region (yellow circle) is selected by the center of fovea and the ONH with radius r, and the peripheral region (red circle) is defined with radius 1.8r. ONH, optic nerve head.
The Wilcoxon matched-pairs signed-rank test for non-normal data was used to compare metrics in the peripheral and macular region before and after image correction. Statistical analysis was performed using StataSE v15.1 (StataCorp, College Station, Texas, USA). The procedures for distortion correction and image quantification are summarized in Figure 5.
Figure 5.
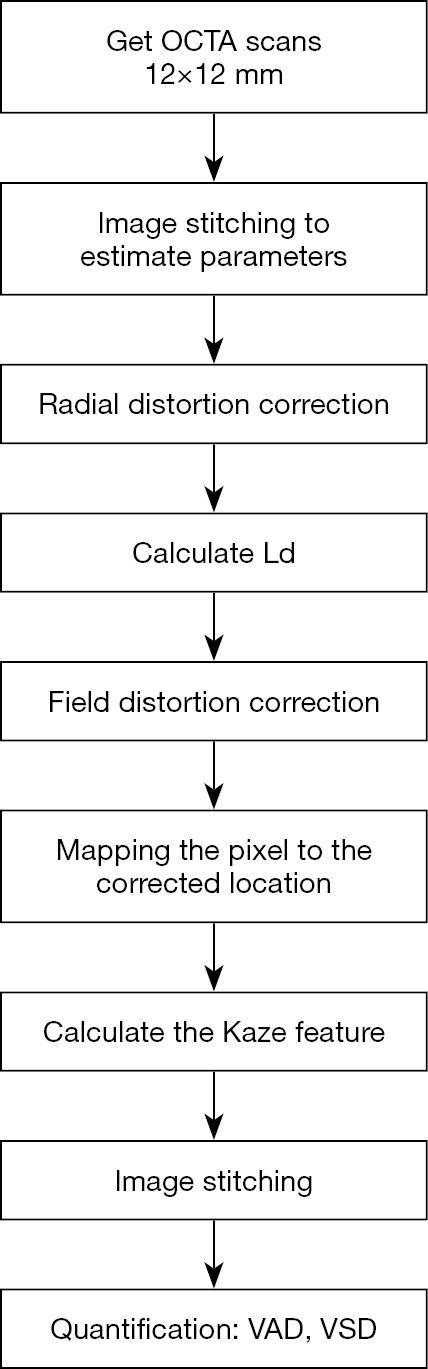
Flow chart describing the procedure for distortion correction and image quantification. OCTA, optical coherence tomography angiography; VAD, vessel area density; VSD, vessel skeleton density.
Results
The changes in metrics before and after image correction in the macular and peripheral regions are shown in Table 1.
Table 1. Average measurements by region, before and after image correction.
| Vessel density | Flow impairment area | Vessel complexity | ||||||
|---|---|---|---|---|---|---|---|---|
| Macular | Peripheral | Macular | Peripheral | Macular | Peripheral | |||
| Before correction | 0.503±0.018 | 0.491±0.025 | 0.089±0.036 | 0.147±0.067 | 4.755±0.477 | 4.476±0.418 | ||
| After correction | 0.504±0.019 | 0.493±0.024 | 0.096±0.039 | 0.172±0.086 | 4.697±0.472 | 4.266±0.423 | ||
| Change (%) | 0.1 | 0.2 | 8.2 | 17.2 | –1.2 | –4.7 | ||
| P value | 0.020 | 0.134 | 0.049 | 0.011 | 0.0004 | 0.0004 | ||
Vessel density changed very slightly before and after correction in the macular and peripheral region. Although the change in the macular region was statistically significant (P=0.02), the magnitude of the absolute change was so small (+0.1%) so as to not be clinically significant. The change in the peripheral region was also quite small and not statistically significant. There was a strong linear relationship in both the macular (R2 =0.983) and peripheral (R2 =0.9992) regions between the uncorrected and corrected vessel density values.
The average flow impairment area changed to a significant degree before and after correction, especially in the peripheral region (+17.2%, P=0.011). In the macular region, there was a strong linear relationship between pre-correction and post-correction flow impairment area (R2 =0.8894). However, the linearity was not as strong in the peripheral region (R2 =0.7579).
The average vessel complexity decreased in both regions following correction, from 4.76 to 4.70 in the macular region and from 4.48 to 4.27 peripherally. These changes were both statistically significant but also small in magnitude (<5%). There was a strong linear relationship between pre- and post-correction vessel complexity in the peripheral and macular regions (R2 =0.9957 and 0.9973, respectively).
Discussion
As the quality and acquisition speed of images produced by commercial OCTA devices continues to improve, widefield angiography imaging is becoming more common in clinical practice. The PLEX Elite device, as with some others, already has automatic montaging software, which can montage five 12×12 mm images with varying fixation points into a single widefield image on the device itself. Ensuring correct presentation of vasculature on widefield montage images is thus increasingly important. Our model is able to estimate the location of a single scan, apply distortion correction, and precisely stitch together single scans into one ultra-widefield montage image.
It is inevitable to introduce distortion when performing projections from a 3D spherical eyeball to a 2D flat surface. The field distortion of a single scan creates a mismatch in the overlapping region between adjacent scans. Distortion correction may benefit the quality of image registration, especially on the border area of the peripheral images. The projection model we applied in this approach is modified from the azimuthal equidistant projection approach. It maintains proportionately correct distances from the central fovea to far peripheral region for ultra-widefield retinal images. A similar approach could be applied to other map projections, such as equidistant or equal-area, to satisfy different goals.
In one prior study on correction of OCT images for eye curvature, Kuo et al. applied a radial correction to spectral domain-OCT B-scans in order to take into account the curvature of the posterior eye (20). They compared metrics from the uncorrected and corrected images to dimensions obtained from magnetic resonance imaging (MRI) scans of the eye. Correction of the OCT images resulted in less variable eye radius curvature values that were closer to those from the reference MRI images. Image correction did not, however, result in a significant change in retinal thickness measurements. The effects of image distortion on quantitative metrics thus may be more relevant in en-face OCT scans, such as those produced by OCTA, than in cross-sectional B-scans.
The prior literature examining correction of widefield ophthalmic imaging has focused largely on fundus photographs and FA images. In a 2016 study, Tan et al. used a stereographic, rather than the conventional azimuthal, projection for ultrawide-field FA images (21). Stereographic projections preserve shape and angle, but do not accurately preserve area information. Tan et al. found non-significant difference in non-perfusion area between the uncorrected and corrected images. Spaide applied a different projection technique, the Lambert azimuthal equal-area projection, which does preserve areas accurately but does not accurately display angles (22). To our knowledge, this methodology is the first that incorporates radial and projection distortion correction into registration of widefield montage OCTA images.
In the present study, the changes in vessel complexity and vessel density were either not statistically significant or were so small in magnitude so as to be clinically insignificant. However, there was a larger degree of change in vessel flow impairment area between uncorrected and corrected montage images. Although both vessel density and flow impairment area increased with correction, primarily due to image stretching, this increase was not equal likely because of variations in the degree of stretching applied to flow and non-flow areas, and different methods to quantify these variables. Flow impairment quantification in widefield OCTA images is increasingly being applied, particularly in studies of diabetic retinopathy, highlighting the importance of considering how distortion correction may affect these metrics (1). This effect was more pronounced peripherally, which is consistent with the greater degree of distortion that occurs in peripheral scans. This finding is particularly relevant in the imaging of diseases, such as diabetic retinopathy, that may present early with peripheral lesions, including neovascularization, microaneurysms, and nonperfusion.
Our results further reveal that the changes in vessel complexity and vessel density were small in magnitude and maintain a very good linear relationship with the original images. The corrected images were locally stretched or compressed as compared to the original images, causing the vessel area to be scaled by the same factor. Thus, the VAD only changed by a small magnitude. The distortion correction did not change the morphological shape of the vessel as the VCI change was also small. To calculate the flow impairment area, our algorithm excludes small discontinuous non-flow areas on the binary vessel map in order to avoid including physiologic non-perfusion areas between capillaries; consequently, the radial distortion did influence calculation of the flow impairment area, especially in the peripheral region.
Generally, the changes in the quantification parameters post-correction can be expressed by a Taylor expression as below:
| [2] |
As the changes in the parameters Δs are small, the high order term of the expression can be ignored. The changes of parameters then followed a linear approximation:
| [3] |
Thus, the small changes in VAD and VCI resulted from a relatively linear relationship (Figures 6,7). However, the changes in flow impairment area were relatively large as they were the result of more non-linear effects (Figure 8).
Figure 6.
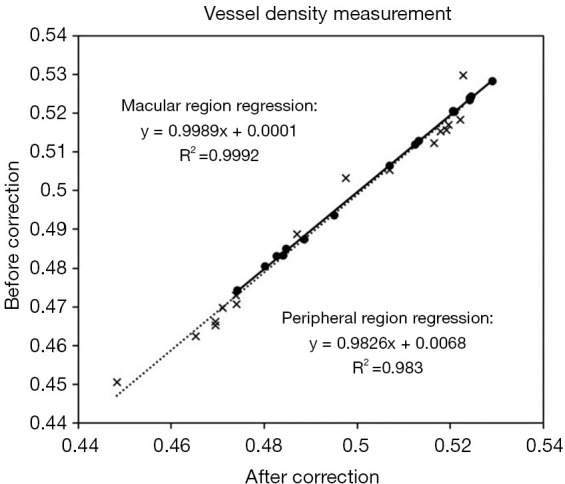
Relationship between before- and after-correction VAD, where the symbols “•” denotes the values from macular region, and “×” from peripheral region, respectively. The solid and dashed lines denote linear regression lines of the macular and peripheral measurements, respectively. VAD, vessel area density.
Figure 7.
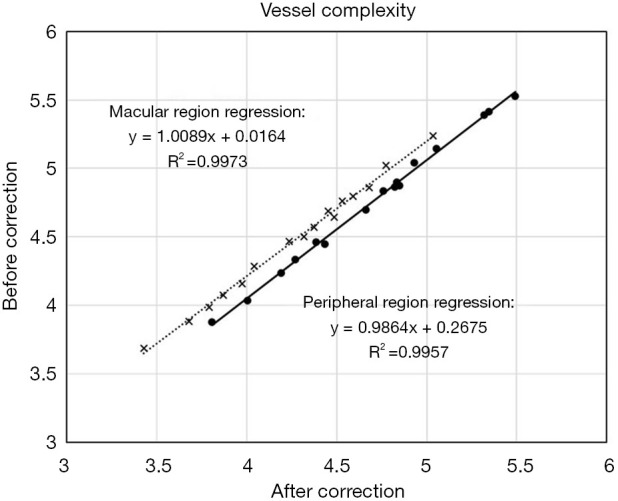
Relationship between before- and after-correction vessel complexity, where the symbols “•” denotes the values from macular region, and “×” from peripheral region, respectively. The solid and dashed lines denote linear regression lines of the macular and peripheral measurements, respectively.
Figure 8.
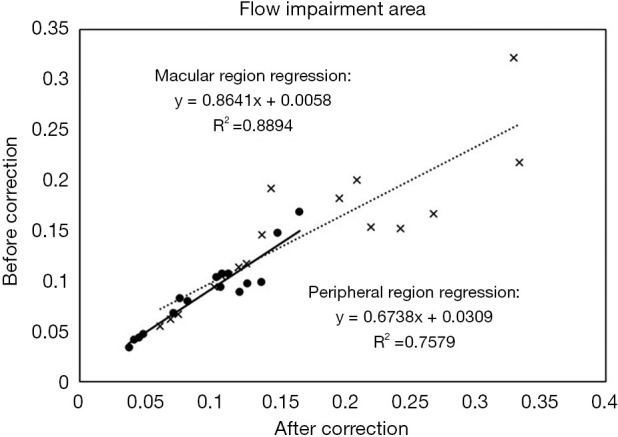
Relationship between before- and after-correction flow impairment area, where the symbols “•” denotes the values from macular region, and “×” from peripheral region, respectively. The solid and dashed lines denote linear regression lines of the macular and peripheral measurements, respectively.
There were several limitations in our study. In some cases, the most peripheral areas of the scan could not be well-visualized due to eye curvature exceeding the visualized window within the depth of the OCT scan. However, we limited our analysis to a portion of the image defined by a 1.8r circle; as a result, the most distorted peripheral regions were not included. In addition, peripheral areas with low signal strength may have impacted quantification. Finally, we restricted our analysis to normal eyes. The effects of distortion correction may be different in imaging of pathologic eyes, particularly for diseases that cause significant peripheral vascular changes. This study’s strengths include our algorithm’s multifaceted approach to image correction, as well as the inclusion of eyes with varying axial lengths—mirroring the makeup of the general population and allowing our analysis to incorporate varying degrees of eye curvature.
Further research is needed to better understand the optimal approach for image correction in widefield imaging, and the impact that image correction has on quantitative metrics relevant for clinical and research practice.
Conclusions
Correction of widefield montage OCTA images for field and radial distortion, as well as precise image stitching, resulted in non-significant or small changes in vessel density and vessel complexity, but a significant change in flow impairment area, which was more pronounced peripherally than centrally.
Acknowledgments
Funding: This study was funded by Macula Vision Research Foundation (West Conshohocken, PA, USA), the Massachusetts Lions Clubs (Belmont, MA, USA), the National Institutes of Health (grant number 5-R01-EY011289-31), the Air Force Office of Scientific Research (grant number FA9550-15-1-0473), the Champalimaud Vision Award (Lisbon, Portugal), the Beckman-Argyros Award in Vision Research (Irvine, CA, USA), Carl Zeiss Meditec, Inc. (Dublin, CA, USA), Research to Prevent Blindness (New York, NY, USA), and the National Eye Institute (R01-EY028753).
Ethical Statement: This prospective study conformed to the Declaration of Helsinki and the Health Insurance Privacy and Portability Act and was approved by the Institutional Review Board at Tufts Medical Center.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
Footnotes
Provenance and Peer Review: With the arrangement by the editorial office, this article has been reviewed by external peers.
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-791). The special issue “Advanced Optical Imaging in Biomedicine” was commissioned by the editorial office without any funding or sponsorship. RKW served as the unpaid Guest Editor of the special issue and serves as an unpaid Deputy Editor of Quantitative Imaging in Medicine and Surgery. JD reports grants from National Institutes of Health, grants and non-financial support from Carl Zeiss Meditec Inc, grants from Air Force Office of Scientific Research, grants from Champalimaud Vision Award, non-financial support from Topcon Medical Systems, Inc., non-financial support from Optovue, Inc., during the conduct of the study. RKW reports grants from National Institutes of Health, grants and non-financial support from Carl Zeiss Meditec Inc, grants from Research to Prevent Blindness, during the conduct of the study. NKW reports grants from National Institutes of Health, grants and non-financial support from Carl Zeiss Meditec Inc, grants from Research to Prevent Blindness, grants from Air Force Office of Scientific Research, grants from Champalimaud Vision Award, grants and non-financial support from Macula Vision Research Foundation, grants from Beckman-Argyros Award in Vision Research, non-financial support from Topcon Medical Systems, Inc., non-financial support from Nidek Medical Products, Inc., non-financial support from Optovue, Inc., during the conduct of the study. The other authors have no other conflicts of interest to declare.
References
- 1.Kashani AH, Chen CL, Gahm JK, Zheng F, Richter GM, Rosenfeld PJ, Shi Y, Wang RK. Optical coherence tomography angiography: a comprehensive review of current methods and clinical applications. Prog Retin Eye Res 2017;60:66-100. 10.1016/j.preteyeres.2017.07.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chen CL, Wang RK. Optical coherence tomography based angiography [Invited]. Biomed Opt Express 2017;8:1056-82. 10.1364/BOE.8.001056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.de Carlo TE, Romano A, Waheed NK, Duker JS. A review of optical coherence tomography angiography (OCTA). Int J Retina Vitreous 2015;1:5. 10.1186/s40942-015-0005-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhang Q, Lee CS, Chao J, Chen CL, Zhang T, Sharma U, Zhang A, Liu J, Rezaei K, Pepple KL, Munsen R, Kinyoun J, Johnstone M, Van Gelder RN, Wang RK. Wide-field optical coherence tomography based microangiography for retinal imaging. Sci Rep 2016;6:22017. 10.1038/srep22017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhang Q, Huang Y, Zhang T, Kubach S, An L, Laron M, Sharma U, Wang RK. Wide-field imaging of retinal vasculature using optical coherence tomography-based microangiography provided by motion tracking. J Biomed Opt 2015;20:066008. 10.1117/1.JBO.20.6.066008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.de Carlo TE, Salz DA, Waheed NK, Baumal CR, Duker JS, Witkin AJ. Visualization of the retinal vasculature using wide-field montage optical coherence tomography angiography. Ophthalmic Surg Lasers Imaging Retina 2015;46:611-6. 10.3928/23258160-20150610-03 [DOI] [PubMed] [Google Scholar]
- 7.Ortiz S, Siedlecki D, Grulkowski I, Remon L, Pascual D, Wojtkowski M, Marcos S. Optical distortion correction in optical coherence tomography for quantitative ocular anterior segment by three-dimensional imaging. Opt Express 2010;18:2782-96. 10.1364/OE.18.002782 [DOI] [PubMed] [Google Scholar]
- 8.Wang D, Liang P, Samuelson S, Jia H, Ma J, Xie H. Correction of image distortions in endoscopic optical coherence tomography based on two-axis scanning MEMS mirrors. Biomed Opt Express 2013;4:2066-77. 10.1364/BOE.4.002066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lee S, Reinhardt JM, Cattin PC, Abràmoff MD. Objective and expert-independent validation of retinal image registration algorithms by a projective imaging distortion model. Med Image Anal 2010;14:539-49. 10.1016/j.media.2010.04.001 [DOI] [PubMed] [Google Scholar]
- 10.Cheung CMG, Wong TY. Clinical use of optical coherence tomography angiography in diabetic retinopathy treatment: ready for showtime? JAMA Ophthalmol 2018;136:729-30. 10.1001/jamaophthalmol.2018.1538 [DOI] [PubMed] [Google Scholar]
- 11.Podoleanu A, Charalambous I, Plesea L, Dogariu A, Rosen R. Correction of distortions in optical coherence tomography imaging of the eye. Phys Med Biol 2004;49:1277-94. 10.1088/0031-9155/49/7/015 [DOI] [PubMed] [Google Scholar]
- 12.Van der Jeught S, Buytaert JAN, Bradu A, Podoleanu AGH, Dirckx JJJ. Real-time correction of geometric distortion artefacts in large-volume optical coherence tomography. Meas Sci Technol 2013;24:057001 10.1088/0957-0233/24/5/057001 [DOI] [Google Scholar]
- 13.Alcantarilla PF, Bartoli A, Davison AJ. KAZE Features. In: Fitzgibbon A, Lazebnik S, Perona P, Sato Y, Schmid C. editors. Computer Vision - ECCV 2012. Heidelberg: Springer, 2012:214-27. [Google Scholar]
- 14.Snyder JP. Map projections: A working manual. Washington, D.C.: U.S. Government Printing Office, 1987. Available online: http://pubs.er.usgs.gov/publication/pp1395 [Google Scholar]
- 15.Fischler MA, Bolles RC. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Commun ACM 1981;24:381-95. 10.1145/358669.358692 [DOI] [Google Scholar]
- 16.Chu Z, Lin J, Gao C, Xin C, Zhang Q, Chen CL, Roisman L, Gregori G, Rosenfeld PJ, Wang RK. Quantitative assessment of the retinal microvasculature using optical coherence tomography angiography. J Biomed Opt 2016;21:66008. 10.1117/1.JBO.21.6.066008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Reif R, Qin J, An L, Zhi Z, Dziennis S, Wang R. Quantifying optical microangiography images obtained from a spectral domain optical coherence tomography system. Int J Biomed Imaging 2012;2012:509783. 10.1155/2012/509783 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ganjee R, Moghaddam ME, Nourinia R. Automatic segmentation of abnormal capillary nonperfusion regions in optical coherence tomography angiography images using marker-controlled watershed algorithm. J Biomed Opt 2018;23:1-16. 10.1117/1.JBO.23.9.096006 [DOI] [PubMed] [Google Scholar]
- 19.Koulisis N, Moysidis SN, Yonekawa Y, Dai YL, Burkemper B, Wood EH, Lertjirachai I, Todorich B, Khundkar TZ, Chu Z, Wang RK, Williams GA, Drenser KA, Capone A, Jr, Trese MT, Nudleman E. Correlating changes in the macular microvasculature and capillary network to peripheral vascular pathologic features in familial exudative vitreoretinopathy. Ophthalmol Retina 2019;3:597-606. 10.1016/j.oret.2019.02.013 [DOI] [PubMed] [Google Scholar]
- 20.Kuo AN, McNabb RP, Chiu SJ, El-Dairi MA, Farsiu S, Toth CA, Izatt JA. Correction of ocular shape in retinal optical coherence tomography and effect on current clinical measures. Am J Ophthalmol 2013;156:304-11. 10.1016/j.ajo.2013.03.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tan CS, Chew MC, van Hemert J, Singer MA, Bell D, Sadda SR. Measuring the precise area of peripheral retinal non-perfusion using ultra-widefield imaging and its correlation with the ischaemic index. Br J Ophthalmol 2016;100:235-9. 10.1136/bjophthalmol-2015-306652 [DOI] [PubMed] [Google Scholar]
- 22.Spaide RF. Peripheral areas of nonperfusion in treated central retinal vein occlusion as imaged by wide-field fluorescein angiography. Retina 2011;31:829-37. 10.1097/IAE.0b013e31820c841e [DOI] [PubMed] [Google Scholar]