Abstract
In this work, we propose a deep learning framework for the classification of COVID-19 pneumonia infection from normal chest CT scans. In this regard, a 15-layered convolutional neural network architecture is developed which extracts deep features from the selected image samples – collected from the Radiopeadia. Deep features are collected from two different layers, global average pool and fully connected layers, which are later combined using the max-layer detail (MLD) approach. Subsequently, a Correntropy technique is embedded in the main design to select the most discriminant features from the pool of features. One-class kernel extreme learning machine classifier is utilized for the final classification to achieving an average accuracy of 95.1%, and the sensitivity, specificity & precision rate of 95.1%, 95%, & 94% respectively. To further verify our claims, detailed statistical analyses based on standard error mean (SEM) is also provided, which proves the effectiveness of our proposed prediction design.
Keywords: COVID19, Data Collection, Deep Learning, Features Fusion, Features Selection, ELM Classifier
1. Introduction
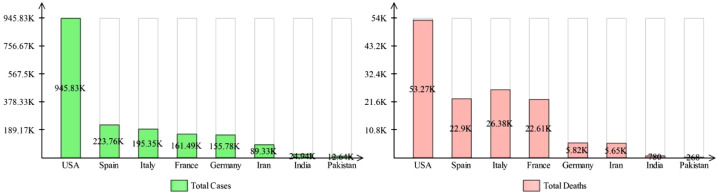
Initially started in the Wuhan city of China in December 2019, SARS-CoV-2 has spread globally with a considerable ratio. Up till 20th May 2020, approximately 5 million cases are reported worldwide in which active cases are around 2.7 million, and the total number of registered deaths are 327,398. From [1], it is noticed that 97% of the patients are having mild symptoms, whilst 3% of cases are critical. A summary of COVID19 cases in different countries are provided in Table 1 . Stats show the critical picture of COVID-19 cases, where it can be observed that the USA is highly affected, compared to other countries. In the USA alone, the total diagnosed cases are 945,833 and total deaths reported are 53,266. Still, the active cases are 781,733 and from them 15,100 are critical. In Spain, the total diagnosed cases are 223,759, total deaths are 22,902, and total recovered cases are 110,834. The active cases in Spain are 105,149, and total critical cases are 7,705. Italy is also adversely affected by this virus and total diagnosed cases are 195,351. The infection is following the same trend in other countries such as France and Germany, where the confirmed cases are 161,488 and 155,782, respectively. In Asian countries like Iran, India, and Pakistan, this virus is rapidly growing and confirm cases are 89,328, 24,942, and 12,644, respectively [1]. The variation in the reported cases of different countries is plotted as a bar chart in Fig. 1 .
Table 1.
| Country | Total Cases | Total Deaths | Total Recovered | Active Cases | Critical Cases | Deaths (Per Million of Population) |
|---|---|---|---|---|---|---|
| USA | 945,833 | 53,266 | 110,834 | 781,733 | 15,100 | 161 |
| Spain | 223,759 | 22,902 | 95,708 | 105,149 | 7,705 | 490 |
| Italy | 195,351 | 26,384 | 63,120 | 105,847 | 2,102 | 436 |
| France | 161,488 | 22,614 | 44,594 | 94,280 | 4,725 | 346 |
| Germany | 155,782 | 5,819 | 109,800 | 40,163 | 2,908 | 69 |
| Iran | 89,328 | 5,650 | 68,193 | 15,485 | 3,096 | 67 |
| India | 24,942 | 780 | 5,498 | 18,664 | - | 0.6 |
| Pakistan | 12,644 | 268 | 2,755 | 9,621 | 111 | 1 |
Fig. 1.
Histogram of registered cases & the total number of deaths for the selected countries. (26 April, 2020) [1]
The COVID-19 is spreading quickly around the globe, and most of the countries are not having an adequate number of resources to handle this large number [2]. Therefore, timely diagnostics are required to identify patients with COVID-19. At present, the nucleic acid amplification test (NAAT) such as RT-PCR (reverse transcription-polymerase chain reaction) is used for the early detection of the infection [3]. The RT-PCR is a time-consuming clinical test which requires trained individuals. The manual prediction of COVID19 pneumonia cases is difficult and time-consuming; therefore, an automated system is required [4]. In this regard, several researchers proposed novel techniques for COVID19-pneumonia detection [5, 6]. Ali et al. [7] presented a CNN based system for the detection of COVID19 infection using X-ray images. They employed three different CNN architectures (ResNet50, Inception-ResNetV2, and Inception V3) for feature extraction. Afterward, the trained architecture on X-ray data detects the COVID19 - pneumonia patients. They analyzed the results based on the ROC and confusion matrix and showed that the ResNet50 model gives an improved performance of 98%. Biraja et al. [8] presented a deep learning model for COVID19 infection detection based on uncertainty. For this purpose, they proposed a drop-weights CNN model which improved the diagnostic performance using X-ray images. Based on the performance of a drop-weights CNN model, they concluded that the presented method is extremely effective under the current conditions. Parnian et al. [9] presented a capsule network based model for COVID-19 prediction from the X-ray images. The capsules in the presented framework are useful to handle a small dataset, which makes the framework quite effective for the applications with limited data resources available. This model achieved an accuracy of 95.7% along with a sensitivity rate of 90% for COVID19 data identification from chest X-ray images. Rajinikanth et al. [10] presented a firefly based evolutionary framework equipped with the Shannon entropy-based algorithm for the salient region detection, which is later extracted using Markov-random field segmentation. They compared the proposed results with the given ground truth images and achieved a mean accuracy of above 92%. Yujin et al. [11] presented a patch-based CNN framework for COVID19 features extraction. They utilized chest X-ray images to train a CNN model to achieving the best results. Rodolfo et al. [12] presented a classification scheme of COVID19 pneumonia and healthy chest CT scans. They presented a hierarchical framework for feature extraction, fusion, and classification. The raw features are extracted by following the CNN framework, which are later fused to improve the feature information to achieving F1-Score of 89%. Shui et al. [13] played their role in extracting the visual features from the CT scans, which help the doctors to diagnose the COVID-19. They used 453 confirmed COVID19 patients’ images for testing and achieved 73.1% testing efficiency. Zhang et al. [14] developed software in which they first used U-Net for the infectious region segmentation, and then provided the segmented region to 3D CNN model for the probability prediction of COVID19. They believe that this system will help to predict the infection.
To classify the COVID-19 pneumonia chest CT scans from the normal is rather a complicated procedure due to a set of challenges. The COVID19 - pneumonia symptoms are visible to the naked eye but it's hard to predict using the machine learning methods. Therefore, quality training and robust algorithms are required for improved accuracy. In the medical domain, state-of-the-art ML techniques exist, which worked exceptionally for different kinds of problems [15], [16], [17], [18]. However, COVID19-pneumonia is diagnosed using chest CT scans, which are collected from 10 patients [19], [20], [21], [22], [23], [24]. The healthy samples are also collected to train the model under all possible scenarios [25]. The main contributions of this work are as follows:
-
i
An imaging database is compiled from the Radiopaedia website - comprising both COVID-19 pneumonia and healthy chest CT scans. The image samples are collected from 10 patients who are diagnosed positive for COVID-19.
-
ii
A 15-layered CNN model is designed which includes two convolutional layers, two max-pooling layers, one global average pool and two fully connected (FC) layers. The convolutional filter is initialized as (2 × 2), whereas the max-pool filter size is (2 × 2) and (3 × 3), respectively.
-
iii
A fusion methodology is opted to fuse deep features extracted from the global average pool layer and FC layer using max-layer detail method.
-
iv
A Correntropy based feature selection criterion is also designed, which is having reliability and time advantages compared to several other meta-heuristic techniques.
The rest of the manuscript is organized as follows. The proposed methodology is presented in Section 2, and detailed results are presented in Section 3. Finally, Section 4 concludes the findings.
2. Proposed Methodology
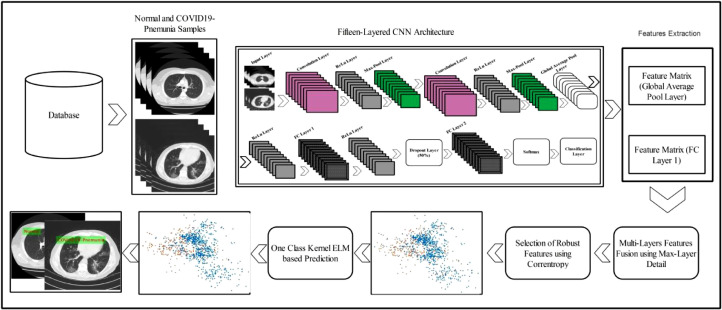
A deep learning based method is presented in this work for the classification of COVID19-pneumonia and normal chest CT scans. The presented method consists of five primary steps. In the first step, data is collected from the Radiopaedia website. Using this data, a 15-layered CNN architecture is implemented in the second step. Feature extraction and fusion are performed in the third step, followed by the selection process in the fourth step. Finally, the selected features are passed to One-Class Kernal ELM for the final classification. Fig. 2 demonstrates each step in detail. 2.
Fig. 2.
Proposed framework: deep learning features based prediction of COVID19-pneumonia and normal chest CT scans
2.1. Database Preparation
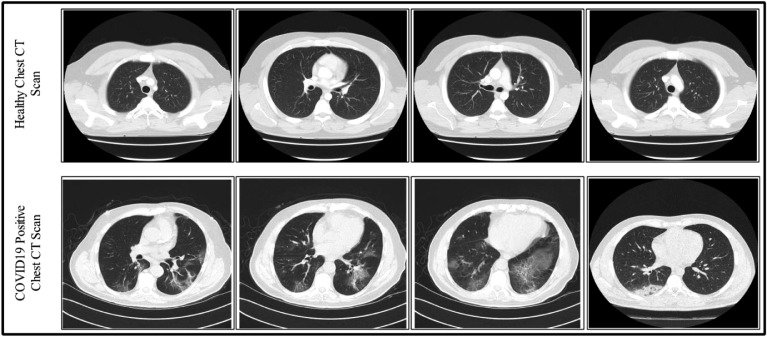
We collected 10 cases of positive COVID19- Pneumonia Chest CT Scans from RadioPaedia [3]. The selected cases are- case 1 (https://radiopaedia.org/cases/covid-19-pneumonia-2), case 3 (https://radiopaedia.org/cases/covid-19-pneumonia-3), case 4 (https://radiopaedia.org/cases/covid-19-pneumonia-4), case 5 (https://radiopaedia.org/cases/covid-19-pneumonia-7), case 8 (https://radiopaedia.org/cases/covid-19-pneumonia-8), case 15 (https://radiopaedia.org/cases/covid-19-pneumonia-23), case 18 (https://radiopaedia.org/cases/covid-19-pneumonia-10), case 20 (https://radiopaedia.org/cases/covid-19-pneumonia-27), case 24 (https://radiopaedia.org/cases/covid-19-pneumonia-36), and case 25 (https://radiopaedia.org/cases/covid-19-pneumonia-38). All these ten cases belong to ten different patients and their RT-PCR COVID-19 test was positive. Based on this, patients considered as COVID19-pneumonia. The patient's history is also provided in the given websites with their detailed traveling history. Similarly, we also collected a few healthy Chest CT Scan data to train a CNN model [26]. A few sample images are shown in Fig. 3 . In this figure, the top row shows healthy/normal scans and the bottom row shows the COVID19-pneumonia images. For training a model, a total of 1500 COVID19-pneumonia and 1300 normal Chest CT Scans are collected from above-given links. All images are resized into 512 × 512.
Fig. 3.
Sample images of COVID19-pneumonia and normal chest CT Scans
2.2. Fifteen-Layered CNN Model
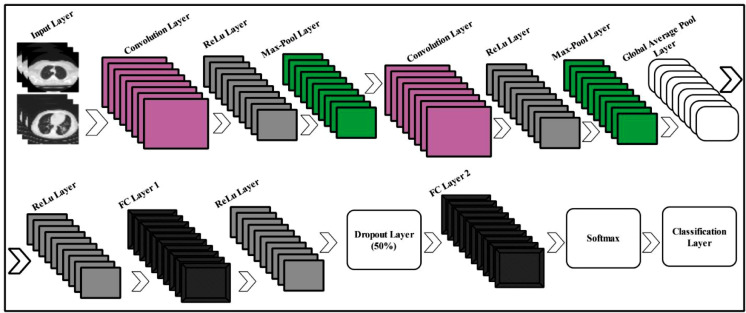
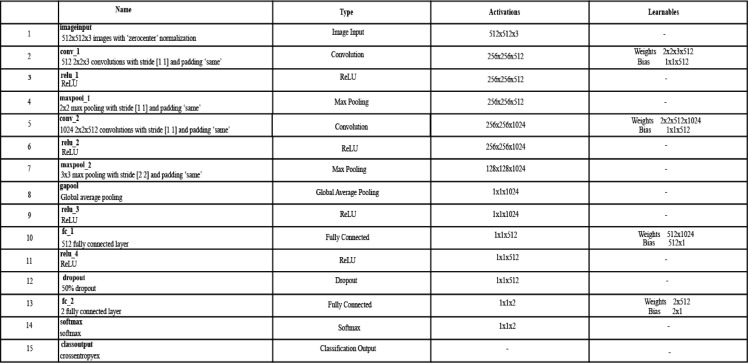
Convolutional Neural Networks (CNN) have received huge attention from the machine learning community due to its capacity to solve complex classification problems [27]. In medical imaging, CNNs performed exceptionally for various problems [28]. For the infected region, complete knowledge is essential, so that a relevant label is assigned. However, due to textural and color variations, the classification task becomes more complex [29]. However, deep methods came with the property of extracting relevant information, and also have a tendency to learn from the complex features. Inspired from the deep methods, we propose a 15-layered CNN architecture for feature extraction. The designed CNN architecture includes two convolutional layers along with ReLu layers, two max-pooling layers, one global average pool layer, 2 fully connected layers, one Softmax, and One-Classification layer. An architecture of 15-layered CNN is shown in Fig. 4 .
Fig. 4.
Proposed 15-layered CNN architecture for feature extraction.
In Fig. 5 , one can observe, the network accepts an image with dimensions 512 × 512 × 3, from the input layer. The second layer is the convolutional layer which includes 512 numbers of channels and the filter size is 2 × 2 along with stride [2, 2]. On this layer, the output learnable weights matrix size is 2 × 2 × 3 × 512 and the bias matrix is having dimensions 1 × 1 × 512. Mathematically, it is defined -by:
| (1) |
Where, denotes input layer feature matrix, denotes learnable weights matrix of lth layer, and denotes bias matrix of lth layer. For the second convolutional layer, the weights and bias matrix are updated as follows:
| (2) |
| (3) |
Where, Cf is the sigmoidal cost function, represent updated weights matrix, represent updated bias matrix, and Lr is a learning rate which is 0.0004. Later, the max-pool layers are also added to solve the problem of overfitting. The main advantage of this layer is to precede only active features to the next layer for processing. Mathematical representation of max-pooling is defined as follows:
| (4) |
Fig. 5.
Visual description of proposed 15-layered deep learning architecture for features extraction
As shown in Fig. 5, two max-pooling layers are included in this architecture. The filter size of a first max-pooling layer is 2 × 2 along with stride [1, 1] and for a second max-pool layer is 3 × 3 along with stride [2, 2]. A global average pool layer also added to minimize the problem of overfitting as well as minimizes the number of tuned parameters. In this layer, the average is calculated for the input feature map. Two fully connected layers are added at the end to compute the high-level features. Through this layer, the weights of previous layers are converted into a single vector for final classification. The formulation of FC layer is defined as follows:
| (5) |
After FC layers, a Softmax is added for the prediction of these features. The formulation of Softmax layer is defined as:
| (6) |
| (7) |
where, Eq. (7) represents the loss of the Softmax classifier. In this equation, represents predicted labels and denotes original image labels, respectively. We extract deep features from the global average pool layer and FC layer (1). The length of extracted vectors is N × 1024 and N × 512, respectively and denoted by λx1(i) and λx2(i), respectively.
2.3. Features Fusion
Consider two feature vectors, obtained from two consecutive CNN layers (Global Average Pool and FC Layer 1) denoted by λx1(i) and λx2(i) where . As we know the feature length of both vectors that is N × 1024 and N × 512, respectively. Initially, equal the length of both vectors by mean value. The sparse coefficient of each vector is denoted by ϕr,c of final vector , where r = {1, 2, 3, …N} and c = {1, 2, 3, …M}. First, CSR model is applied to solve as follows [30]:
| (8) |
Suppose, ϕr,1: N(i, j) denotes substances of ϕr,c at feature location (i, j). The ϕr,1: N is an Nth dimensional vector. The l 1 norm is applied of both vectors ϕr,1: N and ϕc,1: M to acquire the activity level measure of the fused vector. Mathematically, it is defined as follows:
| (9) |
The window based average approach is applied on φr(i,j) as follows:
| (10) |
where, is average approach on the applied window, q represent window size, i and j are features indexes that completed up to k and l. Due to this operation, fewer details may be lost, but it is also dependent on the size of q, so we defined a window size of 2 × 2 along with stride [1, 1]. Later, we obtain the coefficient maps among features by using max-operation [31], given as follows:
| (11) |
Finally, the features are combined as follows:
| (12) |
where, is the final fused vector with d dimensions and contains much more information compared to original extracted single-layered features.
2.4. Correntropy based Feature Selection
Let's consider a fused feature vector denoted by of dimension ξ × N, where ξ denotes the number of input image samples for features extraction and N denotes the length of the fused feature vector. Suppose, two features f 1 and f 2 where , then correntropy is computed among two features as follows:
| (13) |
| (14) |
Where, E[.] denotes the expectation function, KF(.) denotes Mercer Kernel function, ϒ represent nonlinear function, and Hb is a Hilbert space. In this work, we employed Gaussian kernel function [32], which is defined as follows:
| (15) |
Where, σ denotes the kernel bandwidth. Based on kernel function, the loss is formulated as follows:
| (16) |
| (17) |
| (18) |
Using the loss function Loss(f 1, f 2), we follow the property of Correntropy- positive value features. Mathematically, the positive features property is defined as follows:
| (19) |
Here σ is a variance of defined distribution. This property is applied on all features that are included in a fused vector with a stride [1, 1]. The features are selected in pairs. It means that a feature pair is selected who meet Eq. (19). In the end, a final vector is obtained of dimension ξ × N 1, represented by . In this work, only 60% of the features are selected from fused feature vector.
2.5. One-Class Kernel ELM
The One-Class Kernel- ELM (OCK-ELM) is proposed by Leng et al. [33] in 2015. It is an efficient classification technique for two-class problems. In this work, we implemented this classification algorithm for the prediction of COVID19-pneumonia and Normal chest CT Scans. Considering the selected feature vector and , then represent input features and denotes corresponding labels. The symbol N denotes training samples, ξ denotes input training features, and ξk denotes input testing features. Then, the OCK-ELM is described by following Algorithm 1 .
Algorithm 1.
Inputs:
Output: Prediction LabelInitialization:
|
Where the weight matrix w , the network output , the threshold parameter t , and the testing output are defined as follows:
| (20) |
| (21) |
| (22) |
| (23) |
Where, KF denotes the kernel function and ϱ denotes the kernel matrix in ELM defined as: . In the output, the prediction results are obtained based on network error which is measured among output and target labels Y ∈ y.
| (24) |
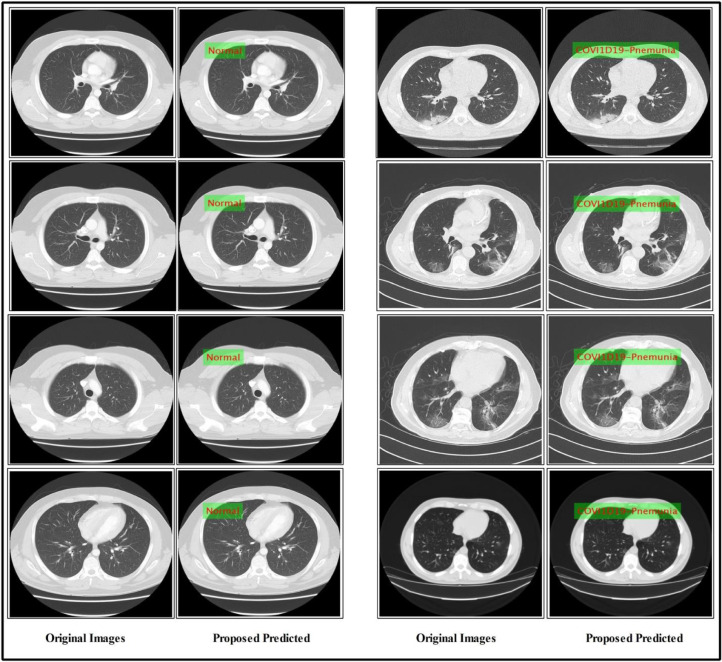
A few predicted labeled results are showing in Fig. 6 .
Fig. 6.
Proposed predicted labeled results
3. Experimental Results
The proposed deep learning prediction method of COVID19-pneumonia is evaluated in this section based on numerical and visual results. For validation, ten different cases of ten patients are considered. The details of collected data is provided in the Section 2.1. The One-Class Kernel ELM is used for the final prediction. The performance of this classifier is compared with a few other classification algorithms such as Fine Tree, SVM, Naïve Bayes, KNN, and Ensemble learning. Six primary performance measures are implemented. These measures are sensitivity rate, specificity rate, precision rate, false positive rate (FPR), area under the curve (AUC), and accuracy. The MATLAB2019b is used to implement the proposed algorithm.
3.1. Explanation of Results
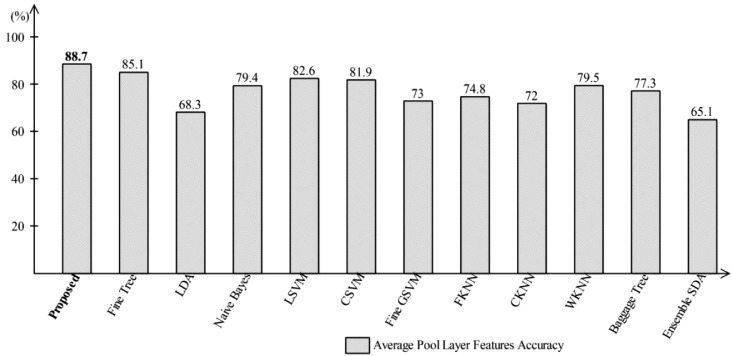
The proposed method results are analyzed through different feature sets. A 70:30 approach is opted along with 10-Fold Cross-validation to confirm the performance of the proposed method. Initially, the prediction results are computed on Global Average Pool Layer features. The extracted features of this layer directly feed to One-Class Kernel ELM and other selected classification algorithms for performance analysis. On this layer features, the proposed achieved an accuracy of 88.7% which is better as compared to other listed classification algorithms. The results are plotted in Fig. 7 . In this Figure, the Fine Tree classifier accomplished an accuracy of 85.1%. The accuracy of linear discriminant analysis (LDA) and Ensemble Discriminant classifier is 68.3% and 65.1% which is almost 20% less as compared to the proposed method. For Naïve Bayes, the reported accuracy is 79.4%. The linear support vector machine (LSVM) shows better accuracy of 82.6% after the Fine Tree classifier. For K-Nearest neighbor (KNN) classifier series, weighted KNN (WKNN) achieved better accuracy of 79.5%.
Fig. 7.
Representation of Average-Pool Layer accuracy using One-Class Kernel ELM where robust features selection technique is not applied.
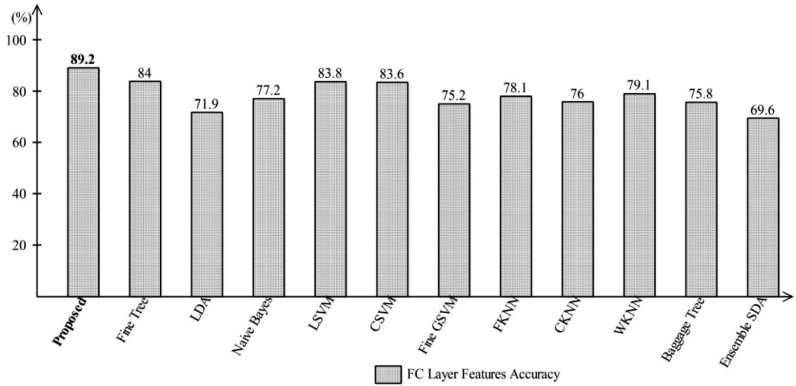
Later, features are extracted from FC Layer one (FC1) and directly passed to One-Class Kernel ELM and other classifiers. The performance of the FC1 layer is shown in Fig. 8 , where one can find the accuracy using proposed method reaches up to 89.2%. It can be observed, with the proposed, the accuracy increases up to 1%. With the FC Layer features, the accuracy of Fine tree classifier decreases compared to the previous. The obtained accuracy is 84% whereas the previous reported accuracy is 85.1%. Moreover, the reported accuracy of Naïve Bayes, LDA, LSVM, CSVM, WKNN, and Ensemble Discriminant Analysis (ESDA) is 77.2%, 71.9%, 83.8%, 83.6%, 79.1%, and 69.6%, respectively. From the results, it is observed that the FC layer features are good compared to global average pool layer features.
Fig. 8.
Representation of FC Layer accuracy using One-Class Kernel ELM where robust features selection technique is not applied.
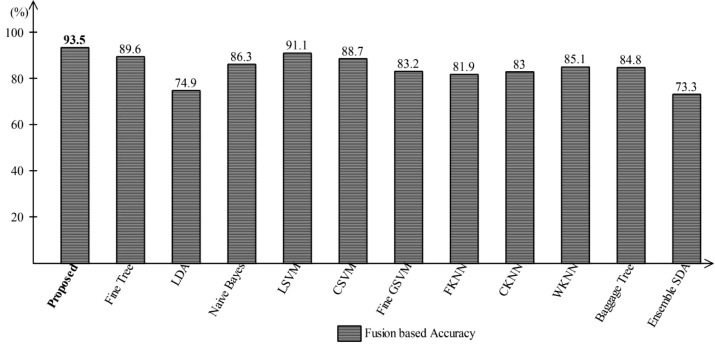
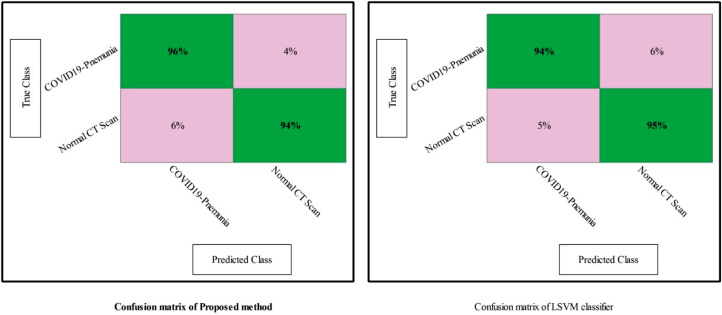
After that, the fusion is performed, and the procedure details are provided in Section 2.3. The fusion of features from both layers produces a resultant matrix, Fig. 9 . In this Figure, it is shown that the maximum noted accuracy is 93.5%, which increases up to 4% compared to the proposed results, Fig. 8. The results plotted in Fig. 9 are improved compared to Fig. 7 and Fig. 8. After fusion, the accuracy of Fine Tree classifier is reached to 89.6%, LDA is 74.9%, Naïve Bayes is 86.3%, LSVM is 91.1%, CSVM is 88.7%, WKNN is 85.1%, Ensemble Baggage method is 84.8%, and ESDA is 73.3%, respectively. However, during fusion few redundant features are added in a fused vector. Moreover, all features in a fused vector are not essential; therefore, it is important to remove them to improve the system's efficiency. For this purpose, a selection method is proposed which is discussed in Section 2.4. The robust selected features are predicted through One-Class Kernel ELM (OCK-ELM) and achieved an improved accuracy of 95.1%. The proposed results are given in Table 2 . In this table, it is shown that the sensitivity rate of OCK-ELM is 95%, the specificity rate is 94%, the precision rate is 95.5%, FPR is 0.05, and AUC is 0.98. The second top accuracy is 94.6% that is achieved by LSVM. For LSVM, the other computed measure such as sensitivity rate is 94.5%, specificity is 95%, and FPR is 0.055. From the results, reported in this table, it is shown that the proposed selected method results are improved as compared to Fig. 7, Fig. 8, and Fig. 9. Moreover, the accuracy of OCK-ELM and LSVM can be verified through Fig. 10 . In this figure, the confusion matrix of the proposed method and LSVM is presented. The diagonal values show the correct prediction rate.
Fig. 9.
Representation of proposed fusion accuracy using One-Class kernel ELM where robust features selection technique is not applied.
Table 2.
Prediction results of proposed heterogeneous method
| Method | Selected Performance Measures | |||||
|---|---|---|---|---|---|---|
| Sensitivity (%) | Specificity (%) | Precision (%) | FPR | AUC | Accuracy (%) | |
| Proposed | 95.0 | 94.0 | 95.5 | 0.05 | 0.98 | 95.1 |
| Fine Tree | 93.0 | 94.0 | 93.5 | 0.07 | 0.94 | 92.8 |
| LDA | 80.0 | 91.0 | 81.5 | 0.20 | 0.80 | 80.0 |
| Naïve Bayes | 91.0 | 93.0 | 91.0 | 0.09 | 0.91 | 91.0 |
| LSVM | 94.5 | 95.0 | 94.5 | 0.055 | 0.98 | 94.6 |
| CSVM | 93.5 | 95.0 | 93.5 | 0.065 | 0.98 | 93.5 |
| Fine GSVM | 90.5 | 87.0 | 90.5 | 0.095 | 0.94 | 90.6 |
| FKNN | 92.0 | 90.0 | 92.0 | 0.08 | 0.92 | 92.0 |
| CKNN | 91.0 | 92.0 | 91.5 | 0.08 | 0.97 | 92.3 |
| WKNN | 90.5 | 92.0 | 91.5 | 0.09 | 0.97 | 92.0 |
| EBT | 92.0 | 92.0 | 92.0 | 0.08 | 0.98 | 92.0 |
| ESDA | 80.5 | 92.0 | 82.0 | 0.195 | 0.90 | 80.4 |
Fig. 10.
Error matrix of proposed method and LSVM for the prediction of COVID19-pneumonia and healthy chest CT Scans
3.2. Analysis of Proposed Results
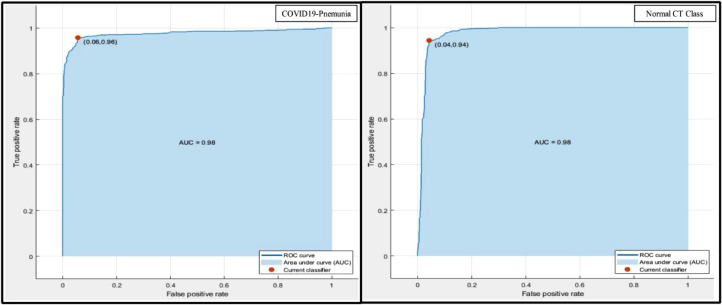
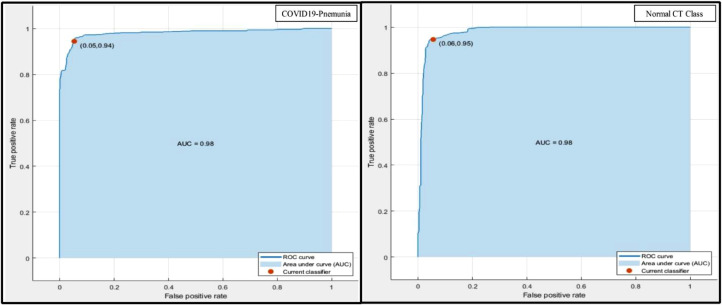
In this section, a detailed analysis of the proposed method is being discussed and both the empirical and graphical results are presented. The proposed approach is shown in Fig. 2 which consists of four primary steps. The novel framework is initiated with the data acquisition step, a few scans are shown in Fig. 3, followed by a feature extraction step using proposed 15-Layered CNN architecture, Fig. 4 & 5. Later, the extracted features from two layers, the global average pool (GAP) and the first FC layers, are fused using the proposed fusion approach. Finally, the features are passed to the OCK-ELM for the final classification. The classification results with both FC layers and max pool layer are plotted in Fig. 7 & 8. The fusion results are also presented in Fig. 9, where it can be observed that the classification results are improved after performing the fusion step. Table 2 demonstrates the results using proposed fusion and selection approach, where it can be seen, using the proposed method the achieved classification accuracy is 95.1%. The accuracy of OCK-ELM is further verified through the confusion matric plotted in Fig. 10. The ROC curve plots are also provided to support the authenticity of FPR and AUC, as shown in Fig. 11 , and ROC is plotted in Fig. 12 .
Fig. 11.
Representation of proposed accuracy in terms of ROC plots
Fig. 12.
Representation of LSVM accuracy in terms of ROC plots
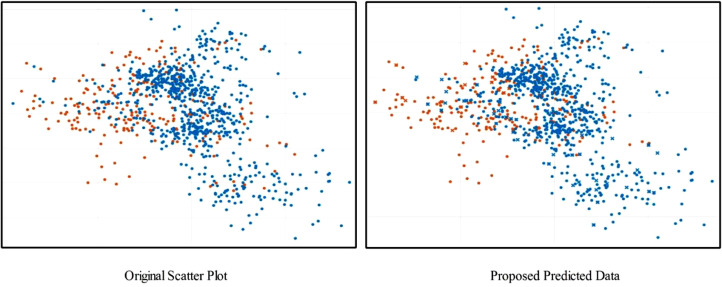
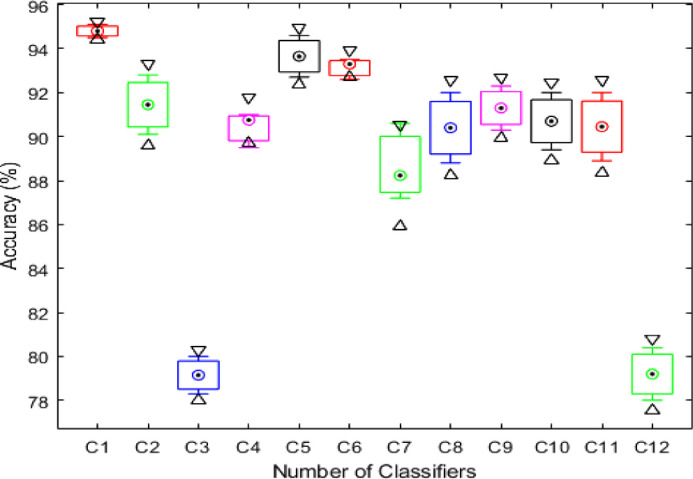
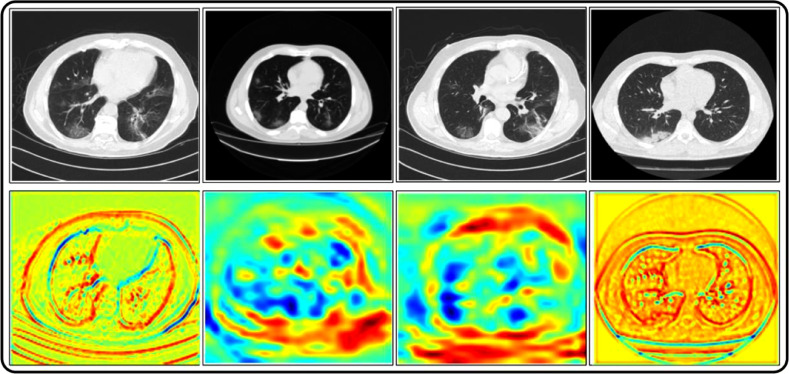
In Fig. 13 , prediction data is plotted in the form of scatter plots; original scatter plot vs proposed predicted data. The original scatter plot (left) shows the actual labelled results, whereas the plot on the right shows the results achieved using the proposed method. It can be observed that a few image features are misclassified, which affect the overall system's accuracy. In addition, a detailed analysis is also conducted in terms of standard error mean (SEM), Table 3 . In this table, it is observed that the SEM of the proposed method (OCK-EML) is minimum and accuracy after 200 iterations are consistent. A minor change has occurred in accuracy for all other classifiers which supports the effectiveness of the proposed scheme. Moreover, this process is also visualized using a box plot given in Fig. 14 - showing the scalability of C1 (proposed method) is better than the other classifiers, C2-C12. In addition, the Gradcam based visualization effects are illustrated in Fig. 15 .
Fig. 13.
Scatter Plot based representation of proposed method performance.
Table 3.
Analysis of proposed method based on Standard Error Mean
| Method | Minimum (%) | Average (%) | Maximum (%) | SEM |
|---|---|---|---|---|
| Proposed (C1) | 94.5 | 94.80 | 95.1 | 0.1414 |
| Fine Tree (C2) | 90.1 | 91.45 | 92.8 | 0.6363 |
| LDA (C3) | 78.3 | 79.15 | 80.0 | 0.4006 |
| Naïve Bayes (C4) | 89.5 | 90.75 | 91.0 | 0.3788 |
| LSVM (C5) | 92.7 | 93.65 | 94.6 | 0.4478 |
| CSVM (C6) | 92.6 | 93.30 | 93.5 | 0.2227 |
| Fine GSVM (C7) | 87.2 | 88.23 | 90.6 | 0.9687 |
| FKNN (C8) | 88.8 | 90.40 | 92.0 | 0.7542 |
| CKNN (C9) | 90.3 | 91.30 | 92.3 | 0.4714 |
| WKNN (C10) | 89.4 | 90.70 | 92.0 | 0.6128 |
| EBT (C11) | 88.9 | 90.45 | 92.0 | 0.7306 |
| ESDA (C12) | 78.0 | 79.20 | 80.4 | 0.5656 |
Fig. 14.
Box plots for the representation of statistical analysis
Fig. 15.
Gradcam based features visualization
4. Conclusion
From the results, it is concluded that the proposed framework outperforms existing methods with greater accuracy. By employing the original features of the GAP and FC layers, the results are not exceptional. On the contrary, the addition of a fusion step improved the system's performance by generating a high average accuracy. Further, by selecting the most discriminant features using the proposed method, the accuracy jumps-up to 95%. One of the limitations of our proposed method is the removal of some useful features in a feature selection step. Adding a feature selector not only eliminates redundant information but also obliterates the useful information. As future work, we will be working to refine the feature selection step, which not only will improve the overall accuracy but also decrease the computational time. Further, we will also consider a CNN model for the detection of infection part in the chest CT scans.
Authors Statement
Authors Muhammad Attique Khan, Seifedine Kadry, and Yu-Dong Zhang are responsible for conceptualization, methodology, and Software. They are also responsible for initial draft. Tallha Akram is responsible for formal analysis of this work. Muhammad Sharif supervised this work. Amjad Rehman and Tanzila Saba are responsible for visualization and edit the original draft.
Declaration of Competing Interest
On the behalf of corresponding author, all authors declare that they have no conflict of interest.
Biographies
Muhammad Attique Khan earned his Master degree in Human Activity Recognition for Application of Video Surveillance from COMSATS University Islamabad, Pakistan. He is currently Lecturer of Computer Science Department in HITEC University Taxila, Pakistan. His primary research focus in recent years is medical imaging, Video Surveillance, Human Gait Recognition, and Agriculture Plants.
Seifedine Kadry: received M.S. degree in computation from Reims University, France, and EPFL, Lausanne, in 2002, the Ph.D. degree from Blaise Pascal University, France, in 2007, and the HDR degree in engineering science from Rouen University, in 2017. His current research interests include education using technology, machine leanring, smart cities, system prognostics, and stochastic systems.
Yu-Dong Zhang: From 2010 to 2012, he worked at Columbia University as a postdoc. From 2012 to 2013, he worked as an assistant research scientist at Columbia University and New York State Psychiatric Institute. At present, he is a Professor in Knowledge Discovery and Machine Learning, in Department of Informatics, University of Leicester, United Kingdom.
Tallha Akram is working as an Assistant Professor at the Department of Electrical Engineering, COMSATS Institute of Information Technology (CIIT), Wah Cantt. He received his MS and PhD degree from University of Leicester, and Chongqing University respectively. His research interests include pattern recognition & machine learning, computer vision, biological inspired computing, and applied optimization.
Muhammad Sharif is Associate Professor at COMSATS University Islamabad, Wah Campus Pakistan. He has worked one year in Alpha Soft UK based software house in 1995. He is OCP in Developer Track. He has more than 200+ research publications and obtained 230+ Impact Factor. His primary research focus in recent years is medical imaging, Video Surveillance, Human Gait Recognition, and Agriculture Plants.
Amjad Rehman received the Ph.D. degree in image processing and pattern recognition from Universiti Teknologi Malaysia, Malaysia, in 2010. During his Ph.D., he proposed novel techniques for pattern recognition based on novel features mining strategies. He is currently conducting research under his supervision for three Ph.D. students.
Tanzila Saba earned PhD in document information security and management from UTM, Malaysia. Currently, she is serving as Associate Prof. and Associate Chair of Information Systems Department. Her primary research focus in recent years is medical imaging, MRI analysis and Soft-computing. She has above one hundred publications that have around 1800 citations with h-index 28.
References
- 1.Worldometer . 2020. COVID-19 Coronavirus Pandemic. https://www.worldometers.info/coronavirus/ [Google Scholar]
- 2.Li L., Qin L., Xu Z., Yin Y., Wang X., Kong B., et al. Artificial intelligence distinguishes COVID-19 from community acquired pneumonia on chest CT. Radiology. 2020 doi: 10.1148/radiol.2020200905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.D. A. K. P. S. a. D. D. J. B. et al., "COVID-19 (https://radiopaedia.org/articles/covid-19-3)," 2020.
- 4.L. Wang and A. Wong, "Covid-net: A tailored deep convolutional neural network design for detection of covid-19 cases from chest x-ray images," arXiv preprint arXiv:2003.09871,2020. [DOI] [PMC free article] [PubMed]
- 5.Amyar A., Modzelewski R., Ruan S. Multi-task Deep Learning Based CT Imaging Analysis For COVID-19: Classification and Segmentation. medRxiv. 2020 doi: 10.1016/j.compbiomed.2020.104037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.F. Shan+, Y. Gao+, J. Wang, W. Shi, N. Shi, M. Han, et al., "Lung infection quantification of covid-19 in ct images with deep learning," arXiv preprint arXiv:2003.04655,2020.
- 7.A. Narin, C. Kaya, and Z. Pamuk, "Automatic detection of coronavirus disease (covid-19) using x-ray images and deep convolutional neural networks," arXiv preprint arXiv:2003.10849, 2020. [DOI] [PMC free article] [PubMed]
- 8.B. Ghoshal and A. Tucker, "Estimating uncertainty and interpretability in deep learning for coronavirus (COVID-19) detection," arXiv preprint arXiv:2003.10769, 2020.
- 9.P. Afshar, S. Heidarian, F. Naderkhani, A. Oikonomou, K. N. Plataniotis, and A. Mohammadi, "Covid-caps: A capsule network-based framework for identification of covid-19 cases from x-ray images," arXiv preprint arXiv:2004.02696, 2020. [DOI] [PMC free article] [PubMed]
- 10.V. Rajinikanth, S. Kadry, K. P. Thanaraj, K. Kamalanand, and S. Seo, "Firefly-Algorithm Supported Scheme to Detect COVID-19 Lesion in Lung CT Scan Images using Shannon Entropy and Markov-Random-Field," arXiv preprint arXiv:2004.09239, 2020.
- 11.Y. Oh, S. Park, and J. C. Ye, "Deep Learning COVID-19 Features on CXR using Limited Training Data Sets," arXiv preprint arXiv:2004.05758, 2020. [DOI] [PubMed]
- 12.R. M. Pereira, D. Bertolini, L. O. Teixeira, C. N. Silla Jr, and Y. M. Costa, "COVID-19 identification in chest X-ray images on flat and hierarchical classification scenarios," arXiv preprint arXiv:2004.05835, 2020. [DOI] [PMC free article] [PubMed]
- 13.Wang S., Kang B., Ma J., Zeng X., Xiao M., Guo J., et al. A deep learning algorithm using CT images to screen for Corona Virus Disease (COVID-19) MedRxiv. 2020 doi: 10.1007/s00330-021-07715-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zheng C., Deng X., Fu Q., Zhou Q., Feng J., Ma H., et al. Deep learning-based detection for COVID-19 from chest CT using weak label. medRxiv. 2020 [Google Scholar]
- 15.Sharif M.I., Li J.P., Khan M.A., Saleem M.A. Active deep neural network features selection for segmentation and recognition of brain tumors using MRI images. Pattern Recognition Letters. 2020;129:181–189. [Google Scholar]
- 16.Khan M.A., Lali I.U., Rehman A., Ishaq M., Sharif M., Saba T., et al. Brain tumor detection and classification: A framework of marker-based watershed algorithm and multilevel priority features selection. Microscopy research and technique. 2019;82:909–922. doi: 10.1002/jemt.23238. [DOI] [PubMed] [Google Scholar]
- 17.Khan M.A., Rubab S., Kashif A., Sharif M.I., Muhammad N., Shah J.H., et al. Lungs cancer classification from CT images: An integrated design of contrast based classical features fusion and selection. Pattern Recognition Letters. 2020;129:77–85. [Google Scholar]
- 18.Khan S.A., Nazir M., Khan M.A., Saba T., Javed K., Rehman A., et al. Lungs nodule detection framework from computed tomography images using support vector machine. Microscopy research and technique. 2019;82:1256–1266. doi: 10.1002/jemt.23275. [DOI] [PubMed] [Google Scholar]
- 19.Macori D.F. 2020. COVID-19 pneumonia. https://radiopaedia.org/cases/covid-19-pneumonia-12. [Google Scholar]
- 20.Dr Chong Keng Sang S. 2020. COVID-19 pneumonia. https://radiopaedia.org/cases/covid-19-pneumonia-2. [Google Scholar]
- 21.Rasuli D.B. 2020. COVID-19 pneumonia. https://radiopaedia.org/cases/covid-19-pneumonia-3. [Google Scholar]
- 22.Rasulii D.B. 2020. COVID-19 pneumonia. https://radiopaedia.org/cases/covid-19-pneumonia-4. [Google Scholar]
- 23.Nicoletti D.D. 2020. COVID-19 pneumonia. https://radiopaedia.org/cases/covid-19-pneumonia-7. [Google Scholar]
- 24.Hosseinabadi D.F. 2020. COVID-19 pneumonia. https://radiopaedia.org/cases/covid-19-pneumonia-8. [Google Scholar]
- 25.Radiopaedia . 2020. Normal CT chest. https://radiopaedia.org/cases/normal-ct-chest. [Google Scholar]
- 26.Dixon D.A. 2020. Normal CT chest. https://radiopaedia.org/cases/normal-ct-chest. [Google Scholar]
- 27.Majid A., Khan M.A., Yasmin M., Rehman A., Yousafzai A., Tariq U. Classification of stomach infections: A paradigm of convolutional neural network along with classical features fusion and selection. Microscopy research and technique. 2020;83:562–576. doi: 10.1002/jemt.23447. [DOI] [PubMed] [Google Scholar]
- 28.Liaqat A., Khan M., Sharif M., Mittal M., Saba T., Manic K., et al. Gastric Tract Infections Detection and Classification from Wireless Capsule Endoscopy using Computer Vision Techniques: A Review. Current Medical Imaging. 2020 doi: 10.2174/1573405616666200425220513. [DOI] [PubMed] [Google Scholar]
- 29.Zahoor S., Lali I.U., Khan M., Javed K., Mehmood W. Breast Cancer Detection and Classification using Traditional Computer Vision Techniques: A Comprehensive Review. Current Medical Imaging. 2020 doi: 10.2174/1573405616666200406110547. [DOI] [PubMed] [Google Scholar]
- 30.Wohlberg B. Efficient algorithms for convolutional sparse representations. IEEE Transactions on Image Processing. 2015;25:301–315. doi: 10.1109/TIP.2015.2495260. [DOI] [PubMed] [Google Scholar]
- 31.Maqsood S., Javed U. Multi-modal Medical Image Fusion based on Two-scale Image Decomposition and Sparse Representation. Biomedical Signal Processing and Control. 2020;57 [Google Scholar]
- 32.Liu W., Pokharel P.P., Príncipe J.C. Correntropy: Properties and applications in non-Gaussian signal processing. IEEE Transactions on Signal Processing. 2007;55:5286–5298. [Google Scholar]
- 33.Leng Q., Qi H., Miao J., Zhu W., Su G. One-class classification with extreme learning machine. Mathematical problems in engineering. 2015;2015 [Google Scholar]