Potential Biases in Studies of Acid-Suppressing Drugs and COVID-19 Infection

Currently, there is great interest in identifying safe and effective existing drug therapies for the prevention of coronavirus-2019 (COVID-19). Recently, there is a surge of observational studies, using big data, examining safety and effectiveness of proton pump inhibitors (PPIs) or histamine-2 receptor antagonists (H2RAs) on the risk of new onset COVID-19.1, 2, 3, 4, 5, 6 The nature of the disease, limitations of large databases, and use of different methodologic approaches have created unique challenges that might have contributed to contradictory studies addressing this question.

Although some recent studies, especially those that tightly controlled for confounding bias, have not found an association,^{1 , 2 , 5} others have shown either a protective^{3 , 4} or a harmful⁶ association with PPIs or H2RAs in COVID-19. These contradictory results can be misleading to clinicians, policymakers, and patients, leading to unnecessary prescribing of PPIs or H2RAs for COVID-19 prevention. Here we discuss potential biases that might have led to these contradictory findings including confounding bias, immortal time bias, selection bias, reverse causality bias, and sparse data bias using examples from published studies and causal directed acyclic graphs (cDAGs). cDAGs are graphical tools that can enable clinician researchers to visualize and better understand the structure of epidemiological biases and allow them to critique the methodologic rigor of observational studies addressing COVID-19 in the area of gastroenterology.7, 8, 9

Specific Biases in Epidemiologic Studies of Acid Suppressing Drug and COVID-19 Studies

The structure of a number of biases that might have affected the studies of gastric-suppressing drugs in COVID-19 can be demonstrated using cDAGs. A more comprehensive discussion on cDAGs is beyond the scope of this review, but can be found elsewhere.^{10 , 11} In brief, cDAGs provide a blueprint of all pertinent variables that play a role in causal questions. Two variables, A and B, are connected with an arrow tail that starts from A and ends on variable B, meaning that A causes B. Variable A cannot cause itself; that is, cDAGs are acyclic. Adjacent arrows, regardless of direction, form paths in a cDAG. Finally, conditioning on a variable means restricting that to a subset of its values. Conditioning can be done at the data analysis stage (eg, regression adjustment) or study design stage (eg, restriction).

Confounding bias

Confounding bias is one of the most prevalent types of bias that can affect the validity of observational studies. In a recent retrospective cohort study, Freedberg et al³ demonstrated a protective effect of famotidine use on COVID-19 death or intubation (hazard ratio, 0.42; 95% confidence interval [CI], 0.21–0.85). The study attempted to control for confounding bias through propensity score (PS) matching, a statistical technique that attempts to balance measured confounders between famotidine users and nonusers. However, PS matching can only adjust for measured confounders and its usefulness depends on how well the PS model can balance measured confounders between the 2 groups.

The authors matched users and nonusers using a 5:1 nearest-neighbor matching strategy and a caliper of 0.2, which means that the PS scores for the 2 members of a matched set could have varied by 20%. They then assessed balance of confounding variables between famotidine users and nonusers in the original and matched sample using hypothesis testing where failure to reject the null hypothesis (P > .05) was used as a metric for good balance of confounders. This approach has been shown to introduce bias⁹ because hypothesis testing is a function of sample size, and with only 84 famotine users, a large P value can erroneously indicate optimal balance of confounders. In fact, in the matched sample, the percentage of the following variables—old age, diabetes, hypertension, and coronary artery disease—among famotidine users remained higher compared with nonusers (at 48%, 29%, 35%, and 11% vs. 43%, 25%, 30%, and 9%, respectively). Standardized mean differences (SMDs)¹² are a useful and accepted metric for examining covariate balance after PS matching. As a general rule, a SMD of ≤10% is indicative of a good balance between variables.¹³ The percentage difference for variables age and hypertension in the matched sample in the Freedberg study was 5%, which translates into a SMD of 10.03% and 10.66%, respectively, which are both slightly >10%. The cohort study by Lee et al,⁵ which did not find an association between PPI use and COVID-19 also used a PS matching analysis and demonstrated a SMD of <10% for all the 14 covariates included in the PS analysis.

Moreover, a caliper of ±0.2 for PSs between matched users and nonusers can lead to residual confounding owing to the substantial variation between the PSs allowed by this approach. A caliper of 0.01–0.05 on the original scale¹⁴ or 0.2 of the standard deviation on the logit scale has been recommended. Residual confounding may explain the protective effect seen with famotidine use in this study.

Residual confounding in this study might have been further accentuated owing to a small ratio of the number of matched exposed to the number of PS model parameters, also referred to as the number of events per variable (EPV). It is recommended EPV to be ≥10 in logistic regression modelling,¹⁵ which for this specific case looks at the number of the exposed as the response variable in the PS model is the exposure. In this study of 84 famotidine users, the investigators included 21 variables as indicators of potential confounders in the estimation of PS model: 84/22 (21 covariates+1, the model intercept) which yields an EPV of 3.8. This number is much less than 10, suggesting the possibility of sparse data bias^{16 , 17} in the PS model coefficients, which can affect the validity of the PS estimation and yield sub-optimal balance of confounders (between famotidine users and nonusers), potentially leading to residual confounding.

Perhaps a more consequential effect of sparse data bias is on the magnitude of the effect size of epidemiologic studies. For example, in the study by Almario et al,⁶ those taking PPIs twice daily experienced an approximately 3.5 higher risk of developing COVID-19 compared with nonusers (odds ratio [OR], 3.67; 95% CI, 2.93–4.60). In this study, the EPV is computed as 198/32 = 6.2 (31 covariates+1) indicative of a low EPV resulting in possibly inflated ORs. Statistical techniques can be used to correct for sparse data bias and shrink the effect size.¹⁸

In another study, Elmunzer et al¹⁹ examined the preadmission exposure to acid-suppressing drugs and the odds of death or need for mechanical ventilation in patients who contract COVID-19. No benefit was observed in the adjusted analysis for H2RA or PPI use with respect to death. Similar to Freedberg et al,³ Elmunzer et al also used a PS-matched analysis using a 0.2 caliper which resulted in a risk difference of 9.72% (95% CI, 1.26%–18.2%). Again, a caliper of 0.2 might mean that the PS matched analysis might not have fully corrected for confounding bias.

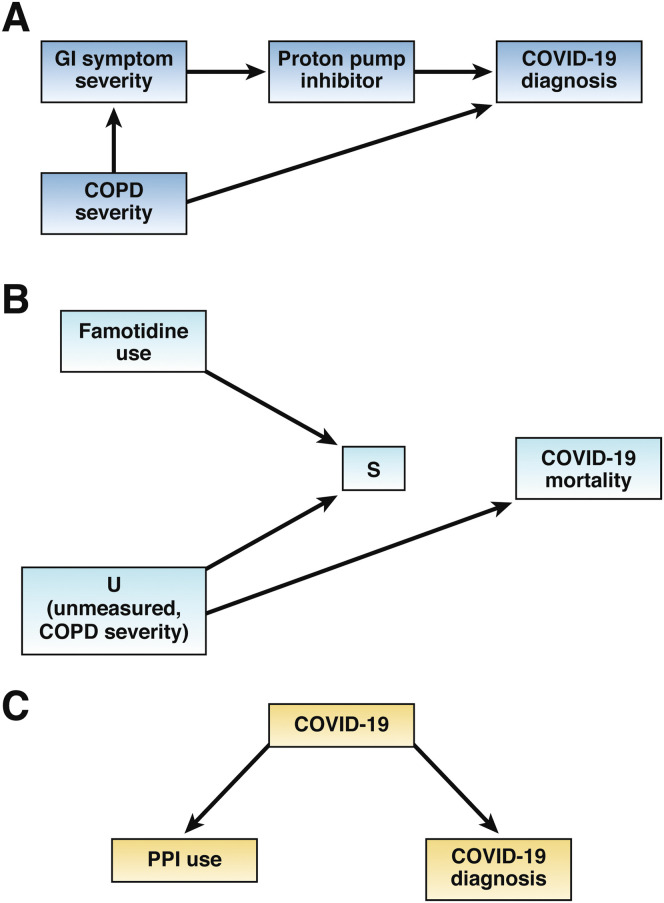
Confounding bias might have also explained harmful association shown between PPI use and COVID-19. Almario et al⁶ undertook a survey in patients with gastrointestinal symptoms who had also contracted COVID-19. The study found that subjects using a PPI once a day had double the odds of contracting COVID-19 compared with nonusers (OR, 2.15; 95% CI, 1.90–2.44). The increase in risk observed might be due to unmeasured confounding such as chronic obstructive pulmonary disease (COPD) severity. This is reflected in Figure 1 A, where subjects with more severe COPD might experience more severe GI symptoms.²⁰ Consequently, those with more severe GI symptoms are more likely to take PPIs. COPD severity is also a recognized risk factor for COVID-19 making it a classic confounder.

Figure 1.

(A) Confounding bias: chronic obstructive pulmonary disease (COPD) severity is a confounder as it is a common cause of coronavirus disease-2019 (COVID-19) and proton pump inhibitor (PPI) use through gastrointestinal (GI) symptom severity. (B) Immortal time bias (selection bias): Conditioning on variable S, which represents selection upon having survived ≤7 days before COVID-19 diagnosis opens a previously blocked path that spuriously associates famotidine use with COVID-19 mortality. (C) Reverse causality: COVID-19 can affect PPI use through early COVID-19 symptoms, and creates a confounded association between PPI use and COVID-19 diagnosis.

Immortal Time Bias

In a recent cohort, Mather et al²² followed 878 famotidine users and assessed the risk of COVID-19 mortality between this group and nonusers. By design, famotidine users could have received the drug within 7 days of COVID-19 screening or hospital admission. This means users had to be alive for ≤7 days (immortal period) before being eligible to receive the drug while nonusers could have incurred the outcome (death) at any time during the study period. This type of conditioning can introduce immortal time bias,²¹ which can lead to a spurious protective effect of a drug as shown by the study which reported an OR of 0.37 (95% CI, 0.16–0.86) consistent with a profound protective effect. The structure of immortal time bias in this example resembles selection bias. Selection bias generally occurs in cohort studies where 1 group of subjects (eg, famotidine users) are treated differently than the other group (nonusers). In this example, users were allowed to be alive ≤7 days before COVID-19 diagnosis, whereas nonusers could have died at any time. Thus, famotidine users with less severe comorbid conditions were more likely to be included in the study, leading to an observed protective effect secondary to selection bias as depicted in Figure 1 B.

In Figure 1 B, variable S represents having been selected into the study based on the 7-day conditioning step defined by the investigators. The arrows from famotidine use and variable U (which represents the unmeasured risk factor COPD severity) to variable S indicate famotidine users with less comorbid conditions (eg, less severe COPD) were more likely to be included in the study. The square around S reflects that the analysis is limited to famotidine users and nonusers included in the sample. Thus, S is a common effect of famotidine and U, also referred to a collider. Unlike in our confounding example where conditioning (through adjustment) on a confounder blocks its effect, conditioning on a collider actually introduces bias by opening a path that was previously closed by variable S. For example, the conditioning step in the study design (variable S) will open the path famotidine → S ← U → mortality. Through this path, famotidine use will be associated with COVID-19 mortality as a result of selection bias, whereas without this conditioning, according to the cDAG, no association exists between famotidine use and COVID-19 mortality. A time-dependent Cox regression analysis should have been used to avoid immortal time bias.

Selection bias might have also affected the study by Almario et al.⁶ In this study, 264,058 potential participants were identified, but only 48.8% patients agreed to participate. It is possible that patients who agreed to participate in the survey did so owing to monetary incentives, a proxy for low socioeconomic status, which can also affect their risk of contracting COVID-19.

Reverse causality bias

Reverse causality bias might explain the protective effect observed with PPI use in the study by Blanc et al.⁴ This was a case-control study among elderly hospitalized patients with an average age of 84 years. PPI use was assessed 15 days before COVID-19 diagnosis. The study found a protective effect with PPI use (OR, 0.43; 95% CI, 0.23-0.81) compared with non-PPI users. This profound protective effect might be explained by reverse causality bias. This bias refers to a situation where symptoms of the disease (which in the case of COVID-19 can start days or weeks before diagnosis) can affect drug use. For example, elderly patients in this study might have decided to discontinue using a PPI, possibly to decrease polypharmacy and maximize adherence, upon experiencing early COVID-19 symptoms and resorted to taking more essential medications such as antidiabetics or antihypertensives. This is reflected in Figure 1 C, where the arrow from COVID-19 to PPI use suggests that early COVID-19 symptoms can affect PPI use, representing reverse causality. Figure 1 C illustrates that a consequence of reverse causality is a confounded association between PPI use and COVID-19 diagnosis.

Summary and Conclusions

We have identified a number of biases including confounding bias, immortal time bias, selection bias and reverse causality bias that might have affected the results of PPI/H2Ras and COVID-19 diagnosis. These biases were identified based on the information available in the studies we have reviewed without having access to the study protocols or data. Thus, we cannot state with certainty if these biases actually affected the results.

In studies of acid-suppressing drugs in COVID-19 where confounding bias was appropriately controlled for, no benefit with these drugs was found. Clinicians should be cognizant of these biases when reviewing future studies on this topic.