Abstract
Background and objective
The novel coronavirus disease 2019 (COVID-19) is considered a pandemic by the World Health Organization (WHO). As of April 3, 2020, there were 1,009,625 reported confirmed cases, and 51,737 reported deaths. Doctors have been faced with a myriad of patients who present with many different symptoms. This raises two important questions. What are the common symptoms, and what are their relative importance?
Methods
A non-structured and incomplete COVID-19 dataset of 14,251 confirmed cases was preprocessed. This produced a complete and organized COVID-19 dataset of 738 confirmed cases. Six different feature selection algorithms were then applied to this new dataset. Five of these algorithms have been proposed earlier in the literature. The sixth is a novel algorithm being proposed by the authors, called Variance Based Feature Weighting (VBFW), which not only ranks the symptoms (based on their importance) but also assigns a quantitative importance measure to each symptom.
Results
For our COVID-19 dataset, the five different feature selection algorithms provided different rankings for the most important top-five symptoms. They even selected different symptoms for inclusion within the top five. This is because each of the five algorithms ranks the symptoms based on different data characteristics. Each of these algorithms has advantages and disadvantages. However, when all these five rankings were aggregated (using two different aggregating methods) they produced two identical rankings of the five most important COVID-19 symptoms. Starting from the most important to least important, they were: Fever/Cough, Fatigue, Sore Throat, and Shortness of Breath. (Fever and cough were ranked equally in both aggregations.) Meanwhile, the sixth novel Variance Based Feature Weighting algorithm, chose the same top five symptoms, but ranked fever much higher than cough, based on its quantitative importance measures for each of those symptoms (Fever - 75 %, Cough - 39.8 %, Fatigue - 16.5 %, Sore Throat - 10.8 %, and Shortness of Breath - 6.6 %). Moreover, the proposed VBFW method achieved an accuracy of 92.1 % when used to build a one-class SVM model, and an NDCG@5 of 100 %.
Conclusions
Based on the dataset, and the feature selection algorithms employed here, symptoms of Fever, Cough, Fatigue, Sore Throat and Shortness of Breath are important symptoms of COVID-19. The VBFW algorithm also indicates that Fever and Cough symptoms were especially indicative of COVID-19, for the confirmed cases that are documented in our database.
Keywords: COVID-19, Feature selection, Importance weights, Important symptoms, Novel coronavirus
1. Introduction
The novel coronavirus disease 2019 (COVID-19) is considered a pandemic by the World Health Organization (WHO). As of August 31, 2020, there are 24,954,140 reported confirmed cases, and 838,924 reported confirmed deaths. In addition, the disease has been transmitted to 208 countries, areas or territories [1]. Doctors have encountered countless COVID-19 patients with many different symptoms. This raises two important questions. What are the common symptoms of COVID-19 patients, and what are the relative importance of these symptoms?
Machine learning methods can be used to analyze the importance of the different symptoms of the disease. However, these methods need a dataset of COVID-19 patients and their symptoms. At this time, few datasets are available on COVID-19 patients, and their symptoms, and the available datasets have some problems that make applying machine learning algorithms to them difficult. Such problems include:
-
•
The data is not well structured.
-
•
The data is of one class – all records in the database are for confirmed COVID-19 cases.
To address the first problem, this work has created a structured dataset, using currently available datasets. To address the second problem, many one-class machine learning approaches have been proposed in the literature. To rank the symptoms, based on their importance, feature selection algorithms can be used.
This paper makes the following contributions:
-
•
We construct a preprocessed, cleaned and organized dataset of COVID-19 symptoms for confirmed cases, available to researchers upon request.
-
•
We propose a novel feature selection and weighting method, called the Variance Based Feature Weighting (VBFW) method for COVID-19 symptoms, for ranking the features (or symptoms) from the most important to least important, and assigning weights of importance to each of them. This assignment is automatically made, based on the change that would occur to the Variance of the training data instances if the selected feature were to be removed from the dataset.
The rest of this paper is organized as follows. Section 2 presents the background and literature review and poses our research question. Section 3 proposes our novel variance-based feature weighting method. It also presents the set of experiments conducted in this work. The results of these experiments are presented in Section 4, and are discussed in Section 5. Finally, Section 6 concludes the paper.
2. Background and literature review
2.1. The coronavirus disease 2019 (COVID-19)
The coronavirus disease 2019 (known as COVID-19) is a new disease that appeared late in 2019 [1].
Lauer et al. [2] investigated the incubation period of the coronavirus. Their study consists of 181 confirmed cases. They found that the incubation period ranges from 5.1–11.5 days.
Bai et al. [3] studied the asymptomatic carrier transmission of COVID-19. Their study included 5 patients who had some symptoms (fever and repository symptoms) and 1 asymptomatic patient. All patients underwent chest CT imaging. Their study was the first to find that a transmission of the disease could occur from an asymptomatic patient with a normal CT scan.
Shi et al. [4] described the CT findings across 81 patients with confirmed COVID-19. They found that abnormalities appeared on the chest CT scans for all COVID-19 patients - even the asymptomatic ones. Thus, the assessment of CT imaging features could facilitate the early diagnosis of the disease.
Bernheim et al. [5] studied chest CT scans of 121 symptomatic patients of confirmed COVID-19. Surprisingly, they found that 20 out of 36 patients imaged 0–2 days after symptom (i.e. 56 %) had normal CT scans. However, with longer time after the symptoms appeared, abnormalities started to appear on the CTs.
Rothan and Byrareddy [6] reviewed and highlighted the symptoms that could present in COVID-19 patients. These symptoms include systematic disorders (such as Fever, Cough, Fatigue, Sputum Production, Headache and Diarrhea) and respiratory disorders (such as Rhinorrhea, Sneezing, Sore Throat and Pneumonia).
Hellewell at al. [7] proposed a stochastic transmission mathematical model to assess whether isolation is an effective method to control the transmission of the COVID-19 disease. They found that case isolation is enough to control the transmission of the disease within 3 months.
The World Health Organization (WHO), in their situation report about COVID-19 [8], defined three cases of COVID-19 patients: suspect case, probable case and confirmed case. A suspect case is defined as a patient with Fever and at least one more symptom (such as Cough, Shortness of Breath … etc.) and, in some cases, a history of travel to a suspicious area. A probable case is defined as a suspect case with a pending lab test, while a confirmed case is defined as a patient with a positive lab test result.
2.2. One-class learning
One-class learning [9,10] is the problem of learning a model from a training dataset that has instances from only one class, with the absence of instances from the counter class. The learnt model should be able to distinguish between instances that belong to either the target class or the absent class. Several one-class learning algorithms are available in the literature. Some of these algorithms employ data generation methods to generate artificial data from the second (absent) class, and then use the traditional two-class learning algorithms [9,11].
Other algorithms try to learn the distribution of the available training instances [9,12] or learn a compact boundary that encloses most of the training instances [9,13]. A new instance that follows the learnt distribution, or lies inside the learnt boundary, is assigned to the target class. Otherwise, it is assigned to the absent class. These algorithms include one-class Support Vector Machines (SVM) [14].
2.3. One-class feature selection
Feature selection [15,16], also known as attribute selection, is the process of selecting a subset of relevant or important features to be used in the learning process, and thus removing all irrelevant and redundant features. The selected features should be able to represent the original dataset without a substantial loss in the prediction performance. This process helps in (1) reducing the time complexity of the learning process by removing all irrelevant features from the feature space and (2) highlighting the most important and informative features that contribute most to the learnt model, and to the predictive variable.
Feature selection can also be used to rank the current features within a given dataset, based on their importance, starting from the most informative features down to the least informative [16]. If a weight that quantifies the importance and informativeness of a feature can be assigned to each feature in the dataset, it helps in the ranking process, and it can be reflected in the learning process as well, by putting more emphasis on the most important features during the learning process.
To do so, several measures can be extracted from the dataset to evaluate the importance of each feature. These measures consider several factors. Liu and Motoda [16] define the importance of a feature as the change that occurs to a specific measure after the removal of that feature from the dataset. In a later study [17], the authors defined a set of categories for feature importance measures. These categories include:
-
•
Distance. This category studies how the feature makes the training instances far from each other.
-
•
Information. This category studies the change in the information gain after and before the removal of the feature of interest.
-
•
Dependency. This category studies how dependent each feature is on the others.
-
•
Consistency. This category studies how consistent each feature is in predicting the output variable.
Although many feature selection methods have been proposed for regular classification problems, few studies have investigated the application of these methods to one-class datasets. One of the most interesting studies on feature selection for one-class problems was done by Lorena et al. [18]. The authors proposed five feature selection measures from the different categories mentioned above. These measures are: Spectral Score, Information Score, Pearson Correlation, Intra-Class Distance and Interquartile Range. The authors then used these measures to rank the features, based on their importance. The resulting rankings were then combined using rank aggregation strategies [19] such as average ranking [20] and majority voting [21,22].
This work employs the five measures proposed in [18]. We also propose an additional measure, called Variance Based Feature Weighting, which allows ranking of the features based on importance, assigning weights of importance to each feature. Next, we explain these feature selection and importance measures.
2.4. Feature importance measures
2.4.1. Spectral score [18]
In this measure, a weighted graph data structure is built using the available dataset. The graph consists of nodes linked by weighted edges. The nodes of the graph are the data instances, while the weights of the edges represent the similarities between the data instances. The similarity between two data instances is computed using the Radial Basis Function (RBF), as shown in Eq. (1).
| (1) |
where, is the similarity between the instances and , and is the standard deviation of the data instances.
The spectrum of the graph is then used to rank the features based on how consistent and similar the data instances are, before and after the removal of each feature.
2.4.2. Information score [18]
The entropy of the data is a measure of its randomness. When the entropy is low, the similarity between the data instances is high. This measure uses the RBF similarity in Eq. (1) to compute the entropy of the data, as shown in Eq. (2).
| (2) |
where, is the entropy of the data, is the number of data instances, and is the similarity matrix for the data instances.
The change in the entropy is then used to rank the features, based on how homogenous and similar the data instances are, before and after the removal of each feature.
2.4.3. Pearson correlation [18]
This measure uses Pearson correlation to compute the correlation between each feature and all other features in the dataset, as shown in Eq. (3).
| (3) |
where, is the total correlation of feature and is the number of features.
The sum of absolute correlation values is then used to rank the features, based on how each feature is associated with other features in the dataset.
2.4.4. Intra-class distance [18]
In this measure, a centroid instance is computed as the average of all data instances. The intra-class distance is then computed as the average distance between the centroid and all data instances, as shown in Eq. (4).
| (4) |
where, is the intra-class distance, is the number of data instances and is the Euclidean distance between the data instance and the centroid .
The change in the intra-class distance is then used to rank the features based on how close the data instances are, before and after the removal of each feature.
2.4.5. Interquartile range [18]
This measure quantifies the variability and dispersion of the data instances by dividing them into four equal parts (, , and ), called quartiles. The interquartile range () is then computed as the difference between the third quartile () and the first one (), as shown in Eq. (5).
| (5) |
The change in the interquartile range is then used to rank the features, based on how dispersed the data instances are, before and after the removal of each feature.
2.5. Summary
The coronavirus disease 2019 (COVID-19) appeared late in 2019. Research is needed to discover the different aspects of the disease, such as its incubation period, its symptoms, its effects on chest CT scans and its transmission.
Some studies identified the main symptoms of the disease. However, none has computationally investigated the importance of each symptom. To do so, a researcher will be faced with datasets that only have information about confirmed COVID-19 cases. This suggests the use of one-class learning and feature selection methods.
Many feature selection methods have been proposed in the literature. However, only a few have focused on a one-class dataset, including spectral score, information score, Pearson correlation, intra-class distance and interquartile range. Also, none of these proposed methods have focused on assigning weights of importance to features in one-class datasets.
With this in mind, we pose the following research question.
Research Question: How could we use feature selection methods to (1) rank the COVID-19 symptoms based on their importance and (2) assign importance weights to each symptom?
3. Methodology
In this section, we present our proposed feature importance measure, as well as the experiments we conducted to evaluate that measure.
3.1. The proposed variance based feature weighting (VBFW) method
This section presents our novel Variance Based Feature Weighting method. First, we define what an important feature is. Then, we describe our feature weighting function. Last, we formally define our proposed VBFW method.
3.1.1. Variance-based importance
If the inclusion of a feature to the training dataset causes the variance of the values of the feature across the data instances to increase, then it is defined to be an important feature. On the other hand, if its inclusion to the dataset causes the variance to decrease, or stay constant, it is not an important feature.
3.1.2. The weighting function
If the dataset contains n instances and m features, then the values of feature i across the n instances form an n-element vector (where n > 1). The variance of the n-element vectors (generated for each of the m features) will also be represented as an n-element vector. The variance comparison in the weighting function will produce an n-element binary vector – with 1 in the jth element if the corresponding element in the original variance (including the feature) is greater than that of the new variance (after removing the feature), and 0 otherwise. The weight of importance of the feature would then depend on the number of ones on that binary vector, which would range between 0 and n. We choose to normalize the weights to values between 0 and 1, by dividing the count of ones in the binary vector by the length of that vector (i.e. n).
3.1.3. Formal definition
In Table 1 , we present the formal definition for our proposed VBFW feature weighting method.
Table 1.
Formal Definition: VBFW Method.
| Let be the dataset of one-class instances with instances and features |
|---|
| Step 1: For each feature , form an n-element feature vector from the values of across the data instances. Each feature vector has a shape of "matrix (n, 1)" and there are m such feature vectors. |
| Step 2: Compute the variance of all feature vectors generated in Step 1. The variance should be taken row-wise resulting in a shape of (n, 1). |
| For each Feature : |
| Step 3: Compute the new variance excluding the n-element vector of feature |
| Step 4: Compare to . The result is an n-element binary vector |
| Step 5: Count the number of ones in . The result is between 0 and |
| Step 6: Assign an importance weight to feature as |
| Output as the set of importance weights of all features |
3.1.4. VBFW method’s intuition
The proposed importance weight of a feature is calculated as the percentage of data instances that saw an inter-feature variance decrease (that is ) after removing said feature. When the proposed VBFW method works in a feature space that binarizes the presence of a feature, the direction of the change of variance from removing a feature is influenced by how many total positive (i.e. present) features a data instance has. The variance of equally likely discrete values can be expressed without referring to the mean as squared deviations of all points from each other. When a negative (i.e. absent) feature is removed, if the remaining features are primarily positive (i.e. present), then the variance is likely to decrease. On the other hand, when a positive feature is removed, if the remaining features are primarily negative, then the variance is likely to decrease.
In other words, features with higher importance weights are essentially those that are less likely to co-exist with other features. The fact that a feature has high importance weight reflects the possibility that it is less likely to be present with other features. The less important features are likely to be regarded as supplementary features that typically accompany more common ones.
Thus, one main characteristic of the proposed VBFW method is that it is largely determined by the co-occurrence of features in a data instance. Therefore, if the data instances are representing an application that correlates with this characteristic, then the proposed VBFW is recommended, otherwise, it is not.
Similarly, the behavior of the proposed VBFW method when dealing with datasets that have features with continuous and/or multiple discrete values could be summarized as follows. The direction of the change of variance from removing a feature is influenced by how many features of relatively high values a data instance has. When a feature of relatively low value is removed, if the remaining features are primarily of relatively high values, then the variance is likely to decrease. On the other hand, when a feature of relatively high value is removed, if the remaining features are primarily of relatively low values, then the variance is likely to decrease.
3.2. Experimental setup
This section presents the experiments that were conducted in this work to evaluate the proposed feature weighting method.
3.2.1. Dataset
A COVID-19 dataset from the COVID-19 Open Research Dataset (CORD-19) repository [23] was used in this work. The data contains information about 14,251 confirmed cases of COVID-19 patients, geographically distributed as shown in Table 2 . This information does not include information about all symptoms in all of the patients. Further, the data is not well structured for learning and data mining algorithms, such as feature selection. Thus, data preprocessing must be performed.
Table 2.
Distribution of Patients with COVID-2019 across the World.
| Country | Number | Country | Number | ||
|---|---|---|---|---|---|
| 1 | Afghanistan | 2 | 27 | Kuwait | 35 |
| 2 | Algeria | 2 | 28 | Lebanon | 4 |
| 3 | Australia | 30 | 29 | Lithuania | 1 |
| 4 | Austria | 4 | 30 | Malaysia | 40 |
| 5 | Bahrain | 37 | 31 | Nepal | 2 |
| 6 | Belgium | 2 | 32 | Nigeria | 1 |
| 7 | Brazil | 1 | 33 | North Macedonia | 1 |
| 8 | Cambodia | 2 | 34 | Norway | 4 |
| 9 | Canada | 22 | 35 | Oman | 6 |
| 10 | China | 10,663 | 36 | Pakistan | 2 |
| 11 | Croatia | 4 | 37 | Philippines | 6 |
| 12 | Ecuador | 1 | 38 | Romania | 3 |
| 13 | Egypt | 2 | 39 | Russia | 4 |
| 14 | Estonia | 1 | 40 | San Marino | 1 |
| 15 | Finland | 3 | 41 | Singapore | 184 |
| 16 | France | 58 | 42 | South Korea | 1052 |
| 17 | Georgia | 2 | 43 | Spain | 47 |
| 18 | Germany | 74 | 44 | Sri Lanka | 2 |
| 19 | Greece | 1 | 45 | Sweden | 10 |
| 20 | Hong Kong | 94 | 46 | Switzerland | 11 |
| 21 | India | 6 | 47 | Taiwan | 34 |
| 22 | Iran | 46 | 48 | Thailand | 81 |
| 23 | Iraq | 6 | 49 | UAE | 41 |
| 24 | Israel | 5 | 50 | UK | 32 |
| 25 | Italy | 591 | 51 | USA | 35 |
| 26 | Japan | 921 | 52 | Vietnam | 32 |
3.2.2. Data preprocessing
The data was preprocessed and organized as follows. First, cases with symptoms were collected. This resulted in 738 patient records, geographically distributed as shown in Table 3 . Then, the reported symptoms were collected, to form a list of 80 symptoms. Many of these symptoms were synonyms for each other. Thus, we were able to reduce the list to 20 symptoms. This was done in an ad-hoc manner by the two medical doctors, who are co-authors of this work. For example, “anorexia” and “loss of appetite” were merged. (The grouping of the 80 symptoms is included as supplementary material.) The final list is shown in Table 4 , along with the distribution of age and gender. This list was then used to create a 738 × 20 data records for the 738 confirmed COVID-19 cases. Each of the 738 rows represents a patient case. While each column represents a binary feature for each of the 20 symptoms. A value of 1 for a feature means that the corresponding symptom was recorded for the patient. On the other hand, a value of 0 means that the symptom was not recorded. As part of our contribution in this work, we make this preprocessed, cleaned and organized dataset available to researchers upon request.
Table 3.
Distribution of Patients with COVID-2019 across the World, whose Symptoms were Recorded.
| Country | Count | |
|---|---|---|
| 1 | Belgium | 1 |
| 2 | Cambodia | 2 |
| 3 | Canada | 1 |
| 4 | China | 289 |
| 5 | Ecuador | 1 |
| 6 | Finland | 1 |
| 7 | France | 3 |
| 8 | Germany | 4 |
| 9 | Hong Kong | 43 |
| 10 | Italy | 1 |
| 11 | Japan | 278 |
| 12 | Lithuania | 1 |
| 13 | Malaysia | 15 |
| 14 | Nepal | 1 |
| 15 | Nigeria | 1 |
| 16 | Philippines | 2 |
| 17 | Russia | 2 |
| 18 | Singapore | 12 |
| 19 | South Korea | 22 |
| 20 | Spain | 3 |
| 21 | Sri Lanka | 1 |
| 22 | Sweden | 2 |
| 23 | Taiwan | 23 |
| 24 | Thailand | 13 |
| 25 | USA | 4 |
| 26 | Vietnam | 12 |
Table 4.
Dataset Characteristics, including the List of Symptoms.
| Count | ||
|---|---|---|
| Age | ||
| 0−14 | 19 | |
| 15−49 | 337 | |
| 50−64 | 200 | |
| >=65 | 182 | |
| Gender | ||
| Female | 307 | |
| Male | 431 | |
| Symptoms | ||
| 1 | Anorexia | 5 |
| 2 | Fatigue | 122 |
| 3 | Conjunctivitis | 2 |
| 4 | Cough | 294 |
| 5 | Fever | 560 |
| 6 | Chill | 48 |
| 7 | Myalgias | 80 |
| 8 | Sore Throat | 49 |
| 9 | Shortness of Breath | 27 |
| 10 | Sputum | 32 |
| 11 | Runny Nose | 16 |
| 12 | Diarrhea | 30 |
| 13 | Headache | 36 |
| 14 | Pneumonia | 3 |
| 15 | Abdominal Pain | 1 |
| 16 | Pleural Effusion | 17 |
| 17 | Chest Pain | 18 |
| 18 | Vomiting | 8 |
| 19 | Flu | 31 |
| 20 | Sweating | 1 |
3.2.3. Experiment I: spectral score
In this experiment, we applied the Spectral Score feature selection measure to our COVID-19 dataset. The features (i.e. 20 symptoms) were then ranked, based on this measure. Below are the detailed steps followed in this experiment.
-
(1)
Compute a 738 × 738 similarity matrix S between the 738 instances in our dataset, using Eq. (1)
-
(2)
Normalize the similarity matrix S to the range [0,1] (Note: Although Eq. (1) already returns values in the range [0,1], this step stretches the components of the matrix to the entire spectrum of [0,1])
-
(3)For each feature f of the 20 features (i.e. symptoms)
-
aCompute a new 738 × 738 similarity matrix Sn after removing the feature f, using Eq. (1)
-
bNormalize Sn to the range [0,1]
-
cCompute the Spectral Score SPEC for the feature f as the Euclidean distance between the two similarity matrices (S, Sn)
-
a
-
(4)
Rank the symptoms (features) based on their spectral scores (higher values indicate more important symptoms).
3.2.4. Experiment II: information score
In this experiment, we applied the Information Score feature selection measure to our COVID-19 dataset. The features (i.e. 20 symptoms) were then ranked based on this measure. Below are the detailed steps followed in this experiment.
-
(1)
Compute a 738 × 738 similarity matrix S between the 738 instances in our dataset, using Eq. (1)
-
(2)
Normalize the similarity matrix S to the range [0.5, 1]
-
(3)
Compute the entropy E for the similarity matrix S, using Eq. (2)
-
(4)For each feature f of the 20 features (i.e. symptoms)
-
(5)
Rank the symptoms (features) based on their information scores (higher values indicate more important symptoms).
3.2.5. Experiment III: Pearson correlation
In this experiment, we applied the Pearson Correlation feature selection measure to our COVID-19 dataset. The features (i.e. 20 symptoms) were then ranked based on this measure. Below are the detailed steps followed in this experiment.
-
(1)For each feature f of the 20 features (i.e. symptoms)
-
aCompute the correlation coefficients between the feature f and the rest of the 19 features
-
bCompute the Pearson Correlation PC for the feature f as the summation of the absolute values of the 19 correlation coefficients, using Eq. (3)
-
a
-
(2)
Rank the symptoms (features) based on their Pearson correlation (higher values indicate more important symptoms – a feature that is highly correlated with all other features can represent and replace all of them, and thus, the feature is highly important).
Note that there are different types of correlation computation methods such as Pearson, Spearman and Kendall. There are some advantages of using one method over another depending on the type and/or distribution of the data. However, in the case of having binary vectors to represent the input data, which is the case of this study, the results of these correlation methods are identical. Hence, there is no need to compare Pearson correlation with the other methods.
3.2.6. Experiment IV: intra-class distance
In this experiment, we applied the Intra-Class Distance feature selection measure to our COVID-19 dataset. The features (i.e. 20 symptoms) were then ranked based on this measure. Below are the detailed steps followed in this experiment.
-
(1)For each feature f of the 20 features (i.e. symptoms)
-
aCompute a centroid instance by averaging all 738 instances, after removing the feature f
-
bCompute the Intra-Class Distance ICD for the feature f as the average of Euclidean distances between the 738 instances and the centroid, using Eq. (4)
-
a
-
(2)
Rank the symptoms (features) based on their intra-class distance (lower values indicate more important symptoms).
-
(3)
To give greater statistical strength to the results in (1) and (2), compute the standard deviation, as well as the 95 % Confidence Interval, for the average of Euclidean distances of each feature f.
3.2.7. Experiment V: interquartile range
In this experiment, we applied the Interquartile Range feature selection measure to our COVID-19 dataset. The features (i.e. 20 symptoms) were then ranked based on this measure. Below are the detailed steps followed in this experiment.
-
(1)
Compute the interquartile range R for the 738 instances in our dataset, using Eq. (5)
-
(2)For each feature f of the 20 features (i.e. symptoms)
-
aCompute a new interquartile range Rn after removing the feature f, using Eq. (5)
-
bCompute the Interquartile Range IQR for the feature f as the Euclidean distance between the two ranges (R, Rn)
-
a
-
(3)
Rank the symptoms (features) based on their interquartile ranges (higher values indicate more important symptoms).
3.2.8. Experiment VI: rank aggregation
In this experiment, we apply rank aggregation to the ranking results in Experiments I – V. We use the Averaging Method as well as the Majority Method. Below are the detailed steps followed in this experiment.
-
(1)
Compute the ranking for the 20 features (i.e. symptoms) in our dataset, using Experiments I – V.
-
(2)For each ranking result
-
aOrder the features from the most important to the least important
-
bAssign a rank to each feature (1, 2, 3 … 20) such that a rank of 1 goes to the feature with the most important measure value and a rank of 20 goes to the feature with least important measure value
-
a
-
(3)For each feature f of the 20 features (i.e. symptoms)
-
aCompute the average rank
-
bCompute the majority vote rank (in case of equal votes, choose the best rank)
-
a
-
(4)
Rank the symptoms (features) based on their average ranks (lower values are more important)
-
(5)
Rank the symptoms (features) based on their majority vote ranks (lower values are more important)
3.2.9. Experiment VII: our VBFW method
In this experiment, we apply the proposed VBFW method on our COVID-19 dataset. Using this method, quantitative importance weights will be computed for each of the 20 symptoms. Below are the detailed steps followed in this experiment.
-
(1)
For each feature f of the 20 features (i.e. symptoms), form a 738-element vector from the values of f across the 738 data instances
-
(2)
Compute a 738-element variance vector V for the 20 vectors computed in (1)
-
(3)For each feature f of the 20 features (i.e. symptoms)
-
aCompute a new 738-element variance vector Vn after removing the feature f
-
bCompute a 738-element binary vector B to check if V is greater than Vn, using the method in Table 1
-
cCompute the Importance Weight W for the feature f
-
a
-
(4)
Rank the symptoms (features) based on their importance weights (higher values are more important)
3.2.10. Experiment VIII: VBFW performance evaluation and validation
The purpose of this experiment is to validate and quantify the performance of the proposed VBFW method. To do so, we use machine learning evaluation metrics as well as rank-aware evaluation metrics.
3.2.10.1. A. Machine learning evaluation metrics
One way to evaluate feature selection methods is to apply the same machine learning model with the features selected from all feature selection methods, and then use some classification evaluation metrics (such as accuracy) to report the performance [24].
In this part of the experiment, we apply the One-Class Support Vector Machines (OCSVM) [14] with the top five features (i.e. symptoms) selected from each of the six feature selection methods. For each method, the classification accuracy is computed using the well-known 10-fold cross validation method [25]. Below are the detailed steps followed in this part of the experiment.
-
(1)
For each of the six feature selection methods (used in Experiments I – VII), select the top five features (i.e. symptoms)
-
(2)
Create an updated version of our COVID-19 dataset for each of the feature selection method based on the five features (i.e. symptoms) selected in (1)
-
(3)For each of the feature selection methods, use the updated version of the dataset to
-
aCompute a prediction model using OCSVM method
-
bCompute the classification accuracy using the 10-fold cross validation method
-
a
3.2.10.2. B. Rank-aware evaluation metrics
Another way to evaluate feature selection methods is to apply rank-aware evaluation metrics [26] to the ranking results from all feature selection methods. A good feature selection method is the one that puts relevant features very high up the list of ranked features. The rank-aware metrics select the feature selection method that aims to achieve this goal.
There are many rank-aware metrics. Some of which are binary relevance-based metrics such as Mean Reciprocal Rank (MRR) [27] and Mean Average Precision (MAP) [27]. These metrics focus on whether a feature is good (relevant) or not. Other metrics are utility-based metrics, which focus on the degree of goodness (relevance) or relative goodness for each feature, such as the Normalized Discounted Cumulative Gain (NDCG) [27]. Since our proposed VBFW method aims at providing relative order of importance between the features (i.e. symptoms), this work uses the NDCG metric to compare the performance of the ranked results of the proposed VBFW method with those of the other five baseline methods.
The NDGC metric [27] provides a measure of the ranking quality. It does so by comparing the ranked results with ground truth ranking. It is usually computed for the first p ranked items (i.e. at a particular rank position p) and is known as NDGC@p or NDGCp. Its value is between 0 and 1. A higher value means a higher quality ranking. It is given by the following formula:
| (6) |
where,
relp is the graded relevance of the item at position i
RELp is the list of relevant items ordered by their relevance up to position p
This work uses the NDCG implementation provided by [28].
In this part of the experiment, we apply the NDCG@p metric to the proposed VBFW method and the five baseline feature selection methods to quantify their ranked results up to feature (i.e. symptom) at rank position p = 5. The ground truth ranking used in this computation is the result of rank aggregation of Experiment VI, plus two additional rankings provided by two medical doctors. Below are the detailed steps followed in this part of the experiment.
-
(1)
Set the two ranked results of Experiment VI as ground truth
-
(2)
Two medical doctors are asked to rank the 20 symptoms (shown in Table 4) based on their importance in predicting COVID-19.
-
(3)
The two rankings from (2) are added to the ground truth in (1)
-
(4)For each of the six feature selection methods
-
aSelect the top five features (i.e. symptoms) with their relative ranking positions
-
bCompute the NDCG@5 metric
-
a
3.2.11. Experiment IX: important features w.r.t gender, age and country
In Experiment VII, we use the proposed VBFW method to find some important features (i.e. symptoms). These features are across the entire population. However, it might be interesting to detect important features (i.e. symptoms) with respect to people with different genders, ages, and countries, which could then be used for each sub-population.
In this experiment, we split our COVID-19 dataset into partitions based on gender, age and country. Then, we apply our VBFW method to each partition to compute quantitative importance weights for each of the 20 symptoms. Below are the detailed steps followed in this experiment.
-
(1)
Split our COVID-19 dataset into two partitions: one for males and one for females. For each partition, apply the proposed VBFW method to compute the importance weights for each of the 20 symptoms and rank the symptoms based on these weights. (As done in Experiment VII)
-
(2)
Split our COVID-19 dataset into four partitions: one for each age range (as presented in Table 4). For each partition, apply the proposed VBFW method to compute the importance weights for each of the 20 symptoms and rank the symptoms based on these weights. (As done in Experiment VII)
-
(3)
Split our COVID-19 dataset into 26 partitions: one for each country (as presented in Table 3). For each partition, apply the proposed VBFW method to compute the importance weights for each of the 20 symptoms and rank the symptoms based on these weights. (As done in Experiment VII)
4. Results
In this section, we present the results of the nine experiments (I – IX), explained in the previous section.
4.1. Experiment I: spectral score
Table 5 shows a sorted list of the Spectral Score measures for the 20 features (i.e. symptoms) in our dataset, derived from Experiment I. Note: Higher Spectral Scores indicate greater importance. Thus, a rank of 1 is assigned to the feature with the highest Spectral Score and a rank of 20 is assigned to the feature with the lowest Spectral Score.
Table 5.
Spectral Score Ranking.
| Symptom | Spectral Score | Rank |
|---|---|---|
| Cough | 230.69 | 1 |
| Fatigue | 123.00 | 2 |
| Fever | 108.42 | 3 |
| Sore Throat | 102.21 | 4 |
| Shortness of Breath | 73.53 | 5 |
| Myalgias | 66.02 | 6 |
| Runny Nose | 65.00 | 7 |
| Sputum | 53.93 | 8 |
| Headache | 53.59 | 9 |
| Pneumonia | 49.16 | 10 |
| Chill | 42.50 | 11 |
| Chest Pain | 30.61 | 12 |
| Flu | 23.52 | 13 |
| Anorexia | 23.47 | 14 |
| Conjunctivitis | 21.30 | 15 |
| Vomiting | 20.97 | 16 |
| Diarrhea | 11.63 | 17 |
| Abdominal Pain | 6.62 | 18 |
| Sweating | 2.01 | 19 |
| Pleural Effusion | 0.28 | 20 |
4.2. Experiment II: information score
Table 6 shows a sorted list of the Information Score measures for the 20 features (i.e. symptoms) in our dataset, derived from Experiment II. Note: Higher Information Scores indicate greater importance. Thus, a rank of 1 is assigned to the feature with the highest Information Score and a rank of 20 is assigned to the feature with the lowest Information Score.
Table 6.
Information Score Ranking.
| Symptom | Information Score | Rank |
|---|---|---|
| Cough | 53509.44 | 1 |
| Fatigue | 15211.86 | 2 |
| Fever | 11817.36 | 3 |
| Sore Throat | 10504.02 | 4 |
| Shortness of Breath | 5436.19 | 5 |
| Myalgias | 4382.19 | 6 |
| Runny Nose | 4248.27 | 7 |
| Sputum | 2924.31 | 8 |
| Headache | 2888.28 | 9 |
| Pneumonia | 2430.30 | 10 |
| Chill | 1816.27 | 11 |
| Chest Pain | 942.35 | 12 |
| Flu | 556.40 | 13 |
| Anorexia | 554.42 | 14 |
| Conjunctivitis | 456.43 | 15 |
| Vomiting | 442.36 | 16 |
| Diarrhea | 136.35 | 17 |
| Abdominal Pain | 44.43 | 18 |
| Sweating | 4.44 | 19 |
| Pleural Effusion | 0.44 | 20 |
4.3. Experiment III: Pearson correlation
Table 7 shows a sorted list of the Pearson Correlation measures for the 20 features (i.e. symptoms) in our dataset, derived from Experiment III. Note: Higher Pearson Correlations indicate greater importance. Thus, a rank of 1 is assigned to the feature with the highest Pearson Correlation and a rank of 20 is assigned to the feature with the lowest Pearson Correlation.
Table 7.
Pearson Correlation Ranking.
| Symptom | Pearson Correlation | Rank |
|---|---|---|
| Fever | 1.261 | 1 |
| Fatigue | 1.148 | 2 |
| Diarrhea | 1.128 | 3 |
| Chill | 1.055 | 4 |
| Cough | 0.944 | 5 |
| Pneumonia | 0.914 | 6 |
| Myalgias | 0.817 | 7 |
| Shortness of Breath | 0.770 | 8 |
| Sputum | 0.746 | 9 |
| Sore Throat | 0.709 | 10 |
| Headache | 0.704 | 11 |
| Runny Nose | 0.659 | 12 |
| Vomiting | 0.644 | 13 |
| Abdominal Pain | 0.611 | 14 |
| Chest Pain | 0.602 | 15 |
| Flu | 0.514 | 16 |
| Sweating | 0.424 | 17 |
| Anorexia | 0.421 | 18 |
| Pleural Effusion | 0.378 | 19 |
| Conjunctivitis | 0.313 | 20 |
4.4. Experiment IV: intra-class distance
Table 8 shows a sorted list of the Intra-Class Distance measures for the 20 features (i.e. symptoms) in our dataset along with their standard deviation and confidence interval measures, derived from Experiment IV. Note: Lower Intra-Class Distance indicated greater importance. Thus, a rank of 1 is assigned to the feature with the lowest Intra-Class Distance and a rank of 20 is assigned to the feature with the highest Intra-Class Distance. Moreover, the resulting narrow Confidence Intervals (≈ ±0.03) indicates that the average Euclidean distance is a good representative of the sample metric.
Table 8.
Intra-Class Distance Ranking.
| Symptom | Intra-Class Distance | Rank | Standard Deviation | 95 % Confidence Interval |
|---|---|---|---|---|
| Cough | 0.792 | 1 | 0.459 | ±0.033 |
| Fever | 0.866 | 2 | 0.379 | ±0.027 |
| Fatigue | 0.890 | 3 | 0.383 | ±0.028 |
| Sore Throat | 0.913 | 4 | 0.382 | ±0.028 |
| Shortness of Breath | 0.931 | 5 | 0.384 | ±0.028 |
| Myalgias | 0.933 | 6 | 0.381 | ±0.027 |
| Pneumonia | 0.938 | 7 | 0.389 | ±0.028 |
| Runny Nose | 0.941 | 8 | 0.388 | ±0.028 |
| Headache | 0.943 | 9 | 0.386 | ±0.028 |
| Chill | 0.943 | 10 | 0.383 | ±0.028 |
| Sputum | 0.944 | 11 | 0.388 | ±0.028 |
| Vomiting | 0.950 | 12 | 0.388 | ±0.028 |
| Chest Pain | 0.951 | 13 | 0.388 | ±0.028 |
| Diarrhea | 0.952 | 14 | 0.386 | ±0.028 |
| Flu | 0.955 | 15 | 0.393 | ±0.028 |
| Anorexia | 0.956 | 16 | 0.394 | ±0.028 |
| Abdominal Pain | 0.958 | 17 | 0.394 | ±0.028 |
| Conjunctivitis | 0.958 | 18 | 0.395 | ±0.029 |
| Pleural Effusion | 0.959 | 19 | 0.395 | ±0.028 |
| Sweating | 0.959 | 20 | 0.395 | ±0.028 |
4.5. Experiment V: interquartile range
Table 9 shows a sorted list of the Interquartile Range measures for the 20 features (i.e. symptoms) in our dataset, derived from Experiment V. Note: Higher Interquartile Ranges indicate greater importance. Thus, a rank of 1 is assigned to the feature with the highest Interquartile Range and a rank of 20 is assigned to the feature with the lowest Interquartile Range.
Table 9.
Interquartile Range Ranking.
| Symptom | Interquartile Range | Rank |
|---|---|---|
| Fever | 1.521 | 1 |
| Cough | 1.392 | 2 |
| Sore Throat | 1.250 | 3 |
| Runny Nose | 1.250 | 4 |
| Myalgias | 1.199 | 5 |
| Fatigue | 1.118 | 6 |
| Shortness of Breath | 1.118 | 7 |
| Diarrhea | 1.118 | 8 |
| Chill | 1.118 | 9 |
| Headache | 1.031 | 10 |
| Chest Pain | 1.000 | 11 |
| Sputum | 0.901 | 12 |
| Pleural Effusion | 0.901 | 13 |
| Vomiting | 0.901 | 14 |
| Flu | 0.901 | 15 |
| Anorexia | 0.791 | 16 |
| Conjunctivitis | 0.791 | 17 |
| Pneumonia | 0.791 | 18 |
| Abdominal Pain | 0.791 | 19 |
| Sweating | 0.791 | 20 |
4.6. Experiment VI: rank aggregation
Table 10 shows the rank aggregation results derived from Experiment VI, using the Averaging rank aggregation method. Note: Lower rank values indicate greater importance. Thus, the features (i.e. symptoms) were ordered from rank 1 (i.e. most important) to rank 20 (i.e. least important).
Table 10.
Average Rank Aggregation.
| Symptom | SPEC | IS | PC | ICD | IQR | Average Rank |
|---|---|---|---|---|---|---|
| Fever | 3 | 3 | 1 | 2 | 1 | 2 |
| Cough | 1 | 1 | 5 | 1 | 2 | 2 |
| Fatigue | 2 | 2 | 2 | 3 | 6 | 3 |
| Sore Throat | 4 | 4 | 10 | 4 | 3 | 5 |
| Shortness of Breath | 5 | 5 | 8 | 5 | 7 | 6 |
| Myalgias | 6 | 6 | 7 | 6 | 5 | 6 |
| Runny Nose | 7 | 7 | 12 | 8 | 4 | 7.6 |
| Chill | 11 | 11 | 4 | 10 | 9 | 9 |
| Headache | 9 | 9 | 11 | 9 | 10 | 9.6 |
| Sputum | 8 | 8 | 9 | 11 | 12 | 9.6 |
| Pneumonia | 10 | 10 | 6 | 7 | 18 | 10.2 |
| Diarrhea | 17 | 17 | 3 | 14 | 8 | 11.8 |
| Chest Pain | 12 | 12 | 15 | 13 | 11 | 12.6 |
| Vomiting | 16 | 16 | 13 | 12 | 14 | 14.2 |
| Flu | 13 | 13 | 16 | 15 | 15 | 14.4 |
| Anorexia | 14 | 14 | 18 | 16 | 16 | 15.6 |
| Conjunctivitis | 15 | 15 | 20 | 18 | 17 | 17 |
| Abdominal Pain | 18 | 18 | 14 | 17 | 19 | 17.2 |
| Pleural Effusion | 20 | 20 | 19 | 19 | 13 | 18.2 |
| Sweating | 19 | 19 | 17 | 20 | 20 | 19 |
Table 11 shows the rank aggregation results derived from Experiment VI, using the Majority voting rank aggregation method. Note: Lower rank values indicate greater importance. Thus, the features (i.e. symptoms) were ordered from rank 1 (i.e. most important) to rank 20 (i.e. least important).
Table 11.
Majority Vote Rank Aggregation.
| Symptom | SPEC | IS | PC | ICD | IQR | Majority Vote Rank |
|---|---|---|---|---|---|---|
| Fever | 3 | 3 | 1 | 2 | 1 | 1 |
| Cough | 1 | 1 | 5 | 1 | 2 | 1 |
| Fatigue | 2 | 2 | 2 | 3 | 6 | 2 |
| Sore Throat | 4 | 4 | 10 | 4 | 3 | 4 |
| Shortness of Breath | 5 | 5 | 8 | 5 | 7 | 5 |
| Myalgias | 6 | 6 | 7 | 6 | 5 | 6 |
| Runny Nose | 7 | 7 | 12 | 8 | 4 | 7 |
| Sputum | 8 | 8 | 9 | 11 | 12 | 8 |
| Headache | 9 | 9 | 11 | 9 | 10 | 9 |
| Pneumonia | 10 | 10 | 6 | 7 | 18 | 10 |
| Chill | 11 | 11 | 4 | 10 | 9 | 11 |
| Chest Pain | 12 | 12 | 15 | 13 | 11 | 12 |
| Flu | 13 | 13 | 16 | 15 | 15 | 13 |
| Anorexia | 14 | 14 | 18 | 16 | 16 | 14 |
| Conjunctivitis | 15 | 15 | 20 | 18 | 17 | 15 |
| Vomiting | 16 | 16 | 13 | 12 | 14 | 16 |
| Diarrhea | 17 | 17 | 3 | 14 | 8 | 17 |
| Abdominal Pain | 18 | 18 | 14 | 17 | 19 | 18 |
| Pleural Effusion | 20 | 20 | 19 | 19 | 13 | 19 |
| Sweating | 19 | 19 | 17 | 20 | 20 | 19 |
Note: Where the rankings produced by both aggregation methods agreed, they are shown in bold in Tables X and XI above.
4.7. Experiment VII: our VBFW method
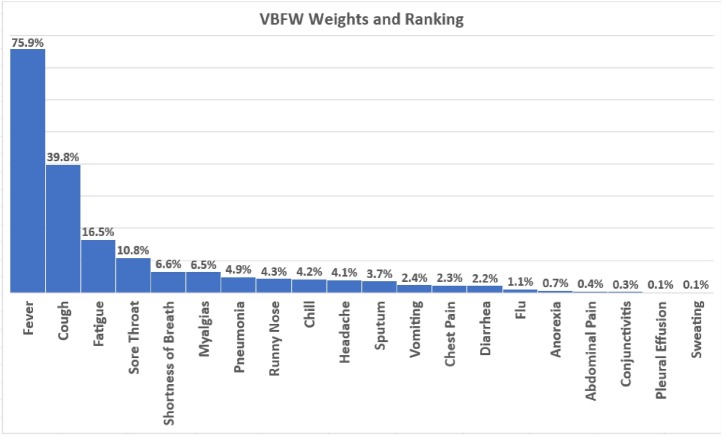
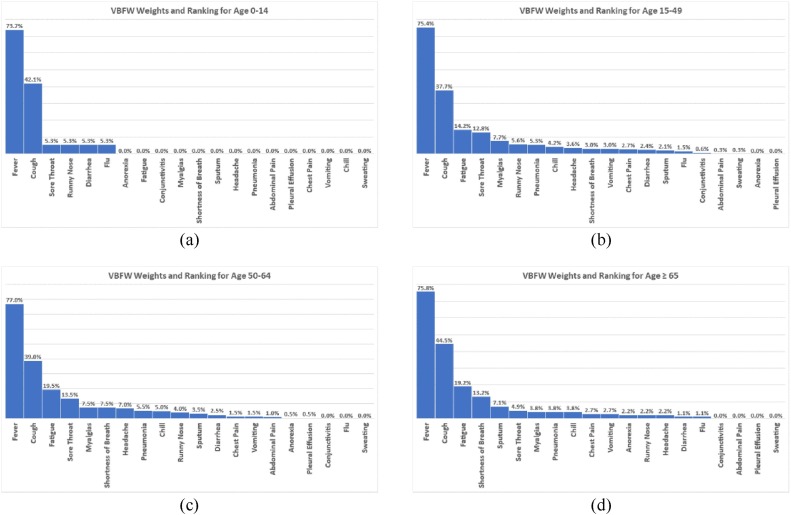
Fig. 1 shows the results of applying the proposed VBFW method to our dataset, derived from Experiment VII. The figure shows the importance weights (in percentages) assigned to each of the 20 features (or symptoms) along with their ranking.
Fig. 1.
VBFW Weights and Ranking.
4.8. Experiment VIII: VBFW performance evaluation and validation
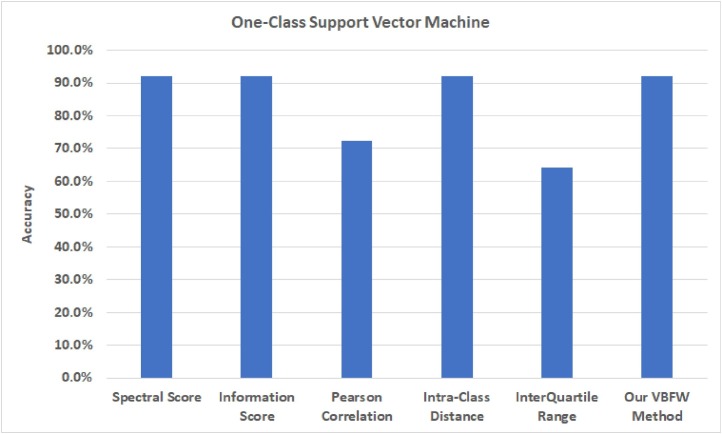
Fig. 2 shows the results of applying one-class Support Vector Machine to our dataset using the top five features (or symptoms) resulted from each of the six feature selection methods, derived from Experiment VIIIA. The figure shows the 10-fold cross validation accuracy (in percentages) for each feature selection method.
Fig. 2.
One-Class SVM Prediction Accuracy.
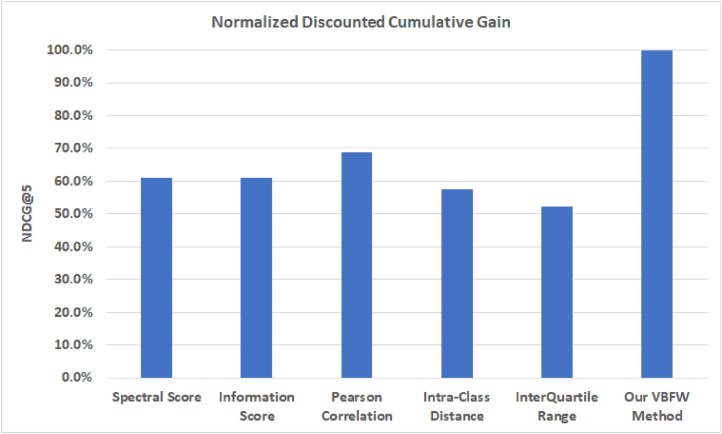
Fig. 3 shows the results of applying rank-aware evaluation and validation to ranked results generated from each of the six feature selection methods, derived from Experiment VIIIB. The figure shows the NDCG@5 (in percentages) for each feature selection method.
Fig. 3.
Rank-Aware Evaluation using Normalized Discounted Cumulative Gain.
4.9. Experiment IX: important features w.r.t gender, age and country
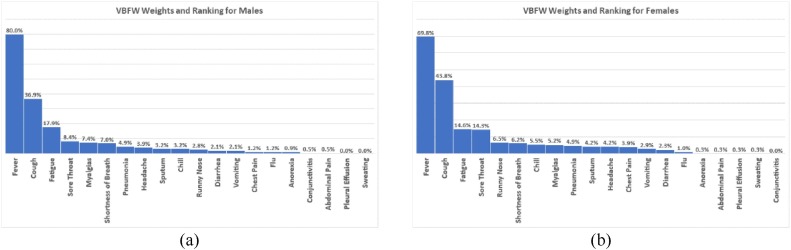
Fig. 4 shows the results of applying the proposed VBFW method to our dataset when split based on gender, derived from Experiment IX. The figure shows the importance weights (in percentages) assigned to each of the 20 features (or symptoms) along with their ranking.
Fig. 4.
VBFW Weights and Ranking for (a) Males and (b) Females.
Fig. 5 shows the results of applying the proposed VBFW method to our dataset when split based on age, derived from Experiment IX. The figure shows the importance weights (in percentages) assigned to each of the 20 features (or symptoms) along with their ranking.
Fig. 5.
VBFW Weights and Ranking for People of Age (a) 0-14, (b) 15-49, (c) 50-64 and (d) ≥ 65.
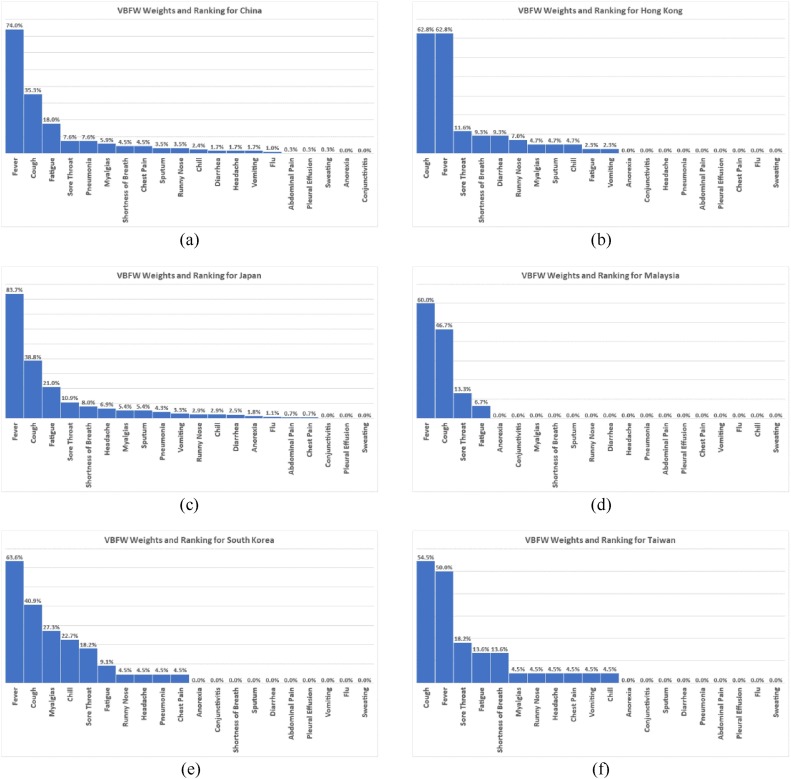
Fig. 6 shows the results of applying the proposed VBFW method to our dataset when split based on country, derived from Experiment IX. The figure shows the importance weights (in percentages) assigned to each of the 20 features (or symptoms) along with their ranking.
Fig. 6.
VBFW Weights and Ranking for People in (a) China, (b) Hong Kong, (c) Japan, (d) Malaysia, (e) South Korea and (f) Taiwan.
5. Discussion of results
5.1. Experiments I – VI: the five feature importance ranking methods
The results presented in Table 5, Table 6 indicate that the five most important symptoms of COVID-19 confirmed cases (based on the spectral score as well as the information score measures) are as follows, starting from the most important to least important:
Cough, Fatigue, Fever, Sore Throat, Shortness of Breath
The results presented in Table 7 indicate that the five most important symptoms of COVID-19 confirmed cases (based on the Pearson correlation measure) are as follows, starting from the most important to least important:
Fever, Fatigue, Diarrhea, Chill, Cough
The results presented in Table 8 indicate that the five most important symptoms of COVID-19 confirmed cases based on the intra-class distance measure are as follows, starting from the most important to least important:
Cough, Fever, Fatigue, Sore Throat, Shortness of Breath
The results presented in Table 9 indicate that the five most important symptoms of COVID-19 confirmed cases (based on the interquartile range measure) are as follows, starting from the most important to least important:
Fever, Cough, Sore Throat, Runny Nose, Myalgias
In summary, for our COVID-19 dataset, the use of different feature selection measures provided different importance levels for the top-five ranked symptoms, and even different sets of important symptoms. This is due to the fact that each of the five measures for feature selection (or importance) ranks the symptoms based on different data characteristics.
For example, the spectral score and information score measures focus on the similarity and consistency of the data, while the intra-class distance measure focuses on the dissimilarity with the centroid artificial instance. On the other hand, the Pearson correlation measure focuses on the association and correlation between the features, while the interquartile range measure focuses on the features with more concentrated values.
Taken together, this suggests that each of the five measures has advantages and disadvantages. All of these rankings can be aggregated, to combine the distinct aspects of the data considered by each measure.
The aggregation results presented in Tables 10 and 11 show that the five most important symptoms of COVID-19 confirmed cases (based on both the average ranking and the majority vote ranking aggregation methods) are as follows, starting from the most important to least important. (Fever and cough were ranked equally in both aggregations.)
Fever/Cough, Fatigue, Sore Throat, Shortness of Breath
The fact that the results for the top five symptoms from both of these aggregation ranking methods were identical supports the identification of these five symptoms as being the most indicative of COVID-19 in these confirmed cases.
5.2. Experiment VII: our VBFW method
The results presented in Fig. 1 indicate that the five most important symptoms of COVID-19 (based on the proposed Variance Based Feature Weighting (VBFW) method) are as follows, starting from the most important to least important:
Fever, Cough, Fatigue, Sore Throat, Shortness of Breath
Note that the VBFW method ranked fever much higher than cough, based on its quantitative importance measures for each of those symptoms (Fever - 75 %, Cough - 39.8 %, Fatigue - 16.5 %, Sore Throat - 10.8 %, and Shortness of Breath - 6.6 %).
These percentages show that, out of the five most important symptoms (i.e. Fever, Cough, Fatigue, Sore Throat, Shortness of Breath), Fever and Cough symptoms are common to a very high percentage of confirmed COVID-19 cases.
Since this work deal with a feature space that binarizes the presence of a feature (i.e. symptom) in unstructured text, the direction of the change of variance from removing a symptom is influenced by how many total present symptoms a case has. Symptoms with higher importance weights are essentially those that are less likely to co-exist with other symptoms. The fact that fever has high importance weight reflects the possibility that it is less likely to be mentioned with other symptoms. In other words, when fever is reported, people may be less inclined to report other symptoms. The less important symptoms such as anorexia and sweating are likely to be regarded as secondary symptoms that typically accompany more common ones such as fever and cough. In this work, the proposed VBFW method is largely determined by the co-occurrence of symptoms in a case.
5.3. Experiment VIII: VBFW performance evaluation and validation
The results presented in Fig. 2 indicate that building a one-class Support Vector Machine model using the five most important features (or symptoms) resulted from our VBFW method (i.e. Fever, Cough, Fatigue, Sore Throat, Shortness of Breath) outperforms that of using other features. The built model achieved an accuracy of 92.1 % using the 10-fold cross validation method. Note that these results represent a rank-less performance evaluation, in which the rank order of the top five features (or symptoms) does not affect the performance of the built model.
On the other hand, the results presented in Fig. 3 indicate that the ranking of the features (or symptoms) based on their importance resulted from our VBFW method outperforms those resulted from the other five feature selection method. The VBFW ranking achieved a normalized discounted cumulative gain of 100 % using the top five symptoms (i.e. NDCG@5). Note that these results represent a rank-aware performance evaluation, in which the rank order of the top five features (or symptoms) affects the performance of the feature selection method.
Taken together, the results of Experiment VIII suggest that our proposed VBFW method outperforms five state-of-the-art feature selection methods.
5.4. Experiment IX: important features w.r.t gender, age and country
5.4.1. Important features w.r.t gender
The results presented in Fig. 4(a) indicate that the five most important symptoms of COVID-19 for males are as follows, starting from the most important to least important:
Fever, Cough, Fatigue, Sore Throat, Myalgias
The results presented in Fig. 4(b) indicate that the five most important symptoms of COVID-19 for females are as follows, starting from the most important to least important:
Fever, Cough, Fatigue, Sore Throat, Runny Nose
This suggests that although the first four important symptoms are common for both males and females who are infected with COVID-19, the fifth symptom indicate that males are likely to suffer from Myalgias while females are likely to suffer from Runny Nose.
5.4.2. Important features w.r.t age
The results presented in Fig. 5(a) indicate that the five most important symptoms of COVID-19 for people of age 0−14 are as follows, starting from the most important to least important:
Fever, Cough, Sore Throat / Runny Nose / Diarrhea / Flu
The results presented in Fig. 5(b) indicate that the five most important symptoms of COVID-19 for people of age 15−49 are as follows, starting from the most important to least important:
Fever, Cough, Fatigue, Sore Throat, Myalgias
The results presented in Fig. 5(c) indicate that the five most important symptoms of COVID-19 for people of age 50−64 are as follows, starting from the most important to least important:
Fever, Cough, Fatigue, Sore Throat, Myalgias
The results presented in Fig. 5(d) indicate that the five most important symptoms of COVID-19 for people of age ≥ 65 are as follows, starting from the most important to least important:
Fever, Cough, Fatigue, Shortness of Breath, Sputum
This suggests that kids of age 0−14 who are infected with COVID-19 are likely to suffer from Runny Nose, Diarrhea and Flu rather than Fatigue and Shortness of Breath. It also suggests that people of age 15–64 are likely to suffer from Myalgias rather than Shortness of Breath, and elderly people are likely to suffer from Sputum rather than Sore Throat.
5.4.3. Important features w.r.t country
The results presented in Fig. 6(a) indicate that the five most important symptoms of COVID-19 for people in China are as follows, starting from the most important to least important:
Fever, Cough, Fatigue, Sore Throat, Pneumonia
The results presented in Fig. 6(b) indicate that the five most important symptoms of COVID-19 for people in Hong Kong are as follows, starting from the most important to least important:
Cough / Fever, Sore Throat, Shortness of Breath / Diarrhea
The results presented in Fig. 6(c) indicate that the five most important symptoms of COVID-19 for people in Japan are as follows, starting from the most important to least important:
Fever, Cough, Fatigue, Sore Throat, Shortness of Breath
The results presented in Fig. 6(d) indicate that the four most important symptoms of COVID-19 for people in Malaysia are as follows, starting from the most important to least important:
Fever, Cough, Sore Throat, Fatigue
The results presented in Fig. 6(e) indicate that the five most important symptoms of COVID-19 for people in South Korea are as follows, starting from the most important to least important:
Fever, Cough, Myalgias, Chill, Sore Throat
The results presented in Fig. 6(f) indicate that the five most important symptoms of COVID-19 for people in Taiwan are as follows, starting from the most important to least important:
Cough, Fever, Sore Throat, Fatigue / Shortness of Breath
This suggests that people in China who are infected with COVID-19 are likely to suffer from Pneumonia rather than Shortness of Breath. It also suggests that people in Hong Kong are likely to suffer from Diarrhea rather than Fatigue, and people in South Korea are likely to suffer from Myalgias and Chill rather than Fatigue and Shortness of Breath.
6. Conclusion and future work
In this paper, we posed the following research question:
Q: How could we use feature selection methods to (1) rank the COVID-19 symptoms based on their importance and (2) assign importance weights to each symptom?
A novel Variance Based Feature Weighting (VBFW) method is proposed in this paper. This method is able to (1) rank the features in one-class datasets based on their importance and (2) assign quantitative importance weights to each of these features.
The results presented in this paper show that the proposed VBFW method provides weight assignment for the features (symptoms) of the COVID-19 one-class dataset that is equal to, or better than, the feature ranking results obtained by state-of-the-art methods. The results also show that the proposed VBFW method achieved an accuracy of 92.1 % when used to build a one-class SVM model, and an NDCG@5 of 100 %.
Overall, the results suggest that symptoms of Fever, Cough, Fatigue, Sore Throat and Shortness of Breath should be considered important symptoms when diagnosing patients for COVID-19, with a particular focus on Fever and Cough symptoms.
The following aspects form future directions and plans for researchers:
-
•
Testing and validating the proposed VBFW method on other available COVID-19 datasets.
-
•
Generalizing the proposed VBFW method to other one-class datasets, beside COVID-19 data.
-
•
Performing further statistical analysis to study the common symptoms on COVID-19 patients with respect to different gender, ages, races and counties. This might include the use of odds ratio.
-
•
Experimenting the proposed VBFW method with datasets that have features with continuous and/or multiple discrete values.
Declaration of Competing Interest
The authors report no declarations of interest.
Footnotes
Supplementary material related to this article can be found, in the online version, at doi:https://doi.org/10.1016/j.artmed.2021.102018.
Appendix A. Supplementary data
The following is Supplementary data to this article:
References
- 1.World Health Organization (WHO) World Health Organization; 2020. Coronavirus disease (COVID-19) pandemic.https://www.who.int/emergencies/diseases/novel-coronavirus-2019 [Google Scholar]
- 2.Lauer Stephen A., Grantz Kyra H., Bi Qifang, Jones Forrest K., Zheng Qulu, Meredith Hannah R., et al. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann Intern Med. 2020 doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bai Yan, Yao Lingsheng, Wei Tao, Tian Fei, Jin Dong-Yan, Chen Lijuan, et al. Presumed asymptomatic carrier transmission of COVID-19. JAMA. 2020 doi: 10.1001/jama.2020.2565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Shi Heshui, Han Xiaoyu, Jiang Nanchuan, Cao Yukun, Alwalid Osamah, Gu Jin, et al. Radiological findings from 81 patients with COVID-19 pneumonia in Wuhan, China: a descriptive study. Lancet Infect Dis. 2020 doi: 10.1016/S1473-3099(20)30086-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bernheim Adam, Mei Xueyan, Huang Mingqian, Yang Yang., Fayad Zahi A., Zhang Ning, et al. Chest CT findings in coronavirus disease-19 (COVID-19): relationship to duration of infection. Radiology. 2020 doi: 10.1148/radiol.2020200463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rothan Hussin A., Byrareddy Siddappa N. The epidemiology and pathogenesis of coronavirus disease (COVID-19) outbreak. J Autoimmun. 2020 doi: 10.1016/j.jaut.2020.102433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hellewell Joel, Abbott Sam, Gimma Amy, Bosse Nikos I., Jarvis Christopher I., Russell Timothy W., et al. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob Health. 2020 doi: 10.1016/S2214-109X(20)30074-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.World Health Organization. Coronavirus disease 2019 (COVID-19): situation report, 67, 2020.
- 9.Tax David Martinus Johannes. 2002. One-class classification: concept learning in the absence of counter-examples; p. 0584. [Google Scholar]
- 10.Khan Shehroz S., Madden Michael G. A survey of recent trends in one class classification. In Irish Conference on Artificial Intelligence and Cognitive Science; Springer, Berlin, Heidelberg; 2009. pp. 188–197. [Google Scholar]
- 11.Bánhalmi András, Kocsor András, Busa-Fekete R.óbert. Counter-example generation-based one-class classification. European Conference on Machine Learning; Springer, Berlin, Heidelberg; 2007. pp. 543–550. [Google Scholar]
- 12.Hempstalk Kathryn, Frank Eibe, Witten Ian H. One-class classification by combining density and class probability estimation. Joint European Conference on Machine Learning and Knowledge Discovery in Databases; Springer, Berlin, Heidelberg; 2008. pp. 505–519. [Google Scholar]
- 13.Schölkopf Bernhard, Platt John C., Shawe-Taylor John, Smola Alex J., Williamson Robert C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001;13(7):1443–1471. doi: 10.1162/089976601750264965. [DOI] [PubMed] [Google Scholar]
- 14.Rätsch Gunnar, Schölkopf Bernhard, Mika Sebastian, Müller Klaus-Robert. GMD-Forschungszentrum Informationstechnik. 2000. SVM and boosting: one class. [Google Scholar]
- 15.Liu Huan, Motoda Hiroshi, Setiono Rudy, Zhao Zheng. Feature selection in data mining. 2010. Feature selection: an ever evolving frontier in data mining; pp. 4–13. [Google Scholar]
- 16.Liu Huan, Motoda Hiroshi., editors. Vol. 453. Springer Science & Business Media; 1998. (Feature extraction, construction and selection: a data mining perspective). [Google Scholar]
- 17.Liu Huan, Yu Lei. Toward integrating feature selection algorithms for classification and clustering. IEEE Trans Knowl Data Eng. 2005;17(4):491–502. [Google Scholar]
- 18.Lorena Luiz H.N., Carvalho AndréC.P.L.F., Lorena Ana C. Filter feature selection for one-class classification. J Intell Robot Syst. 2015;80(1):227–243. [Google Scholar]
- 19.Prati Ronaldo C. Combining feature ranking algorithms through rank aggregation. In The 2012 International Joint Conference on Neural Networks (IJCNN); IEEE; 2012. pp. 1–8. [Google Scholar]
- 20.Wald Randall, Khoshgoftaar Taghi M., Dittman David, Awada Wael, Napolitano Amri. An extensive comparison of feature ranking aggregation techniques in bioinformatics. In 2012 IEEE 13th International Conference on Information Reuse & Integration (IRI); IEEE; 2012. pp. 377–384. [Google Scholar]
- 21.Bauer Eric, Kohavi Ron. An empirical comparison of voting classification algorithms: bagging, boosting, and variants. Mach Learn. 1999;36(1–2):105–139. [Google Scholar]
- 22.Tsymbal Alexey, Pechenizkiy Mykola, Cunningham P.ádraig. Diversity in search strategies for ensemble feature selection. Inf Fusion. 2005;6(1):83–98. [Google Scholar]
- 23.COVID-19 Open Research Dataset (CORD-19). 2020. Version 2020-03-13. Retrieved from https://pages.semanticscholar.org/coronavirus-research. Accessed 2020-03-22. doi:10.5281/zenodo.3715506.
- 24.Čehovin Luka, Bosnić Zoran. Empirical evaluation of feature selection methods in classification. Intell Data Anal. 2010;14(3):265–281. [Google Scholar]
- 25.Tan Pang-Ning, Steinbach Michael, Kumar Vipin. Pearson Education; India: 2016. Introduction to data mining. [Google Scholar]
- 26.The Startup, MRR vs MAP vs NDCG: Rank-Aware Evaluation Metrics and when to Use Them, [online]: https://medium.com/swlh/rank-aware-recsys-evaluation-metrics-5191bba16832, Accessed Aug 2020.
- 27.Harman Donna. Information retrieval evaluation. Synth Lect Inf Concepts Retr Serv. 2011;3(2):1–119. [Google Scholar]
- 28.MathWorks, Normalized Discounted Cumulative Gain (NDCG), [online]: https://www.mathworks.com/matlabcentral/fileexchange/65570-normalized-discounted-cumulative-gain-ndcg, Accessed Aug 2020.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.