Highlights
-
•
The addition of flu could cripple the health care system during the COVID-19 pandemic.
-
•
Fears of coronavirus have intensified the shortage of flu vaccine in developing countries.
-
•
We present an optimization model for equitable flu vaccine distribution.
-
•
The model utilizes an equitable objective function to distribute vaccines to high-risk people.
-
•
We present a case study to exhibit efficacy and demonstrate the model’s applicability.
Keywords: Vaccine supply chain, Healthcare equitability, Inventory-location problem, Mixed-integer linear programming, Influenza virus
Abstract
The addition of other respiratory illnesses such as flu could cripple the healthcare system during the coronavirus disease 2019 (COVID-19) pandemic. An annual seasonal influenza vaccine is the best way to help protect against flu. Fears of coronavirus have intensified the shortage of influenza shots in developing countries that hope to vaccinate many populations to reduce stress on their health services. We present an inventory-location mixed-integer linear programming model for equitable influenza vaccine distribution in developing countries during the pandemic. The proposed model utilizes an equitable objective function to distribute vaccines to critical healthcare providers and first responders, elderly, pregnant women, and those with underlying health conditions. We present a case study in a developing country to exhibit efficacy and demonstrate the optimization model’s applicability.
1. Introduction
The emergence and spread of diseases, such as Middle East Respiratory Syndrome, influenza, and Ebola have threatened people’s health and lives. Vaccines increase the likelihood of preventing the spread of these diseases and save the lives of millions of people, including children and the elderly [1]. Unfortunately, many countries, especially developing countries, often encounter a shortage of vaccines [2]. Many factors can cause a vaccine shortage. Production monopoly, complex production processes, increased oversight of manufacturing facilities, unforeseen fluctuations in demand, and reduced producers are the most frequently cited reasons for vaccine shortage [3], [4], [5], [6].
There are four components in the vaccine supply chain: product (what type of vaccine is needed?), production (how many vaccines should be produced and when?), allocation (who should receive the vaccine?), and distribution (how should the vaccine be distributed?) [7]. An effective vaccine distribution chain used to distribute vaccines from producers to consumers requires an efficient overall structure, an examination of the demand rate and inventory requirements, and identifying suitable vaccine distribution locations. Jacobson et al. [2] proposed a stochastic inventory model for evaluating pediatric vaccine supply. This model aimed to examine the inventory of pediatric vaccines to combat production interruptions in the United States. Their model showed that if the disruption in production is less than six months, the vaccine’s stockpile level would be sufficient; otherwise, some shortages leading to disease spread would occur. Uscher-Pines et al. [8] proposed a systematic analysis for proposing policies to deal with the influenza vaccine shortage in the United States. Using the brainstorming method and Strengths, Weaknesses, Opportunities, and Threats (SWOT) analysis, they developed a framework for purchasing, producing, and distributing vaccines.
Straetemans et al. [9] investigated the distribution prioritization of influenza vaccine in 27 European Union countries and four non-European Union countries. They utilized experts in the distribution planning department and collected data via telephone, email, and fax. Their findings showed that 26 states had considered at least one high-priority group for vaccination. According to their research, essential service providers, healthcare workers, and high-risk individuals were the most common high-priority groups for vaccination. Shrestha et al. [10] studied pediatric vaccine storage and proposed a model for supply shortages, cost, and health impacts. Their model examined the shortage cost of 14 pediatric vaccines and their health impacts using scenario analysis. Samii et al. [11] developed an inventory control model for reserving and allocating the influenza vaccine. Abrahams and Ragsdale [12] presented a decision support system for minimizing total vaccination scheduling costs based on a binary integer programming model and genetic algorithm. Meshkini et al. [13] studied the opportunities and threats associated with vaccine production in Iran required by the world trade organization (WTO). The results showed that the main challenges for joining the WTO were the absence of firm internal intellectual property rules, the use of old equipment, and the lack of cooperation with global vaccine companies. Privett and Gonsalvez [14] identified and prioritized vaccine supply chain challenges in developing countries through interviews and surveys. A multi-objective possibilistic programming model was proposed by Pishvaee et al. [15] to design a sustainable medical supply chain network. They considered the economic, social, and environmental aspects of the needle and syringe supply chain in Iran to validate their model. Lydon et al. [16] analyzed vaccine outsourcing by analyzing data from a vaccine supply chain in South Africa. The results showed that the outsourcing of some parts of the vaccine supply chain could reduce costs and increase supply chain efficiency.
A mixed-integer linear programming (MILP) model was developed by Saif and Elhedhli [17] to design a vaccine supply chain by including environmental considerations. They used a novel hybrid simulation–optimization approach to solve and validate their model. Cernuschi et al. [18] studied the balance between supply and demand for the Bacillus Calmette-Guérin vaccine by examining global demand, global supply, product registration, vaccine shortage, and global demand–supply balance. Gooding et al. [19] conducted a study to investigate vaccine stockouts’ effect on immunization. They presented a conceptual model that showed the relationship between routine immunization and vaccine availability. Their model considered economic status, ethnicity, cultural and religious belief by examining the national immunization supply chain data. Vaccines are highly sensitive to temperature, and their transportation at unfavorable temperatures significantly affects their quality. Lin et al. [20] developed a vaccine transportation model by utilizing a cold supply chain network. Their model analyzed how the inspection policy of the retailer influences the distributor’s decision. Zandkarimkhani et al. [21] proposed a bi-objective MILP model for distributing Avonex (prefilled syringe for multiple sclerosis disease) under uncertainty. Their distribution model simultaneously minimizes total costs and lost demands. They used a fuzzy goal programming approach to solve and validate their model with data collected from Iran’s Avonex distribution chain. Enayati and Özaltın [22] introduced a mathematical programming model for equitable influenza vaccine distribution in a heterogeneous population. Their model minimizes the vaccine doses allocated to subgroups for preventing the disease outbreak at the early stages of the epidemic. They divided the population into different subgroups and distributed the vaccine justifiably to varying subgroups according to an equity constraint.
This study proposes a mathematical model for equitable influenza vaccine distribution, similar to Enayati and Özaltın [22]. However, we go one step further and introduce a new concept for equitable vaccine distribution using a customizable objective function applicable to the COVID-19 vaccine. In addition, unlike the Enayati and Özaltın’s [22] model, we consider the location of distribution centers and storage facilities, vaccine shortage, and budget constraints in the proposed model. In summary, this study addresses the following questions:
-
•
How can an optimization model address the need for an equitable influenza vaccine distribution to a heterogeneous population?
-
•
Which distribution centers should be included in an equitable vaccine distribution model?
-
•
How many vaccine doses should be stored in each distribution center?
-
•
How many vaccine doses should be made available to each group?
The contributions of this study are threefold. We (i) propose an equitable model to classify heterogeneous populations for influenza vaccine distribution during the COVID-19 pandemic; (ii) propose a novel MILP model for equitable influenza vaccine distribution considering inventory-location problems; and (iii) demonstrate the applicability and efficacy of the proposed vaccine distribution model with real-world data.
The remainder of the paper is organized as follows. In Section 2, we define the problem and formulate the model. In Section 3, we present a case study to demonstrate the applicability of the method proposed in this study. In 4, 5, we propose sensitivity analysis and managerial implications, respectively. In Section 6, we conclude with our conclusions and future research directions.
2. Problem definition and proposed model
The prevalence of the seasonal flu virus starts every year with the arrival of the year’s cold seasons (i.e., fall and winter) and the spread of infectious diseases. The seasonal flue affects over five million people annually and leads to 290,000–650,000 deaths annually [23]. Due to the outbreak of coronavirus disease 2019 (COVID-19), the world’s population will experience difficult fall and winter this year (i.e., 2020) since the seasonal flu virus will spread in parallel with COVID-19. Although the flu virus has many mutations, and the mutated virus’s vaccine is produced and distributed each year [24], one of the problems is accessibility to this vaccine as it is produced and distributed by a limited number of countries.
On the other hand, many countries cannot supply the flu vaccine to the entire population due to seasonal shortages. Therefore, it is crucial to develop a practical approach to equitable distribution of vaccines in these countries. Equitable distribution does not always mean equal distribution among individuals, but rather a distribution in which more needy people have a higher priority than less needy people. Accordingly, this paper presents a mixed-integer linear programming model for equitable distribution of the influenza vaccine among different groups of people with varying priorities. The prioritization model requires a balance between helping society and protecting an individual’s health. The supply chain consists of two levels: a supply point (i.e., distribution center) and multiple demand points (i.e., city, state, province, etc.). The health experts group residents in each demand point according to pre-determined criteria. This grouping will determine the need for vaccination in each demand point. The proposed model is used to distribute the vaccines equitably among the demand points according to the following assumptions:
-
•
The proposed model is a single product multi-period distribution model.
-
•
The model determines the optimal location for the distribution center.
-
•
The distribution center is capacitated.
-
•
The demand point (warehouse) has storage facilities for future periods.
-
•
The model considers the possibility of a shortage.
3. Mathematical model
3.1. Indices
| Demand point (Province) | |
|---|---|
| Group type | |
| Distribution center | |
| Time-period |
3.1.1. Parameters
| The total demand of group i for influenza vaccine in province p | |
|---|---|
| Cost of setting up the distribution center k | |
| The per-dose purchasing cost of the influenza vaccine | |
| The per-dose transportation cost of the influenza vaccine from distribution center k to province p | |
| The per-dose holding cost of the influenza vaccine in province p warehouse for each time-period | |
| The minimum percentage of group i to be covered (coverage rate) | |
| The maximum capacity of distribution center k for supplying influenza vaccine in time-period t | |
| Budget | |
| A big number |
3.1.2. Variables
| Binary | If distribution center k is set up | |
|---|---|---|
| Otherwise | ||
| Integer | Number of influenza vaccines allocated to group i in province p in time-period t | |
| Integer | Number of influenza vaccines stored in province p warehouse in time-period t | |
| Integer | Number of influenza vaccines shipped from distribution center k to province p warehouse in time-period t |
3.1.3. Objective function
| (1) |
s.t.
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
The objective function distributes vaccines equitably by maximizing the minimum delivery-to-demand ratio per group in each province and each time-period. This objective function is a novel and new concept for equitable vaccine distribution. The objective function’s underlying premise is the demand at each node, and the trade-off between the nodes, are established according to a delivery-to-demand ratio. To this end, equitability is enforced at each node by maximizing the minimum delivery-to-demand ratio.
Constraint (2) guarantees that vaccines are assigned to each group, at least at the coverage rate. The inventory balance in the provinces’ warehouses is given in Constraints (3), (4) for the first and the subsequent periods. Constraint (5) ensures the capacity of distribution centers is not violated. Constraint (6) ensures the distribution center is already set up and ready to receive vaccines from the distribution center. Constraint (7) ensures that the total cost of the vaccine supply chain, including setting up cost, purchasing cost, and transportation cost, do not exceed the budget.
3.2. Linearization process
The objective function of the proposed model is nonlinear and requires linearization. This linearization is accomplished by introducing a new free variable () to replace in the objective function. Therefore, the following holds true:
| (8) |
Based on Eq. (8), the following formula always holds true:
| (9) |
Therefore, according to Eqs. (8), (9), the proposed nonlinear model is converted into a linear model as follows:
| (10) |
s.t.
| (11) |
4. Case study
Every year, the seasonal flu virus spreads in Iran and other parts of the world with the arrival of cold seasons. The Iranian government annually buys the flu vaccine from the producing countries in limited quantities, proportional to the population. In 2020, the country’s demand for influenza vaccine has increased sharply due to the outbreak of COVID-19. According to the statistics released by the Iran Ministry of Health and Medical Education (MOHME), this amount has increased ten times compared to that in the last year (http://ird.behdasht.gov.ir). The rising demand, on the one hand, and sanctions, on the other hand, has resulted in a shortage of flu vaccine in Iran. Consequently, MOHME needed an efficient and effective vaccine distribution model to cope with the flu vaccine shortage during the cold season and the COVID-19 pandemic. In this case study, we present a prototype model developed for the MOHME for an equitable and fair distribution of the flu vaccine during the fall and winter flu season. Vaccines are generally distributed according to factors such as medical risks, ethics, public health, equity, economic impact, and logistics, among others. The MOHME considers age, pre-existing medical conditions, pregnancy, and healthcare-related jobs to group potential vaccine recipients into the following eight categories:
-
•
Group 1: Infants and toddlers aged 6 to 35 months
-
•
Group 2: Pregnant women with pre-existing medical conditions
-
•
Group 3: Adults aged 65 years and older with pre-existing medical conditions
-
•
Group 4: Critical healthcare providers and first responders
-
•
Group 5: Pregnant women without pre-existing conditions
-
•
Group 6: Adults aged 65 years and older without pre-existing medical conditions
-
•
Group 7: People with pre-existing medical conditions
-
•
Group 8: Other people
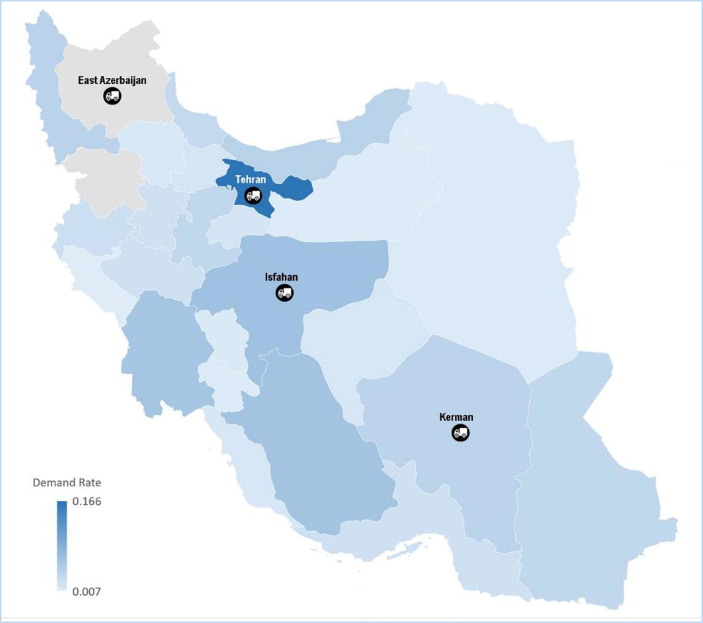
The demand for each group in each province and each group’s coverage rate are presented in Table 1, Table 2 , respectively. The MOHME has selected Tehran, Isfahan, East Azerbaijan, and Kerman (among the 31 available ones) suitable for distribution centers, as shown in Fig. 1 . The transportation cost for each vaccine dose from the four potential distribution centers to the 31 warehouses (provinces) is shown in Table 3 . Each vaccine dose costs the government $14.86, and the total available budget of MOHME for this year is $270,000,000.
Table 1.
The demand for each group in the provinces.
| Province | p | Group |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| East Azerbaijan | 1 | 285,487 | 2250 | 19,557 | 19,157 | 20,252 | 36,324 | 10,040 | 3,516,585 |
| West Azerbaijan | 2 | 209,236 | 842 | 8678 | 13,061 | 15,889 | 42,596 | 4657 | 2,970,260 |
| Ardabil | 3 | 96,045 | 396 | 7059 | 4955 | 5482 | 21,125 | 2275 | 1,133,083 |
| Isfahan | 4 | 543,628 | 2436 | 18,826 | 28,165 | 26,241 | 86,471 | 10,745 | 4,404,338 |
| Alborz | 5 | 444,378 | 1129 | 8504 | 15,732 | 8662 | 32,469 | 4360 | 2,197,166 |
| Ilam | 6 | 50,992 | 99 | 1744 | 1740 | 2086 | 7171 | 1264 | 515,062 |
| Bushehr | 7 | 92,676 | 543 | 2366 | 3490 | 4962 | 12,693 | 3585 | 1,043,085 |
| Tehran | 8 | 1,112,514 | 4598 | 18,135 | 79,606 | 73,328 | 192,077 | 35,476 | 11,751,903 |
| Chaharmahal and Bakhtiari | 9 | 80,727 | 345 | 4360 | 2749 | 3068 | 14,210 | 2709 | 839,592 |
| South Khorasan | 10 | 91,541 | 416 | 1747 | 2922 | 4373 | 10,038 | 1653 | 656,208 |
| Khorasan Razavi | 11 | 555,165 | 1477 | 9157 | 32,173 | 34,646 | 77,489 | 15,706 | 5,708,688 |
| North Khorasan | 12 | 70,181 | 423 | 1830 | 3884 | 4974 | 13,524 | 1615 | 766,661 |
| Khuzestan | 13 | 461,497 | 1286 | 19,525 | 16,958 | 30,037 | 50,966 | 8352 | 4,121,888 |
| Zanjan | 14 | 66,876 | 296 | 2684 | 4230 | 5103 | 12,473 | 2630 | 963,169 |
| Semnan | 15 | 59,558 | 385 | 710 | 2388 | 4214 | 11,302 | 1399 | 622,408 |
| Sistan and baluchestan | 16 | 348,982 | 1449 | 16,537 | 7770 | 18,719 | 39,422 | 5316 | 2,336,819 |
| Fars | 17 | 467,381 | 1066 | 17,138 | 24,256 | 20,367 | 60,885 | 10,672 | 4,249,508 |
| Qazvin | 18 | 97,577 | 379 | 6997 | 5095 | 6727 | 18,116 | 3773 | 1,135,098 |
| Qom | 19 | 74,038 | 481 | 2939 | 5815 | 8002 | 14,176 | 3328 | 1,183,505 |
| Sanandaj | 20 | 140,126 | 1059 | 2123 | 4809 | 5664 | 19,047 | 4993 | 1,425,195 |
| Kerman | 21 | 295,505 | 796 | 4290 | 14,241 | 11,478 | 33,045 | 7671 | 2,797,687 |
| Kermanshah | 22 | 116,921 | 851 | 2222 | 5272 | 7752 | 21,035 | 2369 | 1,796,012 |
| Kohgiluyeh va Buyer Ahmad | 23 | 57,172 | 377 | 3845 | 2068 | 2955 | 7176 | 1350 | 638,116 |
| Golestan | 24 | 166,553 | 1242 | 8662 | 6915 | 8929 | 19,549 | 3770 | 1,653,194 |
| Gilan | 25 | 268,028 | 1671 | 12,551 | 10,123 | 7828 | 33,173 | 7962 | 2,189,354 |
| Lorestan | 26 | 123,254 | 385 | 9020 | 5282 | 11,349 | 17,077 | 5613 | 1,588,669 |
| Mazandaran | 27 | 266,866 | 1129 | 9352 | 14,119 | 21,881 | 32,984 | 10,038 | 2,927,211 |
| Markazi | 28 | 95,074 | 226 | 3773 | 6433 | 8111 | 22,186 | 3320 | 1,290,355 |
| Hormozgan | 29 | 150,240 | 845 | 7141 | 5329 | 7426 | 23,181 | 2560 | 1,579,688 |
| Hamedan | 30 | 156,808 | 258 | 1993 | 6953 | 7755 | 17,034 | 5286 | 1,542,147 |
| Yazd | 31 | 72,962 | 494 | 3263 | 5123 | 7948 | 11,166 | 2923 | 1,034,656 |
Table 2.
The coverage rate for each group.
| Group |
||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Coverage rate | 0.7 | 0.9 | 0.9 | 1 | 0.7 | 0.6 | 0.7 | 0.1 |
Fig. 1.
The geographical location of the potential distribution center.
Table 3.
The transportation cost for each vaccine dose from the potential distribution centers to the warehouses (provinces).
| Province | p | Potential distribution center |
|||
|---|---|---|---|---|---|
| Tehran | Isfahan | East Azerbaijan | Kerman | ||
| East Azerbaijan | 1 | 0.61 | 0.99 | 0.08 | 1.46 |
| West Azerbaijan | 2 | 0.68 | 1.02 | 0.31 | 1.76 |
| Ardabil | 3 | 0.59 | 0.95 | 0.21 | 1.56 |
| Isfahan | 4 | 0.45 | 0.08 | 0.99 | 0.68 |
| Alborz | 5 | 0.12 | 0.40 | 0.60 | 0.96 |
| Ilam | 6 | 0.66 | 0.75 | 0.76 | 1.35 |
| Bushehr | 7 | 0.98 | 0.79 | 1.53 | 1.01 |
| Tehran | 8 | 0.09 | 0.39 | 0.61 | 0.96 |
| Chaharmahal and Bakhtiari | 9 | 0.53 | 0.12 | 0.99 | 0.78 |
| South Khorasan | 10 | 1.01 | 1.21 | 1.39 | 0.81 |
| Khorasan Razavi | 11 | 0.87 | 1.13 | 1.34 | 0.90 |
| North Khorasan | 12 | 0.72 | 1.15 | 1.31 | 0.94 |
| Khuzestan | 13 | 0.81 | 0.74 | 0.98 | 1.28 |
| Zanjan | 14 | 0.33 | 0.72 | 0.29 | 1.17 |
| Semnan | 15 | 0.24 | 0.61 | 0.82 | 1.18 |
| Sistan and baluchestan | 16 | 1.14 | 1.08 | 2.05 | 0.49 |
| Fars | 17 | 0.88 | 0.46 | 1.48 | 0.77 |
| Qazvin | 18 | 0.17 | 0.53 | 0.46 | 1.20 |
| Qom | 19 | 0.22 | 0.32 | 0.51 | 0.98 |
| Sanandaj | 20 | 0.47 | 0.63 | 0.43 | 1.38 |
| Kerman | 21 | 0.96 | 0.68 | 1.46 | 0.08 |
| Kermanshah | 22 | 0.48 | 0.64 | 0.56 | 1.20 |
| Kohgiluyeh va Buyer Ahmad | 23 | 0.74 | 0.70 | 1.43 | 1.00 |
| Golestan | 24 | 0.45 | 0.80 | 0.96 | 1.18 |
| Gilan | 25 | 0.32 | 0.71 | 0.46 | 1.19 |
| Lorestan | 26 | 0.50 | 0.35 | 0.75 | 0.95 |
| Mazandaran | 27 | 0.30 | 0.64 | 0.85 | 1.21 |
| Markazi | 28 | 0.26 | 0.29 | 0.78 | 0.97 |
| Hormozgan | 29 | 1.09 | 0.95 | 1.91 | 0.48 |
| Hamedan | 30 | 0.32 | 0.45 | 0.58 | 1.07 |
| Yazd | 31 | 0.61 | 0.30 | 0.96 | 0.36 |
Table 3 presents the transportation cost from a distribution center to a demand point for each vaccine dose. This cost is proportional to the distance between the two points. For example, $0.61 in the first row of this table asserts if Tehran is used as a distribution center, the cost of transporting each dose of vaccine from Tehran to East Azarbaijan is $0.61. This cost is considered as a function of distance due to the lack of actual transportation costs data in the planning phase.
The GAMS software with BARON solver is used to run the proposed model. The optimal values of the objective function and decision variables are calculated as follows:
-
•
The optimal value of the objective function is equal to 0.029.
-
•
Distribution center 1 (Tehran) was selected among the four potential distribution centers.
-
•
A total of 15,398,713 influenza vaccines were purchased with the available budget of $270,000,000.
-
•
The number of vaccine doses shipped from the Tehran distribution center to other provinces is presented in Table 4 .
Table 4.
The optimal number of vaccines shipped from the Tehran distribution center to other provinces.
| Province | p | t = 1 | t = 2 | t = 3 | t = 4 |
|---|---|---|---|---|---|
| East Azerbaijan | 1 | 121,686 | 479,059 | 0 | 121,801 |
| West Azerbaijan | 2 | 101,452 | 101,452 | 273,385 | 101,608 |
| Ardabil | 3 | 39,553 | 39,551 | 119,452 | 39,550 |
| Isfahan | 4 | 472,270 | 263,003 | 159,432 | 159,432 |
| Alborz | 5 | 84,448 | 374,367 | 84,442 | 94,426 |
| Ilam | 6 | 72,957 | 0 | 18,063 | 18,995 |
| Bushehr | 7 | 177,843 | 0 | 0 | 36,642 |
| Tehran | 8 | 654,387 | 564,517 | 413,071 | 901,950 |
| Chaharmahal and Bakhtiari | 9 | 31,914 | 86,313 | 32,889 | 29,507 |
| South Khorasan | 10 | 28,712 | 81,766 | 26,497 | 23,936 |
| Khorasan Razavi | 11 | 916,739 | 0 | 0 | 306,312 |
| North Khorasan | 12 | 26,871 | 81,371 | 26,871 | 28,130 |
| Khuzestan | 13 | 412,221 | 370,629 | 0 | 146,667 |
| Zanjan | 14 | 32,797 | 32,576 | 32,587 | 87,805 |
| Semnan | 15 | 21,866 | 65,262 | 24,292 | 21,857 |
| Sistan and baluchestan | 16 | 172,794 | 0 | 426,946 | 0 |
| Fars | 17 | 420,040 | 151,039 | 151,039 | 233,203 |
| Qazvin | 18 | 39,656 | 49,247 | 149,679 | 0 |
| Qom | 19 | 40,161 | 40,161 | 145,715 | 0 |
| Sanandaj | 20 | 50,211 | 202,320 | 0 | 48,319 |
| Kerman | 21 | 98,530 | 98,530 | 311,728 | 98,530 |
| Kermanshah | 22 | 121,574 | 0 | 150,898 | 62,360 |
| Kohgiluyeh va Buyer Ahmad | 23 | 22,201 | 22,201 | 22,201 | 66,077 |
| Golestan | 24 | 58,184 | 182,198 | 118,882 | 0 |
| Gilan | 25 | 78,790 | 78,790 | 78,790 | 277,783 |
| Lorestan | 26 | 54,813 | 145,970 | 65,939 | 54,813 |
| Mazandaran | 27 | 358,033 | 0 | 258,006 | 0 |
| Markazi | 28 | 88,692 | 0 | 44,503 | 125,678 |
| Hormozgan | 29 | 110,611 | 0 | 55,308 | 169,390 |
| Hamedan | 30 | 54,118 | 53,800 | 54,116 | 167,794 |
| Yazd | 31 | 35,876 | 89,860 | 0 | 77,435 |
The value 121,686 in the first row and the first column of Table 4 represents that number of flu vaccine doses shipped from distribution center 1 in Tehran to province 1 in East Azarbaijan in time-period 1. Similarly, this table shows the number of vaccine doses shipped to each province in each time-period.
-
•
The optimal number of vaccine doses assigned to Group 1 and each province in each time-period is presented in Table 5 . Similarly, the optimal number of vaccine doses assigned to groups 2–8 in each province for each time-period is presented in the Appendix (See Table A).
Table 5.
The optimal number of vaccine doses assigned to Group 1 and each province in each time-period.
| Province (p) | t = 1 | t = 2 | t = 3 | t = 4 |
|---|---|---|---|---|
| 1 | 8678 | 174,503 | 8330 | 8330 |
| 2 | 6343 | 6343 | 127,276 | 6504 |
| 3 | 2983 | 2983 | 58,463 | 2803 |
| 4 | 329,904 | 16,939 | 16,852 | 16,845 |
| 5 | 13,395 | 270,444 | 13,395 | 13,831 |
| 6 | 30,986 | 1536 | 1581 | 1592 |
| 7 | 56,340 | 2794 | 2848 | 2892 |
| 8 | 34,004 | 184,479 | 34,709 | 525,568 |
| 9 | 2508 | 48,989 | 2513 | 2499 |
| 10 | 2816 | 55,580 | 2784 | 2899 |
| 11 | 231,679 | 17,380 | 16,196 | 123,361 |
| 12 | 2195 | 42,560 | 2191 | 2181 |
| 13 | 280,303 | 15,003 | 13,871 | 13,871 |
| 14 | 2233 | 2017 | 2028 | 40,536 |
| 15 | 1858 | 36,146 | 1846 | 1841 |
| 16 | 11,004 | 10,525 | 212,026 | 10,733 |
| 17 | 283,820 | 14,537 | 14,537 | 14,273 |
| 18 | 3027 | 3014 | 59,273 | 2990 |
| 19 | 2283 | 2284 | 44,977 | 2283 |
| 20 | 4233 | 85,279 | 4355 | 4222 |
| 21 | 9237 | 9117 | 179,405 | 9095 |
| 22 | 3746 | 3545 | 71,010 | 3544 |
| 23 | 1786 | 1789 | 1789 | 34,657 |
| 24 | 5119 | 101,156 | 5006 | 5307 |
| 25 | 8459 | 8082 | 8450 | 162,629 |
| 26 | 3841 | 74,835 | 3802 | 3800 |
| 27 | 162,536 | 8044 | 8135 | 8092 |
| 28 | 3006 | 2969 | 2969 | 57,608 |
| 29 | 4647 | 4384 | 4685 | 91,452 |
| 30 | 4846 | 4852 | 4852 | 95,216 |
| 31 | 2193 | 2198 | 2257 | 44,426 |
The value 8678 in the first row and the first column of Table 5 indicates that 8678 flu vaccine doses have been allocated to Group 1 (Infants and toddlers aged 6 to 35 months) in Province 1 (i.e., East Azarbaijan) in time-period 1. The remaining number of vaccine doses are determined accordingly and presented in Table 5.
-
•
The number of flu vaccine doses stored in the warehouses at provinces in each time-period is reported in Table 6 .
Table 6.
The number of vaccines stored in warehouses at provinces in each time-period.
| Province (p) | t = 1 | t = 2 | t = 3 |
|---|---|---|---|
| 1 | 0 | 121,205 | 0 |
| 3 | 0 | 0 | 1978 |
| 6 | 18,003 | 0 | 0 |
| 7 | 72,011 | 35,766 | 0 |
| 11 | 399,411 | 199,112 | 0 |
| 13 | 0 | 145,980 | 0 |
| 16 | 85,260 | 0 | 86,408 |
| 18 | 0 | 0 | 39,501 |
| 19 | 0 | 0 | 42,388 |
| 20 | 0 | 50,063 | 0 |
| 22 | 60,442 | 0 | 0 |
| 24 | 0 | 0 | 61,179 |
| 27 | 101,315 | 0 | 101,635 |
| 28 | 44,318 | 0 | 0 |
| 29 | 57,069 | 0 | 0 |
| 31 | 0 | 35,229 | 0 |
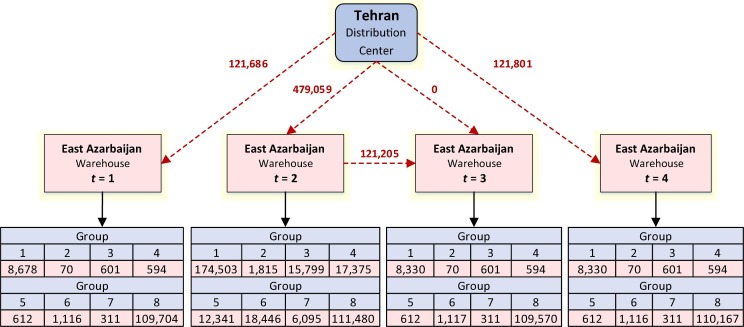
The proposed model equitably distributes the vaccine doses to all provinces. Fig. 2 presents the vaccine distribution from the Tehran distribution center to East Azarbaijan province for all four time-period.
Fig. 2.
The assigned vaccines to groups in each time-period in East Azarbaijan Province.
As shown in Figure 2, 121686, 479059, and 121,801 vaccine doses are shipped from the Tehran distribution center to the East Azarbaijan warehouse in time-periods 1, 2, and 4, respectively. However, no vaccine doses are shipped in time-period 3 since the need for vaccine in this time-period is covered by the available vaccines from time-period 2. Among the 121,686 flue vaccine doses shipped in the first time-period, 8678 doses have been assigned to Group 1 (Infants and toddlers aged 6 to 35 months), 70 doses to Group 2 (Pregnant women with pre-existing medical conditions), 601 doses to Group 3 (Adults aged 65 years and older with pre-existing medical conditions), 594 doses to Group 4 (Critical healthcare providers and first responders), 612 doses to Group 5 (Pregnant women without pre-existing conditions), 1116 doses to Group 6 (Adults aged 65 years and older without pre-existing medical conditions), 311 doses to Group 7 (People with pre-existing medical conditions), and 109,704 doses have been assigned to Group 8 (Other people).
In summary, the optimal solution selected Tehran as a distribution center considering a total budget of $270,000,000) and purchased 15,398,713 doses of the vaccines. The remaining question is the number of vaccine doses that should be bought and distributed if other centers were set up? If the Isfahan distribution center is set up, 15,301,903 doses of vaccine can be purchased and distributed considering the available budget. If the East Azarbaijan is set up, the number of vaccine doses will be reduced to 14,882,527. Finally, if the Kerman is selected as the distribution center, 14,771,554 vaccine doses are purchased and distributed. Therefore, the results show that Tehran is the optimal distribution center. Besides, suppose the decision-makers’ policy is to use the maximum capacity of the distribution center. In that case, the question is how much budget is needed to set up a network with the maximum capacity? This distribution center’s capacity is equal to 18,000,000 vaccine doses for a total of four time-periods, where the amount of $309,933,087 is required for a chain with this capacity. Thus, for an additional $40,000 budget, it is possible to distribute 2,601,287 more vaccine doses in the chain. It is noteworthy that the value of the objective function changes from 0.029 to 0.03 in this case.
5. Sensitivity analysis
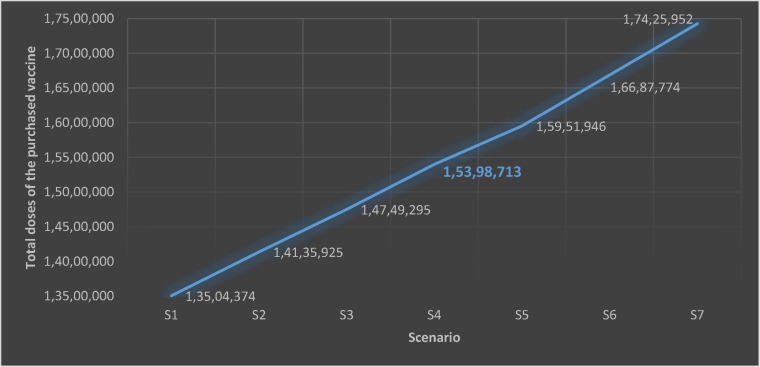
In this section, budgeting scenarios are used to evaluate the performance and behavior of the proposed model. The total vaccine doses are expected to increase by increasing the budget. Similarly, the total vaccine doses are expected to decrease by decreasing the budget. Seven scenarios are considered for sensitivity analysis. Scenarios 1 to 3 consider possible budget decreases, and scenarios 5 to 7 consider possible budget increases. The seven scenarios’ results are presented tabularly in Table 7 and depicted graphically in Fig. 3 .
Table 7.
Sensitivity analysis on budget variations.
| Scenario | Budget | Total doses of the vaccine purchased |
|---|---|---|
| S1 | 240,000,000 | 13,504,374 |
| S2 | 250,000,000 | 14,135,925 |
| S3 | 260,000,000 | 14,749,295 |
| S4 (main problem) | 270,000,000 | 15,398,713 |
| S5 | 280,000,000 | 15,951,946 |
| S6 | 290,000,000 | 16,687,774 |
| S7 | 300,000,000 | 17,425,952 |
Fig. 3.
Total doses of the purchased vaccine for each scenario.
As shown in Table 7 and Fig. 3, the total vaccine doses increase with the increase in budget, and the total vaccine doses decrease with the decrease in budget. This sensitivity analysis confirms the expected behavior of the model proposed in this study.
6. Managerial implications
This study proposes a practical model for equitable influenza vaccine distribution in developing countries. Most developing countries, such as Iran, cannot provide the influenza vaccine to the entire population due to the unavailability of production technology, budgetary constraints, and lack of distribution infrastructure. Therefore, developing an equitable vaccine distribution system and providing vaccines to vulnerable groups is a high priority in developing countries. The model proposed in this study is not only applicable to equitable influenza vaccine distribution; it could be modified for other vaccines (e.g., COVID-19 vaccine) where classification and prioritization are pre-requisites for equitable vaccine distribution. For example, the transportation, storage, and application requirements for the COVID-19 vaccine are similar to those of the influenza vaccine. First, both vaccines belong to the cold supply chain, and storing them at an unsuitable temperature affects their quality and can lead to their perishability. Second, both vaccines are used to kill highly contagious viruses with high outbreak rates. Third, disregard for vulnerable groups in the population can lead to catastrophic events. Fourth, the vaccine’s transportation is an important concern in designing a cold supply chain since improper transportation can impact vaccine quality and perishability. Fifth, the transportation cost in the cold supply chain is strongly influenced by the distance between the distribution point and the demand point. In this study, an attempt is made to develop a comprehensive and equitable vaccine distribution model that is easily adaptable to various vaccine distribution and application requirements in developing countries.
7. Conclusion
Influenza and COVID-19 are both respiratory viruses requiring similar supplies and equipment. Hospitals currently accommodating COVID-19 patients may not be able to manage additional flu patients during the flu season [24]. The flu vaccine supply chain’s role is to ensure that the right product, in the right quantity, is distributed to the right place, at the right time. The risks of inefficient and ineffective flu vaccine supply chains are detrimental to the healthcare sector [25]. In this paper, we proposed a MILP model for the equitable distribution of influenza vaccine doses during the COVID-19 outbreak. The proposed model is a single product multi-period model with distribution centers, storage capabilities, possible shortage, and capacitated distribution centers. According to the MOHME requirements, the population was divided into eight groups according to age, pre-existing medical conditions, pregnancy, and healthcare-related jobs. Each group was allocated an equitable number of vaccine doses according to their coverage rate. The results demonstrate the applicability of the inventory-location optimization model proposed in this study for equitable influenza vaccine distribution During the COVID-19 Pandemic.
The storage and distribution of the influenza vaccine are similar to that of the COVID-19 vaccine. Future research is needed to develop a cold supply chain network for equitable COVID-19 vaccine distribution by considering uncertain, unavailable, or incomplete demand data in developing countries. Moreover, vehicle routing considerations can improve the model’s performance and applicability in rural areas with little or no transportation infrastructure. Finally, the inclusion of other objectives, such as the number of healthcare workers and vaccination stations, may enhance the model’s efficacy in urban areas.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
Dr. Madjid Tavana is grateful for the partial support he received from the Czech Science Foundation (GAˇCR19-13946S) for this research.
Appendix.
Table A. The optimal number of vaccine doses assigned to groups 2–8 and each province in each time-period
| p | Group 2 |
Group 3 |
Group 4 |
Group 5 |
Group 6 |
Group 7 |
Group 8 |
|||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t = 1 | t = 2 | t = 3 | t = 4 | t = 1 | t = 2 | t = 3 | t = 4 | t = 1 | t = 2 | t = 3 | t = 4 | t = 1 | t = 2 | t = 3 | t = 4 | t = 1 | t = 2 | t = 3 | t = 4 | t = 1 | t = 2 | t = 3 | t = 4 | t = 1 | t = 2 | t = 3 | t = 4 | |
| 1 | 70 | 1815 | 70 | 70 | 601 | 15,799 | 601 | 601 | 594 | 17,375 | 594 | 594 | 612 | 12,341 | 612 | 612 | 1116 | 18,446 | 1117 | 1116 | 311 | 6095 | 311 | 311 | 109,704 | 111,480 | 109,570 | 110,167 |
| 2 | 26 | 26 | 680 | 26 | 263 | 263 | 7022 | 263 | 405 | 405 | 11,846 | 405 | 479 | 479 | 9686 | 479 | 1326 | 1326 | 21,580 | 1326 | 145 | 145 | 2830 | 140 | 92,465 | 92,465 | 92,465 | 92,465 |
| 3 | 12 | 12 | 320 | 13 | 218 | 218 | 5695 | 223 | 153 | 153 | 4495 | 154 | 170 | 170 | 3326 | 172 | 649 | 649 | 10,728 | 649 | 69 | 69 | 1386 | 69 | 35,299 | 35,297 | 33,061 | 37,445 |
| 4 | 74 | 1973 | 73 | 73 | 603 | 15,200 | 567 | 574 | 882 | 25,545 | 869 | 869 | 813 | 15,932 | 812 | 812 | 2692 | 43,807 | 2692 | 2692 | 326 | 6548 | 324 | 324 | 136,976 | 137,059 | 137,243 | 137,243 |
| 5 | 35 | 35 | 35 | 912 | 257 | 259 | 257 | 6881 | 487 | 14,264 | 494 | 487 | 268 | 5255 | 273 | 268 | 979 | 16,545 | 979 | 979 | 134 | 134 | 134 | 2650 | 68,893 | 67,431 | 68,875 | 68,418 |
| 6 | 3 | 3 | 3 | 90 | 1408 | 54 | 54 | 54 | 1583 | 52 | 52 | 53 | 1272 | 63 | 63 | 63 | 3637 | 222 | 222 | 222 | 39 | 39 | 39 | 885 | 16,026 | 16,034 | 16,049 | 16,036 |
| 7 | 18 | 16 | 16 | 439 | 1911 | 73 | 73 | 73 | 3166 | 108 | 108 | 108 | 3011 | 156 | 158 | 149 | 6431 | 395 | 395 | 395 | 2177 | 111 | 111 | 111 | 32,778 | 32,592 | 32,057 | 32,475 |
| 8 | 3710 | 143 | 143 | 143 | 14,642 | 560 | 560 | 560 | 72,209 | 2570 | 2323 | 2504 | 44,520 | 2270 | 2270 | 2270 | 97,835 | 5804 | 5804 | 5804 | 21,522 | 1104 | 1104 | 1104 | 365,945 | 367,587 | 366,158 | 363,997 |
| 9 | 11 | 279 | 10 | 11 | 134 | 134 | 3522 | 134 | 2499 | 85 | 80 | 85 | 95 | 1863 | 95 | 95 | 442 | 7200 | 442 | 442 | 85 | 1644 | 84 | 84 | 26,140 | 26,119 | 26,143 | 26,157 |
| 10 | 12 | 339 | 12 | 12 | 53 | 1410 | 53 | 57 | 88 | 88 | 2658 | 88 | 136 | 2654 | 136 | 136 | 5113 | 310 | 293 | 307 | 51 | 1005 | 51 | 51 | 20,443 | 20,380 | 20,510 | 20,386 |
| 11 | 1192 | 46 | 46 | 46 | 7398 | 279 | 276 | 289 | 29,185 | 996 | 996 | 996 | 21,046 | 1069 | 1069 | 1069 | 39,485 | 2329 | 2329 | 2351 | 9534 | 487 | 487 | 487 | 177,809 | 177,713 | 177,713 | 177,713 |
| 12 | 13 | 13 | 13 | 342 | 55 | 1482 | 55 | 55 | 124 | 3526 | 117 | 117 | 154 | 3020 | 154 | 154 | 421 | 6852 | 421 | 421 | 50 | 50 | 50 | 981 | 23,859 | 23,868 | 23,870 | 23,879 |
| 13 | 40 | 1038 | 40 | 40 | 595 | 15,798 | 590 | 590 | 521 | 15,395 | 521 | 521 | 902 | 18,320 | 902 | 902 | 1586 | 25,820 | 1588 | 1586 | 260 | 5067 | 260 | 260 | 128,014 | 128,208 | 128,208 | 128,897 |
| 14 | 9 | 9 | 9 | 240 | 83 | 83 | 83 | 2167 | 131 | 131 | 131 | 3837 | 155 | 153 | 153 | 3112 | 387 | 386 | 386 | 6325 | 81 | 79 | 79 | 1602 | 29,718 | 29,718 | 29,718 | 29,986 |
| 15 | 12 | 311 | 12 | 12 | 22 | 573 | 22 | 22 | 72 | 2165 | 72 | 79 | 130 | 130 | 2558 | 132 | 349 | 5735 | 349 | 349 | 44 | 850 | 43 | 43 | 19,379 | 19,352 | 19,390 | 19,379 |
| 16 | 44 | 42 | 1174 | 45 | 498 | 498 | 13,390 | 498 | 251 | 234 | 7048 | 237 | 578 | 578 | 11,370 | 578 | 1185 | 1185 | 20,064 | 1220 | 164 | 164 | 3230 | 164 | 73,810 | 72,034 | 72,236 | 72,933 |
| 17 | 33 | 33 | 33 | 861 | 559 | 516 | 516 | 13,834 | 754 | 749 | 749 | 22,004 | 614 | 614 | 614 | 12,415 | 1845 | 1845 | 1845 | 30,996 | 328 | 328 | 328 | 6487 | 132,087 | 132,417 | 132,417 | 132,333 |
| 18 | 12 | 308 | 11 | 11 | 215 | 5653 | 215 | 215 | 158 | 158 | 4621 | 158 | 202 | 4081 | 202 | 224 | 564 | 564 | 9178 | 564 | 117 | 117 | 2291 | 117 | 35,361 | 35,352 | 34,387 | 35,222 |
| 19 | 15 | 14 | 390 | 14 | 91 | 91 | 2373 | 91 | 181 | 181 | 5272 | 181 | 249 | 249 | 4855 | 249 | 427 | 427 | 8506 | 428 | 103 | 103 | 103 | 2330 | 36,812 | 36,812 | 36,851 | 36,812 |
| 20 | 32 | 856 | 34 | 32 | 64 | 1718 | 65 | 64 | 145 | 4374 | 145 | 145 | 174 | 3436 | 181 | 174 | 573 | 9708 | 576 | 572 | 151 | 3045 | 150 | 150 | 44,839 | 43,841 | 44,557 | 42,960 |
| 21 | 24 | 24 | 645 | 24 | 130 | 130 | 3471 | 130 | 455 | 429 | 12,911 | 446 | 358 | 357 | 6963 | 357 | 1088 | 996 | 16,742 | 1001 | 245 | 231 | 4663 | 231 | 86,993 | 87,246 | 86,928 | 87,246 |
| 22 | 28 | 25 | 687 | 26 | 68 | 67 | 1798 | 67 | 164 | 164 | 4780 | 164 | 240 | 240 | 4703 | 244 | 651 | 651 | 10,668 | 651 | 78 | 71 | 1439 | 71 | 56,157 | 55,679 | 55,813 | 57,593 |
| 23 | 13 | 11 | 11 | 305 | 119 | 119 | 119 | 3104 | 64 | 64 | 64 | 1876 | 92 | 92 | 92 | 1793 | 217 | 216 | 216 | 3657 | 42 | 42 | 42 | 819 | 19,868 | 19,868 | 19,868 | 19,866 |
| 24 | 38 | 1002 | 41 | 37 | 268 | 6987 | 273 | 268 | 214 | 6273 | 214 | 214 | 278 | 5422 | 269 | 282 | 605 | 9915 | 605 | 605 | 114 | 114 | 113 | 2639 | 51,548 | 51,329 | 51,182 | 51,827 |
| 25 | 52 | 52 | 52 | 1348 | 385 | 378 | 378 | 10,155 | 315 | 315 | 315 | 9178 | 246 | 236 | 245 | 4753 | 1000 | 1000 | 1000 | 16,904 | 257 | 240 | 240 | 4837 | 68,076 | 68,487 | 68,110 | 67,979 |
| 26 | 12 | 12 | 311 | 12 | 276 | 7298 | 272 | 272 | 163 | 5282 | 163 | 163 | 353 | 353 | 7945 | 353 | 539 | 8673 | 516 | 519 | 175 | 179 | 3406 | 170 | 49,454 | 49,338 | 49,524 | 49,524 |
| 27 | 35 | 35 | 912 | 35 | 290 | 290 | 7547 | 290 | 436 | 436 | 12,811 | 436 | 701 | 663 | 13,290 | 663 | 1001 | 1027 | 16,801 | 962 | 307 | 293 | 6117 | 310 | 91,412 | 90,527 | 90,758 | 90,847 |
| 28 | 7 | 7 | 7 | 183 | 117 | 117 | 117 | 3045 | 195 | 195 | 195 | 6433 | 251 | 251 | 251 | 4925 | 685 | 666 | 666 | 11,295 | 102 | 102 | 102 | 2018 | 40,011 | 40,011 | 40,196 | 40,171 |
| 29 | 26 | 26 | 26 | 683 | 221 | 221 | 221 | 5764 | 161 | 161 | 161 | 4846 | 231 | 231 | 231 | 4506 | 723 | 721 | 721 | 11,744 | 81 | 79 | 79 | 1553 | 47,452 | 51,246 | 49,184 | 48,842 |
| 30 | 8 | 8 | 8 | 209 | 62 | 62 | 62 | 1608 | 214 | 209 | 209 | 6321 | 240 | 244 | 240 | 4705 | 526 | 526 | 526 | 8643 | 160 | 159 | 159 | 3223 | 48,062 | 47,740 | 48,060 | 47,869 |
| 31 | 15 | 400 | 15 | 15 | 101 | 2634 | 101 | 101 | 154 | 4661 | 154 | 154 | 246 | 4822 | 250 | 246 | 348 | 5663 | 343 | 346 | 91 | 1774 | 91 | 91 | 32,728 | 32,479 | 32,018 | 32,056 |
References
- 1.Hartmann K., Pagliusi S., Precioso A. Landscape analysis of pharmacovigilance and related practices among 34 vaccine manufacturers’ from emerging countries. Vaccine. 2020;38(34):5490–5497. doi: 10.1016/j.vaccine.2020.06.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Jacobson S.H., Sewell E.C., Proano R.A. An analysis of the pediatric vaccine supply shortage problem. Health Care Management Science. 2006;9(4):371–389. doi: 10.1007/s10729-006-0001-5. [DOI] [PubMed] [Google Scholar]
- 3.Jacobson S.H., Sewell E.C., Jokela J.A. Survey of vaccine distribution and delivery issues in the USA: from pediatrics to pandemics. Expert review of vaccines. 2007;6(6):981–990. doi: 10.1586/14760584.6.6.981. [DOI] [PubMed] [Google Scholar]
- 4.Peter, G., Arvin, A. M., Davis, J. P., & Decker, M. D. (2003). Strengthening the supply of routinely recommended vaccines in the United States: recommendations from the National Vaccine Advisory Committee. JAMA, 290(23), 3122-3122. [DOI] [PubMed]
- 5.Lane K.S., Chu S.Y., Santoli J.M. The United States pediatric vaccine stockpile program. Clin Infect Dis. 2006;42(Supplement_3):S125–S129. doi: 10.1086/499591. [DOI] [PubMed] [Google Scholar]
- 6.Rodewald L.E., Orenstein W.A., Mason D.D., Cochi S.L. Vaccine supply problems: a perspective of the Centers for Disease Control and Prevention. Clin Infect Dis. 2006;42(Supplement_3):S104–S110. doi: 10.1086/499587. [DOI] [PubMed] [Google Scholar]
- 7.Duijzer L.E., van Jaarsveld W., Dekker R. Literature review: The vaccine supply chain. Eur J Oper Res. 2018;268(1):174–192. [Google Scholar]
- 8.Uscher-Pines L., Barnett D.J., Sapsin J.W., Bishai D.M., Balicer R.D. A systematic analysis of influenza vaccine shortage policies. Public Health. 2008;122(2):183–191. doi: 10.1016/j.puhe.2007.06.005. [DOI] [PubMed] [Google Scholar]
- 9.Straetemans M., Buchholz U., Reiter S., Haas W., Krause G. Prioritization strategies for pandemic influenza vaccine in 27 countries of the European Union and the Global Health Security Action Group: a review. BMC Public Health. 2007;7(1):236. doi: 10.1186/1471-2458-7-236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shrestha S.S., Wallace G.S., Meltzer M.I. Modeling the national pediatric vaccine stockpile: Supply shortages, health impacts and cost consequences. Vaccine. 2010;28(38):6318–6332. doi: 10.1016/j.vaccine.2010.06.095. [DOI] [PubMed] [Google Scholar]
- 11.Samii A.B., Pibernik R., Yadav P., Vereecke A. Reservation and allocation policies for influenza vaccines. Eur J Oper Res. 2012;222(3):495–507. [Google Scholar]
- 12.Abrahams A.S., Ragsdale C.T. A decision support system for patient scheduling in travel vaccine administration. Decis Support Syst. 2012;54(1):215–225. [Google Scholar]
- 13.Meshkini A.H., Kebriaeezadeh A., Dinarvand R., Nikfar S., Habibzadeh M., Vazirian I. Assessment of the vaccine industry in Iran in context of accession to WTO: a survey study. DARU Journal of Pharmaceutical Sciences. 2012;20(1):19. doi: 10.1186/2008-2231-20-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Privett N., Gonsalvez D. The top ten global health supply chain issues: perspectives from the field. Operations Research for Health Care. 2014;3(4):226–230. [Google Scholar]
- 15.Pishvaee M.S., Razmi J., Torabi S.A. An accelerated Benders decomposition algorithm for sustainable supply chain network design under uncertainty: A case study of medical needle and syringe supply chain. Transportation Research Part E: Logistics and Transportation Review. 2014;67:14–38. [Google Scholar]
- 16.Lydon P., Raubenheimer T., Arnot-Krüger M., Zaffran M. Outsourcing vaccine logistics to the private sector: the evidence and lessons learned from the Western Cape Province in South-Africa. Vaccine. 2015;33(29):3429–3434. doi: 10.1016/j.vaccine.2015.03.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Saif A., Elhedhli S. Cold supply chain design with environmental considerations: A simulation-optimization approach. Eur J Oper Res. 2016;251(1):274–287. [Google Scholar]
- 18.Cernuschi T., Malvolti S., Nickels E., Friede M. Bacillus Calmette-Guérin (BCG) vaccine: a global assessment of demand and supply balance. Vaccine. 2018;36(4):498–506. doi: 10.1016/j.vaccine.2017.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gooding E., Spiliotopoulou E., Yadav P. Impact of vaccine stockouts on immunization coverage in Nigeria. Vaccine. 2019;37(35):5104–5110. doi: 10.1016/j.vaccine.2019.06.006. [DOI] [PubMed] [Google Scholar]
- 20.Lin Q., Zhao Q., Lev B. Cold chain transportation decision in the vaccine supply chain. Eur J Oper Res. 2020;283(1):182–195. [Google Scholar]
- 21.Zandkarimkhani S., Mina H., Biuki M., Govindan K. A chance constrained fuzzy goal programming approach for perishable pharmaceutical supply chain network design. Ann Oper Res. 2020:1–28. [Google Scholar]
- 22.Enayati S., Özaltın O.Y. Optimal influenza vaccine distribution with equity. Eur J Oper Res. 2020;283(2):714–725. [Google Scholar]
- 23.World Health Organization, Influenza (seasonal), November https://www.who.int/news-room/fact-sheets/detail/influenza-(seasonal), (2018), Accessed date: 9 May 2020.
- 24.Grech V., Borg M. Influenza vaccination in the COVID-19 era. Early Human Dev. 2020;148 doi: 10.1016/j.earlhumdev.2020.105116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jarrett S., Yang L., Pagliusi S. Roadmap for strengthening the vaccine supply chain in emerging countries: Manufacturers’ perspectives. Vaccine:X. 2020;100068 doi: 10.1016/j.jvacx.2020.100068. [DOI] [PMC free article] [PubMed] [Google Scholar]