Identification of dominant risk factor involved in spread of COVID-19 using hesitant fuzzy MCDM methodology

Abstract

The outburst of the pandemic Coronavirus disease since December 2019, has severely impacted the health and economy worldwide. The epidemic is spreading fast through various means, as the virus is very infectious. Medical science is exploring a vaccine, only symptomatic treatment is possible at the moment. To contain the virus, it is required to categorize the risk factors and rank those in terms of contagion. This study aims to evaluate risk factors involved in the spread of COVID-19 and to rank them. In this work, we applied the methodology namely, Fuzzy Analytic Hierarchy Process (FAHP) to find out the weights and finally Hesitant Fuzzy Sets (HFS) with Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) is applied to identify the major risk factor. The results showed that “long duration of contact with the infected person” the most significant risk factor, followed by “spread through hospitals and clinic” and “verbal spread”. We showed the appliance of the Multi Criteria Decision Making (MCDM) tools in evaluation of the most significant risk factor. Moreover, we conducted sensitivity analysis.

Introduction

COVID-19 infectious diseases were earliest reported in the town Wuhan of China in the month of December 2019 [1]. Till date, the number of COVID patients has kept on increasing vigorously, thereby prompting WHO to say publicly COVID-19 to be a pandemic situation. As of August 7, 2020, there were approximately 18,902,735 cases in 216 countries and 709,511patients have lost their lives [1]. WHO has always been in a responsible mode to bring awareness and has updated the countries to take urgent necessary action since the origin of the pandemic. Several preventive measures have been taken by the people and government of different countries. As people are not immune to this disease, this prompted WHO to issue grave reminders regarding the severity of the disease and urged people to act responsibly seeing their neighbors who are suffering and fighting for their existence.

The COVID-19 infection has caused severe respiratory illness syndrome which led to the admission of critical patients largely to the ICU and high mortality among people with comorbidity has been observed. The data collected for the patients was from medical authorities who have made unsung sacrifices and proved to the world, their greatness when it comes for mankind [2]. The virus gets transmitted to other people when an infected person sneezes, speaks or coughs. Moreover, the infection can take place, if a person touches the facade which is contaminated with the virus and then touches his mouth, nose and eyes, findings obtained by the authors of [3], [4], [5]. The infection has been transmitted from human to human contact since the middle of December 2019. The mean incubation period was estimated to be 5.2 days after exposure according to the reference of [6]. The corona virus disease (COVID-19) is strongly associated to SARS but the latter is less severe and has a lower mortality rate than the former and the transmission of corona virus is rapid and affects elderly people more. Men are affected more as compared to women according to the authors of [7]. With the outbreak of COVID-19, it has become mandatory for everyone to use mask to prevent the disease. In such case, selection of proper masks is necessary. MCDM techniques along with the algorithm spherical normal fuzzy environment (SpNoF) was used for the selection of mask, by the authors of [8]. The authors of [9], [10], [11], [12], [13] developed and formulated mathematical models to predict the dynamic behavior of the disease. The model also checked whether the disease was transmitted from dead bodies to human. Further it analyzed whether lockdown was effective or not in saving lives. The authors of [14] reviewed literature on the usage of facemask as which mask could reduce the spread of the novel COVID-19 disease. The authors of reference [15], [16] used mathematical tools for analyzing mathematical model. The authors of [17], [18] forecasted the lessons learnt and epidemic control from this disease. COVID-19 has severely impacted population across the world. The entire world is trying their best to come up with a permanent medical solution i.e. a suitable vaccine so as to put an end to the panic and trauma of the people globally.

Thus, in this paper, with the support of doctors, literature reviews and media survey, we have tried to apply a mathematical model to identify as to which is the most dominant risk factor for the spread of the disease. In this aspect, hesitant fuzzy sets with Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) is used for analyzing the most important risk factor. Multi Criteria Decision Making (MCDM) has also been used.

Review of literature

While making decisions for any situations humans generally are uncertain regarding the choices formed by them from the alternatives available in the system. For example, two decision maker’s debate upon assigning the membership degree of an element to set X, where the first wants to assign 0.1, while the other wants to allocate a value of 0.3. Correspondingly, a general membership degree not being established is neither since there is a edge of fault i.e. Intuitionistic fuzzy set, according to the reference of [19] nor is it due to some possibility of distribution values i.e. type-2 fuzzy set [20], [21] but rather because there is a set of possible values. In order to accord such cases hesitant fuzzy set was developed by the authors of [22], [23] which was a conjecture of fuzzy set according to the reference [24]. Hesitant fuzzy set has been ballooning in its applicability both in terms of qualitative [25] as well as quantitative [26], [27], [28], [29] view points since hesitation can make an appearance while modeling the uncertainty both ways. Hesitant fuzzy set has been used in MCDM problem by the authors of [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40], multi-expert with multi criteria decision making by the reference [41], evaluation processes [42] and in clustering algorithms by the authors of [43], [44], [45], [46], [47]. Aggregation operators were utilized for selection of the optimal production strategy using hesitant fuzzy set by the authors of [48]. Fuzzy TOPSIS was used in the application of a supplier selection problem by the authors of [49]. A wide scale of hesitant power aggregation operators was expanded for hesitant fuzzy ideology by the author [50]. The first algorithm in fuzzy AHP was developed by the authors of [51] using Lootsma’s logarithmic least square method and triangular fuzzy membership functions. The method was further extended with trapezoidal fuzzy numbers and suggestions were made to use geometric mean method in order to gain the fuzzy weights from pairwise comparisons by the author of [52]. An extent analysis method was also proposed for the synthetic extent values of the pairwise comparisons by the author of [53]. A methodology was manifested for interval type-2 fuzzy AHP, according to the authors of [54]. A proposition was made to extend TOPSIS method with fuzzy sets by the author of [55]. Proposals were also made to extend version of fuzzy TOPSIS method to group decision making field, according to the reference of [56]. When the weight information is incomplete then an approach is formulated using TOPSIS to apply in problems of selection of energy policy [38]. In table 1 we briefly discuss the literature review of risk factors for COVID-19 and our proposed model.

Table 1.

Literature review on risk factors for coronavirus disease.

Authors	Method used	Findings	Risk Factors
Mazumdar et al. [57]	GMDH, TOPSIS-1	1. Monitor the main alternative for the pandemic. 2. Contact with infected person was seen as the optimal alternative for the spread of the pandemic	a. Verbal contamination b. Contamination due to eatables c. Contamination due to contact with infected person
Zheng et al. [58]	Meta- Analysis	1. Identified the risk factor for critical, non-critical COVID-19 patients and also analyzed the mortality with Meta-Analysis	a. Smoking patients age over 65 (male) b. Hypertension c. Diabetes d. Cardiovascular disease e. Respiratory disease
Tian et al. [59]	Uni-variate and Multivariate Logistic Regression	1. Patients with malignancy are prone to severe illness with COVID-19 than patient without cancer	a. Cancer patients
Present article	FAHP, HFS-TOPSIS, Sensitivity analysis with three different ranking method.	1. Long duration of contact with the infected person is the significant risk factor	a. Verbal spread b. Long duration of contact with the infected person c. Not maintaining personal hygiene d. Not using quality mask e. Not maintaining social distance in public transport or public places f. Spread through clinic and hospitals

Remarks 1: The proposed study uses FAHP, HFS-TOPSIS. FAHP used Triangular Fuzzy Numbers (TFN) suitable for representing impreciseness [60]. HFS reflects the hesitancy while assigning a particular value during uncertain pandemic situation like COVID-19. HFS can be used when decision makers in which cases that decision maker may not agree on the membership value of an element and discuss it to be whether 0.8 or 0.9 or 0.93. In such cases HFS represent the situation better instead of aggregate single value.

Objectives of the present research

The present study focusses on:

• (a)Identifying the most imperative risk factors for the spread of COVID-19. The factors included in this study are from doctor’s opinion, literature review and media survey.
• (b)Hesitant Fuzzy sets (HFS) along with TOPSIS approach is used for ranking different risk factors. HFS denotes the membership degree of the alternative on basis of the criterion with more flexibility. To the best of our knowledge, for the identification of significant risk factor in COVID-19, there is no work which used integrated FAHP, HFS-TOPSIS methodology in the literature.

The leftovers of the paper are prepared as follows: The section 4 discusses the scientific benefits of the study, section 5 describes the methods used in this research. It provides information about HFS, FAHP, HFS-TOPSIS. Section 6explains the selection of criteria and risk factors taken for the study. Section 7shows the empirical study and ranking of the risk factors using mathematical model. Section 8 includes sensitivity analysis. Section 9 covers the results and discussion part and section10, finally the conclusion.

Scientific benefits of the research

This study identified and ranked the risk factors in the spread of COVID-19. This scientifically obtained result will help the government to formulate administrative strategies to contain the dominant risk factors. As per this research government should implement policies to reduce longer duration of contact i.e. physical distancing to be strictly adhered. Proper transportation to be arranged for COVID-19 warriors. People serving emergency duties like electricity, banking, postal service, conservancy to be provided reliable conveyance conforming to social distancing norms. More safety measures have to be enforced in hospitals, pathological centers and clinics to restrict the spread. Proper disposal of COVID-19 contaminated kits like PPE and sanitization of high-risk areas to be ensured.

Methodology

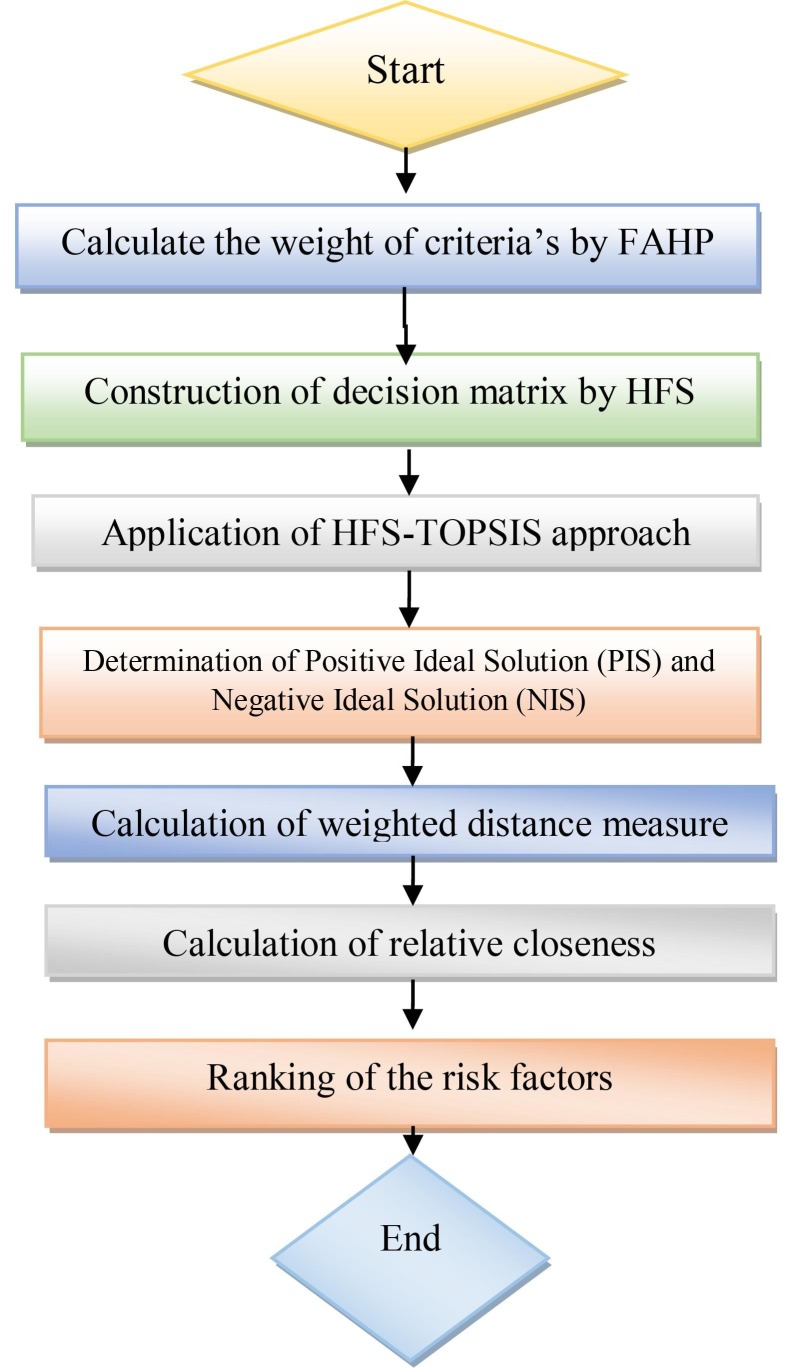
The study focuses on finding the most significant risk factor for the spread of the pandemic coronavirus disease using mathematical Multi Criteria Decision Making (MCDM) technique. Thus, this study used FAHP to obtain the criteria’s weight. The Hesitant Fuzzy Set theory coupled with TOPSIS tool is applied to finding the most significant risk factor for the spread of the COVID-19 disease. Fig. 1 represents the design of the proposed model.

Fig. 1.

Flow chart for the proposed study.

Hesitant fuzzy sets (HFS)

In this section, we will discuss about the fundamental theory of HFS, its basic operational laws and distance measure.

HFS is one of the extensions of fuzzy sets theory. It was introduced by the author of [22] and is applicable when uncertainties and hesitancy exists in assigning the degree of belongingness of the elements. The idea of decision making process involves the hesitancy or uncertainty of the decision makers in terms of preferences, thus HFS can be flexibly used to represent the preferences [38].The authors of reference [61], [62], [63], [64], [65] used fuzzy differential equation, fuzzy delay differential equation, non– linear delay models and fractional calculus to construct biological model, balance Earth’s energy model, dynamics of human- immunodeficiency virus and inventory order problem. The definition given by the author of [22] is as follows:

Definition 1:

Assume a fixed set $X$, a HFS on $X$ is defined in terms of a function, which when applied to $X$ returns a subset of [0,1].

To make it simpler, the authors of [30] represented the HFS in mathematical symbol as follows:

$$F=(〈x|h_F\left(x\right)〉|x\in X)$$ (1)

where $h_F\left(x\right)$ belongs to a set of some values in [0,1], which denotes the degree of belongingness of the element $x\in X$ to the set $F$. For convenience, the authors of [30] called$h=h_F\left(x\right)$, a hesitant fuzzy element (HFE) and $H$ the set of all HFEs.

Let three HFEs be represented by$h,h_{1}and{h}_2$, the following operational rules defined by the author of reference [22] are:

$$h^{\text{'}}={\bigcup }_{\beta \epsilon h}\left\{1-\beta \right\}$$ (2)

$$)h_1\bigcup h_2={\bigcup }_{{\beta }_1∊h_{1,}{\beta }_2∊h_2}\max \left\{{\beta }_1,{\beta }_2\right\}$$ (3)

$$)h_1\bigcap h_2={\bigcup }_{{\beta }_1∊h_{1,}{\beta }_2∊h_2}\min \left\{{\beta }_1,{\beta }_2\right\}$$ (4)

Let $\lambda >0,$assuming three HFEs$h,h_{1}and{h}_2$, the authors of [30] introduced some operations as follows:

$$h^{\lambda }={\bigcup }_{\beta \epsilon h}\left\{{\beta }^{\lambda }\right\}$$ (5)

$$\lambda h={\bigcup }_{\beta \epsilon h}\left\{1-{\left(1-\beta \right)}^{\lambda }\right\}$$ (6)

$$h_1\oplus h_2={\bigcup }_{{\beta }_1∊h_{1,}{\beta }_2∊h_2}\left\{{\beta }_1+{\beta }_2-{\beta }_1{\beta }_2\right\}$$ (7)

$$h_1\otimes h_2={\bigcup }_{{\beta }_1∊h_{1,}{\beta }_2∊h_2}\left\{{\beta }_1{\beta }_2\right\}.$$ (8)

Definition 2:

The authors of [30] defined ranking method for two HFEs. For an particular HFE $\text{'}h\text{'}$, the score function denoted as

$$s_F\left(h\right)=\frac{1}{\#h}\sum _{\beta ∊h}\beta$$

here $\#h$ represented as the number of elements in $h.$

Suppose two HFEs $h_{1}and{h}_2,$

$$\left(1\right)\mathrm{I}\mathrm{f}{s}_F\left(h_1\right)>s_F\left(h_2\right),then{h}_1>h_2$$ (9)

$$\left(2\right)\mathrm{I}\mathrm{f}{s}_F\left(h_1\right)=s_F\left(h_2\right),then{h}_1=h_2.$$ (10)

The definition 2 has some drawbacks, which is illustrated in the example in bellow.

Example 1.

Let $h_1=\left\{0.2,0.4\right\},h_2=\left\{0.3\right\},h_3=\{0.1,0.2,0.4,0.5\}$ be three HFEs. According to definition 2, $s_F\left(h_1\right)=s_F\left(h_2\right)=s_F\left(h_3\right)=0.3,$ which implies $h_1=h_2=h_3.$ Evidently $h_1=h_2=h_3.$ Thus, a contradiction.

The author of [66] proposed a new definition for score function as follows.

Definition 3:

Let $h={\cup }_{\beta ∊h}\left\{\beta \right\}=\{{\beta }_s|s=1,2,\cdots ,\#\left(h\right)\}$ be an HFE, here $\#\left(h\right)$ is the number of elements in $h.$

Therefore, the new score function $s_F\left(h\right)$ is defined as:

$$s_F\left(h\right)=\frac{{\sum }_{s=1}^{\#\left(h\right)}\rho (s){\beta }_s}{{\sum }_{s=1}^{\#\left(h\right)}\rho (s)},$$ (11)

where {$\rho (s)|s=1,2,\cdots .,\#\left(h\right)\}$ is a positive valued monotonic increasing sequence of index $s.$

Fuzzy analytic hierarchy process

The AHP method was developed by the researcher of [67], The logical based analytical setting used in MCDM problem. It is helpful in complex decisions with heuristic methods. Evaluation of criteria’s weights are important for the ranking of risk factors. AHP structures the problem hierarchy by constructing comparison matrices with subjective judgments about the attributes pertinent for ranking. In this present article, FAHP has been used instead of AHP where the problems come with uncertainties. The steps for FAHP is described below.

Step 1: Prepare a comparison matrix associated with TFN by a decision expert or a group of experts using Table 2 .

Table 2.

Linguistic terms in Triangular Fuzzy Number (TFN) for the assessment of Criteria’s weight.

Linguistic Term	THFS
Highly Important	(4.5,5,5.5)
Important	(3.5,4,4.5)
Fairly Important	(2.5,3,3.5)
Less Important	(1.5,2,2.5)
Very Less Important	(0.5,1,1.5)

Let a cluster of ‘$T$’ decision-makers concerned in the pairwise comparison of criteria’s weight. Thus, ‘$t$’ set of matrices are obtained, $p_t=\{p_{\mathit{flt}}\}$

where $p_{\mathit{flt}}=(q_{\mathit{flt}},r_{\mathit{flt}},s_{\mathit{flt}})$ represent the relative preference of $f$ factor to $l$ factor as decided by the $\text{'}t\text{'}$ expert.

$$\left(\begin{array}{c}{q}_{\mathit{fl}}=\underset{t=1,2,\cdots ,T}{\min }(q_{\mathit{flt}}),\\ r_{\mathit{fl}}=\sqrt[T]{{\prod }_{t=1}^T{r}_{\mathit{flt}}}\\ s_{\mathit{fl}}=\underset{t=1,2,\cdots ,T}{\max }(s_{\mathit{flt}})\end{array}\right\}$$ (12)

Step 2: Defuzzification of TFN

A TFN $p_{\mathit{flt}}=\left(q_{\mathit{flt}},r_{\mathit{flt}},s_{\mathit{flt}}\right)$can be defuzzified according to the methodology proposed by the authors of [68]

$$({p_{\mathit{fl}}^{\gamma })}^{\delta }=\left[\delta .q_{\mathit{fl}}^{\gamma }+\left(1-\delta \right).s_{\mathit{fl}}^{\gamma }\right],0\le \delta \le 1,0\le \gamma \le 1,$$ (13)

where $\gamma$ denotes the preference value of the evaluator and $\delta$ is defined as the risk aspect existing in uncertainty.$\delta =1$ implies extremely pessimistic whereas $\delta =0$ implies highly optimistic. The stability increases in decision making with the increase of $\gamma$and diminishes when $\gamma =0$.

The expression $q_{\mathit{fl}}^{\gamma }=\left(r_{\mathit{fl}}-q_{\mathit{fl}}\right)\times \gamma +q_{\mathit{fl}},$ means the lower bound of $\gamma$- cut for $p_{\mathit{fl}}$ and $s_{\mathit{fl}}^{\gamma }=s_{\mathit{fl}}-\gamma .\left(s_{\mathit{fl}}-r_{\mathit{fl}}\right),$means the upper bound of $\gamma$- cut for$p_{\mathit{fl}}$.

Step 3: Construction of comparison matrix in terms of crisp values

Universal presentation of the defuzzified comparison matrix

$$({p_{\mathit{fl}}^{\alpha })}^{\beta }=\left(\begin{array}{ccccc}1& ({p_{12}^{\alpha })}^{\beta }& .& .& ({p_{1n}^{\alpha })}^{\beta }\\ ({p_{21}^{\alpha })}^{\beta }& 1& .& .& ({p_{2n}^{\alpha })}^{\beta }\\ .& .& 1& .& .\\ .& .& .& 1& .\\ ({p_{n1}^{\alpha })}^{\beta }& ({p_{n2}^{\alpha })}^{\beta }& .& .& 1\end{array}\right)$$

Step 4: Normalization of each element of the defuzzified matrix

$$N_{\mathit{fl}}=\frac{p_{\mathit{fl}}}{{\sum }_{f=1}^m{p}_{\mathit{fl}}},\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}f=1,2,\cdots .,m;l=1,2,\cdots .,n$$ (14)

Step 5: Estimation of Criteria priority weight (P.W)

$$P.W=\frac{s^{\mathit{th}}rootvalue}{\sum s^{\mathit{th}}root}$$ (15)

Step 6: Findthe Consistence Index $(C.I)$ of the matrix

$$(C.I)=\frac{{\vartheta }_{\mathit{max}}-n}{n-1}$$ (16)

where $\mathit{n}$ is the size of the matrix.

Step 7: Calculate Consistence ratio (C.R)

$$\left(C.R\right)=\frac{C.I}{R.I}$$ (17)

where Random Index (R.I) varies with the size of the matrix “n”.

The value of C.R $\le 0.1$ means a consistent matrix.

HFS-TOPSIS method

The TOPSIS methods is one of the frequently used MCDM tools introduced by the researchers of [69]. The main concept of TOPSIS methodology is to rank the corresponding alternative, that means giving an scheme as which alternative to favor the most. The efficient alternative obtained is closest to the positive ideal solution (PIS) and furthermost from the negative ideal solution (NIS). Finally, the alternative with higher relative closeness is the best one. The authors of [38] widened the classical TOPSIS method advance to deal with MADM in hesitant fuzzy environment. The authors of [70] used interval type-2 FAHP to evaluate the weights. The best strategy was selected using HFS- TOPSIS with the weights calculated. Based on former studies, the steps for HFS-TOPSIS are described as follows:

Step 1: Determination of PIS and NIS

$$A_p^{+}=\{h_1^{+},h_2^{+},h_3^{+},\cdots ,h_n^{+}\};$$ (18)

where

$$h_c^{+}={\cup }_{b=1}^m{h}_{\mathit{bc}}={\cup }_{{\beta }_{1c}∊h_{1c},\cdots .,{\beta }_{\mathit{mc}}∊h_{\mathit{mc}}}\max \left\{{\beta }_{1c},\cdots ..,{\beta }_{\mathit{mc}}\right\}c=1,2,\cdots ,n$$ (19)

$$A_n^{-}=\{h_1^{-},h_2^{-},h_3^{-},\cdots ,h_n^{-}\};$$ (20)

where

$$h_c^{-}={\cap }_{b=1}^m{h}_{\mathit{bc}}={\cap }_{{\beta }_{1c}∊h_{1c},\cdots .,{\beta }_{\mathit{mc}}∊h_{\mathit{mc}}}\min \left\{{\beta }_{1c},\cdots ..,{\beta }_{\mathit{mc}}\right\}c=1,2,\cdots ,n$$ (21)

Step 2: Measure the distance from PIS and NIS for both the alternative is calculated. The present study used weighted hesitant normalized Hamming distance according to the reference of [44]. The distance of an alternative from PIS can be deliberate as follows:

$$D_b^{+}=\sum _{c=1}^n{w}_c||h_{\mathit{bc}}-h_c^{+}||$$ (22)

where, $w_c$ denotes the weight of cth criteria which is deliberate by FAHP.

In the related way, the distance of an alternative from NIS can be deliberate as follows:

$$D_b^{-}=\sum _{c=1}^n{w}_c||h_{\mathit{bc}}-h_c^{-}||$$ (23)

The literature provides different measure to calculate the distance measure between two HFEs. The authors of [34] proposed Euclidean distance between two HFEs as follows:

$$d\left(h_1,h_2\right)=\sqrt{\frac{1}{\#h}\sum _{c=1}^{\#h}{|h_{1_{\sigma (c)}}-h_{2_{\sigma (c)}}|}^2}$$ (24)

The authors of [39] defined Hamming distance between two different HFEs as follows:

$$d(h_1,h_2)=\frac{1}{\#h}\sum _{c=1}^{\#h}|h_{1_{\sigma (c)}}-h_{2_{\sigma (c)}}$$ (25)

Here, $h_1,h_2$ are HFEs and $\text{'}\#h\text{'}$ denotes the number of elements present in a HFE, also known as length of HFE. Generally, the length of HFEs are diverse and the values in it frequently out of order. To calculate the distance between two HFEs, one should follow these steps:

Assemble the elements in increasing order or declining order.

2. When the lengths of two HFEs are dissimilar, then the shorter length HFE be supposed to be extended by adding the minimal value or maximum value, which is depending on the preference of resolution makers. The optimistic DM prefers addition of maximum value while the pessimistic DM prefers minimum value, according to the reference of [38]

Step 3: The relative closeness to the ideal solution is determined with the following equation:

$${\mathit{RC}}_b=\frac{D_b^{-}}{D_b^{-}+D_b^{+}}$$ (26)

Step 4: Ranking of the alternatives are done on the values of ${\mathit{RC}}_b$, the greater value signifies the optimal alternative.

Note 1: HFS-TOPSIS are extremely helpful in considering the vagueness scenery of the subjective valuations. HFS theory allows the membership degree of a trait to a given set which is being represented by the more than a few probable numerical values.

Selection of criteria’s and risk factors for the study

The objective of this study is to rank the significant risk factors for the spread of the virus. The criteria’s selected by us are Expert opinion i.e. Doctor’s advice, Review of past literature and Media survey.

This research is based on the domain of medical sciences, doctor’s opinion plays a significant role. Doctors, whose domain is infectious disease and those who have been actively treating COVID-19 patients were interviewed. With each passing day, the disease is taking a turn for the worse with the rising asymptomatic symptoms and an expert’s opinion is the only way forward to zero in on the apt risk factors.

The recent research, in this regard has helped us to better highlight the risk factors. The correlation of each risk factor to the various cases studied, has provided clearer links. Thus, review of literature is also an important criterion which helped in identifying the risk factors.

Media survey is an important criterion for selecting the risk factors because in this ongoing pandemic, media has the largest reservoir of the events occurring in connection to COVID-19. The total number of cases be it the confirmed cases, number of deaths or the number of recovered cases in each region, state or the country can be found out by just tuning in to the channels. In this study, reputed media who have a worldwide coverage and an impeccable reputation for delivering true facts have been considered.

Thus, in this research, doctor’s opinion${(\mathrm{\Psi }}_1)$, literature review${(\mathrm{\Psi }}_2)$ and media ${(\mathrm{\Psi }}_3)$ referred by the authors of [57] are the criteria based on which, the most significant risk factors in COVID-19 spread have been identified and considered in this research.

The risk factors selected for the study is depicted in Table 3 .

Table 3.

Representation of different risk factors.

Risk Factors Associated with the disease	Brief description
Verbal Spread, $\stackrel{}{{\mathrm{\Theta }}_1}$	Verbal spread is due to the cough, sneezing and viral load of an infected person. [1], [71]
Long Duration of contact with the Infected person, $\stackrel{}{{\mathrm{\Theta }}_2}$	Time factor significantly depends when a normal person is with an infected person.
Not maintaining personal hygiene, $\stackrel{}{{\mathrm{\Theta }}_3}$	Frequently usage of sanitizer, washing hands, changing clothes if a person comes from outside is highly recommended.
Not using quality mask, $\stackrel{}{{\mathrm{\Theta }}_4}$	N-95 and surgical mask are recommended by doctors, as these masks lowers down the risk, whereas it is seen that the normal mask doesn’t prevent the disease and probability is higher if not using quality masks.
Not maintaining distance in public transport or public places, $\stackrel{}{{\mathrm{\Theta }}_5}$	Maintaining Social distance is very important
Infection spread through hospitals and clinic, $\stackrel{}{{\mathrm{\Theta }}_6}$	A person has higher probability of getting infected, if he/she visits hospitals and clinic.

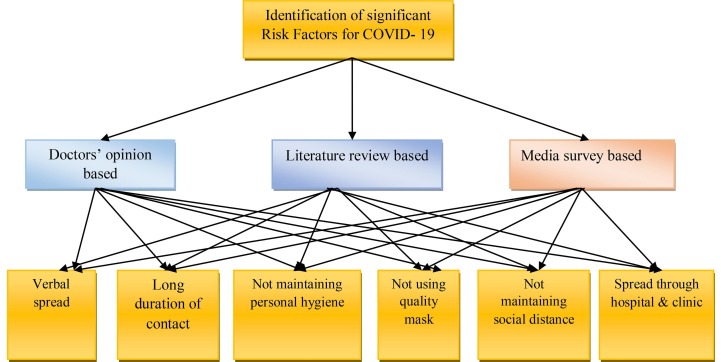
The following hierarchical structure in Fig. 2 represents the three criteria based on which six risk factors are chosen (Fig. 3 ).

Fig. 2.

Hierarchical structure of the study.

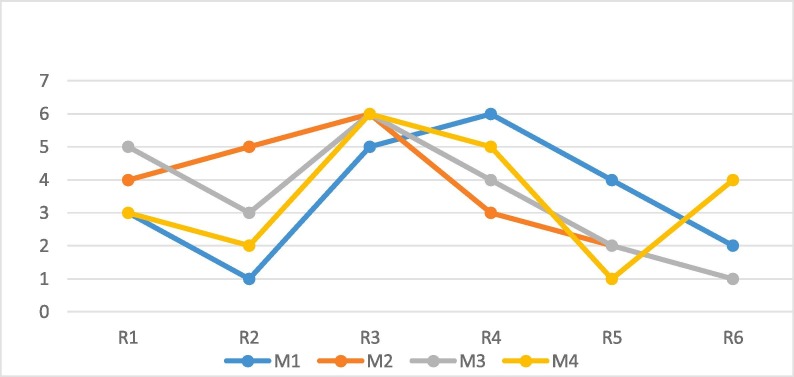
Fig. 3.

Line Chart depicting sensitivity of the ranking based on different methods.

Empirical study

Data Source: The opinion of doctors, literature review [1], [71], [57] and media survey. The DMs comparative preferences for the criteria in terms of TFN are represented in Table 4 using Table 2. The entire process of FAHP used in the study is described below.

Table 4.

Formation of comparison matrix.

Comparison Matrix	DM1			DM2
	${\mathrm{\Psi }}_1$	${\mathrm{\Psi }}_2$	${\mathrm{\Psi }}_3$	${\mathrm{\Psi }}_1{\mathrm{\Psi }}_3$	${\mathrm{\Psi }}_2$	${\mathrm{\Psi }}_3$
${\mathrm{\Psi }}_1$	1	(3.5,4,4.5)	(4.5,5,5.5)	1	(0.22,0.25,0.286)	(4.5,5,5.5)
${\mathrm{\Psi }}_2$	(0.22,0.25,0.286)	1	(3.5,4,4.5)	(3.5,4,4.5)	1	(4.5,5,5.5)
${\mathrm{\Psi }}_3$	(0.18,0.2,0.22)	(0.22,0.25,0.286)	1	(0.18,0.2,0.22)	(0.18,0.2,0.22)	1

Step 1: Construction of comparison matrix

Step 2: Aggregation of TFN using equation (12).

Step 3: Defuzzification of TFN using Eq. (13).

Step 4: Normalization of the matrix using Eq. (14).

Step 5: Determination of Criteria weights using Eq. (15)

Table 5 depicts the criteria weight obtained by FAHP.

Table 5.

Representation of criteria’s weight.

Criteria’s	${\mathrm{\Psi }}_1$	${\mathrm{\Psi }}_2$	${\mathrm{\Psi }}_3$
Weight	0.47	0.45	0.08

Table 6 represents the hesitant fuzzy decision matrix used in TOPSIS approach of this paper for expressing opinion about the risk factors on the basis of criteria used in the study.

Table 6.

Construction of hesitant decision matrix.

Risk Factor’s	${\mathrm{\Psi }}_1$	${\mathrm{\Psi }}_2$	${\mathrm{\Psi }}_3$
Verbal Spread $\stackrel{}{{\mathrm{\Theta }}_1}$	(0.5,0.7,0.9)	(0.6,0.7)	(0.8)
Long Duration of contact $\stackrel{}{{\mathrm{\Theta }}_2}$	(0.9)	(0.6,0.7,0.8,0.9)	(0.7,0.8)
Not maintaining personal hygiene $\stackrel{}{{\mathrm{\Theta }}_3}$	(0.4,0.5,0.6)	(0.1,0.3,0.5)	(0.5)
Not using quality mask $\stackrel{}{{\mathrm{\Theta }}_4}$	(0.2,0.3,0.4,0.5)	(0.3)	(0.4,0.5)
Not maintaining distance in public transport or public places $\stackrel{}{{\mathrm{\Theta }}_5}$	(0.6,0.7)	(0.4,0.5,0.6)	(0.3,0.4,0.5,0.6)
Infection spread through hospitals and clinic $\stackrel{}{{\mathrm{\Theta }}_6}$	(0.8,0.9)	(0.6,0.7,0.8)	(0.4,0.5,0.6)

Step 1: Identification of PIS and NIS using Eq. (18), (21)

$$A_p^{+}=\{0.9,0.9,0.8\}$$

$$A_n^{-}=\{0.2,0.1,0.3\}$$

Step 2: Separation measure$D_b^{+}$ and $D_b^{-}$ are calculatedfor each alternative using (22), (23)

$$D_1^{+}=0.47\times \left|\left|\left\{0.5,0.7,0.9\right\}-\left\{0.9\right\}\right|\right|+0.45\times \left|\left|\left\{0.6,0.7\right\}-\left\{0.9\right\}\right|\right|+0.08\times ||\left\{0.8\right\}-\{0.8\}||$$

The Hamming distance between two HFE is calculated using (25)

$$\left|\left|\left\{0.5,0.7,0.9\right\}-\left\{0.9\right\}\right|\right|=\frac{1}{3}\left[\left|0.5-0.9\right|+\left|0.7-0.9\right|+\left|0.9-0.9\right|\right]=0.2$$

Table 7 represents the separation measures and subsequent relative closeness calculation (Table 8 ).

Table 7.

Relative closeness of the alternatives.

Risk Factors	$D_b^{+}$	$D_b^{-}$	${\mathit{RC}}_b=\frac{D_b^{-}}{D_b^{-}+D_b^{+}}$
$\stackrel{}{{\mathrm{\Theta }}_1}$	0.122	0.5225	0.811
$\stackrel{}{{\mathrm{\Theta }}_2}$	0.0715	0.704	0.91
$\stackrel{}{{\mathrm{\Theta }}_3}$	0.482	0.357	0.42
$\stackrel{}{{\mathrm{\Theta }}_4}$	0.556	0.1725	0.24
$\stackrel{}{{\mathrm{\Theta }}_5}$	0.3255	0.3735	0.53
$\stackrel{}{{\mathrm{\Theta }}_6}$	0.1375	0.615	0.82

Table 8.

Different ranking obtained.

Risk Factors	FAHP HFS-TOPSIS (M1)	Crisp AHP-TOPSIS (M2)	PIVN AHP-TOPSIS (M3)	FAHP-FTOPSIS (M4)
$\stackrel{}{{\mathrm{\Theta }}_1}$(R1)	3	4	5	3
$\stackrel{}{{\mathrm{\Theta }}_2}$(R2)	1	5	3	2
$\stackrel{}{{\mathrm{\Theta }}_3}$(R3)	5	6	6	6
$\stackrel{}{{\mathrm{\Theta }}_4}$(R4)	6	3	4	5
$\stackrel{}{{\mathrm{\Theta }}_5}$(R5)	4	2	2	1
$\stackrel{}{{\mathrm{\Theta }}_6}$(R6)	2	1	1	4

From the analysis, it is seen that the risk factor long duration of contact $\stackrel{}{{\theta }_2}$ is the most significant risk factor. Arranging the rankings in descending order, we see:

$$\stackrel{}{{\theta }_2}\succ \stackrel{}{{\theta }_6}\succ \stackrel{}{{\theta }_1}\succ \stackrel{}{{\theta }_5}\succ \stackrel{}{{\theta }_3}\succ \stackrel{}{{\theta }_4}$$

This shows ‘long duration of contact with the infected person’ is the most significant risk factor, followed by ‘spread through hospitals and clinic’, ‘verbal spread’, ‘not maintaining distance in public transport or public places’, ‘not maintaining personal hygiene’ and ‘not using quality mask’.

Sensitivity analysis

The domain of the paper is based on HFS-TOPSIS approach for the identification of most significant risk factor under FAHP for criterion weight. To explore sensitivity of the ranking obtained, different other ranking techniques has been applied. We applied Crisp values with the AHP- TOPSIS, Parametric Form of Interval Numbers (PIVN) AHP-TOPSIS and Triangular Fuzzy Number (TFN) FAHP-FTOPSIS.

• (a)Crisp AHP-TOPSIS- The MCDM technique in which the linguistic terms are considered as crisp numbers. The linguistic terms used for the comparison matrix are crisp values. The linguistic terms for preferential rating the alternative is also crisp value. The authors of [72] used AHP-TOPSIS to check the preference order of the teachers in an educational institute.
• (b)PIVN AHP-TOPSIS- In this method, parametric form of interval numbers is taken for the study. The authors of [73] represented the interval numbers in various functional forms and explained the concept with arithmetic operations.
• (c)FAHP-FTOPSIS- In FAHP, fuzzy numbers are used for the construction of comparison matrix and the weight’s obtained are fuzzy weights. The FTOPSIS is an extension of classical TOPSIS approach as it solves the decision-making problem with fuzzy uncertainty. The author of [60] used FAHP-FTOPSIS for performance evaluation of industrial practitioner in terms of triangular fuzzy numbers (TFN).

Remark

s: Here $\stackrel{}{{\mathrm{\Theta }}_2}$ (R2), $\stackrel{}{{\mathrm{\Theta }}_6}$ (R6) are identified as significant factor in terms of virus spread clearly visible through this line chart. Government should make policy accordingly.

Results and discussions

This section discusses about the findings obtained. The result obtained by FAHP, HFS-TOPSIS and the result obtained by sensitivity analysis. The methodology FAHP, HFS-TOPSIS ranked “long duration of contact with the infected person” the most significant risk factor, followed by “spread through hospitals and clinic”, “verbal spread”, “not maintaining social distance in public places or public transport”, “not maintaining personal hygiene” and “not using quality mask” .The method crisp AHP-TOPSIS and PIVN AHP-TOPSIS ranks “spread through hospitals and clinic” the most important risk factor. Further, the method FAHP-FTOPSIS ranked “not maintaining social distance in public transport and places” the most significant one.

Conclusion and future scope

In this study, we analyzed the most significant risk factor for the spread of COVID-19 disease using FAHP and HFS-TOPSIS method. Doctor’s opinion, literature review and media survey are the three important criteria’s for the selection of significant risk factor. The criteria’s weight were determined using FAHP. HFS-TOPSIS application identified the most significant risk factor. The advantage of using HFS-TOPSIS is that, it analyzed the risk factors comprehensively. Additional risk factors could be considered in the future based on the way COVID-19 spreads around the globe. Future research can be carried out to scientifically decide the location for building quarantine centers, isolation planning, safe homes, safe mask, epidemic controlling model and bed augmentation model for COVID- 19 hospitals to cater large number of people. Developing mathematical models incorporating different graded interventional effect of lockdown will help in deciding optimal lockdown norms. Research involving population who have developed antibody of COVID-19 can yield better deployment of personnel for COVID-19 management. Detailed research and data analytics will help in understanding the level of community spread. The strategy can be applied in the different sector problem. Anyone can also take the different uncertain parameter rather than fuzzy and hesitant fuzzy setting.

CRediT authorship contribution statement

Neha Ghorui: Conceptualization, Methodology. Arijit Ghosh: Data curation, Writing - original draft. Sankar Prasad Mondal: Supervision, Validation. Mohd Yazid Bajuri: . Ali Ahmadian: Supervision, Validation. Soheil Salahshour: . Massimiliano Ferrara: .

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.