A dynamic generalized fuzzy multi-criteria croup decision making approach for green supplier segmentation

Do Anh Duc; Luu Huu Van; Vincent F Yu; Shuo-Yan Chou; Ngo Van Hien; Ngo The Chi; Dinh Van Toan; Luu Quoc Dat

doi:10.1371/journal.pone.0245187

. 2021 Jan 25;16(1):e0245187. doi: 10.1371/journal.pone.0245187

A dynamic generalized fuzzy multi-criteria croup decision making approach for green supplier segmentation

Do Anh Duc ^1,², Luu Huu Van ¹, Vincent F Yu ³, Shuo-Yan Chou ³, Ngo Van Hien ⁴, Ngo The Chi ⁵, Dinh Van Toan ¹, Luu Quoc Dat ^1,^*

Editor: Yiming Tang⁶

PMCID: PMC7833157 PMID: 33493184

Abstract

Supplier selection and segmentation are crucial tasks of companies in order to reduce costs and increase the competitiveness of their goods. To handle uncertainty and dynamicity in the supplier segmentation problem, this research thus proposes a new dynamic generalized fuzzy multi-criteria group decision making (MCGDM) approach from the aspects of capability and willingness and with respect to environmental issues. The proposed approach defines the aggregated ratings of alternatives, the aggregated weights of criteria, and the weighted ratings by using generalized fuzzy numbers with the effect of time weight. Next, we determine the ranking order of alternatives via a popular centroid-index ranking approach. Finally, two case studies demonstrate the efficiency of the proposed dynamic approach. The applications show that the proposed appoach is effective in solving the MCGDM in vague environment.

Introduction

Supplier segmentation is a step that follows supplier selection and plays an important role in organizations for reducing production costs and optimally utilizing resources. Enterprises classify their suppliers from a selected set into distinct groups with different needs, characteristics, and requirements in order to adopt an appropriate strategic approach for handling different supplier segments [1]. Supplier segmentation is a highly complex decision-making problem that must consider many potential criteria and decision makers under a vague environment [2, 3]. Consequently, supplier segmentation can be viewed as a fuzzy multi-criteria group decision making (MCGDM) problem.

Numerous studies in the literature have proposed fuzzy multi-criteria decision making (MCDM) approaches to select and evaluate (green/sustainable) suppliers, with some recent applications found in [4–10]. While several studies used multi-criteria methods and fuzzy logic systems for solving supplier segmentation problem [2, 3, 11–13], existing studies on segmenting suppliers have paid limited attention to environmentally and socially related criteria [11]. Additionally, few studies have applied generalized fuzzy numbers (GFNs) to select or segment suppliers. Furthermore, they all have converted GFNs into normal fuzzy numbers through a normalization process and then applied fuzzy MCDM methods for normal fuzzy numbers. Nevertheless, the normalization process has a serious disadvantage—that is, the loss of information [14].

Chen [15] indicated in many practical situations that it is not possible to restrict the membership function to the normal form. Furthermore, the existing studies targeting supplier selection and segmentation only address static evaluation information for a certain period. However, in many real-life problems the decision makers are generally provided the information over different periods [16, 17]. Lee et al. [16] proposed a dynamic fuzzy MCGDM method for performance evaluation, while Mehdi et al. [17] presented a new fuzzy dynamic MCGDM approach to assess a subcontractor. Overall, it seems that no study has yet to propose a dynamic MCGDM using GFNs for solving the green supplier segmentation (GSS) problem with the effect of a time weight.

This study primarily proposes a new dynamic generalized fuzzy MCGDM approach from the aspects of capability and willingness with respect to environmental issues. The proposed approach defines the aggregated ratings of alternatives, the aggregated weights of criteria, and the aggregated weighted ratings using GFNs with the effect of time weight. We then determine the ranking order of alternatives via a popular centroid-index ranking approach proposed by [18]. Finally, two case studies demonstrate the efficiency of the proposed approach.

Literature review on methods and criteria for supplier segmentation

This section presents an overview of the methods and criteria that have been used for supplier segmentation in the existing literature.

Supplier segmentation methods

Supplier segmentation models have been widely explored ever since the pioneering works of [19, 20], who specified the variables required for segmenting suppliers [2, 3, 21–26]. Some of these models have been reviewed and discussed in the works of [20, 27–29]. Kraljic [20] presented a comprehensive portfolio approach to purchasing and supply segmentation. To classify materials or components, Kraljic [20] utilized two variables, the profit impact of a given item and the supply risk, under high and low levels that yield four segments: (1) non-critical items (supply risk: low; profit impact: low), (2) leverage items, (supply risk: low; profit impact: high), (3) bottleneck items (supply risk: high; profit impact: low), and (4) strategic items (supply risk: high; profit impact: high). Dyer et al. [30] developed strategic supplier segmentation based on the differences between outsourcing strategies. According to them, firms should maintain high levels of communication with suppliers that provide strategic inputs that contribute to the differential advantage of the buyer’s final product. On the other hand, firms do not need to allocate significant resources to manage and work with suppliers that provide non-strategic inputs. Kaufman et al. [26] developed a strategic supplier typology that explains the differences in the composition and performance of various types of suppliers, using technology and collaboration to segment suppliers.

Svensson [27] applied three principal components, including the source of disturbance, the category of disturbance, and the type of logistics flow, in supplier segmentation. Hallikas et al. [24] described supplier and buyer dependency risks as the variables for classifying supplier relationships. Day et al. [28] presented the taxonomy of segmentation bases in which the buyer assesses the supply base from a purchasing perspective. Che [22] proposed two optimization mathematical models for the clustering and selection of suppliers. Model 1 is based on customer demands to cluster suppliers under a minimal total within cluster variation. Model 2 takes the results of Model 1 to determine the optimal supplier combination based on quantity discount and customer demands. Rezaei & Ortt [31] proposed a framework for classifying suppliers based on supplier capabilities and willingness. Using their framework, it is possible to segment suppliers using multiple criteria, but most existing methods are based on just two criteria.

Rezaei et al. [32] presented an approach for segmenting and developing suppliers using capabilities and willingness criteria. They employed the best worst method (BWM) to define the relative weight of the criteria and further applied a scatter plot to segment the suppliers, where the horizontal and vertical axes are capabilities and willingness, respectively. Segura & Maroto [21] utilized a hybrid MCDM approach based on PROMETHEE and Multi-Attribute Utility Theory and used Analytic Hierarchy Process (AHP) for eliciting the weights of the criteria. The authors further took historical and reliable indicators to classify suppliers. Bai et al. [11] presented a novel methodology based on the rough set theory, VIKOR, and fuzzy C-means for green supplier segmentation, employing the dimensions of willingness and capabilities in their approach. Aineth & Ravindran [8] proposed a quantitative framework for sustainable procurement using the criteria of economic, environmental, and social hazards. Rezaei & Lajimi [33] combined purchasing portfolio matrix, supplier potential matrix, and BWM to segment suppliers. Appendix A in S1 Appendix compares the existing methods for supplier segmentation.

Supplier segmentation is a MCGDM problem that includes many criteria and decision makers within a vague environment. However, only a few studies in the literature applied the multi-criteria method and fuzzy logic systems to segment suppliers. Additionally, previous studies were limited to using normal fuzzy numbers and addressing the static evaluation information at a certain period to segment suppliers. Rezaei & Ortt [2] utilized the fuzzy AHP approach to segment suppliers using their capabilities and willingness criteria. Haghighi & Salahi [13] used the integrated fuzzy AHP approach and c-means algorithm to cluster suppliers. Akman [34] proposed a hybrid approach, including VIKOR, confirmatory factor analysis, and fuzzy c-means, to evaluate and segment suppliers in an automobile manufacturing company. The criteria of suppliers’ capability and willingness were used to cluster suppliers. Lo & Sudjatmika [12] presented a modified fuzzy AHP approach for evaluating suppliers using bell-shaped membership functions. To our knowledge, no prior studies have developed the dynamic generalized fuzzy MCGDM approach with respect to environmental issues for solving supplier segmentation problem.

Green supplier segmentation criteria

Identifying the GSS criteria is one of the main challenges of a business enterprise to formulate proper supplier segmentation. To conduct GSS, several economic, environmental, and social dimensions should be considered [6], yet the majority of prior research only considered the evaluation criteria from the economic aspect. To segment the suppliers, our study’s proposed approach takes into account not only economic criteria, but also environmental and social criteria. Appendix A in S1 Appendix summarizes the capabilities and willingness criteria drawing the greatest attention in recent literature.

Establishment of a new approach for solving green supplier selection and segmentation

This section develops a new generalized fuzzy dynamic MCGDM approach to solve the green supplier selection and segmentation problem. The procedure of the proposed approach is described as follows.

Identifying the green capabilities and willingness criteria

A committee of k decision makers (D_v,v = 1,…,k) is assumed responsible for evaluating m suppliers (A_i,i = 1,…,m) under n selection criteria (C_j,j = 1,…,n) in time sequence t_u,u = 1,…,h, where the ratings of green suppliers versus each criterion and the importance weight of the criteria are expressed by using GTFN. The criteria are classified into two categories: capabilities (C_j,j = 1,…,l) and willingness (C_j,j = l+1,…,n).

A dynamic MCGDM approach can be concisely expressed in matrix format as:

C_{1} (t_{u}) C_{2} (t_{u}) \dots C_{j} (t_{u})

D_{v} (t_{u}) = \begin{array}{l} A_{1} (t_{u}) \\ A_{2} (t_{u}) \\ ⋮ \\ A_{i} (t_{u}) \end{array} [\begin{array}{l} x_{11} (t_{u}) x_{12} (t_{u}) \dots x_{1 j} (t_{u}) \\ x_{21} (t_{u}) x_{22} (t_{u}) \dots x_{2 j} (t_{u}) \\ ⋮ ⋮ ⋮ ⋮ \\ x_{i 1} (t_{u}) x_{i 2} (t_{u}) \dots x_{i j} (t_{u}) \end{array}]

Aggregating the importance weights of the criteria

Let $w_{j v} (t_{u}) = 〈 o_{j v} (t_{u}), p_{j v} (t_{u}), q_{j v} (t_{u}); ϖ_{j v} (t_{u}) 〉, w_{j v} (t_{u}) \in R^{*}, j = 1, \dots, n, v = 1, \dots, k,$ u = 1,…,h, be the weight assigned by decision maker D_v to criterion C_j(C_j,j = 1,…,n) in time sequence t_u. The average weight, w_j = (o_j,p_j,q_j;ϖ_j), of criterion C_j assessed by the committee of k decision makers can be evaluated as:

w_{j} = \frac{1}{h * k} \otimes 〈 w_{j 1} (t_{1}) \oplus w_{j 2} (t_{2}) \oplus … \oplus w_{j k} (t_{u}) 〉,

(1)

where $o_{j} = \frac{1}{h * k} \sum_{v = 1}^{k} o_{j v} (t_{u}), p_{j} = \frac{1}{h * k} \sum_{v = 1}^{k} p_{j v} (t_{u}), q_{j} = \frac{1}{h * k} \sum_{v = 1}^{k} q_{j v} (t_{u})$ and ϖ_j = min(ϖ_j1(t₁),ϖ_j2(t₂),…,ϖ_jk(t_u)}.

Aggregating the ratings of green suppliers versus the criteria

Let $x_{i j v} (t_{u}) = 〈 e_{i j v} (t_{u}), f_{i j v} (t_{u}), g_{i j v} (t_{u}); ϖ_{i j v} (t_{u}) 〉,$ i = 1,…,m,j = 1,…,n, v = 1,…,k, u = 1,…,h, be the suitability ratings assigned to the green suppliers A_i, by decision makers D_v, for criteria C_j in time sequence t_u. The averaged suitability ratings, x_ij = (e_ij,f_ij,g_ij;ϖ_ij), can be evaluated as:

x_{i j} = \frac{1}{h * k} \otimes (x_{i j 1} (t_{1}) \oplus x_{i j 2} (t_{2}) \oplus … \oplus x_{i j v} (t_{u}) \oplus … \oplus x_{i j k} (t_{h})),

(2)

where $e_{i j} = \frac{1}{h * k} \sum_{v = 1}^{k} e_{i j v} (t_{u}),$ $f_{i j} = \frac{1}{h * k} \sum_{v = 1}^{k} f_{i j v} (t_{u}),$ $g_{i j} = \frac{1}{h * k} \sum_{v = 1}^{k} g_{i j v} (t_{u}),$ and ϖ_ij = min(ϖ_ij1(t₁),ϖ_ij2(t₂),…,ϖ_ijk(t_h)}.

Constructing the weighted fuzzy decision matrix

The weighted decision matrices S_i1 = (d_i1,h_i1,i_i1;ϖ_i1) and S_i2 = (d_i2,h_i2,i_i2;ϖ_i2) of the green suppliers A_i versus the capabilities (C_j,j = 1,…,l) and willingness criteria (C_j,j = l+1,…,n) in time t_u are respectively defined as follows:

S_{i 1} = \frac{1}{l} \sum_{j = 1}^{l} {(s_{i j})}_{m . l} = \frac{1}{l} \sum_{j = 1}^{l} x_{i j} \otimes w_{j}, i = 1, \dots, m; j = 1, \dots, l,

(3)

S_{i 2} = \frac{1}{n - l - 1} \sum_{j = l + 1}^{n} {(s_{i j})}_{m . (n - l)} = \frac{1}{n - l - 1} \sum_{j = l + 1}^{n} x_{i j} \otimes w_{j}, i = 1, \dots, m; j = l + 1, \dots, n .

(4)

Defuzzification

This study applies the popular centroid-index ranking approach proposed by [18] to determine the distance values between the centroid and minimum points of green suppliers versus the capabilities and willingness criteria.

Segmenting the green suppliers

Based on the distance values between the centroid and minimum points of the green suppliers in defuzzification process versus the capabilities and willingness criteria, we divide the green suppliers into 2 × 2 segments, including Group 1 (low capabilities and low willingness), Group 2 (low capabilities and high willingness), Group 3 (high capabilities and low willingness), and Group 4 (high capabilities and high willingness). The cut-off points, which are the potential values of the distance, are determined by the decision makers; i.e., all decision makers give the linguistic variables for the ratings of alternatives as Fair = (0.3, 0.5, 0.7; 0.8).

Implementation of the proposed dynamic generalized fuzzy MCGDM approach

This section applies the proposed approach in the case of a medium-sized transport equipment company located in northern Vietnam. The managers of this company have become perplexed on how to effectively manage their suppliers to maximize their profit due to the increase in the number of suppliers. We apply the proposed approach to the process of this firm’s green supplier segmentation to help it segment its suppliers and test the efficacy of the proposed method. Data were collected by conducting semi-structured interviews with the company’s top managers and department heads (decision-makers). Three decision makers (D₁, D₂, and D₃) were requested to separately evaluate the importance weights of the capabilities and willingness criteria and the ratings of GSS at three different times (t₁, t₂, and t₃). We characterize the entire GSS procedure by the following steps.

Step 1: Aggregate the importance weights of the respective capabilities and willingness criteria.
Step 2: Aggregate the ratings of green suppliers versus capabilities and willingness criteria, respectively.
Step 3: Construct the weighted fuzzy decision matrices.
Step 4: Calculation of the distance of each green supplier.
Step 5: Segment the green suppliers.

Steps 1 and 2 were performed by the company’s managers (i.e., the three decision-makers D₁, D₂, and D₃) without any intervention from the authors. Steps 3 to 5 were calculated using the proposed approach.

Aggregation of the importance weights of the respective green capabilities and willingness criteria

Following the review of the literature and discussions with the top managers and department heads, we select six capabilities (i.e., price/cost—C₁, delivery—C₂, quality—C₃, reputation and position in industry—C₄, financial position—C₅, hazardous waste management—C₆) and four willingness criteria (i.e., commitment to quality—W₁, commitment to continuous improvement in product and process—W₂, relationship closeness—W₃, willingness to share information, ideas, technology, and cost savings—W₄) for evaluating and segmenting suppliers. After determining the green suppliers’ criteria, the three company’s managers are asked to define the level of importance of each criterion through a linguistic variable. Table 1 shows the aggregate weights of the criteria using Eq (1).

Table 1. Aggregated weights of the criteria evaluated by the decision makers.

Criterion	Decision maker									w_ij
	t₁			t₂			t₃
	D₁	D₂	D₃	D₁	D₂	D₃	D₁	D₂	D₃
C₁	VI	VI	VI	AI	VI	AI	AI	VI	AI	(0.633, 0.789, 0.944; 0.900)
C₂	VI	I	I	I	I	I	VI	VI	I	(0.433, 0.567, 0.700; 0.800)
C₃	VI	AI	VI	AI	VI	VI	VI	VI	VI	(0.567, 0.744, 0.922; 0.900)
C₄	VI	VI	AI	VI	VI	VI	I	VI	I	(0.511, 0.678, 0.844; 0.800)
C₅	AI	VI	VI	I	VI	I	I	VI	I	(0.489, 0.633, 0.778; 0.800)
C₆	I	VI	I	I	VI	VI	I	VI	VI	(0.456, 0.611, 0.767; 0.800)
W₁	I	I	I	VI	I	I	I	VI	I	(0.422, 0.544, 0.667; 0.800)
W₂	VI	I	VI	I	I	VI	VI	I	I	(0.444, 0.589, 0.733; 0.800)
W₃	I	I	I	I	VI	I	I	VI	I	(0.422, 0.544, 0.667; 0.800)
W₄	I	VI	I	I	VI	VI	VI	VI	I	(0.456, 0.611, 0.767; 0.800)

Open in a new tab

Aggregation of the ratings of green suppliers versus the capabilities and willingness criteria

The decision makers define the suitability ratings of twelve green suppliers (i.e., A₁,…,A₁₂) versus the capabilities and willingness criteria using the linguistic variables. Table 2A to 2E (in Appendix C in S1 Appendix) present the aggregated suitability ratings of the suppliers versus the six capabilities criteria (i.e., C₁,…,C₇) and four willingness criteria (i.e., W₁,…,W₆) from the three decision makers obtained from Eq (2) and Table 1 (in Appendix B in S1 Appendix).

Table 2. Final fuzzy evaluation values of each supplier.

Supplier	Capabilities criteria	Willingness criteria
A₁	(0,214, 0,405, 0,653; 0,700)	(0,126, 0,262, 0,443; 0,700)
A₂	(0,124, 0,261, 0,444; 0,600)	(0,214, 0,387, 0,611; 0,800)
A₃	(0,303, 0,507, 0,762; 0,800)	(0,198, 0,372, 0,598; 0,800)
A₄	(0,131, 0,269, 0,453; 0,600)	(0,214, 0,391, 0,620; 0,800)
A₅	(0,228, 0,422, 0,674; 0,700)	(0,191, 0,358, 0,576; 0,700)
A₆	(0,231, 0,428, 0,685; 0,700)	(0,219, 0,391, 0,611; 0,800)
A₇	(0,298, 0,484, 0,716; 0,700)	(0,212, 0,386, 0,612; 0,800)
A₈	(0,137, 0,286, 0,487; 0,600)	(0,130, 0,266, 0,449; 0,600)
A₉	(0,231, 0,428, 0,683; 0,700)	(0,205, 0,377, 0,601; 0,800)
A₁₀	(0,258, 0,448, 0,692; 0,600)	(0,184, 0,353, 0,575; 0,700)
A₁₁	(0,239, 0,440, 0,699; 0,800)	(0,203, 0,378, 0,605; 0,800)
A₁₂	(0,131, 0,273, 0,464; 0,600)	(0,214, 0,378, 0,589; 0,600)

Open in a new tab

Determination of the weighted rating

Table 2 shows the final fuzzy evaluation values of each green supplier using Eqs (3) and (4).

Calculation of the distance of each green supplier

We obtain the distance between the centroid point and the minimum point Go = (0,124, 0,600) of each green supplier as depicted in Table 3 by using the data in Table 2 and the ranking approach proposed by [18].

Table 3. Distance measurement.

Supplier	Capabilities criteria		Willingness criteria
Supplier	Centroid point A_i $({\bar{x}}_{A}, {\bar{y}}_{A})$	Distance D(A_i, Go)	Centroid point A_i $({\bar{x}}_{A}, {\bar{y}}_{A})$	Distance D(A_i, Go)
A₁	(0,424, 0,233)	0,314	(0,277, 0,233)	0,177
A₂	(0,276, 0,200)	0,172	(0,404, 0,267)	0,298
A₃	(0,524, 0,267)	0,414	(0,389, 0,267)	0,284
A₄	(0,284, 0,200)	0,179	(0,409, 0,267)	0,302
A₅	(0,442, 0,233)	0,331	(0,375, 0,233)	0,266
A₆	(0,448, 0,233)	0,338	(0,407, 0,267)	0,300
A₇	(0,499, 0,233)	0,387	(0,404, 0,267)	0,297
A₈	(0,303, 0,200)	0,197	(0,282, 0,200)	0,175
A₉	(0,447, 0,233)	0,337	(0,394, 0,267)	0,288
A₁₀	(0,466, 0,200)	0,351	(0,370, 0,233)	0,261
A₁₁	(0,459, 0,267)	0,352	(0,396, 0,267)	0,290
A₁₂	(0,289, 0,200)	0,184	(0,394, 0,200)	0,279

Open in a new tab

Segmentation of the suppliers

Based on the distance scores for the capabilities and willingness of each green supplier, we assign 12 green suppliers to one of four segments (Fig 1) using Step 6 of the proposed methodology. In this step, the cut-off points of the green supplier’s capabilities and willingness are 0.2084 and 0.1814, respectively. Fig 1 and Table 4 show that one green supplier is assigned to Group 1, three green suppliers to Group 2, one green supplier to Group 3, and seven green suppliers to Group 4. Thus, the company has seven good green suppliers, but five of them lack capabilities, willingness, or both.

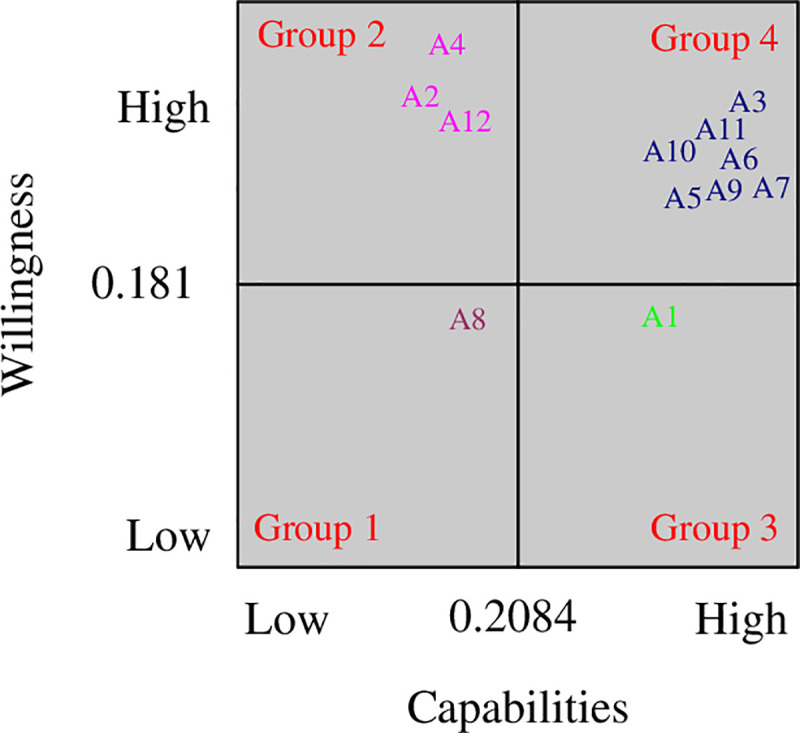
Table 4. Segments of the suppliers.

Segment	No. of suppliers	Supplier(s)
Group 1	1	A₈
Group 2	3	A₂, A₄, A₁₂
Group 3	1	A₁
Group 4	7	A₃, A₅, A₆, A₇, A₀₉, A₁₀, A₁₁

Open in a new tab

The results indicate that the company can use different strategies to handle various segments and may try and develop those green suppliers that are less capable and less willing to cooperate (i.e., Group 1 green suppliers) or terminate its relationship with them in favor of good alternatives [2, 3]. Group 2 green suppliers are willing to cooperate, but are less competent to meet the buyer’s requirements. The company should help these green suppliers improve their capabilities and performance or replace them with capable ones in the short term [35]. Group 3 green suppliers have high capabilities, but exhibit a low-level willingness to cooperate. The company should focus on improving its relationship with these green suppliers and determine various approaches on how to become attractive to them [36]. Group 4 green suppliers, which are the best green suppliers of the company, have great capabilities and a high level of willingness. The company should maintain a close long-term relationship with these green suppliers [31].

Comparison of the proposed method with another fuzzy MCDM method

This section compares the proposed approach in time t_u,u = 1 with another fuzzy MCDM approach to demonstrate its advantages and applicability by reconsidering the example investigated by [2]. In this example, a medium-sized broiler (meat-type chicken) company in the food industry intends to segment its suppliers. Six criteria for capabilities and six criteria for willingness are selected to segment 43 suppliers based on the decision makers (i.e., the managers). Table 5 shows the importance weights of the capabilities and willingness criteria.

Table 5. Importance weights of the capabilities and willingness criteria.

Capabilities criterion	Fuzzy weight	Willingness criterion	Fuzzy weight
$C_{1}^{C}$	(0.065, 0.106, 0.181; 1.0)	$C_{1}^{W}$	(0.114, 0.206, 0.350; 1.0)
$C_{2}^{C}$	(0.110, 0.161, 0.238; 1.0)	$C_{2}^{W}$	(0.086, 0.150, 0.266; 1.0)
$C_{3}^{C}$	(0.148, 0.206, 0.279; 1.0)	$C_{3}^{W}$	(0.094, 0.150, 0.253; 1.0)
$C_{4}^{C}$	(0.115, 0.161, 0.231; 1.0)	$C_{4}^{W}$	(0.094, 0.150, 0.253; 1.0)
$C_{5}^{C}$	(0.109, 0.161, 0.240; 1.0)	$C_{5}^{W}$	(0.127, 0.206, 0.328; 1.0)
$C_{6}^{C}$	(0.132, 0.206, 0.302; 1.0)	$C_{6}^{W}$	(0.074, 0.137, 0.250; 1.0)

Open in a new tab

Table 6 demonstrates the averaged ratings of suppliers versus the capabilities and willingness criteria based on the data presented in Table 3 in the work of [2] and in Table 1 (in Appendix B in S1 Appendix) of this paper.

Table 6. Average ratings of suppliers versus the capabilities and willingness criteria.

Supplier no.	Capabilities criteria	Willingness criteria	Supplier no.	Capabilities criteria	Willingness criteria
1	(0.037, 0.085, 0.170; 0.8)	(0.050, 0.116, 0.250; 0.8)	23	(0.051, 0.105, 0.199; 0.8)	(0.054, 0.122, 0.259; 0.8)
2	(0.051, 0.105, 0.197; 0.8)	(0.061, 0.128, 0.261; 0.8)	24	(0.024, 0.055, 0.112; 0.8)	(0.043, 0.105, 0.235; 0.8)
3	(0.052, 0.106, 0.200; 0.8)	(0.046, 0.110, 0.240; 0.8)	25	(0.039, 0.090, 0.181; 0.8)	(0.040, 0.102, 0.230; 0.8)
4	(0.058, 0.111, 0.204; 0.8)	(0.061, 0.130, 0.266; 0.8)	26	(0.037, 0.088, 0.179; 0.8)	(0.056, 0.123, 0.257; 0.8)
5	(0.041, 0.092, 0.185; 0.8)	(0.049, 0.112, 0.240; 0.8)	27	(0.046, 0.101, 0.197; 0.8)	(0.042, 0.105, 0.236; 0.8)
6	(0.039, 0.089, 0.176; 0.8)	(0.049, 0.113, 0.243; 0.8)	28	(0.058, 0.115, 0.211; 0.8)	(0.040, 0.100, 0.227; 0.8)
7	(0.056, 0.110, 0.203; 0.8)	(0.047, 0.109, 0.235; 0.8)	29	(0.033, 0.082, 0.169; 0.8)	(0.040, 0.100, 0.226; 0.8)
8	(0.063, 0.121, 0.219; 0.8)	(0.014, 0.057, 0.153; 0.8)	30	(0.019, 0.053, 0.115; 0.8)	(0.044, 0.104, 0.226; 0.8)
9	(0.017, 0.050, 0.109; 0.8)	(0.014, 0.057, 0.153; 0.8)	31	(0.039, 0.090, 0.181; 0.8)	(0.045, 0.107, 0.233; 0.8)
10	(0.017, 0.050, 0.109; 0.8)	(0.014, 0.057, 0.153; 0.8)	32	(0.052, 0.101, 0.183; 0.8)	(0.051, 0.117, 0.251; 0.8)
11	(0.043, 0.096, 0.189; 0.8)	(0.065, 0.133, 0.269; 0.8)	33	(0.045, 0.100, 0.195; 0.8)	(0.055, 0.123, 0.261; 0.8)
12	(0.048, 0.100, 0.188; 0.8)	(0.064, 0.133, 0.269; 0.8)	34	(0.046, 0.098, 0.189; 0.8)	(0.013, 0.053, 0.142; 0.8)
13	(0.054, 0.110, 0.207; 0.8)	(0.057, 0.121, 0.249; 0.8)	35	(0.046, 0.097, 0.186; 0.8)	(0.054, 0.122, 0.259; 0.8)
14	(0.031, 0.075, 0.154; 0.8)	(0.038, 0.098, 0.224; 0.8)	36	(0.039, 0.090, 0.181; 0.8)	(0.044, 0.107, 0.238; 0.8)
15	(0.043, 0.096, 0.189; 0.8)	(0.037, 0.092, 0.206; 0.8)	37	(0.061, 0.117, 0.212; 0.8)	(0.053, 0.122, 0.259; 0.8)
16	(0.025, 0.060, 0.124; 0.8)	(0.037, 0.095, 0.218; 0.8)	38	(0.044, 0.094, 0.182; 0.8)	(0.039, 0.100, 0.226; 0.8)
17	(0.025, 0.059, 0.119; 0.8)	(0.060, 0.128, 0.265; 0.8)	39	(0.038, 0.089, 0.180; 0.8)	(0.020, 0.068, 0.173; 0.8)
18	(0.014, 0.045, 0.101; 0.8)	(0.050, 0.117, 0.251; 0.8)	40	(0.047, 0.099, 0.191; 0.8)	(0.051, 0.117, 0.251; 0.8)
19	(0.052, 0.106, 0.201; 0.8)	(0.015, 0.057, 0.149; 0.8)	41	(0.032, 0.078, 0.160; 0.8)	(0.040, 0.100, 0.227; 0.8)
20	(0.039, 0.088, 0.175; 0.8)	(0.033, 0.090, 0.210; 0.8)	42	(0.053, 0.108, 0.202; 0.8)	(0.049, 0.112, 0.240; 0.8)
21	(0.019, 0.059, 0.133; 0.8)	(0.013, 0.052, 0.139; 0.8)	43	(0.031, 0.071, 0.142; 0.8)	(0.059, 0.125, 0.257; 0.8)
22	(0.048, 0.101, 0.193; 0.8)	(0.052, 0.117, 0.249; 0.8)	43	(0.031, 0.071, 0.142; 0.8)	(0.059, 0.125, 0.257; 0.8)

Open in a new tab

We obtain the distance between the centroid and minimum points of 43 suppliers by using the ranking approach proposed by [17] as denoted in Table 7.

Table 7. Distance measurement.

Supplier	Capabilities criteria			Willingness criteria
Supplier	Centroid point	Minimum point	Distance	Centroid point	Minimum point	Distance
1	(0.097, 0.333)	(0.014, 0.333)	0,196	(0.139, 0.333)	(0.013, 0.333)	0,218
2	(0.118, 0.333)	(0.014, 0.333)	0,206	(0.150, 0.333)	(0.013, 0.333)	0,224
3	(0.119, 0.333)	(0.014, 0.333)	0,207	(0.132, 0.333)	(0.013, 0.333)	0,214
4	(0.124, 0.333)	(0.014, 0.333)	0,209	(0.153, 0.333)	(0.013, 0.333)	0,226
5	(0.106, 0.333)	(0.014, 0.333)	0,200	(0.133, 0.333)	(0.013, 0.333)	0,215
6	(0.101, 0.333)	(0.014, 0.333)	0,198	(0.135, 0.333)	(0.013, 0.333)	0,216
7	(0.123, 0.333)	(0.014, 0.333)	0,209	(0.131, 0.333)	(0.013, 0.333)	0,213
8	(0.134, 0.333)	(0.014, 0.333)	0,215	(0.074, 0.333)	(0.013, 0.333)	0,188
9	(0.059, 0.333)	(0.014, 0.333)	0,183	(0.075, 0.333)	(0.013, 0.333)	0,188
10	(0.059, 0.333)	(0.014, 0.333)	0,183	(0.075, 0.333)	(0.013, 0.333)	0,188
11	(0.109, 0.333)	(0.014, 0.333)	0,202	(0.156, 0.333)	(0.013, 0.333)	0,228
12	(0.112, 0.333)	(0.014, 0.333)	0,203	(0.155, 0.333)	(0.013, 0.333)	0,228
13	(0.124, 0.333)	(0.014, 0.333)	0,209	(0.142, 0.333)	(0.013, 0.333)	0,220
14	(0.087, 0.333)	(0.014, 0.333)	0,192	(0.120, 0.333)	(0.013, 0.333)	0,207
15	(0.109, 0.333)	(0.014, 0.333)	0,202	(0.112, 0.333)	(0.013, 0.333)	0,203
16	(0.070, 0.333)	(0.014, 0.333)	0,186	(0.117, 0.333)	(0.013, 0.333)	0,206
17	(0.068, 0.333)	(0.014, 0.333)	0,186	(0.151, 0.333)	(0.013, 0.333)	0,225
18	(0.053, 0.333)	(0.014, 0.333)	0,182	(0.139, 0.333)	(0.013, 0.333)	0,218
19	(0.120, 0.333)	(0.014, 0.333)	0,207	(0.074, 0.333)	(0.013, 0.333)	0,188
20	(0.101, 0.333)	(0.014, 0.333)	0,198	(0.111, 0.333)	(0.013, 0.333)	0,203
21	(0.070, 0.333)	(0.014, 0.333)	0,186	(0.068, 0.333)	(0.013, 0.333)	0,186
22	(0.114, 0.333)	(0.014, 0.333)	0,204	(0.139, 0.333)	(0.013, 0.333)	0,218
23	(0.118, 0.333)	(0.014, 0.333)	0,206	(0.145, 0.333)	(0.013, 0.333)	0,221
24	(0.064, 0.333)	(0.014, 0.333)	0,185	(0.128, 0.333)	(0.013, 0.333)	0,212
25	(0.103, 0.333)	(0.014, 0.333)	0,199	(0.124, 0.333)	(0.013, 0.333)	0,210
26	(0.102, 0.333)	(0.014, 0.333)	0,198	(0.145, 0.333)	(0.013, 0.333)	0,222
27	(0.115, 0.333)	(0.014, 0.333)	0,204	(0.128, 0.333)	(0.013, 0.333)	0,212
28	(0.128, 0.333)	(0.014, 0.333)	0,211	(0.122, 0.333)	(0.013, 0.333)	0,209
29	(0.095, 0.333)	(0.014, 0.333)	0,195	(0.122, 0.333)	(0.013, 0.333)	0,209
30	(0.062, 0.333)	(0.014, 0.333)	0,184	(0.125, 0.333)	(0.013, 0.333)	0,210
31	(0.103, 0.333)	(0.014, 0.333)	0,199	(0.128, 0.333)	(0.013, 0.333)	0,212
32	(0.112, 0.333)	(0.014, 0.333)	0,203	(0.140, 0.333)	(0.013, 0.333)	0,218
33	(0.113, 0.333)	(0.014, 0.333)	0,204	(0.146, 0.333)	(0.013, 0.333)	0,222
34	(0.111, 0.333)	(0.014, 0.333)	0,202	(0.069, 0.333)	(0.013, 0.333)	0,186
35	(0.110, 0.333)	(0.014, 0.333)	0,202	(0.145, 0.333)	(0.013, 0.333)	0,221
36	(0.103, 0.333)	(0.014, 0.333)	0,199	(0.130, 0.333)	(0.013, 0.333)	0,213
37	(0.130, 0.333)	(0.014, 0.333)	0,212	(0.145, 0.333)	(0.013, 0.333)	0,221
38	(0.107, 0.333)	(0.014, 0.333)	0,201	(0.122, 0.333)	(0.013, 0.333)	0,208
39	(0.102, 0.333)	(0.014, 0.333)	0,198	(0.087, 0.333)	(0.013, 0.333)	0,193
40	(0.112, 0.333)	(0.014, 0.333)	0,203	(0.140, 0.333)	(0.013, 0.333)	0,218
41	(0.090, 0.333)	(0.014, 0.333)	0,193	(0.122, 0.333)	(0.013, 0.333)	0,209
42	(0.121, 0.333)	(0.014, 0.333)	0,207	(0.133, 0.333)	(0.013, 0.333)	0,215
43	(0.081, 0.333)	(0.014, 0.333)	0,190	(0.147, 0.333)	(0.013, 0.333)	0,222

Open in a new tab

Based on the distance scores for the capabilities and willingness of each supplier, we assign 43 suppliers to one of four segments using Step 7 of the proposed method. The cut-off points of the supplier’s capabilities and willingness are 0.196 and 0.1996, respectively. Table 8 shows that three suppliers are assigned to Group 1, nine suppliers to Group 2, three suppliers to Group 3, and twenty-eight suppliers to Group 4.

Table 8. Segments of the 43 suppliers.

Segment	No. of suppliers	Suppliers
Group 1	3	A₉, A₁₀, and A₂₁
Group 2	9	A₁₄, A₁₆, A₁₇, A₁₈, A₂₄, A₂₉, A₃₀, A₄₁, andA₄₃
Group 3	3	A₁₉, A₃₄, and A₃₉
Group 4	28	A₁, A₂, A₃, A₄, A₅, A₆, A₇, A₈, A₁₁, A₁₂, A₁₃, and A₁₅, A₂₀, A₂₁, A₂₂, A₂₃, A₂₅, A₂₆, A₂₇, A₂₈, A₃₁, A₃₂, A₃₃, A₃₅, A₃₆, A₃₇, A₃₈, and A₄₀

Open in a new tab

Table 8 shows a slight difference between the segments of the 43 suppliers using the proposed method and the approach introduced by [2, 3]. The reason for the difference is that the techniques proposed by [2, 3] use the crisp values to measure the ratings of the suppliers. This proceeding is unreasonable, because the supplier evaluation criteria include both quantitative and qualitative criteria. The proposed method herein employs GFNs to represent the ratings of suppliers.

Discussions and conclusions

Green supplier segmentation (GSS) is a critical marketing activity for companies having many suppliers. Rather than formulating individual strategies for each supplier, companies can now adopt an appropriate strategic approach for handling different supplier segments. To manage the uncertainty and dynamics of GSS, this study develops a new dynamic generalized fuzzy MCGDM using capabilities and willingness criteria. The proposed approach contributes to the body of GSS literature in four significant directions. First, it expands previous studies by using GFNs instead of fuzzy numbers. Second, it is able to solve the supplier segmentation problem at different periods instead of one period. Third, it considers not only economic criteria, but also environmental and social criteria from the aspects of suppliers’ capability and willingness. Fourth, the approach can solve the GSS problem and also be employed in other management problems under similar settings.

The proposed framework uses GFNs to express the aggregated ratings of alternatives, the aggregated importance weights of criteria, and the aggregated weighted ratings with the effect of time weight. In order to rank the alternatives, we apply the most popular centroid-index ranking approach. We test the proposed approach by segmenting the suppliers of a medium-sized transport equipment company to illustrate its applicability. The company can thus formulate different strategies to handle various segments based on the outcomes obtained using the proposed method. We identify at least four major green supplier strategies: (i) maintain close long-term relationships with suppliers that have strong capabilities and high willingness [31]; (ii) improve and attract relationships with suppliers that have high capabilities, but a low-level willingness to cooperate [36]; (iii) help suppliers that have low capabilities, but are very willing “to green” their products and processes [35]; (iv) terminate relationships with suppliers that are less capable and less willing to cooperate [2, 3]. We further compare the proposed approach with another fuzzy MCDM approach to demonstrate its superiority. Findings show that the proposed approach is an effective tool for practitioners to solve GSS problems.

The study does have some limitations. First, the proposed approach does not consider the correlation of attributes. Therefore, it is difficult to derive the weights of the decision criteria while maintaining judgment consistency. Second, by using fuzzy sets, the proposed approach cannot handle MCGDM problems that have indeterminate and inconsistent information. Future work plans are to integrate an AHP method in MCGDM by defining the importance weights of criteria. Neutrosophic sets and their extension will also be applied to express the vague information in MCGDM.

Supporting information

S1 Appendix

(DOCX)

Click here for additional data file.^{(123.5KB, docx)}

Acknowledgments

This research was completed during and after the stay of Dr. Luu Quoc Dat at the Vietnam Institute for Advanced Study in Mathematics (VIASM).

Data Availability

All relevant data are within the paper and its Supporting Information files.

Funding Statement

This research is funded by “VNU University of Economics and Business, Vietnam National University, Hanoi” and “Korea Foundation for Advanced Studies (KFAS) and the Asia Research Center, Vietnam National University, Hanoi (ARC-VNU)” under project number CA.18.2A. This research was completed during and after the stay of the seventh author at the Vietnam Institute for Advanced Study in Mathematics (VIASM).

References

1.Parkouhi SV, Ghadikolaei AS, Lajimi HF. Resilient supplier selection and segmentation in grey environment. J Cleaner Prod 2019;207;1123–1137. 10.1016/j.jclepro.2018.10.007 [DOI] [Google Scholar]
2.Rezaei J, Ortt R. Multi-criteria supplier segmentation using a fuzzy preference relation based AHP. Eur J Oper Res 2013; 225;75–84. 10.1016/j.ejor.2012.09.037 [DOI] [Google Scholar]
3.Rezaei J, Ortt R. Supplier segmentation using fuzzy logic. Ind Marketing Manage 2013, 42;507–517. 10.1016/j.indmarman.2013.03.003 [DOI] [Google Scholar]
4.Haeri SA, Rezaei J. A grey-based green supplier selection model for uncertain environments. J Cleaner Prod 2019; 221;768–784. 10.1016/j.jclepro.2019.02.193 [DOI] [Google Scholar]
5.Hosseini S, Morshedlou N, Ivanov D, Sarder MD, Khaled AA. Resilient supplier selection and optimal order allocation under disruption risks. Int J Prod Econ 2019;213;124–137. 10.1016/j.ijpe.2019.03.018 [DOI] [Google Scholar]
6.Yu C, Shao Y, Wang K, Zhang L. A group decision making sustainable supplier selection approach using extended TOPSIS under interval-valued Pythagorean fuzzy environment. Expert Syst Appl 2019;121;1–17. 10.1016/j.eswa.2018.12.010 [DOI] [Google Scholar]
7.Memari K, Dargi A, Jokar MRA, Ahmad R, Rahim RA. Sustainable supplier selection: A multi-criteria intuitionistic fuzzy TOPSIS method. J Manuf Syst 2019;50;9–24. 10.1016/j.jmsy.2018.11.002 [DOI] [Google Scholar]
8.Aineth TR, Ravindran AR. Multiple criteria framework for the sustainability risk assessment of a supplier portfolio. J Cleaner Prod 2018;172;4478–4493. 10.1016/j.jclepro.2017.10.304 [DOI] [Google Scholar]
9.Hamdan S, Cheaitou A. Supplier selection and order allocation with green criteria: An MCDM and multi-objective optimization approach. Comput Oper Res 2017;81;282–304. 10.1016/j.cor.2016.11.005 [DOI] [Google Scholar]
10.Yazdani M, Chatterjee P, Zavadskas EK, Zolfani SH. Integrated QFD-MCDM framework for green supplier selection. J Cleaner Prod 2017; 142; 3728–3740. 10.1016/j.jclepro.2016.10.095 [DOI] [Google Scholar]
11.Bai C, Rezaei J, Sarkis J. Multicriteria Green Supplier Segmentation. IEEE Trans Eng Manage 2017; 64;515–528. 10.1109/TEM.2017.2723639 [DOI] [Google Scholar]
12.Lo SC, Sudjatmika FV. Solving multi-criteria supplier segmentation based on the modified FAHP for supply chain management: a case study. Soft Comput 2016;20;4981–4990. 10.1007/s00500-015-1787-1 [DOI] [Google Scholar]
13.Haghighi PS, Salahi MMM. Supplier Segmentation using Fuzzy Linguistic Preference Relations and Fuzzy Clustering. Intell Syst Appl 2014;05;76–82. 10.5815/ijisa.2014.05.08 [DOI] [Google Scholar]
14.Kaufmann A., Gupta M., Introduction to Fuzzy Arithmetic: Theory and Applications, 2nd ed., Van Nostrand Reinhold, New York, 1991. [Google Scholar]
15.Chen SH. Operations on fuzzy numbers with function principal. Tamkang J Manage Sci 1985; 6;13–25. 10.1016/S0020-0255(97)10070-6 [DOI] [Google Scholar]
16.Lee J, Cho H, Kim YS. Assessing business impacts of agility criterion and order allocation strategy in multi-criteria supplier selection. Expert Syst Appl 2015;42;1136–1148. 10.1016/j.eswa.2014.08.041 [DOI] [Google Scholar]
17.Mehdi KG, Amiri M, Zavadskas EK, Turskis Z, Antucheviciene J. A Dynamic Fuzzy Approach Based on the EDAS Method for Multi-Criteria Subcontractor Evaluation. Information 2018;9;68 10.3390/info9030068. [DOI] [Google Scholar]
18.Dat LQ, Vincent FY, Chou SY. An Improved Ranking Method for Fuzzy Numbers Based on the Centroid-Index. Int J Fuzzy Syst 2011;14;413–419. [Google Scholar]
19.Parasuraman A. Vendor segmentation: an additional level of market segmentation. Ind Marketing Manage 1980;9;59–62. 10.1016/S0019-8501(96)00089-2 [DOI] [Google Scholar]
20.Kraljic P. Purchasing must become supply management. Harvard Bus Rev 1983;109–117. [Google Scholar]
21.Segura M, Maroto C. A multiple criteria supplier segmentation using outranking and value function methods. Expert Syst Appl 2017;69;87–100. 10.1016/j.eswa.2016.10.031 [DOI] [Google Scholar]
22.Che ZH. Clustering and selecting suppliers based on simulated annealing algorithms. Comput Math Appl 2012;63;228–238. 10.1016/j.camwa.2011.11.014 [DOI] [Google Scholar]
23.Caniëls MCJ, Gelderman CJ. Power and interdependence in buyer supplier relationships: A purchasing portfolio approach. Ind Marketing Manage 2005;36;219–229. 10.1016/j.indmarman.2005.08.012 [DOI] [Google Scholar]
24.Hallikas J, Puumalainen K, Vesterinen T, Virolainen VM. Risk-based classification of supplier relationships. J Purchasing Supply Manage 2005;11;72–82. 10.1016/j.pursup.2005.10.005 [DOI] [Google Scholar]
25.Svensson G. Supplier segmentation in the automotive industry: A dyadic approach of a managerial model. Int J Phys Distrib Logist Manage 2004;34;12–38. 10.1108/09600030410515664 [DOI] [Google Scholar]
26.Kaufman A, Wood CH, Theyel G. Collaboration and technology linkages: A strategic supplier typology. Strategic Manage J 2000;21;649–663. [DOI] [Google Scholar]
27.Svensson G. A conceptual framework for the analysis of vulnerability in supply chains. International J Phys Distrib Logist Manage 2000;30;731–50. 10.1108/09600030010351444 [DOI] [Google Scholar]
28.Day M, Magnan GM, Moeller MM. Evaluating the bases of supplier segmentation: A review and taxonomy. Ind Marketing Manage 2010;39;625–639. 10.1016/j.indmarman.2009.06.001 [DOI] [Google Scholar]
29.Rezaei J, Davoodi M. A joint pricing, lot-sizing, and supplier selection model. Int J Prod Res 2012;50;4524–4542. 10.1080/00207543.2011.613866 [DOI] [Google Scholar]
30.Dyer JH, Cho DS, Chu W. Strategic supplier segmentation: the next ‘best practice’ in supply chan management. California Manage Rev 1998;40;57–77. 10.2307/41165933 [DOI] [Google Scholar]
31.Rezaei J, Ortt R. A multi-variable approach to supplier segmentation. Int J Prod Res 2012;50;4593–4611. 10.1080/00207543.2011.615352 [DOI] [Google Scholar]
32.Rezaei J, Wang J, Tavasszy L. Linking supplier development to supplier segmentation using Best Worst Method. Expert Syst Appl 2015;42;9152–9164. 10.1016/j.eswa.2015.07.073 [DOI] [Google Scholar]
33.Rezaei J, Lajimi HF. Segmenting supplies and suppliers: bringing together the purchasing portfolio matrix and the supplier potential matrix. Int J Logist Res Appl 2019;22;419–436. 10.1080/13675567.2018.1535649 [DOI] [Google Scholar]
34.Akman G. Evaluating suppliers to include green supplier development programs via fuzzy c-means and VIKOR methods. Comput Ind Eng 2015;86;69–82. 10.1016/j.cie.2014.10.013 [DOI] [Google Scholar]
35.Krause DR, Handfield RB, Tyler BB. The relationships between supplier development, commitment, social capital accumulation and performance improvement. J Oper Manage 2007;25;528–545. 10.1016/j.jom.2006.05.007 [DOI] [Google Scholar]
36.Mortensen M, Arlbjørn J. Inter-organisational supplier development: The case of customer attractiveness and strategic fit. Supply Chain Manage: Int J 2012;17;152–171. 10.1108/13598541211212898 [DOI] [Google Scholar]

PLoS One. doi: 10.1371/journal.pone.0245187.r001

Decision Letter 0

Yiming Tang

15 Jun 2020

PONE-D-20-03268

A DYNAMIC GENERALIZED FUZZY MULTI-CRITERIA GROUP DECISION MAKING APPROACH FOR GREEN SUPPLIER SEGMENTATION

PLOS ONE

Dear Dr. Luu Quoc,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

Please submit your revised manuscript by Jul 30 2020 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.

If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols

We look forward to receiving your revised manuscript.

Kind regards,

Yiming Tang, Ph.D.

Academic Editor

PLOS ONE

Journal Requirements:

When submitting your revision, we need you to address these additional requirements.

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at

https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and

https://journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Partly

Reviewer #2: Partly

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: I Don't Know

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

Reviewer #2: Yes

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: No

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: I would like to thank the authors for this interesting approach in dealing with an important subject. The subject of segmentation and especially weighting using decision makers or "experts" are one of the areas of debate in many fields. I found this approach easy to follow and reproducible. This is an important advantage for the proposed method. However, I have few issues that I want to recommend and clarify:

1- I am not sure that you have presented enough discussion in the literature about the added value for your approach and the need for this approach, not only from operational point of view but also from computational one. In other words, you provided in the second paragraph of the introduction why you are proposing this approach, but there is no justification for where you think it will improve the current method statistically. Is this approach better in your opinion and why?!

2- Tables 6a - 6e are a bit confusing within the manuscript, maybe including these tables in an annex will be more convenient.

3- There must be a discussion section after the section "Comparison of the proposed method with another fuzzy

MCDM method" and the conclusion section. The results are not discussed clearly for the reader. The results need to be interpreted from mathematical and operational point of view, as a reader I am afraid I need more explanation for the numbers. It looked in some places that you jumped from section to another without explaining the results. Moreover, you need to discuss the strengths of your approach, how it tackled current existing problem, and why do you think it should be considered by others. For example, have you considered a simulation study and compare the results with other methods to assess the consistency of the results?! or have you considered comparing this method with more statistically based approaches such as Multidimensional Latent Class Item Response Theory Models?! There should be more discussion before you present your conclusion.

Reviewer #2: While new methods for "green" supplier segmentation is certainly important, interesting, and relevant, there are several issues in this paper.

The methods in this paper appear to be sound, it is very hard to read and comprehend. The organization and visualization of data/results is overall, poor. Additionally:

- Background on fuzzy numbers is lengthy and a bit hard to follow.

- There are an excess of tables, which is incredibly overwhelming and unhelpful given the complexity of the topic and notation. The tables in the literature review section are redundant or unnecessary. If tables really are necessary, for this many tables, they belong in an appendix.

- Some terms or abbreviations are not explained and confusing. For example in Table 6a, I'm assuming "fa" = "fair", "Ve_go" = "Very good"? This needs to be standardized and presented in a more meaningful, insightful, and visually interesting manner. For example, map responses to numbers rather than letter abbreviations, and plot a heat map of responses, rather than use a table. This can be done with ALL of the tables in this section

- Table 8 may be better off as some sort of visual representation (chart) rather than a table

- There are grammatical mistakes throughout the paper

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at figures@plos.org. Please note that Supporting Information files do not need this step.

PLoS One. 2021 Jan 25;16(1):e0245187. doi: 10.1371/journal.pone.0245187.r002

Author response to Decision Letter 0

15 Sep 2020

Response to Referees’ Comments

PONE-D-20-03268

A DYNAMIC GENERALIZED FUZZY MULTI-CRITERIA GROUP DECISION MAKING APPROACH FOR GREEN SUPPLIER SEGMENTATION

The authors greatly appreciate the time and effort the referees spent on reviewing this manuscript. This paper has been revised based on the constructive comments and suggestions made by the referees. Major changes are shown in red color.

Referee 1’s Comments:

I would like to thank the authors for this interesting approach in dealing with an important subject. The subject of segmentation and especially weighting using decision makers or "experts" are one of the areas of debate in many fields. I found this approach easy to follow and reproducible. This is an important advantage for the proposed method. However, I have few issues that I want to recommend and clarify:

1. I am not sure that you have presented enough discussion in the literature about the added value for your approach and the need for this approach, not only from operational point of view but also from computational one. In other words, you provided in the second paragraph of the introduction why you are proposing this approach, but there is no justification for where you think it will improve the current method statistically. Is this approach better in your opinion and why?

2. Tables 6a - 6e are a bit confusing within the manuscript, maybe including these tables in an annex will be more convenient.

3. There must be a discussion section after the section "Comparison of the proposed method with another fuzzy MCDM method" and the conclusion section. The results are not discussed clearly for the reader. The results need to be interpreted from mathematical and operational point of view, as a reader I am afraid I need more explanation for the numbers. It looked in some places that you jumped from section to another without explaining the results. Moreover, you need to discuss the strengths of your approach, how it tackled current existing problem, and why do you think it should be considered by others. For example, have you considered a simulation study and compare the results with other methods to assess the consistency of the results?! or have you considered comparing this method with more statistically based approaches such as Multidimensional Latent Class Item Response Theory Models?! There should be more discussion before you present your conclusion.

Responses:

1. Thank you very much for your comments. The authors have added some sentences in the introduction and literature review section to discuss more about the shortcomings of the existing approaches and the advantages of our approach.

2. Thanks for your suggestion. The authors have moved Tables 6a - 6e to appendix section.

3. Thanks for your comments. The authors have added some paragraphs to discuss about the results of the study and the advantages of our approach. Some sentences have been added in the implementation section to explain more about the calculation process. In this study, a new dynamic generalized fuzzy MCDM approach has been proposed. Then, we have compared the proposed method with another fuzzy MCDM method to show its advantages. The comparison between our proposed approach with more statistically based approaches such as Multidimensional Latent Class Item Response Theory Models should be our further research.

Referee 2’s Comments:

While new methods for "green" supplier segmentation is certainly important, interesting, and relevant, there are several issues in this paper.

1. The methods in this paper appear to be sound, it is very hard to read and comprehend. The organization and visualization of data/results is overall, poor.

2. Background on fuzzy numbers is lengthy and a bit hard to follow.

3. There is an excess of tables, which is incredibly overwhelming and unhelpful given the complexity of the topic and notation. The tables in the literature review section are redundant or unnecessary. If tables really are necessary, for this many tables, they belong in an appendix.

4. Some terms or abbreviations are not explained and confusing. For example, in Table 6a, I'm assuming "fa" = "fair", "Ve_go" = "Very good"? This needs to be standardized and presented in a more meaningful, insightful, and visually interesting manner. For example, map responses to numbers rather than letter abbreviations, and plot a heat map of responses, rather than use a table. This can be done with ALL of the tables in this section.

5. Table 8 may be better off as some sort of visual representation (chart) rather than a table.

6. There are grammatical mistakes throughout the paper

Responses:

1. Thank you very much for your comments. The authors have added some sentences in the implementation section to explain more about the data and results of this study. The authors have also moved the Tables 6a - 6e to the appendix.

2. Thanks for your suggestion. The authors have moved the background on fuzzy numbers to appendix.

3. Thanks for your suggestion. The authors have moved Tables 1-3 to the appendix.

4. Thanks for your suggestion. The authors have tried to change the abbreviations of linguistic variables (Appendix B - Table 2 and other tables).

5. Thanks for your suggestion. The authors have modified the Table 8 to make it more visually.

6. The authors have tried to fix the grammatical mistakes throughout the paper.

The authors would like to thank again the reviewers for the time and expertise they have invested in these reviews. The revised manuscript with marked changes has been resubmitted to your journal. We look forward to your positive response.

Sincerely,

Luu Quoc Dat

Attachment

Submitted filename: Response to Reviewers.doc

Click here for additional data file.^{(49KB, doc)}

PLoS One. doi: 10.1371/journal.pone.0245187.r003

Decision Letter 1

Yiming Tang

26 Dec 2020

A DYNAMIC GENERALIZED FUZZY MULTI-CRITERIA GROUP DECISION MAKING APPROACH FOR GREEN SUPPLIER SEGMENTATION

PONE-D-20-03268R1

Dear Dr. Luu Quoc,

We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.

Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.

An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/, click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

Kind regards,

Yiming Tang, Ph.D.

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #1: All comments have been addressed

Reviewer #3: All comments have been addressed

Reviewer #4: All comments have been addressed

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #1: Yes

Reviewer #3: Partly

Reviewer #4: Yes

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #3: Yes

Reviewer #4: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #1: Yes

Reviewer #3: Yes

Reviewer #4: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #1: Yes

Reviewer #3: Yes

Reviewer #4: Yes

**********

6. Review Comments to the Author

Reviewer #1: I believe all the comments have been addressed by the authors. I reviewed the new version and I find it now easier to follow and more visually appealing. I encourage the authors to do further investigation in the subject and do comparison with more statistically established methods in their future work.

Reviewer #3: The Author should support with evidence during discussion of results. The Author has good presentation but poor discussion on the results found.

Reviewer #4: (No Response)

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #3: Yes: Zerihun Yohannes Amare

Reviewer #4: Yes: Dr. Ghaffar Ali

Attachment

Submitted filename: PONE-D-20-03268_R1_reviewer.pdf

Click here for additional data file.^{(1.5MB, pdf)}

PLoS One. doi: 10.1371/journal.pone.0245187.r004

Acceptance letter

Yiming Tang

13 Jan 2021

PONE-D-20-03268R1

A Dynamic Generalized Fuzzy Multi-Criteria Croup Decision Making Approach for Green Supplier Segmentation

Dear Dr. Dat:

I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

If we can help with anything else, please email us at plosone@plos.org.

Thank you for submitting your work to PLOS ONE and supporting open access.

Kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Professor Yiming Tang

Academic Editor

PLOS ONE

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

S1 Appendix

(DOCX)

Click here for additional data file.^{(123.5KB, docx)}

Attachment

Submitted filename: Response to Reviewers.doc

Click here for additional data file.^{(49KB, doc)}

Attachment

Submitted filename: PONE-D-20-03268_R1_reviewer.pdf

Click here for additional data file.^{(1.5MB, pdf)}

Data Availability Statement

All relevant data are within the paper and its Supporting Information files.

[pone.0245187.ref001] 1.Parkouhi SV, Ghadikolaei AS, Lajimi HF. Resilient supplier selection and segmentation in grey environment. J Cleaner Prod 2019;207;1123–1137. 10.1016/j.jclepro.2018.10.007 [DOI] [Google Scholar]

[pone.0245187.ref002] 2.Rezaei J, Ortt R. Multi-criteria supplier segmentation using a fuzzy preference relation based AHP. Eur J Oper Res 2013; 225;75–84. 10.1016/j.ejor.2012.09.037 [DOI] [Google Scholar]

[pone.0245187.ref003] 3.Rezaei J, Ortt R. Supplier segmentation using fuzzy logic. Ind Marketing Manage 2013, 42;507–517. 10.1016/j.indmarman.2013.03.003 [DOI] [Google Scholar]

[pone.0245187.ref004] 4.Haeri SA, Rezaei J. A grey-based green supplier selection model for uncertain environments. J Cleaner Prod 2019; 221;768–784. 10.1016/j.jclepro.2019.02.193 [DOI] [Google Scholar]

[pone.0245187.ref005] 5.Hosseini S, Morshedlou N, Ivanov D, Sarder MD, Khaled AA. Resilient supplier selection and optimal order allocation under disruption risks. Int J Prod Econ 2019;213;124–137. 10.1016/j.ijpe.2019.03.018 [DOI] [Google Scholar]

[pone.0245187.ref006] 6.Yu C, Shao Y, Wang K, Zhang L. A group decision making sustainable supplier selection approach using extended TOPSIS under interval-valued Pythagorean fuzzy environment. Expert Syst Appl 2019;121;1–17. 10.1016/j.eswa.2018.12.010 [DOI] [Google Scholar]

[pone.0245187.ref007] 7.Memari K, Dargi A, Jokar MRA, Ahmad R, Rahim RA. Sustainable supplier selection: A multi-criteria intuitionistic fuzzy TOPSIS method. J Manuf Syst 2019;50;9–24. 10.1016/j.jmsy.2018.11.002 [DOI] [Google Scholar]

[pone.0245187.ref008] 8.Aineth TR, Ravindran AR. Multiple criteria framework for the sustainability risk assessment of a supplier portfolio. J Cleaner Prod 2018;172;4478–4493. 10.1016/j.jclepro.2017.10.304 [DOI] [Google Scholar]

[pone.0245187.ref009] 9.Hamdan S, Cheaitou A. Supplier selection and order allocation with green criteria: An MCDM and multi-objective optimization approach. Comput Oper Res 2017;81;282–304. 10.1016/j.cor.2016.11.005 [DOI] [Google Scholar]

[pone.0245187.ref010] 10.Yazdani M, Chatterjee P, Zavadskas EK, Zolfani SH. Integrated QFD-MCDM framework for green supplier selection. J Cleaner Prod 2017; 142; 3728–3740. 10.1016/j.jclepro.2016.10.095 [DOI] [Google Scholar]

[pone.0245187.ref011] 11.Bai C, Rezaei J, Sarkis J. Multicriteria Green Supplier Segmentation. IEEE Trans Eng Manage 2017; 64;515–528. 10.1109/TEM.2017.2723639 [DOI] [Google Scholar]

[pone.0245187.ref012] 12.Lo SC, Sudjatmika FV. Solving multi-criteria supplier segmentation based on the modified FAHP for supply chain management: a case study. Soft Comput 2016;20;4981–4990. 10.1007/s00500-015-1787-1 [DOI] [Google Scholar]

[pone.0245187.ref013] 13.Haghighi PS, Salahi MMM. Supplier Segmentation using Fuzzy Linguistic Preference Relations and Fuzzy Clustering. Intell Syst Appl 2014;05;76–82. 10.5815/ijisa.2014.05.08 [DOI] [Google Scholar]

[pone.0245187.ref014] 14.Kaufmann A., Gupta M., Introduction to Fuzzy Arithmetic: Theory and Applications, 2nd ed., Van Nostrand Reinhold, New York, 1991. [Google Scholar]

[pone.0245187.ref015] 15.Chen SH. Operations on fuzzy numbers with function principal. Tamkang J Manage Sci 1985; 6;13–25. 10.1016/S0020-0255(97)10070-6 [DOI] [Google Scholar]

[pone.0245187.ref016] 16.Lee J, Cho H, Kim YS. Assessing business impacts of agility criterion and order allocation strategy in multi-criteria supplier selection. Expert Syst Appl 2015;42;1136–1148. 10.1016/j.eswa.2014.08.041 [DOI] [Google Scholar]

[pone.0245187.ref017] 17.Mehdi KG, Amiri M, Zavadskas EK, Turskis Z, Antucheviciene J. A Dynamic Fuzzy Approach Based on the EDAS Method for Multi-Criteria Subcontractor Evaluation. Information 2018;9;68 10.3390/info9030068. [DOI] [Google Scholar]

[pone.0245187.ref018] 18.Dat LQ, Vincent FY, Chou SY. An Improved Ranking Method for Fuzzy Numbers Based on the Centroid-Index. Int J Fuzzy Syst 2011;14;413–419. [Google Scholar]

[pone.0245187.ref019] 19.Parasuraman A. Vendor segmentation: an additional level of market segmentation. Ind Marketing Manage 1980;9;59–62. 10.1016/S0019-8501(96)00089-2 [DOI] [Google Scholar]

[pone.0245187.ref020] 20.Kraljic P. Purchasing must become supply management. Harvard Bus Rev 1983;109–117. [Google Scholar]

[pone.0245187.ref021] 21.Segura M, Maroto C. A multiple criteria supplier segmentation using outranking and value function methods. Expert Syst Appl 2017;69;87–100. 10.1016/j.eswa.2016.10.031 [DOI] [Google Scholar]

[pone.0245187.ref022] 22.Che ZH. Clustering and selecting suppliers based on simulated annealing algorithms. Comput Math Appl 2012;63;228–238. 10.1016/j.camwa.2011.11.014 [DOI] [Google Scholar]

[pone.0245187.ref023] 23.Caniëls MCJ, Gelderman CJ. Power and interdependence in buyer supplier relationships: A purchasing portfolio approach. Ind Marketing Manage 2005;36;219–229. 10.1016/j.indmarman.2005.08.012 [DOI] [Google Scholar]

[pone.0245187.ref024] 24.Hallikas J, Puumalainen K, Vesterinen T, Virolainen VM. Risk-based classification of supplier relationships. J Purchasing Supply Manage 2005;11;72–82. 10.1016/j.pursup.2005.10.005 [DOI] [Google Scholar]

[pone.0245187.ref025] 25.Svensson G. Supplier segmentation in the automotive industry: A dyadic approach of a managerial model. Int J Phys Distrib Logist Manage 2004;34;12–38. 10.1108/09600030410515664 [DOI] [Google Scholar]

[pone.0245187.ref026] 26.Kaufman A, Wood CH, Theyel G. Collaboration and technology linkages: A strategic supplier typology. Strategic Manage J 2000;21;649–663. [DOI] [Google Scholar]

[pone.0245187.ref027] 27.Svensson G. A conceptual framework for the analysis of vulnerability in supply chains. International J Phys Distrib Logist Manage 2000;30;731–50. 10.1108/09600030010351444 [DOI] [Google Scholar]

[pone.0245187.ref028] 28.Day M, Magnan GM, Moeller MM. Evaluating the bases of supplier segmentation: A review and taxonomy. Ind Marketing Manage 2010;39;625–639. 10.1016/j.indmarman.2009.06.001 [DOI] [Google Scholar]

[pone.0245187.ref029] 29.Rezaei J, Davoodi M. A joint pricing, lot-sizing, and supplier selection model. Int J Prod Res 2012;50;4524–4542. 10.1080/00207543.2011.613866 [DOI] [Google Scholar]

[pone.0245187.ref030] 30.Dyer JH, Cho DS, Chu W. Strategic supplier segmentation: the next ‘best practice’ in supply chan management. California Manage Rev 1998;40;57–77. 10.2307/41165933 [DOI] [Google Scholar]

[pone.0245187.ref031] 31.Rezaei J, Ortt R. A multi-variable approach to supplier segmentation. Int J Prod Res 2012;50;4593–4611. 10.1080/00207543.2011.615352 [DOI] [Google Scholar]

[pone.0245187.ref032] 32.Rezaei J, Wang J, Tavasszy L. Linking supplier development to supplier segmentation using Best Worst Method. Expert Syst Appl 2015;42;9152–9164. 10.1016/j.eswa.2015.07.073 [DOI] [Google Scholar]

[pone.0245187.ref033] 33.Rezaei J, Lajimi HF. Segmenting supplies and suppliers: bringing together the purchasing portfolio matrix and the supplier potential matrix. Int J Logist Res Appl 2019;22;419–436. 10.1080/13675567.2018.1535649 [DOI] [Google Scholar]

[pone.0245187.ref034] 34.Akman G. Evaluating suppliers to include green supplier development programs via fuzzy c-means and VIKOR methods. Comput Ind Eng 2015;86;69–82. 10.1016/j.cie.2014.10.013 [DOI] [Google Scholar]

[pone.0245187.ref035] 35.Krause DR, Handfield RB, Tyler BB. The relationships between supplier development, commitment, social capital accumulation and performance improvement. J Oper Manage 2007;25;528–545. 10.1016/j.jom.2006.05.007 [DOI] [Google Scholar]

[pone.0245187.ref036] 36.Mortensen M, Arlbjørn J. Inter-organisational supplier development: The case of customer attractiveness and strategic fit. Supply Chain Manage: Int J 2012;17;152–171. 10.1108/13598541211212898 [DOI] [Google Scholar]

PERMALINK

A dynamic generalized fuzzy multi-criteria croup decision making approach for green supplier segmentation

Do Anh Duc

Luu Huu Van

Vincent F Yu

Shuo-Yan Chou

Ngo Van Hien

Ngo The Chi

Dinh Van Toan

Luu Quoc Dat

Roles

Abstract

Introduction

Literature review on methods and criteria for supplier segmentation

Supplier segmentation methods

Green supplier segmentation criteria

Establishment of a new approach for solving green supplier selection and segmentation

Identifying the green capabilities and willingness criteria

Aggregating the importance weights of the criteria

Aggregating the ratings of green suppliers versus the criteria

Constructing the weighted fuzzy decision matrix

Defuzzification

Segmenting the green suppliers

Implementation of the proposed dynamic generalized fuzzy MCGDM approach

Aggregation of the importance weights of the respective green capabilities and willingness criteria

Table 1. Aggregated weights of the criteria evaluated by the decision makers.

Aggregation of the ratings of green suppliers versus the capabilities and willingness criteria

Table 2. Final fuzzy evaluation values of each supplier.

Determination of the weighted rating

Calculation of the distance of each green supplier

Table 3. Distance measurement.

Segmentation of the suppliers

Fig 1. Final supplier segmentation results.

Table 4. Segments of the suppliers.

Comparison of the proposed method with another fuzzy MCDM method

Table 5. Importance weights of the capabilities and willingness criteria.

Table 6. Average ratings of suppliers versus the capabilities and willingness criteria.

Table 7. Distance measurement.

Table 8. Segments of the 43 suppliers.

Discussions and conclusions

Supporting information

Acknowledgments

Data Availability

Funding Statement

References

Decision Letter 0

Yiming Tang

Roles

Author response to Decision Letter 0

Decision Letter 1

Yiming Tang

Roles

Acceptance letter

Yiming Tang

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases