Abstract
Background
The high contagiousness and rapid spreading of the coronavirus disease 2019 (COVID-19) has caused a high number of critical to severe life-threatening cases, which required urgent hospital admission and treatment in intensive care units (ICUs). The pandemic has been a tough test for all European national health systems and their capability to provide an adequate reaction.
Methods
The present work aims to reveal correlations between parameters such as COVID-19 incidence, ICU bed occupancy, ICU excess area, and mortality in Italian regions. Public data for the period of March 1 to July 16, 2020, were analyzed using several mathematical and statistical methods.
Results
The analysis defined two separate groups of Italian regions. The examined variables considered within these groups were interlinked and dependent on each other. The regions of the two groups shared the same kind of fitted model (linear) explaining mortality as a function of cumulative incidence, but with higher value of the constant in one group, so characterized by a high intrinsic “strength” of the pandemic, certainly playing a major role in the generation of a large number of severe and life-threatening cases. These results are confirmed at European level. Other factors may condition mortality and be linked to incidence, such as ICU saturation and excess.
Conclusions
These quantitative results could be a very helpful tool to set up preventive measures and optimize biomedical interventions before the pandemic, in its recurrent waves, could overcome the reaction capacity of any public health system.
Keywords: COVID-19, Mortality, Cumulative incidence, Intensive care capability, Mathematical analysis
Introduction
Since its onset, COVID-19 has been characterized by high contagiousness (Zhu et al., 2020, Li et al., 2020, Guan et al., 2020) and different syndromic appearance, from an asymptomatic state or mild signs of discomfort (the majority of cases) to severe manifestation of acute respiratory distress, necessitating intensive care (IC) treatment. Different virus containment measures have been adopted throughout the world. Response to the threat includes individual and collective mobility limitations, physical distancing, quarantine of red zones, in-house confinement, provision of personal protective equipment, identification of infectious cases, and contact tracing via an enhanced effort of direct diagnosis. Rapidly expanding from China, COVID-19 soon became a fierce challenge for all of Europe. It was, in fact, immediately clear that capability of individual European national and regional health systems to sustain the threat mainly relied upon strength of the epidemic (i.e. cumulative number of cases) and was primarily linked to the availability of IC treatment required by the most severely affected patients. Mortality-wise, the pandemic exhibited a great variability in the EU, European Economic Area, and UK countries that share similar welfare-shaped health systems. Different mortality values were also seen in Italian regions, especially in the northern part of Italy, where the pandemic originally struck and was more intense (i.e. Lombardy and Veneto), with the first documented cases on February 21, 2020. Since then, the pandemic has spread over the whole country. When the first outbreaks developed, Italy had a total of 5000 ICU beds. Owing to the spatial and latitudinal heterogeneity, size, and asynchronous insurgence of the outbreaks, local hospitals and ICUs were rapidly saturated in Lombardy. Lockdown measures, implemented at country level on March 12, 2020, and possibly other factors, allowed control of the diffusion of the epidemic. Following the end of March, the COVID-19 incidence started to decrease and at the end of April the pandemic had released its grip on ICUs. Most patients with early symptoms are now treated at home or in COVID-19 specialized wards and hospitals.
In the present investigation, for all Italian regions during the period from March 1 to July 16, 2020, we analyzed a number of variables showing a strong geographical heterogeneity. In particular our intention was to determine whether a direct relation existed among the cumulative number of COVID-19 cases, maximum daily ICU occupancy, ICU excess area (i.e. a condition when COVID-19 critical patients exceed the number of IC available beds), and mortality. The results clearly illustrate how these variables are interconnected and in particular how mortality is influenced by the other parameters.
Material and methods
Daily public data made available by “Protezione Civile Italiana” were downloaded from their website (Anon, a). Temporal sequences between March 1 and July 16, 2020, of cumulative incidence, COVID-19 daily ICU occupancy, and mortality were considered for all Italian regions including Trento and Bolzano autonomous provinces. All sequences referred to 100,000 inhabitants.
The IC sequence data were fitted by means of several functions, the gamma function, and the derivatives of well-known models: logistic and some of its generalizations (Abramowitz and Stegun, 1964, Pearl and Reed, 1920, Gompertz, 1825). After an RMSE comparison, the best type of model was applied to the IC sequence of each region. Whenever an IC fitted curve exceeded the maximum IC capability level, we numerically approximated the area of the geometric region under the curve and above the level. The IC capability at the beginning of the pandemic was taken from (Anon, b). The Mann–Whitney–Wilcoxon rank test was applied to assess statistical significance of the difference between mortality in different groups (Lehmann, 1999).
Hierarchical clustering was used for grouping (Duda and Hart, 1973, Ward, 1963), which minimizes locally the sum of squares of Euclidian distance between cluster elements and the corresponding centroid. Apart from a numerical constant, this is the within variance of the cluster. The associated clusters with their elements are obtained by suitably cutting the dendrogram with a horizontal line. Given an arbitrary number of clusters between 1 and n − 1 (n is the sample size), the corresponding number appearing on the vertical axis, divided by the square root of 2, gives the square root of the difference between the summation over the k clusters of the within-cluster sum of squares and the same quantity for k + 1 clusters. To select the optimal number of clusters we use these heights. Specifically, we follow the elbow criterion slightly modified: we select the number k such that if we decrease it by one, we have a high loss, but if we increase it by one, we have a low gain. More precisely, we maximize the ratio loss/gain, which indeed corresponds to the ratio between the heights relative to k − 1 and k clusters, respectively.
Results
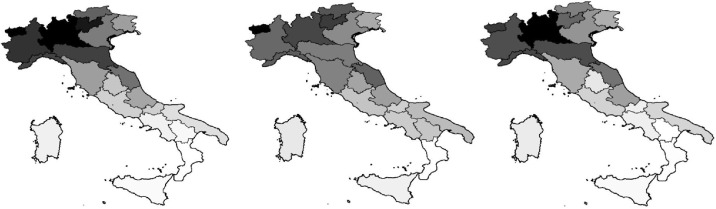
Cumulative incidence, maximum daily ICU occupancy, ICU excess area, and mortality estimates (for 100,000 inhabitants) at July 16, 2020, are reported for each Italian region (Table 1). A map of the Italian regions (Figure 1) shows intensities inversely related to the corresponding COVID-19 cumulative incidence values in Table 1. The analogous maps for maximum daily ICU occupancy and mortality, from data reported in Table 1, are also shown in Figure 1. It is noteworthy that the three maps are very similar. Furthermore, they show the above mentioned latitude-dependent pattern of the epidemic.
Table 1.
COVID-19 cumulative incidence for 100,000 inhabitants, ICU beds for 100,000 inhabitants, maximum daily ICU beds for 100,000 inhabitants, ICU excess area, mortality for 100,000 inhabitants on July 16, 2020, IC group number (from ICU excess area), and HC group number (from hierarchical clustering) for Italian regions.
| Region | N | Cumulative incidence | ICU capacity | Max daily ICU occupancy | ICU excess area | Mortality | GIC | GHC |
|---|---|---|---|---|---|---|---|---|
| Abruzzo | 1 | 252 | 8.24 | 5.75 | 0 | 35.4 | 2 | 2 |
| Basilicata | 2 | 71.2 | 8.59 | 3.33 | 0 | 4.73 | 2 | 2 |
| Bolzano (aut. prov.) | 3 | 504 | 7.53 | 12.2 | 55.3 | 55.0 | 1 | 1 |
| Calabria | 4 | 62.4 | 7.18 | 1.17 | 0 | 4.94 | 2 | 2 |
| Campania | 5 | 82.1 | 8.67 | 3.10 | 0 | 7.40 | 2 | 2 |
| Emilia Romagna | 6 | 653 | 10.1 | 8.43 | 0 | 96.0 | 2 | 1 |
| Friuli Venezia Giulia | 7 | 274 | 10.4 | 5.01 | 0 | 28.3 | 2 | 2 |
| Lazio | 8 | 142 | 9.44 | 3.44 | 0 | 14.4 | 2 | 2 |
| Liguria | 9 | 642 | 11.9 | 11.4 | 0 | 99.9 | 2 | 1 |
| Lombardy | 10 | 951 | 8.98 | 13.8 | 95.9 | 167 | 1 | 1 |
| Marche | 11 | 443 | 7.02 | 11.0 | 65.9 | 64.2 | 1 | 1 |
| Molise | 12 | 144 | 6.12 | 2.90 | 0 | 7.41 | 2 | 2 |
| Piedmont | 13 | 718 | 7.29 | 10.3 | 52.3 | 93.8 | 1 | 1 |
| Apulia | 14 | 112 | 7.53 | 3.91 | 0 | 13.5 | 2 | 2 |
| Sardinia | 15 | 83.8 | 7.44 | 1.88 | 0 | 8.11 | 2 | 2 |
| Sicily | 16 | 69.8 | 8.13 | 1.58 | 0 | 5.60 | 2 | 2 |
| Tuscany | 17 | 277 | 11.9 | 7.94 | 0 | 30.1 | 2 | 2 |
| Trento (aut. prov.) | 18 | 831 | 5.91 | 15.0 | 176 | 74.8 | 1 | 1 |
| Umbria | 19 | 163 | 7.87 | 5.40 | 0 | 9.00 | 2 | 2 |
| Aosta Valley | 20 | 943 | 7.88 | 21.3 | 223 | 115 | 1 | 1 |
| Veneto | 21 | 397 | 10.1 | 7.25 | 0 | 41.7 | 2 | 2 |
Figure 1.
Maps of the COVID-19 cumulative incidence (left) and mortality (right) on July 16, 2020, and maximum daily ICU occupancy in the period March 1 to July 16, 2020, in Italian regions, as in Table 1. High values are plotted in dark.
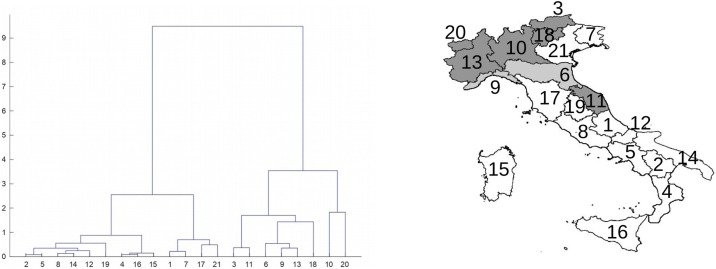
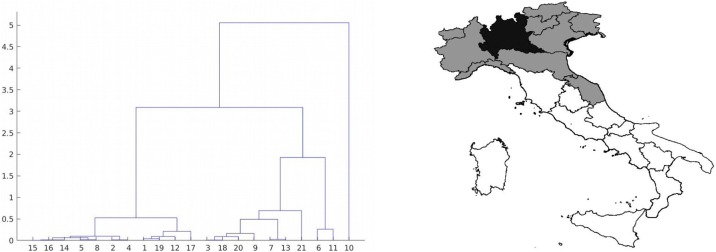
Hierarchical clustering analysis was applied to the whole data set of cumulative incidence, maximum daily ICU occupancy, and mortality of the different regions (Table 1). Figure 2 shows the analysis result by means of a dendrogram, with clear evidence of the presence of two groups GHC. The regions of the first group have a significantly higher mean value for each of the three variables compared with the corresponding values for the other group (Mann–Whitney–Wilcoxon rank test, p < 0.0002). The value 1 (or 2) is assigned as group number GHC to the regions of the first (or second) group (Table 1). The map of the regions of the two groups’ GHC is shown in Figure 2. It should be noted that the regions of group-1 GHC are almost only those “close” to Lombardy, where the epidemic started. The Marche region is included in group 1 although it is “far” from Lombardy. This is likely due to the spread of the epidemic along highways before lockdown (Sebastiani, 2020). In addition, a series of basketball tournament matches in the city of Pesaro during February 13–16, 2020, could have contributed to the early spread of the epidemic in the Marche region. In fact, a very large number of people from Lombardy attended these matches. In contrast, the Veneto region is not included in group-1 GHC although it is close to Lombardy and, in addition, the first COVID-19 death was in Veneto.
Figure 2.
Dendrogram from hierarchical clustering analysis of COVID-19 cumulative incidence, maximum daily ICU occupancy, and mortality data of Italian regions, as in Table 1, (left); and map of the Italian regions of the two groups’ GHC of the dendrogram (right). The regions of group 1 (high values of cumulative incidence, maximum daily ICU occupancy and mortality) are plotted in gray. The regions in dark gray also belong to group 1 GIC. Liguria and Emilia Romagna, in light gray, belong to group 1 GHC, but not to group 1 GIC.
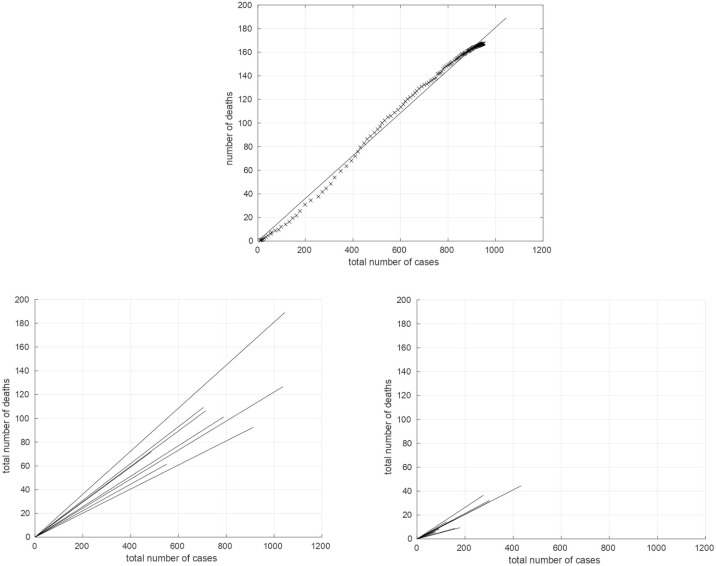
To further characterize the two groups, for each region we studied the relation between the temporal sequences of cumulative incidence and mortality in the period March 1 to July 16, 2020. A simple linear model with one parameter was used. This is a crude approximation as the mortality sequence can be obtained mathematically from the incidence one by convolving it with a suitable kernel. Nevertheless, we take into account the temporal delay by comparing the cumulative incidence to the mortality sequence after shifting the latter along time. An optimal value of the shift was found by minimizing the variance unexplained by the model. In Figure 3 , we present the result of the best linear fit for Lombardy. The results of the fits for the regions of the first and the second groups’ GHC are included in the same figure. The slopes of the best linear model for the regions of the first-group GHC are significantly higher than those of the second group (Mann–Whitney–Wilcoxon rank test, p < 0.003). We repeated the analysis for the relation between cumulative incidence and cumulative daily ICU occupancy. In this case, there is no significant difference between the mean values of the slopes of the regions in the two groups (Mann–Whitney–Wilcoxon rank test, p = 0.1). The results are similar for Spain, United Kingdom, Romania and Germany (Figure 4). The slopes of the lines for Germany and Romania are smaller than for Spain and the UK and comparable to those of the second-group GHC; whereas, the slopes for Spain and the UK are comparable to those of the first-group GHC. The number of critical care beds for Spain, UK, Romania, and Germany are 9.7, 6.6, 21.3, and 29.3 for 100,000 inhabitants, respectively (Anon, c).
Figure 3.
Linear fit between COVID-19 cumulative incidence and mortality sequences for Lombardy (top) and the regions of the first (bottom left) and the second (bottom right) groups’ GHC.
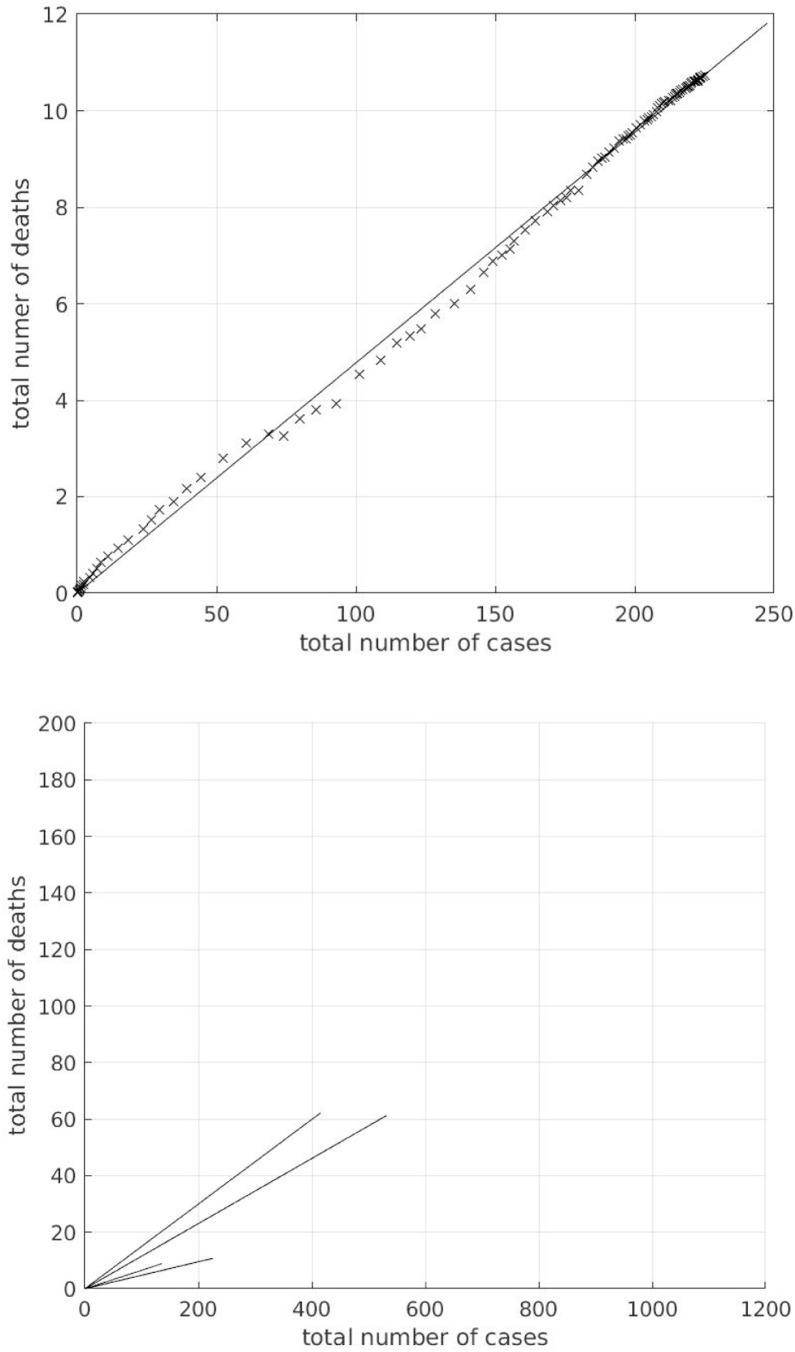
Figure 4.
Linear fit between COVID-19 cumulative incidence and mortality sequences for Germany (top) and for Spain, UK, Romania, and Germany from the highest to the smallest values of slope, respectively (bottom).
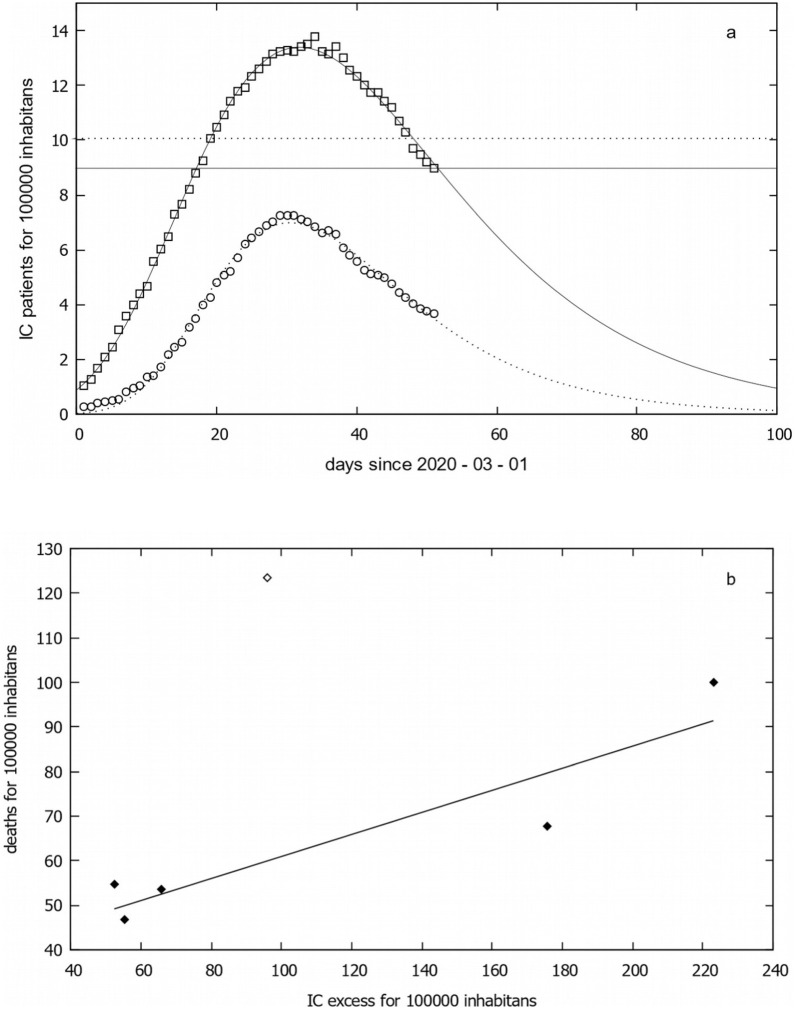
We also studied the influence of ICU excess area on COVID-19 mortality. Examples of IC sequences with and without IC excess are given in Figure 5 a for the Lombardy and Veneto regions. The plot shows that the IC beds for Lombardy are much fewer than the IC patients, for about days 20–60. A value 1 (or 2) is assigned as group number GIC to the regions with (or no) ICU excess area (Table 1). The map of the regions of the two groups’ GIC is illustrated in Figure 2. The values of the mortality in the regions are significantly larger for the first than the second group (Mann–Whitney–Wilcoxon rank test, p < 0.005). It is noteworthy that the two partitions of the Italian regions from IC excess GIC and hierarchical clustering GHC based on cumulative incidence, maximum daily ICU occupancy, and mortality are almost identical. Only the regions of Liguria and Emilia Romagna have different GIC and GHC values. Nevertheless, both regions nearly have IC excess area (data not shown).
Figure 5.
(a) Daily ICU occupancy sequences and IC capability thresholds at the beginning of the pandemic for Lombardy (open squares and continuous line) and Veneto (open circles and dotted lines); and (b) best linear fit between IC excess area and mortality at April 20, 2020. The open symbol represents Lombardy, which was excluded from linear fitting.
The possibility that COVID-19 mortality is directly increased by ICU excess area is also investigated. This is done by a fitting a linear model between ICU excess area and COVID-19 mortality for the regions of the first group of GIC (Figure 5b). Mortality in this case is evaluated at the end of the excess period for all regions, i.e., April 20. The outlier Lombardy, where the Italian epidemic started and reached the highest mortality, is excluded from the analysis that gives a determination coefficient (R2) of 0.85. A similar result is obtained when the area is replaced by the maximum of daily ICU occupancy. Therefore, we test the hypothesis that the mortality mean value in the regions of the first group of GIC is higher than those in the remaining regions of the first group of GHC with no ICU excess area, i.e. Liguria and Emilia Romagna. However, the difference is not significant (Mann–Whitney–Wilcoxon rank test, p = 0.6). This could be tested by performing the analysis at provincial level but, unfortunately, ICU occupancy data are not publicly available at provincial level.
Finally, the partition of the Italian regions into the two groups GHC is almost identical to that obtained by hierarchical clustering from cumulative incidence at the day when the lockdown started at national level in Italy, i.e., March 12, 2020 (Figure 6). Among the regions of group 1 (the one with high cumulative intensity), only Veneto and Friuli Venezia Giulia are not in group 1 GHC (Figure 2). This result is important because the pattern at March 12 helps to predict the one at July 16.
Figure 6.
Dendrogram from hierarchical clustering analysis of COVID-19 cumulative incidence at the day of the lockdown, i.e., March 12, 2020, in Italian regions (left); and map of the regions of the three groups of the dendrogram (right). The regions of group 1 (high values of cumulative incidence) are plotted in gray. The region with highest value of cumulative incidence (i.e. Lombardy) forming a single region group is plotted in black.
Discussion
The results in the above section clearly indicate that, when taken individually, COVID-19 cumulative incidence, maximum daily ICU occupancy, and mortality have the highest values in the same regions, hence these variables show an overlapping geographic distribution. Two groups of regions can be identified in Italy, with mean values related to each of these three parameters that significantly differ between the two groups. These two groups, moreover, can be well separated using specific statistical tools, i.e., hierarchical clustering (GHC). The resulting dendrogram clearly shows the presence of two clusters with higher (GHC1) or lower variable values (GHC2). Lombardy, where the pandemic started and where it has been more intense, is the prototype of the GHC1 cluster. Thus, results show that the viral pandemic affected Italian regions with a dual modality according to the pandemic “strength” and that cumulative incidence of cases, maximum daily ICU occupancy, as well as mortality are somehow interlinked. The spatial proximity to Lombardy of other GHC1 regions along with high mobility of people from Lombardy to non-neighboring regions can explain such a group clustering. The exception to this rule is apparent in the Veneto region, a condition that can derive from a number of public health measures that were adopted by the regional prevention and epidemiology departments: (i) immediate lockdown of the first outbreak centers, (ii) prompt set up of COVID-19 dedicated facilities like first aid, wards, and hospitals together with an increased number of beds in ICUs, (iii) a consolidated capillary territorial distribution of hygiene and preventive services, and (iv) wide adoption of diagnostic tests for symptomatic and at risk populations.
Our mathematical analysis is then extended to dissect the relation between cumulative COVID-19 incidence, mortality, maximum daily ICU occupancy, and ICU excess area comparing clusters GHC1 and GHC2 by means of fitting linear models. The COVID-19 cumulative incidence is highly related to mortality and shows significantly different behavior between the two clusters, a result expected since severe and life-threatening cases increase with pandemic amplification. Cumulative incidence is also linearly related to cumulative daily ICU occupancy but this latter variable varies in the same manner in the two regional clusters, indicating that higher virus circulation has induced the same need for more available IC beds in both groups of regions, without distinction for disease severity.
However, ICU excess area represented by GIC group number 1 (the GIC1 regions: Bolzano, Lombardy, Marche, Piedmont, Trento, and Aosta Valley) is directly related to mortality values significantly larger than those exhibited by GIC group number 2 (the GIC2 regions: all the others), as exemplified by Lombardy. Among GHC1 regions only Liguria and Emilia Romagna do not belong to GIC1 but nearly have IC excess area, a result that indicates that this parameter is also related to the pandemic strength. It is notable in this regard that the IC occupancy in Liguria exceeds 95% of the available units. This suggests that the trend for Liguria should be more similar to the regions of the GIC1 than the GIC2 group. A different situation accounts for Emilia Romagna where the IC occupancy is about 80% of the available ICU beds but COVID-19 incidence is extremely heterogeneous for the different provinces; Piacenza being an example of a highly affected district with respect to others. Data relating ICU excess area to mortality indicate a direct correlation in GIC1 regions (Bolzano, Trento, Piedmont, Marche, and Aosta Valley) with the exception of Lombardy, the worst hit region. This paradox may be because Lombardy had the more intense virus circulation among the general population in Italy; this caused a rapid saturation of hospitals and ICUs that, in turn, became the source of a rapid transmission of contagion from cases with high viral load, a condition that resulted in a serious number of victims (Fagiuoli et al., 2020). The observed pattern is not specific for Italy. In fact, Spain and the UK, which have low ICU capacity, show the same trend as Lombardy and the other regions of the first-group GHC, whereas in Germany and Romania, with high ICU capacity, the situation is similar to the regions of the second-group GHC.
Before general lockdown was introduced, two other regions, Veneto and Friuli Venezia Giulia, had a large virus circulation that clustered together with others at similarly high cumulative incidence (Lombardy, Marche, Piedmont, Liguria, Bolzano, Trento, Aosta Valley, and Emilia Romagna). The fact that both Veneto and Friuli Venezia Giulia had a relatively low mortality and daily ICU occupancy (did not fall within GHC1 group) means that the early public health preventive measures adopted by these regions may have successively affected pandemic spread. Obviously, other virus and host-related factors could influence mortality (e.g., virulence, age, and comorbidities) and could explain some of the discrepant estimates described. Moreover, a high mortality among IC-treated patients cannot be solely related to COVID-19 but to different social, epidemiological, and environmental factors such as the number of days of admission to ICU and the acquisition of multidrug resistant bacterial infections (Rossolini et al., 2014). Our data clearly indicate that IC, albeit life-saving for the most severe COVID-19 complications, should be deferred as much as possible. A substantially reduced IC saturation would mean a better overall survival with new effective treatments being adopted in the community and with a diminished occurrence of nosocomial virus spreading (de Wit et al., 2016). In fact, at the end of the lockdown, with the drop in new SARS-COV-2 positive cases and the reduced admission to ICUs, mortality values steadily decreased (Onder et al., 2020). Unfortunately, since August incidence has progressively increased.
A number of mathematical models have been proposed to predict the biological and medical impact of the ongoing COVID-19 pandemic that could be helpful to optimize preventive and interventional measures (Gatto et al., 2020, Kissler et al., 2020, Sebastiani et al., 2020). In this respect, a simple quantitative estimate of ICU availability and saturation as well as excess thresholds, as reported here, could be of paramount public health relevance. It could help in setting up preparedness plans for surveillance and control of a recurrent wave of SARS-CoV-2 as well as for future emerging and pandemic infections. Moreover, it our opinion that such a parameter, adopted at the European level, could be a critical indicator for establishing sustainability of any health system and preventing its collapse.
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Funding source
Veneto region
Ethical approval
Not required
Acknowledgements
The authors are thankful to the anonymous reviewer for his/her very useful comments and suggestions.
References
- Abramowitz M., Stegun I. Dover; New York: 1964. Handbook of mathematical functions. [Google Scholar]
- https://github.com/pcm-dpc/Covid-19.
- https://www.quotidianosanita.it/studi-e-analisi/articolo.php?articolo_id=82888.
- https://www.covid-19.no/critical-care-bed-numbers-in-europe.
- de Wit E., van Doremalen N., Falzarano D., Munster V.J. SARS and MERS: recent insights into emerging coronavirus. Nat Rev Microbiol. 2016;14:523–534. doi: 10.1038/nrmicro.2016.81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duda R.O., Hart P.E. Wiley; New York: 1973. Pattern classification and scene analysis. [Google Scholar]
- Fagiuoli S., Lorini F.L., Remuzzi G. Adaptations and lessons in the Province of Bergamo. N Engl J Med. 2020;382:e71. doi: 10.1056/NEJMc2011599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatto M., Bertuzzo E., Mari L., Miccoli S., Carraro L., Casagrandi R. Spread and dynamics of the Covid-19 in Italy: effects of emergency containment measures. Proc Natl Acad Sci U S A. 2020;117:10484–10491. doi: 10.1073/pnas.2004978117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gompertz B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos Trans Royal Soc Lond. 1825;115:513–585. doi: 10.1098/rstb.2014.0379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan W., Ni Z., Hu Y., Liang W., Ou C., He J. Clinical characteristics of Coronavirus Disease 2019 in China. N Engl J Med. 2020;382:1708–1720. doi: 10.1056/NEJMoa2002032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kissler S.M., Tedijanto C., Goldstein E., Grad Y.H., Lipsitch M. Projecting the transmission dynamics of SARS-CoV-2 throughout the postpandemic period. Science. 2020 doi: 10.1126/science.abb5793. 10.11267science. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehmann E.L. Springer; 1999. Elements of large-sample theory. [Google Scholar]
- Li Q., Guan X., Wu P., Wang X., Zhou L., Tang Y. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N Engl J Med. 2020;382:1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onder G., Rezza G., Brusaferro S. Case-fatality rate and characteristics of patients dying in relation to COVID-19 in Italy. JAMA (ahead of print) 2020 doi: 10.1001/jama.2020.4683. [DOI] [PubMed] [Google Scholar]
- Pearl R., Reed L. On the rate of growth of the population of the United States. Proc Natl Acad Sci U S A. 1920;6:275–288. doi: 10.1073/pnas.6.6.275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossolini G.M., Arena F., Pecile P., Pollini S. Update on the antibiotic resistance crisis. Curr Opin Pharmacol. 2014;18:56–60. doi: 10.1016/j.coph.2014.09.006. [DOI] [PubMed] [Google Scholar]
- Sebastiani G. 2020. Il coronavirus ha viaggiato in autostrada? Scienza in Rete (in Italian)https://www.scienzainrete.it/articolo/coronavirus-ha-viaggiato-autostrada/giovanni-sebastiani/2020-04-09 [Google Scholar]
- Sebastiani G., Massa M., Riboli E. Covid-19 epidemic in Italy: evolution, projections and impact of government measures. Eur J Epidemiol. 2020;35:341–345. doi: 10.1007/s10654-020-00631-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward J.H. Hierarchical grouping to optimize an objective function. J Am Stat Assoc. 1963;58:236–244. [Google Scholar]
- Zhu N., Zhang D., Wang W., Li X., Yang B., Song J. Novel coronavirus from patients with pneumonia in China, 2019. N Engl J Med. 2020;382:727–733. doi: 10.1056/NEJMoa2001017. [DOI] [PMC free article] [PubMed] [Google Scholar]