A cost-effective plan for global testing - an infection rate stratified, algorithm guided, multiple-level, continuously pooled testing strategy

Abstract

The most effective measure to prevent or stop the spread of infectious diseases is the early identification and isolation of infected individuals through comprehensive screening. At present, in the COVID-19 pandemic, such screening is often limited to isolated regions as determined by local governments. Screening of potentially infectious individuals should be conducted through coordinated national or global unified actions. Our current research focuses on using resources to conduct comprehensive national and regional regular testing with a risk rate based, algorithmic guided, multiple-level, pooled testing strategy. Here, combining methodologies with mathematical logistic models, we present an analytic procedure of an overall plan for coordinating state, national, or global testing. The proposed plan includes three parts 1) organization, resource allocation, and distribution; 2) screening based on different risk levels and business types; and 3) algorithm guided, multiple level, continuously screening the entire population in a region. This strategy will overcome the false positive and negative results in the polymerase chain reaction (PCR) test and missing samples during initial tests. Based on our proposed protocol, the population screening of 300,000,000 in the US can be done weekly with between 15,000,000 and 6,000,000 test kits. The strategy can be used for population screening for current COVID-19 and any future severe infectious disease when drugs or vaccines are not available.

Graphical abstract

1. Introduction

With the new severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) now at the root of a global pandemic, detecting new cases and tracking and identifying infection sources is a critical challenge. Because of combined contact and droplet transmission routes (Sommerstein et al., 2020), a complex response to infection, and asymptomatic carriers, focused and individual population tests are not adequate to identify all infected individuals (Chan et al., 2020; Chen et al., 2020). Faced with this situation, some government entities severely restricted movement by issuing “stay at home” orders or blocking entry by non-residents (Okuhara et al., 2020). Such measures are effective ways to prevent new transmissions. However, this approach takes considerable time to reduce global infection risks and causes great pressure on the economy (Levitt, 2020).

On the other hand, when movement restrictions are relaxed, new waves of infection are observed (Flanders et al., 2020; The New York Times, Oct. 21, 2020). In part, this is due to limited technical, logistical, and financial resources to test every individual continuously in real-time. The most important tool to curb widespread transmission is expanded testing, combined with tracing all exposed individuals. Therefore, the detection of virus carriers has become a necessary global task and an unprecedented challenge.

Most importantly, from Ebola to SARS to SARS-CoV-2, human beings are increasingly facing dangerous, complicated, and difficult-to-control infectious diseases. In case a new type of infectious disease like COVID-19 or even more dangerous infectious disease to humans occurs in the near future, immediate measures must be developed to prevent the disease spread into a pandemic in an extremely short period of time. A whole population screening may be the only way to stop the spreading of such a dangerous infectious disease while waiting for an effective drug or vaccine to be released. Our international collaborating team developed a protocol for whole population screening, which can be applied at state, regional, national, or global levels.

2. Limitations of current evidence and rationale

At present, many countries have accumulated tools and resources for PCR-based nucleotide testing (Yelin et al., 2020), but they have not developed coordinated testing strategies. Currently, a single test provides data for a single individual. Data suggest that test results are positive for about 10% of the total tested population (https://www.worldometers.info/coronavirus/). However, testing is frequently limited to individuals suspected of having the coronavirus. This approach does not detect asymptomatic coronavirus carriers. We conclude that the current one-to-one detection method is a waste of resources. Whole population screening is the only way to identify all individuals, including asymptomatic individuals with SARS-CoV-2 or future similar infectious diseases (Arons et al., 2020).

Statistical pooling methods have been utilized and debated (Lohse et al., 2020; Lee et al., 2020). However, pooling methods cannot be successfully implemented without considering disease risk levels, screening strategies, screening technologies, and resources.

Potential false positive and negative results, missing samples, and difficulty producing results quickly using PCR technology are concerns (Mahase, 2020). Here we present a screening strategy incorporating pooling, mathematical modeling, and overall screening strategies to overcome current testing limitations.

3. Materials and methods

3.1. Objective and aims

Our study question is: What is the best way to detect an infected individual from a large pooled population, e.g., that ranges from 100 to 1000 samples. This study uses mathematical, statistical rules to design a comprehensive testing strategy for a country, a region, or a city.

Hypothesis. We assume that the SARS-CoV-2 global pandemic will continue for at least one to two years at least in some countries and regions. We assume that the successful inoculation of the population worldwide with a vaccine for SARS-CoV-2 will require at least one year or longer, although a vaccine may only reduce rather than stop transmission. We also face the fact that most regions and countries will cease movement restrictions (“reopen”) despite the continuing pandemic or new round of shutdown (Okuhara et al., 2020). Accordingly, we hypothesize that testing the entire human population can be done with a well-planned strategy that takes advantage of new biotechnology, statistical analysis tools, data planning, analytical platforms, public resources, and governments' and organizations' support.

3.2. Strategic considerations

A successful testing program requires public support, especially the allocation and organization of government resources. The leading role of government and unified action on the preparation and implementation of population screening is essential for the proposed strategy's success. We base our testing strategy design on several considerations.

3.2.1. Terminology in this protocol

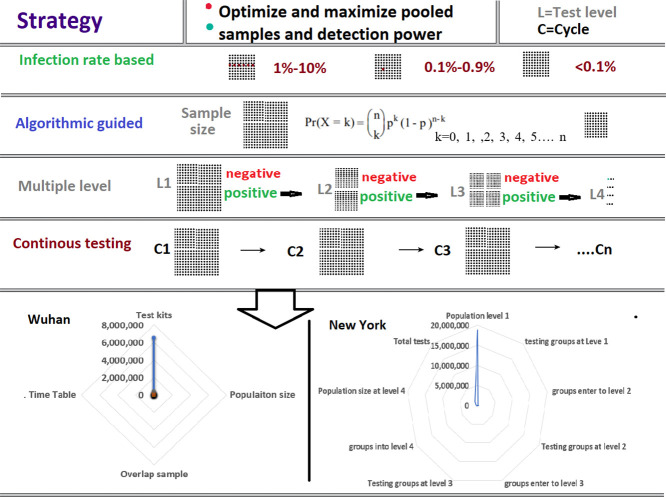
Test levels. We define each cycle of tests into different levels. The first test (level 1) will be a pooled test with several samples as large as all circumstances permit samples in one testing mixture. Sample refers to the testing materials collected from an individual within the population.

After level 1, if a mixture is positive, samples within this positive mixture will be divided into different groups for testing (level 2). If one or more groups at level 2 are positive, the samples within this level 2 group may be divided into smaller groups for testing (level 3). Level 4, for additional sample groups, may be conducted if necessary. Population in this protocol is defined as the entire population of a city, region, state, or country.

3.2.2. Infection rate considerations

The testing strategy will largely depend on the risk of the SARS-CoV-2 transmission in a region, country, or a particular population. For individuals who have already developed symptoms and are suspected of being infected, individual testing should continue as it is currently. The size of the sample tested for a population of individuals with no apparent symptoms of infection depends on the risk levels of the population being infected. The overall degree of infection risk also determines the frequency of testing, e.g., whether testing occurs daily, every few days, or weekly.

3.2.3. Technology considerations

The test accuracy is the primary concern. At present, the accuracy of PCR testing technology has reached near 100% (Dharavath et al., 2020; Garg et al., 2020), while its capability to detect a positive individual in a pooled sample is between 100 and 1000 individuals (Dharavath et al., 2020; Kumari et al., 2019). Thus, within a mixture of 1000 samples, the applied PCR method is sensitive enough to identify the presence of the virus from a single sample. As the accuracy of antibody detection is not as sensitive or specific as PCR technology, the number of mixed individuals in the testing samples need to be determined based on the accuracy of different antibody testing protocols. However, the potential errors and longer time for an accurate result have been concerns for COVID-19 testing (Mahase, 2020). This protocol proposes a strategy that takes advantage of large pooled samples and eliminates experimental errors using continuous multi-level testing.

3.2.4. Population distribution considerations

The number of samples in a pooled test should be determined according to geographic group sizes. For example, if a school has 200 students and 100 teachers, the largest group for this test unit likely would be 300 individuals; it is not advantageous for this school group to be mixed with another group. In a residential area of 50 households, the pool likely would be all residents of the 50 households.

3.2.5. Economic and environmental considerations

When economics are the primary consideration, people may choose a less expensive test with a higher risk of positive errors, but this may reduce the detection power. When environmental conditions, such as budgetary constraints, economic issues, or population distribution, limit the application of the best model, the model most effectively fitting the local environment is the optimal choice.

3.3. Statistical considerations

There is no existing statistical design, particularly for whole population testing. Our definition of the best testing model is based on the model which utilizes the least number of testing kits for the same number of people tested, resulting in equivalent test efficacy. However, different regions and countries have different population sizes, ethnic groups, and government policies and cultures. Therefore, the best practice model may be adjusted based on local requirements.

Our strategy focuses on the statistical aspect to develop a method to utilize the least number of test kits to test the largest number of samples in a reasonable time frame.

3.3.1. Determine the sizes of samples at level 1 using the least number of test kits to test the largest number of samples.

We used the probability formula $Pr\left(X=k\right)=\left(\begin{array}{c}n\\ k\end{array}\right)\cdot p^k{\left(1-p\right)}^{n-k}$ k = 0, 1, 2, 3, 4, 5… n to calculate the sample sizes when the chance of not detecting any infected person at a different rate of risk exists.

3.3.2. We then used the flowing formula to calculate the chance of not detecting a second positive sample under the condition that one positive sample exists in the sample mixture, which determines the samples sizes at level 2:

$P\left(A/B\right)=\frac{P\left(A\circ B\right)}{P\left(B\right)}$ where P(A/B) means the probability of A given that B has occurred. P(A ∘ B) means the probability of both events of A and B occurring. P(B) means the probability of Event B occurring.

3.3.3. We also used the strategy of maximum number (or half of the sample size) of overlap among groups of samples between level 1 and level 2 (e.g., between groups at one level and the following level) to increase the detection power at level 2. The number of overlap groups is one less than the number of total groups. Go = Gt − 1, where Go is the overlap groups, and Gt is the total number of groups.

The maximum sample number in the level-overlap is defined as half of the numbers in the initial total group. Thus, No = Nt / 2. The No is the sample number in the overlap group, while the Nt is the number of samples in the total/initial group.

The advantage of using the level-overlap strategy is to reduce the number of targeted individuals in the screening groups. For example, on the second level, we divide the total number of samples in level 1 into two groups; each contains 50% of the individuals in the first level. If we do not use the overlap strategy, we will be able to determine which set of these two sets of 50% samples contain a positive individual. However, if we use the overlap strategy and calculated the 25% into one overlap group, then 25% of the samples from the first 50% group are also contained in the second sample set. Thus, the second set of samples will test 75% of the samples including, 50% of samples not included in the first set. Possible test results are set 1 positive vs. set 2 negative, set 1 negative vs. set 2 positive, and set 1 positive vs. set 2 positive. This is interpreted as one sample in the 25% samples only in set 1, 50% samples only in set 2, or 25% samples common in set 1 and set 2 are positive, respectively. Thus, using this overlapping method provides a 50% chance to immediately narrow a positive individual to be contained in 25% of the original sample. Consequently, overlapping common samples will be used in all the screening samples among level 2 and level 3 tests to increase detection.

4. Proposed plan

4.1. Organization: global, national, regional, or statewide testing

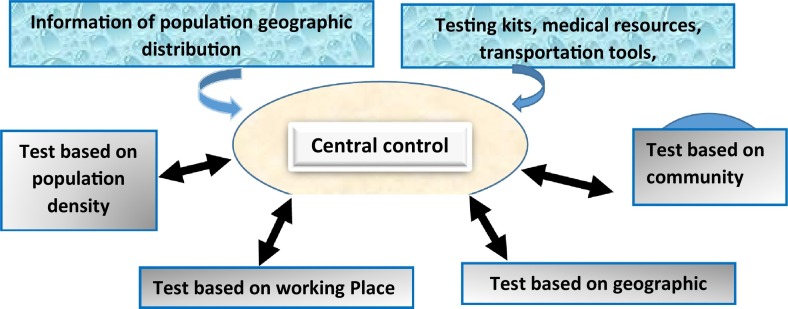
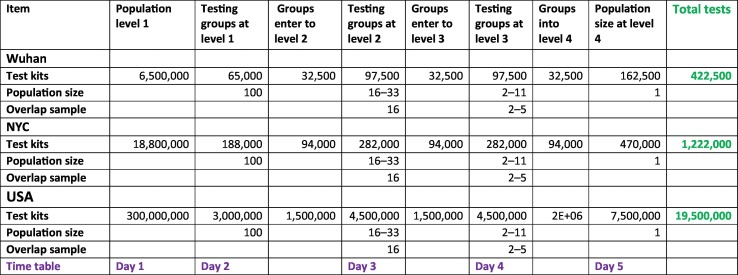
A centralized, powerful command center, appropriate for the size of the organization (business, area, state, region, country, or global levels), must be established. This center must have the right and responsibility to uniformly command and deploy the materials and transportation needed for testing. All the resources for the testing must be under the control of the testing center. The center will determine the screening levels based on the available population information (Fig. 1 ).

Fig. 1.

Overall strategic organization of the population screening. The central control will collect disease test-related information and determine the screening levels accordingly.

4.2. Information collection and assessment

Calculation of required testing materials and determination of degrees of needs in different areas of the countries. The center's first task is to comprehensively evaluate the population's distribution, the development of the epidemic, and the number of test items needed, i.e., test capacity.

Task 1 The population's distribution patterns and estimation of required total tests. The population distribution patterns determine the methodology of the test. Population distributions can be divided into four categories: geographic distribution, including rural areas, suburbs, and cities; workplace distribution, such as institutions, schools, hospitals, and factories; population density, such as the population per square kilometer; and activities-based distribution, such as supermarkets, movie theaters, restaurants, and bars.

Task 2. Identify resources for testing. All testing resources will be collected and analyzed. These testing resources may include but are not limited to test kits, supplying materials, factories, medical testing personnel, test stations, and capability of transporting the testing materials.

Task 3. Assessment of feasibility: After assessing the distribution of the population and the test resources, the next step is to determine whether the testing resources can be allocated based on population distribution. That is, to determine what level of testing can be performed on the group based on testing resources and capabilities.

4.3. Planning and allocation of test materials

Assuming that the information outlined above can be comprehensively collected, the test center (i.e., Central control) will conduct unified testing across the country or the region. This unified testing includes reallocating testing materials and conducting second levels of tests, reallocating testing materials based on the second level testing results, and conducting the third level of testing and/or fourth level of testing if necessary.

4.4. Pooling methodology based on probabilities and algorithms for whole population testing

In some cases, all individuals in a city, a region, or a country need to be tested. In this case, the government may require each citizen to conduct a test in their residence. This testing is the so-called national population detection implemented in some countries. Such a population detection will utilize an infection rate stratified, algorithmic guided, multiple-level, continuously pooled testing approach (Supplementary Fig. 1). For this approach, it is necessary to determine the size of the sample mix and the detection at different levels according to the density of the population's residents, the distribution of the population in the region, and the traffic situation. More importantly, in this last item, the group risk refers to the probability of being infected.

The number of samples in a pooled mixture should be maximized from densely populated areas if conditions permit. In rural areas or remote places, it is necessary to strive for the maximum possible number of mixed samples based on convenient transportation. However, the maximum number of mixed samples must be determined by the accuracy of the test method and the risk probability of the population, i.e., the risk of infection with the disease.

4.4.1. Determine initial pooling size to maximize the test capacity

Statistical condition: It has been reported that the probability of false-negative and false-positive for COVID-19 in the rt-PCR is high (Kucirka et al., 2020; Xiao et al., 2020). However, these high probabilities are not due to the PCR technology; rather, they are due to the samples, including sampling time and tissue types. The actual rate of the false positive and false negative from PCR-based technology is between 5% and 10% (Baron et al., 2020). Different factors affect the accuracy of PCR (Tahamtan and Ardebili, 2020), while PCR technology itself has a high accuracy (Tansarli and Chapin, 2020). With the multiple level strategy in continuous cycles, these false-positive samples will be detected at additional testing, i.e., second level or third level testing will eliminate the false-positive rate. The continuously repeated testing will also eliminate the false-negative results.

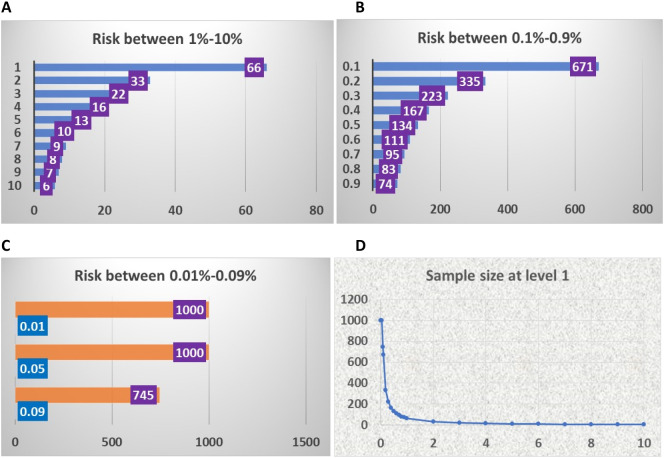
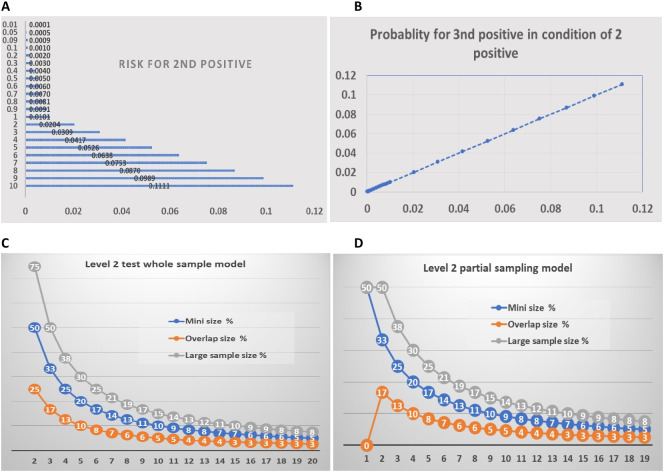
Determining the sample sizes for different risks at level 1 testing. The purpose of the level 1 test is to identify groups of people containing infected individuals and eliminate groups that do not contain infected individuals. Using the probability method, we determined the probability of detecting 0 infected individuals at different levels of infection rate (Supplemental Table s1). To eliminate as many groups as possible and pool the largest sample sizes possible, we set the threshold to more than 50% change to detect 0 infected persons in the sample as the largest sample sizes at a given risk probability of the disease (Table 1). Fig. 2A provides the largest sample sizes for the infection risk at a rate of 1% to 10%. For example, if the rate of infection risk in a population is 10%, at the sample size of 6 pooled persons, the probability of not obtaining a positive result from such a pooled sample group is 56%.

Table 1.

Disease risk probability and detection: Group size at level 1 and potential grouping at level 2.

Disease risk %	Sample size at level 1	Prob for 2nd positive	Group # at level 2	Minimum size independent detection %	Minimum size dependent detection %	Sample size %	Total dependent detection %
10	6	0.111111	2	50	25	75	50
9	7	0.098901	3	33	22	56	67
8	8	0.086957	4	25	19	44	75
7	9	0.075269	5	20	16	36	80
6	10	0.06383	6	17	14	31	83
5	13	0.052632	7	14	12	27	86
4	16	0.041667	8	13	11	23	88
3	22	0.030928	9	11	10	21	89
2	33	0.020408	10	10	9	19	90
1	66	0.010101	11	9	8	17	91
0.9	74	0.009082	12	8	8	16	92
0.8	83	0.008065	13	8	7	15	92
0.7	95	0.007049	14	7	7	14	93
0.6	111	0.006036	15	7	6	13	93
0.5	134	0.005025	16	6	6	12	94
0.4	167	0.004016	17	6	6	11	94
0.3	223	0.003009	18	6	5	11	94
0.2	335	0.002004	19	5	5	10	95
0.1	671	0.001001	20	5	5	10	95
0.09	745	0.000901	20	5	5	10	95
0.05	1000	0.0005	20	5	5	10	95
0.01	1000	0.0001	20	5	5	10	95

Fig. 2.

Sample size at level 1 based on the risk probability of infectious disease. C: Vertical axis: risk probability, Horizontal axis: number of individuals. A. Population sizes of infection rate from 10% to 1%. B. Population sizes of disease risk from 0.9% to 0.1%. C. Population sizes of disease risk from 0.09% to 0.01%. D. The pattern of distribution of population sizes and the probability of disease risk. Vertical axis: number of persons in test group, Horizontal axis: the probability of infected individuals in the population.

In contrast, the sample size can increase to 66 people if the rate of infection risk is 1%. For a rate between 0.9% and 0.1%, the pooled samples for the test can be from 74 to 671 (Fig. 2B). When the rate falls below 0.1%, sample sizes increase to more than 700 up to 1000 individuals (Fig. 2C). Thus, the sample size increases as the risk of infection decreases (Fig. 2D). With these sample sizes, at least half of the pooled sample groups will test negative, meaning these samples will not need to be tested in the following level 2. However, false-negative samples at this level in these half groups need to be detected at subsequent ongoing testing cycles.

4.4.2. Group numbers and potential percentage of infections among the pooled population at levels 2 and 3

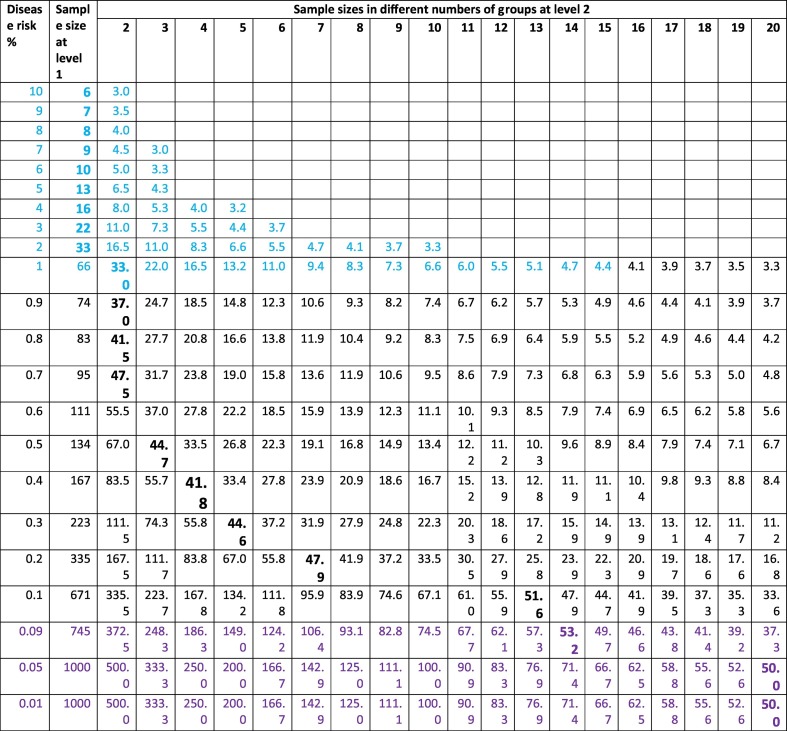
The second level or level 2 testing will be conducted based on the new sets of statistical methods. First, to narrow down the infected individual into a defined group of people, we calculated the probability of the second infected individual given the condition that the first one has been in the sample (Supplemental Table 2, Supplemental Table s3). Accordingly, we estimated the group numbers (Table 1) and samples sizes at level 2 (Table 2). As shown in Fig. 3A, the probability of a second positive in the sample is similar to that of the first sample. Thus, the sizes of the samples can be similar to that of level 1. The third positive sample's probability is the same as that of the second sample (Fig. 3B). Therefore, the sizes of level 2 will be determined according to the infection risk in the population or the risk of a second positive (Fig. 3C and D) (Supplemental Table s4).

Table 2.

Samples sizes at level 2 based on disease risk levels.

Fig. 3.

Overall features of test level 2. On A and B, numbers on vertical axes indicate the disease risk %. Numbers on horizontal axes indicate the risk for 2nd and 3rd positive sample, respectively. Numbers on horizontal axes of C and D indicate the number of groups. A. The probability of having a second positive sample in the sample sets from level 1 positive groups. B. The probability of having a third positive sample in the sample sets given the condition of 2 positive among samples. C. The proposed group numbers and samples' sizes of level 2 test for each of the positive groups at different sizes in level 1. D. The proposed group numbers and samples sizes of level 2 test with the save-one model for each of the positive groups at different sizes in level 1.

The overlapping method will be used at levels 2 and 3. For example, we assume that at level 1, the initial test, a group of 100 samples tested positive for SARS-CoV-2. We propose to divide the 100 samples into two groups, each containing 75 people. In other words, 50 individuals are contained in both samples. The two samples can determine whether the positive individual sample is among 50 people or any one of the two groups of 25 people (Fig. 3C).

An alternative method is a save one model. This model considers the test at level 1 as one of the groups for level 2 testing. Thus, in dividing the 100 samples into two sets, we will only test one set of 50 samples at the second level. Because of the 100 samples' positive result, at least one infected individual exists among these 100 samples. If the pooled 50 samples test negative, then the positive sample is contained within the 50 samples of the original 100 samples not contained in the second group. If the test of the pooled 50 is positive, then the remaining 50 among the 100 samples are assumed not to contain the infected individual (Fig. 3D). However, this is only true in a population of low infection risk. A false negative may exist in the remaining 50 samples in a population at high infection risk, which needs to be detected in the following test cycle.

Alternatively, the tests can use three or more sets of test methods (Fig. 3C and D). For example, if in the second level test, the samples are divided into three groups, 50 people per week, there are 25 individuals shared among the three groups. The test results will put positive individuals into a group of 25 people (Fig. 3C). In the saving one model, in each test grouping, the group numbers will be one less (Fig. 3D).

The level 3 test will be similar to that of level 2. In the case of the 2-group method, in the third level test, we divide 50 or 25 people into two groups and so on. There are a considerable number of common samples and different samples between the two groups. The final result will narrow the group of positive individuals to a few, but not more than 10 people.

Suppose we divide 25 people into three groups in the three-level test. If we include 10 people in every group, there are five common individuals among the three groups. The final test result will place positive individuals among those five people.

The fourth level of testing should be based on the size of the shrinking group. If there is still a large number, such as more than 10, we can also perform two sets of tests at once. Otherwise, a direct individual test can accurately identify positive individuals.

4.4.3. Total numbers of tests used for different sizes of populations at different infection risk levels

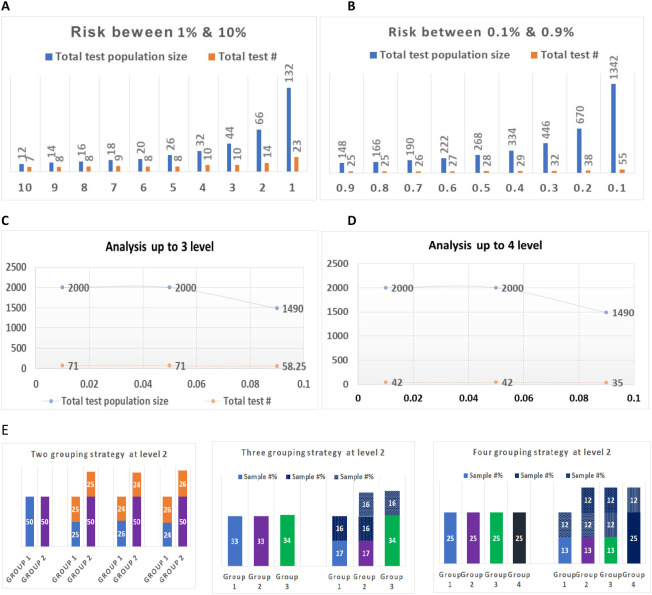
According to the different levels of infection risks, we calculated the number of tests vs. the number of individuals to be tested based on our proposed method. As shown in Fig. 4 , the lower the risk of disease infection, the higher the number of tests will be saved. If the risk of disease infection in a population is 10%, 7 tests are needed for a group of 12 individuals. However, if the infection risk rate is 1%, only 23 tests are needed to screen a group of 132 (Fig. 4A; Table 3 ). When the infection risk rate is lower than 1%, this constitutes a 6 to 25 times saving in tests (Fig. 4B). If the rate is lower than 0.1%, the testing population size can increase to 700 to 1000 individuals. The number of tests needed for all levels of one test cycle will be only one in the average of 30 or 50 people (Fig. 4C and D; Table 4 ). The difference between Fig. 4C and D is that the test will be going to individuals on level 3 (Fig. 4C), and the test will be grouped on level 3 and going to individuals on level 4 (Fig. 4D; Table 4). Fig. 4E demonstrates the percent of samples based on different grouping strategies on screening level 2.

Fig. 4.

Summary of total test groups and populations at each risk and test level. Total test population size refers to the total number of people tested in a group. Total test # refers to the total number of tests needed for the corresponding number of people in the testing group. Sample #% refers to the percent sampled by Group. Numbers on horizontal axes indicate the disease risk of %. Numbers on vertical axes indicate the total number of people in the testing group. A. The total number of people tested and the total number of tests for risk between 1% and 10%. B. The total number of tested people and the total number of tests for risk between 0.1% and 0.9%. C. The total number of tested people and the total number of tests for risk between 0.01% and 0.09% when using three levels of tests. D. The total number of tested people and the total number of tests for risk between 0.01% and 0.09% when using four levels of tests. E. Percentage of samples based on different grouping strategies.

Table 3.

Total number of tests in population with different risk ratio at level 1 and 2.

Sample size at level 1	Disease risk %	Risk for 2nd positive	Probability for 3rd positive sample	Group # at level 2	Sample size at level 2	Total test population size	Total test #
6	10	0.111111	0.111111	2	3	12	7
7	9	0.098901	0.098901	2	3.5	14	8
8	8	0.086957	0.086957	2	4	16	8
9	7	0.075269	0.075269	2	4.5	18	9
10	6	0.06383	0.06383	3	4	20	9
13	5	0.052632	0.052632	3	4	26	9
16	4	0.041667	0.041667	4	5	32	10
22	3	0.030928	0.030928	4	5	44	10
33	2	0.020408	0.020408	10	3	66	14
66	1	0.010101	0.010101	19	3	132	23
74	0.9	0.009082	0.009082	21	3	148	25
83	0.8	0.008065	0.008065	21	3	166	25
95	0.7	0.007049	0.007049	22	3	190	26
111	0.6	0.006036	0.006036	23	3	222	27
134	0.5	0.005025	0.005025	26	3	268	28
167	0.4	0.004016	0.004016	27	3	334	29
223	0.3	0.003009	0.003009	28	3	446	32
335	0.2	0.002004	0.002004	34	3	670	38
671	0.1	0.001001	0.001001	51	3	1342	55
745	0.09	0.000901	0.000901	54	3	1490	58
1000	0.05	0.0005	0.0005	67	3	2000	71
1000	0.01	0.0001	0.0001	67	3	2000	71

Table 4.

Samples sizes and total testing numbers for testing a low risk population.

Sample size at level 1	Disease risk %	Risk for 2nd & 3rd positive	Groups at level 2	Divided size at level 2	Sample size at level 2	Group # at level 3	Divided sample size	Sample size at level 3	Total test population size	Total test #
671	0.1	0.001001	20	33	51	3	11	16	1342	35
745	0.09	0.000901	20	37.25	55	3	13	20	1490	37
1000	0.05	0.0005	20	50	75	3	17	30	2000	41
1000	0.01	0.0001	20	50	75	3	17	30	2000	41

Using this screening strategy, a large population can be tested with a relatively small number of test kits. For example, if the risk of disease in the US is less than 1%, a population of 300,000,000 can be tested between 15,000,000 and 6,000,000 test kits (Table 5 ). Assuming the tests will be conducted at four levels, the entire U.S. population could be tested in one week with current technology.

Table 5.

Tests numbers at different levels in Wuhan, New York City, and USA based on algorithmic guided pooled strategy.

4.5. Application of algorithmic pooling methodologies based on industry types, workplaces, and activity sites

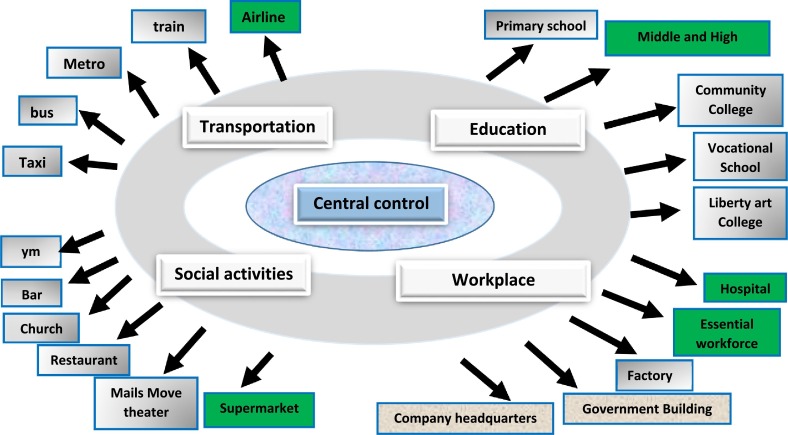
The following is an example of how pooling detection methods are implemented according to the type of work, the nature of the work, and the place of activity (Fig. 5 ). All personnel in the same workplace could be tested on the same day, provided the number of employees is less than a few hundred. All samples would be pooled into one sample for testing under the condition that individuals with symptoms of the disease are found in the workplace prior to the test. An organization with more than xxx employees should use the multiple level pooled grouping test described above (in 4.4 for grouping strategy).

Fig. 5.

Application of algorithmic guided pooled screening method in the different types of industries and business areas. Items with green backgrounds are used as examples of types of essential work and activities.

4.5.1. Transportation system

Transportation is one of the primary transmission tools for infectious disease. An algorithmic guided pooled screening method provides a way to allow transportation systems to function while keeping the infectious disease at bay—for example, passengers on a commercial airline flight number from tens to hundreds. If no passengers have signs of illness, the samples of all passengers can be mixed and tested as one sample. The flight attendant and crew samples can be pooled separately or mixed with passengers. Further tests at level 2 or 3 will be conducted only when a pooled sample tests positive. Practicing social distancing and properly wearing personal protective equipment (PPE) are challenging when traveling by air. In this case, testing of airline passengers and crew can occur daily on every flight. A false negative will be detected in the following test (e.g., additional testing after quarantine on the 14th day or later).

Similarly, subway metro and train transportation systems can collect the samples and conduct the test for all passengers. This kind of test requires sample collection at every line or station exit. The screening of all long-distance travelers can occur at sample collection stations at exits. This screening will be necessary if current PPE and social distancing fail to provide adequate protection.

4.5.2. Education system

The closing of primary and secondary schools has considerably affected the education of children and youth. Keeping social distance and requiring students and teachers to wear PPE in classrooms has proven challenging, if not impossible, particularly with younger children. However, conducting one or two tests per class every day is feasible. As schools' sizes vary, samples of different classes may even be mixed if the class sizes are small. Mixing samples for testing of some or all teachers are also feasible.

4.5.3. Workplace

Employee testing is critical to maintaining a healthy society. In particular, essential business operations must remain open during pandemics. Maintaining workforce health is critical to keeping the essential businesses operating (Fig. 5). Daily screening could be conducted for all employees in workplaces if a pooled sample strategy is used. Employee groups under several hundred can be screened as one sample. Pooled samples from one region or city can be tested in a testing station.

4.5.4. Social and public places

Shopping malls, restaurants, and bars are more complex in terms of personnel and members of the public, with greater mobility. Depending on the number of people at a particular time or on a specific day, the samples can be uniformly mixed for testing. In a similar situation, such as a church event, the samples of all the people who participated in the church event can be mixed as one sample for testing.

4.6. Centralized coordinating, resource sharing and maximization, and continuously multiple cycle testing

Governmental organization and public support are essential for systematic population daily screening. While tests will produce primarily negative results in most places, some locations will have higher numbers of positive results. Resource allocation should be adjusted daily to match testing needs. This can only be achieved if testing resources are shared and under centralized control.

Such a well-organized screening is cost-effective. It will enable governments or organizations to utilize the highly efficient and accurate testing technology for groups that would otherwise be too expensive for individual testing. Because of the lower cost, multiple testing cycles can be conducted to eliminate potential false positive and false negative results in a single test.

5. Discussion

We have provided a comprehensive screening protocol for all populations in a region or at a national level. The implementation of this program provides a guide to effectively use limited testing resources to complete a large area of testing. Uninterrupted nationwide testing strategies can limit the transmission of SARS-CoV-2, particularly during the reopening phase, which will ensure the safety of social and economic activities. A regular population screening program further ensures the normal development of economic activities. For example, it has been reported that, in less than two weeks, Wuhan city tested about 6.5 million residents and discovered a few asymptomatic individuals (The New York Times, May 26, 2020). Although no detailed information is available on the pooled method used in their testing, this study's mathematic model suggests that a total of 6.5 million people could be tested using less than 300,000 test kits in less than a week. If such a screening can be done weekly or at least monthly, the city of Wuhan would operate normally without worrying about future waves of infections from SARS-CoV-2.

Also, if the pooled test method is used in airline passengers and essential workplaces, fewer testing kits can be used to conduct daily tests to ensure the disease spread will not resume because of the reopening.

6. Factors influencing the test

When calculating the number of individuals in a test population and the number of test kits required, we only consider the population's probability of infection. The reasonable groupings and the number of people per group are determined based on the mathematical model and logistic principles. In actual operation, it will be affected by many other factors. These factors include the transportation system, geographic distribution of the population, relevant medical resources, and cultural and policy influence.

Our design requires a reliable test, PCR, or any other reliable test methodology and well organized and carefully handling of samples. Thus, personnel training and standard operation protocol are essential aspects of this strategy.

7. False-positive and false-negative issue

False-positives and false-negatives will be identified during the cycle of multiple tests. One of our testing model's advantages is that all the false positives will be identified between the different levels of the test (Eis-Hübinger et al., 2020). Thus, the false results at one level will be detected at the following level of the test. The false-negative results can be recognized at a lower level because of the positive data from the next level test.

The false-negatives at level 1 will not be identified in the following levels. However, if the whole population test is in continuous multiple cycles, such as conducted once a week, the false-negatives should be identified in the coming cycle of repeated tests.

Additionally, because of the cost-effective nature of this strategy, expensive test methods of high sensitivities and specificities can be utilized.

8. Individuals missing testing or delay of testing

There will be individuals who miss testing, or testing materials may be delayed. The information of these missing individuals should be recorded, and samples should be obtained to add to the next test. We assume all individuals will eventually be included as the test will be multiple levels and continued from time to time (in a time from week/s to week/s). If an individual misses two consecutive tests, this individual may need special attention and be treated as a potentially infected individual.

9. Limitations

Our design is based on the accuracy of the kit reaching more than one-thousandth of the population. Moreover, we assume that the DNA sequence of the virus is precise. If the sequence of the virus is mutated or the kit's test error is large, the number of individuals in each group and the composition of each group should be adjusted accordingly.

10. Conclusion

A well-designed, organized, fully functional plan for whole population testing can be implemented to identify all possible suspected individuals for SARS-CoV-2 and similar infectious transmissions and prevent its spread. This strategy is time efficient and cost-effective. It can be applied for the whole population screening of any severe infectious disease.

The following are the supplementary data related to this article.

Supplemental Table s1

Probability of detection of zero infected persons at different risk rates in different samples.

Supplemental Table 2

Probability of detecting 1 infected person at different risk rates in different sample sizes.

Supplemental Table s3

Probability of detecting 2nd infected person at different risk rate in different sample sizes.

Supplemental Table s4

Testing groups, sizes, and detection power at level 2.

Supplemental Fig. 1

Testing steps of the whole population screening strategy.

CRediT authorship contribution statement

Tianshu Gu: Conceptualization, Formal analysis, Methodology, Writing – original draft, Writing – review & editing. Lan Yao: Conceptualization, Methodology, Validation, Writing – original draft, Writing – review & editing. Xia Meng: Conceptualization, Validation, Writing – review & editing. J. Carolyn Graff: Conceptualization, Validation, Visualization, Writing – review & editing. Donald Thomason: Conceptualization, Validation, Visualization, Writing – review & editing. Jing Li: Investigation, Writing – review & editing. Wei Dong: Investigation, Methodology, Writing – review & editing. Yan Jiao: Investigation, Writing – review & editing. Lotfi Aleya: Conceptualization, Validation, Visualization, Writing – review & editing. Marcello Maida: Conceptualization, Methodology, Validation, Visualization, Writing – review & editing. Cong-Yi Wang: Investigation, Writing – review & editing. Barbara Zangerl: Investigation, Writing – review & editing. Sem Genini: Investigation, Writing – review & editing. Kunal Ray: Investigation, Writing – review & editing. Emanuel Goldman: Investigation, Writing – review & editing. Jiafu Ji: Conceptualization, Resources, Supervision, Validation, Writing – review & editing. Andrei V. Alexandrov: Conceptualization, Resources, Supervision, Validation, Writing – review & editing. Dianjun Sun: Conceptualization, Resources, Supervision, Validation, Writing – review & editing. Weikuan Gu: Conceptualization, Formal analysis, Funding acquisition, Methodology, Project administration, Resources, Supervision, Validation, Writing – original draft, Writing – review & editing. Yongjun Wang: Conceptualization, Funding acquisition, Project administration, Resources, Supervision, Validation, Writing – review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Editor: Dr. Jay Gan