Fractional model of COVID-19 applied to Galicia, Spain and Portugal

Abstract

A fractional compartmental mathematical model for the spread of the COVID-19 disease is proposed. Special focus has been done on the transmissibility of super-spreaders individuals. Numerical simulations are shown for data of Galicia, Spain, and Portugal. For each region, the order of the Caputo derivative takes a different value, that is not close to one, showing the relevance of considering fractional models.

1. Introduction

Coronavirus disease 2019 (COVID-19), the outbreak due to severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), has taken on pandemic proportions in 2020, affecting several millions of individuals in almost all countries [12]. An integrated science and multidisciplinary approach is necessary to fight the COVID-19 pandemic [17], [18]. In particular, mathematical and epidemiological simulation plays a crucial role in predicting, anticipating, and controlling present and future epidemics.

As for the mathematical modelling of coronavirus disease COVID-19, it has been shown to be extremely useful for governments in order to define appropriate policies [19]. In this direction, a number of papers has been recently published related with modelling of this pandemic (see, e.g., [6], [9], just to cite some of them).

In [19], a model including the super-spreader class has been presented, and applied to give an estimation of the infected and death individuals in Wuhan. The collaboration with Galician government [3] has allowed to understand some important considerations in order to perform analysis. In particular, due to the pandemic, some cases have not been reported as expected, but with some days of delay. As a consequence, in this paper we propose to consider not the daily reported cases, but the means in the previous 5 days of daily reported cases. As a result, it seems appropriate to consider fractional derivatives, which have been intensively used to obtain models of infectious diseases since they take into account the memory effect, which is now bigger due to the aforementioned mean of the five previous days of daily reported cases. Having estimates a priori of infected individuals of COVID-19, obtained by using mathematical models, has helped to predict the number of required beds both for hospitalized individuals and mainly at intensive care units [3].

Fractional calculus and fractional differential equations have recently been applied in numerous areas of mathematics, physics, engineering, bio-engineering, and other applied sciences. We refer the reader to the monographs [7], [11], [13], [22], [24], [25], [27] and the articles [1], [2], [20], [26]. In this work we shall consider the Caputo fractional derivative [4] (see also [8]). A fractional model using the Caputo–Fabrizio fractional derivative of COVID-19 in Wuhan (China) has been developed in Prasad and Yadav [21].

The structure of this work is as follows. In Section 2, we introduce a fractional model by using Caputo fractional derivatives on the classical compartmental model presented in Ndaïrou et al. [19], and where the fractional order of differentiation $\alpha$ can be used to describe different strains and genomes of the coronavirus and vary with mutations. In Section 3, some numerical results are presented for three different territories: Galicia, Spain, and Portugal. Galicia is an autonomous community of Spain and located in the northwest Iberian Peninsula and having a population of about 2,700,000 and a total area of 29,574 km${}^2$. Spain (officially, the Kingdom of Spain) is a country mostly located on the Iberian Peninsula, in southwestern Europe, with a population of about 47,000,000 people and a total area of 505,992 km${}^2$. Portugal (officially, the Portuguese Republic) is also a country located mostly on the Iberian Peninsula with a population of about 10,276,000 individuals and a total area of 92,212 km${}^2$. We end with Section 4 of conclusions and discussion.

2. The proposed COVID-19 fractional model

In what follows we shall assume that we have a constant population divided in 8 epidemiological classes, namely:

• 1.susceptible individuals ($S$),
• 2.exposed individuals ($E$),
• 3.symptomatic and infectious individuals ($I$),
• 4.super-spreaders individuals ($P$),
• 5.infectious but asymptomatic individuals ($A$),
• 6.hospitalized individuals ($H$),
• 7.recovery individuals ($R$), and
• 8.dead individuals ($F$) or fatality class.

Our model is based on the one presented in Ndaïrou et al. [19] and substituting the first order derivative by a derivative of fractional order $\alpha$. We use the fractional derivative in the sense of Caputo: for an absolutely continuous function $f:[0,\infty )\to \mathbb{R}$ the Caputo fractional derivative of order $\alpha >0$ is given by Hilfer [11], Kilbas et al. [13], Kumar et al. [15], Samko et al. [22]:

$$D^{\alpha }f\left(t\right)=\frac{1}{\Gamma (1-\alpha )}{\int }_0^t{(t-s)}^{-\alpha }{f}^{\prime }\left(s\right)ds.$$

Fractional calculus and fractional differential equations are an active area of research and, in some cases, adequate to incorporate the history of the processes [1], [10], [14], [15], [16], [23], [27]. The fractional proposed model takes the form

$$\{\begin{array}{c}{\displaystyle D^{\alpha }S\left(t\right)=-\beta \frac{I}{N}S-l\beta \frac{H}{N}S-{\beta }^{{}^{\prime }}\frac{P}{N}S,}\hfill \\ {\displaystyle D^{\alpha }E\left(t\right)=\beta \frac{I}{N}S+l\beta \frac{H}{N}S+{\beta }^{{}^{\prime }}\frac{P}{N}S-\kappa E,}\hfill \\ {\displaystyle D^{\alpha }I\left(t\right)=\kappa {\rho }_{1}E-({\gamma }_a+{\gamma }_i)I-{\delta }_{i}I,}\hfill \\ {\displaystyle D^{\alpha }P\left(t\right)=\kappa {\rho }_{2}E-({\gamma }_a+{\gamma }_i)P-{\delta }_{p}P,}\hfill \\ {\displaystyle D^{\alpha }A\left(t\right)=\kappa (1-{\rho }_1-{\rho }_2)E,}\hfill \\ {\displaystyle D^{\alpha }H\left(t\right)={\gamma }_a(I+P)-{\gamma }_{r}H-{\delta }_{h}H,}\hfill \\ {\displaystyle D^{\alpha }R\left(t\right)={\gamma }_i(I+P)+{\gamma }_{r}H,}\hfill \\ {\displaystyle D^{\alpha }F\left(t\right)={\delta }_{i}I\left(t\right)+{\delta }_{p}P\left(t\right)+{\delta }_{h}H\left(t\right),}\hfill \end{array}$$ (1)

in which we have the following parameters:

• 1.$\beta$ quantifies the human-to-human transmission coefficient per unit time (days) per person,
• 2.${\beta }^{{}^{\prime }}$ quantifies a high transmission coefficient due to super-spreaders,
• 3.$l$ quantifies the relative transmissibility of hospitalized patients,
• 4.$\kappa$ is the rate at which an individual leaves the exposed class by becoming infectious (symptomatic, super-spreaders or asymptomatic),
• 5.${\rho }_1$ is the proportion of progression from exposed class $E$ to symptomatic infectious class $I,$
• 6.${\rho }_2$ is a relative very low rate at which exposed individuals become super-spreaders,
• 7.$1-{\rho }_1-{\rho }_2$ is the progression from exposed to asymptomatic class,
• 8.${\gamma }_a$ is the average rate at which symptomatic and super-spreaders individuals become hospitalized,
• 9.${\gamma }_i$ is the recovery rate without being hospitalized,
• 10.${\gamma }_r$ is the recovery rate of hospitalized patients,
• 11.${\delta }_i$ denotes the disease induced death rates due to infected individuals,
• 12.${\delta }_p$ denotes the disease induced death rates due to super-spreaders individuals,
• 13.${\delta }_h$ denotes the disease induced death rates due to hospitalized individuals.

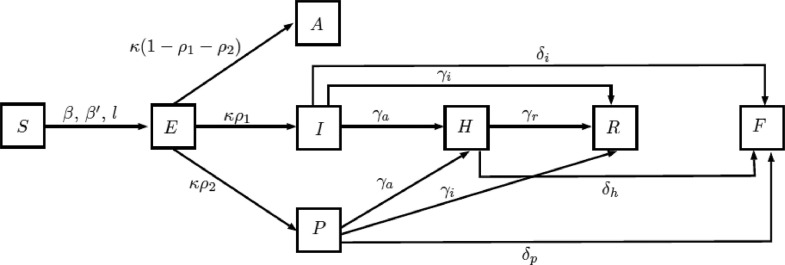
A flowchart of model (1) is presented in Fig. 1 . For additional details and particular values of the parameters we refer the reader to [19].

Fig. 1.

Flowchart of model (1).

3. Numerical simulations

Next, we shall show the numerical simulations in three territories: Galicia, Portugal, and Spain. For all these cases we have considered the official data published by the corresponding authorities and we have computed the means of the five previous reports. As it has been observed during this pandemic, the output of the laboratories has had some delays due to the big pressure and collapse of the public health systems. In this way, some cases have been reported with some delay and some updates have been published days later of the corresponding dates. In order to reduce these problems, we consider the mean of the five previous reported cases, always following the official data. Moreover, in each of the territories there are specificities such as territorial dispersion/concentration, use of public transportation, and mainly the date of starting the confinement, as compared with the initial spread of the COVID-19. These factors imply tiny adjustments in the factor to divide the total population as well as in the value of the fractional parameter $\alpha$. For solving the system of fractional differential Eq. (1) we have used [5], by using Matlab in a MacBook Pro computer with a 2.3 GHz Intel Core i9 processor and 16 GB of 2400 MHz DDR4 memory.

3.1. The case study of Galicia

In the autonomous region of Galicia, we have the values given in Table 1 as for the cumulative cases, the new daily infected individuals, as well as the mean of the 5 previous days.

Table 1.

Data of the autonomous region of Galicia. The list of 51 days includes the cumulative, new infected and mean of the previous 5 days.

Date	Confirmed	New confirmed	5 days mean		Date	Confirmed	New confirmed	5 days mean
03-08	6	1	1		04-03	5625	406	380,4
03-09	22	16	4,2		04-04	5944	319	381
03-10	35	13	6,4		04-05	6151	207	343,8
03-11	35	0	6,4		04-06	6331	180	297,8
03-12	85	50	16		04-07	6538	207	263,8
03-13	115	30	21,8		04-08	6758	220	226,6
03-14	195	80	34,6		04-09	6946	188	200,4
03-15	245	50	42		04-10	7176	230	205
03-16	292	47	51,4		04-11	7336	160	201
03-17	341	49	51,2		04-12	7494	158	191,2
03-18	453	112	67,6		04-13	7597	103	167,8
03-19	578	125	76,6		04-14	7708	111	152,4
03-20	739	161	98,8		04-15	7873	165	139,4
03-21	915	176	124,6		04-16	8013	140	135,4
03-22	1208	293	173,4		04-17	8084	71	118
03-23	1415	207	192,4		04-18	8185	101	117,6
03-24	1653	238	215		04-19	8299	114	118,2
03-25	1915	262	235,2		04-20	8468	169	119
03-26	2322	407	281,4		04-21	8634	166	124,2
03-27	2772	450	312,8		04-22	8805	171	144,2
03-28	3139	367	344,8		04-23	8932	127	149,4
03-29	3723	584	414		04-24	9116	184	163,4
03-30	4039	316	424,8		04-25	9176	60	141,6
03-31	4432	393	422		04-26	9238	62	120,8
04-01	4842	410	414		04-27	9328	90	104,6
04-02	5219	377	416

The data includes 51 values starting 7th March since after that date (27th April) the way of officially computing individuals has changed.

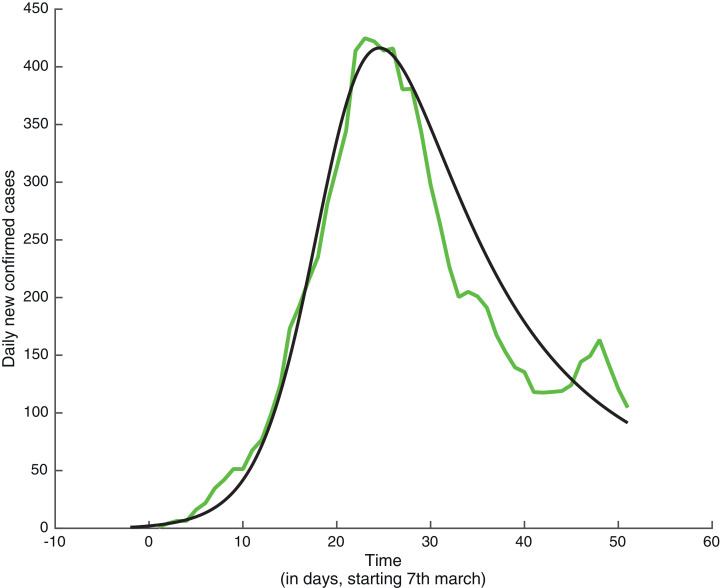
By considering the fractional order $\alpha =0.85$ and the same values of the parameters as in Ndaïrou et al. [19], the results of the numerical simulation are shown in Fig. 2 .

Fig. 2.

Number of confirmed cases per day in Galicia. The green line corresponds to the real data given in Table 1 while the black line ($I+P+H$) has been obtained by solving numerically the system of fractional differential Eq. (1), by using [5]. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The green line denotes the real data while the black line is the numerical solution of the fractional system (1), with total population $N=2,700,000/500,$ where $N=S+E+I+P+A+H+R+F,$ since the population of Galicia is widely dispersed in the territory with very few big cities and low use of public transportation.

3.2. The case study of Spain

As for the Kingdom of Spain, the data of 82 days is collected in Table 2, as for the cumulative cases, the new daily infected individuals, as well as the mean of the 5 previous days, starting 25th February.

Table 2.

Data of the Kingdom of Spain. The list of 82 days includes the cumulative, new infected and mean of the previous 5 days.

Date	Confirmed	New confirmed	5 days mean		Date	Confirmed	New confirmed	5 days mean
02-25	10	6	1,4		04-06	147,717	5213	5676,2
02-26	18	8	3		04-07	153,303	5586	5337,4
02-27	36	18	6,6		04-08	159,051	5748	5151,4
02-28	55	19	10,4		04-09	163,591	4540	4951,8
02-29	83	28	15,8		04-10	168,151	4560	5129,4
03-01	138	55	25,6		04-11	172,054	3903	4867,4
03-02	195	57	35,4		04-12	175,087	3033	4356,8
03-03	270	75	46,8		04-13	178,224	3137	3834,6
03-04	352	82	59,4		04-14	182,662	4438	3814,2
03-05	535	183	90,4		04-15	186,484	3822	3666,6
03-06	769	234	126,2		04-16	190,308	3824	3650,8
03-07	1101	332	181,2		04-17	194,150	3842	3812,6
03-08	1536	435	253,2		04-18	193,437	713	3042,6
03-09	2309	773	391,4		04-19	195,655	2218	2598,6
03-10	3285	976	550		04-20	198,614	2959	2426
03-11	4442	1157	734,6		04-21	200,968	2354	2132
03-12	5976	1534	975		04-22	203,888	2920	1947,6
03-13	7659	1683	1224,6		04-23	206,002	2114	2513
03-14	9806	2147	1499,4		04-24	208,507	2505	2570,4
03-15	11,515	1709	1646		04-25	210,148	1641	2306,8
03-16	14,018	2503	1915,2		04-26	211,807	1659	2167,8
03-17	17,713	3695	2347,4		04-27	213,338	1531	1890
03-18	21,764	4051	2821		04-28	214,215	877	1642,6
03-19	26,333	4569	3305,4		04-29	215,470	1255	1392,6
03-20	31,779	5446	4052,8		04-30	216,757	1287	1321,8
03-21	36,645	4866	4525,4		05-01	217,992	1235	1237
03-22	41,291	4646	4715,6		05-02	218,894	902	1111,2
03-23	48,984	7693	5444		05-03	219,338	444	1024,6
03-24	57,546	8562	6242,6		05-04	220,362	1024	978,4
03-25	66,503	8957	6944,8		05-05	221,236	874	895,8
03-26	75,691	9188	7809,2		05-06	222,145	909	830,6
03-27	83,944	8253	8530,6		05-07	223,305	1160	882,2
03-28	90,371	6427	8277,4		05-08	224,048	743	942
03-29	96,184	5813	7727,6		05-09	224,755	707	878,6
03-30	104,332	8148	7565,8		05-10	227,659	2904	1284,6
03-31	111,745	7413	7210,8		05-11	228,373	714	1245,6
04-01	119,336	7591	7078,4		05-12	228,978	605	1134,6
04-02	126,616	7280	7249		05-13	229,471	493	1084,6
04-03	133,294	6678	7422		05-14	230,228	757	1094,6
04-04	138,832	5538	6900		05-15	230,929	701	654
04-05	142,504	3672	6151,8		05-16	231,350	421	595,4

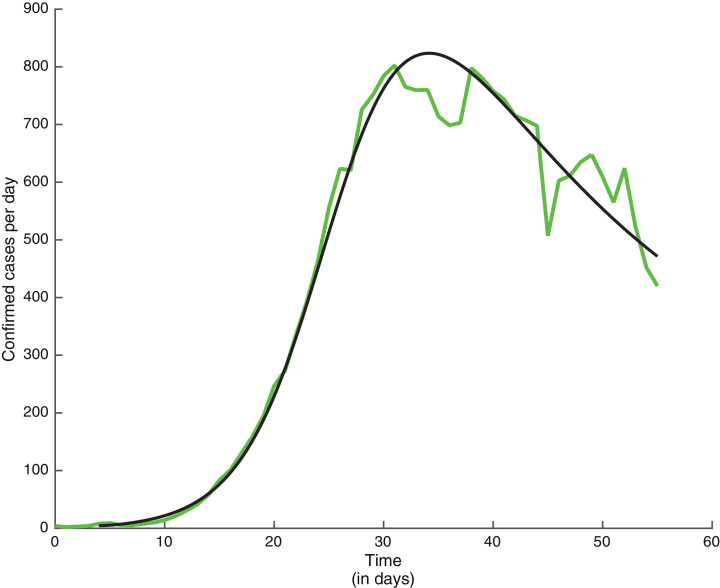
By considering again the fractional order $\alpha =0.85$ and the same values of the parameters as in Ndaïrou et al. [19], the results of the numerical simulation are shown in Fig. 3 .

Fig. 3.

Number of confirmed cases per day in Spain. The green line corresponds to the real data given in Table 2 while the black line ($I+P+H$) has been obtained by solving numerically the system of fractional differential Eq. (1), by using [5].

The green line denotes the real data while the black line is the numerical solution of the fractional system (1), with $N=47,000,000/425$ since in some parts of Spain there is more concentrated population and intensive use of public transportation.

3.3. The case study of Portugal

As for the Republic of Portugal, the data of 56 days starting 3rd March for the cumulative cases, the new daily infected individuals, as well as the mean of the 5 previous days is collected in Table 3.

Table 3.

Data of the Republic of Portugal. The list of 56 days includes the cumulative, new infected and mean of the previous 5 days.

Date	Confirmed	New confirmed	5 days mean		Date	Confirmed	New confirmed	5 days mean
03-03	4	2	4		03-31	7443	1035	725,9
03-04	6	2	2		04-01	8251	808	750,9
03-05	9	3	3		04-02	9034	783	784,3
03-06	13	4	4		04-03	9886	852	802,6
03-07	21	8	8		04-04	10,524	638	764,9
03-08	30	9	9		04-05	11,278	754	759,4
03-09	39	9	5,5		04-06	11,730	452	760,3
03-10	41	2	5,3		04-07	12,442	712	714,1
03-11	59	18	7,6		04-08	13,141	699	698,6
03-12	78	19	9,9		04-09	13,956	815	703,1
03-13	112	34	14,1		04-10	15,472	1516	798
03-14	169	57	21,1		04-11	15,987	515	780,4
03-15	245	76	30,7		04-12	16,585	598	758,1
03-16	331	86	41,7		04-13	16,934	349	743,4
03-17	448	117	58,1		04-14	17,448	514	715,1
03-18	642	194	83,3		04-15	18,091	643	707,1
03-19	785	143	101		04-16	18,841	750	697,9
03-20	1020	235	129,7		04-17	19,022	181	507,1
03-21	1280	260	158,7		04-18	20,206	1184	602,7
03-22	1600	320	193,6		04-19	20,863	657	611,1
03-23	2060	460	247		04-20	21,379	516	635
03-24	2362	302	273,4		04-21	21,982	603	647,7
03-25	2995	633	336,1		04-22	22,353	371	608,9
03-26	3544	549	394,1		04-23	22,797	444	565,1
03-27	4268	724	464		04-24	23,392	595	624,3
03-28	5170	902	555,7		04-25	23,864	472	522,6
03-29	5962	792	623,1		04-26	24,027	163	452
03-30	6408	446	621,1		04-27	24,322	295	420,4

By considering now the fractional order $\alpha =0.75$ and the same values of the parameters as in Ndaïrou et al. [19], the results of the numerical simulation are shown in Fig. 4 . As in the previous figures, the green line denotes the real data while the black line is the numerical solution of the fractional system (1), with $N=10,280,000/1750$ since the Portuguese population is widely dispersed and the confinement started at an earlier stage of the spread of the disease.

Fig. 4.

Number of confirmed cases per day in Portugal. The green line corresponds to the real data given in Table 3 while the black line ($I+P+H$) has been obtained by solving numerically the system of fractional differential Eq. (1), by using [5].

4. Conclusions and discussion

In this paper, we have shown the importance of considering a fractional Caputo differential system, where the order of the derivative $\alpha$ plays a crucial role to fit the number of confirmed cases in the regions of Galicia, Spain and Portugal. In fact, the considered values of $\alpha =0.85$ for Galicia and Spain and $\alpha =0.75$ for Portugal, are not close to 1 (the classical derivative), as it happens in many of the proposed fractional compartmental models in the literature. Note that the same values of the parameters in the differential system (1), taken from [19], were used for the three regions. Therefore, we may conclude that model (1) can be used to approximate the confirmed cases of COVID-19 in regions with different economic, geographical, social and epidemic characteristics, as it happens for the three considered regions in this paper.

Our variables are divided into eight epidemiological sub-populations as in Ndaïrou et al. [19] and they are detailed at the beginning of the second section, dedicated to the introduction of the dynamical model. We have solved our fractional dynamical model using a subroutine called FracPECE [5] to approximate numerically the solution of the proposed fractional system of differential equations. Our numerical simulations show a good agreement between the output of the fractional model given by the sum of the symptomatic and infectious individuals, super-spreaders, and hospitalized individuals and the data collected from the health authorities in Spain, Portugal and Galicia. We plan to consider other countries and regions in our future studies and also, of course, an update of the data. In the future, we also plan to study the stability of the possible equilibrium point, the bifurcation of solutions depending on the parameters, and the role of the basic reproduction number.

Our fractional model is novel and in the future we will study the optimal fractional order of differentiation for the study of the COVID-19 epidemic in different contexts. The system has a unique solution for given initial conditions and a detailed mathematical analysis study will be performed. A crucial point is, of course, to determine the optimal fractional order $\alpha$ adequate for each process and, in this case, each region.

The results obtained here allow us to conjecture that the strains and genomes of the new coronavirus present in Spain and Portugal are different than those that initially hit China: the proposed mathematical model is good to describe the outbreak that was first identified in Wuhan in December 2019 with $\alpha =1$; to describe the spread in Spain and its autonomous community of Galicia, where the virus was first confirmed on January 31 and March 4 2020, respectively, with $\alpha =0.85$; and the COVID-19 situation in Portugal with $\alpha =0.75,$ where the first cases of COVID-19 were recorded in March 2, 2020. We will continue our research using this and other future models, as well as considering different approaches as the COVID-19 evolves and new insights and conjectures emerge.

Funding

This research was partially supported by the Portuguese Foundation for Science and Technology (FCT) within “Project n. 147 – Controlo Ótimo e Modelação Matemática da Pandemia COVID-19: contributos para uma estratégia sistémica de intervenção em saúde na comunidade”, in the scope of the “RESEARCH 4 COVID-19” call financed by FCT; and by the Instituto de Salud Carlos III, within the Project COV20/00617 “Predicción dinámica de escenarios de afectación por COVID-19 a corto y medio plazo (PREDICO)”, in the scope of the “Fondo COVID” financed by the Ministerio de Ciencia e Innovación of Spain. The work of Ndaïrou, Silva and Torres was also partially supported within project UIDB/04106/2020 (CIDMA); the work of Area and Nieto has been partially supported by the Agencia Estatal de Investigación (AEI) of Spain, cofinanced by the European Fund for Regional Development (FEDER) corresponding to the 2014–2020 multiyear financial framework, project MTM2016-75140-P. Moreover, Ndaïrou is also grateful to the support of FCT through the Ph.D. fellowship PD/BD/150273/2019; Nieto also thanks partial financial support by Xunta de Galicia under grant ED431C 2019/02. Silva is also supported by national funds (OE), through FCT, I.P., in the scope of the framework contract foreseen in the numbers 4, 5 and 6 of the article 23, of the Decree-Law 57/2016, of August 29, changed by Law 57/2017, of July 19.

Author contributions

Each author equally contributed to this paper, and read and approved the final manuscript. All authors have read and agreed to the published version of the manuscript.

CRediT authorship contribution statement

Faïçal Ndaïrou: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing - original draft, Writing - review & editing. Iván Area: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing - original draft, Writing - review & editing. Juan J. Nieto: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing - original draft, Writing - review & editing. Cristiana J. Silva: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing - original draft, Writing - review & editing. Delfim F.M. Torres: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing - original draft, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.