Stability analysis and optimal control of covid-19 with convex incidence rate in Khyber Pakhtunkhawa (Pakistan)

Abstract

The dynamic of covid-19 epidemic model with a convex incidence rate is studied in this article. First, we formulate the model without control and study all the basic properties and results including local and global stability. We show the global stability of disease free equilibrium using the method of Lyapunov function theory while for disease endemic, we use the method of geometrical approach. Furthermore, we develop a model with suitable optimal control strategies. Our aim is to minimize the infection in the host population. In order to do this, we use two control variables. Moreover, sensitivity analysis complemented by simulations are performed to determine how changes in parameters affect the dynamical behavior of the system. Taking into account the central manifold theory the bifurcation analysis is also incorporated. The numerical simulations are performed in order to show the feasibility of the control strategy and effectiveness of the theoretical results.

1. Introduction

In December 2019, the capital of Hubei Province i.e., Wuhan city gains attention worldwide, at the end of 2019 as an unknown virus attack people and start killing. Later on, the causative agent was identified as a novel coronavirus and now named as severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). The Chinese government did its best to minimize the spread but unluckily the virus spreads to other countries. The latency period of covid-19 is from 11 to 14 days whereas myalgia, diarrhea, cough, fever, and shortness of breath are common symptoms. Aged people are highly exposed to covid-19 as well as patients having comorbid conditions. The covid-19 transmission rate is very high and the basic reproduction number lies between 2.2 and 3.58. That’s why it spread throughout the world and affected 213 countries. Hence, the world health organization (WHO) declared covid-19 as one of the global pandemics on January 30, 2020. The two main routes of transmission is direct physical contact with the infected person and respiratory droplet coming out from covid-19 patient [1].

At first, Iran and Italy were the highly exposed countries to covid-19 after China. Iran is the neighboring country of Pakistan and every year thousands of people came from Pakistan to Iran for religious ceremonies. While coming back from Iran some of these people were infected and they become the cause for spreading covid-19 in Pakistan. Although the government closed the Pakistan-Iran border but yet the first case was confirmed officially on February 26, 2020, from Karachi. Avoiding the spread and causalities government decided to quarantine most of the people at home [1].

Mathematical modeling is considered an effective tool for describing the dynamical behavior of infections [2], [3], [4], [5], [6]. Mathematicians frequently using the tools of mathematical modeling from the last century. More recently, the field of mathematical modeling got considerable attention and a number of authors put their valuable contributions in this area. For realizing and controlling the outbreak of transmissible diseases in a group, many researchers have formulated models. The second leading source of death around the globe is infectious diseases. The application of mathematical modeling has been in vogue for the study of transmissible infectious diseases. Many scholars have been discussing over the last few years infectious diseases and their dynamics using various approaches. “To study the dynamics of various infectious diseases, mathematical modeling is considered as one of the best techniques to formulate the phenomenon in the system of equations. Several researchers have worked on different infectious diseases. They have developed different mathematical models for these epidemic diseases, and then studied the stability analysis and optimal control of these epidemic models (see e.g., [7], [8], [9], [10], [11], [12]), which not only helps in the control/spread of infectious diseases but also helps in prevention of these diseases in daily life. Many researchers have worked on epidemic models to analyze and control different diseases, for example, hepatitis B, avian influenza, leishmaniasis, tuberculosis, etc. Modeling of epidemic models is helpful to academia as well as to daily life. Mathematical modeling has a rich literature on the transmission dynamics of infectious diseases. Mathematical modeling is one of the powerful tools to describe the dynamical behavior of different diseases [22], [23], [24], [25], [26], [27].

The incidence rate plays a major role in epidemic models. The incidence rate of $g\left(I\right)S=(1-\mathit{cI})\mathit{IS}$ was introduced by Yorke and London [13] whereas $\frac{\beta I^{p}S}{1+\alpha I^q}$ with $\alpha ,\beta ,p,q>0$ was investigated by Liu and coworkers [14]. While this incidence rate is more difficult to deal with than the bilinear one, it seems more reasonable. One of the interesting examples of nonlinear incidence rate is convex incidence rate i.e $f(S,I)=\beta \mathit{SI}(1+\delta I)$, where $\beta$ and $\delta$ are positive constants. For a short time period it corresponds to an increased rate of infection which causes due to two exposure. The contact rate $\beta \mathit{IS}$ results from a single contact, while the term $\beta \delta I^{2}S$ corresponds to a new infective which comes into being due to the double exposure. Until now researchers established stability analysis of epidemic models by geometric approach with non-convex (respect to I) incidence rate. For convex incidence of the approach seems to give very restrictive conditions [33].

One of the reasons why we chose the convex incidence rate is because this function could model the increase in infection, which occurs due to a double exposure situation. This is in parallel with the uncertain mechanisms of infection for a covid-19 pandemic: it has been reported that, until this research work is conducted, there is no evidence whether people have heard or long-term immunity against this covid-19 attack [16], which makes an additional exposure to this novel coronavirus could result in the possibility of infection.

Optimal control is one of the most powerful and effective mathematical tools through which one can formulate the control program for controlling various contagious diseases. We apply the optimal control methods to formulate control mechanisms for the spread of the covid-19 SEIQR model. This technique has been applied over the last few years to prevent various contagious diseases from the community. There are different methods for determining the optimal control for a given mathematical model. For instance, Pontryagin’s maximum principle [15] allows the optimal control calculation for an ordinary equation model system with a given constraint. The aim of this work is to set up an optimal control problem relative to the covid-19 SEIQR model.

To the best of the author’s knowledge, very limited attention has been given to study the convex incidence rate of an epidemic model with control strategies and sensitivity analysis. Therefore, motivated by the above studies, we reformulated the covid-19 SEIQR model by incorporating the convex incidence rate and develop the control strategy for the proposed model [17]. In Section 2, we present the formulation of the model and its basic reproduction number. The local asymptotic stability (LAS) and the global asymptotic stability (GAS) of disease-free equilibrium (DFE) and endemic equilibrium (EE) are discussed in Section 3. In Section 4, we discuss optimal control theory using two control variables. Numerical simulation evaluated in Section 5. The bifurcation analysis sensitivity analysis is performed in Sections 6, 7 respectively while concluding remarks are discussed in Section 8.

2. Model formulation

Due to a large number of reported (covid-19) cases in the KPK province of Pakistan. The authors are interested to formulate a mathematical model for the covid-19 transmission mechanism. The authors divided the total population into five subclasses namely; susceptible individuals $S\left(t\right)$ which denotes individuals vulnerable to the infection; exposed class $E\left(t\right)$ which denotes individuals which take the covid-19 infection but not yet infected i.e., latent class; infectious $I\left(t\right)$ which represent the individuals that are fully infected and ready for spreading the infection to the others; quarantined-treated $Q\left(t\right)$ and $R\left(t\right)$ refers to recovered as well as those individuals whose immune system is strong enough to be safe from covid-19 infection at time t.

Further, the incidence rate plays a major role in epidemic models. According to reports of WHO the covid-19 spread very past in a short time worldwide, that’s why the authors considered that the convex incidence rate is suitable for our model. Because for a short time period it corresponds to an increased rate of infection in which cases due to the two exposures. The contact rate $\beta \mathit{SI}$ results from a single contact, while the term $\beta \delta I^{2}S$ correspond to a new infective which comes into being due to the double exposure.

$$\begin{array}{c}\frac{\mathit{dS}}{\mathit{dt}}=b-\beta \mathit{SI}(1+\delta I)-(\eta +\mu +d_3)S\left(t\right),\hfill \\ \frac{\mathit{dE}}{\mathit{dt}}=\beta \mathit{SI}(1+\delta I)-(\lambda +\mu +d_2)E\left(t\right),\hfill \\ \frac{\mathit{dI}}{\mathit{dt}}=\lambda E\left(t\right)-(\mu +∊+\gamma +d_1)I\left(t\right),\hfill \\ \frac{\mathit{dQ}}{\mathit{dt}}=d_{3}S\left(t\right)+d_{2}E\left(t\right)+d_{1}I\left(t\right)-(\mu +\tau )Q\left(t\right),\hfill \\ \frac{\mathit{dR}}{\mathit{dt}}=\eta S\left(t\right)+\tau Q\left(t\right)+\gamma I\left(t\right)-\mu R,\hfill \end{array}$$ (1)

subject to the conditions

$$S\left(0\right)>0,E\left(0\right)⩾0,I\left(0\right)⩾0,Q\left(0\right)⩾0,R\left(0\right)⩾0\text{.}$$

The parameter b is the constant birth rate, $\beta$ and $\delta$ are positive constants and are the disease transmission coefficients, $\mu$ is the natural death rate, $∊$ is the death rate for the disease of infectious individuals and $\lambda ,\gamma ,d_1,d_2,d_3,\tau$ are the state transition rates. $\eta$ represents those individuals whose immune system is strong enough to prevent them from covid-19 infection (see Fig. 1 ).

Fig. 1.

The flowchart represents the covid-19 epidemic model.

Letting

$$N\left(t\right)=R\left(t\right)+Q\left(t\right)+I\left(t\right)+E\left(t\right)+S\left(t\right),$$

Then

$$\frac{\mathit{dN}}{\mathit{dt}}=b-\mu N-∊I⩽b-\mu N\text{.}$$

Now as $t\to \infty$, we obtain $N⩽\frac{b}{\mu }$. We study $\left(1\right)$ in the following closed set

$$\mathrm{\Gamma }=\left\{(S,E,I,Q,R)\in R_{+}^5:0<S+E+I+Q+R⩽\frac{b}{\mu }\right\}\text{.}$$

2.1. Equilibrium of the model

The DFE of the model $\left(1\right)$ is denoted by $E^0(S_0,0,0,Q_0,R_0)$, where

$$S_0=\frac{b}{\eta +\mu +d_3},Q_0=\frac{d_3{S}_0}{\mu +\tau },R_0=\frac{\eta S_0+\tau Q_0}{\mu }\text{.}$$

This equilibrium is used to compute the threshold number $R_0$, which is actually the basic reproduction number. This number $R_0$ is then conveniently used to study the endemic steady state as well. To calculate the number $R_0$ for our model, it is preferred to use van den Driessche and Watmough method [18].

$$F=\left[\begin{array}{cc}\hfill 0\hfill & \hfill \beta S_0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right],V=\left[\begin{array}{cc}\hfill \lambda +\mu +d_2\hfill & \hfill 0\hfill \\ \hfill -\lambda \hfill & \hfill \mu +∊+\gamma +d_1\hfill \end{array}\right],$$

$$V^{-1}=\frac{1}{(\lambda +\mu +d_2)(\mu +∊+\gamma +d_1)}\left[\begin{array}{cc}\hfill \mu +∊+\gamma +d_1\hfill & \hfill 0\hfill \\ \hfill \lambda \hfill & \hfill \lambda +\mu +d_2\hfill \end{array}\right],$$

$${\mathit{FV}}^{-1}=\left[\begin{array}{cc}\hfill \frac{\beta S_0\lambda }{(\lambda +\mu +d_2)(\mu +∊+\gamma +d_1)}\hfill & \hfill \frac{\beta S_0}{\mu +∊+\gamma +d_1}\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\text{.}$$

Hence

$$R_0=\frac{\lambda \beta b}{(\eta +\mu +d_3)(\lambda +\mu +d_2)(\mu +∊+\gamma +d_1)}\text{.}$$

2.2. Endemic equilibrium point

System (1) is rearranged to get $S_{\ast },E_{\ast },Q_{\ast }$ and $R_{\ast }$ in terms of $I_{\ast }$. Thus

$$\begin{array}{c}{S}_{\ast }=\frac{(\lambda +\mu +d_2)(\mu +∊+\gamma +d_1)I_{\ast }}{\lambda \beta I_{\ast }(1-\delta I_{\ast })},\hfill \\ E_{\ast }=\frac{(\mu +∊+\gamma +d_1)I_{\ast }}{\lambda },\hfill \\ Q_{\ast }=\frac{d_3{S}_{\ast }+d_2{E}_{\ast }+d_1{I}_{\ast }}{\mu +\tau },\hfill \\ R_{\ast }=\frac{\eta S_{\ast }+\tau Q_{\ast }+\gamma I_{\ast }}{\mu }\text{.}\hfill \end{array}$$ (2)

Using the above values in the following equation,

$$b-(\eta +\mu +d_3)S_{\ast }-(\lambda +\mu +d_2)E_{\ast }=0,$$ (3)

gives us

$$P\left(I\right)=A_1{I}^3+A_2{I}^2+A_{3}I=0,$$ (4)

where

$$A_1=(\lambda +\mu +d_2)(\mu +∊+\gamma +d_1)\beta \delta ,$$ (5)

$$A_2=-\left(\right(\lambda +\mu +d_2\left)\right(\mu +∊+\gamma +d_1)\beta +b\lambda \beta \delta ),$$ (6)

$$A_3=b\lambda \beta -(\lambda +\mu +d_2)(\mu +∊+\gamma +d_1)(\eta +\mu +d_3)\text{.}$$ (7)

By the Descarte’s rule of sign if $A_3>0$ then (4) has one positive one negative and one zero roots, and $A_3>0$ implies that $R_0>1$. Hence, for $R_0>1$, a unique positive equilibrium exists for the model.

3. Local stability

We establish the local stability of the system (1) in this section at disease free point $E^0$ as well as at endemic equilibrium point $E^{\ast }$.

Theorem 1

The disease free equilibrium (DFE) point $E^0$ of the system (1) is locally asymptotically stable if $R_0<1$ .

Proof

Jacobian matrix of the system (1) at $E^0$ is

$$J\left(E^0\right)=\left(\begin{array}{ccccc}\hfill -(\eta +\mu +d_3)\hfill & \hfill 0\hfill & \hfill -\frac{\beta b}{\eta +\mu +d_3}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -(\lambda +\mu +d_2)\hfill & \hfill \frac{\beta b}{\eta +\mu +d_3}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \lambda \hfill & \hfill -(\mu +∊+\gamma +d_1)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill d_3\hfill & \hfill d_2\hfill & \hfill d_1\hfill & \hfill -(\mu +\tau )\hfill & \hfill 0\hfill \\ \hfill \eta \hfill & \hfill 0\hfill & \hfill \gamma \hfill & \hfill \tau \hfill & \hfill -\mu \hfill \end{array}\right)\text{.}$$ (8)

The characteristic equation of $J\left(E^0\right)$ takes the following form:

$$({\omega }_1+(\eta +\mu +d_3\left)\right)({\omega }_2+(\mu +\tau \left)\right)({\omega }_3+\mu )(A{\omega }^2+B\omega +C)=0,$$

where

$$\begin{array}{cc}A=\hfill & 1,\hfill \\ B=\hfill & 2\mu +\lambda +∊+\gamma +d_1+d_2,\hfill \\ C=\hfill & (\lambda +\mu +d_2)(\mu +∊+\gamma +d_1)-\frac{\beta \lambda b}{\eta +\mu +d_3}\text{.}\hfill \end{array}$$ (9)

It is clear from the characteristic equation that the first three eigenvalues are negative whereas for the remaining factors we need to find condition under which the real parts of the two eigenvalues are negative.

We see that $A>0,B>0$, and the value of C can either be positive or negative. Therefore, considering the value of C we have the following cases.

• 1:When $C<0$, then the nature of the roots is real with one root positive and the other is negative. Thus DFE is unstable.
• 2:When $C=0$, then the root are real, negative and zero, DFE is stable (not asymptotically), some trajectories will not be heading to the DFE for $t\to \infty$.
• 3:When $B^2-4\mathit{AC}=0$ $(C=\frac{B^2}{4A})$ then the roots are real, negative and repeated, CFE asymptotically stable.
• 4:When $B^2-4\mathit{AC}>0$ $(0<C<\frac{B^2}{4A})$ we obtain two real and negative roots, hence the DFE is asymptotically stable.
• 5:When $B^2-4\mathit{AC}<0$ $(C>\frac{B^2}{4A})$ then the roots are complex conjugate with negative real part, hence DFE is asymptotically stable.

Again from the five cases we can decide that when $C<0$ then DFE is stable, when $C=0$, the DFE is stable (not asymptotically), and if $C>0$ (cases $3,4,5$) then the DFE is asymptotically stable. All trajectories are moving towards the DFE. So the stability of the DFE point depends only on the value of C.

Furthermore, the value of $C>0$ if

$$(\lambda +\mu +d_2)(\mu +∊+\gamma +d_1)-\frac{\beta \lambda b}{\eta +\mu +d_3}>0,$$

$$(\lambda +\mu +d_2)(\mu +∊+\gamma +d_1)(1-R_0)>0\text{.}$$

This shows that for $R_0<1$, the disease free equilibrium point is asymptotically stable. □

3.1. At endemic equilibrium point

Lemma 1

Let M be a $3\times 3$ real matrix. If $\mathit{tr}\left(M\right),\mathit{det}\left(M\right)$ and ${\mathit{detM}}^{\left[2\right]}$ are all negative, then all eigenvalues of M have negative real part.

Theorem 2

If $R_0>1$ , then the endemic equilibrium $E^{\ast }$ of the system (1) is locally asymptotically stable.

Proof

The Jacobian matrix of the system (1) at $E^{\ast }$ is

$$J^{|*|}=\left(\begin{array}{ccccc}\hfill -\left(\beta I_{\ast }\right(1-\delta I_{\ast })+(\eta +\mu +d_3\left)\right)\hfill & \hfill 0\hfill & \hfill -\beta S_{\ast }(1-2\delta I_{\ast })\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \beta I_{\ast }(1-\delta I_{\ast })\hfill & \hfill -(\lambda +\mu +d_2)\hfill & \hfill \beta S_{\ast }(1-2\delta I_{\ast })\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \lambda \hfill & \hfill -(\mu +∊+\gamma +d_1)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill d_3\hfill & \hfill d_2\hfill & \hfill d_1\hfill & \hfill -(\mu +\tau )\hfill & \hfill 0\hfill \\ \hfill \eta \hfill & \hfill 0\hfill & \hfill \gamma \hfill & \hfill \tau \hfill & \hfill -\mu \hfill \end{array}\right)\text{.}$$

Here ${\omega }_1=-\mu ,{\omega }_2=-(\mu +\tau )$ and for the remaining three eigenvalues we have the following reduced matrix:

$$J_1^{|*|}=\left(\begin{array}{ccc}\hfill -\left(\beta I_{\ast }\right(1-\delta I_{\ast })+(\eta +\mu +d_3\left)\right)\hfill & \hfill 0\hfill & \hfill -\beta S_{\ast }(1-2\delta I_{\ast })\hfill \\ \hfill \beta I_{\ast }(1-\delta I_{\ast })\hfill & \hfill -(\lambda +\mu +d_2)\hfill & \hfill \beta S_{\ast }(1-2\delta I_{\ast })\hfill \\ \hfill 0\hfill & \hfill \lambda \hfill & \hfill -(\mu +∊+\gamma +d_1)\hfill \end{array}\right)\text{.}$$

From the Jacobian matrix $J_1^{|*|}$ we have

$$\mathit{tr}\left(J_1^{|*|}\right)=-\left[\right(\beta I_{\ast }(1-\delta I_{\ast })+(\eta +\mu +d_3))+(\lambda +\mu +d_2)+(\mu +∊+\gamma +d_1\left)\right]<0,$$

also

$$\begin{array}{cc}\mathit{det}\left(J_1^{|*|}\right)=\hfill & -\left[\right(\beta I_{\ast }(1-\delta I_{\ast })+(\eta +\mu +d_3)\left)\right((\lambda +\mu +d_2)(\mu +∊+\gamma +d_1)-\lambda \beta S_{\ast }(1-2\delta I_{\ast })\hfill \\ \hfill & +\lambda \beta S_{\ast }(1-2\delta I_{\ast })\beta S_{\ast }{I}_{\ast }(1-2\delta I_{\ast })\left)\right],\hfill \end{array}$$

$$\begin{array}{cc}\mathit{det}\left(J_1^{|*|}\right)=\hfill & -\left[\right(\beta I_{\ast }(1-\delta I_{\ast })+(\eta +\mu +d_3)\left)\right((\lambda +\mu +d_2)(\mu +∊+\gamma +d_1)(1-\frac{(1-2\delta I_{\ast })}{(1-\delta I_{\ast })})\hfill \\ \hfill & +\lambda \beta S_{\ast }(1-2\delta I_{\ast })\beta S_{\ast }{I}_{\ast }(1-2\delta I_{\ast })\left)\right]<0\text{.}\hfill \end{array}$$

Further the second additive compound matrix is

$$J^{\left[2\right]}=\left(\begin{array}{ccc}\hfill -\beta I(1-\delta I)-m\hfill & \hfill \beta S(1-2\delta I)\hfill & \hfill \beta S(1-2\delta I)\hfill \\ \hfill \lambda \hfill & \hfill -\beta I(1-\delta I)-n\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \beta I(1-\delta I)\hfill & \hfill -k\hfill \\ \hfill \hfill \end{array}\right),$$

where

$$\begin{array}{c}m=2\mu +\eta +\lambda +d_2+d_3,\hfill \\ n=2\mu +\eta +\epsilon +\gamma +d_1+d_3,\hfill \\ k=2\mu +\lambda +\epsilon +\gamma +d_1+d_2\text{.}\hfill \end{array}$$

Hence

$$\begin{array}{c}\mathit{det}\left(J^{\left[2\right]}\right)=-\left[\right(\beta I_{\ast }(1-\delta I_{\ast })+m\left)\right(\beta I_{\ast }(1-\delta I_{\ast })+n)k+(\beta I_{\ast }(1-\delta I_{\ast })\left)\right(\lambda \beta I_{\ast }(1-\delta I_{\ast }))\hfill \\ -\left(\beta S_{\ast }\right(1-\delta 2\delta I_{\ast }\left)\lambda k\right)]<0\text{.}\hfill \end{array}$$

Therefore, by Lemma 1, the endemic equilibrium point $E^{\ast }$ is locally asymptotically stable. □

4. Global asymptotic stability

4.1. At disease free equilibrium point

The Castillo Chavez approach [19] is summarized as, let the proposed model (1) is reduced into the following two subsystems given by

$$\begin{array}{cc}\hfill & \frac{d{\chi }_1}{\mathit{dt}}=G({\chi }_1,{\chi }_2),\hfill \\ \hfill & \frac{d{\chi }_2}{\mathit{dt}}=R({\chi }_1,{\chi }_2),\hfill \end{array}$$ (10)

where ${\chi }_1$ and ${\chi }_2$ are the number of uninfected and infected individuals respectively. Thus ${\chi }_1=(S,Q,R)\in R^3$ and ${\chi }_2=(E,I)\in R^2$. Let us denote the disease-free equilibrium by $E_0$ and define as $E_0=({\chi }_1^0,0)$. For disease-free equilibrium the existence of global stability depends on

• 1.If $\frac{d{\chi }_1}{\mathit{dt}}=G({\chi }_1,0),{\chi }_1^0$ is globally asymptotically stable.
• 2. $H({\chi }_1,{\chi }_2)=B{\chi }_2-\bar{H}({\chi }_1,{\chi }_2)$, where $\bar{H}({\chi }_1,{\chi }_2)⩾0$ for $({\chi }_1,{\chi }_2)\in \mathrm{\Delta }$,

where $B=D_{{\chi }_2}H({\chi }_1^0,0)$ is an M-matrix having the positive off-diagonal entries and $\mathrm{\Delta }$ represents the feasible region. Thus the following statement holds.

Lemma 2

The equilibrium point $E_0=({\chi }_1^0,0)$ of the system (1) is globally asymptotically stable, if the above conditions are satisfied and $R_0<1$ [19] .

Now for proving the global stability of (1) at disease-free equilibrium, we apply the above technique.

Theorem 3

At covid-19 free equilibrium $E^0$ , the model (1) is globally asymptotically stable if $R_0<1$ and unstable otherwise.

Proof

Consider ${\chi }_1=(S,Q,R)$, ${\chi }_2=(E,I)$ and define $E^0=({\chi }_1^0,0)$, where

$${\chi }_1^0=\left(\frac{b}{\eta +\mu +d_3},\frac{d_3{S}_0}{\mu +\tau },\frac{\eta S_0+\tau Q_0}{\mu }\right)\text{.}$$ (11)

From the model (1), we have

$$\begin{array}{cc}\hfill \frac{d{\chi }_1}{\mathit{dt}}=& G({\chi }_1,{\chi }_2),\hfill \\ \hfill \frac{d{\chi }_1}{\mathit{dt}}=& \left(\begin{array}{c}\hfill b-\beta \mathit{SI}(1-\delta I)-(\eta +\mu +d_3)S\left(t\right)\hfill \\ \hfill d_{3}S\left(t\right)+d_{2}E\left(t\right)+d_{1}I\left(t\right)-(\mu +\tau )Q\left(t\right)\hfill \\ \hfill \eta S\left(t\right)+\tau Q\left(t\right)+\gamma I\left(t\right)-\mu R\text{.}\hfill \end{array}\right)\text{.}\hfill \end{array}$$ (12)

For $S=S_0,Q=Q_0,R=R_0$, and $G({\chi }_1,0)=0$ , we get

$$G({\chi }_1,0)=\left(\begin{array}{c}\hfill b-(\eta +\mu +d_3)S_0\hfill \\ \hfill d_3{S}_0-(\mu +\tau )Q_0\hfill \\ \hfill \eta S_0+\tau Q_0-\mu R_0\text{.}\hfill \end{array}\right)=0\text{.}$$ (13)

From Eq. (13) as $t\to \infty$, ${\chi }_1\to {\chi }_1^0$. Thus ${\chi }_1={\chi }_1^0$ is globally asymptotically stable.

Now

$$\begin{array}{c}\hfill B{\chi }_2-\bar{H}({\chi }_1,{\chi }_2)=\left(\begin{array}{cc}\hfill -(\lambda +\mu +d_2)\hfill & \hfill \beta S_0(1-2\delta I_0)\hfill \\ \hfill \lambda \hfill & \hfill -(\mu +∊+\gamma +d_1)\hfill \end{array}\right)\left(\begin{array}{c}\hfill E\hfill \\ \hfill I\hfill \\ \hfill \hfill \end{array}\right)\\ \hfill -\left(\begin{array}{c}\hfill \beta S_0{I}_0(1-2\delta I_0)-\beta \mathit{SI}(1-\delta I)\hfill \\ \hfill 0\hfill \\ \hfill \hfill \end{array}\right)\text{.}\end{array}$$ (14)

As $\beta S_0{I}_0(1-2\delta I_0)⩾\beta \mathit{SI}(1-\delta I)$, hence $\bar{H}({\chi }_1,{\chi }_2)⩾0$. Clearly, B is M-matrix and hence both the conditions are proved, so by Lemma 2, the disease free equilibrium point $E^0$ is stable globally asymptotically.

4.2. Endemic equilibrium (global stability)

For the global stability of (1) at endemic equilibrium $E^{\ast }$, we use the geometrical approach [20]. To investigate the sufficient condition through which the $E^{\ast }$ is globally asymptotically stable. Therefore, consider the differential equation

$$\dot{x}=f\left(x\right),$$ (15)

where the open set $U\subset R^n$ is simply connected and $f:U\to R^n$ is a function such that $f\in C^1\left(U\right)$. Assuming that $f\left(x^{\ast }\right)=0$ is the solution of Eq. (15) and for $x(t,x_0)$, the following are true.

• 3. There exist a compact absorbing set $K\in U$.

• 4. System (15) has a unique equilibrium.

The solution $x^{\ast }$ is said to be globally asymptotically stable in U, if it is locally asymptotically stable and all trajectories in U converges to the equilibrium $x^{\ast }$. For $n⩾2$, a condition satisfied for f, which precludes the existence of non-constant periodic solution of Eq. (15) known is Bendixson criteria. The classical Bendixson criteria $\mathit{divf}\left(x\right)<0$ for $n=2$ is robust under $C^1$ [20]. Furthermore a point $x_0\in U$ is wandering for Eq. (15), if there exist a neighborhood N of $x_0$ and $\tau >0$, such that $N\cap x(t,N)$ is empty for all $t>\tau$. Thus the following global stability principle established for autonomous system in any finite dimension.

Lemma 3

If the conditions $\left(3\right)-\left(4\right)$ and Bendixson criterion are satisfied for Eq. (15) (i.e. robust under $C^1$ local perturbation of f at all non equilibrium, non wandering point for Eq. (15) ), then $x^{\ast }$ is globally asymptotically stable (GAS) in U provided it is stable.

Define a matrix valued function P on U by

$$P\left(x\right)=\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)\times \left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)\text{.}$$ (16)

Eq. (16) is a matrix valued function on U. Further assume that $P^{-1}$ exist and is continuous for $x\in K$. Now define a quantity define, such that

$$\overline{q}={\mathit{lim}}_{t\to \infty }\mathit{supsup}\frac{1}{t}{\int }_0^t\left[\mu \right(B\left(x\right(s,x_0\left)\right)\left)\right]\mathit{ds},$$ (17)

where $J^{\left[2\right]}$ is the second additive compound matrix of J i.e. $J\left(x\right)=\mathit{Uf}\left(x\right)$ and $B=P_f{P}^{-1}+{\mathit{PJ}}^{\left[2\right]}{P}^{-1}$. Let $\ell \left(B\right)$ be the Lozinski measure of the matrix B with respect to the norm $\Vert .\Vert$ in $R^n$ [20] defined by

$$\ell \left(B\right)={\mathit{lim}}_{x\to 0}\frac{|I+\mathit{Bx}|-1}{x}\text{.}$$ (18)

Hence if $\overline{q}<0$, which shows that the presence of any orbit that give rise to a simple closed rectifiable curve, such as periodic orbits and heterocyclic cycles.

Lemma 4

Let U is simply connected and the condition $\left(3\right)-\left(4\right)$ are satisfied, then the unique equilibrium $x^{\ast }$ of Eq. (15) is globally asymptotically stable (GAS) in U, if $\overline{q}<0$ . [19]

Theorem 4

If $R_0>1$ , then the model (1) is globally asymptotically stable (GAS) at endemic equilibrium $E^{\ast }$ and unstable otherwise.

Proof

Now examine the sub-system of (1), that is

$$\begin{array}{c}\frac{\mathit{dS}}{\mathit{dt}}=b-\beta \mathit{SI}(1+\delta I)-(\eta +\mu +d_3)S\left(t\right),\hfill \\ \frac{\mathit{dE}}{\mathit{dt}}=\beta \mathit{SI}(1+\delta I)-(\lambda +\mu +d_2)E\left(t\right),\hfill \\ \frac{\mathit{dI}}{\mathit{dt}}=\lambda E\left(t\right)-(\gamma +∊+\mu +d_1)I\left(t\right)\text{.}\hfill \end{array}$$ (19)

The Jacobian matrix becomes

$$J=\left(\begin{array}{ccc}\hfill -\left(\beta I\right(1-\delta I)+(\eta +\mu +d_3\left)\right)\hfill & \hfill 0\hfill & \hfill -\beta S(1-2\delta I)\hfill \\ \hfill \beta I(1-\delta I)\hfill & \hfill -(\lambda +\mu +d_2)\hfill & \hfill \beta S(1-2\delta I)\hfill \\ \hfill 0\hfill & \hfill \lambda \hfill & \hfill -(\mu +∊+\gamma +d_1)\hfill \\ \hfill \hfill \end{array}\right)\text{.}$$

The compound second additive matrix is

$$J^{\left[2\right]}=\left(\begin{array}{ccc}\hfill -\beta I(1-\delta I)-m\hfill & \hfill \beta S(1-2\delta I)\hfill & \hfill \beta S(1-2\delta I)\hfill \\ \hfill \lambda \hfill & \hfill -\beta I(1-\delta I)-n\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \beta I(1-\delta I)\hfill & \hfill -k\hfill \end{array}\right),$$

where

$$\begin{array}{c}m=2\mu +\eta +\lambda +d_2+d_3,\hfill \\ \hfill \\ n=2\mu +\eta +\epsilon +\gamma +d_1+d_3,\hfill \\ \hfill \\ k=2\mu +\lambda +\epsilon +\gamma +d_1+d_2\text{.}\hfill \end{array}$$

The function $P\left(\chi \right)=P(S,E,I)=\mathit{diag}\left(1,\frac{E}{I},\frac{E}{I}\right)$, then

$$P_f=\mathit{diag}\left(0,\frac{E^{\prime }I-I^{\prime }E}{I^2},\frac{E^{\prime }I-I^{\prime }E}{I^2}\right)\text{.}$$

So, it follows

$$P_f{P}^{-1}=\mathit{diag}\left(0,\frac{E^{\prime }}{E}-\frac{I^{\prime }}{I},\frac{E^{\prime }}{E}-\frac{I^{\prime }}{I}\right),$$

$${\mathit{PJ}}^{\left[2\right]}{P}^{-1}=\left(\begin{array}{ccc}\hfill -\beta I(1-\delta I)-m\hfill & \hfill \frac{\beta \mathit{SI}(1-2\delta I)}{E}\hfill & \hfill \frac{\beta \mathit{SI}(1-2\delta I)}{E}\hfill \\ \hfill \frac{\lambda E}{I}\hfill & \hfill -\beta I(1-\delta I)-n\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \beta I(1-\delta I)\hfill & \hfill -k\hfill \\ \hfill \hfill \end{array}\right)\text{.}$$

The matrix $B={\mathit{PJ}}^{\left[2\right]}{P}^{-1}+P_f{P}^{-1}$, can be expressed in the form

$$B=\left(\begin{array}{cc}\hfill B_{11}\hfill & \hfill B_{12}\hfill \\ \hfill B_{21}\hfill & \hfill B_{22}\hfill \end{array}\right),$$

where

$$\begin{array}{cc}\hfill B_{11}=& -\beta I(1-\delta I)-m,\hfill \\ \hfill B_{12}=& \left(\begin{array}{cc}\hfill \frac{\beta \mathit{SI}(1-2\delta I)}{E}\hfill & \hfill \frac{\beta \mathit{SI}(1-2\delta I)}{E}\hfill \\ \hfill \hfill \end{array}\right),\hfill \\ \hfill B_{21}=& \left(\begin{array}{c}\hfill \frac{\delta E}{I}\hfill \\ \hfill 0\hfill \\ \hfill \hfill \end{array}\right),\hfill \\ \hfill B_{22}=& \left(\begin{array}{cc}\hfill \frac{E^{\prime }}{E}-\frac{I^{\prime }}{I}-\beta S(1-2\delta I)-n\hfill & \hfill 0\hfill \\ \hfill \beta S(1-2\delta I)\hfill & \hfill \frac{E^{\prime }}{E}-\frac{I^{\prime }}{I}-k\hfill \\ \hfill \hfill \end{array}\right)\text{.}\hfill \end{array}$$

Suppose $(k_1,k_2,k_3)$ be a vector in ${\mathbb{R}}^3$, with the norm $\Vert .\Vert$ defined by

$$\mathit{max}\left\{\right|k_1|,|k_2|,|k_3\left|\right\}=\Vert (k_1,k_2,k_3)\Vert \text{.}$$

Let $\mu \left(B\right)$ be the Lozinski measure with respect to this norm, we choose

$$\mu \left(B\right)⩽\mathit{sup}\{g_1,g_2\},$$

where

$$g_1=\left|B_{12}\right|+{\mu }_1\left(B_{11}\right),{\mu }_1\left(B_{22}\right)+\left|B_{21}\right|=g_2,$$

$\left|B_{12}\right|,\left|B_{21}\right|$ are matrix norms with respect to the $l_1$ vector norm, and ${\mu }_1$ refers the Lozinski measure with respect to this $l_1$ norm. Then

$${\mu }_1\left(B_{11}\right)=-\beta S(1-2\delta I)-m,\left|B_{21}\right|=\frac{\lambda E}{I},$$

$$\left|B_{12}\right|=\mathit{max}\left\{\frac{\beta \mathit{SI}(1-2\delta I)}{E},\frac{\beta \mathit{SI}(1-2\delta I)}{E}\right\}=\frac{\beta \mathit{SI}(1-2\delta I)}{E},$$

and

$${\mu }_1\left(B_{22}\right)=\mathit{max}\left\{\frac{E^{\prime }}{E}-\frac{I^{\prime }}{I}-n,\frac{E^{\prime }}{E}-\frac{I^{\prime }}{I}-k\right\}=\frac{E^{\prime }}{E}-\frac{I^{\prime }}{I}-\mathit{min}\{n,k\}\text{.}$$

Hence, we have

$$\begin{array}{ccc}\hfill g_1& \hfill =\hfill & -\beta I(1-\delta I)-m+\frac{\beta \mathit{SI}(1-2\delta I)}{E},\hfill \\ \hfill g_2& \hfill =\hfill & \frac{\lambda E}{I}+\frac{E^{\prime }}{E}-\frac{I^{\prime }}{I}-\mathit{min}\{n,k\}\text{.}\hfill \end{array}$$ (20)

From $\left(1\right)$, we get

$$\begin{array}{ccc}\hfill & \hfill \hfill & \frac{E^{\prime }}{E}=\frac{\beta \mathit{SI}(1-\delta I)}{E}-(\lambda +\mu +d_2),\hfill \\ \hfill \\ \hfill & \hfill \hfill & \frac{I^{\prime }}{I}=\frac{\lambda E}{I}-(\mu +\in +\gamma +d_1)\text{.}\hfill \end{array}$$

Thus, we have

$$\begin{array}{ccc}\hfill g_1& \hfill =\hfill & -\beta I(1-\delta I)-m+\frac{\beta \mathit{SI}(1-2\delta I)}{E}+\left[\frac{\beta \mathit{SI}(1-2\delta I)}{E}-\frac{\beta \mathit{SI}(1-\delta I)}{E}\right]\hfill \\ \hfill \\ \hfill & \hfill ⩽\hfill & -\beta I(1-\delta I)-(\mu +\eta +d_3)+\frac{E^{\prime }}{E},\hfill \\ \hfill \\ \hfill g_2& \hfill =\hfill & \frac{I^{\prime }}{I}+(\mu +\in +\gamma +d_1)+\frac{E^{\prime }}{E}-\frac{I^{\prime }}{I}-\mathit{min}\{n,k\}\hfill \\ \hfill \\ \hfill & \hfill ⩽\hfill & \frac{E^{\prime }}{E}-\mu \text{.}\hfill \end{array}$$ (21)

Moreover, we get

$$\mu \left(B\right)⩽\mathit{sup}\{g_1,g_2\}⩽\mathit{sup}\{-\frac{\beta I}{N}-\mu +\frac{E^{\prime }}{E},\frac{E^{\prime }}{E}-\mu \}⩽\frac{E^{\prime }}{E}-\mu ,$$

then

$$\frac{1}{t}{\int }_0^t\mu \left(B\right)\mathit{ds}⩽\frac{1}{t}{\int }_0^t(\frac{E^{\prime }}{E}-\mu )\mathit{ds}=\frac{1}{t}\mathit{ln}\frac{E\left(t\right)}{E\left(0\right)}-\mu ,$$

which implies $q⩽0$, based on Theorem $3.5$ of [21]. We prove that positive equilibrium $(S_{\ast },E_{\ast }.I_{\ast })$ is GAS.

Examine the sub system of system $\left(1\right)$

$$\begin{array}{ccc}\hfill & \hfill \hfill & \frac{\mathit{dQ}}{\mathit{dt}}=d_{3}S+d_{2}E+d_{1}I-(\mu +\tau )Q,\hfill \\ \hfill \\ \hfill & \hfill \hfill & \frac{\mathit{dR}}{\mathit{dt}}=\eta S+\tau Q+\gamma I-\mu R,\hfill \end{array}$$ (22)

the limit system is given by

$$\begin{array}{ccc}\hfill & \hfill \hfill & \frac{\mathit{dQ}}{\mathit{dt}}=d_3{S}_{\ast }+d_2{E}_{\ast }+d_1{I}_{\ast }-(\mu +\tau )Q,\hfill \\ \hfill \\ \hfill & \hfill \hfill & \frac{\mathit{dR}}{\mathit{dt}}=\eta S_{\ast }+\tau Q+\gamma I_{\ast }-\mu R\text{.}\hfill \end{array}$$ (23)

The solution of last equation yields,

$$\begin{array}{cc}\hfill Q\left(t\right)=& e^{-(\mu +\tau )t}\left[Q\right(0)+(d_3{S}_{\ast }+d_2{E}_{\ast }+d_1{I}_{\ast }\left){\int }_0^t{e}^{-(\mu +\tau )s}\mathit{ds}\right],\hfill \\ \hfill R\left(t\right)=& \eta S_{\ast }+\tau Q+\gamma I_{\ast }-\mu R,\hfill \end{array}$$

implies that

$$\begin{array}{cc}\hfill Q\left(t\right)\to & \frac{d_3{S}_{\ast }+d_2{E}_{\ast }+d_1{I}_{\ast }}{\mu +\tau }=Q_{\ast },\hfill \\ \hfill R\left(t\right)\to & \frac{\eta S_{\ast }+\tau Q+\gamma I_{\ast }}{\mu }=R_{\ast },t\to \infty \hfill \end{array}$$

we get that $E^{\ast }$ is GAS.

5. Optimal control strategies

To develop the control strategy, we use optimal control theory [28], [29]. To assess the conditions necessary to indicate the possible optimal control in the proposed epidemic model, we use Pontryagin’s maximum principal [15].

It should be noticed that the social distancing of the vulnerable population and treatment of the infected people makes sense. To incorporate control strategy into the study, we will update the system $\left(1\right)$ by including the controls in the form of treatment and, social distancing. The first control function $u_1\left(t\right)$ refers to show the fraction of the population practicing social distancing. The second control function $u_2\left(t\right)$ represents treatment of infected individual. For minimization of the objective functional, we have

$$J(u_1,u_2)=\mathit{min}{\int }_0^T\left[W_{1}S\left(t\right)+W_{2}E\left(t\right)+W_{3}I\left(t\right)+\frac{1}{2}\left(Z_1{u}_1^2\right(t)+Z_2{u}_2^2(t\left)\right)\right]\mathit{dt},$$ (24)

subject to the state system,

$$\begin{array}{ccc}\hfill & \hfill \hfill & \frac{\mathit{dS}}{\mathit{dt}}=b-\beta \mathit{SI}(1+\delta I)-(\eta +\mu +d_3+u_1(t\left)\right)S\left(t\right),\hfill \\ \hfill & \hfill \hfill & \frac{\mathit{dE}}{\mathit{dt}}=\beta \mathit{SI}(1+\delta I)-(\lambda +\mu +d_2+u_1(t\left)\right)E\left(t\right),\hfill \\ \hfill & \hfill \hfill & \frac{\mathit{dI}}{\mathit{dt}}=\lambda E\left(t\right)-(\mu +∊+\gamma +d_1)I\left(t\right)-\left(u_1\right(t)+u_2(t\left)\right)I\left(t\right),\hfill \\ \hfill & \hfill \hfill & \frac{\mathit{dQ}}{\mathit{dt}}=d_{3}S\left(t\right)+d_{2}E\left(t\right)+d_{1}I\left(t\right)+u_2\left(t\right)I\left(t\right)-(\mu +\tau +u_1(t\left)\right)Q\left(t\right),\hfill \\ \hfill & \hfill \hfill & \frac{\mathit{dR}}{\mathit{dt}}=\eta S\left(t\right)+\tau Q\left(t\right)+\gamma I\left(t\right)+u_1\left(t\right)S\left(t\right)+u_1\left(t\right)E\left(t\right)+u_1\left(t\right)I\left(t\right)+u_1\left(t\right)Q\left(t\right)-\mu R\text{.}\hfill \end{array}$$ (25)

with the initial condition for the above system as

$$S\left(0\right)⩾0,E\left(0\right)⩾0,I\left(0\right)⩾0,Q\left(0\right)⩾0,R\left(0\right)⩾0\text{.}$$

In the objective functional (24), $W_1,W_2$ and $W_3$ and are constants and nonnegative which represent the relative weights of the infected individuals. Similarly, in the objective functional (24), $Z_1$ and $Z_2$ are positive constants and it measures the associated cost on social distancing and treatment, respectively. It is to be noted that (24) translates a clear objective: to decrease the number of susceptible, exposed and infected persons while keeping in view the costs on controls. Our goal is to find the control function, such that,

$$J(u_1^{\ast },u_2^{\ast })=\mathit{min}\left\{J\right(u_1,u_2),u_1,u_2\in U\}$$ (26)

subject to the system (25), where the control set is defined as,

$$U=\left\{\right(u_1,u_2)/u_i(t)0⩽u_i(t)⩽1,i=1,2\}\text{.}$$ (27)

The conditions that an optimal solution must satisfy is obtained by using Pontryagin’s maximum principal [15]. This principal translates Equations (24), (25) into a problem characterizes with minimizing the following Hamiltonian H, with regard to control variables

$$H=W_{1}S\left(t\right)+W_{2}E\left(t\right)+W_{3}I\left(t\right)+\frac{1}{2}(Z_1{u}_1^2+Z_2{u}_2^2)+{\lambda }_1\frac{\mathit{dS}\left(t\right)}{\mathit{dt}}+{\lambda }_2\frac{\mathit{dE}}{\mathit{dt}}+{\lambda }_3\frac{\mathit{dI}}{\mathit{dt}}+{\lambda }_4\frac{\mathit{dQ}\left(t\right)}{\mathit{dt}}+{\lambda }_5\frac{\mathit{dR}\left(t\right)}{\mathit{dt}}\text{.}$$ (28)

where ${\lambda }_1\left(t\right),{\lambda }_2\left(t\right),{\lambda }_3\left(t\right),{\lambda }_4\left(t\right)$ and ${\lambda }_5\left(t\right)$ made up of the adjoint variables. The system solution is determined by taking the partial derivatives of the Hamiltonian (28) with respect to the associated state variable.

Theorem 5

In view of the optimal controls $(u_1^{\ast },u_2^{\ast })$ be the solution of the above control system (24), (25) , then we can find the adjoint variables ${\lambda }_i\left(t\right)$ , for $i=1,2,3,4,5$ , satisfying

$$\frac{-d{\lambda }_i}{\mathit{dt}}=\frac{\partial H}{\partial i},$$ (29)

where $i=S,E,I,Q,R$ and with transversality conditions

$${\lambda }_i\left(T\right)=0\mathrm{for}i=1,2,3,4,5\text{.}$$ (30)

Further more, the optimal controls variables $u_1^{\ast }\left(t\right)$ , $u_2^{\ast }\left(t\right)$ are defined by

$$\begin{array}{cc}\hfill u_1^{\ast }\left(t\right)=& \mathit{max}\left\{\mathit{min}\left\{\frac{X}{Z_1},1\right\},0\right\},\hfill \\ \hfill u_2^{\ast }\left(t\right)=& \mathit{max}\left\{\mathit{min}\left\{\frac{\left({\lambda }_3\right(t)-{\lambda }_4(t\left)\right)I^{\ast }\left(t\right)}{Z_2},1\right\},0\right\},\hfill \end{array}$$ (31)

where, $X=\left({\lambda }_1\right(t)+{\lambda }_5(t\left)\right)S^{\ast }\left(t\right)+\left({\lambda }_2\right(t)+{\lambda }_5(t\left)\right)E^{\ast }\left(t\right)+\left({\lambda }_5\right(t)-{\lambda }_3(t\left)\right)I^{\ast }\left(t\right)+\left({\lambda }_4\right(t)+{\lambda }_5(t\left)\right)Q^{\ast }\left(t\right)$ .

Proof

We use the condition (29), and differentiated the function H with respect to the control variables, to get the corresponding adjoint system. We therefore have the following adjoint system

$$\begin{array}{cc}\hfill \frac{d{\lambda }_1\left(t\right)}{\mathit{dt}}=-& W_1+{\lambda }_1\left(t\right)\left[\beta I(1+\delta I)+\eta +\mu +d_3+{\mu }_1\left(t\right)\right],\hfill \\ \hfill -& {\lambda }_2\left(t\right)\beta I(1+\delta I)-{\lambda }_4\left(t\right)d_3-{\lambda }_5\left(t\right)\left[\eta +{\mu }_1\left(t\right)\right],\hfill \\ \hfill \frac{d{\lambda }_2\left(t\right)}{\mathit{dt}}=-& W_2+{\lambda }_2\left(t\right)\left[\lambda +\mu +d_2+{\mu }_1\left(t\right)\right]-{\lambda }_3\left(t\right)\lambda -{\lambda }_4\left(t\right)d_3-{\lambda }_5\left(t\right){\mu }_1\left(t\right),\hfill \\ \hfill \frac{d{\lambda }_3\left(t\right)}{\mathit{dt}}=-& W_3+{\lambda }_1\left(t\right)\left[\beta S(1+2\delta I)\right]-{\lambda }_2\left(t\right)\left[\beta S(1+2\delta I)\right]\hfill \\ \hfill +& {\lambda }_3\left(t\right)\left[\mu +\in +\gamma +d_1+{\mu }_1\left(t\right)+{\mu }_2\left(t\right)\right]-{\lambda }_4\left(t\right)\left[d_1+{\mu }_2\left(t\right)\right]-{\lambda }_5\left(t\right)\left[\gamma +{\mu }_1\left(t\right)\right],\hfill \\ \hfill \frac{d{\lambda }_4\left(t\right)}{\mathit{dt}}=+& {\lambda }_4\left(t\right)\left[\mu +\tau +{\mu }_1\left(t\right)\right]-{\lambda }_5\left(t\right)\left[\tau +{\mu }_1\left(t\right)\right],\hfill \\ \hfill \frac{d{\lambda }_5\left(t\right)}{\mathit{dt}}=+& {\lambda }_5\left(t\right)\mu \text{.}\hfill \end{array}$$ (32)

Moreover, we apply the condition $\frac{\partial H}{\partial \mathit{ui}}=0$ to get the optimal controls given in (31), for $i=1,2$.

6. Numerical simulation

This section is devoted to the numerical solutions of the optimal system and the associated results of different optimal controls scenarios $u_1$ and $u_2$. The numerical solutions of the optimal system are determined with the help of MATLAB. The adjoint system, was determined to achieve the optimal control solution of the proposed system. A fourth-order Runge–Kutta iterative scheme is used to achieve the solution of the optimal system. To be more specific, we will code state system (25) using forward RK4 method and backward scheme for the adjoint Eq. (32). The scheme will also include the initial data related to state variables and the transversality conditions (30) for the adjoint system. The desired time interval for simulation is taken $t\in [0,10]$. We set some parameter values for the system $\left(1\right)$ as mentioned in Table 1 . Moreover, the weight constant are assumed to be $W_1=400,W_2=1000,W_3=1000,Z_1=0.001$ and $Z_2=0.34$. Consequently, we get the following findings from Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6 . Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6 represents the graphs of susceptible, exposed, infected, quarantine-treated and recovered-treated populations. We consider the most highly sensitive parameter i.e $\beta$ and change its value from $0.5$ to $0.8$. The red color depicts “without control” graphs while the black color depicts “with control” graphs. The dotted graphs are the results when $\beta =0.5$, while the line graphs are the results when $\beta =0.8$.

Table 1.

Parameters value.

Notation	value	Reference
b	$0.04$${\mathit{day}}^{-1}$	[36]
$\delta$	$0.2$${\mathit{day}}^{-1}$	assumed
$\mu$	$0.1$${\mathit{day}}^{-1}$	[36]
$d_1$	$0.2$${\mathit{day}}^{-1}$	[36]
$d_2$	$0.3$${\mathit{day}}^{-1}$	[36]
$d_3$	$0.4$${\mathit{day}}^{-1}$	[36]
$\lambda$	$0.3$${\mathit{day}}^{-1}$	[36]
$\beta$	$0.5$${\mathit{day}}^{-1}$	assumed
$\gamma$	$0.3$${\mathit{day}}^{-1}$	[36]
$\eta$	$0.6$${\mathit{day}}^{-1}$	[36]
$\tau$	$0.1$${\mathit{day}}^{-1}$	assumed
$∊$	$0.3$${\mathit{day}}^{-1}$	[36]

Fig. 2.

The plot demonstrates the dynamic of susceptible population.

Fig. 3.

The plot demonstrates the dynamic of exposed population.

Fig. 4.

The plot demonstrates the dynamic of infected population.

Fig. 5.

The plot demonstrates the dynamic of quarantine population.

Fig. 6.

The plot demonstrates the dynamic of recovered population.

The simulations clearly illustrate the effect as well as the desired goal of the controls, i.e., to reduce the number of exposed, infected, individuals, and to increase $R\left(t\right)$. There is obviously a significance difference between the controlled and without control cases. This positive influence suggests that over the intervention period, the control technique is useful in controlling the disease.

6.1. Case Study: Khyber Pakhtunkhawa (Pakistan)

As other provinces of Pakistan, the Khyber Pakhtunkhawa province is also effected by covid-19 virus. We choose the Khyber Pakhtunkhawa province as a case study to fit our model to the real data of covid-19 cases from this province from ${26}^{\mathit{th}}$ Feb to ${12}^{\mathit{th}}$ May 2020. We use Matlab minimization technique and consider the following initial value in which $E\left(0\right)$ and $Q\left(0\right)$ are estimated while the remaining values are taken from [35]

$$S\left(0\right)=35,00,E\left(0\right)=1000,I\left(0\right)=2,209,Q\left(0\right)=5000,R\left(0\right)=1,086\text{.}$$

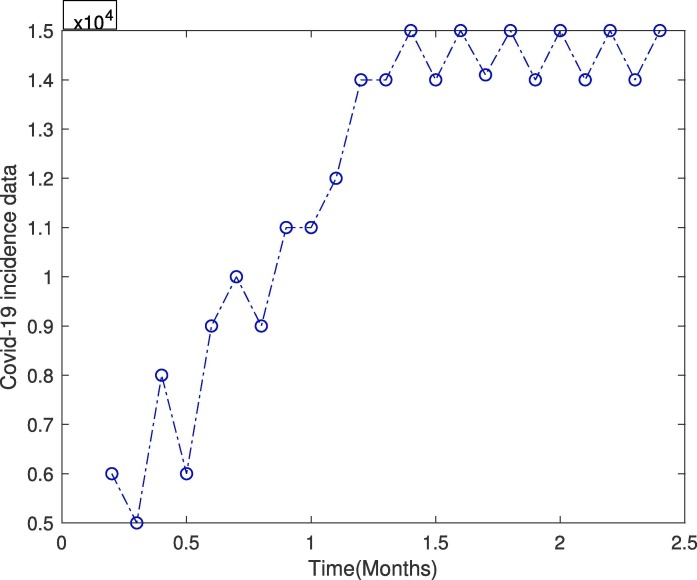
We set some parameter values as mentioned in Table 2 . Fig. 7 depicts the total cases of covid-19 in the Khyber Pakhtunkhawa province from ${26}^{\mathit{th}}$ Feb to ${12}^{\mathit{th}}$ May 2020, which is a period of two and a half months. In Fig. 8 we fit real data with the infected class of our covid-19 model which clearly shows the appropriateness of behavior of the infected class. Fig. 9 shows the long time behavior of the covid-19 cases vs time (months). We can see that the data fits accurately to the model curve, and further, one can observe that the number of cases grows exponentially with time. This case could be alarming that the incidence may increases further in the coming months if the government does not apply the proper optimal control strategies.

Table 2.

Parameters value.

Notation	Value	References
b	0.028	[35]
$\alpha$	0.2	Estimated
$\mu$	0.011	[35]
$d_1$	0.2	Estimated
$d_2$	$0.08$	Estimated
$d_3$	0.06	[35]
$\lambda$	0.3	Estimated
$\beta$	0.5	Estimated
$\gamma$	0.3	[35]
$\eta$	0.6	Estimated
$\tau$	0.1	[35]
$∊$	0.3	[35]

Fig. 7.

The incidence data of covid-19 from Khyber Pakhtunkhwa, Pakistan.

Fig. 8.

Covid-19 model comparison with real data of Khyber Pakhtunkhawa, Pakistan.

Fig. 9.

The incidence data of covid-19 from Khyber Pakhtunkhwa, Pakistan.

7. Bifurcation analysis

Bifurcation analysis plays a pivotal role in controlling and decimating epidemic diseases. In modeling epidemic diseases, to eradicate the disease, a classical condition is imposed on basic reproduction number i.e. $R_0$ must be less than unity [30], [31]. But on the other hand, if a bifurcation takes place, the existence of an endemic equilibria for $R_0>1$ would imply that the disease will persist over time. This goes to show the importance of bifurcation analysis in epidemiology and preventive medicines.To this end, we follow [32], [33] to study the bifurcation phenomenon in our model.

Theorem 6

Let $g:R^n\times R\to R^n$ , where $g\in {\mathcal{C}}^2\left(R^n\times R\right)$ and assume a general system of ODE’s with a parameter $\psi$

$$\frac{\mathit{dx}}{\mathit{dt}}=g(x,\psi )\text{.}$$ (33)

Without loss of generality, we assume that $x=0$ is an equilibrium for system (1).

• i.If $A=D_{x}f(0,0)$ represents the linearized matrix of system (1) around the equilibrium point $x=0$ with $\psi$ evaluated at 0. Zero is a simple eigenvalue and all other eigenvalues having negative real parts.
• ii.Matrix A has a non-negative right eigenvector w and a left eigenvector v corresponding to zero eigenvalues.

Let $g_k$ denotes the $k^{\mathit{th}}$ component of g, and

$$a={\displaystyle \sum _{k,i,j=1}^5}{v}_k{w}_i{w}_j\frac{{\partial }^2{g}_k}{\partial x_i\partial x_j}(0,0),$$

$$b={\displaystyle \sum _{k,i,=1}^5}{v}_k{w}_i\frac{{\partial }^2{g}_k}{\partial x_i\partial \psi }(0,0)\text{.}$$

Then, the local dynamics of system (1) around $x=0$ are determined by the coefficients a and b.

• $\left(i\right)$ $a>0,b>0$. When $\psi <0$ with $\left|\psi \right|\ll 1$, $x=0$ is locally asymptotically stable and there exists a positive unstable equilibrium, when $\mathrm{if}0<\psi \ll 1,x=0$ is unstable and there exist a negative and locally asymptotically equilibrium;
• $\left(\mathit{ii}\right)$ $a<0,b<0$. When $\psi <0$ with $\left|\psi \right|\ll 1,x=0$ is unstable; when $0<\psi <0,x=0$ is locally asymptotically stable and there exist unstable positive equilibrium;
• $\left(\mathit{iii}\right)$ $a>0,b<0$. When $\psi <0$ with $\left|\psi \right|\ll 1,x=0$ is unstable and there exist a locally asymptotically stable negative equilibrium, while in case of $0<\left|\psi \right|\ll 1,x=0$ is stable and there exist a positive unstable equilibrium;
• $\left(\mathit{iv}\right)$ $a<0,b>0$. When $\psi$ varies from negative to positive, $x=0$ changes its stability from stable to unstable. Correspondingly, a negative unstable equilibrium becomes positive and locally asymptotically stable.

The above Theorem prescribes the role of the coefficients a and b of the normal form representing the system dynamics on the central manifold, in deciding the direction of the transcritical bifurcation occurring at $\psi =0$.

More precisely, if $a<0$ and $b>0$, then the bifurcation is forward; if $a>0$ and $b>0$ then the bifurcation is backward.

Taking into account the above theorem we show that our proposed model (1) exhibits bifurcation by using central manifold theory [34]. We put $R_0=1$ to find $b^{\ast }$ as

$$b^{\ast }=\frac{(\eta +\mu +d_3)(\lambda +\mu +d_2)(\mu +∊+\gamma +d_1)}{\lambda \beta }\text{.}$$ (34)

We get the Jacobian at disease free equilibrium as

$$J^0\left(b^{\ast }\right)=\left(\begin{array}{ccccc}\hfill -(\eta +\mu +d_3)\hfill & \hfill 0\hfill & \hfill -\frac{\beta b^{\ast }}{\eta +\mu +d_3}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -(\lambda +\mu +d_2)\hfill & \hfill \frac{\gamma b^{\ast }}{\eta +\mu +d_3}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \lambda \hfill & \hfill -(\mu +∊+\gamma +d_1)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill d_3\hfill & \hfill d_2\hfill & \hfill d_1\hfill & \hfill -(\mu +\tau )\hfill & \hfill 0\hfill \\ \hfill \eta \hfill & \hfill 0\hfill & \hfill \gamma \hfill & \hfill \tau \hfill & \hfill -\mu \hfill \end{array}\right)\text{.}$$ (35)

The corresponding eigenvalues of $J^0\left(b^{\ast }\right)$ are ${\omega }_1=-(\eta +\mu +d_3),{\omega }_2=-(\mu +\tau ),{\omega }_3=-\mu ,{\omega }_4=0$ and ${\omega }_5=-(2\mu +\lambda +∊+\gamma +d_1+d_2)$.

Since one of the eigenvalue is zero, hence it confirms the presence of bifurcation. Following [34], we find the left eigenvectors of $J^0\left(b_1^{\ast }\right)$ as

$$\begin{array}{ccc}\hfill w_1& \hfill =\hfill & -\left(\frac{\beta (\lambda +\mu +d_2)}{(\eta +\mu +d_3)\gamma }\right)w_2,\hfill \\ \hfill w_3& \hfill =\hfill & \left(\frac{(\lambda +\mu +d_2)(\eta +\mu +d_3)}{\gamma b}\right)w_2,\hfill \\ \hfill w_4& \hfill =\hfill & (-(\frac{\beta (\lambda +\mu +d_2)}{(\eta +\mu +d_3)\gamma })d_3+d_2+d_1(\frac{(\lambda +\mu +d_2)(\eta +\mu +d_3)}{\gamma b}\left)\right)w_2,\hfill \\ \hfill w_5& \hfill =\hfill & \eta w_1+\gamma w_3+\tau w_4\text{.}\hfill \end{array}$$ (36)

Also, we find the right eigenvectors as

$$\begin{array}{ccc}\hfill v_1& \hfill =\hfill & 0,\hfill \\ \hfill v_2& \hfill =\hfill & \frac{\lambda }{(\lambda +\mu +d_2)}{v}_3,\hfill \\ \hfill v_4& \hfill =\hfill & 0,\hfill \\ \hfill v_5& \hfill =\hfill & 0\text{.}\hfill \end{array}$$ (37)

Setting $S=x_1,E=x_2,I=x_3,Q=x_4$, and $R=x_5$, in (1), we get

$$\begin{array}{ccc}\hfill f_1\left(x\right)& \hfill =\hfill & b-\beta x_1{x}_3(1-\delta x_3)-(\eta +\mu +d_3)x_1,\hfill \\ \hfill f_2\left(x\right)& \hfill =\hfill & \beta x_1{x}_3(1-\delta x_3)-(\lambda +\mu +d_2)x_2,\hfill \\ \hfill f_3\left(x\right)& \hfill =\hfill & \lambda x_2-(\mu +∊+\gamma +d_1)x_3,\hfill \\ \hfill f_4\left(x\right)& \hfill =\hfill & d_3{x}_1+d_2{x}_2+d_1{x}_3-(\mu +\tau )x_4,\hfill \\ \hfill f_5\left(x\right)& \hfill =\hfill & \eta x_1+\tau x_4+\gamma x_3-\mu x_5\text{.}\hfill \end{array}$$ (38)

Taking into account the left and right eigenvectors we calculate the coefficients a and b as

$$a={\displaystyle \sum _{k,i,j=1}^5}{v}_k{w}_i{w}_j\frac{{\partial }^2{f}_k}{\partial x_i\partial x_j},$$

implies

$$a=-v_3{w}_2\lambda \frac{{(\eta +\mu +d_3)}^2{(\lambda +\mu +d_2)}^3{(\mu +∊+\gamma +d_1)}^2}{{\gamma }^{2}b}\text{.}$$

Also

$$b={\displaystyle \sum _{k,i,=1}^5}{v}_k{w}_i\frac{{\partial }^2{f}_k}{\partial x_i\partial b_1},$$

implies

$$b=\frac{\lambda (\eta +\mu +d_3)v_3{w}_2}{\gamma }\text{.}$$

As $a<0$ and $b>0$, hence it confirms that our proposed model exhibits forward bifurcation (1). The forward bifurcation is highlighted in Fig. 10 .

Fig. 10.

“The solid line (–) denotes stability; the dashed line (- -) denotes instability”.

8. Sensitivity analysis

Determining the parameters which are helpful in decreasing the spread of infectious disease is carried out by sensitivity analysis. Forward sensitivity analysis is considered as vital component of disease modeling although its computation become tedious for complex biological model. Sensitivity analysis of $R_0$ have received much attention from the ecologist and epidemiologist.

Definition 1

The basic reproduction number $R_0$ is the normalized forward sensitivity index that depends differentiability on a parameter $\omega$ is defined as

$$S_{\omega }=\frac{\omega }{R_0}\frac{\partial R_0}{\partial \omega }$$ (39)

Three methods are normally used to calculate the sensitivity indices, (i) by direct differentiation, (ii) by a Latin hypercube sampling method (iii) by linearizing system (1) and then solving the obtain set of linear algebraic equations. We will apply the direct differentiation method as it gives analytical expressions for the indices. The indices not only shows us the influence of various aspects associated with the spreading of infectious disease but also gives us important information regarding the comparative change between $R_0$ and different parameter. Consequently, it helps in developing the control strategies.

Table 3 shows that the parameters $\beta ,b$, and $\lambda$ have a positive influence on the reproduction number $R_0$, which describe that the growth or decay of these parameters say by 10 percent will increase or decrease the reproduction number by 10 percent, 1.0 percent and 9.0 percent, respectively. But on the other hand, the index for parameters $\gamma ,d_1,d_2,\mu ,d_3,\eta$ and $∊$ illustrates that increasing their values by 10 percent will decrease the values of reproduction number $R_0$ by 1.4 percent, 7.1 percent, 8.5 percent, 2.9 percent, 8.1 percent, 0.1 percent and 0.5 percent, respectively.

Table 3.

Sensitivity indices of the reproduction number $R_0$ against mentioned parameters.

Parameters	S.Index	Value	Parameters	S.Index	Value
$\beta$	$S_{\beta }$	1.00000000	$d_2$	$S_{d_2}$	−0.8593749998
b	$S_b$	1.00000000	$\mu$	$S_{\mu }$	−0.2965237119
$\gamma$	$S_{\gamma }$	−0.1428571429	$d_3$	$S_{d_3}$	−0.8196721309
$d_1$	$S_{d_1}$	−0.7142857142	$\eta$	$S_{\eta }$	−0.01639344262
$\lambda$	$S_{\lambda }$	0.9062499999	$∊$	$S_{∊}$	−0.05714285714

Fig. 11 shows sensitivity of $R_0$ against $\eta$ and $∊$. From Table 3, it is clear that both have negative impact on $R_0$, which is depicted in Fig. 11 as it varies very slowly from $0.005$ to its maximum value $0.02$. It shows that the death rate of infectious individuals and those individuals whose immune system is strong enough to prevent them from covid-19 infection has no impact in variation of basic reproduction number.

Fig. 11.

The plot demonstrates the variation of $R_0$ against $\eta$ and $∊$.

Fig. 12 shows sensitivity of $R_0$ against $\eta$ and $\beta$. From Table 3, it is clear that $\eta$ has negative while $\beta$ has positive impact on $R_0$, which is depicted in Fig. 12 as no variation is seen when $\eta$ is increasing while very fast increasing in $R_0$ is felt when $\beta$ is increasing. It shows that the death rate of infectious individuals have no impact on $R_0$ while the transmission rate of covid-19 infection from susceptible people to infected have a very high impact on basic reproduction number.

Fig. 12.

The plot demonstrates the variation of $R_0$ against $\beta$ and $\eta$.

Fig. 13 shows sensitivity of $R_0$ against $\lambda$ and $\beta$. From Table 3, it is clear that $\lambda$ and $\beta$ both have positive impact on $R_0$, which is depicted in Fig. 13 as very big variation of $R_0$ is seen when $\lambda$ and $\beta$ is increasing. It shows that the transmission rate of covid-19 infection from susceptible and exposed people to infected people have a very high impact on basic reproduction number.

Fig. 13.

The plot demonstrates the variation of $R_0$ against $\beta$ and $\lambda$.

Fig. 14 shows sensitivity of $R_0$ against $\gamma$ and $\lambda$. From Table 3, it is clear that $\gamma$ has negative while $\lambda$ has positive impact on $R_0$, which is depicted in Fig. 14 as no variation is seen when $\gamma$ is increasing while very fast increasing in $R_0$ is felt when $\lambda$ is increasing. It shows that the transmission rate of covid-19 infection from infected people to recovered people have no impact on $R_0$ while the transmission rate of covid-19 infection from exposed people to infected have a very high impact on basic reproduction number.

Fig. 14.

The plot demonstrates the variation of $R_0$ against $\gamma$ and $\lambda$.

9. Conclusion

In this article, we performed the stability and bifurcation analysis of covid-19 SEIQR epidemic model with convex incidence rate. First, we investigated the basic reproductive number $R_0$ for the system (1) which completely characterized the stability of the DFE and EE. We obtained sufficient conditions for LAS and GAS. The approach we used for the global stability of DFE was the Lyapunov function theory, whereas, the global stability of EE was carried out using the geometrical approach. Furthermore, we have developed an optimal control strategy with two control variables to minimize the infection in the host population. The controls under consideration are: social distancing and treatment. The sensitivity analysis complemented by simulations are also performed to assess how changes in the parameters affect the dynamical behavior of system (1). It is concluded that with the implementation of such controls strategy for the long run, it is possible to eradicate epidemic diseases from community.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.