Innovative trial designs and analyses for vaccine clinical development

Abstract

In the past decades, the world has experienced several major virus outbreaks, e.g. West African Ebola outbreak, Zika virus in South America and most recently global coronavirus (COVID-19) pandemic. Many vaccines have been developed to prevent a variety of infectious diseases successfully. However, several infections have not been preventable so far, like COVID-19, which induces an immediate urgent need for effective vaccines. These emerging infectious diseases often pose unprecedent challenges for the global heath community as well as the conventional vaccine development paradigm. With a long and costly traditional vaccine development process, there are extensive needs in innovative vaccine trial designs and analyses, which aim to design more efficient vaccines trials. Featured with reduced development timeline, less resource consuming or improved estimate for the endpoints of interests, these more efficient trials bring effective medicine to target population in a faster and less costly way. In this paper, we will review a few vaccine trials equipped with adaptive design features, Bayesian designs that accommodate historical data borrowing, the master protocol strategy emerging during COVID-19 vaccine development, Real-World-Data (RWD) embedded trials and the correlate of protection framework and relevant research works. We will also discuss some statistical methodologies that improve the vaccine efficacy, safety and immunogenicity analyses. Innovative clinical trial designs and analyses, together with advanced research technologies and deeper understanding of the human immune system, are paving the way for the efficient development of new vaccines in the future.

1. Introduction

The vaccine is considered one of the most important achievements of public health during the past century. There are many vaccines that have been made available on market and have fundamentally changed the infectious disease prevention mindset of human beings. However, in the past decades, the world has experienced several new major virus outbreaks, e.g. West African Ebola outbreak, Zika virus in South America and most recently global coronavirus (COVID-19) pandemic. With the recent COVID-19 pandemic, efficient vaccine development is at the frontline and innovative clinical trial designs and analyses are needed more than ever for all vaccine development.

The traditional vaccine development process from discovery to approval is long and costly, which usually requires enrolling huge numbers of subjects in a fixed design. In recent years, increasing needs in innovative vaccine trial designs and analyses have researchers designing more efficient vaccines trials. Featured with reduced development timeline, fewer resources and improved estimates of the endpoints of interests, these more efficient trials bring effective medicine to subjects in a faster and less costly way. For example, adaptive designs [1], which allow trial design modification during the trial based on ongoing available trial data, have become more frequent in recent years and have shown their advantages in accelerating the development timeline, identifying optimal vaccine dose, schedule, and target population, as well as reducing sample size as demonstrated in a few vaccine trial applications. Bayesian designs, with flexibility and ability to incorporate the prior belief about the efficacy of treatment, provide an alternative for vaccine clinical trials where there are challenges due to extremely low incidence rates. Other types of innovative designs, e.g. master protocols, have emerged during the recent global outbreak of endemic COVID-19 in which vaccine development has the advantage of concurrent assessment of multiple candidates. Faced with clinical site shut downs and clinical trials paused due to COVID-19, the rapid increase in the volume, variety, and accessibility of digitized Real-World-Data (RWD) has presented unprecedented opportunities for the use of RWD for the data collection, trial designs and analyses. Another important topic that has gained intensive attention in vaccine development is correlate of protection (CoP). If established successfully, the immune marker could be used as surrogate endpoint to predict vaccine efficacy, which is less costly, and may reduce the vaccine development time. Besides innovative designs and CoP related researches, there are constant efforts to improve vaccine efficacy, safety and immunogenicity analyses. It is essential to summarize these statistical considerations, discuss the assumptions and case study implementations, and promote the usage of those methodologies in a proper setting.

In this paper, Section 2 opens with a general discussion about vaccine design, with the focus on several vaccine innovative design implementations. The design implementations include but are not limited to: treatment arm selection, population enrichment, and sample size re-estimation, followed by Bayesian designs accommodating historical data borrowing, the discussion of master protocols and utilizing RWD in clinical development. In Section 3, we will review a group of methodologies for CoP from the Prentice criteria approach to Qin's framework and other novel CoP trial designs and analyses. In section 4, we will briefly review additional considerations supporting vaccine efficacy, safety, and immunogenicity analyses. In Section 5, we will summarize our discussions and concluding remarks.

2. Innovative designs for vaccine trial

Although each vaccine may follow a different development path that depends on the type of vaccine, disease characteristics, target population, target regions, availability of existing vaccines, administration schedule, etc., all new vaccines need to demonstrate safety, immunogenicity and protective efficacy in subjects before obtaining regulatory licensure. In general, there are two major categories of vaccine trials: immunogenicity trials and vaccine field trials, with safety assessed in all vaccine trials.

Vaccine Immunogenicity Trials: Vaccines function in the human body by exposing the immune system to live or inactivated (or partially inactivated) microorganisms, which are subsequently recognized by the immune system when a natural viral or bacterial infection occurs. Therefore, endpoints based on immune response, e.g. serum antibody levels, immune response rates, etc. are of great interest and used for vaccine dose finding and optimal schedule selection during early phases. The immunogenicity outcomes remain primary endpoints for vaccine bridging trials, combination trials, concomitant trials, and lot-to-lot consistency trials, and play a critical role throughout the vaccine development [2].

Vaccine Field Trials: Vaccine field trials include vaccine efficacy trials and vaccine effectiveness trials. Vaccine efficacy measures the protective effects of vaccination by the reduced risk of vaccinated subjects relative to unvaccinated subjects in clinical Phase II or Phase III, while vaccine effectiveness is usually assessed at population-level post-marketing retrospectively via observational studies.

Prior to obtaining licensure, the focus of a clinical development program is placed on vaccine efficacy. For candidate vaccines, the most common model used to evaluate vaccine efficacy is double blinded randomized trial with active and placebo arms. Under special circumstances, the use of placebo arm may be constrained due to ethical or other reasons, e.g., West African Ebola vaccine [3]. One alternative is to use delayed vaccination as a comparator, which usually has lower power than placebo-controlled ones, and the staggered schedule may also introduce bias to vaccine efficacy estimate [4].

2.1. Adaptive design in vaccine trials

Traditional vaccine efficacy trials usually use fixed designs with fairly large sample size. Recruiting a large number of subjects requires longer follow up time and costs. Therefore, vaccine developers are facing more than ever needs in accelerating the vaccine development to fulfill the public's medical needs. Adaptive design is defined as a clinical trial design that allows for prospectively planned modification to one or more aspects of the design based on accumulating data from subjects in the trial. Adaptive designs attempt to more efficiently select the right treatment arm, population and reduce sample size [1,5,6]. In this section, we will discuss how adaptive designs help to achieve these goals and eventually contribute to bringing promising vaccines to target population earlier.

2.1.1. Treatment arm selection adaptive seamless design

The four-valent human papillomavirus (4vHPV) vaccine was licensed in 2006 for the prevention of HPV 6/11/16/18 related cancer diseases [7]. These four HPV sub-types cause roughly 70% of cervical cancers. Aiming to cover additional five HPV sub-types (31/33/45/52/58), clinical trials were designed to explore the 9vHPV vaccine efficacy [8]. Since the sponsor had extensive knowledge and experience from the 4vHPV vaccine development and both 4vHPV and 9vHPV vaccines used the same mechanisms and other critical development aspects, they believed it was possible to expediate the 9vHPV vaccine development.

A seamless phase II/III design was proposed to accelerate this vaccine development [9]. Unlike traditional clinical trials that have a separate phase II learning stage and a phase III confirmatory stage, a seamless phase II/III design combines these two stages into one seamless clinical trial. This design has several attractive features, including (i) reduction of resources and time by avoiding the gap between phase II and phase III trials, and (ii) incorporation of related phase II data in the final analyses.

In this trial, roughly 1250 subjects were equally randomized into four arms (low dose, medium dose, high dose and 4vHPV) in the phase II stage. The primary endpoint was the post-dose 2 immunogenicity of the original 4vHPV types. Based on the immunogenicity and safety data, the medium dose was selected for the phase III confirmatory doses. In addition, subjects who were in the medium dose arm and 4vHPV arm were followed up continually into phase III stage. In the phase III stage, approximately 13,400 subjects were randomized (1:1) to either the selected medium dose 9vHPV arm or 4vHPV arm. The primary objective of the phase III stage was vaccine efficacy. Approximately 14,200 subjects in both stages contributed to the final vaccine efficacy events. Even though only 620 subjects from phase II stage were included in the final analysis, they contributed roughly 10% of the person-years of follow-up due to the longer observation period.

Despite the attractive features of the seamless phase II/III trials, these designs still have to overcome several statistical and operational challenges. First, the Type I error must be well-controlled. The sponsor carefully chose the phase II endpoint, selected final analysis tests and confidence interval, and demonstrated the small correlation between biomarker endpoint in phase II and efficacy endpoint in phase III. These steps ensured the Type I error was under controlled in this seamless design. Moreover, a large simulation study that was conducted by the sponsor suggested the overall Type I error was well controlled. Secondly, the sponsor also took actions to ensure this seamless phase II/III was operationally efficient. The sponsor's senior management committee (SMC), the external Data Monitoring Committee (eDMC) and other critical functions were set up for the end of phase 2 stage adaptation decision making and built the data blinding firewall. The scope of communication between SMC, eDMC and the study team were also well-planned to protect the integrity of the study. Finally, the sponsor also paid extra attention to vaccine supply, study enrollment, and other logistics aspects for the adaptive designs.

2.1.2. Population selection adaptive design

Adaptive designs which allow population selection or enrichment can be critical in vaccine development. The fundamental principle of adaptations is to select the promising population at an interim analysis to maximize the probability of clinical trial success. Su et al. (2018) proposed a population-enrichment adaptive design strategy for an event-driven vaccine efficacy trial [10]. In their motivating example, the vaccine was targeted for two subpopulations (A and B), which belong to the same general clinical disease family. However, the heterogeneity problem in the response was a concern from the earlier phase I and phase II studies. Two separate phase III clinical trials could be initiated to investigate a vaccine in two different subpopulations, but generally more resources are required. Alternately, one single trial that combines both populations is also feasible. However, the lower vaccine efficacy in one subpopulation may lower the probability of success for the whole trial. Therefore, to balance the probability of success and total sample size in this scenario, an adaptive design which allows population selection in the interim analysis was proposed.

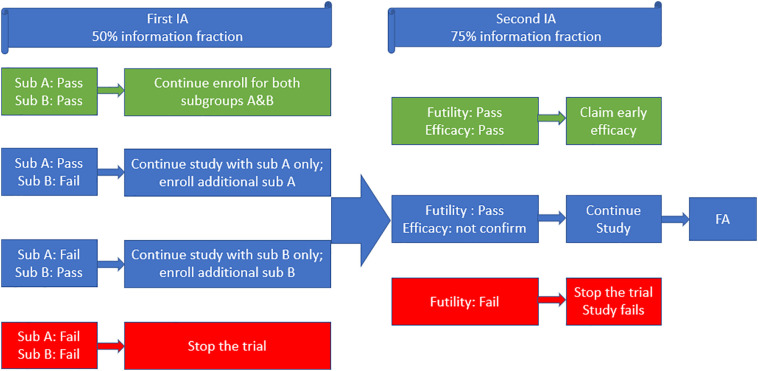
The total sample size in the phase III was around 6000 with equal allocation to both subpopulation A and subpopulation B. For each subpopulation, subjects were equally randomized into active treatment vaccine arm and placebo arm. The lower bound of 95% CI for vaccine efficacy (VE) at the end of the study was defined to be 25%. The conditional exact binomial method proposed by Chan and Zhang was used for the primary analysis [11]. In their proposed adaptive design, three hypotheses (AB combined, subpopulation A and subpopulation B) were planned. Two interim analyses also were scheduled. The first interim analysis (IA) allowed a futility check and a population selection. If the VE passed the futility check in only one subpopulation but failed in other subpopulation, the study would continue with only the selected subpopulation, and enrollment in the selected subpopulation would be increased with an additional 2500 subjects. The second IA allowed another futility check and an early efficacy claim. The process is summarized in Fig. 1 below.

Fig. 1.

Flow chart of population selection design.

Multiplicity adjustment was also evaluated in this design because several efficacy analyses were planned for two subpopulations with an interim analysis across the entire clinical trial. For the most desired case, the vaccine works for both subpopulation A and subpopulation B. It is preferred to test the primary hypothesis (AB) at 1-sided α _(AB) = 2.5% level. Thus, the corresponding test level for the primary hypotheses (A) and (B) would need to be decreased to less than 2.5%. Based on the interim analysis decision rule in Fig. 1, the testing procedure can be summarized as below:

• •If both A and B pass the futility check, the statistical criterion for success requires the lower bound of the 95% confidence interval (CI) (1-sided α _AB = 2.5%) for the estimated vaccine efficacy based on both subpopulations combined to be greater than 25%;
• •If only A passes the futility check, the statistical criterion for success requires that the lower bound of the (1–2 × α _(A))% CI for the estimated vaccine efficacy in subpopulation A to be greater than 25%.
• •If only B passes the futility check, the statistical criterion for success requires that the lower bound of the (1–2 × α _{( B )})% CI for the estimated vaccine efficacy in subpopulation B to be greater than 25%.
• •If vaccine efficacy fails the futility check in both subpopulations, the trial will stop for futility.

They have shown that with α _(A) and α _(B) set to be 0.0115, the overall Type I error was shown to be controlled weakly through theoretical deviation and simulation studies. The simulation results also suggested that the type one error rate was also well maintained in a strong sense. Based on the statistical power in the simulation analyses, the population selection design could still maintain a high power when the treatment effect existed for only one subpopulation. This adaptive design helped to maintain a high probability of success by selecting the promising treatment population at the interim analysis.

2.1.3. Sample size re-estimation adaptive design

Sample size re-estimation (SSR), which allows for the sample size or event size to change after an interim analysis, is also applicable to the vaccine development. The essential idea of SSR is to use interim analysis data (unblinded or blinded) to modify the final sample size. This adaptation feature aims to address the uncertainty in trial design assumptions and allow adaptation as information cumulates. Specifically, for vaccine clinical trials, the assumptions of vaccine efficacy (VE) and incidences rates usually have some uncertainties. Therefore, it would be beneficial to allow sample size adaptations when the information on vaccine efficacy (VE) and incidences rates is cumulated during the clinical trial.

The unblinded SSR allows for sample size or event size adjustment based on the observed treatment effect at the interim analysis. The initial sample size of SSR design can be smaller based on a more optimistic VE assumption. If this optimistic assumption is true, the trial can save sample size and bring the effective vaccine to target population faster. However, if the VE interim result is not as good as the optimistic VE assumption, the sample size can be increased based on the observed treatment effect. Other factors such as chemistry, manufacturing and control (CMC) material or procedure change, or assay scale-up between an earlier phase and a later phase may also change the VE assumptions. With an unblinded SSR feature, one can still use the original VE assumption from earlier phase studies for the originally sample size planning. It allows sample size to be re-estimated during the interim analysis. Despite the attractive features of unblinded SSR, a potential problem of SSR design based on unblinded interim analysis is Type I error inflation. As shown by Proschan and Hunsberger [12], the Type I error can be inflated by two times or more without statistical adjustments. Therefore, several approaches have been proposed to control the overall Type I error including the combination test statistic [13,14], modification the adaptation rule [15,16], and conditional error function [17].

On the other hand, blinded SSR allows sample size adjustment based on the blinded data at an IA. The treatment assignment and treatment effect will still be blinded at the IA. This feature is critical for vaccine clinical trial design when the incidence rate is not quite certain. Li et al. (2012) proposed an adaptive design for a case-driven vaccine study when the incidence rate is unknown [18]. In their proposed design, a modest number of subjects were enrolled in stage I. The incidence rate based on blinded data was estimated and this estimated incidence rate helped to assess the feasibility of the study. If the event feasibility of the study could not be confirmed due to the low case accrual rate, this study can be stopped early. If the feasibility of the study is established, an unblinded interim analysis can be performed at the end of stage I. Based on the IA results, the decision rules for the stage II were as follows: (i) stop the study for either futility or early efficacy; (ii) continue into Stage II without sample size changes; 3) increase the number of events/sample size in Stage II. The event size re-estimation was based on the rejection probability principle (CRP) by Muller and Schafer (2001) [19]. In addition, the sample size re-estimation was based on the pooled incidence rate estimated from the interim analyses. This combined approach ensured not only the high statistical power by re-estimating the event sizes but also a reasonable study duration by increasing the sample size based on the observed incidence rate. Since the incidence rate is low for this type of disease. Li et al. (2012) [18] also provided the adaptation decision table based on observed events for better illustration in different scenarios.

2.2. Bayesian design for vaccines development

To establish the therapeutic effect of novel vaccines, randomized clinical trials are often conducted to evaluate the reduction of the infection or disease incidence rate as compared to placebo or standard of care (SoC). Due to the natural low incidence rate for most of endpoints in vaccine efficacy clinical trials, exact conditional binomial testing is often used for sample size calculation with a large number of subjects needed. It is not uncommon for enrollment to be challenging given the extremely low incidence in certain infectious diseases. Bayesian historical borrowing provides a natural framework to reduce the sample size and increase the efficiency of clinical trials. Contrary to the frequentist approach, Bayesian approaches allow flexibility and incorporation of the prior belief on the efficacy of treatment. However, thoughtful specification of the prior distribution is important for the Bayesian analysis, as the scientific conclusion should be primarily based on the data from the trial itself. As discussed in the 2019 FDA complex innovative design (CID) draft guidance [20], the sponsor should include a borrowing strategy “for evaluating and addressing heterogeneity between the prior data and the concurrent Phase 3 data, such as the use of hierarchical models or other approaches that automatically down weight borrowing in the presence of heterogeneity”.

In general, Bayesian historical borrowing can be categorized into two areas. The first category is to incorporate information from control arms of similar historical trials to augment data. This approach is becoming common in the rare disease or oncology setting. To avoid bias and inflated type I error, the appropriate use of historical control borrowing must take the heterogeneity between the historical and current control data into account (Pocock 1976) [21]. The power prior proposed by Ibrahim and Chen (2000) [22] and modified power prior (Duan et al. 2006 [23], Neuenschwander et al. 2009 [24]) are likelihood-based methods that discount the historical data to account for differences between the pool of historical data and the current control data. However, both power prior and modified power priors could result in inflated type I error rate when historical control data is heterogeneous. These models require pooling in the historical control data and cannot capture the variation between historical trials. Neuenschwander et al. (2010) [25] proposed the meta-analytic-predictive (MAP) prior to accounts for heterogeneity by assuming exchangeability among the historical and current control parameters. This approach explicitly models the between-trial variation with standard normal random effect meta-analysis. Of note, in scenarios where the historical and current data are in conflict, MAP prior could potentially lead to an incorrect conclusion due to an insufficient discount on the historical data. Schmidli et al. (2014) [26] extended the work on MAP and presented a robust version of the MAP (R-MAP) prior to allow for further discounting historical data in the case of extreme conflict between the historic and current control data. R-MAP is a mixture prior where one component is MAP prior, and the other component is a vague prior with appropriate weight that needs to be prespecified in the beginning of the trial.

The second category of historical borrowing is to use the treatment information from a historical trial, which is commonly encountered in pediatric trials, e.g. extrapolation from the adult efficacy data to pediatric subjects. The power prior and modified power priors discussed previously could also be applied in this framework. Schoenfeld et al. (2009) [27] proposed a Bayesian approach for a continuous endpoint to borrow information from previous adult trials in a pediatric efficacy study. Gamalo-Siebers et al. (2017) [28] also summarize the Bayesian methods which leverage available adult data for design and analysis of pediatric studies. Specifically, for vaccine efficacy clinical trials, Jin et al. (2020) [29] considered borrowing information for treatment effects and propose a Bayesian framework under the exact conditional binomial test for vaccine trial sample size determination. Schoenfeld's Bayesian hierarchical model was extended to borrow historical information for vaccine efficacy trials as well as a power beta prior distribution that was proposed with similar results in rejection region and power.

Although there are still very limited publications of Bayesian design for vaccine development and regulatory setting, the conceptual flexibility and historical information borrowing incorporated in the Bayesian design do provide an alternative option for contemporary vaccine clinical trials. In addition, the Bayesian approaches require specification of prior distribution for the possible value, therefore it can allow to incorporate the uncertainty for the unknown vaccine effect. More extensive simulations are often required to evaluate the Bayesian design operating characteristics. As suggested in the FDA guidance on adaptive design and draft guidance on CID design [20,30], early engagement and detailed evaluation of operating characteristics in propose designs and the choice of prior, e.g. type I error and power, will be the key elements to get successful agreement with regulatory agencies.

2.3. Master protocols for vaccines development

Master protocols are becoming popular in recent years due to their ability to allow evaluation of multiple treatments, target populations or both within a single protocol in a more efficient and ethical way (Saville and Berry 2016 [31], Woodcock and LaVange 2017 [32], Lin et al. 2019 [33]). Food and Drug Administration (FDA) also provided a draft guidance on master protocols (September 2018) [34] reflecting an increased interest in these designs by drug developers and major regulatory agencies. In the past few years, there have been many thought-provoking master protocol studies conducted, which include but are not limited to: I-SPY2, BATTLE, NCI MATCH, LUNG-MAP, ALCHEMIST and FOCUS4 (Renfro et al. 2016) [35]. In the recent significant global effort between government, academia and industry to develop therapies and vaccines against COVID-19, master protocols are quickly emerging as a critical tool for evaluating potential promising COVID-19 therapies. Master protocols allow efficient use of a standard shared control arm, generation of rapid efficacy/safety results and assignment of more subjects to more efficacious therapies with multiple comparison during pandemic period. Some of the earlier trial examples include RECOVERY (Randomized Evaluation of COVID-19 Therapy), SOLIDARITY, REMAP-CAP (Randomized, Embedded, Multifactorial Adaptive Platform Trial for Community-Acquired Pneumonia), ASCOT, Adaptive COVID-19 Treatment Trial (ACTT) [[36], [37], [38], [39], [40], [41]].

For the vaccine development, the benefit of utilizing master protocol trial designs are the same as for the therapies. For example, the SOLIDARITY vaccine trial outlined by World Health Organization (WHO) [37,38] will test several preventive candidate SARS-CoV-2 vaccines under development to enable the concurrent evaluation of the benefits and risks of each candidate. The primary outcome of trial is the virologically confirmed COVID-19 disease, regardless of severity. Disease rates for each candidate vaccine will be compared with all concurrently randomized placebo/control arms. Within the adaptive trial design setting, the candidate vaccines might be added or dropped depending on the outcomes compared to placebo or other vaccines. If the early interim analysis suggests that a compound is doing well, then more subjects can be randomized to that treatment arm. This feature will allow the better performing vaccines to graduate from a trial faster with more data generated. This can potentially speed up the timeline by at least few months especially important when there are significant unmet medical needs in this highly infectious and deadly global COVID-19 pandemic.

From design perspective, master protocols can be categorized into the following types: Basket trials, umbrella trials or platform trials. Basket trials usually evaluate a single treatment across different populations. This is particularly common in oncology drug development with the advanced knowledge of the molecular profile of disease. A basket trial will enroll subjects with specific genetic or molecular mutations in a single trial to evaluate the effect of corresponding targeted agents. Umbrella or platform trials, on the other hand, focus on screening multiple treatments simultaneously within one disease type. This will allow investigator to focus on the disease in question, rather than having the specific goal of evaluating a single treatment individually. Bayesian adaptive design framework (Berry 2010) [42] have been increasingly used in the master protocol to expediate the clinical development. Lin and Bunn (2017) [43] gave an overview of different common types of designs for umbrella or platform trials, e.g. response-adaptive randomization (RAR) design and multiple-arm multi-stage (MAMS) design. They compared these two major methods and their extension under several scenarios under the umbrella or platform trial setting. Lin et al. (2019) [33] discussed both advantages and disadvantages of adaptive randomization from a practical perspective of clinical trials as well as illustration of master protocol case studies. In addition, a nonparametric model which was robust to event time distribution in response-adaptive designs for survival trials was also introduced. The simulation studies also compared the operating characteristics of the proposed design and the parametric design, including their robustness properties with respect to model misspecifications.

Though different master protocols might come with a different study size and operational setting, there are many commonly shared features in term of implementation, e.g. increased planning and evaluation as the beginning of trial design, strong coordination between different stakeholders or organizations and more complex infrastructures for clinical trial operations. However, if master protocol is utilized appropriately, these additional efforts are all worthwhile considering the substantial gain in the development efficiency with the potential of running a study for many years, and the benefit of target population.

2.4. Utilizing RWD in the vaccines development

During the COVID-19 outbreak, pharmaceutical companies, clinical research organizations (CROs), university research centers and others have announced the suspension or delay of the enrollment of some clinical trials. These decisions have been made based on the relative benefits and risk assessment of patients' disease type, phase of clinical trials, severity of virus spread and others. Therefore, many clinical sites were closed and large numbers of patients in clinical trials were lost follow up, which could induce massive missing data for the future analyses [44]. Nevertheless, the rapid increase in the volume, variety, and accessibility of digitized RWD has presented unprecedented opportunities for the use of RWD in data collection, trial designs and analyses in the vaccine development during this pandemic.

During the COVID-19 pandemic, electronic health records (EHRs), vaccine registries, and patient-generated data using the mobile app can be beneficial for the clinical trial data collection, which does not require site visits for the subjects. For example, an RWD EHRs platform has fast-tracked updates and incorporates specific COVID-19 terminology into their system, which will help to capture the COVID-19 disease status. Moreover, the vaccine registry system will also contribute to COVID-19 related efficacy and safety data collection. Finally, patient-generated data using a mobile app will allow patients to report their efficacy and safety events at home and avoid site visits. Therefore, if a COVID-19 trial is planned, these RWD sources will contribute to remote data collection, including baseline data, vaccine efficacy data and safety follow up data. Even though RWD cannot capture all the data in the vaccine trial (immunogenicity as an example), these precious data will also contribute to the COVID-19 vaccine designs and analyses.

As reviewed in Section 2.1, adaptive designs with SSR features are helpful when the incidence rate is not clear. As a new disease discovered in 2019, the knowledge of incidence rate is still not clear. In addition, the incidence rate is also based on the degree of social distancing, population density and other factors. Thus, RWD which allow remotely collected data using electronic devices is useful when COVID-19 trials are designed. RWD data sources will assist to estimate the incidence rate and help to calculate an accurate sample size. Especially for the field trials as introduced in Section 2 for COVID-19 vaccine development, accurate sample size is extremely helpful for the massively large urgent international clinical trials.

In order to accelerate COVID-19 vaccine development, a seamless phase 2/3 design using RWD could be considered. The primary endpoint of phase 2 is immunogenicity and the primary endpoint of phase 3 is vaccine efficacy. The data in the phase 2 part of this trial can be captured by traditional clinical trials without using RWD. After the evidence generated through the surrogate endpoint immunogenicity in phase 2, RWD could be beneficial in the phase 3 stage. Although RWD platform cannot capture immunogenicity data easily at the phase 2 stage, the vaccine efficacy and adverse events could be captured relatively easier in the phase 3 stage. Therefore, this hybrid design will contribute to the COVID-19 vaccine design with the RWD embedded into a seamless design frame. Zhu et al. (2019) has summarized practical consideration in implementing this type of hybrid trial including data quality and relevance, site selection, randomization, outcome adjudication, sample size, blinding, and bias [45].

Moreover, ethical concern could be raised for a placebo-controlled randomized efficacy trial for fatal diseases, like the West African Ebola vaccine [3,4], as discussed in Section 2. A similar concern may be raised for COVID-19, then if the efficacy signal in an early phase trial is high, there is a high possibility to adopt a single-arm trial with investigational vaccine only arm. In this scenario, a virtual control arm which used RWD including vaccine registry or natural history study can be beneficial. Through statistical modeling such as exact matching or propensity score-based methods, one can find a virtual control arm that has the similar inclusion/exclusion criteria, disease characters, target populations and other important factors. In this way, a quasi-randomization control arm can be derived to mimic the randomized clinical trial. The vaccine efficacy effect can be evaluated through this virtual control arm derived based on RWD.

However, to wisely use RWD for regulatory decision purpose in vaccine development, one should be cautious about the RWE generation procedure. Without a careful prospective plan on the selection of study, data source, population, endpoints, and a clear operational workflow using RWD, there could be risk of obtaining biased results. The biased results could not be considered as RWE for benefit-risk assessments nor further vaccine registration. More comprehensive considerations of how to use RWD in clinical development could be found in Li et al. (2020) [72].

3. Vaccine correlate of protection

Correlate of protection (COP) is another important topic that has gained extensive attentions in vaccine development. A correlate of protection is an immunological marker that predicts vaccine protection against certain infection or disease. Therefore, COP is often used as surrogate endpoint to vaccine efficacy. Vaccine efficacy endpoints usually require huge sample size to collect required number of events/cases, especially when the incidence rate is low. COP, on the other hand, allows the usage of immunological response to evaluate the vaccine effect, which is less costly, and may accelerate the vaccine development, among other numerous benefits. COP should be associated with immunological marker(s) and an antibody assay only. Although antibody titer is the natural choice of the immunological marker, some researches also considered alternatives like fold rise, or composite biomarkers. In addition, multiple assays might be explored during vaccine development. The COP conclusion needs to explicitly specify the correlation relationship between the assay and biomarker(s). Switching to other biomarker(s), or using new assay may require separately assessment of COP.

3.1. The Prentice criteria

The Prentice criteria were introduced in 1989 [46], when it was first developed to validate substitute endpoints in RCT data. Later his four criteria for validation of a surrogate endpoint was adapted for vaccine trials as follows by WHO [47]:

(1) Protection against vaccine efficacy is significantly related to having received the vaccine;

(2) The immune marker is significantly related to the vaccination status;

(3) The substitute endpoint is significantly related to protection against the vaccine efficacy;

(4) The vaccine efficacy can be explained by the immune marker fully.

Criteria 4 requires the immune marker to fully capture the vaccine's effect. That is, the incidence of the events is the same between vaccinated and unvaccinated subjects given a particular level of the immune marker (e.g., titer value), since the effect of the vaccine disappears after adjusting for the immune marker. This requirement is quite restrictive, making it difficult to validate correlates as surrogates in general. Besides the restrictive criterion 4, the Prentice criteria is also criticized by its post-randomization selection bias by Frangakis and Rubin (2002) [48], since the immune marker is measured after randomization and could be impacted by the vaccination intervention.

3.2. Qin's framework

Qin et al. proposed a framework to assess immunological correlates of protection [49], based on the methods of Prentice and Frangakis and Rubin (2002). Under this framework, the interests have been shifted to address post-randomization bias mentioned above. The proposed framework includes 3 levels of correlate of protection: correlate of risk (COR), level 1 surrogate of protection (SOP) and level 2 surrogate of protection. Qin et al. define the COR as an immune response that is associated with the primary efficacy endpoint. In comparison, a surrogate of protection (level 1 or level 2) is a COR that predicts the level of VE accurately. Level 1 SOP is defined as “an immunological measurement that is a COR within a defined population of vaccinees and is predictive of [vaccine efficacy] VE in the same setting as the trial”, whereas level 2 SOP extends the SOP to different populations or setting, for which meta-analytical approach is usually applied.

Level 1 SoP is further subdivided into two categories: Statistical SOP and Principal SOP. Statistical SOP refers to the traditional SOP that satisfies Prentice criteria. The emphasize is placed on Principal SOP, that essentially evaluates how VE varies among subgroups defined by fixed level of an immune marker. However, there is inherent missing value challenge that the potential immune response given vaccine is unobserved for the placebo arm.

3.3. Methods for correlate of protection

In order to address the inherent missing value issue associated with principal SOP, Follmann (2006) [50] proposed two methods to augment the standard vaccine trials design: 1), utilization of baseline predictors of the immune marker, and 2), vaccination of uninfected placebo subjects at the close out of the trial, to estimate the missing immune values. Accordingly, a few new methodologies have been proposed based on the novel trial design and compared with the estimated likelihood-based methods.

3.3.1. Semiparametric method

Since multiple immune markers may be explored for even used as composite endpoint for COP, Huang and Gilbert (2011) [51] proposed a semiparametric approach that allows multiple potential surrogate markers to be considered, with the goal to estimate the conditional joint CDF F(s₁, …, s_J| W_j). To be more specific, the joint CDF is estimated via a location-scale model on the residuals as follows:

$$F\left(s_1,\dots ,s_J|\mathrm{W}\right)=\mathrm{P}\left(S_1\le s_1,..,S_{\mathrm{J}}\le s_{\mathrm{J}}|\mathrm{W}\right)=\mathrm{P}\left({\epsilon }_1\le \frac{s_1-{\mu }_1\left(W\right)}{{\sigma }_1\left(W\right)},\dots ,{\epsilon }_J\le \frac{s_{\mathrm{J}}-{\mu }_J\left(W\right)}{{\sigma }_J\left(W\right)}\right)=F_{\left(1,..,J\right)}^{\left(0\right)}\left\{\frac{s_1-{\mu }_1\left(W\right)}{{\sigma }_1\left(W\right)},\dots ,\frac{s_{\mathrm{J}}-{\mu }_J\left(W\right)}{{\sigma }_J\left(W\right)}\right\}$$

where F _(1,..,J) ⁽⁰⁾ is the joint CDF for the residuals ε ₁, …, ε _J. The location and scale parameters can be estimated by solving the estimating equations for mean and variance.

3.3.2. Pseudo-score (PS)

Motivated by the observation that incorporating closeout vaccination data into existing estimation procedures resulted in increased estimation error, Huang, Gilbert and Wolfson (2013) [52] proposed a pseudo score method to estimates the score equation instead of the likelihood equation. The score equation of the observed likelihood is defined as

$$\frac{\mathrm{\partial l}\left(\mathrm{\beta },\mathrm{F}\right)}{\mathrm{\partial \beta }}=\sum _{{\mathrm{\delta }}_{\mathrm{i}}=1}{\mathrm{U}}_{\mathrm{\beta }}\left({\mathrm{Y}}_{\mathrm{i}}|{\mathrm{S}}_{\mathrm{i}},{\mathrm{Z}}_{\mathrm{i}},{\mathrm{W}}_{\mathrm{i}}\right)+\sum _{{\mathrm{\delta }}_{\mathrm{j}}=0}\frac{{\mathrm{U}}_{\mathrm{\beta }}\left({\mathrm{Y}}_{\mathrm{j}}|\mathrm{s},{\mathrm{Z}}_{\mathrm{j}},{\mathrm{W}}_{\mathrm{j}}\right)\mathrm{P}\left({\mathrm{Y}}_{\mathrm{j}}|\mathrm{s},{\mathrm{Z}}_{\mathrm{j}},{\mathrm{W}}_{\mathrm{j}}\right)\mathrm{dF}\left(\mathrm{s}|{\mathrm{Z}}_{\mathrm{j}},{\mathrm{W}}_{\mathrm{j}}\right)}{\int \mathrm{P}\left({\mathrm{Y}}_{\mathrm{j}}|\mathrm{s},{\mathrm{Z}}_{\mathrm{j}},{\mathrm{W}}_{\mathrm{j}}\right)\mathrm{dF}\left(\mathrm{s}|{\mathrm{Z}}_{\mathrm{j}},{\mathrm{W}}_{\mathrm{j}}\right)}$$

with Z being the binary treatment indicator; W being baseline covariates; S be the immune marker; Y being vaccine efficacy; F{S} the distribution of S; F(S|Z, W) being the CDF of S conditional on Z and W; P being risk conditional on Z, W and S; U_β(Y_i| S_i, Z_i, W_i) = ∂logP(Y, Z, W)/∂β.

The score type estimator improved the estimation by more efficient use of the augmented data hence but has the limitation requiring the baseline predictor W available for all trial participants.

3.3.3. Semiparametric likelihood and pseudo-likelihood

Liu et al. (2017) [53] proposed a semiparametric likelihood method and a pseudo-likelihood method to explore the potential improvement to the pseudo score method. The semiparametric likelihood approach jointly estimates F(S| W) and the risk parameters β by treating F as an unknown parameter, which allows efficient use of the data. Pseudo-likelihood method defines a weighted estimator for F(S| W) such that

$${\widehat{\mathrm{F}}}_{\mathrm{\beta }}\left(\mathrm{s}|\mathrm{w}\right)=\frac{\sum _{\mathrm{i}}\mathrm{I}\left({\mathrm{S}}_{\mathrm{i}}\le \mathrm{s},{\mathrm{W}}_{\mathrm{i}}=\mathrm{w},{\mathrm{\delta }}_{\mathrm{i}}=1\right)/\widehat{\mathrm{P}}\left({\mathrm{\delta }}_{\mathrm{i}}=1|{\mathrm{S}}_{\mathrm{i}},\mathrm{w};\mathrm{\beta }\right)}{{\sum }_{\mathrm{i}}\mathrm{I}\left({\mathrm{S}}_{\mathrm{i}}\le \mathrm{s},{\mathrm{W}}_{\mathrm{i}}=\mathrm{w}\right)/\widehat{\mathrm{P}}\left({\mathrm{\delta }}_{\mathrm{i}}=1|{\mathrm{S}}_{\mathrm{i}},\mathrm{w};\mathrm{\beta }\right)}$$

Based on simulation results, the pseudo-likelihood method provides computational efficiency and comparable model estimation results compared with the pseudo score method and semiparametric likelihood method.

There are continuous researches based on the principal SOP and/or the novel vaccine trial designs, e.g., three-phase sampling and non-monotone missing sampling design etc. Those likelihood-based approaches discussed could be aimed to address inherent missing value issue for the placebo group, but the implementation relies on the study design, whether a reliable baseline predictor for immune marker exists, and whether the trial design allows additional booster dose by end of the trial to collect missing immune values. In practice, the traditional COP analyses based on VE curve are still used as the primary method as demonstrated in example [54].

4. Other considerations for vaccine development

Besides innovative designs and correlate of protection, continuous efforts have been made to improve statistical methods to several fundamental components of vaccine clinical development, including vaccine efficacy, safety, immunogenicity and more. Heyse et al. (2016) [55] provided a comprehensive review to many aspects of the vaccine development highlighting statistical applications that have contributed to successful vaccine development. This section below, instead, offers a summary of statistical considerations of selected topics that target on ongoing real-world challenges, and are of great interests to many vaccine researchers.

4.1. Vaccine efficacy

In vaccine efficacy trials, vaccine protective effects are investigated. Halloran et al. (2010) [56] provided a theoretical framework to assess vaccine effects, allowing different parameters to be used measuring various effects of vaccine. Prior to licensure, interest of clinical development programs has been placed on the capability of vaccination to prevent or reduce the probability of vaccinated subjects getting the targeted disease or infection, e.g., vaccine efficacy. Commonly used definitions include comparing attach rates, compare person-time, or comparing time-to-event (infection) data. For this subsection, special attention is given to two efficacy related research topics: asymptomatic events and burden of illness (BOI) efficacy measure.

4.1.1. Asymptomatic events

Many pathogens have high proportions of asymptomatic or mild infection, such as Zika virus. However, VE remains an important endpoint of vaccine trials for these pathogens regardless the level of symptom, as it could trigger onward transmission and some long-term sequelae. From an operational perspective, asymptomatic events pose challenges for trial conduction, since those infections require frequent periodic testing of all trial subjects to confirm the real-time infection status.

Kahn et al. (2019) [57] compared seven approaches to estimate vaccine efficacy.

• •Approach 1 is the benchmark. They assume that the exact day of infection is known for all asymptomatic infections. This is the ideal scenario, hence referred as the “perfect knowledge” scenario by Kahn. However, this is not practical because this requires daily testing of infection throughout the trial.
• •Approach 2 assumes that only symptomatic infections are recorded in a trial, and asymptomatic infections are treated as non-event and censored. As expected, this approach introduces bias in vaccine efficacy estimation.
• •Approach 3 performs infection testing only once at the end of the trial to obtain the total counts of injection from each treatment group, and estimate vaccine efficacy using a risk ratio instead of a hazard ratio, e.g., $\mathit{VE}=\frac{\mathit{Attach\; rate\; of\; vaccinated\; subjects}}{\mathit{Attach\; rate\; of\; placebo\; subjects}}$.
• •Approach 4 improved this relative risk estimate by assuming VE can be recovered from the ratio of cumulative hazards e.g., $\mathit{VE}=\frac{ln\left(1-\mathit{Attach\; rate\; of\; vaccinated\; subjects}\right)}{ln\left(1-\mathit{Attach\; rate\; of\; placebo\; subjects}\right)}$.
• •Approaches 5 assumes the day of infection for the symptomatic individuals is known, and asymptomatic infection is tested twice throughout the trial and once at end (3 intervals). This approach further assumes that the serological test is able to distinguish between natural infection and vaccine-introduced immunity.
• •Approach 6 uses the same concept as of approach 5 but only assuming one serological testing at the end of the trial (one interval).
• •Approach 7 assumes that only one serological test at the end of the trial for 10% subjects. For remaining subjects, the infection status is imputed using multiple imputation then approach 6 is used for the imputed datasets.

Based on simulation results, the corrected relative risk estimate (approach 4), the interval-censored Cox models (approaches 5, 6 and 7) yields unbiased VE estimates while approach 2 and 3 returns biased results. In addition, compared with approach 5, approach 6 provides similar estimation in terms of the coverage probability and power but only requires one serological test and hence has the advantage of requiring fewer resources. It is interesting to see that approach 7, testing only 10% subjects at the end of the trial could also provide an accurate estimate but requires even reduced resources. In practice, when “perfect knowledge” posts costs and resources challenges, alternative approaches like corrected relative risk estimate or interval-censored Cox models could be considered.

4.1.2. Burden of illness (BOI)

Vaccine intervention could be assessed by not only incidence but also severity. Chang et al. (1994) [58] proposed the concept of burden of illness (BOI) to take severity of the cases into consideration. First, the investigators graded the severity of each case, and nonevents were graded as zero. Secondly, they set up a BOI score that was simply the sum over all cases for each treatment group. Test statistics were provided alone with sample size and power calculation.

Mehrotra et al. (2006) [59] compared eight methods for testing dual vaccine efficacy endpoints in a proof of concept (POC) HIV vaccine trial. The two endpoints of interests are incidence of HIV infection, and the viral load set point among infected subjects. The first two methods were based on BOI and used a single test for the actual values or ranks of BOI respectively. The remaining six approaches were based on unweighted or weighted two-part z tests, Simes', and Fisher's methods. Simulation results showed that for a POC efficacy trial, the BOI is generally less powerful. Both unweighted Simes' and Fisher's are more powerful even after adjusting for the selection bias, especially when VE is low. When VE is relatively high (>60%), all methods have comparable performance. Hu et al. (2015) [60] also proposed weighted two-part z test based on the combination of two endpoints. In their methods, the optimal weight is obtained by maximizing testing power – assign more weight to the statistic with larger effect size. The paper also proposed conditional exact procedure to handle the issue with excessive number of uninfected subjects.

Another problem for vaccines targeting rare events is that most of the participants do not become infected during the trial. Follmann et al. (2009) [61] introduced chop-lump Wilcoxon and t-tests based on BOI to tackle the issue. Similar to BOI, this approach also assigns a score to each subject, 0 for uninfected subjects and S for severity endpoint assessment. Assuming equal number of subjects in each treatment group, the chop-lump test removes an equal number of zeros from both groups, then performs the test based on the modified BOI, with the null distribution is provided using permutation method.

4.2. Vaccine safety

Vaccines are usually target healthy subjects; therefore, safety performance remains a primary consideration for all vaccines. Vaccine reactogenicity data (also referred as vaccine solicited AEs) and clinical adverse events (AE) data are routinely evaluated throughout the clinical development. Vaccine reactogenicity refers to a set of adverse events of special interests, that are either caused by or attributable to the vaccination. Vaccine trials also collect subject self-reported AE similar to therapy trials, hence share the challenge of multiplicity when multiple safety variables are analyzed.

4.2.1. Multiplicity issue for vaccine safety

Vaccine trial enrollment could be considerably large, resulting in the possibility of an excess of false positive findings although clinically not meaningful. Nauta (2020) [62] discussed five approaches to account for vaccine safety multiplicity:

(1) No correction. False negative is usually of greater concern for vaccine regulatory reviewers than false positives. Therefore, no adjustment is considered as inaccurate but conservative approach, and followed by most vaccine trials.

(2) Strong control of family-wise error rate (FWER) using Bonferroni correction or Holm method.

(3) False discovery rate (FDR) method. Results based on 10,000 simulation showed that FDR approach could address less false positive than uncorrected method but more than Holm methods.

(4) Double false discovery rate approach proposed by Mehrotra and Heyse (2004) [63]. This approach method involves a two-step application of adjusted P values based on the Benjamini and Hochberg false discovery rate (FDR). Step 1, categorize AE by body system or other characteristics and disregard rare AEs that cannot even be rejected at unadjusted α =0.05 level. Step 2, define P_i ^∗ = min {P_i1, P_i2, …, P_ik} to be the ‘representative’ P-value for the i^th body system, as smallest P-value indicates the strongest safety signal. Then apply FDR to P_i ^∗ for all pre-defined groups, e.g., body system. Then apply the second level of FDR adjustment within each body system, e.g., {P_i1, P_i2, …, P_ik} and flags AE (i, j) if final adjusted P_i ^∗ < α₁ and P_ij < α₂. The cutoff α₁ and α₂ are set to be α/2 and α respectively (assuming FDR is controlled at level α) suggested by bootstrap resampling results.

(5) Bayesian 3 level hierarchical mixture model proposed by Berry et al. (2004) [64], that allows borrowing information across body system and potentially within body system.

In practice, most trials follow approach one reporting safety data without correction. Approach 2–5 could be considered as alternative or sensitivity analysis should there be concerns regarding safety profile.

4.2.2. Vaccine safety surveillance

Although a huge number of subjects are usually enrolled in vaccine clinical trials to build up vaccine safety database, rare AEs could still go undetected during clinical development. For example, tetravalent rhesus-human reassortant rotavirus vaccine (RRV-TV) was withdrawn from the market due to reported intussusception, a type of intestinal obstruction.

One goal for post-licensure vaccine safety surveillance is to detect serious AEs as early as possible without too many false positive findings. Sequential statistical analysis allows multiple looks of the data by adjusting for multiple testing issue and control of the overall significance level. Two groups of sequential methods could be considered: continuous or group sequential methods. The former achieves near real-time monitoring by allowing testing as frequently as possible, while the later analyzes data at some time point after data is available for a group of subjects. Silva et al. (2015) [65] systematically compared the performance of two designs and concluded that continuous sequential method has a shorter expected time-to-signal than a group sequential method and data should be collected as frequently as possible. One of the most popular continuous sequential tests, the maximized sequential probability ratio test (MaxSPRT), was proposed by Kulldorff et al. (2011) [66]. MaxSPRT is based off of Wald's clinical sequential probability ratio test (SPRT) but with composite alternative hypothesis instead of a simple alternative hypothesis. The MaxSPRT has been applied to Pediarix vaccine data and showed good performance in terms of statistical power and time-to-signal duration.

As a comparison, Li et al. (2020) [67] proposed a Bayesian paradigm describing how sequential analysis can be performed under Bayesian framework. Comparing with MaxSPRT, the Bayesian approach significantly improves the false negative rate and decreased the earliest time to signal based on both simulation results and a real-world vaccine safety example. As discussed in Section 2, there are very limited applications of a Bayesian approach in vaccine phase I to phase III trials designs. Therefore, although the proposed Bayesian sequential method is for post marketing safety surveillance, this could still be a promising signal for potential further Bayesian approaches implemented in vaccine development.

4.3. Vaccine immunogenicity

Most vaccine immunogenicity trials are based on non-inferiority or equivalence testing. Within the four types of immunogenicity trials mentioned in Section 2, bridging, combination and concomitant trials are usually conducted under a non-inferiority framework while lot-to-lot consistency trial is categorized as equivalence testing. Due to the massive usage of non-inferiority testing, some statistical considerations around this topic would be worth further discussion.

4.3.1. Non-inferiority testing

Non-inferiority designs are often used to demonstrate that the immunogenicity of the candidate vaccine is not less than that of a licensed vaccine, but could provide other benefits, like cost, storage, improved safety, reduced number of injections etc. Non-inferiority methodology could also be used to bridge established vaccine efficacy to extended age groups or regions. For example, an immunogenicity trial was conducted to bridge the efficacy findings for 9-valent human papillomavirus virus-like particle (9vHPV) developed in young women (16–29 years of age) to girls and boys (9–15 years of age).

Although often used, some characteristics of the non-inferiority test should be considered prior to performing analysis. Wang et al. (2001) [68] discussed a series of statistical considerations for noninferiority/equivalence vaccine trials, including endpoints, hypothesis testing, selection of the noninferiority margin, adjustment for stratification factors, missing data and sample size. For stratification factor, different choices of weights that are assigned to different stratum are discussed and compared – Cochran-Mantel-Haenszel (CMH) weights, the precision or inverse-variance (INVAR) weights and the minimum risk (MR) weight strategy that has the smallest asymptotic mean squared error. In addition, MR strategy when used alone with observed variance, could offer notable power advantages for trials with high response rates. Kong et al. (2004) [69] discussed type I error and power testing for multiple endpoints of noninferiority or equivalence when different immune responses are measured. Assuming relatively large sample size, approximately multivariate normal distribution can be assumed, and the distributions of the test statistics can be derived with known covariance matrix. Simulation was conducted to further demonstrate the Type I error and power performance.

5. Concluding remarks

Traditional vaccine development can be time-consuming and high cost. Especially in the global pandemic, e.g. COVID-19, we are increasingly facing the need for efficient designs and analyses in vaccine clinical trials. As such, the purpose of this article was to provide an overview of innovative trial designs and analyses for vaccine clinical trial development. Starting with adaptive design, the first type of adaptive design we reviewed was a 4vHPV seamless phase II/III vaccine efficacy trial. This design allowed dose selection by the end of phase II and incorporated phase II data into final Phase III analyses. Type I error was carefully controlled which was demonstrated through theoretical proof and simulation. The second type of adaptive design featured population enrichment, which allowed dropping sub-populations based on undesired interim analysis results. Type I error was controlled by a pre-specified testing procedure, and simulation results showed that the design had a high probability of success by selecting the promising target population at the interim analysis. A sample size adaptation design which addressed the issue of uncertainty of sample size calculation assumptions at the beginning of the trial was also discussed. More comprehensive considerations of adaptive design implementation, including the role of cross functional team, communication process and documentations could be found in Li et al. (2020) [70].

Although there are still very limited case studies of using Bayesian design for vaccine development, the conceptual flexibility and advantages of borrowing historical information in the Bayesian design do provide a new paradigm for efficient vaccine clinical trials. Of note, early engagement and detailed evaluation of operating characteristics in proposed Bayesian design and choice of prior, e.g. type I error and power, would be the key considerations to get successful endorsements with regulatory agencies. For example, in a recent phase 1/2/3 study of RNA vaccine candidate again COVID-19 in healthy individuals [71], the primary analysis is based on the Bayesian posterior probability with a minimal informative (pessimistic allowing for considerable uncertainty) beta prior is proposed. The study has four interim analyses and overwhelming efficacy can be declared if the posterior probability is higher than the success threshold. Given the use of Bayesian success criteria (e.g. based on the posterior probability P[VE > 30%|data]), the success thresholds for each interim analysis need to be appropriately calibrated through simulations to control the overall type I error rate at 2.5%.

As an emerging new type of innovative trial design, master protocols have been popular for the past several years and have been implemented for several therapy trials. It is newly introduced to vaccine development, triggered by the emergency to develop a vaccine during the global COVID-19 pandemic. In addition, the master protocol has the appealing feature of concurrent evaluation of multiple vaccine candidates, and turned over a new leaf of vaccine development, which allows more ethical and accelerated vaccine development in public health emergencies. More recently, the rapid increase in the volume, variety, and accessibility of digitized RWD has also presented unprecedented opportunities for the use of RWD for the data collection, trial designs and analyses in the vaccine development. However, rigorous statistical methodologies are necessary to ensure the robustness of results are characterized from the RWD, especially for regulatory purpose [72].

Correlate of protection (COP) is another complex yet essential statistical consideration of vaccine development. The traditional Prentice criteria approach and its disadvantages were discussed, prior to introducing Qin's framework that was incorporated in WHO's report. Correlate of protection novel trial designs that utilize baseline predictor or closeout vaccination were discussed, and a series of later research work based on the novel design was summarized in detail. However, for traditional trials without those design features, the usage could be limited.

We also summarized several other statistical considerations for vaccine efficacy, safety and immunogenicity analyses, highlighting asymptomatic event handling, composite vaccine efficacy endpoint using the burden of illness score, multiplicity issues for vaccine safety, post marketing safety surveillance challenges, and some statistical considerations related to non-inferiority testing for immunogenicity endpoints. As expected, with the benefits of novel clinical trial designs and analysis – reduced bias, accelerate development timeline, flexible and efficient trial features etc., comes the requirement of more complex statistical modeling and simulations. Of note, these advances require continuous statistical inputs seamlessly integrated in the clinical development plan. However, the additional quantitative efforts are all worthwhile given the substantial gain of efficient vaccine development, and most importantly, the benefit of the target population.