On a new conceptual mathematical model dealing the current novel coronavirus-19 infectious disease

Abstract

The present paper describes a three compartment mathematical model to study the transmission of the current infection due to the novel coronavirus (2019-nCoV or COVID-19). We investigate the aforesaid dynamical model by using Atangana, Baleanu and Caputo (ABC) derivative with arbitrary order. We derive some existence results together with stability of Hyers-Ulam type. Further for numerical simulations, we use Adams–Bashforth (AB) method with fractional differentiation. The mentioned method is a powerful tool to investigate nonlinear problems for their respective simulation. Some discussion and future remarks are also given.

1. Introduction

studding the existing literature, one can read that in history numerous outbreak came out which totally changed the life situation of the people on this earth. In last four centuries some famous pandemic in which millions of people lasted their lives. In the past century two outbreaks killed many millions people in Europe, Asia and Middle east as well as in Africa [1], [2], [3]. Infectious diseases is a massive threat for humanity and can greatly effect the economy of a state. Proper understanding of a disease’ dynamics could play an important role in elimination of the infection from the community. Further, implementation of suitable control strategies against the disease transmission have been assumed a big challenge. Currently the coronavirus outbreak greatly destroyed the lives of many people around the globe. The mentioned out break was initiated in China Wuhan at the end of 2019 and with a very rapid speed of fifty or sixty days it spread out in the whole globe. WHO announced it as a pandemic. For some detail see [2], [3], [4], [5], [6]. Therefore numerous measures have been taken by different countries to control it. Also researchers have started to form different procedure to cure and control it. In this regards, the approach of mathematical modeling is one of the key tool for handling such and other challenges. A number of general and disease models have been investigated in existing literature which enables us to explore and control the spread of infectious diseases in a better way [7], [8].

The above mentioned epidemic models as well as many other in the literature are actually based on integer-order differential equations (IDEs). However, in the last few years, it is noticed that with the help of fractional-order differential equations (FDEs) one can model universal phenomenon with a greater degree of accuracy [9]. This idea was implemented in many field including engineering, economics, control theory, finance and some up to the mark results were founded. Fractional calculus is the generalization of classical integer-order calculus. The increasing interest of using FDEs in the modeling of complex real world problems is due to its various properties which are could not be founded in IDEs. In contrast of IDEs which are local in nature, the FDEs are non-local and posses the memory effects which make it more superior as in many situations the future state of the model depends not only upon the current state but also on the previous history. These features enables FDEs to effectively model the phenomenon having not only the non-Gaussian but also for non-Markovian behavior. Further, the classical IDEs are unable to provide the information in between two different integer values and it can be make clear with the help of FDEs. Various type of fractional-order operators were introduced in existing literature to over come such limitations of integer-order derivative. The applications of these fractional operators can be found in various fields [10], [11].

During the eighteen century when Reimann, Liouvilli, Euler and Fourier are struggling in producing significant results in ordinary calculus. At the same time, great contributions were made in the area of fractional calculus as well and reinstated and valuable work has been carried out later on. This is due to the various application of fractional calculus in the filed of mathematical modeling where several hereditary materials and memory process cannot be explained clearly by ordinary calculus. Because fractional calculus which include classical calculus is a special case has greater degree of freedom in differential operator as compared to ordinary differential operator which is local in nature. The important applications of the said calculus may be traced out in [12], [13], [14], [15], [16], [17]. Therefore, researchers have given very much attention in studying of fractional derivatives and integrals. In fact fractional derivative is a definite integral which geometrically interpret the accumulation of the whole function or the whole spectrum which globalize it. Investigation of differential equations for qualitative study, numerical and optimization, significant contribution has been made by researchers, we refer few as [18], [19], [20], [21]. It is also remarkable that fractional differential operators have been defined by number of ways. It is a well known fact that the definite integral has no regular kernel, therefore both type of kernel have been involved in various definition. One of the important definition which has very recently attracted the attention is the ABC derivative introduced by Atangana-Baleanu and Caputo [22] in 2016. The mentioned derivative exhibit the singular kernel by nonsingular kernel and therefore were greatly studied [23], [24], [25]. For numerical purposes large numbers of methods have been developed, see for detail [28], [29], [30], [31], [32], [33], [34], [35], [36]. The famous Adams–Bashforth method has also used for numerical purpose in past see [37].

To properly know the mechanism of transmission and hence control the COVID-19 mathematically, we will formulate a model with the help of available literature. The current study is actually divided into three main parts; the statistic, dynamic and control. In the first part, we just studied the qualitative aspects of the disease and estimated the key rates form the real data. In the dynamics part, the authors have tried to answer questions like when the disease will dies out? When does it will persist in the population? Which parameters are more responsible for the disease spreading? Mathematically, we will calculate the possible equilibria of the model and its stability analysis will be carried out using the methods of linearization, the Lyapunov theory and geometrical approach. On the other hand the area devoted to mathematical modelling plays an important role to investigate the dynamics of a disease and hence its control particularly in the absence of vaccination or at early stages of the disease. The area devoted to investigate biological models for infectious diseases is warm area of research in recent time. Many mathematical models can be found in the literature which study stability theory, existence results and optimization of biological models, we refer a few as ([13], [14], [15], [16]). Similar to other diseases [26], [27], we can model COVID-19 [38], [39], and can predict its future behavior. Also, one can look for possible prevention strategies as well. Inspired from the nice properties of FDEs particularly using the definition of $\left(\mathrm{ABC}\right)$ derivative, we intend to capture the transmission of COVID-19 in the from of

$$\left\{\begin{array}{c}{0}^{\mathrm{ABC}}{\mathcal{D}}_{+0}^{r}P\left(t\right)=\lambda -\gamma P\left(t\right)I\left(t\right)-d_{0}P\left(t\right),\hfill \\ 0^{\mathrm{ABC}}{\mathcal{D}}_{+0}^{r}I\left(t\right)=\gamma P\left(t\right)I\left(t\right)-(d_0+h+\eta )P\left(t\right)+\sigma Q\left(t\right),\hfill \\ 0^{\mathrm{ABC}}{\mathcal{D}}_{+0}^{r}Q\left(t\right)=\eta I\left(t\right)-(d_0+\mu +\sigma )Q\left(t\right),\hfill \end{array}\right)$$ (1)

with given initial conditions

$$P\left(0\right)=P0,I\left(0\right)=I_0,Q\left(0\right)=Q_0,$$ (2)

where $0<r⩽1$. Here $P\left(t\right)$ is the susceptible human population, $I\left(t\right)$ represent the people who are infected with COVID-19 and $Q\left(t\right)$ is the people who are quarantined at time $t$. We place the following assumptions on the model:

• $a_1$.All of the parameters and states of the model under discussion are nonnegative.
• $a_2$.The susceptible people move to the infection classes and there is a constant inflow into the susceptible population.
• $a_3$.Initially infected or suspected people move to quarantined class and confirmed cases from quarantined come back to the infected compartment.

The detail of parameters used in model (1) with complete descriptions are given in Table 1 . Further the involve state functions of the model obey $\mathrm{N}\left(t\right)=P\left(t\right)+I\left(t\right)+Q\left(t\right),$ where the total population is $\mathrm{N}$. Since most of iterative methods often faced to convergence problems. Therefore it was needed to search some sophisticated tools of numerical analysis which may help to find the numerical solution with good accuracy and reliability for usual FDEs as well as those problem involving $\mathrm{ABC}$ derivative. Therefore the authors [40] extended the well known Adams–Bashforth numerical procedure for the concerned FDEs. They successfully find numerical results with good accuracy to some chaotic problems. After that the technique mentioned afore has frequently used to deal those problems involving $\mathrm{ABC}$ derivative, see detail in [41], [42], [43]. For numerical purpose stability is also needed so Ulam type stability is investigated for suggested model. Also the existence of the new constructed model is guaranteed by applying fixed point theorems of Banach and Krassnoselskii’s. The mentioned stability has been investigated for usual fractional derivatives in large numbers of research articles like [44], [45], [46], however, the same was not investigated for $\mathrm{ABC}$ derivatives. Finally the results are displayed against real data which has taken from a source about Pakistan during the month of March, 2020.

Table 1.

Description of the parameters used in model (1).

Notation	Parameters description
$\lambda$	Recruitment rate
$\gamma$	The disease transmission rate
$d_0$	Natural death rate
$\eta$	Rate at which infected are getting quarantine
$\mu$	Disease-related death rate in quarantined individuals
$\sigma$	Rate at which quarantined people getting infection
$h$	Disease-related death rate in infected people

2. Deterministic form of our proposed model and its properties

Considering the above discussion, the deterministic form of model (1) is formulated as follows:

$$\begin{array}{c}\frac{d}{\mathit{dt}}P\left(t\right)=\lambda -\gamma P\left(t\right)I\left(t\right)-d_{0}P\left(t\right),\hfill \\ \frac{d}{\mathit{dt}}I\left(t\right)=\gamma P\left(t\right)I\left(t\right)-(d_0+h+\eta )I\left(t\right)+\sigma Q\left(t\right),\hfill \\ \frac{d}{\mathit{dt}}Q\left(t\right)=\eta I\left(t\right)-(d_0+\mu +\sigma )Q\left(t\right),\hfill \end{array}$$ (3)

with initial conditions

$$P\left(0\right)=P_0>0,I\left(0\right)=I_0⩾0,Q\left(0\right)=Q_0⩾0,$$ (4)

The model (3) whose the transmission structure is depicted in the Fig. 1 . We discuss the well possedness of the proposed model (3) then we will use the method of [26], [47], [48] then we have the following axioms.

Proposition 2.1

The model (3) is in orthant $R_{+}^3$ is invariant.

Proof

Let $Y={(P,I,Q)}^T$, then system (3) becomes

$$\frac{\mathit{dY}\left(t\right)}{\mathit{dt}}=\mathit{LY}+C,$$ (5)

where

$$\begin{array}{cc}L\hfill & =\left(\begin{array}{ccc}\hfill -\left(\gamma I\right(t)+d_0)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \gamma I\left(t\right)\hfill & \hfill -(d_0+h+\eta )\hfill & \hfill \sigma \hfill \\ \hfill 0\hfill & \hfill \eta \hfill & \hfill -(d_0+\mu +\sigma )\hfill \end{array}\right),\hfill \\ C\hfill & =\left(\begin{array}{c}\hfill \mathrm{\Lambda }\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)\text{.}\hfill \end{array}$$

Clearly, $C⩾0$ and $L$ preserve the axioms of Metzler matrix, so system (3) is invariant in $R_{+}^3$.

Proposition 2.2

The solution of (3) i.e., $(P,I,Q)$ with (4) are positive.

Proof

It could be clearly noted that the solution of the first equation of system (3) becomes

$$\frac{\mathit{dP}\left(t\right)}{\mathit{dt}}+\left(\gamma I\right(t)+d_0)P\left(t\right)=\lambda \text{.}$$ (6)

The solution of equation (6) is

$$P\left(t\right)=e^{-{\int }_0^t\left(\gamma I\right(t)+d_0)\mathit{dt}}\left(P_0+\lambda \int e^{{\int }_0^t\left(\gamma I\right(t)+d_0)\mathit{dt}}\mathit{dt}\right),$$ (7)

$\forall t>0$, which shows that $P\left(t\right)>0$. Similarly the second equation of (3) gives the form

$$I\left(t\right)=e^{-{\int }_0^t(d_0+h+\eta -\gamma P(t\left)\right)\mathit{dt}}\left(I_0+\sigma \int Q\left(t\right)e^{{\int }_0^t(d_0+h+\eta -\gamma P(t\left)\right)d\tau }\mathit{dt}\right),$$

which implies that $I\left(t\right)⩾0$. Continuing the same process it is very simple to prove that $Q\left(t\right)$ is also positive. Thus $(P,I,Q)$ is nonnegative.

Proposition 2.3

The solution i.e., $(P,I,Q)$ of the proposed problem is given by (3), (4) is bounded.

Proof

Since

$$T\left(t\right)=P\left(t\right)+I\left(t\right)+Q\left(t\right)\text{.}$$ (8)

The differentiation of the above Eq. (8) gives

$$\frac{\mathit{dT}}{\mathit{dt}}+d_{0}T=\lambda -\mu Q-\mathit{hI}\text{.}$$ (9)

Clearly, $\frac{\mathit{dT}}{\mathit{dt}}+d_{0}T⩽\lambda$. Solving we obtain

$$0<T\left(t\right)⩽\frac{\lambda }{d_0}+T\left(0\right)e^{-d_{0}t},$$ (10)

which gives that $0<T(P,I,Q)⩽\frac{\lambda }{d_0}$ as $t\to \infty$.

Proposition 2.4

If $T\left(0\right)⩽\frac{\lambda }{d_0}$ , then the proposed problem is stated by (3), (4) is a well-defined dynamical system the region is given by

$$\mathrm{\Delta }=\left\{(P,I,Q)\in {\mathbb{R}}_{+}^3:0<T⩽\frac{\lambda }{d_0}\right\},$$ (11)

which is biologically feasible. Moreover every solution in $\mathrm{\Delta }$ remains in $\mathrm{\Delta }$ for $t⩾0$ .

Proof

It is very much clear that all the states variables of the proposed problem are nonnegative, so the problem as stated by (3), (4) is well-posed and biologically feasible. From $T\left(0\right)⩽\frac{\lambda }{d_0}$, we concludes that $T\left(t\right)⩽\frac{\mathrm{\Lambda }}{d_0}$. So every solution of (3) along with (4) in $\mathrm{\Delta }$ remains in $\mathrm{\Delta }$.

Fig. 1.

Flowchart of our proposed model (1).

2.1. Basic reproductive number and stability of disease-free equilibrium

Let

$$a=d_0+h+\eta ,b=d_0+\mu +\sigma \text{.}$$ (12)

The disease-free state ($E_1$) takes the form

$$E_1=(P_1,0,0),P_1=\frac{\lambda }{d_0}\text{.}$$ (13)

This disease free state is used to calculate the threshold parameter (${\mathcal{R}}_0$), also called the basic reproduction number i.e., the average of secondary number of infections. Moreover, the threshold parameter (${\mathcal{R}}_0$) is used in the calculating of the endemic state. We follow the Watmough et al.[26], [47] method for the purposes of calculating the threshold parameter.. We know that $I^{\ast }>0$, so

$$I^{\ast }=\frac{\gamma \mathrm{\Lambda }b-d_0\mathit{ab}+d_0\sigma \eta }{\mathit{ab}-\sigma \eta }\text{.}$$

By rearranging the terms, we can write $I^{☆}$ in the following way

$$I^{\ast }=\frac{b\lambda \gamma -d_0\left(b(d_0+h)+\eta (d_0+\mu )\right)}{\gamma \left(b(d_0+h)+\eta (d_0+\mu )\right)}=\frac{d_0}{\gamma }\left({\mathcal{R}}_0-1\right)\text{.}$$ (14)

The term ${\mathcal{R}}_0$ used in (14) and so called the threshold number or threshold quantity which is given by

$${\mathcal{R}}_0=\frac{b\lambda \gamma }{d_0\left(b(d_0+h)+\eta (d_0+\mu )\right)}\text{.}$$ (15)

Lemma 2.5

If ${\mathcal{R}}_0<1$ then model (3) is stable locally at DFE ($E_1$) defined in (13).

Proof

Let $J^{\ast }$ is the Jacobian matrix of model (3) at $E_1$, then

$$J^{\ast }=\left(\begin{array}{ccc}\hfill -d_0\hfill & \hfill -\gamma P_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \gamma P_1-a\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \eta \hfill & \hfill -b\hfill \end{array}\right)\text{.}$$ (16)

For obtaining the characteristic polynomial, we set $|J^{\ast }-\mathrm{\Lambda }A|$=0, where $A$ is identity matrix. Thus The three eigenvalues of the Jacobean matrix at disease free equilibrium (DFE) are ${\mathrm{\Lambda }}_1=-d_0$, ${\mathrm{\Lambda }}_2=-b$ and ${\mathrm{\Lambda }}_3=\frac{b(d_0+h)+\eta (d_0+\mu )}{b}\left({\mathcal{R}}_0-1\right)-\frac{\eta \sigma }{b}$. Clearly, the first two eigenvalues are negative, whereas, the third eigenvalue is negative only if ${\mathcal{R}}_0<1$. Hence the proof.

Theorem 2.6

Assume that ${\mathcal{R}}_0<1$ , then model (3) is stable globally at DFE ( $E_1$ ) (13) . Otherwise unstable.

Proof

We define a function is given by

$$F\left(t\right)=P_1\left(\frac{P}{P_1}-\ln \frac{P}{P_1}\right)+I\left(t\right)+Q\left(t\right)\text{.}$$

Differentiating $F\left(t\right)$, we get

$$\begin{array}{cc}\frac{\mathit{dF}}{\mathit{dt}}\hfill & =\left(\frac{\mathit{dP}}{\mathit{dt}}-\frac{P_1}{P}\frac{\mathit{dP}}{\mathit{dt}}\right)+\frac{\mathit{dI}}{\mathit{dt}}+\frac{\mathit{dQ}}{\mathit{dt}}\hfill \\ \hfill & =-\frac{P_1}{P}\frac{\mathit{dP}}{\mathit{dt}}+\frac{\mathit{dP}}{\mathit{dt}}+\frac{\mathit{dI}}{\mathit{dt}}+\frac{\mathit{dQ}}{\mathit{dt}}\text{.}\hfill \end{array}$$ (17)

Then

$$\frac{\mathit{dF}}{\mathit{dt}}=-\frac{P_1}{P}\left(\lambda -\gamma P\left(t\right)I\left(t\right)-d_{0}P\left(t\right)\right)+\lambda -d_0(P+I+Q)-\mu Q-\mathit{hI}\text{.}$$

The simplification and some re-arrangements gives

$$\frac{\mathit{dF}}{\mathit{dt}}=-\frac{{(\lambda -d_{0}P)}^2}{d_{0}P}+\frac{b\lambda \gamma -d_{0}b(d_0+h)}{{\mathit{bd}}_0}I-(d_0+\mu )Q\text{.}$$

As $Q=\frac{\eta }{b}I$, thus

$$\begin{array}{cc}\hfill \frac{\mathit{dF}}{\mathit{dt}}=& -\frac{{(\lambda -d_{0}P)}^2}{d_{0}P}+\frac{b\lambda \gamma -d_{0}b(d_0+h)}{{\mathit{bd}}_0}I-\frac{\eta (d_0+\mu )}{b}I,\hfill \\ \hfill =& -\frac{{(\lambda -d_{0}P)}^2}{d_{0}P}+\frac{b\lambda \gamma -d_{0}b(d_0+h)-d_0\eta (d_0+\mu )}{{\mathit{bd}}_0}I,\hfill \\ \hfill =& -\frac{{(\lambda -d_{0}P)}^2}{d_{0}P}+\frac{b(d_0+h)+\eta (d_0+\mu )}{b}\left({\mathcal{R}}_0-1\right)I\text{.}\hfill \end{array}$$

Thus, when ${\mathcal{R}}_0<1$, then $\frac{\mathit{dF}}{\mathit{dt}}<0$. Also, $\frac{\mathit{dF}}{\mathit{dt}}=0$ if and only if $P\left(t\right)=P_1$, $I\left(t\right)=0$ and $Q\left(t\right)=0$, which proves the conclusion.

3. Fundamental results

Definition 3.1

If $x\left(t\right)\in {\mathcal{H}}^1(0,\tau )$ and $r\in (0,1]$, then the ABC derivative is defined by

$${}^{\text{ABC}}\mathcal{D}_{+0}^r\varphi \left(t\right)=\frac{\mathrm{ABC}\left(r\right)}{1-r}{\int }_0^t\frac{d}{\mathit{dy}}x\left(y\right){\mathcal{E}}_r\left[\frac{-r}{1-r}{\left(t-y\right)}^r\right]\mathit{dy}\text{.}$$ (18)

We remark that if we replace ${\mathcal{M}}_r\left[\frac{-r}{1-r}{\left(t-y\right)}^r\right]$ by ${\mathcal{E}}_1=\exp \left[\frac{-r}{1-r}\left(t-y\right)\right]$ then we get the so-called Caputo-Fabrizo differential operator. Further it is to be noted that

$${}^{\text{ABC}}\mathcal{D}_{+0}^r\left[\mathit{Constant}\right]=0\text{.}$$

Here $\mathrm{ABC}\left(r\right)$ is known as normalization function which is defined as $\mathrm{ABC}\left(0\right)=\mathrm{ABC}\left(1\right)=1$. Also ${\mathcal{E}}_r$ stands for famous special function called Mittag–Leffler which is a generalization of the exponential function [19].

Definition 3.2

[20], [21] The Mittag–Leffler function ${\mathcal{E}}_r$ is defined as

$${\mathcal{E}}_r\left(t\right)={\displaystyle \sum _{k=0}^{\infty }}\frac{t^k}{\mathrm{\Gamma }(\mathit{kr}+1)},r>0\text{.}$$

In particularly if we take $r=1$ we get ${\mathcal{E}}_1\left(t\right)=\exp \left(t\right)$. In same way two parametric function of Mittag–Leffler is defined as

$${\mathcal{E}}_{r_1,r_2}\left(t\right)={\displaystyle \sum _{k=0}^{\infty }}\frac{t^k}{\mathrm{\Gamma }({\mathit{kr}}_1+r_2)},r_1,r_2>0\text{.}$$

Here again if we have $r_1=r_2=1$, then ${\mathcal{E}}_{1,1}\left(t\right)=\exp \left(t\right)$.

Definition 3.3

Let $x\in L[0,T]$, then the corresponding integral in $\mathrm{ABC}$ sense is given by

$${}^{\text{ABC}}\mathbf{I}_0^{r}x\left(t\right)=\frac{1-r}{\mathrm{ABC}\left(r\right)}x\left(t\right)+\frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}{\int }_0^t{(t-y)}^{r-1}x\left(y\right)\mathit{dy}\text{.}$$ (19)

Lemma 3.4

(See Proposition 3 in [44]) The solution of the given problem for $1>r>0$

$$\begin{array}{cc}\hfill & {}^{\text{ABC}}\mathcal{D}_0^{r}x\left(t\right)=z\left(t\right),t\in [0,T],\hfill \\ \hfill & x\left(0\right)=x_0,\hfill \end{array}$$

is provided by

$$x\left(t\right)=x_0+\frac{(1-r)}{\mathrm{ABC}\left(r\right)}z\left(t\right)+\frac{r}{\mathrm{\Gamma }\left(r\right)\mathrm{ABC}\left(r\right)}{\int }_0^t{(t-y)}^{r-1}z\left(y\right)\mathit{dy}\text{.}$$

Note:  For the qualitative analysis, we define Banach space $\mathbf{H}=\mathcal{X}\times \mathcal{X}\times \mathcal{X}$, where $\mathcal{X}=C[0,T]$ under the norm $\Vert \mathcal{W}\Vert =\Vert (P,I,Q)\Vert ={\max }_{t\in [0,T]}\left[\right|P\left(t\right)+\left|I\right(t\left)\right|+\left|Q\right(t\left)\right|]$.

The following fixed point theorem will be used to proceed in our main results.

Theorem 3.5 [46] —

Let $\mathcal{B}$ be a convex subset of $\mathbf{H}$ and assume that $\mathcal{F},\mathcal{G}$ are two operators with

• 1.  $\mathcal{F}w+\mathcal{G}w\in \mathcal{B}$ for every $w\in \mathcal{B}\text{;}$

• 2.  $\mathcal{F}$ is contraction;

• 3.  $\mathcal{G}$ is continuous and compact.

Then the operator equation $\mathcal{F}w+\mathcal{G}w=w$ has at least one solution.

4. Qualitative analysis of the considered model

Before analyzing any biological model, it is natural to ask weather such dynamical problem really exist or not. This question is guaranteed by fixed point theory. Here, we will try to use the same theory for the proposed problem (1) being part of this research. Regarding to the aforesaid need, we express the right sides of model (1) as

$$\begin{array}{cc}\hfill & {\mathrm{g}}_1(t,P,I,Q)=\lambda -\gamma P\left(t\right)I\left(t\right)-d_{0}P\left(t\right),\hfill \\ \hfill & {\mathrm{g}}_2(t,P,I,Q)=\gamma P\left(t\right)I\left(t\right)-(d_0+h+\eta )P\left(t\right)+\sigma Q\left(t\right),\hfill \\ \hfill & {\mathrm{g}}_3(t,P,I,Q)=\eta I\left(t\right)-(d_0+\mu +\sigma )Q\left(t\right)\text{.}\hfill \end{array}$$ (20)

With the help of (20), the developed system can be written in the form of

$$\begin{array}{cc}\hfill & {}^{\text{ABC}}\mathcal{D}_{+0}^r\mathcal{W}\left(t\right)=\mathrm{\Theta }(t,\mathcal{W}(t\left)\right),t\in [0,\tau ],0<r\le 1,\hfill \\ \hfill & \mathcal{W}\left(0\right)={\mathcal{W}}_0\text{.}\hfill \end{array}$$ (21)

Inview of Lemma 3.4, (21) yields

$$\mathcal{W}\left(t\right)={\mathcal{W}}_0\left(t\right)+\left[\mathrm{\Theta }(t,\mathcal{W}(t\left)\right)-{\mathrm{\Theta }}_0\left(t\right)\right]\frac{(1-r)}{\mathrm{ABC}\left(r\right)}+\frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}{\int }_0^t{(t-y)}^{r-1}\mathrm{\Theta }(y,\mathcal{W}(y\left)\right)\mathit{dy},$$ (22)

where

$$\mathcal{W}\left(t\right)=\left\{\begin{array}{cc}\hfill & P\left(t\right)\hfill \\ \hfill & I\left(t\right)\hfill \\ \hfill & Q\left(t\right)\hfill \end{array}\right),{\mathcal{W}}_0\left(t\right)=\left\{\begin{array}{cc}\hfill & P_0\hfill \\ \hfill & I_0\hfill \\ \hfill & Q_0\hfill \end{array}\right),\mathrm{\Theta }(t,\mathcal{W}(t\left)\right)=\left\{\begin{array}{cc}\hfill & {\mathrm{g}}_1(t,P,I,Q)\hfill \\ \hfill & {\mathrm{g}}_2(t,P,I,Q)\hfill \\ \hfill & {\mathrm{g}}_3(t,P,I,Q)\text{.}\hfill \end{array}\right){\mathrm{\Theta }}_0\left(t\right)=\left\{\begin{array}{cc}\hfill & {\mathrm{g}}_1(0,P_0,I_0,Q_0)\hfill \\ \hfill & {\mathrm{g}}_2(0,P_0,I_0,Q_0)\hfill \\ \hfill & {\mathrm{g}}_3(0,P_0,I_0,Q_0)\text{.}\hfill \end{array}\right)$$ (23)

Due to (22), (23), we define the two operators $\mathcal{F},\mathcal{G}$ from (22)

$$\begin{array}{cc}\hfill \mathcal{F}\left(\mathcal{W}\right)=& {\mathcal{W}}_0\left(t\right)+\left[\mathrm{\Theta }(t,\mathcal{W}(t\left)\right)-{\mathrm{\Theta }}_0\left(t\right)\right]\frac{(1-r)}{\mathrm{ABC}\left(r\right)},\hfill \\ \hfill \mathcal{G}\left(\mathcal{W}\right)=& \frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}{\int }_0^t{(t-y)}^{r-1}\mathrm{\Theta }(y,\mathcal{W}(y\left)\right)\mathit{dy}\text{.}\hfill \end{array}$$ (24)

Expressing some growth condition and Lipschitzian assumption for existence uniqueness as:

• $\left(A_1\right)$
  There exists constants $C_{\mathrm{\Theta }},D_{\mathrm{\Theta }},$ such that

  $$\left|\mathrm{\Theta }\right(t,\mathcal{W}\left(t\right)\left)\right|⩽C_{\mathrm{\Theta }}\left|\mathcal{W}\right|+D_{\mathrm{\Theta }}\text{.}$$
• $\left(A_2\right)$
  There exists constants $L_{\mathrm{\Theta }}>0$ such that for each $\mathcal{W},\bar{\mathcal{W}}\in \mathbf{H}$ such that

  $$\left|\mathrm{\Theta }\right(t,\mathcal{W})-\mathrm{\Theta }(t,\bar{\mathcal{W}}\left)\right|⩽L_{\mathrm{\Theta }}\left[\right|\mathcal{W}|-\bar{\mathcal{W}}|]\text{.}$$

Theorem 4.1

Under the hypothesis $(A_1,A_2)$ , the Integral equation (22) has at least one solution which consequently means that the considered system (1) has the same number of solution if $\frac{(1-r)}{\mathrm{ABC}\left(r\right)}{L}_{\mathrm{\Theta }}<1$ .

Proof

We prove the theorem in two step as bellow:

Step I: Let $\bar{\mathcal{W}}\in \mathcal{B}$, where $\mathcal{B}=\{\mathcal{W}\in \mathbf{H}:\Vert \mathcal{W}\Vert ⩽\rho ,\rho >0\}$ is closed convex set. Then using the definition of $\mathcal{F}$ in (24), one get

$$\begin{array}{cc}\hfill \Vert \mathcal{F}\left(\mathcal{W}\right)-\mathcal{F}\left(\bar{\mathcal{W}}\right)\Vert =& \frac{(1-r)}{\mathrm{ABC}\left(r\right)}{\displaystyle \underset{t\in [0,\tau ]}{\max }}\left|\mathrm{\Theta }\right(t,\mathcal{W}\left(t\right))-\mathrm{\Theta }(t,\bar{\mathcal{W}}\left(t\right)\left)\right|,\hfill \\ \hfill ⩽& \frac{(1-r)}{\mathrm{ABC}\left(r\right)}{L}_{\mathrm{\Theta }}\Vert \mathcal{W}-\bar{\mathcal{W}}\Vert \text{.}\hfill \end{array}$$ (25)

Hence $\mathcal{F}$ is contraction.

Step-II: To show that $\mathcal{G}$ is relatively compact, we must show that $\mathcal{G}$ is bounded, and equi-continuous. To show this, we proceed as: Clearly, $\mathcal{G}$ is continuous as $\mathrm{\Theta }$ is continuous and also for any $\mathcal{W}\in \mathcal{B}$, we have

$$\begin{array}{cc}\hfill \Vert \mathcal{G}\left(\mathcal{W}\right)\Vert =& {\displaystyle \underset{t\in [0,\tau ]}{\max }}\Vert \frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}{\int }_0^t{(t-y)}^{r-1}\mathrm{\Theta }(y,\mathcal{W}(y\left)\right)\mathit{dy}|,\hfill \\ \hfill ⩽& \frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}{\int }_0^{\tau }{(\tau -y)}^{r-1}\left|\mathrm{\Theta }\right(y,\mathcal{W}\left(y\right)\left)\right|\mathit{dy},\hfill \\ \hfill ⩽& \frac{{\tau }^r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}[C_{\mathrm{\Theta }}\rho +D_{\mathrm{\Theta }}]\text{.}\hfill \end{array}$$ (26)

Hence (36) implies that $\mathcal{G}$ is bounded. For equi-continuity we let $t_1>t_2\in [0,\tau ]$, so that

$$\begin{array}{cc}\hfill \left|\mathcal{G}\right(\mathcal{W}\left(t_1\right)-\mathcal{G}\left(\mathcal{W}\right(t_1\left)\right|=& \frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}\left|{\int }_0^{t_1}{(t_1-y)}^{r-1}\mathrm{\Theta }\right(y,\mathcal{W}\left(y\right))\mathit{dy}-{\int }_0^{t_1}{(t_1-y)}^{r-1}\mathrm{\Theta }(y,\mathcal{W}\left(y\right)\left)\mathit{dy}\right|,\hfill \\ \hfill ⩽& \frac{[C_{\mathrm{\Theta }}\rho +D_{\mathrm{\Theta }}]}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}[t_1^r-t_2^r]\text{.}\hfill \end{array}$$ (27)

Right side in (27) becomes zero at $t_1\to t_2$. Since $\mathcal{G}$ is continues and so

$$\left|\mathcal{G}\right(\mathcal{W}\left(t_1\right)-\mathcal{G}\left(\mathcal{W}\right(t_1\left)\right|\to 0,\mathrm{as}{t}_1\to t_2\text{.}$$

Since, $\mathcal{G}$ is a bounded operator and continuous as well, therefore, $\mathcal{G}$ is uniformly continuous and bounded. Thus, by Arzelá-Ascoli theorem $\mathcal{G}$ is relatively compact and so completely continuous. Hence, by Theorem 4.1 the integral equation (22) has at least one solution and consequently the system under consideration has at least one solution.

For uniqueness we give the next result.

Theorem 4.2

Under assumption $\left(A_2\right)$ , the integral equation (22) has unique solution which yields that the system under consideration (1) has the unique result if $\left[\frac{(1-r)L_{\mathrm{\Theta }}}{\mathrm{ABC}\left(r\right)}+\frac{{\tau }^r{L}_{\mathrm{\Theta }}}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}\right]<1$ .

Proof

Let the operator $\mathcal{T}:\mathbf{H}\to \mathbf{H}$ defined by

$$\mathcal{TW}\left(t\right)={\mathcal{W}}_0\left(t\right)+\left[\mathrm{\Theta }(t,\mathcal{W}(t\left)\right)-{\mathrm{\Theta }}_0\left(t\right)\right]\frac{(1-r)}{\mathrm{ABC}\left(r\right)}+\frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}{\int }_0^t{(t-y)}^{r-1}\mathrm{\Theta }(y,\mathcal{W}(y\left)\right)\mathit{dy},t\in [0,\tau ]\text{.}$$ (28)

Let $\mathcal{W},\bar{\mathcal{W}}\in \mathbf{H}$, then one can take

$$\begin{array}{cc}\hfill \Vert \mathcal{TW}-\mathcal{T}\bar{\mathcal{W}}\Vert ⩽& \frac{(1-r)}{\mathrm{ABC}\left(r\right)}{\displaystyle \underset{t\in [0,\tau ]}{\max }}\left|\mathrm{\Theta }\right(t,\mathcal{W}\left(t\right))-\mathrm{\Theta }(t,\bar{\mathcal{W}}\left(t\right)\left)\right|,+\frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}{\displaystyle \underset{t\in [0,\tau ]}{\max }}\left|{\int }_0^t{(t-y)}^{r-1}\mathrm{\Theta }\right(y,\mathcal{W}\left(y\right))\mathit{dy}-{\int }_0^t{(t-y)}^{r-1}\mathrm{\Theta }(y,\bar{\mathcal{W}}\left(y\right)\left)\mathit{dy}\right|,\hfill \\ \hfill ⩽& \mathbf{A}\Vert \mathcal{W}-\bar{\mathcal{W}}\Vert ,\hfill \end{array}$$ (29)

where

$$\mathbf{A}=\left[\frac{(1-r)L_{\mathrm{\Theta }}}{\mathrm{ABC}\left(r\right)}+\frac{{\tau }^r{L}_{\mathrm{\Theta }}}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}\right]\text{.}$$ (30)

Hence, $\mathcal{T}$ is contraction from (29). Thus, the integral equation (22) has a unique solution and so does system (1) has a unique solution.

Next, to develop and present some results on stability of the problem, we will consider a small perturbation $\varphi \in C[0,T]$ which depends only on the solution and $\varphi \left(0\right)=0$. Further.

• • $\left|\varphi \right(t\left)\right|⩽\epsilon ,\mathrm{for}\epsilon >0$;
• • ${}^{\text{ABC}}\mathcal{D}_{+0}^r\mathcal{W}\left(t\right)=\mathrm{\Theta }(t,\mathcal{W}(t\left)\right)+\varphi \left(t\right)\text{.}$

Lemma 4.3

The solution of the perturbed problem

$$\begin{array}{cc}\hfill & {}^{\text{ABC}}\mathcal{D}_{+0}^r\mathcal{W}\left(t\right)=\mathrm{\Theta }(t,\mathcal{W}(t\left)\right)+\varphi \left(t\right),\hfill \\ \hfill & \mathcal{W}\left(0\right)={\mathcal{W}}_0\text{.}\hfill \end{array}$$ (31)

satisfies the following relation

$$\begin{array}{cc}\hfill \left|\mathcal{W}\right(t)-& \left({\mathcal{W}}_0\left(t\right)+\left[\mathrm{\Theta }(t,\mathcal{W}(t\left)\right)-{\mathrm{\Theta }}_0\left(t\right)\right]\frac{(1-r)}{\mathrm{ABC}\left(r\right)}+\frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}{\int }_0^t{(t-y)}^{r-1}\mathrm{\Theta }(y,\mathcal{W}(y\left)\right)\mathit{dy}\right)|,\hfill \\ \hfill ⩽& \frac{\mathrm{\Gamma }\left(r\right)+{\tau }^r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}\epsilon ={\mathrm{\Omega }}_{\tau ,r}\text{.}\hfill \end{array}$$ (32)

Proof

The proof is straight forward so we omit it.

Theorem 4.4

Under assumption $\left(A_2\right)$ together with Result 32 in Lemma 4.3 , the solution of the integral equation (22) is Ulam-Hyers stable and consequently, the analytical results of the considered system are Ulam-Hyers stable if $\mathbf{A}<1$ , where $\mathbf{A}$ is given in (30) .

Proof

Let $\mathcal{W}\in \mathbf{H}$ be any solution and $\bar{\mathcal{W}}\in \mathbf{H}$ be unique solution of (22), then

$$\begin{array}{cc}\hfill \left|\mathcal{W}\right(t)-\bar{\mathcal{W}}(t\left)\right|=& \left|\mathcal{W}\right(t)-\left({\mathcal{W}}_0\left(t\right)+\left[\mathrm{\Theta }(t,\bar{\mathcal{W}}(t\left)\right)-{\mathrm{\Theta }}_0\left(t\right)\right]\frac{(1-r)}{\mathrm{ABC}\left(r\right)}+\frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}{\int }_0^t{(t-y)}^{r-1}\mathrm{\Theta }(y,\bar{\mathcal{W}}(y\left)\right)\mathit{dy}\right)|,\hfill \\ \hfill & ⩽\left|\mathcal{W}\right(t)-\mathcal{W}(t\left)\right|=\left|\mathcal{W}\right(t)-\left({\mathcal{W}}_0\left(t\right)+\left[\mathrm{\Theta }(t,\mathcal{W}(t\left)\right)-{\mathrm{\Theta }}_0\left(t\right)\right]\frac{(1-r)}{\mathrm{ABC}\left(r\right)}+\frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}{\int }_0^t{(t-y)}^{r-1}\mathrm{\Theta }(y,\mathcal{W}(y\left)\right)\mathit{dy}\right)|,\hfill \\ \hfill -& \left({\mathcal{W}}_0\left(t\right)+\left[\mathrm{\Theta }(t,\mathcal{W}(t\left)\right)-{\mathrm{\Theta }}_0\left(t\right)\right]\frac{(1-r)}{\mathrm{ABC}\left(r\right)}+\frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}{\int }_0^t{(t-y)}^{r-1}\mathrm{\Theta }(y,\mathcal{W}(y\left)\right)\mathit{dy}\right)|,\hfill \\ \hfill -& \left({\mathcal{W}}_0\left(t\right)+\left[\mathrm{\Theta }(t,\bar{\mathcal{W}}(t\left)\right)-{\mathrm{\Theta }}_0\left(t\right)\right]\frac{(1-r)}{\mathrm{ABC}\left(r\right)}+\frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}{\int }_0^t{(t-y)}^{r-1}\mathrm{\Theta }(y,\bar{\mathcal{W}}(y\left)\right)\mathit{dy}\right)|,\hfill \\ \hfill ⩽& {\mathrm{\Omega }}_{\tau ,r}+\frac{(1-r)L_{\mathrm{\Theta }}}{\mathrm{ABC}\left(r\right)}\Vert \mathcal{W}-\bar{\mathcal{W}}\Vert +\frac{{\tau }^r{L}_{\mathrm{\Theta }}}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}\Vert \mathcal{W}-\bar{\mathcal{W}}\Vert ,\hfill \end{array}$$

$$\Vert \mathcal{W}-\bar{\mathcal{W}}\Vert ⩽{\mathrm{\Omega }}_{\tau ,r}+\mathbf{A}\Vert \mathcal{W}-\bar{\mathcal{W}}\Vert \text{.}$$ (33)

From (33), we can write

$$\Vert \mathcal{W}-\bar{\mathcal{W}}\Vert ⩽\frac{{\mathrm{\Omega }}_{\tau ,r}}{1-\mathbf{A}}\Vert \mathcal{W}-\bar{\mathcal{W}}\Vert \text{.}$$ (34)

Hence the result (34) concluded that the solution of (22) is Ulam-Hyers stable and consequently the solution of the considered system is Ulam -Hyers stable.

5. Numerical analysis of the constructed model (1)

Here we are going to construct a numerical procedure for the concerned model to perform simulation. Here we use a coupled numerical method due to the combination of “fundamental theorem of fractional calculus and the two-step Lagrange polynomial” as used in [49]. From first equation of model (1), we let

$$\begin{array}{cc}\hfill {}^{\text{ABC}}\mathcal{D}_{+0}^{r}P\left(t\right)=& {\mathrm{g}}_1(t,P(t),I(t),R(t\left)\right),\hfill \\ \hfill P\left(0\right)=& P_0\text{.}\hfill \end{array}$$ (35)

Inview of Lemma 3.4, (35) implies that

$$P\left(t\right)=P_0\frac{1-r}{\mathrm{ABC}\left(r\right)}{\mathrm{g}}_1(t,P(t),I(t),Q(t\left)\right)+\frac{r}{\mathrm{ABC}\left(r\right)}\frac{1}{\mathrm{\Gamma }\left(r\right)}{\int }_0^t{(t-y)}^{r-1}{\mathrm{g}}_1(y,P(y),I(y),R(y\left)\right)\mathit{dy}\text{.}$$ (36)

Now interm of Lagrange interpolation polynomials, we may write over $[t_k,t_{k+1}]$, the function

$${\mathrm{g}}_1(y,P(y),I(y),R(y\left)\right)\mathrm{with}\mathrm{h}=t_k-t_{k-1}$$

as

$${\mathbf{P}}_k\approx \frac{1}{\mathrm{h}}\left[(y-t_{k-1}){\mathrm{g}}_1(t_k,P(t_k),I(t_k),Q(t_k\left)\right)-(y-t_k){\mathrm{g}}_1(t_{k-1},P(t_{k-1}),I(t_{k-1}),Q(t_{k-1}\left)\right)\right]\text{.}$$ (37)

Plugging (37) in (36), we may write (36) as

$$\begin{array}{cc}\hfill P\left(t_{n+1}\right)=& P_0+\frac{(1-r)}{\mathrm{ABC}\left(r\right)}{\mathrm{g}}_1(t_k,P(t_k),I(t_k),Q(t_k\left)\right)+\frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}{\displaystyle \sum _{j=0}^n}\left(\frac{{\mathrm{g}}_1(t_j,P(t_j),I(t_j),Q(t_j\left)\right)}{\mathrm{h}}{\int }_{t_j}^{t_{j+1}}(y-t_{j-1}){(t_{n+1}-y)}^{r-1}\mathit{dy}-\frac{{\mathrm{g}}_1(t_{j-1},P(t_{j-1}),I(t_{j-1}),Q(t_{j-1}\left)\right)}{\mathrm{h}}{\int }_{t_j}^{t_{j+1}}(y-t_j){(t_{n+1}-y)}^{r-1}\mathit{dy}\right)\hfill \\ \hfill =& P_0+\frac{(1-r)}{\mathrm{ABC}\left(r\right)}{\mathrm{g}}_1(t_n,P(t_n),I(t_n),Q(t_n\left)\right)+\frac{r}{\mathrm{ABC}\left(r\right)\mathrm{\Gamma }\left(r\right)}{\displaystyle \sum _{j=0}^n}\left(\frac{{\mathrm{g}}_1(t_j,P(t_j),I(t_j),R(t_j\left)\right)}{\mathrm{h}}{\mathrm{\Omega }}_{j-1,r}-\frac{{\mathrm{g}}_1(t_{j-1},P(t_{j-1}),I(t_{j-1}),Q(t_{j-1}\left)\right)}{\mathrm{h}}{\mathrm{\Lambda }}_{j,r}\right),\hfill \end{array}$$ (38)

where the notions ${\mathrm{\Omega }}_{j-1,r}$ and ${\mathrm{\Lambda }}_{j,r}$ are given bellow

$$\begin{array}{cc}\hfill {\Omega }_{j-1,r}=& {\int }_{t_j}^{t_{j+1}}\left(y-t_{j-1}\right){\left(t_{n+1}-y\right)}^{r-1}\mathit{dy}\hfill \\ \hfill =& -\frac{1}{r}\left[\left(t_{j+1}-t_{j-1}\right){\left(t_{n+1}-t_{j+1}\right)}^r-\left(t_j-t_{j-1}\right){\left(t_{n+1}-t_j\right)}^r\right]-\frac{1}{r\left(r+1\right)}\left[{\left(t_{n+1}-t_{j+1}\right)}^{r+1}-{\left(t_{n+1}-t_j\right)}^{r+1}\right]\hfill \end{array}$$ (39)

and

$$\begin{array}{cc}\hfill {\Lambda }_{j,r}=& {\int }_{t_j}^{t_{j+1}}\left(y-t_j\right){\left(t_{n+1}-y\right)}^{r-1}\mathit{dy}\hfill \\ \hfill =& -\frac{1}{r}\left[\left(t_{j+1}-t_j\right){\left(t_{n+1}-t_{j+1}\right)}^r\right]-\frac{1}{r\left(r+1\right)}\left[{\left(t_{n+1}-t_{j+1}\right)}^{r+1}-{\left(t_{n+1}-t_j\right)}^{r+1}\right]\text{.}\hfill \end{array}$$ (40)

Put $t_j=j\mathrm{h},$ in (39), (40), one has

$$\begin{array}{cc}\hfill {\Omega }_{j-1,r}=& -\frac{{\mathrm{h}}^{r+1}}{r}\left[\left(j+1-\left(j-1\right)\right){\left(n+1-\left(j+1\right)\right)}^r-\left(j-\left(j-1\right)\right){\left(n+1-j\right)}^r\right]-\frac{{\mathrm{h}}^{r+1}}{r\left(r+1\right)}\left[{\left(n+1-\left(j+1\right)\right)}^{r+1}-{\left(n+1-j\right)}^{r+1}\right]\hfill \\ \hfill =& \frac{{\mathrm{h}}^{r+1}}{r\left(r+1\right)}\left[-2\left(r+1\right){\left(n-j\right)}^r+\left(r+1\right){\left(n+1-j\right)}^r-{\left(n-j\right)}^{r+1}+{\left(n+1-j\right)}^{r+1}\right]\hfill \\ \hfill =& \frac{{\mathrm{h}}^{r+1}}{r\left(r+1\right)}\left[{\left(n-j\right)}^r\left(-2\left(r+1\right)-\left(n-j\right)\right)+{\left(n+1-j\right)}^r\left(r+1+n+1-j\right)\right]\hfill \\ \hfill =& \frac{{\mathrm{h}}^{r+1}}{r\left(r+1\right)}\left[{\left(n+1-j\right)}^r\left(n-j+2+r\right)-{\left(n-j\right)}^r\left(n-j+2+2r\right)\right]\text{.}\hfill \end{array}$$ (41)

and

$$\begin{array}{cc}\hfill {\Lambda }_{j,r}=& -\frac{{\mathrm{h}}^{r+1}}{r}\left[\left(j+1-j\right){\left(n+1-\left(j+1\right)\right)}^r\right]-\frac{h^{r+1}}{r\left(r+1\right)}\left[{\left(n+1-\left(j+1\right)\right)}^{r+1}-{\left(n+1-j\right)}^{r+1}\right]\hfill \\ \hfill =& \frac{{\mathrm{h}}^{r+1}}{r\left(r+1\right)}\left[-\left(r+1\right){\left(n-j\right)}^r-{\left(n-j\right)}^{r+1}+{\left(n+1-j\right)}^{r+1}\right]\hfill \\ \hfill =& \frac{{\mathrm{h}}^{r+1}}{r\left(r+1\right)}\left[{\left(n-j\right)}^r\left(-\left(r+1\right)-\left(n-j\right)\right)+{\left(n+1-j\right)}^{r+1}\right]\hfill \\ \hfill =& \frac{{\mathrm{h}}^{r+1}}{r\left(r+1\right)}\left[{\left(n+1-j\right)}^{r+1}-{\left(n-j\right)}^r\left(n-j+1+r\right)\right]\text{.}\hfill \end{array}$$ (42)

Substituting (41), (42) into (38), we get

$$P\left(t_{n+1}\right)=P\left(t_0\right)+\frac{1-r}{\mathrm{ABC}\left(r\right)}{\mathrm{g}}_1(t_n,P(t_n),I(t_n),Q(t_n\left)\right)+\frac{r}{\mathrm{ABC}\left(r\right)}{\displaystyle \sum _{j=0}^n}\left(\frac{{\mathrm{g}}_1(t_j,P(t_j),I(t_n),Q(t_n\left)\right)}{\mathrm{\Gamma }(r+2)}{\mathrm{h}}^r\left[{(n+1-j)}^r(n-j+2+r)-{(n-j)}^r(n-j+2+2r)\right]\right)-\left(\frac{{\mathrm{g}}_1(t_{j-1},P(t_{j-1}),I(t_{j-1}),Q(t_{j-1}\left)\right)}{\mathrm{\Gamma }(r+2)}{\mathrm{h}}^r\left[{(n+1-j)}^{r+1}-{(n-j)}^r(n-j+1+r)\right]\right)\text{.}$$ (43)

Similarly

$$I\left(t_{n+1}\right)=I\left(t_0\right)+\frac{1-r}{\mathrm{ABC}\left(r\right)}{\mathrm{g}}_2(t_n,P(t_n),I(t_n),Q(t_n\left)\right)+\frac{r}{\mathrm{ABC}\left(r\right)}{\displaystyle \sum _{j=0}^n}\left(\frac{{\mathrm{g}}_1(t_{j-1},P(t_{j-1}),I(t_{j-1}),Q(t_{j-1}\left)\right)}{\mathrm{\Gamma }(r+2)}{\mathrm{h}}^r\left[{(n+1-j)}^r(n-j+2+r)-{(n-j)}^r(n-j+2+2r)\right]\right)-\left(\frac{{\mathrm{g}}_2(t_{j-1},P(t_{j-1}),I(t_{j-1}),Q(t_{j-1}\left)\right)}{\mathrm{\Gamma }(r+2)}{\mathrm{h}}^r\left[{(n+1-j)}^{r+1}-{(n-j)}^r(n-j+1+r)\right]\right)$$ (44)

and

$$Q\left(t_{n+1}\right)=Q\left(t_0\right)+\frac{1-r}{\mathrm{ABC}\left(r\right)}{\mathrm{g}}_3(t_n,P(t_n),I(t_n),Q(t_n\left)\right)+\frac{r}{\mathrm{ABC}\left(r\right)}{\displaystyle \sum _{j=0}^n}\left(\frac{{\mathrm{g}}_3(t_{j-1},P(t_{j-1}),I(t_{j-1}),Q(t_{j-1}\left)\right)}{\mathrm{\Gamma }(r+2)}{\mathrm{h}}^r\left[{(n+1-j)}^r(n-j+2+r)-{(n-j)}^r(n-j+2+2r)\right]\right)-\left(\frac{{\mathrm{g}}_3(t_{j-1},P(t_{j-1}),I(t_{j-1}),Q(t_{j-1}\left)\right)}{\mathrm{\Gamma }(r+2)}{\mathrm{h}}^r\left[{(n+1-j)}^{r+1}-{(n-j)}^r(n-j+1+r)\right]\right)\text{.}$$ (45)

6. Numerical interpretation and discussion

This part is composed on two subsections. In first subsection we simulation the model 1 corresponding to integer order derivative by taking different initial values.

6.1. Numerical results and discussion for model 1 at $r=1$

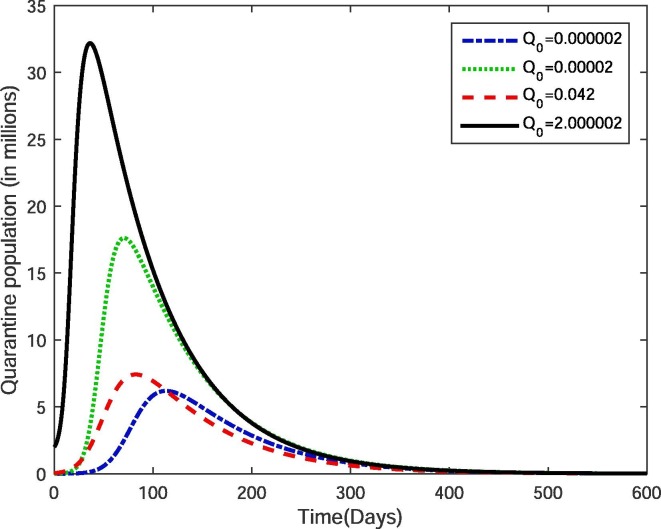
We carry out the simulation of the model 3 to verify the previous analytical results with the help of graphical representations. We used the data where its corresponding numerical values and sources are presented in Table 2 . By using the values shown in Table 2, sample simulation were carried out for susceptible population. We have consider four different initial population of susceptible individual, that is, $P_0=58.498998,65.498998,50.498998$, $70.498998$ where the population was considered in million and $58.498998$ million is the actual population. Whenever ${\mathcal{R}}_0<1$. In the case of ${\mathcal{R}}_0<1$, each solution curve $S\left(t\right)$ almost taking $550$ days in order to reach to its equilibrium value $P^0=5.343818752$. It means that if we wish to eliminate the disease from the community, still it will take enough time. Further, the figures show that the disease will effect a major portion of the population during the indicated course of outbreak. Further, Fig. 2, Fig. 3, Fig. 4 verify our theoretical findings that the disease-free equilibrium is locally and globally asymptotically stable if and only if ${\mathcal{R}}_0<1$.

Table 2.

Values and sources of parameter used in numerical simulation.

Parameter	Value	Source
$\mathrm{\Lambda }$	0.03805333333	fitted
$\gamma$	0.00594474	estimated
$d_0$	0.007121000000	[47]
$\eta$	0.144211141	estimated
$\nu$	0.007121000000	[47]
$\sigma$	0.0052281	estimated
$k$	0.027864676	estimated

Fig. 2.

Dynamics of susceptible individuals $S\left(t\right)$ for ${\mathcal{R}}_0<1$.

Fig. 3.

Behavior of infected population when ${\mathcal{R}}_0<1$.

Fig. 4.

Quarantine population in case of ${\mathcal{R}}_0<1$.

6.2. Numerical results under fractional order derivative

Now we taking Numerical simulation for model 1. We take some approximation to real values of the parameters of some locality which is considered in the model. The assumed values of the parameters are presented as given in Table 3 . We took hypothetical initial population of susceptible, infected and quarantined to be $10,0.01,0.0011$ millions, respectively. The approximate percentage of the density in the total population twenty-one thousands of the selected people susceptible people were $0.6$, infected were $0.2$ and quarantined were of $0.2$. Thank to the numerical procedure is given in Section 5, we simulate the results in the following Fig. 5, Fig. 7 as: We have simulated the results by using the afore established numerical method of in Section 5 subject to the given numerical values. From 5, we see that as the papulation of susceptible class is decreasing with different rate due to fractional order. As a results infection is going on increasing at various fractional order in Fig. 6. Smaller the order faster the growth and decay rate and hence these classes rapidly approaching to their concerned stable position. On the other hand when the infected papulation is increasing as a result more people should be sent to quarantined and hence the density of this class is also growing as shown in Fig. 7. From Fig. 5, Fig. 6, Fig. 7 , one can observe that fractional derivative produces the global dynamics of the concerned model in which smaller the order faster will be the growth and decay rate of the concerned papulation and vice versa.

Table 3.

Description of the parameters that are involved in the considered model (1).

Notation	Parameters description	Numerical value
$\lambda$	Recruitment rate	$0.003$
$\gamma$	Disease transmission rate	$0.009$
$d_0$	Natural death rate	$0.009$
$\eta$	Rate at which infected are getting quarantine	$0.004$
$\mu$	Disease-related death rate in quarantined individuals	$0.004$
$\sigma$	Rate at which quarantined people getting infection	$0.003$
$h$	Disease-related death rate in infected people	$0.007$
$P_0$	Initial population of susceptible	$10$ million
$I_0$	Initially infected population	$0.01$ million
$Q_0$	Quarantined people at $t=0$	$0.0011$ million

Fig. 5.

Fractional dynamics of susceptible class in model (1) at various values of fractional order $r$.

Fig. 7.

Fractional dynamics of quarantined class in model (1) at various values of fractional order $r$.

Fig. 6.

Fractional dynamics of infected class in model (1) at various values of fractional order $r$.

7. Conclusion

A new mathematical model of three different compartments of present novel coronavirus infection has been established under the nonlocal and nonsingular kernel type derivative. Further its existence has been demonstrated via the use of classical fixed point results of Banach and Guo -Krasnoselskii. Also stability results have been established. By using Adams–Bashforth numerical method of fractional type the numerical simulations were performed which addressed as the infection go on increasing, then more people will be pushed into quarantined so that other people may be saved from being infected in a community. On the other hand if before self quarantined is adopted then the process may go on reverse direction and infection will be deceasing and hence healthy community may be restored.

Funding

There is no Funding source available to support this research work.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.