Abstract
The corona pandemic significantly changes the processes of aircraft and passenger handling at the airport. In our contribution, we focus on the time-critical process of aircraft boarding, where regulations regarding physical distances between passengers will significantly increase boarding time. The passenger behavior is implemented in a field-validated stochastic cellular automata model, which is extended by a module to evaluate the transmission risk. We propose an improved boarding process by considering that most of the passengers are travel together and should be boarded and seated as a group. The NP-hard seat allocation of groups with minimized individual interactions between groups is solved with a genetic algorithm. Then, the improved seat allocation is used to derive an associated boarding sequence aiming at both short boarding times and low risk of virus transmission. Our results show that the consideration of groups will significantly contribute to a faster boarding (reduction of time by about 60%) and less transmission risk (reduced by 85%) compared to the standard random boarding procedures applied in the pandemic scenario.
Keywords: Aircraft boarding, Virus transmission, COVID19, Pandemic requirements, Cabin operations, Passenger groups, Optimization model, Genetic algorithm
1. Introduction
Air transportation offers international mobility in a globally well-connected network. Given the current pandemic situation caused by the new coronavirus SARS-CoV2, air transportation is part of the transmission chains and is sustainably affected (International Civil Aviation Organization (ICAO), 2020a). Along the passenger journey, the cabin operations demand to share a constricted environment with other passengers during boarding, flight, and deboarding. Thus, these operations hold the potential for virus transmissions between passengers and require appropriate seat allocation and strategies to reduce the transmission risk significantly. We assume that the requirements for future air traffic will also take into account pandemic-related regulations in addition to the safety and security regulations that are inherent in today’s air traffic. The constraints from pandemic situations lead to changes in passenger handling. Currently, airlines aim to protect passengers and crews from Covid-19 and see face covering as one mandatory action for passengers onboard (International Civil Aviation Organization (ICAO), 2020b, International Aviation Transport Association (IATA), 2020a). There are further key elements to efficiently face the transmission risk, such as temperature and symptom screening, cleaning and disinfection, or COVID-19 testing (International Aviation Transport Association (IATA), 2020b). A physical distance between passengers during aircraft boarding and deboarding is also part of these risk mitigation strategies (International Aviation Transport Association (IATA), 2020c). Within our contribution, we focus on the operational consequence of the distance requirement and provide a customer-oriented solution for both airlines and passengers. This enables a situational approach to establish both an appropriate seat allocation and aircraft entry sequence considering passenger groups and minimum interactions between groups of passengers.
1.1. Review of research on virus transmission in aircraft
The SARS outbreak in 2002 emphasizes the important role of air transportation in pandemic situations (Olsen et al., 2003a). The climate control system of aircraft seems to reduce the spreading of airborne pathogens by frequently recirculating the cabin air through high efficiency particulate air (HEPA) filters (Mangili and Gendreau, 2005, International Aviation Transport Association (IATA), 2020b). These filters are designed to filter at least 99.95% of aerosols and are capable of removing viruses and bacteria attached to droplets. But the transmission of infectious diseases is likely to be more frequent than reported for several reasons, such as much shorter flight times than incubation periods. When considering the passenger path to and in the aircraft cabin, upstream and downstream processes can also lead to infections (e.g. baggage handling, security checks). To minimize physical interactions, current handling approaches aim at a contactless passenger journey through the airport terminal. In a post-pandemic scenario, this contactless journey could include biometric scans or the use of personal mobile devices for services or inflight entertainment. Studies on reported in-flight transmissions emphasize that proximity to the index case increases the risk of transmission (Olsen et al., 2003a, Hertzberg and Weiss, 2016). The simulation of transmissions during flight, based on actual passenger behaviors in single-aisle aircraft, indicate a low probability of direct transmission to passengers not seated close to an infectious passenger (Hertzberg et al., 2018). An investigation of a long-haul flight indicates a low risk of pandemic influenza transmission close to infected passengers with symptoms (Baker et al., 2010). The calculation of the spatial and temporal distributions of droplets in an aircraft cabin showed a reduced influenza transmission risk if the respirator masks are used by the passengers (Gupta et al., 2012). The documentation of a symptomatic SARS-CoV2 index case flying a 15 h trip in economy class shows that all 25 passengers being seated within a range of 2 m from the index case were tested negative for SARS-CoV2 (Schwartz et al., 2020). Two other case studies reports 11 transmissions (Qian et al., 2020) and one potential infection during a flight (Eldin et al., 2020). A brief introduction about the understanding of SARS-CoV2 in the context of passenger boarding is given at Schultz and Fuchte (2020).
1.2. Review of aircraft boarding approaches
Comprehensive overviews are provided for aircraft ground operations, passenger boarding, and corresponding economic impact (Schmidt, 2017, Jaehn and Neumann, 2015, Schultz, 2018c, Nyquist and McFadden, 2008, Mirza, 2008, Cook and Tanner, 2015, Delcea et al., 2018, Schultz and Fricke, 2008). A common goal of simulation-based approaches for passenger boarding is to minimize boarding time. Thus, the efficiency of different boarding strategies was the focus of several research activities (Marelli et al., 1998, Van Landeghem and Beuselinck, 2002, Ferrari and Nagel, 2005, van den Briel et al., 2005, Bachmat and Elkin, 2008, Schultz et al., 2008, Bachmat et al., 2013, Steffen, 2008a). Whereas these models are based on cellular automaton or analytical approaches, there are also models from various fields, such as statistical mechanics (Steffen, 2008b), discrete-event simulations (Jafer and Mi, 2017), or mixed integer linear programs (Bazargan, 2007, Soolaki et al., 2012).
The quantity and quality of hand luggage determine the duration of boarding significantly. Thus, research was conducted with a particular focus on the physique of passengers (maximum speed), the quantity of hand luggage, and individually preferred distance (Tang et al., 2012), seats assigned to passengers with regards to hand luggage (Qiang et al., 2014, Milne and Salari, 2016, Steffen, 2008a, Milne and Kelly, 2014). Furthermore, the fact that passengers travel in groups has an impact on the boarding efficiency (Zeineddine, 2017, Schultz, 2018c). Other research aims at the evaluation of pre-boarding areas (Steiner and Philipp, 2009, Wallace, 2020), consideration of passenger expectations (Wittmann, 2019), use of apron busses (Milne et al., 2019), and real-time seat allocation (Schultz, 2018a, Yazdani et al., 2019). The impact of different aircraft cabin layouts on passenger boarding were focused on the following studies: aircraft interior design (seat pitch and passengers per row) (Bachmat et al., 2009), aircraft seating allocation and alternative designs single and twin-aisle configuration (Schultz et al., 2013, Chung, 2012), impact of aircraft cabin modifications (Fuchte, 2014), novel aircraft configurations and seating concepts (Schmidt et al., 2015, Schmidt et al., 2017), and dynamic change of the cabin infrastructure (Schultz, 2017b). Only a few experimental tests have been conducted to provide data for the calibration of input parameters and validation of simulation results: using a mock Boeing 757 fuselage (Steffen and Hotchkiss, 2012), time to store hand luggage items in the overhead compartments (Kierzkowski and Kisiel, 2017), small-scale laboratory tests (Gwynne et al., 2018), evaluation of passenger perceptions during boarding/deboarding (Miura and Nishinari, 2017), operational data and passenger data from field trial measurements (Schultz, 2017a, Schultz, 2018b), field trials for real-time seat allocation in connected aircraft cabin (Schultz, 2018a), and using a B737-800 mock-up (1/3 size) to explore the factors affecting the time of luggage storage (Ren et al., 2020).
The particular movement behavior of pedestrians depends significantly on group constellations (e.g. friends or families) and impacts the self-organization capabilities of crowds (Moussaïd et al., 2010, Schultz et al., 2013b, Zanlungo et al., 2019). Also in the context of passenger dynamics in the airport, it is an important fact that up to 70% of the tourists and 30% of the business passengers are traveling in groups (Schultz, 2010, Schultz and Fricke, 2011). The resulting group behavior is indirectly considered as non-compliant behavior of passengers when boarding the aircraft (e.g. couples should not be separated during boarding). In the literature, there are two definitions of the term “group”. The first one refers to a group as a batch of passengers which boards separately, e.g. “Group F boards last”. The second definition considers a group as a set of interconnected passengers, e.g. couples board together, and sit together. In our research, we focus on the second definition and assume that the self-organization within a group will minimize the time to take the individual seats. A very good example of considering both types of batches and sets of passengers is the concept of the flying carpet (Wallace, 2020). After passing the boarding counter a batch of passengers (up to 40) enter an area where the aircraft seat layout is painted/projected on the floor. Here each passenger takes his/her seat location and the whole batch will be easily pre-sorted. This smart idea prevents both passing passengers in the aisle and the separation of passengers traveling together. Operational tests (Wallace, 2020) and simulation studies (Schultz, 2018c) prove a significant reduction of the boarding time, even for small batch sizes (more than 20% reduction). Boarding an aircraft is mainly affected by interferences between passengers in the aisle and during the seating process. Group behavior may shorten the boarding time since conflicts during the seating process are reduced (Tang et al., 2018). Since passenger groups book seats in the same rows, aircraft boarding by rows should be the recommended practice (Kierzkowski and Kisiel, 2017). An approach of a dynamically optimized boarding indicates that the passenger boarding benefits from the consideration of groups (Zeineddine, 2017). Less complex boarding strategies (e.g. random or block boarding) benefit from the consideration of groups (approx. 5% faster boarding), while seat-based strategies (separation of window, middle, and aisle seats) lead to longer boarding times (Schultz, 2018c).
There are two new research contributions available, which set a focus on behaviors during pandemic situations and their impact on the aircraft boarding procedures. The first research addresses the quantity and quality of passenger interactions (Cotfas et al., 2020) and the second research additionally develops and implements a transmission model to provide a more detailed evaluation (Schultz and Fuchte, 2020). With a focus on airport operations, the impact of physical distances on the performance of security control lanes was analyzed to provide a reliable basis for appropriate layout adaptations (Kierzkowski and Kisiel, 2020). The particular requirements for the cabin cleaning and disinfection during the aircraft turnaround also demand adjusted procedures (Schultz et al., 2020).
1.3. Focus and structure of the document
We provide in this contribution an approach for aircraft boarding considering pandemic scenarios. These scenarios are mainly driven by the requirement of physical distance between passengers to ensure a minimal virus transmission risk during the boarding, flight, and deboarding. We consider passenger groups as an important factor to derive an appropriate seat allocation and boarding sequence. The main idea behind the group approach is that members of one group are allowed to be close to each other, as they are already in close contact with each other before boarding, while different groups should be separated as far apart as necessary. Deboarding is not explicitly considered in our contribution. The paper is structured as follows. After the introduction (Section 1), we present a stochastic cellular automata approach, which is used for modeling the passenger movements in the aircraft cabin (Section 2). A transmission model is implemented to evaluate the virus transmission risk during passenger movements and applied to evaluate standard boarding procedures. In Section 3, we introduce a problem description and optimization strategies considering passenger groups. The results of the optimization model are presented in Section 4, where we use a genetic algorithm for solving the complex problem. The achieved seat allocations are used as input for the passenger movement model to derive an appropriate boarding sequence with a minimized transmission risk during boarding. Finally, our contribution ends with a conclusion and outlook (Section 5).
2. Passenger boarding model using operational, individual, pandemic constraints
The initial model for movements of pedestrians was developed to provide a stochastic approach covering short (e.g. avoid collisions, group behavior (Schultz et al., 2013b)) and long-range interactions (e.g. tactical wayfinding) of human beings (Schultz, 2010). This cellular automata model is based on an individual transition matrix, which contains the transition probabilities to move to adjacent positions around the the current position of the passenger (Schultz, 2013).
2.1. Operational constraints and rules of movement
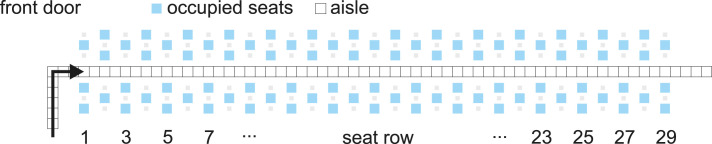
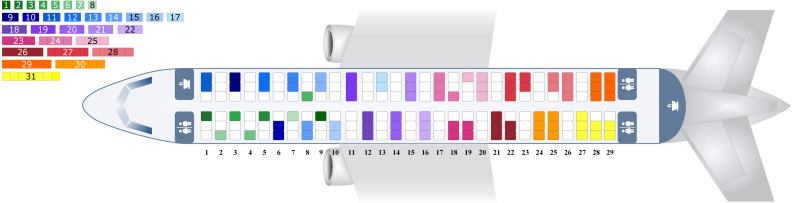
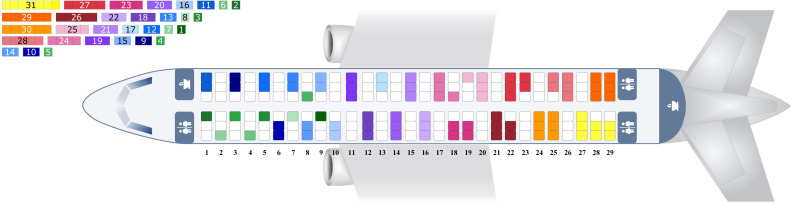
To reflect operational conditions of aircraft and airlines (e.g. seat load factor, conformance to the boarding procedure) as well as the non-deterministic nature of the underlying passenger processes (e.g. hand luggage storage) the stochastic model was developed (Schultz et al., 2008, Schultz et al., 2013) and calibrated (Schultz, 2017a, Schultz, 2018b). The model will be used for the passenger movements during the aircraft boarding. The passenger boarding is modeled with a cellular automata approach based on a regular grid (Fig. 1). This regular grid consists of equal cells with a size of 0.4 × 0.4 m, whereas a cell can either be empty or contain exactly one passenger.
Fig. 1.
Grid-based model — Airbus A320 with 29 seat rows and 6 seats per row (reference layout).
The boarding progress consists of a simple set of rules for the passenger movement: (a) enter the aircraft at the assigned door (based on the current boarding scenario), (b) move forward from cell to cell along the aisle until reaching the assigned seat row, and (c) store the luggage (aisle is blocked for other passengers) and take the seat. The storage time for the hand luggage depends on the individual number of hand luggage items. The seating process depends on the constellation of already used seats in the corresponding row. A scenario is defined by the seat allocation, the number of passengers to board, the number of available doors, the boarding strategy, and the conformance of passengers in following the current strategy. Further details about the model and the simulation environment can be found in Schultz (2018c) and for parameter validation in Schultz (2018b).
In the simulation environment, the boarding process is implemented as follows. Depending on the seat load, a specific number of randomly chosen seats are used for boarding. For each seat, an agent (passenger) is created. Each agent can walk along the aisle with a maximum of 0.8 m/s (Schultz, 2018a). The individual time for storing the hand luggage is derived from a Weibull distribution with the shape parameter and the scale parameter s (Schultz, 2018c). This distribution is derived during field trials and replaces the assumption of a given distribution of a specific number of hand luggage items (Schultz, 2018b). Within the model, there is no consideration of specific challenges during boarding, which are arising from blocked overhead compartments or limited capacity to store individual hand luggage items.
Each necessary interaction between agents (movements) during the seating processes (seat shuffle) is defined by a triangular distribution with 1.8 s, 2.4 s, and 3 s for , , and respectively (Schultz et al., 2013). The chronological order of occupying the seat rows affects the boarding time, due to the required coordination of position changes (seat shuffle, cf. Bazargan, 2007, Schultz et al., 2008). In the worst case, the aisle and the middle seats are already occupied and the arriving passenger wants to sit in the window seat. For this constellation, 9 movements are necessary for stepping out of the row, (re-) entering the row, and unblocking the aisle. The other seat occupation patterns demand 4 (aisle seat blocked) and 5 movements (middle seat is blocked and the window seat is the target). If the passenger can enter his seat without any interference, the time for entering the seat row is defined with 1 movement (Schultz, 2018c).
The agents are sequenced with regard to the active boarding strategy. From this sequence, a given percentage of agents are taken out of the sequence (non-conforming behavior) and inserted into a position, which contradicts the current strategy (e.g. inserted into a different boarding block). A waiting queue at the aircraft door is implemented and each agent enters this queue at the arrival time. In each simulation step, the first agent of the queue enters the aircraft by moving to the entry cell of the aisle grid (aircraft door), if this cell is free. Then, all agents located in the aisle move forward to the next cell, if possible (free cell and not arrived at the seat row), using a shuffled sequential update procedure (emulate parallel update behavior (Schultz, 2010, Schultz, 2013)). If the agent arrives at the assigned seat row, the corresponding cell at the aisle is blocked until the hand luggage is stored. When the seating process is finished the aisle cell is set free. Each boarding scenario is simulated 125,000 times, to achieve statistically relevant results defined by the average boarding time (starts when the first passenger arrives the aircraft and finished when the last passenger is seated) and the standard deviation of boarding times.
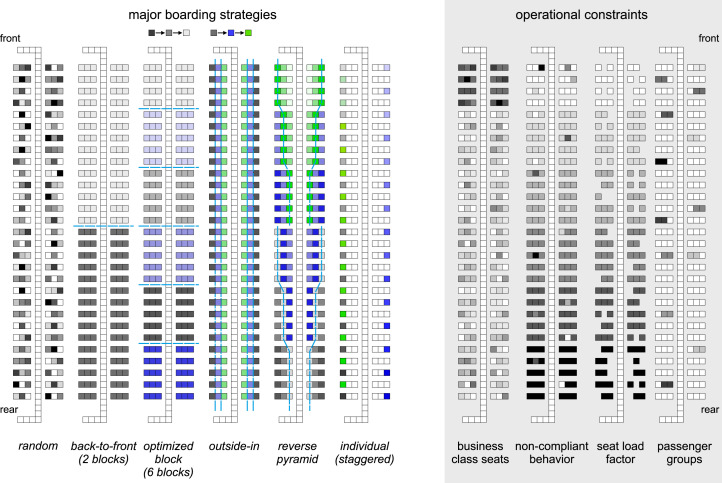
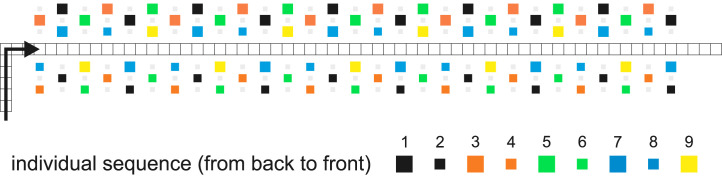
Boarding strategies are derived from three major approaches: boarding per row (aggregated to blocks), boarding per seat (window, middle, aisle), and sequences of specific seats. Fig. 2 (left) depicts how the boarding strategies and operational constraints are implemented in the boarding model. The seats are color-coded to emphasize the order of aircraft seats in the boarding sequence. Six different boarding strategies are generally considered: random, back-to-front (based on 2 blocks), optimized block (based on 6 blocks), outside-in (window seats first, aisle seats last), reverse pyramid (back-to-front plus outside-in with 6 blocks), and individual seating.
Fig. 2.
Overview of different boarding strategies (darker seats are boarded first; black–blue–green) and implementation of operational constraints in the cellular automata model (Schultz, 2018c). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Thus, boarding strategies range from random boarding without a specific order to individual boarding, which is a specific solution of the optimized block (alternating seats) and the outside-in strategy (each block contains only one seat). Fig. 2 (right) illustrates how the operational constraints of 1 class seats, passenger conformance, seat load factor, and the existence of passenger groups are covered by the boarding model.
2.2. Transmission model
The fundamental cellular automata model for the stochastic passenger movements is extended by an approach to evaluate the risk of virus transmission during the boarding process. The transmission risk can be defined by two major input factors: distance to the index case and reduction of contact time. A straight forward approach is to count both the individual interactions (passengers located in adjacent cells) and the duration of these contacts in the aisle and during the seating process. However, counting the individual contacts will only provide a first indication about potential ways of infections.
We derived a more comprehensive approach, which is based on the transmission model (Smieszek, 2009) defining the spread of SARS-CoV2 as a function of different public distancing measures (Müller et al., 2020). The probability of a person to become infected by person is described in (1).
| (1) |
defined by:
-
the probability of the person to receive an infectious dose. This shall not be understood as “infection probability”, because this strongly depends on the immune response by the affected person.
-
the calibration factor for the specific disease.
-
the shedding rate, the amount of virus the person spreads during the time step .
-
the intensity of the contact between and during the time step , which corresponds to their distance.
-
the time the person interacts with person during the time step .
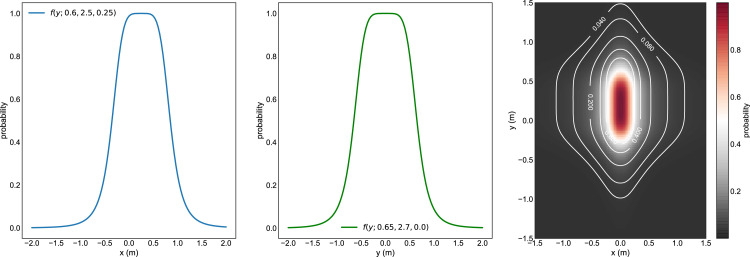
In our approach, we define the shedding rate as a normalized bell-shaped function (2) with for both longitudinal and lateral dimensions, respectively. The parameters are (scaling factor), (slope of leading and falling edge), and (offset) to determine the shape of the curve.
| (2) |
In a preceding study (Schultz and Fuchte, 2020), was calibrated on the transmission events of an actual flight (Olsen et al., 2003b). Thus, we are using the corresponding parameter setting with , , , , , and . This generates a slightly smaller footprint in -direction (lateral to moving direction) than in -direction (longitudinal to moving direction). Additionally, the spread in -direction is higher in front of the index case than behind it (see Fig. 3). Consequently, the moving direction is changed by 90 degrees with a heading to the aircraft window, when the passenger arrives his/her seat row.
Fig. 3.
Transmission probability for longitudinal (x) and lateral (y) components and as two-dimensional probability field (right).
Finally, the individual probability for virus transmission is corresponds to , the specific intensity (dose) per time step (3). In accordance with Schultz and Fuchte (2020), is set to , which means a passenger reaches a probability of after standing 20 s in closest distance in front of an infected passenger (SR ). The parameter is 1 and changed to 2 when the passenger stores the luggage or enters the seat row. This doubled shedding rate reflects the higher physical activities within a short distance to surrounding passengers.
| (3) |
2.3. Implementation and analysis of standard boarding approaches
We introduce a baseline setup to depict the results for the evaluation of transmission risks, considering a seat load factor of 85%, a conformance rate of 85%, and a passenger inter-arrival time of 3.7 s (exponential distributed) (Schultz, 2018c). Table 1 shows the comprehensive evaluation of transmissions around one infected passenger, which is randomly seated in the aircraft cabin. Two different scenarios are evaluated against the reference implementation (R) of the boarding strategies: (A) applying a minimum physical distance between two passengers of 1.6 m, and (B) additionally to the physical distance, the number of hand luggage items is reduced by 50% (implemented by reducing the storing time by 50%). Scenarios A and B are additionally extended by the use of two aircraft doors (one in the front and at the rear) during boarding, scenarios A2 and B2. The transmission risk and the boarding time are used as evaluation criteria.
Table 1.
Evaluation of transmissions risk assuming one SARS-CoV2 passenger in the cabin. The simulated scenarios are: (R) reference implementation (Schultz, 2018c), (A) 1.6 m minimum physical distance between two passengers, (B) additional reduction of hand luggage by 50%, (A2) and (B2) use of two door configuration (Schultz and Fuchte, 2020).
| Boarding strategy | Transmission risk |
Boarding time (%) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R | A | B | A2 | B2 | R | A | B | A2 | B2 | |
| Random | 5.9 | 1.6 | 1.1 | 1.4 | 1.0 | 100 | 198 | 154 | 133 | 103 |
| Back-to-front (2 blocks) | 5.6 | 1.4 | 1.0 | 1.2 | 0.8 | 96 | 220 | 169 | 153 | 116 |
| Optimized block (6 blocks) | 6.5 | 2.3 | 1.5 | 1.5 | 1.0 | 95 | 279 | 210 | 166 | 125 |
| Outside-in | 3.5 | 0.4 | 0.2 | 0.3 | 0.1 | 80 | 161 | 116 | 107 | 77 |
| Reverse pyramid | 3.0 | 0.2 | 0.1 | 0.2 | 0.1 | 75 | 185 | 128 | 119 | 82 |
| Individual | 2.0 | 0.2 | 0.1 | 0.2 | 0.1 | 66 | 114 | 104 | 103 | 74 |
| Deboarding | 10.0 | 9.7 | 7.8 | 7.6 | 6.0 | 55 | 97 | 68 | 52 | 36 |
In the context of physical distance, the International Aviation Transport Association (IATA) demands a distance of at least 1 m (International Aviation Transport Association (IATA), 2020c) and the Federal Aviation Administration (FAA) a minimum of 6 feet (2 m) (Federal Aviation Administration (FAA), 2020). In consideration of the underlying cellular automaton, which uses a grid structure with cells of 0.4 × .4 m size, and to maintain comparability of our results with preliminary studies (Schultz and Fuchte, 2020, Schultz et al., 2020), the minimum physical distance was set to 1.6 m. At this point, we assume that passengers are informed that a distance of 1.6 m corresponds to the distance of 2 seat rows, which offers proper visual guidance.
The analysis points out that, in particular, the back-to-front strategy (2 blocks: front block with rows 1–15, rear block with rows 16–29) exhibits lower values for the transmission probability than the optimized block strategy (using 6 blocks of aggregated seat rows) (see Schultz (2018c)). When passengers board (block-wise) from the back to the front, the chance to pass an infected person is reduced to a minimum, which is confirmed by the reduced transmission probability exhibited in Table 1. This effect is also a root cause of the low transmission risks of the outside-in, reverse pyramid, and individual boarding strategy.
The use of two aircraft doors for boarding will provide an appropriate solution for a reduced transmission risk inside and outside the cabin if near apron stands could be used and passengers could walk from the terminal to the aircraft. This kind of walk boarding also prevents passengers from standing in the badly ventilated jetway during the boarding. Deboarding is difficult to control by specific procedures given that passengers demonstrated little discipline and high eagerness to leave the aircraft. More attention should be paid to this process and consideration should also be given to procedural or technical solutions to provide passengers better guidance and control.
3. Improved boarding of passenger groups
We provide a new optimization method that incorporates passenger groups and required distances between members from different groups. In the following, we describe the mathematical problem and formulate the optimization model.
3.1. Problem description and formulation
We develop a new mathematical model to determine an optimal strategy for assigning seats in the cabin to minimize the virus transmission risk. The idea to create an appropriate seat allocation for a pandemic situation includes three assumptions. The first one is that an airline could assign just a percentage of the available seats (e.g. 50%) to reduce the virus transmissions in the cabin and this strategy will be the primary solution to face the pandemic situation. The next assumption is about minimizing passenger contacts or maximizing the distances between passengers in the cabin and guaranteeing at the same time that the confined space inside the aircraft is used efficiently.
Looking at Fig. 4, passengers have maximized distances from each other respecting the limitation that only 50% of the seats can be occupied. Each airline company could determine the seat load factor for each flight individually also considering risk assessments or economic reasons. To enable airlines to resume flights, many of them accepted the policy of empty middle seats in the beginning.
Fig. 4.
Fifty percent of the seats will be allocated to passengers during the pandemic situation according to a pattern with maximum physical separation.
Although complex boarding strategies, such as outside-in, reverse pyramid, and individual lead to better boarding times, there will be an issue. The boarding process is driven by the willingness of passengers to follow the proposed strategy. We will assume a group of four members (e.g. a family) to be seated. If one of these boarding strategies is applied, the members will have just two options. The first one is seating near each other, therefore they have to split during the boarding (see Fig. 2). The next option is remaining as one group in the boarding sequence and as a result, they have to seat in different rows. Both options are inconvenient for group members (families). Here we propose to look at the group members as a community since they were already in close contact before boarding. The strategy that is used in Fig. 4 depicts a general solution, but it could be improved considering groups. Without loss of generality, we could suppose that the transmission rate for the members of each group is zero, which will result in better use of space and create a new pattern.
The introduced concept of a shedding rate of infected passengers will be used here as well. If an infected passenger was assigned to different columns, the several shedding rates must be counted based on the location of the adjacent locations. Taking Fig. 5 as an example, when a passenger seated in row and column C (aisle), we compute the shedding rate for the passenger from other groups that seat in the same row ( at column A (window), B (middle), and D (aisle)) and previous row (column B (middle), C (aisle), and D (aisle)).
Fig. 5.
Types of passenger interactions (orange) in the aircraft cabin around the infected passengers (red) considering different seat positions: besides (1 and 4), in front (2), diagonally in front (3), and across the aisle (5 and 6). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
3.2. Optimization model
Based on the assumptions of the problem description, we list the sets, parameters, and decision variables for achievement of the purposes of the research. The number of rows, columns, groups and interaction types are defined as , , and , respectively. In the Airbus A320 reference layout (see Fig. 1), the number of rows and columns are and , six types of interactions exists (see Fig. 5), and we exemplary separated the passengers into thirty-one groups (). We define the parameter of SR (2) considering an aisle and seat width of 0.4 m, and a seat pitch of 0.8 m. This results in the following values SR =0.99987, SR =0.9226, SR =0.9126, SR SR =0.6833, and SR =0.6315.
| Notation | Definition |
|---|---|
| Sets and Indexes | |
| Index set of row | |
| Index set of column | |
| Index set of group | |
| Index set of interaction type | |
| Notation | Definition |
|---|---|
| Parameters | |
| Number of members in the group | |
| SR | The related shedding rate for interaction |
| Decision Variables | |
| Binary variable, equals one if a passenger from group is seated in a seat in row and column ; equals zero otherwise | |
| The summation of shedding rates that the passengers of other groups can cause for a passenger from group who is seated in a seat in row and column | |
The proposed a mixed-integer linear programming model for the problem is introduced as follows.
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
The summation of shedding rates of all passengers, as the objective function, is minimized in Eq. (4). Constraints (5) guarantee that each seat would be assigned to not more than one passenger. The number of group members is indicated by constraints (6). To calculate the sum of shedding rates () for a passenger of group k who seats in row and column , we count the shedding rates based on the location of the passengers of other groups who seat in row and previous row (see Fig. 5). Constraints (7)–(11) correspond to the shedding rates of passengers that are seated in the first row (=1) in cabin. For instance, if a passenger was seated in a seat in column C (=3), then the shedding rate for that passenger can be calculated based on the other passengers of different groups that were seated in columns A (=1), B (=2), and D (=4) on constraints (9). Also, the shedding rates of passengers that are seated in other rows in the cabin are computed by constraints (12)–(16). Here, we must consider the shedding rates not only for a passenger in the same row but also for the previous row. For instance, if a seat in the second row which located in column C (=3), was assigned to a passenger, then the shedding rates of the other passengers from different groups that were seated in column A (=1), B (=2), and D (=4) of that row and columns B (=2), C (=3), and D (=4) of the first row are calculated based on constraints (14) as well. The left hand side of the constraints (7)–(16) includes two terms. The first term takes a value of zero if the seat (,) is assigned to group and takes a negative value otherwise. The second term calculates the sum of shedding rates based on the locations of other passengers. We must deactivate calculating the sum of shedding rates when there is not a passenger of the group in a seat (,) and as the maximum value of the shedding rate is one, therefore, we consider the different multipliers for each equation based on the numbers of shedding rates in each equation. For example, in the constraints (7), the second term includes two shedding rate, therefore if a seat (,) is assigned to a passenger of the group , the first terms take zero and the sum of shedding rates calculates accordingly. On the other hand, if there is not any passenger then the first term takes , which is lower than the sum of two shedding rates and as a result, the decision variable is related to the sum of shedding rate takes zero. Finally, the requirements for decision variables are denoted by constraints (17).
4. Application of the model and evaluation of the results
We solved the mathematical model for a small size problem (). When we increased the size of the problem to the medium size (e.g. and ), the time run increased significantly and the optimization software (GAMS with CPLEX solver) could not find an optimal solution in a reasonable time (10 h). Therefore, we propose a Genetic Algorithm (GA) for the real size problem. The problems run on a computer with the specifications the AMD Ryzen 7, 3700U, 2.30 GHz CPU, 16 GB RAM, and Matlab 2013 software is used for running the GA. We choose six scenarios for the optimization and used the optimal seat allocation in the passenger boarding simulation to derive an appropriate boarding sequence with a low transmission risk.
4.1. Solution procedure and result
The GA has many applications in the optimization problems. In light of the NP-hard class of the seat allocation and boarding problem, several methods were conducted to present optimal/near-optimal solutions (van den Briel et al., 2005, Soolaki et al., 2012). In this context, we designed a GA with the following chromosome structure.
The value of each array of the matrix such as is the group’s number of related decision variable , which is if the seat (row , column ) is assigned to a passenger group , otherwise it takes zero. The population of chromosomes for the first generation is created based on the structure above. We evaluate each chromosome with its fitness function value, which is determined by the value of the original objective function. After that, we implement several operators as follows to create the next generations from the current generation: selection, crossover, mutation, migration, and elitism operator.
The selection operator (roulette wheel) ensures that each chromosome with a lower fitness function value is more likely to be selected. New offsprings are created by the recombination of parental genes. Therefore, the group’s numbers are divided into two separate sets. The first offspring receives their genes (the value of arrays in Matrix ) of the first set from the first parent and the second part from the second parent and vice versa for the second offspring (see Fig. 6). Here, we explain with colors and numbers of each group to clarify the implication of operation. For example, the first offspring receives their genes which are colored with light green (group 7), light blue (group 15), purple (group 20), dark pink (group 23), and red (group 27) from the first parent and receives the genes which are colored with dark green (group 2), navy (group 10), pink (group 24), orange (group 30), and yellow (group 31) from the second parent. If there is overlap between a gene’s location of the first and second parent, then we use a random strategy to select another array in a matrix and value it (e.g. for the first offspring, instead of , we randomly set because the array (5,5) was colored with light green before or ). Thus, the next generation always contains valid solutions for seat allocation.
Fig. 6.
Principle of crossover operator using a seat allocation within in the first seven seat rows. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
In the first generation, the solutions are produced based on the chromosome structure of Matrix . We start with the parameter . For each group, we randomly generate a value for and . If the array is taken zero, we assign the number of that group to the seat (row , column ) otherwise we randomly generate another and until takes zero. As a result, for each seat (, ) we consider just one value as the group and the number of seats that are assigned to each group is . Therefore, the constraints (5)–(6) are considered in the process of generating solutions. Other constraints would be considered in the decision variable of the sum of shedding rates. Also, the GA operators such as the crossover and mutation operators generate the new feasible solutions. The number of groups is deterministic and certain (i.e. ). We consider one value per passenger group and assign this number to every seat used by the group members.
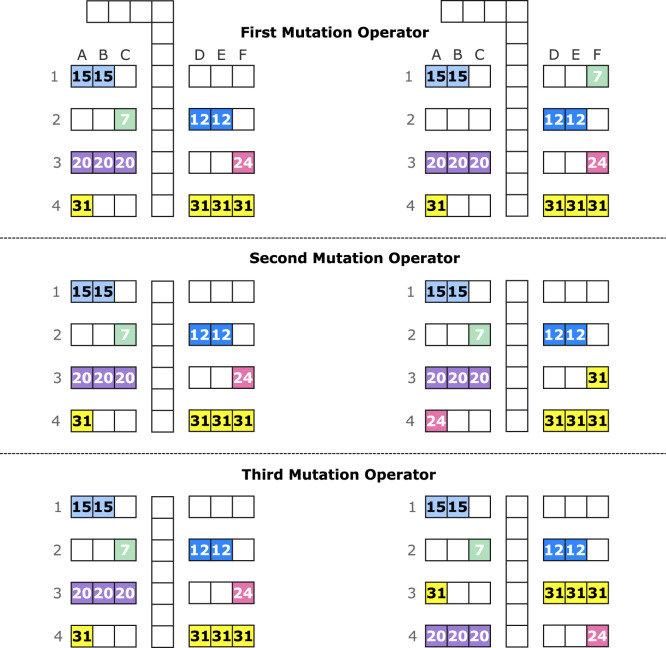
The mutation operator is used to maintain the diversity of solutions. Therefore, we designed three operators to change some genes in a chromosome to create a new chromosome for the next generation (see Fig. 7).
Fig. 7.
Principle of the three implemented mutation operators: move of a single seat location (first), exchanging two occupied seats (second), and switch seat rows (third). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
In the first mutation operator, we change the seat location of a passenger (), as a gene in a chromosome, to an unoccupied seat (). In the second operator, we change the locations of two occupied seats ( and ). Therefore, after implementation of the operator, we have: and . Finally, the arrays of two random rows (the third and fourth rows) are changed in the last mutation operator. A low percentage of each generation is randomly transferred to the next generation (migration operator). The elitism operator selects the best chromosomes in terms of fitness function value, and transfer them from the current generation to the next generation. The following parameters were used for executing the code: initial population = 1000, number of generations = 1000, crossover rate = 0.55, mutation rate = 0.35, elitism = 0.075, and migration rate = 0.025.
As already mentioned, we consider the passengers of other groups that seat near that passenger to determine the individual shedding rate. This individual shedding rate is defined as the sum of shedding rates of all affected passengers. As an example, in Fig. 6 (second offspring), the sum of shedding rates for a passenger of group 20 who seats in the seat 6D (,) is calculated based on a passenger of group 30 in the seat 6F (,) with interaction type (SR ), a passenger of group 24 in the seat 5D (,) with interaction type (SR ), and a passenger of group 15 in the seat 5C (,) with interaction type 6 (i.e. SR ). Therefore, equals the sum of SR , SR and SR .
We consider 8 groups with one member (i.e. G1 to G8 which coded with green color), 9 groups of two members (i.e. G9 to G17 which coded with blue color), 5 groups of three members (i.e. G18 to G22 which coded with purple color), 3 groups of four members (i.e. G23 to G25 which coded with ping color), 3 groups of five members (i.e. G26 to G28 which coded with red color), 2 groups of six members (i.e. G29 to G30 which coded with orange color), and finally a group of seven members (i.e. G31 which coded with yellow color). Fig. 8 depicts an improved solution for the seat allocation based on the designed GA generated for the 31 groups (87 passengers).
Fig. 8.
Improved allocation layout to seat 31 groups (87 passengers, 50% seat load) solved by GA approach. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
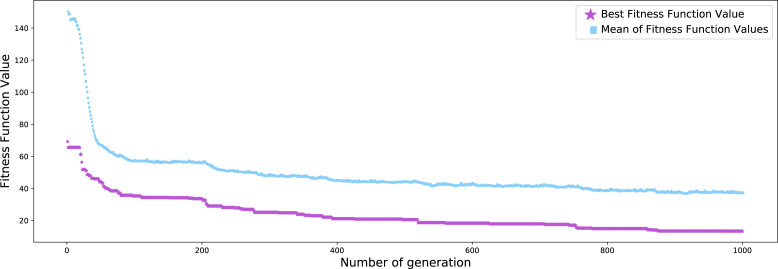
The run time for GA is 1805 s, the value of the objective function for the best solution is 13.3347. The evolutionary diagram concerning the GA is shown in Fig. 9. The fitness function of the elite and the mean of each generation demonstrates the increasing quality of generated solutions (decreasing fitness function).
Fig. 9.
Progress of GA fitness function.
To understand the impact of our group approach, we introduce six scenarios and their related solutions based on the assumptions below and compare them by the values of the objective function and the number of passengers considered.
-
•
Scenario 1: Aircraft seats are assigned randomly to passengers with a maximum distance (alternating seats) and a seat load of 50% (87 passengers).
-
•
Scenario 2: Similar to scenario 1, while the group members are seated close to each other in the same area (87 passengers).
-
•
Scenario 3: Improved allocation from mathematical modeling and GA application (87 passengers), shown in Fig. 8.
-
•
Scenario 4: Middle seat empty solution (116 passengers, 66% seat load).
-
•
Scenario 5: Improved allocation considering the increased seat load of 66% (116 passengers).
-
•
Scenario 6: Improved allocation considering the maximum number of passengers (174 passengers).
The corresponding solutions for the first three scenarios are illustrated in Fig. 10. In these scenarios, the number of passengers is fixed to 87 passengers. The values of the objective function (O.F.) of these three scenarios indicate that our approach (scenario 3) for an improved seat allocation should also result in a significant reduction of the transmission risk: a reduction of 91% of O.F. value compared to scenario 1 (seats are assigned randomly to passengers with a maximum distance), and a reduction of 85% compared to scenario 2 (seats are assigned randomly, group members in the same zone). The solutions for scenario 4, 5, and 6 are depicted in Fig. 11. The optimization method uses the available space in the best way (minimizing the objective value), depending on the actual number of passengers and groups. For example, we were increasing the number of passengers by 33% (from 87 to 116 passengers) and implemented the “empty middle seat policy” (scenario 4). Our group-based optimization (scenario 5) leads to a lower value (31%) of the objective function against scenario 4 (empty middle seat). Finally, the consideration of a seat load of 100% indicates an upper boundary (scenario 6) for the objective function.
Fig. 10.
Seat allocation in the aircraft cabin considering 87 passengers (31 groups) assigned to different groups using regular pattern (scenario 1 and 2) and improved group-based seat allocation (scenario 3). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Fig. 11.
Seat allocation in the aircraft cabin considering 116 passengers (38 groups) in an empty middle seat (scenario 4) and improved group-based approach (scenario 5), scenario 6 as an example for a fully utilized aircraft cabin (174 passengers, 62 groups). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
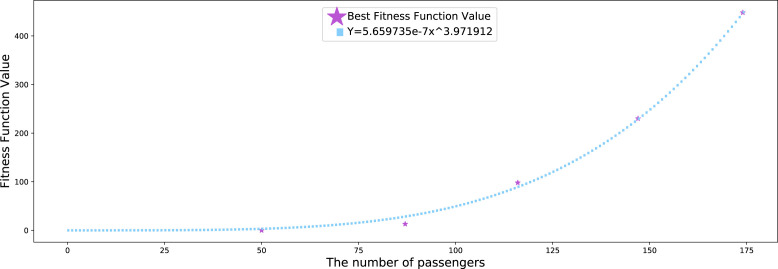
To show the general behavior of the objective function, we use a power-law function with and , which fits the O.F. values from scenarios 3, 5, and 6 (group-based optimization). Furthermore, we calculated scenarios with 50 passengers (17 groups) and 147 passengers (reference case with 85% seat load, 51 groups) to provide intermediate values. If the seat load increases over 50% (87 passengers) the values of the objective function progressively increases as shown in Fig. 12.
Fig. 12.
Progressive increase of transmission risk over the number of seated passengers.
4.2. Boarding times and evaluation
The implementation of the mixed-integer linear programming model and the genetic algorithm results in an improved allocation for the passengers to be seated in the aircraft cabin. This seat allocation will be used as input for the passenger boarding model, which was extended by a transmission module to evaluate transmission risk during aircraft boarding, to derive an optimum sequence to board the passengers. In our contribution, we will not provide an optimization of the deboarding process.
Analyses in the context of appropriate boarding sequence accompanied by the introduction of infrastructural changes showed that an improved sequence comprises a mix of boarding per seat (from window to aisle) and per seat row (from the rear to the front) (Schultz, 2017b). First and foremost, per-seat boarding (window seats first) is the most important rule to ensure seating without additional interaction in the seat rows. Starting with an outer seat in the last row, the number of group members, and the necessary physical distance between passengers (1.6 m) defines the subsequently following seat row, which could be used in parallel: e.g. 6 passengers with seat row 29 will block the aisle until seat row 27 (waiting), the physical distance requires to block row 26 and 25, the next group must have seats in front of row 25. This process of seat and row selection is repeated until the front of the aircraft is reached and is repeated until all passengers are seated. We further assume that the passengers in each group will organize themselves appropriately to minimize local interactions. In Fig. 13, the result of this sequencing algorithm is exemplarily illustrated.
Fig. 13.
Improved boarding sequence considering passengers as individuals and a physical distance of 1.6 m between passengers (scenario 1). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
If the sequencing algorithm is applied to the optimized seat allocation from scenario 3, the passenger groups are boarded in five segments. Inside each group, the distance between passengers is not restricted but between groups, it is constrained by 1.6 m (last member of the first group and the first member of the following group). The first segment starts with group no. 31 and the last segment with group no. 14 (see Fig. 14). As an example, the passengers inside group no. 31 (yellow) are organized by the following sequence of seats, which results in a minimum of the individual seat and row interactions: 29A, 29B, 28A, 28B, 27A, 27B, and 27C. Considering distances between groups, the best candidate will be group no. 27 (red) with the seats 23F, 23E, 22F, 22E, and 22D. This sequence allows both groups to start the seating process in parallel, without waiting time due to insufficient distance between the seat rows.
Fig. 14.
Optimized boarding of 31 groups considering a physical distance of 1.6 m between passengers of different groups (scenario 3). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
In the first three scenarios 87 passengers are boarded with different strategies (cf. Fig. 10): individual passengers in a regular pattern (scenario 1), groups in a regular pattern (scenario 2), and groups in an optimized seat allocation (scenario 3). Scenario 1 is used as a reference case to evaluate the performance (boarding time) and the transmission risk of scenarios 2 and 3 (Table 2). Therefore, a passenger sequence is established for both random and individual boarding strategy (optimized for physical distance, Fig. 13). The boarding time for the random strategy is set to 100%, as reference. As shown in Table 2, the implementation of the individual strategy will reduce the boarding time to 45.2% at a minimum of transmission risk. The consideration of groups (scenarios 2 and 3) using the random strategy already reduces the boarding time by about a third at a comparable level of transmission risk. If the optimized seat allocation is used together with the individual (group) boarding the boarding time could be further reduced to 41.1% at a low transmission risk of 0.09 new infected passengers at average (85% reduction). Table 2 emphasizes the portability of the results achieved by the evaluation of scenarios 4, 5, and 6. A corresponding baseline was calculated (random boarding of individual passengers) and compared against the achieved improvement. Scenario 4 (empty middle seat with improved seat allocation) already exhibits a reduced boarding time (by 55%) and transmission risk (by 54%), but could be further improved by our group-based approach (4% faster and 18% lower risk). In general, this improvement can also be demonstrated with a fully occupied cabin (scenario 6).
Table 2.
Evaluation of average aircraft boarding times and transmission risk during boarding assuming one randomly located infectious passenger.
| Scenario | Strategy | Passengers | Time (%) | Transmission risk |
|---|---|---|---|---|
| 1 | Random | 87 | 100.0 | 0.58 |
| Best sequence | 87 | 45.2 | 0.00 | |
| 2 | Groups, random sequence | 87 | 68.0 | 0.62 |
| Groups, best sequence | 87 | 51.9 | 0.20 | |
| 3 | Groups, optimal allocation, random sequence | 87 | 69.0 | 0.57 |
| Groups, optimal allocation, best sequence | 87 | 41.1 | 0.09 | |
| 4 | Random sequence | 116 | 100.0 | 1.12 |
| Groups, best sequence | 116 | 45.2 | 0.52 | |
| 5 | Groups, optimal allocation, random sequence | 116 | 64.9 | 0.94 |
| Groups, optimal allocation, best sequence | 116 | 40.9 | 0.31 | |
| 6 | Random sequence | 174 | 100.0 | 2.09 |
| Groups, optimal allocation, random sequence | 174 | 65.1 | 1.96 | |
| Groups, optimal allocation, est sequence | 174 | 34.4 | 0.66 | |
Finally, our results show that the improved group boarding of 174 passengers (scenario 5) possesses a transmission risk of 0.66, which is close to the random strategy in scenario 1 (0.58). Furthermore, this particular scenario 5 performs about 20% faster than the random strategy in scenario 1 (87 passengers) and reaches pre-pandemic boarding times.
5. Discussion and outlook
Along the passenger journey, the processes in the aircraft cabin require sharing a confined environment with other passengers during boarding and flight. These processes have the risk of virus transmission between passengers and require appropriate seat configuration and risk mitigation strategies. The physical distance between passengers during boarding and staggered seat configurations are part of the risk mitigation strategy. However, the side effect from an operational point of view is a doubled boarding time compared to the situation before the coronavirus pandemic situation.
In our contribution, we consider passenger groups as an important factor for operational efficiency. The main idea behind our approach is that members of one group are allowed to be close to each other, as they already are before boarding, while different groups should be as far apart as necessary. We provide a customer-oriented solution for both airlines and passengers, which enables a situational approach to establish appropriate seat allocation and aircraft entry sequences considering a minimum transmission risk between groups of passengers. Thus, we developed a new mathematical model, which provides an improved seat allocation, while minimizing the sum of shedding rates that an infected passenger can cause. This model was used to evaluate the transmission risk of a seat allocation scheme and to solve the corresponding optimization problem with a genetic algorithm. We created, evaluated, and improved three different scenarios of grouped passengers (87, 116, 174). The optimization of a standard scenario with a seat load of 50% (87 passengers) shows that with the consideration of groups the value for the objective function was reduced from 147 to 13, which indicates a significant reduction of the transmission risk induced by the improved seat allocation. This trend was also valid for the other scenarios.
In the next step, the derived seat allocations were used as input for the boarding simulation (stochastic cellular automata), which evaluates the transmission risk during the passenger movements in the cabin (walk the aisle, store luggage, take the seat). The entry sequence of the passenger groups was optimized to keep boarding time as short as possible. Our simulation results exhibit that the improved seat allocation for groups (scenario 3) performs best for the boarding time (41.1% in relation to random boarding with no groups) at a low level of transmission risk (0.09, while random boarding without groups leads to a risk of 0.58). We could also demonstrate that the effective consideration of passenger groups is a major impact factor for fast and safe passenger boarding (e.g., board more passengers at the same level of transmission risk). In the context of aircraft ground operations (turnaround), shorten boarding times could compensate for the extended ground times caused by additional disinfection procedures in the aircraft cabin.
Our approach is based on the definition of a shedding rate, which was adopted from previous research. This approach is used as a proxy for the evaluation of the transmission risk and allows a simplified differentiation between seat allocations (ranked by order). Also, our aircraft environment does not allow any detailed analysis of infection chains or air flows in the cabin. At present, the coronavirus pandemic challenges our society to find appropriate solutions for the present and future mobility of people. However, there are only a few studies on infection chains and simplified assumptions have to be made. We hope that the results from other research groups will provide more accurate input parameters for our model and that we can further improve our method. In our operational scenarios, we have generated exemplary passenger groups within an acceptable range. If we could obtain airline data, especially on the number of passengers and the number of group bookings on each flight, more airline-related results could be provided.
CRediT authorship contribution statement
Michael Schultz: Conceptualization, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing - original draft, Writing - review & editing. Majid Soolaki: Conceptualization, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing - original draft, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix.
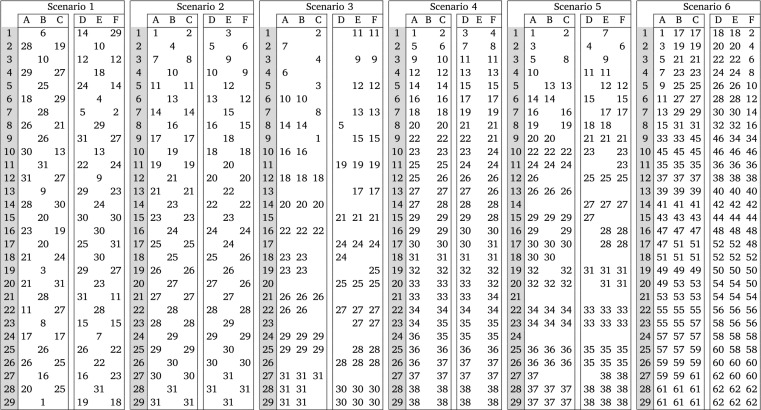
The detailed seat allocation of the six scenarios is given using a numerical description without color-coding in Table 3.
Table 3.
Numerical representation of passenger groups seated in the aircraft cabin.
References
- Bachmat E., Berend D., Sapir L., Skiena S., Stolyarov N. Analysis of airplane boarding times. Oper. Res. 2009;57:499–513. [Google Scholar]
- Bachmat E., Elkin M. Bounds on the performance of back-to-front airplane boarding policies. Oper. Res. Lett. 2008;36:597–601. [Google Scholar]
- Bachmat E., Khachaturov V., Kuperman R. Optimal back-to-front airplane boarding. Phys. Rev. E (3) 2013;87 doi: 10.1103/PhysRevE.87.062805. [DOI] [PubMed] [Google Scholar]
- Baker M.G., Thornley C.N., Mills C., Roberts S., Perera S., Peters J., Kelso A., Barr I., Wilson N. Transmission of pandemic A/H1N1 2009 influenza on passenger aircraft: retrospective cohort study. BMJ. 2010;340 doi: 10.1136/bmj.c2424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bazargan M. A linear programming approach for aircraft boarding strategy. European J. Oper. Res. 2007;183:394–411. [Google Scholar]
- van den Briel M.H.L., Villalobos J.R., Hogg G.L., Lindemann T., Mulé A.V. America west airlines develops efficient boarding strategies. INFORMS J. Appl. Anal. 2005;35:191–201. [Google Scholar]
- Chung C. Simulation design approach for the selection of alternative commercial passenger aircraft seating configurations. J. Aviat. Technol. Eng. 2012;2 [Google Scholar]
- Cook A., Tanner G. EUROCONTROL Performance Review Unit; Brussels: 2015. European Airline delay cost reference values - updated and extended values (version 4.1) [Google Scholar]
- Cotfas L.A., Delcea C., Milne R.J., Salari M. Evaluating classical airplane boarding methods considering COVID-19 flying restrictions. Symmetry. 2020;12:1087. [Google Scholar]
- Delcea C., Cotfas L.A., Paun R. Agent-based evaluation of the airplane boarding strategies’ efficiency and sustainability. Sustainability. 2018;10:1879. [Google Scholar]
- Eldin C., Lagier J.C., Mailhe M., Gautret P. Probable aircraft transmission of Covid-19 in-flight from the central African Republic to France. Travel Med. Infect. Dis. 2020 doi: 10.1016/j.tmaid.2020.101643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Federal Aviation Administration (FAA) 2020. COVID-19: Updated interim occupational health and safety guidance for air carriers and crews.https://www.faa.gov/other_visit/aviation_industry/airline_operators/airline_safety/safo/all_safos/#2020 [Google Scholar]
- Ferrari P., Nagel K. Robustness of efficient passenger boarding strategies for airplanes. Transp. Res. Rec. 2005;1915:44–54. [Google Scholar]
- Fuchte J.C. Technische Universität Hamburg-Harburg; Hamburg: 2014. Enhancement of aircraft cabin design guidelines with special consideration of aircraft turnaround and short range operations. (Ph.D. thesis) [Google Scholar]
- Gupta J.K., Lin C.H., Chen Q. Risk assessment of airborne infectious diseases in aircraft cabins. Indoor Air. 2012;22:388–395. doi: 10.1111/j.1600-0668.2012.00773.x. [DOI] [PubMed] [Google Scholar]
- Gwynne S.M.V., Senarath Yapa U., Codrington L., Thomas J.R., Jennings S., Thompson A.J.L., Grewal A. Small-scale trials on passenger microbehaviours during aircraft boarding and deplaning procedures. J. Air Transp. Manag. 2018;67:115–133. [Google Scholar]
- Hertzberg V.S., Weiss H. On the 2-row rule for infectious disease transmission on aircraft. Ann. Glob. Health. 2016;82:819–823. doi: 10.1016/j.aogh.2016.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hertzberg V.S., Weiss H., Elon L., Si W., Norris S.L. Behaviors, movements, and transmission of droplet-mediated respiratory diseases during transcontinental airline flights. Proc. Natl. Acad. Sci. 2018;115:3623–3627. doi: 10.1073/pnas.1711611115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Aviation Transport Association (IATA) 2020. Health safety standards checklist for airline operators.https://www.icao.int/safety/CAPSCA/Pages/Coronavirus.aspx [Google Scholar]
- International Aviation Transport Association (IATA) 2020. Restarting aviation following COVID-19.https://www.iata.org/en/programs/covid-19-resources-guidelines/ [Google Scholar]
- International Aviation Transport Association (IATA) 2020. Guidance for cabin operations during and post pandemic, edt. 4.https://www.iata.org/en/programs/covid-19-resources-guidelines/ [Google Scholar]
- International Civil Aviation Organization (ICAO) 2020. Effects of novel coronavirus (COVID-19) on civil aviation.https://www.icao.int/sustainability/Documents/Covid-19 [Google Scholar]
- International Civil Aviation Organization (ICAO) 2020. COVID-19 response and recovery platform.https://www.icao.int/covid [Google Scholar]
- Jaehn F., Neumann S. Airplane boarding. European J. Oper. Res. 2015;244:339–359. [Google Scholar]
- Jafer S., Mi W. Comparative study of aircraft boarding strategies using cellular discrete event simulation. Aerospace. 2017;4(4):57. [Google Scholar]
- Kierzkowski A., Kisiel T. The human factor in the passenger boarding process at the airport. Procedia Eng. 2017;187:348–355. [Google Scholar]
- Kierzkowski A., Kisiel T. Simulation model of security control lane operation in the state of the COVID-19 epidemic. J. Air Transp. Manag. 2020;88 doi: 10.1016/j.jairtraman.2020.101868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangili A., Gendreau M.A. Transmission of infectious diseases during commercial air travel. Lancet (London, England) 2005;365 doi: 10.1016/S0140-6736(05)71089-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marelli S., Mattocks G., Merry R. The role of computer simulation in reducing airplane turn time. Boeing AERO Mag. 1998;01 [Google Scholar]
- Milne R.J., Delcea C., Cotfas L.A., Salari M. New methods for two-door airplane boarding using apron buses. J. Air Transp. Manag. 2019;80 [Google Scholar]
- Milne R.J., Kelly A.R. A new method for boarding passengers onto an airplane. J. Air Transp. Manag. 2014;34:93–100. [Google Scholar]
- Milne R.J., Salari M. Optimization of assigning passengers to seats on airplanes based on their carry-on luggage. J. Air Transp. Manag. 2016;54:104–110. [Google Scholar]
- Mirza M. Economic impact of airplane turn-times. Aeronaut. Q. 2008;04 [Google Scholar]
- Miura A., Nishinari K. A passenger distribution analysis model for the perceived time of airplane boarding/deboarding, utilizing an ex-Gaussian distribution. J. Air Transp. Manag. 2017;59:44–49. [Google Scholar]
- Moussaïd M., Perozo N., Garnier S., Helbing D., Theraulaz G. The walking behaviour of pedestrian social groups and its impact on crowd dynamics. PLOS ONE. 2010;5:1–7. doi: 10.1371/journal.pone.0010047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller S.A., Balmer M., Neumann A., Nagel K. Mobility traces and spreading of COVID-19. medRxiv. 2020 [Google Scholar]
- Nyquist D.C., McFadden K.L. A study of the airline boarding problem. J. Air Transp. Manag. 2008;14:197–204. [Google Scholar]
- Olsen Sonja J., Chang Hsiao-Ling, Cheung Terence Yung-Yan, Tang Antony Fai-Yu, Fisk Tamara L., Ooi Steven Peng-Lim, Kuo Hung-Wei, Jiang Donald Dah-Shyong, Chen Kow-Tong, Lando Jim, Hsu Kwo-Hsiung, Chen Tzay-Jinn, Dowell Scott F. Transmission of the severe acute respiratory syndrome on aircraft. N. Engl. J. Med. 2003;349:2416–2422. doi: 10.1056/NEJMoa031349. [DOI] [PubMed] [Google Scholar]
- Olsen S.J., Chang H.L., Cheung T.Y.Y., Tang A.F.Y., Fisk T.L., Ooi S.P.L., Kuo H.W., Jiang D.D.S., Chen K.T., Lando J., Hsu K.H., Chen T.J., Dowell S.F. Transmission of the severe acute respiratory syndrome on aircraft. N. Engl. J. Med. 2003;349:2416–2422. doi: 10.1056/NEJMoa031349. [DOI] [PubMed] [Google Scholar]
- Qian G Q, Yang N B, Ding F, Ma A H Y, Wang Z Y, Shen Y F, Shi C W, Lian X, Chu J G, Chen L, Wang Z Y, Ren D W, Li G X, Chen X Q, Shen H J, Chen X M. Epidemiologic and clinical characteristics of 91 hospitalized patients with COVID-19 in Zhejiang, China: A retrospective, multi-centre case series. QJM: Int. J. Med. 2020;hcaa089 doi: 10.1093/qjmed/hcaa089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiang S.J., Jia B., Xie D.F., Gao Z.Y. Reducing airplane boarding time by accounting for passengers’ individual properties: A simulation based on cellular automaton. J. Air Transp. Manag. 2014;40:42–47. [Google Scholar]
- Ren X., Zhou X., Xu X. A new model of luggage storage time while boarding an airplane: An experimental test. J. Air Transp. Manag. 2020;84 [Google Scholar]
- Schmidt M. A review of aircraft turnaround operations and simulations. Prog. Aerosp. Sci. 2017;92:25–38. [Google Scholar]
- Schmidt M., Heinemann P., Hornung M. 55th AIAA Aerospace Sciences Meeting AIAA SciTech Forum. American Institute of Aeronautics and Astronautics; 2017. Boarding and turnaround process assessment of single- and twin-aisle aircraft. [Google Scholar]
- Schmidt M., Nguyen P., Hornung M. SAE International; Warrendale, PA: 2015. Novel aircraft ground operation concepts based on clustering of interfaces; pp. 2688–3627. [Google Scholar]
- Schultz M. Technische Universität Dresden, Faculty of Transport and Traffic Sciences Friedrich List; Dresden: 2010. Entwicklung eines individuenbasierten modells zur abbildung des bewegungsverhaltens von passagieren im flughafenterminal. (Ph.D. thesis) [Google Scholar]
- Schultz M. Pedestrian and Evacuation Dynamics 2012. Springer International Publishing; 2013. Stochastic transition model for pedestrian dynamics; pp. 971–985. [Google Scholar]
- Schultz M. Aircraft boarding - data, validation, analysis. In: 12th USA/Europe Air Traffic Management Research and Development Seminar. 2017 [Google Scholar]
- Schultz M. Dynamic change of aircraft seat condition for fast boarding. Transp. Res. C. 2017;85:131–147. [Google Scholar]
- Schultz M. Fast aircraft turnaround enabled by reliable passenger boarding. Aerospace. 2018;5(1) [Google Scholar]
- Schultz M. Field trial measurements to validate a stochastic aircraft boarding model. Aerospace. 2018;5(1) [Google Scholar]
- Schultz M. Implementation and application of a stochastic aircraft boarding model. Transp. Res. C. 2018;90:334–349. [Google Scholar]
- Schultz M., Evler J., Asadi E., Preis H., Fricke H., Wu C.L. Future aircraft turnaround operations considering post-pandemic requirements. J. Air Transp. Manag. 2020;89 doi: 10.1016/j.jairtraman.2020.101886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz M., Fricke H. Improving aircraft turnaround reliability. In: 3rd International Conference on Research in Airport Transportation. 2008:335–343. [Google Scholar]
- Schultz M., Fricke H. Managing passenger handling at airport terminal. In: 9th USA/Europe Air Traffic Management Research and Development Seminar. 2011 [Google Scholar]
- Schultz M., Fuchte J. Evaluation of aircraft boarding scenarios considering reduced transmissions risks. Sustainability. 2020;12:5329. [Google Scholar]
- Schultz M., Kunze T., Fricke H. Boarding on the critical path of the turnaround. In: 10th USA/Europe Air Traffic Management Research and Development Seminar. 2013 [Google Scholar]
- Schultz M., Rößger L., Fricke H., Schlag B. Pedestrian and Evacuation Dynamics 2012. Springer International Publishing; 2013. Group dynamic behavior and psychometric profiles as substantial driver for pedestrian dynamics; pp. 1097–1111. [Google Scholar]
- Schultz M., Schulz C., Fricke H. Efficiency of aircraft boarding procedures. In: 3rd International Conference on Research in Airport Transportation. 2008:371–377. [Google Scholar]
- Schwartz K.L., et al. Lack of COVID-19 transmission on an international flight. Can. Med. Assoc. J. 2020;192 doi: 10.1503/cmaj.75015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smieszek T. A mechanistic model of infection: why duration and intensity of contacts should be included in models of disease spread. Theor. Biol. Med. Model. 2009;6 doi: 10.1186/1742-4682-6-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soolaki M., Mahdavi I., Mahdavi-Amiri N., Hassanzadeh R., Aghajani A. A new linear programming approach and genetic algorithm for solving airline boarding problem. Appl. Math. Model. 2012;36:4060–4072. [Google Scholar]
- Steffen J.H. Optimal boarding method for airline passengers. J. Air Transp. Manag. 2008;14:146–150. arXiv:0802.0733. [Google Scholar]
- Steffen J.H. A statistical mechanics model for free-for-all airplane passenger boarding. Amer. J. Phys. 2008;76:1114–1119. [Google Scholar]
- Steffen J.H., Hotchkiss J. Experimental test of airplane boarding methods. J. Air Transp. Manag. 2012;18:64–67. [Google Scholar]
- Steiner A., Philipp M. 2009. Speeding up the airplane boarding process by using pre-boarding areas. in 9th swiss transport research conference. p. 30. [Google Scholar]
- Tang T.Q., Wu Y.H., Huang H.J., Caccetta L. An aircraft boarding model accounting for passengers’ individual properties. Transp. Res. C. 2012;22:1–16. [Google Scholar]
- Tang T.Q., Yang S.P., Ou H., Chen L., Huang H.J. An aircraft boarding model accounting for group behavior. J. Air Transp. Manag. 2018;69:182–189. [Google Scholar]
- Van Landeghem H., Beuselinck A. Reducing passenger boarding time in airplanes: A simulation based approach. European J. Oper. Res. 2002;142:294–308. [Google Scholar]
- Wallace R. 2020. The flying carpet.https://the-flying-carpet.com/ (accessed September 26, 2020) [Google Scholar]
- Wittmann J. Customer-oriented optimization of the airplane boarding process. J. Air Transp. Manag. 2019;76:31–39. [Google Scholar]
- Yazdani D., Omidvar M.N., Deplano I., Lersteau C., Makki A., Wang J., Nguyen T.T. Real-time seat allocation for minimizing boarding/alighting time and improving quality of service and safety for passengers. Transp. Res. C. 2019;103:158–173. [Google Scholar]
- Zanlungo F., Yücel Z., Kanda T. Intrinsic group behaviour II: On the dependence of triad spatial dynamics on social and personal features; and on the effect of social interaction on small group dynamics. PLOS ONE. 2019;14:1–28. doi: 10.1371/journal.pone.0225704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeineddine H. A dynamically optimized aircraft boarding strategy. J. Air Transp. Manag. 2017;58:144–151. [Google Scholar]