Population Size Estimation Using Multiple Respondent-Driven Sampling Surveys

Abstract

Respondent-driven sampling (RDS) is commonly used to study hard-to-reach populations since traditional methods are unable to efficiently survey members due to the typically highly stigmatized nature of the population. The number of people in these populations is of primary global health and demographic interest and is usually hard to estimate. However, due to the nature of RDS, current methods of population size estimation are insufficient. We introduce a new method of estimating population size that uses concepts from capture-recapture methods while modeling RDS as a successive sampling process. We assess its statistical validity using information from the CDC’s National HIV Behavioral Surveillance system in 2009 and 2012.

1. INTRODUCTION

In some populations, such as people at high risk for HIV—for example, female sex workers (FSW), men who have sex with men (MSM), or people who inject drugs (PWID)—or recent migrants, obtaining a probability sample can be practically impossible. This can be for a variety of reasons, including social stigma, unwillingness to self-identify, or simply because the people in the group may have engaged in an illegal activity.

In many cases, finding the size of these hard-to-reach populations is of great interest. When deciding how much aid to send for HIV prevention, getting an accurate count of people at high risk for HIV is crucial for efficient allocation of resources (UNAIDS and World Health Organization 2010). Since these populations are hard to reach, traditional methods of sampling, such as random digit dialing telephone numbers or household surveys, are infeasible. In addition, due to the stigma attached to many hidden populations, individuals may refuse to release information to protect their or others’ privacy (Heckathorn 1997).

An alternative way of surveying these hidden populations involves exploiting their highly connected nature. For example, PWID are much more likely to know someone else who injects drugs. In addition, it is much more likely that a person in the population would know that someone else is also in that population (e.g., it is more likely for PWID to know who among people they know is also a PWID). Therefore, researchers have developed various link-tracing sampling methods in which the network links from sampled members of the population are traced out to unsampled members in the population in order to grow the sample (Spreen 1992; Gile and Handcock 2010; Handcock and Gile 2011).

One link-tracing method that has recently become very popular with researchers for studying hidden populations is respondent-driven sampling (RDS). Introduced by Heckathorn (1997) as an alternative to traditional snowball sampling and time-location sampling techniques, RDS employs a link-tracing design in the following manner:

1. Start with a small initial sample, usually a convenience sample.

2. Give each respondent a few coupons to recruit others, with incentives for both the recruiter and the new recruit.

3. Include each recruit in the study and give them a limited number of coupons, typically approximately three (Malekinejad, Johnston, Kendall, Kerr, Rifkin, et al. 2008), to hand out to other members of the population.

4. People who receive a coupon may choose to come in to join the study.

5. Each new participant is included in the study and given coupons to recruit others.

6. The process continues until a stopping condition is reached, such as a target sample size. If the chain stops before the stopping condition is reached (e.g., due to unfruitful referrals), new seeds may be chosen to start new chains.

Respondent-driven sampling has several benefits over more conventional methods. First and most prominent is that it enables researchers to survey a population for which a sampling frame does not exist. Since respondents know others in the population (a reasonable assumption for populations like MSM and FSW), it is much easier to ask them to find more people for the study rather than for researchers to try to find them. In addition, as opposed to other network sampling designs, RDS involves a dual incentive system, with incentives for both the recruiter for recruiting others and participants for joining the study. In addition, the long chains generated by RDS result in samples that are not as prone to bias by the initial convenience sample, whereas other recruitment sampling methods may be (Heckathorn 1997; Gile 2011). In particular, RDS is able to reach the less visible members of the population that may be missed by other link-tracing designs (Kendall, Kerr, Gondim, Werneck, Macena, et al. 2008). Further, RDS does not require participants to give up any information about others. Instead, they are simply asked to recruit them into the study, giving agency to the possible recruits. This avoids the issue of asking respondents to reveal information about their friends or acquaintances (Heckathorn 1997).

Due to its many benefits, respondent-driven sampling has increasingly been the method of choice when surveying these hard-to-reach populations (Platt, Wall, Rhodes, Judd, Hickman, et al. 2006; UNAIDS and World Health Organization 2010; Bengtsson, Lu, Nguyen, Camitz, Hoang, et al. 2012). A review in 2008 found that there had been over 120 studies that have used RDS to sample the populations most at risk for HIV (Malekinejad et al. 2008). Much of the previous work has been done using respondent-driven sampling to find proportions or other statistics (Volz and Heckathorn 2008; Gile 2011). Many studies comparing RDS with other methods found that RDS is an effective and efficient method for sampling hard-to-reach populations (Magnani, Sabin, Saidel, and Heckathorn 2005; Abdul-Quader, Heckathorn, Sabin, and Saidel 2006; Platt et al. 2006; Semaan 2010).

However, the current literature on estimating the population size using only RDS data is quite limited and has mostly focused on using a multiplier method (Wattana, van Griensven, Rhucharoenpornpanich, Manopaiboon, Thienkrua 2007; Paz-Bailey, Jacobson, Guardado, Hernandez, Nieto, et al. 2011). Some research has been done regarding using other forms of network sampling, such as incorporating general link-tracing design to capture-recapture (Vincent and Thompson 2016), but very few model-based methods have been developed specifically for RDS data (Handcock, Gile, and Mar 2014; Crawford, Wu, and Heimer 2018). In addition, the current model-based methods for RDS do not take full advantage of the multiple capture population size estimation literature from animal abundance. Because RDS is so popular among researchers of hidden populations, methods must be developed to estimate population size using RDS data.

In this article, we develop a new method to estimate population size using two RDS surveys. In section 2, we discuss traditional capture-recapture methods for population size estimation and methods developed specifically for RDS data. In section 3, we introduce our new population size estimation method that uses concepts from both traditional capture-recapture and RDS-based methods. In section 4, we use simulation studies to assess our new model and compare it with existing methods. Finally, we provide concluding remarks in section 5.

2. POPULATION SIZE ESTIMATION

Even though using RDS data for population size estimation has not been studied thoroughly, there is a rich literature on size estimation in general. The basis of these methods comes from animal abundance. Researchers interested in finding the number of animals in a certain area developed methods to count them. These methods were applied to surveys of human populations, and extensions were developed to relax some of the assumptions.

2.1 Capture-Recapture

A classic method of estimating the abundance of animals is using capture-recapture. A basic capture-recapture design as it applies to animal abundance can be described as follows:

1. Capture a certain number of animals.

2. Tag them and then release them back into the wild.

3. Perform a second capture (recapture).

4. Count how many of the recaptured animals are tagged.

5. Use the overlap to estimate the abundance.

We can express the simple capture-recapture data in the form of a collapsed two-by-two table, as in figure 1. Then we see the data as capture histories. That is, we know the capture history of “1, 1,” “1, 0,” and “0, 1,” although we do not observe the capture history “0, 0”. This is a condensed version of the complete data, and multiple list methods typically approach the problem in this way, estimating the frequency of capture history of all “0”s.

Figure 1.

Contingency table for a simple capture-recapture design.

If we assume independence of the two lists and equal capture probabilities for each unit in the population, we get what Paz-Bailey et al. (2011) and Berchenko and Frost (2011) refer to as the naive estimator,

$${\widehat{N}}_{\text{naive}}=\frac{(a_{1,0}+a_{1,1})(a_{0,1}+a_{1,1})}{a_{1,1}},$$

where $a_{1,0}$ is the number of people who were captured in only the first sample, and $a_{0,1}$ is the number of people who were captured in only the second sample. This is also called the Lincoln-Petersen estimator. An alternative formulation of this capture-recapture design uses the hypergeometric distribution. That is, we model the second capture as a hypergeometric process, with a “success” defined as a unit that was already observed in the first list (e.g., a tagged animal) and a “failure” defined as one that was not observed (e.g., an untagged animal). A Bayesian implementation of this is provided by Cosenza, Eudey, Kerr, and Trumbo (2014).

2.2 Multiple List Methods

The basic capture-recapture method of estimating population size can be generalized to include more lists. For example, one might consider using three lists. This would result in a three-dimensional version of the contingency table in figure 1, and the aim would once again be to estimate every unit that was not captured in any list. In addition, various methods have been developed to try to account for heterogeneity in capture probabilities and for heterogeneity in lists (that is, a different propensity to capture animals) or time effects (for example, if an animal that is tagged is more likely to be captured because of the tagging) (Fienberg, Johnson, and Junker 1999; Rivest and Baillargeon 2007; Manrique-Vallier 2016).

2.3 Network-Based Population Size Estimation Methods

One method to find the size of a population without directly sampling that population is the network scale-up method (Bernard, Hallett, Iovita, Johnsen, Lyerla, et al. 2010; Salganik, Fazito, Bertoni, Abdo, Mello, et al. 2011). The network scale-up method uses information about personal network sizes of respondents in the general population and known population proportions to make size estimates. For example, suppose we want to know how many men who have sex with other men (MSM) in a particular group of one million people. If a respondent knows two hundred people (i.e., their personal network size is 200) and knows two people who are MSM, then we can conclude that 1 percent of the population are MSM. Known populations are used to estimate the size of each respondentof personal network; for example, if a person reports knowing 2 people named Joe and there are ten thousand Joes out of one million people in the population, then that respondent's personal network size would be two hundred.

The network scale-up method provides an advantage in that it does not need to sample the population of interest directly, but it does require an assumption that the unobserved and observed members have the same distribution of characteristics. In addition, the population of interest is hidden, which means that the general population most likely does not know whether their acquaintances really are in that hidden population. Therefore, respondents might report knowing many fewer members of the hidden population even if they actually know many more members.

Successive sampling–population size estimation (SS-PSE) was developed specifically to use RDS data, estimating population size using a single RDS sample and modeling the RDS process rather than treating it as a probability sample (Handcock et al. 2014). While performing the RDS, information on each respondent’s degree (i.e., how many people they know in the population) is collected, along with the order of observation. The RDS process is treated as sampling with probability proportional to size without replacement (PPSWOR) (Gile 2011).

Intuitively, if we are sampling with PPSWOR, we would expect the people with higher degrees to be sampled first and the people with lower degrees to be sampled later on. Successive sampling–population size estimation leverages this information to estimate the population size, modeling RDS with a successive sampling approximation, which accounts for the without-replacement nature of RDS and has been found to be effective in estimation of population means (Gile 2011).

Crawford et al. (2018) introduce another population size estimation method specifically developed for a single RDS survey. They assume that the population social network follows an Erdős-Rényi distribution and use the timing of recruitment and network degree of recruits to gain information about the unsampled members of the population. As opposed to SS-PSE, the RDS process is more exactly modeled (rather than treating it as sampling with PPSWOR), but it also requires a stronger assumption that the population network is an Erdős-Rényi graph, such that ties are independent and that there is an equal probability of each tie.

One large limitation of both SS-PSE and the method described by Crawford et al. (2018) is that they both only use one RDS sample. More conventional size estimation methods use multiple samples; so while the RDS process is actually modeled, there is potential for improvement since adding a subsequent RDS survey adds valuable recapture information. In the next section, we will build on the network-based approaches by estimating population size using two RDS surveys.

3. CAPTURE-RECAPTURE WITH SUCCESSIVE SAMPLING FOR POPULATION SIZE ESTIMATION

One of the biggest benefits of using RDS data is the ability to collect multiple samples on a hidden population relatively easily. In a review of RDS studies related to HIV surveillance, Malekinejad et al. (2008) found that RDS studies took, on average, nine weeks to complete. Because of this, we want to adapt capture-recapture methods to work with RDS data so that we can use as much information as possible. Currently, capture-recapture and other multiple list methods have not been tailored for RDS data. Paz-Bailey et al. (2011) used RDS in the recapture stage, but there have been no published studies using RDS for each stage of multiple captures in population size estimation. In addition, Paz-Bailey et al. (2011) only used an adjusted ratio estimator. We aim to take a model-based approach, which will not only give us better estimates but also better measures of variance.

We aim to improve on current methods by utilizing the degrees of each respondent and the order in which they were sampled to develop a method specifically for multiple RDS lists. In this section, we introduce Capture-Recapture SS-PSE, a method to estimate population size using two RDS surveys.

We assume the existence of a population (for example, FSW in a city) with an associated unit size. This can generally be anything about the individual that affects their catchability, but for our purposes in RDS surveys, the unit sizes will be the personal network size (or degree). Our observed data consists of two RDS surveys that serve as our lists, or captures, in which the personal network size of each observation is recorded in order of observation. That is, we track both the unit size (degree) and the sequential order of the when units were included into the study for both RDS surveys. We note that in practice, this is done in the order that respondents come into the research center to be included in the study, regardless of which wave or which seedee chain they are a part of. In addition, the second RDS survey includes a question about whether the respondent was recruited and participated in the first RDS survey. Notably in these methods, we do not assume that we have unique matching between the first and second list for those captured in both. Instead, we only know that the unit was part of the first sample. This is similar to the information collected in previous RDS studies that have tried to use capture-recapture methodologies, as the researchers would ask whether the respondent had previously received a unique keychain (Paz-Bailey et al. 2011).

3.1 Likelihood Formulation

We start by describing the likelihood. Let the total population size be N, with each individual person in the population indexed $1,\dots ,N$. Since we want to estimate the population size, N is unknown. Each person has an associated unit size representing the number of people they know in the population (e.g., the number of FSW they know). These unit sizes are treated as an i.i.d. sample from a superpopulation model. Let $U_1,\dots ,U_N$ be the random variables representing the unit sizes. Let $n\prime$ and $n″$ be the sample size of the first list and second list, respectively, and n₀ refer to the size of the overlap, while n refers to the overall unique sample size (so that $n\prime +n″-n_0=n$).

We have an ordered sampling design, with $G\prime =(G{\prime }_1,\dots ,G{\prime }_{n\prime })$ representing the random indices of the sequentially sampled units with realization $g\prime =(g{\prime }_1,\dots ,g{\prime }_{n\prime })$ in the first list, and $G″=(G\prime {\prime }_1,\dots ,G\prime {\prime }_{n″})$ representing the random indices of the sequentially sampled units with realization $g″=(g\prime {\prime }_1,\dots ,g\prime {\prime }_{n″})$ in the second list. The unit sizes are $U{\prime }_{\mathit{obs}}=(U_{g{\prime }_1},\dots ,U_{g{\prime }_{n\prime }})$, in order of the first list, and $U{″}_{\mathit{obs}}=(U_{g\prime {\prime }_1},\dots ,U_{g\prime {\prime }_{n″}})$ the ordered unit sizes in order of the second list, with realizations $u_{\mathit{obs}}^{\prime }=(u_{g{\prime }_1},\dots ,u_{g{\prime }_{n\prime }})$ and $u{″}_{\mathit{obs}}=(u_{g\prime {\prime }_1},\dots ,u_{g\prime {\prime }_{n″}})$, respectively. $Y{″}_{\mathit{obs}}=(Y\prime {\prime }_{g\prime {\prime }_1},\dots ,Y\prime {\prime }_{g\prime {\prime }_{n″}})$ with realizations $y{″}_{\mathit{obs}}=(y\prime {\prime }_{g\prime {\prime }_1},\dots ,y\prime {\prime }_{g\prime {\prime }_{n″}})$ represent the recapture information. In other words, $y_{g_i}″=1$ if unit g_i was observed in the first list and zero otherwise. $U=(U_1,\dots ,U_N)$ and $u=(u_1,\dots ,u_N)$ are the unit sizes of the population. We will assume that the unit sizes are independent and identically distributed by some probability mass function $f(·|\eta )$. The choice of parametric model for the unit size distribution is discussed further in section 3.4. Finally, for simplicity, we will use ${\mathbf{U}}_{o\mathit{bs}}=\{U_{\mathit{obs}}^{\prime },U{″}_{\mathit{obs}},Y{″}_{\mathit{obs}}\}$, with realizations ${\mathbf{u}}_{o\mathit{bs}}=\{u_{\mathit{obs}}^{\prime },u{″}_{\mathit{obs}},y{″}_{\mathit{obs}}\}$ to represent all observed data, including both lists and information about their overlap.

$$\begin{array}{c}\begin{array}{cc}\hfill & L(N,\eta |{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})\hfill \\ \hfill & \propto p({\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}}|N,\eta )\hfill \\ \hfill & =p(U_{\mathit{ob}{s}^{\prime }}=u_{\mathit{ob}{s}^{\prime }}|N,\eta ) p(U_{\mathit{ob}{s}^{″}}=u_{\mathit{ob}{s}^{″}},Y_{\mathit{ob}{s}^{″}}=y_{\mathit{ob}{s}^{″}}|U_{\mathit{ob}{s}^{\prime }}=u_{\mathit{ob}{s}^{\prime }},N,\eta )\hfill \\ \hfill & =p(U_{\mathit{ob}{s}^{\prime }}=u_{\mathit{ob}{s}^{\prime }}|N,\eta ) p(U_{\mathit{ob}{s}^{″}}=u_{\mathit{ob}{s}^{″}}|Y_{\mathit{ob}{s}^{″}}={y^{″}}_{\mathit{obs}},U_{\mathit{ob}{s}^{\prime }}=u_{\mathit{ob}{s}^{\prime }},N,\eta )\times \hfill \\ \hfill & p(Y_{\mathit{ob}{s}^{″}}=y_{\mathit{ob}{s}^{″}}|U_{\mathit{ob}{s}^{\prime }}=u_{\mathit{ob}{s}^{\prime }},N,\eta )\hfill \end{array}\\ \begin{array}{cc}\hfill & =\sum ^u[(\sum ^{g^{\prime }}p({U^{\prime }}_{\mathit{obs}}={u^{\prime }}_{\mathit{obs}}|U=u,G^{\prime }=g^{\prime },\eta )p(G^{\prime }=g^{\prime }|U=u,\eta ))\times \hfill \\ \hfill & (\sum _{g^{″}}^{}p({U^{″}}_{\mathit{obs}}={u^{″}}_{\mathit{obs}}|U_{\mathit{ob}{s}^{\prime }}={u^{\prime }}_{\mathit{obs}},{Y^{″}}_{\mathit{obs}}={y^{″}}_{\mathit{obs}},U=U,G^{″}=g^{″},\eta )·\hfill \\ \hfill & p(G^{″}=g^{″}|{Y^{″}}_{\mathit{obs}}={y^{″}}_{\mathit{obs}},U_{\mathit{ob}{s}^{\prime }}={u^{\prime }}_{\mathit{obs}},U=u)\times \hfill \\ \hfill & p({Y^{″}}_{\mathit{obs}}={y^{″}}_{\mathit{obs}}|U_{\mathit{ob}{s}^{\prime }}={u^{\prime }}_{\mathit{obs}},U=u,\eta ))·p(U=u|\eta )]\hfill \\ \hfill & =\frac{N!}{(N-n)!}\sum _{v\in \mathcal{U}}[p(G^{\prime }=(1\cdots n^{\prime })|U=v)\times \hfill \\ \hfill & p(G^{″}=g^{*}|U_{\mathit{ob}{s}^{\prime }}={u^{\prime }}_{\mathit{obs}},{Y^{″}}_{\mathit{obs}}={y^{″}}_{\mathit{obs}},U=v,\eta )\times \hfill \\ \hfill & p({Y^{″}}_{\mathit{obs}}={y^{″}}_{\mathit{obs}}|U_{\mathit{ob}{s}^{\prime }},U=v,\eta )\prod _{j=1}^{N}f(u_j|\eta )].\hfill \end{array}\end{array}$$

Here $\mathcal{U}$ is the set of equivalence classes of unit sizes possible for the N units, given that the observed data was ${\mathbf{u}}_{o\mathit{bs}}$. Intuitively, the elements of $\mathcal{U}$ include all possible unit sizes for each of the N units, except n of them are constrained to be the observed unit sizes. Since the likelihood is equivalent for all values of $g\prime$ and $g″$ as long as they have the same unit sizes, we assign the labels sequentially starting from one and incrementing up when we sample a previously unobserved unit, then multiply by the number of permutations outside the sum. So in the first list, we have $g\prime =\{1,\dots ,n\prime \}$, and in the second list, we have $g″=g^{*}$, where the values of $g^{*}$ take on the original label from the first list if it was already observed in the first list and the next available sequential value if it was not observed in the first list. In other words, the newly observed units in $g^{*}$ are in order from $n\prime +1$ to n (recall that n refers to the combined sample size, or the number of unique units sampled in the two lists), while the previously observed units retain their original labeling. Since we choose $n\prime$ indices from N possible in the first list and $n\prime -n_0$ indices from $N-n\prime$ possible in the second list, the multiplicative factor is

$$\frac{N!}{(N-n\prime )!}·\frac{(N-n\prime )!}{(N-n\prime -(n″-n_0))!}=\frac{N!}{(N-n)!}.$$

We note that even though n is not fixed by the study design as $n\prime$ and $n″$ are, it is determined by the observed data (specifically, the overlap information), and we are able to apply the multiplicative factor outside the summation due to how we have constructed $\mathcal{U}$.

3.2 Modeling RDS as PPSWOR

Respondent-driven sampling is a complex process for which it is extremely difficult to find a statistical representation because it relies on the network structure of the population and is not fully controlled by surveyors. There have been many attempts at approximating the RDS process (Heckathorn 1997; Volz and Heckathorn 2008; Gile 2011). Gile (2011) provides theoretical and empirical justification for treating the RDS process as a successive sampling process, using a probability proportional to size without replacement (PPSWOR) sampling scheme to approximate RDS, showing that it reduces finite population biases for RDS estimates of population characteristics.

As such, we model the RDS process as a successive sampling procedure, following Gile (2011). Specifically, our model for the first list is the same as in SS-PSE (Handcock et al. 2014):

$$\begin{array}{cc}\hfill & L(N,\eta |{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})\hfill \\ \propto \frac{N!}{(N-n)!}\sum _{v\in \mathcal{U}}[\hfill & (\prod _{k=1}^{n^{\prime }}\frac{u_{{g^{\prime }}_k}}{{r^{\prime }}_k})p(G^{″}=g^{*}|U_{\mathit{ob}{s}^{\prime }}={u^{\prime }}_{\mathit{obs}},{Y^{″}}_{\mathit{obs}}={y^{″}}_{\mathit{obs}},U=v,\eta )\times \hfill \\ \hfill & p({Y^{″}}_{\mathit{obs}}={y^{″}}_{\mathit{obs}}|U_{\mathit{ob}{s}^{\prime }},U=v,\eta )\prod _{j=1}^{N}f(u_j|\eta )],\hfill \end{array}$$

where

$$r{\prime }_k=\sum _{i=1}^{n\prime }{u}_{g{\prime }_i}-\sum _{j=1}^{k-1}{u}_{g{\prime }_j}.$$ (1)

We can think of $r{\prime }_k$ as representing the remaining total degree (i.e., the sum of the degrees of everyone in the population who has not yet been sampled). For the second list, we split it up into two parts: whether the units in the second list were in the first list and the order in which they were captured, given the information about whether they were in the first list. We start with the latter.

Given that we know whether or not the unit was in the first list, we can treat the sampling process as PPSWOR out of the two groups: captured in first list and not captured in first list. Let $g_k^{+},k\in \{1,\dots ,n_0\}$ refer the indices of units caught in the first list and $g_k^{-},k\in \{1,\dots ,N-n\prime \}$ refer to the indices of units not caught in the first list. Then, we obtain

$$p(G″=g^{*}|U_{\mathit{obs}}^{\prime }=u{\prime }_{\mathit{obs}},Y\prime {\prime }_{\mathit{obs}}=y\prime {\prime }_{\mathit{obs}},U=v,\eta )=\prod _{k=1}^{n″-n_0}\frac{u_{g_k^{+}}}{r_k^{+}}\prod _{k=1}^{n_0}\frac{u_{g_k^{-}}}{r_k^{-}},$$

where

$$r_k^{+}=\sum _{i=1}^{n″}{u}_{g\prime {\prime }_i}-\sum _{j=1}^{k-1}{u}_{g_j^{+}} \text{and} r_k^{-}=\sum _{i=1}^{n″}{u}_{g\prime {\prime }_i}-\sum _{j=1}^{k-1}{u}_{g_j^{-}}.$$ (2)

So, our full likelihood becomes

$$L(N,\eta |{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})$$

$$\propto \frac{N!}{(N-n)!}\sum _{v\in \mathcal{U}}[\prod _{k=1}^{n\prime }\frac{u_{g{\prime }_k}}{r{\prime }_k}\prod _{k=1}^{n″-n_0}\frac{u_{g_k^{+}}}{r_k^{+}}\prod _{k=1}^{n_0}\frac{u_{g_k^{-}}}{r_k^{-}}·p(Y\prime {\prime }_{\mathit{obs}}=y\prime {\prime }_{\mathit{obs}}|U_{\mathit{obs}}^{\prime },U=v,\eta )\prod _{j=1}^{N}f(u_j|\eta )].$$

Recall that $Y\prime {\prime }_{\mathit{obs}}$ represents a vector of indicator variables for whether the units in the second list were captured in the first list. Again, we model the process as PPSWOR so that

$$p(Y\prime {\prime }_{\mathit{obs}}=y\prime {\prime }_{\mathit{obs}}|U{\prime }_{\mathit{obs}}=u{\prime }_{\mathit{obs}},U=v,\eta )=\prod _{k=1}^{n″}\frac{1}{{r″}_k}\prod _{k=1}^{n″-n_0}{r}_k^{+}\prod _{k=1}^{n_0}{r}_k^{-},$$

where

$$r\prime {\prime }_k=\sum _{i=1}^{n″}{u}_{g\prime {\prime }_i}-\sum _{j=1}^{k-1}{u}_{g\prime {\prime }_j}.$$

After simplification, we obtain

$$L(N,\eta |{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})\propto \frac{N!}{(N-n)!}\sum _{v\in \mathcal{U}}[\prod _{k=1}^{n\prime }\frac{u_{g{\prime }_k}}{r{\prime }_k}\prod _{k=1}^{n″-n_0}{u}_{g_k^{+}}\prod _{k=1}^{n_0}{u}_{g_k^{-}}\prod _{k=1}^{n″}\frac{1}{r\prime {\prime }_k}\prod _{j=1}^{N}f(u_j|\eta )].$$

3.3 Bayesian Inference for Unit Size Distribution and Population Size

The joint posterior is given by

$$p(\eta ,N|{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})\propto \pi (\eta ,N)·L[\eta ,N|{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}}],$$

where $\pi (\eta ,N)$ is the joint prior for the unit size distribution parameter and the population size. West (1996) and Handcock et al. (2014) note that the likelihood is difficult to compute due to the complexity of $\mathcal{U}$. They develop an ancillary variable to finesse this. We use a variant of this method to sample from the augmented posterior,

$$p(N,\eta ,U_{\mathit{unobs}}=u_{\mathit{unobs}},\hspace{0.17em}\Psi |{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}}),$$

using a four-component Gibbs sampler. This method is developed and detailed in appendices A.1 and B.1. The full specification of the Markov Chain Monte Carlo (MCMC) algorithm is given in appendix C.1.

3.4 Unit Size Distribution Model

For our purposes, we need a super-population model for unit size. Here we focus on the cases in which the unit sizes are the personal network sizes (or degrees). There has been a considerable amount of work done on modeling the degree distribution of a network. Handcock et al. (2014) notes that certain long-tailed distributions such as the Poisson-log-normal and the Waring and Yule distributions, which allow for power-law over-dispersion (Handcock and Jones 2006), are not able to represent the under-dispersion in degree counts, suggesting the Conway-Maxwell-Poisson distribution (Shmueli, Minka, Kadane, Borle, and Boatwright 2005) as an alternative.

For the applications in this article, we chose to use the Conway-Maxwell-Poisson distribution because it offers greater flexibility over similar distributions such as the Poisson while using only one additional parameter.

3.5 Prior Specification

We can parametrize the Conway-Maxwell-Poisson distribution in terms of its mean and standard deviation. We then put priors on the log mean and variance parameters using the normal distribution for the prior log mean, μ, given the prior standard deviation σ, and scaled inverse χ² for the variance ${\sigma }^2$, so

$$\text{log}(\mu )|\sigma \sim N({\mu }_0,\sigma /d{f}_{\mathit{mean}}) \text{and} {\sigma }^2\sim \text{Inv}{\chi }^2({\sigma }_0^2;d{f}_{\mathit{sigma}}).$$

In our applications, we use diffuse priors with df_mean = 1 and df_sigma = 5.

For the population size, Handcock et al. (2014) uses a two-parameter class of priors,

$$\pi (N)=\frac{\beta n{(N-n)}^{\beta -1}}{N^{\alpha +\beta }}\text{for} N>n,\alpha >0,\beta >0.$$

This prior can be thought of specifying knowledge about the sample fraction $(n/N)$ as a beta (α, β) distribution. This class of priors was chosen after consultation with field researchers; the hyperparameters can be specified by them based on budget and logistic considerations for their choice of sample size. For more information about this prior choice, see Handcock et al. (2014).

4. ASSESSMENT OF CR-SS-PSE

In this section we compare our method, capture-recapture successive sampling–population size estimation (CR-SS-PSE) with other population size estimation methods. One approach to assessment would be using asymptotic approximations of its statistical properties. However, in the case of population size estimation, there are a number of different asymptotic frameworks involving the relative sizes of n and N, and the real-world relevance of each proposed asymptotic approximation would need to be carefully considered. Instead, we assess the performance of CR-SS-PSE via simulation studies using ranges of n and N that are commonly met in practice. We can also precisely specify the statistical properties of the networked populations and RDS schemes. This allow us to see how CR-SS-PSE performs under known conditions and the dimensions under which it breaks down.

4.1 Simulation of Networks with Known Statistical Properties

In general, we do not expect people to form networks completely randomly. Therefore, we tried to simulate networks with network characteristics as close to the populations of interest as possible. We want to incorporate some of the factors that affect network structure, as they can greatly affect how the RDS process samples from the population. Therefore, we will look at several key aspects of network formation.

Exponential-family random graph models (ERGMs) were used to generate each of the simulated population networks discussed in this chapter (Snijders, Pattison, Robins, and Handcock 2006; Gile and Handcock 2010; Spiller, Gile, Handcock, Mar, and Wejnert 2017). That is, y, an N by N binary matrix representation of a network (with y_ij = 1 if there is a tie between node i and node j, and y_ij = 0 otherwise) is represented as a realization of the random variable Y with distribution

$$P_{\eta }(Y=y|x)=\text{exp}\hspace{0.17em}\{\eta ·g(y,x)-\kappa (\eta ,x)\}y\in \mathcal{Y},$$ (3)

where x are covariates, g(y, x) is a p-dimensional vector of network statistics, $\eta \in {\mathbb{R}}^p$ is a parameter vector, $\mathcal{Y}$ is the set of all possible undirected networks with N nodes, and $\text{exp}\hspace{0.17em}\{\kappa (\eta ,x)\}=\sum _{u\in \mathcal{Y}}\hspace{0.17em}\text{exp}\hspace{0.17em}\{\eta ·g(u,x)\}$ is the normalizing constant (Handcock et al. 2014).

The ERGM provides a way for us to put a probability on every possible network with a certain number of nodes, N, based on characteristics of the network we want to simulate. In the simulations discussed in this chapter, we use parameters for homophily, differential activity, and overall mean degree that acts as a baseline level of propensity to form ties. We use the ERGM to draw networks from the space of all possible networks with a probability described by (3).

For the first part of our simulation studies, we use two simulated networks—called Faux Sycamore and Faux Madrona—and a real network from the Add Health data set. The Faux Sycamore and Faux Madrona network data sets were taken from the RDS package in R (Handcock, Fellows, and Gile 2016). These simulated data was used by Gile and Handcock (2010) in simulation studies to test RDS estimators and was created to include characteristics similar to the data from the CDC surveillance program (Abdul-Quader et al. 2006). In these networks, individuals had a dichotomous characteristic of being infected or uninfected. The networks were generated using homophily and differential activity. Homophily was such that two infected individuals were five times as likely to be linked with a tie than a mixed pair of individuals. Differential activity on their disease status was such that the mean degree of infected individuals was twice that of uninfected individuals.

The Add Health data set was constructed from a series of questionnaires given to students in school. The students were asked to nominate friends either in the same school or in a “sister” school, and a friendship network was generated based on these responses (Harris, Halpern, Whitsel, Hussey, Tabor, et al. 2009). We used a network with N = 2,587 for our simulations. Though the networks generated were directed, we treated them as undirected by turning each tie into an undirected one.

Then we simulated networks based on RDS data collected on people who inject drugs (PWID) from ten cities collected by the CDC (Centers for Disease Control and Prevention 2012). To create the simulated networks, five network characteristics were measured: the prevalence of a binary trait, HIV infection, homophily for that trait, mean degree, and differential activity. Using the estimated mean values of these characteristics from the RDS studies, natural parameters were calculated for the ERGMs, which were then used to simulate many networks for each of the cities: 1,000 networks for the N = 10,000 case and 250 each for the N = 5,000 and N = 1,000 cases. We will refer to these cases as the CDC PWID studies.

4.2 Simulation of RDS

In addition to simulating the population network, we simulate the RDS process. When we apply traditional capture-recapture models, we implicitly make assumptions about the RDS process. That is, we may be treating the RDS as a simple random sample as in the basic Lincoln-Petersen estimator. However, we have reason to believe that the RDS process is actually very different from this (Gile 2011). Therefore in these simulations, we try to get as close to real RDS surveys as possible.

In the simulations performed in this chapter, we will define a trial as consisting of collecting two respondent-driven samples and recording the order of observation and personal network size (unit size), in addition to recapture information. The latter is only collected in the second sample as the answer to “Were you in the first sample?” In other words, we do not track unique matching between the two lists.

For the Add Health, Faux Madrona, and Faux Sycamore networks, we started with a random sample of ten initial seeds, which is consistent with a review of over 120 RDS studies that found an average of ten seeds used (Malekinejad et al. 2008) and the number used in a pilot study run by the CDC (Abdul-Quader et al. 2006). We used two coupons for each respondent. In the simulation, starting with the seeds, we sampled two recruits randomly from the nodes connected to each respondent. Then we used the newest wave of recruits to repeat the process. If a respondent had only one available link to an unsampled person, that person only recruited one person. We stopped the RDS recruitment when we reached our target sample size. The recruiting was assumed to have been done at random from each respondent's personal network.

For the simulated networks based on CDC PWID studies, we used real network characteristics for each of the cities and then performed one RDS trial for each of the networks. The networks were generated for N = 10,000 and N = 1,000. The RDS simulation that was performed on each of the networks was based on the real RDS that was taken in the real city. That is, the simulated RDS had the same number of starting seeds, number of coupons given out, number of seeds with or without the trait (HIV infection), and distribution of number of recruits per respondent as the actual RDS run in that city.

4.3 Population Size Estimation Methods

We compare our method, CR-SS-PSE, with five other methods. We include two methods that used multiple list concepts: simple capture-recapture using the hypergeometric distribution (Cosenza et al. 2014) and the nonparametric latent class model (NPLCM) (Manrique-Vallier 2016). We used a Bayesian implementation of the hypergeometric model so that we could use the same priors as in all of our other methods.

We also used three variants of the SS-PSE model: SS-PSE with just the first list (which we call SS-PSE); SS-PSE using the first list and then SS-PSE with the second list using the posterior from the first as the prior (which we call independent SS-PSE); and SS-PSE with one combined list consisting of all unique units in the order they were sampled, removing any double-counting from the second list (which we call combined SS-PSE).

4.4 Faux Sycamore Friendship Network

The Faux Sycamore network had a true population size of N = 715, and the sample size for each list was $n\prime =n″=150$. Table 1 gives some numerical summaries of the performance of the point estimates. Capture-recapture successive sampling–population size estimation and hypergeometric CR have the lowest MSE values, while CR-SS-PSE has the lowest bias.

Table 1.

Mean Squared Error (MSE), Bias, Variance of the Posterior Means, and the Bias Proportion of MSE ( ${\text{Bias}}^2/\text{MSE})$ for Each of the Six Methods with the Faux Sycamore Network

Method	MSE	Bias	Variance	Bias proportion of MSE
CR-SS-PSE	$1.7\times {10}^4$	36	$1.6\times {10}^4$	0.077
SS-PSE	$9.6\times {10}^4$	−264	$2.7\times {10}^4$	0.722
Independent SS-PSE	$9.3\times {10}^4$	−259	$2.6\times {10}^4$	0.719
Combined SS-PSE	$2.2\times {10}^5$	307	$1.2\times {10}^5$	0.434
Hypergeometric CR	$1.7\times {10}^4$	−70	$1.2\times {10}^4$	0.287
NPLCM	$3.0\times {10}^4$	–145	$8.6\times {10}^3$	0.708

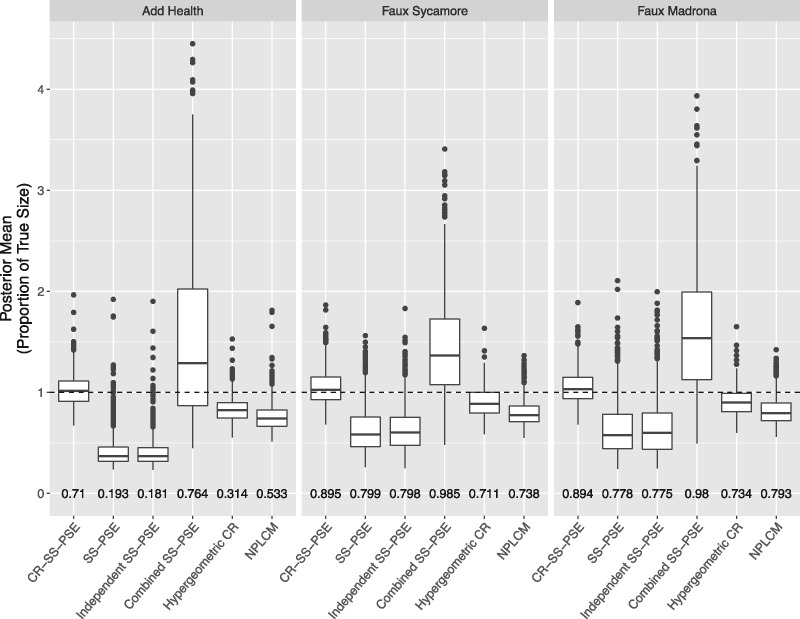
Figure 2 shows the posterior means using the six methods and their coverage rates. As the bias and MSE values showed, CR-SS-PSE seems to do the best job, with the posterior means centered at the true value. Successive sampling–population size estimation and independent SS-PSE both underestimate the population size, while the combined SS-PSE model overestimates the population size and has the largest variation in posterior means. The hypergeometric capture-recapture model and NPLCM both also tend to underestimate the true population size. Capture-recapture successive sampling–population size estimation and combined SS-PSE have the best coverage rates.

Figure 2.

Boxplots of posterior means with six methods for the Add Health, Faux Sycamore, and Faux Madrona networks. Posterior means are shown as a proportion of the true population size. Coverage rate of the 1,000 90% confidence interval estimates is shown below each boxplot.

4.5 Faux Madrona Friendship Network (N = 1,000)

The Faux Madrona network had a true population size of N = 1,000, and the sample size for both lists was $n\prime =n″=200$. Figure 2 shows the posterior means using the six methods. We see similarities to what we saw from the Faux Sycamore data set. Capture-recapture successive sampling–population size estimation performs the best, with a median posterior mean very close to the true population size, while most of the other methods tend to underestimate, and the combined SS-PSE method overestimates. Capture-recapture successive sampling–population size estimation and combined SS-PSE again have the best coverage rates.

Table 2 shows the performance of the point estimates. Capture-recapture successive sampling–population size estimation has the lowest MSE, followed by hypergeometric CR and NPLCM. Capture-recapture successive sampling–population size estimation also has the lowest bias. Combined SS-PSE has the highest variance of posterior means, which is supported by the wide boxplot in figure 2.

Table 2.

Mean Squared Error (MSE), Bias, Variance of the Posterior Means, and the Bias Proportion of MSE ( ${\text{Bias}}^2/\text{MSE})$ for Each of the Six Methods with the Faux Madrona Network

Method	MSE	Bias	Variance	Bias proportion of MSE
CR-SS-PSE	$2.6\times {10}^6$	52	$2.5\times {10}^4$	0.095
SS-PSE	$1.3\times {10}^8$	−360	$7.2\times {10}^4$	0.642
Independent SS-PSE	$1.2\times {10}^8$	−347	$7.8\times {10}^4$	0.608
Combined SS-PSE	$3.6\times {10}^8$	599	$3.8\times {10}^5$	0.487
Hypergeometric CR	$7.2\times {10}^6$	−85	$2.0\times {10}^4$	0.266
NPLCM	$3.3\times {10}^7$	−182	$1.8\times {10}^4$	0.646

4.6 Add Health Friendship Network (N = 2,587)

One aspect of the Add Health friendship network that may affect the performance compared with the two previous networks is the possible existence of a bottleneck. Since this network consists of two schools, we might be concerned about a possible bottleneck due to a high level of homophily by school.

We again use 1,000 simulated RDS trials, apply each of the six methods, and compare their posterior means and 95 percent highest posterior density, as shown in figure 2. We again see that CR-SS-PSE performs the best, with every single other method—besides the combined SS-SPE—underestimating the true population size. The difference is even more drastic in this case, with every single point estimate in the SS-PSE and independent SS-PSE methods coming under the true population size. Table 3 shows this difference even more clearly. Capture-recapture successive sampling–population size estimation again has the lowest MSE, and the bias for the SS-PSE methods are all quite high. Combined SS-PSE again does well in coverage rate due to very wide interval estimates, but CR-SS-PSE performs better than every other method.

Table 3.

Mean Squared Error (MSE), Bias, Variance of the Posterior Means, and the Bias Proportion of MSE ( ${\text{Bias}}^2/\text{MSE})$ for Each of the Six Methods with the Add Health Network

Method	MSE	Bias	Variance	Bias proportion of MSE
CR-SS-PSE	$1.7\times {10}^5$	80	$1.7\times {10}^5$	0.037
SS-PSE	$2.4\times {10}^6$	−1,497	$2.0\times {10}^5$	0.919
Independent SS-PSE	$2.5\times {10}^6$	−1,523	$1.6\times {10}^5$	0.935
Combined SS-PSE	$6.5\times {10}^6$	1,373	$4.7\times {10}^6$	0.288
Hypergeometric CR	$2.9\times {10}^5$	−433	$9.9\times {10}^4$	0.656
NPLCM	$5.1\times {10}^5$	−617	$1.3\times {10}^5$	0.749

4.7 Comparison Based on the National HIV Behavioral Surveillance Studies

In order to try to emulate real networks, we used simulated networks that were based on RDS studies for people who inject drugs (PWID) by the CDC National HIV Behavioral Surveillance system (NHBS) in 2009 and 2012 (Centers for Disease Control and Prevention 2012, 2015). For each of these networks, one RDS trial was simulated using the same number of starting seeds, number of coupons given out, number of seeds with or without the trait, and the distribution of the number of recruits as was used in the original RDS study. Every population size estimation method in this section is the same as in previous sections in terms of methods and priors used.

4.8 Population with N = 10,000

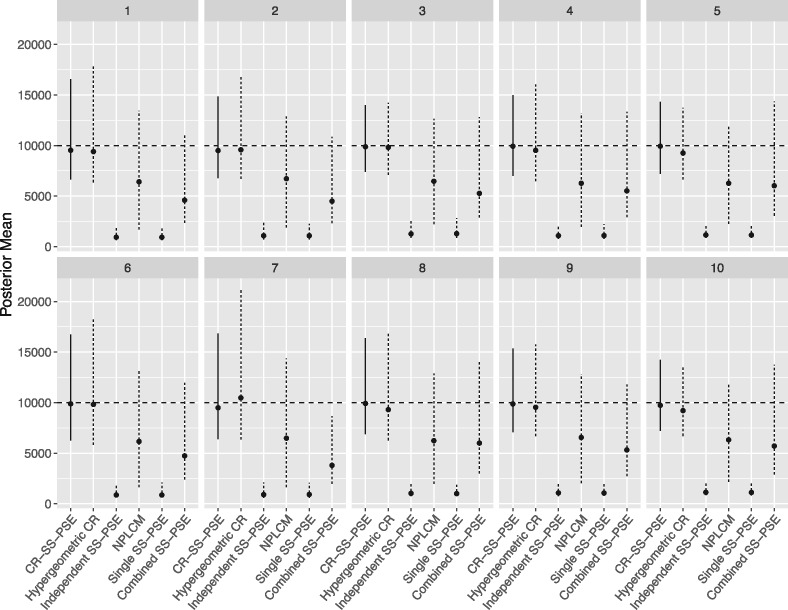
Figure 3 shows the posterior means from the cities with a population size of N = 10,000, with the point showing the median posterior mean and the line representing the middle 95 percent of the posterior means (i.e., the 97.5 and 2.5 percentile). The CR-SS-PSE method seems to be doing very well, though the hypergeometric capture-recapture model seems to be doing very similarly. In general, the posterior means for these two methods are near the true population size. By contrast, the SS-PSE methods and NPLCM all tend to greatly underestimate the population size.

Figure 3.

Posterior means from ten simulated cities for N = 10,000. The median and middle 95 percent of the posterior mean are shown with the point and line for each method. The CR-SS-PSE is shown with a solid line, while the other five methods are shown with dashed lines.

Table 4 shows the coverage rates of the interval estimates. We see that CR-SS-PSE and hypergeometric capture-recapture are both very similar and relatively high, getting close to the 90-percent coverage level, with CR-SS-PSE generally performing slightly better. The performance of the other methods by this metric falls off considerably. Independent and single SS-PSE both have extremely low coverage rates, while NPLCM and combined SS-PSE both have coverage rates that hover around 0.60.

Table 4.

Nominal 90% Confidence Interval Coverage Rates from Ten Simulated Cities for N = 10,000

City	1	2	3	4	5	6	7	8	9	10
CR-SS-PSE	0.86	0.87	0.91	0.88	0.87	0.85	0.87	0.85	0.87	0.88
Hypergeometric	0.85	0.87	0.87	0.84	0.81	0.82	0.87	0.77	0.82	0.80
Indep. SS-PSE	0.01	0.02	0.01	0.01	0.00	0.01	0.01	0.00	0.01	0.00
NPLCM	0.53	0.56	0.56	0.52	0.52	0.52	0.57	0.49	0.52	0.50
Single SS-PSE	0.01	0.01	0.01	0.00	0.00	0.01	0.01	0.00	0.01	0.00
Comb. SS-PSE	0.58	0.53	0.62	0.69	0.74	0.64	0.45	0.75	0.65	0.69

4.9 Population with N = 1,000

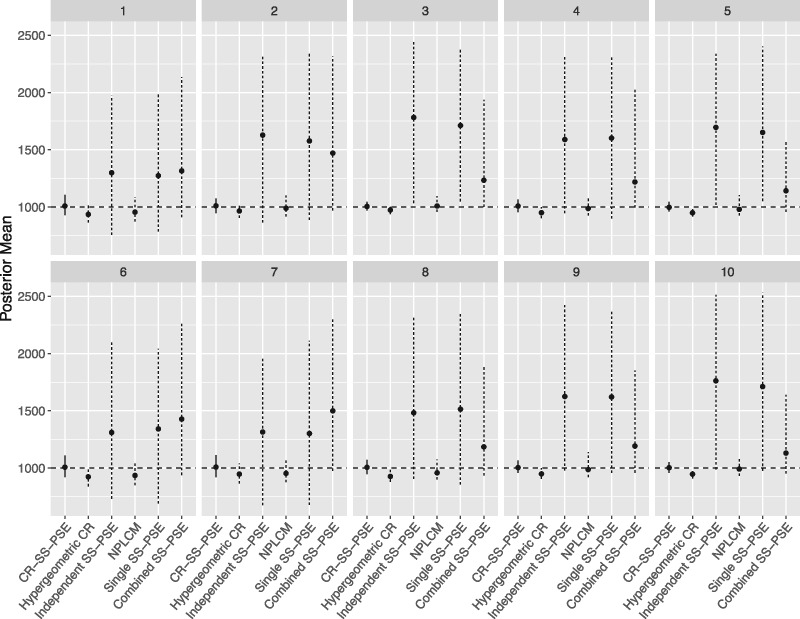
Figure 4 shows the posterior means from the cities with a population size of N = 1,000, with the point showing the median posterior mean and the line representing the middle 95 percent of the posterior means (i.e., the 97.5 and 2.5 percentile). The CR-SS-PSE method again seems to be doing very well, while the hypergeometric capture-recapture model tends to underestimate slightly. The NPLCM does better with N = 1,000 than with N = 10,000, with point estimates that seem to be close or slightly underestimated. The SS-PSE methods all overestimate this time, with a very wide range of point estimates.

Figure 4.

Posterior means from ten simulated cities for N = 1,000. The median and middle 95 percent of the posterior means are shown with the point and line for each method. The CR-SS-PSE is shown with a solid line, while the other five methods are shown with dashed lines.

Table 5 shows the coverage rates for each of the cities with N = 1,000. We see that CR-SS-PSE is again relatively high, getting close to the 90-percent coverage level. Hypergeometric capture-recapture does much poorer by this metric, with coverage rates going as high as 0.70 and as low as 0.18. However, all the other methods seem to do quite well in coverage; though in the case of the SS-PSE methods, it is due to quite large interval estimates, which is undesirable for practical purposes.

Table 5.

Coverage Rates from Ten Simulated Cities for N = 1,000

City	1	2	3	4	5	6	7	8	9	10
CR-SS-PSE	0.87	0.90	0.93	0.94	0.93	0.90	0.89	0.89	0.88	0.92
Hypergeometric	0.47	0.68	0.60	0.44	0.22	0.44	0.70	0.18	0.42	0.24
Indep. SS-PSE	0.98	0.91	0.64	0.88	0.61	0.98	0.98	0.89	0.80	0.69
NPLCM	0.95	0.98	0.96	0.98	0.91	0.94	0.98	0.94	0.95	0.94
Single SS-PSE	0.98	0.92	0.71	0.85	0.67	1.00	0.99	0.85	0.85	0.67
Comb. SS-PSE	0.81	0.72	0.69	0.80	0.86	0.85	0.84	0.82	0.84	0.83

4.10 Overview of CDC PWID Simulations

For each of the different population sizes, CR-SS-PSE had good point and interval estimates, and though there were cases in which other methods may have performed just as well, they were not consistent across all population sizes. We also note that the coverage rates for the CR-SS-PSE were relatively consistent, with lower spikes and drops compared with the other methods, and they were generally around 90 percent coverage.

5. CONCLUSION

We have proposed a new method of estimating the size of a hidden population using multiple RDS surveys. This model, called capture-recapture successive sampling for population size estimation—or CR-SS-PSE—uses information from RDS samples more efficiently than existing methods and is shown to have good properties when applied to networks with known statistical properties and has outperformed many existing methods. Due to the popularity of RDS because of the relative ease with which RDS surveys can be implemented, CR-SS-PSE can be useful in providing better estimates by using more of the available information rather than only the network information or a simple capture-recapture approximation.

Appendix A.1: Bayesian Inference for the unit size distribution

We start by developing inference for the unit size distribution conditional on known N. The posterior is given by

$$p(\eta |{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})\propto \pi (\eta )·L[\eta |{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}}],$$

where $\pi (\eta )$ is the prior for the unit size distribution parameter. West (1996) and Handcock et al. (2014) note that the likelihood is difficult to deal with and use

$$p(U=u|G\prime =g\prime ,G″=g″,\eta )=\frac{N!}{(N-n)!}\prod _{k=1}^{n\prime }\frac{u_{g{\prime }_k}}{r{\prime }_k}\prod _{h=1}^{n″}\frac{u_{g\prime {\prime }_h}}{r\prime {\prime }_h}\prod _{j=1}^{N}f(u_j|\eta ).$$ (4)

So from (4),

$$p(U_{\mathit{unobs}}=u_{\mathit{unobs}}|\eta ,{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})\propto \prod _{k=1}^{n\prime }\frac{1}{r{\prime }_k}\prod _{h=1}^{n″}\frac{1}{r\prime {\prime }_h}\prod _{j=n+1}^{N}f(u_j|\eta ).$$

West (1996) and Handcock et al. (2014) note that the $r{\prime }_k$ and $r\prime {\prime }_k$ terms are difficult to deal with and use a method involving augmenting the data. We adapt the method to include multiple lists. For $k\in \{1,\dots ,n\prime \},\hspace{0.17em}h\in \{1,\dots ,n″\}$, let $\psi {\prime }_k$ and $\psi \prime {\prime }_h$ have the exponential distribution with rate parameter $r{\prime }_k$ and $r\prime {\prime }_h$, respectively. Then,

$${\int }_0^{\infty }r{\prime }_k{e}^{-r_k^{\prime }{\psi }_k^{\prime }}d\psi {\prime }_k=1\Rightarrow {\int }_0^{\infty }{e}^{-r_k^{\prime }{\psi }_k^{\prime }}d\psi {\prime }_k=\frac{1}{r{\prime }_k}$$

and

$${\int }_0^{\infty }r\prime {\prime }_h{e}^{-r_h^{″}{\psi }_h^{″}}d\psi \prime {\prime }_h=1\Rightarrow {\int }_0^{\infty }{e}^{-r_h^{″}{\psi }_h^{″}}d\psi \prime {\prime }_h=\frac{1}{r\prime {\prime }_h}.$$

In other words,

$$p(\psi {\prime }_k=\psi \prime |\eta ,U_{\mathit{unobs}}=u_{\mathit{unobs}},{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})=r{\prime }_k\hspace{0.17em}\text{exp}(-r{\prime }_k\psi \prime )$$

and

$$p(\psi \prime {\prime }_h=\psi ″|\eta ,U_{\mathit{unobs}}=u_{\mathit{unobs}},\eta ,{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})=r\prime {\prime }_h\hspace{0.17em}\text{exp}(-r\prime {\prime }_h\psi ″).$$

We can then augment the data with $\Psi \prime =(\psi {\prime }_1,\dots ,\psi {\prime }_{n\prime })$ and $\Psi ″=(\psi \prime {\prime }_1,\dots ,\psi \prime {\prime }_{n″})$, where the components of $\Psi \prime$ and $\Psi ″$ are all conditionally independent of one another. Let $\Psi =(\Psi \prime ,\Psi ″)$. Then,

$$\begin{array}{c}p(U_{\mathit{unobs}}=u_{\mathit{unobs}},\Psi |\eta ,{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})\\ \begin{array}{cc}=\hfill & p(\Psi \prime =\psi \prime |\eta ,{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})p(\Psi ″=\psi ″|\eta ,{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})·\hfill \\ \hfill & p(U_{\mathit{unobs}}=u_{\mathit{unobs}}|\eta ,{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})\hfill \end{array}\\ \propto \prod _{j=1}^{n\prime }{e}^{-r_j^{\prime }{\psi }_j^{\prime }}\prod _{j=1}^{n″}{e}^{-r_j^{″}{\psi }_j^{″}}\prod _{j=n+1}^{N}f(u_j|\eta ).\end{array}$$ (5)

Using (1), (2), and (5),

$$\begin{array}{cc}\hfill & p(U_{\mathit{unobs}}=u_{\mathit{unobs}}|{\Psi }^{\prime },{\Psi }^{″},\eta ,{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})\hfill \\ \hfill & \propto \prod _{j=1}^{n^{\prime }}{e}^{-{r^{″}}_j{{\psi }^{\prime }}_j}\prod _{k=1}^{n^{″}}{e}^{-{r^{″}}_j{{\psi }^{″}}_j}\prod _{j=n+1}^{N}f(u_j|\eta )\hfill \\ \propto \hfill & \prod _{i=1}^{n^{\prime }}{e}^{-{{\psi }^{\prime }}_i\sum _{j=n^{\prime }+1}^N{u}_{{g^{\prime }}_j}}\prod _{i=1}^{n^{\prime }}{e}^{-{{\psi }^{\prime }}_i\sum _{j=i}^{n^{\prime }}{u}_{{g^{\prime }}_j}}\prod _{i=1}^{n^{″}}{e}^{-{{\psi }^{″}}_i\sum _{j=n^{″}+1}^N{u}_{{g^{″}}_j}}\hfill \\ \hfill & \prod _{i=1}^{n^{″}}{e}^{-{{\psi }^{″}}_i\sum _{j=i}^{n^{″}}{u}_{{g^{″}}_j}}\prod _{j=n+1}^{N}f(u_j|\eta )\hfill \\ \hfill & \propto \prod _{j=n+1}^N\hspace{0.17em}\text{exp}\hspace{0.17em}(-u_j\sum _{i=1}^{n^{\prime }}{{\psi }^{\prime }}_i)\hspace{0.17em}\text{exp}(-u_j\sum _{i=1}^{n^{″}}{{\psi }^{″}}_i)f(u_{g_j}|\eta )\hfill \\ \hfill & =\prod _{j=n+1}^N\hspace{0.17em}\text{exp}\hspace{0.17em}(-u_j(\sum _{i=1}^{n^{\prime }}{{\psi }^{\prime }}_i+\sum _{i=1}^{n^{″}}{{\psi }^{″}}_i))f(u_{g_j}|\eta ).\hfill \end{array}$$ (6)

We see that the unobserved units are conditionally independent from the unnormalized PMF $\text{exp}(-u_j({\sum }_{i=1}^{n^{\prime }}\psi {\prime }_i+{\sum }_{i=1}^{n^{″}}\psi \prime {\prime }_i))f(u_{g_j}|\eta )$. In addition, they are independent of all observed information. Thus we can get draws from the augmented posterior,

$$p(\eta ,U_{\mathit{unobs}}=u_{\mathit{unobs}},\Psi |{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}}),$$

using a three-component Gibbs sampler.

Appendix B.1: Bayesian Inference for the population size

In the previous section, we assumed a known N. However, when estimating the population size, we do not know N and want to estimate it. To do this, we adjust the method in the previous section to treat N as a parameter.

We derive the conditional for N.

$$\begin{array}{c}p(N|\eta ,\Psi \prime ,\Psi ″,{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}})\propto \pi (N)p({\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}}|N,\eta ,\Psi \prime ,\Psi ″)\\ =\frac{N!}{(N-n)!}\pi (N)\sum _{v\in \mathcal{U}}\left[\prod _{j=n+1}^N\hspace{0.17em}\text{exp}\hspace{0.17em}(-u_j(\sum _{i=1}^{n\prime }\psi {\prime }_i+\sum _{i=1}^{n″}\psi \prime {\prime }_i))f(u_{g_j}|\eta )\right]\\ =\frac{N!}{(N-n)!}\pi (N)\prod _{j=n+1}^N\left[\sum _{v_j=1}^{\infty }\hspace{0.17em}\text{exp}\hspace{0.17em}(-v_j(\sum _{i=1}^{n\prime }\psi {\prime }_i+\sum _{i=1}^{n″}\psi \prime {\prime }_i))f(j|\eta )\right]\\ =\frac{N!}{(N-n)!}\pi (N){\left[\gamma (\sum _{i=1}^{n\prime }\psi {\prime }_i+\sum _{i=1}^{n″}\psi \prime {\prime }_i,\eta )\right]}^{N-n},\text{where} \gamma (\alpha ,\eta )=\sum _{\mathrm{j}=1}^{\infty }{\mathrm{e}}^{-\alpha \mathrm{j}}\mathrm{f}(\mathrm{j}|\eta ).\end{array}$$ (7)

We can use (7) to obtain samples from the joint augmented posterior,

$$p(N,\eta ,U_{\mathit{unobs}}=u_{\mathit{unobs}}\Psi |{\mathbf{U}}_{o\mathit{bs}}={\mathbf{u}}_{o\mathit{bs}}),$$

which we can then use to obtain the marginal posterior distribution of N and η. The full details of the MCMC algorithm are given in appendix C.1.

Appendix C.1: Algorithmic Details

Here we describe in the detail the algorithm for drawing from the joint posterior.

1. Draw d from $f(·|\eta )$ and independently $u\sim U(0,1)$.

2. If $\text{log}(u)>-({\sum }_{i=1}^{n^{\prime }}\psi {\prime }_i+{\sum }_{i=1}^{n^{″}}\psi \prime {\prime }_i)·d$, reject d and return to (i). Otherwise, save d and repeat until N ann elements of u_unobs have been sampled.

3. Repeat until convergence.

		list 2
		1	0
list 1	1	$a_{1,1}$	$a_{1,0}$	$a_{1,+}$
	0	$a_{0,1}$	$a_{0,0}$	$a_{0,+}$
		$a_{+,1}$	$a_{+,0}$	$a_{+,+}$