A new study of unreported cases of 2019-nCOV epidemic outbreaks

Abstract

2019-nCOV epidemic is one of the greatest threat that the mortality faced since the World War-2 and most decisive global health calamity of the century. In this manuscript, we study the epidemic prophecy for the novel coronavirus (2019-nCOV) epidemic in Wuhan, China by using q-homotopy analysis transform method (q-HATM). We considered the reported case data to parameterise the model and to identify the number of unreported cases. A new analysis with the proposed epidemic 2019-nCOV model for unreported cases is effectuated. For the considered system exemplifying the model of coronavirus, the series solution is established within the frame of the Caputo derivative. The developed results are explained using figures which show the behaviour of the projected model. The results show that the used scheme is highly emphatic and easy to implementation for the system of nonlinear equations. Further, the present study can confirm the applicability and effect of fractional operators to real-world problems.

1. Introduction

Besides the deadly infectious virus known as severe acute respiratory syndrome (SARS) and the Middle East respiratory syndrome Coronavirus (MERS-CoV), there is another one called novel coronavirus (2019-nCOV) [1]. 2019-nCOV is more transmissible than the previous ones. The first outbreak of the 2019-NCOV has been observed in China in the city of Wuhan, in December 2019. The main source of this virus is not yet completely confirmed but the seafood market of Wuhan is considered as the main source of infection [2].Coronavirus is found in both sexes and most of all age groups and affecting more than 190 countries and territories around the world. Current reports acquaint that COVID-19 transmission may occur from an infectious individual, who is not yet symptomatic. It is recorded that appearance of the symptoms of this virus taking two to fourteen days.

From the date of its origin it exponentially growth in the mankind and infected more than 41, 78, 110 with 283,734 deaths on May 10 throughout the globe. Breathing difficulty, fatigue, fever, dry cough, tiredness, conjunctivitis, chest pain, loss of speech, diarrhoea and sore throat are the most serious symptoms in the infected peoples of COVID-19. Specifically, fatigue with 68.3%, 64.4% of taste and smell commotion, dry cough with 60.4%, fever of about 55.5%, the pain of muscle is about 44.6%, 42.6% of headache, breathing problem with 41.1% and sore throat with 31.2%, and others are the main available symptoms of COVID-19 in the general category [3]. But, it varies from gender to gender and also with different age. The symptoms include breathing difficulties, coughing, and fever. This is also be noted that if the individuals are above 60 years old then this virus becomes more deadly and effects very fast [4]. This virus is Coronaviridae family and the Nidovirales order and enveloped positive-sense, non-segmented RNA viruses and widely distributed in mammals particularly, humans [5].

In order to overcome this challenge, every day numerous tests, analysis, examination, estimation and predictions are held via research. The antibody responses for the novel virus have been discussed by researchers in [6] and presented some important and simulated results. Authors in [7] presented the impact on the environment of glob and effects on society with COVID-19 and also discussed and illustrated the possible ways of controlling its effect on humankind. A model-based analysis has been exemplified by authors in [8] and predictions and prevention approaches are presented and many researchers [9].

Nature is always provided with the all essential needs for the leaving beings for systematic life. But, mankind is tried to overcome limitations raised by nature in order to prove he is best and first for the world and as its response we have the above. However, we have many tools in order to analyse and predict the behaviour of the models illustrating various phenomena including virus and its corresponding consequences. Particularly, researchers considered mathematics as a pivotal tool in order to model the evaluation of various phenomena. The concept of calculus with integral and differential operators is the most favourable and efficient weapon to examine and build models of epidemics and pandemics. In this connection, many researchers investigate various model exemplifying the evaluation, prediction and effects of 2019-nCOV on mortality. With the aid of dataset, the COVID-2019 epidemic is analysed by researchers in [10] using ARIMA model, in [11] illustrated the effect of COVID-19 in China with undetected infections and cited some interesting results. Some researchers are mathematical models to illustrate the effect of coronavirus in country wise with the help of real data [12], [13], [14] and reference therein.

On other hand, many researchers pointed out some limitations about the study of the concept of calculus with integer order, specifically while analysing the phenomena associated to diffusion, long-range wave, hereditary properties, history-based phenomena and others. These consequences are very vital to understand the behaviour of the models which describes various phenomena. In this connection, many pioneers suggested the generalization of calculus with fractional order called fractional calculus (FC) to incorporate the above-cited consequences [15], [16], [17]. There have been distinct definitions for differential and integrals with fractional calculus [16,17]. In this paper, we used the most familiar and highly employed operator called Caputo fractional operator. Recently, many researchers are hired theory and applications of FC in order to illustrate their viewpoints while analysing various problems. For instance, authors in [18] analysed Pine Wilt Disease model with convex rate using semi-analytical technique within the frame of fractional calculus, the harmonic oscillator is studies by researchers in [19] using fractional operator with position-dependent mass, pollution of lake model has been analysed and presented some simulating results by authors in [20], some interesting consequences of mathematical exemplifying human liver is illustrated in by authors in [21] using recently proposed fractional operator, and many other interesting phenomena by numerous researchers [22], [23], [24], [25], [26], [27], [28].

The aim of this paper is to clearly describe the reported and unreported cases by the help of Caputo derivative by analysing a time-fractional model and finding its solution by the q-homotopy analysis transform method. Since, for every differential system, we don't have an exact or analytical solution, and hence we referred to semi-analytical or numerical schemes. There have numerous techniques in the literature. Most of them have their own limitations, for instance, accuracy, linearization, huge computation, perturbation, huge time of simplification, dissertation and many others. However, recently many researchers showed that homotopy analysis scheme with Laplace transform to overcome the above-cited limitations. The considered solution procedure is proposed by Singh et al. [29] with the aid of q-HAM and LT. Later, it has been hired by many researchers to find the solution for various classes of nonlinear differential equations describing various phenomena including fluid mechanics, optics, chaotic behaviour, human disease, biological models, economic growth, chemical and others [30], [31], [32], [33], [34], [35], [36], [37], and also presented some interesting simulating consequences with the comparison of other traditional and modified techniques. Recently, it has been proved by many researchers, the considered method offers two parameters and which can assist us to converge our solution to an analytical solution with the minimum number of iterations and so on [33], [34], [35], [36], [37], [38], [42], [43], [44], [45], [46], [47], [48], [49], [50], [51], [52], [53], [54], [55], [56], [57], [58], [59], [60], [61], [62], [63].

2. Preliminaries

Here, basic notations are recalled for the FC and Laplace transform.

Definition 1

The fractional Riemann-Liouville derivative of a function f(t) is defined as [15]

$$J^{\alpha }f\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}\underset{0}{\overset{t}{\int }}{\left(t-\vartheta \right)}^{\alpha -1}f\left(\vartheta \right)d\vartheta .$$ (1)

Definition 2

The Caputo fractional order derivative of$f\in C_{-1}^n$ is presented as follows [15], [16], [17]

$$D_t^{\alpha }f\left(t\right)=\{\begin{array}{cc}{\displaystyle \frac{d^{n}f\left(t\right)}{d{t}^n},}\hfill & \alpha =n\in N,\hfill \\ {\displaystyle \frac{1}{\Gamma \left(n-\alpha \right)}\underset{0}{\overset{t}{\int }}{\left(t-\vartheta \right)}^{n-\alpha -1}{f}^{\left(n\right)}\left(\vartheta \right)d\vartheta ,}\hfill & n-1<\alpha <n,n\in \mathbb{N}.\hfill \end{array}$$ (2)

Definition 3

Laplace transform (LT) of f(t) with respect to fractional Caputo derivative [15], [16], [17] is

$$L\left[D_t^{\alpha }f\left(t\right)\right]=s^{\alpha }F\left(s\right)-\sum _{r=0}^{n-1}{s}^{\alpha -r-1}{f}^{\left(r\right)}\left(0^{+}\right),\left(n-1<\alpha \le n\right),$$ (3)

where F(s) is LT of f(t).

3. Model descriptions

In the present investigation, we consider the epidemic model studied by Liu et al. [39]. In [39], the authors presented and derived some interesting results for the projected model by comparison with some practical values and also cited interesting results. The considered model consists of four compartments with individuals of susceptible S(t), asymptomatic infectious I(t), reported symptomatic infectious R(t), unreported symptomatic infectious U(t). Now, the ordinary nonlinear differential system is considered as follows [39]

$$\begin{array}{ccc}\hfill \frac{dS\left(t\right)}{dt}& =& -\rho S\left(t\right)\left[I\left(t\right)+U\left(t\right)\right],\hfill \\ \hfill \frac{dI\left(t\right)}{dt}& =& \rho S\left(t\right)\left[I\left(t\right)+U\left(t\right)\right]-\beta I\left(t\right),\hfill \\ \hfill \frac{dR\left(t\right)}{dt}& =& {\beta }_{1}I\left(t\right)-\mu R\left(t\right),\hfill \\ \hfill \frac{dU\left(t\right)}{dt}& =& {\beta }_{2}I\left(t\right)-\mu U\left(t\right).\hfill \end{array}$$ (4)

The considered model is generalised to fractional order with the aid of novel fractional operator called Caputo derivative. Now, the generalised system of the considered model defined in Eq. (4) is as follows

$$\begin{array}{ccc}\hfill D_t^{\alpha }S\left(t\right)& =& -\rho S\left(t\right)\left[I\left(t\right)+U\left(t\right)\right],\hfill \\ \hfill D_t^{\alpha }I\left(t\right)& =& \rho S\left(t\right)\left[I\left(t\right)+U\left(t\right)\right]-\beta I\left(t\right),\hfill \\ \hfill D_t^{\alpha }R\left(t\right)& =& {\beta }_{1}I\left(t\right)-\mu R\left(t\right),\hfill \\ \hfill D_t^{\alpha }U\left(t\right)& =& {\beta }_{2}I\left(t\right)-\mu U\left(t\right).\hfill \end{array}$$ (5)

4. Fundamental solution procedure of q-HATM

In this segment, to illustrate the solution procedure of the proposed technique we consider fractional differential equation [[29], [30], [31],40,41]

$$D_t^{\alpha }v(x,t)+\mathcal{R}v(x,t)+\mathcal{N}v(x,t)=f(x,t),n-1<\alpha \le n,$$ (6)

with the initial condition

$$v(x,0)=\mathcal{g}\left(x\right),$$ (7)

where$D_t^{\alpha }v\left(x,t\right)$ symbolise the Caputo derivative of v(x, t). By applying LT on Eq. (6), one can get

$$L\left[v(x,t)\right]-\frac{\mathcal{g}\left(x\right)}{s}+\frac{1}{s^{\alpha }}\{L\left[\mathcal{R}v(x,t)\right]+L\left[\mathcal{N}v(x,t)\right]-L\left[f(x,t)\right]\}=0.$$ (8)

Then we define the nonlinear operator for corresponding real-valued function φ(x, t; q)

$$\begin{array}{ccc}\hfill N\left[\phi (x,t;q)\right]& =& L\left[\phi (x,t;q)\right]-\frac{\mathcal{g}\left(x\right)}{s}\hfill \\ & & +\frac{1}{s^{\alpha }}\{L\left[\mathcal{R}\phi (x,t;q)\right]+L\left[\mathcal{N}\phi (x,t;q)\right]-L\left[f(x,t)\right]\}.\hfill \end{array}$$ (9)

where $q\in \left[0,\frac{1}{n}\right]$. Now, the homotopy is defined as follows

$$(1-\mathit{nq})L[\phi (x,t;q)-v_0(x,t)]=\hslash q\mathcal{N}\left[\phi (x,t;q)\right],$$ (10)

where L is signifying LT, $q\in \left[0,\frac{1}{n}\right]\left(n\ge 1\right)$ is the embedding parameter and ℏ ≠ 0 is an auxiliary parameter. For $q=0$ and$q=\frac{1}{n}$, the results are given below hold true

$$\phi \left(x,t;0\right)=v_0\left(x,t\right),\phi \left(x,t;\frac{1}{n}\right)=v\left(x,t\right).$$ (11)

Now, by intensifying q from 0 to $\frac{1}{n}$, then φ(x, t; q) varies from v ₀(x, t) to v(x, t). By applying Taylor theorem near to q, we have

$$\phi \left(x,t;q\right)=v_0\left(x,t\right)+\sum _{m=1}^{\infty }{v}_m\left(x,t\right)q^m,$$ (12)

where

$$v_m\left(x,t\right)=\frac{1}{m!}\frac{{\partial }^m\phi \left(x,t;q\right)}{\partial q^m}{|}_{q=0}.$$ (13)

On m-times differentiating Eq. (10) with q and then multiply by $\frac{1}{m!}$ and later substituting $q=0$, we have

$$L[v_m(x,t)-k_m{v}_{m-1}(x,t)]=\hslash {\mathfrak{R}}_m\left({\overrightarrow{v}}_{m-1}\right),$$ (14)

where the vectors are defined as

$${\overrightarrow{v}}_m=\left\{v_0\left(x,t\right),v_1\left(x,t\right),\dots ,v_m\left(x,t\right)\right\}.$$ (15)

On applying inverse LT to Eq. (14), it reduces to

$$v_m(x,t)=k_m{v}_{m-1}(x,t)+{\hslash }^{-1}\left[{\mathfrak{R}}_m\left({\overrightarrow{v}}_{m-1}\right)\right],$$ (16)

where

$$\begin{array}{ccc}\hfill {\mathfrak{R}}_m\left({\overrightarrow{v}}_{m-1}\right)& =& L\left[v_{m-1}(x,t)\right]-(1-\frac{k_m}{n})(\frac{\mathcal{g}\left(x\right)}{s}+\frac{1}{s^{\alpha }}L\left[f(x,t)\right])\hfill \\ & & +\frac{1}{s^{\alpha }}L[\mathcal{R}{v}_{m-1}+{\mathcal{H}}_{m-1}],\hfill \end{array}$$ (17)

and

$$k_m=\{\begin{array}{c}0,m\le 1,\\ n,m>1.\end{array}$$ (18)

In Eq. (17), H _m is homotopy polynomial and which is defined as

$${\mathcal{H}}_m=\frac{1}{m!}{\left[\frac{{\partial }^m\phi (x,t;q)}{\partial q^m}\right]}_{q=0}\text{and}\phi (x,t;q)={\phi }_0+q{\phi }_1+q^2{\phi }_2+\cdots$$ (19)

By the aid of Eqs. (16) and (17), one can get

$$\begin{array}{ccc}\hfill v_m(x,t)& =& (k_m+\hslash )v_{m-1}(x,t)-(1-\frac{k_m}{n})L^{-1}(\frac{\mathcal{g}\left(x\right)}{s}+\frac{1}{s^{\alpha }}L\left[f(x,t)\right])\hfill \\ & & +\hslash L^{-1}\left\{\frac{1}{s^{\alpha }}L[\mathcal{R}{v}_{m-1}+{\mathcal{H}}_{m-1}]\right\}.\hfill \end{array}$$ (20)

Then, the terms of v_m(x, t) can be getting by the help of Eq. (20). The q-HATM series solution is defined below

$$v\left(x,t\right)=v_0\left(x,t\right)+\sum _{m=1}^{\infty }{v}_m\left(x,t\right).$$ (21)

5. Solution for the projected model using q-HATM

Now, we consider the fractional-order system of equations illustrating the dynamics of the presented in Eq. (5)

$$\begin{array}{c}{D}_t^{\alpha }S\left(t\right)+\rho S\left(t\right)\left[I\left(t\right)+U\left(t\right)\right]=0,\hfill \\ D_t^{\alpha }I\left(t\right)-\rho S\left(t\right)\left[I\left(t\right)+U\left(t\right)\right]+\beta I\left(t\right)=0,\hfill \\ D_t^{\alpha }R\left(t\right)-{\beta }_{1}I\left(t\right)+\mu R\left(t\right)=0,\hfill \\ D_t^{\alpha }U\left(t\right)-{\beta }_{2}I\left(t\right)+\mu U\left(t\right)=0,\hfill \end{array}$$ (22)

with initial conditions

$$S\left(0\right)=S_0,I\left(0\right)=I_0,R\left(0\right)=R_0\text{and}U\left(0\right)=U_0.$$ (23)

Now, applying LT on Eq. (22) and with the assist of Eq. (23), one can get

$$\begin{array}{ccc}& & L\left[S\left(t\right)\right]-\frac{1}{s}\left(S_0\right)+\frac{1}{s^{\alpha }}L\left\{\rho S\left(t\right)\left[I\left(t\right)+U\left(t\right)\right]\right\}=0,\hfill \\ & & L\left\{I\left(t\right)\right\}-\frac{1}{s}\left(I_0\right)-\frac{1}{s^{\alpha }}L\left\{\rho S\left(t\right)\left[I\left(t\right)+U\left(t\right)\right]+\beta I\left(t\right)\right\}=0,\hfill \\ & & L\left\{R\left(t\right)\right\}-\frac{1}{s}\left(R_0\right)-\frac{1}{s^{\alpha }}L\left\{{\beta }_{1}I\left(t\right)+\mu R\left(t\right)\right\}=0,\hfill \\ & & L\left\{U\left(t\right)\right\}-\frac{1}{s}\left(U_0\right)-\frac{1}{s^{\alpha }}L\left\{{\beta }_{2}I\left(t\right)+\mu U\left(t\right)\right\}=0.\hfill \end{array}$$ (24)

Now, the nonlinear operator is presented as

$$\begin{array}{ccc}\hfill N^1\left[{\phi }_1,{\phi }_2,{\phi }_3,{\phi }_4\right]& =& L\left[{\phi }_1\left(t;q\right)\right]-\frac{1}{s}\left(S_0\right)\hfill \\ & & +\frac{1}{s^{\alpha }}L\left\{\rho {\phi }_1\left(t;q\right)\left[{\phi }_2\left(t;q\right)+{\phi }_4\left(t;q\right)\right]\right\},\hfill \\ \hfill N^2\left[{\phi }_1,{\phi }_2,{\phi }_3,{\phi }_4\right]& =& L\left[{\phi }_2\left(t;q\right)\right]-\frac{1}{s}\left(I_0\right)\hfill \\ & & -\frac{1}{s^{\alpha }}L\{\rho {\phi }_1\left(t;q\right)[{\phi }_2\left(t;q\right)+{\phi }_4\left(t;q\right)]\hfill \\ & & -\left(\rho +\gamma \right){\phi }_3\left(t;q\right)+\beta {\phi }_2\left(t;q\right)\},\hfill \\ \hfill N^3\left[{\phi }_1,{\phi }_2,{\phi }_3,{\phi }_4\right]& =& L\left[{\phi }_3\left(t;q\right)\right]-\frac{1}{s}\left(R_0\right)\hfill \\ & & -\frac{1}{s^{\alpha }}L\left\{{\beta }_1{\phi }_2\left(t;q\right)+\mu {\phi }_3\left(t;q\right)\right\},\hfill \\ \hfill N^4\left[{\phi }_1,{\phi }_2,{\phi }_3,{\phi }_4\right]& =& L\left[{\phi }_4\left(t;q\right)\right]-\frac{1}{s}\left(U_0\right)\hfill \\ & & -\frac{1}{s^{\alpha }}L\left\{{\beta }_2{\phi }_2\left(t;q\right)+\mu {\phi }_4\left(t;q\right)\right\}.\hfill \end{array}$$ (25)

By employing the projected scheme and for $H\left(t\right)=1$, the m-th order deformation equation is presented as

$$\begin{array}{c}L\left[S_m\left(t\right)-k_m{S}_{m-1}\left(t\right)\right]=\hslash {}_{1,m}\left[{\overrightarrow{S}}_{m-1},{\overrightarrow{I}}_{m-1}{\overrightarrow{R}}_{m-1},{\overrightarrow{U}}_{m-1}\right],\hfill \\ L\left[I_m\left(t\right)-k_m{I}_{m-1}\left(t\right)\right]=\hslash {}_{2,m}\left[{\overrightarrow{S}}_{m-1},{\overrightarrow{I}}_{m-1}{\overrightarrow{R}}_{m-1},{\overrightarrow{U}}_{m-1}\right],\hfill \\ L\left[R_m\left(t\right)-k_m{R}_{m-1}\left(t\right)\right]=\hslash {}_{3,m}\left[{\overrightarrow{S}}_{m-1},{\overrightarrow{I}}_{m-1}{\overrightarrow{R}}_{m-1},{\overrightarrow{U}}_{m-1}\right],\hfill \\ L\left[U_m\left(t\right)-k_m{U}_{m-1}\left(t\right)\right]=\hslash {}_{4,m}\left[{\overrightarrow{S}}_{m-1},{\overrightarrow{I}}_{m-1}{\overrightarrow{R}}_{m-1},{\overrightarrow{U}}_{m-1}\right],\hfill \end{array}$$ (26)

where

$$\begin{array}{ccc}& & {\mathcal{R}}_{1,m}[{\overrightarrow{S}}_{m-1},{\overrightarrow{I}}_{m-1},{\overrightarrow{R}}_{m-1},{\overrightarrow{U}}_{m-1}]\hfill \\ & & =L\left[S_{m-1}\left(t\right)\right]-(1-\frac{k_m}{n})\frac{1}{s}\left(S_0\right)\hfill \\ & & +\frac{1}{s^{\alpha }}L\left\{\rho (\sum _{i=0}^{m-1}{S}_i{I}_{m-1-i}-\sum _{i=0}^{m-1}{S}_i{U}_{m-1-i})\right\},\hfill \\ & & {\mathcal{R}}_{2,m}[{\overrightarrow{S}}_{m-1},{\overrightarrow{I}}_{m-1},{\overrightarrow{R}}_{m-1},{\overrightarrow{U}}_{m-1}]\hfill \\ & & =L\left[I_{m-1}\left(t\right)\right]-(1-\frac{k_m}{n})\frac{1}{s}\left(I_0\right)\hfill \\ & & -\frac{1}{s^{\alpha }}L\{\rho [\sum _{i=0}^{m-1}{S}_i{I}_{m-1-i}-\sum _{i=0}^{m-1}{S}_i{U}_{m-1-i}]+\beta I_{m-1}\left(t\right)\},\hfill \\ & & {\mathcal{R}}_{3,m}[{\overrightarrow{S}}_{m-1},{\overrightarrow{I}}_{m-1},{\overrightarrow{R}}_{m-1},{\overrightarrow{U}}_{m-1}]\hfill \\ & & =L\left[R_{m-1}\left(t\right)\right]-(1-\frac{k_m}{n})\frac{1}{s}\left(R_0\right)-\frac{1}{s^{\alpha }}L\{{\beta }_1{I}_{m-1}\left(t\right)+\mu R_{m-1}\left(t\right)\},\hfill \\ & & {\mathcal{R}}_{4,m}[{\overrightarrow{S}}_{m-1},{\overrightarrow{I}}_{m-1},{\overrightarrow{R}}_{m-1},{\overrightarrow{U}}_{m-1}]\hfill \\ & & =L\left[U_{m-1}\left(t\right)\right]-(1-\frac{k_m}{n})\frac{1}{s}\left(U_0\right)-\frac{1}{s^{\alpha }}L\{{\beta }_2{I}_{m-1}\left(t\right)+\mu U_{m-1}\left(t\right)\}.\hfill \end{array}$$ (27)

Eq. (26) simplifies by the help of inverse LT as follows

$$\begin{array}{ccc}\hfill S_m\left(t\right)& =& k_m{S}_{m-1}\left(t\right)+\hslash L^{-1}\left\{{}_{1,m}[{\overrightarrow{S}}_{m-1},{\overrightarrow{I}}_{m-1},{\overrightarrow{R}}_{m-1},{\overrightarrow{U}}_{m-1}]\right\},\hfill \\ \hfill I_m\left(t\right)& =& k_m{I}_{m-1}\left(t\right)+\hslash L^{-1}\left\{{}_{2,m}[{\overrightarrow{S}}_{m-1},{\overrightarrow{I}}_{m-1},{\overrightarrow{R}}_{m-1},{\overrightarrow{U}}_{m-1}]\right\},\hfill \\ \hfill R_m\left(t\right)& =& k_m{R}_{m-1}\left(t\right)+\hslash L^{-1}\left\{{}_{3,m}[{\overrightarrow{S}}_{m-1},{\overrightarrow{I}}_{m-1},{\overrightarrow{R}}_{m-1},{\overrightarrow{U}}_{m-1}]\right\},\hfill \\ \hfill U_m\left(t\right)& =& k_m{U}_{m-1}\left(t\right)+\hslash L^{-1}\left\{{}_{4,m}[{\overrightarrow{S}}_{m-1},{\overrightarrow{I}}_{m-1},{\overrightarrow{R}}_{m-1},{\overrightarrow{U}}_{m-1}]\right\}.\hfill \end{array}$$ (28)

On simplifying the above system and with the assist of initial values, we obtained the required series solution. Then for Eq. (22), the q-HATM series solution is defined as

$$\begin{array}{c}S\left(t\right)=S_0\left(t\right)+\sum _{m=1}^{\infty }{S}_m\left(t\right){\left(\frac{1}{n}\right)}^m,\hfill \\ I\left(t\right)=I_0\left(t\right)+\sum _{m=1}^{\infty }{I}_m\left(t\right){\left(\frac{1}{n}\right)}^m,\hfill \\ R\left(t\right)=R_0\left(t\right)+\sum _{m=1}^{\infty }{R}_m\left(t\right){\left(\frac{1}{n}\right)}^m,\hfill \\ U\left(t\right)=U_0\left(t\right)+{\sum }_{m=1}^{\infty }{U}_m\left(t\right){\left(\frac{1}{n}\right)}^m.\hfill \end{array}$$ (29)

5. Results and discussion

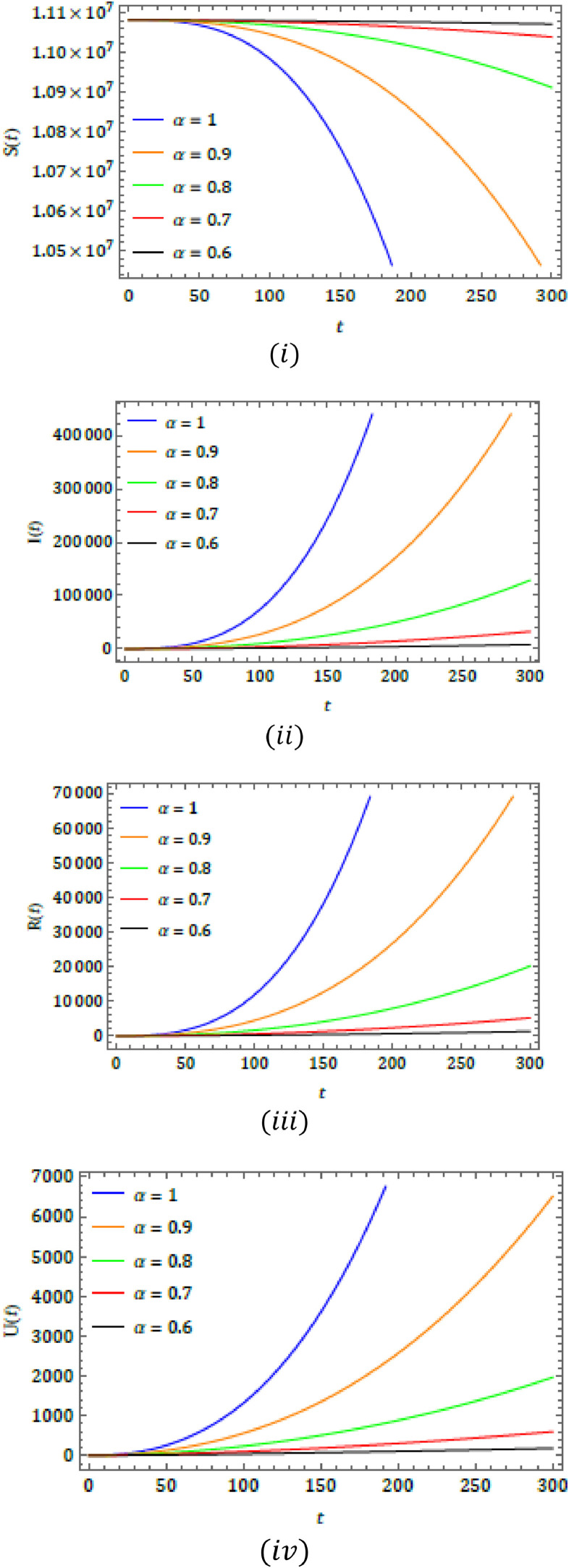
In this paper, we consider the initial conditions for the projected epidemic model as $S\left(0\right)=S_0=11.081\times {10}^6,I\left(t\right)=I_0=3.62,R\left(0\right)=R_0=0$ and $U\left(0\right)=U_0=4.13.$We evaluate up to a third-order series solution to capture the behaviour for the model. Fig. 1 exemplifies the behaviour of achieved results by projected solution procedure for S(t), I(t), R(t) and U(t) for different fractional order (α) with respect to time (t) and we consider values of all the parameters with the help of Table 1 . The considered system contains the four compartments and which exemplifies the current situation in the globe and also these types of models can aid to examine the nature and predict the exponential growth of the greatest threat of present days. We can observe from the plots that susceptible S(t), asymptomatic infectious I(t), reported symptomatic R(t) and unreported symptomatic infectious U(t) are effectively depends on the time and order of the system. Further, we capture corresponding behaviour with the values of $\alpha =0.6,0.7,0.8,0.9$ and for classical order $\left(\alpha =1\right)$ and we can see that the projected system has to simulate behaviour with respect to parameters cited in Table 1 and fractional order. The behaviour cited shows the ability and efficiency of the considered solution procedure andfrom the cited figures it is clear that the projected model extremely depends on the order and offers more degree of flexibility. Moreover, the considered fractional operator provides more interesting consequences to examine and predict the future of the considered model. The epidemic models are highly dependent on hereditary properties and hence, the present investigation may help to understand the deadly virus.

Fig. 1.

Nature of obtained solution for (i) S(t), (ii) I(t), (iii) R(t) and (iv) U(t) for different α at $\hslash =-1,n=1$ and using Table 1.

Table 1.

Parameters cited in Eq. (4) and their corresponding value [39].

Parameter	ρ	β	μ	β1	β2
Value	$4.48\times {10}^{-8}$	$\frac{1}{7}$	$\frac{1}{7}$	0.8  × μ	0.2  × μ

6. Conclusion

In the neoteric decade, so many deadly diseases have apparent their existence in many countries around the world. We studied a time-fractional model of 2019-nCOV with the successful application of q-HATM. For the given model series solutions are obtained. We achieved these results by using the fractional derivative called Caputo derivative. Our results are helpful to make an idea of unreported cases in Wuhan, China of this virus. The behaviour of the achieved third-order solution has been exemplified with the aid of plots and which demonstrate the effect and essence generalizing the integer order system into an arbitrary order system with the specific theory of fractional calculus. The projected scheme is strong and highly credible in finding the solution to fractional models of biological, physical and medical importance. For the solution of the epidemic model, we presented various graphical results at the different values of α.The present study exemplifies the applications of the projected method and considered fractional operator while analysing real word problems and understanding as well as predicting the corresponding consequences.

Credit author statement

P. Veeresha and D.G. Prakasha combined of the presented idea. H.M. Baskonus, W. Gao and P. Kumar have analyzed the results. All authors discussed the results and contributed to the final manuscript.

Declaration of Competing Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.