Mathematical modeling for the outbreak of the coronavirus (COVID-19) under fractional nonlocal operator

Abstract

A mathematical model for the spread of the COVID-19 disease based on a fractional Atangana–Baleanu operator is studied. Some fixed point theorems and generalized Gronwall inequality through the AB fractional integral are applied to obtain the existence and stability results. The fractional Adams–Bashforth is used to discuss the corresponding numerical results. A numerical simulation is presented to show the behavior of the approximate solution in terms of graphs of the spread of COVID-19 in the Chinese city of Wuhan. We simulate our table for the data of Wuhan from February 15, 2020 to April 25, 2020 for 70 days. Finally, we present a debate about the followed simulation in characterizing how the transmission dynamics of infection can take place in society.

1. Introduction

Mathematical modeling allows for rapid assessment and applied it within the dynamic frameworks used to speculation the evolution of a hypothetical or ongoing pandemic spread. These models play a significant role in aid to define strategies to control communicable diseases and mitigate their potential impacts [1], [2], [3], There are a number of extensive studies of infectious diseases in the form of mathematical models, we refer to [4], [5].

Coronaviruses are a widespread family of viruses known to cause diseases ranging from common colds to more severe diseases, such as Middle East Respiratory Syndrome (MERS) and Severe Acute Respiratory Syndrome (SARS). The emerging coronavirus (COVID-19) is a new strain of the virus that has not been previously discovered in humans. This emerging virus is an infectious and rapidly spreading disease, that was alleged to the outbreak have first spread at a Chinese city called Wuhan on 28 November [6]. It has since prevalence globally, resulting in the continuing 2020 pandemic outbreak. The COVID-19 pandemic is considered the largest global threat in the world, almost the economic and health system of every country in the world has been pushed to a very dangerous situation. Moreover, it has caused thousands of confirmed infections, it is accompanied by thousands of deaths worldwide. According to the latest statistics to date 16-May-2020, confirmed infections with the Coronavirus have exceeded 4,641,376 worldwide, while the number of deaths has reached 308,845, and the number of people recovered has risen to 1,767,389, according to the World-Meter website that specialized in counting COVID-19 victims.

Infectious diseases pose a big menace to humans also to the country’s economy. A strict understanding of the dynamics of disease plays a considerable role in decrease infection in society. So, implementation of a convenient strategy contra disease transportation is another defy. Mathematical modeling style is one of the main tools for dealing with these challenges. Numerous disease models were developed in the recent literature that allows us to better scout the spread and control of infectious diseases. Most of these models are established on ordinary differential equations see [7], [8], [9], [10], [11], [12]. However, in recent years the role of fractional calculus that deals with fractional order has appeared, as it has a prominent role in the interpretation of real-world problems, as well as in modeling real phenomena due to of its accurate description of genetic characteristics and memory [13], [14], [15], [16], [17], [18], [19], [20], [21].

In the given paper, we consider the model in the integer-order derivative introduced by [22] and then we generalize this model by applying the Atangana–Baleanu (AB) fractional derivative. The aim of utilizing the AB fractional derivative to the model is that it has kernel is nonsingular and nonlocal, and the intersection behavior can be better described in the model using this operator than other fractional operators such as Caputo, Caputo-Fabrizio [23], [24], [25], [26], [27], [28], [29], and other. Some recent research related to the AB fractional derivatives and their applications to different models emerging in science and engineering can be found in [30], [31], [32], [33], [34], [35], [36], [37], [38]. Some other related works to the modeling infectious diseases of AB fractional derivative can be seen in [39], [40], [41], [42], [43], [44], [45].

The global problem of the spread of the disease attracted the attention of researchers from various fields, which led to the emergence of a number of proposals to analyze and anticipate the development of the epidemic [46], [47]. The purpose of the paper is to consider the reported cases in the Chinese city of Wuhan since February 15, 2020 till April 25, 2020 for 70 days, and formulate a mathematical model involving AB fractional derivatives. Then we discuss the existence, uniqueness and stability results for the COVID-19 model (3)–(4) by means of fixed point theorems and generalized Gronwall inequality. Moreover, the fractional Adams–Bashforth method is effective to approximate the AB fractional operator. Through numerical simulation, the graphical representation of numerical solutions is shown accurately. For the numerical simulation, we apply a strong two-step numerical instrument named fractional Adams–Bashforth technique. The intended numerical technique is stronger than the classical Euler technique also Taylor technique. Due to the aforementioned technique is quicker convergent and stable as a comparison to other techniques that are slowly convergent, see [48], [49], [50], [51].

The rest of this paper is arranged as follows. In Section 2, we recall some fundamental properties of the AB fractional operators and the results of nonlinear functional analysis. Brief details about the fractional mathematical modeling of the novel COVID-19 pandemic are present in Section 3. The existence and uniqueness solutions of the fractional model have been investigated via some fixed point theorems in Section 4. In Section 5, we apply the Gronwall inequality in the frame of the AB fractional integral to obtain the Ulam stability results. We then, present an Adams–Bashforth numerical scheme to solve the proposed model in Section 6. Moreover, the behavior of the approximate solution in terms of graphs are presented via numerical simulations with many values of the fractional order. The conclusion will be given in last Section.

2. Preliminaries

For short, setting $\mathbb{Z}=(\mathbb{S},\mathbb{E},\mathbb{I},\mathbb{P},\mathbb{A},\mathbb{H},\mathbb{R}$, $\mathbb{F})$. Let $\mathbb{J}=\left[0,T\right]$ $(T>0)$ and define the Banach space $\Xi =C\left(\mathbb{J},{\mathbb{R}}^8\right)$ under the norm

$${\Vert \left(\mathbb{Z}\right)\Vert }_{\Xi }=\underset{t\in \mathbb{J}}{max}\left\{\left|\mathbb{Z}\left(t\right)\right|,\mathbb{Z}\in \Xi \right\},$$

where

$$\left|\mathbb{Z}\left(t\right)\right|=\left|\mathbb{S}\left(t\right)\right|+\left|\mathbb{E}\left(t\right)\right|+\left|\mathbb{I}\left(t\right)\right|+\left|\mathbb{P}\left(t\right)\right|+\left|\mathbb{A}\left(t\right)\right|+\left|\mathbb{H}\left(t\right)\right|+\left|\mathbb{R}\left(t\right)\right|+\left|\mathbb{F}\left(t\right)\right|$$

and $\mathbb{S},\mathbb{E},\mathbb{I},\mathbb{P},\mathbb{A},\mathbb{H},\mathbb{R}$, $\mathbb{F}\in C\left(\mathbb{j},\mathbb{R}\right)$.

Definition 1 [20] —

The ABC fractional derivative of order $q$ for a function $\phi$ is defined by

$${}^{ABC}{\mathcal{D}}_{0^{+}}^q\phi \left(t\right)=\frac{\Upsilon \left(q\right)}{1-q}{\int }_0^t{\mathbb{E}}_q\left(\frac{-q}{q-1}{(t-\theta )}^q\right){\phi }^{\prime }\left(\theta \right)d\theta ,t>0,$$

where $q\in (0,1]$, $\phi \in H^1(0,T)$, $\Upsilon \left(q\right)$ is the normalization function satisfies the fact $\Upsilon \left(0\right)=\Upsilon \left(1\right)=1$, and ${\mathbb{E}}_q$ is the Mittag-Leffler function given by

$${\mathbb{E}}_q\left(\phi \right)=\sum _{k=0}^{\infty }\frac{{\phi }^k}{\Gamma \left(qk+1\right)}.$$ (1)

Definition 2 [20] —

The AB fractional integral of order $q$ for $\mathcal{\phi }\left(t\right)$ is described by

$${}^{AB}{\mathcal{I}}_{0^{+}}^q\phi \left(t\right)=\frac{1-q}{\Upsilon \left(q\right)}\phi \left(t\right)+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\theta )}^{q-1}\phi \left(\theta \right)d\theta ,t>0.$$

where $0<q\le 1$ and $\phi \left(t\right)\in L^1(0,T)$.

Definition 3 [20] —

The Laplace transform of ${}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathcal{\phi }\left(t\right)$ is defined by

$$\mathcal{L}\left[{}^{ABC}{\mathcal{D}}_{0^{+}}^q\phi \left(t\right)\right]=\Upsilon \left(q\right)\frac{\left[s^q\mathcal{L}\left[\phi \left(t\right)\right]-s^{q-1}\phi \left(0\right)\right]}{s^q\left(1-q\right)+q}.$$

Lemma 1 [15] —

For $0<q\le 1$ , the solution of the following system

$${}^{ABC}{\mathcal{D}}_{0^{+}}^q\phi \left(t\right)=\varsigma \left(t\right),$$

$$\phi \left(0\right)={\phi }_0$$ (2)

is defined by

$$\phi \left(t\right)={\phi }_0+\frac{1-q}{\Upsilon \left(q\right)}\varsigma \left(t\right)+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\theta )}^{q-1}\varsigma \left(\theta \right)d\theta .$$

Definition 4 [18] —

Let $\mathbb{U}$ be a Banach space. For all ${\varsigma }_1,{\varsigma }_2\in \mathbb{U}$

$$\Vert \mathbb{Q}{\varsigma }_1-\mathbb{Q}{\varsigma }_2\Vert \le \vartheta \Vert {\varsigma }_1-{\varsigma }_2\Vert ,$$

• 1.If the Lipschitz constant $\vartheta >0$, then the operator $\mathbb{Q}:\mathbb{U}\to \mathbb{U}$ is a Lipschitzian
• 2.If $\vartheta <1$ then the operator $\mathbb{Q}:\mathbb{U}\to \mathbb{U}$ is a contraction.

Theorem 1 [18] —

Let $\mathbb{U}$ be a Banach space, and $\mathbb{B}$ be non empty and closed subset of $\mathbb{U}$ . If the operator $\mathbb{Q}:\mathbb{B}⟶\mathbb{B}$ is a contraction, then, $\mathbb{Q}$ has a unique fixed point.

Theorem 2 [18] —

Let $\mathbb{B}$ be a nonempty, convex, closed subset of a Banach space $\mathbb{U}$ . Assume ${\mathbb{Q}}_1$ and ${\mathbb{Q}}_2$ map $\mathbb{B}$ into itself and that ${\mathbb{Q}}_{1}x+{\mathbb{Q}}_{2}y\in \mathbb{B}$ for all $x,y\in \mathbb{B}$ , ${\mathbb{Q}}_1$ is compact and continuous; and ${\mathbb{Q}}_2$ is a contraction. Then, there exists $s\in \mathbb{B}$ such that ${\mathbb{Q}}_{1}s+{\mathbb{Q}}_{2}s=s$ .

Theorem 3 [52] —

Suppose that $q>0$ , $a\left(t\right){\left(1-\frac{1-q}{\Upsilon \left(q\right)}b\left(t\right)\right)}^{-1}$ is a non-negative, nondecreasing and locally integrable function on $[c,d)$ , $\frac{qb\left(t\right)}{\Upsilon \left(q\right)}{\left(1-\frac{1-q}{\Upsilon \left(q\right)}b\left(t\right)\right)}^{-1}$ is non-negative and bounded on $[c,d)$ and $\sigma \left(t\right)$ is nonnegative and locally integrable on $[c,d)$ with

$$\sigma \left(t\right)\le a\left(t\right)+b\left(t\right)\left({}^{AB}{\mathcal{I}}_{0^{+}}^q\sigma \right)\left(t\right).$$

Then

$$\sigma \left(t\right)\le \frac{a\left(t\right)\Upsilon \left(q\right)}{\Upsilon \left(q\right)-\left(1-q\right)b\left(t\right)}{\mathbb{E}}_q\left(\frac{qb\left(t\right)t^q}{\Upsilon \left(q\right)-\left(1-q\right)b\left(t\right)}\right).$$

3. Formulation of the model

Based on an epidemiological model introduced in [22], and taking into account the presence of superior prevalence in the coronavirus family [53], we generalize the considered model in [22] under novel fractional operator depend on the Mittag-Leffler function which take the following form:

$$\left\{\begin{array}{c}\hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{S}\left(t\right)=-\beta \frac{1}{N}\mathbb{S}-\iota \beta \frac{\mathbb{H}}{N}\mathbb{S}-{\beta }^{\prime }\frac{\mathbb{P}}{N}\mathbb{S},\hfill \\ \hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{E}\left(t\right)=\beta \frac{1}{N}\mathbb{S}+\iota \beta \frac{\mathbb{H}}{N}\mathbb{S}+{\beta }^{\prime }-\kappa \mathbb{E},\hfill \\ \hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{I}\left(t\right)=\kappa {\rho }_1\mathbb{E}-({\gamma }_a+{\gamma }_i)\mathbb{I}-{\delta }_i\mathbb{I},\hfill \\ \hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{P}\left(t\right)=\kappa {\rho }_2\mathbb{E}-({\gamma }_a+{\gamma }_i)\mathbb{P}-{\delta }_p\mathbb{P},\hfill \\ \hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{A}\left(t\right)=\kappa (1-{\rho }_1-{\rho }_2)\mathbb{E},\hfill \\ \hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{H}\left(t\right)={\gamma }_a(\mathbb{I}+\mathbb{P})-{\gamma }_r\mathbb{H}-{\delta }_h\mathbb{H},\hfill \\ \hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{R}\left(t\right)={\gamma }_i(\mathbb{I}+\mathbb{P})+{\gamma }_r\mathbb{H},\hfill \\ \hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{F}\left(t\right)={\delta }_i\mathbb{I}\left(t\right)+{\delta }_p\mathbb{P}\left(t\right)+{\delta }_h\mathbb{H}\left(t\right),\hfill \end{array}\right)$$ (3)

with the initial conditions

$$\left\{\begin{array}{c}\hfill \mathbb{S}\left(0\right)={\mathbb{S}}_0,\mathbb{E}\left(0\right)={\mathbb{E}}_0,\mathbb{I}\left(0\right)={\mathbb{I}}_0,\mathbb{P}\left(0\right)={\mathbb{P}}_0,\hfill \\ \hfill \mathbb{A}\left(0\right)={\mathbb{A}}_0,\mathbb{H}\left(0\right)={\mathbb{H}}_0,\mathbb{R}\left(0\right)={\mathbb{R}}_0,\mathbb{F}\left(0\right)={\mathbb{F}}_0,\hfill \end{array}\right)$$ (4)

where ${\mathbb{S}}_0,{\mathbb{E}}_0,{\mathbb{I}}_0,{\mathbb{P}}_0,{\mathbb{A}}_0,{\mathbb{H}}_0,{\mathbb{R}}_0,{\mathbb{F}}_0\ge 0$, the constant total population $N$ is partition into 8 epidemiological categories, we will mention the parameters and variables for this model in Table 1, Table 2.

Table 1.

The physical interpretation of the variables.

Variables	Description
$\mathbb{S}$	Susceptible class
$\mathbb{E}$	Exposed class
$\mathbb{I}$	Symptomatic and infectious class
$\mathbb{P}$	Super-spreaders class
$\mathbb{A}$	Infectious but asymptomatic class
$\mathbb{H}$	Hospitalized
$\mathbb{R}$	Recovery class
$\mathbb{F}$	Fatality class

Table 2.

The physical interpretation of the parameters.

Parameters	Physical description
$\beta$	Transmission coefficient from an infected person
$\iota$	Relative disease transmission in the hospitalized
${\beta }^{\prime }$	Transmission coefficient due to the high propagation
$\kappa$	Rate exposed infectious
${\rho }_1$	Rate that exposed individuals become infected
${\rho }_2$	Average at which exposed individuals become super-spreaders
${\gamma }_a$	Rate of hospitalized admission
${\gamma }_i$	Recovery rate unaccompanied by go hospitalized
${\gamma }_r$	Hospitalization rate
${\delta }_i$	Death rate due to infected class
${\delta }_p$	Death rate due to super-spreaders
${\delta }_h$	Death rate due to hospitalized class

The following formula gives the number of death because of the disease at each immediate of time

$$\mathcal{D}\mathbb{(}t\mathbb{)}≔{\delta }_i\mathbb{I}\left(t\right)+{\delta }_p\mathbb{P}\left(t\right)+{\delta }_h\mathbb{H}\left(t\right)=\frac{d\mathbb{F}\left(t\right)}{dt}.$$

In the model (3), ${}^{ABC}{\mathcal{D}}_{0^{+}}^q$ is the generalized Caputo fractional derivative introduced by Atangana and Baleanu in [20], and ${\mathbb{S}}_0,{\mathbb{E}}_0$, ${\mathbb{I}}_0$ $,{\mathbb{P}}_0$, ${\mathbb{A}}_0,{\mathbb{H}}_0$, ${\mathbb{R}}_0$ and ${\mathbb{F}}_0$ are initial values corresponding to the eight categories in Table 1.

4. Existence and uniqueness analysis

In this section, we discuss the existence and uniqueness theorems of the proposed model (3)–(4) by employing the fixed point technique. Now we reformulate the model (3) in an appropriate pattern, as follows

$$\left\{\begin{array}{c}\hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{S}\left(t\right)={\mathcal{G}}_1(t,\mathbb{Z}),\hfill \\ \hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{E}\left(t\right)={\mathcal{G}}_2(t,\mathbb{Z}),\hfill \\ \hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{I}\left(t\right)={\mathcal{G}}_3(t,\mathbb{Z}),\hfill \\ \hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{P}\left(t\right)={\mathcal{G}}_4(t,\mathbb{Z}),\hfill \\ \hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{A}\left(t\right)={\mathcal{G}}_5(t,\mathbb{Z}),\hfill \\ \hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{H}\left(t\right)={\mathcal{G}}_6(t,\mathbb{Z}),\hfill \\ \hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{R}\left(t\right)={\mathcal{G}}_7(t,\mathbb{Z}),\hfill \\ \hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\mathbb{F}\left(t\right)={\mathcal{G}}_8(t,\mathbb{Z}),\hfill \end{array}\right)$$

where

$$\left\{\begin{array}{c}\hfill {\mathcal{G}}_1(t,\mathbb{Z})=-\beta \frac{1}{N}\mathbb{S}-\iota \beta \frac{\mathbb{H}}{N}\mathbb{S}-{\beta }^{\prime }\frac{\mathbb{P}}{N}\mathbb{S},\hfill \\ \hfill {\mathcal{G}}_2(t,\mathbb{Z})=\beta \frac{1}{N}\mathbb{S}+\iota \beta \frac{\mathbb{H}}{N}\mathbb{S}+{\beta }^{\prime }-\kappa \mathbb{E},\hfill \\ \hfill {\mathcal{G}}_3(t,\mathbb{Z})=\kappa {\rho }_1\mathbb{E}-({\gamma }_a+{\gamma }_i)\mathbb{I}-{\delta }_i\mathbb{I},\hfill \\ \hfill {\mathcal{G}}_4(t,\mathbb{Z})=\kappa {\rho }_2\mathbb{E}-({\gamma }_a+{\gamma }_i)\mathbb{P}-{\delta }_p\mathbb{P},\hfill \\ \hfill {\mathcal{G}}_5(t,\mathbb{Z})=\kappa (1-{\rho }_1-{\rho }_2)\mathbb{E},\hfill \\ \hfill {\mathcal{G}}_6(t,\mathbb{Z})={\gamma }_a(\mathbb{I}+\mathbb{P})-{\gamma }_r\mathbb{H}-{\delta }_h\mathbb{H},\hfill \\ \hfill {\mathcal{G}}_7(t,\mathbb{Z})={\gamma }_i(\mathbb{I}+\mathbb{P})+{\gamma }_r\mathbb{H},\hfill \\ \hfill {\mathcal{G}}_8(t,\mathbb{Z})={\delta }_i\mathbb{I}\left(t\right)+{\delta }_p\mathbb{P}\left(t\right)+{\delta }_h\mathbb{H}\left(t\right).\hfill \end{array}\right)$$ (5)

Consider the model (3) is equivalent to the following fractional system

$$\left\{\begin{array}{c}\hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\Phi \left(t\right)=\mathcal{Z}(t,\Phi \left(t\right)),\hfill \\ \hfill \Phi \left(0\right)={\Phi }_0\ge 0,\hfill \end{array}\right)$$ (6)

where

$$\Phi \left(t\right)=\left(\begin{array}{c}\hfill \mathbb{S}\hfill \\ \hfill \mathbb{E}\hfill \\ \hfill \mathbb{I}\hfill \\ \hfill \mathbb{P}\hfill \\ \hfill \mathbb{A}\hfill \\ \hfill \mathbb{H}\hfill \\ \hfill \mathbb{R}\hfill \\ \hfill \mathbb{F}\hfill \end{array}\right),{\Phi }_0=\left(\begin{array}{c}\hfill {\mathbb{S}}_0\hfill \\ \hfill {\mathbb{E}}_0\hfill \\ \hfill {\mathbb{I}}_0\hfill \\ \hfill {\mathbb{P}}_0\hfill \\ \hfill {\mathbb{A}}_0\hfill \\ \hfill {\mathbb{H}}_0\hfill \\ \hfill {\mathbb{R}}_0\hfill \\ \hfill {\mathbb{F}}_0\hfill \end{array}\right),\mathcal{Z}(t,\Phi \left(t\right))=\left(\begin{array}{c}\hfill {\mathcal{G}}_1(t,\mathbb{Z})\hfill \\ \hfill {\mathcal{G}}_2(t,\mathbb{Z})\hfill \\ \hfill {\mathcal{G}}_3(t,\mathbb{Z})\hfill \\ \hfill {\mathcal{G}}_4(t,\mathbb{Z})\hfill \\ \hfill {\mathcal{G}}_5(t,\mathbb{Z})\hfill \\ \hfill {\mathcal{G}}_6(t,\mathbb{Z})\hfill \\ \hfill {\mathcal{G}}_7(t,\mathbb{Z})\hfill \\ \hfill {\mathcal{G}}_8(t,\mathbb{Z})\hfill \end{array}\right),$$ (7)

According to Lemma 1, the system (6) can be turned to the following fractional formula

$$\Phi \left(t\right)={\Phi }_0+\frac{1-q}{\Upsilon \left(q\right)}\mathcal{Z}(t,\Phi \left(t\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\mathcal{Z}(\xi ,\Phi \left(\xi \right))d\xi .$$ (8)

The following assumptions for analysis of the existence and uniqueness will be satisfied:

(H1)

$\mathcal{Z}:\mathbb{j}\times \Xi \to \mathbb{R}$ is continuous and there exist two constants ${\mu }_{\mathcal{Z}},{\eta }_{\mathcal{Z}}$ such that

$$\left|\mathcal{Z}(t,\Phi )\right|\le {\mu }_{\mathcal{Z}}\left|\Phi \right|+{\eta }_{\mathcal{Z}},\text{for}t\in \mathbb{j}\text{ and }\Phi \in \Xi .$$

(H2)

There exists $L_{\mathcal{Z}}>0$ such that

$$|\mathcal{Z}(t,{\Phi }_1)-\mathcal{Z}(t,{\Phi }_2)|\le L_{\mathcal{Z}}|{\Phi }_1-{\Phi }_2|,\text{for}t\in \mathbb{j}\text{ and }\Phi \in \Xi .$$

Theorem 4

Suppose (H1) and (H2) are satisfied. The equivalent equation (8) to the considered model (3) – (4) has a solution, provided that

$$\frac{1-q}{\Upsilon \left(q\right)}{L}_{\mathcal{Z}}<1,\text{ and }{\mathbb{A}}_1≔\left[\frac{1-q}{\Upsilon \left(q\right)}+\frac{T^q}{\Upsilon \left(q\right)\Gamma \left(q\right)}\right]{\mu }_{\mathcal{Z}}<1.$$ (9)

Proof

We convert the fractional system (6) into a fixed point problem through the following equation

$$\Phi =\mathbb{Q}\Phi ,\Phi \in \Xi ,$$

where the operator $\mathbb{Q}:\Xi \to \Xi$ defined by

$$\left(\mathbb{Q}\Phi \right)\left(t\right)={\Phi }_0+\frac{1-q}{\Upsilon \left(q\right)}\mathcal{Z}(t,\Phi \left(t\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\times {\int }_0^t{(t-\xi )}^{q-1}\mathcal{Z}(\xi ,\Phi \left(\xi \right))d\xi .$$ (10)

Let ${\mathbb{K}}_{\sigma }=\{\Phi \in \Xi :{\Vert \Phi \Vert }_{\Xi }\le \sigma \}$ which is closed, convex, bounded subset of $\Xi$ with $\sigma \ge \frac{{\mathbb{A}}_2}{1-{\mathbb{A}}_1}$, where

$${\mathbb{A}}_2≔\left|{\Phi }_0\right|+\left[\frac{1-q}{\Upsilon \left(q\right)}+\frac{T^q}{\Upsilon \left(q\right)\Gamma \left(q\right)}\right]{\eta }_{\mathcal{Z}}.$$ (11)

Define the operators ${\mathbb{Q}}_1$ and ${\mathbb{Q}}_2$ on ${\mathbb{K}}_{\sigma }$ such that ${\mathbb{Q}}_1+{\mathbb{Q}}_2=\mathbb{Q}$ and

$${\mathbb{Q}}_1\Phi \left(t\right)={\Phi }_0+\frac{1-q}{\Upsilon \left(q\right)}\mathcal{Z}(t,\Phi \left(t\right)),$$

$${\mathbb{Q}}_2\Phi \left(t\right)=\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\mathcal{Z}(\xi ,\Phi \left(\xi \right))d\xi ,$$ (12)

Now, we give the proof in several steps:

Step1: ${\mathbb{Q}}_1{\Phi }_1+{\mathbb{Q}}_2{\Phi }_2\in$ ${\mathbb{K}}_{\sigma }$, for ${\Phi }_1,{\Phi }_2\in$ ${\mathbb{K}}_{\sigma }$.

By (H1), (9), (11), then for ${\Phi }_1,{\Phi }_2\in$ ${\mathbb{K}}_{\sigma }$ and $t\in \mathbb{j}$, we have

$${\Vert {\mathbb{Q}}_1{\Phi }_1+{\mathbb{Q}}_2{\Phi }_2\Vert }_{\Xi }\le \underset{t\in \mathbb{j}}{max}\left\{\left|{\Phi }_0\right|+\frac{1-q}{\Upsilon \left(q\right)}\left|\mathcal{Z}(t,\Phi \left(t\right))\right|\right)\left(+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\left|\mathcal{Z}(\xi ,\Phi \left(\xi \right))\right|d\xi \right\}\le \left\{\left|{\Phi }_0\right|+\frac{1-q}{\Upsilon \left(q\right)}\left[{\mu }_{\mathcal{Z}}\underset{t\in \mathbb{j}}{max}\left|\Phi \left(t\right)\right|+{\eta }_{\mathcal{Z}}\right]\right)\left(+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\left[{\mu }_{\mathcal{Z}}\underset{t\in \mathbb{j}}{max}\left|\Phi \left(t\right)\right|+{\eta }_{\mathcal{Z}}\right]d\xi \right\}\le \left\{\left|{\Phi }_0\right|+\frac{1-q}{\Upsilon \left(q\right)}\left[{\mu }_{\mathcal{Z}}{\Vert \Phi \Vert }_{\Xi }+{\eta }_{\mathcal{Z}}\right]\right)\left(+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\left[{\mu }_{\mathcal{Z}}{\Vert \Phi \Vert }_{\Xi }+{\eta }_{\mathcal{Z}}\right]d\xi \right\}=\left|{\Phi }_0\right|+\left[\frac{1-q}{\Upsilon \left(q\right)}+\frac{T^q}{\Upsilon \left(q\right)\Gamma \left(q\right)}\right]{\eta }_{\mathcal{Z}}+\left[\frac{1-q}{\Upsilon \left(q\right)}+\frac{T^q}{\Upsilon \left(q\right)\Gamma \left(q\right)}\right]{\mu }_{\mathcal{Z}}\sigma ={\mathbb{A}}_2+{\mathbb{A}}_1\sigma \le \sigma .$$

This proves that ${\mathbb{Q}}_1{\Phi }_1+{\mathbb{Q}}_2{\Phi }_2\in {\mathbb{K}}_{\sigma }$.

Step2: ${\mathbb{Q}}_1$ is contraction.

Let $\Phi ,{\Phi }^{\ast }\in {\mathbb{K}}_{\sigma }$. Then by (H2) we have

$${\Vert {\mathbb{Q}}_1\Phi -{\mathbb{Q}}_1{\Phi }^{\ast }\Vert }_{\Xi }=\underset{t\in \mathbb{j}}{max}\frac{1-q}{\Upsilon \left(q\right)}|\mathcal{Z}(t,\Phi \left(t\right))-\mathcal{Z}(t,{\Phi }^{\ast }\left(t\right))|\le \frac{1-q}{\Upsilon \left(q\right)}{L}_{\mathcal{Z}}\underset{t\in \mathbb{j}}{max}|\Phi \left(t\right)-{\Phi }^{\ast }\left(t\right)|\le \frac{1-q}{\Upsilon \left(q\right)}{L}_{\mathcal{Z}}{\Vert \Phi -{\Phi }^{\ast }\Vert }_{\Xi }.$$

As $\frac{1-q}{\Upsilon \left(q\right)}{L}_{\mathcal{Z}}<1$, the operator ${\mathbb{Q}}_1$ is a contraction.

Step3: ${\mathbb{Q}}_2$ is relatively compact.

First, we prove that ${\mathbb{Q}}_2$ given by (12) is continuous. Let $\left({\Phi }_n\right)$ be a sequence such that ${\Phi }_n\to \Phi$. Then for $t\in \mathbb{j}$

$$|{\mathbb{Q}}_2{\Phi }_n-{\mathbb{Q}}_2{\Phi }^{\ast }|=\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}|\mathcal{Z}(\xi ,{\Phi }_n\left(\xi \right))-\mathcal{Z}(\xi ,\Phi \left(\xi \right))|d\xi \le \frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\underset{\xi \in \mathbb{j}}{max}|\mathcal{Z}(\xi ,{\Phi }_n\left(\xi \right))-\mathcal{Z}(\xi ,\Phi \left(\xi \right))|d\xi \le \frac{T^q}{\Upsilon \left(q\right)\Gamma \left(q\right)}{\Vert \mathcal{Z}(t,{\Phi }_n\left(t\right))-\mathcal{Z}(t,\Phi \left(t\right))\Vert }_{\Xi }.$$

Since $\mathcal{Z}$ is continuous and ${\Phi }_n\to \Phi$, the operator ${\mathbb{Q}}_2$ is continuous.

Next, we need to prove that ${\mathbb{Q}}_2$ is uniformly bounded and equicontinuous on ${\mathbb{K}}_{\sigma }$.

Indeed, let $\Phi \in {\mathbb{K}}_{\sigma }$, and $t\in \mathbb{j}$. Then we have

$${\Vert {\mathbb{Q}}_2\Phi \Vert }_{\Xi }\le \underset{t\in \mathbb{j}}{max}\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\left|\mathcal{Z}(\xi ,\Phi \left(\xi \right))\right|d\xi \le \frac{q}{\Upsilon \left(q\right)\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\left[{\mu }_{\mathcal{Z}}\underset{t\in \mathbb{j}}{max}\left|\Phi \right|+{\eta }_{\mathcal{Z}}\right]d\xi \le \frac{q}{\Upsilon \left(q\right)\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\left[{\mu }_{\mathcal{Z}}{\Vert \Phi \Vert }_{\Xi }+{\eta }_{\mathcal{Z}}\right]d\xi \le \frac{T^q}{\Upsilon \left(q\right)\Gamma \left(q\right)}\left[{\mu }_{\mathcal{Z}}\sigma +{\eta }_{\mathcal{Z}}\right].$$

Thus, $\left({\mathbb{Q}}_2\Phi \right)$ is bounded on ${\mathbb{K}}_{\sigma }$. For the equicontinuity of ${\mathbb{Q}}_2$. Let $\Phi \in {\mathbb{K}}_{\sigma }$ and $t_1,t_2\in \mathbb{j}$ such that $t_1<t_2$. Then

$$|{\mathbb{Q}}_2\Phi \left(t_2\right)-{\mathbb{Q}}_2\Phi \left(t_1\right)|\le \frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_{t_1}^{t_2}{(t_2-\xi )}^{q-1}\left|\mathcal{Z}(\xi ,\Phi \left(\xi \right))\right|d\xi +\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\left|{\int }_0^{t_1}\left[{(t_1-\xi )}^{q-1}-{(t_2-\xi )}^{q-1}\right]\mathcal{Z}(\xi ,\Phi \left(\xi \right))d\xi \right|\le \frac{\left[{\mu }_{\mathcal{Z}}{\Vert \Phi \Vert }_{\Xi }+{\eta }_{\mathcal{Z}}\right]}{\Upsilon \left(q\right)\Gamma \left(q\right)}\left[{(t_2-t_1)}^q\right]++\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\left|{\int }_0^{t_1}\left[{(t_1-\xi )}^{q-1}-{(t_2-\xi )}^{q-1}\right]\mathcal{Z}(\xi ,\Phi \left(\xi \right))d\xi \right|\le \frac{\left[{\mu }_{\mathcal{Z}}\sigma +{\eta }_{\mathcal{Z}}\right]}{\Upsilon \left(q\right)\Gamma \left(q\right)}{(t_2-t_1)}^q+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\left|{\int }_0^{t_1}\left[{(t_1-\xi )}^{q-1}-{(t_2-\xi )}^{q-1}\right]\mathcal{Z}(\xi ,\Phi \left(\xi \right))d\xi \right|.$$

As $t_1\to t_2$, the continuity of $\mathcal{Z}$ tends R.H.S of above inequality to zero. Consequently, ${\mathbb{Q}}_2$ is equicontinuous on ${\mathbb{K}}_{\sigma }$. The Arzelá–Ascoli theorem shows that ${\mathbb{Q}}_2$ is completely continuous. It follows from Theorem 2 that Eq. (8) has at least one solution, i.e., the model (3)–(4) has at least one solution. □

Theorem 5

Suppose that (H2) holds, Eq. (8) has a unique solution which leads that the model (3) – (4) has unique solution too, if

$${\mathbb{A}}_3≔\left(\frac{1-q}{\Upsilon \left(q\right)}+\frac{T^q}{\Upsilon \left(q\right)\Gamma \left(q\right)}\right)L_{\mathcal{Z}}<1.$$ (13)

Proof

Taking the operator $\mathbb{Q}:\Xi \to \Xi$ defined by (10). Let $\Phi$ and ${\Phi }^{\ast }$ in $\Xi$ and $t\in \mathbb{j}$. Then

$${\Vert \mathbb{Q}\Phi \left(t\right)-\mathbb{Q}{\Phi }^{\ast }\left(t\right)\Vert }_{\Xi }\le \underset{t\in \mathbb{j}}{max}\frac{1-q}{\Upsilon \left(q\right)}|\mathcal{Z}(t,\Phi \left(t\right))-\mathcal{Z}(t,{\Phi }^{\ast }\left(t\right))|+\underset{t\in \mathbb{j}}{max}\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\times |\mathcal{Z}(\xi ,\Phi \left(\xi \right))-\mathcal{Z}(\xi ,{\Phi }^{\ast }\left(\xi \right))|d\xi \le \left(\frac{1-q}{\Upsilon \left(q\right)}+\frac{T^q}{\Upsilon \left(q\right)\Gamma \left(q\right)}\right)L_{\mathcal{Z}}{\Vert \Phi -{\Phi }^{\ast }\Vert }_{\Xi }.$$

Due to (13), $\mathbb{Q}$ is contraction. Thus (8) has unique solution. It follows that the model (3)–(4) has unique solution. □

5. Stability analysis

A concept of Ulam stability was begun by Ulam [54], [55]. Then foregoing stability has been investigated for ordinary fractional derivatives in many of the published papers, see [56], [57], [58]. So, the stability standard is one of the significant qualitative properties of the solution of differential equations that gives a description of the behavior of such solutions. Besides, the stability is a necessary condition in relation to an approximate solution, therefore we seek to Ulam–Hyers (UH) stability for the model (3) by means of Theorem 3.

Theorem 6

Suppose that (H1) holds. If

$$\left(1-q+\frac{T^q}{\Gamma \left(q\right)}\right)\frac{L_{\mathcal{Z}}}{\Upsilon \left(q\right)}<1.$$

Then, the zero solution of the model (3) is stable and bounded.

Proof

Thanks of Lemma 1, the following fractional system

$$\left\{\begin{array}{c}\hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\Phi \left(t\right)=\mathcal{Z}(t,\Phi \left(t\right)),\hfill \\ \hfill \Phi \left(0\right)={\Phi }_0\ge 0,\hfill \end{array}\right)$$

has a unique solution which is given by

$$\Phi \left(t\right)={\Phi }_0+\frac{1-q}{\Upsilon \left(q\right)}\mathcal{Z}(t,\Phi \left(t\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\mathcal{Z}(\xi ,\Phi \left(\xi \right))d\xi .$$

Set ${sup}_{\xi \in \mathbb{j}}\Vert \mathcal{Z}(\xi ,0)\Vert ≔{\mathcal{A}}_1$. Then by (H1), we have

$${\Vert \Phi \Vert }_{\Xi }\le \Vert {\Phi }_0\Vert +\frac{1-q}{\Upsilon \left(q\right)}\left[\Vert \mathcal{Z}(t,\Phi \left(t\right))-\mathcal{Z}(t,0)\Vert +\Vert \mathcal{Z}(t,0)\Vert \right]+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\left[\Vert \mathcal{Z}(\xi ,\Phi \left(\xi \right))-\mathcal{Z}(\xi ,0)\Vert +\Vert \mathcal{Z}(\xi ,0)\Vert \right]d\xi \le \Vert {\Phi }_0\Vert +\frac{1-q}{\Upsilon \left(q\right)}\left[L_{\mathcal{Z}}{\Vert \Phi \Vert }_{\Xi }+{\mathcal{A}}_1\right]+\frac{T^q}{\Upsilon \left(q\right)\Gamma \left(q\right)}{\mathcal{A}}_1+\frac{T^q}{\Upsilon \left(q\right)\Gamma \left(q\right)}{L}_{\mathcal{Z}}{\Vert \Phi \Vert }_{\Xi }=\Vert {\Phi }_0\Vert +\left(1-q+\frac{T^q}{\Gamma \left(q\right)}\right)\frac{{\mathcal{A}}_1}{\Upsilon \left(q\right)}+\left(1-q+\frac{T^q}{\Gamma \left(q\right)}\right)\frac{L_{\mathcal{Z}}}{\Upsilon \left(q\right)}{\Vert \Phi \Vert }_{\Xi }$$

which implies

$${\Vert \Phi \Vert }_{\Xi }\le \frac{\Vert {\Phi }_0\Vert +\left(1-q+\frac{T^q}{\Gamma \left(q\right)}\right)\frac{{\mathcal{A}}_1}{\Upsilon \left(q\right)}}{1-\left(1-q+\frac{T^q}{\Gamma \left(q\right)}\right)\frac{L_{\mathcal{Z}}}{\Upsilon \left(q\right)}}≔\ell .$$

So, ${\Vert \Phi \Vert }_{\Xi }\le \ell$, $\ell >0$. Hence, the zero solution of the model (3) is stable and bounded. □

Definition 5

The model (3)–(4) is UH stable if there exists $ħ>0$ such that for each $ϵ>0$, and each a solution $\tilde{\Phi }\in \Xi$satisfies

$$\begin{array}{c}\hfill |{}^{ABC}{\mathcal{D}}_{0^{+}}^q\tilde{\Phi }\left(t\right)-\mathcal{Z}(t,\tilde{\Phi }\left(t\right))|\le ϵ,\hfill \end{array}$$ (14)

then there exists a solution $\Phi \in \Xi$ of the model (3) such that

$$|\tilde{\Phi }\left(t\right)-\Phi \left(t\right)|\le ħϵ.$$

where

$$\tilde{\Phi }\left(t\right)={\left(\tilde{\mathbb{Z}}\right)}^T=\left(\begin{array}{c}\hfill \tilde{\mathbb{S}}\hfill \\ \hfill \tilde{\mathbb{E}}\hfill \\ \hfill \tilde{\mathbb{I}}\hfill \\ \hfill \tilde{\mathbb{P}}\hfill \\ \hfill \tilde{\mathbb{A}}\hfill \\ \hfill \tilde{\mathbb{H}}\hfill \\ \hfill \tilde{\mathbb{R}}\hfill \\ \hfill \tilde{\mathbb{F}}\hfill \end{array}\right),{\tilde{\Phi }}_0={\left(\widetilde{{\mathbb{Z}}_0}\right)}^T=\left(\begin{array}{c}\hfill {\tilde{\mathbb{S}}}_0\hfill \\ \hfill {\tilde{\mathbb{E}}}_0\hfill \\ \hfill {\tilde{\mathbb{I}}}_0\hfill \\ \hfill {\tilde{\mathbb{P}}}_0\hfill \\ \hfill {\tilde{\mathbb{A}}}_0\hfill \\ \hfill {\tilde{\mathbb{H}}}_0\hfill \\ \hfill {\tilde{\mathbb{R}}}_0\hfill \\ \hfill {\tilde{\mathbb{F}}}_0\hfill \end{array}\right),\mathcal{Z}(t,\tilde{\Phi }\left(t\right))=\left(\begin{array}{c}\hfill {\mathcal{G}}_1(t,\tilde{\mathbb{Z}})\hfill \\ \hfill {\mathcal{G}}_2(t,\tilde{\mathbb{Z}})\hfill \\ \hfill {\mathcal{G}}_3(t,\tilde{\mathbb{Z}})\hfill \\ \hfill {\mathcal{G}}_4(t,\tilde{\mathbb{Z}})\hfill \\ \hfill {\mathcal{G}}_5(t,\tilde{\mathbb{Z}})\hfill \\ \hfill {\mathcal{G}}_6(t,\tilde{\mathbb{Z}})\hfill \\ \hfill {\mathcal{G}}_7(t,\tilde{\mathbb{Z}})\hfill \\ \hfill {\mathcal{G}}_8(t,\tilde{\mathbb{Z}})\hfill \end{array}\right),$$

and

$$ϵ=max\left(\begin{array}{c}\hfill {ϵ}_1\hfill \\ \hfill {ϵ}_2\hfill \\ \hfill {ϵ}_3\hfill \\ \hfill {ϵ}_4\hfill \\ \hfill {ϵ}_5\hfill \\ \hfill {ϵ}_6\hfill \\ \hfill {ϵ}_7\hfill \\ \hfill {ϵ}_8\hfill \end{array}\right),\lambda =max\left(\begin{array}{c}\hfill {ħ}_1\hfill \\ \hfill {ħ}_2\hfill \\ \hfill {ħ}_3\hfill \\ \hfill {ħ}_4\hfill \\ \hfill {ħ}_5\hfill \\ \hfill {ħ}_6\hfill \\ \hfill {ħ}_7\hfill \\ \hfill {ħ}_8\hfill \end{array}\right).$$

Remark 1

Suppose a small perturbation $m\left(t\right)\in C(\mathbb{j},\mathbb{R})$ with $m\left(0\right)=0$ satisfying

• 1. $\left|m\left(t\right)\right|\le ϵ$, for $t\in \mathbb{j}$.
• 2. ${}^{ABC}{\mathcal{D}}_{0^{+}}^q\tilde{\Phi }\left(t\right)=\mathcal{Z}(t,\tilde{\Phi }\left(t\right))+m\left(t\right)$, for $t\in \mathbb{j}$, where $m\left(t\right)={\left(m_1\left(t\right),m_2\left(t\right),\dots ,m_8\left(t\right)\right)}^T$.

Lemma 2

If $\tilde{\Phi }\in \Xi$ satisfies (14) , then $\tilde{\Phi }\in \Xi$ is a solution of the inequality

$$|\tilde{\Phi }\left(t\right)-{\tilde{\Phi }}_0-\frac{1-q}{\Upsilon \left(q\right)}\mathcal{Z}(t,\tilde{\Phi }\left(t\right))-\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\mathcal{Z}(\xi ,\tilde{\Phi }\left(\xi \right))d\xi |\le \left(1-q+\frac{T^q}{\Gamma \left(q\right)}\right)\frac{ϵ}{\Gamma \left(q\right)}.$$

Proof

By Remark 1 and Lemma 1, the solution of the perturbed system

$$\left\{\begin{array}{c}\hfill {}^{ABC}{\mathcal{D}}_{0^{+}}^q\tilde{\Phi }\left(t\right)=\mathcal{Z}(t,\tilde{\Phi }\left(t\right))+m\left(t\right),\hfill \\ \hfill \tilde{\Phi }\left(0\right)={\tilde{\Phi }}_0\hfill \end{array}\right)$$ (15)

is given by

$$\tilde{\Phi }\left(t\right)={\tilde{\Phi }}_0+\frac{1-q}{\Upsilon \left(q\right)}\mathcal{Z}(t,\tilde{\Phi }\left(t\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\mathcal{Z}(\xi ,\tilde{\Phi }\left(\xi \right))d\xi +\frac{1-q}{\Upsilon \left(q\right)}m\left(t\right)+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}m\left(\xi \right)d\xi .$$

Then Remark 1 gives

$$|\tilde{\Phi }\left(t\right)-{\tilde{\Phi }}_0-\frac{1-q}{\Upsilon \left(q\right)}\mathcal{Z}(t,\tilde{\Phi }\left(t\right))-\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\mathcal{Z}(\xi ,\tilde{\Phi }\left(\xi \right))d\xi |=|\frac{1-q}{\Upsilon \left(q\right)}m\left(t\right)+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}m\left(\xi \right)d\xi |\le \frac{1-q}{\Upsilon \left(q\right)}\left|m\left(t\right)\right|+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\left|m\left(\xi \right)\right|d\xi \le \frac{1-q}{\Upsilon \left(q\right)}ϵ+\frac{T^q}{\Upsilon \left(q\right)\Gamma \left(q\right)}ϵ\le \left(1-q+\frac{T^q}{\Gamma \left(q\right)}\right)\frac{ϵ}{\Gamma \left(q\right)}.\square$$

Theorem 7

Under assumptions of Theorem 5 . The model (3) – (4) is UH stable in $\Xi$ .

Proof

Let $\tilde{\Phi }\in \Xi$ be the solution of (14) and $\Phi \in \Xi$ is the solution of (6) with the initial condition

$$\Phi \left(0\right)=\tilde{\Phi }\left(0\right).$$ (16)

By (16), ${\Phi }_0=\widetilde{{\Phi }_0}$, it follows from Lemma 1 that

$$\Phi \left(t\right)=\widetilde{{\Phi }_0}+\frac{1-q}{\Upsilon \left(q\right)}\mathcal{Z}(t,\Phi \left(t\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\mathcal{Z}(\xi ,\Phi \left(\xi \right))d\xi .$$ (17)

By Eq. (17), assumption (H1) and Lemma 2, we obtain

$$|\tilde{\Phi }\left(t\right)-\Phi \left(t\right)|\le \left|\tilde{\Phi }\left(t\right)-{\tilde{\Phi }}_0-\frac{1-q}{\Upsilon \left(q\right)}\mathcal{Z}(t,\Phi \left(t\right))\right)\left(-\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\mathcal{Z}(\xi ,\Phi \left(\xi \right))d\xi \right|\le \left|\tilde{\Phi }\left(t\right)-{\tilde{\Phi }}_0-\frac{1-q}{\Upsilon \left(q\right)}\mathcal{Z}(t,\tilde{\Phi }\left(t\right))\right)\left(-\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}\mathcal{Z}(\xi ,\tilde{\Phi }\left(\xi \right))d\xi \right|+\frac{1-q}{\Upsilon \left(q\right)}|\mathcal{Z}(t,\tilde{\Phi }\left(t\right))-\mathcal{Z}(t,\Phi \left(t\right))|+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}|\mathcal{Z}(\xi ,\tilde{\Phi }\left(\xi \right))-\mathcal{Z}(\xi ,\Phi \left(\xi \right))|d\xi \le \left(1-q+\frac{T^q}{\Gamma \left(q\right)}\right)\frac{ϵ}{\Gamma \left(q\right)}+\frac{1-q}{\Upsilon \left(q\right)}{L}_{\mathcal{Z}}|\tilde{\Phi }\left(t\right)-\Phi \left(t\right)|+\frac{q}{\Upsilon \left(q\right)}\frac{L_{\mathcal{Z}}}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}|\tilde{\Phi }\left(\xi \right)-\Phi \left(\xi \right)|d\xi =\left(1-q+\frac{T^q}{\Gamma \left(q\right)}\right)\frac{ϵ}{\Gamma \left(q\right)}+L_{\mathcal{Z}}\left({}^{AB}{\mathcal{I}}_{0^{+}}^q|\tilde{\Phi }\left(\xi \right)-\Phi \left(\xi \right)|\right)\left(t\right).$$

Applying Theorem 3 with $a\left(t\right)=\left(1-q+\frac{T^q}{\Gamma \left(q\right)}\right)\frac{ϵ}{\Gamma \left(q\right)}$ and $b\left(t\right)=L_{\mathcal{Z}}$, we get

$$|\tilde{\Phi }\left(t\right)-\Phi \left(t\right)|\le \frac{\left(1-q+\frac{T^q}{\Gamma \left(q\right)}\right)\frac{\Upsilon \left(q\right)}{\Gamma \left(q\right)}ϵ}{\Upsilon \left(q\right)-\left(1-q\right)L_{\mathcal{Z}}}{\mathbb{E}}_q\left(\frac{q{L}_{\mathcal{Z}}{t}^q}{\Upsilon \left(q\right)-\left(1-q\right)L_{\mathcal{Z}}}\right)\le \frac{\left(1-q+\frac{T^q}{\Gamma \left(q\right)}\right)\frac{\Upsilon \left(q\right)}{\Gamma \left(q\right)}ϵ}{\Upsilon \left(q\right)-\left(1-q\right)L_{\mathcal{Z}}}{\mathbb{E}}_q\left(\frac{q{L}_{\mathcal{Z}}{T}^q}{\Upsilon \left(q\right)-\left(1-q\right)L_{\mathcal{Z}}}\right).$$

For $ħ=\frac{\left(1-q+\frac{T^q}{\Gamma \left(q\right)}\right)\frac{\Upsilon \left(q\right)}{\Gamma \left(q\right)}}{\Upsilon \left(q\right)-\left(1-q\right)L_{\mathcal{Z}}}{\mathbb{E}}_q\left(\frac{q{L}_{\mathcal{Z}}{T}^q}{\Upsilon \left(q\right)-\left(1-q\right)L_{\mathcal{Z}}}\right)$, we obtain

$$|\tilde{\Phi }\left(t\right)-\Phi \left(t\right)|\le ħϵ.$$

This shows that the model (3)–(4) is UH stable. □

6. Derivation of a numerical algorithm for model (3)–(4)

In this part, we provide the numerical results of model (3)–(4) through the proposed scheme of fractional Adam Bashforth. To this end, we need to approximate the AB fractional integral by applying the Adams–Bashforth method.

By the initial conditions and the definition of ${}^{ABC}{\mathcal{I}}_{0^{+}}^q$, we turn fractional model (3) into the following fractional system

$$\left\{\begin{array}{c}\hfill \mathbb{S}\left(t\right)-\mathbb{S}\left(0\right)={}^{AB}{\mathcal{I}}_{0^{+}}^q{\mathcal{K}}_1(t,\mathbb{S}\left(t\right)),\hfill \\ \hfill \mathbb{E}\left(t\right)-\mathbb{E}\left(0\right)={}^{AB}{\mathcal{I}}_{0^{+}}^q{\mathcal{K}}_2(t,\mathbb{E}\left(t\right)),\hfill \\ \hfill \mathbb{I}\left(t\right)-\mathbb{I}\left(0\right)={}^{AB}{\mathcal{I}}_{0^{+}}^q{\mathcal{K}}_3(t,\mathbb{I}\left(t\right)),\hfill \\ \hfill \mathbb{P}\left(t\right)-\mathbb{P}\left(0\right)={}^{AB}{\mathcal{I}}_{0^{+}}^q{\mathcal{K}}_4(t,\mathbb{P}\left(t\right)),\hfill \\ \hfill \mathbb{A}\left(t\right)-\mathbb{A}\left(0\right)={}^{AB}{\mathcal{I}}_{0^{+}}^q{\mathcal{K}}_5(t,\mathbb{A}\left(t\right)),\hfill \\ \hfill \mathbb{H}\left(t\right)-\mathbb{H}\left(0\right)={}^{AB}{\mathcal{I}}_{0^{+}}^q{\mathcal{K}}_6(t,\mathbb{H}\left(t\right)),\hfill \\ \hfill \mathbb{R}\left(t\right)-\mathbb{R}\left(0\right)={}^{AB}{\mathcal{I}}_{0^{+}}^q{\mathcal{K}}_7(t,\mathbb{R}\left(t\right)),\hfill \\ \hfill \mathbb{F}\left(t\right)-\mathbb{F}\left(0\right)={}^{AB}{\mathcal{I}}_{0^{+}}^q{\mathcal{K}}_8(t,\mathbb{F}\left(t\right)),\hfill \end{array}\right)$$ (18)

which gives

$$\left\{\begin{array}{c}\hfill \mathbb{S}\left(t\right)-\mathbb{S}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_1(t,\mathbb{S}\left(t\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}{\mathcal{K}}_1(\xi ,\mathbb{S}\left(\xi \right))d\xi ,\hfill \\ \hfill \mathbb{E}\left(t\right)-\mathbb{E}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_2(t,\mathbb{E}\left(t\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}{\mathcal{K}}_2(\xi ,\mathbb{E}\left(\xi \right))d\xi ,\hfill \\ \hfill \mathbb{I}\left(t\right)-\mathbb{I}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_3(t,\mathbb{I}\left(t\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}{\mathcal{K}}_3(\xi ,\mathbb{I}\left(\xi \right))d\xi ,\hfill \\ \hfill \mathbb{P}\left(t\right)-\mathbb{P}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_4(t,\mathbb{P}\left(t\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}{\mathcal{K}}_4(\xi ,\mathbb{P}\left(\xi \right))d\xi ,\hfill \\ \hfill \mathbb{A}\left(t\right)-\mathbb{A}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_5(t,\mathbb{A}\left(t\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}{\mathcal{K}}_5(\xi ,\mathbb{A}\left(\xi \right))d\xi ,\hfill \\ \hfill \mathbb{H}\left(t\right)-\mathbb{H}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_6(t,\mathbb{H}\left(t\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}{\mathcal{K}}_6(\xi ,\mathbb{H}\left(\xi \right))d\xi ,\hfill \\ \hfill \mathbb{R}\left(t\right)-\mathbb{R}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_7(t,\mathbb{R}\left(t\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}{\mathcal{K}}_7(\xi ,\mathbb{R}\left(\xi \right))d\xi ,\hfill \\ \hfill \mathbb{F}\left(t\right)-\mathbb{F}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_8(t,\mathbb{F}\left(t\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}{\int }_0^t{(t-\xi )}^{q-1}{\mathcal{K}}_8(\xi ,\mathbb{F}\left(\xi \right))d\xi ,\hfill \end{array}\right)$$ (19)

To obtain an iterative scheme, we set $t=t_{\Delta +1}$, for $\Delta =0,1,\dots$, in the above system which leads to the following model

$$\left\{\begin{array}{c}\hfill \mathbb{S}\left(t_{\Delta +1}\right)-\mathbb{S}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_1(t_{\Delta },\mathbb{S}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }{\int }_{t_m}^{t_{m+1}}{(t_{\Delta +1}-\xi )}^{q-1}{\mathcal{K}}_1(\xi ,\mathbb{S}\left(\xi \right))d\xi ,\hfill \\ \hfill \mathbb{E}\left(t_{\Delta +1}\right)-\mathbb{E}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_2(t_{\Delta },\mathbb{E}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }{\int }_{t_m}^{t_{m+1}}{(t_{\Delta +1}-\xi )}^{q-1}{\mathcal{K}}_2(\xi ,\mathbb{E}\left(\xi \right))d\xi ,\hfill \\ \hfill \mathbb{I}\left(t_{\Delta +1}\right)-\mathbb{I}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_3(t_{\Delta },\mathbb{I}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }{\int }_{t_m}^{t_{m+1}}{(t_{\Delta +1}-\xi )}^{q-1}{\mathcal{K}}_3(\xi ,\mathbb{I}\left(\xi \right))d\xi ,\hfill \\ \hfill \mathbb{P}\left(t_{\Delta +1}\right)-\mathbb{P}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_4(t_{\Delta },\mathbb{P}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }{\int }_{t_m}^{t_{m+1}}{(t_{\Delta +1}-\xi )}^{q-1}{\mathcal{K}}_4(\xi ,\mathbb{P}\left(\xi \right))d\xi ,\hfill \\ \hfill \mathbb{A}\left(t_{\Delta +1}\right)-\mathbb{A}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_5(t_{\Delta },\mathbb{A}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }{\int }_{t_m}^{t_{m+1}}{(t_{\Delta +1}-\xi )}^{q-1}{\mathcal{K}}_5(\xi ,\mathbb{A}\left(\xi \right))d\xi ,\hfill \\ \hfill \mathbb{H}\left(t_{\Delta +1}\right)-\mathbb{H}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_6(t_{\Delta },\mathbb{H}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }{\int }_{t_m}^{t_{m+1}}{(t_{\Delta +1}-\xi )}^{q-1}{\mathcal{K}}_6(\xi ,\mathbb{H}\left(\xi \right))d\xi ,\hfill \\ \hfill \mathbb{R}\left(t_{\Delta +1}\right)-\mathbb{R}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_7(t_{\Delta },\mathbb{R}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }{\int }_{t_m}^{t_{m+1}}{(t_{\Delta +1}-\xi )}^{q-1}{\mathcal{K}}_7(\xi ,\mathbb{R}\left(\xi \right))d\xi ,\hfill \\ \hfill \mathbb{F}\left(t_{\Delta +1}\right)-\mathbb{F}\left(0\right)=\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_8(t_{\Delta },\mathbb{F}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }{\int }_{t_m}^{t_{m+1}}{(t_{\Delta +1}-\xi )}^{q-1}{\mathcal{K}}_8(\xi ,\mathbb{F}\left(\xi \right))d\xi .\hfill \end{array}\right)$$ (20)

Using the two points interpolation polynomial for approximate the functions

$${\mathcal{K}}_j(\xi ,\mathbb{Z}),\mathbb{Z}\in \{\mathbb{S},\mathbb{E},\mathbb{I},\mathbb{P},\mathbb{A},\mathbb{H},\mathbb{R},\mathbb{F}\},j=1,2,\dots ,8,$$

that lie inside the integral in (20) on the interval $[t_m,t_{m+1}]$, we get

$$\left\{\begin{array}{c}\hfill {\mathcal{K}}_1(\xi ,\mathbb{S}\left(\xi \right))\cong \frac{{\mathcal{K}}_1(t_m,\mathbb{S}\left(t_m\right))}{h}(t-t_{m-1})+\frac{{\mathcal{K}}_1(t_{m-1},\mathbb{S}\left(t_{m-1}\right))}{h}(t-t_m),\hfill \\ \hfill {\mathcal{K}}_2(\xi ,\mathbb{E}\left(\xi \right))\cong \frac{{\mathcal{K}}_2(t_m,\mathbb{E}\left(t_m\right))}{h}(t-t_{m-1})+\frac{{\mathcal{K}}_2(t_{m-1},\mathbb{E}\left(t_{m-1}\right))}{h}(t-t_m),\hfill \\ \hfill {\mathcal{K}}_3(\xi ,\mathbb{I}\left(\xi \right))\cong \frac{{\mathcal{K}}_3(t_m,\mathbb{I}\left(t_m\right))}{h}(t-t_{m-1})+\frac{{\mathcal{K}}_3(t_{m-1},\mathbb{I}\left(t_{m-1}\right))}{h}(t-t_m),\hfill \\ \hfill {\mathcal{K}}_4(\xi ,\mathbb{P}\left(\xi \right))\cong \frac{{\mathcal{K}}_4(t_m,\mathbb{P}\left(t_m\right))}{h}(t-t_{m-1})+\frac{{\mathcal{K}}_4(t_{m-1},\mathbb{P}\left(t_{m-1}\right))}{h}(t-t_m),\hfill \\ \hfill {\mathcal{K}}_5(\xi ,\mathbb{A}\left(\xi \right))\cong \frac{{\mathcal{K}}_5(t_m,\mathbb{A}\left(t_m\right))}{h}(t-t_{m-1})+\frac{{\mathcal{K}}_5(t_{m-1},\mathbb{A}\left(t_{m-1}\right))}{h}(t-t_m),\hfill \\ \hfill {\mathcal{K}}_6(\xi ,\mathbb{H}\left(\xi \right))\cong \frac{{\mathcal{K}}_6(t_m,\mathbb{H}\left(t_m\right))}{h}(t-t_{m-1})+\frac{{\mathcal{K}}_6(t_{m-1},\mathbb{H}\left(t_{m-1}\right))}{h}(t-t_m),\hfill \\ \hfill {\mathcal{K}}_7(\xi ,\mathbb{R}\left(\xi \right))\cong \frac{{\mathcal{K}}_7(t_m,\mathbb{R}\left(t_m\right))}{h}(t-t_{m-1})+\frac{{\mathcal{K}}_7(t_{m-1},\mathbb{R}\left(t_{m-1}\right))}{h}(t-t_m),\hfill \\ \hfill {\mathcal{K}}_8(\xi ,\mathbb{F}\left(\xi \right))\cong \frac{{\mathcal{K}}_8(t_m,\mathbb{F}\left(t_m\right))}{h}(t-t_{m-1})+\frac{{\mathcal{K}}_8(t_{m-1},\mathbb{F}\left(t_{m-1}\right))}{h}(t-t_m),\hfill \end{array}\right)$$

which implies

$$\left\{\begin{array}{c}\hfill \mathbb{S}\left(t_{\Delta +1}\right)=\mathbb{S}\left(0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_1(t_{\Delta },\mathbb{S}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_1(t_m,\mathbb{S}\left(t_m\right))}{h}{I}_{m-1,q}-\frac{{\mathcal{K}}_1(t_{m-1},\mathbb{S}\left(t_{m-1}\right))}{h}{I}_{m,q}\right),\hfill \\ \hfill \mathbb{E}\left(t_{\Delta +1}\right)=\mathbb{E}\left(0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_2(t_{\Delta },\mathbb{E}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_2(t_m,\mathbb{E}\left(t_m\right))}{h}{I}_{m-1,q}-\frac{{\mathcal{K}}_2(t_{m-1},\mathbb{E}\left(t_{m-1}\right))}{h}{I}_{m,q}\right),\hfill \\ \hfill \mathbb{I}\left(t_{\Delta +1}\right)=\mathbb{I}\left(0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_3(t_{\Delta },\mathbb{I}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_3(t_m,\mathbb{I}\left(t_m\right))}{h}{I}_{m-1,q}-\frac{{\mathcal{K}}_3(t_{m-1},\mathbb{I}\left(t_{m-1}\right))}{h}{I}_{m,q}\right),\hfill \\ \hfill \mathbb{P}\left(t_{\Delta +1}\right)=\mathbb{P}\left(0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_4(t_{\Delta },\mathbb{P}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_4(t_m,\mathbb{P}\left(t_m\right))}{h}{I}_{m-1,q}-\frac{{\mathcal{K}}_4(t_{m-1},\mathbb{P}\left(t_{m-1}\right))}{h}{I}_{m,q}\right),\hfill \\ \hfill \mathbb{A}\left(t_{\Delta +1}\right)=\mathbb{A}\left(0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_5(t_{\Delta },\mathbb{A}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_5(t_m,\mathbb{A}\left(t_m\right))}{h}{I}_{m-1,q}-\frac{{\mathcal{K}}_5(t_{m-1},\mathbb{A}\left(t_{m-1}\right))}{h}{I}_{m,q}\right),\hfill \\ \hfill \mathbb{H}\left(t_{\Delta +1}\right)=\mathbb{H}\left(0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_6(t_{\Delta },\mathbb{H}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_6(t_m,\mathbb{H}\left(t_m\right))}{h}{I}_{m-1,q}-\frac{{\mathcal{K}}_6(t_{m-1},\mathbb{H}\left(t_{m-1}\right))}{h}{I}_{m,q}\right),\hfill \\ \hfill \mathbb{R}\left(t_{\Delta +1}\right)=\mathbb{R}\left(0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_7(t_{\Delta },\mathbb{R}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_7(t_m,\mathbb{R}\left(t_m\right))}{h}{I}_{m-1,q}-\frac{{\mathcal{K}}_7(t_{m-1},\mathbb{R}\left(t_{m-1}\right))}{h}{I}_{m,q}\right),\hfill \\ \hfill \mathbb{F}\left(t_{\Delta +1}\right)=\mathbb{F}\left(0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_8(t_{\Delta },\mathbb{F}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\frac{1}{\Gamma \left(q\right)}\hfill \\ \hfill \times \sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_8(t_m,\mathbb{F}\left(t_m\right))}{h}{I}_{m-1,q}-\frac{{\mathcal{K}}_8(t_{m-1},\mathbb{F}\left(t_{m-1}\right))}{h}{I}_{m,q}\right),\hfill \end{array}\right)$$ (21)

where

$$I_{m-1,q}={\int }_{t_m}^{t_{m+1}}\left(t-t_{m-1}\right){\left(t_{\Delta +1}-t\right)}^{q-1}dt,$$

and

$$I_{m,q}={\int }_{t_m}^{t_{m+1}}\left(t-t_m\right){\left(t_{\Delta +1}-t\right)}^{q-1}dt.$$

By simple calculations of the integrals $I_{m-1,q}$ and $I_{m,q}$ we get

$$I_{m-1,q}=-\frac{1}{q}\left[\left(t_{m+1}-t_{m-1}\right){\left(t_{\Delta +1}-t_{m+1}\right)}^q-\left(t_m-t_{m-1}\right){\left(t_{\Delta +1}-t_m\right)}^q\right]-\frac{1}{q\left(q+1\right)}\left[{\left(t_{\Delta +1}-t_{m+1}\right)}^{q+1}-{\left(t_{\Delta +1}-t_m\right)}^{q+1}\right],$$

and

$$I_{m,q}=-\frac{1}{q}\left[\left(t_{m+1}-t_m\right){\left(t_{\Delta +1}-t_{m+1}\right)}^q\right]-\frac{1}{q\left(q+1\right)}\left[{\left(t_{\Delta +1}-t_{m+1}\right)}^{q+1}-{\left(t_{\Delta +1}-t_m\right)}^{q+1}\right].$$

Taking $t_m=mh$, we can conclude that

$$I_{m-1,q}=\frac{h^{q+1}}{q\left(q+1\right)}\left[{\left(\Delta +1-m\right)}^q\left(\Delta -m+2+q\right)\right)\left(-{\left(\Delta -m\right)}^q\left(\Delta -m+2+2q\right)\right].$$ (22)

and

$$I_{m,q}=\frac{h^{q+1}}{q\left(q+1\right)}\left[{\left(\Delta +1-m\right)}^{q+1}-{\left(\Delta -m\right)}^q\left(\Delta -m+1+q\right)\right].$$ (23)

By replacing (22), (23) into (21), we obtain

$$\mathbb{S}\left(t_{\Delta +1}\right)=\mathbb{S}\left(t_0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_1(t_{\Delta },\mathbb{S}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_1(t_m,\mathbb{S}\left(t_m\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^q(\Delta -m+2+q)\right)\right)\left(-{(\Delta -m)}^q(\Delta -m+2+2q)\right]-\frac{{\mathcal{K}}_1(t_{m-1},\mathbb{S}\left(t_{m-1}\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^{q+1}\right)\left(\left(-{(\Delta -m)}^q(\Delta -m+1+q)\right]\right),$$ (24)

$$\mathbb{E}\left(t_{\Delta +1}\right)=\mathbb{E}\left(t_0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_2(t_{\Delta },\mathbb{E}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_2(t_m,\mathbb{E}\left(t_m\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^q(\Delta -m+2+q)\right)\right)\left(-{(\Delta -m)}^q(\Delta -m+2+2q)\right]-\frac{{\mathcal{K}}_2(t_{m-1},\mathbb{E}\left(t_{m-1}\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^{q+1}\right)\left(\left(-{(\Delta -m)}^q(\Delta -m+1+q)\right]\right),$$ (25)

$$\mathbb{I}\left(t_{\Delta +1}\right)=\mathbb{I}\left(t_0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_3(t_{\Delta },\mathbb{I}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_3(t_m,\mathbb{I}\left(t_m\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^q(\Delta -m+2+q)\right)\right)\left(-{(\Delta -m)}^q(\Delta -m+2+2q)\right]-\frac{{\mathcal{K}}_3(t_{m-1},\mathbb{I}\left(t_{m-1}\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^{q+1}\right)\left(\left(-{(\Delta -m)}^q(\Delta -m+1+q)\right]\right),$$ (26)

$$\mathbb{P}\left(t_{\Delta +1}\right)=\mathbb{P}\left(t_0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_4(t_{\Delta },\mathbb{P}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_4(t_m,\mathbb{P}\left(t_m\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^q(\Delta -m+2+q)\right)\right)\left(-{(\Delta -m)}^q(\Delta -m+2+2q)\right]-\frac{{\mathcal{K}}_4(t_{m-1},\mathbb{P}\left(t_{m-1}\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^{q+1}\right)\left(\left(-{(\Delta -m)}^q(\Delta -m+1+q)\right]\right),$$ (27)

$$\mathbb{A}\left(t_{\Delta +1}\right)=\mathbb{A}\left(t_0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_5(t_{\Delta },\mathbb{A}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_5(t_m,\mathbb{A}\left(t_m\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^q(\Delta -m+2+q)\right)\right)\left(-{(\Delta -m)}^q(\Delta -m+2+2q)\right]-\frac{{\mathcal{K}}_5(t_{m-1},\mathbb{A}\left(t_{m-1}\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^{q+1}\right)\left(\left(-{(\Delta -m)}^q(\Delta -m+1+q)\right]\right),$$ (28)

$$\mathbb{H}\left(t_{\Delta +1}\right)=\mathbb{H}\left(t_0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_6(t_{\Delta },\mathbb{H}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_6(t_m,\mathbb{H}\left(t_m\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^q(\Delta -m+2+q)\right)\right)\left(-{(\Delta -m)}^q(\Delta -m+2+2q)\right]-\frac{{\mathcal{K}}_6(t_{m-1},\mathbb{H}\left(t_{m-1}\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^{q+1}\right)\left(\left(-{(\Delta -m)}^q(\Delta -m+1+q)\right]\right),$$ (29)

$$\mathbb{R}\left(t_{\Delta +1}\right)=\mathbb{R}\left(t_0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_7(t_{\Delta },\mathbb{R}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_7(t_m,\mathbb{R}\left(t_m\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^q(\Delta -m+2+q)\right)\right)\left(-{(\Delta -m)}^q(\Delta -m+2+2q)\right]-\frac{{\mathcal{K}}_7(t_{m-1},\mathbb{R}\left(t_{m-1}\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^{q+1}\right)\left(\left(-{(\Delta -m)}^q(\Delta -m+1+q)\right]\right),$$ (30)

$$\mathbb{F}\left(t_{\Delta +1}\right)=\mathbb{F}\left(t_0\right)+\frac{1-q}{\Upsilon \left(q\right)}{\mathcal{K}}_8(t_{\Delta },\mathbb{F}\left(t_{\Delta }\right))+\frac{q}{\Upsilon \left(q\right)}\sum _{m=0}^{\Delta }\left(\frac{{\mathcal{K}}_8(t_m,\mathbb{F}\left(t_m\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^q(\Delta -m+2+q)\right)\right)\left(-{(\Delta -m)}^q(\Delta -m+2+2q)\right]-\frac{{\mathcal{K}}_8(t_{m-1},\mathbb{F}\left(t_{m-1}\right))}{\Gamma (q+2)}{h}^q\left[{(\Delta +1-m)}^{q+1}\right)\left(\left(-{(\Delta -m)}^q(\Delta -m+1+q)\right]\right),$$ (31)

6.1. Numerical simulations and discussion

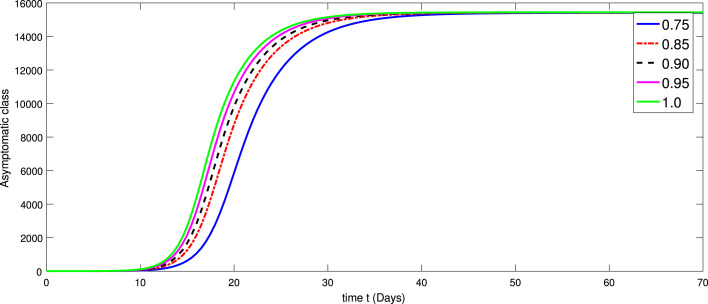
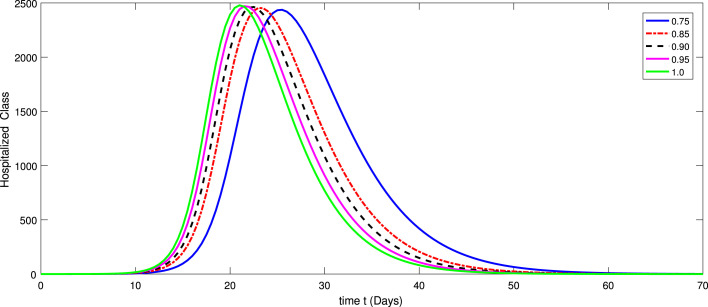
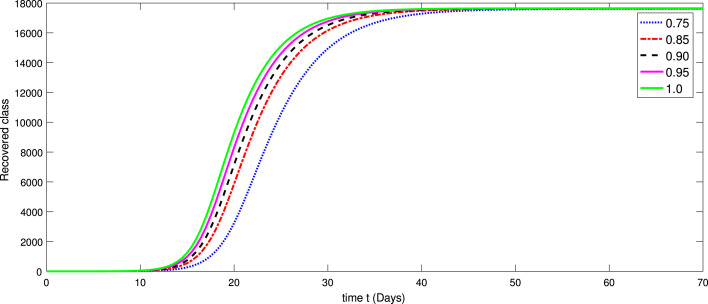
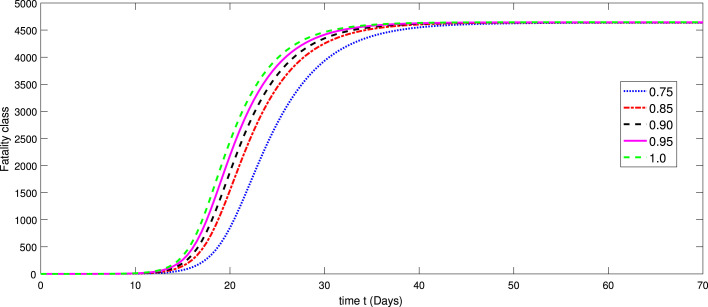
Numerical simulations are performed for the suggested model of COVID-19 pandemic originated from Wuhan (China) by using the real data of Wuhan city taken from [22], [59] since mid-February 2020 to April 25, 2020. Now to give the numerical simulation of the fractional model (3)–(4) involving AB fractional operator, we will use the iterative solution given in (24)–(31). Here the time as days. The numerical quantities of the parameters utilized in the simulation are provided in Table 1. The dynamical behavior of various compartments including $\mathbb{S},\mathbb{E},\mathbb{I},\mathbb{P},\mathbb{A},\mathbb{H},\mathbb{R},\mathbb{F}$ corresponding to various fractional orders as $q=0.75,0.85,0.90,0.95,1.0$ of the proposed model (3) is given in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7, Fig. 8. Further, we consider the initial values as a proportion of the total population as follows with taking $N=11000000∕250$ and

$${\mathbb{S}}_0\left(0\right)=N-6,{\mathbb{E}}_0\left(0\right)=0,{\mathbb{I}}_0\left(0\right)=1,{\mathbb{P}}_0\left(0\right)=5,$$

$${\mathbb{A}}_0\left(0\right)=0,{\mathbb{H}}_0\left(0\right)=0,{\mathbb{R}}_0\left(0\right)=0,{\mathbb{F}}_0\left(0\right)=0.$$

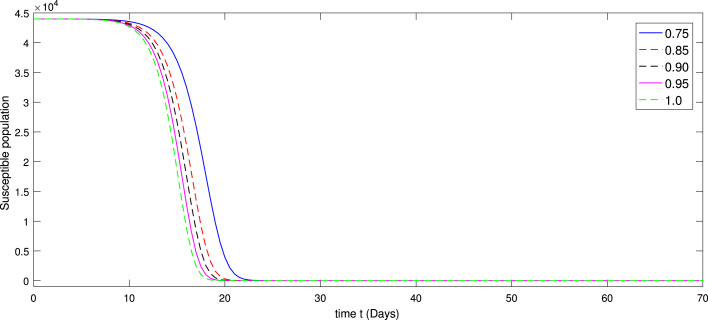
Fig. 1.

Dynamical behavior of $\mathbb{S}$ class of model (3) at various values of fractional order $q$.

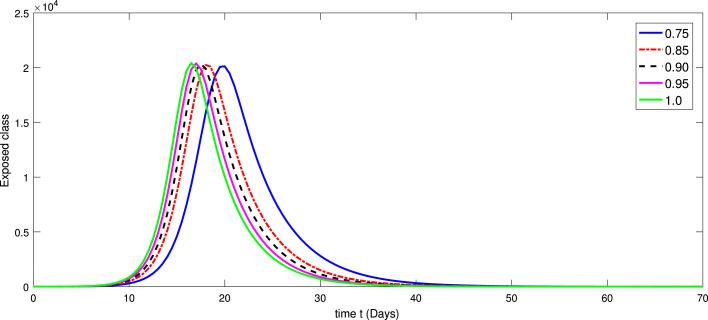
Fig. 2.

Dynamical behavior of $\mathbb{E}$ class of model (3) at various values of fractional order $q$.

Fig. 3.

Dynamical behavior of $\mathbb{I}$ class of model (3) at various values of fractional order $q$.

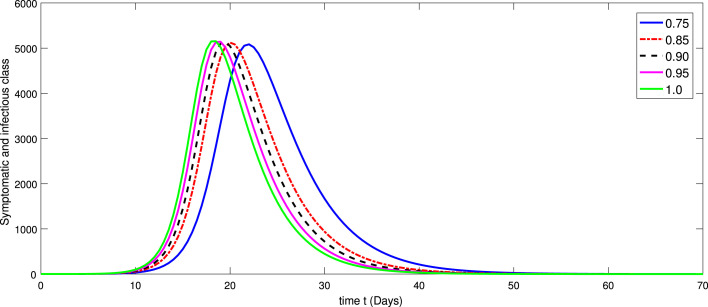
Fig. 4.

Dynamical behavior of $\mathbb{P}$ class of model (3) at various values of fractional order $q$.

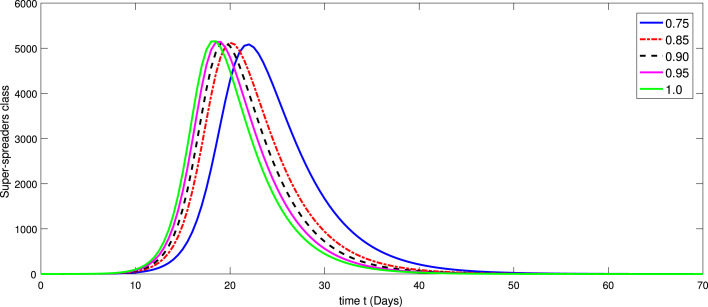
Fig. 5.

Dynamical behavior of $\mathbb{A}$ class of model (3) at various values of fractional order $q$.

Fig. 6.

Dynamical behavior of $\mathbb{H}$ class of model (3) at various values of fractional order $q$.

Fig. 7.

Dynamical behavior of $\mathbb{R}$ class of model (3) at various values of fractional order $q$.

Fig. 8.

Dynamical behavior of $\mathbb{F}$ class of model (3) at various values of fractional order $q$.

In Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7, Fig. 8, we provide dynamics of each class of the model (3) with respect to different values of fractional order $q$ on using numerical values in Table 3. From Fig. 1, one can observe that after two weeks of the outbreak being reported the decline in susceptible class was very fast on small fractional order as and it is slow at integer order. In first few days the infection was increasing very rapidly with different scenario due to fractional orders as shown in Fig. 2. On the other hand the infectious was then decreasing. In same line the exposed class i Fig. 2 raises with different rate of fractional order and it is faster at greater order as compared to small value of fractional order . The other classes have been increased with different rate of fractional order. In Fig. 4, Fig. 5, Fig. 6, the dynamics of symptomatic and infectious class, Super-spreaders class, symptomatic class, have same behaviors of increasing and then after a month the dynamics reversed as the Chinese government after a month took strict action to control the disease from further speeding. After the strict action the recovered class was raising as many people got ride from infection (see Fig. 7). Also initially the fatality was increasing. Therefore, the increase was different at different fractional order (see Fig. 8). We have simulated the results for the seventy days from mid-February 2020 to April 25, 2020. From the graphical presentation, we see that the fractional derivative approach can also be used to describe the transmission dynamics of the novel coronavirus disease in the community. The said approach provides global dynamics of disease transmission. From these dynamics we concluded that fractional order derivatives provides global dynamics and hence help in better understanding the dynamics of COVID-19.

Table 3.

The physical interpretation of the parameters and numerical values  [22].

Parameters	Physical description	Numerical value
$\beta$	Transmission coefficient from an infected person	2.55/day
$\iota$	Relative disease transmission in the hospitalized	1.56
${\beta }^{\prime }$	Transmission coefficient due to the high propagation	7.65/day
$\kappa$	Rate exposed infectious	0.25/day
${\rho }_1$	Rate that exposed individuals become infected	0.580
${\rho }_2$	Average at which exposed individuals become super-spreaders	0.001
${\gamma }_a$	Rate of hospitalized admission	0.94/day
${\gamma }_i$	Recovery rate unaccompanied by go hospitalized	0.27/day
${\gamma }_r$	Hospitalization rate	0.5/day
${\delta }_i$	Infected class death rate	0.35/day
${\delta }_p$	Super-spreaders death rate	1/day
${\delta }_h$	Hospitalized class death rate	0.3/day

7. Conclusion

The given investigation focused to develop and generalize a mathematical model and the dynamics of the novel coronavirus (COVID-2019) pandemic which is protruded recently with considered the reported cases in the Chinese city of Wuhan since February 15, 2020 till April 25, 2020 for 70 days, and formulate a generalized mathematical model involving AB fractional derivatives. Then we have discussed the existence, uniqueness, and Ulam stability results for the proposed model (3)–(4) with the help of fixed point theorems and generalized Gronwall inequality. Moreover, the fractional Adams–Bashforth method was effective to approximate the AB fractional operator. Also, we have used the data of Wuhan city under some suitable parametric values and presented the graphs. Through numerical simulation, the graphical representation of numerical solutions is shown accurately. For the numerical simulation, we have applied a strong two-step numerical instrument named the fractional Adams–Bashforth–Moulton technique. The intended numerical technique is stronger than the classical Euler technique also Taylor technique. So, the aforementioned technique is quicker convergent and stable as a comparison to other techniques that are slowly convergent. We see that fractional derivative can also be used as a powerful tools to describe the transmission dynamics with global nature. This study may also help the researchers in further investigation of the current novel coronavirus disease.

CRediT authorship contribution statement

Saleh S. Redhwan: Writing - original draft. Mohammed S. Abdo: Visualization, Investigation, Analysis. Kamal Shah: Developed the concept, methodology. Thabet Abdeljawad: Supervision, Editing. S. Dawood: Validation. Hakim A. Abdo: Software. Sadikali L. Shaikh: Reviewing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

This is not applicable in this research work.