When will the Covid-19 pandemic peak?

Abstract

We carry out some analysis of the daily data on the number of new cases and the number of new deaths by (191) countries as reported to the European Centre for Disease Prevention and Control (ECDC). Our benchmark model is a quadratic time trend model applied to the log of new cases for each country. We use our model to predict when the peak of the epidemic will arise in terms of new cases or new deaths in each country and the peak level. We also predict how long the number of new daily cases in each country will fall by an order of magnitude. Finally, we also forecast the total number of cases and deaths for each country. We consider two models that link the joint evolution of new cases and new deaths.

1. Introduction

We implement econometric models of daily data on the number of new cases of and new deaths from COVID-19 in countries worldwide. Our benchmark model is a regression of log outcomes on a quadratic trend function for each country. Since April 5th 2020 we have been estimating our model every day and providing outlooks for the future development of the pandemic in different countries. Our primary purpose when we initiated this study was to estimate the turnaround dates, the expected peak to trough times, and the expected total number of cases and deaths using only the data at hand, which was before the peak had been achieved. The results have been updated daily at the website http://covid.econ.cam.ac.uk/linton-uk-covid-cases-predicted-peak; R-code is available upon request. On this website we have also provided various robustness tests: we considered quantile estimation in place of mean estimation to limit the effect of large measurement error; we provided a one-step ahead forecasting exercise that keeps track of the model performance. We evaluated the residuals from our model along several dimensions. In particular, we found little evidence of day of the week effects in most countries, although the United States and the United Kingdom do appear to have a seasonal effect in deaths. We find some evidence of autocorrelation in the residuals but it varies widely across countries, with the mean effect (across countries) being positive autocorrelation. We find some limited evidence of time varying cross-sectional heteroskedasticity. We find the error distribution pooled across countries is not far from symmetric for cases and slightly less so for deaths. There appears to be substantial cross sectional contemporaneous correlation between the errors from cases and deaths within a country (positive) and between cases in one country and another (here, the mean is small and positive but there is wide dispersion meaning there are also negative correlations in some cases). The SUR models we fit cannot benefit from GLS, but the error properties can affect the standard errors and test statistics. We also develop a joint model for the evolution of new cases and new deaths and test the restrictions it implies and estimate the restricted model.

Our model is purely statistical and we do not pretend to model the disease dynamics per se, just the data. However, the epidemiological models themselves do not have perfect forecasting records and our approach is complementary to the large literature produced by professional epidemiologists and biostatisticians.3 One advantage of our model over dynamic epidemiological models is that the publicly available data from many countries is subject to a wide range of errors that make dynamic models very suspect without some additional model for the measurement error, which typically requires many untestable assumptions.

Literature Review. Many researchers apply or extend the SIR or its variants (SIRD, SEIR) to model the dynamics of the Covid-19 outbreak. For example, Wu et al. (2020), Anastassopoulou et al. (2020), and Lin et al. (2020). A short description of the baseline SIR model is as follows. The fixed population (N) can be split into three non-intersecting classes: susceptibles (S), infectious (I) and recovered (R). The number of individuals in each of these classes changes over time and satisfies

$$N\left(t\right)=S\left(t\right)+I\left(t\right)+R\left(t\right).$$

The dynamics of each class can be described using ordinary differential equations (ODEs) as follows:

$$\frac{dS}{dt}=-\beta IS,\frac{dI}{dt}=\beta IS-\alpha I,\frac{dR}{dt}=\alpha I,$$

where $\beta$ is the transmission rate constant, $\beta I$ is the force of infection, and $\beta IS$ is the number of individuals who become infected per unit of time. The susceptible individuals who become infected move to the class I and individuals who recover (the constant recovery rate is $\alpha$) leave the infectious class and move to the recovered class. Equipped with initial conditions $S\left(0\right),I\left(0\right),R\left(0\right)$, the model can be easily solved. Elaborations on the basic SIR model that are used in the study of Covid19 includes SIRD (eg. Anastassopoulou et al., 2020) and SEIR (eg. Wu et al., 2020 as well as Read et al. (2020)). Since there are daily data available on the number of deaths, an additional class ‘Deceased’ (D) can be included as well, which corresponds to SIRD model. The other popular variant of baseline SIR is SEIR, which separately considers susceptibles (S) and exposed (E).

Chudik et al. (2020) contrast government-mandated social distancing policies with voluntary self-isolation in an SEIR model. They decompose the population, $N$, into two categories: the exposed $N_E$ and the rest, $N_I$, which are isolated. The strength of a mitigation policy can be measured by $1-\lambda$ where $\lambda =\frac{N_E}{N}$, and it integrates social distancing policy in the traditional SIR model. They evaluate the costs and benefits of alternative societal decisions on the degree and the nature of government-mandated containment policies by considering alternative values of $\lambda$ in conjunction with an employment loss elasticity $\alpha$. They found that the employment loss can be reduced if the social distancing policy is targeted towards people that are most likely to spread the infection. Besides, other articles also discuss this model, see Wu et al. (2020), Read et al. (2020), and Peng et al. (2020) for details.

One feature of Covid-19 is that different sub-populations face different risks. Taking that into account, Acemoglu et al. (2020) develop a heterogeneous agent multi-risk SIR model (MR-SIR) where infection, hospitalization and fatality rates vary between groups. Describing the laws of motion of the susceptible, infectious and recovered populations by group, they found that better social outcomes can be achieved with targeted policy that applies an aggressive lockdown on the oldest group instead of a uniform lockdown policy.

However, these kinds of models have a high requirement on the data availability and quality, to which the estimates are very sensitive. One of the limitations of Covid-19 data is that the number of susceptible and recovered people are seldom reported. Apart from this reason, Li et al. (2020) point out the limitations of SIR style models, arguing that the real situation could be much more complicated and changing all the time.

Another strand of time series analysis originated from Generalized Logistic Model (GLM), first proposed by Richards (1959), developed for modelling growth curves. Allowing for more flexible S-shaped aggregation, the infection curve $Y\left(t\right)$ evolves as

$$Y\left(t\right)=A+\frac{K-A}{{(1+Q{e}^{-Bt})}^{1∕v}},$$

where $A$ and $K$ are lower and upper asymptotes; $B$ is the growth rate; $v$ affects the maximum asymptote growth; and $Q$ is related to the value $Y\left(0\right)$. An extension of GML called sub-epidemic modelling was studied by Chowell et al. (2019), where they model each group sub-epidemic by a GLM and then comprise a set of n overlapping sub-epidemics to describe the whole epidemic waves. Roosa et al. (2020) extend the aforementioned GML to fit the cumulative number of confirmed Covid-19 cases and forecast short-run new cases in Hubei and other provinces in China, and they found the S-shape curve fits the initial data well, based on the information until 9th Feb. Additionally, they also compare their model with the Richard curve and sub-epidemic modelling. All models provide good visual fits to the epidemic curves, and their estimates obtained from GLM consistently illustrate that the epidemic growth is nearly exponential in Hubei and sub-exponential in other provinces at early stages.

Liu et al. (2020) consider a panel regression model for the infection growth rates. Like us, they suppose a deterministic trend, in their case a piecewise linear trend for the growth rates with breakpoint at the peak of the curve. They also explicitly include first order autocorrelation in the error term, which after quasi differencing introduces a lagged dependent variable into the mean equation. They assume a common value across countries for the autocorrelation, but allow the other parameters to vary across countries. They specify prior distributions for all parameters. For example, the prior for the common autocorrelation is a normal with mean 0.5 truncated to $[0,0.99]$. They assume normality for the innovation process of the regression and independence of these error terms across country and independence of the random coefficients across countries. They provide Bayesianist inference and predictive density forecasts. This paper has some impressive results. However, it is not clear what the evidence base is for some of their choices, since they do not elucidate on them. In fact, we have found negative autocorrelations in the residuals from our mean model to be quite common (perhaps due to stale reporting in some countries, Lo and MacKinlay, 1990).4 Also, we find strong evidence of cross-sectional correlation between the error terms, which seems eminently plausible as countries like Belgium and Netherlands, say, share a lot common shocks, a point that has led to the developments in Hafner (2020).

Apart from GLM, several other time trend modelling are worth reviewing, some of which verifies the parabola time trend of daily new cases and deaths. Deb and Majumdar (2020) showed that a time-dependent quadratic trend successfully captures the log incidence pattern of the disease among Chinese provinces. Li et al. (2020) use time series modelling to fit the infections and fatalities in China, an apparent quadratic trend and turning points are found. They also demonstrate that the distribution of daily deaths is similar to that of daily infections with a 5 to 6 days delay. Furthermore, Flaxman et al. (2020) develop a semi-mechanistic Bayesian hierarchical model to accommodate the impact of government interventions on both daily new infections and fatalities among 11 European countries. Especially, most of their online plots based on data from European CDC present second-order polynomial time trend, which are consistent with the evidence from China. Moreover, Hafner (2020) considers both serial correlation and spillover effects of Covid-19 by spatial autoregressive models. Finally, Hu et al. (2020) apply artificial intelligence method for real-time forecasting of Covid-19 cases data. By using cumulative confirmed cases data until the end of February 2020, they predicted that the provinces/cities would enter plateaux eventually, although with varied time points.

Trend modelling has been a major activity in econometrics. The class of nonstationary processes is extremely broad, and different types of nonstationarity can generate quite different behaviour and require quite different analytical techniques. There are two main approaches to depict the structure of nonstationary data. One is the unit root theory for integrated time series, or similar techniques for fractional integrated time series that covers unit root process as a special case. This theory and associated techniques are studied and developed by Park and Phillips, 1999, Park and Phillips, 2001, Marinucci and Robinson (2001), Hualde et al. (2011), and Wang, 2014, Wang, 2015, among others. The other is locally stationary processes and deterministic trends. In economics, many data series feature increasing trends that are quite close to linear. For epidemic data, the situation is more complex so that typically there is an upward exponential growth, a plateaux, and a declining trend part, all of which needs to be captured.

2. Transformation regression model

We model the number of new cases and new deaths per day for each country or territory. For national health services, these are key quantities that determine peak resource needs. Let $y_{it}$ denote either the number of new cases or the number of new deaths in country $i$ on day $t$. We sometimes add one to the count as this is necessary for some countries with sparse data records or at early stages of the epidemic when zero counts were common. We also sometimes work with the data normalized by population, i.e., $\left(y_{it}+1\right)∕n_i$, where $n_i$ is the population of country $i$ and rescaled time. Division by population only affects the constant term in our regressions, but is done to aid comparability across countries.

We suppose that for some monotonic transformation $\tau$ (such as the logarithm)

$$x_{it}=\tau \left(y_{it}\right)=m_i\left(t\right)+{\epsilon }_{it},$$ (1)

where $m_i$ is the trend in the mean of the process $x_{it}$, i.e., $m_i\left(t\right)=E\left(x_{it}\right)$, and the error term ${\epsilon }_{it}$ is mean zero. We also define the mean of the original process $y_{it}$, as $M_i\left(t\right)=E\left(y_{it}\right)$. We will allow all aspects of the model to vary across countries without restriction, but we sometimes drop the subscript $i$ in the discussion for convenience. Although the data are counts, i.e., integer values, we do not impose this property; this can matter a bit at the beginning and at the end of the trajectory for small countries, but otherwise it does not seem to be necessary or helpful to impose some Poisson type process for large countries in the middle of the episode. We focus on the mean regression and we do not restrict the error process beyond the zero mean property, it may be autocorrelated and heteroskedastic within some limits. Nevertheless, statistical folklore suggests that the transformation can help in reducing heteroskedasticity and other issues that arise from the non-negative count nature of $y$, Box and Cox (1964). The long run behaviour is fully determined by the trend $m$. We discuss both nonparametric and parametric (local and global) approaches to choosing $m$.

Other models involve dynamic processes for $y_t;$ one problem with this approach is the presence of measurement error in $y$, which in our framework is simply averaged out, whereas in a dynamic model some additional structure regarding the measurement error would have to be imposed to mitigate its effects on parameter estimation.

2.1. Parametric forms

We first discuss the transformation $\tau$. We have considered the Box–Cox family of transforms ${\tau }_v\left(y\right)=(y^v-1)∕v$, where $v$ is an unknown parameter. In several of the web updates we provide a discussion of inference in this model and provide prediction based on estimating the parameter $v$. However, we found (see the website) that identification of the parameter $v$ from short time series to be challenging, so in the sequel we suppose that $v=0$ (i.e., $\tau$ is the logarithm of $y$ or $y+1$) is given.5

We next discuss the trend function $m$. We consider polynomials in $t$ and $log\left(t\right)$. Suppose that

$$m\left(t\right)=a+bt+c{t}^2,$$ (2)

where $a,b,c$ are parameters to be determined. A quadratic is the simplest function that reflects the possibility of a turning point. A well defined maximum of $m$ occurs if and only if $c<0$ and occurs at the time ${\tau }_{max}=-b∕2c$, which results in the maximal value of cases per day of $m\left({\tau }_{max}\right)=a-b^2∕4c;$ finally, the value of $t$ after which no cases would be reported (the end of the epidemic) is the larger root of $m\left(t\right)=0$. A quadratic function can also be rewritten in vertex form so that $m\left(t\right)=\alpha +\gamma {(t-\mu )}^2$, where $\mu ={\tau }_{max}$ and $\alpha =m\left({\tau }_{max}\right)$, and the parameter $\gamma =c$. The vertex form is good for interpretation since it is parameterized in terms of the quantities of interest (but it does require some nonlinear estimation, whereas the parameters of the standard form all have linear parameter effects, which makes it easier to implement). We consider a generalization of the vertex form of the quadratic model

$$m\left(t\right)=\alpha +\gamma {|t-\mu |}^{\lambda },$$ (3)

where $\alpha ,\gamma ,\mu ,\lambda$ are parameters to be determined. For any $\lambda$, a well defined maximum of $m$ occurs if and only if $\gamma <0$ and occurs at the time ${\tau }_{max}=\mu$, which results in the maximal value of (log) cases per day of $m\left({\tau }_{max}\right)=\alpha$. The parameter $\lambda$ controls the shape of the curve around the peak. When $\lambda >2$, this is called the leptobottomed case, that is, the peak is elongated relative to the $\lambda =2$ case. When $\lambda =1$, the platybottomed case, the peak is sharper than the $\lambda =2$ case. The parameter $\gamma$ measures the speed of approach to the peak and decline from the peak. We look at values $\lambda =2$ and $\lambda =4$ primarily. In the case $\lambda =2$, Eqs. (2), (3) are in one to one relation. The case $\lambda =4$ is a special case of a quartic polynomial. For any $\lambda$ this model is symmetric about the peak, which enables prediction from before the peak is achieved, although it is restrictive.

We have also worked with the mixed polynomial logarithmic functional form, that is,

$$m\left(t\right)=a-bt+clog\left(t\right),t>0,$$ (4)

which is consistent with the typical unimodal trajectory under some restrictions. It suffices that $b>0$ and $c>0$, in which case the peak is located at time $c∕b$. The curve can be reparameterized as $m\left(t\right)=\alpha -\beta t+\beta \mu ln\left(t\right)$, where $t=\mu$ is the peak time. This functional form can generate asymmetric behaviour around the peak. The UK government promoted this type of curve, perhaps as a way of encouraging “prudent” behaviour during the lockdown easing process, UK gov (2020).

Our model is for the transformed value of cases, the implied model for the cases themselves is obtained by taking the inverse transformation. Specifically, for the general model (1) we obtain

$$M\left(t\right)=E\left[{\tau }^{-1}(m\left(t\right)+{\epsilon }_t)\right].$$ (5)

If the distribution of ${\epsilon }_t$ is time invariant and $\tau$ is increasing, then the maximum of $M$ and $m$ are achieved at the same time. In the logarithmic special case, $M\left(t\right)=exp\left(m\left(t\right)\right){\kappa }_0$, where ${\kappa }_0=E\left[exp\left({\epsilon }_t\right)\right]$. If ${\epsilon }_t$ were $N(0,{\sigma }^2)$, then ${\kappa }_0=exp({\sigma }^2∕2)$ and for small ${\sigma }^2$ we have ${\kappa }_0\simeq 1+{\sigma }^2∕2$, and macroeconomists refer to this as the Jensen’s inequality term, and often drop it, (Campbell, 1993). We do not specify any distributional shape for ${\epsilon }_t$, since we do not need to, and we account for the presence of the stochastic error term in our predictions by estimating ${\kappa }_0$.

In the case where $\tau$ is logarithmic, when $\lambda =2$ the model $m$ is quadratic in time and the implied model for $M\left(t\right)$ is proportional to a Gaussian density. When $\lambda =4$, the implied model for $M\left(t\right)$ is proportional to a “fat bottomed” density with a flatter peak and faster curvature before and after the peak. The mixed functional form (4) for $m$ implies a shape for $M\left(t\right)$ proportional to a gamma density, i.e., $M\left(t\right)\propto t^{c+1}exp(-bt)$.

2.1.1. Parameters of interest

The curves $m(.),M(.)$ themselves are of interest and follow directly once the parameters are known or estimated. Parameters of interest are the time ${\tau }_{max}=\mu$ where the maximum of $m$ and $M$ occurs and the maximal value of (log) cases per day, $m\left({\tau }_{max}\right)$, which in the model (3) is $\alpha$, since this is embedded in the vertex form. Transforming back to cases we obtain for that model

$$y_{max}=exp\left(\alpha \right)E\left[exp\left({\epsilon }_t\right)\right],$$ (6)

which is the maximum of $M\left(t\right)$. For the log and linear curve (4), the peak is located at ${\tau }_{max}=-b∕d=\mu$ and $m\left({\tau }_{max}\right)=\alpha +\beta \mu (log\left(\mu \right)-1)$ and $y_{max}=exp(\alpha -\beta \mu ){\mu }^{\beta \mu }E\left[exp\left({\epsilon }_t\right)\right]$. The peak time could be in the future relative to the estimation window or could already have past.

We may be interested in the expected first passage time to some trough level from the peak. For example, suppose that trough is defined as the expected peak number of new cases divided by some number $L$. Then

$$t_{TP}=\underset{t>{\tau }_{max}}{min}\left\{\frac{y_{max}}{M\left(t\right)}\ge L\right\}.$$

For the quadratic model, this is equivalent to finding the first point $t>{\tau }_{max}$ for which $(t-\mu )\ge \sqrt{-logL∕\gamma }$.

We are also interested in the total number of cases that would occur in a given country, which is ${\sum }_{t=-\infty }^{\infty }exp\left(m\left(t\right)\right)$. We work with rescaled time below, that is, $t\mapsto t∕K$ for some large $K$. In this framework we can replace the sum by an integral and obtain a closed form in terms of the parameters. In the case $\lambda =2$, this is approximately

$$N_{total}=K\times {\int }_{-\infty }^{\infty }exp\left(m\left(t\right)\right)dt=K\sqrt{\frac{-\pi }{\gamma }}exp\left(\alpha \right)$$ (7)

and in the case $\lambda =4$

$$N_{total}=K\frac{2\Gamma \left(\frac{5}{4}\right)}{\sqrt[4]{-\gamma }}exp\left(\alpha \right)=\frac{1.812K}{\sqrt[4]{-\gamma }}exp\left(\alpha \right).$$ (8)

Finally, for the (4) family we have

$$N_{total}=K\frac{\Gamma \left(c+1\right)}{{(-b)}^{c+1}}exp\left(a\right).$$ (9)

The reproduction number, also known as $R$ or $R_0$, is the average number of people that one person with an infectious disease will likely infect in the future. It measures how fast the epidemic will increase over time. In the context of our model, we may define $R_0$ as $m^{\prime }\left(t\right)+1;$ this has the property that $R_0$ starts out above one and declines to one at the peak and then declines further towards zero as the episode ends. (it measures the rate of growth of the epidemic)

3. Asymptotic framework

We suppose that time is relative to December 31st 2019, which is the putative starting point of the epidemic. However, the first time point $t_{min}$ for a given country may be some time after this. The last time point $t_{max}$ we hope is finite, so that $y_t=0$ and $log(y_t+1)=0$ for all $t<t_{min}$ and $t>t_{max}$. It follows that there are a finite, albeit potentially quite large, number of time periods with information about $m$. We may use the traditional long horizon setting subject to this limitation. Instead, we use an infill asymptotic scheme. We suppose that time is rescaled according to the number of observations being used. That is, we if we label today as time $t_1$, and if use we use the $K$ most recent observations, we suppose they fall in the interval $[t_0,t_1]$ for some $t_0$, so that observation times are $t_0+(t_1-t_0)∕K,\dots ,t_1$ (with an abuse of notation we say $t=1,\dots ,K$). As $K\to \infty$ our observations fill up the interval $[t_0,t_1]$. The data generating process is consequently a triangular array indexed by $K$. The model however is assumed to operate over all time, i.e., from $-\infty$ to $\infty$ (or from $0$ to $+\infty$ for the model containing a logarithmic trend). We note that some parameters are relative to the coordinate system $[t_0,t_1]$ induced by $K$, and we may want to convert them back to calendar time relative to December 31st 2019 or today), which we do by linear transformation. If we interpret the model as parametric and true for all data (the model is global), the model can extrapolate both forward and backward.

Consider the nonparametric point of view. In this case the function $m(.)$ is not specified except that it is a smooth function of (rescaled time), and our quadratic regressions can be interpreted as approximations (the model is local). In this case we take the one-sided estimation window of size $K$ to be a small fraction of the total available observations $T$. In this case, the interpretation is that we are estimating the level of the regression function at the point $u\in [t_0,t_1]$ using data from previous periods and a local quadratic fit. For the local quadratic regression (Fan and Gijbels, 1996, Gozalo and Linton, 2000), $a=m\left(u\right)$, $b=h{m}^{\prime }\left(u\right)$, and $c=h^2{m}^{″}\left(u\right)∕2$ so that $\gamma =h^2{m}^{″}\left(u\right)∕2$, $\mu =-m^{\prime }\left(u\right)∕h{m}^{″}\left(u\right)$, and $\alpha =m\left(u\right)-(m^{\prime }{\left(u\right)}^2∕2m^{″}\left(u\right))$, where $h$ is a bandwidth parameter ($1∕K$). This suggests that the $\gamma$ parameter may be hard to estimate since it depends on the second derivative of the regression function and also is scaled by a small quantity. In this case, the model itself has limited extrapolative properties based on the assumption of smoothness.

4. Estimation

Our estimation methodology is very simple. We work with daily data that is available for all countries since December 31st 2019. Each country in the database has a day of first case $t_{min}^c$ and day of first death $t_{min}^d;$ these vary by country with China having its first recorded cases (as far as this database is concerned) on December 31st, but other countries enter into the fray subsequently. The current time period is denoted $t_1$ and so we have data $\{y_{it}^c,y_{it}^d,t=1,\dots ,K,i=1,\dots ,n\}$, which are count data with many zeros at the beginning.6

• 1.To estimate (3) we fix $\lambda =2$ or $\lambda =4$ and estimate the parameters $\alpha ,\gamma$ for given $\mu$ by OLS of the log of counts plus one ($log(y+1)$) for each country using the estimation window data, which contains the most recent $K$  datapoints with rescaled time ($t∕K$).7 We then search for the minimum squared error across different $\mu$. For (4) we estimate by OLS directly. We allow country specific case and country specific death values for all parameters. We also include day of the week dummy variables in each regression. We provide standard errors for the parameter estimates based on NLLS theory, which is detailed in the Appendix. We use the LS standard errors for simplicity, given the small sample size we have for each country the HAC-based standard errors can be subject to a lot of noise. We comment on the residual properties below.
• 2.We then extrapolate the estimated regression curves outside the estimation window and take exponentials to deliver predictions of the number of new cases and new deaths per day. That is, we calculate $\widehat{m}\left(s\right)$ and $\widehat{M}\left(s\right)=exp\left(\widehat{m}\left(s\right)\right){\widehat{\kappa }}_0$ for any $s$ from $-\infty$ to $+\infty$,8 where ${\widehat{\kappa }}_0={\sum }_{t=1}^{K}exp\left({\widehat{\epsilon }}_t\right)∕K$ and ${\widehat{\epsilon }}_t=log{y}_t-\widehat{m}\left(t\right)$ are the least squares residuals. We forecast $y_s$ for ANY TIME $s$ by $\widehat{M}\left(s\right)$. This is an asymptotically, i.e., as the estimation error disappears $(K\to \infty )$, unbiased forecast.
• 3.
  We provide frequentist prediction intervals for $M\left(s\right)$ for any fixed $s$,

  $$\mathcal{I}\left(s\right)=\left[\widehat{M}\left(s\right)exp\left({\widehat{q}}_{\alpha ∕2}\right),\widehat{M}\left(s\right)exp\left({\widehat{q}}_{1-\alpha ∕2}\right)\right],$$ (10)

  where ${\widehat{q}}_{\alpha }$ is the $\alpha$-quantile of the residuals $\{{\widehat{\epsilon }}_t,t=1,\dots ,K\}$. As the estimation error disappears $(K\to \infty )$, this interval will contain $M\left(s\right)$ with probability converging to $1-\alpha$.
• 4.We provide a forecast of the total number of cases: the total number of cases so far plus ${\sum }_{s>today}\widehat{M}\left(s\right)$. Alternatively, we use the formula for the total number of cases from the model $m$, which is approximately given by (7), (8), and (9)
• 5.Selection of $K$. Our choice of $K$ is often limited by data availability. We investigate in Section 9 a specific algorithm for choosing $K$.

When viewed as a parametric model, the choice of specification is crucial to obtain consistent estimates of parameters. However, there is one robustness result that does hold, namely, in the vertex model with ${\lambda }_0>0$, provided there is data on either side of the peak, our estimation procedures will robustly estimate the location of the peak $\mu$ for other values of $\lambda$, although other parameters will not be consistently estimated.

Regarding the prediction intervals, a full disclosure. These are intended to assist the reader in gauging the fundamental uncertainty that would be present were the parameter values known and the model were true. The reality is that neither of these conditions are met. If one takes account of parameter uncertainty, then the prediction intervals expand rapidly with horizon. Technically, the parameter uncertainty overwhelms the prediction uncertainty when the horizon is greater than the square root of estimation sample size. We would argue that this is true of any model in this setting unless one believes in Bayesian magic. We discuss short term prediction intervals that take account of parameter uncertainty in more detail in the Appendix.

5. Data

We use daily data on new cases and fatalities downloaded from the website of the European Centre for Disease Protection and Control (ECDC), which is an agency of the European Union. According to that website, the first case worldwide was recorded as December 31st 2019 (day 1). We have the daily number of (new) cases and the number of (new) deaths up to today’s date, which is 180+ days at the time of writing since day 1. These are count data with some zeros initially but the counts get quite big quite quickly for the major countries.

We consider the 191+ countries and entities in the ECDC dataset but report separately only the thirty countries with the largest number of cases (excluding China) and with at least $K$ days of data. Specifically, cases are the reported daily count of detected and laboratory (and sometimes, depending on the country reporting them and the criteria adopted at the time, also clinically) confirmed positive and sometimes – depending on the country reporting standards – also presumptive, suspect, or probable cases of detected infection. The size of the gap between detected (whether confirmed, suspect or probable) and reported cases versus actual cases will depend on the number of tests performed and on the country’s transparency in reporting. Most estimates have put the number of undetected cases at several multiples of detected cases. There are a number of reporting issues. Some of these include official governmental channels changing or retracting figures, or publishing contradictory data on different official outlets. National or State figures with old or incomplete data compared to regional, local (counties, in the US) government’s reports is the norm.

6. Results

We consider the thirty countries with the largest number of cases (excluding China) and with at least $K$ days of data. We re-estimate every day as new data comes in. We fully expect the parameters to change over time and to vary across country, and they do.

6.1. Estimation of trend models

We fit the models (3), (4) on each country’s case and death data separately with the most recent $K$ datapoints (and using rescaled time with estimation window $[t_0,t_1]$) and report the most recent results below in: Table 1a (cases, $\lambda =2$), Table 1b (cases, $\lambda =4$), Table 1c (cases, (4)), Table 2a (fatalities, $\lambda =2$) and Table 2b (fatalities, $\lambda =4$) and Table 1c (fatalities, (4)). We use $K$=$100$ here. The regressions generally have high $R^2$ (not reported). There is quite a bit of heterogeneity across the parameters consistent with different countries being at different stages of the cycle and having taken different approaches to managing the epidemic and having different demographics. By now most countries have $\mu$ significantly in the past, which means their peak has passed, but a number of countries still have yet to reach their peak. The $\gamma$ parameters are mostly negative but the standard errors are quite wide, and in some cases the confidence intervals around these estimates include zero. The $y_{max}$ parameter is quite well estimated for most countries with some exceptions. Most countries do not exhibit strong seasonal effects, although generally Monday and Tuesday seem to report lower cases and deaths than other days of the week (see Table 2c).

Table 1a.

Empirical Results of the quadratic model with K $=$ 100.

Name	$y_{max}$	$\hat{\mu }$	$\hat{\gamma }$	Mon	Tue	Wed	Thu	Fri	Sat	log_likelihood
USA	32600	139	−2.17	−0.18	−0.16	−0.11	−0.19	−0.03	−0.04	−37.69*
	(3262)	(4)	(0.5)	(0.14)	(0.14)	(0.14)	(0.14)	(0.14)	(0.14)
Brazil	33548	180	−4.89	−0.32	−0.36	0.05	0.09	0.09	0.15	8.39***
	(3217)	(3)	(0.32)	(0.09)	(0.09)	(0.09)	(0.09)	(0.09)	(0.09)
Russia	15655	145	−13.01	0.09	−0.29	0.02	0.01	0.07	0.02	−82.68*
	(2352)	(1)	(0.78)	(0.22)	(0.22)	(0.22)	(0.22)	(0.22)	(0.22)
India	13710	174	−5.88	−0.03	−0.11	−0.09	−0.08	−0.11	−0.03	−18.04 *
	(1460)	(3)	(0.41)	(0.12)	(0.12)	(0.12)	(0.11)	(0.11)	(0.12)
UK	5107	121	−6.53	−0.05	−0.2	−0.1	−0.16	−0.03	0.03	−30.5**
	(480)	(1)	(0.47)	(0.13)	(0.13)	(0.13)	(0.13)	(0.13)	(0.13)
Peru	7075	145	−11.54	0.14	−1.35	−0.48	0.33	0.12	−0.07	−166.64***
	(1925)	(3)	(1.82)	(0.51)	(0.51)	(0.51)	(0.5)	(0.5)	(0.51)
Chile	17642	235	−2.09	−0.09	−0.15	−0.16	0	0.01	0.03	−41.85***
	(9555)	(27)	(0.52)	(0.15)	(0.15)	(0.15)	(0.14)	(0.14)	(0.15)
Spain	53	278	1.34	−0.43	−0.03	−0.03	0.22	0.22	0.11	−55.61***
	(65)	(68)	(0.6)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)
Italy	NA	−265	−0.49	−0.14	−0.32	−0.2	−0.04	−0.01	−0.04	−16.66**
	(NA)	(323)	(0.41)	(0.11)	(0.11)	(0.11)	(0.11)	(0.11)	(0.11)
Iran	1730	99	1.28	−0.04	0.01	0.01	0.03	0	−0.49	−117.07**
	(353)	(27)	(1.11)	(0.31)	(0.31)	(0.31)	(0.31)	(0.31)	(0.31)
Mexico	4594	171	−5.46	0.01	−0.16	−0.01	0.02	0.1	0.11	30.96*
	(289)	(2)	(0.25)	(0.07)	(0.07)	(0.07)	(0.07)	(0.07)	(0.07)
France	315	218	1.56	−0.84	−0.25	0.1	−0.16	0.06	−0.1	−94.4***
	(184)	(52)	(0.88)	(0.25)	(0.25)	(0.25)	(0.24)	(0.24)	(0.25)
Pakistan	13561	205	−3.27	−0.03	−0.1	−0.09	−0.46	−0.29	−0.88	−150.55***
	(9385)	(37)	(1.55)	(0.43)	(0.43)	(0.43)	(0.43)	(0.43)	(0.43)
Turkey	2847	124	−4.88	−0.04	−0.09	0.01	−0.1	0.01	0.03	−97.42*
	(460)	(2)	(0.91)	(0.26)	(0.26)	(0.26)	(0.25)	(0.25)	(0.26)
Germany	418	180	2.94	−0.23	−0.01	0.1	0.18	−0.15	0.35	−121.23***
	(128)	(21)	(1.15)	(0.32)	(0.32)	(0.32)	(0.32)	(0.32)	(0.32)
Saudi Arabia	4241	163	−6.05	−0.13	−0.08	−0.06	−0.12	−0.07	−0.49	−92.9**
	(747)	(5)	(0.87)	(0.24)	(0.24)	(0.24)	(0.24)	(0.24)	(0.24)
Bangladesh	3283	162	−11.15	0.14	0.2	0.22	0.17	0.23	0.17	−101.7*
	(570)	(3)	(0.95)	(0.27)	(0.27)	(0.27)	(0.26)	(0.26)	(0.27)
South Africa	0	−178	0.86	0.19	0.09	−0.01	0.08	0.26	0.28	−56.7**
	(1)	(21)	(0.6)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)
Canada	1757	124	−7.57	−0.06	−0.06	−0.08	−0.01	0.04	−0.03	−33.81**
	(171)	(1)	(0.48)	(0.14)	(0.14)	(0.14)	(0.13)	(0.13)	(0.14)
Qatar	2391	149	−10.93	−0.07	−0.14	−0.03	−0.15	−0.1	−0.48	−76.59**
	(336)	(2)	(0.74)	(0.21)	(0.21)	(0.21)	(0.2)	(0.2)	(0.21)
Colombia	10458	272	−1.41	−0.19	−0.16	0	0.03	−0.62	0.07	−115.23**
	(20669)	(112)	(1.09)	(0.31)	(0.31)	(0.31)	(0.3)	(0.3)	(0.31)
Sweden	688	132	−4.7	−0.26	0.18	0.6	0.76	0.79	0.14	−152.85*
	(163)	(5)	(1.58)	(0.44)	(0.44)	(0.44)	(0.44)	(0.44)	(0.44)
Egypt	2528	188	−3.63	−0.65	−0.36	−0.1	−0.89	−0.19	−0.31	−157.87***
	(1198)	(28)	(1.66)	(0.47)	(0.47)	(0.47)	(0.46)	(0.46)	(0.47)
Belgium	1371	96	−5.45	−0.3	−0.51	−0.27	−0.26	0.02	0.03	−106.07**
	(238)	(6)	(0.99)	(0.28)	(0.28)	(0.28)	(0.27)	(0.27)	(0.28)
Belarus	1414	144	−14.66	−0.14	0.59	0.45	0.42	0.62	0.56	−154.17**
	(315)	(2)	(1.6)	(0.45)	(0.45)	(0.45)	(0.44)	(0.44)	(0.45)
Argentina	25	−46	1.02	−1.27	−0.26	−0.96	−0.39	−1.39	−0.41	−192.34**
	(97)	(401)	(2.35)	(0.66)	(0.66)	(0.66)	(0.65)	(0.65)	(0.66)
Ecuador	881	150	−4.51	−0.14	−0.15	0.02	−0.03	−0.38	0.13	−133.09**
	(136)	(7)	(1.3)	(0.36)	(0.36)	(0.36)	(0.36)	(0.36)	(0.36)
Indonesia	1137	178	−2.76	−0.15	−0.27	−0.07	−0.33	−0.03	0	−69.65*
	(215)	(13)	(0.69)	(0.19)	(0.19)	(0.19)	(0.19)	(0.19)	(0.19)
Netherlands	1561	42	−1.67	0	−0.57	−0.2	−0.16	0.11	0.08	−88.65**
	(817)	(43)	(0.83)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)
UAE	1956	142	−12.36	−0.56	0.01	−0.08	−0.43	−0.18	−1.01	−151.5*
	(426)	(2)	(1.56)	(0.44)	(0.44)	(0.44)	(0.43)	(0.43)	(0.44)

This table uses the latest K $=$ 100 days’ data (until 2020-06-26) to fit the quadratic model.

Standard errors are in parentheses below the estimates.

$\hat{\mu }$ is the estimated day of the peak, taking 201-12-31 as day 0.

The number of * at the last column denotes the relative goodness of fit based on log likelihood, where *** indicates the model of the best fit among others.

Table 1b.

Empirical Results of Quartic Model of Cases with K $=$ 100.

Name	$y_{max}$	$\hat{\mu }$	$\hat{\gamma }$	Mon	Tue	Wed	Thu	Fri	Sat	log_likelihood
USA	31178	138	−9.69	−0.19	−0.17	−0.13	−0.17	−0.02	−0.03	−15.73***
	(37612)	(126)	(2.51)	(0.11)	(0.11)	(0.11)	(0.11)	(0.11)	(0.11)
Brazil	38309	250	−0.63	−0.33	−0.37	0.04	0.1	0.1	0.15	2.21*
	(7695)	(21)	(0.12)	(0.09)	(0.09)	(0.09)	(0.09)	(0.09)	(0.09)
Russia	10149	158	−15.87	0.07	−0.33	−0.03	0.01	0.05	0.04	−65.09***
	(25297)	(266)	(3.6)	(0.18)	(0.18)	(0.18)	(0.18)	(0.18)	(0.18)
India	17207	247	−0.72	−0.03	−0.11	−0.1	−0.07	−0.11	−0.03	−5.52**
	(3825)	(23)	(0.13)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
UK	4233	125	−28.99	−0.05	−0.2	−0.1	−0.13	−0.01	0.04	−48.42*
	(3602)	(92)	(2.54)	(0.16)	(0.16)	(0.16)	(0.15)	(0.15)	(0.16)
Peru	5575	176	−5.7	0.13	−1.38	−0.52	0.31	0.08	−0.06	−168.7*
	(16008)	(402)	(4.33)	(0.52)	(0.52)	(0.52)	(0.51)	(0.51)	(0.52)
Chile	6730	250	−0.52	−0.09	−0.15	−0.16	0.04	0.04	0.03	−60.14*
	(2325)	(39)	(0.22)	(0.18)	(0.18)	(0.18)	(0.17)	(0.17)	(0.18)
Spain	318	250	0.46	−0.41	−0.01	−0.04	0.2	0.23	0.12	−72.63*
	(123)	(44)	(0.25)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)
Italy	5692	0	−0.4	−0.14	−0.32	−0.2	0	0.03	−0.05	−53.04*
	(1778)	(34)	(0.19)	(0.16)	(0.16)	(0.16)	(0.16)	(0.16)	(0.16)
Iran	1634	11	0.11	−0.04	0.01	0	0.04	0.01	−0.49	−117.27*
	(1034)	(73)	(0.43)	(0.31)	(0.31)	(0.31)	(0.31)	(0.31)	(0.31)
Mexico	5761	244	−0.67	0.01	−0.17	−0.02	0.02	0.1	0.11	45.53***
	(808)	(14)	(0.08)	(0.06)	(0.06)	(0.06)	(0.06)	(0.06)	(0.06)
France	485	250	0.33	−0.85	−0.25	0.1	−0.17	0.06	−0.09	−98.55*
	(224)	(57)	(0.32)	(0.26)	(0.26)	(0.26)	(0.25)	(0.25)	(0.26)
Pakistan	8976	250	−0.6	−0.03	−0.1	−0.09	−0.43	−0.27	−0.87	−152.75*
	(6400)	(97)	(0.55)	(0.44)	(0.44)	(0.44)	(0.44)	(0.44)	(0.44)
Turkey	2566	131	−24.26	−0.05	−0.11	−0.02	−0.07	0.03	0.04	−90.66 **
	(3154)	(147)	(3.94)	(0.24)	(0.24)	(0.24)	(0.23)	(0.24)	(0.24)
Germany	395	250	0.37	−0.23	−0.01	0.1	0.17	−0.16	0.35	−122.87*
	(243)	(72)	(0.41)	(0.33)	(0.33)	(0.33)	(0.32)	(0.32)	(0.33)
Saudi Arabia	4865	226	−0.98	−0.13	−0.09	−0.07	−0.12	−0.08	−0.49	−92.69***
	(3092)	(70)	(0.47)	(0.24)	(0.24)	(0.24)	(0.24)	(0.24)	(0.24)
Bangladesh	3957	221	−2.03	0.13	0.19	0.2	0.17	0.22	0.18	−99.87***
	(2643)	(81)	(0.57)	(0.26)	(0.26)	(0.26)	(0.26)	(0.26)	(0.26)
South Africa	70	0	0.54	0.19	0.09	−0.01	0.02	0.21	0.28	−85.11*
	(29)	(47)	(0.26)	(0.23)	(0.23)	(0.23)	(0.22)	(0.22)	(0.23)
Canada	1426	127	−34.37	−0.07	−0.06	−0.08	0.02	0.07	−0.03	−38.58*
	(1071)	(80)	(2.27)	(0.14)	(0.14)	(0.14)	(0.14)	(0.14)	(0.14)
Qatar	1969	180	−5.18	−0.09	−0.17	−0.06	−0.16	−0.13	−0.46	−78.82*
	(2625)	(146)	(1.5)	(0.21)	(0.21)	(0.21)	(0.21)	(0.21)	(0.21)
Colombia	2122	250	−0.48	−0.19	−0.16	0	0.07	−0.58	0.07	−119.27*
	(1262)	(70)	(0.39)	(0.32)	(0.32)	(0.32)	(0.31)	(0.31)	(0.32)
Sweden	626	130	−23.51	−0.27	0.18	0.6	0.79	0.82	0.15	−151.51***
	(1122)	(260)	(7.14)	(0.44)	(0.44)	(0.44)	(0.43)	(0.43)	(0.44)
Egypt	2440	250	−0.53	−0.65	−0.36	−0.1	−0.88	−0.18	−0.31	−159.25*
	(1858)	(104)	(0.58)	(0.47)	(0.47)	(0.47)	(0.47)	(0.47)	(0.47)
Belgium	1690	19	−0.6	−0.29	−0.5	−0.27	−0.27	0.01	0.03	−109.04*
	(1009)	(73)	(0.46)	(0.29)	(0.29)	(0.29)	(0.28)	(0.28)	(0.29)
Belarus	954	165	−12.01	−0.16	0.55	0.4	0.4	0.57	0.57	−154.66*
	(3185)	(510)	(6.31)	(0.45)	(0.45)	(0.45)	(0.45)	(0.45)	(0.45)
Argentina	164	0	0.37	−1.27	−0.26	−0.96	−0.42	−1.42	−0.41	−193.39*
	(128)	(139)	(0.76)	(0.67)	(0.67)	(0.67)	(0.66)	(0.66)	(0.67)
Ecuador	742	170	−3.04	0.01	−0.12	−0.01	−0.06	−0.34	0.23	−121.02***
	(1471)	(303)	(3.5)	(0.32)	(0.32)	(0.32)	(0.32)	(0.32)	(0.32)
Indonesia	1129	232	−0.53	−0.15	−0.27	−0.07	−0.32	−0.02	0	−66.93**
	(530)	(50)	(0.32)	(0.19)	(0.19)	(0.19)	(0.19)	(0.19)	(0.19)
Netherlands	1156	0	−0.3	0	−0.57	−0.2	−0.15	0.12	0.08	−92.16*
	(512)	(51)	(0.28)	(0.24)	(0.24)	(0.24)	(0.24)	(0.24)	(0.24)
UAE	1187	145	−27.54	−0.58	−0.02	−0.14	−0.42	−0.19	−0.99	−150.17**
	(5939)	(724)	(12.04)	(0.43)	(0.43)	(0.43)	(0.43)	(0.43)	(0.43)

This table uses the latest K $=$ 100 days’ (until 2020-06-26) data to fit the quartic model.

Standard errors are in parentheses below the estimates.

$\hat{\mu }$ is the estimated day of the peak, taking 2020-12-31 as day 0.

The number of * at the last column denotes the relative goodness of fit based on log likelihood, where *** indicates the model of the best fit among others.

Table 1c.

Empirical Results of Gamma Model of Cases with K $=$ 100.

Name	$y_{max}$	$\hat{\mu }$	$\hat{c}$	Mon	Tue	Wed	Thu	Fri	Sat	log_likelihood
USA	33085	133	8.21	−0.19	−0.16	−0.11	−0.18	−0.03	−0.04	−31.09**
	(22014)	(3)	(1.41)	(0.13)	(0.13)	(0.13)	(0.13)	(0.13)	(0.13)
Brazil	50411	218	14.64	−0.33	−0.37	0.04	0.09	0.09	0.15	7.69 **
	(57481)	(11)	(0.95)	(0.09)	(0.09)	(0.09)	(0.09)	(0.09)	(0.09)
Russia	13501	143	40.48	0.08	−0.31	0	0.02	0.07	0.03	−70.12**
	(16091)	(1)	(2.08)	(0.19)	(0.19)	(0.19)	(0.19)	(0.19)	(0.19)
India	16085	194	18.57	−0.03	−0.11	−0.1	−0.07	−0.11	−0.03	−4.5***
	(17871)	(7)	(1.08)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
UK	5369	118	21.01	−0.05	−0.21	−0.11	−0.15	−0.03	0.03	−11.21***
	(1777)	(1)	(1.15)	(0.11)	(0.11)	(0.11)	(0.11)	(0.11)	(0.11)
Peru	6187	145	34.37	0.13	−1.36	−0.5	0.33	0.11	−0.06	−167.02**
	(15394)	(5)	(5.47)	(0.51)	(0.51)	(0.51)	(0.5)	(0.5)	(0.51)
Chile	NA	4101	5.69	−0.09	−0.15	−0.17	0	0.01	0.03	−43.4**
	(NA)	(37121)	(1.59)	(0.15)	(0.15)	(0.15)	(0.15)	(0.15)	(0.15)
Spain	NaN	−127	−2.53	−0.43	−0.03	−0.02	0.22	0.22	0.11	−57.38**
	(NaN)	(186)	(1.83)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)
Italy	14321	42	2.48	−0.14	−0.32	−0.2	−0.04	−0.01	−0.04	−15.14***
	(32526)	(13)	(1.2)	(0.11)	(0.11)	(0.11)	(0.11)	(0.11)	(0.11)
Iran	1698	101	−4.13	−0.03	0.01	0.01	0.03	0	−0.49	−116.95***
	(375)	(16)	(3.32)	(0.31)	(0.31)	(0.31)	(0.31)	(0.31)	(0.31)
Mexico	5206	189	16.81	0.01	−0.17	−0.02	0.02	0.1	0.11	45.47**
	(3470)	(4)	(0.65)	(0.06)	(0.06)	(0.06)	(0.06)	(0.06)	(0.06)
France	NaN	−787	−3.03	−0.84	−0.25	0.1	−0.15	0.06	−0.1	−95.27**
	(NaN)	(5143)	(2.67)	(0.25)	(0.25)	(0.25)	(0.25)	(0.25)	(0.25)
Pakistan	NA	436	8.76	−0.03	−0.11	−0.1	−0.46	−0.3	−0.87	−151.06**
	(NA)	(594)	(4.67)	(0.44)	(0.44)	(0.44)	(0.43)	(0.43)	(0.44)
Turkey	3058	121	17.89	−0.04	−0.09	0	−0.08	0.02	0.04	−88.89***
	(2248)	(2)	(2.51)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)
Germany	220	264	−7.1	−0.23	−0.01	0.1	0.19	−0.14	0.35	−122.49**
	(980)	(152)	(3.51)	(0.33)	(0.33)	(0.33)	(0.32)	(0.32)	(0.33)
Saudi Arabia	4358	175	18.17	−0.13	−0.09	−0.07	−0.12	−0.07	−0.49	−92.94*
	(9388)	(11)	(2.61)	(0.24)	(0.24)	(0.24)	(0.24)	(0.24)	(0.24)
Bangladesh	3346	172	33.73	0.13	0.19	0.2	0.17	0.23	0.17	−100.57**
	(6902)	(6)	(2.82)	(0.26)	(0.26)	(0.26)	(0.26)	(0.26)	(0.26)
South Africa	18	42	−3.33	0.19	0.09	−0.01	0.07	0.26	0.28	−55.94***
	(58)	(15)	(1.8)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)
Canada	1819	120	23.89	−0.07	−0.07	−0.09	−0.01	0.04	−0.03	−17.07***
	(711)	(1)	(1.22)	(0.11)	(0.11)	(0.11)	(0.11)	(0.11)	(0.11)
Qatar	2103	149	33.02	−0.08	−0.16	−0.04	−0.15	−0.11	−0.47	−75.16***
	(2862)	(2)	(2.18)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)
Colombia	NaN	−1177	4.55	−0.19	−0.16	0	0.03	−0.62	0.07	−115.09***
	(NaN)	(8904)	(3.26)	(0.3)	(0.3)	(0.3)	(0.3)	(0.3)	(0.3)
Sweden	670	128	14.22	−0.27	0.18	0.59	0.76	0.79	0.15	−152.78**
	(975)	(5)	(4.75)	(0.44)	(0.44)	(0.44)	(0.44)	(0.44)	(0.44)
Egypt	7702	292	9.4	−0.65	−0.36	−0.1	−0.9	−0.2	−0.31	−158.55**
	(46487)	(217)	(5.03)	(0.47)	(0.47)	(0.47)	(0.46)	(0.46)	(0.47)
Belgium	1451	100	17.61	−0.3	−0.51	−0.28	−0.25	0.02	0.04	−103.37***
	(244)	(3)	(2.9)	(0.27)	(0.27)	(0.27)	(0.27)	(0.27)	(0.27)
Belarus	1202	143	44.67	−0.15	0.57	0.43	0.42	0.61	0.56	−152.79***
	(2332)	(3)	(4.75)	(0.44)	(0.44)	(0.44)	(0.44)	(0.44)	(0.44)
Argentina	109	59	−4.04	−1.27	−0.26	−0.96	−0.39	−1.39	−0.41	−192.26***
	(466)	(54)	(7.05)	(0.66)	(0.66)	(0.66)	(0.65)	(0.65)	(0.66)
Ecuador	862	150	14.54	−0.2	−0.16	0.01	−0.03	−0.4	0.12	−136.54*
	(1344)	(11)	(4.04)	(0.38)	(0.38)	(0.38)	(0.37)	(0.37)	(0.38)
Indonesia	1184	193	9.51	−0.15	−0.27	−0.07	−0.32	−0.02	0	−66.76***
	(2348)	(24)	(2.01)	(0.19)	(0.19)	(0.19)	(0.18)	(0.18)	(0.19)
Netherlands	1098	80	6.45	0	−0.57	−0.2	−0.16	0.11	0.08	−87.18***
	(1030)	(11)	(2.46)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)
UAE	1717	139	38.15	−0.57	0	−0.1	−0.42	−0.18	−1.01	−149.51***
	(3063)	(3)	(4.59)	(0.43)	(0.43)	(0.43)	(0.42)	(0.42)	(0.43)

This table uses the latest K $=$ 100 days’ data (until 2020-06-26) to fit the Gamma model.

Standard errors are in parentheses below the estimates.

$\hat{\mu }$ is the estimated day of the peak, taking 2019-12-31 as day 0.

The number of * at the last column denotes the relative goodness of fit based on log likelihood, where *** indicates the model of the best fit among others.

Table 2a.

Empirical Results of Quadratic model with K $=$ 100.

Name	$y_{max}$	$\hat{\mu }$	$\hat{\gamma }$	Mon	Tue	Wed	Thu	Fri	Sat	log_likelihood
USA	2500	131	−9.57	−0.33	−0.23	0.25	0.25	0	0.14	−112.99*
	(457)	(1)	(1.06)	(0.3)	(0.3)	(0.3)	(0.29)	(0.29)	(0.3)
Brazil	1146	155	−8.71	−0.4	−0.3	0.22	0.1	0.18	0.07	−2.69*
	(83)	(1)	(0.35)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
Russia	164	152	−10.02	0	−0.12	0.23	0.21	0.25	0.25	−31.22*
	(15)	(1)	(0.47)	(0.13)	(0.13)	(0.13)	(0.13)	(0.13)	(0.13)
India	349	173	−5.76	0.14	0.02	0.19	0.12	0.07	0.07	−53.9*
	(50)	(5)	(0.59)	(0.17)	(0.17)	(0.17)	(0.16)	(0.16)	(0.17)
UK	801	122	−8.41	−0.69	−0.6	0.3	0.18	0.06	0.13	−87.75**
	(120)	(1)	(0.82)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)
Peru	215	153	−8.26	−0.28	−0.8	−0.3	0.01	−0.06	−0.1	−118.37*
	(43)	(4)	(1.12)	(0.31)	(0.31)	(0.31)	(0.31)	(0.31)	(0.31)
Chile	29522	427	−0.79	0.13	−0.46	−0.62	−0.09	−0.07	0.01	−96.64**
	(198732)	(342)	(0.9)	(0.25)	(0.25)	(0.25)	(0.25)	(0.25)	(0.25)
Spain	1353	85	−6.43	0.66	0.82	0.18	0.19	0.68	0.21	−153.85*
	(182)	(11)	(1.6)	(0.45)	(0.45)	(0.44)	(0.44)	(0.45)	(0.45)
Italy	1110	52	−2.34	−0.36	−0.29	−0.17	−0.1	−0.07	−0.05	7.88**
	(192)	(10)	(0.32)	(0.09)	(0.09)	(0.09)	(0.09)	(0.09)	(0.09)
Iran	68	134	3.32	−0.02	0.04	0.03	0.07	0.05	−0.36	−72.4***
	(10)	(3)	(0.71)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)
Mexico	547	165	−7.97	−0.38	−0.09	0.24	0.29	0.23	0.28	−56.89*
	(70)	(3)	(0.61)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)
France	385	100	−6.4	−0.37	0.35	0.76	0.21	0.36	0.22	−85.53**
	(55)	(4)	(0.81)	(0.23)	(0.23)	(0.23)	(0.22)	(0.22)	(0.23)
Pakistan	141	197	−3.17	0.02	0	0.07	−0.14	−0.02	−0.15	−69.82**
	(42)	(15)	(0.69)	(0.19)	(0.19)	(0.19)	(0.19)	(0.19)	(0.19)
Turkey	87	124	−7.82	0	0	0.01	−0.03	0.04	−0.05	−86.86**
	(13)	(1)	(0.82)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)
Germany	101	115	−8.88	−0.23	0.61	0.88	0.62	0.41	0.49	−128.69**
	(21)	(2)	(1.24)	(0.35)	(0.35)	(0.35)	(0.34)	(0.34)	(0.35)
Saudi Arabia	546	342	−0.83	−0.09	−0.24	−0.06	−0.18	−0.09	−0.29	−43.32**
	(1223)	(137)	(0.53)	(0.15)	(0.15)	(0.15)	(0.15)	(0.15)	(0.15)
Bangladesh	115	235	−1.86	−0.11	−0.09	−0.09	−0.05	−0.17	−0.15	−63.09***
	(75)	(37)	(0.64)	(0.18)	(0.18)	(0.18)	(0.18)	(0.18)	(0.18)
South Africa	0	−775	0.27	−0.22	0.16	−0.15	0.22	0.14	0.31	−83.78**
	(0 )	(2621)	(0.79)	(0.22)	(0.22)	(0.22)	(0.22)	(0.22)	(0.22)
Canada	229	133	−13.43	−0.4	−0.39	−0.21	−0.07	−0.02	−0.06	−65.95*
	(29)	(1)	(0.66)	(0.19)	(0.19)	(0.19)	(0.18)	(0.18)	(0.19)
Qatar	1	90	1.86	0.2	0.04	0.1	0.11	0.01	0.18	−59.19**
	(0 )	(13)	(0.62)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)
Colombia	153	234	−1.79	0.07	−0.03	−0.02	−0.18	−0.26	0.09	−85.05**
	(119)	(48)	(0.8)	(0.23)	(0.23)	(0.23)	(0.22)	(0.22)	(0.23)
Sweden	62	127	−9.41	−1.46	0.36	1.01	1.2	0.63	0.72	−120.28*
	(11)	(2)	(1.14)	(0.32)	(0.32)	(0.32)	(0.32)	(0.32)	(0.32)
Egypt	1390	393	−0.58	−0.18	−0.12	−0.09	−0.56	−0.19	−0.2	−107.9**
	(8209)	(462)	(1.01)	(0.28)	(0.28)	(0.28)	(0.28)	(0.28)	(0.28)
Belgium	151	114	−10.99	−0.03	−0.06	0.27	0.44	0.25	0.37	−100.86**
	(24)	(2)	(0.94)	(0.26)	(0.26)	(0.26)	(0.26)	(0.26)	(0.26)
Belarus	7	150	−4.05	−0.04	0.03	−0.09	−0.09	0.1	−0.13	−26.8*
	(1)	(3)	(0.45)	(0.13)	(0.13)	(0.13)	(0.12)	(0.12)	(0.13)
Argentina	44	234	−1.14	−0.65	0.04	−0.14	−0.01	−0.01	−0.09	−78.22**
	(32)	(70)	(0.75)	(0.21)	(0.21)	(0.21)	(0.21)	(0.21)	(0.21)
Ecuador	58	143	−5.27	0.12	−0.03	−0.02	0.25	−0.53	0.78	−166.03*
	(12)	(7)	(1.8)	(0.51)	(0.51)	(0.51)	(0.5)	(0.5)	(0.51)
Indonesia	59	206	−1.06	0.05	−0.27	−0.2	−0.29	0.02	−0.04	−74.89*
	(23)	(54)	(0.73)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)
Netherlands	124	102	−7.21	−0.56	−0.8	0.15	−0.01	0	0.05	−72.11**
	(16)	(3)	(0.71)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)
UAE	6	132	−6.52	0	0.15	0.11	0.05	0.06	−0.05	−71.67**
	(1)	(1)	(0.7)	(0.2)	(0.2)	(0.2)	(0.19)	(0.19)	(0.2)

This table uses the latest K $=$ 100 days’ data (until 2020-06-26) to fit the quadratic model.

Standard errors are in parentheses below the estimates.

$\hat{\mu }$ is the estimated day of the peak, taking 201-12-31 as day 0.

The number of * at the last column denotes the relative goodness of fit based on log likelihood, where *** indicates the model of the best fit among others.

Table 2b.

Empirical Results of Quartic Model of Deaths with K $=$ 100.

Name	$y_{max}$	$\hat{\mu }$	$\hat{\gamma }$	Mon	Tue	Wed	Thu	Fri	Sat	log_likelihood
USA	1885	132	−42.44	−0.34	−0.25	0.22	0.29	0.03	0.15	−94.9***
	(2730)	(171)	(4.31)	(0.25)	(0.25)	(0.25)	(0.25)	(0.25)	(0.25)
Brazil	1057	194	−3	−0.41	−0.31	0.19	0.1	0.17	0.08	19.77***
	(402)	(39)	(0.35)	(0.08)	(0.08)	(0.08)	(0.08)	(0.08)	(0.08)
Russia	146	189	−3.8	0	−0.14	0.2	0.21	0.24	0.26	−30.11**
	(101)	(72)	(0.68)	(0.13)	(0.13)	(0.13)	(0.13)	(0.13)	(0.13)
India	414	241	−0.79	0.14	0.01	0.18	0.13	0.07	0.08	−46.97**
	(140)	(37)	(0.22)	(0.15)	(0.15)	(0.15)	(0.15)	(0.15)	(0.15)
UK	643	126	−39.88	−0.69	−0.61	0.29	0.22	0.1	0.14	−90.82*
	(730)	(136)	(3.83)	(0.24)	(0.24)	(0.24)	(0.24)	(0.24)	(0.24)
Peru	199	193	−2.85	−0.29	−0.82	−0.32	0.01	−0.07	−0.1	−117.82**
	(269)	(158)	(1.43)	(0.31)	(0.31)	(0.31)	(0.31)	(0.31)	(0.31)
Chile	125	250	−0.55	0.13	−0.46	−0.62	−0.04	−0.02	0.01	−108.52*
	(61)	(63)	(0.35)	(0.29)	(0.29)	(0.29)	(0.28)	(0.28)	(0.29)
Spain	1417	0	−0.56	0.69	0.82	0.18	0.21	0.67	0.2	−153.01**
	(495)	(93)	(0.51)	(0.45)	(0.45)	(0.44)	(0.44)	(0.45)	(0.45)
Italy	903	0	−0.38	−0.36	−0.29	−0.17	−0.1	−0.05	−0.05	−8.6*
	(191)	(22)	(0.12)	(0.11)	(0.11)	(0.11)	(0.1)	(0.1)	(0.11)
Iran	77	130	13.89	−0.02	0.04	0.03	0.05	0.03	−0.36	−75.17*
	(89)	(124)	(3.36)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)
Mexico	586	219	−1.62	−0.38	−0.1	0.22	0.3	0.23	0.29	−45.97**
	(264)	(48)	(0.34)	(0.15)	(0.15)	(0.15)	(0.15)	(0.15)	(0.15)
France	499	17	−0.59	−0.37	0.35	0.77	0.19	0.34	0.21	−94.57*
	(256)	(62)	(0.38)	(0.25)	(0.25)	(0.25)	(0.24)	(0.24)	(0.25)
Pakistan	116	250	−0.53	0.02	0	0.06	−0.12	−0.01	−0.15	−73.2*
	(46)	(44)	(0.25)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)
Turkey	70	129	−35.23	−0.01	−0.02	−0.02	0.01	0.06	−0.04	−88.75*
	(79)	(133)	(3.75)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)
Germany	80	122	−39.19	−0.24	0.61	0.88	0.66	0.45	0.5	−139.68*
	(153)	(272)	(6.8)	(0.39)	(0.39)	(0.39)	(0.38)	(0.38)	(0.39)
Saudi Arabia	40	250	−0.41	−0.09	−0.24	−0.06	−0.15	−0.05	−0.28	−56.95*
	(14)	(37)	(0.21)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)
Bangladesh	48	250	−0.47	−0.11	−0.09	−0.09	−0.02	−0.14	−0.15	−71.67*
	(19)	(43)	(0.24)	(0.2)	(0.2)	(0.2)	(0.19)	(0.19)	(0.2)
South Africa	2	0	0.5	−0.21	0.16	−0.14	0.16	0.09	0.3	−102.88*
	(1)	(56)	(0.31)	(0.27)	(0.27)	(0.27)	(0.27)	(0.27)	(0.27)
Canada	150	132	−55.41	−0.42	−0.41	−0.23	−0.02	0.02	−0.04	−60.63**
	(164)	(119)	(3.04)	(0.18)	(0.18)	(0.18)	(0.17)	(0.17)	(0.18)
Qatar	1	1	0.16	0.2	0.04	0.1	0.11	0.01	0.18	−59.86
	(0 )	(37)	(0.2)	(0.18)	(0.18)	(0.18)	(0.17)	(0.17)	(0.18)
Colombia	69	250	−0.45	0.07	−0.03	−0.02	−0.15	−0.23	0.09	−87.21*
	(30)	(51)	(0.28)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)
Sweden	47	129	−43.7	−1.47	0.35	0.99	1.24	0.67	0.73	−116.64**
	(63)	(176)	(4.96)	(0.31)	(0.31)	(0.31)	(0.3)	(0.3)	(0.31)
Egypt	66	250	−0.36	−0.18	−0.12	−0.09	−0.52	−0.16	−0.2	−111.47*
	(34)	(64)	(0.36)	(0.29)	(0.29)	(0.29)	(0.29)	(0.29)	(0.29)
Belgium	128	66	−2.61	−0.02	−0.04	0.3	0.39	0.22	0.36	−123.1*
	(176)	(183)	(1.72)	(0.33)	(0.33)	(0.33)	(0.32)	(0.32)	(0.33)
Belarus	7	177	−2.36	−0.04	0.02	−0.1	−0.09	0.09	−0.12	−23.64***
	(6)	(94)	(1)	(0.12)	(0.12)	(0.12)	(0.12)	(0.12)	(0.12)
Argentina	26	250	−0.29	−0.65	0.04	−0.14	0.01	0.01	−0.09	−79.16*
	(11)	(47)	(0.26)	(0.21)	(0.21)	(0.21)	(0.21)	(0.21)	(0.21)
Ecuador	48	150	−9.62	0.12	−0.05	−0.05	0.26	−0.54	0.79	−165.18***
	(234)	(876)	(13.38)	(0.5)	(0.5)	(0.5)	(0.49)	(0.49)	(0.5)
Indonesia	51	250	−0.2	0.05	−0.27	−0.2	−0.28	0.03	−0.04	−74.63**
	(20)	(45)	(0.25)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)
Netherlands	147	32	−0.93	−0.56	−0.79	0.16	−0.03	−0.02	0.05	−84.25*
	(86)	(67)	(0.46)	(0.22)	(0.22)	(0.22)	(0.22)	(0.22)	(0.22)
UAE	5	133	−22.67	−0.01	0.14	0.09	0.06	0.06	−0.04	−82.18*
	(6)	(153)	(3.83)	(0.22)	(0.22)	(0.22)	(0.22)	(0.22)	(0.22)

This table uses the latest K $=$ 100 days’ (until 2020-06-26) data to fit the quartic model.

Standard errors are in parentheses below the estimates.

$\hat{\mu }$ is the estimated day of the peak, taking 2020-12-31 as day 0.

The number of * at the last column denotes the relative goodness of fit based on log likelihood, where *** indicates the model of the best fit among others.

We provide likelihood ratio test statistics $\ell$ that can be used to test the difference between the three models$;$ the critical value for the likelihood ratio test is ${\chi }_{0.95}^2=3.84$. In the past there was not much to choose between the models, for most countries. Currently, the US strongly prefers the fat-bottomed model, Brazil favours the quadratic regression, whereas the UK favours the model (4).

The table below gives $log(cas{e}_t+1)=\alpha +\gamma {|t-\mu |}^2+{\sum }_{d=1}^6{\beta }_d{D}_d$.

The table below gives $log(cas{e}_t+1)=\alpha +\gamma {|t-\mu |}^4+{\sum }_{d=1}^6{\beta }_d{D}_d$.

The table below gives $log(cas{e}_t+1)=a+bt+clog\left(t\right)+{\sum }_{d=1}^6{\beta }_d{D}_d$.

The table below gives $log(deat{h}_t+1)=\alpha +\gamma {|t-\mu |}^2+{\sum }_{d=1}^6{\beta }_d{D}_d$.

The table below gives $log(deat{h}_t+1)=\alpha +\gamma {|t-\mu |}^4+{\sum }_{d=1}^6{\beta }_d{D}_d$.

The table below gives $log(deat{h}_t+1)=a+bt+clog\left(t\right)+{\sum }_{d=1}^6{\beta }_d{D}_d$.

Table 2c.

Empirical Results of Gamma Model of Deaths with K $=$ 100.

Name	$y_{max}$	$\hat{\mu }$	$\hat{c}$	Mon	Tue	Wed	Thu	Fri	Sat	log_likelihood
USA	2512	127	31.76	−0.33	−0.24	0.24	0.26	0	0.14	−101.92**
	(2532)	(1)	(2.85)	(0.27)	(0.27)	(0.27)	(0.26)	(0.26)	(0.27)
Brazil	1055	159	26.76	−0.4	−0.31	0.2	0.1	0.18	0.08	16.49**
	(697)	(2)	(0.87)	(0.08)	(0.08)	(0.08)	(0.08)	(0.08)	(0.08)
Russia	148	154	30.35	0	−0.13	0.22	0.21	0.25	0.25	−26.6***
	(138)	(2)	(1.34)	(0.13)	(0.13)	(0.13)	(0.12)	(0.12)	(0.13)
India	395	191	18.34	0.14	0.01	0.18	0.12	0.07	0.08	−46.76***
	(623)	(10)	(1.64)	(0.15)	(0.15)	(0.15)	(0.15)	(0.15)	(0.15)
UK	854	118	27.57	−0.69	−0.61	0.29	0.19	0.07	0.14	−75.29***
	(505)	(1)	(2.19)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)
Peru	198	156	25.09	−0.29	−0.81	−0.31	0.01	−0.06	−0.1	−117.66***
	(423)	(6)	(3.34)	(0.31)	(0.31)	(0.31)	(0.31)	(0.31)	(0.31)
Chile	NaN	−101	2.64	0.13	−0.47	−0.62	−0.09	−0.07	0.02	−96.54***
	(NaN)	(190)	(2.71)	(0.25)	(0.25)	(0.25)	(0.25)	(0.25)	(0.25)
Spain	1325	94	21.65	0.66	0.81	0.17	0.2	0.68	0.19	−151.52***
	(261)	(5)	(4.69)	(0.44)	(0.44)	(0.43)	(0.43)	(0.44)	(0.44)
Italy	857	78	7.55	−0.37	−0.29	−0.17	−0.09	−0.07	−0.05	12.87***
	(355)	(3)	(0.91)	(0.08)	(0.08)	(0.08)	(0.08)	(0.08)	(0.08)
Iran	71	131	−9.34	−0.01	0.04	0.03	0.07	0.05	−0.37	−73.89**
	(67)	(4)	(2.16)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)
Mexico	551	175	24.96	−0.38	−0.1	0.23	0.29	0.23	0.28	−47.77***
	(778)	(5)	(1.66)	(0.16)	(0.16)	(0.16)	(0.15)	(0.15)	(0.16)
France	417	103	21.52	−0.38	0.34	0.75	0.22	0.36	0.22	−75.8***
	(72)	(2)	(2.2)	(0.21)	(0.21)	(0.21)	(0.2)	(0.2)	(0.21)
Pakistan	336	284	9.59	0.02	0	0.06	−0.14	−0.03	−0.15	−69.67***
	(995)	(81)	(2.07)	(0.19)	(0.19)	(0.19)	(0.19)	(0.19)	(0.19)
Turkey	92	120	26.33	0	−0.01	0	−0.01	0.05	−0.05	−71.7***
	(58)	(1)	(2.11)	(0.2)	(0.2)	(0.2)	(0.19)	(0.19)	(0.2)
Germany	111	113	29.33	−0.24	0.6	0.87	0.63	0.42	0.5	−122.37***
	(75)	(2)	(3.5)	(0.33)	(0.33)	(0.33)	(0.32)	(0.32)	(0.33)
Saudi Arabia	NaN	−371	3.29	−0.09	−0.24	−0.06	−0.18	−0.08	−0.28	−42.3***
	(NaN)	(715)	(1.57)	(0.15)	(0.15)	(0.15)	(0.14)	(0.14)	(0.15)
Bangladesh	15240	1098	5.54	−0.12	−0.09	−0.09	−0.05	−0.17	−0.15	−63.15 **
	(84165)	(3050)	(1.94)	(0.18)	(0.18)	(0.18)	(0.18)	(0.18)	(0.18)
South Africa	0	19	−1.11	−0.22	0.16	−0.15	0.22	0.14	0.31	−83.73***
	(2)	(35)	(2.38)	(0.22)	(0.22)	(0.22)	(0.22)	(0.22)	(0.22)
Canada	216	129	41.48	−0.41	−0.4	−0.23	−0.06	−0.02	−0.05	−50.83***
	(153)	(1)	(1.71)	(0.16)	(0.16)	(0.16)	(0.16)	(0.16)	(0.16)
Qatar	1	95	−5.7	0.2	0.04	0.1	0.1	0.01	0.18	−58.99***
	(0 )	(8)	(1.86)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)	(0.17)
Colombia	530	412	6.69	0.07	−0.03	−0.02	−0.18	−0.26	0.09	−83.52***
	(2282)	(346)	(2.38)	(0.22)	(0.22)	(0.22)	(0.22)	(0.22)	(0.22)
Sweden	63	123	30.12	−1.46	0.35	0.99	1.21	0.63	0.72	−114.89***
	(58)	(1)	(3.25)	(0.3)	(0.3)	(0.3)	(0.3)	(0.3)	(0.3)
Egypt	NaN	−219	2.44	−0.18	−0.12	−0.1	−0.55	−0.19	−0.2	−107.73***
	(NaN)	(757)	(3.03)	(0.28)	(0.28)	(0.28)	(0.28)	(0.28)	(0.28)
Belgium	169	112	35.51	−0.03	−0.07	0.26	0.45	0.26	0.37	−87.33***
	(74)	(1)	(2.47)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)	(0.23)
Belarus	7	150	12.48	−0.04	0.02	−0.1	−0.09	0.1	−0.12	−24.4**
	(6)	(4)	(1.32)	(0.12)	(0.12)	(0.12)	(0.12)	(0.12)	(0.12)
Argentina	85	386	4.41	−0.65	0.03	−0.14	−0.01	−0.01	−0.09	−77.38***
	(330)	(421)	(2.23)	(0.21)	(0.21)	(0.21)	(0.21)	(0.21)	(0.21)
Ecuador	55	141	16.67	0.12	−0.04	−0.03	0.26	−0.53	0.79	−165.51**
	(97)	(8)	(5.39)	(0.5)	(0.5)	(0.5)	(0.5)	(0.5)	(0.5)
Indonesia	66	252	4.06	0.05	−0.27	−0.2	−0.28	0.02	−0.04	−74.16***
	(179)	(142)	(2.16)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)	(0.2)
Netherlands	137	103	23.39	−0.57	−0.8	0.14	−0.01	0	0.05	−61.35***
	(22)	(2)	(1.9)	(0.18)	(0.18)	(0.18)	(0.18)	(0.18)	(0.18)
UAE	6	129	19.69	−0.01	0.15	0.1	0.05	0.05	−0.05	−71.11***
	(5)	(2)	(2.1)	(0.2)	(0.2)	(0.2)	(0.19)	(0.19)	(0.2)

This table uses the latest K $=$ 100 days’ data (until 2020-06-26) to fit the Gamma model.

Standard errors are below the estimates.

$\hat{\mu }$ is the estimated day of the peak, taking 2019-12-31 as day 0.

The number of * at the last column denotes the relative goodness of fit based on log likelihood, where *** indicates the model of the best fit among others.

6.2. Prediction of the future

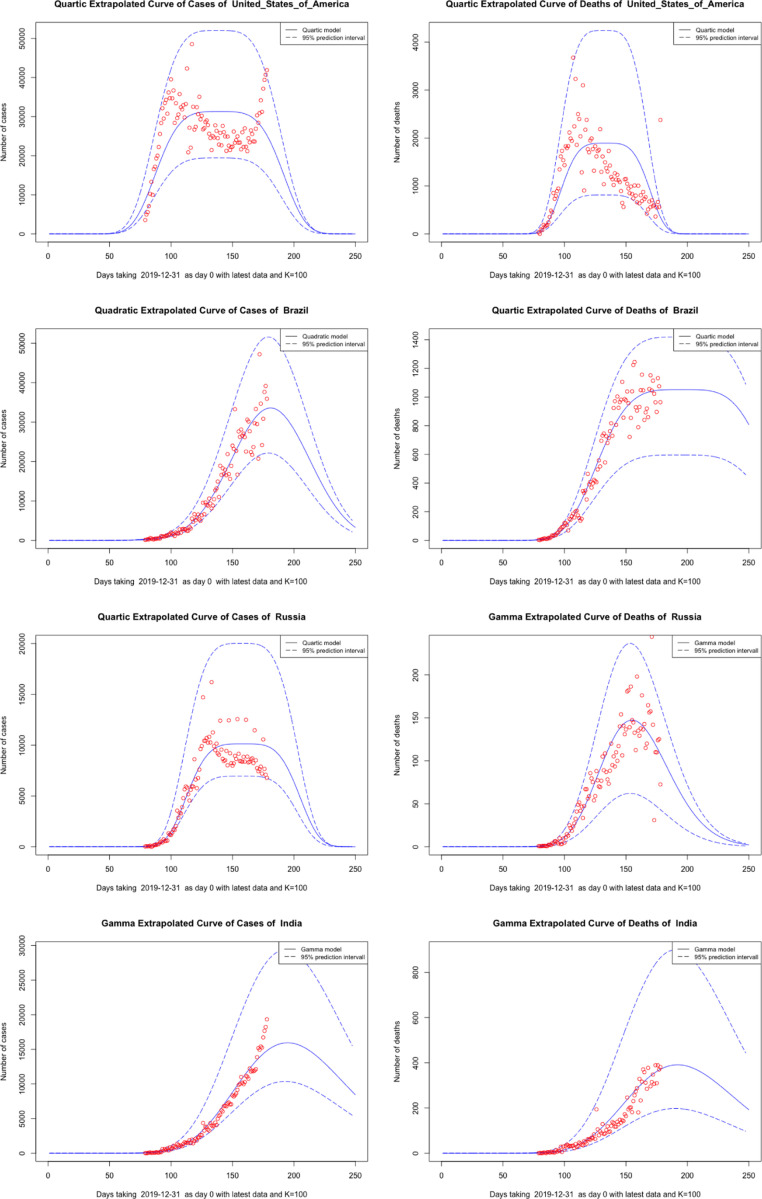
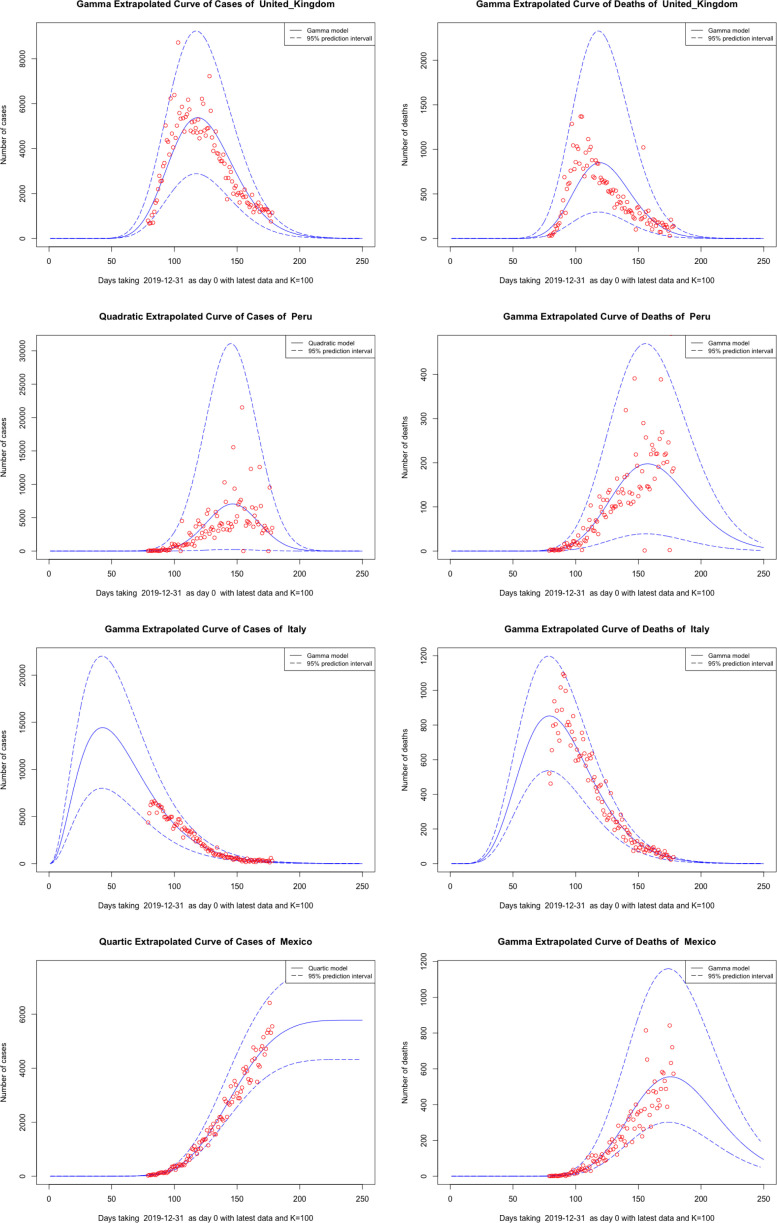
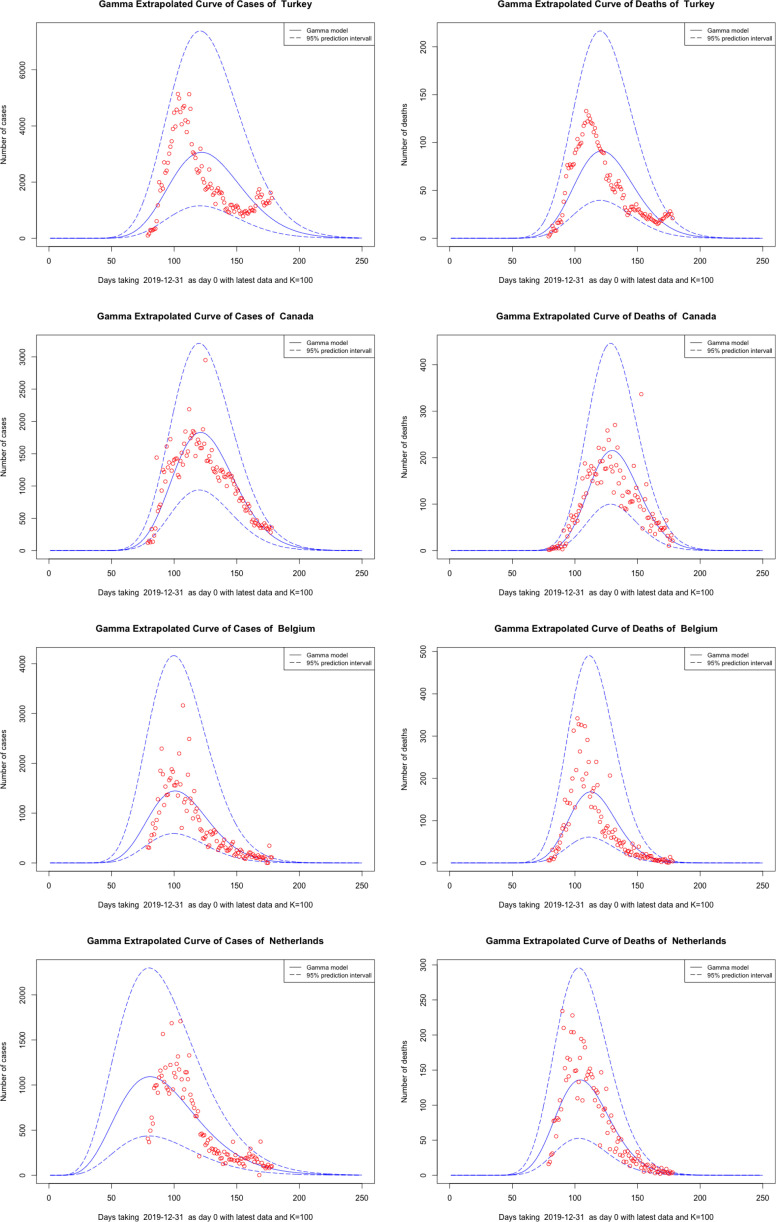
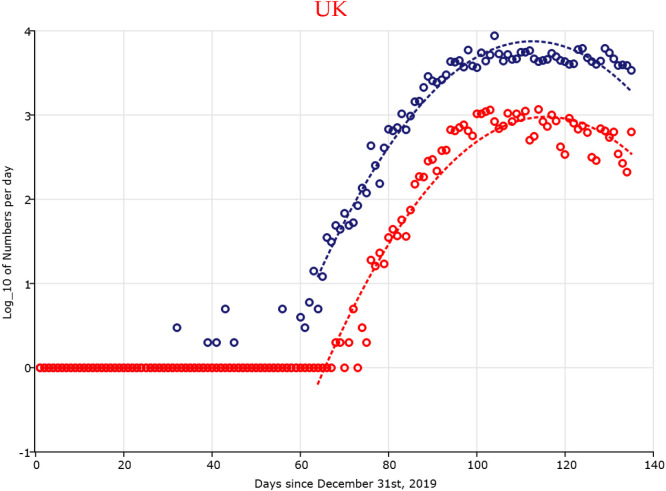
We present the estimated curves along with their 95% prediction intervals for selected countries in the graphs below. The estimated curve in solid blue, confidence intervals in dotted blue, and data points in red. The extrapolation curve is a scaled density function as mandated by our curve models (see Fig. 1, Fig. 2, Fig. 3).

Fig. 1.

Plots of cases and deaths of the best models of selected countries Part1.

Fig. 2.

Plots of cases and deaths of the best models of selected countries Part2.

Fig. 3.

Plots of cases and deaths of the best models of selected countries Part3.

We estimate the time that it has taken for selected countries to pass from peak to trough, where trough is defined as the estimated peak number of new cases divided by 10. Admittedly, this is not a very exacting standard, but the advantage is that there are several countries that have effectively satisfied this. An empirical estimator is just based on the first passage time

$${\widehat{t}}_{TP}=\underset{t>{\tau }_{max}}{min}\left\{{log}_{10}\left(y_{{\tau }_{max}}\right)-{log}_{10}\left(y_t\right)\ge 1\right\},$$

where ${log}_{10}\left(10\right)\simeq 1$ and ${\tau }_{max}=arg{max}_s{log}_{10}\left(y_s\right)$. For New Zealand, Australia, and Austria, ${\widehat{t}}_{TP}=14$, for South Korea ${\widehat{t}}_{TP}=15$, for China ${\widehat{t}}_{TP}=19$, for Norway ${\widehat{t}}_{TP}=21$, for Israel ${\widehat{t}}_{TP}=21,$ while for Switzerland ${\widehat{t}}_{TP}=31$. These estimates are rather rough and in each case there was some bounce back. Incidentally, looking at these successful countries’ trajectories, there seems to be a fairly symmetric curve around the peak, see below the case of New Zealand.

We can also estimate the passage time from the model for countries that have not yet passed the threshold by computing

$$min\left\{t:m\left({\tau }_{max}\right)-m({\tau }_{max}+t)\ge 1\right\},$$

This is equivalent to $(t-\mu )\ge \sqrt{-1∕\gamma }$. For the UK, this gives around 28 days based on the latest estimates, although the confidence interval is rather wide.

7. Model tests and robustness

7.1. One step ahead prediction

The choice of K.

This section illustrates the selection of the window width $K$. Let today (2020-06-26) be the day 0, $K$ ranges from 14 to 100 and $L$ is the length of the test data. Due to the missing data, we only list 27 out of top 30 countries. We compute the one step ahead forecast $\hat{m}(1-l;K)$ of $log{y}_{1-l}$ based on the data from $\{-l,-l-1,\dots ,-l-K\}$ for $l=1,2,\dots ,L$ and calculate:

$$\hat{Q}(K;L)=\frac{1}{L}\sum _1^L|(log{y}_{i-l})-\hat{m}(1-l;K)|.$$

And we show the empirical results for both daily infections and fatalities below. Although $K$=$100$ is not the best choice for all countries with top cases, it still works well for most of them.

7.2. Residual properties

In this section we look at the properties of the residuals from the trend fitting. The model assumptions do not exclude autocorrelation or heteroskedasticity but there is limited scope to improve efficiency by exploiting these properties. They would however affect standard errors and might suggest alternative short term predictors (see Table 5, Table 6).

Table 5.

One Step Ahead Prediction of Cases.

	Predicted Cases			Reported Cases	$t$-statistics
Name	1a	1b	1c		1a	1b	1c
USA	20555	21768	19793	40949	−1.8	−0.79	−2.04
Brazil	35116	35861	40111	39483	−0.55	−0.08	−0.05
Russia	3970	10810	5149	7113	−1.13	0.21	−0.74
India	11443	12221	12610	17296	−1.38	−0.27	−1.23
UK	568	437	624	1118	−2	−1.08	−2.1
Peru	2268	6038	3203	3913	−0.64	0.02	−0.38
Chile	9787	6095	10446	4648	1.69	0.06	1.85
Spain	237	474	212	400	−1.29	0.01	−1.52
Italy	171	102	164	296	−1.89	−0.05	−2.09
Iran	3973	3944	3782	2595	0.34	0.01	0.29
Mexico	4722	5363	5412	6104	−1.26	−0.16	−0.72
France	421	607	377	0	8.48	1.44	8.32
Pakistan	8678	6818	9694	2775	0.66	0.07	0.75
Turkey	631	691	610	1458	−1.41	−0.56	−1.58
Germany	329	391	282	477	−0.59	−0.07	−0.76
Saudi Arabia	3391	4314	3996	3372	−0.18	0.04	0.04
Bangladesh	3138	4618	4169	3946	−0.58	−0.01	−0.2
South Africa	8717	19777	8774	6579	0.39	0.03	0.42
Canada	194	136	223	369	−1.9	−1.24	−1.77
Qatar	844	1791	1131	1060	−0.57	0.22	−0.04
Colombia	1334	937	1390	3486	−1.3	−0.29	−1.26
Sweden	454	297	525	1566	−1.34	−0.71	−1.22
Egypt	1830	1586	2165	2989	−0.62	−0.12	−0.49
Belgium	32	32	35	109	−1.87	−0.08	−1.79
Belarus	523	1819	749	437	−0.2	0.25	0.11
Argentina	743	1275	783	2606	−1.03	−0.01	−1
Indonesia	1088	1025	1094	1178	−0.29	−0.1	−0.28
Netherlands	77	61	75	110	−0.74	−0.02	−0.78
UAE	325	967	419	430	−0.58	0.11	−0.35
${\tau }_{PY}$					1.18	−0.39	1.43

This table presents the results of one step ahead prediction of new cases for 2020-06-26 along with the reported values and $t$-statistics of the prediction. All three models are applied. K $=$ 100 and ${\tau }_{PY}$ is the joint prediction test statistics of all listed countries as Pesaran and Yamagata (2012), see Appendix.

Table 6.

One Step Ahead Prediction of Deaths.

	Predicted Deaths			Reported Deaths	$t$-statistics
Name	2a	2b	2c		2a	2b	2c
USA	214	194	241	2437	−3.31	−1.64	−3.55
Brazil	859	1259	1032	1141	−1.08	0.1	−0.52
Russia	113	196	147	92	0.44	0.59	1.23
India	350	377	395	407	−0.55	−0.08	−0.28
UK	54	36	59	149	−1.8	−1.07	−1.84
Peru	120	183	148	175	−0.64	−0.04	−0.39
Chile	193	94	193	172	−0.09	−0.18	−0.09
Italy	24	19	25	34	−1.39	−0.04	−1.31
Iran	129	157	115	134	−0.2	0.05	−0.42
Mexico	579	691	680	718	−0.66	−0.07	−0.31
France	10	12	10	21	−1.34	−0.04	−1.36
Pakistan	134	101	142	59	1.36	0.13	1.5
Turkey	8	8	8	21	−1.68	−0.7	−1.84
Germany	3	1	3	21	−1.99	−1.15	−2.02
Saudi Arabia	54	32	52	41	0.47	−0.12	0.41
Bangladesh	51	34	55	39	0.35	−0.08	0.48
South Africa	146	355	147	87	0.62	0.03	0.64
Canada	15	14	20	20	−0.77	−0.34	−0.21
Qatar	4	4	4	2	0.83	0.02	0.71
Colombia	53	41	54	163	−2.02	−0.41	−2.04
Sweden	8	5	9	21	−1.39	−0.77	−1.25
Egypt	63	43	64	168	−1.5	−0.33	−1.49
Belgium	1	0	1	4	−1.49	−1.04	−1.48
Belarus	5	6	5	5	−0.11	0.15	0.08
Argentina	27	22	26	39	−0.84	−0.2	−0.89
Indonesia	53	48	51	47	−0.04	−0.05	−0.08
Netherlands	1	1	1	3	−1.66	−0.06	−1.64
UAE	1	1	1	1	−0.57	−0.07	−0.26
${\tau }_{PY}$					0.38	−0.46	0.58

This table presents the results of one step ahead prediction of new deaths for 2020-06-26 along with the reported values and $t$-statistics of the prediction. All three models are applied. K $=$ 100 and ${\tau }_{PY}$ is the joint prediction test statistics of all listed countries as Pesaran and Yamagata (2012), see Appendix.

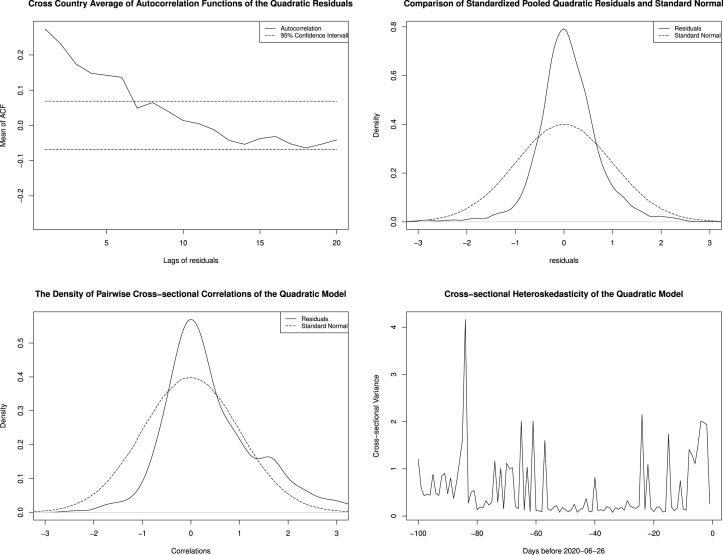
Autocorrelation.

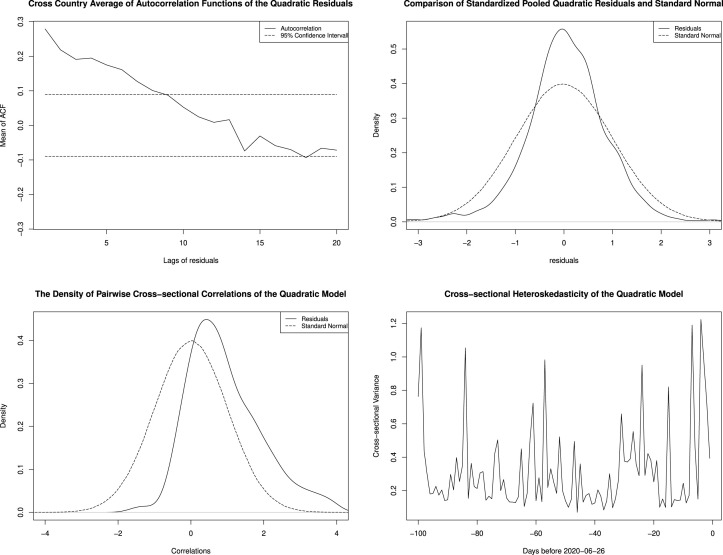
We first estimate the autocorrelation function of $\{{\widehat{ϵ}}_{it},t=1,2,\dots ,K\}$ denoted ${\hat{\rho }}_i\left(j\right)$, $j=1,2,\dots ,J$ for all the available countries that have at least 100 observations, currently, $n=150$ countries. We take $J=21$ to allow for long lag effects, which might be predicted for deaths by epidemiological models. We calculated the estimated mean value of ${\hat{\rho }}_i\left(j\right)$ across countries along with standard errors that take account of the cross-sectional averaging but allow for cross sectional correlation as Linton (2020). The pattern of autocorrelation is similar in both cases and deaths for all three models, the weak positive correlation at low lags that declines across horizon to negative autocorrelation after around ten days, and then remains a very low level closed to zero.

Distributional properties.

We next show the kernel density estimate of the pooled standardized residuals of both cases and death of all three models, which appears not far from a Gaussian shape, at least, roughly symmetrical.

Cross-sectional correlation.

We analysis cross-sectional correlation by computing the $n\times n$ pairwise correlation matrix of time series residuals. We compare the plot of the pairwise correlation density and normal distribution. For cases, the mean value of the pairwise correlation is very close to zero and distributed similarly to normal distribution for all three models. However, for deaths, the mean value is slightly positive, such as 0.18 for the quadratic model (2a), 0.09 for the quartic model (2b) and 0.13 for the Gamma model (2c).

Heteroskedasticity.

We look at time-varying heteroskedasticity in the residuals, specifically we graph the time series of mean squared residuals ${\sum }_{i=1}^n{\widehat{ϵ}}_{it}^2∕n$. It seems that there are limited spikes for residuals of cases models while more outliers of deaths models in the cross country variability of the error terms. However, it moves, generally speaking, in a modest range.

We show the results of all four residual properties of the quadratic model of cases (1a) in Fig. 4 and deaths (1b) in Fig. 5.

Fig. 4.

Residual properties of quadratic model of cases.

Fig. 5.

Residual properties of quadratic model of deaths.

8. Combining case and fatality models

Total fatalities should be a fraction of the total cases reported, and fatalities should follow cases, at least individually. For this reason we consider the following model, which imposes that the fatality curve is a delayed and shifted (because this is the log of cases) version of the case curve. Let $y_{it}^d$ denote deaths and $y_{it}^c$ denote cases, where:

$$log\left(y_{it}^d\right)=m_i^d\left(t\right)+{\epsilon }_{it}^d,$$

$$log\left(y_{it}^c\right)=m_i^c\left(t\right)+{\epsilon }_{it}^c.$$

We suppose that for some ${\theta }_i<0$ and $k_i\ge 0$

$$m_i^d\left(t\right)={\theta }_i+m_i^c(t-k),$$ (11)

which is a special case of the model considered by Hardle and Marron (1990). This imposes restrictions across the coefficients of the two quadratic equations. The turning point for $m^d$ occurs $k$ periods after the turning point for $m^c$, that is, ${\alpha }^d={\alpha }^c+\theta$ and ${\mu }^d={\mu }^c+k$. The only equality restriction is that the $\gamma$ parameter is the same across both cases and deaths. We can test this by comparing the statistic

$$\frac{{\widehat{\gamma }}^d-{\widehat{\gamma }}^c}{\sqrt{\widehat{\mathrm{var}}({\widehat{\gamma }}^d-{\widehat{\gamma }}^c)}}$$ (12)

with the standard normal critical values. Regarding the inequality restrictions ${\alpha }^d-{\alpha }^c<0$ and ${\mu }^d-{\mu }^c>0$, these can also be tested separately by similar $t$-statistics with one-sided critical values. Specifically, we consider

$$\frac{{\hat{\mu }}^c-{\hat{\mu }}^d}{\sqrt{\mathrm{var}({\hat{\mu }}^c-{\hat{\mu }}^d)}}.$$

The tests results are presented below in two tables. The model does not fare well on either count (although the significance mostly disappears when HAC standard errors are used)

We estimate the constrained model as described in the Appendix, the results are shown below graphically. For the UK the results look quite plausible (see Table 7, Table 8).

Table 7.

The Hypotheses Test On ${\hat{\gamma }}_{case}={\hat{\gamma }}_{death}$ of Top 30 Countries Until 2020-06-26 and K $=$ 100.

countryname	${\hat{\gamma }}_{case}$	${\hat{\gamma }}_{death}$	s.e($\Delta \hat{\gamma }$)	$t$-stat
UAS	−2.1263	−9.3089	0.731	9.826
Brazil	−4.7037	−8.4341	0.334	11.169
Russia	−12.7193	−9.7444	0.764	−3.894
India	−5.7853	−5.638	0.478	−0.308
UK	−6.4149	−8.1086	0.716	2.366
Peru	−11.06	−7.9733	0.95	−3.249
Chile	−2.013	−0.7313	0.888	−1.443
Spain	1.6029	−8.809	1.806	5.765
Italy	−0.4951	−2.1971	0.406	4.192
Iran	1.303	3.3044	0.566	−3.536
Mexico	−5.3239	−7.6995	0.567	4.19
France	−0.1307	−6.2251	1.189	5.126
Pakistan	−3.2801	−3.1389	1.089	−0.13
Turkey	−4.7904	−7.6543	0.355	8.067
Germany	2.8744	−8.622	0.794	14.479
Saudi Arabia	−5.9082	−0.8122	0.873	−5.837
Bangladesh	−10.9014	−1.8296	0.833	−10.891
South Africa	0.8659	0.3374	0.988	0.535
Canada	−7.3964	−13.0866	0.635	8.961
Qatar	−10.7066	1.8031	0.893	−14.009
Colombia	−1.4845	−1.8614	0.757	0.498
Sweden	−4.3263	−8.8669	1.446	3.14
Egypt	−3.6688	−0.6793	1.033	−2.894
Belgium	−5.3037	−10.6704	0.828	6.482
Belarus	−14.2614	−3.9488	1.462	−7.054
Argentina	0.8656	−1.0505	1.975	0.97
Ecuador	−2.0516	−5.2959	1.792	1.81
Indonesia	−2.7413	−1.0625	0.675	−2.487
Netherlands	−1.5925	−6.9629	0.762	7.048
UAE	−12.1046	−6.3816	1.561	−3.666

Table 8.

The Hypotheses Test On ${\hat{\mu }}_{case}<{\hat{\mu }}_{death}$ of Top 30 Countries Until 2020-06-26 and K $=$ 100.

countryname	${\hat{\mu }}_{case}$	${\hat{\mu }}_{death}$	s.e($\Delta \hat{\mu }$)	$t$-stat
USA	−0.389	−0.4642	0.03	2.507
Brazil	0.0396	−0.2182	0.037	6.968
Russia	−0.3254	−0.2524	0.016	−4.563
India	−0.0311	−0.0364	0.041	0.129
UK	−0.5664	−0.5593	0.012	−0.592
Peru	−0.3159	−0.2354	0.018	−4.472
Chile	0.5982	2.6875	3.871	−0.54
Spain	0.6927	−0.8921	0.443	3.577
Italy	−4.3904	−1.2917	3.126	−0.991
Iran	−0.7841	−0.4399	0.255	−1.35
Mexico	−0.0593	−0.1186	0.03	1.977
France	−12.2877	−0.7758	102.432	−0.112
Pakistan	0.272	0.1937	0.264	0.297
Turkey	−0.5309	−0.5346	0.013	0.285
Germany	0.0299	−0.6219	0.201	3.243
Saudi Arabia	−0.1377	1.6637	1.348	−1.336
Bangladesh	−0.1499	0.5781	0.348	−2.092
South Africa	−3.4868	−7.7151	16.794	0.252
Canada	−0.5359	−0.4478	0.009	−9.789
Qatar	−0.2855	−0.8835	0.132	4.53
Colombia	0.8555	0.5091	0.74	0.468
Sweden	−0.4535	−0.5077	0.043	1.26
Egypt	0.0942	1.7521	3.007	−0.551
Belgium	−0.8177	−0.642	0.054	−3.254
Belarus	−0.3293	−0.273	0.031	−1.816
Argentina	−2.4996	0.6446	4.894	−0.642
Ecuador	−0.3769	−0.3477	0.178	−0.164
Indonesia	0.0011	0.2768	0.467	−0.59
Netherlands	−1.3903	−0.7647	0.45	−1.39
UAE	−0.3542	−0.4502	0.027	3.556

We calculate the ratio of expected total deaths to expected total cases (the fatality ratio) by country as

$$Fr=exp({\alpha }^d-{\alpha }^c)=exp\left(a^d-a^c-\frac{{\left(b^d\right)}^2}{c}+\frac{{\left(b^c\right)}^2}{c}\right).$$

At the time of writing, UK has 0.136, France has 0.170, Italy has $0.132$, Spain has 0.101, Germany has 0.045, Australia has 0.052, and USA has 0.051. This may be saying more about the disparity between countries in testing rather than the quality of treatment.

Epidemiological models often build in the effect of lagged cases on deaths, reflecting the natural causal ordering of cases on deaths. We consider an alternative model that combines that feature with our quadratic regression. Suppose that the log death regression is a weighted delay of the log cases regression

$$m^d\left(t\right)={\int }_0^{\infty }{w}_s{m}^c(t-s)ds.$$ (13)

In principle, if $m^c,m^d$ were both nonparametric and estimable one might be able to estimate the function $w$ by sieve expansion, using the methods described in inter alia (Chen, 2007) and (Chen and Christensen, 2015). We take a parametric approach where both $m$ functions are quadratic. This is possible provided

$$a^d+b^{d}t+c^d{t}^2={\int }_0^{\infty }{w}_s\left(a^c+b^c(t-s)+c^c{(t-s)}^2\right)ds={\int }_0^{\infty }{w}_s\left(a^c+b^{c}t+c^c{t}^2\right)ds-{\int }_0^{\infty }{w}_{s}s\left(b^c+2c^{c}t\right)ds+c^c{\int }_0^{\infty }{w}_s{s}^{2}ds=a^c{\int }_0^{\infty }{w}_{s}ds-b^c{\int }_0^{\infty }{w}_{s}sds+c^c{\int }_0^{\infty }{w}_s{s}^{2}ds+t\left(b^c{\int }_0^{\infty }{w}_{s}ds-2c^c{\int }_0^{\infty }{w}_{s}sds\right)+t^2{c}^c{\int }_0^{\infty }{w}_{s}ds.$$

We suppose that $w$ is a constant $\psi$ times the density of a normal random variable whose mean is $\vartheta$ and whose variance is one. This shape seems plausible since it implies a peak loading some days previous. We need the constants ${\phi }_j={\int }_0^{\infty }{s}^j{w}_{s}ds$. Suppose that ${\phi }_j\left(\theta \right)$, where $\theta =(\psi ,\vartheta )\in {\mathbb{R}}^2;$ these constants are obtainable in closed form as integrals of normal densities, (Barr and Sherrill, 1999):

$${\int }_0^{\infty }{w}_{s}ds=\psi {\int }_{-\vartheta }^{\infty }\varphi \left(s\right)ds=\psi \left(1-\Phi (-\vartheta )\right)=\psi \Phi \left(\vartheta \right){\int }_0^{\infty }{w}_{s}sds=\psi {\int }_{-\vartheta }^{\infty }\varphi \left(s\right)sds=\psi E\left(Z\right|Z>-\vartheta )Pr(Z>-\vartheta )=\psi \varphi \left(\vartheta \right)$$

$${\int }_0^{\infty }{w}_s{s}^{2}ds=\psi {\int }_{-\vartheta }^{\infty }\varphi \left(s\right)s^{2}ds=\psi E\left(Z^2\right|Z>-\vartheta )Pr(Z>-\vartheta )=\psi \frac{1}{2}\underset{{\vartheta }^2}{\overset{\infty }{\int }}\frac{1}{2^{3∕2}\Gamma (3∕2)}{u}^{1∕2}{e}^{-u∕2}du=\psi \frac{1}{2}\left(1-F_{{\chi }^2\left(3\right)}\left({\vartheta }^2\right)\right),$$

where $\varphi ,\Phi$ are the density function and c.d.f. of a standard normal random variable. This expresses the parameters of the death curve uniquely as a function of the parameters of the case curve and the two parameters $\psi ,\vartheta$. In particular, the location of the death peak is related to the case peak as follows

$${\mu }^d=\frac{-b^d}{2c^d}=-\frac{b^c{\int }_0^{\infty }{w}_{s}ds-2c^c{\int }_0^{\infty }{w}_{s}sds}{2c^c{\int }_0^{\infty }{w}_{s}ds}=\frac{-b^c}{2c^c}+\frac{{\int }_0^{\infty }{w}_{s}sds}{{\int }_0^{\infty }{w}_{s}ds}=\frac{-b^c}{2c^c}+\frac{\varphi \left(\vartheta \right)}{\Phi \left(\vartheta \right)}={\mu }^c+\lambda \left(\vartheta \right).$$

Since the Heckman correction $\lambda \left(\vartheta \right)\ge 0$, this implies that ${\mu }^d\ge {\mu }^c$ as for the previous model. This equation allows the determination of $\vartheta$ because the function $\lambda \left(\vartheta \right)=\varphi \left(\vartheta \right)∕\Phi \left(\vartheta \right)>0$ is monotonic decreasing. That is, $\vartheta ={\lambda }^{-1}({\mu }^d-{\mu }^c)$. Whence, $\psi =c^d∕{\phi }_0\left(\vartheta \right)c^c$. It follows that the quadratic model for both cases and deaths is compatible with the posited relation between deaths and cases.

Regarding the peak of the two curves, we have

$$m_{max}^d=a^d-\frac{{\left(b^d\right)}^2}{4c^d}=\psi \left[{\phi }_0{m}_{max}^c+c^c\left({\phi }_2-\frac{{\phi }_1^2}{{\phi }_0}\right)\right].$$

By the Cauchy–Schwarz inequality, ${\phi }_2-\frac{{\phi }_1^2}{{\phi }_0}\ge 0$ so that with negative $c^c$ we have $m_{max}^d\le \psi {\phi }_0{m}_{max}^c$. This model imposes exactly one restriction like the shape invariant model but the nature of the restrictions are quite different. We plan to investigate this model in the sequel.

9. Concluding remarks

There are many challenges in modelling the COVID data. Countries differ widely in their reporting methods and standards, which makes the data noisy and sometimes very unreliable. Our model does not impose any restrictions across countries for the evolution of the epidemic and we find there are very large differences across countries in all the key parameters. Another complication is due to different interventions implemented in different countries at different times. Actually, most European countries introduced lockdown measures within the month of March 2020 so that whatever effects these measures have had will be fully reflected in the subsequent data. Our model allows us to estimate future turning points of the curves without imposing much structure. It also allows the forecasting of total number of cases, although the confidence intervals around such estimates are extremely large when proper attention is given to parameter uncertainty.

The one day ahead forecasting record of our model has been quite good, discounting the problems arising from late and incorrect reporting of data. The main source of forecasting error was late reporting. On the other hand, longer term forecasting has proved more challenging. We have consistently underestimated the likely total number of cases and deaths for the UK and US.

We have some specific findings from the empirical work that is worth commenting. First, the shapes of the curves appear to be quite different across countries. Second, the timing of peak deaths in some countries precedes the peak of cases, which seems to be against the epidemiological models. This may be because testing capacity has increased a lot and treatment has improved. Third, the characteristics of endgame countries vary a lot: being a small island seems to help, but countries as diverse as Luxembourg, China, South Korea, Israel, Switzerland have also reached the endgame relatively quickly. There are also differences across countries in terms of the ratios of deaths to cases. Part of this is due to how much testing is done (USA) and different death definitions (Russia), but there must be more factors at play such as demographics, lifestyle choices and social norms.

The models we have considered impose a single peak, although when we use a rolling window analysis, a second peak will be detected from the updated sample. We may allow for multiple peaks in a global model by taking higher order polynomial time trends. For example, quartic polynomials allow two peaks. We may parameterize this explicitly as the double peak model

$$m\left(t\right)=\alpha -\gamma {\left(t-{\mu }_1\right)}^2\left({\left(t-{\mu }_2\right)}^2+\delta \right)$$

has twin peaks at ${\mu }_1$ and ${\mu }_2$ with the difference in peak heights given by $\gamma \delta {\left({\mu }_2-{\mu }_1\right)}^2$. Using this model we have found that South Korea and China and Portugal show signs of a second peak, although the height of this second peak is an order of magnitude lower than the first round.

Appendix.

A.1. Missing data

In all the datasources we have worked with there are sometimes clearly “erroneous” data, such as negative values. Health agencies sometimes report negative values to correct earlier mistakes, and they often do not break down the corrections by date rather just post a single correction. For example, on 21/05/2020 the UK posted — 515 new cases, while on 03/07/2020 they posted — 29726. This was accompanied by the statement

We have updated the methodology of reporting positive cases, to remove duplicates within and across pillars 1 and 2, to ensure that a person who tests positive is only counted once. Methodologies between nations differ and we will be making future revisions to align approaches as much as possible across the 4 nations. Due to this change, and a revision of historical data in pillar 1, the cumulative total for positive cases is 30,302 lower than if you added the daily figure to yesterday’s total. We will revise the methodology note explaining this in more detail in due course

We take the following steps to adjust our estimation for these data issues. Suppose that at dates $t_1,\dots ,t_r$, the outcome variable is negative for country $i$. We then exclude $y_{i{t}_1},\dots ,y_{i{t}_r}$ and estimate the model using the data excluding these observations. We then impute the missing observations by

$${\widehat{y}}_{i{t}_s}=exp\left(\widehat{m}\left(t_s\right)\right){\widehat{\kappa }}_0.$$ (14)

Then we take the original negative values and the imputed ones $y_{i{t}_s}-{\widehat{y}}_{i{t}_s}$ and redistribute them to all the observations $\{y_{it},t\le t_s\}$ equally. Finally we reestimate the model with the full sample reflecting the level shift(s). We have also carried out quantile regressions instead, which provides some robustness to missrecording. The results are quite similar to the least squares ones.

A.2. Standard errors

Here, we consider standard errors for a regression function of the form $m\left(t\right)=\alpha +\gamma {|t-\mu |}^{\lambda }+{\sum }_{j=1}^6{\beta }_j{D}_{jt}$, where $\mu$ is the location of the peak and $\lambda >1$ is a known parameter that measures the type of peak, while $D_{jt}$ are day of the week dummies. We let $\theta ={(\alpha ,\gamma ,\mu ,{\beta }^{{}^{⊺}})}^{{}^{⊺}}$, where $\beta ={({\beta }_1,\dots ,{\beta }_6)}^{{}^{⊺}}$, and let $\widehat{\theta }$ minimize

$$Q_K\left(\theta \right)=\frac{1}{K}\sum _{t=1}^K{\left(y_t-\alpha -\gamma {|t-\mu |}^{\lambda }-\sum _{j=1}^6{\beta }_j{D}_{jt}\right)}^2.$$

In fact we solve this in two steps: for given $\mu$, ${(\alpha ,\gamma ,{\beta }^{{}^{⊺}})}^{{}^{⊺}}$ can be found by closed form OLS estimation, we then do grid search over $\mu$. By standard theory for profile likelihood, this procedure is equivalent to the MLE.

The score function components are

$$\frac{\partial Q_K\left(\theta \right)}{\partial \alpha }=\frac{1}{K}\sum _{t=1}^K\left(y_t-\alpha -\gamma {|t-\mu |}^{\lambda }-\sum _{j=1}^6{\beta }_j{D}_{jt}\right)$$

$$\frac{\partial Q_K\left(\theta \right)}{\partial \gamma }=\frac{1}{K}\sum _{t=1}^K\left(y_t-\alpha -\gamma {|t-\mu |}^{\lambda }-\sum _{j=1}^6{\beta }_j{D}_{jt}\right){|t-\mu |}^{\lambda }$$

$$\frac{\partial Q_K\left(\theta \right)}{\partial \mu }=\frac{1}{K}\sum _{t=1}^K\left(y_t-\alpha -\gamma {|t-\mu |}^{\lambda }-\sum _{j=1}^6{\beta }_j{D}_{jt}\right)\lambda \gamma {|t-\mu |}^{\lambda -1}.$$

$$\frac{\partial Q_K\left(\theta \right)}{\partial \beta }=\frac{1}{K}\sum _{t=1}^K\left(y_t-\alpha -\gamma {|t-\mu |}^{\lambda }-\sum _{j=1}^6{\beta }_j{D}_{jt}\right)D_t,$$

where $D_t={(D_{1t},\dots ,D_{6t})}^{{}^{⊺}}$. We can drop the constant term $\lambda \gamma$ from the score for $\mu$ (assuming that $\gamma \ne 0$). Define the $K\times 9$ data matrix

$$X={\left(\begin{array}{cccccc}\hfill 1\hfill & \hfill {|t_i-\widehat{\mu }|}^{\lambda }\hfill & \hfill {|t_i-\widehat{\mu }|}^{\lambda -1}\hfill & \hfill D_{1t}\hfill & \hfill \cdots \hfill & \hfill D_{6t}\hfill \end{array}\right)}_{i=1}^K$$

$$\widehat{\mathcal{M}}=X^{{}^{⊺}}X∕K.$$

It follows that (under iid error assumptions) as $K\to \infty$

$${\widehat{\mathcal{M}}}^{-1∕2}\sqrt{K}\left(\widehat{\theta }-\theta \right)⟹N(0,{\sigma }_{\epsilon }^2),$$

where ${\sigma }_{\epsilon }^2$ is the error variance. Standard errors are computed as

$${\widehat{\sigma }}_{\epsilon }\mathrm{sqrt}\left(\mathrm{diag}\left({\widehat{\mathcal{M}}}^{-1}\right)\right),$$

where ${\widehat{\sigma }}_{\epsilon }^2$ is the residual variance. We use these standard errors for the quadratic and quartic vertex models; for the log model we just use OLS standard errors. The Gaussian log likelihood is

$$-Klog{\sigma }_{\epsilon }^2-\frac{1}{2{\sigma }_{\epsilon }^2}\sum _{t=1}^K{\left(y_t-\alpha -\gamma {|t-\mu |}^{\lambda }-\sum _{j=1}^6{\beta }_j{D}_{jt}\right)}^2.$$

To compare across different $\lambda$ we can consider the likelihood ratio statistic, ${\ell }_{\lambda }-{\ell }_2$, where

$${\ell }_{\lambda }=Klog\left({\widehat{\sigma }}_{\epsilon }\left(\lambda \right)\right),$$

which should be approximately ${\chi }^2$ with one degree of freedom under the null hypothesis that the true $\lambda =2$.

A.3. Forecasting test

We discuss here our approach to obtaining prediction intervals. We have a classical linear regression with $K$ observations:

$$y_t={\theta }^{{}^{⊺}}{x}_t+{\epsilon }_t,t=1,\dots ,K$$

$$\widehat{\theta }={\left(X^{{}^{⊺}}X\right)}^{-1}{X}^{{}^{⊺}}y$$

$$V^{-1∕2}(\widehat{\theta }-\theta )⟹N(0,I),V={\sigma }_{\epsilon }^2{\left(X^{{}^{⊺}}X\right)}^{-1}$$

$$y_{K+s|K}={\widehat{\theta }}^{{}^{⊺}}{x}_{K+s}.$$

We have

$$y_{K+s}-y_{K+s|K}={(\widehat{\theta }-\theta )}^{{}^{⊺}}{x}_{K+s}+{\epsilon }_{K+s}\simeq N\left(0,{\sigma }_{\epsilon }^2{x}_{K+s}^{{}^{⊺}}{\left(X^{{}^{⊺}}X\right)}^{-1}{x}_{K+s}\right)+{\epsilon }_{K+s},$$

where we assume that the two random variables are independent.

As $K\to \infty$, the parameter uncertainty is small for given $s$, but as $s\to \infty$, the parameter uncertainty grows without bound (in our case since $x_{K+s}={(1,1+s∕K,{(1+s∕K)}^2)}^{{}^{⊺}}$). In fact the estimator of $m$ is only consistent in the range where $s^2∕K\to 0$. Our intervals, or any intervals, are only valid over short horizons without strong additional assumptions or Bayesian magic. In our graphs above we have ignored the contribution from estimation uncertainty, which mostly affects long term prediction intervals, and affects them dramatically.

A simple approach is to assume normality for ${\epsilon }_{K+s}$, in which case ${\epsilon }_{K+s|K}=y_{K+s}-y_{K+s|K}\sim N\left(0,{\sigma }_{\epsilon }^2(1+x_{K+s}^{{}^{⊺}}{\left(X^{{}^{⊺}}X\right)}^{-1}{x}_{K+s})\right)$. We provide a test of the vector of one step ahead predictions for $n=30$ countries. We have for the vector of one step ahead predictions

$${\epsilon }_{K+1|K}\sim N\left(0,(1+x_{K+1}^{{}^{⊺}}{\left(X^{{}^{⊺}}X\right)}^{-1}{x}_{K+1}){\Omega }_{\epsilon }\right),$$

where ${\Omega }_{\epsilon }$ is the error covariance matrix, so that

$$t_i=\frac{y_{K+1}-y_{K+1|K}}{\sqrt{(1+x_{K+1}^{{}^{⊺}}{\left(X^{{}^{⊺}}X\right)}^{-1}{x}_{K+1}){\widehat{\sigma }}_{ii}}},$$

is approximately standard normal for each $i$. Since $n>K$, we use a version of the Pesaran and Yamagata (2012) statistic to aggregate across countries

$${\tau }_{PY}=\frac{\sum _{i=1}^n{t}_i^2-n}{\sqrt{2i_n^{{}^{⊺}}\left({\widehat{R}}_{\epsilon }\odot {\widehat{R}}_{\epsilon }\right)i_n}},{\widehat{R}}_{\epsilon }=\mathrm{diag}{\left({\widehat{\Omega }}_{\epsilon }\right)}^{-1∕2}{\widehat{\Omega }}_{\epsilon }\mathrm{diag}{\left({\widehat{\Omega }}_{\epsilon }\right)}^{-1∕2},$$

which is asymptotically standard normal under the null (provided $n$ is large and the cross-sectional dependence is weak); the test is rejected if ${\tau }_{PY}>z_{1-\alpha }$, where $\Phi \left(z_a\right)=a$. Here,  $\odot$ denotes Hadamard product and ${\widehat{\Omega }}_{\epsilon }$ is the residual covariance matrix estimate

$${\widehat{\Omega }}_{\epsilon }=\frac{1}{K}\sum _{t=1}^K{\widehat{\epsilon }}_t{\widehat{\epsilon }}_t^{⊺}.$$

These are the statistics reported in Table 3, Table 4.

Table 3.

One Step Ahead Prediction Loss of Cases.

	Minimum Average Loss			Average Loss of K $=$ 100
Name	1a	1b	1c	1a	1b	1c
USA	6463	9480	5186	16247	14250	16755
Brazil	3263	2395	2753	6139	5737	4130
Russia	103	845	120	2440	2757	1499
India	2761	1004	2612	5348	4902	4529
UK	109	93	109	292	258	267
Peru	1553	1800	1583	1677	2968	1885
Chile	1115	949	1100	3606	1143	3840
Italy	94	67	98	139	165	140
Iran	38	100	46	1102	1086	1014
Mexico	956	547	872	1448	1072	1050
France	207	202	211	207	304	213
Pakistan	706	1012	825	4907	3081	5554
Turkey	115	64	137	679	479	717
Germany	74	50	63	210	110	246
Saudi Arabia	77	95	86	302	745	594
South Africa	346	297	371	364	3837	397
Canada	32	21	27	64	65	44
Qatar	163	160	221	330	1110	613
Colombia	917	681	875	1248	1595	1194
Sweden	797	787	798	1310	1368	1281
Egypt	361	554	420	1256	767	1310
Belgium	86	75	88	91	95	90
Belarus	196	209	203	257	1132	443
Argentina	1099	1067	1108	1680	2023	1643
Indonesia	47	62	46	155	213	155
Netherlands	6	14	6	13	14	14
UAE	40	76	43	127	633	170

This table summarizes the average loss of one step prediction for new daily cases when L $=$ 5. And K ranges from 14 to 100 days. The second column presents the minimum average loss of 5 days within that range. And the corresponding results of K $=$ 100 are provided for comparisons.

Table 4.

One Step Ahead Prediction Loss of Deaths.

	Minimum Average Loss			Average Loss of K $=$ 100
Name	2a	2b	2c	2a	2b	2c
USA	389	149	393	609	564	595
Brazil	48	70	58	225	89	120
Russia	16	19	20	22	60	31
India	27	26	28	57	53	43
UK	43	29	45	74	75	72
Peru	86	80	84	102	82	89
Chile	34	48	35	76	155	69
Italy	18	15	18	18	17	18
Iran	13	3	20	19	20	26
Mexico	240	268	245	344	284	288
France	8	6	8	12	9	11
Pakistan	27	28	30	47	33	50
Turkey	2	3	2	15	12	15
Germany	4	4	4	8	8	7
Saudi Arabia	2	2	2	5	12	4
South Africa	20	14	20	32	110	32
Canada	7	11	9	7	14	9
Qatar	2	1	2	2	2	2
Colombia	31	31	39	49	58	49
Sweden	13	13	14	24	25	23
Egypt	38	33	38	45	58	47
Belgium	5	5	5	5	5	5
Belarus	1	1	1	1	1	1
Argentina	9	8	9	11	13	11
Indonesia	4	3	4	4	6	4
Netherlands	1	1	1	1	1	1
UAE	0	0	0	1	1	1

This table summarizes the average loss of one step prediction for new daily deaths when L=5. And K ranges from 14 to 100 days. The second column presents the minimum average loss of 5 days within that range. And the corresponding results of K $=$ 100 are provided for comparisons.

A.4. Restricted model estimation

We next discuss how to estimate the restricted model of Section 5. In this case we have a pair of quadratic equations with an equality restriction,

$$log\left(y_t^c+1\right)={\alpha }^c+{\beta }^{c}t+{\gamma }^c{t}^2+{\epsilon }_t^c,$$

$$log\left(y_t^d+1\right)={\alpha }^d+{\beta }^{d}t+{\gamma }^d{t}^2+{\epsilon }_t^d,$$

where

$$E\left[\left(\begin{array}{c}\hfill {\epsilon }_t^c\hfill \\ \hfill {\epsilon }_t^d\hfill \end{array}\right)\left(\begin{array}{cc}\hfill {\epsilon }_t^c\hfill & \hfill {\epsilon }_t^d\hfill \end{array}\right)\right]=\Omega .$$

This is a SUR with a cross-equation restriction and the optimal estimator is a GLS. The unrestricted estimator vector $\widehat{\theta }=$ ${({\widehat{\alpha }}^c,{\widehat{\beta }}^c,{\widehat{\gamma }}^c,{\widehat{\alpha }}^d,{\widehat{\beta }}^d,{\widehat{\gamma }}^d)}^{{}^{⊺}}$ has variance $\Omega \otimes {\left(X^{{}^{⊺}}X\right)}^{-1}$. We define $\theta =$ ${({\alpha }^c,{\beta }^c,{\alpha }^d,{\beta }^d,\gamma )}^{{}^{⊺}}$ and $L$ the 6 × 5 matrix of zeros and ones that picks out the right element

$$\tilde{\theta }={\left(L^{{}^{⊺}}\left({\widehat{\Omega }}^{-1}\otimes \left(X^{{}^{⊺}}X\right)\right)L\right)}^{-1}{L}^{{}^{⊺}}\left({\widehat{\Omega }}^{-1}\otimes \left(X^{{}^{⊺}}X\right)\right)\widehat{\theta }$$

with asymptotic variance

$${\left(L^{{}^{⊺}}\left({\Omega }^{-1}\otimes \left(X^{{}^{⊺}}X\right)\right)L\right)}^{-1}.$$

In our second model, the quasi likelihood can be used with one step taken from initial consistent estimators of $\theta ={(a^c,b^c,c^c,\psi ,\vartheta )}^{{}^{⊺}}$. The quasi-likelihood is

$$\ell (\theta ,\Omega )=-\frac{K}{2}logdet\Omega -\frac{1}{2}\sum _{t=1}^K{\left(y_t-m_t\left(\theta \right)\right)}^{{}^{⊺}}{\Omega }^{-1}\left(y_t-m_t\left(\theta \right)\right),$$

where $y_t={(y_t^c,y_t^d)}^{{}^{⊺}}$ and $m_t={(m_t^c,m_t^d)}^{{}^{⊺}}$, where, with ${\phi }_0\left(\vartheta \right)=\Phi \left(\vartheta \right)$, ${\phi }_1\left(\vartheta \right)=\varphi \left(\vartheta \right)$, and ${\phi }_2\left(\vartheta \right)=\frac{1}{2}(1-F_{{\chi }^2\left(3\right)}\left({\vartheta }^2\right))$, we have

$$m_t^d=\psi \left(a^c{\phi }_0\left(\vartheta \right)-b^c{\phi }_1\left(\vartheta \right)+c^c{\phi }_2\left(\vartheta \right)\right)+t\psi \left(b^c{\phi }_0\left(\vartheta \right)-2c^c{\phi }_1\left(\vartheta \right)\right)+t^2\psi c^c{\phi }_0\left(\vartheta \right).$$

This is an SUR system with a nonlinear cross equation restriction. The efficient estimator should use the error covariance matrix.

We can alternatively estimate the unrestricted model ${(a^c,b^c,c^c,a^d,b^d,c^d)}^{{}^{⊺}}$ and then impose the restrictions afterwards by minimum distance where

$$\left(\begin{array}{c}\hfill a^d\hfill \\ \hfill b^d\hfill \\ \hfill c^d\hfill \end{array}\right)=\psi \left(\begin{array}{ccc}\hfill {\phi }_0\left(\vartheta \right)\hfill & \hfill -{\phi }_1\left(\vartheta \right)\hfill & \hfill {\phi }_2\left(\vartheta \right)\hfill \\ \hfill 0\hfill & \hfill {\phi }_0\left(\vartheta \right)\hfill & \hfill -2{\phi }_1\left(\vartheta \right)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\phi }_0\left(\vartheta \right)\hfill \end{array}\right)\left(\begin{array}{c}\hfill a^c\hfill \\ \hfill b^c\hfill \\ \hfill c^c\hfill \end{array}\right).$$

for some norm. This is similar to the case we have already studied because there are five unrestricted parameters and 6 estimable quantities.