Learning versus habit formation: Optimal timing of lockdown for disease containment

Abstract

We analyze a model where the government has to decide whether to impose a lockdown in a country to prevent the spread of a possibly virulent disease. If the government decides to impose a lockdown, it has to determine its intensity, timing and duration. We find that there are two competing effects that push the decision in opposite directions. An early lockdown is beneficial not only to slow down the spread of the disease, but creates beneficial habit formation (such as social distancing, developing hygienic habits) that persists even after the lockdown is lifted. Against this benefit of an early lockdown, there is a cost from loss of information about the virulence and spread of the disease in the population in addition to a direct cost to the economy. Based on the prior probability of the disease being virulent, we characterize the timing, intensity and duration of a lockdown with the above mentioned tradeoffs. Specifically, we show that as the precision of learning goes up, a government tends to delay the imposition of lockdown. Conversely, if the habit formation parameter is very strong, a government is likely to impose an early lockdown.

1. Introduction

The entire world has been severely affected by the emergence of a new respiratory illness, named coronavirus 2 (SARS-CoV-2), popularly known as Covid-19. Since the first recorded hospitalization in China on the 12th of December, $2019$ (Wu et al., 2020, Zhou et al., 2020), the disease has rapidly spread to other regions across the globe taking on the nature of a pandemic. Yet, because of its novelty, many decisions on how to respond to the possible pandemic had to be taken at a stage when much remained unknown about the disease, including its virulence and how to mitigate against that.

One of the common responses to preventing the spread of the disease has been through lockdown, a broad term by which we mean drastically reducing movement of individuals which includes severe restrictions on human to human contact. This has consisted of restrictions on when to leave one’s residence, where to go and whom to meet with, as well as shutting down non-essential parts of the economy. While these measures no doubt lower the spread of the infection, they come with a huge cost to the economy. Additionally, given that the disease is novel, a lockdown also leads to a loss of information.1 about the dynamics i.e. the spread and severity of the disease within the population had it been allowed to take its own course.

In this paper, we analyze a model of lockdown where the government (either a benevolent autocrat or a democratically elected leader) has to decide when (if at all) to impose a lockdown. Imposing a lockdown lowers the harm from the disease through lowering the rate of reproduction of the disease (the so-called R number). A lockdown also signals to the population the probable seriousness of the disease and makes them conscious of the need to take precautions against the disease via e.g. social distancing, wearing masks and practicing good hygiene. We posit that these precautionary actions often turn into habits even after a lockdown is lifted through inducing non-transitory changes in the behavior of the citizenry (see Gardner and Rebar, 2019). This behavioral response is indeed being seen in many countries where a majority of citizens maintain social distancing and continue to reduce their social contact and take precautions against the disease even after the government eases some of the restrictions imposed earlier. As Susskind and Vines (2020) point out, the use of lockdowns thus had an additional effect of signaling how important it was to change behavior, obviating the need for long drawn out draconian lockdowns for disease containment. This idea is formalized through our habit formation parameter $\beta$ which internalizes some of the messages that a lockdown conveys. Thus, an early lockdown has a benefit of inducing changes in behavior in the population that lasts beyond the lockdown.2

Against this benefit of an early lockdown, there is a cost from loss of information (in addition to a direct cost to the economy). An early lockdown prevents the natural course of the disease and reduces its consequent public health cost but its suppression does not allow us to discover the dynamics of the disease and its consequent costs with any precision. Given the enormous cost to the economy of the lockdown, an early lockdown based on imperfect information on the severity of the disease may lead to a possibly inoptimal response e.g. imposing huge social and economic costs not warranted by the true severity of the disease.

While this effect has not been emphasized, there are a group of eminent scientists who have argued against a lockdown at least partly on the grounds that the data available was not precise enough to warrant a lockdown. For example, Sunetra Gupta, a professor of theoretical epidemiology at the University of Oxford, U.K. does not believe that the disease is likely to be virulent enough to justify a lockdown given its huge economic and social costs.3 Their model as well as a modification run by James Hay4 point out that the limited data available at the time of the U.K. lockdown was consistent with different probabilities of the severity of the disease. Given this uncertainty, the case for waiting (i.e. not locking down early) would be to get more data which would allow us to form more precise estimates. This learning effect would push towards a delay in the timing of a lockdown. The present paper studies the interplay of these two independent aspects, namely, the informational loss and the behavioral benefit, and its net effect on the optimal timing and severity of a lockdown. We now describe the model in more detail, explain the main results and discuss what questions it allows us to answer.

We consider a three-period model, with the third period representing the end of the current planning horizon. We assume that the decision on whether and for how long to impose a lockdown is restricted to the first two periods. In period 1, the government gets information (via a signal with a certain level of precision) and forms its belief about the probability that the disease is virulent. If it decides to impose a lockdown, it has to determine for how many periods and with what intensity. The lockdown reduces the spread of the disease but we assume no further information is forthcoming on the virulence of the disease during the lockdown.5 If there is no lockdown in period 1, the government gets a further signal about the virulence of the disease and decides whether or not to impose a lockdown in period 2. Further, as mentioned earlier, an early lockdown changes the way people behave and induces a behavioral response whereby people continue to take voluntary steps to prevent the spread of the disease through habit formation. Lockdowns are however economically and socially costly and thus each lockdown period has a cost.6

If the government is democratically elected, it may also face a cost from imposing a lockdown that is decreasing in the prior probability that the disease is virulent. We can think of this as a backlash from the economic hardship faced by the population. The strength of the backlash effect depends on various factors which we can think of summarily as representing trust in government. For a given belief about the probability of the disease being virulent, a lower trust is likely to cause people to impose higher electoral costs on the government. We denote this cost of public opposition to lockdown, particularly of consideration in a democracy by a parameter $\delta$.

This model thus allows us to answer a number of important questions of relevance to a policy maker. Given the information in any period that the disease is virulent, we can analyze whether the government should impose a lockdown, how intense should the lockdown be and if imposed early, for how long should it be. We are further interested in understanding the cutoff probability that the disease is virulent at which a government decides to lockdown and how this shifts over time as a function of (i) the accuracy of the signal each period, (ii) the strength of the behavioral response, (iii) the cost to the economy, (iv) the magnitude of the backlash effect and (v) the expected time of arrival of a vaccine/treatment.

We characterize the tradeoff between information and habit formation. When the strength of the habit formation parameter ($\beta$) is high, early lockdown is optimal. In particular, we show that for any given $\beta$, as long as the signal precision ($p$) is below a certain threshold, the cutoff belief for imposing a lockdown is lower in the first period than in the second period. Conversely, if the signal precision is higher than the threshold, the opposite holds as the possible information loss would make the government delay lockdown. Hence, the cutoff belief for imposing a lockdown is higher in the first period than in the second period. The democracy parameter $\delta$ also plays a role, as this acts to delay the timing, duration and intensity of the lockdown given the possible public backlash against lockdowns. This also tilts towards waiting for a more precise signal that may reduce public opposition to the backlash. This suggests that democratic governments in populations distrustful of governments may delay lockdowns because of possible electoral consequences emanating from public backlash against a lockdown.

There are a number of other important comparative static results. The intensity of lockdown is increasing in $\beta$ and the beliefs that the disease is virulent but decreasing in the loss to the economy. The parameter $\gamma$ represents the extent of the economic impact of the lockdown, with a higher value indicating a more negative impact. Consistent with the intuition in Susskind and Vines (2020), we characterize how under some parameter values, optimal lockdowns are not draconian or long drawn out i.e. of low intensity and only for one period. Somewhat counterintuitively, while intensity of lockdowns go down as economic costs increase, we also see if $\beta$ is high, the cutoff belief for early lockdowns is lower than that for later lockdowns. This is because if economic costs of a lockdown are high, conditional on imposing a lockdown, it is better to do so early than late to get the full benefit of disease reduction because of habit formation.

Our model’s assumptions on disease propagation and benefits of a lockdown are consistent with standard models in epidemiology and economics. Lockdowns in epidemiological models of disease propagation are a vital tool for slowing the incidence of the disease. The basic models (see Anderson and May, 1992) assume that the hazard rate is an increasing function of prevalence in the population. Economic models however assume people are rational and hence even without a lockdown, they update information about disease prevalence and take precautions to reduce their chances of infection through (individually) optimal social distancing (see Geoffard and Philipson, 1996). Nonetheless even in these fully rational models, the individual decision (i.e. choice of how much to socially distance) is not in general socially optimal as rational agents do not consider the external benefits of social distancing (see Toxvaerd, 2019). Hence, imposing lockdowns to reduce human contact can be justified even in such models to reach the social optimum. Our model is agnostic about whether agents are fully rational and indeed abstracts from the decision of the population to focus on the government’s optimal timing of lockdown.

The economic costs of lockdown as well as the public health benefits are broadly consistent with both the epidemiological and economic models.7 Indeed in the Covid-$19$ context there are a large number of recent papers modeling the trade-off between the public health benefit (disease suppression) and the economy (see Alvarez et al., 2020, Favero et al., 2020, Miclo and Spiro, 2020, Pindyck, 2020). What is novel in our model is the trade-off between acquiring information on the dynamics of an unknown disease (which acts in favor of delaying a lockdown as it will generate data points allowing for more precise estimates via Bayesian updating) versus altering habits of the population (which acts in favor of an early lockdown). This has been generally neglected in the literature. In fact, even any analysis of uncertainty in the reproduction number has been largely missing while focusing on the trade-off in a lockdown, with one of the few papers that considers this uncertainty being (Gollier, 2020).8 It assumes the disease is virulent and the reproduction number is uncertain. Its focus is on lockdown intensity allowing for some learning during a (partial) lockdown, though it assumes the virus is necessarily lethal. The model does not consider the trade-off between information acquisition versus allowing disease-reducing behavior to kick in early through behavioral changes.

To the best of our knowledge, our model’s insights on the trade-off between acquiring information and changing behavior have not been formalized before. It has some similarities with the literature on adoption of new technology where there is an optimal period at which one should adopt the technology where there is uncertainty in the costs and benefits of adoption. Waiting delays the potential benefits from the technology but allows us to learn more about the actual costs and benefits from adoption (see e.g. Jensen, 1982, Bhattacharya et al., 1986, Hoppe, 2002, Chavas and Nauges, 2020 for a survey with regard to adoption in agriculture). The insight is also similar to the concept of option value (see Dixit and Pindyck, 1994). This literature however does not consider the tradeoff with habit formation.

At a more macro level, the impact of diseases on the economy has been looked at both empirically and theoretically including the endogeneity of diseases, labour supply and human capital accumulation and hence growth, including the possibility of a growth trap (Goenka and Liu, 2012, Goenka and Liu, 2019, Goenka et al., 2014, Chakraborty et al., 2010). While these papers consider the impact of interventions on growth, they do not consider interventions in the context of a novel disease that has a trade-off between the informational value of delaying interventions and kicking in habit formation early.

2. Environment

We consider a three-period discrete time model, i.e. $t=1,2,3$. A new disease hits a population at $t=1$. The transmission potential of this disease is measured by the basic rate of reproduction $R>0$. Let $r^{\prime }$ be the harm caused by the disease which is dependent on the value of $R$. Formally, $r^{\prime }$ is defined as a continuous strictly increasing function $r^{\prime }:\mathcal{R}\to \mathcal{R}$, $R\mapsto r^{\prime }\left(R\right)$.

Given it is a novel disease, $R$ is unknown and can take two values; $R_L$ or $R_H$ with $0<R_L<1<R_H$. Thus the disease is either potentially virulent in which case the reproduction rate $R=R_H>1$, or less harmful with the reproduction rate $R=R_L<1$.9 Let ${\rho }_0$ be the prior in period $1$ that it is virulent. We define

$$r=r_H^{\prime }-r_L^{\prime }$$

such that $r_H^{\prime }=r^{\prime }\left(R_H\right)$ and $r_L^{\prime }=r^{\prime }\left(R_L\right)$. Thus, $r$ reflects the added harm from the disease in the event it is virulent. Since $r^{\prime }$ is a strictly increasing function, $r>0$.

In periods $t=1,2$, new data on the disease produces a partially informative signal $S_t\in \{L,H\}$ about the true value of $R$. Signal $H$ ($L$) can be thought of as the data on the number of patients infected with the disease, which leads to Bayesian updating on the probability that the disease is virulent. The signals are iid across periods with precision $p\in (\frac{1}{2},1)$; This means $Pr[S_t=L|R=R_L]=Pr[S_t=H|R=R_H]=p$. Given a prior ${\rho }_{t-1}$ in period $t$ ($t=1,2$), after the realization of the signal $S_t$, ${\rho }_{t-1}$ is updated using Bayes’ rule giving us the posterior ${\rho }_t$ which can take two values. If $S_t=H$,

$${\rho }_t={\rho }_t^H=\frac{{\rho }_{t-1}p}{{\rho }_{t-1}p+(1-{\rho }_{t-1})(1-p)}.$$ (1)

If $S_t=L$,

$${\rho }_t={\rho }_t^L=\frac{{\rho }_{t-1}(1-p)}{{\rho }_{t-1}(1-p)+(1-{\rho }_{t-1})p}$$ (2)

Since the signals are informative (i.e. $p>\frac{1}{2}$) following a $H\left(L\right)$ signal, the updated value ${\rho }_t>(<){\rho }_{t-1}$. In our model $p<1$, i.e. signals are not fully informative.

Our model consists of a population of fixed size and a government. We assume that the government is the only decision maker, and interpret period $2$ as the end of the current planning horizon. Period $3$ represents the expected length of time after the current planning horizon but before the arrival of a vaccine or treatment. We denote the expected length of this period by $A>0$.

2.1. Actions and payoffs

In each period $t=1,2$, the government can take two actions. It can either implement a lockdown, or it can wait. In the event the government decides to implement a lockdown, it also determines its length and intensity. Further, if a lockdown is implemented, then during the lockdown, the precision of the signal goes down. This is because during a lockdown, we lose some information of the dynamics of the spread of the disease in the population i.e. which groups are most affected, what is the complication rate absent intervention etc. For analytical tractability, we assume the precision of the signal during a lockdown to be $p=\frac{1}{2}$. From (1), (2) we can conclude that this implies during a lockdown there is no learning, and hence the value of $\rho$ is not updated.10

If the government imposes a lockdown, it has to choose its intensity $a$. The choice set of $a$ is $(0,1]$, with $a=1$ representing the highest intensity.11 The intensity of the lockdown reduces the expected harm caused by the disease slowing its transmission because of enforced changes in social behavior. This continues to an extent beyond the lockdown due to habit formation which we denote by $\beta$. If in period $t(t=1,2)$ a lockdown for $T$ periods with intensity $a$ is implemented, then the payoff to the government is given by

$$W_t={\rho }_t\left[-rT\{1-(a-a^2)\}-r[3-(T+t)]\{1-\beta (a-a^2)\}\right]+{\rho }_t[-rA\{1-\beta (a-a^2)\}]-\gamma [1+(1-{\rho }_t)\delta ](a^2+T^2)$$ (3)

We now explain each of the terms in (3). Note that $W_t$ is strictly negative implying that the payoff reflects the net expected harm from a particular lockdown policy. During the lockdown, in the event the disease is virulent, the effective net harm per period is reduced from $-r$ to $-r\{1-(a-a^2)\}$.12 This implies the total net harm during the lockdown in the event the disease is virulent is $-rT\{1-(a-a^2)\}$. Once the lockdown is lifted, part of the disease reducing impact stays due to habit formation which is captured by the parameter $\beta \in (0,1)$.13 As discussed in the introduction, the idea behind this is that the rules mandated during a lockdown i.e. restricting interactions through social distancing; adopting hygiene measures continue to an extent beyond the lockdown through beneficial habit formation. This means the effective net harm per period after the lockdown is lifted is $-r\{1-\beta (a-a^2)\}$. Thus for the remaining periods in the planning horizon, in the event the disease is virulent, the net harm is given by $-r[3-(T+t)]\{1-\beta (a-a^2)\}$. Finally, because of this habit formation, in the event the disease is virulent, the net harm after the planning horizon until the vaccine or treatment arrives is $-rA\{1-\beta (a-a^2)\}$. This explains the first two terms of (3). Thus in our model, periods $1$ and $2$ are the current planning horizon, but the actions taken in those periods have longer term consequences due to habit formation.

Imposing a lockdown entails an economic cost which is directly proportional to the intensity and the duration of the lockdown captured by $(a^2+T^2)$. $\gamma >0$ is a cost parameter which reflects the efficacy of a government in managing the economy during a lockdown. The expression $(1-{\rho }_t)\delta$ in the final term of (3) captures an additional cost for a democratically elected leader due to public backlash against lockdown. The higher the probability the disease is virulent, the lower is the backlash while $\delta$ captures a country specific parameter with a higher $\delta$ indicating a greater backlash against the lockdown. This might represent trust in government such that the trust is inversely proportional to the value of $\delta$.

Note that the functional forms $(1-(a-a^2))$, $(1-\beta (a-a^2))$ and the convex economic cost ensure that the payoff $W_t$ is strictly concave in $a$ for $a\in (0,1]$.

Remark 1

The habit formation parameter $\beta$ may of course affect the economy after the lockdown is lifted. Incorporating $\beta$ in the cost component of imposing the lockdown will push up the thresholds for imposing the lockdown in both periods. The qualitative features of all our results remain unchanged.

3. Optimal action by the government

In this section, we determine the optimal action of the government in each period $t(t=1,2)$ as a function of the likelihood of the disease being virulent. We begin our analysis in the following subsection by considering period $2$.

3.1. Optimal action in period $2$

Consider a situation when the government waits until period $2$, i.e. it does not impose a lockdown in period $1$. In that case, the government’s decision consists of two actions. It can either impose a lockdown for $1$ period, or not impose it at all.

Let ${\rho }_2$ be the posterior in period $2$. If the government decides to impose a lockdown, then it chooses $a$ to maximize:

$$W_2={\rho }_2[-r\{(A+1)-(1+A\beta )(a-a^2)\}]-\gamma [1+(1-{\rho }_2)\delta ](a^2+1)$$

From the first order condition we obtain14

$$a_2^{\ast }=\frac{{\rho }_{2}r[1+A\beta ]}{2[{\rho }_{2}r[1+A\beta ]+\gamma [1+(1-{\rho }_2)\delta ]]}$$ (4)

As explained in the previous section, as a consequence of the choice of our functional forms, $W_2$ is strictly concave in $a$ for $a\in (0,1)$. Further, it is strictly increasing (decreasing) at $a=0$ ($a=\frac{1}{2}$). Thus the optimal $a_2^{\ast }$ should satisfy $a_2^{\ast }<\frac{1}{2}$. This is confirmed by the expression in (4).

Remark 2

Direct computation confirms that $a_2^{\ast }$ is strictly increasing in $A$, $\beta$ and ${\rho }_2$. It is strictly decreasing in $\gamma$.

These comparative static results can be explained intuitively. When it is more likely that the disease is virulent i.e. ${\rho }_2$ is higher, the expected benefit of a lockdown is also higher. This induces the government to optimally impose a lockdown with a higher intensity, and hence it chooses a higher value of $a$. Coming to the habit formation parameter $\beta$, the marginal benefit of $a$ increases with $\beta$, which implies that the optimal value of $a$ in increasing in $\beta$. Next, an increase in $A$ implies that the arrival of the vaccine will be delayed. This results in the government choosing a higher level of $a$ so that the total net harm beyond the planning horizon is reduced through habit formation. Finally, the lower is the efficacy of a government in managing an economy during the lockdown (reflected in higher $\gamma$), the lower will be the intensity of lockdown chosen by the government.

Substituting the value of $a_2^{\ast }$ from (4), we obtain the optimal welfare from lockdown in period $2$. This is given by

$$W_2^{\ast }=-{\rho }_{2}r(A+1)+\frac{{\rho }_2^2{r}^2{(1+A\beta )}^2}{4[{\rho }_{2}r(1+A\beta )+\gamma [1+(1-{\rho }_2)\delta ]]}-\gamma [1+(1-{\rho }_2)\delta ]$$ (5)

If the government on the other hand decides not to impose a lockdown in period $2$, then it obtains a payoff of $=-{\rho }_{2}r-{\rho }_{2}rA=-{\rho }_{2}r(A+1)$. This implies imposing a lockdown is optimal as long as

$${\rho }_2\ge {\rho }_2^{\ast }=\frac{2\gamma (1+\delta )}{(\sqrt{2}-1)r(1+A\beta )+2\gamma \delta }$$ (6)

Direct computation shows that ${\rho }_2^{\ast }<1$ as long as $r>\frac{2\gamma }{(\sqrt{2}-1)(1+A\beta )}$. ${\rho }_2^{\ast }>1$ means that it is not optimal to impose a lockdown in period $2$. One implication of this is that the higher is the value of $A$, the lower is the value of ${\rho }_2^{\ast }$ and hence, it is more likely lockdown will be imposed in period $2$. Similarly, the higher is the value of $\beta$, it is more likely lockdown will be imposed in period $2$.

We now move to the analysis of period $1$ in the following subsection.

3.2. Optimal action in period $1$

In this subsection, we analyze the optimal action of the government in period $1$. Suppose ${\rho }_1$ is the posterior in period $1$. In the current setting, the planning horizon begins from period $1$.

As mentioned earlier, given ${\rho }_1$, the government can either impose a lockdown, or it can wait. In period $1$, if the government decides to impose a lockdown, then it has to decide whether the lockdown will be imposed for one period or two periods. W.L.O.G we can rule out the possibility of the government imposing a lockdown for one period in both $t=1$ and $t=2$ as given the informational assumptions (i.e. no updating of $\rho$ during a lockdown) of the current model, it is equivalent to imposing a lockdown in period $1$ for two periods.

We begin our analysis by determining the expected payoff to the government if it decides to wait and not impose a lockdown in period $1$. In order to do that, we need to compute the continuation payoff to the government from such an action. This continuation payoff is the sum of the payoff from inaction in period $1$, and the expected optimal payoff in period $2$. The latter as demonstrated in the previous subsection, depends on the optimal action in period $2$, which is determined by the updated belief after the realized signal in that period. This implies that the general expression for the continuation payoff to the government from waiting and not imposing a lockdown in period $1$ is given by

$$\Gamma \left({\rho }_1\right)=-{\rho }_{1}r+\left[Pr(S_2=H|{\rho }_1)W_2^{\ast }\left({\rho }_2^H\right)\right]+\left[Pr(S_2=L|{\rho }_1)W_2^{\ast }\left({\rho }_2^L\right)\right]$$ (7)

The first term represents the expected payoff in period $1$ if no lockdown is imposed. The second and the third term represent the expected payoff in period $2$ in the event a high and low signal is received respectively. Since $Pr(S_2=S|{\rho }_1)$ and the resulting ${\rho }_2^S$ ($S=H,L$) are functions of ${\rho }_1$, we can express $\Gamma$ as a function of ${\rho }_1$ only.

In order to determine $\Gamma$, define two thresholds of ${\rho }_1$, $\widetilde{{\rho }_1}$ and $\overline{{\rho }_1}$ such that

$${\rho }_2^{\ast }=\frac{\widetilde{{\rho }_1}p}{\widetilde{{\rho }_1}p+(1-p)(1-\widetilde{{\rho }_1})}\text{ ; and }{\rho }_2^{\ast }=\frac{\overline{{\rho }_1}(1-p)}{\overline{{\rho }_1}(1-p)+p(1-\overline{{\rho }_1})}$$ (8)

Suppose ${\rho }_1\le \widetilde{{\rho }_1}$, and the government decides to wait. In this case, irrespective of the signal received next period, the updated belief will be less than the threshold ${\rho }_2^{\ast }$. From our analysis in the previous subsection, we can conclude that in this case no lockdown will be imposed in period $2$. Similarly, if ${\rho }_1\ge \overline{{\rho }_1}$, and the government decides to wait, irrespective of the signal next period, the updated belief will be higher than the threshold ${\rho }_2^{\ast }$. Thus in this case lockdown will be imposed in period $2$. Finally consider $\widetilde{{\rho }_1}<{\rho }_1<\overline{{\rho }_1}$. Suppose the government decides to wait. In this case, if in period $2$, a high (low) signal is received, then lockdown is (not) imposed in period $2$. The analysis in the previous subsection along with these arguments allow us to express (please see Appendix A for a detailed derivation) $\Gamma \left({\rho }_1\right)$ as

$$\Gamma \left({\rho }_1\right)=-{\rho }_{1}r(A+2)$$

$$+max\{0,\left[Pr(S_2=H|{\rho }_1)\right]\{\frac{{\rho }_2^{H2}{r}^2{(1+A\beta )}^2}{4[{\rho }_2^{H}r(1+A\beta )+\gamma [1+(1-{\rho }_2^H)\delta ]]}-\gamma [1+(1-{\rho }_2^H)\delta ]\}\}$$

$$+max\{0,\left[Pr(S_2=L|{\rho }_1)\right]\{\frac{{\rho }_2^{L2}{r}^2{(1+A\beta )}^2}{4[{\rho }_2^{L}r(1+A\beta )+\gamma [1+(1-{\rho }_2^L)\delta ]]}-\gamma [1+(1-{\rho }_2^L)\delta ]\}\}$$ (9)

The first term of (9) gives the welfare if no action is taken in both periods $1$ and $2$. The second and the third term reflect the net expected premium obtained from the optimal action in period $2$ after receiving a high and low signal respectively. The second (third) term is strictly positive if following a high (low) signal in period $2$, the government finds it optimal to impose a lockdown. From our arguments made in the previous paragraph we can conclude that $\Gamma \left({\rho }_1\right)\ge -{\rho }_{1}r(A+2)$ with strict inequality for ${\rho }_1>\widetilde{{\rho }_1}$.

We now determine the payoff from imposing a lockdown of optimal length and intensity in period $1$.

Payoff from lockdown in period $1$ :

In period $1$, if a government imposes a lockdown, then it also has to decide whether it will be for one period or two periods. First, we evaluate the optimal payoff if the government decides to impose a lockdown in period $1$ for two periods ($T=2$). From (3), we can say that the government in this case chooses $a$ to maximize

$$W_1={\rho }_1\left[-r\{(2+A)-(2+A\beta )(a-a^2)\}\right]-\gamma [1+(1-{\rho }_1)\delta ](a^2+4)$$

Evaluating the first order condition we obtain

$$a_1^{\ast }=\frac{{\rho }_{1}r(2+A\beta )}{2[{\rho }_{1}r(2+A\beta )+\gamma [1+(1-{\rho }_1)\delta ]]}$$ (10)

Remark 3

As in (4), direct computation confirms that $a_1^{\ast }$ is strictly increasing in $A$, $\beta$ and ${\rho }_1$. It is strictly decreasing in $\gamma$.

Substituting the value of $a_1^{\ast }$ from (10), we get the optimal welfare of the government from a lockdown for 2 periods in period $1$ as

$$W_1^{\ast }=-{\rho }_{1}r(A+2)+\frac{{\rho }_1^2{r}^2{(2+A\beta )}^2}{4[{\rho }_{1}r(2+A\beta )+\gamma [1+(1-{\rho }_1)\delta ]]}-4\gamma [1+(1-{\rho }_1)\delta ]$$ (11)

The following lemma illustrates that the optimal payoff to the government from imposing a lockdown in period $1$ for two periods intersects the continuation payoff $\Gamma \left({\rho }_1\right)$ from not imposing any lockdown in period $1$ at a belief ${\rho }_1^{\prime }>{\rho }_2^{\ast }$. Thus, Lemma 1 looks at what the threshold for lockdown in period 1 would be had it been restricted to a choice between a 2 period lockdown or no lockdown in period 1.

Lemma 1

$W_1^{\ast }\left({\rho }_1\right)$ intersects $\Gamma \left({\rho }_1\right)$ at a belief ${\rho }_1^{\prime }$ such that ${\rho }_1^{\prime }>{\rho }_2^{\ast }$ .

The formal proof of this lemma is relegated to Appendix B. Here we provide the intuition for the result. First, we show that the welfare $W_1^{\ast }=-{\rho }_{1}r(A+2)$ at a belief that is strictly higher than the threshold ${\rho }_2^{\ast }$. From the expression of the continuation payoff in (9), we know that $\Gamma$ is strictly higher than $-{\rho }_{1}r(A+2)$ for all ${\rho }_1>\widetilde{{\rho }_1}$. Since ${\rho }_2^{\ast }>\widetilde{{\rho }_1}$, we can conclude that ${\rho }_1^{\prime }>{\rho }_2^{\ast }$.

An implication of the above lemma is that if in period $1$, the government is constrained to impose a lockdown for two periods or no lockdown, then the likelihood of lockdown in period $2$ is higher than that in period $1$. This can be intuitively explained as follows. Consider the alternate policies of imposing a lockdown in period $1$ for two periods and imposing a lockdown in period $2$. The benefit due to habit formation from both these policies are for the same number of periods, i.e. $A$. However, the latter policy has the additional advantage of acting after receiving a more precise signal about the virulence of the disease. Additionally, a later lockdown reduces the negative impact on the economy by one period. This makes imposition of lockdown more likely in period $2$.

We will now determine the optimal payoff from imposing a lockdown in period $1$ for $1$ period only. From (3) we can say that the government in this case chooses $a$ to maximize

$$W_1={\rho }_1\left[-r\{(2+A)-(1+(A+1)\beta )(a-a^2)\}\right]-\gamma [1+(1-{\rho }_1)\delta ](a^2+1)$$

From the first order condition, we obtain

$$a_1^{\ast n}=\frac{(1+(A+1)\beta ){\rho }_{1}r}{2[(1+(A+1)\beta ){\rho }_{1}r+\gamma [1+(1-{\rho }_1)\delta ]]}$$ (12)

Substituting the value of $a_1^{\ast n}$, we obtain the optimal welfare from lockdown of one period duration in period $1$.15 This is given by

$$W_1^{{}^{\prime }\ast }\left({\rho }_1\right)=-{\rho }_{1}r(A+2)+\frac{{[1+(A+1)\beta ]}^2{\rho }_1^2{r}^2}{4[[1+(A+1)\beta ]{\rho }_{1}r+\gamma [1+(1-{\rho }_1)\delta ]]}-\gamma [1+(1-{\rho }_1)\delta ]$$ (13)

Thus, if in period $1$ the government decides to impose a lockdown of optimal length and intensity, then welfare from lockdown is given by

$$W_1^f=max\{\underset{1}{\overset{\ast }{W}},W_1^{{}^{\prime }\ast }\}$$

The government finds it beneficial to impose a lockdown in period $1$ if $W_1^f\left({\rho }_1\right)\ge \Gamma \left({\rho }_1\right)$. Both $W_1^f$ and $\Gamma$ are continuous functions of ${\rho }_1$. Let ${\rho }_1^{\ast }$ be the threshold of ${\rho }_1$ such that when ${\rho }_1>{\rho }_1^{\ast }$, the government finds it optimal to impose a lockdown in period $1$. Since at ${\rho }_1=0$, $W_1^f\left({\rho }_1\right)<\Gamma \left({\rho }_1\right)$, ${\rho }_1^{\ast }>0$. It is possible to have ${\rho }_1^{\ast }>1$ which implies that under no circumstances, does the government find it beneficial to impose a lockdown in period $1$.

In the following proposition we establish that as long as there is a positive degree of habit formation (i.e. $\beta >0$), then up to some precision level of the signal, the threshold for imposing the lockdown increases over time with the converse holding if the precision level is higher than the threshold. Further, for low precision level of learning, at the vicinity of the threshold in period $1$, lockdown is always imposed for one period.

Proposition 1

For any $\beta >0$ , there exists a $p^{\ast }\in (\frac{1}{2},1]$ such that if ${\rho }_t^{\ast }<1$ ( $t=1,2$ ), then for all $p\in (\frac{1}{2},p^{\ast })$ ,

$${\rho }_1^{\ast }\le {\rho }_2^{\ast }$$

and $W_1^f\left({\rho }_1^{\ast }\right)=W_1^{{}^{\prime }\ast }\left({\rho }_1^{\ast }\right)$ . This shows that for $p<p^{\ast }$ , at the right neighborhood of the threshold ${\rho }_1^{\ast }$ , lockdown is always imposed for one period.

Further, if $p^{\ast }<1$ , then for all $p\in (p^{\ast },1)$ ,

$${\rho }_1^{\ast }>{\rho }_2^{\ast }$$

The formal proof of this proposition is relegated to Appendix C. The idea behind the proof is discussed here. In the present paragraph, by lockdown, unless otherwise stated, we will refer to lockdown imposed in period $1$. We first show that the payoff from lockdown for one period is higher than $-{\rho }_{1}r(A+2)$ if ${\rho }_1$ exceeds a threshold ${\rho }_1^{″}$, which is strictly lower than ${\rho }_2^{\ast }$, the threshold for imposing a lockdown in the second period. From Lemma 1, we know that the payoff from lockdown for two periods exceeds $-{\rho }_{1}r(A+2)$ if ${\rho }_1$ is above a threshold, which is strictly higher than ${\rho }_2^{\ast }$. Hence, we can conclude that at the neighborhood of the ${\rho }_1={\rho }_1^{″}$, the payoff from lockdown for one period exceeds the payoff from a lockdown for two periods. This implies in this neighborhood, the optimal payoff from lockdown is equal to the payoff from lockdown for one period. When there is no learning, i.e. $p=\frac{1}{2}$, the continuation payoff from not imposing a lockdown in period $1$ is equal to $-{\rho }_{1}r(A+2)$. Thus, with no learning the optimal threshold ${\rho }_1^{\ast }$ for imposing a lockdown in period $1$ is equal to ${\rho }_1^{″}$, which is strictly less than that in period $2$. Since payoff functions are continuous, we know that the conclusion will continue to hold for some $p$ at the right neighborhood of $\frac{1}{2}$, and let $p^{\ast }\in (\frac{1}{2},1]$ be the supremum of such $p$’s. This means whenever $p<p^{\ast }$, we have ${\rho }_1^{\ast }<{\rho }_2^{\ast }$. From Lemma 1 we can further conclude that when $p<p^{\ast }$, at the right neighborhood of ${\rho }_1^{\ast }$, lockdown will always be imposed for one period. Finally, suppose $p^{\ast }<1$. From the definition of $p^{\ast }$, we can conclude that at the right neighborhood of $p^{\ast }$, the optimal welfare from lockdown at the belief ${\rho }_2^{\ast }$ will be less than or equal to the continuation payoff at that belief. While the optimal payoff from lockdown in period $1$ is unaffected by the learning parameter $p$, the continuation payoff is strictly increasing in it. Hence, we can conclude that for all $p>p^{\ast }$, we have ${\rho }_1^{\ast }>{\rho }_2^{\ast }$.

The above result can be intuitively explained as follows. The tradeoff between imposing a lockdown early and waiting is as follows. If a lockdown is imposed earlier, the benefit through behavioral change in the event that the disease is virulent lasts longer. On the other hand, imposing a lockdown earlier means the government is unable to learn about the nature of the disease. Thus it may impose a lockdown when the disease happens to be relatively mild and needlessly suffer the economic costs. Given a behavioral pattern, which is captured by the parameter $\beta$, the government has a higher incentive to impose the lockdown earlier if the precision of the learning is below a certain level in which case there would not be much gain in learning by waiting for one period. This explains why the threshold for imposing a lockdown in period $1$ is lower than that in period $2$. In Proposition 1 we have shown that at the right neighborhood of the threshold in period $1$, the government always imposes a lockdown for one period. However, if the value of ${\rho }_1$ is very high, it is possible that the government optimally chooses to impose a lockdown for two periods.

On the other hand, a higher precision of signal increases the gains from learning via the signal and hence reduces the incentive of the government to impose the lockdown earlier. As a consequence, the threshold for imposing the lockdown in period $1$ is higher than that in period $2$.

This intuition is now illustrated with a numerical example.

Example 1

We calibrate our model for $r=2.5$; $\beta =0.6$; $A=2$; $\gamma =0.45$ and $\delta =0.8$.

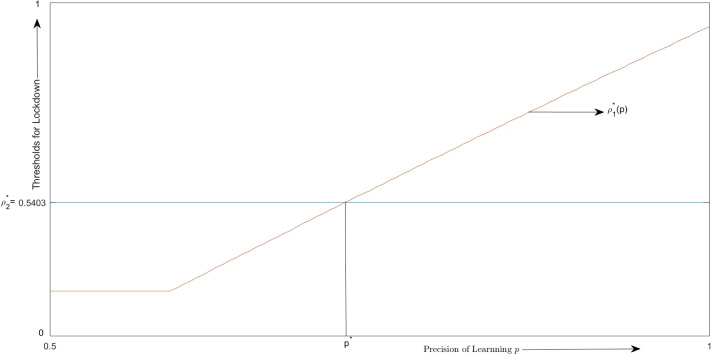
Fig. 1 exhibits how the threshold for imposing the lockdown in period $1$ changes as the precision of learning $p$ varies from 0.5 to $1$. We can observe that for low values of $p$, ${\rho }_1^{\ast }$ is unaffected by $p$, but as $p$ increases, ${\rho }_1^{\ast }$ also increases in $p$. To understand this, recall from our model that ${\rho }_1^{\ast }$ is determined by the point of intersection of the payoff from lockdown in period $1$, and the continuation payoff $\Gamma \left({\rho }_1\right)$. For values of ${\rho }_1<\widetilde{{\rho }_1}$, $\Gamma \left({\rho }_1\right)=-{\rho }_{1}r(A+2)$, which is independent of $p$. The lower is the precision of the signal, the more likely $\Gamma \left({\rho }_1\right)$ and the optimal payoff from lockdown in period $1$ intersect at a point where $\Gamma =-{\rho }_{1}r(A+2)$. Thus ${\rho }_1^{\ast }$ is independent of $p$. This explains the horizontal part of the ${\rho }_1^{\ast }$ curve. The period $2$ threshold ${\rho }_2^{\ast }$ on the other hand is independent of $p$. It can be observed in Fig. 1 that there exists a threshold $p^{\ast }$ such that for all $p$ lower (higher) than this threshold ${\rho }_1^{\ast }<(>){\rho }_2^{\ast }$, illustrating Proposition 1.

Fig. 1.

Ranking of thresholds with respect to precision of learning $p$.

4. Numerical examples

In this section we present some numerical examples of how the lockdown thresholds for periods $1$ and $2$ change with the strength of the habit formation parameter, the cost to the economy, the backlash from a lockdown and the expected time of the arrival of a treatment or vaccine. We also demonstrate how the variables interact e.g. we show that the impact of the economy on lockdown thresholds is different when the habit formation parameter takes high or low values.

4.1. Variation of lockdown thresholds with respect to the habit formation parameter ($\beta$)

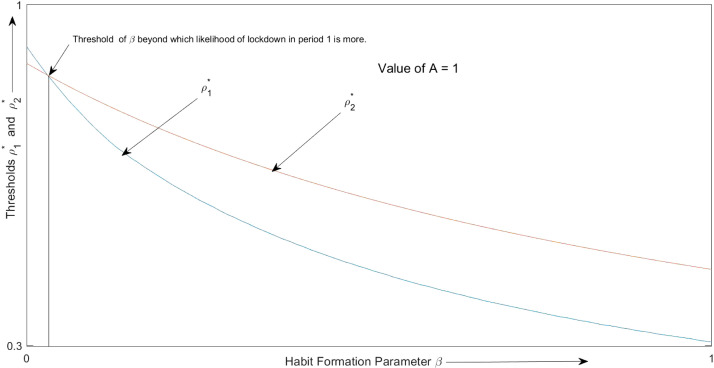
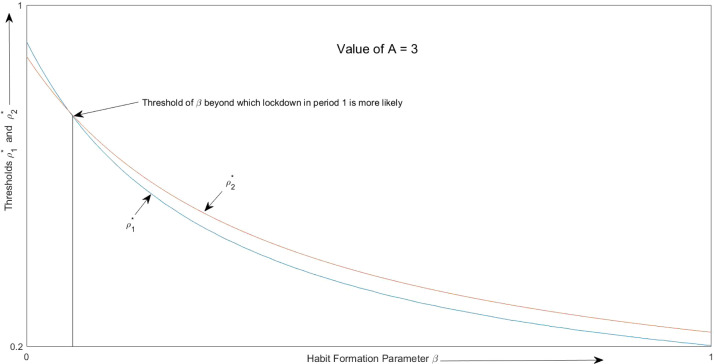
In this subsection, we examine how the thresholds for imposing the lockdown in periods $1$ and $2$, ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ respectively, vary with the value of the habit formation parameter $\beta$. We calibrate our model for $r=2.5$; $\gamma =0.45$; $\delta =0.8$, and $p=0.6$. As we will see below, the thresholds ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ are decreasing in $\beta$ across a range of values of $A$ (i.e. length of period $3$). However, $A$ affects the difference between ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ for each $\beta$. Fig. 2, Fig. 3 depict the variation of ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ with respect to $\beta$ for $A=1$ and $A=3$ respectively.

Fig. 2.

Variation of the thresholds ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ with respect to $\beta$.

Fig. 3.

Variation of the thresholds ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ with respect to $\beta$.

These findings can be explained as follows. Once lockdown is imposed, the government gets a future benefit from habit formation. While an imposition of lockdown in period $2$ generates the benefit from habit formation during period $3$, a lockdown imposed in period $1$ for one period, generates the benefit from habit formation in both periods $2$ and $3$.16 In the absence of any habit formation, i.e. $\beta =0$, it is more beneficial to impose the lockdown in period $2$, as this comes with the benefit of getting a more precise signal about the likelihood of the virulence of the disease, allowing for a more informed choice of $a$ in period $2$. This explains why at $\beta =0$, ${\rho }_2^{\ast }$ lies below ${\rho }_1^{\ast }$. However, as $\beta$ increases, the option of imposing an early lockdown in period $1$ becomes more attractive as it now comes with the benefit of habit formation for an additional period. Thus, as $\beta$ crosses a threshold, ${\rho }_1^{\ast }$ lies below ${\rho }_2^{\ast }$. In both Fig. 2, Fig. 3, this pattern is displayed. Next, we explain the effects of an increase in the value of $A$. First, the threshold of $\beta$ above which ${\rho }_1^{\ast }$ is below ${\rho }_2^{\ast }$ increases. Second, the relative difference between ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ goes down. These observations can be intuitively explained as follows. Irrespective of the timing of the lockdown, the benefit of habit formation is always present during the third period. The imposition of an early lockdown brings in the additional benefit of habit formation in period $2$. As $A$, the length of period $3$ goes up, the relative significance of this additional benefit in period $2$ from early lockdown declines. This explains why as $A$ increases, the difference between ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ (for a given $\beta$) becomes smaller.

4.2. Lockdown thresholds and the cost parameter ($\gamma$)

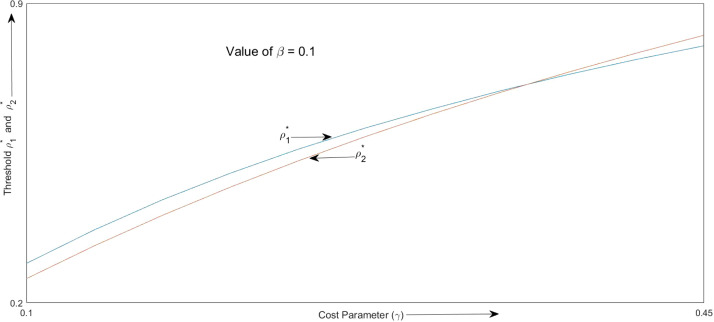
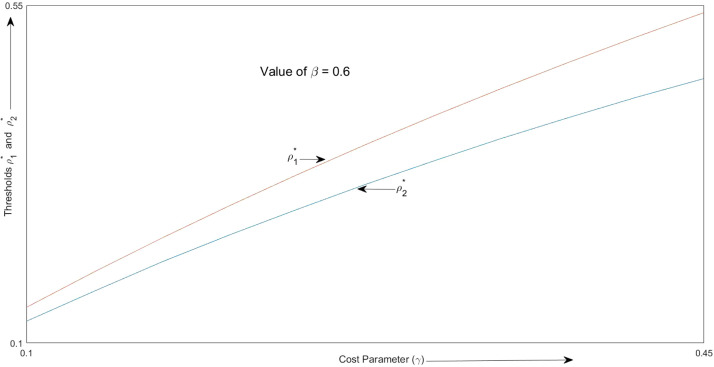
In this subsection we will analyze how the thresholds ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ interact with the cost parameter $\gamma$. For this exercise, we calibrate the model for $r=2.5$; $\delta =0.8$; $p=0.6$ and $A=2$. We look at the variation of the thresholds ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ as the value of $\gamma$ continuously varies from 0.1 to 0.45. Fig. 4, Fig. 5 depict this variation for fixing $\beta =0.1$ and $\beta =0.6$ respectively. Again, it is verified that at the right neighborhood of the threshold ${\rho }_1^{\ast }$, optimal length of lockdown is always equal to $1$.

Fig. 4.

Variation of the thresholds ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ with respect to $\gamma$.

Fig. 5.

Variation of the thresholds ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ with respect to $\gamma$.

It is evident from both the figures that as the magnitude of the cost parameter goes up, both the thresholds increase. This follows from the fact that the less able a government is in handling the economy during a lockdown (i.e. higher values of $\gamma$), the more reluctant a government is to impose a lockdown in a particular period, i.e. ${\rho }_t^{\ast }$ higher ($t=1,2$). Thus, from both the figures we can observe that as $\gamma$ goes up, both ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ go up. However, the rate of increase in ${\rho }_1^{\ast }$ is lower than the rate of increase in ${\rho }_2^{\ast }$. This implies that for higher values of $\gamma$ the relative benefit of early lockdown is higher. The first observation follows from the fact that as $\gamma$ goes up, the cost of lockdown in any period goes up, raising the thresholds for lockdown in both periods. To understand the second observation, consider a government which is deciding between an early or a late lockdown. Irrespective of the timing of the lockdown, the cost incurred will be the same. However, the early lockdown has the additional benefit of habit formation in period $2$. A government with a higher value of $\gamma$ is less efficient in managing the economy during a lockdown. This implies, at the new optimum, the marginal benefit from imposing a lockdown should be equal to this higher marginal cost. The government achieves this by imposing an early lockdown so that it can reap the additional benefit from habit formation in period $2$. This explains why ${\rho }_1^{\ast }$ increases less in comparison to ${\rho }_2^{\ast }$ as $\gamma$ increases. This effect is more prominent for higher values of $\beta$ as evident from Fig. 5.

An implication of this finding is that if a country with higher $\gamma$ has to impose a lockdown, then it is better to impose an early lockdown to get the benefit of habit formation.

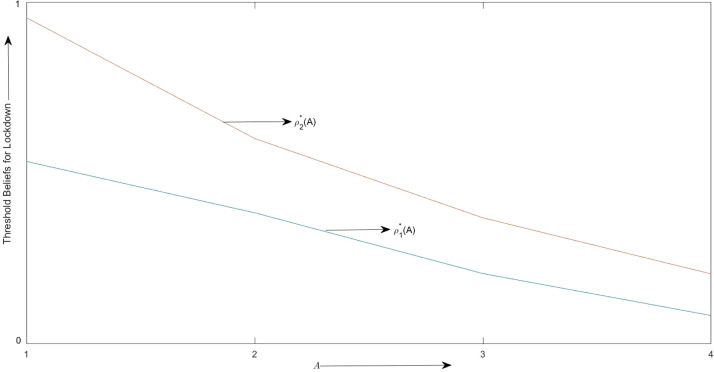
4.3. Effect of the length of period $3$ ($A$) and the democracy parameter ($\delta$) on the lockdown thresholds

We begin this subsection by examining the effect of the length of period $3$, i.e. $A$ on the lockdown thresholds ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$. This is depicted in Fig. 6. We can observe that as there is an increase in the expected time of the arrival of vaccine or treatment (i.e. $A$ increases), the thresholds for imposing the lockdown goes down in both periods.17 The intuition follows from the fact that an increase in $A$ entails more harm in the event the disease is virulent and hence the government wants to kick in disease reduction measures earlier.

Fig. 6.

Variation of thresholds with respect to $A$.

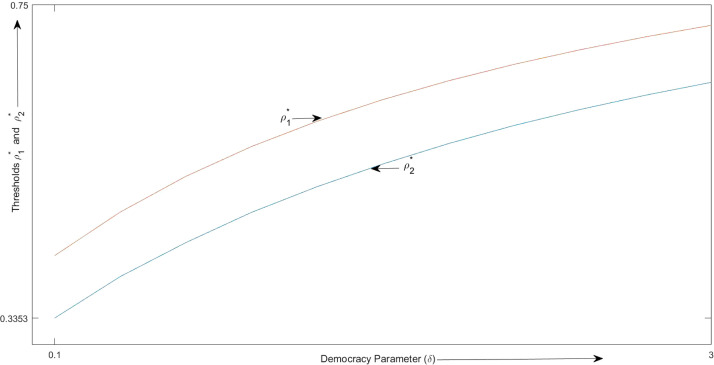
Next, in Fig. 7 we represent the variation of the thresholds ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ with respect to the parameter $\delta$. In our model, the parameter $\delta$ captures the public backlash in the event a lockdown is imposed when the disease is not virulent. We can interpret this parameter as representing the trust of the public on the incumbent government. The higher is the value of $\delta$, the lower is the trust of the public in the government.

Fig. 7.

Variation of the thresholds ${\rho }_1^{\ast }$ and ${\rho }_2^{\ast }$ with respect to $\delta$.

We can observe that as the level of trust of the public goes down, the government becomes more reluctant to impose a lockdown. This is demonstrated by the increasing thresholds for both periods. However, because of the benefit from habit formation, the relative benefit of early lockdown is higher and hence, the thresholds ${\rho }_1^{\ast }$ is always below the threshold ${\rho }_2^{\ast }$.

5. Discussion and concluding remarks

We have presented a stylized model of a disease with unknown virulence to illustrate the trade-off between learning and habit formation that have opposing impacts on the timing of a lockdown. To isolate this trade-off, we simplify on a number of dimensions including not explicitly modeling the decision of other agents in the population as well as ruling out strategic considerations. We believe strategic considerations to be minimal in a large population. Political considerations do play a role in a government’s decisions to impose a lockdown in terms of its timing and intensity. While we do not model this explicitly, political issues are partly captured by the variable $\delta$ which proxies for how much trust there is in government. A lower $\delta$ implies a higher trust and thus lower public backlash against the lockdown. We have also simplified the disease propagation mechanism by a single parameter that can be interpreted as the virulence or harm. Assuming this is proportional to the reproduction rate, this could have been embedded in a standard SIR model.18 where this reproduction rate would need to be greater than $1$ for the disease to spread over time. While the harm or virulence $r$ being modeled as a binary variable is a simplification, we think it captures the key qualitative features of a more realistic model where the virulence can take on more values. There are other simplifying assumptions, e.g. habit formation can also directly affect the economy if people stay home post lockdown and reduce demand in certain sectors, whereas in our model this is only captured through the equilibrium choice of $a$. Allowing a more direct impact would push towards a later lockdown but once again preserve the qualitative features of the model.

Our model suggests some interesting implications for the timing of lockdown both within and across countries. Holding everything else constant, one might have expected countries facing the pandemic later to adopt earlier lockdowns as they already had recourse to information from other countries. But as the model shows, this effect is moderated by factors such as the cost to the economy, trust in the government and country specific information (e.g. age composition) that can affect the virulence of the disease. Importantly, governments may over-estimate or under-estimate the strength of the habit formation parameter of the population. One can estimate differences in values of $\beta$ across countries by the level of compliance of the population with the suggested guidelines from the government. However, a government may not necessarily estimate the value of $\beta$ accurately. In the U.K., the government was criticized for delaying the lockdown, but it seems (from copies of meetings of the scientific advisory group) that there was a general belief that the U.K. population would not comply or reach behavioral fatigue (see Mahase, 2020).19 While the government may have underestimated the degree of compliance in the population with the guidelines on social distancing, it nonetheless rationalizes the ex ante decision of the government. Reports of the U.K.’s scientific advisory committee minutes also reveal how initial decisions were being reformulated as new data arrived on the disease and expert advice was being sought how to induce lasting behavioral changes through messaging during the lockdown20 in line with our model. These suggest that the tradeoffs we suggest in our model indeed played a crucial role in the decision to lockdown. Further, it points out that countries that have been ex post criticized for acting late may have been gathering data before taking the extreme step of a lockdown.

Coming to the parameters $\delta$ and $\gamma$, the early lockdown in India is consistent with the high support it enjoyed at that time (suggesting a low $\delta$) in the population as well as the fact that it had more precise signals already because of the spread in other countries. The fact that the economic cost to a lockdown in a country like India might be high is also consistent with our comparative static result that if a lockdown is imposed where $\gamma$ is high, it is better to impose it early. The distrust in government seen in the U.S.A (suggesting a high $\delta$) is also consistent with the lower intensity of lockdowns in many states.

The model shows the complex tradeoffs involved in a situation where the initial signals about the nature and spread of the disease were imprecise and the decisions on when and with what intensity to lockdown were based on the ex ante beliefs of governments on not just the damage to the economy and political backlash but on the degree to which this would change habits in the population. Thus, while ex post Italy’s lockdown may seem late,21 as the first country in Europe to see the spread of the virus, it may have felt it needed to know more before taking this step, which in fact may have resulted in a somewhat more stringent lockdown later. This phenomenon is consistent with our model i.e. when lockdown is imposed in period $2$ following a high signal, the value of ${\rho }_2$ is higher implying a high intensity of lockdown $a_2^{\ast }$.

There are a number of other things we have simplified or not considered. A more extended model would look at how different governments with different resources (e.g. ability to have track and trace in place in a short time) would use more targeted measures that allow for both some containment22 while gaining some information on disease propagation. We leave this for future work which should also look at empirical measures on trust in government, ability of the economy to adapt to virtual working etc. to see if they affected the timing and intensity of the lockdown as predicted by the model.

Manuscript handled by Editor Raouf Boucekkine

Appendix A. Expected continuation payoff in period $1$ from not imposing a lockdown

The general expression for continuation payoff from waiting and not imposing a lockdown in period $1$ is given by

$$\Gamma \left({\rho }_1\right)=-{\rho }_{1}r+\left[Pr(S_2=H|{\rho }_1)W_2^{\ast }\left({\rho }_2^H\right)\right]+\left[Pr(S_2=L|{\rho }_1)W_2^{\ast }\left({\rho }_2^L\right)\right]$$

First, consider ${\rho }_1<\widetilde{{\rho }_1}$. We have argued above that for any signal $S_2\in \{H,L\}$ received in period $2$, ${\rho }_2^i$, the posterior in period $2$ is less than or equal to ${\rho }_2^{\ast }$. This means we have

$$W_2^{\ast }\left({\rho }_2^H\right)=-{\rho }_2^{H}r(A+1);W_2^{\ast }\left({\rho }_2^L\right)=-{\rho }_2^{L}r(A+1)$$

Substituting this in the general expression of $\Gamma \left({\rho }_1\right)$ we obtain

$$\Rightarrow \Gamma \left({\rho }_1\right)=-{\rho }_{1}r+\{[{\rho }_{1}p+(1-p){(1-\rho )}_1]-\frac{{\rho }_{1}p}{{\rho }_{1}p+(1-p){(1-\rho )}_1}r(A+1)\}+$$

$$\{[{\rho }_1(1-p)+p{(1-\rho )}_1]-\frac{{\rho }_1(1-p)}{{\rho }_1(1-p)+p{(1-\rho )}_1}r(A+1)\}$$

$$\Rightarrow \Gamma \left({\rho }_1\right)=-{\rho }_{1}r(A+2)$$

Next, consider ${\rho }_1\in (\widetilde{{\rho }_1},\overline{{\rho }_1})$. Only if a high signal is received in period $2$, a lockdown is imposed. This gives us

$$Pr(S_2=H|{\rho }_1)W_2^{\ast }\left({\rho }_2^H\right)=-{\rho }_{1}pr(A+1)$$

$$+\left[Pr(S_2=H|{\rho }_1)\right]\{\frac{{\rho }_2^{H2}{r}^2{(1+A\beta )}^2}{4[{\rho }_2^{H}r(1+A\beta )+\gamma [1+(1-{\rho }_2^H)\delta ]]}-\gamma [1+(1-{\rho }_2^H)\delta ]\}$$

and

$$Pr(S_2=L|{\rho }_1)W_2^{\ast }\left({\rho }_2^L\right)=-{\rho }_1(1-p)r(A+1)$$

Thus, we have

$$\Gamma \left({\rho }_1\right)=-{\rho }_{1}r(A+2)+\left[Pr(S_2=H|{\rho }_1)\right]\times \{\frac{{\rho }_2^{H2}{r}^2{(1+A\beta )}^2}{4[{\rho }_2^{H}r(1+A\beta )+\gamma [1+(1-{\rho }_2^H)\delta ]]}-\gamma [1+(1-{\rho }_2^H)\delta ]\}$$

Finally, consider ${\rho }_1>\overline{{\rho }_1}$. Irrespective of the signal received in period $2$, a lockdown is imposed. This gives us

$$Pr(S_2=H|{\rho }_1)W_2^{\ast }\left({\rho }_2^H\right)=-{\rho }_{1}pr(A+1)$$

$$+\left[Pr(S_2=H|{\rho }_1)\right]\{\frac{{\rho }_2^{H2}{r}^2{(1+A\beta )}^2}{4[{\rho }_2^{H}r(1+A\beta )+\gamma [1+(1-{\rho }_2^H)\delta ]]}-\gamma [1+(1-{\rho }_2^H)\delta ]\}$$

and

$$Pr(S_2=L|{\rho }_1)W_2^{\ast }\left({\rho }_2^L\right)=-{\rho }_1(1-p)r(A+1)$$

$$+\left[Pr(S_2=L|{\rho }_1)\right]\{\frac{{\rho }_2^{L2}{r}^2{(1+A\beta )}^2}{4[{\rho }_2^{L}r(1+A\beta )+\gamma [1+(1-{\rho }_2^L)\delta ]]}-\gamma [1+(1-{\rho }_2^L)\delta ]\}$$

From this we can say

$$\Gamma \left({\rho }_1\right)=-{\rho }_{1}r(A+2)+\left[Pr(S_2=H|{\rho }_1)\right]\times \{\frac{{\rho }_2^{H2}{r}^2{(1+A\beta )}^2}{4[{\rho }_2^{H}r(1+A\beta )+\gamma [1+(1-{\rho }_2^H)\delta ]]}-\gamma [1+(1-{\rho }_2^H)\delta ]\}+\left[Pr(S_2=L|{\rho }_1)\right]\{\frac{{\rho }_2^{L2}{r}^2{(1+A\beta )}^2}{4[{\rho }_2^{L}r(1+A\beta )+\gamma [1+(1-{\rho }_2^L)\delta ]]}-\gamma [1+(1-{\rho }_2^L)\delta ]\}$$

From the above arguments, we can indeed confirm that $\Gamma \left({\rho }_1\right)\ge -{\rho }_{1}r(A+2)$ with strict inequality for ${\rho }_1>\widetilde{{\rho }_1}$. We can express $\Gamma \left({\rho }_1\right)$ as

$$\Gamma \left({\rho }_1\right)=-{\rho }_{1}r(A+2)$$

$$+max\{0,\left[Pr(S_2=H|{\rho }_1)\right]\{\frac{{\rho }_2^{H2}{r}^2{(1+A\beta )}^2}{4[{\rho }_2^{H}r(1+A\beta )+\gamma [1+(1-{\rho }_2^H)\delta ]]}-\gamma [1+(1-{\rho }_2^H)\delta ]\}\}$$

$$+max\{0,\left[Pr(S_2=L|{\rho }_1)\right]\{\frac{{\rho }_2^{L2}{r}^2{(1+A\beta )}^2}{4[{\rho }_2^{L}r(1+A\beta )+\gamma [1+(1-{\rho }_2^L)\delta ]]}-\gamma [1+(1-{\rho }_2^L)\delta ]\}\}$$ (14)

Appendix B. Proof of Lemma 1

First we determine the belief at which $W_1^{\ast }$ intersects the line $-{\rho }_{1}r(A+2)$.

$$W_1^{\ast }\ge -{\rho }_{1}r(A+2)\Rightarrow {\rho }_1\ge \frac{4\gamma (1+\delta )}{(\sqrt{5}-2)r(2+A\beta )+4\gamma \delta }>{\rho }_2^{\ast }>\widetilde{{\rho }_1}$$

From (9) we know that for ${\rho }_1>\widetilde{{\rho }_1}$, $\Gamma \left({\rho }_1\right)>-{\rho }_{1}r(A+2)$. This implies

$${\rho }_1^{\prime }>\frac{4\gamma (1+\delta )}{(\sqrt{5}-2)r(2+A\beta )+4\gamma \delta }>{\rho }_2^{\ast }$$

This concludes the proof of the lemma.

Appendix C. Proof of Proposition 1

Suppose ${\rho }_1^{\ast }$ is the belief where $W_1^f$ intersects $\Gamma$. ${\rho }_1^{\ast }$ is a function of $p$. For notational convenience we do away with writing the argument of ${\rho }_1^{\ast }$.

First we find the value of ${\rho }_1$ at which $W_1^{{}^{\prime }\ast }$ intersects $-{\rho }_{1}r(A+2)$. This is

$${\rho }_1^{″}=\frac{2\gamma [1+\delta ]}{[\sqrt{2}-1]r\{1+(A+1)\beta \}+2\gamma \delta }<{\rho }_2^{\ast }$$

Consider $p=\frac{1}{2}$. In this case $\Gamma \left({\rho }_1\right)=-{\rho }_{1}r(A+2)$. Since ${\rho }_1^{″}<{\rho }_2^{\ast }$, and from Lemma 1, ${\rho }_1^{″}$ is strictly less than the belief at which $W_1^{\ast }$ intersects $\Gamma$. This means we have

$$W_1^{{}^{\prime }\ast }\left({\rho }_1^{″}\right)=\Gamma \left({\rho }_1^{″}\right)>W_1^{\ast }\left({\rho }_1^{″}\right)$$

Thus $W_1^f=W_1^{{}^{\prime }\ast }$, and ${\rho }_1^{\ast }={\rho }_1^{″}<{\rho }_2^{\ast }$.

This implies at the right neighborhood of $p=\frac{1}{2}$, we have ${\rho }_1^{\ast }<{\rho }_2^{\ast }$. Let

$$p^{\ast }=\underset{p}{sup}\{p\in (\frac{1}{2},1]|{\rho }_1^{\ast }<{\rho }_2^{\ast }\}$$

Thus, for all $p\in (\frac{1}{2},p^{\ast })$ we have ${\rho }_1^{\ast }<{\rho }_2^{\ast }$.

Suppose $p^{\ast }<1$. This means for $p=p^{\ast }-ϵ$, ${\rho }_1^{\ast }={\rho }_2^{\ast }-\psi$ such that $ϵ>0$, $\psi >0$ and $\psi \to 0$ as $ϵ\to 0$.

Thus, at the right neighborhood of $p^{\ast }$, $W_1^f\left({\rho }_2^{\ast }\right)\le \Gamma \left({\rho }_2^{\ast }\right)$. $\Gamma \left({\rho }_1\right)$ is increasing in $p$, and $W_1^f$ is unaffected by $p$. Therefore, it follows that for all $p>p^{\ast }$, ${\rho }_1^{\ast }>{\rho }_2^{\ast }$.

This concludes the proof.