Abstract
B-cells are the poster child for cellular diversity and heterogeneity. The diverse repertoire of B lymphocytes, each expressing unique antigen receptors, provides broad protection against pathogens. However, B-cell diversity goes beyond unique antigen receptors. Side-stepping B-cell receptor (BCR) diversity through BCR-independent stimuli or engineered organisms with monoclonal BCRs still results in seemingly identical B-cells reaching a wide variety of fates in response to the same challenge. Identifying to what extent the molecular state of a B-cell determines its fate is key to gaining a predictive understanding of B-cells and consequently the ability to control them with targeted therapies. Signals received by B-cells through transmembrane receptors converge on intracellular molecular signaling networks, which control whether each B-cell divides, dies, or differentiates into a number of antibody-secreting distinct B-cell subtypes. The signaling networks that interpret these signals are well known to be susceptible to molecular variability and noise, providing a potential source of diversity in cell fate decisions. Iterative mathematical modeling and experimental studies have provided quantitative insight into how B-cells achieve distinct fates in response to pathogenic stimuli. Here, we review how systems biology modeling of B-cells, and the molecular signaling networks controlling their fates, is revealing the key determinants of cell-to-cell variability in B-cell destiny.
Keywords: systems biology, B-cells, computational modeling, heterogeneity, cell signaling, cell fate, NF-κB, cell-to-cell variability
Introduction
Following antigen exposure, B-cells are activated, often with the help of T-cells, to secrete antibodies essential for resolving infections. In addition to this well-studied humoral immune function, an important role for B-cells in cellular immunity is emerging (Hoffman et al., 2016). B-cell diversity is vital, with loss of diversity correlating with frailty and reductions in overall survival (Gibson et al., 2009). Each B-cell’s destiny can range from apoptosis within hours, rapid differentiation into a short-lived plasma blast in the initial days of an infection (Lam and Baumgarth, 2019), to that of a memory B-cell surviving for decades (Seifert and Küppers, 2016), or long-lived plasma cells found in the bone marrow > 40 years after vaccination (Brynjolfsson et al., 2017). Even B-cells stimulated ex vivo, without the complexities of T-cells and the germinal center, will undergo varied fates (Hawkins et al., 2009; Mitchell et al., 2018). Single-cell measurements of B-cells, stimulated with B-cell receptor (BCR)-independent stimuli, show vast cell-to-cell heterogeneity (Shih et al., 2002; Hawkins et al., 2013). Therefore, it seems that non-genetic B-cell diversity is an intrinsic property of B-cells. This has led to substantial efforts to identify the molecular determinants of B-cell destiny with pivotal studies combining insight from experimental models with in silico systems biology models. We will first discuss molecular determinants of each fate decision in isolation, followed by the molecular signaling pathways that interpret the cell’s environment. Finally, we will put the pieces together to describe how cell-to-cell variability in B-cell fates is understood through systems biology.
Cell Cycle
In response to antigen challenge, the B-cell population expands due to a portion of the cell population undergoing repeated rounds of cell division. In vitro, between 0 and 8 divisions occur, while multiple rounds of proliferation in the germinal center can lead to substantially higher (30+) divisions (Duffy et al., 2012; Tas et al., 2016; Mitchell and Hoffmann, 2018).
Mathematical models have been central to studies of the cell cycle since the 1960s, starting with phenomenological models recapitulating cell-cycle phase transitions (Smith and Martin, 1973). Dowling et al. (2014) observed that time spent in both G1 and S/G2/M phases is highly variable in B-cells. As a result, they proposed an alternative to the highly influential Smith–Martin model, in which all phases of the cell cycle stretch depending on a stochastically determined total division time (Smith and Martin, 1973). The timing of cell-cycle phases was found to be highly correlated in sister cells, suggesting a pre-existing non-genetic source of variability strongly inherited through cell division (Dowling et al., 2014). Interestingly, this stretching of all cell-cycle phases proportional to total cell-cycle length does not seem to be maintained in B lymphoma cell lines (Pham et al., 2018). An inherited molecular source of cell-to-cell variability is consistent with results from lineage-tracking of division times across multiple generations in proliferating B lymphocytes (Duffy et al., 2012; Mitchell et al., 2018). Heinzel et al. (2017) identified c-Myc as this molecule and fit a mathematical model to experimental data based on distributed c-Myc controlling a distributed division destiny. B-cell-specific modeling of cell division has been restricted to phenomenological modeling without explicitly representing molecular processes (Callard and Hodgkin, 2007; Zilman et al., 2010).
Kinetic modeling of the eukaryotic cell cycle became possible as increasing molecular mechanistic detail was revealed in the 1990s (Novak and Tyson, 1993; Csikasz-Nagy, 2009). The foundations for this progress was provided by the seminal work of Novák and Tyson, whose models have a striking ability to generate predictions validated many years later by experiments (Pomerening et al., 2003; Sha et al., 2003; Novák and Tyson, 2004). By adapting metabolic control analysis approaches to this model of the cell cycle, Conradie et al. (2010) found that variation in Cdk2 and its interactions with cyclin-dependent kinase inhibitor (p27Kip1) and CyclinE were the most likely sources of cell-to-cell variability in the cell cycle. Later, live-cell Cdk2 tracking identified a bifurcation in Cdk2 trajectories, controlled by p27, as a source of cell-to-cell heterogeneity (Spencer et al., 2013; Figure 1). Despite the fact that much of this mechanistic insight has been generated from models of non-lymphatic cell lines, the ability of mechanistic cell-cycle models to generate insights into multiple model organisms from yeast to xenopus suggests that the molecular architecture of such models can also be informative in B-cells (Pomerening et al., 2005; Skotheim et al., 2008). Indeed, a generic model of the mammalian cell cycle was incorporated into a multiscale B-cell model by Shokhirev et al. (2015), which replicated single-cell B-cell proliferation measured by time-lapse microscopy.
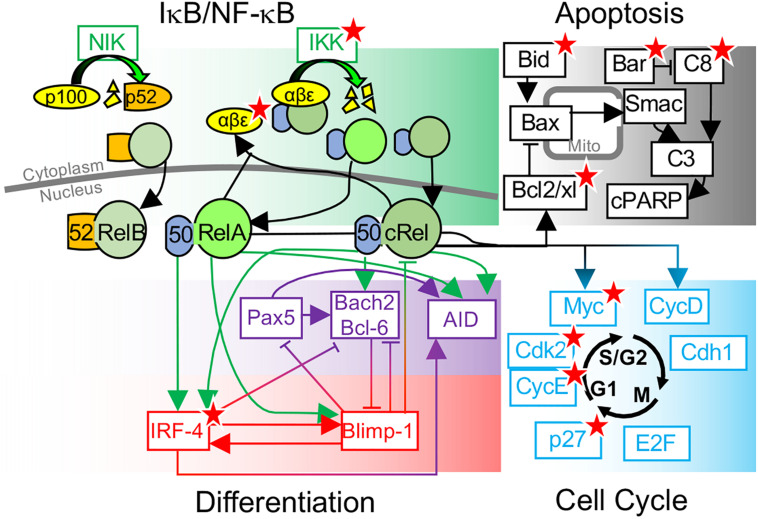
FIGURE 1.
Overview of key molecular determinants of B-cell fate decisions. Schematic of B-cell fate decisions determined by molecular networks controlling NF-κB, Apoptosis, differentiation, and the cell cycle. Key molecular determinants of cell-to-cell variability in B-cell fate decisions, identified through systems biology modeling and experimental studies, are indicated (★).
Cell Death
Mounting an antibody response requires a balance of B-cell proliferation and cell death. Inadequate apoptosis leads to auto-immunity and malignancies while excess apoptosis can cause immunodeficiency (Cossu, 2010; Correia et al., 2015; Li et al., 2016; Yang et al., 2016). Mathematical models have been widely used to illuminate the cell-to-cell variation in the timing of apoptosis (Spencer and Sorger, 2011). The first kinetic models of apoptosis were published two decades ago (Fussenegger et al., 2000), as single-cell analysis revealed switch-like effector caspase kinetics in individual cells (Goldstein et al., 2000; Tyas et al., 2000). This switch-like behavior motivated construction of computational models, with multiple mechanisms being proposed from receptor clustering to cooperativity in apoptosome formation or pore formation (Eissing et al., 2004; Hua et al., 2005; Bagci et al., 2006; Legewie et al., 2006; Ho and Harrington, 2010). Comprehensive mechanistic models constructed by Peter Sorger’s group, combined with single-cell fate tracking, have been instrumental in understanding cell-to-cell variability in apoptosis (Albeck et al., 2008; Spencer et al., 2009). These studies attributed variability in cell death timings to differences in BID truncation and a threshold determined by the Bcl-2 family proteins (Spencer et al., 2009; Figure 1). Apoptosis timing was found to be correlated in recently divided cells, but correlations between sister cells were lost quickly following cell division (t1/2 = 1.5 h) due to intrinsic gene expression noise (Spencer et al., 2009). Similar analysis in B-cells found similar transient correlations in sibling cell apoptosis timing (Hawkins et al., 2009). This may seem inconsistent with results showing that, in proliferating B-cells, the majority of cells that are progeny of a single founder cell will undergo apoptosis in the same generation, even following 100+ hours of proliferation (Hawkins et al., 2009; Mitchell et al., 2018). It seems that the cell-to-cell variability in the decision to undergo apoptosis in a particular generation, and the precise timing of apoptosis, have distinct sources. This is consistent with an analysis of the Albeck et al. (2008) model performed by Loriaux et al. (2013), which found that molecular determinants of the timing of apoptosis are not equivalent to molecular determinants of whether or not a cell undergoes apoptosis. This analysis suggests that Procaspase 8 and its negative regulator Bar are key determinants of cell-to-cell differences in apoptotic decision making (Loriaux et al., 2013). Recent Luria–Delbrück analysis of gene expression revealed that the set of genes whose expression is reliably inherited differs between cell types (Luria and Delbrück, 1943; Shaffer et al., 2020). Therefore, key to predictive mechanistic modeling of B-cell apoptosis will be understanding the molecular determinants of apoptotic decisions, along with how reliably these factors are inherited during proliferation.
B-Cell Differentiation
Following proliferation, activated B-cells differentiate into short-lived plasma blasts or long-lived plasma cells, both of which are antibody-secreting cells (ASCs) (Shapiro-Shelef and Calame, 2005). Cell division is required but not sufficient for ASC production, and considerable cell-to-cell differences in the timing of differentiation following activation exist, even in vitro (Tangye and Hodgkin, 2004; Zhou et al., 2018).
Recent single-cell RNAseq data indicate a bifurcation during the early stages of B-cell activation, committing a portion of cells to an ASC destiny (Scharer et al., 2020). This requires Interferon Regulatory Factor 4 (IRF4) induction, with higher and sustained activation biasing cells toward ASC fates (Ochiai et al., 2013). This was also seen by Xu et al. (2015) who constructed a minimal mathematical model of mutual inhibition between IRF4 and IRF8 in B-cells, with initial conditions obtained by flow cytometry, and found bifurcating fates recreating experiments showing a fraction of cells undergo rapid differentiation into plasma blasts. Sciammas et al. (2011) modeled the core regulatory network controlling terminal differentiation of activated B-cells including the mutual inhibition between Blimp1 and Bcl6/Bach2, along with the incoherent effects of IRF4 activating both somatic hypermutation (through AID) and differentiation (through Blimp1). This molecular model was incorporated into multiscale stochastic simulations, which revealed that differences in the time spent undergoing class-switch recombination and somatic hypermutation could be explained by the initial rate of IRF4 activation (Sciammas et al., 2011). Subsequent kinetic modeling found that interactions between Irf4, Bcl6, and Blimp1 were sufficient to capture a broad variety of B-cell differentiation dynamics (Martínez et al., 2012). Taken together, these results show that cell-to-cell differences in terminal differentiation of B-cells result from differences in IRF4 signaling.
NF-κB
NF-κB is a dimeric transcription factor, first discovered in B-cells and later revealed to have near-ubiquitous expression (Sen and Baltimore, 1986; William et al., 1995; Xu et al., 1996; Inlay et al., 2002; Baltimore, 2009). NF-κB’s important role in B-cell development, survival, and function has been widely studied (Vallabhapurapu and Karin, 2009; Gerondakis and Siebenlist, 2010; Kaileh and Sen, 2012; Heise et al., 2014; Almaden et al., 2016). In response to increasing BCR activation, B-cells show a digital all-or-nothing NF-κB response, with an increasing number of cells responding, rather than each cell increasing its response, with increasing NF-κB (Shinohara et al., 2014). The all-or-nothing response suggests the presence of a positive feedback loop, enabling cells that cross a cell-specific threshold of activation to invariably achieve maximum activation. Through iterative computational and experimental modeling, a positive feedback was identified between TAK1 (MAP3K7) and inhibitor of NF-κB (IκB) kinase-β (IKKβ) complex, resulting in switch-like single-cell behaviors; disruption of this feedback results in a more graded response (Shinohara et al., 2014). These all-or-nothing responses are consistent with studies applying information theoretic approaches to NF-κB signaling, which reveal that intrinsic noise in NF-κB limits the information the pathway can encode about each cell’s environment to only a few states, e.g., absence, low and high stimuli (Cheong et al., 2011; Selimkhanov et al., 2014; Mitchell and Hoffmann, 2018). It seems unlikely that the intricate environmental stimuli received by B-cells through diverse receptors can be accurately encoded through noisy NF-κB signaling in single cells (Rawlings et al., 2012). This may be reconciled by a model-aided analysis that revealed a trade-off between reliable single-cell responses and reliable population-scale responses, with distributed switch-like responses enabling an appropriate fraction of cells within a population to reliably respond (Suderman et al., 2017).
Core to NF-κB signaling is its regulation through sequestration in the cytoplasm by inhibitory proteins (IκBs) (Mitchell et al., 2016). IκBs are themselves induced by nuclear NF-κB, resulting in a negative feedback in which NF-κB inhibits itself with a delay due to gene expression and protein synthesis (Figure 1). Such systems can create the oscillatory dynamics seen in NF-κB signaling, and mathematical modeling has been central to understanding NF-κB (Hoffmann et al., 2002; Lipniacki et al., 2004; Nelson et al., 2004; Basak et al., 2012). Each IκB family member has distinct kinetics of induction, degradation, and NF-κB sequestration, resulting in distinct contributions to cell-to-cell variability. IκBα displays rapid and robust stimulus-dependent degradation and subsequent NF-κB-dependent induction, creating a noise-insensitive first peak of NF-κB activity. IκBε has slower kinetics than IκBα (Kearns et al., 2006). Incorporating IκBε with slower negative feedback into mathematical simulations revealed that IκBε enables a more reliable dose-dependent response to sustained signals, minimizing the impact of stochastic gene expression on late-phase NF-κB activity (Longo et al., 2013). Through both kinetic modeling and experimental investigation, IκBε has been found to limit B-cell expansion through limiting NF-κB cRel and RelA (Alves et al., 2014).
Whether cell-to-cell differences in NF-κB signaling result from intrinsically generated noise, such as transcriptional noise, or pre-existing differences between B-cells prior to stimulation has been debated (Williams et al., 2014). Both sources of variation have been simulated through mathematical modeling of NF-κB, with intrinsic noise recreated through stochastic simulation using the Gillespie algorithm (Gillespie, 1977) and pre-existing variability simulated by sampling parameters prior to deterministic simulations (Hayot and Jayaprakash, 2006; Cheng et al., 2015; Hughey et al., 2015). Recent studies combining mathematical modeling with single-cell analysis find that pre-existing cell-to-cell differences best explain distributed single-cell NF-κB dynamics and the similar responses observed in daughter cells (Cheng et al., 2015; Hughey et al., 2015).
Putting the Pieces Together
In studying the regulatory networks controlling the B-cell fate decisions described above, a pattern emerges. Key molecular determinants of cell-to-cell variability in B-cell fate decisions are NF-κB target genes. Indeed, recent single-cell RNA-sequencing analysis found that the most highly variable genes in lymphoid cells were functionally significant and centered around NF-κB and its target genes, including NFKBIA, MYC, IRF4, and AID (Osorio et al., 2020).
Myc and Bcl2 are NF-κB target genes that have been shown to control B-cell division and apoptosis (Duyao et al., 1990; Chen et al., 1999; Catz and Johnson, 2001; Figure 1). This was used by Shokhirev et al. (2015) in order to connect models of NF-κB signaling, the cell cycle, and apoptosis networks discussed above, recapitulating cellular statistics from single-cell time-lapse microscopy and revealing that NF-κB cRel was essential to protect growing B-cells from apoptosis. Mitchell et al. (2018) used this model to determine the source of cell-to-cell variability using single-cell lineage tracking experiments and discovered that B-cell fates were determined by molecular differences in the naïve B-cell population that are reliably inherited during proliferation. Interestingly, predictions of the most significant molecular determinants of cell-to-cell fate variability depend on the magnitude of variability. Perturbing parameters controlling NF-κB signaling resulted in the largest changes in B-cell proliferation; however, this required relatively large parameter changes of twofold or more. Smaller changes in parameters, and logistic regression on simulated cell populations with experimentally determined molecular heterogeneity, did not identify NF-κB-related biochemical processes as the largest determinants of cell-to-cell variability in B-cell proliferation. Instead, apoptotic signaling regulators such as Bar, Caspase 3, and XIAP were predicted to be the most significant determinants of B-cell proliferative outcome, a result tested through caspase inhibition (Mitchell et al., 2018).
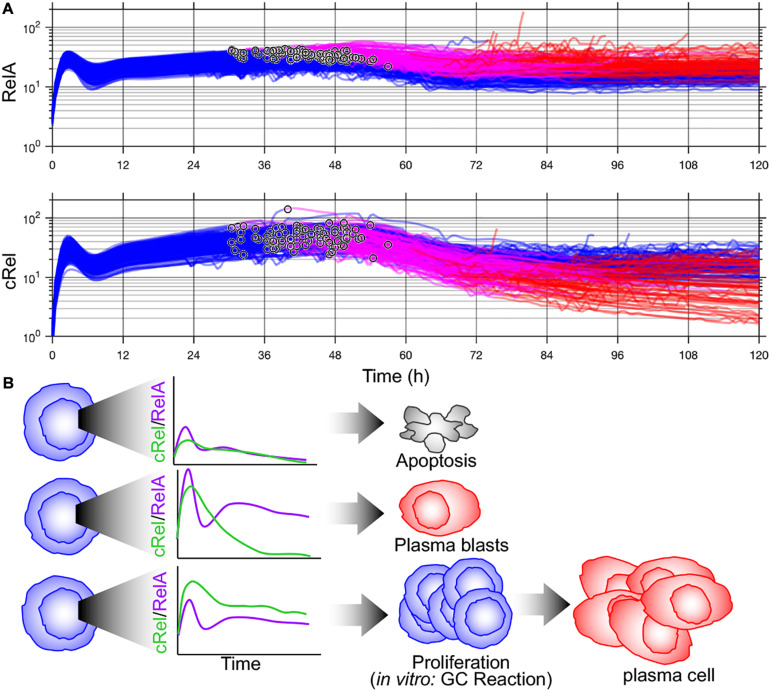
Key determinants of cell-to-cell variability in B-cell terminal differentiation including Blimp1 and IRF4 are also NF-κB target genes (Grumont and Gerondakis, 2000; Morgan et al., 2009; Heise et al., 2014). This led Roy et al. (2019) to add NF-κB regulation to the model of Sciammas et al. (2011) and discover that a previously unidentified regulatory interaction was required to recapitulate experimental results. Roy et al. (2019) discovered that the missing interaction was transcriptional inhibition of NF-κB cRel by Blimp1 and that dynamic downregulation of cRel by Blimp1 was required for plasma cell differentiation (Roy et al., 2019). Once this new regulatory interaction was incorporated into the multiscale model of Shokhirev et al. (2015), the model recapitulated cell-to-cell variability in B-cell proliferation and differentiation dynamics from wild-type and knockout mice (Roy et al., 2019). Given the overlap between NF-κB target genes and key determinants of B-cell fate decisions, well characterized cell-to-cell variability in NF-κB may coordinate diverse B-cell fates. Indeed, if Blimp1 upregulation time is noted in simulations from Roy et al. (2019), this model predicts that B-cells with the highest NF-κB RelA differentiate more quickly (Figure 2). As NF-κB integrates BCR and toll-like receptor signaling and induces IRF4, this prediction is consistent with the rapid differentiation by high-affinity BCR-expressing B-cells into plasma blasts (Paus et al., 2006) and the rapidly differentiating subset of cells with high IRF4 activation (Xu et al., 2015). Subsequent cRel downregulation is required to complete differentiation (Roy et al., 2019). The distinct roles of NF-κB cRel and RelA in B-cell survival and differentiation, respectively, seen in these multiscale models are consistent with in vivo requirements for germinal center maintenance and plasma cell generation (Heise et al., 2014) and an emerging picture of subunit-specific dysregulation of NF-κB in lymphoid malignancies (Kennedy and Klein, 2018).
FIGURE 2.
Multiscale modeling of B-cell fates predicts cell-to-cell variability in NF-κB subunits that can orchestrate distinct fates. (A) Time course of NF-κB RelA (top) and NF-κB cRel (bottom) from multiscale simulation data from Mitchell et al. (2018). Blimp-1 upregulation time is indicated (°). Activated B-cells (blue), high Blimp1 (pink), and high Blimp1 with low AID (complete differentiation, red). (B) Proposed orchestration of cell fates through NF-κB. Inadequate NF-κB induction results in apoptosis (top). High RelA induction followed and subsequent dynamic cRel downregulation results in rapid plasma blast differentiation. High cRel with lower RelA (and therefore lower IRF4) results in a proliferative/germinal center phenotype.
Discussion
The decision each B-cell faces, between proliferation, apoptosis, and differentiation, is vitally important to thread the needle between autoimmunity and immunodeficiency. An effective immune response requires a portion of B-cells to rapidly express antibodies, in order to buy time for the germinal center reaction to iteratively refine and expand an antigen-specific B-cell population to resolve the infection. Not only does this require careful coordination of multiple cell fates within each B-cell, but it requires cells to reach distinct decisions to the same challenge. Mathematical modeling provides unique opportunities to quantitatively disentangle the cell-intrinsic and extrinsic sources of cell-to-cell variability. Through combined modeling and single-cell experiments, we now know that distinct B-cell fates are achieved through molecular differences in the founder cell of each lineage, which are reliably inherited across many rounds of cell division (Hawkins et al., 2009; Mitchell et al., 2018).
B-cell differentiation takes place in the germinal centers of the spleen and lymph nodes. These structures spatially organize and traffic B-cells, enabling interactions with antigen-presenting cells and T-cells (De Silva and Klein, 2015; Mesin et al., 2016). Recently, these extra- and intercellular processes have been modeled through stochastic approaches (Thomas et al., 2019; Pélissier et al., 2020). Integrating the molecular determinants of B-cell fate decision into models of B-cell fates within the germinal center will be informative for therapeutic targeting of B-cells (Kepler and Perelson, 1993; Figge, 2005; Meyer-Hermann et al., 2012; Robert et al., 2017; Thomas et al., 2019; Pélissier et al., 2020; Verheijen et al., 2020).
The ultimate goal of many of the studies discussed here, and systems biology as a whole, is to use models to enable predictive control over cells in health and disease. While the emerging picture from experiments and models is that measuring one or even 5+ (Mitchell et al., 2018) molecular abundances is unlikely to reliably predict a B-cell’s fate, this does not preclude reliable interventions. Modeling has identified molecular targets to control B-cell fates and predicted how mutations will skew proportions and timings of cell fate decisions in experimental systems (Mitchell et al., 2018; Roy et al., 2019). One challenge to predictive modeling is that many models have been parameterized in other cell types, and B-cell specific parameterization is daunting. However, the prevalence of single-cell data, along with promising model-generated experiment-validated results, suggests that a systems biology approach to predictably controlling B-cell responses is a realistic goal.
Author Contributions
SM conceived the study and wrote the manuscript.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Alexander Hoffman, Koushik Roy, and Haripriya Vaidehi Narayanan for insightful discussion of the topic and many useful comments on the manuscript.
Footnotes
Funding. This work was funded by Leukaemia UK John Goldman Fellowship (2020/JGF/003) and Beat: Cancer Research Grant.
References
- Albeck J. G., Burke J. M., Spencer S. L., Lauffenburger D. A., Sorger P. K. (2008). Modeling a snap-action, variable-delay switch controlling extrinsic cell death. PLoS Biol. 6:e299. 10.1371/journal.pbio.0060299 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almaden J. V., Liu Y. C., Yang E., Otero D. C., Birnbaum H., Davis-Turak J., et al. (2016). B-cell survival and development controlled by the coordination of NF-κB family members RelB and cRel. Blood J. Am. Soc. Hematol. 127 1276–1286. 10.1182/blood-2014-10-606988 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alves B. N., Tsui R., Almaden J., Shokhirev M. N., Davis-Turak J., Fujimoto J., et al. (2014). IκBε is a key regulator of B cell expansion by providing negative feedback on cRel and RelA in a stimulus-specific manner. J. Immunol. 192 3121–3132. 10.4049/jimmunol.1302351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bagci E., Vodovotz Y., Billiar T., Ermentrout G., Bahar I. (2006). Bistability in apoptosis: roles of bax, bcl-2, and mitochondrial permeability transition pores. Biophys. J. 90 1546–1559. 10.1529/biophysj.105.068122 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baltimore D. (2009). Discovering NF-κB. Cold Spring Harbor Perspect. Biol. 1:a000026. 10.1101/cshperspect.a000026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basak S., Behar M., Hoffmann A. (2012). Lessons from mathematically modeling the NF-κB pathway. Immunol. Rev. 246 221–238. 10.1111/j.1600-065x.2011.01092.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brynjolfsson S. F., Mohaddes M., Kärrholm J., Wick M.-J. (2017). Long-lived plasma cells in human bone marrow can be either CD19+ or CD19–. Blood Adv. 1:835. 10.1182/bloodadvances.2017004481 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Callard R., Hodgkin P. (2007). Modeling T-and B-cell growth and differentiation. Immunol. Rev. 216 119–129. [DOI] [PubMed] [Google Scholar]
- Catz S. D., Johnson J. L. (2001). Transcriptional regulation of bcl-2 by nuclear factor κB and its significance in prostate cancer. Oncogene 20 7342–7351. 10.1038/sj.onc.1204926 [DOI] [PubMed] [Google Scholar]
- Chen F., Demers L. M., Vallyathan V., Lu Y., Castranova V., Shi X. (1999). Involvement of 5′-Flanking κB-like Sites withinbcl-x Gene in Silica-induced Bcl-x Expression. J. Biol. Chem. 274 35591–35595. 10.1074/jbc.274.50.35591 [DOI] [PubMed] [Google Scholar]
- Cheng Z., Taylor B., Ourthiague D. R., Hoffmann A. (2015). Distinct single-cell signaling characteristics are conferred by the MyD88 and TRIF pathways during TLR4 activation. Sci. Signal. 8:ra69. 10.1126/scisignal.aaa5208 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheong R., Rhee A., Wang C. J., Nemenman I., Levchenko A. (2011). Information transduction capacity of noisy biochemical signaling networks. Science 334 354–358. 10.1126/science.1204553 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conradie R., Bruggeman F. J., Ciliberto A., Csikász-Nagy A., Novák B., Westerhoff H. V., et al. (2010). Restriction point control of the mammalian cell cycle via the cyclin E/Cdk2: p27 complex. FEBS J. 277 357–367. 10.1111/j.1742-4658.2009.07473.x [DOI] [PubMed] [Google Scholar]
- Correia C., Schneider P. A., Dai H., Dogan A., Maurer M. J., Church A. K., et al. (2015). BCL2 mutations are associated with increased risk of transformation and shortened survival in follicular lymphoma. Blood J. Am. Soc. Hematol. 125 658–667. 10.1182/blood-2014-04-571786 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cossu F. (2010). Genetics of SCID. Italian J. Pediatr. 36:76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csikasz-Nagy A. (2009). Computational systems biology of the cell cycle. Briefings Bioinform. 10 424–434. 10.1093/bib/bbp005 [DOI] [PubMed] [Google Scholar]
- De Silva N. S., Klein U. (2015). Dynamics of B cells in germinal centres. Nat. Rev. Immunol. 15 137–148. 10.1038/nri3804 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dowling M. R., Kan A., Heinzel S., Zhou J. H., Marchingo J. M., Wellard C. J., et al. (2014). Stretched cell cycle model for proliferating lymphocytes. Proceed. Natl. Acad. Sci. 111 6377–6382. 10.1073/pnas.1322420111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duffy K. R., Wellard C. J., Markham J. F., Zhou J. H., Holmberg R., Hawkins E. D., et al. (2012). Activation-induced B cell fates are selected by intracellular stochastic competition. Science 335 338–341. 10.1126/science.1213230 [DOI] [PubMed] [Google Scholar]
- Duyao M. P., Buckler A. J., Sonenshein G. E. (1990). Interaction of an NF-kappa B-like factor with a site upstream of the c-myc promoter. Proc. Natl. Acad. Sci. U S A. 87 4727–4731. 10.1073/pnas.87.12.4727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eissing T., Conzelmann H., Gilles E. D., Allgöwer F., Bullinger E., Scheurich P. (2004). Bistability analyses of a caspase activation model for receptor-induced apoptosis. J. Biol. Chem. 279 36892–36897. 10.1074/jbc.m404893200 [DOI] [PubMed] [Google Scholar]
- Figge M. T. (2005). Stochastic discrete event simulation of germinal center reactions. Phys. Rev. E 71:051907. [DOI] [PubMed] [Google Scholar]
- Fussenegger M., Bailey J. E., Varner J. (2000). A mathematical model of caspase function in apoptosis. Nat. Biotechnol. 18 768–774. 10.1038/77589 [DOI] [PubMed] [Google Scholar]
- Gerondakis S., Siebenlist U. (2010). Roles of the NF-κB pathway in lymphocyte development and function. Cold Spring Harbor Perspect. Biol. 2:a000182. 10.1101/cshperspect.a000182 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson K. L., Wu Y. C., Barnett Y., Duggan O., Vaughan R., Kondeatis E., et al. (2009). B-cell diversity decreases in old age and is correlated with poor health status. Aging Cell 8 18–25. 10.1111/j.1474-9726.2008.00443.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie D. T. (1977). Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81 2340–2361. 10.1021/j100540a008 [DOI] [Google Scholar]
- Goldstein J. C., Waterhouse N. J., Juin P., Evan G. I., Green D. R. (2000). The coordinate release of cytochrome c during apoptosis is rapid, complete and kinetically invariant. Nat. Cell Biol. 2 156–162. 10.1038/35004029 [DOI] [PubMed] [Google Scholar]
- Grumont R. J., Gerondakis S. (2000). Rel induces interferon regulatory factor 4 (IRF-4) expression in lymphocytes: modulation of interferon-regulated gene expression by rel/nuclear factor κB. J. Exp. Med. 191 1281–1292. 10.1084/jem.191.8.1281 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawkins E., Markham J., Mcguinness L., Hodgkin P. (2009). A single-cell pedigree analysis of alternative stochastic lymphocyte fates. Proc. Natl. Acad. Sci. 106 13457–13462. 10.1073/pnas.0905629106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawkins E., Turner M., Wellard C., Zhou J., Dowling M., Hodgkin P. (2013). Quantal and graded stimulation of B lymphocytes as alternative strategies for regulating adaptive immune responses. Nat. Commun. 4:2406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayot F., Jayaprakash C. (2006). NF-κB oscillations and cell-to-cell variability. J. Theoret. Biol. 240 583–591. 10.1016/j.jtbi.2005.10.018 [DOI] [PubMed] [Google Scholar]
- Heinzel S., Giang T. B., Kan A., Marchingo J. M., Lye B. K., Corcoran L. M., et al. (2017). A Myc-dependent division timer complements a cell-death timer to regulate T cell and B cell responses. Nat. Immunol. 18 96–103. 10.1038/ni.3598 [DOI] [PubMed] [Google Scholar]
- Heise N., De Silva N. S., Silva K., Carette A., Simonetti G., Pasparakis M., et al. (2014). Germinal center B cell maintenance and differentiation are controlled by distinct NF-κB transcription factor subunits. J. Exp. Med. 211 2103–2118. 10.1084/jem.20132613 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho K. L., Harrington H. A. (2010). Bistability in apoptosis by receptor clustering. PLoS Comput. Biol. 6:e1000956. 10.1371/journal.pcbi.1000956 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman W., Lakkis F. G., Chalasani G. (2016). B cells, antibodies, and more. Clin. J. Am. Soc. Nephrol. 11 137–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann A., Levchenko A., Scott M. L., Baltimore D. (2002). The IκB-NF-κB signaling module: temporal control and selective gene activation. Science 298 1241–1245. 10.1126/science.1071914 [DOI] [PubMed] [Google Scholar]
- Hua F., Cornejo M. G., Cardone M. H., Stokes C. L., Lauffenburger D. A. (2005). Effects of Bcl-2 levels on Fas signaling-induced caspase-3 activation: molecular genetic tests of computational model predictions. J. Immunol. 175 985–995. 10.4049/jimmunol.175.2.985 [DOI] [PubMed] [Google Scholar]
- Hughey J. J., Gutschow M. V., Bajar B. T., Covert M. W. (2015). Single-cell variation leads to population invariance in NF-κB signaling dynamics. Mol. Biol. Cell 26 583–590. 10.1091/mbc.e14-08-1267 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inlay M., Alt F. W., Baltimore D., Xu Y. (2002). Essential roles of the kappa light chain intronic enhancer and 3′ enhancer in kappa rearrangement and demethylation. Nat. Immunol. 3 463–468. 10.1038/ni790 [DOI] [PubMed] [Google Scholar]
- Kaileh M., Sen R. (2012). NF-κB function in B lymphocytes. Immunol. Rev. 246 254–271. 10.1111/j.1600-065x.2012.01106.x [DOI] [PubMed] [Google Scholar]
- Kearns J. D., Basak S., Werner S. L., Huang C. S., Hoffmann A. (2006). IκBε provides negative feedback to control NF-κB oscillations, signaling dynamics, and inflammatory gene expression. J. Cell Biol. 173 659–664. 10.1083/jcb.200510155 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy R., Klein U. (2018). Aberrant activation of NF-κB signalling in aggressive lymphoid malignancies. Cells 7:189. 10.3390/cells7110189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kepler T. B., Perelson A. S. (1993). Cyclic re-entry of germinal center B cells and the efficiency of affinity maturation. Immunol. Today 14 412–415. 10.1016/0167-5699(93)90145-b [DOI] [PubMed] [Google Scholar]
- Lam J. H., Baumgarth N. (2019). The multifaceted B cell response to influenza virus. J. Immunol. 202 351–359. 10.4049/jimmunol.1801208 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legewie S., Blüthgen N., Herzel H. (2006). Mathematical modeling identifies inhibitors of apoptosis as mediators of positive feedback and bistability. PLoS Comput. Biol. 2:e120. 10.1371/journal.pcbi.0020120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y., Takahashi Y., Fujii S.-I., Zhou Y., Hong R., Suzuki A., et al. (2016). EAF2 mediates germinal centre B-cell apoptosis to suppress excessive immune responses and prevent autoimmunity. Nat. Commun. 7: 10836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipniacki T., Paszek P., Brasier A. R., Luxon B., Kimmel M. (2004). Mathematical model of NF-κB regulatory module. J. Theoret. Biol. 228 195–215. 10.1016/j.jtbi.2004.01.001 [DOI] [PubMed] [Google Scholar]
- Longo D. M., Selimkhanov J., Kearns J. D., Hasty J., Hoffmann A., Tsimring L. S. (2013). Dual delayed feedback provides sensitivity and robustness to the NF-κ B signaling module. PLoS Comput. Biol. 9:e1003112. 10.1371/journal.pcbi.1003112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loriaux P. M., Tesler G., Hoffmann A. (2013). Characterizing the relationship between steady state and response using analytical expressions for the steady states of mass action models. PLoS Comput. Biol. 9:e1002901. 10.1371/journal.pcbi.1002901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luria S. E., Delbrück M. (1943). Mutations of bacteria from virus sensitivity to virus resistance. Genetics 28:491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martínez M. R., Corradin A., Klein U., Álvarez M. J., Toffolo G. M., Di Camillo B., et al. (2012). Quantitative modeling of the terminal differentiation of B cells and mechanisms of lymphomagenesis. Proc. Natl. Acad. Sci. U S A. 109 2672–2677. 10.1073/pnas.1113019109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mesin L., Ersching J., Victora G. D. (2016). Germinal center B cell dynamics. Immunity 45 471–482. 10.1016/j.immuni.2016.09.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer-Hermann M., Mohr E., Pelletier N., Zhang Y., Victora G. D., Toellner K.-M. (2012). A theory of germinal center B cell selection, division, and exit. Cell Rep. 2 162–174. 10.1016/j.celrep.2012.05.010 [DOI] [PubMed] [Google Scholar]
- Mitchell S., Hoffmann A. (2018). Identifying noise sources governing cell-to-cell variability. Curr. Opin. Systems Biol. 8 39–45. 10.1016/j.coisb.2017.11.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell S., Roy K., Zangle T. A., Hoffmann A. (2018). Nongenetic origins of cell-to-cell variability in B lymphocyte proliferation. Proc. Natl. Acad. Sci. U S A. 115 E2888–E2897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell S., Vargas J., Hoffmann A. (2016). Signaling via the NFκB system. Wiley Interdiscip. Rev. Systems Biol. Med. 8 227–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan M. A., Magnusdottir E., Kuo T. C., Tunyaplin C., Harper J., Arnold S. J., et al. (2009). Blimp-1/Prdm1 alternative promoter usage during mouse development and plasma cell differentiation. Mol. Cell. Biol. 29 5813–5827. 10.1128/mcb.00670-09 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson D. E., Ihekwaba A. E. C., Elliott M., Johnson J. R., Gibney C. A., Foreman B. E., et al. (2004). Oscillations in NF-κB signaling control the dynamics of gene expression. Science 306 704–708. 10.1126/science.109996 [DOI] [PubMed] [Google Scholar]
- Novak B., Tyson J. J. (1993). Numerical analysis of a comprehensive model of M-phase control in xenopus oocyte extracts and intact embryos. J. Cell Sci. 106 1153–1168. [DOI] [PubMed] [Google Scholar]
- Novák B., Tyson J. J. (2004). A model for restriction point control of the mammalian cell cycle. J. Theoret. Biol. 230 563–579. 10.1016/j.jtbi.2004.04.039 [DOI] [PubMed] [Google Scholar]
- Ochiai K., Maienschein-Cline M., Simonetti G., Chen J., Rosenthal R., Brink R., et al. (2013). Transcriptional regulation of germinal center B and plasma cell fates by dynamical control of IRF4. Immunity 38 918–929. 10.1016/j.immuni.2013.04.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osorio D., Yu X., Zhong Y., Li G., Serpedin E., Huang J. Z., et al. (2020). Single-Cell expression variability implies cell function. Cells 9:14. 10.3390/cells9010014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paus D., Phan T. G., Chan T. D., Gardam S., Basten A., Brink R. (2006). Antigen recognition strength regulates the choice between extrafollicular plasma cell and germinal center B cell differentiation. J. Exp. Med. 203 1081–1091. 10.1084/jem.20060087 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pélissier A., Akrout Y., Jahn K., Kuipers J., Klein U., Beerenwinkel N., et al. (2020). computational model reveals a stochastic mechanism behind germinal center clonal bursts. Cells 9:1448. 10.3390/cells9061448 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pham K., Kan A., Whitehead L., Hennessy R., Rogers K., Hodgkin P. (2018). Converse smith-martin cell cycle kinetics by transformed B lymphocytes. Cell Cycle 17 2041–2051. 10.1080/15384101.2018.1511511 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pomerening J. R., Kim S. Y., Ferrell J. E., Jr. (2005). Systems-level dissection of the cell-cycle oscillator: bypassing positive feedback produces damped oscillations. Cell 122 565–578. 10.1016/j.cell.2005.06.016 [DOI] [PubMed] [Google Scholar]
- Pomerening J. R., Sontag E. D., Ferrell J. E. (2003). Building a cell cycle oscillator: hysteresis and bistability in the activation of Cdc2. Nat. Cell Biol. 5 346–351. 10.1038/ncb954 [DOI] [PubMed] [Google Scholar]
- Rawlings D. J., Schwartz M. A., Jackson S. W., Meyer-Bahlburg A. (2012). Integration of B cell responses through Toll-like receptors and antigen receptors. Nat. Rev. Immunol. 12 282–294. 10.1038/nri3190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robert P. A., Rastogi A., Binder S. C., Meyer-Hermann M. (2017). “How to simulate a germinal center,” in Germinal Centers. Methods in Molecular Biology, ed. Calado D. (New York, NY: Humana Press; ), 303–334. 10.1007/978-1-4939-7095-7_22 [DOI] [PubMed] [Google Scholar]
- Roy K., Mitchell S., Liu Y., Ohta S., Lin Y.-S., Metzig M. O., et al. (2019). A regulatory circuit controlling the dynamics of NFκB cRel transitions B cells from proliferation to plasma cell differentiation. Immunity 50 616.–628 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scharer C. D., Patterson D. G., Mi T., Price M. J., Hicks S. L., Boss J. M. (2020). Antibody-secreting cell destiny emerges during the initial stages of B-cell activation. Nat. Commun. 11:3989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sciammas R., Li Y., Warmflash A., Song Y., Dinner A. R., Singh H. (2011). An incoherent regulatory network architecture that orchestrates B cell diversification in response to antigen signaling. Mol. Systems Biol. 7:495. 10.1038/msb.2011.25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seifert M., Küppers R. (2016). Human memory B cells. Leukemia 30 2283–2292. [DOI] [PubMed] [Google Scholar]
- Selimkhanov J., Taylor B., Yao J., Pilko A., Albeck J., Hoffmann A., et al. (2014). Accurate information transmission through dynamic biochemical signaling networks. Science 346 1370–1373. 10.1126/science.1254933 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sen R., Baltimore D. (1986). Multiple nuclear factors interact with the immunoglobulin enhancer sequences. Cell 46 705–716. 10.1016/0092-8674(86)90346-6 [DOI] [PubMed] [Google Scholar]
- Sha W., Moore J., Chen K., Lassaletta A. D., Yi C.-S., Tyson J. J., et al. (2003). Hysteresis drives cell-cycle transitions in Xenopus laevis egg extracts. Proc. Natl. Acad. Sci. U S A. 100 975–980. 10.1073/pnas.0235349100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaffer S. M., Emert B. L., Hueros R. A. R., Coté C., Harmange G., Schaff D. L., et al. (2020). Memory sequencing reveals heritable single-cell gene expression programs associated with distinct cellular behaviors. Cell 182 947–959. 10.1016/j.cell.2020.07.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapiro-Shelef M., Calame K. (2005). Regulation of plasma-cell development. Nat. Rev. Immunol. 5 230–242. 10.1038/nri1572 [DOI] [PubMed] [Google Scholar]
- Shih T.-A. Y., Roederer M., Nussenzweig M. C. (2002). Role of antigen receptor affinity in T cell–independent antibody responses in vivo. Nat. Immunol. 3 399–406. 10.1038/ni776 [DOI] [PubMed] [Google Scholar]
- Shinohara H., Behar M., Inoue K., Hiroshima M., Yasuda T., Nagashima T., et al. (2014). Positive feedback within a kinase signaling complex functions as a switch mechanism for NF-κB activation. Science 344 760–764. 10.1126/science.1250020 [DOI] [PubMed] [Google Scholar]
- Shokhirev M. N., Almaden J., Davis-Turak J., Birnbaum H. A., Russell T. M., Vargas J. A., et al. (2015). A multi-scale approach reveals that NF-κB cR el enforces a B-cell decision to divide. Mol. Systems Biol. 11:783. 10.15252/msb.20145554 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skotheim J. M., Di Talia S., Siggia E. D., Cross F. R. (2008). Positive feedback of G1 cyclins ensures coherent cell cycle entry. Nature 454 291–296. 10.1038/nature07118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith J., Martin L. (1973). Do cells cycle? Proc. Natl. Acad. Sci. U S A. 70 1263–1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer S. L., Cappell S. D., Tsai F.-C., Overton K. W., Wang C. L., Meyer T. (2013). The proliferation-quiescence decision is controlled by a bifurcation in CDK2 activity at mitotic exit. Cell 155 369–383. 10.1016/j.cell.2013.08.062 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer S. L., Gaudet S., Albeck J. G., Burke J. M., Sorger P. K. (2009). Non-genetic origins of cell-to-cell variability in TRAIL-induced apoptosis. Nature 459 428–432. 10.1038/nature08012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer S. L., Sorger P. K. (2011). Measuring and modeling apoptosis in single cells. Cell 144 926–939. 10.1016/j.cell.2011.03.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suderman R., Bachman J. A., Smith A., Sorger P. K., Deeds E. J. (2017). Fundamental trade-offs between information flow in single cells and cellular populations. Proc. Natl. Acad. Sci. U S A. 114 5755–5760. 10.1073/pnas.1615660114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tangye S. G., Hodgkin P. D. (2004). Divide and conquer: the importance of cell division in regulating B-cell responses. Immunology 112 509–520. 10.1111/j.1365-2567.2004.01950.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tas J. M., Mesin L., Pasqual G., Targ S., Jacobsen J. T., Mano Y. M., et al. (2016). Visualizing antibody affinity maturation in germinal centers. Science 351 1048–1054. 10.1126/science.aad3439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas M. J., Klein U., Lygeros J., Rodríguez Martínez M. (2019). A probabilistic model of the germinal center reaction. Front. Immunol. 10:689. 10.3389/fimmu.2019.00689 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyas L., Brophy V. A., Pope A., Rivett A. J., Tavaré J. M. (2000). Rapid caspase-3 activation during apoptosis revealed using fluorescence-resonance energy transfer. EMBO Rep. 1 266–270. 10.1093/embo-reports/kvd050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vallabhapurapu S., Karin M. (2009). Regulation and function of NF-κB transcription factors in the immune system. Ann. Rev. Immunol. 27 693–733. 10.1146/annurev.immunol.021908.132641 [DOI] [PubMed] [Google Scholar]
- Verheijen M., Rane S., Pearson C., Yates A. J., Seddon B. (2020). Fate mapping quantifies the dynamics of B cell development and activation throughout life. Cell Rep. 33:108376. 10.1016/j.celrep.2020.108376 [DOI] [PMC free article] [PubMed] [Google Scholar]
- William C. S., Liou H.-C., Tuomanen E. I., Baltimore D. (1995). Targeted disruption of the p50 subunit of NF-κB leads to multifocal defects in immune responses. Cell 80 321–330. 10.1016/0092-8674(95)90415-8 [DOI] [PubMed] [Google Scholar]
- Williams R. A., Timmis J., Qwarnstrom E. E. (2014). Computational models of the NF-KB signalling pathway. Computation 2 131–158. 10.3390/computation2040131 [DOI] [Google Scholar]
- Xu H., Chaudhri V. K., Wu Z., Biliouris K., Dienger-Stambaugh K., Rochman Y., et al. (2015). Regulation of bifurcating B cell trajectories by mutual antagonism between transcription factors IRF4 and IRF8. Nat. Immunol. 16 1274–1281. 10.1038/ni.3287 [DOI] [PubMed] [Google Scholar]
- Xu Y., Davidson L., Alt F. W., Baltimore D. (1996). Deletion of the Ig kappa light chain intronic enhancer/matrix attachment region impairs but does not abolish V kappa J kappa rearrangement. Immunity 4 377–385. 10.1016/s1074-7613(00)80251-4 [DOI] [PubMed] [Google Scholar]
- Yang J., Zhao S., Yang X., Zhang H., Zheng P., Wu H. (2016). Inhibition of B-cell apoptosis is mediated through increased expression of Bcl-2 in patients with rheumatoid arthritis. Int. J. Rheumat. Dis. 19 134–140. 10.1111/1756-185x.12706 [DOI] [PubMed] [Google Scholar]
- Zhou J. H., Markham J. F., Duffy K. R., Hodgkin P. D. (2018). Stochastically timed competition between division and differentiation fates regulates the transition from B lymphoblast to plasma cell. Front. Immunol. 9:2053. 10.3389/fimmu.2018.02053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zilman A., Ganusov V. V., Perelson A. S. (2010). Stochastic models of lymphocyte proliferation and death. PLoS One 5:e12775. 10.1371/journal.pone.0012775 [DOI] [PMC free article] [PubMed] [Google Scholar]