Abstract
Along the pathway from behavioral symptoms to the development of psychotic disorders sits the multivariate mediating brain. The functional organization and structural topography of large-scale multivariate neural mediators among patients with brain disorders, however, are not well understood. Here, we design a high-dimensional brain-wide functional mediation framework to investigate brain regions that intermediate between baseline behavioral symptoms and future conversion to full psychosis among individuals at clinical high risk (CHR). Using resting-state functional magnetic resonance imaging (fMRI) data from 263 CHR subjects, we extract an brain atlas and a brain atlas: the former underlines brain areas associated with prodromal symptoms and the latter highlights brain areas associated with disease onset. In parallel, we identify and separate mediators that potentially positively and negatively mediate symptoms and psychosis, respectively, and quantify the effect of each neural mediator on disease development. Taken together, these results paint a brain-wide picture of neural markers that are potentially mediating behavioral symptoms and the development of psychotic disorders; additionally, they underscore a statistical framework that is useful to uncover large-scale intermediating variables in a regulatory biological system.
1. Introduction
How does the human brain intermediate between behavioral symptoms and the development of brain diseases? Which brain areas are involved in this process? Can we chart these areas’ functional characteristics and structural organization?
Researchers studying brain diseases often observe that brain signals are on the one hand associated with behavioral symptoms, and on the other hand linked to disease status. Conventionally, the former is called an independent variable, the latter is called a dependent variable (or an outcome), and the brain areas interposed in-between are called mediators. A central problem in neural mediation analysis is to identify which brain regions are positioned along the pathway between behavioral symptoms and disease status. Equally important is to quantify the effect of each identified brain area on developing the disease and to determine its relative prominence in the mediation system.
Disorganization symptoms, such as bizarre thoughts and behaviors, are considered to be associated with conversion to psychosis among individuals at clinical high risk (CHR); empirical studies have shown a significantly higher hazard ratio for psychosis onset in CHR subjects with higher disorganization symptoms at baseline (Cannon et al., 2008; Demjaha et al., 2012; Carrión et al., 2013). Yet, as properties associated with a mental disorder, the disorganization symptoms and disease development are reflected by the measured brain signals. Probing into the neural basis of human behavior and disease development, mediation analysis can help us to understand the functional attributes and structural topography of the brain areas that potentially mediate behavioral symptoms and disease development. But it can only do so by first charting the neural pathways that make brain mediation possible.
A beginning in this direction can be made by identifying and isolating neural mediators that are interposed between behavioral symptoms and disease development (see Fig. 1). Central to this enquiry is a high-dimensional brain mediation analysis: examining hundreds of thousands of brain areas to find a subset of potential mediators. To uncover high-dimensional functional neural mediators with binary outcomes (e.g., whether one has a full-blown psychotic disorder or not), one, however, must confront several challenges. First, although existing mediation models have made the search for mediators fruitful, they are not suitable for studying high-dimensional mediation analysis with binary outcomes. For example, existing multi-level mediation models assume that the outcomes are continuously distributed (Chén et al., 2018; Geuter et al., 2020; Huang and Pan, 2016; VanderWeele and Vansteelandt, 2014); mediation frameworks concerning binary outcomes are at present restricted to a relatively small number of mediators (VanderWeele and Vansteelandt, 2014; Nguyen, 2016); high-dimensional mediation models whose outcomes are not normally distributed do not have a closed form solution (therefore it is difficult to estimate parameters analytically, as, for example, in (Chén et al., 2018)). Second, although functional mediation analysis (Lindquist, 2012) has considerably advanced knowledge about the functional signal organization of the brain in relation to independent and outcome variables, it remains unclear whether it is suitable for analyzing high-dimensional brain data, and if so, how the underlying data configuration, such as the sample size and noise level, would affect parameter estimation. In parallel, its efficacy needs to be evaluated for brain disease studies. Third, signals from brain mediators could be orthogonal or non-orthogonal. Whether and how their orthogonality would affect mediation analysis is an as-of-yet less-well-charted area. If not properly treated, this set of circumstances could generate inconsistent results and confusing interpretations. Finally, the search for functional neural mediators among subjects with severe behavioral symptoms raises the question of which mediators are positively, and which are negatively, mediating the development of brain disorders.
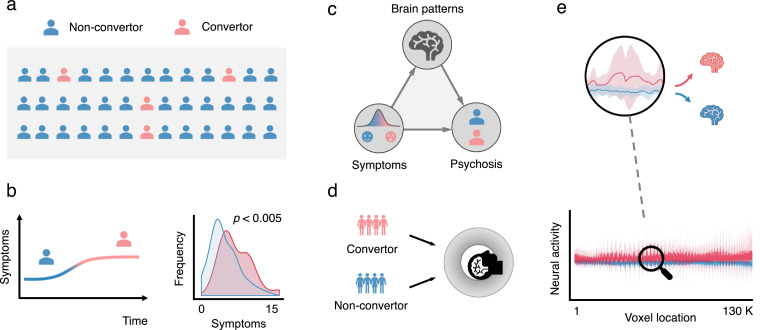
Fig. 1.
The study layout of the neural mediation analysis.(a) We considered a sample of 263 subjects recruited from eight study sites across the United States and Canada who met criteria for a prodromal risk syndrome at the point of recruitment and had been clinically followed up for two years as part of the NAPLS-2 project. During the follow-up period, 25 subjects developed a full-blown psychotic disorder (CHR convertors); 238 did not (CHR non-convertors). (b) The behavioral symptoms of convertors were significantly more severe than those of non-convertors. (c) The neural mediation analysis investigated which brain regions were intermediating between psychosis symptoms and disease status. Once neural mediators were identified, one could further quantify the mediation effect of each mediator to determine its relative prominence in the mediation system. (d) Both convertors and non-convertors received an eyes-open resting-state functional magnetic resonance imaging (fMRI) scan at the point of recruitment. (e) Resting-state brain activities from both convertor and non-convertor samples were plotted along 130,992 brain areas. The red shade represented brain signals stacked across the convertor group along the whole-brain space and the blue shade represented those from the non-convertor group.
To address these questions, here we propose a high-dimensional functional mediation model. Through simulation studies and empirical data analysis, we demonstrate that the model may be useful to (a) analyze large-scale intermediating brain signals (e.g., resting-state brain activities from hundreds of thousands of voxels); (b) distinguish distinctive functional brain regions between different groups in relation to behavior symptoms; (c) quantify each neural mediator's effect on disease outcome; and (d) identify and separate brain areas that are potentially positively and negatively mediating brain disorders.
In clinical practice, one assumes that an irregular change of brain signals can first cause prodromal signs and symptoms, followed in some cases by later conversion to psychosis. In this paper, we aimed at studying the influence of the underlying brain signals on the link between two directly and clinically observable sets of variables: prodromal signs and symptoms on the one hand, and conversion state on the other hand. The framework we designed to map the pathways contained directed arrows. The arrows clarified that the statistical model was a mediation one they did not suggest definitive causal flows from prodromal signs via brain areas towards conversion status (see Figs. 1 and 2). When confusion about the causal direction arises, one can interpret the identified neural mediators as brain areas that are jointly associated with behavioral symptoms and psychosis conversion. In other words, the neural mediators exclude brain areas that are associated with conversion, but that are not associated with prodromal symptoms, and vice versa. One should also note that in cases where the brain signals first have an effect on the symptoms and then on the disease status (namely when the symptoms are the mediator), the identified brain regions are identical to the alpha atlas estimated by the proposed model (see Results). Although there are overlaps between the two models, the interpretations are different. The key differences between brain areas identified by these two models are (1) the identified brain areas in the current study are potential neural mediators whereas those identified using the other model (where the symptom is treated as the mediator) are multivariate independent variables; and (2) the neural mediators from the present study are a subset of brain areas identified using the other model. In the Supporting Information, we extend the proposed model to causal mediation setting using counterfactuals; additionally, we discuss how to interpret the model when causal inference is concerned; in cases where brain signals can be manually controlled (e.g., via transcranial magnetic stimulation (TMS)), under some identification conditions, the proposed model may unveil potential causal direct effect and indirect effect on the odds ratio scale.
Fig. 2.
A schematic representation of mediation analysis. (a) Univariate mediation analysis. The circles indicate an independent variable, a univariate mediator, an outcome variable, and covariates. The arrows denote pathways. The letter denotes the effect from the independent variable to the mediator, after accounting for the covariate effect. The letter denotes the effect of the mediator on the outcome, after controlling the independent variable and covariates. The letter denotes the effect from the independent variable to the outcome, after accounting for the covariate effect. (b)Multivariate neural mediation analysis. Each circle within the brain represents a potential neural mediator. The arrows denote pathways. The letter ( denotes the effect from the independent variable to the neural mediator (represented by a red circle). The letter denotes the effect of the neural mediator on the outcome, after controlling the independent variable and covariates. The letter indicates the direct effect from the independent variable to the outcome, after accounting for the covariate effect.
In the following, we begin with a brief overview of the mediation analytical frameworks concerning univariate and multivariate mediators. After discussing these basic concepts, we introduce the high-dimensional functional mediation framework. To demonstrate its utility, we perform both simulation and case studies. During the simulation study, we consider various experimental settings, including different levels of noise, sample sizes, and both orthogonal and non-orthogonal basis functions, to ensure that the proposed framework is suitable for studying high-dimensional functional mediation. During the case study, we uncover brain areas that potentially mediate psychosis symptoms and disease status from whole-brain resting-state functional magnetic resonance imaging (rs-fMRI) data obtained from 263 subjects at clinical high risk (CHR) for psychosis.
1.1. Univariate mediation analysis
Univariate mediation analysis considers a single mediator () (see Fig. 2(a)). In other words, a variable is a mediator if, after accounting for covariates , the effect of an independent variable on an outcome variable is at least partially carried through (Baron and Kenny, 1986; Robins and Greenland, 1992). In the following, we use upper cases to indicate random variables, and lower cases to indicate observed values. We use nonbold letters to represent univariate variables and observations; we use bold letters to represent multivariate variables and observations. Examples of univariate mediators are pain catastrophizing, which mediates the clinical treatment and disability status (Whittle et al., 2017), and intention, which mediates attitudes and behavior (Fishbein and Ajzen, 1975).
The identification of a univariate mediator consists of two steps (Alwin and Hauser, 1975; Baron and Kenny, 1986; Hyman, 1955; Judd and Kenny, 1981; Sobel, 1982) (see Supporting Information for a comparison between two common mediation analysis frameworks). The first step examines if the independent variable has an effect on the mediator after controlling for the covariates , using the following conditional model:
| (i) |
where refers to the expectation operation; , , are coefficients for the intercept, the observed independent variable , and the observed covariates . If is significantly different from zero, then the independent variable has an effect on the mediator.
The second step evaluates if the mediator has an effect on the outcome , after controlling for the independent variable and covariates , using the following conditional model:
| (ii) |
where , , and are coefficients for the intercept, the observed independent variable , the observed value of the mediator , and the observed covariates . The prime in is to differentiate it from its counterpart in (i). If is significantly different from zero, then the mediator has an effect on the outcome.
The univariate variable is said to significantly mediate the relationship between and , if both and are significantly different from zero. Said in a different way, if the product is non-zero, then is a mediator for and , and the value of quantifies the mediation effect. In the language of a graphical model, this means that both and edges in Fig. 2(a) exist, connecting nodes and via a pathway passing through node .
1.2. Multivariate mediation analysis
Mediation analysis concerning a multivariate mediator can be conducted using structural equation models (SEMs) (Lindquist, 2012; VanderWeele and Vansteelandt, 2014) (see Fig. 2(b)). Formally, consider mediators (), denoted as , an independent variable , and an outcome variable . Multivariate mediation analysis considers two conditional models as follows.
| (iii) |
where is the mediator; , , and are coefficients for the intercept, the observed independent variable , and the observed covariates that are associated with the mediator.
| (iv) |
where is a vector representing observed mediators; , and are coefficients for the intercept, the observed independent variable , and the observed covariates ; is the coefficient associated with the mediator.
The mediator , for , is said to significantly mediate the relationship between and , if both and are significantly different from zero after accounting for the covariates. The product, , quantifies the mediation effect for the mediator (see Fig. 3).
Fig. 3.
A hypothetical experiment and how multivariate mediation analysis can be used to study brain mediation in health and disease.(a1) Three individuals’ behavioral symptom scores are measured at baseline. (a2) Resting-state brain activities for one individual is collapsed into activities averaged over time across voxels in the whole brain. Each circle corresponds to one voxel. (a3) Individuals’ two-year clinical outcome for psychosis. We use a blue icon to refer to a non-convertor and a red icon to refer to a convertor. (b1) Measured individual brain signals are arranged corresponding to their behavioral symptom scores and psychosis statuses. Each column contains data from a particular subject. (b2) The input system of the brain mediation framework studies the association between the behavioral symptom score (the box) and measured brain signals (the circles). The colored arrows indicate significant pathways from the behavioral symptom score to brain areas. The width of the arrows indicates effect size, and the color indicates sign (where orange means positive and blue means negative). (b3) The output system of the brain mediation framework studies the association between the measured brain signals (the circles) and disease status (the box). (c1) The mediation analysis framework combines the input and output systems, and studies how the effect of behavioral symptom score (the left box) on the psychosis status (the right box) is intermediated by neural mediators (the circles). A voxel significantly mediates the relationship if its signal is associated with both the behavioral symptom score and the psy-chosis status. (c2) The mediation effect of a particular voxel is calculated by multiplying the effect sizes from the input and the output pathways corresponding to the voxel.
1.3. High-dimensional brain-wide functional mediation
High-dimensional mediation analysis aims at identifying mediators from a high-dimensional multivariate variable. For example, a neurobiologist is interested in searching through the entire brain to look for neural mediators using signals recorded from hundreds of thousands of brain regions. The framework introduced in the paper consists of a dual system: the input system investigates how an independent variable (e.g., behavioral symptoms) may be associated with signals of brain mediators, after controlling for covariates; the output system examines how signals of brain mediators may give rise to the outcome variable (e.g., psychosis disease status), after controlling for the independent variable and covariates (see Fig. 3). For brevity, from now on we will refrain from mentioning covariate control in our writing; readers should note that this has been included during the mediation analysis.
In the following, we introduce the key concepts of the framework and leave derivations and discussions to the Material and Methods and Supporting Information sections.
Consider subjects and brain areas, where is high-dimensional (in our study and ). Let and be the independent and outcome variables for subject , respectively. Let , , and ) denote the covariates of subject , for example, the site (from which data are collected), age, gender, frame-wise displacement (FD), and whole-brain gray matter volume, respectively. Finally, let be the neural activity from the brain area of subject . The high-dimensional functional brain-wide mediation framework consists of an input system and an output system.
The following conditional model describes the input system (see Fig. 3 (b2)):
| (v) |
where , , and are coefficients for the intercept, the independent variable, and covariates that are associated with the mediator. It is worthwhile mentioning that the estimated parameters (see the alpha atlas in the Results section) are closely related to canonical correlation (CCA) between multivariate brain signals and the independent variable and are remotely related to the Partial Least Squares (PLS) estimates (see Supporting Information for details).
The following generalized functional linear model (a generalized linear model containing functional PCs in its regressors) represents the output system (see Fig. 3 (b3)):
| (vi) |
where , , and are coefficients for the intercept, the independent variable, and covariates. Here, denotes the data and are the Karhunen-Loève expansion (Loève, 1945; Karhunen, 1947) of , the mediator of subject ; in other words (without loss of generality, assume is zero centered), where , , for , , and is a finite integer such that captures the importance of modes of variations of (see Material and Methods for more detailed explanation). Additionally, denotes the basis functions and is the coefficient associated with the mediator. The link function takes various forms based on the outcome distribution. For example, when is Gaussian, binary, or Poisson, the link function is , , or , respectively.
The first basis functions or in Eq. (vi) are functional representations of dominant population-specific (i.e., shared by all subjects) information of brain data, ranked decreasingly (according to ) based on the amount of information each basis function explains about the multivariate neural mediator . Although by Mercer's theorem (see Chapter 4 of Indritz, 1963), the basis functions are orthogonal, and researchers indeed are oftentimes interested in uncovering orthogonal brain signals in relation to mediation, it remains possible that the brain signals consist of non-orthogonal information. Despite the central focus herein being on mediation studies, it is important to understand how the underlying orthogonality of brain data's basis functions may affect the identification of neural mediators and the estimation of the mediation effect. To that end, we performed simulation studies using both orthogonal and non-orthogonal basis functions with different noise levels and sample sizes, and the results showed that our framework was successful to uncover neural mediators regardless of the orthogonality. Naturally, the mediation analysis performance was better when the underlying basis functions were orthogonal, and the estimation results improved as the noise decreased or the sample size increased (see Supporting Information).
We summarize the key steps of the framework as follows. First, it estimates the effect of the independent variable on each brain area; this yields an brain atlas (see Fig. 3(b2)). Next, it extracts subject-specific principal component (PC) scores from each individual ’s brain signals (), and estimates the effect of the transformed lower-dimensional mediators (i.e., ) on the disease outcome after controlling for the independent variable and the covariates. Subsequently, the low-dimensional mediator-on-outcome effect is translated to the high-dimensional brain space using the estimated brain-wide basis functions (i.e., ); this produces a brain atlas (see Fig. 3 (b3)), Material and Methods and Supporting Information). Finally, it obtains the brain-wide mediation effect using the and brain atlases and bootstrap tests (see Fig. 3(c1) - (c2) and Methods).
2. Material and methods
2.1. The NAPLS-2 data
The fMRI data were drawn from the second phase of the North American Prodrome Logitudinal Study (NAPLS-2) consortium (Addington et al., 2012), which included 263 subjects recruited from eight study sites across the United States and Canada. All subjects met the criteria for the prodromal syndromes at the point of recruitment according to the Structured Interview for Prodromal Syndromes (SIPS) (McGlashan et al., 2001) and were clinically followed-up for two years. During follow-up, 25 subjects developed one type of the Axis-I psychotic disorders (CHR convertors, age 18.52 ± 4.08 years, 17 males) and 238 did not (CHR non-convertors, 19.07 ± 4.16 years, 136 males). The conversion was defined as the individual either met the Diagnostic and Statistical Manual of Mental Disorders, fourth edition (DSM-IV) (Bell, 1994) criteria for an Axis-I psychotic disorder or had at least one fully psychotic symptom assessed by the Structured Interview for Prodromal Syndromes (SIPS) at follow-up (Miller et al., 2002; Miller et al., 2003). See Table 1 for details on the studied sample. All subjects received an eyes-open resting-state functional magnetic resonance imaging (fMRI) scan at the point of recruitment.
Table 1.
Demographic and clinical information for the studied sample. The two groups showed significant differences in disorganization symptoms.
| CHR converters (N = 25) | CHR non-converters (N = 238) | p-value | |
|---|---|---|---|
| Age (years) | 18.52±4.08 | 19.07±4.16 | 0.52 |
| Sex (M/F) | 17/8 | 136/102 | 0.30 |
| Site | 7/4/1/0/8/1/3/1 | 36/41/28/26/44/21/36/6 | 0.23 |
| SOPS disorganized symptoms | 7.52±3.38 | 5.04±3.15 | <0.001 |
| Mean frame-wise displacement (mm) | 0.14±0.10 | 0.11±0.08 | 0.17 |
2.2. Data acquisition
During the 5-min eyes-open resting-state scan (154 whole-brain volumes), participants were asked to lay still in the scanner, relax, gaze at a fixation cross, and not engage in any particular mental activity. After the scan, investigators confirmed with the participants that they had not fallen asleep in the scanner. Data were acquired from 3T MR scanners located at eight study sites with identical fMRI protocols. Siemens scanners were used at Emory, Harvard, University of California Los Angeles (UCLA), University of North Carolina at Chapel Hill (UNC), and Yale; GE scanners were used at Calgary, University of California San Diego (UCSD), and Zucker Hillside Hospital (ZHH). Functional images were collected using gradient-recalled echo-planar imaging (GRE-EPI) sequences: TR/TE 2000/30 ms, 77° flip angle, 30 4-mm slices, 1-mm gap, 220-mm FOV. In addition, we also acquired high-resolution T1-weighted images for each participant with the following sequence: 1) Siemens scanners: magnetization-prepared rapid acquisition gradient-echo (MPRAGE) sequence with 256 mm × 240 mm × 176 mm FOV, TR/TE 2300/2.91 ms, 9° flip angle; 2) GE scanners: spoiled gradient recalledecho (SPGR) sequence with 260 mm FOV, TR/TE 7.0/minimum full ms, 8° flip angle.
2.3. Preprocessing of rs-fMRI data
Data were preprocessed using the standard pipeline implemented in the Statistical Parametric Mapping (SPM12, http://www.fil.ion.ucl.ac.uk/spm/) software following previously published work (Cao et al., 2018; Cao et al., 2019; Cao et al., 2019; Cao et al., 2019), including slice-timing correction, realignment, individual structural-functional image coregistration, normalization to the Montreal Neurological Institute (MNI) template, and spatial smoothing with 8-mm full width at half maximum (FWHM). Preprocessed images were further corrected for white matter, cerebrospinal, and global signals, 24 head motion parameters (6 translation and rotation parameters, their first derivatives, and the square of these 12 parameters), and frame-wise displacement (FD). To mitigate potential head motion effect, 8 subjects (1 converter, 7 non-converters) with mean FD > 0.35 mm were excluded from further analysis. The activities of each gray matter voxel during resting state were quantified by fractional amplitude of low-frequency fluctuation (fALFF), a well-established measure evaluating the ratio of power spectrum of low-frequency (0.01–0.1 Hz) to that of the entire frequency range (Zou et al., 2008). After computation, fALFF values were extracted from a total of 130,992 voxels covering the gray matter of the entire brain for each subject. Secondary data analysis was conducted using the R software.
2.4. The model
Here we introduce the high-dimensional functional mediation analysis framework. The input system of the framework tests if the independent variable (e.g., behavioral symptoms) has an effect on each brain area (see Fig. 3(b2)). The output system examines if each brain area has an effect on the outcome (see Fig. 3(b3)).
Formally, consider subjects and brain areas, where and in this study. Let be the independent variable for subject , be the covariates consisting of the site (from which data are collected), age, gender, frame-wise displacement (FD), and whole-brain gray matter volume, respectively, of subject , be the measured brain signals of subject spanning brain areas, and be the outcome for subject (in this study ).
We first review the basics of functional principal component analysis (fPCA) (Ramsay and Silverman, 2005; Wang et al., 2016). Let , be a squared integrable random function with mean and covariance function . In other words, and . By Mercer's theorem (see Chapter 4 of Indritz, 1963), one can obtain the spectral decomposition of as:
where are decreasingly ordered nonnegative eigenvalues and ’s are their corresponding orthogonal eigenfunctions with unit norms.
Karhunen-Loève expansion (Loève, 1945; Karhunen, 1947) of the random function yields:
where are uncorrelated random variables with zero mean and variance . For a given functional sample, the mean function and covariance function can be consistently estimated using the method of moments. The eigen-values and -functions are estimated from the empirical covariance function, and the principal component scores (’s) can be estimated by numeric integration.
Next, we inquire further into Eqs. (v) and (vi) from the Introduction section. Resume the notations used in Eqs. (v) and (vi). Consider subjects and brain areas, where is high-dimensional. Let and be the independent and outcome variables for subject , respectively. Let , , , , ) denote the covariates of subject , for example, the site (from which data are collected), age, gender, frame-wise displacement (FD), and whole-brain gray matter volume, respectively. Finally, let be the neural activity from the brain area of subject .
The input system consists of the following model:
where , , and are coefficients for the intercept, the independent variable, and covariates that are associated with the mediator. Specifically, captures the effect of the independent variable on the mediator, indicates an intercept, and denotes the coefficients for the covariates with respect to the mediator. Without loss of generality, consider .
The output system consists of the following generalized functional linear model:
| (vii) |
where , is called a linear predictor with , , denotes the data, , and , where , , for and , and is a set of basis functions. denotes the corresponding parameters for . , and are proper functions. is a vector, whose entry estimates the effect of the mediator on the outcome, controlling the independent variable and covariates. is a nuisance parameter.
By taking the expected value of conditioning on , Eq. (vii) yields Eq. (vi) in the Introduction section. Particularly, when is binary, Eq. (vi) has the following form:
| (viii) |
where
Thanks to spectral decomposition of , parameter estimation of can be performed on , where . To see this, rewrite in Eq. (vi) as , where . The estimation problem now translates to estimating the low-dimensional mediator-on-outcome effect, or . Subsequently, the estimation of can be retrieved by projecting the estimated back to the brain space using the estimated basis functions ; in other words, , where represents a generalized inverse.
Although in real-world brain data, the (unknown) basis functions can be either orthogonal or non-orthogonal, simulation studies showed that, regardless of the orthogonality of basis functions, our framework was successful to uncover the and brain atlases under different noise levels and sample sizes (see Supporting Information). Since has a one-to-one relationship to the voxel's mediation effect (see Supporting Information), for simplicity we estimate , for . In words, is the voxel's natural indirect mediation effect on the log odds-ratio scale per unit increase of the independent variable. When is small, Sobel's Test (Sobel, 1982) evaluates the statistical significance of . When is high-dimensional, the statistical significance of can be evaluated using a bootstrap approach (Efron, 1979) (see Supporting Information); the results are further adjusted for multiple comparisons.
2.5. Brain-wide functional mediation analysis
We conducted brain-wide functional mediation analysis on the rs-fMRI data from the NAPLS-2 sample using the proposed framework. We first assessed if there was any effect from the independent variable (SOPS disorganization symptom scores) on each voxel, controlling for age, sex, study site, FD, and whole-brain gray matter volume, using Eq. (v) and obtained the brain atlas. We then estimated the effect each brain area had on the outcome, controlling for the independent variable and all covariates, using Eq. (vi) and obtained the brain atlas. Finally, we identified positive and negative neural mediators and estimated their mediation effect via bootstrap experiments. We presented the empirical results in Fig. 4.
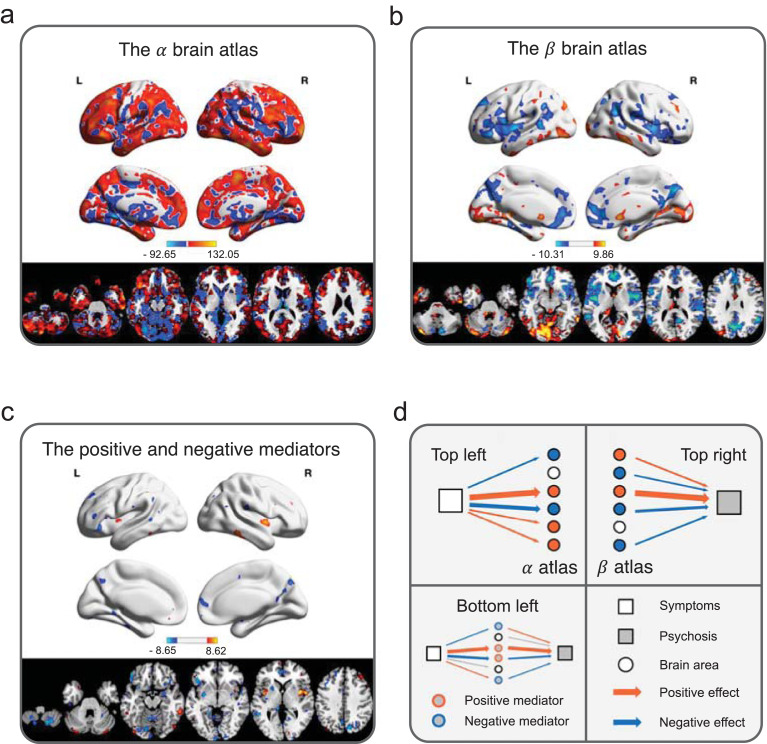
Fig. 4.
Brain areas potentially mediating behavioral symptoms and the development of psychosis. A high-dimensional mediation analysis on 130,992 brain voxels of 263 subjects suggests that the pathway between behavioral symptoms and psychosis is potentially positively mediated by the right lateral prefrontal cortices, bilateral insular and opercular areas, bilateral sensorimotor areas, striatum, and cerebellar lobules 4, 5, and 6, and negatively mediated by the bilateral medial frontal and orbitofrontal cortices, left lateral prefrontal cortices, posterior cingulate, precuneus, visual cortex, and cerebellar Crus 1 and lobule 9. (a)Thebrain atlas. The brain atlas shows surface and subcortex areas associated with behavioral symptoms when controlled for covariates. (b)Thebrain atlas. The brain atlas shows surface and subcortex areas associated with psychosis status when controlled for behavioral symptoms and covariates. (c)The positive and negative neural mediators. The neural mediators include surface and subcortex areas that are jointly associated with behavioral symptoms and brain disease status, after all covariates are controlled. The areas highlighted in orange are positive mediators, and those highlighted in blue represent negative mediators. (d)Explanations regarding the pathways and color codes of figures (a)–(c). The color bars in (a)–(c) indicate effect sizes from bootstrap experiments.
3. Results
3.1. Simulation studies
We conducted simulation studies to ensure that the proposed framework was able to identify brain areas that intermediate the independent and the outcome variables under different settings. We first simulated covariates such that their distributions were similar to those from the empirical data. We then simulated symptom data using the covariates. Next, we simulated brain signals and disease outcomes using Eqs. (v) and (vi), respectively (see more details in the Supporting Information). When simulating brain signals, we examined different combinations of eigenfunctions, idiosyncratic noises, and sample sizes. For eigenfunctions, we considered both orthogonal and non-orthogonal cases (to cover the two general scenarios where the brain signals consist of orthogonal and non-orthogonal information). For noises, we considered a range of magnitudes, from small, moderate, to very large scales; we considered very large noise because we wanted to see to what degree the estimates would be able to (and unable to) uncover the signals, and whether, even under very large noise level, signals could be recovered using more samples. We considered dimensionality of 130,992 (the same as the empirical study) and sample sizes of 100 and 500. Together, we examined 12 simulation conditions; for each condition, we conducted 100 bootstrap simulations. From the estimation performance, one can relatively easily peer into how the model would perform under other combinations of basis functions, noise levels, and sample sizes.
Overall, the proposed framework was able to uncover (simulated) brain areas involved in mediation. Particularly, (1) the framework successfully uncovered neural mediators across different combinations of eigenfunctions, idiosyncratic noises, and sample sizes. (2) The performance on estimating the input map was better than it on estimating the output map . With larger samples, however, the estimation of improved. Both estimations of and deteriorated when more noises were added; but for each noise level, the estimation performance improved with more samples. At perhaps the extreme end when the noise was very large, the algorithm was still able to uncover some signals using large samples. The estimation using signals simulated from orthogonal basis functions outperformed those from non-orthogonal basis functions. Both cases saw improvement when less noise or larger a sample size was considered. The detailed simulation procedures and results can be found in the Supporting Information.
3.2. Empirical results
We applied the framework to an empirical study to identify and isolate functional brain regions that mediate prodromal symptoms at baseline and two-year clinical outcome in subjects at clinical high risk (CHR) for psychosis. The sample included 263 subjects recruited from eight study sites across the United States and Canada who met criteria for a prodromal risk syndrome (Miller et al., 2003) at the point of recruitment and were clinically followed up for two years as part of the NAPLS-2 project (Addington et al., 2012) (see Table 1). During the follow-up period, 25 subjects developed a full-blown psychotic disorder (CHR convertors); 238 did not (CHR non-convertors). All participants received an eyes-open resting-state functional magnetic resonance imaging (fMRI) scan at the point of recruitment. After data preprocessing and noise correction, the fractional amplitude of low-frequency fluctuation (fALFF) (Zou et al., 2008) for each voxel within a binary gray-matter mask (130,992 voxels in total) was extracted. The prodromal symptoms were quantified using the Scale of Prodromal Symptoms (SOPS) (McGlashan et al., 2001), and the clinical outcome was labeled as convertor or non-convertor.
Since disorganization symptoms have been shown to be a potential clinical predictor for psychosis (Cannon et al., 2008; Demjaha et al., 2012; Carrión et al., 2013), we first investigated whether the SOPS scores of disorganization symptoms were significantly different between convertors and non-convertors at baseline. Using the Welch two sample t-test and Pearson's (product moment) correlation coefficient test, the data confirmed that the convertors and non-convertors in the study indeed had significantly different behavioral symptom scores (, p < 0.005; Pearson correlation , p < 0.001) (see Fig. 1 (b)). We then continued to investigate which brain regions would functionally mediate this association. First, we tested if behavioral symptoms had an effect on any of the 130,992 voxels, controlling for age, sex, study site, head motion parameter, and total gray-matter volume (see Fig. 3(b2)). This analysis yielded the brain atlas (see Fig. 4(a)): each of its 130,992 elements indicated the effect of behavioral symptoms on a brain voxel. Second, we tested if activity from a brain voxel would increase (or decrease) the likelihood of developing psychosis, while controlling for behavioral symptoms and the aforementioned covariates (see Fig. 3(b3)). This was conducted using a generalized functional linear model (see Methods). This analysis yielded the brain atlas (see Fig. 4(b)): each of its 130,992 elements represented the effect from a brain voxel to the likelihood of developing psychosis, controlling behavioral symptoms and covariates. Third, we obtained the brain-wide functional mediators using the and brain atlases and classified them into two categories: the positive and negative neural mediators (see Fig. 4 (c)). Finally, we conducted bootstrap experiments to test whether the mediation effect corresponding to each voxel was statistically significant (see Methods). Results were reported after Bonferroni correction across all voxels in the brain (see Fig. 4).
3.3. The α and β brain atlases
We further inquired into the brain atlas (Fig. 4(a)) and the brain atlas (Fig. 4(b)) in order to investigate how the input and output systems contribute to overall mediation. Specifically, the brain atlas included brain regions that were associated with behavioral symptoms; the brain atlas consisted of brain areas that were associated with psychosis status when controlled for behavioral symptoms. On the brain atlas, activities of the majority of brain regions were positively associated with behavioral symptoms, while activities of the striatum, thalamus, insular and opercular areas, middle cingulate cortex, sensorimotor area, lingual gyrus, together with cerebellar lobules 4, 5, 6, crus 1, and crus 2 were negatively correlated with behavioral symptoms. On the brain atlas, positive associations were present mainly in the middle cingulate cortex, inferior parietal lobule, striatum, thalamus, lingual gyrus, calcarine sulcus, inferior and middle temporal gyri, and cerebellar lobule 6, crus 1, and crus 2. In contrast, negative associations were shown in the lateral and medial prefrontal cortices, anterior cingulate cortex, posterior cingulate cortex, precuneus, insular and opercular areas, angular gyrus, fusiform gyrus, and cerebellar lobule 8.
3.4. The positive and negative mediators
Discovering brain areas that are positively and negatively mediating behavioral symptoms and disease development is a central problem in neuropathology. To promote discussion, here we defined the positive mediators as brain areas whose activities were positively mediating higher behavioral symptoms and increased chance of conversion to psychosis (see regions with positive weights in Fig. 4(c)). Our results suggested that the positive mediators were mainly present at the bilateral insular and opercular areas, left inferior parietal cortex, right middle frontal gyrus, bilateral inferior temporal gyrus, and cerebellar crus 1 and 2. In parallel, we defined the negative mediators as brain areas whose activities were negatively mediating higher behavioral symptoms and increased chance of conversion to psychosis (see regions with negative weights in Fig. 4(c)). Our results suggested that the negative mediators were located chiefly at the bilateral medial frontal cortex, anterior cingulate cortex, orbitofrontal cortex, precuneus, cuneus, calcarine sulcus, striatum, thalamus, and cerebellar vermis and lobule 8. The direct effect after accounting for the mediators remained significant (γ > 0, bootstrap p < 0.05), suggesting that the identified mediation effect was partial mediation.
4. Discussion
In this study, we designed a high-dimensional brain-wide functional mediation analysis framework. Through its lenses, we identified and isolated positive and negative neural mediators that potentially mediate psychosis prodromal behavioral symptoms and disease status among individuals at CHR and quantified each mediator’ effects on developing psychosis. The positive mediators consisted of brain areas associated with positive mediation, which were primarily distributed in the brain's sensorimotor system, insular and opercular areas, and striatum. The negative mediators consisted of areas associated with negative mediation, which were chiefly located in the brain's default-mode system and visual system. The identification and isolation of the positive and negative mediators provide insights regarding the neurobiological pathways from early psychotic signs to full-blown psychosis, and demonstrate the potential utility of the proposed methodological framework in clinical neuroscience studies.
The proposed framework showed promise to study how brain signals may intermediate between an independent variable (such as prodromal behavioral symptoms) and an outcome variable (such as psychosis disease status). The framework extends multivariate mediation analysis to high-dimensional functional mediation analysis with non-Gaussian outcomes by incorporating functional data analysis and a generalized linear model. To inquire into the functional organization of the mediator, the model extracts subject-specific principal component (PC) scores and functional representations (population-specific brain-wide basis functions) of measured brain signals. The estimated effect from PC scores to psychosis status is then translated to the whole brain space via the brain-wide basis functions. A logit link function was employed to couple measured brain signals and the independent variable with the disease outcome. Since the model allows for a variety of link functions, it may assist other mediation problems with different outcome distributions from the exponential family.
There are a few additional properties of the proposed framework that may be useful in other studies. First, the framework integrates a generalized functional linear model into a dual regulatory system connecting an input system and an outcome system. This technique may provide some insights regarding designing biological models consisting of sub-systems. Second, when the outcomes are binary, one can use the framework to evaluate controlled direct effects, and natural direct and indirect effects on the odds-ratio scale (see Supporting Information). Third, high-dimensional brain signals may contain multilevel information. The proposed framework allows us to extract both group-level (i.e., the group-level basis functions) and subject-specific features (i.e., the subject-specific PC scores) of the brain data. The subject-specific features may be used as low-dimensional neural features to assess individual differences in the future (see Supporting Information).
We applied the proposed framework in a psychosis neuroimaging study, where we investigated how functional brain activities may mediate prodromal behavioral symptoms and clinical outcome. The findings provided some insights into psychotic disorders. First, our results suggest that the positive mediators mainly involved the insular-opercular areas, temporal areas, frontoparietal areas, and part of cerebellum (crus 1 and 2). With extensive connections with both sensory areas and limbic system, the insula is a critical structure in the brain for the integrating and processing of visual and auditory emotional information and supporting subjective feeling states (Wylie and Tregellas, 2010; Namkung et al., 2017). A large number of studies have demonstrated that increased activity in the insular-opercular area is strongly associated with auditory hallucinations in patients with schizophrenia (Dierks et al., 1999; Shergill et al., 2000; Powers et al., 2017). Increased connectivity was found between insula and multiple perceptual areas such as sensorimotor cortex and visual cortex, together with decreased connectivity between insula and prefrontal cortex (Tian et al., 2019). The exact mechanism underlying the hyperactivity state of this area is unclear; it, however, may relate to sensory gating deficits disrupted by excessive mesolimbic dopamine input (Braff, 1990). The frontoparietal network, inferior temporal gyrus, and cerebellar crus 1 and crus 2 are key cognitive areas in humans (Dosenbach et al., 2007; Dosenbach et al., 2008; Buckner et al., 2011; Marek et al., 2018); increased activity and connectivity in these regions have been shown to be predictive of psychosis onset in previous studies (Cao et al., 2018; Cao et al., 2019). In line with previous findings, the current study further shows that these increased activities are potential mediators positively mediating psychosis conversion in individuals with prodromal symptoms. Second, the negative mediators are primarily distributed in the brain's default mode network or DMN (including medial prefrontal cortex, anterior cingulate cortex, and precuneus), together with thalamus, visual cortex, and cerebellar lobule 8. The DMN is one of the most frequently reported systems whose function is strongly associated with psychosis. Perhaps the most prominent finding regarding the DMN in patients is the failure to deactivate this network during cognitive tasks (Pomarol-Clotet et al., 2008; Fryer et al., 2013), which may relate to exaggerated internally-focused thoughts and lack of sufficient suppression of these thoughts during cognition (Whitfield-Gabrieli and Ford, 2012). Here, the finding of negative mediation effect in DMN activities during resting state is parallel to such interpretation, suggesting lower activity (indicating insufficient activation) during rest may potentially mediate prodromal symptoms and psychosis onset. In addition, this finding also corresponds well with the “triple network” model of psychosis, where the dysregulation of insula (as a positive mediator) on the DMN has been reported in individuals at risk for psychosis (Wotruba et al., 2014; Bolton et al., 2020). Cerebellar lobule 8 is a key region for processing sensorimotor-related errors (Buckner et al., 2011; Schmahmann, 2019). Higher activity in this region and the visual cortex may therefore imply a compensatory mechanism or an amplification of neural representations of perceptual information, potentially related to resolving or attenuating the existing perceptual deficits.
A few reasons have made the blood-oxygen-level-dependent functional magnetic resonance imaging (BOLD fMRI) data suitable for studying brain-wide mediation. First, although studies have used resting state electroencephalography (EEG) data and discovered brain areas, such as the frontal regions, that are associated with psychosis (Sollychin et al., 2019), imaging modalities with greater spatial resolution, such as fMRI, may both confirm and extend neural signatures beyond those identified using EEG. Second, reduced auditory P300 event-related potential (ERP) amplitude (from a functional neurophysiological test) is a primary candidate electrophysiologic biomarker of psychosis (Hamilton et al., 2019); it nevertheless may not capture as much variability that occurs in spontaneous brain activity as fMRI data to work well as a biomarker for conversion. Third, slow wave power has been shown to correlate with reduced blood flow and glucose utilization in schizophrenia patients, and is therefore thought to reflect reduced functioning in the frontal area (Ingvar et al., 1976; Guich et al., 1989). This supports the utility of fMRI BOLD data in mediation studies. Finally, structural MRI studies are beginning to discover associations between structural brain information and conversion to psychosis (Chung et al., 2019); here we showed that functional MRI data may add new insights into studies of neural markers associated with psychosis.
There are several limitations in this study. First, the nature of the imaging and clinical data suggests that the identified mediating pathways are associative; our results do not conclude definitive causal flows from prodromal signs via brain areas towards conversion status (see Introduction). Second, we were mainly interested in identifying brain regions that were simultaneously mediating behavioral symptoms and psychosis status. This naturally left out the cases where some mediators were interposed before or after other mediators. Future analysis may incorporate dynamic mediating systems and information feedback components. Third, throughout, we assumed that behavioral symptoms did not interact with the mediators. Future work that includes interaction between the independent variable and the mediator may be useful to expand current analysis (see Supporting Information for an example and see (Muller et al., 2005) for a special case). Fourth, although dimension reduction could reduce biases caused by spurious correlation, our framework cannot remove the coincidental association between some (voxel) features and the residual term (i.e., incidental endogeneity). This is an active research area in high-dimensional data analysis (see, for example, (Fan and Liao, 2014)). Fifth, the proposed model focused on neural markers by averaging the brain time courses over time. This omitted the territory of mediation analysis where the mediation effect changes over time. Future work could extend the framework to longitudinal settings: such extensions are particularly useful for studying mediation effect related to brain development during childhood and adolescence, brain aging between health and disease, and brain degeneration along the trajectory of a neurodegenerative disease development. We are currently investigating how to extend the techniques used in our framework to improve our understanding about large-scale longitudinal mediation; potential directions include combing functional data analysis (FDA) and a dual mediation system with autoregressive models (Gollob and Reichardt, 1991; Cole and Maxwell, 2003), latent growth curve (LGM) (Muthén and Curran, 1997), parallel process models (Cheong et al., 2009), latent difference score (LDS) models (McArdle, 2001), and autoregressive LGM models (Bollen and Curran, 2004).
Although we demonstrated high-dimensional functional neural mediation analysis in the domain of brain studies, the framework may also be useful to study other high-dimensional mediation problems, such as how genome-wide genotypes mediate the effect of environmental factors on phenotypes. With the recent convergence in neuroimaging, genomics, health informatics, wearable and digital sensors, the model may be useful to study a broad range of intermediating variables. For example, the model may be used to understand how gene expression, brain physiology, and circadian patterns jointly mediate environment and biological phenotypes, uncover brain regions that mediate sensory input and behavior outcome collected by wearable devices, and study how computers may act as a mediating artificial intelligence (AI), transferring human input into computer-generated intelligent responses.
To summarize, in the present study, we propose a framework that leverages mediation analysis concept and neuroscientific insights to inquire into the properties of large-scale functional neural markers that mediate the relationship between an independent variable and a binary disease outcome. The framework's capacity of treating high-dimensional data and flexibility in handling non-normally distributed outcomes make it potentially useful in a variety of scenarios to uncover intermediating pathways in complex regulative systems.
Author contributions
O.Y.C. designed the model and performed the mediation analysis. H.C. provided neurobiological intepretations. G.N. and J.M.R. provided neurobiological support. H.P. and J.P. provided simulation support. J.G., T.Q., and J.D. provided statistical support. T.D.C. and M.D.V. provided funding, support, and guidance. O.Y.C. and H.C. wrote the manuscript, with comments from all other authors.
Declaration of Competing Interest
The authors declare no competing interests.
Acknowledgement
The research was supported by the Wellcome Trust SCNI (098461/Z/12/Z) and the Flemish Government (AI Research Program) to Dr. de Vos, the NARSAD Young Investigator Grant (No. 27068) to Dr. Cao, and the NIH grant U01 MH081902 to Dr. Cannon. T.C. Dr. Cannon would like to acknowledge gifts from the Staglin Music Festival for Mental Health and International Mental Health Research Organization. The authors wish to thank the principal investigators of the North American Prodrome Longitudinal Study for allowing use of the project's imaging data in this demonstration analysis: Jean Addington, Carrie Bearden, Kristin Cadenhead, Barbara Cornblatt, Diana Perkins, Larry Seidman, Elaine Walker, and Scott Woods. The authors thank the Editor and three anonymous reviewers for their constructive suggestions which improved the quality and readability of the paper.
Footnotes
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.neuroimage.2020.117508.
Appendix. Supplementary materials
References
- Addington J. North American Prodrome Longitudinal Study (NAPLS 2): overview and recruitment. Schizophr. Res. 2012;142:77–82. doi: 10.1016/j.schres.2012.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alwin D.F., Hauser R.M. The decomposition of effects in path analysis. Am. Sociol. Rev. 1975;40:37. [Google Scholar]
- Baron R.M., Kenny D.A. The moderator-mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. J. Pers. Soc. Psychol. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Bell C.C. DSM-IV: diagnostic and Statistical Manual of Mental Disorders. J. Am. Med. Assoc. 1994;272:828–829. [Google Scholar]
- Bollen K.A., Curran P.J. Autoregressive Latent Trajectory (ALT) models: a synthesis of two traditions. Sociol. Methods Res. 2004;32:336–383. [Google Scholar]
- Bolton T.A.W. Triple network model dynamically revisited: lower salience network state switching in pre-psychosis. Front. Physiol. 2020;11:66. doi: 10.3389/fphys.2020.00066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braff D.L., Geyer M.A. Sensorimotor gating and Schizophrenia. Arch. Gen. Psychiatry. 1990;47:181–188. doi: 10.1001/archpsyc.1990.01810140081011. [DOI] [PubMed] [Google Scholar]
- Buckner R.L. The organization of the human cerebellum estimated by intrinsic functional connectivity. J. Neurophysiol. 2011;106:2322–2345. doi: 10.1152/jn.00339.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cannon T.D. Prediction of psychosis in youth at high clinical risk. Arch. Gen. Psychiatry. 2008;65:28–37. doi: 10.1001/archgenpsychiatry.2007.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao H. Cerebello-thalamo-cortical hyperconnectivity as a state-independent functional neural signature for psychosis prediction and characterization. Nat. Commun. 2018;9:3836. doi: 10.1038/s41467-018-06350-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao H. Altered brain activation during memory retrieval precedes and predicts conversion to psychosis in individuals at clinical high risk. Schizophr. Bull. 2019;45:924–933. doi: 10.1093/schbul/sby122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao H. Progressive reconfiguration of resting-state brain networks as psychosis develops: preliminary results from the North American Prodrome Longitudinal Study (NAPLS) consortium. Schizophr. Res. 2019 doi: 10.1016/j.schres.2019.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao H. Evidence for cerebello-thalamo-cortical hyperconnectivity as a heritable trait for schizophrenia. Transl. Psychiatry. 2019;9:1–8. doi: 10.1038/s41398-019-0531-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrión R.E. Prediction of functional outcome in individuals at clinical high risk for psychosis. JAMA Psychiatry. 2013;70:1133–1142. doi: 10.1001/jamapsychiatry.2013.1909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chén O.Y. High-dimensional multivariate mediation with application to neuroimaging data. Biostatistics. 2018;19:121–136. doi: 10.1093/biostatistics/kxx027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheong J., Mackinnon D.P., Toon S. Investigation of mediational processes using parallel process latent growth curve modeling. Struct. Equ. Model. 2009;10:238–262. doi: 10.1207/S15328007SEM1002_5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung Y. Adding a neuroanatomical biomarker to an individualized risk calculator for psychosis: a proof-of-concept study. Schizophr. Res. 2019;208:41–43. doi: 10.1016/j.schres.2019.01.026. [DOI] [PubMed] [Google Scholar]
- Cole D.A., Maxwell S.E. Testing mediational models with longitudinal data: questions and tips in the use of structural equation modeling. J. Abnorm. Psychol. 2003;112:558–577. doi: 10.1037/0021-843X.112.4.558. [DOI] [PubMed] [Google Scholar]
- Demjaha A. Disorganization/cognitive and negative symptom dimensions in the at-risk mental state predict subsequent transition to psychosis. Schizophr. Bull. 2012;38:351–359. doi: 10.1093/schbul/sbq088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dierks T. Activation of Heschl's gyrus during auditory hallucinations. Neuron. 1999;22:615–621. doi: 10.1016/s0896-6273(00)80715-1. [DOI] [PubMed] [Google Scholar]
- Dosenbach N.U.F. Distinct brain networks for adaptive and stable task control in humans. Proc. Natl. Acad. Sci. U. S. A. 2007;104:11073–11078. doi: 10.1073/pnas.0704320104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenbach N.U. A dual-networks architecture of top-down control. Trends Cogn. Sci. 2008;12:99–105. doi: 10.1016/j.tics.2008.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B. Bootstrap methods: another look at the Jackknife. Ann. Stat. 1979;7:1–26. [Google Scholar]
- Fan J., Liao Y. Endogeneity in high dimensions. Ann. Stat. 2014;42:872–917. doi: 10.1214/13-AOS1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fishbein M., Ajzen I. Addison-Wesley, Reading; MA, USA: 1975. Belief, Attitude, Intention, and Behavior: An Introduction to Theory and Research. [Google Scholar]
- Fryer S.L. Deficient suppression of default mode regions during working memory in individuals with early psychosis and at clinical high-risk for psychosis. Front. Psychiatry. 2013;4:92. doi: 10.3389/fpsyt.2013.00092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geuter S. Multiple brain networks mediating stimulus-pain relationships in humans. Cereb. Cortex. 2020;30:4204–4219. doi: 10.1093/cercor/bhaa048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gollob H.F., Reichardt C.S. Interpreting and estimating indirect effects assuming time lags really matter. In: Collins L.M., Horn J.L., editors. Best Methods For the Analysis of change: Recent advances, Unanswered Questions. American Psychological Association; 1991. pp. 243–259. future directions, edited by. [Google Scholar]
- Guich S.M. Effect of attention on frontal distribution of delta activity and cerebral metabolic rate in schizophrenia. Schizophr. Res. 1989;2:439–448. doi: 10.1016/0920-9964(89)90012-1. [DOI] [PubMed] [Google Scholar]
- Hamilton H.K. Association between P300 responses to auditory oddball stimuli and clinical outcomes in the psychosis risk syndrome. JAMA Psychiatry. 2019;76:1187–1197. doi: 10.1001/jamapsychiatry.2019.2135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y.T., Pan W.C. Hypothesis test of mediation effect in causal mediation model with high-dimensional continuous mediators. Biometrics. 2016;72:402–413. doi: 10.1111/biom.12421. [DOI] [PubMed] [Google Scholar]
- Hyman H.H. The Free Press; Glencoe, Illinois, USA: 1955. Survey Design and Analysis: Principles, Cases and Procedures. [Google Scholar]
- Indritz J. Macmillan; New York, USA: 1963. Methods in Analysis. [Google Scholar]
- Ingvar D.H., Sjölund B., Ardö A. Correlation between dominant EEG frequency, cerebral oxygen uptake and blood flow. Electroencephalogr. Clin. Neurophysiol. 1976;41:268–276. doi: 10.1016/0013-4694(76)90119-x. [DOI] [PubMed] [Google Scholar]
- Judd C.M., Kenny D.A. Process analysis: estimating mediation in treatment evaluations. Eval. Rev. 1981;5:602–619. [Google Scholar]
- Karhunen K. Über lineare Methoden in der Wahrscheinlichkeitsrechnung (On linear methods in probability and statistics) Ann. Acad. Sci. Fenn. Ser. A. I. Math.-Phys. 1947;31:1–79. [Google Scholar]
- Lindquist M.A. Functional causal mediation analysis with an application to brain connectivity. J. Am. Stat. Assoc. 2012;107:1297–1309. doi: 10.1080/01621459.2012.695640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loève M. Calcul des probabilités – sur la covariance d’une fonction aléatoire (Calculating probabilities – on the covariance of a random function). Note by M. Michel Loéve, present by M. Henri Villat. In Comptes rendus de l’Académie des Sciences (Comptes rendus, or Proceedings of the Academy of sciences) 1945;220:295–296. [Google Scholar]
- Marek S. Spatial and temporal organization of the individual human cerebellum. Neuron. 2018;100:977–993. doi: 10.1016/j.neuron.2018.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McArdle J.J. A latent difference score approach to longitudinal dynamic structural analysis. In: Cudeck R., du Toit S., Sörbom D, editors. Structural Equation Modeling: Present and Future. Scientific Software International; Lincolnwood, IL, USA: 2001. pp. 342–380. [Google Scholar]
- McGlashan T.H. Instrument for the assessment of prodromal symptoms and states. In: Miller T., Mednick S.A., McGlashan T.H., Libiger J., Johannessen J.O., editors. Early Intervention in Psychotic Disorders. Springer; Dordrecht, the Netherlands: 2001. pp. 135–149. byNATO Science Series (Series D: Behavioural and Social Sciences) [Google Scholar]
- Miller T.J. Prospective diagnosis of the initial prodrome for schizophrenia based on the structured interview for prodromal syndromes: preliminary evidence of interrater reliability and predictive validity. Am. J. Psychiatry. 2002;159:863–865. doi: 10.1176/appi.ajp.159.5.863. [DOI] [PubMed] [Google Scholar]
- Miller T.J. Prodromal assessment with the structured interview for prodromal syndromes and the scale of prodromal symptoms: predictive validity, interrater reliability, and training to reliability. Schizophr. Bull. 2003;29:703–715. doi: 10.1093/oxfordjournals.schbul.a007040. [DOI] [PubMed] [Google Scholar]
- Muller D., Judd C.M., Yzerbyt V.Y. When moderation is mediation and mediation is moderated. J. Pers. Soc. Psychol. 2005;89:852–863. doi: 10.1037/0022-3514.89.6.852. [DOI] [PubMed] [Google Scholar]
- Muthén B.O., Curran P.J. General longitudinal modeling of individual differences in experimental designs: a latent variable framework for analysis and power estimation. Psychol. Methods. 1997;2:371–402. [Google Scholar]
- Namkung H., Kim S.H., Sawa A. The insula: an underestimated brain area in clinical neuroscience, psychiatry, and neurology. Trends Neurosci. 2017;40:200–207. doi: 10.1016/j.tins.2017.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen T.Q. Causal mediation analysis with a binary outcome and multiple continuous or ordinal mediators: Simulations and application to an alcohol intervention. Structural equation modeling. 2016;23:368–383. doi: 10.1080/10705511.2015.1062730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pomarol-Clotet E. Failure to deactivate in the prefrontal cortex in schizophrenia: dysfunction of the default mode network. Psychol. Med. 2008;38:1185–1193. doi: 10.1017/S0033291708003565. [DOI] [PubMed] [Google Scholar]
- Powers A.R., Mathys C., Corlett P.R. Pavlovian conditioning–induced hallucinations result from overweighting of perceptual priors. Science. 2017;357:596–600. doi: 10.1126/science.aan3458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsay J., Silverman B.W. Springer-Verlag; New York, USA: 2005. Functional Data Analysis. [Google Scholar]
- Robins J.M., Greenland S. Identifiability and exchangeability for direct and indirect effects. Epidemiology. 1992;3:143–155. doi: 10.1097/00001648-199203000-00013. [DOI] [PubMed] [Google Scholar]
- Schmahmann J.D. The cerebellum and cognition. Neurosci. Lett. 2019;688:62–75. doi: 10.1016/j.neulet.2018.07.005. [DOI] [PubMed] [Google Scholar]
- Shergill S.S. Mapping auditory hallucinations in schizophrenia using functional magnetic resonance imaging. Arch. Gen. Psychiatry. 2000;57:1033–1038. doi: 10.1001/archpsyc.57.11.1033. [DOI] [PubMed] [Google Scholar]
- Sobel M.E. Asymptotic confidence intervals for indirect effects in structural equation models. Sociol. Methodol. 1982;13:290–312. [Google Scholar]
- Sollychin M. Frontal slow wave resting EEG power is higher in individuals at ultra high risk for psychosis than in healthy controls but is not associated with negative symptoms or functioning. Schizophr. Res. 2019;208:293–299. doi: 10.1016/j.schres.2019.01.039. [DOI] [PubMed] [Google Scholar]
- Tian Y. Insula functional connectivity in schizophrenia: subregions, gradients, and symptoms. Biol. Psychiatry Cogn. Neurosci. Neuroimaging. 2019;4:399–408. doi: 10.1016/j.bpsc.2018.12.003. [DOI] [PubMed] [Google Scholar]
- VanderWeele T.J., Vansteelandt S. Mediation analysis with multiple mediators. Epidemiol. Method. 2014;2:95–115. doi: 10.1515/em-2012-0010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.-.L., Chiou J.-.M., Müller1 H.-.G. Functional data analysis. Ann. Rev. Stat. Appl. 2016;3:257–295. [Google Scholar]
- Whitfield-Gabrieli S., Ford J.M. Default mode network activity and connectivity in psychopathology. Ann. Rev. Clin. Psychol. 2012;8:49–76. doi: 10.1146/annurev-clinpsy-032511-143049. [DOI] [PubMed] [Google Scholar]
- Whittle R., Mansell G., Jellema P., van der Windt D. Applying causal mediation methods to clinical trial data: what can we learn about why our interventions (don't) work. Eur. J. Pain. 2017;21:614–622. doi: 10.1002/ejp.964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wotruba D. Aberrant coupling within and across the default mode, task-positive, and salience network in subjects at risk for psychosis. Schizophr. Bull. 2014;40:1095–1104. doi: 10.1093/schbul/sbt161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wylie K.P., Tregellas J.R. The role of the insula in schizophrenia. Schizophr. Res. 2010;123:93–104. doi: 10.1016/j.schres.2010.08.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou Q.H. An improved approach to detection of amplitude of low-frequency fluctuation (ALFF) for resting-state fMRI: fractional ALFF. J. Neurosci. Methods. 2008;172:137–141. doi: 10.1016/j.jneumeth.2008.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.