Impact of reproduction number on the multiwave spreading dynamics of COVID-19 with temporary immunity: A mathematical model

Graphical abstract

Abstract

Objectives

The recent discoveries of phylogenetically confirmed COVID-19 reinfection cases worldwide, together with studies suggesting that antibody titres decrease over time, raise the question of what course the epidemic trajectories may take if immunity were really to be temporary in a significant fraction of the population. The objective of this study is to obtain an answer for this important question.

Methods

We construct a ground-up delay differential equation model tailored to incorporate different types of immune response. We considered two immune responses: (a) short-lived immunity of all types, and (b) short-lived sterilizing immunity with durable severity-reducing immunity.

Results

Multiple wave solutions to the model are manifest for intermediate values of the reproduction number R; interestingly, for sufficiently low as well as sufficiently high R, we find conventional single-wave solutions despite temporary immunity.

Conclusions

The versatility of our model, and its very modest demands on computational resources, ensure that a set of disease trajectories can be computed virtually on the same day that a new and relevant immune response study is released. Our work can also be used to analyse the disease dynamics after a vaccine is certified for use and information regarding its immune response becomes available.

Introduction

Between 24-08 and 10-11-2020, nine phylogenetically confirmed cases of COVID-19 reinfection have been discovered worldwide; the first of these was in Hong Kong (To et al., 2020), followed by two more in Greater Noida, India (Sinha, 2020, Gupta et al., 2020), two in Belgium (van Elslande et al., 2020; Selhorst et al., 2020), two in USA (Goldman et al., 2020, Tillett et al., 2020), one in Ecuador (CGTN, 2020), and one in the Netherlands (Mulder et al., 2020). In eight of these cases, the patients were presumed to be immunocompetent; of these, the second infections were milder than the first in six cases and more severe in two. Little is known about the immune response to SARS-CoV-2. Edridge et al. (2020) reported that immunity against infection by benign coronaviruses (excluding SARS-CoV, MERS-CoV or SARS-CoV-2) lasts for a few months and that reinfection is common from one year onwards. Wajnberg et al. (2020) found that among a cohort of almost 20,000 patients at Mount Sinai Hospital in New York, USA, all but one demonstrated significant antibody titre levels in their blood plasma three months after the original infection. Siddiqui et al. (2020) corroborated these results via a smaller study conducted at Max Hospital, New Delhi, India.

An observational cohort study (Crawford et al., 2020) of 34 patients conducted at the University of Washington at Seattle found that over a 3- to 5-month period, antibody concentrations decreased over time, in a manner consistent with the immune responses to acute infections by other viruses including influenza, SARS, and MERS. In these infections, the initial reduction in titres was followed by a plateau; whether this is true of SARS-CoV-2 is unknown at present. Abu-Raddad et al. (2020) reported that out of more than 130,000 patients infected with COVID-19 in Doha, Qatar, 243 reported a positive swab 45 or more days after the original positive test; 54 out of these 243 had “strong or good evidence for reinfection”. All of the reinfections were asymptomatic or presented with mild symptoms on the second bout; however the initial symptom profile of these patients had been mild or asymptomatic as well. Kowitdamrong et al. (2020) reported upto a 20% post-infection seroconversion failure rate in mild or asymptomatic patients in Thailand but did not document any cases of reinfection. More recently, Lumley et al. (2020) reported an antibody half-life of 85 days and a median time of 137 days to the loss of positivity; these results were corrborated by Robertson et al. (2020). A few potential cases of reinfection have also been reported in the media for some time prior to the first documented case; however, in these instances, the evidence was not fully credible (McCamon, 2020, Saplakoglu, 2020, Ackerly, 2020).

Two systematic reviews have focussed on the antibody response (Post et al., 2020) and cellular immune response (Shrotri et al., 2020) to the virus. The former expanded upon the results we describe above; the latter highlighted that the response of T-cells to SARS-CoV-2 is currently unknown. Lavine et al. (2020) proposed that the immune response to the virus will determine the manner of transition of COVID-19 to endemicity; however, in the absence of known facts, this work is predominantly speculative at this time. Recent cross-sectional studies from both Paris (Anna et al., 2020) and London (Ward et al., 2020) reported decreasing seroprevalence as a function of time; this may be related to decreasing titre levels and might indicate the possibility of reinfection. In two recent, reassuring developments, Zuo et al. (2020) in Manchester, UK, and Ogega et al. (2020) in Baltimore, USA, reported significant levels of T- and B-cells in recovered patients at 25 and 15 weeks, respectively, following infection; both studies included mild or asymptomatic patients as well as patients with very low antibody titre levels. This indicates that durable cellular immunity may be present against this virus even if antibodies decay over time.

Although the reinfection cases so far are isolated, the almost daily updates on the immune response to SARS-CoV-2 make us contemplate what the epidemiological consequences might be if the immunity duration indeed turns out to be finite for a significant fraction of the population. The only approach that can attempt to answer this question is mathematical modeling. Giordano et al. (2020) and Bjørnstad et al. (2020) both account for the possibility of reinfection, with the latter identifying an oscillatory approach towards the eventual endemic equilibrium. Kosinski (2020) however, finds multiple waves of COVID-19 if the immunity duration is finite. Sandmann et al. (2020), in an analysis of this situation in the context of a vaccine, reported smooth oscillations about an endemic equilibrium, which change to jerky oscillations with periodic lockdown. In this article, we show that the case trajectories with temporary immunity actually depend in an intricate manner on the reproduction number R. Before commencing our analysis, we clarify that we are currently treating large-scale temporary immunity as a hypothetical, hopefully worst-case scenario; the validity of this assumption remains uncertain due to the lack of sufficient data. Furthermore, in this research, we do not attempt to model the effects of vaccination; all the possibilities that might come into play after introduction of this new variable will be considered in a subsequent analysis.

Methods

We start from a delay differential equation (DDE) model constructed by our group (Shayak and Sharma, 2020, Sharma and Shayak, 2020), hereinafter referred to as “References Shayak and Sharma, 2020, Sharma and Shayak, 2020”) which accounts for many realistic features associated with COVID-19 transmission. This model can be easily adapted to accommodate a given immune response. The dependent variable y(t) denotes the cumulative number of corona cases in the region of interest (typically a town, neighbourhood, village, or other area with good interaction among the inhabitants) as a function of time, measured in days. The parameters in the model are:

• • m ₀: the per-case spreading rate which accounts for factors such as the degree of mobility (i.e. lockdown/unlock), extent of mask use, extent of handwashing, and other public health measures
• • τ ₁: the asymptomatic transmission period which we take to be 7 days throughout
• • τ ₂: the pre-symptomatic transmission period which we take to be 3 days throughout
• • μ ₁: the fraction of patients who are asymptomatic (0 < μ ₁ < 1)
• • μ ₃: the fraction of patients (both symptomatic and asymptomatic) who are NOT detected in contact tracing drives and quarantined (0 < μ ₃ < 1)
• • N: the total number of susceptible people in the region at the start of the epidemic

In our previous work [26,27], we had assumed that one bout of infection renders everlasting immunity (practically, immunity lasting longer than the epidemic’s progression). Now, we account for two different types of immune response, as follows.

• •Simple response: In this scenario, one bout of infection renders a person insusceptible to fresh infection for a time τ ₀ days (τ ₀ much greater than τ ₁ and τ ₂) following recovery, after which s/he again turns susceptible to the disease in its original form.
• •Complex response: In this scenario, adapted from Lavine et al. (2020), a person is initially susceptible to the current, highly virulent form of the disease. The first bout of infection renders him/her completely insusceptible for τ ₀ days following recovery, after which s/he turns susceptible to a lower virulence form of the disease. If infected the second time, then s/he becomes permanently insusceptible to further infection.

As is customary in lumped parameter or compartmental models, the value of τ ₀ used in the model must be an average over the entire population. The experiences of the first few confirmed reinfections may well indicate a general trend favouring the second immune response to the first; in the absence of data, we shall work with both assumptions.

It can be shown (Section 2 of the Supplementary material) that with the simple immune response, the dynamics of the disease is governed by the DDE

$$\frac{\text{d}y}{\text{d}t}=m_0\left[1-\frac{y\left(t\right)-y(t-{\tau }_0)}{N}\right]\left[y\left(t\right)-\left(1-{\mu }_3\right)y(t-{\tau }_2/2)-\left(1-{\mu }_1\right){\mu }_{3}y(t-{\tau }_2)-{\mu }_1{\mu }_{3}y\left(t-{\tau }_1\right)\right]$$ (1)

With the complex immune response, we need two dependent variables : y(t), the cumulative number of cases of the high virulence form and z(t), the cumulative number of cases of the lower virulence form. We let μ _{1 a} and μ _{1 b} (presumably greater than μ _{1 a}) be the asymptomatic fractions for the two forms and keep all other parameters identical for both. Then, the dynamics of y and z are governed by the following coupled system of DDEs

$$\frac{\text{d}y}{\text{d}t}=m_0\left[1-\frac{y(t)}{N}\right]\left[\begin{array}{l}y(t)-\left(1-{\mu }_3\right)y(t-{\tau }_2/2)-\left(1-{\mu }_{1a}\right){\mu }_{3}y(t-{\tau }_2)-{\mu }_{1a}{\mu }_{3}y(t-{\tau }_1)\\ +z(t)-\left(1-{\mu }_3\right)z(t-{\tau }_2/2)-\left(1-{\mu }_{1b}\right){\mu }_{3}z(t-{\tau }_2)-{\mu }_{1b}{\mu }_{3}z(t-{\tau }_1)\end{array}\right]$$ (2a)

$$\frac{\text{d}z}{\text{d}t}=m_0\left[\frac{y(t-{\tau }_0)-z}{N}\right]\left[\begin{array}{l}y(t)-\left(1-{\mu }_3\right)y(t-{\tau }_2/2)-\left(1-{\mu }_{1a}\right){\mu }_{3}y(t-{\tau }_2)-{\mu }_{1a}{\mu }_{3}y(t-{\tau }_1)\\ +z(t)-\left(1-{\mu }_3\right)z(t-{\tau }_2/2)-\left(1-{\mu }_{1b}\right){\mu }_{3}z(t-{\tau }_2)-{\mu }_{1b}{\mu }_{3}z(t-{\tau }_1)\end{array}\right]$$ (2b)

whose derivation is again given in the Supplementary material, Section 2.

For both models, we present the solutions in a Notional City having an initial susceptible population of N = 300,000 (the epidemic durations and case trajectory shapes are almost independent of N and the case counts scale as N for large N) and 80% asymptomatic carriers i.e. μ ₁ = 0·8 (or μ _{1 a} = 0·8 if appropriate) in the current, highly virulent form of the disease. We let μ _{1 b} = 0·95 for the lower virulence form and take the immunity duration τ ₀ to be 200 days. We solved the equations numerically in Matlab using the 2nd order Runge Kutta method with a step size of 0·001 day. The initial condition function we take is zero cases for the first 193 days followed by linear growth of cases at 100 cases/day for the next seven days (with the complex immune response, this growth refers to the high virulence cases; the lower virulence cases remain zero). We take t = 0 to be the 194th day of the initial condition period.

One issue needs special mention. In a numerical simulation, the case rate will never be identically zero but will be something like 0·001 cases/day (or machine epsilon cases/day). This can pose a serious problem in a situation where there are potential second waves of the epidemic. To circumvent this issue, we have arranged for manual termination of the run if the case rate becomes sufficiently low. Defining the number of active cases at time t to be y(t)−y(t−14), we stop the run if there is less than one active case for 14 consecutive days. While the number 14 (twice) may be somewhat arbitrary, the criterion of a low enough active case count for a long enough period is a very reasonable indicator of the true end of the outbreak. We run all simulations either upto t = 1400 days or until they terminate, whichever is earlier.

Results

All results in this described herein are based on an assumed immunity period of 200 days. The exact value is not of the greatest significance; as we shall see, the important thing is whether this period is shorter or longer than the evolution of the outbreak with permanent immunity. Six different solution classes, corresponding to different parameter values and labelled as Notional Cities A through F, of the model with permanent immunity have been derived previously [26,27] and are recapitulated in Section 1 of the Supplementary material. We shall consider the same Cities in the present analysis.

Scenario 1: simple immune response

We first consider the simple immune response, modelled by (1). Notional City A has m ₀ = 0·23 and μ ₃ = 0.5, which, with permanent immunity, resulted in the epidemic being driven monotonically to containment in 120 days. With the simple immune response, the time-trace of the disease is shown in Figure 1 . Here and henceforth, we show three things in the same plot : y(t) as a blue line, its derivative as a green line and the “epi-curve” or weekly increments in cases scaled down by a factor of 7, in grey bars.

Figure 1.

City A eliminated the epidemic via non-pharmaceutical interventions alone.

The response remained the same as it was with permanent immunity. Next, we present City C, which has μ ₃ = 3/4 and m ₀ = 0·5 all the time. (We use 0·23 for a “low” value of m ₀ since we obtained it from data fits in previous studies [26,27]; the chosen “high” value of m ₀ = 0·5 generates a 90% infection level at the end of the outbreak). With a simple immune response, the trajectory is shown in Figure 2 .

Figure 2.

City C reached herd immunity well before the 200-day mark. ‘k’ Denotes thousand and ‘L’ denotes hundred thousand.

Once again, there is no change in behaviour from the permanent immunity case. City B had an m ₀ of 0·23 as with City A but had a μ ₃ of 3/4 as with City C. With permanent immunity, City B crawled up to an infection level of approximately 26% over a period of 220 days. Here however, the 220-day run becomes longer than the assumed immunity duration of 200 days; the result, now labelled as City B1, is shown in Figure 3 .

Figure 3.

City B1 (we used B2 to denote the same city with a complex immune response) was a less effective form of A and had multiple waves of COVID-19. ‘k’ Denotes thousand and ‘L’ denotes hundred thousand. We stopped the simulation at 1400 days but it is important to note that the waves persisted after this time.

There are wave after wave of outbreaks in this scenario. While we do not believe that the disease can really run unmitigated for four years, the long simulation runtime demonstrated the perfect periodicity of the case trajectories. The case count at the end of the run was greater than the city’s initial susceptible population, thus, at least some people were infected at least twice.

Cities D and E of References Shayak and Sharma (2020), Sharma and Shayak (2020) were similar to C and A, respectively, and again, did not show any change when the new immune response is incorporated. City F, was more interesting as it features reopening-induced second waves. We began our analysis of this City with the parameter values of B, on a path to multiple waves. One hundred and fifty days into the outbreak it reopened completely, raising m ₀ to 0·5, aiming to infect its entire population before immunity ran out (Figure 4 ).

Figure 4.

City F took a bold approach and “beat the virus to the finish line”. ‘k’ Denotes thousand and ‘L’ denotes hundred thousand.

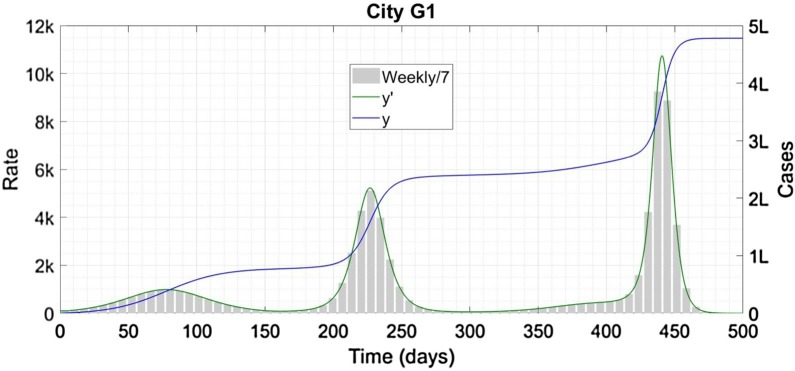
However controversial this strategy might appear, it works. The reopening generates an immediate second wave but it did not succeed in making epidemic vanish completely after 210 days and 246,000 infections. This strategy however has an unhappy variant. City G, instead of reopening at one shot, shows a linear increase in m ₀ from 0·23 to 0·50 over the interval from 150 to 250 days. The resulting infection profile is shown in Figure 5 .

Figure 5.

City G1 represents a failed version of City F; the error in this case carries a significant price. ‘k’ Denotes thousand and ‘L’denotes hundred thousand.

There are three separate waves of infections here; each more severe than the first. Furthermore, the cumulative case count exceeded 150% of the total population.

Scenario 2: complex immune response

Next, we considered the complex immune response, as modelled previously (2). Numerical research confirmed our expectation that Cities A, C, and F showed no difference from the simple immune response case since the epidemic terminates before the immunity duration lapsed. Next, we focus on City B, now renamed as B2 (Figure 6 ).

Figure 6.

City B with a complex immune response. ‘k’ Denotes thousand and ‘L’ denotes hundred thousand. W/7 denotes the weekly increments in cases scaled down by 7 as described previously, while HVF and LVF refer to the higher and lower virulence forms of the disease, respectively. y Is shown in blue, $\dot{y}$ in green, z in red, $\dot{z}$ in magenta, and the epi-curves in grey for y and cyan for z.

Again, we observe multiple waves. However, this time, the waves are progressively attenuated so that the total fraction of the high virulence infection remained less than 60%. An equally significant difference between the two immune responses was evident in City G (Figure 7 ).

Figure 7.

City G with a complex immune response. In the right third of the plot, the cyan bars obscure the smaller grey bars; the latter are enveloped by the green curve which is still visible. ‘k’ Denotes thousand and ‘L’ denotes hundred thousand. W/7 denotes the weekly increments in cases scaled down by 7 as described previously, while HVF and LVF refer to the higher and lower virulence forms of the disease, respectively.

A massive third wave of G1 then occured almost entirely in the lower virulence form.

Discussion

The difference between the cities A, B, and C, lies in their reproduction number R, which is proportional to m ₀ if other parameters are held constant. City A had the starting value R ₀ = 0·886, City B had R ₀ = 1·16, and City C hasd R ₀ = 2·5. With permanent immunity, a low but greater-than-unity R ₀ leads to a long epidemic duration with a lower caseload, while high R ₀ leads to a shorter duration with a higher caseload. The latter carries a significant risk of overwhelming healthcare facilities and causing unnecessary deaths. With temporary immunity, however, we observe multiple waves of disease if the cutoff interval τ ₀ fall below the evolution time with permanent immunity (Supplement, Section 3 features more pedagogical examples that substantiate these findings).

In this example, we took τ ₀ to be 200 days, which is towards the longer end of the free evolution duration with time-independent parameters (with time-dependent parameters like periodic lockdown, the epidemic durations can become much longer). Hence, we observe wave solutions in a small region of parameter space. We find that with a simple immune response, for all parameters except m ₀ being held to their City B values, a containment (City A) solution for low m ₀ gave way to a multiple wave (City B1) solution as m ₀ increased above 0·20, while that reverts to a one-shot logistic-like (City C) solution at m ₀ = 0·25 and higher. A shorter immunity duration would have caused multiple waves over a larger range of m ₀. In our example, the waves were close to sinusoidal near m ₀ = 0·20; as m ₀ was increased, the crests become higher and narrower and the troughs become lower and wider. From a public health perspective, a low and wide trough might represent an opportunity to intensify test-trace-treat efforts and stamp the disease out. With the complex immune response, the total numbers of cases are bounded by 300,000 infections of both y and z. Hence, the infinite periodic waves are no longer possible; instead, they keep attenuating in size before the epidemic terminates outright. In both Cities B and G, the time interval between successive waves appeared to be in the range 1·5τ ₀–2τ ₀. Cities F and G show possible scenarios with reopening. In Table 1 , we summarize the different case trajectories possible for different values of R with three types of immune response: permanent, simple, and complex.

Table 1.

Different possible scenarios with different levels of intervention combined with different types of immune response.

Value of R	Example Notional City	Permanent immunity	Immune response 1	Immune response 2
R < 1 throughout	A	Containment of epidemic in time
Constant intervention level; R0 > 1 but not too high	B	Slow growth of cases, long epidemic duration	Slow growth of cases, infinite waves of epidemic	Slow growth of cases, two to three attenua-ting waves
Constant intervention level; R0 very high	C	Entire population infected rapidly
Abrupt increase in R after a time interval	F	Two waves of disease with high case counts and rates in the second
Gradual increase in R after a time interval	G	Two waves of disease with high case counts and rates in the second	Three waves of disease with progressively increasing counts and rates	Three waves of disease but third (most severe) wave in lower virulence form

We note that the second waves seen after relaxing public health interventions were fundamentally different from the second and subsequent waves exhibited under the aegis of temporary immunity. The former was caused by more susceptible people getting exposed and infected, as in the second wave of City F, while the latter was caused by recovered cases turning re-susceptible and thus increasing the size of the susceptible pool, much like the waves in City B1. The waves in City G1 were of both types; the second wave was of the former type and the third wave was of the latter type. This explains why City G2 (Figure 7), where previously infected people suffered a “different” disease, the second wave occurred primarily in the high virulence form while the third occurred in the lower virulence form. The phenomenon we are currently seeing in European countries and elsewhere is overwhelmingly the result of weakening of public health intervention measures and not because immunity ran out. We are unsure as to what factors governed the successive waves of the deadly 1918–1919 influenza pandemic and how that disease eventually ended.

A search of the existing literature (Giordano et al., 2020, Bjørnstad et al., 2020, Cooke and Van Den Driessche, 1996, Trawicki, 2017, Kiran et al., 2020) suggests the omission of the multiple wave solutions possible with temporary immunity. While Kosinski (2020) and Sandmann et al. (2020) do find these waves, they do not obtain the diverse possible epidemic trajectories depending on R. Since R is governed by public health interventions, our analysis revealed a subtle interconnection between immunity and public health; collectively, these factors influence the fate of the pandemic. In Section 3 of the Supplementary material, we provide an explanation for why we find the present results to be more realistic. Finally, we have never seen an S-E-I-R framework being used to model a situation such as the complex immune response where a person can be infected exactly twice but not more.

Some of the limitations of the present study are the natural constraints associated with any compartmental or lumped parameter model. For example, the immunity duration used in the model has to be an average over the entire population, which can be refined to some degree by introducing age- or vulnerability-structuring (Sandmann et al., 2020). When there are very few cases in a region, the lumped parameter model will no longer be valid. The actual end of the outbreak will be determined by the testing, tracing, and treatment, of each individual case. Another limitation arises from the current lack of knowledge regarding the human immune response to the new pathogen SARS-CoV-2. Here, we have assumed two (plausible) types of response, one where immunity completely lapses after a given time frame and the second where severity-reducing immunity persists indefinitely. Future work may reveal the actual immune response to be more complex than either of these assumptions. Moreover, at least six strains of SARS-CoV-2 have been identified to date (Mercatelli and Giorgi, 2020). At present, we know little about the spreading dynamics of these individual strains (Zhang et al., 2020) and even less about the degree of cross-immunity provided by one strain against another.

In this variability, however, also lies our model’s primary strength. The structure of our model makes it easy to incorporate any form of immune response (Shayak et al., 2020). The computational requirement is negligible, with the run for each Notional City taking approximately one second on a personal computer. Yet, the model is quite powerful since it can generate diverse classes of solutions which are beyond the scope of other models. This means that the moment more information regarding the immune response becomes known, the new information can be encoded into the model framework and accurate case trajectories predicted forthwith. Our analysis will also be of considerable value in calculating the epidemic dynamics after a vaccine is released and mass vaccination is initiated. We shall wait for such an analysis until a vaccine release is imminent or confirmed, since, by that time much more information regarding the immune response to infection and vaccination will be fact instead of speculation.

Funding statement

This research did not involve any funding whatsoever.

Conflict of interest statement

None of the authors have any conflicts of interest to declare.

Data availability statement

This article does not use or feature any data.

Appendix A. Supplementary data

The following is Supplementary data to this article: