Abstract
This study aims to find the association between short-term exposure to air pollutants, such as particulate matters and ground-level ozone, and SARS-CoV-2 confirmed cases. Generalized linear models (GLM), a typical choice for ecological modeling, have well-established limitations. These limitations include apriori assumptions, inability to handle multicollinearity, and considering differential effects as the fixed effect. We propose an Ensemble-based Dynamic Emission Model (EDEM) to address these limitations. EDEM is developed at the intersection of network science and ensemble learning, i.e., a specialized approach of machine learning. Generalized Additive Model (GAM), i.e., a variant of GLM, and EDEM are tested in Los Angeles and Ventura counties of California, which is one of the biggest SARS-CoV-2 clusters in the US. GAM depicts that a 1 μg/m3, 1 μg/m3, and 1 ppm increase (lag 0–7) in PM 2.5, PM 10, and O3 is associated with 4.51% (CI: 7.01 to −2.00) decrease, 1.62% (CI: 2.23 to −1.022) decrease, and 4.66% (CI: 0.85 to 8.47) increase in daily SARS-CoV-2 cases, respectively. Subsequent increment in lag resulted in the negative association between pollutants and SARS-CoV-2 cases. EDEM results in an R2 score of 90.96% and 79.16% on training and testing datasets, respectively. EDEM confirmed the negative association between particulates and SARS-CoV-2 cases; whereas, the O3 depicts a positive association; however, the positive association observed through GAM is not statistically significant. In addition, the county-level analysis of pollutant concentration interactions suggests that increased emissions from other counties positively affect SARS-CoV-2 cases in adjoining counties as well. The results reiterate the significance of uniformly adhering to air pollution mitigation strategies, especially related to ground-level ozone.
Keywords: Air pollution, COVID-19, California, Ensemble learning, Machine learning, Network science, Centrality measures
1. Introduction
Prolonged exposure to particulate matters, PM 2.5 and PM 10, is related to severe health impacts, including respiratory, cardiovascular, and neurocognitive diseases (Brook et al., 2004; Ciencewicki and Jaspers, 2007; Di et al., 2017; Wellenius et al., 2012). After the SARS-CoV-2 virus (COVID-19, henceforth) outbreak, the researchers have established that the people having protracted exposure to PM 2.5 are prone to COVID-19 (Saez et al., 2020; Stieb et al., 2020). This exposure gravely affects the respiratory and cardiovascular systems that exacerbate the impact of COVID-19. A consequence of this is the worse COVID-19 outbreaks in the industrial cities.
Proximity to infected persons (Chan et al., 2020; Li et al., 2020), population mobility (Kraemer et al., 2020), long-term exposure to particulate matters (Saez et al., 2020; Stieb et al., 2020), and ambient temperature (Xie and Zhu, 2020) have been well-associated with COVID-19 pandemic. In addition, the existing state-of-the-art in the field has established the potential existence of traces of COVID-19 RNA on PM (Setti et al., 2020a). This finding is consistent with the evidence available for other viruses (Ma et al., 2017; Qin et al., 2020; Reche et al., 2018; Zhao et al., 2019). In addition, Setti et al. (2020c) have found that initial spread of COVID-19 is significantly associated with daily PM 10 exceedances in Italy. However, no conclusion can be obtained regarding the existence of the virus on PM and severity of the COVID-19 incidences as we are not certain about the vitality of the virus on particulates (Setti et al., 2020a, 2020b). The analysis of historical exposure to pollution can neither validate nor rule out the possibility of airborne transmission. Therefore, data-driven analysis exposure to air pollutants for a short period of time is required to bridge this technical gap.
Los Angeles is one of the biggest COVID-19 clusters in the US, and Ventura is in geographical proximity to it. Thus, Ventura is considered as an extension to Los Angeles, which is also a part of Los Angeles–Long Beach Combined statistical area (CSA, Figure S.8). Los Angeles county has been associated with bad air quality and greenhouse gas emissions. Bashir et al. (2020) unravel the link between air pollution and COVID-19 cases and mortality in California. However, there exists three limitations that needs to be addressed. Firstly, this study did not consider the use of well-established ecological modeling techniques (Saez et al., 2020; Stieb et al., 2020; Zheng et al., 2020). On the contrary, it employs fundamental techniques, such as Spearman, and Kendall correlation. Subsequently, lagged effect of exposure is not introduced in this study. Notably, the impact of pollution can manifest after numerous days (Lin et al., 2018; Myung et al., 2019; Yang et al., 2020). Finally, ground-level ozone (O3), i.e., an essential pollutant in the Californian context (Bytnerowicz and Fenn, 2019; Kahn, 2000) is not included.
In this work, we aim to examine the association between interim exposure to three pollutants: PM 2.5, PM 10, and O3, and COVID-19 incidences. We begin by modeling the pollutants with Generalized Linear Models (GLMs), a classical technique in ecological modeling. However, the GLM has well-established limitations: apriori assumptions (Ngufor et al., 2019), inability to handle multicollinearity (Chen et al., 2018; Dastoorpoor et al., 2019; Phosri et al., 2019), and quantifying differential county-level (or city-level) effects as fixed effects (Zheng et al., 2020). We address these limitations by devising a novel modeling approach, Ensemble-based Dynamic Emission Modeling (EDEM), at the intersection of network science and machine learning. The study focuses on quantifying the emission interactions among counties using state-of-the-art in network science. Both of these approaches, GLM and EDEM, were examined in Los Angeles and Ventura counties of California.
2. Methods
This section details the methods used for ecological modeling. The architecture of the GLM is described. In addition, the architecture of a novel EDEM is proposed that takes into account the effect of pollutant concentrations from adjoining counties while addressing other major challenges of the GLM. Subsequently, detailed sensitivity analyses for both approaches are outlined.
2.1. Data collection
We have used well established sources of ambient air pollution data, ambient meteorological data, county-level COVID-19 data, and county-level demographic data. These sources and their web links are listed in Table A1.
2.1.1. COVID-19 cases
The Johns Hopkins University hosts the most extensive county-level data in the US. The available COVID data consists of the cumulative count of confirmed, deceased, and recovered cases. However, we are interested in daily incidences that are to be modeled against short-term exposure (Zheng et al., 2020). The daily incidences for confirmed cases and deaths were calculated from the cumulative data (see Fig. A.1, Fig. A.2). The delay in reporting and testing practices was accommodated by obtaining a moving average of 7 days on the data. Later, the population bias among counties was addressed by computing the fraction of COVID-19 incidences by the population of the county.
2.1.2. Air pollution and meteorological data
The county-level exposure to pollutants is collected from US EPA (Environmental Protection Agency) monitoring stations spread across these counties. These pollutants include PM 2.5, PM 10, and O3. The maximum daily concentration of the pollutants was collected across these monitoring stations, and the median concentration of these monitoring stations defines the county-level concentration. In addition, daily meteorological data are obtained from US EPA monitoring stations. These meteorological data include mean temperature, relative humidity (RH), air pressure, and wind speed.
2.2. Study area
The contemporary GLM approach and proposed EDEM were applied in Los Angeles and Ventura counties of California. Data are collected from January 22, 2020. As of 1st July 2020, the air pollution data for Los Angeles and Ventura counties are available until 31st March 2020 and 30th April 2020, respectively. All the necessary files, code, and data sources are publicly available on GitHub repository newtein / pollution_science to ensure replication of the study.
2.3. Generalized linear models
Generalized Additive Model (GAM) is a special type of GLM with an added advantage of introducing smooth functions on the predictor variables. GAM is an established choice for modeling the impact of pollutants on the health (Hu et al., 2020; Ma et al., 2020a,b; Peng et al., 2006; Ravindra et al., 2019). Zhu et al. use the same method for determining the relationship between short-term exposure to air pollutants, and COVID-19 confirmed cases in China. In contrast, we explore the effect of exposure on both COVID cases and mortality in the US through GAM and extend the approach to propose EDEM.
2.3.1. Statistical methods
Although the exposure to these pollutants is hazardous, their effect can manifest after numerous days (Lin et al., 2018; Myung et al., 2019; Yang et al., 2020). Thus, the moving-average is employed to reflect the cumulative lag effect of these pollutants (Lin et al., 2018; Yang et al., 2020; Zheng et al., 2020). The model is tested for the lag of 7, 14, and 21 days. The motivation behind choosing the 14-day lag frame is the official COVID-19 incubation period issued by the US Centers for Disease Control and Prevention (The White House, 2020). However, research suggests that our understanding of this incubation period is limited (Lauer et al., 2020); thus, we have included additional multiples of 7, i.e., 7 and 21 days, to determine the effect of exposure to pollution, which is also consistent with the related research in the field (Zheng et al., 2020).Three different models were built for three pollutants due to their inability to handle multicollinearity (Chen et al., 2018; Dastoorpoor et al., 2019; Phosri et al., 2019).
Each pollutant is modeled against positive cases and mortalities. Adhering to the established principles, these models are assumed to take the following form,
| (1) |
| (2) |
Here, and denote the COVID-19 cases and mortalities observed on day in city , respectively (Liu et al., 2017, Zhu and Xie, 2020). Unity has been added to these terms to facilitate their logarithm transformation. represents the lagged moving average concentration of the pollutant (Chen et al., 2018; Phosri et al., 2019; Zheng et al., 2020). The confounding effect of meteorological variables was controlled by introducing mean pressure, temperature, RH, and wind speed. The term represents these four meteorological variables. is the smooth function of a particular meteorological variable (Zhu and Xie, 2020). Potential serial correlation is handled in our model by introducing terms and , which depict reported cases and deaths on a previous day (Liu et al., 2017). The represents the fixed effects affecting all the cities in a particular day (Amuakwa-Mensah et al., 2017; Zheng et al., 2020). This also aims to check time independent characteristics, e.g. population; however, it disregards the time variant effects, such as pollution from the adjoining counties.
The statistical tests were conducted with a two-tailed confidence interval, and p-value of less than 0.05 was categorized as significant. Owing to the logarithmic transformation of the independent variable, effect estimates were represented by the percentage change in daily COVID -19 incidences per unit increase in the pollutant. In this study, GAM is built using the mgcv package (v 1.8–31) in R (v 3.5.3). Notably, the mgcv package uses implicit generalized cross validation mechanism (Wood, 2006).
2.3.2. Sensitivity analyses
We conduct five sensitivity analyses. First, the lagged term for cases and deaths was removed from the model, since we are analyzing daily coronavirus cases and not the communitive ones. Thus, any COVID-19 related trend is essential for the analysis. Second, Los Angeles had the most COVID-19 cases in California; thus, we excluded Los Angeles from our data and analyzed Ventura County only. Third, we created a combined model of pollutants, PM 2.5, PM 10, and O3, to compare the results from single pollutant models, thereby validating the methodology (Chen et al., 2018; Phosri et al., 2019). Forth, we divided cases and deaths with the pollution of the city to overcome the population bias. Fifth, emission coefficient was modeled along with other parameters. To rephrase, GLM was trained with dynamic emission parameters while keeping all other parameters constant, e.g., pollutants, meteorological factor, lagging function with an exception to the city fixed effects.
2.4. Limitations
Three significant limitations of the GLM are summarized as follows. Firstly, GLMs are constructed on assumptions. For instance, equations (1), (2)), delineate our assumption for the linear dependence of COVID-19 cases and deaths, respectively. Although the knowledge is obtained from existing studies, the use of such assumptions is highly discouraged in association analysis (Ngufor et al., 2019). Nevertheless, data-driven machine learning approaches have the potential to obtain associations, both linear and non-linear, without facilitating the model with linear apriori assumptions.
Next, the inability of GLMs to accommodate multicollinearity. For instance, most of the pollutants depict high correlations among themselves; this compels the researchers to develop separate models for each pollutant (Chen et al., 2018; Dastoorpoor et al., 2019; Phosri et al., 2019). However, ensemble learning or tree-based machine learning approaches are equipped with handling multicollinearity (Ma et al., 2020a,b; Parsa et al., 2020; Zhai and Chen, 2018). In addition, this helps us to obtain the relative importance of each pollutant in the prediction of the outcome, which we cannot obtain by developing separate models for each pollutant.
Subsequently, GLMs quantify differential interactions between counties or states as fixed effects. For instance, we replace counties belonging to the same states with a fixed intercept to accommodate diverse demographics, policy implementations, testing procedures, etc. followed by the states (Amuakwa-Mensah et al., 2017; Lu and Lu, 2017; Zheng et al., 2020). In the era of the plethora of data, this approach leads to considerable information loss. We propose the use of network science to quantify these county-level interactions.
2.5. Ensemble-based Dynamic Emission Model
Pollutants are influenced by transport systems (e.g., wind) and meteorological variables (e.g., pressure). The GLM categorizes the differential effects among counties as fixed, which leads to a colossal information loss. However, a county is a part of a large complex emission system experience several state-level and county-level effects. For instance, the effect of pollution of adjoining counties needs to be quantified. Thus, to quantify these effects, we construct a weighted emission network for the pollutants. Each node in the network represents a county, and an edge represents the magnitude of emission (or air pollution) interaction between two counties. Emission interactions for each county are quantified based on its role in the network.
COVID-19 incidences were than mapped by county-level pollutant (lag 0–14), emission interactions (lag 0–14), meteorological variables (wind, RH, temperature, and pressure), geographic, and demographic information. State-of-the-art machine learning technique, i.e., ensemble learning, is used to determine the outcome. Tree-based ensemble learning technique is not affected by multicollinearity, which is one of the limitations of GLMs. To rephrase, multiple pollutants can be modeled by a single model and thereby comparing the relative effect of pollutants on the outcome. In addition, these models can map complex and non-linear associations; however, GLMs only focus on linear associations. The cutting-edge SHAP technique is employed to understand the directionality and degree of these associations, including the relative importance of all the independent variables.
Therefore, in this study, we introduce EDEM that uses a combination of network science and machine learning techniques. EDEM is scripted in python programming language (v 3.7.9) using Networkx (v 2.4), XGBoost (v 1.0.2), SHAP (v 0.35.0), FastDTW (v 0.3.4), CDTW (v 0.0.1), Haversine (v 2.2.0), and SciPy (v 1.0.0).
2.5.1. Emission network
A short-term emission network, for a pollutant with a lag of 14 days, is constructed. Each node represents the monitoring sites, and the edge represents the observed interaction among them. This interaction is quantified using the following methodology. The emission coefficient quantifies the effect of emissions of various counties on a particular county c,
| (3) |
where denotes the total number of counties minus one (excluding c). denotes the emission coefficient between counties c and d,
| (4) |
where denotes the maximum daily value of the emission recording for the county , denotes the observed similarity between the emissions (lag 0–14), is the geometrical nearness factor and is a min-max normalized scalar.
The emission recorded at the monitoring sites is represented by time series; therefore, time series similarity metrics were employed to compute the similarity among emissions. One of the well-established similarity metrics is the Pearson correlation coefficient. Prior to computing correlation, both of the time series were de-trended to eliminate bi-weekly trends (Li et al., 2019; Tong et al., 2020; Zou et al., 2019). The correlations below 98% significance were not considered. Therefore, the can be obtained by cross-correlation,
| (5) |
where and are de-trended values of air pollution concentrations in city c and d, respectively, and n is the number of data points. Notably, the air pollution concentrations is referred to as emissions. Moreover, three additional state-of-the-art similarity metrics were employed for sensitivity analyses: Euclidean distance, dynamic time wrapping (DTW), and constrained dynamic time wrapping (CDTW). The rationale of employing DTW and CDTW involves their capability of computing similarity between two time series that can vary disproportionately with time. This virtue makes them suitable for computing the similarity due to the lag between emissions. Notably, , which represents the observed similarity between two time series of pollutant , is an empirical quantity that can be computed by a wide variety of methods. In this study, we have reported results from Pearson correlation, Euclidean distance, DTW, and CDTW. In addition, Spearman correlation can be employed to compute monotonic relationships (Okada, 2018).
The nearness factor aims to amplify the emission similarity for counties situated at a close distance from each other. The nearness factor is obtained by,
| (6) |
where and denote the set of latitude and longitude for county c and d, respectively. The haversine distance, i.e., the actual circular distance between two places, is used to compute the physical distance.
Three weighted networks were constructed for three pollutants. Notably, a county consists of multiple monitoring sites; thus, the median effect of various monitoring sites is considered the net county-level effect.
2.5.2. Quantification of the interactions
Network centralities metrics provide quantitative tools to pick out fine interactions in complex networks. In terms of emission network, betweenness denotes the extent to which a node is influenced by the other nodes in the emission network. To rephrase, the extent to which a node is influenced (as a bridge) when information, i.e., emission, is passed around the network. Current flow betweenness, i.e., inspired by the random-walk, focuses on the flow of emissions across all the paths by incorporating a component of randomness in the flow (Brandes and Fleischer, 2005), which makes it suitable for emission modeling. In addition, we introduce diverse centrality metrics in sensitivity analyses.
The emission network for pollutant p,
| (7) |
where is the network of the pollutant p and is the emission coefficients, i.e., the edge weights of the network. Current flow betweenness centrality of pollutant p for county c is defined as:
| (8) |
where represents the net emission of pollutant p received at county c. Net emission for county c is calculated by combining the net impact from the emission based on the edge weight, i.e.,. Brandes and Fleischer (2005) compute by Kirchhoff's Current Law and Potential Law. is the normalizing constant .
2.5.3. Association analysis using machine learning
The features fed to the ensemble learning model broadly covers four domains. First, daily pollutant maximum concentration (lag 0–14), second, daily mean values for meteorological variables (e.g., wind, pressure, temperature, and RH), and third, quantification of county-level interactions (lag 0–14). These features were modeled against COVID incidences. The data are split randomly between training and testing set in the ratio of 7:3. XGBoost (eXtreme Gradient Boosting) technique was used to train the model (Chen et al., 2019; Ma et al., 2020a,b; Pan, 2018). The details of hyperparameter tuning of XGBoost using five-fold cross validation is listed in Table S.9. Subsequently, the associations obtained from the model are interpreted using SHapley Additive exPlanations or SHAP (García and Aznarte, 2020; Stojić et al., 2019; Zheng et al., 2020).
2.5.4. Quantifying unmeasured confounding bias
We take potential meteorological and demographic confounding factors into consideration. These include the daily average value of temperature, pressure, RH, wind, and population. In addition, we quantify the county-level emissions to account for the differential emissions. We conduct various sensitivity analyses to determine statistical significance and robustness of the results.
2.5.5. Sensitivity analyses
We conduct 39 sensitivity analyses. First, we create three separate ensemble learning models separately for three pollutants. Second, we create two separate models for Los Angeles and Ventura counties because out of 170 total data points – 100 belong to Ventura and 70 belong to Los Angeles. Third, an incremental term is added to our original ensemble learning model similar to Equations (1), (2)). Forth, the independent variable, i.e., coronavirus cases, was transformed into the logarithmic domain. The subsequent 35 sensitivity analyses involves variation in metrics for (1) computing similarity between observed emissions, i.e., used for network creation, and (2) quantification of the influence of the county by network centralities. Thus, the next 35 sensitivity analyses involve exploring various combinations of similarity and centrality metrics. We use four methods for similarity metrics, namely Pearson correlation coefficient, Euclidian distance, DTW, and CDTW, in combination with 9 methods for centrality metrics, e.g., degree, betweenness, closeness, harmonic, current flow betweenness, current flow closeness, communicability betweenness, load, and clustering.
3. Results
This section presents the results obtained by modeling exposure to air pollution and daily COVID-19 cases. The results can be classified into descriptive, association, and sensitivity analyses. The descriptive analysis focuses on the overall statistics and correlations observed in the data, whereas the association analysis aims to determine the relationship between interim exposure to airborne pollutants and COVID-19 cases. The sensitivity analyses focus on ensuring the robustness and significance of the results.
3.1. Descriptive analysis
The observed mean and standard deviation (mean ± std) for daily maximum values for the pollutants, PM 2.5, PM 10 and O3, were 14.68 ± 7.55 μg/m3, 42.48 ± 28.20 μg/m3, and 0.05 ± 0.008 ppm, respectively. Meteorological variables, namely daily mean pressure, RH, temperature, and wind, depicted the mean and standard deviations of 961.56 ± 26.69 mbar, 61.08 ± 17.55%, 56.05 ± 7.09 °F, and 5.11 ± 2.12 kn, respectively (Table 1 ).
Table 1.
Descriptive statistics of air pollutants and meteorological variables.
| PM 2.5 | PM 10 | O3 | Pressure | RH | Temperature | Wind | |
|---|---|---|---|---|---|---|---|
| count | 170 | 170 | 170 | 170 | 170 | 170 | 170 |
| mean | 14.68 | 42.48 | 0.05 | 961.57 | 61.08 | 56.06 | 5.11 |
| std | 7.55 | 28.2 | 0.01 | 26.7 | 17.56 | 7.1 | 2.13 |
| min | 4 | 4 | 0.03 | 921.04 | 21.38 | 36.07 | 1.48 |
| 25% | 9.18 | 25.25 | 0.04 | 930.59 | 47.64 | 51.32 | 3.96 |
| 50% | 13.4 | 37 | 0.05 | 980.35 | 65.15 | 55.02 | 5.18 |
| 75% | 17 | 55 | 0.06 | 984.42 | 76.2 | 59.36 | 6.01 |
| max | 48 | 213 | 0.08 | 991.04 | 91.25 | 81.33 | 12.55 |
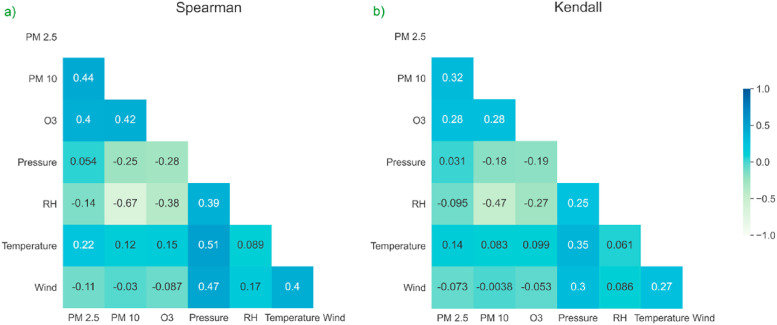
Fig. 1(a–b) illustrate the Spearman and Kendall coefficients of correlation among air pollutants and meteorological variables. Notably, the usage of Spearman and Kendall coefficients for obtaining correlation among meteorological variables and pollutants is established in the literature because data is not assumed to be normally distributed (Copat et al., 2020; Liu et al., 2017). All three pollutants were observed to be significantly correlated with each other. The pressure is significantly correlated with the other meteorological variables. However, the strength of correlation is weak in all these cases. Notably, a statistically significant correlation does not imply the strength of the correlation (Akoglu, 2018). To rephrase, the significant correlation reassures its strength, whether weak or strong. In addition, the temperature is significantly correlated with the wind. However, pollutants are not observed to be strongly correlated with meteorological variables.
Fig. 1.
Observed correlation among pollutants and meteorological variables.
3.2. Association analysis
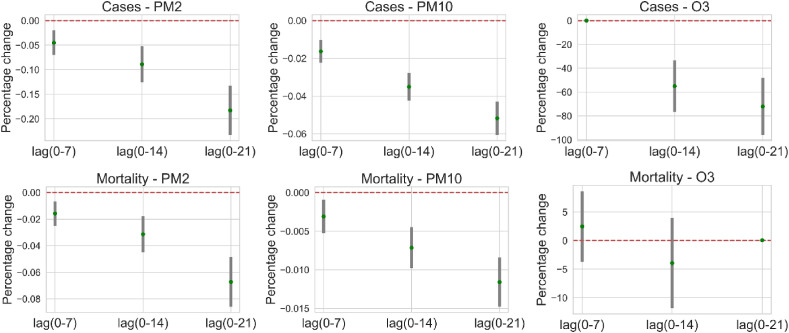
By applying GAM, i.e., a specialized model of GLM family, we have observed a negative association between particulate matter and COVID-19 cases and mortality across all the lags. Specifically, for (1) PM 2.5 at lag 0–21 percentage change equals −18.2% (95% CI: 23.28 to −13.26) for cases and −6.7% (95% CI: 8.59 to −4.84) in mortality, (2) PM 10 at lag 0–21 percentage change equals −5.1% (95% CI: 6.06 to −4.29) and −1.1% (95% CI: 1.47 to −0.84). However, for the lag of 7 days, O3 is observed to be positively associated with the COVID-19 incidences. Specifically, for O3 at lag 0–7 percentage change equals 4.6% (95% CI: 0.85 to 8.47) for cases and 246.83% (95% CI: 369.02 to 862.69) in mortality.
Notably, the observed significance of these pollutants is as follows. Firstly, PM 2.5 is negatively associated with COVID-19 incidences for 14-day lag with 99% confidence. However, similar confidence (or p-value) is not observed for 7 and 21 days. Secondly, the negative association of PM 10 and COVID-19 cases for 7-day lag depicts 95% confidence; however, the confidence is decreased to 90% with an increment in the lag. Finally, O3 is positively associated with COVID-19 cases for 7-day lag; however, the p-value is much higher to be statistically significant. Along with other pollutants, O3 depicts a negative association with COVID-19 cases for 14- and 21- day lag with 99% and 95% confidence, respectively. These results are delineated in Table 2 . The moving average lag effects for pollutants, PM 2.5, PM 10, and O3, on daily cases and mortality related to COVID -19 is illustrated in Fig. A.3.
Table 2.
Intercept – P value table depicting relationship between lagged exposure to air pollutants and COVID-19 incidences.
| Pollutants | lag(0–7) days |
lag(0–14) days |
lag(0–21) days |
||||
|---|---|---|---|---|---|---|---|
| Cases | Mortality | Cases | Mortality | Cases | Mortality | ||
| PM 2.5 | Intercept | −0.045. | −0.015. | −0.089* | −0.031* | −0.182*** | −0.067*** |
| P value | 0.0733 | 0.0882 | 0.0164 | 0.0223 | 0.0003 | 0.0004 | |
| PM 10 | Intercept | −0.016** | −0.003 | −0.035*** | −0.007** | −0.051*** | −0.011*** |
| P value | 0.0080 | 0.1582 | 3.71e-06 | 0.0077 | 2.68e-08 | 0.0003 | |
| O3 | Intercept | 0.046 | 2.468 | −55.00* | −3.931 | −72.14** | 0.057. |
| P value | 0.2227 | 0.6891 | 0.0122 | 0.6183 | 0.0029 | 0.0910 | |
‘***‘, ‘**‘, and ‘*’ shows the significance at 10%, 5%, and 1%.
Although GAM has been a classical modeling approach for modeling health outcomes, the proposed EDEM addresses some of its well-established limitations, which are detailed in Section 2.4. In essence, these are its dependence on apriori assumptions, inability to handle multicollinearity, and quantifying differential county-level (or city-level) effects as fixed effects. To address these limitations, EDEM is built at the intersection of two cutting-edge technologies: network science and machine learning.
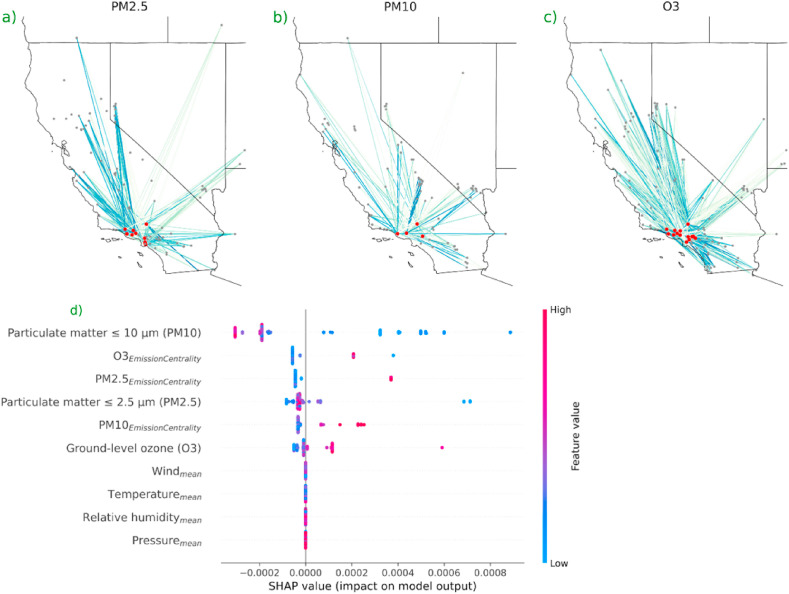
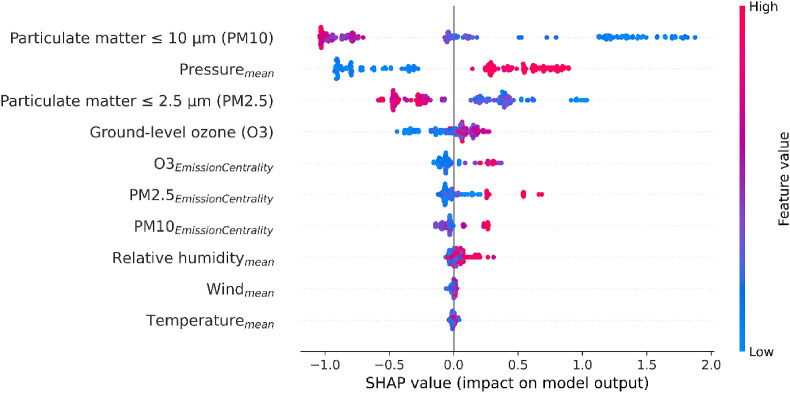
By introducing EDEM, the county-level interactions were quantified. Fig. 2 (a–c) represents the emission network for PM 2.5, PM 10, and O3, respectively. The network comprises short-term exposure information about the particular pollutants. Stronger influence is represented by the bolder edge in the network. EDEM results in an R2 score of 90.96% and 79.16% on training and testing datasets, respectively. Fig. 2 d illustrates the relative importance of features and the directionality of their impact on COVID-19 cases. The result suggests that particulates negatively associated with the cases; however, the ozone factor positively associates. In addition, a positive association is observed between county-level emission interactions and COVID-19 cases. Since EDEM can handle multicollinearity, the decreasing importance of pollutants for determining COVID-19 cases are as follows: PM 10, PM 2.5, and O3 (Fig. 2 d). The airborne nature of COVID-19 is still not explicit; thus, we have reported the results of both models separately without delineating final decisions.
Fig. 2.
The results obtained from EDEM. (a) Represents an emission network of PM 2.5 for an arbitrary day. The nodes (in red) represents the monitoring stations in counties of Los Angeles and Ventura. The influence of the emissions of adjoining counties, grey nodes, are represented by the edge. A stronger edge represents a higher influence. (b) Represents the emission network of PM 10 for an arbitrary day. (c) Represents the emission network of O3 for an arbitrary day. (d) Depicts the impact, direction, and relative importance of the association between exposure to pollutants for a short period of time and COVID-19 cases (also refer to Fig. A.4). Emission centrality reflects the county-level effects obtained from Equation (8) through the current flow betweenness centrality measure. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
3.3. Sensitivity analyses
Five sensitivity analyses were conducted for the GLM. As part of the first sensitivity analysis, the association between COVID-19 incidences and pollutants become more robust after removing the incremental lagging term from the model (Table A.2). As part of the second sensitivity analysis, the removal of Los Angeles from the data has resulted in positive associations between particulate matter and coronavirus incidences. However, the association with O3 is observed to be significantly negative (Table A.3). The third sensitivity analysis involves modeling all pollutants together, which has resulted in the decline of the association (Table S.1). In the fourth sensitivity analysis, the association has become most robust with multiple significant relationships (Table S.2). Notably, the association of COVID-19 cases with all three pollutants is significant. The fifth sensitivity analysis introduces the emission coefficient in the GLM model; the results show a negative association (Table S.7).
Thirty-nine sensitivity analyses were conducted for the EDEM. The first sensitivity analysis confirms the positive association between county-level emissions and COVID-19 cases separately for each pollutant (Figure S.1). However, the separate O3 model has yielded the worst performance with 0.72 and 0.54 R2 scores on training and testing datasets, respectively (Table A.4). Thus, the associations in separate O3 model is not entirely reliable. In the second sensitivity analysis, a higher influence of PM 2.5 and PM 10 is observed by separately modeling Los Angeles and Ventura counties, respectively (Figure S.2). It is intriguing to note that the combined model is influenced by Ventura county, and PM 2.5 is the only influential component in Los Angeles context. The third sensitivity analysis involves the introduction of an incremental term, i.e., day of the year. The results are robust and validate the dependence between pollutants and COVID-19 cases. Consistent with the original model, the particulates are observed to be negatively associated; in addition, the ozone is positively associated (Figure S.3).
As part of the fourth sensitivity analysis, the results became more robust and significant after transforming COVID-19 cases into the logarithmic domain. As compared to the baseline model (Fig. 2 d), the impact and association of pollutants have increased after log transformation, as shown in Fig. A.4. Specifically, the number of data points showing associations is significantly increased; this effect is observed for all the pollutants: PM 10, PM 2.5, and O3. In addition, Fig. A.4 shows that a significant positive association is observed between meteorological variables, namely pressure and Rh, and COVID-19 cases. The R2 score observed across training, and testing dataset for these four sensitivity analyses is delineated in Table A.4.
The next thirty-five sensitivity analyses confirm the robustness of results by introducing diverse methods for computing emission similarity and network centrality. The results are detailed in Table S.3-S.6 and Figure S.4-S.7. We compare the R2 scores across several similarity and centrality metrics, as shown in Figure S.9. The observed results for four similarity metrics: Pearson correlation, Euclidean distance, DTW, and CDTW, are as follows. Firstly, when used with the Pearson correlation, the current flow closeness achieved the highest R2 score of 0.9375 and 0.9088 for training and testing datasets, respectively. Secondly, the usage of harmonic centrality metrics with the Euclidean distance outperformed other network centralities. This combination observed an R2 score of 0.9542 and 0.9575 on training and testing datasets, respectively. Moreover, Figure S.5 h shows the model impact of this combination. In addition to confirming the directionality of associations of the baseline model, the county-level interactions of O3 are most prominent.
In essence, the aforementioned Euclidean distance (between two time-series) is the square root of the sum of the squared distances between data-points belonging to these time-series (Iglesias and Kastner, 2013). In contrast, DTW and CDTW emphasize capturing similar patterns between two time-series by calculating the longest common subsequence. Finally, for DTW and CDTW, harmonic and communicability betweenness metrics yielded approximately 95% of R2 scores, as shown in Table S.5-S.6, respectively. Although R2 scores slightly vary with various centralities, the difference is not significant. The current flow betweenness, harmonic, and communicability betweenness yielded significant results in all the scenarios. Since there exists limited research at the intersection of air pollution and network science, an in-depth analysis of these metrics across various pollutants remains future work.
4. Discussions
This study is focused on devising a novel approach to quantify county-level interactions by mapping air pollution to emission networks. The association analysis is conducted by ensemble learning techniques. The proposed method that lies at the intersection of network science and machine learning addresses several well-established limitations of the GLM. We applied the contemporary method and proposed EDEM to the Los Angeles and Ventura counties. The GLM depicts a negative association between particulate matters and COVID-19 incidences. In addition, our proposed method validates these negative associations; however, the emission interactions were observed to be positively associated with corona cases. To rephrase, the emissions from the adjoining counties are positively related to COVID-19 cases.
The analysis of O3 through GLM delineated a mixed association with coronavirus incidences. The GLM has reported a positive relationship for lag (0–7) days; however, a negative association is observed for lag (0–14) days and lag (0–21) days. Nevertheless, EDEM depicted the positive association between O3 and COVID-19 incidences. Bernardini et al. (2020) found a positive association between exposure to ground-level ozone and hospitalizations in Umbria, Italy. The authors conclude that short-term exposure to ground-level ozone may be linked with increased psychiatric emergency related hospitalizations in Umbria; however, the mental health implication of ground-level ozone is not clear. On the other hand, there exist studies that focus on growing mental health issues during COVID-19. Shi et al. (2020) have reported that the mental health symptoms may have been common in the general population of China during the COVID-19 outbreak. In addition, Lai et al. report mental health outcomes among frontline workers (Lai et al., 2020). However, the role of ground-level ozone is yet to be determined.
The observation of the negative association between particulate matters and corona incidences is perplexing. This negative association between particulates and COVID-19 incidences is consistent with Bashir et al. (2020). This can be attributed to the stringent drop in particulate matter during lockdown (stay at home order) and subsequent increment in the COVID-19 incidences. Berman and Ebisu (2020) show that urban areas of the US are associated with a statistically significant reduction in PM 2.5 during COVID-19. In addition, this is validated by the second sensitivity analysis, where the removal of Los Angeles, i.e., highly polluted, has resulted in a positive association between particulates and corona cases. Chan et al. (2020) have observed a positive association between short term exposure to particulates and corona incidences in China, which is contested to be spurious by Copiello and Grillenzoni (2020). With a systematic review of the literature, Copat et al. (2020) point out that PM 2.5 is closely associated with COVID-19 than PM 10 due to the inability of the latter to penetrate type II alveolar cells.
Los Angeles has struggled with high levels of ground-level ozone, a major constituent of photochemical smog (Bytnerowicz and Fenn, 2019; Haagen-Smit and Arie, 1952; Kahn, 2000). Reducing ozone levels requires dedicated and continuous efforts. Studies show that temporary measures fail to reduce ozone concentration (Su et al., 2017). Implementing strict emission standards can be expensive, albeit research shows that fiscal health advantages associated with decreased ambient air pollution would compensate 26–1050% of the expenditure of US policies to reduce greenhouse gas emissions (Thompson et al., 2014). In addition, the literature has established strong link between air pollution and airborne viral respiratory diseases (Chauhan and Johnston, 2003; Mehta et al., 2013), along with the subsequent hospitalization (Phosri et al., 2019; Xie et al., 2019).
Despite the inherent challenges in designing an ecological study (Saez et al., 2020; Stieb et al., 2020; Zheng et al., 2020), the results obtained from EDEM through network analyses reiterate the importance of (1) uniformly abiding by the air pollution regulations across counties, and (2) continuing to reinforce existing air pollution mitigation strategies to ensure healthy living during and after the pandemic. The implications of our results in the control and prevention of COVID-19 as are follows. First, it suggests that federal and county-level administrations should work uniformly in all the counties to reduce the pollution as emission from one county affects the other, which in turn positively associates with coronavirus incidences. Second, stringer automobile standards to limit ground-level ozone could aid in bringing down the net ozone emissions that might lead to the reduction in COVID-19 cases. Third, urban city dwellers might avoid areas with high ozone concentration, e.g., parking lots and traffic jams, since automobiles are the major contributor to ozone and its precursors.
Although we devise a novel approach at the intersection of network science and machine learning, the major limitation of our work is its application in Los Angeles and Ventura counties only. Since this work is focused on the introduction of EDEM, a country wide cross-county analysis of the complete USA remains the future work. In addition, we did not include multi-dimensional demographic information e.g., gender, population composition. Future studies are required to address these limitations.
5. Conclusions
In this work, we examined the association between short-term exposure to air pollution and COVID cases using two modeling techniques. These models include classical GLMs and proposed EDEMs. EDEM was implemented at the intersection of network science and machine learning for ecological modeling. We modeled particulate and ground-level ozone pollution as networks. Subsequently, we used ensemble learning, i.e., a specialized machine learning technique due to its virtue of handling multicollinearity. Finally, we obtained a deeper-understanding of the association through SHAP, i.e., a specialized machine learning interpretability technique inspired by the Shapley values. The models were evaluated using the R2 score, the training and testing datasets yielded R2 score of 90.96% and 79.16%, respectively. The results suggested a significant relationship between airborne pollutants and COVID-19 cases. The results showed that short-term exposure to ground-level ozone is positively related to daily confirmed cases; however, exposure to particulates, PM 2.5 and PM 10, depicts a negative association. The analysis of county-level emission interactions suggests that increased influence from other counties positively affects the COVID-19 confirmed cases. Although the empirical results depict positive associations, considering the paucity of data, it would be early to present a conclusive decision. Currently, the possible setbacks of the pandemic cannot be averted until potent vaccines or immunoprophylaxis with recombinant antibodies will be adequately administered; however, adhering to the existing air pollution standards, especially ground-level ozone regulations, can potentially ameliorate the situation.
Author contribution statement
HG: Conceptualization; Formal analysis; Methodology; Software; Visualization; Roles/Writing - original draft; Writing – review & editing. AS: Supervision; Validation; Writing – review & editing.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors acknowledge the sincere efforts of Deepak Mittal (Project Engineer, Wipro Limited, Bangalore, India.), Manas Gujral (Medical Student, Atal Bihari Vajpayee Institute of Medical Sciences and Dr. RML Hospital, New Delhi, India.), and Tanya Gupta (Associate Applied Data Scientist, Dunnhumby India Pvt. Ltd., Gurugram, India.).
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.envres.2020.110704.
Appendix A.
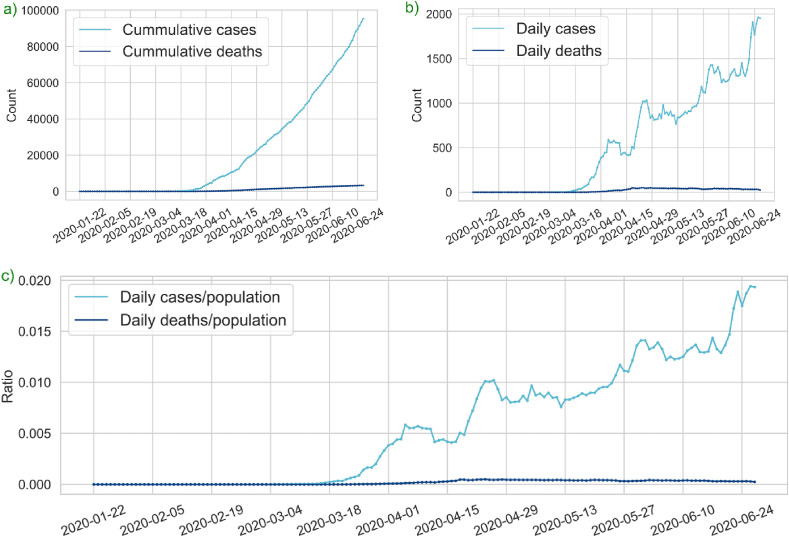
Fig. A.1.
Los Angeles County COVID-19 Statistics
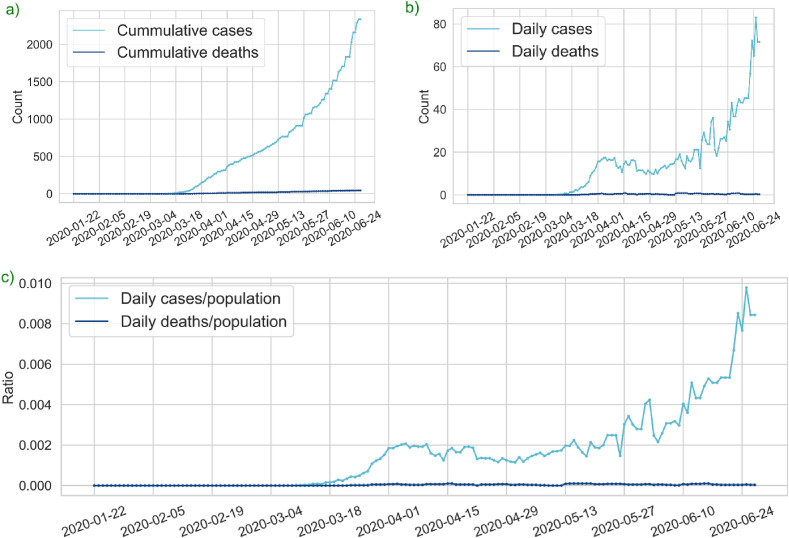
Fig. A.2.
Ventura County COVID-19 Statistics
Fig. A.3.
Association between short - term exposure to pollutants and COVID Incidences across lags
Fig. A.4.
Results of 4th sensitivity analysis of the proposed EDEM. COVID-19 cases were transformed by log scale.
Table A.1.
Data Sources
| Source | Access link | |
|---|---|---|
| COVID-19 incidences | Johns Hopkins University COVID-19 Resource Center |
GitHub Repository: CSSEGISandData/COVID-19 Full address: https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_time_series |
| Air Pollution and Meteorological data | US EPA – AQS API | API documentation: https://aqs.epa.gov/aqsweb/documents/data_api.html Data files: https://aqs.epa.gov/aqsweb/airdata/download_files.html |
| Demographic data | 2014-18 release of the American Community Survey | Module documentation: https://walker-data.com/tidycensus/ Full address: https://www.kaggle.com/headsortails/covid19-us-county-jhu-data-demographics |
Table A.2.
Generalized linear models – 1st Sensitivity Analysis. The lagged term for cases and deaths is removed from the model since we are analyzing daily COVID cases and not communitive COVID cases.
| Pollutant | Feature | Cases | Deaths | Cases | Deaths | Cases | Deaths |
|---|---|---|---|---|---|---|---|
| Pollution exposure lag | lag(0–7) | lag(0–7) | lag(0–14) | lag(0–14) | lag(0–21) | lag(0–21) | |
| PM2 | Intercept | −0.057* | −0.025** | −0.122** | −0.050*** | −0.239*** | −0.097*** |
| P-value | 0.0277 | 0.0092 | 0.0014 | 0.0004 | 1.67E-06 | 1.76E-07 | |
| PM10 | Intercept | −0.022*** | −0.004* | −0.043*** | −0.010*** | −0.058*** | −0.016*** |
| P-value | 0.0001 | 0.0367 | 4.00E-10 | 9.17E-05 | 5.16E-13 | 1.86E-07 | |
| O3 | Intercept | −29.19 | 2.5875 | −76.61*** | 0.0464* | −1.046e+02*** | −21.80* |
| P-value | 0.1073 | 0.6983 | 0.0007 | 0.0491 | 2.13E-05 | 0.0195 | |
Table A.3.
Generalized linear models – 2nd Sensitivity Analysis. Los Angeles has most COVID cases in the California; thus, we exclude Los Angeles from our data and conduct analysis only on Ventura County.
| Pollutant | Feature | Cases | Deaths | Cases | Deaths | Cases | Deaths |
|---|---|---|---|---|---|---|---|
| Pollution exposure lag | lag(0–7) | lag(0–7) | lag(0–14) | lag(0–14) | lag(0–21) | lag(0–21) | |
| PM2 | Intercept | 0.014 | −0.006 | 0.0464 | 0.015 | −0.006 | 0.001 |
| P-value | 0.6484 | 0.5448 | 0.3497 | 0.3417 | 0.9219 | 0.9647 | |
| PM10 | Intercept | −0.015 | −0.004 | −0.034*** | −0.004 | −0.057*** | −0.008* |
| P-value | 0.0517 | 0.1078 | 0.0004 | 0.1157 | 1.01E-06 | 0.0165 | |
| O3 | Intercept | −0.012*** | −0.014 | −67.73* | −0.009 | −1.287e+02*** | −19.13 |
| P-value | 9.10E-05 | 0.6415 | 0.0117 | 0.6347 | 7.98E-05 | 0.0602 | |
Table A.4.
Evaluation metrics of 1st – 4th sensitivity analyses for EDEM. These four sensitivity analyses are as follows. First, we create three separate ensemble learning models separately for three pollutants. Second, we create two separate models for Los Angeles and Ventura counties because out of 170 total data points – 100 belong to Ventura and 70 belong to Los Angeles. Third, an incremental term is added to our original ensemble learning model similar to Equations (1), (2)). Forth, the independent variable, i.e., coronavirus cases, was transformed into the logarithmic domain.
| Sensitivity Analysis | Details | Training R2 score | Testing R2 score |
|---|---|---|---|
| 1 | Three models for three pollutants | 0.7871 0.8776 0.7247 |
0.6869 0.7457 0.5471 |
| 2 | Two models for Los Angeles and Ventura | 0.8820 0.9059 |
0.6210 0.8323 |
| 3 | Added incremental term, i.e., day of the year. | 0.9576 | 0.9229 |
| 4 | Logarithmic transformation of covid-19 cases | 0.9999 | 0.9635 |
Appendix B. Supplementary data
The following is the Supplementary data to this article:
References
- Akoglu Haldun. User's guide to correlation coefficients. Turkish journal of emergency medicine. 2018;18(3):91–93. doi: 10.1016/j.tjem.2018.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amuakwa-Mensah Franklin, George Marbuah, Mubanga Mwenya. Climate variability and infectious diseases nexus: evidence from Sweden. Infectious Disease Modeling. 2017;2(2):203–217. doi: 10.1016/j.idm.2017.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bashir Muhammad Farhan, Bilal BenJiang MA., Komal Bushra. Correlation between environmental pollution indicators and COVID-19 pandemic: a brief study in Californian context. Environ. Res. 2020:109652. doi: 10.1016/j.envres.2020.109652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman Jesse D., Ebisu Keita. Changes in US air pollution during the COVID-19 pandemic. Sci. Total Environ. 2020;739:139864. doi: 10.1016/j.scitotenv.2020.139864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernardini F., Attademo L., Trezzi R., Gobbicchi C., Balducci P.M., Del Bello V., Menculini G., et al. Air pollutants and daily number of admissions to psychiatric emergency services: evidence for detrimental mental health effects of ozone. Epidemiol. Psychiatr. Sci. 2020;29 doi: 10.1017/S2045796019000623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandes Ulrik, Fleischer Daniel. Annual Symposium on Theoretical Aspects of Computer Science. Springer; Berlin, Heidelberg: 2005. Centrality measures based on current flow; pp. 533–544. [Google Scholar]
- Brook Robert D., Franklin Barry, Wayne Cascio, Hong Yuling, Howard George, Lipsett Michael, Russell Luepker, et al. Air pollution and cardiovascular disease: a statement for healthcare professionals from the expert panel on population and prevention science of the American heart association. Circulation. 2004;109(21):2655–2671. doi: 10.1161/01.CIR.0000128587.30041.C8. [DOI] [PubMed] [Google Scholar]
- Bytnerowicz Andrzej, Fenn Mark E. Ricardo cisneros, donald schweizer, joel burley, and susan L. Schilling. "Nitrogenous air pollutants and ozone exposure in the central sierra Nevada and white mountains of California–distribution and evaluation of ecological risks. Sci. Total Environ. 2019;654:604–615. doi: 10.1016/j.scitotenv.2018.11.011. [DOI] [PubMed] [Google Scholar]
- Chan Jasper Fuk-Woo, Yuan Shuofeng, Kok Kin-Hang, Kelvin Kai-Wang To. Chu Hin, Jin Yang, Xing Fanfan, et al. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster. Lancet. 2020;395:514–523. doi: 10.1016/S0140-6736(20)30154-9. 10223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chauhan Anoop J., Johnston Sebastian L. Air pollution and infection in respiratory illness. Br. Med. Bull. 2003;68(1):95–112. doi: 10.1093/bmb/ldg022. [DOI] [PubMed] [Google Scholar]
- Chen Chen, Liu Cong, Chen Renjie, Wang Weibing, Li Weihua, Kan Haidong, Fu Chaowei. Ambient air pollution and daily hospital admissions for mental disorders in Shanghai, China. Sci. Total Environ. 2018;613:324–330. doi: 10.1016/j.scitotenv.2017.09.098. [DOI] [PubMed] [Google Scholar]
- Chen Songchao, Liang Zongzheng, Webster Richard, Zhang Ganlin, Zhou Yin, Teng Hongfen, Hu Bifeng, Arrouays Dominique, Zhou Shi. A high-resolution map of soil pH in China made by hybrid modeling of sparse soil data and environmental covariates and its implications for pollution. Sci. Total Environ. 2019;655:273–283. doi: 10.1016/j.scitotenv.2018.11.230. [DOI] [PubMed] [Google Scholar]
- Ciencewicki Jonathan, Jaspers Ilona. Air pollution and respiratory viral infection. Inhal. Toxicol. 2007;19(14):1135–1146. doi: 10.1080/08958370701665434. [DOI] [PubMed] [Google Scholar]
- Copat Chiara, Cristaldi Antonio, Fiore Maria, Grasso Alfina, Zuccarello Pietro, Salvatore Santo Signorelli. Conti Gea Oliveri, Ferrante Margherita. The role of air pollution (PM and NO2) in COVID-19 spread and lethality: a systematic review. Environ. Res. 2020:110129. doi: 10.1016/j.envres.2020.110129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Copiello Sergio, Grillenzoni Carlo. The spread of 2019-nCoV in China was primarily driven by population density. Comment on “Association between short-term exposure to air pollution and COVID-19 infection: evidence from China” by Zhu et al. Sci. Total Environ. 2020;744:141028. doi: 10.1016/j.scitotenv.2020.141028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Qian, Wang Yan, Zanobetti Antonella, Wang Yun, Koutrakis Petros, Choirat Christine, Dominici Francesca, Joel D., Schwartz Air pollution and mortality in the Medicare population. N. Engl. J. Med. 2017;376(26):2513–2522. doi: 10.1056/NEJMoa1702747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dastoorpoor Maryam, Sekhavatpour Zohreh, Masoumi Kambiz, Mohammadi Mohammad Javad, Aghababaeian Hamidreza, Khanjani Narges, Hashemzadeh Bayram, Vahedian Mostafa. Air pollution and hospital admissions for cardiovascular diseases in Ahvaz, Iran. Sci. Total Environ. 2019;652:1318–1330. doi: 10.1016/j.scitotenv.2018.10.285. [DOI] [PubMed] [Google Scholar]
- García María Vega, Aznarte José L. Shapley additive explanations for NO2 forecasting. Ecol. Inf. 2020;56:101039. [Google Scholar]
- Haagen-Smit, Arie J. Chemistry and physiology of Los Angeles smog. Ind. Eng. Chem. 1952;44(6):1342–1346. [Google Scholar]
- Hu Yabin, Xu Zhiwei, Jiang Fan, Li Shenghui, Liu Shijian, Wu Meiqin, Yan Chonghuai, et al. Relative impact of meteorological factors and air pollutants on childhood allergic diseases in Shanghai, China. Sci. Total Environ. 2020;706:135975. doi: 10.1016/j.scitotenv.2019.135975. [DOI] [PubMed] [Google Scholar]
- Iglesias Félix, Kastner Wolfgang. Analysis of similarity measures in times series clustering for the discovery of building energy patterns. Energies. 2013;6(2):579–597. [Google Scholar]
- Kahn Matthew E. Smog reduction's impact on California county growth. J. Reg. Sci. 2000;40(3):565–582. [Google Scholar]
- Kraemer, Moritz U.G., Yang Chia-Hung, Gutierrez Bernardo, Wu Chieh-Hsi, Klein Brennan, Pigott David M. Louis Du Plessis et al. "The effect of human mobility and control measures on the COVID-19 epidemic in China. Science. 2020;368(6490):493–497. doi: 10.1126/science.abb4218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai Jianbo, Ma Simeng, Wang Ying, Cai Zhongxiang, Hu Jianbo, Ning Wei, Wu Jiang, et al. Factors associated with mental health outcomes among health care workers exposed to coronavirus disease 2019. JAMA network open. 2020;3(3) doi: 10.1001/jamanetworkopen.2020.3976. e203976-e203976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauer Stephen A., Grantz Kyra H., Bi Qifang, Jones Forrest K., Zheng Qulu, Meredith Hannah R., Azman Andrew S., Reich Nicholas G., Lessler Justin. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann. Intern. Med. 2020;172(9):577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Qun, Guan Xuhua, Wu Peng, Wang Xiaoye, Zhou Lei, Tong Yeqing, Ren Ruiqi, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. N. Engl. J. Med. 2020;382:1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Rui, Wang Zhenzhen, Cui Lulu, Fu Hongbo, Zhang Liwu, Kong Lingdong, Chen Weidong, Chen Jianmin. Air pollution characteristics in China during 2015–2016: spatiotemporal variations and key meteorological factors. Sci. Total Environ. 2019;648:902–915. doi: 10.1016/j.scitotenv.2018.08.181. [DOI] [PubMed] [Google Scholar]
- Lin Hualiang, Tao Jun, Kan Haidong, Qian Zhengmin, Chen Ailan, Du Yaodong, Liu Tao, et al. Ambient particulate matter air pollution associated with acute respiratory distress syndrome in Guangzhou, China. J. Expo. Sci. Environ. Epidemiol. 2018;28(4):392. doi: 10.1038/s41370-018-0034-0. [DOI] [PubMed] [Google Scholar]
- Liu Yuewei, Xie Shuguang, Yu Qing, Huo Xixiang, Ming Xiaoyan, Wang Jing, Zhou Yun, et al. Short-term effects of ambient air pollution on pediatric outpatient visits for respiratory diseases in Yichang city, China. Environ. Pollut. 2017;227:116–124. doi: 10.1016/j.envpol.2017.04.029. [DOI] [PubMed] [Google Scholar]
- Lu Susan Feng, Lu Lauren Xiaoyuan. Do mandatory overtime laws improve quality? Staffing decisions and operational flexibility of nursing homes. Manag. Sci. 2017;63(11):3566–3585. [Google Scholar]
- Ma Jun, Ding Yuexiong, Cheng Jack CP., Jiang Feifeng, Tan Yi, Vincent JL Gan, Wan Zhiwei. Identification of high impact factors of air quality on a national scale using big data and machine learning techniques. J. Clean. Prod. 2020;244:118955. [Google Scholar]
- Ma Yueling, Zhao Yadong, Liu Jiangtao, He Xiaotao, Wang Bo, Fu Shihua, Yan Jun, Niu Jingping, Zhou Ji, Luo Bin. Effects of temperature variation and humidity on the death of COVID-19 in Wuhan, China. Sci. Total Environ. 2020:138226. doi: 10.1016/j.scitotenv.2020.138226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma Yuxia, Zhou Jianding, Yang Sixu, Zhao Yuxin, Zheng Xiaodong. Assessment for the impact of dust events on measles incidence in western China. Atmos. Environ. 2017;157:1–9. [Google Scholar]
- Mehta Sumi, Shin Hwashin, Burnett Rick, North Tiffany, Aaron J., Cohen Ambient particulate air pollution and acute lower respiratory infections: a systematic review and implications for estimating the global burden of disease. Air Quality, Atmosphere & Health. 2013;6(1):69–83. doi: 10.1007/s11869-011-0146-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myung Woojae, Lee Hyewon, Kim Ho. Short-term air pollution exposure and emergency department visits for amyotrophic lateral sclerosis: a time-stratified case-crossover analysis. Environ. Int. 2019;123:467–475. doi: 10.1016/j.envint.2018.12.042. [DOI] [PubMed] [Google Scholar]
- Ngufor Che, Van Houten Holly, Caffo Brian S., Shah Nilay D., McCoy Rozalina G. Mixed Effect Machine Learning: a framework for predicting longitudinal change in hemoglobin A1c. J. Biomed. Inf. 2019;89:56–67. doi: 10.1016/j.jbi.2018.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okada Shinichi. Towards Data Science; 2018. The Subtlety of Spearman's Rank Correlation Coefficient.https://towardsdatascience.com/the-subtlety-of-spearmans-rank-correlation-coefficient-29478653bbb9 [Accessed 15th October 2020] [Google Scholar]
- Pan Bingyue. vol. 113. 2018. Application of XGBoost algorithm in hourly PM2. 5 concentration prediction. (IOP Conference Series: Earth and Environmental Science). [Google Scholar]
- Parsa A.B., Movahedi A., Taghipour H., Derrible S., Mohammadian A.K. Toward safer highways, application of XGBoost and SHAP for real-time accident detection and feature analysis. Accid. Anal. Prev. 2020;136:105405. doi: 10.1016/j.aap.2019.105405. [DOI] [PubMed] [Google Scholar]
- Peng Roger D., Dominici Francesca, Louis Thomas A. Model choice in time series studies of air pollution and mortality. J. Roy. Stat. Soc. 2006;169(2):179–203. [Google Scholar]
- Phosri Arthit, Ueda Kayo, Vera Ling Hui Phung. Tawatsupa Benjawan, Honda Akiko, Takano Hirohisa. Effects of ambient air pollution on daily hospital admissions for respiratory and cardiovascular diseases in Bangkok, Thailand. Sci. Total Environ. 2019;651:1144–1153. doi: 10.1016/j.scitotenv.2018.09.183. [DOI] [PubMed] [Google Scholar]
- Qin Nan, Liang Peng, Wu Chunyan, Wang Guanqun, Xu Qian, Xiong Xiao, Wang Tingting, et al. Longitudinal survey of microbiome associated with particulate matter in a megacity. Genome Biol. 2020;21(1):1–11. doi: 10.1186/s13059-020-01964-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ravindra Khaiwal, Rattan Preety, Mor Suman, Nath Aggarwal Ashutosh. Generalized additive models: building evidence of air pollution, climate change and human health. Environ. Int. 2019;132:104987. doi: 10.1016/j.envint.2019.104987. [DOI] [PubMed] [Google Scholar]
- Reche Isabel, D'Orta Gaetano, Mladenov Natalie, Winget Danielle M., Suttle Curtis A. Deposition rates of viruses and bacteria above the atmospheric boundary layer. ISME J. 2018;12(4):1154–1162. doi: 10.1038/s41396-017-0042-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saez Marc, Tobias Aurelio, Barceló Maria A. Effects of long-term exposure to air pollutants on the spatial spread of COVID-19 in Catalonia, Spain. Environ. Res. 2020:110177. doi: 10.1016/j.envres.2020.110177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setti Leonardo, Passarini Fabrizio, De Gennaro Gianluigi, Barbieri Pierluigi, Grazia Perrone Maria, Borelli Massimo, Palmisani Jolanda, et al. SARS-Cov-2RNA found on particulate matter of bergamo in northern Italy: first evidence. Environ. Res. 2020:109754. doi: 10.1016/j.envres.2020.109754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setti Leonardo, Passarini Fabrizio, De Gennaro Gianluigi, Barbieri Pierluigi, Alberto Pallavicini, Ruscio Maurizio, Piscitelli Prisco, Colao Annamaria, Miani Alessandro. 2020. Searching for SARS-COV-2 on Particulate Matter: A Possible Early Indicator of COVID-19 Epidemic Recurrence; p. 2986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setti Leonardo, Passarini Fabrizio, De Gennaro Gianluigi, Barbieri Pierluigi, Licen Sabina, Grazia Perrone Maria, Piazzalunga Andrea, et al. Potential role of particulate matter in the spreading of COVID-19 in Northern Italy: first observational study based on initial epidemic diffusion. BMJ open. 2020;10(9) doi: 10.1136/bmjopen-2020-039338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi Le, Lu Zheng-An, Que Jian-Yu, Huang Xiao-Lin, Liu Lin, Ran Mao-Sheng, Gong Yi-Miao, et al. Prevalence of and risk factors associated with mental health symptoms among the general population in China during the coronavirus disease 2019 pandemic. JAMA network open. 2020;3(7) doi: 10.1001/jamanetworkopen.2020.14053. e2014053-e2014053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stieb David M., Greg J., Evans Teresa M., To Jeffrey R. Brook, Burnett Richard T. "An ecological analysis of long-term exposure to PM2. 5 and incidence of COVID-19 in Canadian health regions. Environ. Res. 2020;191:110052. doi: 10.1016/j.envres.2020.110052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stojić Andreja, Stanić Nenad, Vuković Gordana, Stanišić Svetlana, Perišić Mirjana, Šoštarić Andrej, Lazić Lazar. Explainable extreme gradient boosting tree-based prediction of toluene, ethylbenzene and xylene wet deposition. Sci. Total Environ. 2019;653:140–147. doi: 10.1016/j.scitotenv.2018.10.368. [DOI] [PubMed] [Google Scholar]
- Su Wenjing, Liu Cheng, Hu Qihou, Fan Guangqiang, Xie Zhouqing, Huang Xin, Zhang Tianshu, et al. Characterization of ozone in the lower troposphere during the 2016 G20 conference in Hangzhou. Sci. Rep. 2017;7(1):1–11. doi: 10.1038/s41598-017-17646-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The White House Press briefing by members of the president's coronavirus task force. 2020. www.whitehouse.gov/briefings-statements/press-briefing-members-presidents-coronavirus-task-force 31 January, Online Source: 15th October 2020.
- Thompson Tammy M., Rausch Sebastian, Saari Rebecca K., Selin Noelle E. A systems approach to evaluating the air quality co-benefits of US carbon policies. Nat. Clim. Change. 2014;4(10):917–923. [Google Scholar]
- Tong Ruipeng, Liu Jiefeng, Wang Wei, Fang Yingqian. Health effects of PM2. 5 emissions from on-road vehicles during weekdays and weekends in Beijing, China. Atmos. Environ. 2020;223:117258. [Google Scholar]
- Wellenius Gregory A., Burger Mary R., Coull Brent A., Schwartz Joel, Suh Helen H., Koutrakis Petros, Gottfried Schlaug, Gold Diane R., Mittleman Murray A. Ambient air pollution and the risk of acute ischemic stroke. Arch. Intern. Med. 2012;172(3):229–234. doi: 10.1001/archinternmed.2011.732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood Simon N. Generalized additive models: an introduction with R. Chapman and Hall/CRC. Texts Stat. Sci. 2006;67:391. [Google Scholar]
- Xie J., Zhu Y. Association between ambient temperature and COVID-19 infection in 122 cities from China. Sci. Total Environ. 2020;724 doi: 10.1016/j.scitotenv.2020.138201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Zhiyi, Jiayuan Hao, Huang Shuqiong, Yang Wenwen, Zhu Zhongmin, Tian Liqiao, Lu Yuanan, Xiang Hao, Liu Suyang. Acute effects of air pollution on the incidence of hand, foot, and mouth disease in Wuhan, China. Atmos. Environ. 2020;225:117358. [Google Scholar]
- Zhai Binxu, Chen Jianguo. Development of a stacked ensemble model for forecasting and analyzing daily average PM2. 5 concentrations in Beijing, China. Sci. Total Environ. 2018;635:644–658. doi: 10.1016/j.scitotenv.2018.04.040. [DOI] [PubMed] [Google Scholar]
- Zhao Yang, Richardson Brad, Takle Eugene, Chai Lilong, Schmitt David, Xin Hongwei. Airborne transmission may have played a role in the spread of 2015 highly pathogenic avian influenza outbreaks in the United States. Sci. Rep. 2019;9(1):1–10. doi: 10.1038/s41598-019-47788-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Saina, He Chenhang, Hsu Shu-Chien, Sarkis Joseph, Jieh-Haur Chen Corporate environmental performance prediction in China: an empirical study of energy service companies. J. Clean. Prod. 2020:121395. [Google Scholar]
- Zhu Yongjian, Xie Jingui. Science of the Total Environment; 2020. Association between ambient temperature and COVID-19 infection in 122 cities from China; p. 138201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou Y., Charlesworth E., Yin C.Q., Yan X.L., Deng X.J., Li F. The weekday/weekend ozone differences induced by the emissions change during summer and autumn in Guangzhou, China. Atmos. Environ. 2019;199:114–126. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.