Short-term forecasts of the COVID-19 pandemic: a study case of Cameroon

Highlights

• •A COVID-19 model with free coronaviruses in the environment is formulated.
• •States and unknown parameters of model are estimated using the Ensemble Kalman filter.
• •The implementation is performed using real data of the current COVID-19 pandemic in Cameroon.
• •The basic reproduction number in Cameroon R0  ≈  2:9495.
• •There is a necessity to maintain the surveillance and sensibilisation of population.

Abstract

In this paper, an Ensemble of Kalman filter (EnKf) approach is developed to estimate unmeasurable state variables and unknown parameters in a COVID-19 model. We first formulate a mathematical model for the dynamic transmission of COVID-19 that takes into account the circulation of free coronaviruses in the environment. We provide the basic properties of the model and compute the basic reproduction number ${\mathcal{R}}_0$ that plays an important role in the outcome of the disease. After, assuming continuous measurement of newly COVID-19 reported cases, deceased and recovered individuals, the EnKf approach is used to estimate the unmeasured variables and unknown COVID-19 transmission rates using real data of the current COVID-19 pandemic in Cameroon. We present the forecasts of the current pandemic in Cameroon and explore the impact of non-pharmaceutical interventions such as mass media-based sensitization, social distancing, face-mask wearing, contact tracing and the desinfection and decontamination of infected places by using suitable products against free coronaviruses in the environment in order to reduce the spread of the disease. Through numerical simulations, we find that at that time (i) ${\mathcal{R}}_0\approx 2.9495$ meaning that the disease will not die out without any control measures, (ii) the infection from COVID-19 infected cases is more important than the infection from free coronaviruses in the environment, (iii) the number of new COVID-19 cases will still increase and there is a necessity to increase timely the surveillance by using contact tracing and sensibilisation of the population to respect social distancing, face-masks wearing through awareness programs and (iv) the eradication of the pandemic is highly dependent on the control measures taken by governments.

1. Introduction

On November 17, 2019, a disease appeared in the city Wuhan in China [1], [2], [3]. Having the symptoms of an ordinary flu, it happened to be caused by the coronavirus SARS-CoV-2 discovered in 2002 (to quote) [4], [5]. The disease has then spread to several cities in China and research showed that it is a new coronavirus named COVID-19, and it was declared as an epidemic in late December 2019 [6], [7], [8]. The opening of this host country to the outside world (with trade, tourism and others ...) have promoted the spread of this epidemic to other countries and on January 13, 2020, a first case was discovered outside of mainland China [4], [9], [10]. The epidemic progressed on all continents and a public health emergency of international scope was declared by the World Health Organization on January 30, 2020, since it was then the COVID-19 pandemic.

0n March 06, 2020, a first patient tested positive of the novel coronavirus COVID-19 Yaoundé, Cameroon. Two days later, one of these acquaintances was also tested positive. The virus has spread from city to city all over Cameroon and a first state of alert was announced on March 17, with more than 13 drastic measures: wearing a mask in all areas open to the public, intensification of the awareness campaign in urban and rural areas, the stopping of presensial lessons in all schools, closing leisure places after 6 p.m. and practising barriers [11]. According to the report of the Center for Analysis and Research on Policies in Cameroon, the restriction of movement of people strongly affects transport, catering and accommodation away from usual home (hotels), cultural and leisure activities, etc. The cancellation or postponement of major international events planned in Cameroon (CHAN, Trade Fairs, Conferences, etc.) are an illustration of this. With the evolution of the pandemic, the wearing of a mask and the distance become an obligation for all Cameroonian residents as of April 06. According to the Inter-Patronal Grouping of Cameroon (Gicam) [12], 92% of the sampled companies declared that the Covid-19 pandemic has had a very negative (52%) or negative (40%) impact on their activities. Also, Small and Medium-sized Enterprises in Cameroon (SMEs) and service companies are the most affected. The proportion of SMEs reporting a very negative impact is higher (61%) than that of large companies (27%). Similarly, 58% of service companies reported being very negatively impacted by the Covid-19 pandemic compared to 38% of industrial companies. The country should experience a loss of economic growth of 3%. The deterioration in the budgetary balance would be 2.8% and the deterioration in the current balance by 1.4%. This socio-economic situation was at the origin of the lifting of drastic measures on May 01 and the return to the classrooms on June 01. However, it is possible that the pandemic continues her spread. So, many studies need to be done to help the government to apply the best control measures in the process of fighting against the COVID-19 pandemic.

Mathematical tools are used to understand several evils which plague societies today. In public health, mathematical models rule on the dynamics of the infectious diseases. Several compartmental models have been implemented to complete the epidemiology and statistical analysis in order to prevent and control epidemics [13], [14], [15], [16], [17]. Despite the difficulty of understanding the evolution of the new coronavirus at this time, most studies on epidemiological observations and hypotheses have been done [18], [19], [20], [21]. More results indicate that there are indirect contaminations through the environment and direct contaminations human to human. Some models may shed light on past epidemics, while some may help us to forecast the future via a fitting process. In the fitting process of an epidemic, it is important to have some informations that help either to develop better control or to predict the future of the epidemic with food accuracy. For this, it is important to design a model that will help to reconstruction some of unknown informations having another ones. The data are used to have or reconstruct these informations that we call estimated states and parameters. Since its inception in the 1960s for the estimation of states in linear system, the Kalman Filter (KF) has undergone substantive improvements and today we can estimate the states and parameters of non-linear systems [22], [23], [24], [25]. The Extended Kalman filter (EKf) proceeds by adopting the formulae of the classical Kalman filter with the Jacobian of the dynamics matrix (in both continuous and discrete time) playing the role of the linear dynamics matrix [25], but this would increase estimation errors.

The Ensemble Kalman filter (EnKf) belongs to a broader category of filters known as particle filters [25], [26]. Unlike (EKf) estimation and unscented Kalman filter estimation, particle filters use neither the Jacobian of the dynamics nor frozen linear dynamics. In the case of the unscented Kalman filter [27], the number of sample points required is equal to the dimension of the system. On the other hand, the number of ensembles required in the (EnKf) is heuristic. While one would expect that a large ensemble would be needed to obtain appropriate estimates, the literature on EnKf suggests that an ensemble of 50 to 100 points is often adequate for systems with thousands of states [25]. With the complexity of many phenomena, estimating of both states and parameters for dynamical systems are of high interest. EnKf has dealt with this interrogation [28], [29].

In order to understand and control COVID-19 within a human community, several researchers have proposed different mathematical models for the dynamics of the new coronavirus [30], [31], [32], [33], [34], [35], [36], [37], [38]. However, several of these works do not take into account the fact that susceptible individuals can also contract the COVID-19 by an indirect transmission by adequate contacts with free coronaviruses in the environment [39]. Other researchers study the problems of estimation and forecasting of Covid-19 using the methods of either Least Square or Monte Carlo Markov Chain (MCMC) [40], [41], [42], [43]. Micheal Li et All [44] used MCMC to estimate the parameters related to COVID-19 transmission in China. The author presents the trends of the epidemic in the same country and explains why it it difficult to predict the COVID-19.

In this paper, we develop the EnKf approach for the estimation of unmeasurable state variables and unknown parameters using real data of the current COVID-19 pandemic for a study case in Cameroon. We first formulate a mathematical model for the transmission dynamics of the COVID-19 pandemic. The particularity of this model is that it takes into account the circulation of free coronaviruses in the environment. We study the basic properties of the model such as the positivity of the solutions and the boundedness of trajectories. We compute the disease-free equilibrium and derive the basic reproduction number ${\mathcal{R}}_0$ that determines the outcome of the pandemic. After, we assume that the newly COVID-19 infected cases, deceased and recovered individuals are accessible to measurements and the transmission rates from COVID-19 infected cases and free coronaviruses in the environment are unknown parameters. Then, we use the EnKf method to investigate both states and parameters estimation in the considered model. This estimation method is applied to real data from March 6, 2020 to April 30, 2020 of the current COVID-19 pandemic in Cameroon [45]. We use the estimate values of the transmission rates to estimate the basic reproduction number ${\mathcal{R}}_0$ in Cameroon. Without any control measures, we found that ${\mathcal{R}}_0\approx 2.9495$ which implies that the disease will not die out. The sensitivity index of the basic reproduction number ${\mathcal{R}}_0$ indicates that most of the COVID-19 transmission is coming from COVID-19 infected cases. We also use these results to make a short-term forecasts of the current COVID-19 pandemic in Cameroon using control measures such as mass media-based sensitization, social distancing, face-mask wearing and the desinfection and decontamination of infected places (markets, offices, churches, public places,...) by using suitable products against free coronaviruses in the environment to reduce the transmission of the pandemic as recommended by the World Heath Organization (WHO). We find that the number of newly COVID-19 infected cases will increase and there will always free coronaviruses circulating in the environment. This study represents the first work that provides an in-depth parameters and states estimation using real demographic and epidemiological data of COVID-19 in a country of Sub-saharan Africa.

The paper is organized as follows. In Section 2, we present material and methods. Section 3 gives the results of this work. The last Section is devoted to ours conclusions.

2. Materials and methods

2.1. Model formulation

We consider a SIRS model for the COVID-19 transmission within a human community and free coronaviruses concentration in the environment. These populations under consideration are grouped into disjoint classes. We divide the human population into four states: Susceptible individuals S (individuals who are susceptible to COVID-19), COVID-19 infected I (who are infected and able to transmit the COVID-19 infection); Recovered individuals R (infected individuals who are recovered). Thus, the total human population at time t is

$$N\left(t\right)=S\left(t\right)+I\left(t\right)+R\left(t\right).$$ (1)

The complexity of the COVID-19 into human population resides in the ability of free coronaviruses to live in the environment. According to some studies [47], [48], the virus can alive free in the environment between 12 hours and 9 days mainly depending on the temperature. Then, we consider in this work the free coronaviruses living in the environment and we denote it by V. We point out that the class of COVID-19 infected cases comprises asymptomatic (susceptible individuals who were exposed to the virus but clinical signs of COVID-19 have not yet developed) and symptomatic individuals (susceptible individuals who were exposed to the virus and present the clinical symptoms of COVID-19). For mathematical simplicity, we do not consider the exposed class in our model. Indeed, exposed individuals can be detected using the contact-tracing strategy. In many countries of Sub-saharan Africa, a contact-tracing strategy is difficult to implement, since it involves searching or identifying individuals who have come in contact with, or been in the vicinity of, anybody who is known to have been sick or died of COVDI-19 or virus in the environment. Also most people exposed to COVID-19 refuse to present themselves to the authorities in charge of the disease because of the stigmatization or the lack of information on the harmful effects of this disease.

Susceptible individuals are recruited into the human population at rate Λ. Susceptible individuals can contract COVID-19 after having adequate contact with COVID-19 infected at rate β_h that is assumed to be a constant. Also, they can contract the disease through the free coronaviruses in the environment at rate β_v. We assume that the transmission of COVID-19 disease from COVID-19 infected to susceptible individuals is modelled by a standard incidence, while the transmission of COVID-19 disease from the free virus in the environment to susceptible individuals is modelled by the Holling function. Thus, susceptible individuals are exposed at rate λ(I, V) given by

$$\lambda (I,V)={\beta }_h\frac{I}{N}+{\beta }_v\frac{V}{K+V},$$ (2)

where K is the concentration of free coronaviruses in the environment that yields 50% of chance for a susceptible individual to catch the infection

After carry the infection, susceptible individuals become either asymptomatic or symptomatic at rate λ(I, V). Susceptible individuals, COVID-19 infected cases and recovered individuals succumb to natural death at rate μ where 1/μ is approximately the live span of the human. The COVID-19 infected recover from the disease after a therapeutic of treatment at rate ρ. The COVID-19 infected is affected by COVID-19 induced mortality at rate d. COVID-19 infected cases contribute to free coronaviruses in the environment at rate δ. As suggested by many studies, recovered individuals may only have partial immunity [46], [47], [48]. Indeed, there is no evidence that recovered individuals of COVID-19 acquire a permanent immunity. That is, just because an individual recovers from the virus does not mean he/she cannot catch it again. Indeed, on 24 April, the World Health Organization (WHO) in a statement said ”there is currently no evidence that people who have recovered from COVID-19 and have antibodies are protected from a second infection” [49].

Since the recovery from the disease does not confer a total immunity to recovered individuals, recovered individuals loss their protection and return to the susceptible class S at rate θ. Free coronaviruses concentration in the environment die at rate ν. With respect to other studies [30], [31], [32], [33], [34], [35], [36], [37], [38], the formulated model incorporates some demographic effects by assuming a proportional natural death rate in each of the human sub-population and a net inflow of susceptible individuals (which includes births, immigration and emigration) into the region or country. Indeed, in many countries of Sub-saharan Africa, the daily number of COVID-19 induced mortality is very low compared to the daily number of new birth so that it is not possible to neglect the demographic in modelling of COVID-19.

A flowchart characterizes the model in Fig. 1 , where the solid lines represent the flows between individuals compartments, the dashed lines represent the infected classes shedding the environment and the curves dashed lines stand from new infections coming from the interaction of susceptible individuals with free coronaviruses in the environment.

Fig. 1.

Flowchart of the model. Solid lines represent flow between compartments, while the dashed lines represent the interaction between human individuals and the free coronaviruses in the environment.

Using the flowchart in Fig. 1, the COVID-19 transmission model is expressed by the following system of differential equations:

$$\{\begin{array}{ccc}\dot{S}\hfill & =& \Lambda +\theta R-(\mu +\lambda )S,\hfill \\ \dot{I}\hfill & =& \lambda S-(\mu +d+\rho )I,\hfill \\ \dot{R}\hfill & =& \rho I-(\theta +\mu )R,\hfill \\ \dot{V}\hfill & =& \delta I-\nu V.\hfill \end{array}$$ (3)

Tables 1 and 2 summarize, respectively the model variables and the parameter values used for the numerical simulations.

Table 1.

Variables with units for the model system (3).

Symbols	Description	Units
S	Susceptible individuals	Individual
I	COVID-19 infected cases	Individual
R	Recovered individuals	Individual
V	Free coronaviruses concentration in the environment	Cells

Table 2.

Parameter values for the model system (3).

Symbols	Description	Value/range	Reference
Λ	Human recruitment rate	1305 $indiv.da{y}^{-1}$	[52]
μ	Natural mortality rate in the	13.27/365000 $da{y}^{-1}$	[52]
	human population
ν	Decrease rate of free coronaviruses in	1/5 $da{y}^{-1}$	[53]
	the environment
ρ	Recovery rate of COVID-19 infected	[0,1] $da{y}^{-1}$	[45]
θ	Recovery waning induced rate	1/14 $da{y}^{-1}$	[45]
d	COVID-19 induced mortality	[0,1] $da{y}^{-1}$	[45]
δ	Shedding rate of COVID-19 infected	0.4 $cells.(day.indiv){}^{-1}$	[53]
	individuals to the environment
K	Positive constant	106cells	Constant
βh	COVID-19 transmission rate from	[0,1] $da{y}^{-1}$	To be estimated
	COVID-19 infected cases
βv	COVID-19 transmission rate from	[0,1] ${\mathit{day}}^{-1}$	To be estimated
	free coronaviruses in the environment

2.2. States space formulation with EnKf using data

In this section, we present an estimation method for the reconstruction of unmeasurable state variables and the unknown parameters of the model system (3). We also use the parameter estimates to subsequently estimate the value of the basic reproduction number ${\mathcal{R}}_0$. The goal of this step is to shed light on the beginning of the epidemic until today by a dual estimating of the state variables and parameter of model system (3). Then, we will give short-term forecasts of the COVID-19 pandemic using as initial conditions the last state variables estimates. Note that the short-term forecasts is very useful for control and prevention the spread. To do so, we will use the EnKf approach [50]. The advantage of the dual estimation is that the estimation state is mined for the estimation of the parameters, that conserve the stability of the estimation process [28], [51].

Fig. 5.

Fitting results of the current COVID-19 pandemic in Cameroon using the estimated value of the transmission rates β_h and β_v given in Fig. 3 and the estimated value of state variables given in Fig. 4. (a) COVID-19 newly reported cases; (b) Newly recovered individuals; (c) Newly deceased cases; (d) COVID-19 cumulative infected cases and (e) COVID-19 active cases.

The estimation problem with the EnKf method is formulated via recurrent equations on the states and the parameters to be estimated. In addition to these equations, the observations of system are used as inputs to the system. For the model system (3), all the states are not directly observed. As more outbreak, the data of COVID-19 on line that one can use in model system (3) are the newly COVID-19 reported cases λ(I, V)S, newly recovered individuals ρI and newly deceased dI. The daily number of new COVID-19 reported cases is rather easy to be detected or suspected and counted by the health authorities in charge of COVID-19. The measurable variable of the COVID-19 model (3) denoted by y is modelled as:

$$y\left(t\right)=\left(\begin{array}{c}\lambda (I,V)S\\ \rho I\\ dI\end{array}\right)+v_t,$$ (4)

where $v_t\in {\mathbb{R}}^3$ is white noise that is assumed to be a Gaussian distribution with deviation Z_t. We point out that v_t can be interpreted as the number of COVD-19 infected cases that are not reported by the health authorities in charge of COVID-19.

Even if the recovery and deceased rates are known, in more realistic situations, several uncertainties may appear. For instance, the force of infection is not well known. Indeed, the COVID-19 transmission rate from the COVID-19 infected cases β_h and free coronaviruses in the environment β_v are uncertain (it is very difficult to know the exact effective contacts between human and COVID-19 infected cases or free coronaviruses in the environment within an African community, since control measures such as the hygiene rules and confinement are not well respected by many people). Thus, the COVID-19 transmission rates β_h and β_v are the unknown parameters in model system (3). As in Refs [29], [54]., the unknown parameters ${\beta }_t=({\beta }_{h,t},{\beta }_{v,t})$ can be written into a simple state space model following a Markov process as

$${\beta }_{t+1}={\beta }_t+{\eta }_t,$$ (5)

where β_t is the uncertainty at time t given by a Gaussian white noise in ${\mathbb{R}}^2$ with standard deviations T_t. One can interpret η_t as the behavior change that makes contacts grow or fall beyond a certain limit 0 and 1.

Finally, we simulate the model system (3) using the Runge Kutta method. Since each variable of (3) follows a Markov process [28], [29], we use the following discrete model:

$$x_{t+1}=f(x_t,{\beta }_t)+w_t,$$ (6)

where w_t is the incertitude at time t of the discretization (error) that is assumed to be a white noise process with the covariance matrix Q_t that appreciates the estimation of the exact value of the state variables x(t) at time t [28], $x_t=(S\left(t\right),I\left(t\right),R\left(t\right),V\left(t\right)){}^T,$ f(x_t, β_t) is the approximated value of $x(t+1)$ given by the discrete model obtained by discretizing (3) using the Runge Kutta method.

Herein, we use the EnKf procedure [28] to estimate the states x_t and the parameters β_t for each data y_t using the following system:

$$\{\begin{array}{ccc}{x}_{t+1}& =\hfill & f(x_t,{\beta }_t,u_t)+w_t,\hfill \\ y_t& =\hfill & h(x_t,{\beta }_t)+v_t,\hfill \\ {\beta }_{t+1}& =\hfill & {\beta }_t+{\eta }_t,\hfill \end{array}$$ (7)

where $h(x_t,{\beta }_t)=(\lambda (I,V)S,\rho I,dI){}^t$. In the sequel, we apply the Kalman Ensemble filtering process described in Appendix C to system (7) in order estimate unmeasurable states and unknown parameters using real data of any country affected by COVID-19 pandemic.

2.3. Impact of control measures

Herein, we analyse how control measures can influence the spread of the disease. Many intervention measures can be considered to reduce day-to-day transmission rates by using face-mask wearing. We assume that the transmission rates are non constant and different control measures will be tested to give the trend of the COVID-19 pandemic in any country affected by this pandemic. Herein, we do not consider the contact-tracing strategy since in many countries of Sub-saharan Africa affected by this pandemic, as a response to the ongoing COVID-19 outbreak, contact-tracing strategy has been implemented via the mass-media sensitization campaigns [46].

We first study the face-mask wearing to reduce the transmission of COVID-19 within human individuals and the disinfection and decontamination of infected places by using suitable products against free coronaviruses in the environment as control measures. The transmission rates from COVID-19 infected cases and free coronaviruses in the environment can be respectively modelled as follows.

$${\beta }_h\left(t\right)=\{\begin{array}{cc}{\beta }_{h,0},\hfill & t>t_0,\hfill \\ {\beta }_{h,0}(1-{\epsilon }_h{\pi }_h),\hfill & t\le t_0,\hfill \end{array}$$ (8)

and

$${\beta }_v\left(t\right)=\{\begin{array}{cc}{\beta }_{v,0},\hfill & t>t_0,\hfill \\ {\beta }_{v,0}(1-{\epsilon }_v{\pi }_v),\hfill & t\le t_0,\hfill \end{array}$$ (9)

where t ₀ is the start time of control measures, π_h the proportion of susceptible individuals who wearing face-masks, ε_h the efficacy of face-mask wearing, β _h,0 the mean value of the estimated value of β_h, π_v the proportion of cleaned places, ɛ_v the efficacy of disinfection and decontamination and β _{v, 0} the mean value of the estimated value of β_v.

We also consider non-pharmaceutical interventions to reduce the transmission rates to minimal values by taking into account a containment, the face-mask wearing and social distancing. We assume that control measures are applied after t ₀ days in order to reduce the transmission rates β_h and β_v to minimal values β _h,min and β _{v, min}. According to Tang et al. [55], the transmission rates can be modelled as follows:

$${\beta }_h\left(t\right)=\{\begin{array}{cc}{\beta }_{h,0},\hfill & t>t_0,\hfill \\ {\beta }_{h,min}+({\beta }_{h,0}-{\beta }_{h,min})e^{-r_h(t-t_0)},\hfill & t\le t_0,\hfill \end{array}$$ (10)

and

$${\beta }_v\left(t\right)=\{\begin{array}{cc}{\beta }_{v,0},\hfill & t>t_0,\hfill \\ {\beta }_{v,min}+({\beta }_{v,0}-{\beta }_{v,min})e^{-r_v(t-t_0)},\hfill & t\le t_0,\hfill \end{array}$$ (11)

where β _h,0 and β _{v, 0} are defined as in Eqs. (10) and (11), and r_h is the decay rate of individuals due to barrier measures, face-masks wearing, washing hands with soap and regular use of hydro-alcoholic gels, while r_v is the decay rate of free coronaviruses in the environment due to the disinfection and decontamination of infected places.

3. Results

In this section, we show how the estimation method proposed in the previous section can be used to calibrate the model system (3) by using real data of the current COVID-19 pandemic in Cameroon.

3.1. Basic properties

Herein, we study the positivity and boundedness of solutions of system (3) using the Laplace transform [56], [57]. Obviously, system (3) where the right part is a C ^∞ differential system (a C ^∞ function is a function that is differentiable for all degrees of differentiation which shows the regularity of every solution) admits a unique maximal solution for any associated Cauchy problem. We have the following result.

Theorem 1

Model system (3) is a dynamical system on the biologically feasible compact domain:

$$\Omega =\{(S,I,R,V)\in {\mathbb{R}}_{+}^4,N\left(t\right)\le \frac{\Lambda }{\mu }\text{and}V\left(t\right)\le \frac{\Lambda \delta }{\nu \mu }\}.$$ (12)

The proof of Theorem 1 is given in Appendix A.

3.2. The basic reproduction number ${\mathcal{R}}_0$

Herein, we compute the basic reproduction number of system (3), which is the average number of secondary cases produced by a single infective individual which is introduced into an entirely susceptible population [58].

System (3) has a disease-free equilibrium X ₀ obtained by setting the right-hand side of the equations to zero with $I=0$:

$$X_0=(\frac{\Lambda }{\mu },0,0,0).$$ (13)

Using the next generation matrix [58], the basic reproduction number of model system (3) (see Appendix B for the computation) is

$${\mathcal{R}}_0=\frac{1}{\mu +d+\rho }({\beta }_h+{\beta }_v\frac{\delta \Lambda }{K\mu \nu }).$$ (14)

The relevance of the reproduction number (14) is due to the following result established from Theorem 2 in [58].

Theorem 2

The disease-free equilibrium X ₀ of model system (3) is locally-asymptotically stable if ${\mathcal{R}}_0<1,$ and unstable if ${\mathcal{R}}_0>1$ .

This theorem is crucial in epidemiology. Indeed, if ${\mathcal{R}}_0\le 1,$ we are sure that the COVID-19 pandemic will disappear, while for ${\mathcal{R}}_0>1,$ it will persist within the community. After the estimation of the unknown parameters in the next section, we will estimate the value of ${\mathcal{R}}_0$ in order to predict the outcome of pandemic. However, estimating the value of ${\mathcal{R}}_0$ alone would be non-significant, since the urgency is also to estimate the number of new infectious infected by an infected individual of COVID-19 disease within the human population. Thus, it is important to estimate the value of the basic reproduction number for only the human population ${\mathcal{R}}_{0h}$ (assuming that only the human population carry the coronavirus) defined by

$${\mathcal{R}}_{0h}=\frac{{\beta }_h}{\mu +d+\rho }.$$ (15)

3.3. The endemic equilibrium and its stability

According to the instability of the DFE when ${\mathcal{R}}_0\ge 1,$ it’s crucially to proof that the COVID-19 pandemic will not increase indefinitely. To do so, we calculate the endemic equilibrium and study its stability.

Let $X^{*}=(S*,I^{*},R^{*},V^{*}){}^T$ be the endemic equilibrium of model system (3). This endemic equilibrium (steady state with I* > 0 and V* > 0) is obtained by setting the right hand side of model system (3) to zero, giving

$$\{\begin{array}{c}\Lambda +\theta R^{*}-({\lambda }^{*}+\mu )S^{*}=0,\hfill \\ {\lambda }^{*}{S}^{*}-(d+\rho +\mu )I^{*}=0,\hfill \\ \rho I^{*}-(\theta +\mu )R^{*}=0,\hfill \\ \delta I^{*}-\nu V^{*}=0,\hfill \end{array}$$ (16)

where

$${\lambda }^{*}={\beta }_h\frac{I^{*}}{N^{*}}+{\beta }_v\frac{V^{*}}{K+V^{*}},$$ (17)

is the force of infection at the steady state X*. Solving the first sixth equations in Eq. (16) in term of λ* gives

$$\begin{array}{c}{\displaystyle S^{*}=\frac{A\Lambda }{A\mu +B{\lambda }^{*}},I^{*}=\frac{A\Lambda {\lambda }^{*}}{(\mu +d+\rho )(A\mu +B{\lambda }^{*})},}\hfill \\ {\displaystyle R^{*}=\frac{\rho \Lambda \lambda }{A\mu +B{\lambda }^{*}}\text{and}{V}^{*}=\frac{A\delta \Lambda \lambda }{\nu (\mu +d+\rho )(A\mu +B{\lambda }^{*})},}\hfill \end{array}$$ (18)

where

$$A=(\theta +\mu )(\mu +d+\rho )\text{and}B=(\theta +\mu )(\mu +d)+\mu \rho .$$

Now, using the expressions of N given in Eq. (1), the dynamics of the total human population at the endemic equilibrium X* is

$$N^{*}=\frac{A\Lambda (1+C{\lambda }^{*})}{A\mu +B{\lambda }^{*}},$$ (19)

where $C=\frac{\theta +\rho +\mu }{(\theta +\mu )(d+\rho +\mu )}$. Now, substituting the expressions of S*, I*, R* and N* in Eq. (17), we finally obtain the following equation in term of λ*:

$$a_2\left({\lambda }^{*}\right){}^2+a_1{\lambda }^{*}+a_0=0,$$ (20)

where

$$\begin{array}{ccc}{a}_0\hfill & =& (\mu +d+\rho ){}^3(\theta +\mu )\nu \mu K(1-{\mathcal{R}}_0),\hfill \\ a_1\hfill & =& {\displaystyle (\mu +d+\rho ){}^2\left[\right(\nu \left(\right(\theta +\mu \left)\right(\mu +d)+\mu \rho )K}\hfill \\ & & {\displaystyle +\delta (\theta +\mu )\Lambda )(1-\frac{{\beta }_h}{\mu +d+\rho })}\hfill \\ & & {\displaystyle +\nu (\theta +\mu +d)\mu K(1-\frac{{\beta }_v\delta \Lambda }{K\mu (\mu +d+\rho )\nu })],}\hfill \\ a_2\hfill & =& {\displaystyle \frac{(\theta +d+\mu )(\mu +d+\rho )}{\theta +\mu }(\nu ((\theta +\mu )(\mu +d)+\mu \rho )K}\hfill \\ & & +\delta (\theta +\mu )\Lambda ).\hfill \end{array}$$

It is clearly a ₂ > 0 and a ₀ is positive or negative depending whether ${\mathcal{R}}_0$ is less or greater than the unity, respectively. Thus, the number of possible real roots of the polynomial (20) depends on the signs of all coefficients. This can be analyzed using the Descartes Rule of Signs on the polynomial (20). However, according to the signs of a ₂ > 0 and a ₀, one can conclude that there is a unique endemic equilibrium if ${\mathcal{R}}_0>1$. Thus, we have proved the following result for existence of the endemic equilibrium X*.

Lemma 1

Model system (3) has a unique endemic equilibrium X* when ${\mathcal{R}}_0>1$ .

Now, using the center manifold theory, we are going to show that if ${\mathcal{R}}_0>1,$ model system (3) has exactly one endemic equilibrium which is locally asymptotically stable. To do this, we use the theorem of Castillo-Chavez and Song [60].

We have the following result.

Theorem 3

Model system (3) undergoes a unique endemic equilibrium X* which is locally asymptotically stable for ${\mathcal{R}}_0>1$ .

The proof of Theorem 3 is given in Appendix D.

3.4. Parameters and states estimation of the current COVID-19 pandemic in Cameroon

Here, we demonstrate how the estimation method developed in the previous section can be used to reconstruct the unmeasurable state variables and unknown parameters using real data of the current COVID-19 pandemic in Cameroon. For numerical simulations, we use the parameter values given in Table 2. The covariance matrices of error are chosen according to the evolution process of each object that we want to estimate. The deviations are chosen to be $Q_t=0.2{\mathcal{I}}_4,$ $T_t=diag(0.005,0.00001)$ and $Z_t=diag(0.02,0.02,0.03)$. We use the COVID-19 real data from March 6, 2020 to May 17, 2020 in Cameroon for the calibration of the COVID-19 model (3) [45]. We point out that the Cameroonian government still collect data of the COVID-19 pandemic in Cameroon. In the present study, we consider the following two periods: the first period concerns the period of the beginning of the pandemic when the containment was not been applied (March 6, 2020 until April 06, 2020), while the second period corresponds to the period when the containment has been applied by the Cameroonian government (from April 07, 2020 until April 30, 2020) and the third period corresponds to the period when the containment has been lived in Cameroon (from May 01, 2020 until May 17, 2020).

Fig. 2 presents the daily number of newly COVID-19 reported cases, recovered individuals and deceased from March 6, 2020 to May 17, 2020 in Cameroon during before, during and after the containment (magenta, blue and red lines).

Fig. 2.

Reported data of COVID-19 from 06-03-2020 to 17-05-2020 in Cameroon [45]. (a) Newly COVID-19 cases, (b) Newly recovered individuals and (c) COVID-19 newly deceased.

Model system (7) was simulated with the following initial condition: $S\left(0\right)=26371000,$ $I\left(0\right)=1,$ $R\left(0\right)=5$ and $V\left(0\right)=700$ so that $S\left(0\right)+I\left(0\right)+R\left(0\right)$ is the number of the cameroonian population at the begining of estimate. We use the real data given in Fig. 2 and the EnKf procedure for the reconstruction of both the state variables and unknown transmission rates of COVID-19 in Cameroon. The results of the numerical simulations are depicted in Figs. 3 and 4.

Fig. 3.

Reconstruction of COVID-19 transmission rates β_h and β_v of model system (3) using the initial condition (26371000,1,5,700) and the initial parameter $(0.41,1.384\times {10}^{-6})$. (a) COVID-19 transmission rate β_h and (b) COVID-19 transmission rate β_v. All other parameter values are as in Table 2.

Fig. 4.

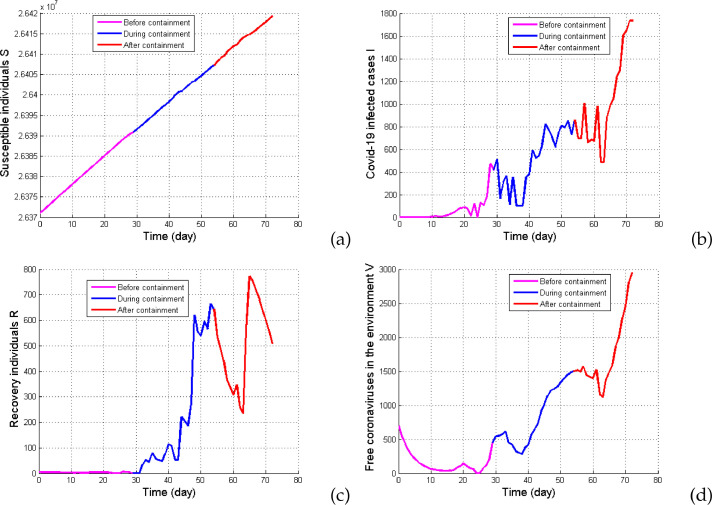
Reconstruction of the state variables of model system 3) with the initial condition (26371000,1,5,700) and initial parameter $(0.473,2.859\times {10}^{-6})$. (a) Susceptible individuals S, (b) COVID-19 infected cases I, (c) Recovered individuals R and (d) Free coronaviruses in the environment V. All other parameter values are as in Table 2.

Fig. 3 shows the reconstruction of the COVID-19 transmission rates. It clearly appears that during the first period of non-containment, the transmission rates β_h varied but β_v did not vary enough (see the magenta line in Fig. 3-(a)-(b)). But, at the same period the daily number of COVID-19 infected cases increased, as shown in Fig. 4-(b) (magenta line). However, during the period of containment, one can observe an increase of the daily number of recovered individuals R as shown in the blue line of Fig. 4-(c). One can also observe the persistence of COVID-19 infected individuals and free coronaviruses in the environment (see the blue line in Fig. 4-(b) and (d)). The results in Fig. 4 also illustrate that COVID-19 infected individuals and free coronaviruses concentration in the environment still increase after the containment period (see the red line in Fig. 4-(b) and (d)). This implies that the COVID-19 pandemic will persist in Cameroon. We point out that even if the COVID-19 transmission rate β_h reaches his maximal value during and after the period of containment, it also reach to the origin at sometime (see the blue and red lines in Fig. 3-(a)). Also, during and after the period of containment, the COVDI-19 transmission rate from free coronaviruses in the environment β_v increases (see the blue and red lines in Fig. 3-(b)). In order to add further evidence of this result, we give the estimated values of all state variables, COVID-19 transmission rates and the basic reproduction number in Cameroon at May 17, 2020. The result is depicted in Table 3 . We find that the basic reproduction number in Cameroon is approximately ${\mathcal{R}}_0=2.949509412,$ i.e. that the disease will not die out without any control measures. It is then important to apply control measures such as contact tracing, social distancing, face-mask wearing, isolation of patient, pharmaceutical interventions and the desinfection and decontamination of infected places by using suitable products against free coronaviruses in the environment. Also, the fact that the number of susceptible individuals increases means that the disease had no significant influence on the evolution of the total human population (see the magenta, blue and red lines in Fig. 4-(a)).

Table 3.

Estimated values of state variables and parameters on May 17, 2020.

Variables	S	I	R	V	βh	βv	${\mathcal{R}}_0$
Values	$26,420,359$	1570	567	2644	0.29461694	0.000038625	2.949509412

Using the parameter values given in Tables 2 and 3, the value of the basic reproduction number within the human individuals without free coronaviruses in the environment is ${\mathcal{R}}_{0h}\approx 2.796109713$. Also, despite an increase of the COVID-19 transmission rate from free coronaviruses in the environment β_v, one has $2<{\mathcal{R}}_{0h}\approx {\mathcal{R}}_0$. This means that the infection of COVID-19 in Cameroon coming from contacts between susceptible individuals and COVID-19 infected cases (i.e. human to human) is much more important than the infection of COVID-19 coming from contacts between susceptible individuals and free coronaviruses in the environment (i.e; human to virus).

Now, to get an overview of the most influential parameters, we compute the normalized sensitivity indices of the model parameters with respect to ${\mathcal{R}}_0$. We use the estimated parameters from Tables 2 and 3 for the baseline values. The rest of the parameter values are the same as in Table 2. The mathematical definition of the normalized forward sensitivity index of the basic reproduction number ${\mathcal{R}}_0$ with respect to a parameter τ is given as:

$${\displaystyle X_{{\mathcal{R}}_0}^{\tau }=\frac{\partial {\mathcal{R}}_0}{\partial \tau }\frac{\tau }{{\mathcal{R}}_0}}$$ (21)

The sensitivity indices of ${\mathcal{R}}_0$ with respect to the model parameters are given in Table 4 . The fact that $X_{{\mathcal{R}}_0}^{{\beta }_h}=0.897$ means that if we increase 1% in β_h, by keeping the other parameters ${\mathcal{R}}_0$ fixed, will produce 0.897% increase in ${\mathcal{R}}_0$. Similarly, $X_{{\mathcal{R}}_0}^{\nu }=-0.102$ implies an increasing of ${\mathcal{R}}_0$ parameter ν by 1%, the value of ${\mathcal{R}}_0$ will decrease by 0.102% keeping the value of the other parameters fixed. Thus, the transmission rate between susceptible humans and COVID-19 infected humans is positively correlated and the recovery rate of COVID-19 infected cases is negatively correlated with respect to the basis reproduction number respectively. Also, ours results confirm that the infection of COVID-19 from human to human has the strongest greatest influence on the spread of the current COVID-19 pandemic in Cameroon. Therefore, the first control measures should be social distancing with the face-mask wearing of the population.

Table 4.

Sensitivity index of the basic reproduction number ${\mathcal{R}}_0$.

Sensitivity index	$X_{{\mathcal{R}}_0}^{{\beta }_h}$	$X_{{\mathcal{R}}_0}^{{\beta }_v}$	$X_{{\mathcal{R}}_0}^{\delta }$	$X_{{\mathcal{R}}_0}^{\Lambda }$	$X_{{\mathcal{R}}_0}^{\nu }$	$X_{{\mathcal{R}}_0}^{\mu }$	$X_{{\mathcal{R}}_0}^K$	$X_{{\mathcal{R}}_0}^{\rho }$	$X_{{\mathcal{R}}_0}^d$
Values	0.897	0.102	0.102	0.102	$-0.102$	$-0.102$	$-0.103$	$-0.896$	$-0.103$

In addition, we draw the contour plots of ${\mathcal{R}}_0$ with respect to the transmission rates β_h, β_v and the recovery rate for model system (3) to investigate the effect of these parameters on the basic reproduction number ${\mathcal{R}}_0$ as shown in Fig. 6. The contours of Fig. 6-(a) indicates that, decreasing β_h and β_v decreases the basic reproduction number ${\mathcal{R}}_0$ and, therefore, COVID-19 cases. Also, with these parameter values, keeping β_h or β_v constant, as the recovery rate ρ increases, ${\mathcal{R}}_0$ decreases (see Figs. 6(a) and (b)). But, in the both cases ${\mathcal{R}}_0>1,$ and therefore the disease will persist in the population (i.e. the above control measures cannot lead to carry effective control of the epidemic).

Fig. 6.

Effect of COVID-19 transmission rates β_h and β_v and the recovery rate of patients on the forecasts of COVID-19 in Cameroon when $r_h=r_v=0.1,$${\beta }_{h,min}=0.001$ and ${\beta }_{v,min}={10}^{-7}$. All other parameter values are as in Table 2.

Now, to assess the accuracy of the short-term forecasts, we calculate two performance metrics, namely the Mean Absolute Error (MAE) and the Root Mean Square Error (RMSE) defined using a set of performance metrics as follows:

$$\text{MAE}=\frac{1}{n}\sum _{i=1}^n|Y\left(i\right)-\widehat{Y}\left(i\right)|,$$ (22)

and

$$\text{RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^n{|Y\left(i\right)-\widehat{Y}\left(i\right)|}^2},$$ (23)

where Y(i) represent the original cases, $\widehat{Y}\left(i\right))$ are the estimated values and n is the size of the data.

These performance metrics are reported in Table 5 . From Table 5, it is evident that the model performs perfectly in case of Cameroon.

Table 5.

Performance of the estimations.

Performance	COVID-19 newly	COVID-19 newly	COVID-19 newly
metrics	reported cases	deceased cases	recovered individuals
MAE	5.05608	0.37365	4.78483
RMSE	13.06629	1.27825	14.92217

3.5. Forecasts of COVID-19 pandemic in Cameroon

The main goal of this analysis is to uncover the trend of the current COVID-19 pandemic in Cameroon using the values of the transmission rates estimated in the previous section. To do so, we take the finale estimated state variables (in Table 3) as the new initial condition of model system (3).

We first assume that the only control measures are face-mask wearing and the desinfection and decontamination of infected places. In this case, the COVID-19 transmission rates from COVID-19 Infected cases and free coronaviruses in the environment are respectively defined as in Eqs. (8) and (9).

Fig. 7 gives the results of the trend the spread of COVID-19 when ${\epsilon }_h={\epsilon }_v=0.45,$ ${\pi }_h={\pi }_v=50\%$ and $t_0=15$. From this figure, it is evident that when the face-mask wearing and the desinfection and decontamination of infected places are applied as control measures, the disease will first increase with more 8 millions COVID-19 infected cases after 70 days (see the cyan line in Fig. 7-(b)) but will decrease after this words. However, the number of newly COVID-19 infected cases will quickly increase to reach a peak with more than 700 000 cases after 70 days as shown in Fig. 7-(f)) (cyan line). One can also observe that the concentration of free coronaviruses in the environment will increase (see the cyan line in Fig. 7-(d)). This implies that the pandemic will continuous to increase in Cameroon if the face-mask wearing and, the disinfection and decontamination of infected places are adopted as the only control measures without the containment.

Fig. 7.

Forecasts of the current COVID-19 pandemic in Cameroon using the estimated values given in Table 4 when ${\epsilon }_h={\epsilon }_v=0.45,$${\pi }_h={\pi }_v=50\%$ and $t_0=15$. (a) Susceptible individuals S, (b) COVID-19 infected cases I, (c) Recovered individuals R, (d) Free coronaviruses in the environment V, (e) Daily deceased cases dI and (f) COVID-19 newly reported cases y_t. All other parameter values are as in Table 2.

Now, we use another non-pharmaceutical interventions to reduce the contacts between susceptible individuals with infected cases or free coronaviruses in the environment by using the containment, the face-mask wearing and the social distancing. To do so, we assume that the transmission rates from susceptible individuals to COVID-19 infected cases or free coronaviruses in the environment are defined as in Eqs. (10) and (11).

The results of numerical simulations are depicted in Fig. 8 for $r=0.5,$ ${\beta }_{h,min}=0.001,$ ${\beta }_{v,min}={10}^{-8}$ and $t_0=15$. It illustrates that using all these following non-pharmaceutical interventions, the number of newly COVID-19 infected cases will quickly increase to reach a peak but with only a few cases around June 5, 2020 (see the cyan line in Fig. 7-(f)). One can also see that the pandemic could disappear after September 2020. Comparing to the results obtained in Fig. 7 where only the face-mask wearing and the desinfection and decontamination of infected places have been considered as control measures, the pandemic could rapidly disappear in Cameroon if the non-pharmaceutical interventions such as the containment, the face-mask wearing and the social distancing are applied.

Fig. 8.

Forecasts of the current COVID-19 pandemic in Cameroon with control measures using the estimated values given in Table 4 and $r=0.5,$${\beta }_{h,min}=0.001,$${\beta }_{v,min}={10}^{-8}$ and $t_0=15$. We use (a) Susceptible individuals S, (b) COVID-19 infected cases I, (c) Recovered individuals R, (d) Free coronaviruses in the environment V, (e) Daily deceased cases u₁ and (f) newly COVID-19 reported cases. All other parameter values are as in Table 2.

Now, we test the ability of these control measures for different values of t ₀.

Figs. 9 and 10 present the forecasts of COVID-19 pandemic in Cameroon using different hypotheses of control measures. From these figures, one observe that the time t ₀ influences especially the disappear of the pandemic of COVID-19 in Cameroon. In fact, if we apply quickly such control measures, the disease will quickly disappear (see the blue lines in Fig. 9-(a) and (b)) compared to the case when we apply the control measures later (see the red lines in Fig. 9-(a) and (b)).

Fig. 9.

Forecast of infected cases of the current COVID-19 pandemic in Cameroon with control measures using the estimated values given in Table 4 and ${\beta }_{h,min}=0.001$ and ${\beta }_{v,min}={10}^{-8}$. (a) COVID-19 newly cases and (b) COVID-19 infected cases. All other parameter values are as in Table 2.

Fig. 10.

Forecasts of infected cases of the current COVID-19 pandemic in Cameroon with control measures using the estimated values given in Table 4 and ${\beta }_{h,min}=0.001$ and ${\beta }_{v,min}={10}^{-8}$. (a) COVID-19 newly cases and (b) COVID-19 infected cases. All other parameter values are as in Table 2.

Furthermore, we study the impact of the transmission rates β_h and β_v on the COVID-19 newly infected cases and the cumulative infected cases.

Fig. 11 presents the effect of the transmission rates β_h and β_v on the forecasts of COVID-19 in Cameroon when $r_h=r_v=0.1,$ ${\beta }_{h,min}=0.001$ and ${\beta }_{v,min}={10}^{-7}$. This indicates that a reduction in the transmission rates will slow down the epidemic significantly. Also, this means that the transmission rate β_h has a significant effect on the cumulative outcome of the pandemic by observing how one can attend the origin with decreasing β_h (see Fig. 11-(a) and (b)) to the detriment of decreasing β_v (see Fig. 11-(c) and (d)).

Fig. 11.

Effect of COVID-19 transmission rates β_h and β_v on the forecasts of COVID-19 in Cameroon when $r_h=r_v=0.1,$${\beta }_{h,min}=0.001$ and ${\beta }_{v,min}={10}^{-7}$. All other parameter values are as in Table 2.

4. Conclusion

This paper has considered the problem of the reconstruction of unmeasurable state variables and unknown transmission rates in a COVID-19 mathematical model using real data of the COVID-19 pandemic in the study case Cameroon. We have proposed a SIRS comprehensive continuous model for the transmission dynamics of COVID-19 that incorporates the interaction between the human individuals and the free coronaviruses in the environment. We have studied the basic properties of the model. More precisely, we have showed the positivity of solutions and the boundedness of the trajectories of the formulated model. We also have computed the disease-free equilibrium and derived the basic reproduction number ${\mathcal{R}}_0$ that determines the outcome of COVID-19. Then, an EnKf framework has been applied to fit the non-linear dynamics model for COVID-19 transmission using real date. We have applied this method to reconstruct the unmeasurable state variables and unknown transmission rates using real data from March 6, 2020 to May 17, 2020 of the current COVID-19 pandemic outbreak in Cameroon. Our main findings on the short-term forecasts of the COVID-19 pandemic in Cameroon can be summarized as follows. (i) The estimation of the state variables and unknown parameters fit the data well. (ii) There is an increases of the numbers of susceptible individuals which implies that the spread of the COVID-19 pandemic has not a significant influence on the human population in Cameroon during the estimation period. (iii) The number of contaminations from free coronaviruses in the environment has increased during and after the period of containment (from April 07 to May 17, 2020), This means that the disease will still persist in Cameroon in the future. (iv) The number of COVID-19 infected cases will rapidly increase when only the use of face-masks wearing is used as control measures. This seems realistic since the estimated value of basic reproduction number at the date of the end of confinement is clearly larger than the unity (that is ${\mathcal{R}}_0>2$). (v) The forecasts of susceptible individuals show that the pandemic will affect the evolution of the population. (vi) The pandemic can quickly disappear if more comprehensive control measures such as containment, the face-mask wearing of individuals and the distancing of people aiming to reduce effective contacts between individuals are applied.

CRediT authorship contribution statement

C. Hameni Nkwayep: Methodology, Validation. S. Bowong: Conceptualization, Writing - original draft. J.J. Tewa: Data curation, Writing - review & editing. J. Kurths: Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Proof of the basic properties of model system (3)

In this Appendix, we prove that any solution of model system (3) with a positive initial condition remains positive and bounded. The proof is done in two steps.

Step 1: We show that the solution X(t) of model system (3) corresponding to initial conditions such that X(0) > 0 are non negative for all t > 0.

Suppose that X(0) > 0. Then from the model equation and properties of continuous functions, there exists some t ₀ > 0 so that X(t) remain non-negative for all t ∈  ]0, t ₀[. We are now going to show that $t_0=\infty$.

Suppose that t ₀ < ∞. Hence, there exists t ₁ ≥ t ₀ which vanish at least one component of X. We define

$$t^{*}=\inf \{t_1\ge t_0:S\left(t_1\right)=0\text{or}I\left(t_1\right)=0\text{or}R\left(t_1\right)=0\text{or}V\left(t_1\right)=0\}.$$

Suppose that $S_h\left(t_1\right)=0$ and let us consider the first equation of model system (3):

$$\dot{S}\left(t\right)=\Lambda -(\lambda +\mu )S\left(t\right).$$

From the above equation, one has that

$$\dot{S}\left(t\right)+({\lambda }_h+{\mu }_h)S\left(t\right)>0.$$

Integrating the above inequality from 0 to t*, one can deduce that

$${\int }_0^{t^{*}}\frac{d}{dt}\left[S\left(t\right)\exp ({\int }_0^t\lambda \left(s\right)ds+\mu t)\right]>0.$$

Since S(0) > 0, one has that

$$S\left(t^{*}\right)>S\left(0\right)\exp (-{\int }_0^{t^{*}}\lambda \left(s\right)ds-\mu t^{*})>0,$$

which is a contradiction with the fact that $S\left(t^{*}\right)=0$. Using the same arguments, we prove by the absurdity of t ₀ < ∞ that I(t*) > 0, R(t*) > 0 and V(t*) > 0. Therefore, the trajectories of the solutions of model system (3) remains positive for all $t\in [0,+\infty [$.

Step 2: We prove that the total population human and the free coronaviruses in the environment at time t, $N_{(}t)$ and V(t) are bounded.

• 1.
  Adding the first, second and fourth equations in model system (3), the dynamics of total human population satisfies

  $$\frac{dN}{dt}=\Lambda -\mu N\left(t\right)-dI\left(t\right)\le \Lambda -\mu N\left(t\right).$$ (24)

  We consider the function M which is the solution of the following equation:

  $$\frac{dM}{dt}=\Lambda -\mu M\left(t\right),$$ (25)

  with the initial condition defined by $M\left(0\right)=N\left(0\right)$. Applying the Laplace transform and it inverse [56] to both sides of Eq. (25), we get the following solution:

  $$M\left(t\right)=\frac{\Lambda }{\mu }(1-\exp (-\mu t))+N\left(0\right)\exp (-\mu t).$$ (26)

  Using the comparison principle related to the classical Cauchy problems, it follows the following relationship:

  $$N\left(t\right)\le \frac{\Lambda }{\mu }(1-\exp (-\mu t))+N\left(0\right)\exp (-\mu t).$$ (27)

  Thus the solution is bound; with the blow-up concept, we obtain the existence of the solution for all t ≥ 0. Furthermore when t tends to $+\infty ,$ then

  $$0\le N\left(t\right)\le \frac{\Lambda }{\mu }.$$ (28)
• 2.
  Finally, using the last equation of model system (3) and the fact that $I\left(t\right)\le \frac{\Lambda }{\mu }$ for all time t ≥ 0, one obtains

  $$\dot{V}\left(t\right)\le \frac{\delta \Lambda }{\mu }-{\nu }_{v}V\left(t\right).$$ (29)
  Applying the same principle as in the first item, one has when t tends to $+\infty ,$

  $$0\le V\left(t\right)\le \frac{\Lambda \delta }{\mu \nu }.$$ (30)

Therefore, combining Step 1 and Step 2, the result about the positivity and the boundedness of solutions are proved. This complete the proof. □

Appendix B. Computation of the basic reproduction number ${\mathcal{R}}_0$ of model system (3)

Herein, we show how to calculate the basic reproduction number ${\mathcal{R}}_0$ of model system (3).

Using the notations in van den Driessche and Watmough [58] for model system (3), the new infection term and the remaining transfer term are $\mathcal{F}=(\lambda S,0){}^T$ and $\mathcal{W}=((\rho +d+\mu )I,-\delta I+\nu V){}^T,$ respectively. Their Jacobian matrices evaluated at the DFE X ₀ are

$$F=\left[\begin{array}{cc}{\beta }_h& {\beta }_v\frac{\Lambda }{K\mu }\\ 0& 0\end{array}\right]\text{and}W=\left[\begin{array}{cc}\rho +d+\mu & 0\\ -\delta & \nu \end{array}\right].$$

A simple computation gives

$$W^{-1}=\left[\begin{array}{cc}\frac{1}{\rho +d+\mu }& 0\\ \frac{\delta }{(\rho +d+\mu )\nu }& \frac{1}{\nu }\end{array}\right].$$

Then, the basic reproduction number of model system (3) is the maximum eigenvalue of the next generation matrix $F{W}^{-1}$ given as:

$$F{W}^{-1}=\left[\begin{array}{cc}\frac{1}{\rho +d+\mu }({\beta }_h+\frac{{\beta }_v\Lambda \delta }{K\mu })& \frac{{\beta }_v\Lambda \delta }{K\nu }\\ 0& 0\end{array}\right].$$

With this in mind, the basic reproduction number of model system (3) is

$${\mathcal{R}}_0=\frac{1}{\mu +d+\rho }({\beta }_h+{\beta }_v\frac{\delta \Lambda }{K\mu \nu }).$$ (B.1)

 □

Appendix C. Ensemble Kalman filter approach

Herein, we use the EnKf procedure [28] to estimate the states x_t and the unknown parameters β_t of the model system (32) for each data y_t using the following system:

$$\{\begin{array}{ccc}\hfill x_{t+1}& =& f(x_t,{\beta }_t,u_t)+w_t,\hfill \\ \hfill y_t& =& h(x_t,{\beta }_t)+v_t,\hfill \\ \hfill {\beta }_{t+1}& =& {\beta }_t+{\eta }_t.\hfill \end{array}$$ (32)

The estimate state-parameter mechanism of Eq. (32) is based on a prediction-correction scheme for the state x_t and the parameter β_t at time t.

We begin by the design of estimating the state. In the forecast step, we prepare both of the ensemble of n forecasted states with random sampling error and the set of predicted outputs as

$$x_{t+1}^{fi}=f(x_t^{ai},{\beta }_t^a,u_t)+w_t^i\text{and}{y}_{t+1}^{fi}=h(x_{t+1}^{fi},{\beta }_t^a),i=1,2,\dots ,n,$$ (33)

where the superscript fi refers to the i-th member of the ensemble of data, ${\beta }_t^a$ is the estimate value of β_t at time t and the vector $x_t^{ai}$ corresponds to the i-th member of the set of states corrected at the moment t. Then, for the step of correction, the set means defined as ${\overline{x}}_{t+1}^f$ and ${\overline{y}}_{t+1}^f$ are respectively given by

$${\overline{x}}_{t+1}^f=\frac{1}{n}\sum _{i=1}^n{x}_{t+1}^{fi}\text{and}{\overline{y}}_{t+1}^f=\frac{1}{n}\sum _{i=1}^n{y}_{t+1}^{fi}.$$ (34)

Thus, the forecast ensemble mean which is the best forecast estimate of the state, and the spread of the ensemble members around the mean as the error between the best estimate and the actual state by

$$R_{t+1}=\frac{1}{n-1}\sum _{i=1}^n{v}_{t+1}^i\left(v_{t+1}^i\right){}^T.$$ (35)

Thus, the covariance matrices of the error at time $t+1$ are

$$\begin{array}{c}{\displaystyle P_{xy,t+1}=\frac{1}{n-1}\sum _{i=1}^n{E}_{x,t+1}^{fi}\left(E_{y,t+1}^{fi}\right){}^T}\hfill \\ {\displaystyle \text{and}{P}_{yy,t+1}=\frac{1}{n-1}\sum _{i=1}^n{E}_{y,t+1}^{fi}\left(E_{y,t+1}^{fi}\right){}^T,}\hfill \end{array}$$ (36)

where $E_{x,t+1}^{fi}=x_{t+1}^{fi}-{\overline{x}}_{t+1}^f$ and $E_{y,t+1}^{fi}=y_{t+1}^{fi}-{\overline{y}}_{t+1}^f$.

$P_{xy,t+1}$ is the unbiased empirical estimator of the covariance matrix of the cross-prediction error between the state and the output at time $t+1$. Similarly, $P_{yy,t+1}$ represents the unbiased estimator of the covariance matrix of the prediction error of the output at time $t+1$.

The second step is the analysis. To obtain the estimate analysis of the state, the EnKf performs an ensemble of parallel data assimilation cycles. This step consists of updating each available member of the set of draft states using the current observation. For this, the following linear correction equation is applied

$$x_{t+1}^{ai}={\overline{x}}_{t+1}^{fi}+K_{t+1}(y_{t+1}+v_{t+1}^i-y_{t+1}^{fi}),i=1,2,\dots ,n,$$ (37)

where $K_{t+1}$ is the Ensemble Kalman filter gain is defined as

$$K_{t+1}=P_{xy,t+1}(P_{yy,t+1}+R_{t+1}){}^{-1}.$$ (38)

Finally, the estimate state of $x_{t+1}$ is the mean of all estimation $x_{t+1}^{ai}$ defined as follows:

$$x_{t+1}^a=\frac{1}{n}\sum _{i=1}^n{x}_{t+1}^{ai}.$$ (39)

The second design concerns the estimation ${\beta }_{t+1}^a$ of the vector of parameters ${\beta }_{t+1}$ at time $t+1$.

As at the state estimation, we prepare the ensemble of N forecasted states with random sampling error as

$${\beta }_{t+1}^{fi}={\beta }_t^{fi}+{\eta }_t^i,i=1,2,\dots ,n.$$ (40)

The ensemble mean is defined as

$${\overline{\beta }}_{t+1}^f=\frac{1}{n}\sum _{i=1}^n{\beta }_{t+1}^{fi}.$$ (41)

The ensemble error matrix for the state variable is defined as follows

$$E_{\beta ,t+1}^{fi}={\beta }_{t+1}^{fi}-{\overline{\beta }}_{t+1}^f,i=1,\dots ,n.$$ (42)

and the ensemble error matrix for the observed variables is defined as follows:

$$E_{y,t+1}^{fi}=y_{t+1}^{\beta fi}-{\overline{y}}_{t+1}^{\beta f},i=1,2,\dots ,n,$$ (43)

where $y_{t+1}^{\beta fi}=h(x_{t+1}^a,{\beta }_{t+1}^{fi})i=1,2,\dots ,n$.

For the analysis steps, the Kalman gain matrix of EnKf $K_{t+1}$ is

$$K_{\beta ,t+1}=P_{\beta y,t+1}(P_{\beta yy,t+1}+R_{t+1}){}^{-1},$$ (44)

where the error covariance matrices $P_{\beta y,t+1}$ and $P_{\beta yy,t+1}$ are given by

$$\begin{array}{c}{\displaystyle P_{\beta y,t+1}=\frac{1}{n-1}\sum _{i=1}^n{E}_{\beta ,t+1}^{fi}\left(E_{y,t+1}^{fi}\right){}^T}\hfill \\ {\displaystyle \text{and}{P}_{\beta yy,t+1}=\frac{1}{n-1}\sum _{i=1}^n{E}_{\beta yy,t+1}^{fi}\left(E_{yy,t+1}^{fi}\right){}^T.}\hfill \end{array}$$ (45)

Appendix D. Proof of Theorem 3

In this Appendix, we give the proof of Theorem 3 on the local stability of the endemic equilibrium point X* of model system (3). To apply this theory, the following simplification and change of variables are made first of all. Let $z=(z_1,z_2,z_3,z_4){}^T$ with $z_1=S\left(t\right)-S_0,$ $z_2=I\left(t\right),$ $z_3=R\left(t\right)$ and $z_4=V\left(t\right)$. It then follows that ${\dot{z}}_1=\dot{S}\left(t\right),$ ${\dot{z}}_2=\dot{I}\left(t\right)$ ${\dot{z}}_3=\dot{R}\left(t\right)$ and ${\dot{z}}_4=\dot{V}\left(t\right)$. With this in mind, model system (3) can be written in the form $\dot{z}=f\left(z\right),$ with $f=(f_1,f_2,f_3,f_4){}^T,$ as follows:

$$\{\begin{array}{ccc}{\dot{z}}_1\hfill & =& f_1=\Lambda +\theta z_3-(\lambda +\mu )(z_1+S_0),\hfill \\ {\dot{z}}_2\hfill & =& f_2=\lambda (z_1+S_0)-(d+\rho +\mu )z_2,\hfill \\ {\dot{z}}_3\hfill & =& f_3=\rho z_2-(\theta +\mu )z_3,\hfill \\ {\dot{z}}_4\hfill & =& f_4=\delta z_2-\nu z_4,\hfill \end{array}$$ (46)

where

$$\lambda ={\beta }_h\frac{z_2}{N}+{\beta }_v\frac{z_4}{K+z_4}\text{and}N=\frac{\Lambda }{\mu }+z_1+z_2+z_3.$$ (47)

System (46) has a DFE given by $X_0=(z_1^0,0,0,0)$ with $z_1^0=S_0$.

Let ${\alpha }^{*}={\beta }_h$ be the bifurcation parameter. Solving ${\mathcal{R}}_0=1$ gives

$${\alpha }^{*}=\mu +d+\rho -{\beta }_v\frac{\delta \Lambda }{K\mu \nu }.$$ (48)

The Jacobian of model system (46) at X ₀ is

$$J^{*}\left(X_0\right)=\left[\begin{array}{cccc}-\mu & -{\alpha }^{*}& \theta & -\frac{{\beta }_v}{K}{S}_0\\ 0& {\alpha }^{*}-(\rho +d+\mu )& 0& \frac{{\beta }_v}{K}{S}_0\\ 0& \rho & -(\theta +\mu )& 0\\ 0& \delta & 0& -\nu \end{array}\right],$$

where ${\upsilon }^{*}=1-\upsilon$ and ${\omega }^{*}=1-\omega$.

The eigenvalues of the Jacobian (J*(X ₀)) of model system (46) at the DFE X ₀ are: μ, $-(\theta +\mu ),$ $-\frac{{\beta }_v\Lambda }{K\mu }-\nu$ and has zero as a simple eigenvalue. Hence, the Centre Manifold theory [59] can be used to analyse the dynamics of model system (46). In particular, the theorem in Castillo and Song [60], reproduced below for convenience, will be used to show that when ${\mathcal{R}}_0>1,$ there can exist a unique endemic equilibrium of model system (46) (as shown in Lemma 1) which is locally asymptotically stable for ${\mathcal{R}}_0$ near 1 under certain condition.

Theorem 4

(Castillo-Chavez $\&$ Song [60] ): Consider the following general system of ordinary differential equations with a parameter ϕ:

$${\displaystyle \frac{dz}{dt}=f(z,\varphi ),f:{\mathbb{R}}^n\times \mathbb{R}\to \mathbb{R}\text{and}f\in C^2({\mathbb{R}}^n,\mathbb{R}),}$$ (49)

where 0 is an equilibrium point of the system (that is, f(0, ϕ) ≡ 0 for all ϕ) and assume

• 1. $A=D_{z}f(0,0)=\left({\displaystyle \frac{\partial f_i}{\partial z_j}(0,0)}\right)$ is the linearization matrix of system (49) around the equilibrium 0 with ϕ evaluated at 0. Zero is a simple eigenvalue of A and other eigenvalues of A have negative real parts;
• 2. Matrix A has a right eigenvector u and a left eigenvector v (each corresponding to the zero eigenvalue).

Let f_k be the k^th component of f and

$$\begin{array}{ccc}a\hfill & =& {\displaystyle \sum _{k,i,j=1}^n{v}_k{u}_i{u}_j\frac{{\partial }^2{f}_k}{\partial z_i\partial z_j}(0,0),}\hfill \\ \\ b\hfill & =& {\displaystyle \sum _{k,i=1}^n{v}_k{u}_i\frac{{\partial }^2{f}_k}{\partial z_i\partial \varphi }(0,0),}\hfill \end{array}$$

then, the local dynamics of the system around the equilibrium point 0 is totally determined by the signs of a and b.

• 1. a > 0, b > 0. When ϕ < 0 with |ϕ| ≪ 1, 0 is locally asymptotically stable and there exists a positive unstable equilibrium; when 0 < ϕ ≪ 0, 0 is unstable and there exists a negative, locally asymptotically stable equilibrium;
• 2. a < 0, b < 0. When ϕ < 0 with |ϕ| ≪ 1, 0 is unstable; when 0 < ϕ ≪ 1, 0 is locally asymptotically stable equilibrium, and there exists a positive unstable equilibrium;
• 3. a > 0, b < 0. When ϕ < 0 with |ϕ| ≪ 1, 0 is unstable, and there exists a locally asymptotically stable negative equilibrium; when 0 < ϕ ≪ 1, 0 is stable, and a positive unstable equilibrium appears;
• 4. a < 0, b > 0. When ϕ changes from negative to positive, 0 changes its stability from stable to unstable. Correspondingly a negative unstable equilibrium becomes positive and locally asymptotically stable.

Particularly, if a > 0 and b > 0, then a backward bifurcation occurs at $\varphi =0$ .

In order to apply the above theorem, the following computations are necessary (it should be noted that we use α* as the bifurcation parameter, in place of ϕ in Theorem (Castillo-Chavez $\&$ Song [60])).

Eigenvectors of J*(X₀): For the case when ${\mathcal{R}}_0=1,$ it can be shown that the Jacobian of model system (46) at ${\beta }_h={\alpha }^{*}$ (denoted by J*(X ₀)) has a right eigenvector (corresponding to the zero eigenvalue), given by $w=(w_1,w_2,w_3,w_4){}^T$ where

$$\begin{array}{c}{\displaystyle w_1=-\frac{\nu \left(\right(\theta +\mu \left)\right(\mu +d)+\mu \rho )}{\mu (\theta +\mu )},w_2=\nu ,w_3=\frac{\rho \nu }{\theta +\mu },}\hfill \\ {\displaystyle \text{and}{w}_4=\delta .}\hfill \end{array}$$

Similarly, the components of the left eigenvectors of $J_{{\alpha }^{*}}$ (corresponding to the zero eigenvalue), denoted by $v=(v_2,v_2,v_3,v_4){}^T$ where

$$v_1=v_3=0,v_2=\nu \text{and}{v}_4=\frac{{\beta }_v\Lambda }{\mu K}.$$

Computation of b: For the sign of b, it can be shown that the associated non-vanishing partial derivative of f is

$${\displaystyle \frac{{\partial }^2{f}_2}{\partial z_2\partial {\alpha }^{*}}=1.}$$

Substituting the respective partial derivatives into the expression

$$\begin{array}{ccc}b\hfill & =& {\displaystyle v_2{w}_2\frac{{\partial }^2{f}_2}{\partial z_2\partial {\alpha }^{*}},}\hfill \\ \\ & =& {\nu }^2>0.\hfill \end{array}$$ (50)

Computation of a: For model system (46), the associated non-zero partial derivatives of f (at the DFE X ₀) are given by

$$\begin{array}{cc}& {\displaystyle \frac{{\partial }^2{f}_2}{\partial z_1\partial z_4}=\frac{{\partial }^2{f}_2}{\partial z_4\partial z_1}=\frac{{\beta }_v}{K},\frac{{\partial }^2{f}_2}{\partial z_2\partial z_3}=\frac{{\partial }^2{f}_2}{\partial z_3\partial z_2}=-\frac{{\alpha }^{*}}{N_0},}\hfill \\ & {\displaystyle \frac{{\partial }^2{f}_2}{\partial z_2^2}=-\frac{2{\alpha }^{*}}{N_0}\text{and}\frac{{\partial }^2{f}_2}{\partial z_4^2}=-\frac{2{\beta }_v}{K^2}{S}_0,}\hfill \end{array}$$

where $S_0=N_0=\Lambda /\mu$. Then, it follows that

$$\begin{array}{ccc}{\displaystyle a}\hfill & =& {\displaystyle \sum _{k,i,j=1}^7{v}_k{w}_i{w}_j\frac{{\partial }^2{f}_k}{\partial z_i\partial z_j},}\hfill \\ & =& {\displaystyle -2\nu [\frac{{\beta }_v\delta }{K}(\frac{(\theta +\mu )(\mu +d)+\mu \rho }{\mu (\theta +\mu )}+\frac{\delta S_0}{K})}\hfill \\ & & {\displaystyle +\frac{{\alpha }^{*}}{N_0}({\delta }^2+\frac{\rho {\nu }^2}{\theta +\mu })]<0.}\hfill \end{array}$$ (51)

Observe that the coefficient b is always positive so that, according to the sign of the coefficient a which is negative around the disease-free equilibrium for ${\beta }_h={\alpha }^{*}$. Thus, it follows that the endemic equilibrium is locally asymptotically stable (according to the fourth step of Theorem 4). This concludes the proof. □