Pseudo-likelihood based logistic regression for estimating COVID-19 infection and case fatality rates by gender, race, and age in California

Abstract

In emerging epidemics, early estimates of key epidemiological characteristics of the disease are critical for guiding public policy. In particular, identifying high-risk population subgroups aids policymakers and health officials in combating the epidemic. This has been challenging during the coronavirus disease 2019 (COVID-19) pandemic because governmental agencies typically release aggregate COVID-19 data as summary statistics of patient demographics. These data may identify disparities in COVID-19 outcomes between broad population subgroups, but do not provide comparisons between more granular population subgroups defined by combinations of multiple demographics.

We introduce a method that helps to overcome the limitations of aggregated summary statistics and yields estimates of COVID-19 infection and case fatality rates — key quantities for guiding public policy related to the control and prevention of COVID-19 — for population subgroups across combinations of demographic characteristics. Our approach uses pseudo-likelihood based logistic regression to combine aggregate COVID-19 case and fatality data with population-level demographic survey data to estimate infection and case fatality rates for population subgroups across combinations of demographic characteristics.

We illustrate our method on California COVID-19 data to estimate test-based infection and case fatality rates for population subgroups defined by gender, age, and race/ethnicity. Our analysis indicates that in California, males have higher test-based infection rates and test-based case fatality rates across age and race/ethnicity groups, with the gender gap widening with increasing age. Although elderly infected with COVID-19 are at an elevated risk of mortality, the test-based infection rates do not increase monotonically with age. The workforce population, especially, has a higher test-based infection rate than children, adolescents, and other elderly people in their 60–80. LatinX and African Americans have higher test-based infection rates than other race/ethnicity groups. The subgroups with the highest 5 test-based case fatality rates are all-male groups with race as African American, Asian, Multi-race, LatinX, and White, followed by African American females, indicating that African Americans are an especially vulnerable California subpopulation.

1. Introduction

Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has spread from its zoonotic origins in Hubei Province, China, causing a global pandemic of coronavirus disease 2019 (COVID-19) (Phelan et al., 2020, Cucinotta and Vanelli, 2020). As of October 13, 2020, COVID-19 has infected over 38 million people across 189 countries and regions (COVID, 2020). In the early stages of an emerging epidemic such as COVID-19, estimating the infection rate (IR) and case fatality rate (CFR) of the infectious disease is of utmost importance to health officials, policymakers, and the population at large. Accurate population and subgroup estimates of CFRs provide an evidence-based rationale for policies designed to mitigate the spread of the infectious disease, help identify disparities in disease vulnerability, and inform resource allocation to communities in greatest need.

Official COVID-19 data released by governmental health agencies and other public sources are prohibited by U.S. law from containing personally identifiable information. Consequently, these data are generally summarized in an aggregate format that comprises only univariate or limited bivariate summary statistics of patient demographics, providing valuable but limited information on the heterogeneity of patient attributes. Indeed, in New York City, the epicenter of the COVID-19 outbreak in the U.S., the reported infection rates and case fatality rates for African Americans were disproportionately higher than other races, according to data released by the New York City Department of Health and Mental Hygiene (Garg, 2020). Data from several other U.S. states, including New Jersey (New Jersey Department of Health, 2020), California (California Department of Public Health, 2020c), and Illinois (Illinois Department of Public Health, 2020), exhibited similar trends. Gender and age-disaggregated national case data from a vast array of countries across the globe reveal that males and older individuals generally have substantially higher case fatality rates. Furthermore, evidence from numerous clinical studies of COVID-19 risk factors has established that gender and age are risk factors for COVID-19 infection mortality (Zheng et al., 2020, Jin et al., 2020, Docherty et al., 2020, Du et al., 2020). However, by aggregating, data from governmental health agencies or other public sources do not provide granular information on the combined effect of the risk factors under consideration. In particular, how IRs and CFRs vary across population subgroups characterized by gender, age, and race jointly has not yet received substantial attention. Understanding the gender-age-race dynamics of COVID-19 infection and mortality would provide deeper insights into the disparities that exist in the effects of COVID-19 on the population.

Various methods for using information contained in aggregate data have been proposed in a wide array of applications (see, e.g. Mavridis and Salanti, 2013, Simmonds and Higgins, 2016, Chang et al., 2000), and there is growing interest in leveraging summary statistics in publicly released COVID-19 datasets to quantify the impact of various risk factors on COVID-19 mortality (Caramelo et al., 2020). In this paper, we propose a method that helps overcome the limitations of having only aggregate summary statistics on COVID-19 cases and fatalities to obtain early estimates of COVID-19 IRs and CFRs for population subgroups defined by combinations of risk factors. A major contribution of our proposed method is that we provide a way to incorporate multivariate population demographic data, which provides estimates of the probability distribution of multiple risk factors for the disease, into the analysis of publicly released aggregate data. Specifically, we propose a pseudo-likelihood based multivariable logistic regression approach that combines publicly released aggregate COVID-19 case and fatality data with multivariate population-level demographic survey data. The proposed method, compared to the prevalent approaches, includes the information of inner correlation across different risk factors and allows statistical control for confounds to obtain more reliable inferences.

The proposed method is composed of two main steps. First, we model COVID-19 IRs using a multivariable logistic regression model, estimating its parameter values from publicly available COVID-19 case data. Second, we estimate COVID-19 CFRs based on the recovered IRs and publicly available COVID-19 fatality data. This paper uses California as an example case study, but the approach is easily generalized to other states. We carry out the analysis using the most recent COVID-19 case and fatality data from the California Department of Public Health (CDPH) (California Department of Public Health, 2020c, California Department of Public Health, 2020a, California Department of Public Health, 2020b) and population-level demographic data from the California Health Interview Survey (CHIS) (California Health Interview Survey, 2020) to obtain estimates of IRs and CFRs for subgroups of the California state population characterized by gender, age, and race.

Not every person who may be infected with COVID-19 is tested, and in some locations only symptomatic people are tested. This was especially true at the beginning of the epidemic when patients that were deemed high risk and/or symptomatic were given priority for testing. This introduces sampling bias into the COVID-19 data that prevents a straightforward estimation of the true IRs and CFRs. To circumvent this issue, we estimate test-based IR (T-IRs) and test-based CFRs (T-CFRs) that depend on the availability and use of testing and may differ from the true IRs and CFRs. In particular, we expect true IRs to be greater than T-IRs and true CFRs to be less than T-CFRs due to the presence of asymptomatic and undiagnosed infections. While the test-based rates do not estimate the overall population rates, they capture the vast majority of severe or fatal COVID-19 infections, because these individuals are very likely to be tested. Consequently, the T-IRs and T-CFRs estimated by our method provide valuable insights into the disparities in COVID-19 outcomes that exist across gender, age, and race/ethnicity groups and furnish guidance for public policy related to the control and prevention of COVID-19.

2. Data

Our method for estimating COVID-19 T-IRs and T-CFRs relies on two data sources: daily COVID-19 data for California from the California Department of Public Health (CDPH) (California Department of Public Health, 2020c, California Department of Public Health, 2020a, California Department of Public Health, 2020b), and the 2017–2018 wave of the California Health Interview Survey (CHIS) (California Health Interview Survey, 2020).

CDPH data are publicly available and provide up-to-date information on the number of COVID-19 cases and fatalities in California by gender (California Department of Public Health, 2020a), age (California Department of Public Health, 2020b), and race/ethnicity (California Department of Public Health, 2020c), separately. The case and fatality data as of October 13, 2020 are presented in Table 1. CDPH divides the population into ten age groups: less than 5, 5–17, 18–34, 35–49, 50–59, 60–64, 65–69, 70–74, 75–79, and 80 and above. Age group is missing from less than 0.1% of the confirmed cases and no missing for deaths reported by CDPH. The eight race and ethnicity groups in the publicly released dataset are LatinX/ Hispanic (LatinX), White/ Caucasian (White), Asian, African American/Black (AA), Multi-Race, American Indian or Alaska Native (AIAN), Native Hawaiian and other Pacific Islander, and others. We combined the last two race and ethnicity groups due to their small size in the California population. Race and ethnicity are missing in almost 30% of confirmed cases and 1% of the deaths.

Table 1.

Confirmed COVID-19 cases and fatalities by gender, age and race/ethnicity in California as of October 13, 2020 California Department of Public Health, 2020a, California Department of Public Health, 2020b, California Department of Public Health, 2020c.

Demographic	Group	Confirmed cases	Deaths	Death rate (%)
Gender	Male	416,579	9,439	2.27%
	Female	431,587	7,055	1.63%
Age group	0–17	89,843	2	0.00%
	18–34	300,957	257	0.09%
	35–49	210,997	932	0.44%
	50–59	118,522	1,761	1.49%
	60–64	42,807	1,405	3.28%
	65–69	29,268	1,699	5.80%
	70–74	20,380	1,840	9.03%
	75–79	14,056	1,848	13.15%
	80+	27,347	6,778	24.79%
Race & Ethnicity	LatinX	366,314	7,959	2.17%
	White	104,140	4,929	4.73%
	Asian	33,342	1,914	5.74%
	AA	25,515	1,237	4.85%
	Multi-race	6,604	122	1.85%
	AIAN	1,676	51	3.04%
	Other	62,418	177	0.28%

To supplement the CDPH COVID-19 data, we used demographic data on the California population collected by the California Health Interview Survey (CHIS) (California Health Interview Survey, 2020). CHIS is the largest state health survey in the U.S., conducted by the UCLA Center for Health Policy Research in collaboration with the California Departments of Public Health and Health Care Services. CHIS interviews over 20,000 Californians each year, collecting information on a wide range of demographic and health variables. CHIS oversamples certain population subgroups to achieve more reliable and precise estimates for these subgroups, and estimates a sampling weight for each respondent to represent the reciprocal of the probability of selection. We use the 2017–2018 wave of CHIS in our analysis, that consists of 45,369 subjects interviewed, focusing on the following three demographic variables recorded: gender, age, and race and ethnicity groups.

3. Methods

3.1. Infection rate estimation procedure

We propose estimating COVID-19 T-IRs given gender, age and race using a multivariable logistic regression model. The variables we use in our analysis are listed in Table 2. Let female, age 0–17 and LatinX be the reference category for gender, age group and race and ethnicity, respectively; thus we need $p=1+8+6=15$ variables to represent all demographic characteristics. We let $\mathit{z}\in {\{0,1\}}^p\in {\mathbb{R}}^p$ denote the gender-age-race covariate setting of the covariates $\mathit{Z}$ in Table 2. The postulated IR model follows

$$log\left[\frac{\mathbb{P}(\mathcal{I}=1\mid \mathit{z})}{1-\mathbb{P}(\mathcal{I}=1\mid \mathit{z})}\right]={\gamma }_0+{\mathit{z}}^{\top }\mathit{\gamma },$$ (1)

where $\mathcal{I}\in \{0,1\}$ represents infection status, ${\gamma }_0$ is the log odds of infection for the female age 0–17 Latinx group, and $\mathit{\gamma }\in {\mathbb{R}}^p$ are the log odds ratios of infection associated with the other demographic categories.

Table 2.

Variables used in the infection rate estimation procedure.

Variable	Definition
Infection status	Dichotomous outcome indicating COVID-19 infection (0 = No, 1 = Yes)
Gender	Dichotomous covariate indicating male or female (0 = Female, 1 = Male)
Age	Categorical covariate with the following age groups: 0–17 (reference level), 18–34, 35–49, 50–59, 60–64, 65–69, 70–74, 75–79, 80+
Race/Ethnicity	Categorical covariate with the following race categories: LatinX (reference level), White, Asian, African American/Black, Multi-Race, American Indian or Alaska Native, Other

The CDPH data provide the gender, age, and race distributions of COVID-19 infections separately (California Department of Public Health, 2020a). To estimate the T-IRs given gender, age, and race jointly, we employ a pseudo-likelihood approach that maximizes a likelihood function constructed from univariate logistic regression models obtained by marginalizing over the covariates. The proposed method begins by first expressing Eq. (1) in terms of the probability of infection conditional on the covariates,

$$\mathbb{P}(\mathcal{I}=1|\mathit{z})=\frac{exp({\gamma }_0+{\mathit{z}}^{\top }\mathit{\gamma })}{1+exp({\gamma }_0+{\mathit{z}}^{\top }\mathit{\gamma })}.$$ (2)

We introduce ${\mathbb{P}}_{\mathit{X}}\left(\mathit{x}\right)$ as the probability mass function of a $p^{\ast }$-dimensional discrete random variable $\mathit{X}$ with support $\mathcal{X}\subset {\{0,1\}}^{p^{\ast }}$, $p^{\ast }>p$, that represents the proportion of the California population with gender-age-race attributes $\mathit{x}$, that is simply an augmentation of the covariate setting $\mathit{z}$ in (1) to include the reference levels listed in Table 2. We then define the conditional probability mass function of ${\mathit{X}}_{-i}$ given ${\mathit{X}}_i=1$ to be ${\mathbb{P}}_{{\mathit{X}}_{-i}|X_i}\left({\mathit{x}}_{-i}|x_i=1\right)$, where $X_i$ is the $i$th element of $\mathit{X}$, and ${\mathit{X}}_{-i}$ is the subset of $\mathit{X}$ that omits $X_i$. Defining ${\mathcal{X}}_{(X_i=1)}$ to be the subset of $\mathcal{X}$ with the constraint that $X_i=1$ and taking the expectation of both sides of Eq. (2) conditional on $X_i=1$, by the Law of Iterated Expectations we have

$$\mathbb{P}(\mathcal{I}=1\mid X_i=1)={\mathbb{E}}_{{\mathit{X}}_{-i}|X_i=1}\left[\mathbb{P}\left(\mathcal{I}=1|\mathit{z}\right)\right]=\sum _{\tilde{\mathit{x}}\in {\mathcal{X}}_{(X_i=1)}}\mathbb{P}\left(\mathcal{I}=1|\mathit{z}\left(\tilde{\mathit{x}}\right)\right){\mathbb{P}}_{{\mathit{X}}_{-i}|X_i}\left({\tilde{\mathit{x}}}_{-i}|x_i=1\right)=\sum _{\tilde{\mathit{x}}\in {\mathcal{X}}_{(X_i=1)}}\frac{exp({\gamma }_0+{\mathit{\gamma }}^{\top }\mathit{z}\left(\tilde{\mathit{x}}\right))}{1+exp({\gamma }_0+{\mathit{\gamma }}^{\top }\mathit{z}\left(\tilde{\mathit{x}}\right))}{\mathbb{P}}_{{\mathit{X}}_{-i}|X_i}\left({\tilde{\mathit{x}}}_{-i}|x_i=1\right).$$ (3)

Next, we construct the individual log-likelihoods corresponding to each univariate logistic regression of $\mathcal{I}$ on $X_i=1$ for each $X_i\in \mathit{X}$. Let $N$ denote the total population size, $N_{i1}$ denote the number of individuals in the population with $X_i=1$, and $N_{i1}^{\left(\mathcal{I}\right)}$ denote the total number of individuals with $X_i=1$ who have been or will be infected with COVID-19. Therefore, $N_{i1}^{\left(\mathcal{I}\right)}$ follows a binomial distribution,

$$\text{Binomial}\left(N_{i1},\sum _{\tilde{\mathit{x}}\in {\mathcal{X}}_{(X_i=1)}}\frac{exp({\gamma }_0+{\mathit{\gamma }}^{\top }\mathit{z}\left(\tilde{\mathit{x}}\right))}{1+exp({\gamma }_0+{\mathit{\gamma }}^{\top }\mathit{z}\left(\tilde{\mathit{x}}\right))}{\mathbb{P}}_{{\mathit{X}}_{-i}|X_i}\left({\tilde{\mathit{x}}}_{-i}|x_i=1\right)\right)$$ (4)

for $i=1,\dots ,p^{\ast }$. We define the individual log-likelihood of $({\gamma }_0,\mathit{\gamma })$ for $X_i$ corresponding to the binomial distribution (4) as ${\mathcal{L}}_{X_i}^{\left(\mathcal{I}\right)}({\gamma }_0,\mathit{\gamma }|N_{i1}^{\left(\mathcal{I}\right)},N_{i1})$, and we define the full log-likelihood of $({\gamma }_0,\mathit{\gamma })$ as the sum of the individual log-likelihoods

$$\mathcal{L}({\gamma }_0,\mathit{\gamma })=\sum _{i=1}^{p^{\ast }}{\mathcal{L}}_{X_i}^{\left(\mathcal{I}\right)}({\gamma }_0,\mathit{\gamma }\mid N_{i1}^{\left(\mathcal{I}\right)},N_{i1}).$$ (5)

We use the CHIS data to approximate ${\mathbb{P}}_{\mathit{X}}\left(\mathit{x}\right)$, which we denote ${\hat{\mathbb{P}}}_{\mathit{X}}\left(\mathit{x}\right)$. Let $N^{\left(\mathcal{I}\right)}$ denote the total number of individuals in the population who have been or will be infected with COVID-19, and let ${\pi }_{\mathcal{I}}=\mathbb{P}(\mathcal{I}=1)$ denote the overall infection rate in the population. Thus, the total population size is $N=N^{\left(\mathcal{I}\right)}∕{\pi }_{\mathcal{I}}$. From the CDPH data presented in Table 1, we have the cumulative number of reported COVID-19 infections as of October 13, 2020, which we denote ${\hat{N}}^{\left(\mathcal{I}\right)}$. Because ${\hat{N}}^{\left(\mathcal{I}\right)}$ measures the cumulative number of COVID-19 infections up to October 13, 2020, and increases daily, ${\hat{N}}^{\left(\mathcal{I}\right)}$ is smaller than $N^{\left(\mathcal{I}\right)}$, perhaps substantially. Furthermore, ${\pi }_{\mathcal{I}}$ is unknown, and for a given estimate ${\hat{\pi }}_{\mathcal{I}}$ of ${\pi }_{\mathcal{I}}$, we define $\hat{N}$ to be $\hat{N}={\hat{N}}^{\left(\mathcal{I}\right)}∕{\hat{\pi }}_{\mathcal{I}}$. Therefore, even for accurate estimates of ${\pi }_{\mathcal{I}}$, $\hat{N}$ will be smaller, perhaps substantially, than the total number of individuals in the population. However, we assume here that the relative size of $\hat{N}$ to $N$ is approximately equal to the relative size of ${\hat{N}}^{\left(\mathcal{I}\right)}$ to $N^{\left(\mathcal{I}\right)}$. Hence, $\hat{N}$ may be interpreted as an appropriately scaled version of $N$ with respect to ${\hat{N}}^{\left(\mathcal{I}\right)}$ and ${\hat{\pi }}_{\mathcal{I}}$ as of October 13, 2020. Likewise, we define ${\hat{N}}_{i1}=\hat{N}\times {\sum }_{\tilde{\mathit{x}}\in {\mathcal{X}}_{(X_i=1)}}{\hat{\mathbb{P}}}_{\mathit{X}}\left(\tilde{\mathit{x}}\right)$, with ${\hat{N}}_{i1}$ having the same interpretation as $\hat{N}$ but for the subset of the population with $X_i=1$. We denote ${\hat{N}}_{i1}^{\left(\mathcal{I}\right)}$ to be the cumulative number of infected individuals with $X_i=1$ as of October 13, 2020, and present $\{{\hat{N}}_{i1}^{\left(\mathcal{I}\right)}:i=1,\dots ,p^{\ast }\}$ in Table 1.

Substituting ${\hat{\mathbb{P}}}_{{\mathit{X}}_{-i}|X_i}\left({\tilde{\mathit{x}}}_{-i}|x_i=1\right)$ for ${\mathbb{P}}_{{\mathit{X}}_{-i}|X_i}\left({\tilde{\mathit{x}}}_{-i}|x_i=1\right)$, $\{{\hat{N}}_{i1}^{\left(\mathcal{I}\right)}:i=1,\dots ,p^{\ast }\}$ for $\{N_{i1}^{\left(\mathcal{I}\right)}:i=1,\dots ,p^{\ast }\}$, and $\{{\hat{N}}_{i1}:i=1,\dots ,p^{\ast }\}$ for $\{N_{i1}:i=1,\dots ,p^{\ast }\}$ in the log-likelihood (5), we obtain a pseudo-likelihood

$$\tilde{\mathcal{L}}({\gamma }_0,\mathit{\gamma })=\sum _{i=1}^{p^{\ast }}{\tilde{\mathcal{L}}}_{X_i}^{\left(\mathcal{I}\right)}({\gamma }_0,\mathit{\gamma }|{\hat{N}}_{i1}^{\left(\mathcal{I}\right)},{\hat{N}}_{i1}).$$ (6)

We maximize the pseudo-likelihood (6) with respect to $\left({\gamma }_0,\mathit{\gamma }\right)$ to obtain our estimates

$$\left({\hat{\gamma }}_0,\hat{\mathit{\gamma }}\right)=\underset{{\gamma }_0,\mathit{\gamma }}{argmax}\left\{\tilde{\mathcal{L}}({\gamma }_0,\mathit{\gamma })\right\}.$$ (7)

The optimization is implemented through the ‘optim’ function in R (Version 3.6.3) using Limited-Memory Broyden–Fletcher–Goldfarb–Shanno Optimization for finite solutions  (Team et al., 2020, Zhu et al., 1995). Here, we use term “pseudo-likelihood” since the calculation of likelihood is based on a combination of real data and population information approximated by CHIS data. A combination of pseudo samples and real data is necessary here since only infected cases are recorded at the early stage of a pandemic. In Section 3.3 we will show how to use pseudo samples that simulate population by bootstrapping CHIS data to calculate the pseudo-likelihood.

Lastly, by plugging $\left({\hat{\gamma }}_0,\hat{\mathit{\gamma }}\right)$ into Eq. (2), we obtain the predicted test-based infection probabilities for individuals with gender-age-race covariate setting $\mathit{z}$

$$\hat{\mathbb{P}}(\mathcal{I}=1|\mathit{z})=\frac{exp({\hat{\gamma }}_0+{\mathit{z}}^{\top }\hat{\mathit{\gamma }})}{1+exp({\hat{\gamma }}_0+{\mathit{z}}^{\top }\hat{\mathit{\gamma }})}.$$ (8)

3.2. Case fatality rate estimation procedure

Similar to the T-IR estimation method, we model the T-CFRs given gender, age, and race using a multivariable logistic regression model. The gender-age-race covariate we use for CFR estimation (see Table 3) is the same as the covariate we use for IR estimation, except that we combined the 0–17 and 18–34 age groups due to low numbers of fatalities among the 0–17 age group. With a slight abuse of notation, we denote $\mathit{z}\in {\{0,1\}}^q\in {\mathbb{R}}^q$ to be the covariate setting of the vector of non-reference group covariates $\mathit{Z}$, where $q=14$. The corresponding random variable $\mathit{X}$ and its covariate setting $\mathit{x}$ are as defined in the preceding subsection and have dimension $q^{\ast }$, where $q^{\ast }=17$. We give the T-CFR model as

$$\text{log}\left[\frac{\mathbb{P}(\mathcal{M}=1\mid \mathit{z},\mathcal{I}=1)}{1-\mathbb{P}(\mathcal{M}=1\mid \mathit{z},\mathcal{I}=1)}\right]={\delta }_0+{\mathit{z}}^{\top }\mathit{\delta },$$ (9)

where $\mathcal{M}\in \{0,1\}$ represents mortality status, ${\delta }_0$ is the log odds of mortality for the LatinX female age 0–34 group, and $\mathit{\delta }\in {\mathbb{R}}^q$ are the log odds ratios of mortality for other covariate settings.

Table 3.

Variables used in the case fatality rate estimation procedure.

Variable	Definition
Mortality status	Dichotomous outcome indicating fatality status (0 = No, 1 = Yes)
Gender	Dichotomous covariate indicating gender (0 = Female, 1 = Male)
Age	Categorical covariate with the following age groups: 0–34 (reference level), 35–49, 50–59, 60–64, 65–69, 70–74, 75–79, 80+
Race/Ethnicity	Categorical covariate with the following race categories: LatinX (reference level), White, Asian, African American/Black, Multi-Race, American Indian or Alaska Native, Other

We again employ a pseudo-likelihood approach to estimate $\left({\delta }_0,\mathit{\delta }\right)$ that maximizes a likelihood function constructed from univariate logistic regression models. Following similar steps as shown in the preceding subsection, we have

$$\mathbb{P}(\mathcal{M}=1\mid X_i=1,\mathcal{I}=1)$$$$=\sum _{\tilde{\mathit{x}}\in {\mathcal{X}}_{(X_i=1)}}\frac{exp({\delta }_0+{\mathit{\delta }}^{\top }\mathit{z}\left(\tilde{\mathit{x}}\right))}{1+exp({\delta }_0+{\mathit{\delta }}^{\top }\mathit{z}\left(\tilde{\mathit{x}}\right))}{\mathbb{P}}_{{\mathit{X}}_{-i}|X_i}\left({\tilde{\mathit{x}}}_{-i}|x_i=1,\mathcal{I}=1\right).$$ (10)

We use the CHIS data and the IR model (1) with coefficient estimates (7) to estimate ${\mathbb{P}}_{{\mathit{X}}_{-i}|X_i}\left({\tilde{\mathit{x}}}_{-i}|x_i=1,\mathcal{I}=1\right)$. First, we estimate $\mathbb{P}\left(\mathit{z}\right|\mathcal{I}=1)$ using Bayes’ Rule

$$\hat{\mathbb{P}}\left(\mathit{z}\right|\mathcal{I}=1)=\frac{\hat{\mathbb{P}}(\mathcal{I}=1|\mathit{z}){\hat{\mathbb{P}}}_{\mathit{X}}\left(\mathit{x}\left(\mathit{z}\right)\right)}{{\hat{\pi }}_{\mathcal{I}}},$$ (11)

where $\hat{\mathbb{P}}(\mathcal{I}=1|\mathit{z})$ comes from Eq. (8), and ${\hat{\mathbb{P}}}_{\mathit{X}}\left(\mathit{x}\left(\mathit{z}\right)\right)$ is obtained from the CHIS dataset. Then, by the definition of conditional probability, we estimate ${\mathbb{P}}_{{\mathit{X}}_{-i}|X_i}\left({\tilde{\mathit{x}}}_{-i}|x_i=1,\mathcal{I}=1\right)$ by

$${\hat{\mathbb{P}}}_{{\mathit{X}}_{-i}|X_i}\left({\tilde{\mathit{x}}}_{-i}|x_i=1,\mathcal{I}=1\right)=\frac{\hat{\mathbb{P}}\left(\mathit{z}\left(\tilde{\mathit{x}}\right)\right|\mathcal{I}=1)}{\sum _{\tilde{\mathit{x}}\in {\mathcal{X}}_{(X_i=1)}}\hat{\mathbb{P}}\left(\mathit{z}\left(\tilde{\mathit{x}}\right)\right|\mathcal{I}=1)},$$ (12)

where $\hat{\mathbb{P}}\left(\mathit{z}\left(\tilde{\mathit{x}}\right)\right|\mathcal{I}=1)$ comes from Eq. (11).

Analogous to the IR model, we denote $N_{i1}^{\left(\mathcal{M}\right)}$ to be the number of individuals with $X_i=1$ who have died or will die from COVID-19. Therefore, $\{N_{i1}^{\left(\mathcal{M}\right)}:i=1,\dots ,q^{\ast }\}$ each follows a binomial distribution

$$N_{i1}^{\left(\mathcal{M}\right)}\sim \text{Binomial}(N_{i1}^{\left(\mathcal{I}\right)},\sum _{\tilde{\mathit{x}}\in {\mathcal{X}}_{(X_i=1)}}\frac{exp({\delta }_0+{\mathit{\delta }}^{\top }\mathit{z}\left(\tilde{\mathit{x}}\right))}{1+exp({\delta }_0+{\mathit{\delta }}^{\top }\mathit{z}\left(\tilde{\mathit{x}}\right))}{\mathbb{P}}_{{\mathit{X}}_{-i}|X_i}\left({\tilde{\mathit{x}}}_{-i}|x_i=1,\mathcal{I}=1\right)).$$ (13)

We then construct the full log-likelihood of $({\delta }_0,\mathit{\delta })$ as the sum of the individual log-likelihoods of $({\delta }_0,\mathit{\delta })$ for $X_i$ corresponding to binomial distribution (13)

$$\mathcal{L}({\delta }_0,\mathit{\delta })=\sum _{i=1}^{q^{\ast }}{\mathcal{L}}_{X_i}^{\left(\mathcal{M}\right)}({\delta }_0,\mathit{\delta }|N_i^{\left(\mathcal{M}\right)},N_i^{\left(\mathcal{I}\right)}).$$ (14)

From the CDPH data presented in Table 1, we have the cumulative number of COVID-19 deaths by gender, age, and race. We denote ${\hat{N}}_{i1}^{\left(\mathcal{M}\right)}$ to be the cumulative number of reported deaths of infected individuals with $X_i=1$ as of October 13, 2020. Analogous to the infection risk model, we assume that the relative size of ${\hat{N}}_i^{\left(\mathcal{I}\right)}$ to $N_i^{\left(\mathcal{I}\right)}$ is approximately equal to the relative size of ${\hat{N}}_i^{\left(\mathcal{M}\right)}$ to $N_i^{\left(\mathcal{M}\right)}$. Substituting ${\hat{N}}_i^{\left(\mathcal{I}\right)}$ for $N_i^{\left(\mathcal{I}\right)}$, ${\hat{N}}_i^{\left(\mathcal{M}\right)}$ for $N_i^{\left(\mathcal{M}\right)}$, and ${\hat{\mathbb{P}}}_{{\mathit{X}}_{-i}|X_i}\left({\tilde{\mathit{x}}}_{-i}|x_i=1\right)$ for ${\mathbb{P}}_{{\mathit{X}}_{-i}|X_i}\left({\tilde{\mathit{x}}}_{-i}|x_i=1\right)$, $i=1,\dots ,q^{\ast }$, in the likelihood (14), we obtain a pseudo-likelihood

$$\tilde{\mathcal{L}}({\delta }_0,\mathit{\delta })=\sum _{i=1}^{q^{\ast }}{\tilde{\mathcal{L}}}_{X_i}^{\left(\mathcal{M}\right)}({\delta }_0,\mathit{\delta }|{\hat{N}}_i^{\left(\mathcal{I}\right)},{\hat{N}}_i^{\left(\mathcal{M}\right)})$$ (15)

and maximize it with respect to $\left({\delta }_0,\mathit{\delta }\right)$ to obtain our estimates

$$\left({\hat{\delta }}_0,\hat{\mathit{\delta }}\right)=\underset{{\delta }_0,\mathit{\delta }}{argmax}\left\{\tilde{\mathcal{L}}({\delta }_0,\mathit{\delta })\right\}.$$ (16)

Lastly, from $\left({\hat{\delta }}_0,\hat{\mathit{\delta }}\right)$, we can obtain the predicted COVID-19 test-based case fatality rates for individuals with gender-age-race covariate setting $\mathit{z}$,

$$\hat{\mathbb{P}}(\mathcal{M}=1|\mathit{z},\mathcal{I}=1)=\frac{exp({\hat{\delta }}_0+{\mathit{z}}^{\top }\hat{\mathit{\delta }})}{1+exp({\hat{\delta }}_0+{\mathit{z}}^{\top }\hat{\mathit{\delta }})}.$$ (17)

3.3. Monte Carlo simulation procedure

To quantify the uncertainty of the T-IR and T-CFR estimates in (8), (17), respectively, we carry out a Monte Carlo procedure that repeatedly performs the T-IR and T-CFR estimation procedures described in Sections 3.1, 3.2 sequentially, introducing sampling variation in the data in three stages. The first stage bootstraps the CHIS data with selection probabilities proportional to the sampling weights. The second stage introduces variation in $\left\{{\hat{N}}_{i1}^{\left(\mathcal{I}\right)}\right\}$ immediately prior to maximizing the pseudo-log-likelihood (6), by simulating values of ${\hat{N}}_{i1}^{\left(\mathcal{I}\right)}$ for each $i$ independently from a binomial distribution with success probability equal to ${\hat{N}}_{i1}^{\left(\mathcal{I}\right)}∕{\hat{N}}_{i1}$, i.e., 

$${\tilde{N}}_{i1}^{\left(\mathcal{I}\right)}\stackrel{ind}{\sim }\text{Binomial}\left({\hat{N}}_{i1},\frac{{\hat{N}}_{i1}^{\left(\mathcal{I}\right)}}{{\hat{N}}_{i1}}\right).$$ (18)

Similarly, the third stage introduces variation in the $\left\{{\hat{N}}_{i1}^{\left(\mathcal{M}\right)}\right\}$ prior to maximizing the pseudo-log-likelihood (15) by simulating values of ${\hat{N}}_{i1}^{\left(\mathcal{M}\right)}$ for each $i$ independently from a binomial distribution with success probability equal to ${\hat{N}}_{i1}^{\left(\mathcal{M}\right)}∕{\hat{N}}_{i1}^{\left(\mathcal{I}\right)}$,

$${\tilde{N}}_{i1}^{\left(\mathcal{M}\right)}\stackrel{ind}{\sim }\text{Binomial}\left({\hat{N}}_{i1}^{\left(\mathcal{I}\right)},\frac{{\hat{N}}_{i1}^{\left(\mathcal{M}\right)}}{{\hat{N}}_{i1}^{\left(\mathcal{I}\right)}}\right).$$ (19)

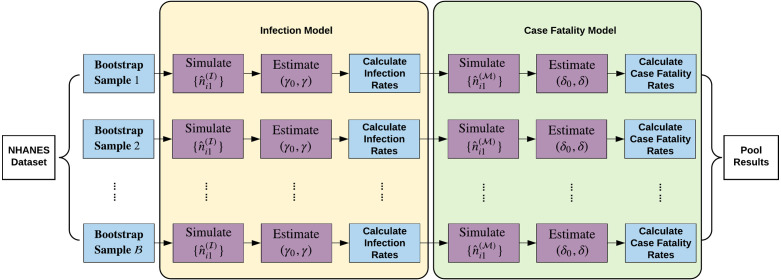
The entire Monte Carlo simulation procedure can be summarized in 5 steps:

Monte Carlo Simulation Procedure
Step 1:	Bootstrap the CHIS dataset with selection probabilities proportional to the sampling weights.
Step 2:	Perform the T-IR estimation procedure, simulating a value of ${\hat{N}}_{i1}^{\left(\mathcal{I}\right)}$ from (18) for each $X_i$, subsequently obtaining estimates $\left({\hat{\gamma }}_0,\hat{\mathit{\gamma }}\right)$.
Step 3:	Using $\left({\hat{\gamma }}_0,\hat{\mathit{\gamma }}\right)$ obtained in Step 2, perform the T-CFR estimation procedure, simulating a value of ${\hat{N}}_{i1}^{\left(\mathcal{M}\right)}$ from (19) for all $X_i$, subsequently obtaining estimates $\left({\hat{\delta }}_0,\hat{\mathit{\delta }}\right)$.
Step 4:	Repeat Steps 1–3 to obtain a total of $\mathcal{B}$ estimates of $\left({\gamma }_0,\mathit{\gamma }\right)$ and $\left({\delta }_0,\mathit{\delta }\right)$, which we denote $\left\{\left({\hat{\gamma }}_0^{\left(b\right)},{\hat{\mathit{\gamma }}}^{\left(b\right)}\right):b=1,\dots ,\mathcal{B}\right\}$ and $\left\{\left({\hat{\delta }}_0^{\left(b\right)},{\hat{\mathit{\delta }}}^{\left(b\right)}\right):b=1,\dots ,\mathcal{B}\right\}$, respectively.
Step 5:	For each set of bootstrap coefficient estimates $\left({\gamma }_0^{\left(b\right)},{\mathit{\gamma }}^{\left(b\right)},{\delta }_0^{\left(b\right)},{\mathit{\delta }}^{\left(b\right)}\right)$, $b=1,\dots ,\mathcal{B}$, estimate the T-IR and T-CFR for covariate setting $\mathit{z}$ using Eqs. (8), (17), respectively.

In Fig. 1, We illustrate the Monte Carlo simulation procedure in a flow chart.

Fig. 1.

Flow chart depicting the Monte Carlo simulation procedure.

3.4. Summary statistics for infection and case fatality rate estimates

In addition to estimating the T-IR and T-CFR for specific covariate settings $\mathit{z}$ through Eqs. (8), (17), respectively, we can provide collapsed estimates of T-IRs and T-CFRs for specific values of any subset $\{X_{j_1},\dots ,X_{j_r}\}$ of $\mathit{X}$. Let $J_r=\{j_1,\dots ,j_r\}$, where $J_r\subset \{1,\dots ,p^{\ast }\}$; ${\mathit{c}}_r=\left(c_{j_1},\dots ,c_{j_r}\right)$, where $c_{j_1},\dots ,c_{j_r}\in \{0,1\}$; and ${\mathcal{X}}_{\left(J_r\right)}^{\left({\mathit{c}}_r\right)}$ denotes the subset of $\mathcal{X}$ with the constraint that $X_{j_1}=c_{j_1}$, …, $X_{j_r}=c_{j_r}$. Estimates of collapsed T-IRs given $X_{j_1}=c_{j_1}$, …, $X_{j_r}=c_{j_r}$ can be obtained using the marginalization formula

$$\hat{\mathbb{P}}(\mathcal{I}=1|X_{j_1}=c_{j_1},\dots ,X_{j_r}=c_{j_r})=\frac{\sum _{\tilde{\mathit{x}}\in {\mathcal{X}}_{\left(J_r\right)}^{\left({\mathit{c}}_r\right)}}\hat{\mathbb{P}}(\mathcal{I}=1|\mathit{z}\left(\tilde{\mathit{x}}\right)){\hat{\mathbb{P}}}_{\mathit{X}}\left(\mathit{z}\left(\tilde{\mathit{x}}\right)\right)}{\sum _{\tilde{\mathit{x}}\in {\mathcal{X}}_{\left(J_r\right)}^{\left({\mathit{c}}_r\right)}}{\hat{\mathbb{P}}}_{\mathit{X}}\left(\mathit{z}\left(\tilde{\mathit{x}}\right)\right)}.$$ (20)

Likewise, collapsed estimates of T-CFRs given $X_{j_1}=c_{j_1}$, …, $X_{j_r}=c_{j_r}$ can be obtained using the marginalization formula

$$\hat{\mathbb{P}}(\mathcal{M}=1|X_{j_1}=c_{j_1},\dots ,X_{j_r}=c_{j_r},\mathcal{I}=1)=\frac{\sum _{\tilde{\mathit{x}}\in {\mathcal{X}}_{\left(J_r\right)}^{\left({\mathit{c}}_r\right)}}\hat{\mathbb{P}}(\mathcal{M}=1|\mathit{z}\left(\tilde{\mathit{x}}\right),\mathcal{I}=1)\hat{\mathbb{P}}\left(\mathit{z}\left(\tilde{\mathit{x}}\right)\right|\mathcal{I}=1)}{\sum _{\tilde{\mathit{x}}\in {\mathcal{X}}_{\left(J_r\right)}^{\left({\mathit{c}}_r\right)}}\hat{\mathbb{P}}\left(\mathit{z}\left(\tilde{\mathit{x}}\right)\right|\mathcal{I}=1)},$$ (21)

where $\hat{\mathbb{P}}\left(\mathit{z}\left(\tilde{\mathit{x}}\right)\right|\mathcal{I}=1)$ comes from Eq. (11).

4. Results

T-IRs and T-CFRs are estimated by our IR (1) and CFR (8) models fit to the California data described in Section 2 and summarized according to Section 3.4. All standard errors were computed using the bootstrapping method with sample size the same as the CHIS data as 45,369 and the number of replicates as $\mathcal{B}=100$. As a baseline estimate, we assume an estimated overall California COVID-19 infection rate ${\hat{\pi }}_{\mathcal{I}}$ equal to the cumulative test-based positive rate as 5.2% (855,072/16,425,487), which is the ratio of total confirmed cases and total tests in California as of October 13, 2020 (California Department of Public Health, 2020a). However, there is still substantial uncertainty surrounding the true COVID-19 infection rate primarily due to the lack of testing and the large prevalence of asymptomatic cases. Recent studies suggest that the true overall infection rate in the U.S. is much higher than what was initially hypothesized (Bendavid et al., 2020, Sutton et al., 2020).

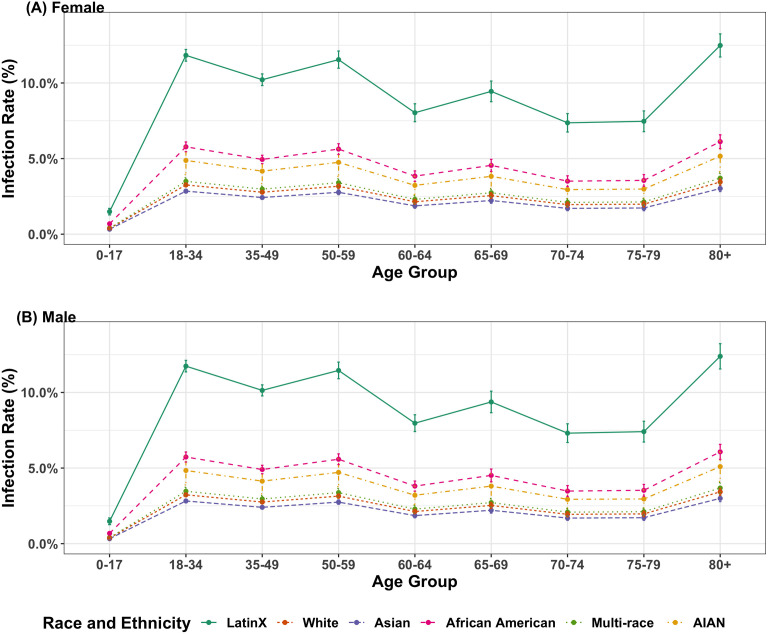
Fig. 2 depicts T-IR estimates and error bars indicating two bootstrap standard errors (SEs) for different combinations of gender and age group under the assumption of an overall California infection rate of 5.2%. The T-IR estimates range from 0.3% to 12.5% for females and 0.3% to 12.4% for males, which is almost the same. It is because both the infection cases of COVID-19 and the gender ratio in California are quite balanced. Six different race/ethnicity groups have been presented including LatinX/ Hispanic (LatinX), White/ Caucasian (White), Asian, African American/Black (AA), Multi-Race, and American Indian or Alaska Native (AIAN). LatinX has the highest T-IRs, followed by African Americans. Population aged 80 and older have higher T-IRs compared with other age groups across race/ethnicity groups. The people in age groups of 18–34, 35–49, and 50–59 share a relatively higher T-IRs comparing with teenagers and senior citizens, except for the population aged 80 and above. Meanwhile, T-IRs were non-monotonic, with age groups 60–64 and 70–74 having slightly lower T-IRs than the preceding age groups, 50–59 and 65–69 respectively.

Fig. 2.

Estimated test-based infection rates given age and race/ethnicity, stratified by gender. ((A) and (B) present the bootstrapped mean infection rates for female and male respectively. Only 6 racial and ethnicity groups are considered in the figures, including LatinX/ Hispanic (LatinX), White/ Caucasian (White), Asian, African American/Black (AA), Multi-Race, and American Indian or Alaska Native (AIAN). The overall infection rate was assumed to be 5.2%, and the error bars denote two bootstrap standard errors.).

We also considered alternate values for the overall California IR. Table 4 presents the point estimates and associated two SE intervals of the marginal T-IRs for gender and age group obtained from marginalization formula (20) using three types of test-based positive rates as the assumed overall IRs. In addition to the cumulative positive rate stated above as 5.2%, Coronavirus Resource Center provides a 7-day average daily positive rate as 2.7% for California and a cumulative positive rate for the U.S. as 6.1% as of October 14, 2020 (Coronavirus Resource Center at Johns Hopkins University & Medicine, 2020a, Coronavirus Resource Center at Johns Hopkins University & Medicine, 2020b). The 7-day average daily positive rate stands for the rolling average of 7 daily positive rates for testing, while cumulative positive rates are calculated by taking the ratio of the total confirmed cases and the total number of testings. Due to misleading peaks resulting from the limited test capacity and uneven reporting cadences, the 7-day average daily positive rate is also considered here. The estimated marginal T-IRs for gender, age groups, and race and ethnicity groups are consistent with the results presented in Fig. 2, including males and older individuals having higher estimated T-IRs.

Table 4.

Estimated marginal test-based infection rates of each risk group with different overall infection rates.

Variable	Category	Default infection rate (Mean $\pm$ 2 SE)
		2.7%	5.2%	6.1%
	Overall	2.68% (0.00%)	5.16% (0.01%)	6.06% (0.01%)
Gender	Male	2.66% (0.02%)	5.13% (0.05%)	6.02% (0.05%)
	Female	2.70% (0.02%)	5.19% (0.04%)	6.09% (0.05%)
Age group	0–17	0.96% (0.02%)	1.85% (0.04%)	2.18% (0.04%)
	18–34	4.08% (0.07%)	7.86% (0.14%)	9.22% (0.16%)
	35–49	3.48% (0.07%)	6.69% (0.14%)	7.85% (0.15%)
	50–59	3.16% (0.08%)	6.09% (0.16%)	7.14% (0.19%)
	60–64	2.11% (0.07%)	4.06% (0.14%)	4.76% (0.17%)
	65–69	2.16% (0.11%)	4.17% (0.20%)	4.89% (0.23%)
	70–74	1.70% (0.08%)	3.27% (0.17%)	3.84% (0.19%)
	75–79	1.53% (0.08%)	2.95% (0.15%)	3.46% (0.19%)
	80$+$	2.48% (0.12%)	4.77% (0.23%)	5.60% (0.27%)
Race & Ethnicity	LatinX	4.10% (0.05%)	7.90% (0.10%)	9.27% (0.12%)
	White	1.24% (0.02%)	2.39% (0.03%)	2.81% (0.04%)
	Asian	1.09% (0.03%)	2.10% (0.05%)	2.46% (0.06%)
	AA	2.22% (0.09%)	4.27% (0.19%)	5.01% (0.21%)
	Multi-race	1.08% (0.07%)	2.08% (0.12%)	2.44% (0.15%)
	AIAN	2.21% (0.43%)	4.23% (0.80%)	4.98% (0.98%)
	Other	32.61% (2.96%)	62.97% (5.74%)	73.90% (6.72%)

Table 5 presents the point estimates and associated two SE intervals of the bootstrap estimated marginal T-CFRs obtained from marginalization formula (21), assuming an estimated overall infection rate of ${\hat{\pi }}_{\mathcal{I}}=5.2\text{\%}$; T-CFR estimates do not vary in expectation for different values of ${\hat{\pi }}_{\mathcal{I}}$. Males have an estimated mean T-CFR 0.70% higher than females (2.51% and 1.81%), and estimated T-CFRs increase with age, ranging from less than 0.07% for the 0–34 age group to over 26.68% for the 80+ age group. Among six race and ethnicity groups, Asian, African American, and White are high-risk groups with point estimated T-CFRs as 4.55%, 3.86%, and 3.74% respectively. Other, LatinX and Multi-race subgroups have T-CFRs below the overall 1.95% T-CFR for California.

Table 5.

Estimated marginal test-based case fatality rates of each risk group.

Variable	Category	Case fatality rate (MEAN $\pm$ 2 SE)	Observed death rate (from Table 1)
Overall	Overall	2.15% (0.02%)	1.95%
Gender	Male	2.51% (0.04%)	2.27%
	Female	1.81% (0.04%)	1.63%
Age group	0–34	0.07% (0.01%)	0.07%
	35–49	0.49% (0.03%)	0.44%
	50–59	1.64% (0.07%)	1.49%
	60–64	3.63% (0.18%)	3.28%
	65–69	6.37% (0.28%)	5.80%
	70–74	9.91% (0.48%)	9.03%
	75–79	14.34% (0.58%)	13.15%
	80$+$	26.68% (0.51%)	24.79%
Race & Ethnicity	LatinX	1.71% (0.03%)	2.17%
	White	3.74% (0.08%)	4.73%
	Asian	4.55% (0.17%)	5.74%
	AA	3.86% (0.20%)	4.85%
	Multi-race	1.46% (0.28%)	1.85%
	AIAN	2.38% (0.72%)	3.04%
	Other	0.22% (0.04%)	0.28%

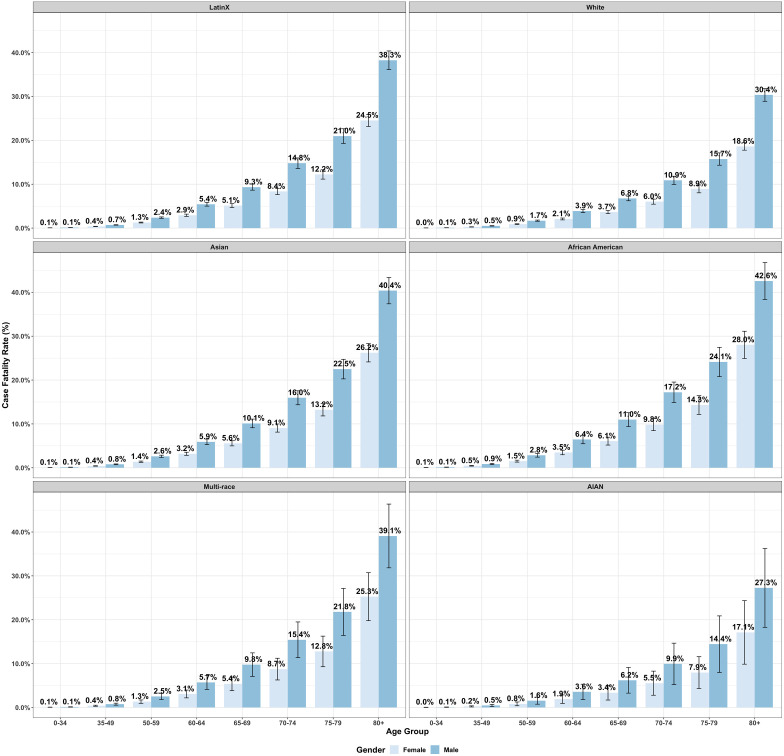
Fig. 3 presents the estimated T-CFRs, obtained from formula (21), with error bars displaying two SEs of uncertainty for different combinations of gender and age groups, stratified by six race and ethnicity groups as shown in Fig. 2. Males have higher estimated T-CFRs than females across all age-race levels, and the estimations and the gender gap increases with age, which shows a different pattern comparing with the T-IR estimations. African American female even has a higher T-CFRs than AIAN, and slightly lower T-CFRs than White male for each age group correspondingly.

Fig. 3.

Estimated test-based case fatality rates by age and gender, stratified by race/ethnicity. (The bootstrap mean case fatality rates are presented separately for LatinX, White, Asian, African American, Multi-Race, and AIAN groups. The overall infection rate was assumed to be 5.2%, and the error bars denote two bootstrap standard errors.).

Besides, African Americans and Asians have higher estimated T-CFRs than other race groups in general across different age groups based on the stratified results. CHIS dataset indicates that Asians have a higher proportion of elderly people (i.e. the high-risk age groups 75–80 and 80+) than the African Americans. Therefore, although Asians have a higher overall estimated T-CFR than African Americans shown in Table 5, the ranks are flipped due to different age distributions for two race/ethnicity groups, which is an example of Simpson’s paradox. Similarly, the multi-race has higher estimated T-CFRs at each age group compared with the LatinX and White, while the overall estimation is a bit lower. The Multi-races are younger than the Whites in California. For example, we can compare the number of adults (18 and above) and the number of children and adolescents (0 to 17 years old) within each race and ethnicity group. An overall adult–child ratio is defined as the total number of adults over that of children and adolescents ignoring race and ethnicity groups. Multi-race population in California has 0.43 times the overall adult–child ratio (1.7% of adults and 4% of children and adolescents), while it is 1.3 times the overall adult-child ratio for the White population (38.8% of adults and 29.2% of children and adolescents) (California Department of Public Health, 2020c). Since the T-CFRs increase with the age, a higher adult-child ratio in the age structure for Multi-race leads to a higher marginal T-CFR. The case still holds when we have multiple age groups. Meanwhile, the small proportions of Multi-race and AIAN in the general population also result in large error bars.

5. Discussion

In this paper, we combined aggregate COVID-19 case and fatality data with population demographic data in a pseudo-likelihood based multivariable logistic regression approach for obtaining early estimates of COVID-19 T-IRs and T-CFRs for subgroups of the California population. Overall, our models uncover and compare the test-based infection rates and case fatality rates across risk groups with different combinations of age, gender, and race/ethnicity. Our results revealed that males, the elderly, and LatinX are marginally at a relatively higher risk of COVID-19 infection. The workforce population with age from 18–59 have a higher infection rate comparing with children, adolescents, and other senior citizens, except for people in their 80 and above. One possible reason is that more workforce population have been back to work already and therefore they have more exposure to the COVID-19 virus, while the older workforce group (i.e. age group 60–64) and retired population (i.e. with age 65 and above) tend to be more flexible to keep the social distance. Besides, the results of the CFR model indicate that males, the elderly, Asians, Africa Americans, and Whites are marginally at elevated risk of mortality after COVID-19 infection. However, due to the imbalance in the age distribution of different races in California, the subgroups with the top 5 T-CFRs are all-male groups with race as African American, Asian, Multi-race, LatinX, and White for each age group, followed by African American females. The pattern of estimated T-CFRs matches with the observations in other studies on COVID-19 mortality (see, e.g. Yehia et al., 2020, Gu et al., 2020, Golestaneh et al., 2020). The difference in T-CFRs across different races may partially be explained by pre-existing diseases. Previous research has (e.g. Yehia et al., 2020, Gu et al., 2020) shown that non-Hispanic Black/African-Americans patients were disproportionately affected by obesity and kidney disease, which has been proved to have a significant positive association with a high mortality rate for COVID patients. Overall, therefore, African Americans are the race/ethnicity group most vulnerable to COVID-19 in California. We also found that the elevated infection and mortality risk for males and the greater mortality risk for all races increase with age.

We propose a model to estimate the infection and case fatality rates for population subgroups defined by combinations of demographic characteristics through publicly available stacked data and population-level demographic survey data in this work. We estimate infection and case fatality rates for COVID-19 for different population subgroups through the proposed method. Here, we provide a further discussion on the estimates of coefficients in the proposed model. Since we consider as many risk factors as possible in the model to increase the precision of estimation, we might include risk factors that are highly correlated with each other, causing multicollinearity. Multicollinearity does not influence the estimated infection and case fatality rates for population subgroups, but it can affect the coefficients in the model. Hence, the estimates of coefficients ${\lambda }_0,\lambda$ and ${\delta }_0,\delta$ might be biased, and we do not recommend the proposed method for research on analyzing the effect of individual risk factors.

The proposed methods are subject to three general limitations. First, the analysis is based on publicly available test-based infection rates and case-fatality rates. It has been well documented that the lack of testing for COVID-19 in the U.S. has hindered efforts to estimate the true COVID-19 infection rate. Further compounding this issue is the high prevalence of asymptomatic COVID-19 cases. These two issues may lead to substantial underestimates of the infection rates and/or substantial overestimates of the case fatality rates from our analyses. Second, race/ethnicity is missing in 30% of the reported cases from CDPH as of October 13, 2020, which is a considerable amount that weakens the rationality of assuming race and ethnicity data is missing at random. A violation of the missing at random assumption might introduce substantial bias in our estimates of T-IR and T-CFR. However, it is hard to analyze the missing pattern for stacked data, which does not provide any information at individual level. So we have limited statistical tools and extra information to reduce the impact of a high missing rate on the inferences of our model. Moreover, the case and fatality data released by CDPH provide marginal summary statistics for a subset of risk factors, and we do not have direct information on the joint distribution of all risk factors. Although the central goal of our proposed methods is to circumvent this limitation, the absence of direct multivariate information on the risk factors of COVID-19 infection and mortality as well as the sampling bias should be taken into account when interpreting the results of our models. Third, in this paper, we do not consider regularity conditions ensuring concavity associated with the pseudo-log-likelihood functions constructed in Eqs. (6), (15), nor do we examine the asymptotic properties of the parameter estimates in Eqs. (7), (16). Future research investigating the mathematical theory of the proposed methods is warranted.

Another promising avenue for future work is combining this method with a COVID-19 prediction model (Watson et al., 2020) to provide detailed demographic projections of COVID-19 cases and mortalities. This would be a substantial improvement over most COVID-19 prediction models, as they tend to be quite limited in their ability to forecast the demographic characteristics of the infected.

In summary, this paper provides a pragmatic tool for producing early estimates of COVID-19 T-IRs and T-CFRs for the California population, which offer valuable information to guide health policies concerning the control and prevention of COVID-19. In addition, our methods can be generalized into a general framework for early estimation of subpopulation IRs and CFRs from aggregate case and fatality data in other locations and for future epidemics.

CRediT authorship contribution statement

Di Xiong: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data curation, Writing - original draft, Visualization. Lu Zhang: Methodology, Software, Validation, Formal analysis, Data curation, Writing - original draft. Gregory L. Watson: Methodology, Software, Writing - original draft. Phillip Sundin: Investigation, Software, Writing - review & editing. Teresa Bufford: Investigation, Software, Writing - review & editing. Joseph A. Zoller: Software, Writing - review & editing. John Shamshoian: Software, Writing - review & editing. Marc A. Suchard: Conceptualization, Software, Writing - review & editing. Christina M. Ramirez: Conceptualization, Investigation, Writing - original draft, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.