Modeling the coronavirus disease 2019 pandemic: A comprehensive guide of infectious disease and decision-analytic models

What is new?

• •This commentary discusses the different types of models that are being used to support planning for coronavirus disease 2019 (COVID-19).
• •The commentary uses a previously proposed taxonomy to compare and contrast different types of models (dynamic transmission modeling vs. decision-analytic modeling) and modeling techniques for readers to assess the tradeoffs.
• •We highlight challenges with modeling in the early phases of the pandemic, and the need for local data availability and early collaboration between researchers and decision-makers.
• •This article highlights the intersection of infectious disease modeling and decision-analytic modeling to support decision-making through an example from Ontario, Canada.

1. Introduction

The coronavirus disease 2019 (COVID-19) pandemic has prompted many countries to rapidly implement public health interventions to mitigate spread and reallocate health care resources to prevent overwhelming their health care systems. Models play a critical role in informing pertinent policy questions such as: What impact will physical distancing have on the number of expected cases and deaths? When do we expect the peak? Will we have sufficient health care system capacity? What is the best combination of strategies, and how does the optimal combination vary over populations and by stages of a local epidemic? A wide range of model types is used to answer these questions, including forecasting, quantifying trade-offs, explanatory modeling, intervention modeling, and economic evaluation.

Models are a simulated and simplified representation of the real-world. For the COVID-19 pandemic, a nonpeer-reviewed summary of current models, conducted by the Center for Evidence-Based Medicine (CEBM) from the University of Oxford, identified 43 models indexed on PubMed, and 13 released separately by Imperial College London. The review focused only on epidemic models projecting severe acute respiratory syndrome coronavirus 2 (SARS-CoV2) transmission and epidemic trajectory of COVID-19 in various settings. CEBM reported a substantial variation among models with respect to their input parameters and estimates of case fatality rate [1]. In addition to models that simulate transmission of SARS-CoV2, there are others that have been developed to predict the impact of COVID-19 on acute care resources, the need for personal protective equipment and other resources [2]. The variety of models used during this pandemic may be a source of confusion for those unfamiliar with modeling.

In this commentary, we draw on a previously proposed model taxonomy to highlight the different infectious disease and decision-analytic model types. We describe the conceptualization of these models, benefits and limitations, and outline some of the challenges based on our experience in Ontario, Canada.

2. Model taxonomy

Multiple model taxonomies exist, while some are specifically for infectious diseases [[3], [4], [5]], others capture a broader range of model types. Here, we use a previously proposed taxonomy that can accommodate decision-analytic and infectious disease models [6]. We use this taxonomy's three broad criteria: individual level vs. cohort level, with vs. without interaction, and discrete vs. continuous time.

2.1. Cohort vs. individual level

Cohort models stratify a population of individuals into mutually exclusive health states or compartments. Members of a given health state are assumed to be homogenous with respect to the risk of subsequent events. Cohort models are configured to follow entire populations over time and allow for changing event probabilities or rates to accurately reflect disease progression or the influence of time on the risk of events. An important assumption is that future behavior of individuals depends only on the present health state and transition probabilities (i.e., past events are not remembered). While cohort models require less data, and save computational costs, they typically consider population averages and are unable to explore individual heterogeneity with respect to risk factors and also variations in individual outcomes due to chance and complex network effects.

Individual-level models simulate everyone separately as they progress through health states, with each simulated person having heterogeneous characteristics (e.g., age, comorbidities, and risk factors) which may change the risk of subsequent events. Individual-level models generally require more data and are more computationally intensive than cohort models. Stochasticity, or randomness, can be incorporated in these models so that each individual's probability of subsequent events is randomly determined, reflecting uncertainty from random processes (e.g., if the probability of being admitted to hospital due to COVID-19 is 0.2, and individual patient may or may not be admitted; however, at the population level approximately 20% of patients would be admitted to hospital). Each stochastic model simulation produces a different result, but over a large number of simulations, the results should converge to the average result from a deterministic model. Stochastic models are especially useful modeling rare events, or small populations, when uncertainty due to chance can have a large effect, for example, superspreader events. Key reasons for selecting an individual-level model over a cohort model are: to easily capture additional layers of modeled heterogeneity among individuals (e.g., age and sex) and environmental characteristics (e.g., household composition and workplace); to capture uncertainty due to random processes; and to use individual-level data and history of events to determine future risk for events [6].

2.2. With or without interactions

The second aspect is whether the model allows for interactions and feedback loops. Interactions may refer to contacts between people leading to chains of transmission in the context of infectious diseases. With interactions, a case becomes a risk factor for other individuals and creates a feedback loop between prevalent and incident infections. Modeling with interactions is especially important for infectious diseases, the spread of which relies on interaction for individual-level models. In deterministic compartmental models, these interactions are not formally modeled but can be built into equations with prespecified parameters. Interactions can also refer to individuals with their environment, such as competition among individuals for resources. For example, if infected cases admitted to hospital exceed available acute system resources, this results in queuing among subsequent cases and delayed care.

2.3. Discrete vs. continuous time

The third aspect is how time is incorporated. Discrete-time models divide time from the beginning of a simulation into equally long time segments. Transitions among health states or compartments are assigned a distinct value at each point in time. Continuous time models view variables as having a value at any infinitesimally short amount of time (i.e., time is not distinct). Transitions among compartments are assigned instantaneous rates which are often calculated as systems of differential equations.

3. Infectious disease models

3.1. Phenomenological models

Phenomenological models are commonly used for estimating the time-variant reproductive ratio at time point t, Rt (i.e., the average number of secondary infections per infectious individual at any given point in time) and near-forecasting in real time. Such models do not simulate the causal pathway of transmission. Phenomenological models use observed data from one time step, with an understanding of key biological properties such as generation time of an infectious disease, to project expected number of cases at the next time step. A benefit of these models is that they use very few parameters alongside observed cases to project forward without causal mechanisms [7,8]. Examples are provided in Box 1 .

Box 1. Glossary of model types mentioned in commentary.

Term	Definition
Agent-based models	Also referred to as individual-level models. See “Individual-level models” for definition.
Compartmental models	Compartmental models are cohort-based transmission dynamic models that involve interaction and usually treat time as continuous. The biological structure is applied to homogenous groups of individuals (compartments), which can be further stratified across other domains. Examples include SIR and SEIR models among the many.
	Also referred to as cohort-level models.
Decision-analytic models	Decision analytic models are used to analyze decisions under uncertainty. This group of models include decision trees, Markov cohort models, state-transition models, and discrete event simulation models.
	Also referred to as health economic models if used for economic evaluations.
Deterministic models	A model where random processes and uncertainty due to random chance of events are not captured. Each simulation will result in identical average results. Deterministic model results are often viewed as the average of many stochastic model simulations.
Discrete event simulation (DES) models	Discrete event simulation models are individual-level models that simulate events at a particular point in time. These models involve interaction, generally between individuals and their environment, and treat time as continuous. They require extensive individual-level time-to-event data.
Individual-level models	Individual-level models are dynamic models allowing for interactions between individuals to produce a complex network effect.
	In individual-level infectious disease models, the biologic structure, demographic characteristics, and risk factors are applied at the individual level, so that natural history, risk level, and contacts/interactions can vary between people.
	Also referred to as agent-based models.
	In individual-level decision-analytic models, the probability of transition, risk for events, or time-to-event apply to each individual. Each simulation represents an individual, often introducing heterogeneity and stochasticity.
	Sometimes referred to as microsimulations.
Phenomenological models	Phenomenological models are commonly used for estimating the time-variant Rt (effective reproductive number), and near-forecasting in real time. Such models do not simulate the causal pathway of transmission.
	These models have been used to estimate time-varying reproduction numbers during epidemics for measles (Germany, 1861), pandemic influenza (USA, 1918), smallpox (Kosovo, 1972), SARS (Hong Kong, 2003), and pandemic influenza (USA, 2009) [9].
	Examples of phenomenological models include regression analyses or statistical model, branching processes, and renewal equation models. Branching process is a mathematical process where nodes (which represent infected individuals) give rise to other nodes to show an infection tree. The probability of nodes proliferating or diminishing is described by statistics and mathematics. Renewal equation models use an equation that defines the relationship between the number of new infections as being proportional to the number of prevalent cases and their infectiousness.
SEIR	A type of infectious disease compartmental transmission model with the compartments: Susceptible, Exposed, Infectious, and Recovered.
SEIRS	A type of infectious disease compartmental transmission model with the compartments: Susceptible, Exposed, Infectious, Recovered, and Susceptible (again).
SIR	A type of infectious disease compartmental transmission model with the compartments: Susceptible, Infectious, and Recovered.
SIRS	A type of infectious disease compartmental transmission model with the compartments: Susceptible, Infectious, and Recovered, and Susceptible (again).
State-transition models	Simulations (or expected value calculations) conceptualized in terms of health states, transitions, and transition probabilities. The most common types are Markov cohort models and individual-level state-transition models.
Stochastic model	A model that captures uncertainty due to random chance. Each stochastic model simulations produce different results (realizations), but over a large number of simulations, they should converge to the average result generated from a deterministic model. Stochastic models are especially useful when events are rare or if there are smaller populations; when uncertainty due to chance can have a large effect.
Transmission dynamic models	Models for infectious disease transmission explicitly capture interactions and feedback loops as mechanisms of infectious diseases dynamics

All provided definitions and examples are adapted from Gambhir et al. [4], Mishra et al. [5], Cori et al. [9], Fraser et al. [10], Thompson et al. [11] Please refer to these papers for more details about infectious disease modeling.

3.2. Transmission dynamic models

Models for infectious disease transmission explicitly capture interactions and feedback loops as mechanisms of infectious disease dynamics [3,12]. Transmission dynamic (TD models can be used for forecasting (e.g., number of cases and deaths and final outbreak size) [13], explanatory modeling (e.g., identifying mechanistic areas of uncertainty), estimating epidemic characteristics [14], assessing interventions (e.g., vaccines, public health interventions, and treatment), and for economic evaluations [15].

TD models are abstractions of the natural history of an infectious pathogen as it passes between people and moves through a population. The basic biological structure is that of S-I (susceptible and infectious), but various structures are possible depending on the characteristics of the pathogen, such as whether there is a period of time wherein a person may be infected but not yet infectious, usually called an “exposed” or “latent” period or whether reinfection is possible. Common structures include Susceptible, Infectious, and Recovered (SIR) [16], Susceptible, Exposed, Infectious, Recovered (SEIR), and others where individuals can return to the susceptible compartment (e.g., SEIRS). The key decision points surrounding the development of the biological structure is specified by how the pathogen plays out in the host. Such decisions are often challenging in the setting of emerging infectious diseases such as SARS-CoV-2 until key biological properties (e.g., presymptomatic transmission) are available. A key component of these models includes the mixing pattern across each of these domains (biological, demographic, and risk level) with respect to contact encounters. Subsets of a population (e.g., regions or neighborhoods) can be linked via mixing matrices or by proxy measures such as travel patterns or spatial distance between regions. TD models are considered mechanistic models because they simulate the mechanisms of the feedback loops. TD models can be compartmental (cohort level) or individual level.

3.3. Compartmental transmission dynamic models

Compartmental TD models are cohort-based, involve interaction, and usually treat time as continuous. The biological structure is applied to homogenous groups of individuals (compartments), which can be further stratified across other domains including demographic (e.g., age- and/or sex-stratified) and infection risk level (subgroups with higher contact rates or who cannot self-isolate). Compartmental TD models can be deterministic or stochastic. Deterministic models generate an average trajectory for each set of data inputs, whereas stochastic models allow several “epidemic realizations.” The average of many stochastic realizations approximates that of a deterministic model. Stochastic simulations are well suited for small populations or when there are few cases.

3.4. Individual-level transmission dynamic models

If TD models simulate individuals, they are referred to as agent-based or individual-level models and usually treat time as discrete. In individual-level TD models, the biologic structure, demographic characteristics, and risk factors are applied at the individual level, so that natural history, risk level, contacts/interactions can vary between people [17]. These interactions can produce complex network effects. The benefits of an individual-level TD model, despite added complexity, are added layers of heterogeneity, ability to incorporate stochasticity (i.e., they can still be deterministic), and better capture of emergent phenomena such as specific transmission dynamics (e.g., superspreader or rare events). However, individual-level TD models require extensive individual-level data for each characteristic under consideration and are resource-intensive to develop, calibrate (i.e., to reproduce population-level network features), and analyze [18,19].

4. Health system models in the context of a pandemic

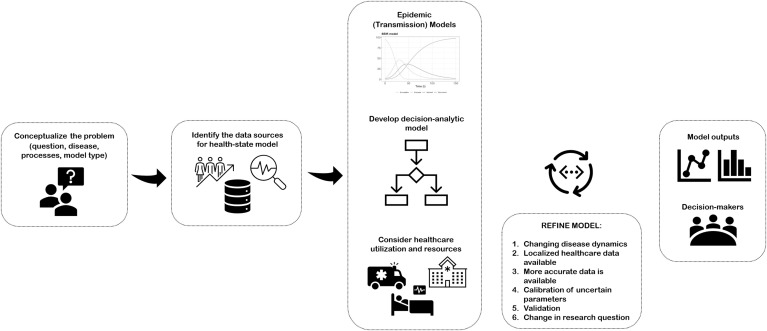
Phenomenological and TD models inform one part of pandemic planning by forecasting the potential rate of increase, time to peak and ultimate magnitude of local outbreaks, and the effect of public health interventions on flattening the epidemic curve [[20], [21], [22]]. Another key element of pandemic planning is preparing the health system response, which will be more accurately modeled using synergistic modeling of the health system alongside TD models (Fig. 1 ). Health system models, commonly using decision-analytic tools, can forecast health care utilization, patient outcomes over time, dynamic resource constraints, queuing and priority setting, and the consequences of resource constraints. These models can be useful in the early stages of a pandemic and can be used to answer future-minded health system questions such as restarting clinical services that were curtailed.

Fig. 1.

Conceptualizing a health system model for pandemic planning.

4.1. Decision-analytic models

Decision analysis is the application of systematic, quantitative, and transparent methods to analyze decisions under uncertainty [23]. These models often incorporate multiple aspects of the decision problem, including epidemiology, dynamic populations, patient characteristics, disease progression, and resource utilization.

State-transition models are simulations (or expected value calculations) conceptualized in terms of health states, transitions, and transition probabilities. They are the most common type of decision-analytic models and include Markov cohort- and individual-level models [24]. Individual-level models are often useful for resource constraint and capacity planning purposes in a pandemic due to its ability to capture interaction and dynamics of transmission.

4.2. Individual-level state-transition models

Individual-level state-transition models allow each individual with unique characteristics to traverse any number of health states (e.g., healthy, sick, and dead) and treat time as discrete. They can include a dynamic population (i.e., people entering and leaving the model to accommodate interaction with the environment), incorporate stochasticity (randomness), capture dynamics of transmission, and provide individual-level outcomes based on heterogeneity in the base-case analysis [24,25]. Individuals can be modeled in parallel, allowing them to interact with each other (i.e., contribute to transmission) and compete for resources, which, if unavailable, may result in adverse outcomes [24,26]. While these models are flexible, its complexity and need for multiple data sources can lead to the possibility of competing risks [25,27].

4.3. Discrete event simulation

Discrete event simulation (DES) models are individual level, involve interaction, generally between individuals and their environment, and treat time as continuous [28]. The main concepts of DES models include entities (e.g., patients), attributes (e.g., patient characteristics), events, resources, queues, and time. DES models involve time segments as well but, unlike state transition models, the length of each time step is variable and continuous. A given step involves the movement of an individual from one discrete event (e.g., arrival at an emergency department) to another (e.g., admission to critical care). DES models are also flexible and computationally efficient. However, one major limitation is its extensive requirement of time-to-event data [29], which is unlikely to be available early in an outbreak.

4.4. Conceptualizing a health system model for pandemic planning

In Box 2 , we describe steps to conceptualize a health-system model for pandemic planning, which were adapted from the International Society for Pharmacoeconomics and Outcomes Research & Society of Medical Decision Making Modeling Good Research Practices Task Force [30]. For conceptualization of compartmental model, refer to “An introduction to infectious disease modeling” by Vynnycky et al. [31]. An example for Ontario, Canada is described in Box 3 .

Box 2. Conceptualizing a health system model for pandemic planning.

Step	Description
[1] Develop the research question and assess available data	•The question that the model ultimately answers will determine what data and type of model will be required. For example, in a health system model for pandemic planning of health care resources, the model would need to start at the time where the patient first contacts the health care system. •This model would simulate patient flow in the hospital (facility) due to COVID-19 and identify resource constraints and all potential health outcomes (death). Because resource constraints require individual interaction, Markov cohort models and decision-tree models are inadequate choices.
[2] Selecting a decision-analytic model	•Due to the unique nature of a pandemic (sudden, limited data, and uncertainty) and the understanding that models are highly data-driven, model selection is very important to timeliness of evidence. •While discrete event simulation (DES) models would be traditionally used for resource constraints, a discrete-time, dynamic, individual state-transition model is also appropriate given the likely lack of time-to-event data required to build a DES model. •This model's population of interest should be dynamic following observed case data. •This can usually be incorporated by integrating the decision-analytic model with a transmission model component or simple short-term forecasting of daily incidence rates of cases from epidemic curves. •An appropriate time horizon and time measurement (daily time steps) should also be considered.
[3] Mapping out disease progression and patient pathway through health system	• The model's schematic and patient trajectory should consider: • The health care facility's resources, • All potential disease progression pathways for patients presenting with the disease, and • Logic on how to resolve resource constraints and queues in accordance with clinical practice.
[4] Selecting the outcomes to report	• This is usually informed by the research question. Outcomes to inform pandemic planning can include: • the number of hospitalizations, • days until resource depletion (ward beds, intensive care unit (ICU) beds, and ventilators), • resources required (beds, personal protective equipment, and medication), and • health outcomes, for example, mortality, associated with resource constraints. •Additional outcomes that can be reported include patient-specific outcomes (e.g., quality-adjusted life years) and costs.
[5] Refining the model	•Steps 1 to 4 are similar to those described in the literature [30]. However, modelling pandemics is a unique challenge due to the constantly changing environment. •After developing the model and running analyses, the model will need to be refined when higher quality data is available and when questions being addressed change. •Initially, the model will likely address the consequences (magnitude and speed) of the outbreak, but then turn to understanding how to sustain adequate health care, and finally how to plan normalization as the outbreak is controlled.

Box 3. COVID-19 example in Ontario, Canadaa.

Steps	Description
Model selection	•At the beginning of the epidemic in Ontario, we developed a dynamic, discrete-time, individual-level state-transition model [2] informed by data from the epidemic in China. •We used data from published observational studies for disease progression and health care needs (e.g., needing mechanical ventilation) [32,33].
Data sources and challenges	•As the pandemic evolved, the model was refined using data from the epidemic in Italy [34], and as local evidence emerged, Canadian-specific data [35]. •Because of different populations, health care systems, and medical practices, we acknowledge that the use of other jurisdictions' data to inform the model can be misleading but is the only practical solution at the earliest phases of an outbreak. •Model assumptions and data sources need to be clearly explained, and the model was refined as local data became available. •For pandemic trajectories, that is, predicted cases over time, initial projections had to be based on observed data from other countries (Italy and South Korea) [36] but were updated to Ontario's expected cases using the integrated Public Health Information System (iPHIS) database as the epidemic in Ontario continued. •Data availability and quality is a major challenge during an outbreak (e.g., changes in case definitions, testing criteria, reporting, right censoring, especially for clinical data). •However, modelling for pandemic planning needs to find a balance between perfect data and timeliness of generated evidence from the model.
Refining the model	•As more data becomes available, calibration of uncertain parameters can be conducted (e.g., probability of ward and intensive care unit (ICU) admissions in Ontario). • Calibration is a technique comparing model outputs with an independent data set (e.g., observed data), also known as calibration targets, to explore variations of an uncertain model parameter to provide a better fit of the model [37]. •Another method to improve model credibility and accuracy is through model validation. •Some forms of validation include face validity, where experts confirm whether the model reflects their understanding of the disease and patient pathways, and external validity, where model results are compared with actual event data [38].

^aThis box describes the COVID-19 Resource Estimator model developed by COVID-19-MC [2].

5. Challenges

A common aphorism is: “All models are wrong, but some are useful” [39]. Models are useful when they are driven by a specific question for which the model is well designed to answer. After framing the modeling question, the challenges thereafter are often driven by data availability and the timeliness of providing information for decision makers.

5.1. Timing vs. comprehensiveness

Models can provide qualitative insights and quantitative projections. Both are highly data-driven, depending on data which are typically sparse, right censored, and reported in aggregate without comprehensive detail (e.g., demographic, clinical, and biological features) in early phases of an outbreak. Thus, simpler models often predominate in the early phase of an epidemic, with data borrowed from what was known before. With COVID-19, early analyses based on experience elsewhere, especially in the absence of local data, were used to explore “what-if” scenarios in local jurisdictions. These scenario-based analyses were helpful because while they borrowed heavily from estimated reproductive rates from other settings, they provided decision makers with initial estimates of best and worst-case scenarios in the absence of further action.

In the context of modeling for an emerging infectious disease, there will remain a tension between comprehensiveness and timeliness of model-based information for decision makers: a simple model developed quickly, albeit with recognized caveats may be more useful to the response than a detailed model completed after the worst of the pandemic has passed. The key is clarity in how the modeling question is framed, how model outputs are interpreted, and transparency around the justification for model selection and data inputs.

5.2. Data availability and quality

Local or regional data is critical at all phases of the pandemic. Data components that are especially important include:

• aInfection/transmission (e.g., reported cases and deaths, proportion of those confirmed positive through diagnostic testing, and presenting to the hospital).
• bResource use (e.g., length of stay and health care utilization).
• cDisease progression (e.g., proportion of patients transitioning to ICU (deteriorate), proportion of ICU patients needing a ventilator, proportion of patients recovering, and time to all events).
• dDemographics (e.g., age, sex, gender, and comorbidities).

Often, health system and transmission modelers do not have this real-time data, which highlights the importance of close collaborations between decision makers and modelers [15]. In the context of modeling to support a pandemic response, there is considerable strength in defining questions and interrogating the data and model assumptions in partnership with stakeholders who may use the modeling results. Beyond their role as knowledge users, stakeholders (e.g., decision makers, Ministries of Health, public health organizations, and frontline service providers) also provide expertise in context-specific considerations and how data were collected. Ensuring a clear understanding of how the data were collected, and the potential biases, is a critical component of modeling.

6. Conclusions

Modeling can be a useful tool to provide evidence to support policymakers and decision-making throughout a pandemic. In this commentary, we provided a description of common model types that policymakers are likely to encounter, and discuss reasons for why specific model types are more suitable over another for specific research questions, conceptualization, and data availability.

CRediT authorship contribution statement

Stephen Mac: Conceptualization, Writing - original draft, Visualization. Sharmistha Mishra: Conceptualization, Writing - original draft. Raphael Ximenes: Writing - review & editing. Kali Barrett: Writing - review & editing. Yasin A. Khan: Writing - review & editing. David M.J. Naimark: Writing - review & editing. Beate Sander: Conceptualization, Writing - original draft, Supervision.