Abstract
Novel Coronavirus is a highly infectious disease, with over one million confirmed cases and thousands of deaths recorded. The disease has become pandemic, affecting almost all nations of the world, and has caused enormous economic, social and psychological burden on countries. Hygiene and educational campaign programmes have been identified to be potent public health interventions that can curtail the spread of the highly infectious disease. In order to verify this claim quantitatively, we propose and analyze a non-linear mathematical model to investigate the effect of healthy sanitation and awareness on the transmission dynamics of Coronavirus disease (COVID-19) prevalence. Rigorous stability analysis of the model equilibrium points was performed to ascertain the basic reproduction number R0, a threshold that determines whether or not a disease dies out of the population. Our model assumes that education on the disease transmission and prevention induce behavioral changes in individuals to imbibe good hygiene, thereby reducing the basic reproduction number and disease burden. Numerical simulations are carried out using real life data to support the analytic results.
Keywords: Education, Exploratory data analysis, Hygiene, Reproduction number, Stability
Introduction
Coronavirus disease (COVID-19) is an infectious disease caused by a newly discovered type of coronavirus which belongs to a family of viruses [1] that are usually found in animals globally; however, up until now very few human infection have been found [2]. The World Health Organization (WHO) coined the term, COVID-19, to describe the coronavirus that affect the lower respiratory tract of patients with pneumonia in Wuhan, China on the 29th of December 2019 [3], [4], [5]. The present reference name for the virus is severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) [5]. Fig. 1 describes the club-shaped glycoprotein spikes in the envelope that gives the virus a crownlike or coronal view. The systemic and respiratory disorder caused by COVID-19 infection is a strain of coronavirus that is newly identified in humans [1]. Coronaviruses cause ailments from common cold to severe diseases such as MERS and SARS [6], [7],
Fig. 1.
Diagram of an Isolated Corona virus, Pilch, R. (2020). World War : The COVID-19 Pandemic. Director, CNS Chemical and Biological Weapons Nonproliferation Program. Middlebury Institute of International Studies at Monterey. Available at https://www.nonproliferation.org/world-war-v-the-covid-19-pandemic/. Accessed on April 1, 2020.
Other than SARS-CoV-2, there are six known coronaviruses in humans: HCoV-229E, HCoV-OC43, SARS-CoV, HCoVNL63, HCoV-HKU1, and MERS-CoV [4], [6], [8], [9]. Two out of these coronaviruses have caused two large-scale pandemics in the last two decades: SARS [10] and MERS [11], [12]. When people are infected with the COVID-19 virus, they contract mild to moderate respiratory disorder and may recuperate without the need for special treatment. The elderly and those with terminal illnesses, such as cardiovascular ailments and cancer, are prone to becoming severely sick. The full range of the clinical symptoms is not totally clear, but it can lead to the death of the infected [3]. Symptoms that are commonly reported include fever, cough, aches, tiredness, pneumonia, and complicated dyspnea. Less common symptoms are headache, diarrhea, hemoptysis, runny nose, and phlegm-producing cough [3], [13]. Reports indicate that patients with mild symptoms take a week or more to recover, while cases that are severe gradually progress to respiratory failure, which may lead to death [14]. Death is common in middle-aged and elderly patients who already suffer from such diseases as tumor, cirrhosis, hypertension, coronary heart disease, diabetes, and Parkinson’s disease [14]. The incubation period of COVID-19 infection is approximately 5.2 days.
The COVID-19 virus spreads predominantly when an infected person coughs or sneezes, and releases droplets of saliva or discharge from the nose in the process. This makes it crucial to adopt respiratory etiquette (for example, coughing into a flexed elbow) [15]. At first, it was opined that the infections was zoonotic in nature, that is, animal-to-human transmission; however, recent published report [4], as well as the rate of spread of the infection show compelling evidence of human-to-human secondary transmission, which is believed to be fueled by travels, going by the spread to every continent [4]. This geographic extension beyond the initial epicenter of Wuhan makes studying the pathogenic history of COVID-19 infection pertinent. Isolating the virus from biologic samples revealed the virus as genus betacoronavirus, which places it together with other Severe Acute Respiratory Syndrome (SARS) and Middle East Respiratory Syndrome (MERS) [3]. Primary cases of COVID-19 have been traced back to the Huanan seafood market, with secondary cases occurring at hospitals among nurses and physicians, who had extensive contact with COVID-19 patients. Furthermore, several individuals who did not have direct contact with the primary sources contracted the virus from the secondary sources. MERS also spreads through close person-to-person contact (primarily in health care settings during the symptomatic phase of the disease), although the transmission was significantly reduced at the height of the MERS epidemic [1]. Similarly, the transmission of SARS increases at a rapid rate during close person-to-person contact and from respiratory droplets from sneezing or coughing, but not as fast as is the case with the current COVID-19 outbreak. Furthermore, fomites, fecal transmission and handling of animals (killing, selling or preparing wild animals) were less common methods of transmission [15], [16]. The modes of transmission, regarding COVID-19, are thought to be the same mechanism for the three viruses. Infections as a result of respiratory droplets or secretions from infected individuals appear to be the primary mode of transmission from human to human. The spread of infection for the current outbreak is occurring more rapidly than the SARS epidemic. The rates of human-to-human transmission were generally lower for MERS, possibly in part due to the higher case fatality ratio (CFR) among those diagnosed with the disease. When compared with SARS and MERS, COVID-19 has a more rapid spread, partly due to increased globalization [1]. Patients were assessed for viral pneumonia through the ascertainment and testing of bronchialveolarlavage fluid utilizing whole genome sequencing, cell cultures and polymerase chain reaction (PCR). At the time of writing, the number of persons infected by the virus globally has now surpassed 1,004,500 and authorities have reported 52,600 deaths from the virus. Over 30 countries, in almost all continents, have confirmed cases to date. The spread of the virus became international within 1 month of its first identification, as humans move from one location to another [3]. The World Health Organization (WHO) declared COVID-19 a public health emergency of international concern on the 1st of February, 2020. Insufficient risk assessment about the emergency nature of the situation, as well as inadequate reporting on the virus within China has, to an extent, led to the rapid spread of COVID-19 throughout mainland China and into proximal and distant countries. The lack of transparency of the Chinese health ministry has been cited as one of the largest contributors to the spread of the virus globally [5].
The SARS global outbreak was contained in July 2003, and no other cases about it has been reported since 2004. After the emergence of SARS, MERS was the second coronavirus resulting in a major global public health crisis. It first emerged in 2012 in Saudi Arabia, when a 60 year old man presented with severe pneumonia [17]. An outbreak of the virus did not occur until 2 years later, in 2014, with a total number of 662 identified cases and a 32.97% case-fatality rate [18]. From 2014 to 2016, 1364 cases were observed in Saudi Arabia. A total of 27 countries were affected by MERS during the outbreaks spanning Europe, Asia, the Middle East and North America [19]. Since 2012, 2494 laboratory confirmed cases of MERS have been reported, and 858 associated deaths have occurred with 34.4% case-fatality ratio [20]. The major difference between COVID-19 and its predecessors is that while runny noses or gastrointestinal symptoms are features of MERS and SARS, they are rare in the virus of interest to this study. The global spread of 2019 novel coronavirus (COVID-19) infections from the epicenter of Wuhan, China, has made it critical to investigate the history, as well as ways of curbing the spread of the virus, particularly due to the high rate of human international mobility. Although it is still too early to predict susceptible populations, early patterns have shown a trend similar to Severe Acute Respiratory Syndrome (SARS) and Middle East respiratory syndrome (MERS) coronaviruses. Susceptibility seems to be associated with age, biological sex, and other health conditions [18]. A study conducted on Covid-19 infected pregnant women in their third trimester revealed that there was no evidence of mother-to-child transmission. However, precaution is taken by making all pregnant mothers deliver via cesarean sections; hence, it is difficult to determine if transmission can occur during vaginal birth. This study is essential because pregnant mothers are relatively more vulnerable to infection from respiratory pathogens and severe pneumonia. Furthermore, fomites, fecal transmission and handling of animals (killing, selling or preparing wild animals) were less common methods of transmission [20] The severe acute respiratory syndrome (SARS) outbreak in 2003 resulted in more than 8000 cases and 800 deaths. SARS was contained by means of syndromic surveillance, speedy isolation of infected persons, strict enforcement of quarantine of all contacts, and top-down enforcement of community quarantine in some locations. In contrast, by Feb 28, 2020, within a matter of 2 months since the beginning of the outbreak of coronavirus disease 2019 (COVID-19), more than 1, 004, 500 confirmed cases of COVID-19 have been reported, with more than 52, 600 deaths. Although there are conspicuous similarities in both SARS and COVID-19, the differences in the characteristics of the viruses will, in the end, define whether or not the same measures for SARS will hold in successfully curbing the spread and subsequent elimination of COVID-19. The two coronaviruses are reported to differ in terms of period of infection, transmissibility, clinical severity, and the extent of community spread. Owing to the rapid spread of the new coronavirus and its impacts on human health, scholars are rapidly responding to the new virus. It was suggested that the best way to prevent and slow down the transmission is to create awareness about the COVID-19 virus: how it spreads, protecting oneself and others from infection by hand washing, frequent use of alcohol-based sanitizer, and avoiding face touching (personal and environmental hygiene). Reducing the spread of Covid-19 is critical, so it was advised that patients with mild symptoms should stay home, as much as possible, and that workers should be permitted to, where feasible, telecommute. Given the wide spread of Covid-19, governments have had to impose quarantines and travel bans. For instance, China locked down whole cities, Italy imposed draconian restrictions, and in the United States, thousands of people have been made to subject to legally enforced quarantines, or are in self-quarantine. However, in spite of all these, the numbers of cases and deaths continue to rise, implying that travel bans and mandatory quarantine are not enough. There is need for a more effective response to Covid-19, using more creative legal tools.
Containing COVID-19 should be the current target, since the closure of institutions and public places, and restrictions on travels and trades, cannot be upheld indeterminately. Individual-case containment might not be possible in the long run, and there might be the need to move from containment to mitigation, thereby balancing the costs and benefits of public health measures. Countries need to accept that even if public health measures are not able to fully contain the spread of COVID-19, owing to its characteristics, they will still be effective in reducing widespread community transmission, reducing peak incidences and the impact on public services, and decreasing the overall attack rate. In addition, the present study suggests that the outbreak can be minimized, its peak can be suppressed, and global deaths can be reduced by providing two factors: awareness and hygiene. This is because while quarantines and travel bans are usually the first response to new infectious diseases, they are old measures, of limited use for highly transmissible diseases, and if imposed too heavily and/or haphazardly, they can be counterproductive [1].
Mathematical modeling has been used to gain meaningful insight to study the spread of infectious diseases such as malaria, dengue fever, Zika virus, and influenza, among others. For example, the effect of vaccine on the control of dengue disease was considered by [21] while a nonautonomous mathematical model was used to describe the dynamics of malaria transmission with age structure for the vector population in [22]. The biting rate of mosquitoes was considered as a positive periodic function which depends on climatic factors. Multiple routes transmitted system of epidemics was considered in [23] by deriving equations to accurately calculate the epidemic threshold and the outbreak size in a multiplex network. Several researchers, including [4], [24], [25], [26] have generated mathematical and statistical models considering different variables, but no work had been done that considers quarantine, hygiene, treatment and awareness. This research work employs a deterministic non-linear mathematical model to ascertain the impact of the variables: awareness and hygiene, on preventing or slowing down the COVID-19.
Model formulation
In the population under consideration, we assumed that the population is homogeneously mixed and that disease spreads via direct contact between susceptible and infected persons, as well as indirectly through corona virus shed in the environment by infected individuals. Furthermore, it is assumed that the mean value of infective in the population does change significantly. Hence, we shall consider an SQIRES model with restriction in the recruitment rate into the population as we described in Table 1. The total human population is denoted by N(t) at time t with sub-populations according to their health status namely: Susceptible individual S(t), Quarantined humans Q(t), Infected and infectious humans I(t) and Recovered/removed humans R(t). Quarantined individuals Q(t) who show symptoms of the infection progress to the infected compartment at a rate α 1 while those who test negative move back to the susceptible class S(t) at a rate α 2. Infected and infectious humans I(t) are recovered at a rate α 3 while COVID-19 induce death rate is assumed to be σ. All humans die naturally (i.e. those whose death are not due to COVID-19) at a rate μ. In the present situation where there is outbreak of novel corona virus disease (also referred to as COVID-19), the information regarding the spread and how it could be controlled is propagated through social media, radio, TV, organizing informative and educative programmes by government and non-governmental organizations. This awareness about the disease and the mode of transmission stimulates susceptible individuals to take precautionary measures and brings about behavioral changes towards self-protection and reduction of contacts with infected persons during the outbreak of the disease. Thus, the dynamics of education/information propagation E(t) is considered in the present work. We assume that information about the disease and the need to protect oneself is proportional to the densities of infected individual is denoted by F(I(t)). This type of growth rate was used in [27] and we make use of same here.
Table 1.
Description of the variables in system (6).
| Variable | Description |
|---|---|
| S(t) | Susceptible humans |
| Q(t) | Quarantined humans |
| I(t) | Infectious humans |
| R(t) | Recovered humans |
| E(t) | Education/Campaign |
Maintaining good sanitation and personal hygiene plays a critical role in reducing the spread of the virus from person-to-person, person-to-surface, person-to-surface-to person transmission. To achieve this, the use of sanitizers and frequent hand washing with soap and clean running tap water has been suggested among other precautionary measures. To this end, we shall assume that the transmission rate of COVID-19 reduces, as function of good hygiene. Also, the form of this function is not too clear; however, we shall adopt the linear function here as used in [28], [29]. Consequently, the transmission rate of the disease denoted by β(H) where H is the sanitation level is defined as a linear function of H as follows:
| (1) |
Observe that the parameters and denote the maximum and minimum transmission rate of COVID-19 respectively. The simple implication of Eq. (1) is that if maximum hygiene is maintained i.e. so that disease transmission is at its barest minimum while disease transmission will be maximum if . In order that individual imbibe good hygienic habits, we put in place a campaign strategy to educate and create awareness for the locals. This is motivated as follows: It is assumed that a fraction H 0 of individuals practice good sanitation habits before the outbreak of COVID-19, while the remaining fraction who do not take sanitation seriously are influenced to practice healthy habits as the rate of education campaign on good hygiene grows at rate ω 0. Thus, as the rate of awareness on good hygiene saturate the population, we relate educational campaign to good sanitation H according to
| (2) |
Further,(2) implies that, when there is no campaign strategy (i.e ) in place to warn people on how to protect themselves against the disease, then . However, if an awareness strategy is adopted to propagate information on how individuals can protect themselves over time, we have an increase in sanitation initial level from H 0 to .
Suppose p 1 is the probability that an individual get infected due to his/her interaction with an infected and infectious human, then we assume the force of infection λ(H) follows a simple mass action and is defined as
| (3) |
In addition to the assumptions made while motivating the construction of the model, the following assumptions were considered:
-
(1)
COVID-19 is transmitted by an infected and infectious human; and by coming in contact with surface infested with the virus
-
(2)Creating awareness on how susceptible individuals could protect themselves is propagated by a saturating function which depends on infected population density given by
This type of saturating function was used in [27], where ω 0, ω 1 and ω 2 are information growth rate, the half saturation point for F(I) [[27],[30]] as it attains half of its maximum value when infected population arrives at ω 1 and saturation constant of information respectively.(4) -
(3)
It is not clear from literature whether COVID-19 confers proper immunity on recovered humans, thus we assume in this study that recovered people from COVID-19 lose their immunity δ (both natural and immunity due to medication) and progress back to the susceptible class over time.
-
(4)
Due to human lackadaisical attitude and lack of resources, awareness/information degenerate at rate d
-
(5)Since the human population is not constant, we assume that the recruitment rate into the population is
where ΛT are those who are recruited through migration, ΛB are rate of births while γ is a restriction parameter on immigration(5)
In view of the foregoing discussions, the dynamics of the model is presented in the following system of non-linear differential equations:
| (6) |
with the following initial conditions S(0) > 0, Q(0) ≥ 0, I(0) ≥ 0, R(0) ≥ 0 and E(0) ≥ 0. Since we are dealing with human dynamics, we shall assume all parameters are positive with dynamic variables description provided in Table 1 . The flow chart for the model is provided in Fig. 2
Fig. 2.
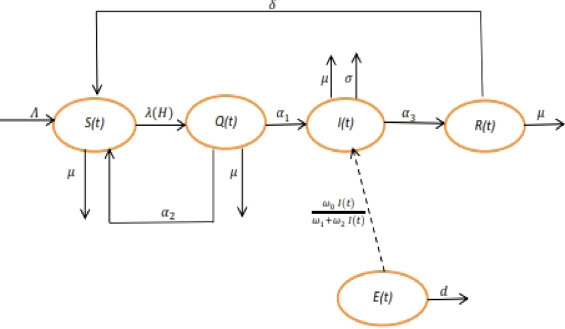
Schematic diagram of model dynamics between humans under the influence of Education.
Model analysis
In this section, we focus on the analysis of the model by carrying out rigorous stability analysis on the model by considering the positivity and boundedness of solutions, the model steady states and their stability.
Positivity and boundedness of solutions
In this part, we show that model system (6) is epidemiological well-posed and realistic if all the variables of system (6) are non-negative for all time t. Thus, we establish this through the following Lemma:
Lemma 0.1
The solution S(t), Q(t), I(t), R(t) and E(t) of system(6)with initial conditions S(0) > 0, Q(0) ≥ 0, I(0) ≥ 0, R(0) ≥ 0 and E(0) ≥ 0 are positive for all t > 0.
Proof
: Now, following the approach in [27] we have ; ; ; ; Since all the above rates are non-negative on bounding plane then it is easy to show that the region is positively invariant and attracting [31], [32]. For system (6), the region of attraction is given by
(7) Hence, it is sufficient to consider the dynamics of system (6) in Ω which attracts all solutions initiating in the interior positive orthant [27]. □
Equilibrium points of the model
The model system (6) is non-linear and so, it may be difficult to determine the analytic/exact solutions. Consequently, we apply stability theories to study the qualitative behavior of the equilibrium points, in order to gain insight concerning the disease dynamics and how it can be controlled. In this part of the work, the existence of all equilibriums of the model are investigated by equating the rate of change with respect to time t of all dynamical variables to zero. Suppose H is a known quantity, then we can obtain the equilibrium points of system (6) by solving the following set of algebraic equations simultaneously:
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
The simultaneous solution of Eqs. (8)–(12) yields
| (13) |
where Furthermore, taking into account of I from (13) in Eq. (3), we obtain
| (14) |
The solution of Eq. (14) for λ(H) gives
| (15) |
From solutions in (15) it follows that we have the following cases:
; COVID-19 Free Equilibrium, C0
Observe that when in Eq. (13), we have
| (16) |
C 0 is a COVID-19 Free Equilibrium, which represent a state where there is no presence of novel Corona virus disease and infection in the population under consideration in the absence of hygiene.
Local stability of COVID-19 Free Equilibrium (CFE), C0
The local stability of C 0 is investigated through the following Theorem:
Theorem 1
The COVID-19 Free Equilibrium (CFE), C0of system(6)is locally asymptotically stable if R0 < 1 otherwise unstable.
Proof
Consider the Jacobian matrix of system (6) evaluated at (C 0) in the absence of sanitation
(17) It is easy to see that the eigenvalues of (2.17) are and while the remaining two eigenvalues are obtained from the 2 × 2 matrix
(18) According to Routh-Hurwitz condition, all eigenvalues of matrix M are real and negative if
Clearly,
where
(19) Thus, all eigenvalues of (2.17) are real and negative if R 0 < 1 so that CFE, C 0 is locally asymptotically stable and unstable if R 0 > 1 □
Remark 1
The quantity R 0 is popularly referred to as the basic reproduction number. It is defined as the number of secondary infected individuals caused by an infected individual due to direct or indirect contact during his/her whole infectious period in a wholly susceptible population. In particular if R 0 < 1(orR 0 > 1), it implies that on average, an infected individual will produce less than (or more than) one secondary infected individuals during his/her whole infectious period in a wholly susceptible population and thus the disease will die out (or persist) in the population, respectively. It is worthy of note here that the basic reproduction number R 0 can be obtained by applying the next generation matrix approach [33], [34].
Global asymptotic stability of CFE, C0
Suppose the stability of CFE, C 0 did not depend on the initial size of the population while the prevailing conditions did not allow local stability of C 0 to hold, then we need to consider the global asymptotic stability (GAS). To do this, a Lyapunov function is constructed. Consider the Lyapunov function defined as follows:
| (20) |
By differentiating Eq. (20) along the solutions of (6) gives
Thus, at CFE, C 0, we have so that
Therefore,
| (21) |
Hence, the CFE, C 0 is globally asymptotically stable if R 0 ≤ 1 otherwise unstable. The foregoing considerations is summarized as follows:
Theorem 2
Then CFE, C0is globally asymptotically stable if R0 ≤ 1 otherwise unstable.
; COVID-19 endemic equilibrium (CEE), C⋆
Firstly, recall the components of the dynamical variables in (13) which we now denote as C ⋆ and written as follows:
| (22) |
Now, C ⋆ denote the Corona Virus Endemic Equilibrium (COVID-19 EE) which represent a state where there is a presence of corona virus disease or infection in the population of interest. Assuming H is known, then, there is at most one endemic equilibrium C ⋆ as defined in (2.22). In order to ensure that (22) does indeed specify an endemic equilibrium, we must ensure that all components of (22) are positive. Of course, this is the case if and only if λ(H) > 0 i.e.
| (23) |
Furthermore, from (23) we have
| (24) |
Taking into account of (1) in (24) and making H the subject gives
| (25) |
For convenience, let
| (26) |
We summarize the above result in the following Lemma:
Lemma 0.2
Suppose H is known, then model system (6) has a unique positive endemic equilibrium C⋆if the force of infection.
Determination of H
In order to be able to completely study the endemic equilibrium C ⋆, it is important to derive an equation for H and determine its uniqueness.The equation for H is obtained by taking into account the value of in (13) to get
| (27) |
where . Then the solution of H in (27) is feasible and unique if:
-
(i)
(28) -
(ii)
(29) -
(iii)
(30)
Now, if in (27) we have
Then the result follows immediately that f(H 0) > 0 if R 0 > 1. Clearly, if in (27), f(H ⋆) < 0 i.e
Lastly, the derivative of (27) with respect to H yields
Note that . The result follows immediately that Eq. (27) has a unique solution in (H 0, H ⋆) if R 0 > 1.
Lemma 0.3
Model system(6)has a positive unique endemic equilibrium C⋆if H ∈ (H 0, H ⋆) and if R 0 > 1.
Local stability of COVID-19 EE, C⋆
Theorem 3
The COVID-19 PE, C ⋆ is locally asymptotically stable if the inequality
holds otherwise unstable
Consider the Jacobian matrix of system (6) at C ⋆ given as
| (31) |
where
One eigenvalue of (31) is while the remaining eigenvalues can be obtained from
| (32) |
Now, it is easy to see that Trace(M ⋆) < 0 from Lemma 3.2 i.e.
Then Det(M⋆) > 0 if:
Thus, C ⋆ is locally asymptotically stable.
Sensitivity analysis of the model
The following section is dedicated to consider the sensitive parameters in the model. Following the approach of Arriola and Hyman [35], [36], the sensitivity of model parameters are calculated using
| (33) |
where q is the parameter whose sensitivity is to be determined, R 0 retain its original meaning. Sensitive indices measures the relative change in state variables when the parameter changes. The result of the sensitivity analysis of parameter in the model is given in Table 1 Observe that and ΛB are all positive and sensitive to R 0. It is also clear that R 0 is most sensitive to both and p 1 while γ is next in line to both and p 1. The implication of this is that p 1 and γ will bring about an increase of the same proportion in R 0 and vice-versa. Sensitivity analysis of H 0, α 2, α 3, σ and μ have an inverse proportional relationship with R 0 implying that any increase in H 0, α 2, α 3, σ and μ will reduces the value of R 0 as reported in Table 2 . However, this is not practical in real life except for α 2. Results from the sensitivity analysis suggest that more effort in particular should be concentrated at reducing the risk p 1 of contracting and the transmission rate of the disease. Particularly, Fig. 4 shows that if the immigration restriction parameter meaning border is completely closed to immigrants, then basic reproduction number (R 0) will be 0.165; but if the border is completely opened to immigrants (), then R 0 will increase to 1.604. It should be noted that since the disease is communicable, then the probability that an individual gets infected (p 1), transmission rate per day () and the rate quarantined individuals move to the infected class (α 1) are strictly greater than zero (i.e, p 1 > 0, and α 1 > 0). Hence, the need for public health workers and international bodies in charge of health should ensure that transmission rate and α 1 are kept relatively low as they can cause the reproduction number R 0 to increase as shown in Fig. 3 . This can be achieved through the propagation of awareness/information on disease transmission and protection strategies such as imbibing good hygiene and restriction through various social media available.
Table 2.
Sensitivity Analysis of Model Parameters and their Values.
| Parameter | Sensitivity Value |
|---|---|
| 1 | |
| 0 | |
| γ | 0.15092 |
| α1 | 0.06361 |
| p1 | 1 |
| H0 | -0.02522 |
| ΛT | 0.15092 |
| ΛB | 0.84909 |
| α2 | -0.06087 |
| α3 | -0.98402 |
| σ | -0.01565 |
| μ | -1.0031 |
Fig. 4.

Simulations of system (2.6) for the total human population level as a function of time for R0 < 1 with parameters set at .
Fig. 3.
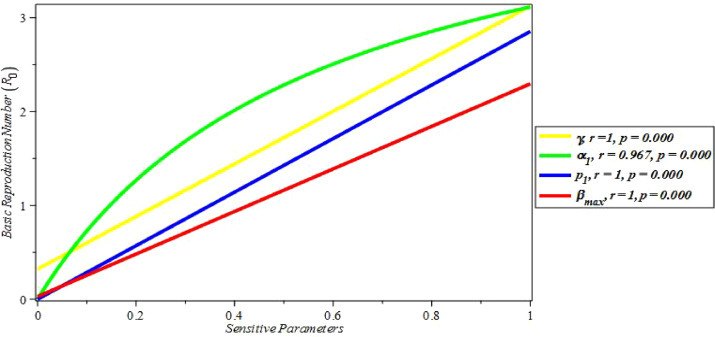
Correlation between Basic Reproduction Number R0 and Sensitive parameters of the model.
It must be clarified here that the term ”restriction” γ refers to screening individuals who enters the country through our sea, land and air borders, aside from social distancing. In order to achieve this feat, it is suggested here that a test and isolation center should be created at our borders, especially at our airports. This will ensure that only individuals who test negative will be allowed into the population while those who test positive or are suspected to have contracted the virus will be moved to the isolation center for further test and treatment
Remark 2
Observe from Fig. 3 that there is a significant direct relationship between the basic reproduction number, R 0 and the sensitive parameters at 5% level of significance.
Numerical simulation
In previous sections,we have qualitatively analyzed the behavior of the non-linear model system about the equilibrium points to gain meaningful and deep understanding regarding COVID-19 dynamics and obtained analytical results for the equilibria, the stability properties for COVID-19FE, C 0 and COVID-19EE, C ⋆. In this section, the model parameters were estimated from real data, using least square estimation method and is used for the numerical simulation. The data used for this analysis is a daily report on the novel coronavirus (COVID-19) collected from the World Health Organization (WHO), Coronavirus disease (COVID-2019) situation reports citeworld2020coronavirus and the recovered cases retrieved from worldometer (2020): https://www.worldometers.info/coronavirus/country/italy/. See Appendix A1 (all the data are real data except for S and Q, which were estimated). The estimated parameters are used to simulate the dynamical variables of the model system (6). Each compartment is simulated at different hygiene levels and for different awareness values over time. This process is repeated for times. The dynamical variables of (2.6) are plotted against time to exploit how hygiene and awareness can affect these variables over time. Several numerical methods has been used to simulate epidemiological studies including fractional derivative technique [37], variational iteration method (IVM), Modified Initial Guess Variational Iterative Method (MIGVIM) [38], [39] and Runge-Kutta-Fehlberg method (RKF45). In present study, the simulations solution of the system (2.6) is analyzed using MAPLE 18 with RKF45 Ordinary Differential Equation (ODE) solver which is among the family of implicit and explicit iterative methods; these include the well- known routine called the Euler’s method using temporal discretization for approximate solutions of ODE with order fourth and error estimator order fifth. We used Italy’s time series for cumulative confirmed cases, infected cases, recovered and mortality data collected from the 31st of January to the 30th of March, 2020 by WHO (2020), to standardize the initial conditions of the model. Parameter fitting was accomplished through a nonlinear least squares algorithm implemented using R. For these set of parameter values, it may be verified for equilibrium C 0 (i.e. R 0 < 1) and C ⋆ (i.e. R 0 > 1) is satisfied. For parameter values such that R 0 < 1, a plot of the variation of total population is presented in Fig. 4. We observed that the susceptible population increases over time; while over the same time, quarantined, infected and recovered population decline asymptotically. To show the impact of educational campaign on respective human classes, we have drawn plots of susceptible, quarantined, infected and recovered/removed classes against awareness. It is observed from these figures that educating the populace has great impact on COVID-19 control. It can be seen from Figure 5a that number of susceptible individuals increased significantly as information propagation on the disease grows over time. This is because susceptible people are now aware of how to protect themselves against the disease. In Fig. 5 (b) and (c) it can be seen that as the rate of information on COVID-19 increases, there is a sharp decline in the number of quarantined and infected individuals while the number of recovered people witnessed a significant rise over the same period as shown in Fig. 5(d). Fig. 6 (a) depicts the graph of susceptible human population against time for various values of hygiene H level. It is observed that the susceptible population increased significantly as the level of sanitation increases around twenty (20) days before settling down to a stable level. In contrast, the Quarantine class decreases sharply around 10 days before reaching a constant value, (see Fig. 6 (b)) due to increase in hygiene level resulting from creating awareness about the disease. Similarly from Fig. 6(c), it can be seen that the number of infected individuals reduces significantly as less people are exposed to the disease as a result of taking precautionary measures such as good hygiene informed by educating individuals on how to protect oneself against the disease. It is observed from Fig. 6 (d) that for low level of hygiene more individuals are infected. This account for the initial high number of people that would need to be recovered but this number decreased with increase in hygiene level.
Fig. 5.
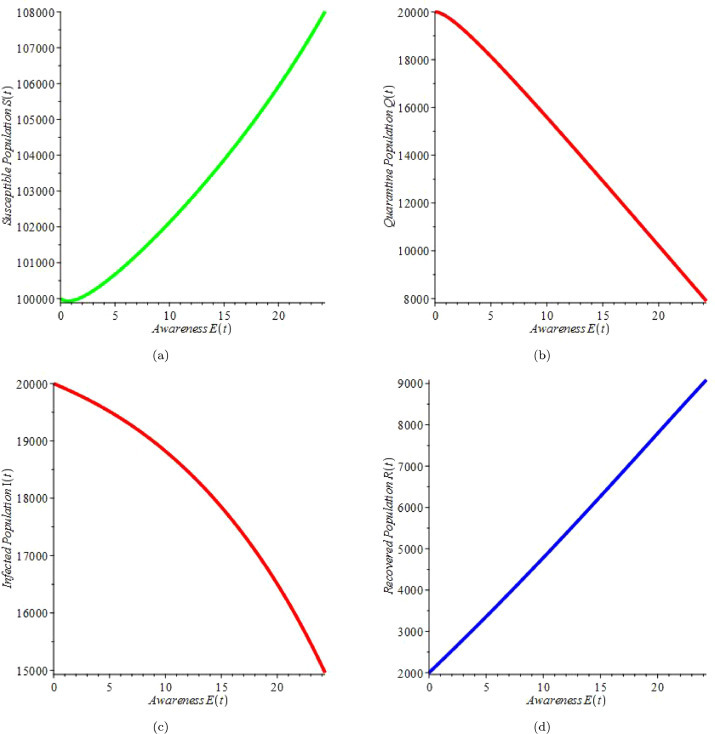
Simulation showing the impact of Education on Susceptible, Quarantined, Infected and Recovered human populations over time with parameters set .
Fig. 6.
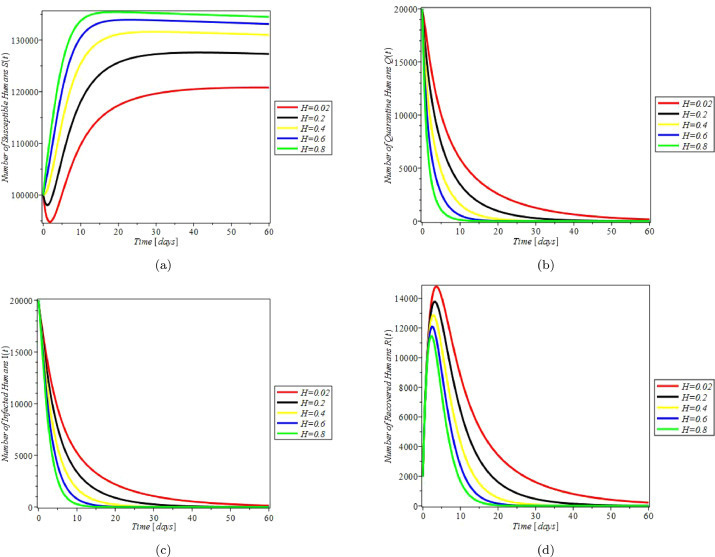
Simulation showing the impact of good Hygiene (H) on Susceptible, Quarantined, Infected and Recovered human populations over time with parameter set .
Exploratory data analysis (EDA)
In recent times, dynamic models are defined based on parameter assumption without necessarily considering the real life data to be modeled. In this research, the real data to be modeled is collected and analyzed using data harvested from WHO [40] and worldometer (2020): https://www.worldometers.info/coronavirus/country/italy/. The EDA helps to reveal some hidden feature in a data set. Table and plots are used to explain the hidden features in COVID-19 data of Italy for the first 60 days since the index cases was recorded on 31st January 2020. (Fig. 6.1).
Fig. 6.1.
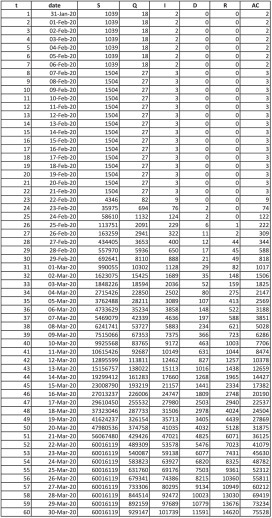
Italy Data.
Table 4 shows the descriptive statistics of the data. The data was collected from 31st January 2020 when the index case in Italy was reported. Two cases were reported on this day. For the period under review (31st January - 30th March), the minimum daily laboratory confirmed cases is zero and the maximum is 6,557, and the mean is 1696 with standard deviation of 2,271.07. This gives a coefficient of variation of 133.94%, which is a very high deviation, thus causing high variability in the number of COVID-19 reported cases in Italy. For this period under review, on the average, 232 individuals recovered per day, while 193 deaths are recorded per day. Thus, the recovery and mortality rates per day are 13.7% and 11.4% respectively.
Fig. 7 shows time plots representing infected individuals, recovered individuals and reported deaths per day and their daily totals. Fig. 7a depicts that daily reported laboratory confirmed cases of COVID-19 in Italy peaked at 6557 on the 50th day of infection in the country (20th March 2020) and later decreased to 4050 on the 30th of March. Fig. 7b is a non decreasing curve, it is a cumulative frequency curve of infected individuals per day. This curve cannot decrease but can be flattened. The figure shows that it will flatten in coming days. Fig. 7 also shows that recovery rate and mortality rate are trending up. It is a good report for recovery but not a good one for death. As recovery and death compartment increase, the active cases reduces, reducing rate of transmission of the virus.
Fig. 7.
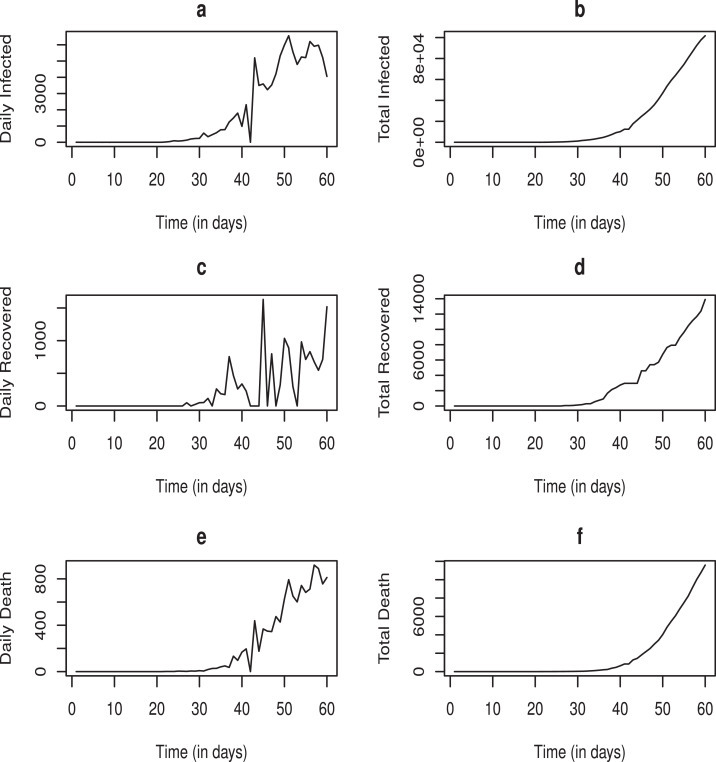
Time Plots of COVID-19 situation in Italy.
Fig. 8 shows the histogram of daily and total infected, recovered and death compartment. The histogram reveal that the data are positively skewed, with the mean being affected by outliers in the data sets. These outlines can be seen in the box plots presented in Fig. 9 .
Fig. 8.
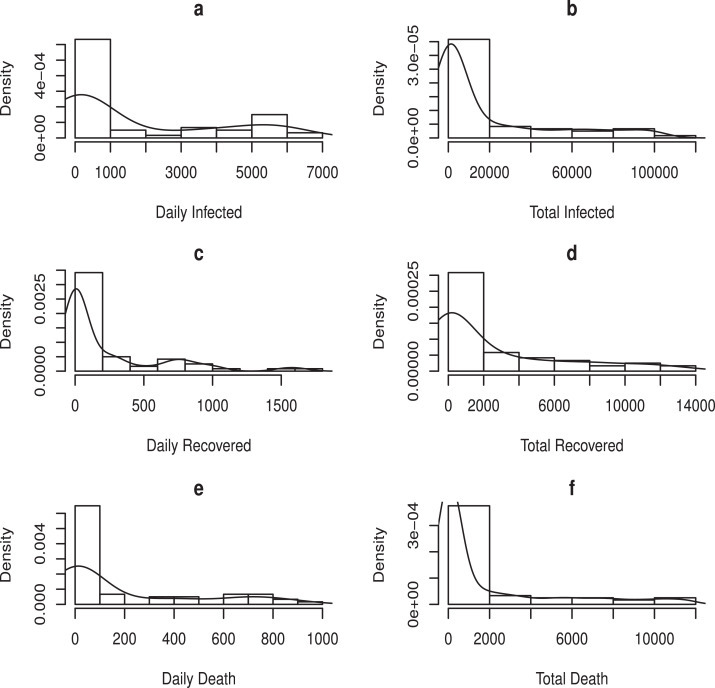
Histogram and Density Plots of COVID-19 situation in Italy.
Fig. 9.
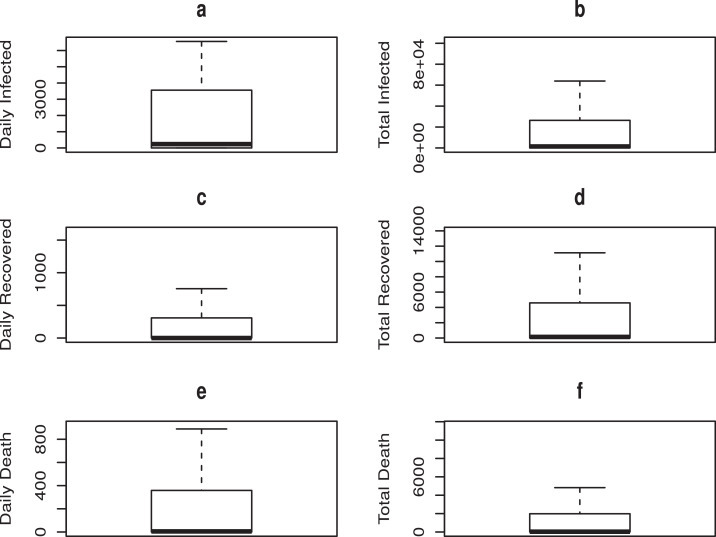
Box Plots of COVID-19 situation in Italy.
The box plots in Fig. 9 show that there are outliers and widespread extreme values, except for daily infected data. This exploratory data analysis has revealed the shape of the real data set, which can be used by statisticians and users of statistics in generating convoluted distributions that best fit the data. The data for daily infected, recovered and death individuals have tendencies of bimodality (two peaks), which can be modelled by T-R{Y} family of distributions [41] and subsequently used in generalized regression model of infectious disease.
The EDA helps readers to see the real situation of the data being modelled. Thus, the parameters of the modelled can be estimated or fitted from these data using available estimation techniques. The estimated parameters will then be used in dynamic modelling of the disease in question. Dynamic modelling will help to control and manage the disease in question by varying some parameters values in the parameter space within its confident limits.
Conclusions and recommendations
Conclusion
In this work, we have proposed and analyzed a non-linear mathematical model to consider the impact of sanitation and education campaigns on controlling the transmission dynamics of COVID-19 in the population of interest. In the course of modeling, it was assumed that susceptible individuals contract the infection through direct contact with infected persons, as well as indirectly through the presence of coronavirus in the environment. It was assumed that education on COVID-19 saturate throughout the population over time. Further, we also assumed that the transmission rate of COVID-19 is interrupted by healthy hygiene. First, the deterministic non-linear mathematical model was qualitatively analyzed. Positivity of solutions, boundedness and basic reproduction number R 0 in the absence of hygiene was obtained. It was found that the COVID-19FE, C 0 is locally and globally stable if R 0 ≤ 1 and that an endemic state COVID-19EE,C ⋆ exist for R 0 > 1. Furthermore, the sensitivity analysis of the model parameters to the reproduction number, R 0 is determined. This study reveals that the probability of getting infected p 1, maximum transmission rate of COVID-19 and restriction rate γ are most sensitive. In addition, it was also discovered that the propagation of information on good hygiene over time induce behavioral change in individuals leading to significant reduction in the number of quarantined and infected individuals.
Based on the results and findings of this study, the following recommendations are made:
-
(1)
Restriction (γ) is one of the most sensitive parameters that increases the basic reproduction number (R 0). It is recommended that restriction on land, sea and airport borders should be considered to control who comes into the country at a time like this. The restriction in this context could be total or partial depending on the severity of the spread of the disease.
-
(2)
In view of recommendation (1) above, we are also submitting that testing and isolation centers should be made available and fully functional at the borders in particular, the airports. This is to ensure that only immigrants who test negative or who had been observed to be free from symptoms of the disease at the isolation center, within the disease incubation period (for COVID-19, a maximum of 14 days is recommended globally) would be allowed into the country.
-
(3)
The result of the sensitivity analysis shows that the probability of getting infected is high when an individual comes in contact with an infected person. Thus, the stay at home policy, social distancing, and hand washing with alcohol-based sanitizer should be strictly maintained. Since the virus cannot spread without a medium, then the best policy is the stay at home order.
-
(4)
Maximum transmission rate is high, which is another sensitive parameter. It is very important that people are educated on personal and societal hygiene. The more the campaign on the spread of the virus, the more aware people become and this may bring about behavioral changes in individuals to practice healthy hygiene, which has been known to interrupt the rate of transmission of the coronavirus.
-
(5)
The present study revealed that promoting good hygiene via education/creating awareness (information) can help induce attitudinal change among the people, thereby influencing individuals to emulate good and healthy habits to protect themselves against the disease.
-
(6)
Information degenerate over time and can be attributed to factors, such as human lackadaisical attitude, and lack of resources, among other reasons. Thus, education campaign on the disease transmission and how it could be prevented must be sustained through social media, TV, Radio, Talk shows e.t.c.
If these recommendations are taken seriously by all stakeholders, then, we might be on the right path to flattening the curve.
Conclusively, as efforts to effectively combat COVID-19 rage on, further analysis can be done to improve the present work by looking into social distancing, isolation, palliative measures and budgetary allocation. The latter is important due to the emergency state of COVID-19, as most nations have insufficient funds to tackle the disease. Thus, it is essential to consider a mathematical model that will take into account social distancing, isolation and budget to propagate information to warn people on how to maintain good sanitation to curtail the spread of the disease. All these shall form the foundation for another research work.
Declaration of Competing Interest
All authors have agreed and approved the manuscript and have contributed significantly towards the article. There is no conflict of interest among the authors.
Acknowledgment
One of the authors (SIO) acknowledges with thanks to the support of South African DST-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS) for Post-doctoral Fellowship position. The authors are grateful to the anonymous reviewers and handling editor for their constructive comments.
Appendix A
Appendix A1: Estimation of Parameters in the Model
In most mathematical models, parameters are assumed. In this research, the parameters are estimated from the available data. Data on new cases, deaths, recovered and active cases of COVID-19, immigration, birth and population of Italy were collected from WHO and macro trends. These data form the basis of the estimation. The relationship between variables of interest are used to estimate the parameters using least square and maximum likelihood estimation methods. Eqs. (6), (8), (9), (10), (11) and (12) form the basis of the parameter estimation. It is easy to see from Eq. (13) that infected I(t) and recovered R(t) individuals are related to hygiene H. The data for I(t) and R(t) are available from which H(t) was estimated. Since H and E(t) are related, then, H is related to both S(t) and Q(t). The dynamic variables S(t), Q(t), I(t) and H(t) were predicted values from equation (13) based on the parameter estimated. It should be noted that S, Q, I, R, H and E are all time dependent variables, . The parameters are estimated with the use of R3.6.1 package. Information growth rate ω 0 was sourced from [27] and recovery rate of infected individuals was gotten from [42], all other parameters were estimated from data. The parameters were estimated from the data as follows: The natural death rate of humans, μ, is calculated by
| (6.1) |
where is the life expectancy of Italy before the outbreak of COVID-19 https://www.worldometers.info/coronavirus/country/. Without loss of generality, R(t) can be written as Rt and the same follows for other variables. The COVID-19 induced death rate, σ, is estimated by
| (6.2) |
where Dt is number of reported COVID-19 induced deaths in Italy at time t, It is the number of reported confirmed laboratory infected individuals at time t, . Since, the number of individuals exposed are not reported, it is assumed that approximately 50% of the individuals exposed may tested positive and move to the infected compartment, while the remaining percentage will move back to the susceptible class. Thus, which after using maximum likelihood method, we obtained and . The number of quarantined individuals at time t can be estimated from equation (13) by
| (6.3) |
where and are the estimates of α 1, α 3 and σ respectively, while It is actual reported confirmed laboratory infected individuals at time t. The rate at which immunity is lost, δ, is estimated by
| (6.4) |
Information growth rate, is assumed, so that the linear model
| (6.5) |
Where and et is the error term, then
| (6.6) |
So that
| (6.7) |
The parameter of the linear model, is estimated using the least square estimate given by
| (6.8) |
Appendix A2: Italy Data in the Model
Table 3.
Symbols, values and units of the parameters used in model.
| Description of Parameters | Symbol | Value | Source |
|---|---|---|---|
| Natural death rate of humans | μ | 0.0122 | Estimated |
| Rate at which immunity is lost (loss of immunity) | δ | 0.4335 | Estimated |
| Rate of COVID-19 induced deaths | σ | 0.1139 | Estimated |
| Rate of progression of quarantined individuals to the infected class | α1 | 0.5 | Estimated |
| Rate of progression of quarantined individuals to susceptible class | α2 | 0.56 | Estimated |
| Recovery rate of infected individuals | α3 | 0.547 | [27] |
| Recruitment rate by immigration | λT | 0.0628 | Estimated |
| Restriction parameter | γ | 0.7 | Estimated |
| Probability that an individual gets infected | p1 | 0.8 | Estimated |
| Maximum transmission rate of COVD-19 | 0.9943 | Estimated | |
| Minimum transmission rate of COVD-19 | 0.5027 | Estimated | |
| Information growth rate | ω0 | 0.025 | [27] |
| Level of hygiene in the absence of information | H0 | 0.0246 | Estimated |
| Rate at which information degenerate | d | 0.975 | Estimated |
| Half saturation point for F(I) | |||
| as it attains half of its | |||
| maximum value | |||
| when infected | |||
| population arrives at ω1 | ω1 | 0.9495 | Estimated |
| Saturation constant of information | ω2 | 0.0263 | Estimated |
Table 4.
Descriptive Summary of Italy COVID-19 Data.
| Statistic | Infected | Recovered | Death |
|---|---|---|---|
| Min | 0 | 0 | 0 |
| Max | 6557 | 1631 | 919 |
| 1st Quartile | 0 | 0 | 0 |
| 3rd Quartile | 3542 | 302 | 353.8 |
| Mean | 1696 | 232 | 193 |
| Std. Dev. | 2,271.07 | 391.41 | 293.08 |
| Median | 237 | 0 | 0 |
| Skewness | 0.9462 | 1.8660 | 1.2417 |
| Kurtosis | 2.2177 | 5.9308 | 2.9893 |
| Total | 101,739 | 13,911 | 11,591 |
References
- 1.Al-Rousan N., Al-Najjar H. The correlation between the spread of covid-19 infections and weather variables in 30 chinese provinces and the impact of chinese government mitigation plans. Eur. Rev. Med. Pharmacol. Sci. 2020;24(8) doi: 10.26355/eurrev_202004_21042. [DOI] [PubMed] [Google Scholar]
- 2.Adhikari S.P., Meng S., Wu Y.-J., Mao Y.-P., Ye R.-X., Wang Q.-Z., Sun C., Sylvia S., Rozelle S., Raat H., et al. Epidemiology, causes, clinical manifestation and diagnosis, prevention and control of coronavirus disease (covid-19) during the early outbreak period: a scoping review. Infect. Dis. Pover. 2020;9(1):1–12. doi: 10.1186/s40249-020-00646-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.for Disease Control C., Prevention, et al. Novel coronavirus, Wuhan, China. Prevention. 2020 [Google Scholar]
- 4.Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y., Ren R., Leung K.S., Lau E.H., Wong J.Y., et al. Early transmission dynamics in wuhan, china, of novel coronavirus–infected pneumonia. N. Engl. J. Med. 2020 doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Novel C.P.E.R.E., et al. The epidemiological characteristics of an outbreak of 2019 novel coronavirus diseases (covid-19) in china. Zhonghua liu xing bing xue za zhi= Zhonghua liuxingbingxue zazhi. 2020;41(2):145. doi: 10.3760/cma.j.issn.0254-6450.2020.02.003. [DOI] [PubMed] [Google Scholar]
- 6.Chen Y., Liu Q., Guo D. Emerging coronaviruses: genome structure, replication, and pathogenesis. J. Med. Virol. 2020;92(4):418–423. doi: 10.1002/jmv.25681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wang W., Tang J., Wei F. Updated understanding of the outbreak of 2019 novel coronavirus (2019-ncov) in wuhan, china. J. Med. Virol. 2020;92(4):441–447. doi: 10.1002/jmv.25689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lin L., Li T. Interpretation of” guidelines for the diagnosis and treatment of novel coronavirus (2019-ncov) infection by the national health commission (trial version 5)”. Zhonghua Yi Xue Za Zhi. 2020;100:E001. doi: 10.3760/cma.j.issn.0376-2491.2020.0001. [DOI] [PubMed] [Google Scholar]
- 9.Su S., Wong G., Shi W., Liu J., Lai A.C., Zhou J., Liu W., Bi Y., Gao G.F. Epidemiology, genetic recombination, and pathogenesis of coronaviruses. Trends Microbiol. 2016;24(6):490–502. doi: 10.1016/j.tim.2016.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Poon L.L., Leung C.S., Tashiro M., Chan K.H., Wong B.W., Yuen K.Y., Guan Y., Peiris J.S. Rapid detection of the severe acute respiratory syndrome (sars) coronavirus by a loop-mediated isothermal amplification assay. Clin. Chem. 2004;50(6):1050–1052. doi: 10.1373/clinchem.2004.032011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zaki A.M., Van Boheemen S., Bestebroer T.M., Osterhaus A.D., Fouchier R.A. Isolation of a novel coronavirus from a man with pneumonia in saudi arabia. N. Engl. J. Med. 2012;367(19):1814–1820. doi: 10.1056/NEJMoa1211721. [DOI] [PubMed] [Google Scholar]
- 12.Zhou P., Yang X.-L., Wang X.-G., Hu B., Zhang L., Zhang W., Si H.-R., Zhu Y., Li B., Huang C.-L., et al. Discovery of a novel coronavirus associated with the recent pneumonia outbreak in humans and its potential bat origin. BioRxiv. 2020 [Google Scholar]
- 13.Huang C., Wang Y., Li X., Ren L., Zhao J., Hu Y., Zhang L., Fan G., Xu J., Gu X., et al. Clinical features of patients infected with 2019 novel coronavirus in wuhan, china. The Lancet. 2020;395(10223):497–506. doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Li T., Wei C., Li W., Hongwei F., Shi J. Beijing union medical college hospital on” pneumonia of novel coronavirus infection” diagnosis and treatment proposal (v2. 0) Med J Peking Union Med Coll Hosp. 2020 [Google Scholar]
- 15.Peeri N.C., Shrestha N., Rahman M.S., Zaki R., Tan Z., Bibi S., Baghbanzadeh M., Aghamohammadi N., Zhang W., Haque U. The sars, mers and novel coronavirus (covid-19) epidemics, the newest and biggest global health threats: what lessons have we learned? Int. J. Epidemiol. 2020 doi: 10.1093/ije/dyaa033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Backer J.A., Klinkenberg D., Wallinga J. Incubation period of 2019 novel coronavirus (2019-nCoV) infections among travellers from Wuhan, China, 20–28 January 2020. Eurosurveillance. 2020;25(5):2000062. doi: 10.2807/1560-7917.ES.2020.25.5.2000062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Corman V.M., Landt O., Kaiser M., Molenkamp R., Meijer A., Chu D.K., Bleicker T., Brünink S., Schneider J., Schmidt M.L., et al. Detection of 2019 novel coronavirus (2019-ncov) by real-time rt-pcr. Eurosurveillance. 2020;25(3) doi: 10.2807/1560-7917.ES.2020.25.3.2000045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fehr A.R., Channappanavar R., Perlman S. Middle east respiratory syndrome: emergence of a pathogenic human coronavirus. Annu. Rev. Med. 2017;68:387–399. doi: 10.1146/annurev-med-051215-031152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sohrabi C., Alsafi Z., O’Neill N., Khan M., Kerwan A., Al-Jabir A., Iosifidis C., Agha R. World Health Organization declares global emergency: A review of the 2019 novel coronavirus (COVID-19) International Journal of Surgery. 2020 doi: 10.1016/j.ijsu.2020.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rothan H.A., Byrareddy S.N. The epidemiology and pathogenesis of coronavirus disease (covid-19) outbreak. J. Autoimmun. 2020:102433. doi: 10.1016/j.jaut.2020.102433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chanprasopchai P., Tang I.M., Pongsumpun P. Sir model for dengue disease with effect of dengue vaccination. Comput. Math. Method. Med. 2018;2018 doi: 10.1155/2018/9861572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Traoré B., Sangaré B., Traoré S. A mathematical model of malaria transmission with structured vector population and seasonality. J. Appl. Math. 2017;2017 [Google Scholar]
- 23.Zhao D., Li L., Peng H., Luo Q., Yang Y. Multiple routes transmitted epidemics on multiplex networks. Phys. Lett. A. 2014;378(10):770–776. [Google Scholar]
- 24.Al-qaness M.A., Ewees A.A., Fan H., Abd El Aziz M. Optimization method for forecasting confirmed cases of covid-19 in china. J Clin Med. 2020;9(3):674. doi: 10.3390/jcm9030674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hellewell J., Abbott S., Gimma A., Bosse N.I., Jarvis C.I., Russell T.W., Munday J.D., Kucharski A.J., Edmunds W.J., Sun F., et al. Feasibility of controlling covid-19 outbreaks by isolation of cases and contacts. Lancet Glob. Health. 2020 doi: 10.1016/S2214-109X(20)30074-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shen M., Peng Z., Xiao Y., Zhang L. Modelling the epidemic trend of the 2019 novel coronavirus outbreak in China. bioRxiv. 2020 doi: 10.1016/j.xinn.2020.100048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kumar A., Srivastava P.K., Takeuchi Y. Modeling the role of information and limited optimal treatment on disease prevalence. J. Theor. Biol. 2017;414:103–119. doi: 10.1016/j.jtbi.2016.11.016. [DOI] [PubMed] [Google Scholar]
- 28.Agusto F.B., Del Valle S.Y., Blayneh K.W., Ngonghala C.N., Goncalves M.J., Li N., Zhao R., Gong H. The impact of bed-net use on malaria prevalence. J. Theor. Biol. 2013;320:58–65. doi: 10.1016/j.jtbi.2012.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gbadamosi B., Ojo M.M., Oke S.I., Matadi M.B. Qualitative analysis of a dengue fever model. Math. Comput. Applic. 2018;23(3):33. [Google Scholar]
- 30.Misra A.K., Rai R.K., Takeuchi Y. Modeling the control of infectious diseases: effects of tv and social media advertisements. Math. Biosci. Eng. 2018;15(6):1315. doi: 10.3934/mbe.2018061. [DOI] [PubMed] [Google Scholar]
- 31.Freedman H., So J.-H. Global stability and persistence of simple food chains. Math. Biosci. 1985;76(1):69–86. [Google Scholar]
- 32.Okedoye A., Salawu S., Oke S., Oladejo N. Mathematical analysis of affinity hemodialysis on t-cell depletion. Sci. Afr, 2020:e00427. [Google Scholar]
- 33.Diekmann O., Heesterbeek J.A.P., Metz J.A. On the definition and the computation of the basic reproduction ratio r 0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990;28(4):365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
- 34.Van den Driessche P., Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002;180(1–2):29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- 35.Arriola L., Hyman J. Lecture Notes, Forward and Adjoint Sensitivity Analysis: with Applications in Dynamical Systems. Linear Algebra and Optimisation Mathematical and Theoretical Biology Institute, Summer; 2005. [Google Scholar]
- 36.Olabisi O.T., Olaniyi A.M. Mathematical analysis of malaria-pneumonia model with mass action. Int. J. Appl. Math. 2014;29(2):1333. [Google Scholar]
- 37.Iyiola O.S., Zaman F. A fractional diffusion equation model for cancer tumor. AIP Adv. 2014;4(10):107121. [Google Scholar]
- 38.Adeniyi M., Kolawole M. Solution of lie’nard equations using modified initial guess variational iterative method (migvim) J. Nig. Assoc. Math. Phys. 2012;20(1):61–64. [Google Scholar]
- 39.Oke S., Matadi M., Xulu S. Cost-effectiveness analysis of optimal control strategies for breast cancer treatment with ketogenic diet. Far. East J. Math. Sci. 2018;109(2):303–342. [Google Scholar]
- 40.Cheng V.C., Wong S.C., Chen J.H., Yip C.C., Chuang V.W., Tsang O.T., Sridhar S., Chan J.F., Ho P.L., Yuen K.Y. Escalating infection control response to the rapidly evolving epidemiology of the Coronavirus disease 2019 (COVID-19) due to SARS-CoV-2 in Hong Kong. Infection Control & Hospital Epidemiology. 2020;41(5):493–498. doi: 10.1017/ice.2020.58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Alzaatreh A., Lee C., Famoye F. T-Normal family of distributions: a new approach to generalize the normal distribution. J. Stat. Distrib. Appl. 2014;1(1):16. [Google Scholar]
- 42.Jandrić P. Postdigital research in the time of covid-19. Postdig. Sci. Educ. 2020:1–6. [Google Scholar]


