Abstract
Classification of COVID-19 X-ray images to determine the patient’s health condition is a critical issue these days since X-ray images provide more information about the patient’s lung status. To determine the COVID-19 case from other normal and abnormal cases, this work proposes an alternative method that extracted the informative features from X-ray images, leveraging on a new feature selection method to determine the relevant features. As such, an enhanced cuckoo search optimization algorithm (CS) is proposed using fractional-order calculus (FO) and four different heavy-tailed distributions in place of the Lévy flight to strengthen the algorithm performance during dealing with COVID-19 multi-class classification optimization task. The classification process includes three classes, called normal patients, COVID-19 infected patients, and pneumonia patients. The distributions used are Mittag-Leffler distribution, Cauchy distribution, Pareto distribution, and Weibull distribution. The proposed FO-CS variants have been validated with eighteen UCI data-sets as the first series of experiments. For the second series of experiments, two data-sets for COVID-19 X-ray images are considered. The proposed approach results have been compared with well-regarded optimization algorithms. The outcomes assess the superiority of the proposed approach for providing accurate results for UCI and COVID-19 data-sets with remarkable improvements in the convergence curves, especially with applying Weibull distribution instead of Lévy flight.
Keywords: COVID-19, Heavy-tailed distributions, Cuckoo search, Fractional-order cuckoo search, Lévy fight
1. Introduction
The first cases of coronavirus disease (COVID-19) were registered in Wuhan, an important city of China, in December 2019. COVID-19 is originated by a virus called SARS-CoV-2, and currently, it is one of the major concerns worldwide. By the middle of April 2020, the affectations of COVID-19 in humans can be summarized in more than 150,000 deaths and almost 1,700,00 confirmed cases worldwide [1]. These amounts are evidence of the fast dissemination in the population. The symptoms of COVID-19 known until now include fever, cough, sore throat, headache, fatigue, muscle pain, among others [2]. The test for detection of COVID-19 commonly used is invasive, and it is called a reverse transcription-polymerase chain reaction (RT-PCR) [3]. COVID-19 is not only affecting the health of the nations but also the consequences of the diseases are important (e.g., economic and psychological [4], [5]). Another important consideration is that prompt detection could be reflected in early treatment. Then COVID-19 is a pandemic whit a large number of challenges to face. Based on the above information, they are required tools that permit the detection of this mortal disease in a timely manner.
On the other hand, the use of medical images to diagnose disease has increased in the latest years. Different computer vision and image processing tools can be used to identify the abnormalities produced by the illnesses. One of the main advantages of using this kind of system is that the detection is fast and accurate. However, the results must be validated by an expert. In this way, medical image processing algorithms can be used as a primary diagnosis that provides a clue about a possible disease. In the case of COVID-19, the use of X-ray images permits to study how the virus is affecting the lungs. Since COVID-19 is a recent virus, only a few data-sets are available, and the number of works related to them is also reduced.
A number of studies have been proposed to classify COVID-19 from X-ray scan images using different techniques, such as DenseNet201 [6], MobileNet v2 [7], DarkNet [8], and others [9], [10], [11], [12]. In general, the medical images can be directly analyzed to identify certain elements in the scene that permits the diagnosis. However, it is also common to extract different features from all the images and create a set that contained the information of the objects contained in the images [13]. In this case, not all the features extracted could provide essential information about the disease that is going to be detected; for that reason, it is necessary to use automatic tools that remove the non-desired (irrelevant or duplicated) elements.
Feature Selection (FS) is an important pre-processing tool that helps to extract the information desired from the irrelevant data [14], [15], [16]. FS helps in reducing the dimensionality of the data by selecting only the relevant information in the next steps. With this pre-processing, the machine learning could be applied more efficiently over the data-set by decreasing computational effort [17], [18]. The use of FS has been extended for to different domains, for example in bio-medicine for diagnosis of neuromuscular disorders [19], in signal processing for speech emotion recognition [20], in internet of things specially for medicine with EEG signals [21], human activity recognition [22] and text classification [23], to mention some. The FS works by maximizing the relevance of the features, but also the redundancy could be minimized. In comparison to other methods, FS preserver the data by not applying domain transformations; then, the FS operates by including and excluding the attributes in the data-set without any modification. The FS has three main advantages, (1) it improves the prediction performance, (2) it permits a better understanding of the processes that fastly generate the data, and (3) it has more effective predictors with lower computational cost [24]. According to Pinheiro et al. [25], they exist two kinds of FS method, namely the wrapper and filter methods. The most popular approaches are the wrapper-based because they provide more accurate results [26]. The wrapper FS method needs an internal classifier to find a better subset of features; this could affect their performance, especially with large data-sets. Moreover, they also have backward and forward strategies to add or remove features that become non-suitable for a larger amount of features. Considering these drawbacks, meta-heuristic algorithms (MA) are used to increase the performance of FS processes.
MA have become more popular in recent years due to their flexibility and adaptability [27]. MA can be used in a wide range of applications, and FS is not an exception. Some classical approaches Genetic Algorithms (GA) [28], Particle Swarm Optimization (PSO) [29] and Differential Evolution (DE) [30] have been successfully used to solve the FS problem. More so, modern MA algorithms also have been applied for FS, such as Grasshopper Optimization Algorithm (GOA) [31], Competitive Swarm Optimizer (CSO) [32], Gravitational Search Algorithm (GSA) [33], and others. since FS can be seen as an optimization problem, there is not MA able to handle all the difficulties in FS. This last fact is defined according to the No-Free-Lunch (NFL) theorem [34]; therefore, it is necessary to continue exploring new alternative MA.
An interesting MA is the Cuckoo Search (CS) algorithm introduced by Yang and Deb [35], [36] as a global optimization method inspired by the breeding behavior of Cuckoo birds (CB). CS is a population-based method that employs three basic rules that mimic the brood parasitism of the Cuckoo bird. In nature, the female CB lays the eggs in the nest of other species. Some CB species can imitate the color of the eggs of the nest where they will be laid. In the CS context, a set of host nest containing eggs (candidate solutions) are randomly initialized, then only one Cuckoo egg is generated in each generation using Lévy Flights. After that, a random host nest is chosen, and its egg is evaluated using a fitness function. The fitness value of the Cuckoo egg and the one selected from a random host nest are compared, the best egg is preserved in the host nest. A fraction of the worst nest is abandoned in each generation, and the best solutions are preserved [35]. The use of CS for several applications has been increased in recent years [37], [38]. The CS is an interesting alternative for solving complex optimization problems. However, the CS has the disadvantage that it can fall into sub-optimal solutions [39]; this is caused due to inappropriate balance between exploration and exploitation phases. To overcome such drawbacks, they have been introduced some modifications of the standard CS.
Recently, an interesting approach called fractional-order cuckoo search (FO-CS) is proposed to include the use of fractional calculus to enhance the performance of the CS [40]. The FO-CS possesses better convergence speed than the CS; besides, the balance between exploration and exploitation produced by the fractional calculus permits more accurate solutions to complex optimization problems. Nevertheless, several other approaches can be included with FO-CS for further performance enhancement.
This paper presents the use of heavy-tailed distributions instead of Lévy flights in the FO-CS. This kind of distribution has been used to enhance the mutation operator in evolutionary algorithms and other MA [41], [42]. Using the heavy-tailed distributions, it is possible to escape from non-prominent regions of the search space [41]. The distributions used in to enhance the FO-CS are the Mittag-Leffler distribution (ML) [43], the Pareto distribution (P) [44], the Cauchy distribution (C) [45], and the Weibull distribution (W) [46]. The FO-CS based on heavy-tailed distributions is proposed as an alternative method for solving features selection problems. In this context, the experimental results include different tests considering eighteen data-sets from the UCI repository [47]. The comparisons included different MA from the state-of-the-art, where the proposed approach provides better results in terms of accuracy and convergence. Moreover, the most important contribution of this work is the use of the FO-CS based on heavy-tailed distributions for FS over a COVID-19 data-set. Over this experiment, the results obtained by the proposed method permits to accurately identify three different classes, namely normal patients, COVID-19 infected patients, and Pneumonia patients. Regarding the results of UCI and COVID-19 data-sets, different statistical and metrics validate the good performance of the FO-CS based on heavy-tailed distributions, especially Weibull distribution. The main contribution of the current study can be summarized as follows:
-
1.
Provide an alternative COVID-19 X-ray image classification method which aims to detect the COVID-19 patient from normal and abnormal cases.
-
2.
Extracting features from X-ray images then using a new feature selection method to select the relevant features.
-
3.
Develop feature selection method using a modified CS based on the fractional concept and heavy-tailed distributions.
-
4.
Evaluate the developed method using two data-set for real COVID-19 X-ray images.
-
5.
Compare the new developed FS method with other recently implemented FS methods.
The rest of the paper is organized as follows. Section 2 presents the related works. Section 3 introduces the basics of heavy-tailed distributions, CS, and FO-CS. Section 4 explains the proposed modified FO-CS, in Section 5 presents the experimental results and comparisons. Finally, in Section 6, the conclusions and future work are discussed.
2. Related works
In this section, we present a simple review of the existing works of COVID-19 medical image classification, the applications of MA for feature selection, and the recent applications of the CS.
Recently, some studies have been presented to classify and identify COVID-19 from chest X-ray images using different techniques. Pereira et al. [48] applied CNN to extract texture features from chest X-ray images. They applied resampling techniques to balance the distribution of the classes to implement a multi-classification process. Ozturk et al. [8] applied a deep learning-based approach for determining COVID-19 for X-ray scan images. They used DarkNet model to classify images into binary classification and multi-classification. For binary classification, images were classified into COVID or no-findings. For the multi-classification, images were classified into three classes, COVID, pneumonia, and no-findings. Elaziz et al. [49] proposed a machine learning-based model to classify COVID-19 X-ray images into two classes, COVID or non-COVID. They proposed a feature extraction method called fractional multichannel exponent moments to extract features from X-ray scan images. Thereafter, they applied an improved Manta-Ray Foraging Optimization algorithm as a feature selection method to select the most relevant features. In [9], the authors evaluated several convolutional neural network models with different X-ray scan images that include, COVID-19, normal incidents and bacterial pneumonia. Ouchicha et al. [50] proposed a deep learning-based approach for COVID-19 classification, called CVDNet, which is built by using the residual neural network. The evaluation outcomes showed that CVDNet could achieve a high detection accuracy on a small dataset. In [51], the authors proposed a deep learning approach, namely COVIDX-Net for COVID-19 diagnosis from chest x-ray scan images. COVIDX-Net depends on seven deep learning architectures. It was evaluated with 50 X-ray images, and it showed a good performance. In [52], a new model called CoroNet is proposed for COVID-19 detection from both of CT and X-ray images. Xception architecture is used to build CoroNet, and ImageNet datasets are applied to train it. It showed an acceptable performance for several classes with an average accuracy of 89.6 Toraman et al. [53] presented a Convolutional CapsNet model for COVID-19 detection from X-ray images. The proposed model was applied for binary classification (COVID-19, and None- COVID) and also for multi-class classification. Furthermore, Jain et al. [54] applied a deep learning model based on ResNet-101 for COVID-19 X-ray image classification. The proposed model achieved significant performance using several performance measures. Hassantabar et al. [55] applied deep neural network (DNN) and convolutional neural network (CNN) to detect infected lung tissue of COVID-19 patients form X-ray scans. Furthermore, there are different approaches for COVID-19 X-ray images classification, such as MobileNet v2 [7], DenseNet201 [6], and others [10], [11], [12]. In recent years, the modern MA have been widely applied for FS. for example, in [56] it has been proposed the use of the Grasshopper Optimization Algorithm (GOA) to identify the best subset of features, the use of Crow Search Algorithm (CSA) with chaotic maps has also been proposed for FS using different benchmark data-sets [31]. Another interesting work includes the implementation of the Competitive Swarm Optimizer (CSO) for FS [32]; the advantage of CSO is its capability to handle high-dimension optimization problems. In [33], an evolutionary version of the Gravitational Search Algorithm (GSA) is introduced for FS, and the use of mutation and crossover operators enhance the performance of the standard GSA. Besides using the hybrid Particle Swarm Optimization (PSO) to extract the optimal features of different benchmark data-sets. Too and Mirjalili [57] proposed an FS approach based on a hyper learning binary dragonfly algorithm. They applied the proposed approach for different FS datasets, including the COVID-19 patient health prediction dataset. All these approaches are novel, and their performance is relevant. However, they have some disadvantages; the first is that, like many other meta-heuristics, they can fail into sub-optimal solutions; the second is related to their use only in benchmark sets. Finally, since FS can be seen as an optimization problem, there is not MA able to handle all the difficulties in FS. This last fact is defined according to the No-Free-Lunch (NFL) theorem [34]; therefore, it is necessary to continue exploring new alternative MA.
The cuckoo search (CS) is one of the algorithms that have been applied for several applications has been increased in recent years [37], [38]. The CS is an interesting alternative for solving complex optimization problems. However, the CS has the disadvantage that it can fall into sub-optimal solutions [39]; this is caused due to inappropriate balance between exploration and exploitation phases. To overcome such drawbacks, they have been introduced some modifications of the standard CS. For example, in [58], the authors proposed the hybridization of CS with the Chaotic Flower Pollination algorithm (CFPA) for maximizing area coverage in Wireless Sensor Networks. The Reinforced Cuckoo Search Algorithm (RCSA) is presented by Thirugnanasambandam et al. [59] for multi-modal optimization, the RCSA contains three operators called modified selection strategy, Patron-Prophet concept, and self-adaptive strategy. An enhanced version of the CS that includes the quasi-opposition based learning and other two strategies is introduced in [60] for the parameter estimation of photovoltaic models. Another recent approach of fractional-order cuckoo search (FO-CS) including the use of fractional calculus was proposed for identifying the unknown parameters of the chaotic, hyper-chaotic fractional-order financial systems [40]. The proposed FO-CS exposed its efficiency in solving set of known mathematical benchmarks as well with a remarkable convergence speed in comparison with the basic CS.
3. Background
In this section, the essential knowledge about the features extraction and feature selection approaches from images are explained in detail. Moreover, we introduce an overall background about the integrated parts in the novel optimizer variants that are the heavy-tailed distributions and the novel fractional-order cuckoo search optimizer (FO-CS) as described below:
3.1. Image features extraction techniques
In this study, the image features are extracted using the following techniques, the Fractional Zernike Moments (FrZMs), Wavelet Transform (WT), Gabor Wavelet Transform (GW), and Gray Level Co-Occurrence Matrix (GLCM). Brief descriptions of these techniques are listed below.
3.1.1. Fractional Zernike Moments (FrZMs)
The FrZMs are used to extract gray images features as presented by [61]. This process is shown in Eq. (1) [62].
| (1) |
where denotes the fractional parameter, . is a gray image. denotes the real valued radial polynomial as, and it is calculated by Eq. (2). and define the order which and be even, .
| (2) |
The calculation of need a linear mapping transformation of image coordinates system to a proper space inside a unit circle because they are determined in polar coordinates () where [63]. This step is calculated by Eq. (3)
| (3) |
| (4) |
where , . N defines the pixels number in the image.
3.1.2. Wavelet Transform (WT)
The WT is a method used for signal analysis and feature extraction [64]. It breaks up a signal into scaled and shifted versions of the mother wavelet. It is represented by the sum of the signal multiplied by the shifted and scaled versions of the wavelet function (). The continuous WT (CWT) of a signal can be computed as:
| (5) |
| (6) |
where denotes the mother wavelet. and and represent the shifted and scaled parameters, respectively. is not equal to zero.
3.1.3. Gabor Wavelet Transform (GW)
The GW is a popular technique used filters for extracting image features [65]. It is calculated by Eq. (7).
| (7) |
where and represent the kernels’ orientation and scale. denotes the Gabor vector as in Eq. (8).
| (8) |
where, equals . represents the max frequency. represents the spacing factor among kernels in the frequency space. equals .
3.1.4. Gray Level Co-Occurrence Matrix (GLCM)
The GLCM technique is a statistical technique which applied to extract the texture features from an image [66].
The GLCM uses five equations to perform its task as follow:
-
•The contrast () equation represents the amount of local variations in an image . Eq. (9) calculates this equation.
(9) -
•The correlation () equation represents the relationship among the image pixels. Eq. (10) calculates this equation.
(10) -
•The energy equation represents the textural uniformity. Eq. (11) calculates this equation.
(11) -
•The entropy equation defines the intensity distribution randomness. Eq. (12) calculates this equation.
(12) -
•The homogeneity () equation defines the distribution closeness. Eq. (13) calculates this equation.
where defines the gray levels in the image. is the number of transitions between and .(13)
3.2. Heavy-tailed distributions overview
Random walking has an important effect on the efficiency and quality of the MA. The Lévy flight distribution may consider the most popular random walk whereby the jump-lengths have a heavy-tailed probability distribution. That is why the Lévy flight distribution is employed in MA to be a more effective source for the random walk than the Gaussian distribution.
For the heavy-tailed distributions, there are several types of distributions, such as Mittag-Leffler distribution, Cauchy distribution, Pareto distribution, and Weibull distribution can be applied to the MA to emulate the random walk in the algorithms. In this section, we present the details and the mathematical formulas of those heavy-tied distributions and their charts as follows;
-
•Mittag-Leffler distribution (ML) [43]: a random variable has been followed the ML distribution that its distribution can be defined via the following function;
where ML distribution is a heavy-tailed when the ¿ 0 and . The symbols and are the scale and shape parameters, and they take the value of 4.5, and 0.8, respectively. The symbols of and denote uniform random numbers. The is a Mittag-Leffler random number.(14) -
•Pareto distribution (P) [44]: a random variable has been followed the Pareto distribution if it has the following tail pattern as below:
where and are the scale and shape parameters and have values of 1.5 and 4.5, respectively.(15) -
•Cauchy distribution (C) [45]: a random variable has been followed the Cauchy distribution if it has the following tail formula as below:
where and are the scale and location parameters, and they have values of 4.5 and 0.8, respectively.(16) -
•Weibull distribution (W) [46]: a random variable has been shown to follow the Weibull distribution if it has the following tail formula as below:
where and are the scale and shape parameters. The Weibull Distribution is a heavy-tied when has values less than 1. Therefore in the current work, the tuned values of , and are 4 and 0.3, respectively.(17)
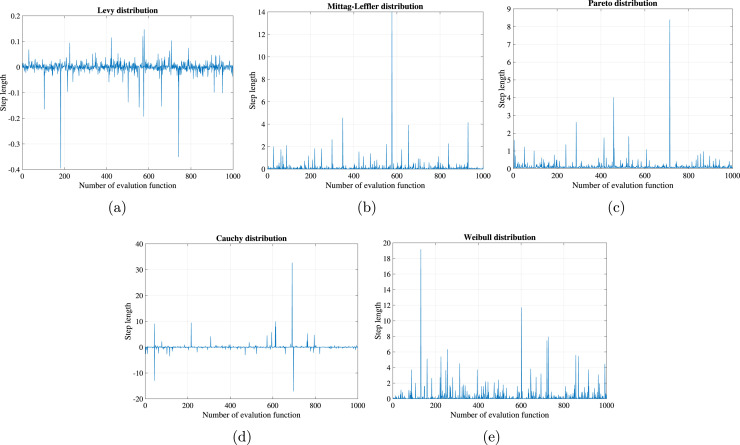
The charts for the jump-length of the proposed distributions with a scaling factor of 0.01 against the number of functions evaluation are plotted in Fig. 1. By inspecting the figures, once can detect that (I) the Lévy and Cauchy distributions are two-sided distributions where the random numbers have positive and negative values. (II) Mittag-Leffler, Pareto, and Weibull distributions are one-side distributions as the random numbers have positive values. (III) All the distributions expose long jumps (steps) frequently with different step values.
Fig. 1.
Heavy-tailed distributions for (a) Lévy distribution, (b) Mittag-Leffler, (c) Pareto distribution, (d) Cauchy distribution, and (e) Weibull distribution.
3.3. Cuckoo search
The cuckoo search (CS) has been innovated by Yang et al. ([36]) inspiriting from the natural behavior of cuckoo breeding parasitism. In ([36]), authors modeled that behavior mathematically via three hypotheses mainly (I) each cuckoo lays one egg at a time, and (II) cuckoo puts egg in a nest that chosen randomly, and the fittest is retained for the next generation (III) the available host nests number is bounded, and a host cuckoo can detect a stranger egg with a probability . These behaviors can be formulated mathematically using fights. For each cuckoo , a new solution is obtained based on flight as in Eq. (18).
| (18) |
where 0 is the step size, as per the literature, it is tuned as . flight is a random walk, and its jumps are computed from a distribution.
For the local random walk, the solution will be updated using the following equation;
| (19) |
where the product denotes entry-wise multiplications. Where and are two randomly selected solutions. The is a Heaviside function, is the step size, and is a random number drawn from a uniform distribution. Yang et al. ([36]) utilized a switching probability to transmit amongst the local and global random walk and assumed its values as 0.25 to achieve a balance in the transmission stage.
3.4. Fractional-order cuckoo search
Recently Yousri et al. [40] proposed a novel variant for CS algorithm to improve the global cuckoo walk of Eq. (18) via accounting the memory prospective of cuckoo during motion based on fractional-calculus (FC) method. In the FO-CS, four previous terms from memory are saved for each cuckoo during its motion, and that memory has been modified based on the first input first output concept. Moreover, the switching probability has been computed based on Beta function and FC parameters as follow:
-
•The enhanced global random walk of cuckoo based on the previous four terms from memory (m 4) is updated as follow;
where refers to the derivative order coefficient [40]. The authors strongly believe that with increasing the memory terms, the execution time has been increased; therefore, in the current study, the number of terms is selected as m = 4 to maintain an acceptable execution time.(20) -
•In the FO-CS, the switching probability has generated using the distribution. The function is calculated for from 0.1 to with step 0.1 and number of memory terms () using Eq. (21b).
(21a)
where refers to the beta function with inputs of the derivative order vector () that is varied from 0.1 to with step 0.1 and memory terms is . The generated distribution has minimum and maximum values and . The normalization interval ranges are and . The denotes the index of the derivative order. The recommended value of the derivative order is 0.3 therefore the index is 3 [40].(21b)
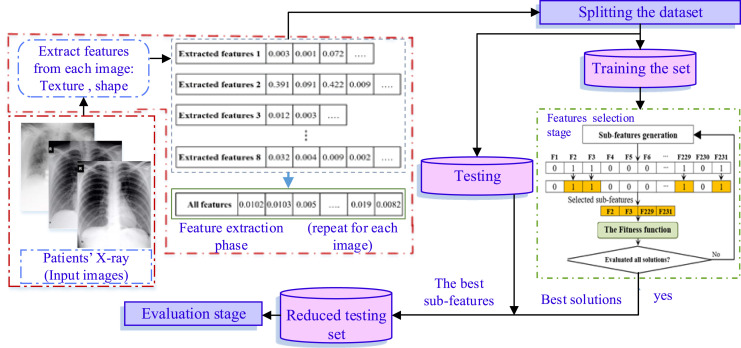
4. Proposed methodology
The structure of the proposed COVID-19 classification approach is given in Fig. 2, and the following steps summarized this structure. In general, the proposed COVID-19 classification method consists of two stages. The first stage is to extract the features using a set of methods, as discussed in Section 3.1. The second stage is to select the relevant features from those extracted features. To achieve this task, a modified FO-CS based on heavy-tailed distributions is implemented as a feature selection method. Where combining among the heavy-tailed distributions and FO-CS in place of the lévy flight distribution, open the door for new four variants of the FO-CS algorithm that can be viewed as FO-CS, FO-CS, FO-CS, FO-CS, and FO-CS. For the first variant FO-CS, the Mittag-Leffler used in place of lévy flight. For the FO-CS, FO-CS, FO-CS, and FO-CS variants, the Pareto, Cauchy, and Weibull distributions, respectively, merged with FO-CS in place of lévy flight. Sequentially, the mathematical equation of Eq. (20) can be rewritten as follows for the four variants:
| (22) |
| (23) |
| (24) |
| (25) |
Fig. 2.
The structure of FO-CS FS COVID-19 detection/classification approach.
The details of the stages of the proposed method are given as presented below:
4.1. Stage 1: Extract features
In this stage, the X-ray COVID-19 images are used as input to our methods. Then, for each image in the current data-set, a set of features are extracted using Fractional Zernike moments, Wavelet, Gabor Wavelet, and GLCM, as discussed in Section 3.1. All of these features are collected in one matrix, where each row represents the extracted features from its corresponding COVID-19 image. This matrix of extracted features is used as an input to the second stage (i.e., to the developed FO-CS method) to determine the irrelevant features that are removed and the relevant features that are kept.
4.2. Stage 2: Features selection
This stage is considered the main core of the proposed COVID-19 detection using X-ray images. Since it aims to normal and abnormal images first, then determines COVID-19 patients from abnormal images. This aim is achieved by using the following steps:
4.2.1. Step 1: Construct initial population
The developed feature selection FO-CS method begins by dividing the data-set (features from the first stage) into training and testing sets, which represent 80% and 20% from the data-set, respectively. Then constructing a population of real-valued solutions generated from a uniform random number. This step is formulated as:
| (26) |
In the above equation, the and denote the lower and upper boundaries of search space at dimension , and is a random number drawn from uniform distribution in the interval of [0 1].
4.2.2. Step 2: updating solutions
In this step, the solutions starting their updating by computing the fitness value of each of them. Since the FS problem is a discrete problem, so we convert the real-value of each solution to binary to deal with this type of problem. This process is formulated using the following equation.
| (27) |
Then features that corresponding 1’s in are selected, and the other features are removed. Followed by using Eq. (28) to evaluate the performance of those selected features.
| (28) |
represents the fitness value of the th solution. denotes the error of classification using the KNN classifier. is the number of selected features (i.e., the number of features which corresponding to ones in ). denotes a uniform random number used to make a balance between two parts of the fitness value.
The next process is that the solutions will be updated using the operators of the FO-CS algorithm and one of the heavy tail distributions. This performed by generating a step size in basis of the utilized distribution (i.e., Mittag Leffler Eq. (22), or Pareto Eq. (23), or Cauchy Eq. (24), or Weibull Eq. (25), or Levy flight Eq. (20)), respectively to update the current solution. Then using Eq. (21b) to compute the switching probability and applied to discover the solution that will be replaced by new ones. Before starting a new iteration, the memory window can be updated using first in first out approach, as depicted in Algorithm 1.
4.2.3. Step 3: Terminal conditions of training
The main target of this step is to check whether the second step will be conducted again or not. This is achieved by checking if the terminal conditions are reached or not. In the case they are not reached, then step 2 (i.e., updating solution) is repeated again; otherwise, it will return by best solution .
4.2.4. Step 4: Evaluate best solution
In this step, the testing set is used as input to KNN; however, their features that are corresponding to 0’s in will be removed. Then predict the target of the testing set and compute the performance of this output using different metrics.
5. Simulation and results
To validate the performance of the developed COVID-19 detection method, a set of experimental series is performed. The main aim of the first experimental series is to evaluate the performance of the main core of our COVID-19 detection (i.e., FO-CS based on heavy-tailed distributions), a set of eighteen UCI data-sets is used. Meanwhile, the second experimental series aims to test the applicability of the developed COVID-19 detection method by using two real-world COVID-19 images which have different characteristics.
5.1. Experimental Series 1: FS using UCI data-sets
In this experimental, eighteen well-regarded data-sets of UCI [47] source are used. These data-sets specifications are listed in Table 1. As noted from Table 1, the examined benchmark problems diverse from the small to the high dimension to evaluate the efficiency of the proposed algorithm. In this study, the first stage of the proposed classification COVID-19 X-ray images (i.e., feature extraction) not used.
Table 1.
Data-sets description [47].
| Data-sets | Number of features | Number of instances | Number of classes | Data category |
|---|---|---|---|---|
| Breastcancer (DS1) | 9 | 699 | 2 | Biology |
| BreastEW (DS2) | 30 | 569 | 2 | Biology |
| CongressEW (DS3) | 16 | 435 | 2 | Politics |
| Exactly (DS4) | 13 | 1000 | 2 | Biology |
| Exactly2 (DS5) | 13 | 1000 | 2 | Biology |
| HeartEW (DS6) | 13 | 270 | 2 | Biology |
| IonosphereEW (DS7) | 34 | 351 | 2 | Electromagnetic |
| KrvskpEW (DS8) | 36 | 3196 | 2 | Game |
| Lymphography (DS9) | 18 | 148 | 2 | Biology |
| M-of-n (DS10) | 13 | 1000 | 2 | Biology |
| PenglungEW (DS11) | 325 | 73 | 2 | Biology |
| SonarEW (DS12) | 60 | 208 | 2 | Biology |
| SpectEW (DS13) | 22 | 267 | 2 | Biology |
| Tic-tac-toc (DS14) | 9 | 958 | 2 | Game |
| Vote (DS15) | 16 | 300 | 2 | Politics |
| WaveformEW (DS16) | 40 | 5000 | 3 | Physics |
| WineEW (DS17) | 13 | 178 | 3 | Chemistry |
| Zoo (DS18) | 16 | 101 | 6 | Artificial |
5.2. Comparative algorithms
We compared the improved FO-CS variants with several existing MA, including the original CS, Henry gas solubility optimization (HGSO) [67], Harris hawks optimization (HHO) [68], Genetic Algorithm (GA) [69], Salp Swarm Algorithm (SSA) [70], Whale optimization algorithm (WOA) [71], and Grey wolf optimizer (GWO) [72]. These algorithms are employed based on their original implementation and parameter values. All the algorithms have been implemented with a population size of 15 and a number of iterations of 50 using Matlab R2018b working on Windows 10, 64 bit. Computations were performed on a 2.5 GHz CPU processor with 16 GB RAM.
5.3. Performance measures
In this paper, we employed several performance measures to evaluate the improved FO-CS variants as follows.
-
•Average of accuracy : It is applied to test the efficiency of the algorithm for predicting target labels of each class during a set of runs:
(29) -
•Standard deviation (STD): It is applied to for calculating dispersion between the accuracy value overall runs their average values:
(30) -
•Average of selected features : It is used to test the ability of the algorithm for selecting the smallest relevant features set during all runs as defined by the following equation:
where represents the cardinality of at th run.(31) -
•Average of fitness value : It is employed to test the performance of the algorithm in balancing between the ratio of selecting features and the error:
(32)
5.3.1. Results and discussion
In this section, the results of the proposed fractional-order cuckoo search algorithm using five types of distributions approaches are given; Levy distribution (FO-CS), Mittag-Leffler distribution (FO-CS), Pareto distribution (FO-CS), Cauchy distribution (FO-CS), and Weibull distribution (FO-CS). Table 2 describes the accuracy results of the proposed methods compared to other competitor optimization methods.
Table 2.
Accuracy results for the FO-CS variants along with the compared algorithms.
| Data-set | CS | FO-CS | FO-CS | FO-CS | FO-CS | FO-CS | HHO | HGSO | WOA | SSA | GWO | GA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DS1 | 0.9633 | 0.9729 | 0.9774 | 0.9662 | 0.9695 | 0.9695 | 0.9643 | 0.9752 | 0.9476 | 0.9790 | 0.9567 | 0.9462 |
| DS2 | 0.9476 | 0.9594 | 0.9912 | 0.9611 | 0.9629 | 0.9716 | 0.9731 | 0.9333 | 0.9433 | 0.9719 | 0.9415 | 0.9351 |
| DS3 | 0.9651 | 0.9410 | 0.9877 | 0.9728 | 0.9567 | 0.9322 | 0.9640 | 0.9854 | 0.9448 | 0.9594 | 0.9157 | 0.9609 |
| DS4 | 0.9893 | 0.9998 | 0.9923 | 0.9885 | 0.9915 | 0.9968 | 0.9720 | 0.9743 | 0.8960 | 0.9587 | 0.8987 | 0.8667 |
| DS5 | 0.7403 | 0.7567 | 0.8050 | 0.7395 | 0.7737 | 0.7500 | 0.7450 | 0.7260 | 0.7703 | 0.7653 | 0.7900 | 0.7130 |
| DS6 | 0.8911 | 0.8605 | 0.8802 | 0.9160 | 0.8198 | 0.8691 | 0.9062 | 0.8914 | 0.7988 | 0.8975 | 0.8272 | 0.8753 |
| DS7 | 0.9793 | 0.8704 | 0.9394 | 0.9864 | 0.9343 | 0.9249 | 0.9268 | 0.9117 | 0.9174 | 0.9700 | 0.9380 | 0.9577 |
| DS8 | 0.9370 | 0.9682 | 0.9679 | 0.9753 | 0.9692 | 0.9705 | 0.9725 | 0.9495 | 0.9507 | 0.9655 | 0.9577 | 0.9616 |
| DS9 | 0.9351 | 0.9978 | 0.8767 | 0.9263 | 0.9667 | 0.9943 | 0.9133 | 0.9319 | 0.8821 | 0.9685 | 0.8756 | 0.8844 |
| DS10 | 0.9970 | 1.0000 | 0.9993 | 0.9985 | 0.9965 | 0.9988 | 0.9947 | 0.9853 | 0.9497 | 0.9637 | 0.9627 | 0.9477 |
| DS11 | 0.9133 | 0.9333 | 0.8733 | 0.9333 | 0.9333 | 0.9978 | 0.9556 | 1.0000 | 0.9686 | 1.0000 | 0.9822 | 0.8667 |
| DS12 | 0.9473 | 0.9730 | 0.9008 | 0.9905 | 0.9833 | 0.9730 | 0.9571 | 0.9556 | 0.9825 | 0.9190 | 0.9381 | 0.9937 |
| DS13 | 0.8919 | 0.8889 | 0.9580 | 0.9235 | 0.8401 | 0.8654 | 0.9308 | 0.9148 | 0.7593 | 0.8099 | 0.7716 | 0.8580 |
| DS14 | 0.8389 | 0.8247 | 0.8194 | 0.8399 | 0.8408 | 0.8229 | 0.8177 | 0.8101 | 0.7809 | 0.7990 | 0.7819 | 0.8250 |
| DS15 | 0.9056 | 0.9356 | 0.9317 | 0.9789 | 0.9744 | 0.9289 | 0.9667 | 0.9844 | 0.9622 | 0.9567 | 0.9700 | 0.9600 |
| DS16 | 0.7246 | 0.7538 | 0.7464 | 0.7478 | 0.7444 | 0.7567 | 0.7287 | 0.7283 | 0.7283 | 0.7381 | 0.7186 | 0.75333 |
| DS17 | 0.9741 | 1.0000 | 0.9991 | 1.0000 | 0.9954 | 1.0000 | 0.9981 | 0.9981 | 0.9759 | 1.0000 | 0.9833 | 0.9833 |
| DS18 | 1.0000 | 0.9984 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9968 | 1.0000 | 0.9841 | 1.0000 |
It is apparent from Table 2 that the proposed FO-CS and FO-CS got almost the same response over the proposed methods; each method got five best results out of eighteen. They gave better results than the other proposed methods (i.e., FO-CS, FO-CS, and FO-CS) in terms of the classification accuracy measure. The proposed FO-CS and FO-CS also show almost the same performance over the proposed methods; each method excelled in three cases. They gave better results than only one of the other proposed methods (i.e., FO-CS) according to used measure. The conventional CS performed better than only one of the proposed methods (FO-CS) over all the data-sets utilized in this paper in terms of the classification accuracy measure.
It is worthwhile to mention that the proposed FO-CS and FO-CS got better results in five out of eighteen compared to all other comparative methods (i.e., HHO, HGSO, WOA, SSA, GWO, and GA). Meantime, SSA got the best results in four cases (i.e., DS1, DS11, DS17, and DS18) compared to all other methods. Generally, in terms of the accuracy measure, the proposed FO-CS outperformed the other state-of-the-art methods using various distribution approaches, mainly when used FO-CS and FO-CS.
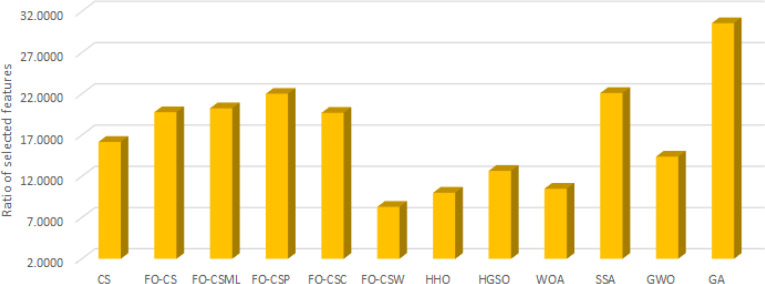
Table 3 shows the number of selected features achieved by the feature selection algorithms. From this Table, we can notice that the proposed FO-CS made the smallest number of features selected in seven data-sets (DS6, DS7, DS11, DS13, DS16, DS17, and DS18). In comparison with the proposed FO-CS methods, the FO-CS got the smallest optimal number of the selected features according to the results of the proposed FO-CS with the used distribution approaches, followed by FO-CS. As well, in comparison with all tested methods, most of the best cases (in terms of the best number of selected features) have been accomplished by the FO-CS. WOA achieved the smallest number of selected features in three data-sets. FO-CS BDA gave a better performance than other methods on most of the used data-sets according to the number of selected feature measures. The high-performance of the FO-CS with Weibull distribution (FO-CS) enhances its capability in reducing the number of selected features.
Table 3.
Selected features results for the FO-CS variants along with the compared algorithms.
| Data-set | CS | FO-CS | FO-CS | FO-CS | FO-CS | FO-CS | HHO | HGSO | WOA | SSA | GWO | GA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DS1 | 1.87 | 3.47 | 3.43 | 2.37 | 3.60 | 3.00 | 1.80 | 3.40 | 2.40 | 3.27 | 2.60 | 4.80 |
| DS2 | 7.97 | 12.47 | 12.67 | 15.33 | 11.90 | 6.30 | 8.60 | 9.33 | 5.67 | 15.73 | 8.47 | 20.87 |
| DS3 | 4.50 | 7.50 | 4.73 | 7.80 | 7.53 | 4.20 | 2.73 | 2.73 | 3.87 | 8.47 | 5.07 | 10.67 |
| DS4 | 7.00 | 6.87 | 7.13 | 7.37 | 7.23 | 7.07 | 6.73 | 8.07 | 8.60 | 8.27 | 6.53 | 9.40 |
| DS5 | 6.73 | 2.97 | 2.03 | 7.43 | 2.83 | 2.10 | 3.50 | 5.67 | 4.33 | 8.20 | 3.40 | 9.40 |
| DS6 | 7.17 | 5.53 | 8.40 | 8.07 | 6.90 | 2.97 | 3.80 | 4.20 | 4.53 | 6.87 | 6.27 | 10.87 |
| DS7 | 13.43 | 15.57 | 17.77 | 19.90 | 16.70 | 5.40 | 9.47 | 8.93 | 8.47 | 19.07 | 8.80 | 28.07 |
| DS8 | 20.83 | 21.33 | 21.43 | 21.03 | 22.27 | 21.80 | 19.07 | 17.80 | 19.00 | 22.93 | 20.67 | 28.87 |
| DS9 | 10.23 | 11.60 | 11.23 | 10.63 | 9.50 | 10.63 | 8.60 | 7.13 | 4.07 | 9.93 | 8.00 | 14.00 |
| DS10 | 7.17 | 7.07 | 7.40 | 7.03 | 7.40 | 7.37 | 7.47 | 8.27 | 9.40 | 8.73 | 8.60 | 9.20 |
| DS11 | 103.67 | 168.63 | 167.13 | 184.17 | 159.20 | 11.73 | 37.20 | 77.73 | 40.53 | 185.33 | 106.80 | 267.27 |
| DS12 | 38.53 | 36.87 | 36.07 | 40.13 | 36.10 | 33.43 | 24.80 | 25.93 | 30.93 | 35.33 | 24.47 | 50.00 |
| DS13 | 11.57 | 5.37 | 14.97 | 13.13 | 11.63 | 1.77 | 8.33 | 7.67 | 3.73 | 12.60 | 6.53 | 16.93 |
| DS14 | 6.00 | 6.00 | 5.80 | 5.93 | 5.90 | 5.97 | 5.93 | 4.67 | 5.40 | 5.87 | 5.27 | 6.33 |
| DS15 | 7.17 | 6.63 | 7.27 | 7.30 | 6.90 | 2.40 | 4.87 | 5.20 | 1.87 | 6.93 | 4.20 | 11.07 |
| DS16 | 24.73 | 26.37 | 24.93 | 25.57 | 25.77 | 16.70 | 18.53 | 19.87 | 22.00 | 26.80 | 19.73 | 34.20 |
| DS17 | 6.80 | 5.73 | 6.70 | 7.27 | 7.27 | 4.07 | 6.20 | 5.27 | 6.27 | 6.60 | 5.47 | 9.47 |
| DS18 | 5.80 | 6.10 | 5.50 | 5.77 | 6.10 | 2.50 | 2.60 | 6.20 | 8.07 | 6.87 | 8.27 | 9.00 |
Table 4 summarizes the mean fitness function values obtained by the proposed algorithms. According to this measure, we can reveal that the proposed FO-CS is a superior method compared to the other proposed methods that are based on using the modified fractional-order cuckoo search algorithm with five various distributions approaches. The proposed FO-CS got the best mean fitness values in four cases, and it is not worse than any other method on most of the use of data-sets. In comparison with all of the given methods in Table 4, FO-CS also outperformed the comparative methods in terms of the mean fitness function except HGSO; they got an equal number of best-obtained results (each method got the best results in two cases).
Table 4.
Results of the mean fitness values for the FO-CS variants along with the compared algorithms.
| Data-set | CS | FO-CS | FO-CS | FO-CS | FO-CS | FO-CS | HHO | HGSO | WOA | SSA | GWO | GA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DS1 | 0.0537 | 0.0629 | 0.0585 | 0.0567 | 0.0674 | 0.0608 | 0.0712 | 0.0601 | 0.0738 | 0.0552 | 0.0679 | 0.1018 |
| DS2 | 0.0647 | 0.0781 | 0.0501 | 0.0861 | 0.0731 | 0.0465 | 0.0636 | 0.0911 | 0.0699 | 0.0777 | 0.0809 | 0.1280 |
| DS3 | 0.0595 | 0.1000 | 0.0406 | 0.0732 | 0.0860 | 0.0873 | 0.0364 | 0.0302 | 0.0738 | 0.0895 | 0.1075 | 0.1018 |
| DS4 | 0.0601 | 0.0530 | 0.0618 | 0.0670 | 0.0633 | 0.0572 | 0.0607 | 0.0852 | 0.1598 | 0.1008 | 0.1415 | 0.1923 |
| DS5 | 0.2855 | 0.2418 | 0.1834 | 0.2916 | 0.2178 | 0.2327 | 0.2155 | 0.2902 | 0.2170 | 0.2743 | 0.1998 | 0.3306 |
| DS6 | 0.1351 | 0.1681 | 0.1724 | 0.1376 | 0.2153 | 0.1406 | 0.1555 | 0.1301 | 0.2160 | 0.1450 | 0.2038 | 0.1958 |
| DS7 | 0.0581 | 0.1624 | 0.1068 | 0.0708 | 0.1083 | 0.0835 | 0.0415 | 0.1057 | 0.0993 | 0.0831 | 0.0817 | 0.1206 |
| DS8 | 0.0815 | 0.0879 | 0.0884 | 0.0806 | 0.0896 | 0.0871 | 0.0739 | 0.0949 | 0.0971 | 0.0947 | 0.0955 | 0.1148 |
| DS9 | 0.1152 | 0.0664 | 0.1734 | 0.1254 | 0.0828 | 0.0642 | 0.1058 | 0.1009 | 0.1287 | 0.0835 | 0.1564 | 0.1818 |
| DS10 | 0.0578 | 0.0544 | 0.0575 | 0.0555 | 0.0601 | 0.0577 | 0.0540 | 0.0768 | 0.1176 | 0.0999 | 0.0998 | 0.1179 |
| DS11 | 0.0919 | 0.1119 | 0.1654 | 0.1167 | 0.1090 | 0.0056 | 0.0121 | 0.0239 | 0.0408 | 0.0570 | 0.0489 | 0.2022 |
| DS12 | 0.0757 | 0.0857 | 0.1494 | 0.0755 | 0.0752 | 0.0800 | 0.0690 | 0.0832 | 0.0673 | 0.1317 | 0.0965 | 0.0890 |
| DS13 | 0.1254 | 0.1244 | 0.1058 | 0.1286 | 0.1968 | 0.1291 | 0.1584 | 0.1115 | 0.2336 | 0.2284 | 0.2353 | 0.2047 |
| DS14 | 0.2117 | 0.2245 | 0.2269 | 0.2100 | 0.2088 | 0.2257 | 0.2360 | 0.2228 | 0.2572 | 0.2461 | 0.2548 | 0.2279 |
| DS15 | 0.0623 | 0.0995 | 0.1069 | 0.0646 | 0.0661 | 0.0790 | 0.0390 | 0.0465 | 0.0457 | 0.0823 | 0.0533 | 0.1052 |
| DS16 | 0.2909 | 0.2875 | 0.2905 | 0.2909 | 0.2945 | 0.2832 | 0.3662 | 0.2942 | 0.2996 | 0.3027 | 0.3026 | 0.3075 |
| DS17 | 0.0531 | 0.0441 | 0.0524 | 0.0559 | 0.0601 | 0.0390 | 0.0429 | 0.0422 | 0.0699 | 0.0508 | 0.0571 | 0.0878 |
| DS18 | 0.0363 | 0.0396 | 0.0344 | 0.0360 | 0.0381 | 0.0063 | 0.0371 | 0.0388 | 0.0533 | 0.0429 | 0.0660 | 0.0563 |
The standard deviation (STD) values of the proposed algorithm’s fitness function are given in Table 5. From these results, it can be seen that the proposed FO-CS exceeded the other proposed methods on most of the used data-sets. According to the STD measure, FO-CS achieved the best results in four cases in terms of the STD measure. Moreover, FO-CS achieved better fitness function results with excellent STD values compared to other comparative methods in the majority of data-sets. Compared to all comparative methods in Table 5, HGSO got the best cases in most data-sets, which means that HGSO is a powerful competitor method in this research. Thus, the proposed FO-CS beets all the comparative methods according to the STD measure.
Table 5.
STD results of the fitness values for the FO-CS variants along with the compared algorithms.
| Data-set | CS | FO-CS | FO-CS | FO-CS | FO-CS | FO-CS | HHO | HGSO | WOA | SSA | GWO | GA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DS1 | 0.0024 | 0.0046 | 0.0055 | 0.0043 | 0.0062 | 0.0038 | 0.0059 | 0.0018 | 0.0113 | 0.0053 | 0.0061 | 0.0120 |
| DS2 | 0.0097 | 0.0109 | 0.0100 | 0.0078 | 0.0107 | 0.0058 | 0.0087 | 0.0058 | 0.0115 | 0.0081 | 0.0114 | 0.0067 |
| DS3 | 0.0125 | 0.0099 | 0.0179 | 0.0104 | 0.0128 | 0.0073 | 0.0064 | 0.0019 | 0.0153 | 0.0087 | 0.0196 | 0.0119 |
| DS4 | 0.0157 | 0.0048 | 0.0202 | 0.0193 | 0.0204 | 0.0110 | 0.0211 | 0.0330 | 0.0963 | 0.0418 | 0.0810 | 0.0823 |
| DS5 | 0.0131 | 0.0172 | 0.0014 | 0.0135 | 0.0095 | 0.0000 | 0.0022 | 0.0417 | 0.0262 | 0.0164 | 0.0049 | 0.0164 |
| DS6 | 0.0101 | 0.0196 | 0.0093 | 0.0112 | 0.0248 | 0.0026 | 0.0175 | 0.0182 | 0.0225 | 0.0240 | 0.0319 | 0.0105 |
| DS7 | 0.0115 | 0.0243 | 0.0136 | 0.0087 | 0.0146 | 0.0096 | 0.0128 | 0.0165 | 0.0177 | 0.0174 | 0.0094 | 0.0091 |
| DS8 | 0.0059 | 0.0066 | 0.0060 | 0.0073 | 0.0053 | 0.0069 | 0.0104 | 0.0079 | 0.0150 | 0.0092 | 0.0141 | 0.0106 |
| DS9 | 0.0220 | 0.0110 | 0.0207 | 0.0209 | 0.0253 | 0.0132 | 0.0256 | 0.0134 | 0.0597 | 0.0132 | 0.0255 | 0.0271 |
| DS10 | 0.0090 | 0.0040 | 0.0053 | 0.0078 | 0.0100 | 0.0085 | 0.0148 | 0.0236 | 0.0410 | 0.0384 | 0.0416 | 0.0425 |
| DS11 | 0.0149 | 0.0027 | 0.0160 | 0.0041 | 0.0017 | 0.0115 | 0.0044 | 0.0116 | 0.0314 | 0.0025 | 0.0266 | 0.0023 |
| DS12 | 0.0104 | 0.0116 | 0.0175 | 0.0109 | 0.0093 | 0.0139 | 0.0213 | 0.0170 | 0.0128 | 0.0168 | 0.0202 | 0.0106 |
| DS13 | 0.0118 | 0.0122 | 0.0166 | 0.0101 | 0.0109 | 0.0158 | 0.0213 | 0.0152 | 0.0072 | 0.0158 | 0.0177 | 0.0119 |
| DS14 | 0.0068 | 0.0062 | 0.0018 | 0.0061 | 0.0120 | 0.0078 | 0.0085 | 0.0093 | 0.0180 | 0.0188 | 0.0177 | 0.0231 |
| DS15 | 0.0070 | 0.0141 | 0.0164 | 0.0089 | 0.0160 | 0.0029 | 0.0050 | 0.0053 | 0.0168 | 0.0173 | 0.0201 | 0.0232 |
| DS16 | 0.0079 | 0.0079 | 0.0071 | 0.0096 | 0.0092 | 0.0089 | 0.0111 | 0.0103 | 0.0174 | 0.0102 | 0.0115 | 0.0085 |
| DS17 | 0.0059 | 0.0078 | 0.0097 | 0.0067 | 0.0118 | 0.0073 | 0.0068 | 0.0097 | 0.0139 | 0.0091 | 0.0117 | 0.0161 |
| DS18 | 0.0050 | 0.0198 | 0.0051 | 0.0042 | 0.0055 | 0.0000 | 0.0056 | 0.0035 | 0.0119 | 0.0052 | 0.0157 | 0.0075 |
For the all feature selection algorithms, the minimum results of the fitness function values are given in Table 6. The obtained results proved that the proposed FO-CS and FO-CS are able to get better results compared to other proposed methods. It got the best results in six out of eighteen cases. However, FO-CS provides average of the best fitness value better than FO-CS overall the tested datasets. The obtained high-performance by the proposed FO-CS algorithm demonstrates its capability to equilibrium the exploration and exploitation during the optimization process. As per the obtained-results, the performance of the proposed FO-CS algorithm is proven on the small-sized data-sets and large-sized data-sets. The three data-sets (i.e., DS17, and DS16) are comparatively large, and the minimum fitness values of the proposed FO-CS is obviously less compared to all other comparative methods.
Table 6.
Min results of the fitness values for the FO-CS variants along with the compared algorithms.
| Data-set | CS | FO-CS | FO-CS | FO-CS | FO-CS | FO-CS | HHO | HGSO | WOA | SSA | GWO | GA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DS1 | 0.0479 | 0.0590 | 0.0526 | 0.0479 | 0.0590 | 0.0590 | 0.0766 | 0.059 | 0.059 | 0.0462 | 0.0573 | 0.083 |
| DS2 | 0.0470 | 0.0582 | 0.0267 | 0.0674 | 0.0516 | 0.0358 | 0.0561 | 0.0786 | 0.0491 | 0.0646 | 0.0607 | 0.1107 |
| DS3 | 0.0313 | 0.0726 | 0.0166 | 0.0541 | 0.0519 | 0.0726 | 0.1056 | 0.0291 | 0.056 | 0.0769 | 0.0664 | 0.0769 |
| DS4 | 0.0462 | 0.0462 | 0.0462 | 0.0462 | 0.0462 | 0.0462 | 0.093 | 0.0538 | 0.0462 | 0.0538 | 0.0462 | 0.0615 |
| DS5 | 0.2455 | 0.2327 | 0.1832 | 0.2455 | 0.2147 | 0.2327 | 0.2327 | 0.2417 | 0.2102 | 0.2505 | 0.1967 | 0.3032 |
| DS6 | 0.1128 | 0.1385 | 0.1308 | 0.1205 | 0.1808 | 0.1397 | 0.1487 | 0.1064 | 0.1731 | 0.1128 | 0.1628 | 0.1692 |
| DS7 | 0.0303 | 0.0976 | 0.0733 | 0.0509 | 0.0713 | 0.0654 | 0.1025 | 0.0654 | 0.0742 | 0.0441 | 0.0674 | 0.1048 |
| DS8 | 0.0683 | 0.0753 | 0.0725 | 0.0669 | 0.0781 | 0.0738 | 0.1004 | 0.0809 | 0.0660 | 0.0822 | 0.0683 | 0.1003 |
| DS9 | 0.0800 | 0.0500 | 0.1289 | 0.0800 | 0.0111 | 0.0333 | 0.0967 | 0.0624 | 0.0471 | 0.0444 | 0.1065 | 0.1322 |
| DS10 | 0.0462 | 0.0462 | 0.0462 | 0.0462 | 0.0462 | 0.0462 | 0.0782 | 0.0538 | 0.0615 | 0.0538 | 0.0538 | 0.0615 |
| DS11 | 0.0640 | 0.1068 | 0.1132 | 0.1086 | 0.1046 | 0.0006 | 0.0652 | 0.0108 | 0.0031 | 0.0532 | 0.0203 | 0.1982 |
| DS12 | 0.0500 | 0.0617 | 0.1126 | 0.0567 | 0.0500 | 0.0500 | 0.1112 | 0.0564 | 0.0481 | 0.1045 | 0.0648 | 0.075 |
| DS13 | 0.1030 | 0.0970 | 0.0667 | 0.1045 | 0.1803 | 0.0939 | 0.1379 | 0.0894 | 0.2182 | 0.2045 | 0.1939 | 0.1773 |
| DS14 | 0.2073 | 0.2214 | 0.2243 | 0.2073 | 0.2026 | 0.2214 | 0.2495 | 0.2179 | 0.2354 | 0.229 | 0.2307 | 0.212 |
| DS15 | 0.0525 | 0.0788 | 0.0663 | 0.0400 | 0.0313 | 0.0700 | 0.0813 | 0.0375 | 0.0363 | 0.0525 | 0.0338 | 0.0625 |
| DS16 | 0.2775 | 0.2688 | 0.2745 | 0.2677 | 0.2751 | 0.2649 | 0.3018 | 0.2758 | 0.273 | 0.2843 | 0.2847 | 0.2951 |
| DS17 | 0.0385 | 0.0308 | 0.0385 | 0.0462 | 0.0308 | 0.0231 | 0.0462 | 0.0308 | 0.0462 | 0.0385 | 0.0385 | 0.0692 |
| DS18 | 0.0250 | 0.0063 | 0.0250 | 0.0313 | 0.0250 | 0.0063 | 0.0063 | 0.0313 | 0.0375 | 0.0313 | 0.0438 | 0.0438 |
According to the last evaluation measure (worst fitness function values), the proposed algorithms using the FO-CS with the used distribution approaches, as shown in Table 7, got better results than the other comparative methods relatively. The proposed FO-CS achieved better results in comparison with the proposed algorithms as well as in comparison with other comparative methods. It obtained high-performance results (worst mean fitness values) in five out of eighteen experimented data-sets.
Table 7.
Worst results of the fitness values for the FO-CS variants along with the compared algorithms.
| Data-set | CS | FO-CS | FO-CS | FO-CS | FO-CS | FO-CS | HHO | HGSO | WOA | SSA | GWO | GA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DS1 | 0.0561 | 0.0766 | 0.0684 | 0.0655 | 0.0766 | 0.0766 | 0.0818 | 0.0637 | 0.0976 | 0.0637 | 0.0818 | 0.1228 |
| DS2 | 0.0819 | 0.0986 | 0.0633 | 0.0995 | 0.0940 | 0.0561 | 0.0774 | 0.1023 | 0.0856 | 0.0882 | 0.1011 | 0.1365 |
| DS3 | 0.0748 | 0.1183 | 0.0769 | 0.0955 | 0.1039 | 0.1056 | 0.0519 | 0.0332 | 0.1037 | 0.1080 | 0.1431 | 0.1330 |
| DS4 | 0.0975 | 0.0660 | 0.1187 | 0.1322 | 0.1412 | 0.0930 | 0.1277 | 0.1547 | 0.2822 | 0.1727 | 0.2372 | 0.3096 |
| DS5 | 0.3090 | 0.2852 | 0.1909 | 0.3130 | 0.2479 | 0.2327 | 0.2211 | 0.3334 | 0.3117 | 0.3000 | 0.2121 | 0.3559 |
| DS6 | 0.1526 | 0.2026 | 0.1859 | 0.1603 | 0.2782 | 0.1487 | 0.1846 | 0.1577 | 0.2513 | 0.2026 | 0.2692 | 0.2090 |
| DS7 | 0.0803 | 0.1924 | 0.1319 | 0.0871 | 0.1378 | 0.1025 | 0.0616 | 0.1299 | 0.1279 | 0.1057 | 0.0996 | 0.1389 |
| DS8 | 0.0951 | 0.1004 | 0.1003 | 0.1003 | 0.1018 | 0.1004 | 0.0891 | 0.1051 | 0.1160 | 0.1089 | 0.1215 | 0.1340 |
| DS9 | 0.1511 | 0.0967 | 0.2278 | 0.1456 | 0.1156 | 0.0967 | 0.1630 | 0.1198 | 0.2467 | 0.1022 | 0.2052 | 0.2278 |
| DS10 | 0.0795 | 0.0615 | 0.0705 | 0.0750 | 0.0917 | 0.0782 | 0.1007 | 0.1219 | 0.1836 | 0.1868 | 0.1785 | 0.2106 |
| DS11 | 0.1197 | 0.1182 | 0.1751 | 0.1274 | 0.1111 | 0.0652 | 0.0206 | 0.0542 | 0.0852 | 0.0618 | 0.0905 | 0.2065 |
| DS12 | 0.0964 | 0.1062 | 0.1721 | 0.0948 | 0.0898 | 0.1112 | 0.1043 | 0.1110 | 0.0867 | 0.1621 | 0.1243 | 0.1081 |
| DS13 | 0.1545 | 0.1379 | 0.1273 | 0.1470 | 0.2227 | 0.1379 | 0.1939 | 0.1439 | 0.2379 | 0.2591 | 0.2652 | 0.2227 |
| DS14 | 0.2325 | 0.2495 | 0.2307 | 0.2290 | 0.2401 | 0.2495 | 0.2465 | 0.2418 | 0.2917 | 0.2964 | 0.2924 | 0.2793 |
| DS15 | 0.0775 | 0.1338 | 0.1288 | 0.0825 | 0.0925 | 0.0813 | 0.0488 | 0.0550 | 0.0950 | 0.1100 | 0.0975 | 0.1438 |
| DS16 | 0.3016 | 0.3074 | 0.3030 | 0.3071 | 0.3074 | 0.3018 | 0.2883 | 0.3152 | 0.3229 | 0.3157 | 0.3215 | 0.3215 |
| DS17 | 0.0635 | 0.0538 | 0.0712 | 0.0692 | 0.0769 | 0.0462 | 0.0558 | 0.0538 | 0.0865 | 0.0692 | 0.0712 | 0.1192 |
| DS18 | 0.0438 | 0.0866 | 0.0438 | 0.0438 | 0.0500 | 0.0063 | 0.0375 | 0.0438 | 0.0804 | 0.0500 | 0.0866 | 0.0688 |
In general, the previous results showed that the best values obtained by FO-CS variants equal to 60% of all measures namely, they obtained the best values in 67% of the accuracy measure in all datasets, 0.50% of the selected features, and 78% of the standard deviation, also 56% of the fitness function values, the minimum, and the worst values. These results indicate that the variants of the proposed method can effectively compete with other algorithms in selecting the most relevant features.
Besides, from the given results, it can be recognized that the fractional-order calculus has increased the efficacy of the proposed algorithms, especially with the Weibull distribution approach in terms of fitness function values. The main reason here is that the proposed FO-CS has evaded from converging towards the local area and improved its exploration functions to address more complex cases. Hence, it can make an excellent trade-off between the exploration and exploitation strategies.
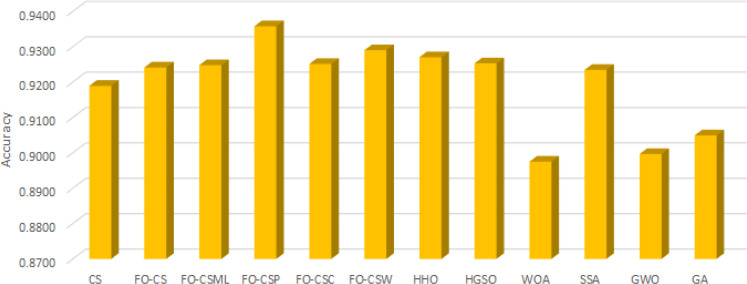
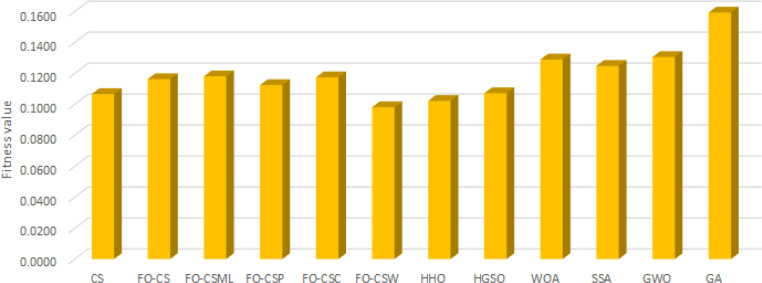
Furthermore, Fig. 3, Fig. 4, Fig. 5 depict the results of the average of the accuracy, the fitness value, and the number of selected features, respectively, for each algorithm overall the tested data-sets. These figures provide extra evidence about the high performance of the proposed FO-CS variants with heavy-tailed distributions as feature selection approaches, which provide better results than the other methods.
Fig. 3.
Average of accuracy overall tested for each algorithm.
Fig. 4.
Average of fitness value overall tested for each algorithm.
Fig. 5.
Average of number of selected feature overall tested for each algorithm.
For further analysis of the results of FO-CS variants, as feature selection approaches, the non-parametric Friedman test [73] is used as in Table 8. From this table, it can be noticed that the FO-CS provides better results in terms of accuracy overall the tested data-set. Whereas, in terms of the number of selected features, FO-CS allocates the first rank with a mean rank of nearly 3.5, and it has the smallest mean rank in terms of fitness value. Moreover, we can see that the FO-CS obtained the first rank in the fitness function and the smallest selected attributes (in these measures, the smallest value is the best), whereas it was ranked third in the accuracy measure (in this measures the largest value is the best). Although the FO-CS was ranked third, the first and the second rank were for the other variants of the proposed method (i.e., FO-CS and FO-CS); therefore, the proposed method variants obtained the first five ranks compared with the other algorithms.
Table 8.
Friedman test results for the first experiment.
| Measure | CS | FO-CS | FO-CS | FO-CS | FO-CS | FO-CS | HHO | HGSO | WOA | SSA | GWO | GA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fitness | 4.47 | 6.11 | 5.94 | 5.42 | 6.67 | 4.06 | 4.33 | 5.56 | 8.11 | 7.61 | 8.72 | 11.00 |
| Rank | 3 | 7 | 6 | 4 | 8 | 1 | 2 | 5 | 10 | 9 | 11 | 12 |
| Attributes | 6.36 | 6.83 | 7.36 | 8.31 | 7.53 | 3.53 | 3.72 | 4.58 | 4.50 | 8.89 | 4.44 | 11.94 |
| Rank | 6 | 7 | 8 | 10 | 9 | 1 | 2 | 5 | 4 | 11 | 3 | 12 |
| Accuracy | 5.72 | 7.22 | 7.78 | 8.86 | 7.42 | 7.69 | 7.14 | 6.36 | 3.69 | 7.17 | 3.86 | 5.08 |
| Rank | 9 | 5 | 2 | 1 | 4 | 3 | 7 | 8 | 12 | 6 | 11 | 10 |
Generally, the proposed FO-CS has a superior exploration search capability due to the used fractional-order calculus between the candidate solutions, which encourage its exploration abilities over the search processes when it is needed and in the following phase, it can efficiently converge on the neighborhood of explored locations by using the Weibull distribution approach, chiefly, through the final iterations. Consequently, this proposed method (FO-CS) has stabilized a balance between the exploration and exploitation strategies, so its influence can be recognized in the enhanced fitness results and the smallest number of selected features compared to all other comparative methods in this research.
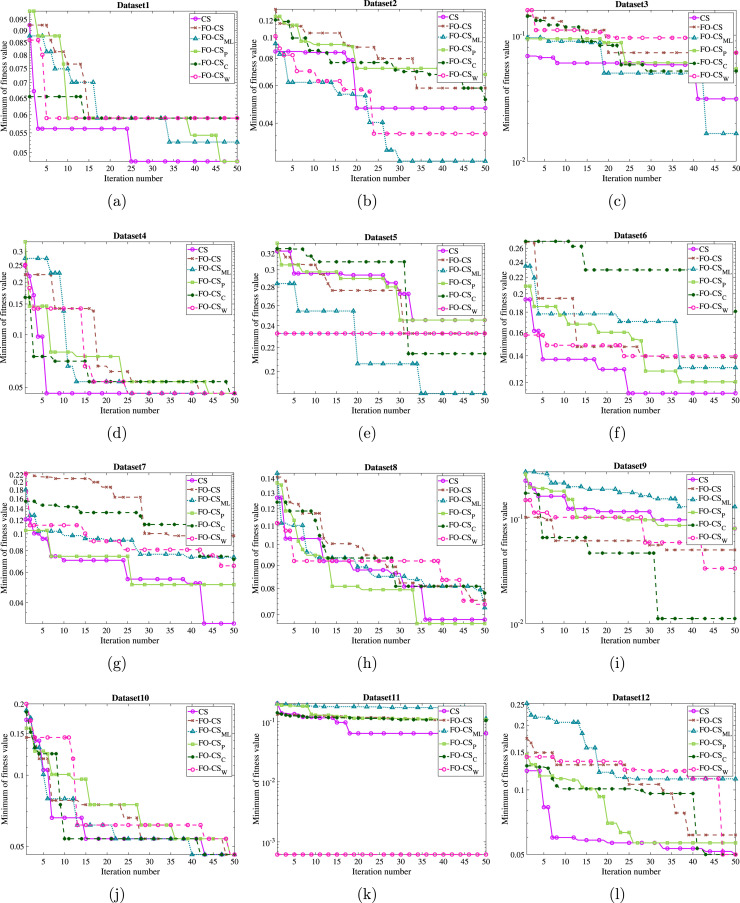
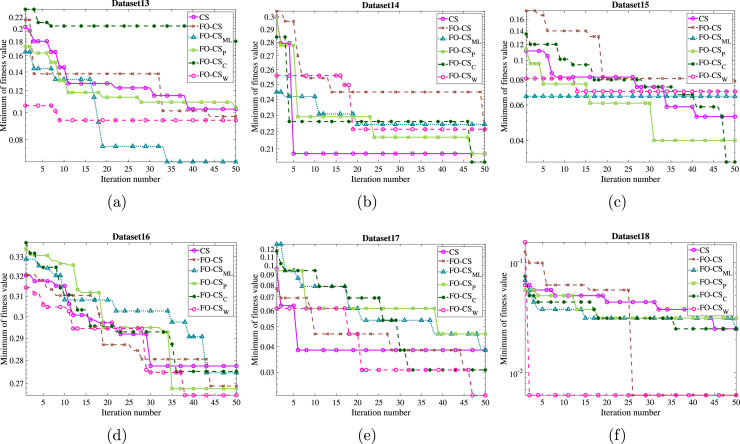
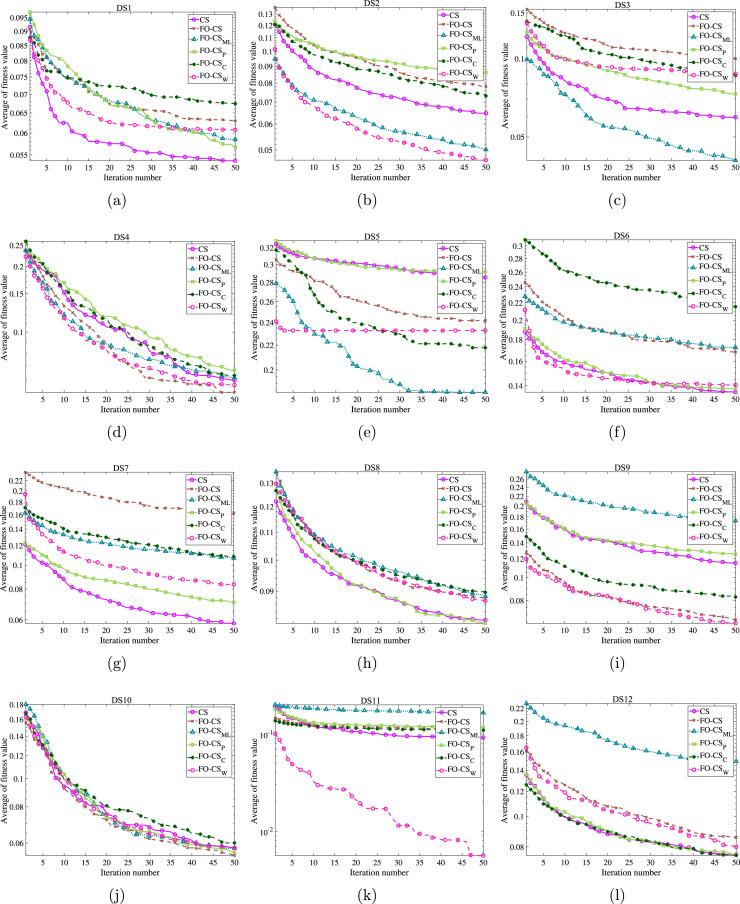
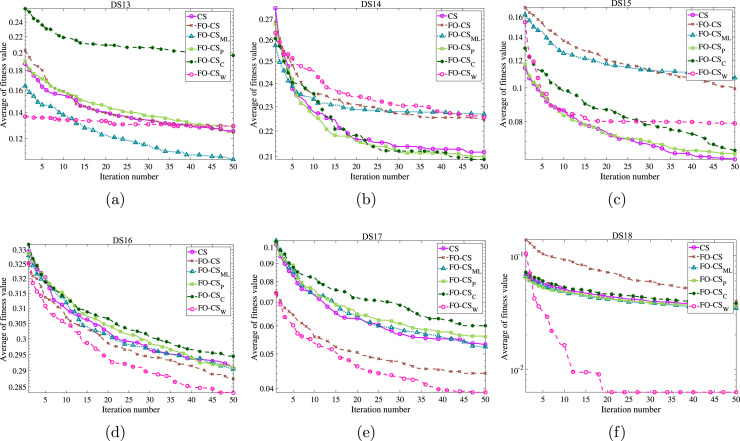
As the acceleration convergence speed is the other aspect that should be discussed and evaluated for the recommended FO-CS variant, the convergence curves based on the optimal fitness function and the mean convergence curves for the basic CS and FO-CS variants have been drawn for the eighteen datasets to demonstrate the efficiency of the recommended FO-CS as in Figs. 6, 7 and 8, 9, respectively. By inspecting the convergence curves of the minimum fitness functions of Figs. 6–7, it can be seen that the CS suffers from stagnation in several functions in nearly 80% of the studied datasets. In contrast, the FO-CS variants expose high qualified performance, especially FO-CS, FO-CS, and FO-CS as they show successful performance for 6, 6 and 5 datasets, respectively. The average convergence curves across the set of independent runs are drawn as in Figs. 8–9 for achieving unbiased comparison. By inspecting the figures, it can be seen from this convergence that, in most cases, the FO-CS has faster convergence, for example, DS2, DS9, DS11, DS12, DS16, DS17, and DS18. However, FO-CS provides better convergence at DS3, DS5, and DS13. Also, CS has the best convergence rate at DS1 and DS7. From all these graphs, it can be observed that the high effect of Fractional-order and Heavy-tailed distributions on the convergence CS.
Fig. 6.
Minimum of fitness values by the recommended FO-CS and the other FO-CS variants as well as the basic CS for (a) DS1, (b) DS2, (c) DS3, (d) DS4, (e) DS5, (f) DS6, (g) DS7, (h) DS8, (i) DS9, (j) DS10, (k) DS11, and (l) DS12.
Fig. 7.
Minimum of fitness values by the recommended FO-CS and the other FO-CS variants as well as the basic CS for (a) DS13, (b) DS14, (c) DS15, (d) DS16, (e) DS17 and, (f) DS18.
Fig. 8.
Average of fitness values by the recommended FO-CS and the other FO-CS variants as well as the basic CS for (a) DS1, (b) DS2, (c) DS3, (d) DS4, (e) DS5, (f) DS6, (g) DS7, (h) DS8, (i) DS9, (j) DS10, (k) DS11, and (l) DS12.
Fig. 9.
Average of fitness values by the recommended FO-CS and the other FO-CS variants as well as the basic CS for (a) DS13, (b) DS14, (c) DS15, (d) DS16, (e) DS17 and, (f) DS18.
5.4. Experimental series: FS using COVID-19 data-sets
In this section, the FO-CS variants are evaluated using two real-world COVID-19 images which have different characteristics.
5.4.1. Data-sets description
In this study, two data-sets are used to assess the performance of the developed FO-CS as the COVID-19 X-ray classification method. These data-sets are contained only two classes (i.e., COVID and No-Findings), which are used for binary classification, or they have three classes (i.e., COVID, No-Findings, Pneumonia) which used for multi-class classification. The description of these data-sets are given in the following
-
1.
Data-set 1: This is an X-ray image data-set which collects from different two sources. The first source is the COVID-19 X-ray images collected by Cohen JP [74]. This source has 127 COVID-19 X-ray. The second source named Chest X-ray, which collected by Wang et al. [58]. This data-set contains normal and pneumonia X-ray images. From this source, 500 no-findings and 500 pneumonia are used. Fig. 10 depicts sample from this data-set (Data-set 1).
-
2.
Data-set 2: This data-set has 219 and 1341 for positive and negative COVID-19 images, respectively. It is collected collaboration between different teams such as Qatar University, University of Dhaka (Bangladesh), also collaborators from Malaysia and Pakistan medical doctors [75]. In addition, the Italian Society of Medical and Interventional Radiology (SIRM) [76]. Fig. 11 shows sample of Data-set 2.
Fig. 10.
Sample of COVID-19 X-ray from Data-set 1 [74].
Fig. 11.
5.4.2. Results and discussion
In this section, the comparison results between the variants of FO-CS and other algorithms are discussed. All of the algorithms used the extracted features from algorithms introduced in Section 5.1. In this section, the extracted features from the COVID-19 x-ray images are the input for the proposed approach that aimed to reduce these features by removing the irrelevant ones. The parameter settings for each algorithm are similar to the previous experiments of the UCI data-set.
Table 9 shows the average of results in terms of accuracy, fitness value, and the number of selected features. One can be observed from this table that the FO-CS algorithm provides better results than other algorithms in terms of accuracy. In general, it has the first rank according to the STD, and the worst of accuracy. However, according to the Best value of the accuracy, the FO-CS has the higher. By analyzing the results of COVID-19 Data-set 1 in terms of fitness value, it has been observed that the FO-CS has better value according to the Mean and Best fitness value. However, the GA and FO-CS provide better results in terms of STD and worst of fitness value, respectively.
Table 9.
FS results of the FO-CS variants along with the compared algorithms in both COVID-19 data-sets.
| Data-set1 |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CS | FO-CS | FO-CS | FO-CS | FO-CS | FO-CS | HHO | HGSO | WOA | SSA | GWO | SGA | ||
| Accuracy | Best | 0.7133 | 0.8067 | 0.8467 | 0.8333 | 0.8267 | 0.8400 | 0.7600 | 0.7867 | 0.8267 | 0.7933 | 0.7533 | 0.7667 |
| Mean | 0.6907 | 0.7613 | 0.8267 | 0.8133 | 0.8093 | 0.8267 | 0.7267 | 0.7653 | 0.7587 | 0.7680 | 0.7080 | 0.7373 | |
| STD | 0.0167 | 0.0307 | 0.0249 | 0.0163 | 0.0130 | 0.0105 | 0.0267 | 0.0173 | 0.0417 | 0.0238 | 0.0272 | 0.0180 | |
| Worst | 0.6667 | 0.7333 | 0.7933 | 0.7933 | 0.7933 | 0.8133 | 0.6933 | 0.7400 | 0.7200 | 0.7333 | 0.6800 | 0.7200 | |
| Fitness value | Mean | 0.2814 | 0.0180 | 0.0159 | 0.0166 | 0.0187 | 0.0098 | 0.0328 | 0.0324 | 0.0388 | 0.2555 | 0.1374 | 0.3990 |
| STD | 0.0048 | 0.0027 | 0.0047 | 0.0028 | 0.0023 | 0.0023 | 0.0089 | 0.0060 | 0.0078 | 0.0072 | 0.0088 | 0.0058 | |
| Best | 0.2747 | 0.0144 | 0.0118 | 0.0144 | 0.0175 | 0.0066 | 0.0219 | 0.0228 | 0.0281 | 0.2468 | 0.1285 | 0.3900 | |
| Worst | 0.2878 | 0.0214 | 0.0227 | 0.0214 | 0.0228 | 0.0123 | 0.0455 | 0.0389 | 0.0491 | 0.2638 | 0.1521 | 0.4035 | |
| Attr | 177.2 | 25.6 | 27.6 | 27.6 | 25.4 | 27.4 | 23.4 | 25.4 | 26.4 | 172.4 | 72.2 | 263.4 | |
| Data-set 2 | |||||||||||||
| Accuracy | Best | 0.9895 | 0.9842 | 0.9895 | 0.9947 | 0.9737 | 1.0000 | 0.9789 | 0.9789 | 0.9526 | 0.9895 | 0.9579 | 0.9842 |
| Mean | 0.9779 | 0.9779 | 0.9874 | 0.9842 | 0.9705 | 0.9926 | 0.9632 | 0.9579 | 0.9337 | 0.9789 | 0.9347 | 0.9811 | |
| STD | 0.0094 | 0.0069 | 0.0029 | 0.0064 | 0.0047 | 0.0060 | 0.0134 | 0.0144 | 0.0177 | 0.0064 | 0.0228 | 0.0047 | |
| Worst | 0.9632 | 0.9684 | 0.9842 | 0.9789 | 0.9632 | 0.9842 | 0.9474 | 0.9421 | 0.9105 | 0.9737 | 0.9000 | 0.9737 | |
| Fitness value | Mean | 0.2814 | 0.0180 | 0.0159 | 0.0166 | 0.0187 | 0.0098 | 0.0328 | 0.0324 | 0.0388 | 0.2555 | 0.1374 | 0.3990 |
| STD | 0.0048 | 0.0027 | 0.0047 | 0.0028 | 0.0023 | 0.0023 | 0.0089 | 0.0060 | 0.0078 | 0.0072 | 0.0088 | 0.0058 | |
| Best | 0.2747 | 0.0144 | 0.0118 | 0.0144 | 0.0175 | 0.0066 | 0.0219 | 0.0228 | 0.0281 | 0.2468 | 0.1285 | 0.3900 | |
| Worst | 0.2878 | 0.0214 | 0.0227 | 0.0214 | 0.0228 | 0.0123 | 0.0455 | 0.0389 | 0.0491 | 0.2638 | 0.1521 | 0.4035 | |
| Attr | 123.8 | 23.2 | 24.4 | 24 | 21.8 | 22.8 | 26.6 | 25.2 | 22.6 | 112.2 | 68 | 178.4 | |
According to the results of the algorithms using the second COVID-19 data-set (i.e., Data-set 2), it can be observed that mean and Best of the accuracy of FO-CS is better than others. Also, in the worst value of accuracy, FO-CS and FO-CS have the same performance, but FO-CS is more stable in terms of accuracy. In addition, the FO-CS provides better performance in terms of Mean, Best, and Worst fitness value, but FO-CS is more stable than FO-CS in terms of fitness value. From all of these results, it can be noticed that the following observation, firstly, the variants of FO-CS, in general, provide better results than other algorithms. Secondly, the heavy-tailed distribution has the largest effect on FO-CS, which has high accuracy and smaller fitness value than levy flight distribution. Finally, using the content of FO leads to improve the performance of CS and the conclusion from the results of FO-CS when compared with traditional CS algorithms in real-world COVID-19 X-ray images.
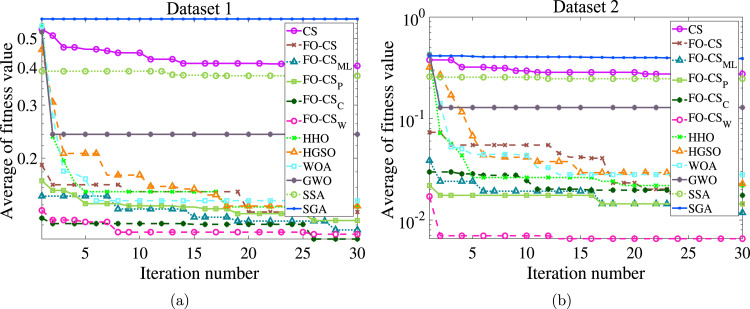
Fig. 12(a) shows the average of the fitness value cross the number iterations. From this convergence curve, it can be observed that FO-CS and FO-CS are the most competitive FS algorithms applied to COVID-19 X-ray images, and they converge faster than other algorithms, followed by FO-CS and FO-CS, respectively for the first data-set. The FO-CS is the superior one in the case of the second data-set.
Fig. 12.
Average of fitness values by the proposed FO-CS variants and other counterparts for (a) Data-set 1, and (b) Data-set 2.
From the previous results, we noticed that the proposed FO-CS based on heavy-tailed distributions provide better results than other algorithms for both UCI datasets and COVID-19 X-ray images. However, there are some limitations of these variants, such as determine the optimal value of the parameters for heavy-tailed distributions. In addition, determine the number of terms and derivative order coefficient.
6. Conclusions
In this study, we present four variants of the recent fractional-order cuckoo search optimization algorithm (FO-CS) using heavy-tailed distributions instead of Lévy flights to classify the extracted features from COVID-19 x-ray data-sets. The considered heavy-tailed distributions included the Mittag-Leffler distribution, the Pareto distribution, the Cauchy distribution, and the Weibull distribution. The application of these distributions can be used to improve mutation operators of MA, and it can be used to escape from non-prominent regions of the search space. For appraising the performance of the proposed variants before applying to the COVID-19 classification approach, we used eighteen data-sets from the UCI repository, and we compared their results with several well-regarded MA utilizing several statistical measures. At this end, the FO-CS based on heavy-tailed distributions variants have been employed for the COVID-19 classification optimization task to classify the data-sets for normal patients, COVID-19 infected patients, and Pneumonia patients. Two different data-sets have been studied, and the FO-CS novel approaches have been compared with numerous MA to evaluate the proposed approach for classifying such of those important data-sets to introduce a reliable and robust technique that helped in classifying the COVID-19 data-sets efficiently and with high accuracy. The FO-CS based on Weibull distribution showed its superiority compared to the other proposed variants and recent well-regarded MA. In future work, we will try to evaluate the proposed method in different applications, such as parameters estimation and solving various engineering problems.
CRediT authorship contribution statement
Dalia Yousri: Conceptualization, Data curation, Formal analysis, Methodology, Software, Visualization, Writing - review & editing. Mohamed Abd Elaziz: Data curation, Formal analysis, Methodology, Software, Visualization, Writing - original draft. Laith Abualigah: Formal analysis, Supervision, Writing - review & editing. Diego Oliva: Conceptualization, Validation, Writing - review & editing. Mohammed A.A. Al-qaness: Conceptualization, Investigation, Writing - original draft. Ahmed A. Ewees: Formal analysis, Project administration, Software, Writing - original draft.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
This project is supported financially by the Academy of Scientific Research and Technology (ASRT) , Egypt, Grant No 6619.
References
- 1.Nishiura H., Linton N.M., Akhmetzhanov A.R. Serial interval of novel coronavirus (COVID-19) infections. Int. J. Infect. Dis. 2020 doi: 10.1016/j.ijid.2020.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Singhal T. A review of coronavirus disease-2019 (COVID-19) Indian J. Pediatrics. 2020:1–6. doi: 10.1007/s12098-020-03263-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zu Z.Y., Jiang M.D., Xu P.P., Chen W., Ni Q.Q., Lu G.M., Zhang L.J. Coronavirus disease 2019 (COVID-19): a perspective from China. Radiology. 2020 doi: 10.1148/radiol.2020200490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Arslan G., Yıldırım M., Tanhan A., Buluş M., Allen K.-A. Coronavirus stress, optimism-pessimism, psychological inflexibility, and psychological health: Psychometric properties of the coronavirus stress measure. Int. J. Mental Health Addict. 2020:1. doi: 10.1007/s11469-020-00337-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fernandes N. 2020. Economic effects of coronavirus outbreak (COVID-19) on the world economy. Available at SSRN 3557504. [Google Scholar]
- 6.Jaiswal A., Gianchandani N., Singh D., Kumar V., Kaur M. Classification of the COVID-19 infected patients using densenet201 based deep transfer learning. J. Biomol. Struct. Dyn. 2020:1–8. doi: 10.1080/07391102.2020.1788642. [DOI] [PubMed] [Google Scholar]
- 7.Apostolopoulos I.D., Aznaouridis S.I., Tzani M.A. Extracting possibly representative COVID-19 biomarkers from X-Ray images with deep learning approach and image data related to pulmonary diseases. J. Med. Biol. Eng. 2020:1. doi: 10.1007/s40846-020-00529-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ozturk T., Talo M., Yildirim E.A., Baloglu U.B., Yildirim O., Acharya U.R. Automated detection of COVID-19 cases using deep neural networks with X-ray images. Comput. Biol. Med. 2020 doi: 10.1016/j.compbiomed.2020.103792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Apostolopoulos I.D., Mpesiana T.A. Covid-19: automatic detection from x-ray images utilizing transfer learning with convolutional neural networks. Phys. Eng. Sci. Med. 2020:1. doi: 10.1007/s13246-020-00865-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ucar F., Korkmaz D. Covidiagnosis-net: Deep Bayes-squeezenet based diagnostic of the coronavirus disease 2019 (COVID-19) from X-Ray images. Med. Hypotheses. 2020 doi: 10.1016/j.mehy.2020.109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Islam M.Z., Islam M.M., Asraf A. A combined deep cnn-lstm network for the detection of novel coronavirus (covid-19) using x-ray images. Inform. Med. Unlocked. 2020 doi: 10.1016/j.imu.2020.100412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Toğaçar M., Ergen B., Cömert Z. COVID-19 detection using deep learning models to exploit social mimic optimization and structured chest X-ray images using fuzzy color and stacking approaches. Comput. Biol. Med. 2020 doi: 10.1016/j.compbiomed.2020.103805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Nixon M., Aguado A. Academic press; 2019. Feature Extraction and Image Processing for Computer Vision. [Google Scholar]
- 14.Abualigah L.M.Q. Springer; 2019. Feature Selection and Enhanced Krill Herd Algorithm for Text Document Clustering. [Google Scholar]
- 15.Abualigah L.M., Khader A.T., Hanandeh E.S. A new feature selection method to improve the document clustering using particle swarm optimization algorithm. J. Comput. Sci. 2018;25:456–466. [Google Scholar]
- 16.Ibrahim R.A., Oliva D., Ewees A.A., Lu S. International Conference on Neural Information Processing. Springer; 2017. Feature selection based on improved runner-root algorithm using chaotic singer map and opposition-based learning; pp. 156–166. [Google Scholar]
- 17.Ibrahim R.A., Abd Elaziz M., Ewees A.A., Selim I.M., Lu S. Galaxy images classification using hybrid brain storm optimization with moth flame optimization. J.Astron. Telesc. Instrum. Syst. 2018;4(3) [Google Scholar]
- 18.Neggaz N., Ewees A.A., Abd Elaziz M., Mafarja M. Boosting salp swarm algorithm by sine cosine algorithm and disrupt operator for feature selection. Expert Syst. Appl. 2020;145 [Google Scholar]
- 19.Benazzouz A., Guilal R., Amirouche F., Slimane Z.E.H. 2019 International Conference on Networking and Advanced Systems (ICNAS) IEEE; 2019. EMG Feature selection for diagnosis of neuromuscular disorders; pp. 1–5. [Google Scholar]
- 20.Alex S.B., Mary L., Babu B.P. Attention and feature selection for automatic speech emotion recognition using utterance and syllable-level prosodic features. Circuits Systems Signal Process. 2020:1–29. [Google Scholar]
- 21.Chatterjee R., Maitra T., Islam S.H., Hassan M.M., Alamri A., Fortino G. A novel machine learning based feature selection for motor imagery eeg signal classification in internet of medical things environment. Future Gener. Comput. Syst. 2019;98:419–434. [Google Scholar]
- 22.Al-qaness M.A. Device-free human micro-activity recognition method using wifi signals. Geo-Spatial Inform. Sci. 2019;22(2):128–137. [Google Scholar]
- 23.Deng X., Li Y., Weng J., Zhang J. Feature selection for text classification: A review. Multimedia Tools Appl. 2019;78(3):3797–3816. [Google Scholar]
- 24.Han J., Pei J., Kamber M. Elsevier; 2011. Data Mining: Concepts and Techniques. [Google Scholar]
- 25.Pinheiro R.H., Cavalcanti G.D., Correa R.F., Ren T.I. A global-ranking local feature selection method for text categorization. Expert Syst. Appl. 2012;39(17):12851–12857. [Google Scholar]
- 26.Beezer R.A., Hastie T., Tibshirani R., Springer J.F. 2002. The elements of statistical learning: Data mining, inference and prediction. by. [Google Scholar]
- 27.Abualigah L. Multi-verse optimizer algorithm: a comprehensive survey of its results, variants, and applications. Neural Comput. Appl. 2020:1–21. [Google Scholar]
- 28.Tsai C.-F., Eberle W., Chu C.-Y. Genetic algorithms in feature and instance selection. Knowl.-Based Syst. 2013;39:240–247. [Google Scholar]
- 29.Xue B., Zhang M., Browne W.N. Particle swarm optimization for feature selection in classification: A multi-objective approach. IEEE Trans. Cybern. 2012;43(6):1656–1671. doi: 10.1109/TSMCB.2012.2227469. [DOI] [PubMed] [Google Scholar]
- 30.Hancer E. Differential evolution for feature selection: a fuzzy wrapper–filter approach. Soft Comput. 2019;23(13):5233–5248. [Google Scholar]
- 31.Sayed G.I., Hassanien A.E., Azar A.T. Feature selection via a novel chaotic crow search algorithm. Neural Comput. Appl. 2019;31(1):171–188. [Google Scholar]
- 32.Gu S., Cheng R., Jin Y. Feature selection for high-dimensional classification using a competitive swarm optimizer. Soft Comput. 2018;22(3):811–822. [Google Scholar]
- 33.Taradeh M., Mafarja M., Heidari A.A., Faris H., Aljarah I., Mirjalili S., Fujita H. An evolutionary gravitational search-based feature selection. Inform. Sci. 2019;497:219–239. [Google Scholar]
- 34.Wolpert D.H., Macready W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997;1(1):67–82. [Google Scholar]
- 35.Yang X.-S., Deb S. 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC) IEEE; 2009. Cuckoo search via Lévy flights; pp. 210–214. [Google Scholar]
- 36.Gandomi A.H., Yang X.-S., Alavi A.H. Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013;29(1):17–35. [Google Scholar]
- 37.Yang X.-S., Deb S. Cuckoo search: recent advances and applications. Neural Comput. Appl. 2014;24(1):169–174. [Google Scholar]
- 38.Shehab M., Khader A.T., Al-Betar M.A. A survey on applications and variants of the cuckoo search algorithm. Appl. Soft Comput. 2017;61:1041–1059. [Google Scholar]
- 39.Liu L., Liu X., Wang N., Zou P. Modified cuckoo search algorithm with variational parameters and logistic map. Algorithms. 2018;11(3):30. [Google Scholar]
- 40.Yousri D., Mirjalili S. Fractional-order cuckoo search algorithm for parameter identification of the fractional-order chaotic, chaotic with noise and hyper-chaotic financial systems. Eng. Appl. Artif. Intell. 2020;92 [Google Scholar]
- 41.T. Friedrich, F. Quinzan, M. Wagner, Escaping large deceptive basins of attraction with heavy-tailed mutation operators, in: Proceedings of the Genetic and Evolutionary Computation Conference, 2018, pp. 293–300.
- 42.B. Doerr, H.P. Le, R. Makhmara, T.D. Nguyen, Fast genetic algorithms, in: Proceedings of the Genetic and Evolutionary Computation Conference, 2017, pp. 777–784.
- 43.Huillet T.E. On Mittag-Leffler distributions and related stochastic processes. J. Comput. Appl. Math. 2016;296:181–211. [Google Scholar]
- 44.Arnold B.C. Wiley StatsRef: Statistics Reference Online. 2014. Pareto distribution; pp. 1–10. [Google Scholar]
- 45.Arnold B.C., Beaver R.J. The skew-Cauchy distribution. Statist. Probab. Lett. 2000;49(3):285–290. [Google Scholar]
- 46.Kharazmi O. Generalized weighted Weibull distribution. J. Math. Ext. 2016;10:89–118. [Google Scholar]
- 47.Dua D., Graff C. 2019. UCI machine learning repository. URL: http://archive.ics.uci.edu/ml, accessed: April 20, 2020 5PM. [Google Scholar]
- 48.Pereira R.M., Bertolini D., Teixeira L.O., Silla Jr C.N., Costa Y.M. COVID-19 identification in chest X-ray images on flat and hierarchical classification scenarios. Comput. Methods Programs Biomed. 2020 doi: 10.1016/j.cmpb.2020.105532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Elaziz M.A., Hosny K.M., Salah A., Darwish M.M., Lu S., Sahlol A.T. New machine learning method for image-based diagnosis of COVID-19. PLoS One. 2020;15(6) doi: 10.1371/journal.pone.0235187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ouchicha C., Ammor O., Meknassi M. Cvdnet: A novel deep learning architecture for detection of coronavirus (Covid-19) from chest x-ray images. Chaos Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hemdan E.E.-D., Shouman M.A., Karar M.E. 2020. Covidx-net: A framework of deep learning classifiers to diagnose covid-19 in x-ray images. arXiv preprint arXiv:2003.11055. [Google Scholar]
- 52.Khan A.I., Shah J.L., Bhat M.M. Coronet: A deep neural network for detection and diagnosis of COVID-19 from chest x-ray images. Comput. Methods Programs Biomed. 2020 doi: 10.1016/j.cmpb.2020.105581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Toraman S., Alakus T.B., Turkoglu I. Convolutional capsnet: A novel artificial neural network approach to detect COVID-19 disease from X-ray images using capsule networks. Chaos Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Jain G., Mittal D., Thakur D., Mittal M.K. A deep learning approach to detect Covid-19 coronavirus with X-Ray images. Biocybern. Biomed. Eng. 2020;40(4):1391–1405. doi: 10.1016/j.bbe.2020.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hassantabar S., Ahmadi M., Sharifi A. Diagnosis and detection of infected tissue of COVID-19 patients based on lung x-ray image using convolutional neural network approaches. Chaos Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Zakeri A., Hokmabadi A. Efficient feature selection method using real-valued grasshopper optimization algorithm. Expert Syst. Appl. 2019;119:61–72. [Google Scholar]
- 57.Too J., Mirjalili S. A hyper learning binary dragonfly algorithm for feature selection: A COVID-19 case study. Knowl.-Based Syst. 2020 [Google Scholar]
- 58.Binh H.T.T., Hanh N.T., Dey N., et al. Improved cuckoo search and chaotic flower pollination optimization algorithm for maximizing area coverage in wireless sensor networks. Neural Comput. Appl. 2018;30(7):2305–2317. [Google Scholar]
- 59.Thirugnanasambandam K., Prakash S., Subramanian V., Pothula S., Thirumal V. Reinforced cuckoo search algorithm-based multimodal optimization. Appl. Intell. 2019;49(6):2059–2083. [Google Scholar]
- 60.Kang T., Yao J., Jin M., Yang S., Duong T. A novel improved cuckoo search algorithm for parameter estimation of photovoltaic (PV) models. Energies. 2018;11(5):1060. [Google Scholar]
- 61.Xiao B., Li L., Li Y., Li W., Wang G. Image analysis by fractional-order orthogonal moments. Inform. Sci. 2017;382:135–149. [Google Scholar]
- 62.Chen B., Yu M., Su Q., Shim H.J., Shi Y.-Q. Fractional quaternion zernike moments for robust color image copy-move forgery detection. IEEE Access. 2018;6:56637–56646. [Google Scholar]
- 63.Chen B., Qi X., Sun X., Shi Y.-Q. Quaternion pseudo-zernike moments combining both of RGB information and depth information for color image splicing detection. J. Vis. Commun. Image Represent. 2017;49:283–290. [Google Scholar]
- 64.Nenadic Z., Burdick J.W. Spike detection using the continuous wavelet transform. IEEE Trans. Biomed. Eng. 2004;52(1):74–87. doi: 10.1109/TBME.2004.839800. [DOI] [PubMed] [Google Scholar]
- 65.Raghavendra U., Acharya U.R., Fujita H., Gudigar A., Tan J.H., Chokkadi S. Application of gabor wavelet and locality sensitive discriminant analysis for automated identification of breast cancer using digitized mammogram images. Appl. Soft Comput. 2016;46:151–161. [Google Scholar]
- 66.Abd Elaziz M., Ewees A.A., Ibrahim R.A., Lu S. Opposition-based moth-flame optimization improved by differential evolution for feature selection. Math. Comput. Simulation. 2020;168:48–75. [Google Scholar]
- 67.Hashim F.A., Houssein E.H., Mabrouk M.S., Al-Atabany W., Mirjalili S. Henry gas solubility optimization: A novel physics-based algorithm. Future Gener. Comput. Syst. 2019;101:646–667. [Google Scholar]
- 68.Heidari A.A., Mirjalili S., Faris H., Aljarah I., Mafarja M., Chen H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019;97:849–872. [Google Scholar]
- 69.Oreski S., Oreski G. Genetic algorithm-based heuristic for feature selection in credit risk assessment. Expert Syst. Appl. 2014;41(4):2052–2064. [Google Scholar]
- 70.Ibrahim R.A., Ewees A.A., Oliva D., Elaziz M.A., Lu S. Improved salp swarm algorithm based on particle swarm optimization for feature selection. J. Ambient Intell. Humaniz. Comput. 2019;10(8):3155–3169. [Google Scholar]
- 71.Mirjalili S., Lewis A. The whale optimization algorithm. Adv. Eng. Softw. 2016;95:51–67. [Google Scholar]
- 72.Ibrahim R.A., Elaziz M.A., Lu S. Chaotic opposition-based grey-wolf optimization algorithm based on differential evolution and disruption operator for global optimization. Expert Syst. Appl. 2018;108:1–27. [Google Scholar]
- 73.Zimmerman D.W., Zumbo B.D. Relative power of the wilcoxon test, the friedman test, and repeated-measures ANOVA on ranks. J. Exp. Educ. 1993;62(1):75–86. [Google Scholar]
- 74.Cohen J.P., Morrison P., Dao L. 2020. COVID-19 image data collection. arXiv preprint arXiv:2003.11597. [Google Scholar]
- 75.Chowdhury M.E., Rahman T., Khandakar A., Mazhar R., Kadir M.A., Mahbub Z.B., Islam K.R., Khan M.S., Iqbal A., Al-Emadi N., et al. 2020. Can AI help in screening viral and COVID-19 pneumonia? arXiv preprint arXiv:2003.13145. [Google Scholar]
- 76.o. M. a. I. Radiology S.S. 2020. Italian society of medical and interventional radiology. URL: https://www.sirm.org/category/senza-categoria/covid-19, Accessed: April 22, 2020 12AM. [Google Scholar]