COVID-19 classification by CCSHNet with deep fusion using transfer learning and discriminant correlation analysis

Highlights

• •We proposed a novel (L, 2) transfer feature learning (L2TFL) approach.
• •L2TFL can elucidate the optimal layers to be removed prior to selection.
• •We developed a novel selection algorithm of pretrained network for fusion approach.
• •SAPNF can determine the best two pretrained models for fusion.
• •We introduced a deep CCT fusion discriminant correlation analysis fusion method.

Abstract

Aim

: COVID-19 is a disease caused by a new strain of coronavirus. Up to 18th October 2020, worldwide there have been 39.6 million confirmed cases resulting in more than 1.1 million deaths. To improve diagnosis, we aimed to design and develop a novel advanced AI system for COVID-19 classification based on chest CT (CCT) images.

Methods

: Our dataset from local hospitals consisted of 284 COVID-19 images, 281 community-acquired pneumonia images, 293 secondary pulmonary tuberculosis images; and 306 healthy control images. We first used pretrained models (PTMs) to learn features, and proposed a novel (L, 2) transfer feature learning algorithm to extract features, with a hyperparameter of number of layers to be removed (NLR, symbolized as L). Second, we proposed a selection algorithm of pretrained network for fusion to determine the best two models characterized by PTM and NLR. Third, deep CCT fusion by discriminant correlation analysis was proposed to help fuse the two features from the two models. Micro-averaged (MA) F1 score was used as the measuring indicator. The final determined model was named CCSHNet.

Results

: On the test set, CCSHNet achieved sensitivities of four classes of 95.61%, 96.25%, 98.30%, and 97.86%, respectively. The precision values of four classes were 97.32%, 96.42%, 96.99%, and 97.38%, respectively. The F1 scores of four classes were 96.46%, 96.33%, 97.64%, and 97.62%, respectively. The MA F1 score was 97.04%. In addition, CCSHNet outperformed 12 state-of-the-art COVID-19 detection methods.

Conclusions

: CCSHNet is effective in detecting COVID-19 and other lung infectious diseases using first-line clinical imaging and can therefore assist radiologists in making accurate diagnoses based on CCTs.

1. Introduction

COVID-19 (coronavirus disease 2019) was declared as a Public Health Emergency of International Concern on 30/Jan/2020, and a worldwide pandemic on 11/March/2020. Up to 18/Oct/2020, globally there have been 39.6 million confirmed cases and more than 1.1 million deaths (including US 222.5k Brazil 153.6k, India 114.0k, Mexico 86.0k, UK 43.5k, etc.) [1].

Two prevailing diagnostic methods are available for COVID-19 detection. One is viral testing by nasopharyngeal swabs [2] to test the existence of viral RNA fragments using real-time reverse-transcriptase PCR (rRT-PCR) and the other is imaging methods such as chest X-ray (CXR) [3] and chest computed tomography (CCT) [4]. Compared to viral testing, CCT can avoid the problem of sample contamination. For example, the swab can touch contaminated surfaces or gloves, samples can be cross-contaminated, etc. It was reported that in March 2020, due to the problem of reagent contamination, the US Center for Disease Control and Prevention (CDC) withdrew testing kits [5]. As an alternative, CCT scans can help to detect hazy, patchy, “ground glass” white spots in the lung, a tell-tale sign of COVID-19 infection, which can provide a more accurate result than viral tests. Furthermore, previous studies have shown that CCT can detect 97% of COVID-19 infections; whereas viral testing only detected 52% of patients with COVID-19 infection [6].

There are currently two imaging modalities that are used to detect COVID-19 infection. CXR is the most widely used diagnostic X-ray examination in medical practice, producing images of the blood vessels, airways, lungs, heart, bones of the spine, and chest. On the other hand, CCT uses computer-processed combinations of numerous X-ray images taken at different angles to produce a cross-sectional image of the region being scanned and to examine abnormalities. CCT is able to detect very small nodules in the lung compared to CXR [7]. In addition, CCT has advantages over CXR since it generates high-quality, detailed images by taking a 360-degree image of the chest and its internal organs. Moreover, CXR provides a 2D image that contains less information; whereas CCT provides 3D volumetric data that can highlight additional spatial features and abnormalities.

For diagnosis of COVID-19, CXR is sub-optimal since important abnormalities are undetectable due to the normal black appearance of the lung. However, CCT can clearly show a combination of multifocal peripheral lung changes of ground-glass opacity (GGO) [8] and/or consolidation [9], which indicate infection with COVID-19. Hence, in this study we used CCT to aid diagnosis of COVID-19 infection. Nevertheless, manual labeling by radiologists is tedious and time-consuming, while being affected by inter- and/or intra-expert factors (e.g., emotion, tiredness, lethargy, etc.). Further, diagnostic throughputs of radiologists are not comparable with digital methods and early symptoms are more difficult to measure and hence can potentially be missed by experts.

Improved diagnostic systems using image processing and machine learning can potentially benefit patients, experts, radiologists, consultants, and hospitals. Currently, most AI methods can differentiate COVID-19 infection in images from healthy subjects and/or community acquired pneumonia (CAP). Deep learning (DL) approaches are an emerging new type of machine learning, which consists of stacks of convolution layers and fully connected layers (FCLs).

For example, Li and Liu [10] employed wavelet packet Tsallis entropy as a feature descriptor, and used a real-coded biogeography-based optimization (RCBO) approach as a classifier. Lu [11] employed bat algorithm to optimize extreme learning machine. Their method was called ELM-BA. Jiang [12] proposed a six-level convolutional neural network (6L-CNN) towards therapy and rehabilitation, while improving performance by replacing the traditional rectified linear unit with leaky rectified linear unit. Guo and Du [13] used ResNet-18 (RN-18) to classify thyroid ultrasound standard plane (TUSP), achieving a classification accuracy of 83.88%. Their experiment verified the effectiveness of RN-18. Fulton, et al. [14] utilized ResNet-50 to classify Alzheimer's disease (RN-50-AD) with and without imagery. The authors stated that ResNet-50 models might help identify AD patients prior to provider review. Although these previous five studies did not analyze COVID-19 positive patients, their algorithms can be easily transferred to the multi-class classification task of COVID-19 diagnosis in this study.

Numerous cutting-edge AI methods have been proposed to diagnose COVID-19 using either CXR or CCT. For CXR, Loey, et al. [15] employed generative adversarial network (GAN) to produce new simulated images showing that the combination of GAN and GoogleNet (GAN-GN) is optimal for two-class classification than AlexNet and ResNet-18. Togacar, et al. [16] utilized SqueezeNet and MobileNetV2 to obtain image descriptors. The authors chose social mimic optimization (SMO) as a feature selection tool. The obtained features were then combined and passed into support vector machines. Cohen, et al. [17] employed a sizable non-COVID-19 CXR set to improve extracted features from images of CXRs from COVID-19 patients and predicted two scores: (i) lung opacity score; and (ii) geographic extent score. Their method could gage severity of COVID-19. The method (termed COVID severity score or CSS) achieved a mean absolute error (MAE) of 1.14 on geographic extent score, and a MAE of 0.78 on lung opacity score. Tabik, et al. [18] built COVIDGR-1.0, a homogeneous and balanced database that includes all levels of severity, and presented a novel COVID-SDNet in order to classify COVID-19 based on CXR images.

For CCT, Ni, et al. [19] proposed NiNet, utilizing both 3D U-Net and MVP-Net on more than 90 COVID-19 patients in CCT scanning, for the aim of (i) pulmonary lobe segmentation, (ii) lesion segmentation, and (iii) lesion detection. The authors found the deep learning algorithm could assist radiologists to make quicker diagnosis (all p values are less than 0.01%) with first-class performances. Ko, et al. [20] presented a straigtforward 2D fast-track deep learning system for single CCT image termed FCONet (fast-track COVID-19 classification network). They analyzed 4 pretrained models: ResNet-50, VGG16, Xception, and Inception-V3, finding that ResNet-50 performed the best when classifying COVID-19 positive patients. They used two augmentation methods: zoom and image rotation, while proposing extra layers consisting of a flatten layer, a FCL (32 neurons), and a FCL (3 neurons). The final FCL has 3 neurons since their task is to classify 3 categories: COVID-19, other pneumonia, and non-pneumonia. As validation, the authors tested the FCONet approaches on an external set from embedded low-quality CCT images of COVID-19 patients. Li, et al. [21] developed COVNet, choosing ResNet50 as the backbone network. In their study, the deep representations were merged by a max-pooling procedure, with the obtained feature map being passed into a FCL to produce the probability score of three categories: (i) COVID-19 infection, (ii) CA), and (iii) non-pneumonia. Wang, et al. [22] proposed DeCovNet, a weakly-supervised DL framework via three-dimensional CT data for (i) lesion localization; and (ii) COVID-19 classification. The lung region was firstly segmented via a pre-trained UNet. Next, the segmented 3D lung region was passed to a three-dimensional deep network to predict the probability of COVID-19. When using a probability threshold of 0.5, the DeCovNet yielded an accuracy of 90.1%, a negative predictive value of 98.2%, and a positive predictive value of 84.0%. Satapathy, et al. [23] proposed a seven-layer CNN by stochastic pooling. Their method achieved a specificity of 93.63%, a sensitivity of 94.44%, and an accuracy of 94.03%. Wu [24] combined wavelet Renyi entropy with a three-segment biogeography-based optimization (TSBO). Their proposed TSBO can optimize weights, biases, and order of Renyi entropy at the same time.

The inspiration for this study was to improve detection of COVID-19 infection in CCT images by developing a novel method to fuse the features from two neural network models. The main contributions of this paper are that: (i) We proposed a novel (L, 2) transfer feature learning (L2TFL) approach to elucidate the optimal layers to be removed prior to selection by testing various pretrained networks with various settings. (ii) We developed a novel selection algorithm of pretrained network for fusion (SAPNF) approach that can determine the best two pretrained models and proved it gives better performance than the proposed greedy selection algorithm for fusion (GSAF). (iii) We introduced a deep CCT fusion discriminant correlation analysis (DCFDCA) fusion method that gives better performance than traditional addition and concatenation fusion methods; and (iv) we improved performance over current methods by implementing multiple-way data augmentation.

The structure of the paper is organized as below. Section 2 introduces the dataset, imaging protocol, slice selection method, ground-truth labeling, and preprocessing of the images. Section 3 describes every component of the proposed AI model for COVID-19 detection, and Section 4 presents the experimental results and discussions. Finally, Section 5 concludes the paper.

2. Dataset and preprocessing

Table 10 in Appendix.A and Table 11 in Appendix.B list the abbreviation and variable meanings exercised for easy reading.

2.1. Slice selection

Four types of CCT were used in this study: (i) COVID-19 positive; (ii) community-acquired pneumonia (CAP); (iii) second pulmonary tuberculosis (SPT); (iv) healthy control (HC). The three diseased classes were chosen since they are all infectious diseases of the chest regions. Our aim was to develop an AI system that can automatically predict the four categories.

For each subject, $s=\left\{1,2,3,4\right\}$ slices were chosen and a slice level selection (SLS) method was employed: For the three diseased groups, the slice displaying the largest number of lesions and size was chosen. For healthy subjects, any slice of the 3D image was randomly chosen.

The resolutions of all images were $1024\times 1024\times 3$. In total, we enrolled 521 subjects, and generated 1164 slice images using the SLS method, viz., 284 COVID-19 images, 281 CAP images, 293 SPT images; and 306 HC images. Image collection is challenging since it is expensive and labor-intensive, as well as requiring expert curation. Table 1 lists the demographics of the four-category subject cohort.

Table 1.

Subjects and images of four categories.

Category	Patients (n)	CCT Images (n)
COVID-19	125	284
CAP	123	281
SPT	134	293
HC	139	306

(n = number).

2.2. Ground-truth labelling

Three radiologists (Two juniors: ${\mathcal{B}}_1$ and ${\mathcal{B}}_2$, and one senior: ${\mathcal{B}}_3$) were assigned to curate all the images. Suppose $x_0$ means one CCT scan, $Z$ means the labeling of each individual expert, and the final labeling $Z^{CCT}$ of the CCT scan is obtained by

$$Z^{CCT}\left[x_0\right]=\{\begin{array}{cc}Z\left[{\mathcal{B}}_1,x_0\right]\hfill & Z\left[{\mathcal{B}}_1,x_0\right]==Z\left[{\mathcal{B}}_2,x_0\right]\hfill \\ \text{MV}\left\{Z_{all}\left[x_0\right]\right\}\hfill & \text{otherwise}\hfill \end{array}$$ (1)

Where $Z_{all}$ denotes the labeling of all radiologists, viz.,

$$Z_{all}\left[x_0\right]=\left[Z\left({\mathcal{B}}_1,x_0\right),Z\left({\mathcal{B}}_2,x_0\right),Z\left({\mathcal{B}}_3,x_0\right)\right]$$ (2)

MV denotes majority voting. The above equation means the situation of disagreement between the analyses of two junior radiologists $\left({\mathcal{B}}_1,{\mathcal{B}}_2\right)$, we need to consult a senior radiologist $\left({\mathcal{B}}_3\right)$to reach a consensus.

2.3. Preprocessing

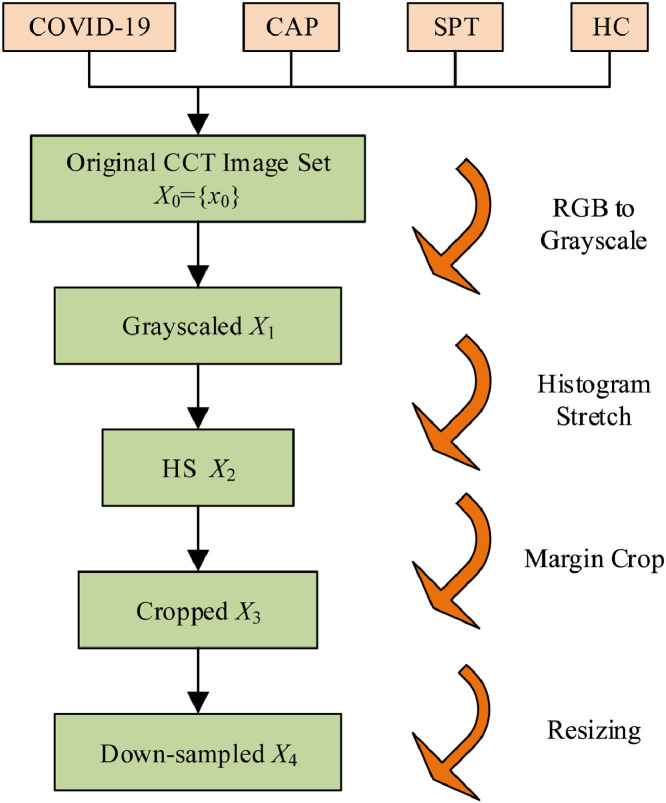
Preprocessing has already shown its success in medical image analysis [25, 26]. The original dataset contained $|X_0|$ slice images $\left\{x_0\left(i\right),i=1,2,\cdots ,\left|X_0\right|\right\}$. The size of each image was $size\left[x_0\left(i\right)\right]=W_0\times H_0\times C_0$. Fig. 1 shows the pipeline for preprocessing of our dataset.

Fig. 1.

Illustration of preprocessing. (CAP: community-acquired pneumonia; SPT: secondary pulmonary tuberculosis; HC: healthy control; CCT: chest CT; HS: histogram stretching).

First, the color CCT images from four classes were converted into grayscale by retaining the luminance channel, and yielding the grayscale data set $X_1$:

$$X_1=F_G\left(X_0\right)=\left\{x_1\left(1\right),x_1\left(2\right),\dots ,x_1\left(i\right),\dots x_1\left(\left|X\right|\right)\right\}$$ (3)

where $F_G$ means the grayscale operation. Note that $size\left[x_1\left(i\right)\right]=W_1\times H_1\times C_1$

Second, the histogram stretching (HS) [27, 28] was utilized to increase the contrast of all images. Take the i th image $x_1\left(i\right),i=1,2,\cdots ,\left|X\right|$ as an example, its minimum and maximum grayscale values $a_l\left(i\right)$ and $a_h\left(i\right)$ were calculated as:

$$\{\begin{array}{c}{a}_l\left(i\right)=\underset{w=1}{\overset{W_1}{\min }}\underset{h=1}{\overset{H_1}{\min }}\underset{c=1}{\overset{C_1}{\min }}{x}_1\left(i\right|x,y,c)\hfill \\ a_h\left(i\right)=\underset{w=1}{\overset{W_1}{\max }}\underset{h=1}{\overset{H_1}{\max }}\underset{c=1}{\overset{C_1}{\max }}{x}_1\left(i\right|x,y,c)\hfill \end{array}$$ (4)

here (w, h, c) means the index of width, height, and channel directions along image $x_1\left(i\right)$, respectively. The new histogram stretched image set $X_2$ was calculated as:

$$X_2=HS\left(X_1\right)=\left\{x_2\left(i\right)\underset{\_}{\underset{\_}{def}}\frac{x_1\left(i\right)-a_l\left(i\right)}{a_h\left(i\right)-a_l\left(i\right)}\right\}$$ (5)

Third, cropping was carried out to remove the checkup bed at the bottom area, and to remove the texts at the margin areas. The cropped dataset $X_3$ is obtained as

$$X_3=F_C\left(X_2,\left[c_t,c_b,c_l,c_r\right]\right)=\left\{x_3\left(1\right),x_3\left(2\right),\cdots ,x_3\left(i\right),\cdots ,x_3\left(\left|X\right|\right)\right\}$$ (6)

where $F_C$ represents crop operation. Parameter $\left(c_t,c_b,c_l,c_r\right)$ means pixels to be cropped in unit of pixel from four directions. The subscript $\left(t,b,l,r\right)$ is the initial letter of top, bottom, left, and right, respectively. After this step, the resolution of each image $size\left[x_3\left(i\right)\right]=W_3\times H_3\times C_3$.

Fourth, we down-sampled each image to a size of $\left[W_4,H_4\right]$, obtaining the resized image set $X_4$ as

$$X_4=F_D\left(X_3,\left[W_5,H_5\right]\right)=\left\{x_4\left(1\right),x_4\left(2\right),\dots ,x_4\left(i\right),\dots x_4\left(\left|X\right|\right)\right\}$$ (7)

where $F_D:a\mapsto b$ represents the downsampling (DS) function, in which b is a down-sampled image of the raw image a.

After the preprocessing procedure, each image was approximately 1.64% (explained below) of its original storage or size. The compression ratio (CR) rates of i th image of the final stage $X_4$ to the raw stage $X_0$ was measured by two variables: the storage CR $\left({\delta }_1\right)$ and size CR $\left({\delta }_2\right)$

$$\{\begin{array}{c}{\displaystyle {\delta }_1=\frac{storage\left[x_4\left(i\right)\right]}{storage\left[x_0\left(i\right)\right]}}\hfill \\ {\displaystyle {\delta }_2=\frac{size\left[x_4\left(i\right)\right]}{size\left[x_0\left(i\right)\right]}}\hfill \end{array}$$ (8)

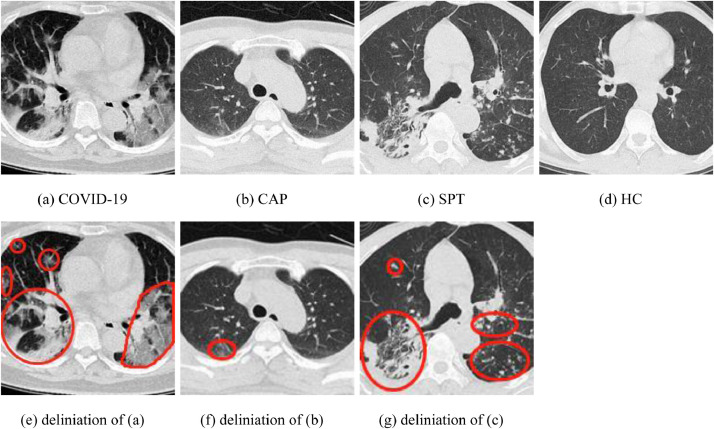
We can have ${\delta }_1=206,116/12,582,912$, and ${\delta }_2=51,529/3,145,728$. Hence, we can obtain ${\delta }_1\left(i\right)={\delta }_2\left(i\right)=1.64\%$, $\forall i=1,2,\dots ,\left|X\right|$. Hence, it proves the importance of preprocessing. Furthermore, Fig. 2 displays four samples from the preprocessed set $X_4$. The top row presents the preprocessed images, and the bottom row the delineated results in red curves. Overall, the advantages of preprocessing is three-fold: (i) Compression ratio helps to minimize the storage size; (ii) Histogram stretching helps to normalize the contrast of all samples; (iii) Cropping removes irrelevant contents from CCT images, so the AI model will focus on the lung region. Table 2 compares the storage and size of every image $x_s\left(i\right),s=0,\cdots ,4,i=1,\cdots ,\left|X\right|$ at each preprocessing step.

Fig. 2.

Samples of X₄. (CAP: community-acquired pneumonia; SPT: secondary pulmonary tuberculosis; HC: healthy control).

Table 2.

Storage and size per preprocessing step.

Preprocessing Step	Variable	W	H	C	Storage*	Size*
Raw	$x_0\left(i\right)$	1024	1024	3	12,582,912	$3,145,728$
Grayscale	$x_1\left(i\right)$	1024	1024	1	4194,304	$1,048,576$
HS	$x_2\left(i\right)$	1024	1024	1	4194,304	$1,048,576$
Crop	$x_3\left(i\right)$	724	724	1	2096,704	$524,176$
DS	$x_4\left(i\right)$	227	227	1	206,116	$51,529$

* Storage and size are measured per image.

3. Methodology

The motivation of our algorithm was to use pretrained models to generate features from CCT images, and fuse those features using the discriminant correlation analysis (DCA) method. Section 3.1 introduces what transfer learning is. Section 3.2 briefs several state-of-the-art pretrained models and proposes a novel (L, 2) transfer feature learning (L2TFL) algorithm, to answer the question of how to extract features using pretrained networks. Section 3.3 determines how to choose the optimal two pretrained models, and proposes a novel selection algorithm of pretrained networks for fusion (SAPNF). Section 3.4 details how to fuse, and introduces the DCA technology. Section 3.5 presents a novel data augmentation method to further improve the performance. Section 3.6 presents the experimental setup and measures. Section 3.7 summarizes and gives the pseudocode of the proposed algorithms.

3.1. Transfer learning

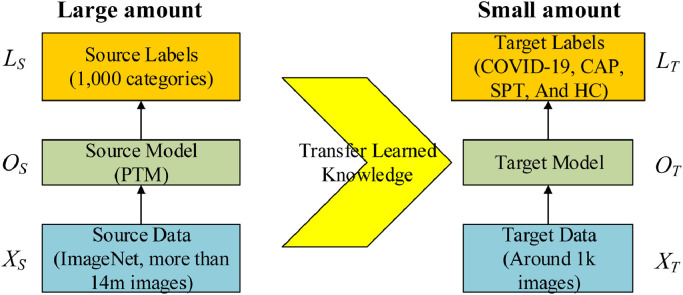
The basic ideas of transfer learning (TL) are utilizing a complicated and successfully pre-trained model (PTM) [29], taught from a sizable amount of source data, viz., (1000 categories from ImageNet), and then “transfer” the learnt knowledge [30] to the relatively simple task (4 categories of COVID-19, CAP, SPT and HC in this study) with a small quantity of data.

Mathematically, suppose the source data is $X_S$ representing ImageNet, the source label $L_S$ the 1000-category labeling, and $O_S$ means the source objective-predictive function (i.e., the classifier), we have the source domain knowledge $\mathcal{S}$ as a triple variable of

$$\mathcal{S}=\left\{X_S,L_S,O_S\right\}$$ (9)

Now we have the triple target: target data $X_T$ represents the training set, $L_T$ presents the 4-class labeling (COVID-19, CAP, SPT, or HC), and $O_T$ represents the classifier to be established.

$$\mathcal{T}=\left\{X_T,L_T,O_T\right\}$$ (10)

Using TL, the classifier to be created can be written as $O_T\left(X_T,L_T|\mathcal{S}\right)$. Without using transfer learning, the classifier is written as $O_T\left(X_T,L_T\right)$.

$$O_T=\{\begin{array}{cc}{O}_T\left(X_T,L_T|\mathcal{S}\right)=O_T\left(X_T,L_T|X_S,L_S,O_S\right)\hfill & \text{using}\text{TL}\hfill \\ O_T\left(X_T,L_T\right)\hfill & \text{not}\text{using}\text{TL}\hfill \end{array}$$ (11)

Then we can say $O_T\left(X_T,L_T|\mathcal{S}\right)$ is expected to be much closer to the ideal classifier $O_T^{Ideal}$ than the classifier using only the target domain $O_T\left(X_T,L_T\right)$, viz. suppose we have a large number of samples $X$ and its labels $L$.

$$\begin{array}{c}err\left[O_T\left(X_T,L_T|\mathcal{S}\right)\left(X\right),L\right]\\ <err\left[O_T\left(X_T,L_T\right)\left(X\right),L\right]\end{array}$$ (12)

Where $err\left(a,b\right)$ is an error function measuring the two inputs $a$ and $b$.

In practice, three elements are vital to help transfer learning improve its performance than building and training a network [31] from scratch: (i) Successful PTM can help the user remove hyper-parameter tuning; (ii) The initial layers in PTM can be thought of as feature descriptors, which extract low-level features, e.g., tints, edges, blobs, shades, and textures; (iii) The target model may only need to re-train the last several layers of the pre-trained model, since we believe the last several layers carry out the complex identification tasks. The basic idea of transfer learning is shown in Fig. 3 .

Fig. 3.

Idea of transfer learning. (PTM: pretrained mode; CAP: community-acquired pneumonia; SPT: secondary pulmonary tuberculosis; HC: healthy control).

3.2. Novelty 1: (L, 2) transfer feature learning

As shown in Table 3 , $N_{PTM}$ pretrained models were tested in this study: AlexNet, DenseNet201, ResNet50, ResNet101, VGG16, and VGG19. Traditional transfer learning usually modifies the neuron number of the last fully connected layer. Then the user may choose to retrain the whole network (The weights of reserved layers may be initialized by either pretrained models or re-initialization) or only retrains the modified layer.

Table 3.

Candidate pretrained models.

PTM	PTM Symbol	Parameters (millions)	Input Size
AlexNet	$M^{PTM}\left(1\right)$	61.0	227×227
DenseNet201	$M^{PTM}\left(2\right)$	20.0	224×224
ResNet50	$M^{PTM}\left(3\right)$	25.6	224×224
ResNet101	$M^{PTM}\left(4\right)$	44.6	224×224
VGG16	$M^{PTM}\left(5\right)$	138	224×224
VGG19	$M^{PTM}\left(6\right)$	144	224×224

In this study, we proposed a new (L, 2) transfer feature learning algorithm (abbreviated as L2TFL). The motivation for L2TFL is two-fold: (i) We make $L$, the number of layers to be removed (NLR), adaptive, and the value of $L$ was optimized to improve performance. (ii) We chose to add two newly fully connected layers due to the arbitrary width case of universal approximation theorem.

For ease of understanding, the pseudocode of proposed L2TFL algorithm is presented in Algorithm 1, where $L$ is a parameter and its value was optimized.

• Step 1. Read the PTM network in Table 3, and store it into variable $M_0$, suppose its number of learnable layers is $L^0$.

• Step 2. Remove the last NLR l-learnable layers from $M_0$ and get $M_1$,

  $$M_1=F_{rl}\left(M_0,L\right)$$ (13)

where $F_{rl}$ means remove layer function, and parameter $L$ means the number of last layers to be removed. If there are shortcuts with their outputs located within the last $L$ learnable layers, those shortcuts must be removed.

Step 3. Add 2 new fully connected layers

$$M_2=F_{afcl}\left(M_1,2\right)$$ (14)

where $F_{afcl}$ means add fully-connected layer function, and the constant 2 means the number of fully-connected layers to be appended to $M_1$. Here the number of learnable layers $L_2$ of network $M_2$ can be calculated as $L_2=L_0-L+2$. The first layer FCL layer has $N_{FCL}\left(1\right)$ nodes, and the second FCL layer has $N_{FCL}\left(2\right)$ nodes.

Step 4. Keep the learning rate [32] of all the transfer layers zero, in order to freeze those layers

$$\overrightarrow{l_r}\left[M_2\left(1:L_0-L\right)\right]\leftarrow 0$$ (15)

Where $l_r$ means the leaning rate, and $M\left(a:b\right)$ means the layers from $a$ to $b$ in network $M$, in total $b-a+1$ layers are considered in $M\left(a:b\right)$.

Step 5. Let the last two added new fully connected layers be retrainable, i.e., set their learning rate as 1

$$\overrightarrow{l_r}\left[M_2\left(L_2-1:L_2\right)\right]\leftarrow 1$$ (16)

Step 6. Retrain the whole network $M_2$ using our four-class data and get the trained network $M_3$.

$$M_3=F_{rt}\left(M_2,X\right)$$ (17)

where $X$ is some dataset, and $F_{rt}$ means the retrain function.

Step 7. Using $M_3$ to generate learnt features

$$f_M\left(L\right)=F_{ac}\left(M_3,L_2-1\right)$$ (18)

where $F_{ac}$ is the activation function, $f_{ac}\left(a,b\right)$ means to extract the activation functions from network $a$ at the $b$-th layer, $f_M\left(L\right)$ means features learnt from network $M$ by removing $L$ learnable layers.

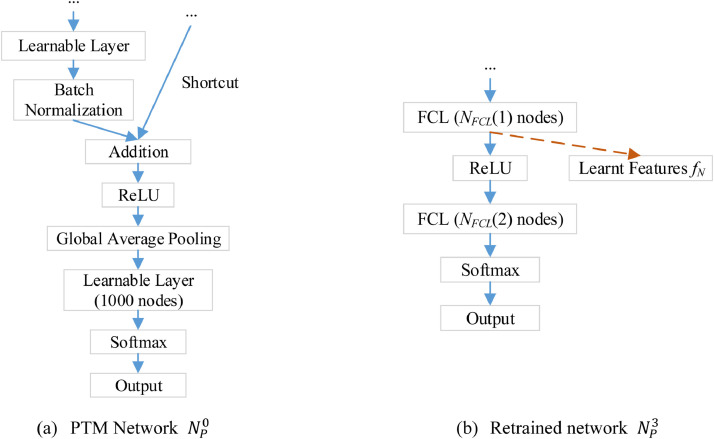
Take ResNet18 as an example, Fig. 4 shows the diagram of our L2TFL algorithm, where $L=2$. Fig. 4(a) shows the part of ResNet18 with the last two learnable layers. Fig. 4(b) shows the structure of using our L2TFL, by which the last two learnable layers of ResNet18 were replaced by two newly added FCL layers with number of nodes of $N_{FCL}\left(1\right)$ and $N_{FCL}\left(2\right)$, respectively.

Fig. 4.

A simplistic example of L2TFL algorithm for ResNet18 (Here NLR L = 2). (ReLU: rectified linear unit; FCL: fully-connected layer; L2TFL: (L, 2) transfer feature learning; NLR: number of layers to be removed).

To search the optimal value of NLR $L$, we set a range of $\left[1,L_{\text{max}}\right]$, where we searched the optimal NLR $L$ value from this range for each PTM. $L_{\text{max}}$ is the maximum removable layer (MRL). Note that SqueezeNet [33] and GoogleNet [34] were not considered since their structure contains parallel branches and were not appropriate in our L2TFL algorithm.

3.3. Novelty 2: selection algorithm of pretrained networks for fusion

Previously, we discussed how to extract features from PTMs. Now the question is how to select the two pretrained models? The naive idea is to use greedy selection algorithm for fusion (GSAF), i.e., select the best two pretrained models, and extract their features, and fuse those two features.

Suppose there is a dataset $Y$ will be split into a training set $Y_1$, a validation set $Y_2$, and a test set $Y_3$, resulting in $|Y_1|+|Y_2|+|Y_3|=|Y|$. The GSAF uses $Y_2$ to create a performance rank list $R_L$, choose the best two PTMs from that list, and fuse their corresponding features.

The procedure of GSAF is briefly described as: For a given $k$-th PTM $M_0\left(k\right)$, we use L2TFL via data $Y_1$ and removing $L$ layers to obtain $M_3\left(k,L\right)$

$$M_3\left(k,L\right)=F_{L2TFL}\left[M_0\left(k\right),L,Y_1\right]$$ (19)

where $F_{L2TFL}$ is our proposed L2TFL operation. Subsequently, an empty one-hidden layer neural network (OHNN) [35] $B$ was created for validation. The initial and trained one-hidden neural network are symbolized as $B^i$ and $B^t$, respectively. The input of $B$ is $f_M\left(k,L\right)$, and the number of hidden neurons is symbolized to $N_{HL}$. Performance indicator $I$ was calculated by comparing the output of $B^t$ over validation set $Y_2$, viz.,

$$O_2=B^t\left(Y_2\right)$$ (20)

with its ground truth labels $Z\left(Y_2\right)$, so $I$ is calculated as

$$I=F_{MI}\left[O_2,Z\left(Y_2\right)\right]$$ (21)

Where $F_{MI}$ is the measuring indicator function. It can be accuracy or sensitivity or specificity or any other measuring indicators. The $I$ is gathered overall all possible hyperparametric combination, so we get indicator vector

$$\overrightarrow{I\left(k,L\right)}\underset{\_}{\underset{\_}{def}}\left(k,L|\begin{array}{c}k=1,\cdots ,N_{PTM}\hfill \\ L=1\cdots ,L_{\text{max}}\hfill \end{array}\right)$$ (22)

The indicator vector $\overrightarrow{I\left(k,L\right)}$ is used to compare all the $N_{PTM}$ possible models and all $L_{\text{max}}$ possible removable layers, and we obtain the rank list $\overrightarrow{R}$ by

$$\overrightarrow{R_{GSAF}}=F_{SD}\left(\overrightarrow{I\left(k,L\right)}\right)$$ (23)

Where $F_{SD}$ is the sort function in descending way, and $I\left(k,L\right)$ means the indicator by learnt features from k-th PTM with removing NLR $L$ learnable layers. Now $\overrightarrow{R_{GSAF}}\left(1\right)$ and $\overrightarrow{R_{GSAF}}\left(2\right)$ means the index of the top two best models by GSAF method, as shown in Table Algorithm 2.

Nevertheless, this greedy selection algorithm cannot ensure the fused feature can obtain the best performance. For example, if the two best models are all focusing on one region, their fusion does not help improve the performance.

Hence, we proposed a novel selection algorithm of pretrained networks for fusion (SAPNF) to help choose the best two pretrained models that can specifically improve the performance of the fused features. The difference between SAPNF and GSAF is the former will investigate a larger search space that covers both PTM candidates to be fused, while the latter only searches a smaller space which contains only one PTM candidate. The pseudocode of SAPNF is presented in Algorithm 3.

Mathematically, we retrained two models (with hyperparameters as PTM and NLR) in SAPNF. Hence, Eq (19) was updated as

$$\{\begin{array}{c}{M}_3\left(k_1,L_1\right)=F_{L2TFL}\left[M_0\left(k_1\right),L_{M1},Y_1\right]\\ M_3\left(k_2,L_2\right)=F_{L2TFL}\left[M_0\left(k_2\right),L_{M2},Y_1\right]\end{array}$$ (24)

where the subscript $1\text{or}2$ in $\left(k_1,k_2\right)$ and $\left(L_{M1},L_{M2}\right)$ means the index of candidate model. Note we should guarantee

$$k_1\ne k_2\vee L_{M1}\ne L_{M2}$$ (25)

Which helped ensure the two candidate models are not the same one.

Now we can generate two features $f_M\left(k_1,L_{M1}\right)$ and $f_M\left(k_2,L_{M2}\right)$ from two different models $M_3\left(k_1,L_{M1}\right)$ and $M_3\left(k_2,L_{M2}\right)$, respectively. We used some fusion operation to generate a fused feature $f_F$ as

$$f_F\left(k_1,L_{M1},k_2,L_{M2}\right)=F_{DF}\left[f_M\left(k_1,L_{M1}\right),f_M\left(k_2,L_{M2}\right)\right]$$ (26)

Where $F_{DF}$ is the deep fusion function, which will be discussed in next Section.

The indicator vector $\overrightarrow{I}$ is updated as

$$\overrightarrow{I\left(k_1,L_{M1},k_2,L_{M2}\right)}\underset{\_}{\underset{\_}{def}}\overrightarrow{\left(k_1,L_1,k_2,L_2|\begin{array}{c}\left(k_1,k_2\right)=1,\cdots ,N_{PTM}\hfill \\ \left(L_{M1},L_{M2}\right)=1\cdots ,L_{\text{max}}\hfill \\ k_1\ne k_2\vee L_{M1}\ne L_{M2}\hfill \end{array}\right)}$$ (27)

Similarly, we obtain the rank list $\overrightarrow{R_{SAPNF}}$ by

$$\overrightarrow{R_{SAPNF}}=F_{SD}\left(\overrightarrow{I\left(k_1,L_{M1},k_2,L_{M2}\right)}\right)$$ (28)

3.4. Novelty 3: deep CCT fusion by discriminant correlation analysis

Feature-level fusion (FLF) aims to combine discriminative multiple features, while decision-level fusion (DLF) combines multiple decision answers. Commonly, DLF is simpler than FLF, but FLF outperforms DLF [36, 37]. In this study we chose feature-level fusion. In our future research, we will also consider some advanced fusion rules, such as score-level fusion, DLF, and hybrid fusion methods [38].

We have discussed how to carry out transfer feature learning and how to select pretrained models. Now we need to answer the question of how to fuse those extracted features. There are two commonly used FLF methods. Based on having two $N_{FCL}\left(1\right)$-dimension features from two PTMs, the features were generated by our L2TFL method, and the selection of PTM was by SAPNF method.

Assume the two features are symbolized as $f_{M1}$ with length $q_1$ and $f_{M2}$ with length $q_2$, the fused feature is symbolized as $f_F$. Serial fusion (SF) [39] concatenates the two features into one single feature

$$\underset{q_1+q_2}{\underbrace{f_F}}=F_{SF}\left(\underset{q_1}{\underbrace{f_{M1}}},\underset{q_2}{\underbrace{f_{M2}}}\right)$$ (29)

where $F_{SF}$ represents the SF operation. The length of $f_F$ equals $|f_{M1}|+|f_{M2}|=q_1+q_2$.

Parallel fusion (PF) [40] combines $f_{M1}$ and $f_{M2}$ into one complex vector

$$f_F=F_{PF}\left(f_{M1},f_{M2}\right)=f_{M1}+i\times f_{M2}$$ (30)

where $F_{PF}$ represents the PF operation, and $i$ the imaginary unit.

Sun, et al. [41] proposed a canonical correlation analysis (CCA), which finds optimal linear combination of $f_{M1}$ and $f_{M2}$ which have maximum correlation with each other. Suppose $f_{M1}\in R^{q_1\times N_{TF}}$, $f_{M2}\in R^{q_2\times N_{TF}}$, where $N_{TF}$ means the number of trained features. First, we can define two covariance matrixes $S_{\left(M1,M1\right)}$ and $S_{\left(M2,M2\right)}$ as

$$\{\begin{array}{c}{S}_{\left(M1,M1\right)}=F_{CCOV}\left(f_{M1},f_{M1}\right)\in R^{q_1\times q_1}\hfill \\ S_{\left(M2,M2\right)}=F_{CCOV}\left(f_{M2},f_{M2}\right)\in R^{q_2\times q_2}\hfill \end{array}$$ (31)

where $F_{CCOV}$ is the cross-covariance operation. Also, we can define the covariance matrix $S_{\left(M1,M2\right)}$ as

$$S_{\left(M1,M2\right)}=F_{CCOV}\left(f_{M1},f_{M2}\right)$$ (32)

We have $S_{\left(M1,M2\right)}=S_{\left(M2,M1\right)}^T$.

The overall covariance matrix can be computed as

$$S=\left[\begin{array}{cc}{S}_{\left(M1,M1\right)}& S_{\left(M1,M2\right)}\\ S_{\left(M2,M1\right)}& S_{\left(M2,M2\right)}\end{array}\right]\in R^{\left(q_1+q_2\right)\times \left(q_1+q_2\right)}$$ (33)

The aim of CCA is to seek the best linear projection

$$\{\begin{array}{c}\overline{f_{M1}}=W_{CCA,M1}^T{f}_{M1}\\ \overline{f_{M2}}=W_{CCA,M2}^T{f}_{M2}\end{array}$$ (34)

where $W_{CCA,M1}$ and $W_{CCA,M2}$ are transformation matrices of CCA. The aim is to find the optimal $\left(W_{CCA,M1},W_{CCA,M2}\right)$ that maximizes the pair-wise correlation $F_{PWC}$ over the two feature sets:

$$\left(W_{CCA,M1},W_{CCA,M2}\right)=\underset{W_{M1},W_{M2}}{\text{argmax}}\left[F_{PWC}\left(\overline{f_{M1}},\overline{f_{M2}}\right)\right]$$ (35)

Where $F_{PWC}$ means the pair-wise correlation, defined as

$$F_{PWC}\left(\overline{f_{M1}},\overline{f_{M2}}\right)=\frac{W_{CCA,M1}^T{S}_{\left(M1,M2\right)}{W}_{CCA,M2}}{\sqrt{W_{CCA,M1}^T{S}_{\left(M1,M1\right)}{W}_{CCA,M1}}\times \sqrt{W_{CCA,M2}^T{S}_{\left(M2,M2\right)}{W}_{CCA,M2}}}$$ (36)

The detailed derivation and solution can be found in [41]. For the optimal weights $\left(W_{CCA,M1},W_{CCA,M2}\right)$, we have $\overline{f_{M1}}=W_{CCA,M1}^T{f}_{M1}$, and $\overline{f_{M2}}=W_{CCA,M2}^T{f}_{M2}$. Hence, the combination of the transformed features is carried out by either concatenation or summation as:

$$\{\begin{array}{c}{f}_{CCCA}=\left(\begin{array}{c}\overline{f_{M1}}\\ \overline{f_{M2}}\end{array}\right)={\left(\begin{array}{cc}{W}_{CCA,M1}& 0\\ 0& W_{CCA,M2}\end{array}\right)}^T\left(\begin{array}{c}{f}_{M1}\\ f_{M2}\end{array}\right)\hfill \\ f_{SCCA}=\overline{f_{M1}}+\overline{f_{M2}}={\left(\begin{array}{c}{W}_{CCA,M1}\\ W_{CCA,M2}\end{array}\right)}^T\left(\begin{array}{c}{f}_{M1}\\ f_{M2}\end{array}\right)\hfill \end{array}$$ (37)

where $f_{CCCA}$ and $f_{SCCA}$ represent the concatenation and summation of CCA features, respectively.

CCA has two issues: (i) The number of samples is less than the number of features in many real world scenarios: $N_{TF}<q_1\vee N_{TF}<q_2$, which makes the covariance matrices non-invertible and singular. (ii) CCA neglects the class structure information. To solve these two issues, Haghighat, et al. [42] presented a discriminant correlation analysis (DCA) approach. DCA has been proven to offer improved performance than recent fusion approaches.

In this study, we used DCA to fuse features from CCT images, and we named it as deep CCT fusion by discriminant correlation analysis (DCFDCA). Similar to CCA, suppose $f_{M1}\in R^{q_1\times N_{TF}}$, where $N_{TF}$ means the number of trained features. The $N_{TF}$ columns of the data matrix can be segmented into $\mathcal{C}$ classes, suppose $N_i$ columns belong to the i th class, we have

$$N_{TF}={\sum }_{i=1}^{\mathcal{C}}{N}_i$$ (38)

Let $f_{M1}^{ij}\in f_{M1}$ denotes feature extracted from i th image of j-th category via model $M1$, and $\overline{f_{M1}^i}$ and $\overline{f_{M1}}$ denotes the mean of $f_{M1}^{ij}$ over i th class and the whole set, respectively. We can get

$$\{\begin{array}{c}\overline{f_{M1}^i}=\frac{1}{N_{TF}}{\sum }_{j=1}^{N_i}{f}_{M1}^{ij}\\ \overline{f_{M1}}=\frac{1}{N_{TF}}{\sum }_{i=1}^{\mathcal{C}}{N}_i\overline{f_{M1}^i}\end{array}$$ (39)

Thus, the between-class scatter (BCS) matrix $S_{BCS,M1}\in R^{q_1\times q_1}$ is defined as

$$S_{BCS,M1}={\sum }_{i=1}^{\mathcal{C}}{N}_i\left(\overline{f_{M1}^i}-\overline{f_{M1}}\right)\left(\overline{f_{M1}^i}-\overline{f_{M1}}\right)\underset{\_}{\underset{\_}{\text{def}}}{\Phi }_{BCS,M1}{\Phi }_{BCS,M1}^T$$ (40)

where ${\Phi }_{BCS,M1}\in R^{q_1\times \mathcal{C}}$ is defined as

$${\Phi }_{BCS,M1}=\left[\sqrt{N_1}\left(\overline{f_{M1}^1}-\overline{f_{M1}}\right),\sqrt{N_2}\left(\overline{f_{M1}^2}-\overline{f_{M1}}\right),\dots ,\sqrt{N_{\mathcal{C}}}\left(\overline{f_{M1}^{\mathcal{C}}}-\overline{f_{M1}}\right)\right]$$ (41)

Note the number of features is greater than the number of classes in this study, i.e., $\left(q_1\gg \mathcal{C}\right)$, so a method [43] is chosen here to calculate the covariance matrix of ${\Phi }_{BCS,M1}^T{\Phi }_{BCS,M1}\in R^{\mathcal{C}\times \mathcal{C}}$. The most significant eigenvectors of ${\Phi }_{BCS,M1}{\Phi }_{BCS,M1}^T$ can be economically attained by mapping the eigenvectors of ${\Phi }_{BCS,M1}^T{\Phi }_{BCS,M1}$. Hence, it is ncessary to acquire the eigenvectros of this $\mathcal{C}\times \mathcal{C}$ covraicne matrix ${\Phi }_{BCS,M1}^T{\Phi }_{BCS,M1}$. Assue the classes were well-separated, ${\Phi }_{BCS,M1}^T{\Phi }_{BCS,M1}$ is a diagonal matrix as

$$P_{OE}^T\left({\Phi }_{BCS,M1}^T{\Phi }_{BCS,M1}\right)P_{OE}=\widehat{\Lambda }$$ (42)

where $P_{OE}$ denotes the matrix of orthogonal eigenvectors, $\widehat{\Lambda }$ the diagonal matrix of real and non-negtive eigenvalue in decreasing order.

Assue $Q_{OE}\in R^{r\times r}$ entails the first $r$ eigenvectors from $P_{OE}$, so $Q_{OE}$ corrresponds to the $r$ largest non-zero eigenvalues in $\widehat{\Lambda }$. We can deduce folowing equation as

$$Q_{OE}^T\left({\Phi }_{BCS,M1}^T{\Phi }_{BCS,M1}\right)Q_{OE}=\Lambda \in R^{r\times r}$$ (43)

Therefore, the $r$ most significant eigenvectors of $S_{BCS,M1}$ are acquired by the mapping $Q_{OE}\Rightarrow {\Phi }_{BCS}{Q}_{OE}$ as

$${\left({\Phi }_{BCS,M1}{Q}_{OE}\right)}^T{S}_{BCS,M1}\left({\Phi }_{BCS,M1}{Q}_{OE}\right)=\Lambda$$ (44)

Assume $W_{BCS,M1}={\Phi }_{BCS,M1}{Q}_{OE}{\Lambda }^{-1/2}$ is the transformation which uses $S_{BCS}$ and reduces the data's dimensionality from $q_1$ to $r$, we have

$$W_{BCS,M1}^T{S}_{BCS,M1}{W}_{BCS,M1}=I$$ (45)

and

$$\underset{r\times N_{TF}}{\underbrace{{f^{\prime }}_{M1}}}=\underset{r\times q_1}{\underbrace{W_{BCS,M1}^T}}\times \underset{q_1\times N_{TF}}{\underbrace{f_{M1}}}$$ (46)

where $f_{M1}^{\prime }$ denotes the projection of $f_{M1}$ in a temporary space, in which the BCS matrix of the 1st feature set to be fused is $I$ and the classes are all separated. Notice that

$$r\le \min \left[F_{rank}\left(f_{M1}\right),F_{rank}\left(f_{M2}\right),\mathcal{C}-1\right]$$ (47)

where $F_{rank}$ is the rank function.

Similarly, to the second feature set $f_{M2}$, we can find a transform matrix $W_{BCS,M2}$, which employes the BCS matrix for the second feature sets to be fused $S_{BCS,M2}$ and reduces the dimensionality of $f_{M2}$ from $q_2$ to $r$ as

$$W_{BCS,M2}^T{S}_{BCS,M2}{W}_{BCS,M2}=I$$ (48)

$$\underset{r\times N_{TF}}{\underbrace{{f^{\prime }}_{M2}}}=\underset{r\times q_2}{\underbrace{W_{BCS,M2}^T}}\times \underset{q_2\times N_{TF}}{\underbrace{f_{M2}}}$$ (49)

The updated ${\Phi }_{BCS,M1}^{\prime }$ and ${\Phi }_{BCS,M2}^{\prime }$ are now non-square $r\times \mathcal{C}$ orthonormal matrices. Note that $S_{BCS,M1}^{\prime }=S_{BCS,M2}^{\prime }=I$, nevertheless, the matrices ${\left({\Phi }_{BCS,M1}^{\prime }\right)}^T{\Phi }_{BCS,M1}^{\prime }$ and ${\left({\Phi }_{BCS,M2}^{\prime }\right)}^T{\Phi }_{BCS,M2}^{\prime }$ are strictly diagonally dominant matrices (DDMs), namely, if $b_{ij}$ denotes the entry of a DDM, then $\left(\forall i:|b_{ii}|>{\sum }_{i\ne j}\left|b_{ij}\right|\right)$. In our study, the diagonal entries are near to 1 and the off-diagonal entries are near to zero.

So far, we have transformed $f_{M1}\to f_{M1}^{\prime }$ and $f_{M2}\to f_{M2}^{\prime }$, i.e., we have finished the unitization of BCS matrices. The next step is to transform the features in one set to have nonzero correlation with their cognate features in the other set.

Mathematically, the between-set covariance (BSC) matrix $S_{M1,M2}^{\prime }=f_{M1}^{\prime }{\left(f_{M2}^{\prime }\right)}^T\in R^{r\times r}$ of the transformed features set need to be diagonalized. The singular value decomposition (SVD) approach is utilized at this step.

$$S_{M1,M2}^{\prime }=U\Sigma V^T\Rightarrow U^T{S}_{M1,M2}^{\prime }V=\Sigma$$ (50)

Remember that $f_{M1}^{\prime }$ and $f_{M2}^{\prime }$ are of rank $r$ and $S_{M1,M2}^{\prime }$ is non-degenerate. We can deduce $\Sigma$ is a diagonal matrix, of which the main diagonal elements are non-zero. Assume

$$\{\begin{array}{c}{W}_{BSC,M1}\underset{\_}{\underset{\_}{\text{def}}}U{\Sigma }^{-1/2}\\ W_{BSC,M2}\underset{\_}{\underset{\_}{\text{def}}}V{\Sigma }^{-1/2}\end{array}$$ (51)

We have

$${\left(U{\Sigma }^{-1/2}\right)}^T{S}_{M1,M2}^{\prime }\left(V{\Sigma }^{-1/2}\right)=I$$ (52)

which unitizes the BSC matrix $S_{M1,M2}^{\prime }$. Finally, the DCA-transformed features can be written as

$$\{\begin{array}{c}{g}_{M1}=W_{BSC,M1}^T{f^{\prime }}_{M1}=W_{BSC,M1}^T{W}_{BCS,M1}^T{f}_{M1}\underset{\_}{\underset{\_}{\text{def}}}{W}_{DCA,M1}{f}_{M1}\hfill \\ g_{M2}=W_{BSC,M2}^T{f^{\prime }}_{M2}=W_{BSC,M2}^T{W}_{BCS,M2}^T{f}_{M2}\underset{\_}{\underset{\_}{\text{def}}}{W}_{DCA,M2}{f}_{M2}\hfill \end{array}$$ (53)

Where $W_{DCAM1}\underset{\_}{\underset{\_}{\text{def}}}{W}_{BSC,M1}^T{W}_{BCS,M1}^T$ and $W_{DCA,M2}\underset{\_}{\underset{\_}{\text{def}}}{W}_{BSC,M2}^T{W}_{BCS,M2}^T$ are the final transformation matrices of DCA for $f_{M1}$ and $f_{M2}$, respectively. Similarly, the combination of the transformed DCA features is done by either concatenation or summation as:

$$\{\begin{array}{c}{g}_{CDCA}=\left(\begin{array}{c}{g}_{M1}\\ g_{M2}\end{array}\right)={\left(\begin{array}{cc}{W}_{DCA,M1}& 0\\ 0& W_{DCA,M2}\end{array}\right)}^T\left(\begin{array}{c}{f}_{M1}\\ f_{M2}\end{array}\right)\hfill \\ g_{SDCA}=g_{M1}+g_{M2}={\left(\begin{array}{c}{W}_{DCA,M1}\\ W_{DCA,M2}\end{array}\right)}^T\left(\begin{array}{c}{f}_{M1}\\ f_{M2}\end{array}\right)\hfill \end{array}$$ (54)

where $g_{CDCA}$ and $g_{SDCA}$ represent the concatenation and summation of DCA features, respectively. In this study, $g_{SDCA}$ was chosen, since (i) summation procedure features in lower number of dimensions, and (ii) the summation and concatenation have similar results reported in [42]. In addition, feature fusion can help improve the performance compared to using a single PTM model (See Sections 4.3 and 4.4).

3.5. Data augmentation

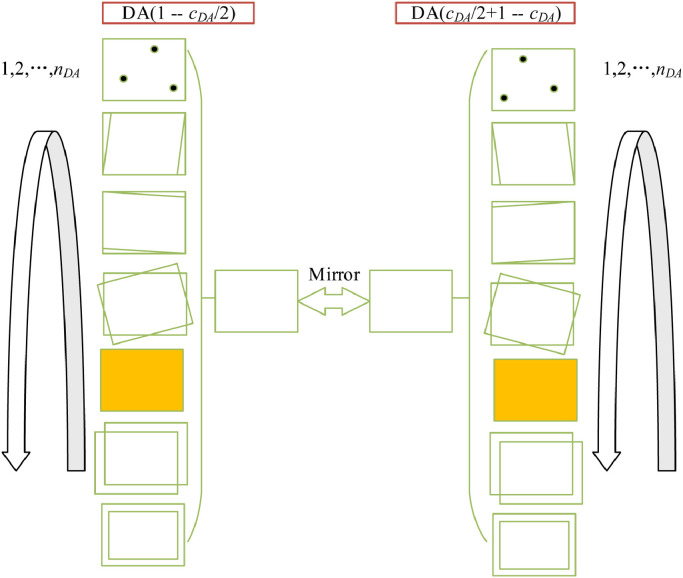
Multiple-way data augmentation (MDA) technology [44] was used in this study. The disparity of MDA to conventional DA is that MDA utilizes a large number of different data augmentation methods. There are two types [45] of MDA, offline and online. Offline means editing and storing data on the disk, and online means on-the-fly augmentation. In this study, we chose to use offline multiple-way data augmentation, as shown in Fig. 6 . Usually, online data augmentation is mainly applied when the dataset is large. The transformations happen in mini-batches and then, the transformed data is fed into the model to improve the generalization of the model. However, we have a small dataset in this study. Therefore, we chose offline data augmentation as a preprocessing step to expand the dataset.

Fig. 6.

Diagram of proposed offline MDA technology. (DA: data augmentation; MDA: multiple-way DA).

Suppose the number of different DA techniques used is $c_{DA}$, and there is one training image $x^{tr}\left(i\right)\in X^{tr}$, where $X^{tr}$ means the training set. Assume each offline MDA technique will generate $n_{DA}$ images, so for each image, we will generate $c_{DA}\times n_{DA}$ new images. Over the entire training image set $X^{tr}$, we perform the subsequent seven DA methods:

(i) noise injection

The $h_m^{NI}$-mean $h_v^{NI}$-variance Gaussian noises were added to all training images to produce $n_{DA}$ new noised images.

$\overrightarrow{x^{tr1}\left(i\right)}\begin{array}{c}|=F_{NI}\left[x^{tr}\left(i\right)\right]\hfill \\ |=\left[x_1^{tr1}\left(i\right),\cdots x_{n_{DA}}^{tr1}\left(i\right)\right]\hfill \end{array}$

$$\begin{array}{c}\overrightarrow{x^{tr1}\left(i\right)}=F_{NI}\left[x^{tr}\left(i\right)\right]\hfill \\ =\left[x_1^{tr1}\left(i\right),\dots x_{n_{DA}}^{tr1}\left(i\right)\right]\hfill \end{array}$$ (55)

where $F_{NI}$ means the noise injection function.

(ii) horizontal shear (HS) transform

New $n_{DA}$ images were made by HS transform

$$\overrightarrow{x^{tr2}\left(i\right)}\begin{array}{c}|=F_{HS}\left[x^{tr}\left(i\right)\right]\hfill \\ |=\left[x_1^{tr2}\left(i,h_1^{HS}\right),\cdots x_{n_{DA}}^{tr2}\left(i,h_{n_{DA}}^{HS}\right)\right]\hfill \end{array}$$ (56)

Where $F_{HS}$ denotes the HS transform function. HS factors $h^{HS}$ does not include the value of $h^{HS}=0$.

(iii) vertical shear (VS) transform

$$\overrightarrow{x^{tr3}\left(i\right)}\begin{array}{c}|=F_{VS}\left[x^{tr}\left(i\right)\right]\hfill \\ |=\left[x_1^{tr3}\left(i,h_1^{VS}\right),\cdots x_{n_{DA}}^{tr3}\left(i,h_{n_{DA}}^{VS}\right)\right]\hfill \end{array}$$ (57)

where $F_{VS}$ means VS transform function, which operates similarly as ST transform. The VS factor has the same value of HS factor $h_j^{VS}=h_j^{HS},\forall j\in 1,2,\cdots ,n_{DA}$.

(iv) rotation

(i) Rotation angle vector $h^{RO}$skips the value of 0.

$$\begin{array}{c}\overrightarrow{x^{tr4}\left(i\right)}=F_{RO}\left[x^{tr}\left(i\right)\right]\hfill \\ =\left[x_1^{tr4}\left(i,h_1^{RO}\right),\dots x_{n_{DA}}^{tr4}\left(i,h_{n_{DA}}^{RO}\right)\right]\hfill \end{array}$$ (58)

where $F_{RO}$ means rotation operation.

(v) gamma correction (GC)

The factor of GC $h^{GC}$ skips the value of 1.

$$\begin{array}{c}\overrightarrow{x^{tr5}\left(i\right)}=F_{GC}\left[x^{tr}\left(i\right)\right]\hfill \\ =\left[x_1^{tr5}\left(i,h_1^{GC}\right),\dots x_{n_{DA}}^{tr5}\left(i,h_{n_{DA}}^{GC}\right)\right]\hfill \end{array}$$ (59)

Where $F_{GC}$ means GC operation.

(vi) random translation (RT)

Every image in the training set $x^{tr}\left(i\right),i=1,2,\dots ,\left|X^{tr}\right|$ is translated $n_{DA}$ times with random vertical shift $h_{rvs}$ and random horizontal shift $h_{rhs}$. The values of $h_{rhs}$ and $h_{rvs}$ are in the range of $\left[-a_Z,a_Z\right]$, and obey uniform distribution $\mathcal{V}$.

$$\{\begin{array}{c}{h}_{rhs}^i\sim \mathcal{V}\left[-M_{SR},+M_{SR}\right]\\ h_{vhs}^i\sim \mathcal{V}\left[-M_{SR},+M_{SR}\right]\end{array},\forall i\in \left[1,n_{DA}\right]$$ (60)

where $M_{SR}$ is the maximum shift range. Hence, we have

$$\begin{array}{c}\overrightarrow{x^{tr6}\left(i\right)}=F_{RT}\left[x^{tr}\left(i\right)\right]\hfill \\ =\left[x_1^{tr6}\left(i,h_{rhs}^1,h_{vhs}^1\right),\dots x_{n_{DA}}^{tr6}\left(i,h_{rhs}^{n_{DA}},h_{vhs}^{n_{DA}}\right)\right]\hfill \end{array}$$ (61)

(vii) scaling

All training images $\left\{x^{tr}\left(i\right)\right\}$ are scaled with scaling factor $h^{SC}$, skipping $h^{SC}=1$.

$$\begin{array}{c}\overrightarrow{x^{tr7}\left(i\right)}=F_{SC}\left[x^{tr}\left(i\right)\right]\hfill \\ =\left[x_1^{tr7}\left(i,h_1^{SC}\right),\dots x_{n_{DA}}^{tr7}\left(i,h_{n_{DA}}^{SC}\right)\right]\hfill \end{array}$$ (62)

where $F_{SC}$ is the scaling operation.

(ix) mirror

All the above $\frac{c_{DA}}{2}$ results are mirrored:

$$\begin{array}{c}\overrightarrow{x^{tr\left(k+\frac{c_{DA}}{2}\right)}\left(i\right)}=F_{MIR}\left[\overrightarrow{x^{tr\left(k\right)}\left(i\right)}\right]\end{array},\forall k\in \left\{1,2,\cdots ,\frac{c_{DA}}{2}\right\}$$ (63)

where $F_{MIR}$ represents the mirror function.

(x) concatenation

All the $c_{DA}$-way results are concatenated as

$$\overrightarrow{{\underbrace{x^{DA}\left(i\right)}}_{{\alpha }_{DA}}}=F_{CON}\left\{\underset{1}{\underbrace{x^{tr}\left(i\right)}},\underset{1}{\underbrace{F_{MIR}\left[x^{tr}\left(i\right)\right]}},\overrightarrow{{\underbrace{x^{tr1}\left(i\right)}}_{n_{DA}}},\cdots \overrightarrow{{\underbrace{x^{tr}\left(C_{DA}\right)\left(i\right)}}_{n_{DA}}}\right\}$$ (64)

where $F_{CON}$ means concatenation operation, $\overrightarrow{x^{DA}\left(i\right)},i=1,2,\cdots ,\left|X^{DA}\right|$ is the collection of generated MDA images with original image $x^{tr}\left(i\right)$. $X^{DA}$ is the set of all augmented images. $|X^{DA}|$ is the size of the augmented dataset. $a_{DA}$ the data augmentation factor (DAF), representing the ratio of size of augmented training set to the size of original training set. $a_{DA}$ is calculated as

$$a_{DA}=\frac{\left|\overrightarrow{x^{DA}\left(i\right)}\right|}{\left|x^{tr}\left(i\right)\right|}=\frac{\left|X^{DA}\right|}{\left|X^{tr}\right|}$$ (65)

We can calculate $a_{DA}=n_{DA}\times c_{DA}+2$. Therefore, the MDA is a function making the enhanced training set $a_{DA}$ times as large as the original training set $X^{tr}$.

$$\left\{x^{tr}\left(i\right)\in X^{tr}\right\}\stackrel{\text{MDA}}{\to }\left\{\to x^{DA}\left(i\right)\in X^{DA}\right\}$$ (66)

3.6. Experiment setup and measures

Two types of measures were performed in our experiment. One is for validation to choose the best PTMs, and the other is on the test set to relate the unbiased performances so as to compare with state-of-the-art approaches. the whole preprocessed dataset $X_4$ is split into a non-test set $X_4^{ntest}$, and a test set $X_4^{test}$, i.e., $X_4\to \left\{X_4^{ntest},X_4^{test}\right\}$. Roughly, the non-test set $X_4^{ntest}$comprises 80% of the whole dataset, and the test set $X_4^{test}$ the remaining 20%. So we have

$$N_k^{ntest}+N_k^{test}=N_k\left(k=1,2,3,4\right)$$ (67)

where $N_k^{ntest}$ means the number of samples in the non-test set in k-th class and $N_k^{test}$ the number of samples of the test set in k-th class. Hence, $N_k^{ntest}/N_k\approx 80\%$, and $N_k^{test}/N_k\approx 20\%$.

For the validation phase, a $R_v$ runs of 10-fold cross validation [46] was run to obtain the validation performance. The ideal confusion matrix $L_{Val}^I$ combining all $R_v$ runs of 10 folds is

$$L_{Val}^I=R_v\times \left[\begin{array}{cccc}{N}_1^{ntest}& & & \\ & N_2^{ntest}& & \\ & & N_3^{ntest}& \\ & & & N_4^{ntest}\end{array}\right]$$ (68)

In the test phase, we ran our selected best models with $R_t$ times, each run with various initial seeds, the ideal confusion matrix $L_{Test}^I$ is

$$L_{Test}^I=R_t\times \left[\begin{array}{cccc}{N}_1^{test}& & & \\ & N_2^{test}& & \\ & & N_3^{test}& \\ & & & N_4^{test}\end{array}\right]$$ (69)

For realistic runs, suppose $r_i$ is the run index, and each run we will generate either validation confusion matrix [47] $L_{Val}\left(r_i\right)$ or test confusion matrix $L_{Test}\left(r_i\right)$. After summarizing all runs, we can obtain the summation of validation confusion matrix $L_{Val}$ as

$$L_{Val}={\sum }_{r_i=1}^{R_v}{L}_{Val}\left(r_i\right)$$ (70)

And the summation of test confusion matrix $L_{Test}$ as

$$L_{Test}={\sum }_{r_i=1}^{R_t}{L}_{Test}\left(r_i\right)$$ (71)

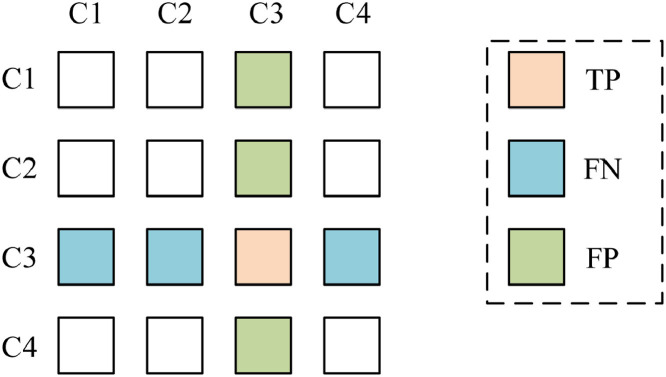
For each class $k=1,2,3,4$, we set the that class label as “positive”, and all other three classes are “negative”. Fig. 7 shows a schematic of a multiple-class confusion matrix, where we focus on the 3rd class. Hence, the element on the 3rd row and 3rd column is TP, the summation of the remaining entries on the 3rd row is FN, and the summation of the remaining entries in the 3rd column is FP. So, we can define this measure per class as

$$Sen\left(k\right)=\frac{TP\left(k\right)}{TP\left(k\right)+FN\left(k\right)}$$ (72)

$$Prc\left(k\right)=\frac{TP\left(k\right)}{TP\left(k\right)+FP\left(k\right)}$$ (73)

$$F1\left(k\right)=\frac{2*Prc\left(k\right)*Sen\left(k\right)}{Prc\left(k\right)+Sen\left(k\right)}$$ (74)

Fig. 7.

Confusion matrix of multiple class conditions.

Measures can also be given at an overall level. One is called macro-level, which computes the metric independently for each class and takes the average that gives equal weight to each class (treating all classes equally) [48]. In contrast, the other is micro-level, weighting all samples equally [49]. In this multiple classification research, we prefer the micro-averaged (MA) F1 as the dataset is slightly unbalanced. The MA F1 [50] ($F{1}_{\mu }$) is defined below as the main indicator in the validation phase.

$$F{1}_{\mu }=\frac{2*Pr{c}_{\mu }*Se{n}_{\mu }}{Pr{c}_{\mu }+Se{n}_{\mu }}$$ (75)

where $Pr{c}_{\mu }$ and $Se{n}_{\mu }$ are micro-averaged precision and micro-averaged sensitivity, defined as

$$Se{n}_{\mu }=\frac{{\sum }_{k}TP\left(k\right)}{{\sum }_{k}TP\left(k\right)+FN\left(k\right)}$$ (76)

$$Pr{c}_{\mu }=\frac{{\sum }_{k}TP\left(k\right)}{{\sum }_{k}TP\left(k\right)+FP\left(k\right)}$$ (77)

We used $F{1}_{\mu }$ in this study, since its values equals $Se{n}_{\mu }$ and $Pr{c}_{\mu }$.

3.7. Pseudocode of CCSHNet

Algorithm 4 lists the pseudocode of proposed AI model, named CCSHNet, which is an acronym of the four categories analyzed in this study: COVID-19, CAP, SPT, and HC. The proposed algorithm and experiment setup consisted of five phases: Phase I shows the preprocessing. Phase II shows $R_v$ runs of ten-folds CV on the non-test set. Phase III shows the PTM selection. Phase IV presents CCSHNet model creation, and Phase V reports the test performance of the CCSHNet model.

Gradient-weighted Class Activation Mapping (Grad-CAM) [51] was used to give an explainable heat map. It utilizes the gradient of the classification score in terms of the convolutional features regulated by the AI model to help users comprehend which regions of the input image are the most vital for AI model to make decisions.

4. Experiments, results, and discussions

4.1. Hyperparameter values

Table 4 itemizes the hyperparameter setting. The image size using slice level section was obtained as $|X_0|=1164$. The size of each raw image was $1024\times 1024\times 3$. The crop values along four directions were all set to 150 (We tested larger values and found some important chest regions are removed). The number of PTM candidates was set to 6. The number of the first FCL was set to 512, and the number of the second FCL was set to 4, which corresponds to the number of classes in this task. The maximum removable layer was set 3, so we searched the best $L$ at the range of $\left[1,3\right]$. The number of hidden neurons in OHNN was set to 10.

Table 4.

Hyperparameter Setting.

Parameter	Value
$|X_0|$	$|X_0|=284+281+293+306=1164$
$W_0$	1024
$H_0$	1024
$C_0$	3
$c_t$	150
$c_b$	150
$c_l$	150
$c_r$	150
$N_{PTM}$	6
$N_{FCL}\left(1\right)$	512
$N_{FCL}\left(2\right)$	4
$L_{\text{max}}$	3
$N_{HL}$	10
$c_{DA}$	14
$n_{DA}$	30
$h_m^{NI}$	0
$h_v^{NI}$	0.01
$h^{HS}$	$h_{1-15}^{HS}=\left[-0.15,-0.14,\dots ,-0.01\right]$, $h_{16-30}^{HS}=\left[+0.01,+0.02,\dots ,+0.15\right]$.
$h^{RO}$	$h_{1-15}^{RO}=\left[-{30}^{\circ },-{28}^{\circ },\dots ,-2^{\circ }\right]$, $h_{16-30}^{RO}=\left[+2^{\circ },+4^{\circ },\dots ,+{30}^{\circ }\right]$.
$h^{GC}$	$h_{1-15}^{GC}=\left[0.4,0.44,\dots ,0.96\right]$, $h_{16-30}^{GC}=\left[1.04,1.08,\dots ,1.6\right]$.
$M_{SR}$	20
$h^{SC}$	$h_{1-15}^{SC}=\left[0.7,0.72,\dots ,0.98\right]$, $h_{16-30}^{SC}=\left[1.02,1.04,\dots ,1.3\right]$.
$a_{DA}$	422
$R_v$	10
$R_t$	10

For the offline MDA technique, the number of different DA techniques was adjusted to 14. The number of generated images by each offline MDA technique was 30. The mean and variance of Gaussian noise injected were 0 and 0.01, respectively. The HS factor $h^{HS}$ ranged from −0.15 to +0.15, excluding the value of 0. The RO factor $h^{RO}$ ranged from −30 to 30 excluding the value of 0. The GC factor $h^{GC}$ ranged from 0.4 to 1.6 skipping the value of 1. The maximum shift range was set to 20. The SC factor $h^{SC}$ ranged from 0.7 to 1.3 excluding the value of 1. Data augmentation factor was calculated as 422. The number of runs over validation and test sets were all set to 10.

Table 5 itemizes the training, validation, and test set for each category. For the non-test set, 10-fold cross validation was used for validation, with 9 folds being for training and the remaining fold for validation, which repeated 10 times, so all the non-test set was used in the validation set. The above 10-fold cross validation repeat $R_v$ runs, and thus generated a summation of validation confusion matrix $L_{Val}$. For the test set, $R_t$ runs generated a summation of test confusion matrix $L_{Test}$.

Table 5.

Training, validation, and test set.

	Non-test (9 folds for training and 1-fold for validation)	Test	Total
COVID-19	$N_1^{ntest}=227$	$N_1^{test}=57$	$N_1=284$
CAP	$N_2^{ntest}=225$	$N_2^{test}=56$	$N_2=281$
SPT	$N_3^{ntest}=234$	$N_3^{test}=59$	$N_3=293$
HC	$N_4^{ntest}=245$	$N_4^{test}=61$	$N_4=306$

4.2. Illustration of multiple data augmentation

Fig. 8 displays the MDA results, where the hyperparameters can be found in Section 4.1. The raw image is Fig. 2(a), which generates 421 new images (1 mirror image, 210 new images obtained from the original image, and 210 new images obtained from the mirrored original image). Fig. 8(a-g) shows the noise injection, HS transform, VS transform, rotation, GC, RT, and scaling results, respectively.

Fig. 8.

Results of proposed MDA.

4.3. Top three models of the validation set

On the validation set, we found the best three models using GSAF were: (i) $M^{PTM}\left(2\right)$, i.e., DenseNet201 with NLR of 1; (ii) DenseNet201 with NLR of 2; and (iii) ResNet1–1 with NLR of 1. Those top best three models found by GSAF are listed in Table 6 . For the best model (DenseNet201 with NLR of 1), we observed the sensitivity of the four classes were 94.63%, 93.16%, 98.12%, and 99.18%, the precision of the four classes were 96.45%, 96.68%, 96.15%, and 96.16%, the F1 score of the four classes were 95.53%, 94.88%, 97.12%, and 97.65%. The MA F1 score was 96.35%. For the other two best models, their $F{1}_{\mu }$ values were 96.06%, and 95.83%, respectively.

Table 6.

Top best three models on validation set.

Model	Class	Sen (%)	Prc (%)	F1 (%)
DensetNet201 (NLR=1)	C1	94.63	96.45	95.53
	C2	93.16	96.68	94.88
	C3	98.12	96.15	97.12
	C4	99.18	96.16	97.65
	MA			96.35
DensetNet201 (NLR=2)	C1	94.93	97.07	95.99
	C2	93.91	95.57	94.73
	C3	97.26	94.09	95.65
	C4	97.92	97.52	97.72
	MA			96.06
ResNet101 (NLR=1)	C1	96.91	96.57	96.74
	C2	96.22	94.45	95.33
	C3	94.44	95.75	95.09
	C4	95.79	96.50	96.14
	MA			95.83

(MA: micro-averaged; Sen: Sensitivity; Prc: Precision).

4.4. GSAF against SAPNF

Using the greedy version GSAF to select the two models, we chose the best two models as DenseNet201 with NLR of 1, and DenseNet201 with NLR of 2. Conversely, using the non-greedy algorithm SAPNF showed the two best models to be fused were DenseNet201 with NLR of 1 and ResNet101 with NLR of 1. The comparative results are presented in Table 7 .

Table 7.

GSAF against SAPNF on validation set.

Selection Approach	Selected Model	Class	Sen (%)	Prc (%)	F1 (%)
GSAF	DenseNet201 (NLR =1) & DenseNet201 (NLR =2)	C1	94.80	96.58	95.68
		C2	93.42	96.59	94.98
		C3	97.90	96.22	97.05
		C4	99.06	96.11	97.56
		MA			96.37
SAPNF	DenseNet201 (NLR=1) & ResNet101 (NLR=1)	C1	96.43	98.07	97.24
		C2	95.95	97.03	96.49
		C3	97.64	96.82	97.23
		C4	98.53	96.83	97.67
		MA			97.18

(MA: micro-averaged; Sen: Sensitivity; Prc: Precision).

There are two findings we can observe from comparing Table 7 with Table 6. (i) First, fusion can give improved performance than individual models alone. The MA F1 score $F{1}_{\mu }$ of the best single model was 96.35%, while the two fused model gave improved performance, with GSAF of 96.37%, and SAPNF of 97.18%. (ii) A non-greedy selection approach (SAPNF) can obtain better results than the greedy selection approach, GSAF. The reason is the two best models have similar advantages. For example, both DenseNet201 (NLR=1) and DenseNet201 (NLR=2) work optimally on the 3rd and 4th classes, so their fusion will not help to handle the weak spots (1st and 2nd classes). Nevertheless, the 3rd best model, i.e., RESNet101 (NLR = 1) shows exceptional classification ability on 1st and 2nd classes. Hence, fusing the 1st best model and 3rd best model is more logical, which is the core idea of our SAPNF.

4.5. Visual explanation of fusion

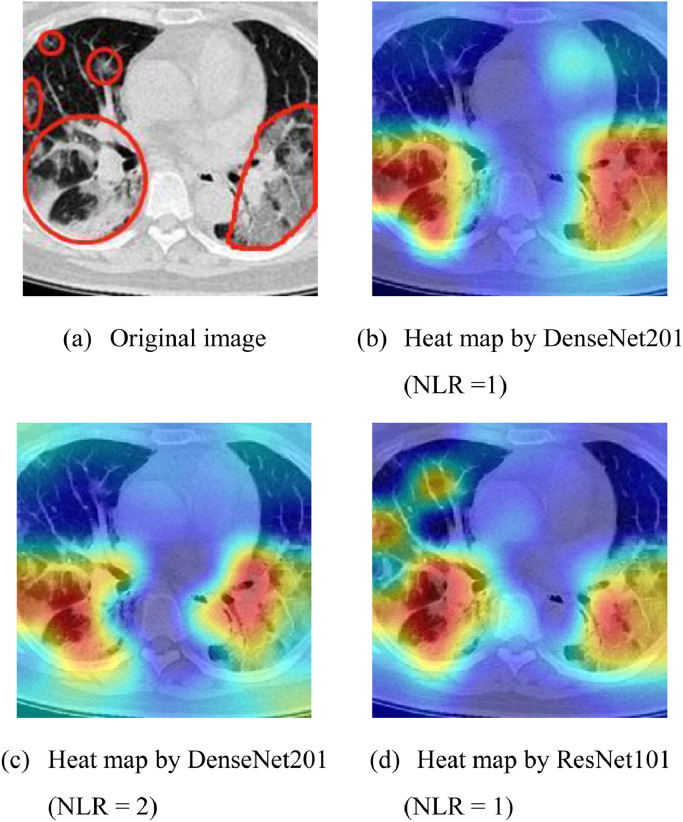
Grad-CAM [51] was used to illustrate why the fusion of Heat map by DenseNet201 (NLR =1) and Heat map by ResNet101 (NLR = 1) works the best among all possible fusion model combinations.

Fig. 9 displays the heat map results of a COVID-19 CCT slice by Grad-CAM over three models. Fig. 9(b, c, & d) presents the heat maps generated by DenseNet201 (NLR =1), DenseNet201 (NLR = 2), and ResNet101 (NLR = 1), respectively. We can observe that DenseNet201 networks with NLR equaling 1 & 2 capture the same GGO lesion on the bottom-half of the pictures (See Fig. 9b & c), so their fusion will not aid the other model. In contrast, ResNet101 (NLR=1) captures the top left GGO areas, which are neglected by the two DenseNet models. Thus, fusing DenseNet201 (NLR =1) and ResNet101 (NLR=1) is reasonable and has a solid visual explanation.

Fig. 9.

Grad-CAM result of a COVID-19 slice. (The “jet” pseudo-color was used. Red colors mean part and parcel areas for AI diagnosis, and blue colors less important areas for AI decision.).

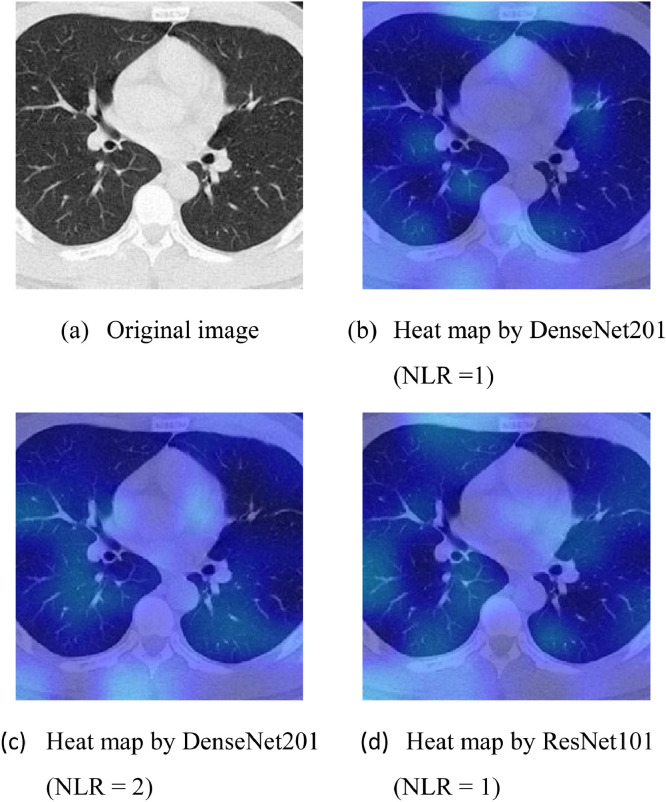
Fig. 10 displays the Grad-CAM heat map of a normal CCT slice using the top three models. Fig. 10(a) shows the original CCT image, and Fig. 10(b-d) gives the heat maps using DenseNet201 (NLR=1), DenseNet201 (NLR=2), and ResNet101 (NLR=1). All three AI models did not locate any strong indications of suspicious areas. Therefore, all three AI models classified this image as “normal”, which was subsequently confirmed by a radiologist.

Fig. 10.

Grad-CAM result on a normal case.

4.6. Performance of CCSHNet on the test set

After completing our previous experiments on the validation set, and selecting the optimal pretrained models and optimal NLR values, we ran our model CCSHNet, i.e., fusion of DenseNet201 (NLR =1) and ResNet101 (NLR=1) via DCA, on the test set and reported its performance. Test results are summarized in Table 8 . The sensitivities of four classes were 95.61%, 96.25%, 98.30%, and 97.86%, respectively. The precision values for the four classes were 97.32%, 96.42%, 96.99%, and 97.38%, respectively. The F1 scores of the four classes were 96.46%, 96.33%, 97.64%, and 97.62%, respectively. The MA F1 score $F{1}_{\mu }$ of CCSHNet on test set was 97.04%, which is slight lower than the validation $F{1}_{\mu }$ of 97.18% (See Table 7).

Table 8.

Performance of proposed CCSHNet on test set (%).

Class	Sen (%)	Prc (%)	F1 (%)
C1	95.61	97.32	96.46
C2	96.25	96.42	96.33
C3	98.30	96.99	97.64
C4	97.86	97.38	97.62
MA			97.04

(MA: micro-averaged; Sen: Sensitivity; Prc: Precision).

4.7. Comparison to state-of-the-art approaches

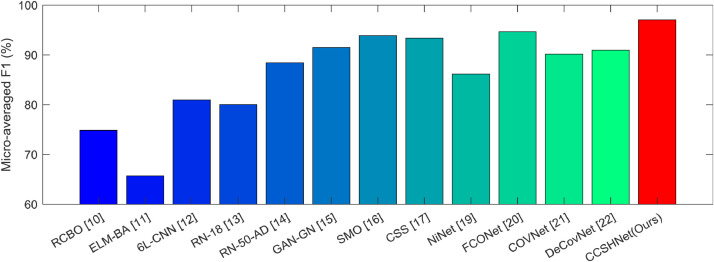
Proposed CCSHNet method was compared with 12 state-of-the-art approaches: RCBO [10], ELM-BA [11], 6L-CNN [12], RN-18 [13], RN-50-AD [14], GAN-GN [15], SMO [16], CSS [17], NiNet [19], FCONet [20], COVNet [21], and DeCovNet [22]. All these approaches were compared using our dataset. The comparison and their MA F1 $F{1}_{\mu }$ plots are presented in Table 9 and Fig. 11 , respectively.

Table 9.

Comparison results of state-of-the-art methods.

Method	Class	Sen (%)	Prc (%)	F1 (%)
RCBO [10]	C1	71.93	84.19	77.58
	C2	72.86	72.73	72.79
	C3	73.56	76.41	74.96
	C4	80.66	68.91	74.32
	MA			74.85
ELM-BA [11]	C1	62.63	67.61	65.03
	C2	64.29	65.10	64.69
	C3	71.86	66.77	69.22
	C4	63.93	63.52	63.73
	MA			65.71
6L-CNN [12]	C1	72.46	83.94	77.78
	C2	78.93	77.82	78.37
	C3	81.86	75.00	78.28
	C4	89.84	87.54	88.67
	MA			80.94
RN-18 [13]	C1	82.81	82.66	82.73
	C2	81.07	74.43	77.61
	C3	74.24	76.98	75.58
	C4	82.13	86.38	84.20
	MA			80.04
RN-50-AD [14]	C1	87.72	85.03	86.36
	C2	87.68	91.26	89.44
	C3	93.39	89.89	91.60
	C4	84.92	87.65	86.26
	MA			88.41
GAN-GN [15]	C1	91.75	89.86	90.80
	C2	92.86	91.87	92.36
	C3	89.83	89.98	89.91
	C4	91.64	94.27	92.93
	MA			91.50
SMO [16]	C1	97.02	92.63	94.77
	C2	89.11	95.23	92.07
	C3	94.92	94.92	94.92
	C4	94.26	92.89	93.57
	MA			93.86
CSS [17]	C1	94.04	92.25	93.14
	C2	93.75	95.11	94.42
	C3	91.36	93.58	92.45
	C4	94.43	92.75	93.58
	MA			93.39
NiNet [19]	C1	87.89	91.59	89.70
	C2	80.89	85.47	83.12
	C3	83.22	82.11	82.66
	C4	92.30	85.95	89.01
	MA			86.18
FCONet [20]	C1	92.28	95.64	93.93
	C2	96.79	94.43	95.59
	C3	94.75	95.88	95.31
	C4	94.92	92.94	93.92
	MA			94.68
COVNet [21]	C1	89.82	86.63	88.20
	C2	89.82	92.63	91.21
	C3	93.73	90.66	92.17
	C4	87.38	90.96	89.13
	MA			90.17
DeCovNet [22]	C1	91.05	90.58	90.81
	C2	93.75	90.99	92.35
	C3	90.51	86.97	88.70
	C4	88.69	95.58	92.01
	MA			90.94
CCSHNet (Ours)	C1	95.61	97.32	96.46
	C2	96.25	96.42	96.33
	C3	98.30	96.99	97.64
	C4	97.86	97.38	97.62
	MA			97.04

Fig. 11.

Comparison plot of MA F1 for our algorithm compared to 12 state-of-the-art methods.

The results in Table 9 and Fig. 11 demonstrate that our CCSHNet accomplished the best outcomes among all methods. The reason our CCSHNet obtains the best overall performance is that we have proposed several new algorithms to improve our fusion model: (L, 2) transfer feature learning (L2TFL), the selection algorithm of pretrained network for fusion (SAPNF), and deep CCT fusion discriminant correlation analysis (DCFDCA). The fusion framework demonstrates their effectiveness. Meanwhile, the proposed multiple-way data augmentation prevents our AI model from overfitting, thus increasing its performances.

Our method is unique in comparison to other strategies. The RCBO [10] used real-coded strategy in traditional biogeography-based optimization method; however, their method still needs to manually select the features, and they cannot validate their manually curated features to fit this four-class classification task. ELM-BA [11] used extreme learning classifier as the backbone, which employed random features (i.e., non-tuned random hidden nodes), so its performance may not be reliable. 6L-CNN [12] was proposed for fingerspelling classification during patients’ rehabilitation. It used leaky rectified linear unit to replace traditional rectified linear unit. Nevertheless, the structure itself is shallow (only six layers), thus may not handle the complicated internal mapping from CCT images to the four class labels. RN-18 [13] and RN-50-AD [14] used two variants of ResNet to classify thyroid ultrasound standard plane and Alzheimer's disease, respectively. The weights of the corresponding two networks were already adapted to their corresponding data, so retraining of the weights is required, which results in suboptimal performance. GAN-GN [15] combined generative adversarial network (GAN) and GoogleNet, but the image size and size of the dataset affects the generated images produced by GAN. SMO [16] used social mimic optimization for feature selection and fusion. Nevertheless, SMO's performance needs further verification. CSS [17] predicted COVID severity score in their model. We transferred the score prediction in their paper to COVID-19 recognition in this task. Those geographic extent score and lung opacity score may not have direct relation to our COVID-19 recognition, so this transfer is cross-field, which makes it more challenging. NiNet [19] combined 3D U-Net and MVP-Net. However, the 3D neural network needs more samples to train; otherwise it is susceptible to overfitting. FCONet [20] is a type of fast-track COVID-19 classification network. Again, the authors used ResNet50 and trained their models on three categories. In contrast our CCSHNet used deeper models and four categories of CCT images; hence, our model is more complicated and effective. COVNet [21] chose ResNet50, which has fewer layers than our proposed models (DenseNet201 and ResNet101). They trained their models with three categories; in contrast, our model was trained with four categories, which provides an additional class such as secondary pulmonary tuberculosis. DeCovNet [22] is a weakly-supervised DL method. Nevertheless, their model needs to train a UNet to extract lung regions, which requires more samples and more precise expert annotations.

5. Conclusions

This paper proposed a novel CCSHNet for COVID-19 detection in CCTs. Our model is based on the proposed DCFDCA algorithm of the selected two optimal models, of which we developed a SAPNF algorithm to optimally determine the best PTM and NLR. The feature learning procedures of the two models were achieved by the proposed L2TFL algorithm. Overall, our experiments showed our CCSHNet can achieve the best performance compared to 12 state-of-the-art approaches, and potentially aid radiologists in making more accurate, quicker diagnoses of COVID-19 using CCTs.

The impacts of our method in hospitals and society are promising. From the experimental results, our CCSHNet system can aid decision making when diagnosing lung-related diseases using CCTs. Furthermore, our CCSHNet can be improved by integration with other AI models developed by other teams from other universities/countries. In addition; our algorithm has the potential to be re-deployed to a new hospital's server, with little costs if using cloud-computing based techniques.

The shortcomings of our CCSHNet are three-fold: (i) It cannot handle heterogeneous data, such as the mixed data of CCT with CXR and patient history and other data. (ii) It has not yet been through a strict clinical verification. (iii) The dataset in this study is size-limited and category-limited.

The future work contains following aspects: (i) Expand the size of the dataset and test CCSHNet model on a larger and heterogeneous dataset. (ii) Try to use some advanced PTMs, particularly those trained from medical lung images. (iii) Try some advanced data preprocessing techniques to check whether the performance of our AI system can be improved. (iv) Our AI system can be embedded into other automated healthcare systems [52], [53], [54]. (v) IoT [55], [56], [57], [58] and communication technologies [59] can help make our AI system more powerful. (vi) Some advanced or hybrid fusion rules will be tested.

CRediT authorship contribution statement

Shui-Hua Wang: Conceptualization, Methodology, Software, Validation, Data curation, Writing - original draft, Investigation, Data curation. Deepak Ranjan Nayak: Formal analysis, Writing - original draft, Writing - review & editing. David S. Guttery: Writing - original draft, Writing - review & editing. Xin Zhang: Writing - original draft, Writing - review & editing. Yu-Dong Zhang: Resources, Formal analysis, Investigation, Data curation, Writing - review & editing, Supervision, Project administration, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A

Table 10

Table 10.

Abbreviation List.

Abbreviation	Full Name
(M)DA	(multiple-way) data augmentation
BCS	between-class scatter
BSC	between-set covariance
CAP	community-acquired pneumonia
CCA	canonical correlation analysis
CCT	chest computed tomography
DAF	data augmentation factor
DCA	discriminant correlation analysis
DCFDCA	deep CCT fusion by discriminant correlation analysis
DDM	diagonally dominant matrix
DL	deep learning
DLF	decision-level fusion
FCL	fully-connected layer
FLF	feature-level fusion
GSAF	greedy selection algorithm for fusion
HC	healthy control
ISP	incompatible size problem
L2TFL	(L,2) transfer feature learning
MRL	maximum removable layer
MV	Majority voting
NLR	number of layers to be removed
OHNN	one-hidden layer neural network
PF	parallel fusion
PTM	pre-trained model
SAPNF	selection algorithm of pretrained networks for fusion
SF	serial fusion
SPT	secondary pulmonary tuberculosis
SVD	singular value decomposition
TL	transfer learning

Appendix B

Table 11

Table 11.

Symbol List.

Symbol	Meaning
$X_0$	raw dataset
$x_0$	raw slice CCT image
$\left[W_0,H_0,C_0\right]$	size of $x_0$
$\left[w,h,c\right]$	index of $\left[W,H,C\right]$
$Z$	labeling
$\mathcal{B}$	radiologist
$\mathcal{C}$	class (viz., COVID, CAP, SPT, HC)
$F_G$	grayscale operation
$a_l$	minimum grayscale of an image
$a_h$	maximum grayscale of an image
$F_C$	crop operation
$\left(c_t,c_b,c_l,c_r\right)$	crop values in unit of pixel from four directions
$X_4$	preprocessed dataset
$x_4$	preprocessed slice CCT image
$\left[W_4,H_4,C_4\right]$	size of $x_4$
${\delta }_1$	storage compression ratio
${\delta }_2$	size compression ratio
$\left\{X_S,L_S,O_S\right\}$	data, labeling, and classifier of source domain
$\left\{X_T,L_T,O_T\right\}$	data, labeling, and classifier of target domain
$err$	error function
$l_r$	learning rate
$N_{PTM}$	number of PTMs
$M^{PTM}$	a specified model among all six models. See Table 3.
$M_0$	a pretrained model
$M_1$	$M_0$ with last L layers removed
$M_2$	$M_1$ with 2 new fully connected layers added
$M_3$	retrained $M_2$
$M\left(k\right)$	k-th PTM
$M1$	1st model
$M2$	2nd model
$L$	number of last layers to be removed
$L_{M1}$	number of last layers to be removed at 1st model
$L_{M2}$	number of last layers to be removed at 2nd model
$L_0$	number of learnable layers of $M_0$
$L_2$	number of learnable layers of $M_2$
$L_{\text{max}}$	maximum removable layer
$M\left(a:b\right)$	layers from $a$ to $b$ in network $M$
$f_M$	features learnt from network $M$
$F_{rl}$	remove layer function
$F_{afcl}$	add fully-connected layer function
$F_{rt}$	retrain function
$F_{ac}$	activation function
$N_{FCL}\left(1\right)$	node number of first added FCL layer
$N_{FCL}\left(2\right)$	node number of second added FCL layer
$\left\{Y_1,Y_2,Y_3\right\}$	training, validation, and test set of a dataset $Y$.
$N_{HL}$	number of hidden neurons
$B^i$	initialized OHNN
$B^t$	trained OHNN
$F_{SD}$	sort function in descending way
$\overrightarrow{R}$	rank list
$I\left(k,L\right)$	indicator by k-th PTM and removing $L$ layers
$\overrightarrow{I}$	indicator vector
$F_{L2TFL}$	proposed L2TFL operation
$O_2$	output on validation set
$O_3$	output on test set
$F_{MI}$	measuring indicator function
$f_F$	fused feature
$F_{DF}$	deep fusion function
$\left(f_{M1},f_{M2}\right)$	features to be fused from two models $\left(M1,M2\right)$
$F_{SF}$	serial fusion operation
$F_{PF}$	parallel fusion operation
$q$	length of feature
$N_{TF}$	number of trained features.
$F_{CCOV}$	cross-covariance operation
$W_{CCA,M1}$	transformation matrix of CCA for model 1
$W_{CCA,M2}$	transformation matrix of CCA for model 1
$\left(\overline{f_{M1}},\overline{f_{M2}}\right)$	transformed features by CCA
$f_{CCCA}$	concatenation of CCA features
$f_{SCCA}$	summation of CCA features
$f_{M1}^{ij}$	feature extracted from i th image of j-th category via model $M1$
$S_{BCS}$	between-class scatter matrix
$P_{OE}$	matrix of orthogonal eigenvectors
$\widehat{\Lambda }$	diagonal matrix of real and non-negtive eigenvalue in decreasing order.
$F_{rank}$	rank function
$f_{M1}^{\prime }$	projection of $f_{M1}$ where the BCS matrix is $I$
$S_{M1,M2}^{\prime }$	between-set covariance matrix of transformed feature sets
$W_{DCA,M1}$	transform matrix of DCA for model 1
$W_{DCA,M2}$	transform matrix of DCA for model 2
$\left(g_{M1},g_{M2}\right)$	transformed feature sets by DCA
$g_{CDCA}$	concatenation of DCA features
$g_{SDCA}$	summation of DCA features
$c_{DA}$	number of different DA techniques
$n_{DA}$	number of generated images by each offline MDA technique
$x^{tr}\left(i\right)$	one training image
$X^{tr}$	training set
$X^{va}$	validation set
$h_m^{NI}$	mean of Gaussian noise injected
$h_v^{NI}$	variance of Gaussian noise injected
$F_{NI}$	noise injection operation
$F_{HS}$	horizontal shift transform function
$F_{VS}$	vertical shift transform function
$F_{GC}$	Gamma correction operation
$F_{RO}$	image rotation operation
$F_{RT}$	random translation operation
$h_{rhs}$	random horizontal shift
$h_{rvs}$	random vertical shift
$M_{SR}$	maximum shift range
$\mathcal{V}$	uniform distribution
$F_{SC}$	image scaling operation
$F_{MIR}$	mirror function
$F_{CON}$	concatenation operation
$\overrightarrow{x^{DA}\left(i\right)}$	collection of generated MDA images with original image
$X^{DA}$	set of all augmented images
$a_{DA}$	data augmentation factor
$X_4^{ntest}$	non-test set of preprocessed dataset
$X_4^{test}$	test set of preprocessed dataset
$N_k^{ntest}$	number of samples of non-test set in k-th class
$N_k^{test}$	number of samples of test set in k-th class.
$L_{Val}^I$	ideal confusion matrix over validation set
$L_{Test}^I$	ideal confusion matrix over test set
$R_v$	number of runs on validation set
$R_t$	number of runs on test set
$F{1}_{\mu }$	micro-averaged F1
$Pr{c}_{\mu }$	micro-averaged precision
$Se{n}_{\mu }$	micro-averaged sensitivity
$r_i$	run index
$f_i$	fold index

Algorithm 1.

Proposed L2TFL algorithm.

Step 1 Read one raw PTM network $M_0$,

Step 2 Remove the last NLR l-learnable layers from $M_0$ and get $M_1$, $M_1=F_{rl}\left(M_0,L\right)$,

Step 3 Add two new fully connected layers, $M_2=F_{afcl}\left(M_1,2\right)$,

Step 4 Freeze early layers, $\overrightarrow{l_r}\left[M_2\left(1:L_0-L\right)\right]\leftarrow 0$,

Step 5 Let last two layers retrainable, $\overrightarrow{l_r}\left[M_2\left(L_2-1:L_2\right)\right]\leftarrow 1$,

Step 6 Retrain the whole network, and obtain the new network $M_3=F_{rt}\left(M_2,X\right)$,

Step 7 Output learnt features $f_N=F_{ac}\left(M_3,L_2-1\right)$.

Algorithm 2.

Proposed GSAF for PTM selection.

Step 1 Input: Training set $Y_1$ and validation set $Y_2$

Step 2 for k = 1: $N_{PTM}$ (k is the index of PTM)

for $L=1:L_{\text{max}}$ (L is the index of NLR)

Step 2.1 PTM Retrain

Import $k$-th PTM $M_0\left(k\right)$,

Use L2TFL via data $Y_1$ and removing $L$ layers,

Obtain $M_3\left(k,L\right)$,

Step 2.2 Feature Extraction

Generate features $f_M\left(k,L\right)$ from $M_3\left(k,L\right)$.

Step 2.3 Train OHNN

Initialize OHNN $B^i\left(k,L\right)$,

Train OHNN $B^i\left(k,L\right)$ using input as $f_M\left(k,L\right)$,

Obtain $B^t\left(k,L\right)$,

Step 2.4 Obtain Indicator

Obtain performance indicator $I\left(k,L\right)$ over validation set $Y_2$

end

end

Step 3 Generate and sort the indicator vector $\overrightarrow{I\left(k,L\right)},$

Step 4 Obtain the rank list $\overrightarrow{R_{GSAF}}$,

Step 5 Choose the top two best models (determine PTM and NLR):

$M\left[\overrightarrow{R_{GSAF}}\left(1\right)\right]$ and $M\left[\overrightarrow{R_{GSAF}}\left(2\right)\right]$

Algorithm 3.

Proposed SAPNF for PTM selection.

Step 1 Input: Training set $Y_1$ and validation set $Y_2$

Step 2 for $k_1=1:N_{PTM}$ ($k_1$ is the index of PTM of 1st model)

for $L_{M1}=1:L_{\text{max}}$ ($L_{M1}$ is the index of NLR of 1st model)

for $k_2=1:N_{PTM}$ ($k_2$ is the index of PTM of 1st model)

for $L_{M2}=1:L_{\text{max}}$ ($L_{M2}$ is the index of NLR of 1st model)

Step 2.1 1st model Retrain

Import $k_1$-th PTM $M_0\left(k_1\right)$,

Use L2TFL via data $Y_1$ and removing $L_{M1}$ layers,

Obtain $M_3\left(k_1,L_{M1}\right)$,

Step 2.2 2nd model Retrain

Import $k_2$-th PTM $M_0\left(k_2\right)$,

Use L2TFL via data $Y_1$ and removing $L_{M2}$ layers,

Obtain $M_3\left(k_2,L_{M2}\right),$

Step 2.3 Feature Extraction from two retrained PTMs

Generate features $f_M\left(k_1,L_{M1}\right)$ from $M_3\left(k_1,L_{M1}\right)$,

Generate features $f_M\left(k_2,L_{M2}\right)$ from $M_3\left(k_2,L_{M2}\right)$,

Step 2.4 Feature Fusion

Obtain $f_F\left(k_1,L_{M1},k_2,L_{M2}\right)$

Step 2.5 Train OHNN

Initialize OHNN $B^i\left(k_1,L_{M1},k_2,L_{M2}\right)$,

Train OHNN $B^i\left(k_1,L_{M1},k_2,L_{M2}\right)$ using input as $f_F\left(k_1,L_{M1},k_2,L_{M2}\right)$,

Obtain $B^t\left(k_1,L_{M1},k_2,L_{M2}\right)$,

Step 2.6 Obtain Indicator

Obtain performance indicator $I\left(k_1,L_{M1},k_2,L_{M2}\right)$ over validation set $Y_2$

end

end

end

end

Step 3 Generate and sort the indicator vector $\overrightarrow{I\left(k_1,L_{M1},k_2,L_{M2}\right)},$

Step 4 Obtain the rank list $\overrightarrow{R_{SAPNF}}$,

Step 5 Choose the top two best models (determine PTM and NLR)

$M\left[\overrightarrow{R_{SAPNF}}\left(1\right)\right]$ and $M\left[\overrightarrow{R_{SAPNF}}\left(2\right)\right]$

Algorithm 4.

Pseudocode of our CCSHNet algorithm.

Input: Original Image Set $X_0$ and its ground truth label $Z^{CCT}$.

Phase I: Preprocessing$X_0\to X_4$

Grayscaling: $X_0\to X_1$. See Eq. (3).

HS: $X_1\to X_2$, See Eq. (5).

Crop: $X_2\to X_3.$ See Eq. (6).

Downsampling: $X_3\to X_4.$ See Eq. (7).

Phase II: Ten-folds CV on Non-test Set

Split $X_4$ into nontest set and test set: $X_4\to \left\{X_4^{ntest},X_4^{test}\right\}$

for $r_i=1:R_v$% $r_i$ is run index

for $f_i=1:10$% $f_i$ is fold index

Step II.A Split into 10 folds

Split nontest set $X_4^{ntest}$ into 10 folds $\left\{F_4^{ntest}\left(1|r_i\right),\cdots ,F_4^{ntest}\left(10|r_i\right)\right\}$.

Step II.B Create Training and Validation set

Training Set: $X^{tr}\left(r_i\right)=F_4^{ntest}(1,\dots f_{i-1},f_{i+1},\dots ,10|r_i)$

Validation Set: $X^{va}\left(r_i\right)=F_4^{ntest}\left(f_i|r_i\right)$

Step II.C MDA on training set

for $i=1:|X^{tr}|$

Training image: $x^{tr}\left(i,r_i\right)$ and its ground truth labels $Z^{CCT}\left[x^{tr}\left(i,r_i\right)\right]$.

$x^{tr}\left(i,r_i\right)$: i th training image in $r_i$-th run

$x^{tr}\left(i,r_i\right)\to \overrightarrow{x^{DA}\left(i,r_i\right)}$. See Eq. (66).

end

DA enhanced training set: $X^{DA}\left(r_i\right)=\left\{\overrightarrow{x^{DA}\left(i,r_i\right)}|i=1,\cdots ,|X^{tr}\left(r_i\right)|\right\}$.

Enhanced training set labels: $Z^{CCT}\left(r_i\right)=\left\{Z^{CCT}\left[x^{tr}\left(i,r_i\right)\right]|i=1,\cdots ,|X^{tr}\left(r_i\right)|\right\}$.

Step II.D Model Selection by SAPNF, L2TFL, and DCFDCA.

See Algorithm 3, Algorithm 1, and Fig. 5.

Step II.E Validation confusion matrix at$r_i$-th run and$f_i$-th fold

Record $L_{Val}\left(r_i,f_i\right)$, See Eq. (68)

End

Validation confusion matrix at $r_i$-th run $L_{Val}\left(r_i\right)={\sum }_{f_i=1}^{10}{L}_{Val}\left(r_i,f_i\right)$

end

Phase III: PTM and NLR Selection

Validation confusion matrix. See Eq. (70).

Indicator is chosen as micro-averaged F1.

Obtain $F{1}_{\mu }$. See Eq. (75)

Obtain the rank list $\overrightarrow{R_{SAPNF}}$. See Eq. (28).

Output the top two models, i.e., best PTM and NLR combinations.

Output $M\left[\overrightarrow{R_{SAPNF}}\left(1\right)\right]$ and $M\left[\overrightarrow{R_{SAPNF}}\left(2\right)\right]$ and the corresponding removed layers $L_{M1}$ and $L_{M2}$

Phase IV: Create CCSHNet Model

Select the two optimal models $M\left[\overrightarrow{R_{SAPNF}}\left(1\right)\right]$ and $M\left[\overrightarrow{R_{SAPNF}}\left(2\right)\right]$.

Feature learning by L2TFL with NLR $L_{M1}$ and $L_{M2}$ layers removed.

Deep CCT fusion by DCFDCA.

OHNN $B^i$.

Phase V: Report the test performance of the CCSHNet model

Training set is $X_4^{ntest}$, and its labels $Z^{CCT}\left(X_4^{ntest}\right)$.

Test set is $X_4^{test}$, and its labels $Z^{CCT}\left(X_4^{test}\right)$.

for $r_i=1:R_t$% $r_i$ is run index

We initialized a random seed $S\left(r_i\right)$ at each run.

Trained CCSHNet Model $\text{trainnetwork}\left\{\text{CCSHNet},MDA\left[X_4^{ntest}\right],Z^{CCT}\left(X_4^{ntest}\right),S\left(w\right)\right\}$

Prediction: $Pred\left(r_i\right)=\text{predict}\left[\text{CCSHNet},X_4^{test}\right]$;

Test confusion matrix at $r_i$-th run: $L_{Test}\left(r_i\right)=\text{compare}\left[Pred\left(r_i\right),Z^{CCT}\left(X_4^{test}\right)\right]$.

Calculate Indicators. See Eq. (72)-(77).

End

Test confusion matrix: See Eq. (71).

Calculate indicators.

Output: The best model CCSHNet and its test performances.

Fig. 5.

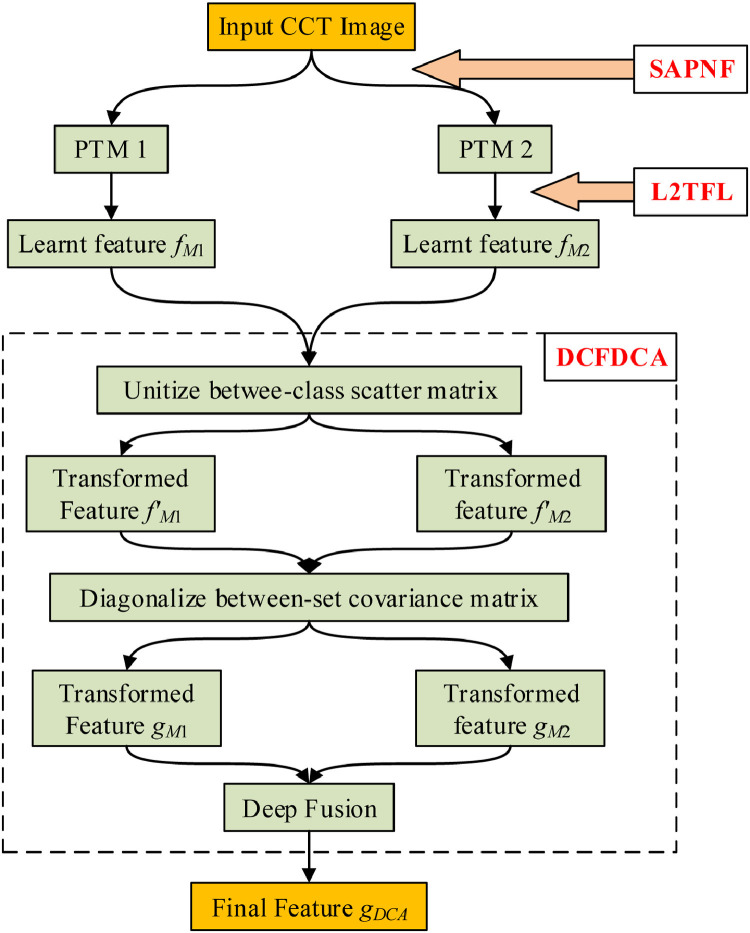
Diagram of our proposed fusion method, indicating the relation among SAPNF, L2TFL, and DCFDCA. (SAPNF: selection algorithm of pretrained networks for fusion; L2TFL: (L, 2) transfer feature learning; DCFDCA: deep CCT fusion by discriminant correlation analysis; CCT: chest CT; PTM: pretrained model).