Tuning the Thermal Stability and Photoisomerization of Azoheteroarenes through Macrocycle Strain

Abstract

Azobenzene and its derivatives are one of the most widespread molecular scaffolds used in a range of modern applications, as well as in fundamental research. After photoexcitation, azo‐based photoswitches revert back to the most stable isomer on a timescale ($t_{1/2}$ ) that determines the range of potential applications. Attempts to bring $t_{1/2}$ to extreme values prompted the development of azobenzene and azoheteroarene derivatives that either rebalance the E‐ and Z‐isomer stabilities, or exploit unconventional thermal isomerization mechanisms. In the former case, one successful strategy has been the creation of macrocycle strain, which tends to impact the E/Z stability asymmetrically, and thus significantly modify$t_{1/2}$ . On the bright side, bridged derivatives have shown an improved optical switching owing to the higher quantum yields and absence of degradation. However, in most (if not all) cases, bridged derivatives display a reversed thermal stability (more stable Z‐isomer), and smaller $t_{1/2}$ than the acyclic counterparts, which restricts their potential interest to applications requiring a fast forward and backwards switch. In this paper, the impact of alkyl bridges on the thermal stability of phenyl‐azoheteroarenes is investigated by using computational methods, and it is revealed that it is indeed possible to combine such improved photoswitching characteristics while preserving the regular thermal stability (more stable E‐isomer), and increased $t_{1/2}$ values under the appropriate connectivity and bridge length.

Taking the strain: The thermal relaxation and photoisomerization of bridged azoheteroarenes based on 3‐pyrazole and 2‐imidazole have been investigated computationally, revealing the impact of the bridge length on the thermal stability, half‐life time, kinetics, and the preferred pathway for this class of molecules.

Introduction

Molecular switches are able to modify their properties upon application of an external stimulus like heat, pressure, pH, or light, the latter being especially advantageous owing to is selectivity and immediacy. As a result, photoswitches are being used in material sciences, ^[1] medicine, ^[2] biology, ^[3] optical data storage, ^[4] and molecular machines or actuators. ^[5] One of the most studied families of photoswitches are azobenzene (AB) derivatives, ^[6] which display a trans–cis isomerization upon excitation to the low‐lying nπ* (S₀→S₁) or ππ* (S₀→S₂) bands. Once in its metastable state (generally the Z‐isomer), the molecule can be switched back to its most stable state (generally the E‐isomer) through either a similar photochemical process, or through thermal relaxation to the ground state. The timescale associated with the latter process ($t_{1/2}$ ) is a key characteristic of a photoswitch, as it defines the range of potential applications for which it can be used. Those with $t_{1/2}$ on the order of nanoseconds are promising candidates to be used in real‐time information transmission, ^[7] whereas those with $t_{1/2}$ longer than a year can be used for optical data storage, ^[4] as they ensure the integrity of the data for an extended period of time.

Such diversity of potential applications has motivated the development of new types of photoswitches. An example is azoheteroarenes, which replace one or the two Ph rings of AB with an heteroarene. ^[8] The plethora of available heteroaryl rings offer a larger structural diversity[ ⁹ , ¹⁰ , ¹¹ , ¹² ] and leads to a broader range of $t_{1/2}$ , which spans from 281 ns for an azopyridine derivative, ^[13] to 46 years for an ortho‐substituted arylazopyrazole. ^[14] A strategy to further modify $t_{1/2}$ is to incorporate the azo‐bond into a macrocycle, as it generates ring strain, which modifies the relative thermal stability of the E/Z‐isomers.[ ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ , ²¹ ] This strategy has been recently exploited to modify the half‐life time (i.e., $t_{1/2}$ ) of a hydrazone‐based photoswitch. ^[22] The acyclic compound had an extraordinary half‐life time of 5357 years, whereas that of bridged derivatives spanned 0.047 and 996 years. ^[22] The impact of ring strain on cyclic AB‐polymers has been discussed in the past by Rau,[ ¹⁵ , ¹⁶ ] Nobuyuki,[ ¹³ , ¹⁴ ] and others.[ ²³ , ²⁴ ] More recently, experimental ^[25] and computational[ ²⁶ , ²⁷ , ²⁸ , ²⁹ ] work described the photoisomerization of a bridged AB, in which the two phenyl rings are connected with an alkyl chain. The constrained AB presented several advantages compared with the acyclic AB: the band separation was larger, the quantum yield was enhanced, and the photoisomerization was faster.[ ²⁵ , ²⁶ , ²⁷ , ²⁸ , ²⁹ ] As a side‐effect, the bridge reversed the relative stability of the two isomers, converting the E‐isomer into the metastable one, with a very fast thermal back‐reaction to the Z‐isomer of only 4.5 h. ^[19] The decrease of $t_{1/2}$ is, indeed, a general trend when bridges are employed together with azo‐dyes. That is only useful for applications benefiting from a fast forward and backward switching, essentially limiting the range of applications of bridged azo‐dyes. It is thus important to understand whether bridged azo derivatives unavoidably lead to reversed E/Z stabilities and short$t_{1/2}$ , or alternatively, if it is possible to preserve the regular E/Z stability and increase $t_{1/2}$ through the adequate bridge length and design.

In this computational study, we aim at answering this point by investigating the impact of alkyl bridges on the thermal stability of phenyl‐azoheteroarenes based on 3‐pyrazole and 2‐imidazole (3‐pz 1 and 2‐im 2). Our selection is based on the fact that these heteroarene families showed E/Z thermal stabilities that were at the edge of the explored values in a recent computational screening. ^[30] Moreover, azopyrazoles and azoimidazoles are two of the azoheteroarenes families that have received the most attention in recent years.[ ³¹ , ³² , ³³ , ³⁴ , ³⁵ , ³⁶ , ³⁷ , ³⁸ ] Herein, we present the evolution of the half‐life times associated with both the inversion and rotation thermal relaxation mechanisms with bridge length. Although bridges tend to shorten$t_{1/2}$ , we could identify some cases in which the E‐isomer remains as the most stable, and $t_{1/2}$ is enhanced with respect to the acyclic compound. Given the importance of steric constrains on the molecular motion, we also investigated the photoisomerization mechanism and kinetics of selected bridged derivatives by using surface hopping molecular dynamics. The impact of bridges on the photoisomerization is significant, especially in shorter ones, leading to much faster relaxation kinetics, and to the photoswitch exclusively exploring the rotational mechanism, which is traditionally associated with higher quantum yields. Therefore, this study might contribute to the design of improved azoheteroarenes undergoing a fast and efficient (i.e., with high quantum yield) photoisomerization, and extreme $t_{1/2}$ values.

Methodology and Computational Details

Compounds and nomenclature

The compounds studied in this work are derived from 3‐pyrazole and 2‐imidazole, in which an alkyl bridge connects the phenyl and heteroarene rings. The length of the bridge varies, generating series of compounds based on the same heteroarene and connectivity. The nomenclature of those series follows a three‐digit code. The first number indicates the heteroarene fragment (1 for 3‐pyrazole, 2 for 2‐imidazole). The second and third digits indicate the position (see Scheme 1) to which the bridge is attached on the phenyl and heteroarene rings (in this order). To mention a specific compound in a series, a fourth digit indicates the number of carbon atoms in the alkyl bridge. In the first series, labelled 111n, the alkyl bridge connects the ortho position of the Ph group, and the ortho‐C atom of the 3‐Pz. This series spans bridges having from 1 to 6 C atoms (i.e., from 1111 to 1116). The equivalent series using 2‐imidazole as the heteroarene leads to series 211n, which also spans from 2111 to 2116 (n=1–6). A difference with respect to the 111n series is that in 211n the bridge is attached to the heteroarene through the N atom. Therefore, the comparison between the two series serves to evaluate the importance of the bridge–ring connectivity. Finally, the substitution at the ortho‐ (Ph) and the meta‐C atom (het) is studied in the series labelled 112n, which spans from 1122 to 1128 (n=2–8). Preliminary studies have been carried out by exploring other possible connectivities (section S4 in the Supporting Information). However, the impact of the bridge on $t_{1/2}$ was found to be either much smaller, or very similar to that of the main series discussed here. Therefore, we did not pursue a more complete study.

Scheme 1.

(Top): Nomenclature scheme and (below) representation of the heteroarene families explored in this manuscript. The red numbers are used in the series nomenclature to indicate the bridge anchoring sites.

Rotation versus inversion mechanism of thermal relaxation

The rotation and inversion mechanisms compete in the photo‐ and thermal isomerization of AB and its derivatives.[ ³⁹ , ⁴⁰ , ⁴¹ , ⁴² , ⁴³ , ⁴⁴ , ⁴⁵ , ⁴⁶ , ⁴⁷ , ⁴⁸ ] Under light irradiation, the preferred pathway depends on the region of the S₁ potential energy surface (PES), which is explored after excitation (and subsequent decay) to either S₁ or S₂.[ ⁴⁹ , ⁵⁰ , ⁵¹ , ⁵² ] In turn, the thermal relaxation occurs completely in the ground state (S₀) PES, without involvement of any excited state. In that case, inversion occurs through a transition state (TS) with one of the CNN angles at approximately 180° (${\mathrm{T}\mathrm{S}}_{\mathrm{i}\mathrm{n}\mathrm{v}}$ ), ^[53] whereas rotation goes through a TS with a CNNC dihedral angle of approximately 90° (${\mathrm{T}\mathrm{S}}_{\mathrm{r}\mathrm{o}\mathrm{t}}$ ). Under the thermal pathway, the rotation mechanism along S₀ requires the hemolytic cleavage of the azo N=N bond at sufficiently twisted geometries. Therefore, the TS needs to be described as either a triplet (T₁) or as a singlet bi‐radical (open‐shell singlet, OSS), with one unpaired electron in each azo N atom. Notice that in the latter case, the OSS description must be forced within DFT by using the broken symmetry (BS) approach, ^[54] and spin decontamination techniques (e.g., Yamaguchi equation ^[55] ) can be applied to correct its energy (see section S6 in the Supporting Information).

In AB, evidence for both mechanisms associated with thermal relaxation can be found in the literature.[ ⁶ , ⁴⁴ , ⁵⁶ ] A computational study ^[44] (at the CASPT2 level) and earlier experimental work ^[57] suggest that a non‐adiabatic rotational pathway (S₀→T₁→S₀) should be accessible and lower in energy. However, experimental studies showed that the rate of isomerization and the activation free volume are independent of the solvent polarity, which excludes the rotational pathway (as the associated TS is polar).[ ⁵⁷ , ⁵⁸ ] In push–pull AB derivatives (ppAB), it has been reported that the mechanism depends on the solvent, with a preference towards rotation in polar environments.[ ⁵⁹ , ⁶⁰ , ⁶¹ ] Considering that our computations are conducted in the gas phase, and that azoheteroarenes based on 1 and 2 (even unsubstituted ones) have a different degree of push–pull character (which implies that both AB and ppAB could be regarded as the reference),[ ⁸ , ³⁰ , ⁶² ] it is hardly possible to anticipate the preferred thermal relaxation pathway of the systems studied herein. Therefore, we considered both inversion and rotation as possible mechanisms. As we will see later, the results suggest that inversion is the active thermal pathway.

Half‐life times and conformers

The rate constant k of the thermal relaxation and its corresponding half‐life time ($t_{1/2}$ ) are calculated from the relative free energy difference (${\Delta G}^{\ne }$ ) between the lowest TS and the metastable state, using Eyring equation with T=300 K and assuming a first‐order relaxation kinetics (for k). The transmission coefficient is taken as 1 for simplicity, although a study determined that it ranges between 0.2 and 0.4 for AB and a ppAB. ^[59] The Eyring equation is routinely used to assess the thermal relaxation in azo‐dyes.[ ¹¹ , ⁶⁰ ]

The minima and TS of the acyclic azoheteroarenes 1 and 2 have multiple conformers as the two aromatic rings attached to the azo group are different, and the heteroarenes are non‐symmetric upon rotation about the NNCC/N angle. In alkyl‐bridged derivatives, the conformational space is further enlarged owing to the rotational flexibility of the bridge. It is important to search for the most stable conformers among them, as errors in the evaluation of ${\Delta G}^{\ne }$ lead to significant changes to $t_{1/2}$ owing to the exponential term in Eyring equation. To do so, we have used the protocol described in section S1 (in the Supporting Information). It includes the explicit evaluation of the ring conformers, an energy scan along dihedral angles in the bridge, and a more thorough evaluation by using metadynamics for specific systems. In the Eyring equation, we have employed the ${\Delta G}^{\ne }$ computed from the lowest‐energy conformers at each stationary point (minima and TS). Thus, we assume that higher‐energy conformers can interconvert towards the most stable without a barrier. An alternative is to Boltzmann‐weight the different conformer energies in the calculation of the rate constants and the resulting$t_{1/2}$ . This has been done for series 111n, with negligible changes on the estimated $t_{1/2}$ values.

Computational details

The optimization of the E‐ and Z‐isomer minima, and the TS search has been done at the ωB97X‐D/6‐31G(d) level as implemented in Gaussian09 (G09). ^[63] Computations using the PBE0‐D3BJ and M06‐L functionals can be found in section S2 (in the Supporting Information). All zero‐gradient points are further verified with a frequency computation, which also provides the thermal corrections to evaluate the free energy of each point.

The metadynamics mentioned in section 2.3 (in the Supporting Information) ran at the xTB level (see section S3 in the Supporting Information). ^[64] The output of such metadynamics is a trajectory consisting of a large collection of conformers. These are then clustered (see Figure S2.1. in the Supporting Information) by using the T‐distributed Stochastic Neighbor Embedding (t‐SNE) projection, and the OPTICS algorithm as implemented in the Scikit‐learn package. ^[65] The two t‐SNE main coordinates are obtained from dihedral angles inside the ring containing the azo group, and hence the clustering focuses on conformers created by the alkyl bridge.

The Non‐Adiabatic Molecular Dynamics (NAMD) simulations were performed with Newton‐X[ ⁶⁶ , ⁶⁷ ] interfaced with G09. Based on previous benchmarks,[ ³⁰ , ⁶⁸ , ⁶⁹ ] we used linear‐response TDDFT[ ⁷⁰ , ⁷¹ ] within the Tamm–Dancoff approximation (TDA), the ωB97X‐D functional,[ ⁷² , ⁷³ ] and the 6‐31G(d) basis set. 500 Initial conditions were generated from the Wigner distribution based on the harmonic oscillator, four states (S₀–S₃), a Lorentzian broadening of 0.1 eV, an anharmonicity factor of 3, and a temperature of 300 K. From these initial conditions, we obtain the initial geometries and velocities for the trajectories. The trajectories are initiated at S₁ and S₂ by using the respective Franck–Condon (FC) energies and a width of +/−0.1 eV. 25 Trajectories are propagated for each state and compound. Time‐derivative couplings ^[74] were computed between all states except S₀, which is excluded due to the difficulties of TDA to describe the multi‐reference character of the electronic wavefunction near a S₁–S₀ conical intersection (CoIn). Accordingly, trajectories ran for a maximum of 1000 fs or until an S₁–S₀ energy gap below 0.1 eV is reached. In the latter case, it is assumed that the actual CoIn is very similar to the final geometry, and that it should be reached immediately after in time. Trajectories are propagated in the microcanonical NVE ensemble, and the energy is conserved within 0.5 eV. Notice that the termination criterion does not presuppose the character of the S₁ (nπ* or ππ*). In practice, however, in all terminated trajectories, S₁ is the nπ* state. In general, we favor the nomenclature nπ*/ππ* to specifically refer to these states, and the S₁–S₂ nomenclature when the state character is not relevant, only the order.

Results and Discussion

E/Z thermal stability

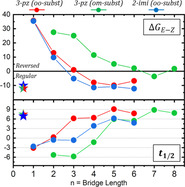
In acyclic AB and azoheteroarene derivatives, the E‐isomer is typically the most stable one, so the thermal relaxation refers to the conversion from the metastable Z‐isomer to the most‐stable E‐isomer. That is the case of the bare 1 and 2, in which ${\Delta G}_{E-Z}$ is −12 and −10 kcal mol⁻¹, respectively. This scenario is reversed in the short bridge derivatives (n=1, 2) for the 111n and 211n series (positive${\Delta G}_{E-Z}$ , see Figure 1 a), in agreement with what has been reported for AB.[ ²⁵ , ²⁶ ] A major contribution to this trend is that shorter bridges enforce much more strain to the E‐ than to the Z‐isomer (see Figure 1 b), mainly on the aromatic system (see Figures S3.1 and S3.2 in the Supporting Information). Such strain on the E‐isomer diminishes with longer bridges, but that of the Z‐isomer evolves differently depending on the connectivity (see Figure 1 b–c), remaining almost constant in the ortho/ortho substitution, and decreasing slowly in the ortho/meta. As a result, the regular E/Z thermal stability is eventually recovered (negative${\Delta G}_{E-Z}$ values in Figure 1 a). This occurs from n=3 onwards in the ortho/ortho series (i.e., 111n and 211n), and from n=6 onwards in the ortho/meta series (i.e., 112n). The latter case is especially interesting as ${\Delta G}_{E-Z}$ never reaches similar values to the acyclic compounds (ca. −10 kcal mol⁻¹). That is because the E‐isomer strain remains larger for long bridges under the ortho/meta substitution (112n case, see Figure 1 c) than under the ortho/ortho substitution (111n case, see Figure 1 b). As a result, the E‐ and Z‐isomers are almost degenerate during a window of bridge lengths that extends from n=6 to a least n=8 (see Figure 1 a). Within that window, neither of the two states is particularly destabilized, unlike the TS energies, which are still largely affected by strain. That is the perfect scenario to obtain long half‐life times.

Figure 1.

(a) Computed values for the relative E/Z‐isomer energy in the 111n (red), 112n (green), and 211n (blue) series. The values of the non‐substituted 1 and 2 compounds are shown with stars (1 in green/red and 2 in blue). Also shown is the energy penalty associated with strain in the most stable conformers of the stationary points along the (b) 111n and (c) 112n series. Our strain evaluation method does not capture the portion of strain arising from the two bonds connecting the bridge with the two rings (see section S2 in the Supporting Information). Given that this the major source of strain in 1111, a reliable value for this system could not be provided in (b). All energies are computed at the ωB97X‐D/6‐31G(d) level (see results with M06L and PBE0 in section S2 in the Supporting Information).

Half‐life times (${\mathbf{t}}_{1/2}$ )

The half‐life time of the metastable state is proportional to the energy difference between itself and the TS (${\Delta G}^{\ne }$ ). As discussed above, shorter bridges penalize the stability of the E‐ more than the Z‐isomer, which leads to a reversed thermal stability, and very short $t_{1/2}$ values (see Figure 2). The strain of the minima is reduced when using longer bridges, but the penalty on the TS energies (both ${\mathrm{T}\mathrm{S}}_{\mathrm{i}\mathrm{n}\mathrm{v}}$ and${\mathrm{T}\mathrm{S}}_{\mathrm{r}\mathrm{o}\mathrm{t}}$ ) remains much larger (see Figure 1 b–c). ^[75] As a result, ${\Delta G}^{\ne }$ and the associated $t_{1/2}$ are systematically increased along with the bridge length (see Figure 2). Series 111n and 211n display the same trend, which suggests that the impact of the bridge is similar for 1 and 2. However, the 211n series is generally shifted towards shorter $t_{1/2}$ values with respect to the 111n one (compare blue and red lines in Figure 2). Such difference cannot be explained by the intrinsic differences in the heteroarene, as the acyclic compounds barely display any difference in ${\Delta G}_{E-Z}$ or $t_{1/2}$ (see stars in Figures 1 and 2). Instead, it might be due to the change in connectivity, as the bridge is attached to the heteroarene ring through either a C or a N atom in the 111n and 211n series, respectively. A similar observation is discussed in section S4 (in the Supporting Information). Finally, we notice that compounds 1112 and 2112 display slightly shorter $t_{1/2}$ values (2 and 0.25 s, respectively) than the C ₂‐AB reported by Siewertsen and collaborators (4.5 h).

Figure 2.

Calculated thermal relaxation half‐life times ($t_{1/2})$ associated with the (left) inversion and (right) rotation thermal pathways in the 111n (red), 112n (green), and 211n (blue) series. Colored stars indicate the values associated with the acyclic counterparts (1 in green/red and 2 in blue). These are computed from the ωB97X‐D/6‐31G(d) energies of the isomers′ minima (Figure 1 a) and transition states, together with the Eyring equation. In the rotation pathway, the TS is computed as an open‐shell singlet (OSS) bi‐radical with the two unpaired electrons in each azo N atom. The rotational TS could not be characterized for compound 2111, and hence the associated $t_{1/2}$ could not be estimated and plotted.

When comparison between experimental and computational $t_{1/2}$ values is possible, differences of one order of magnitude are common in the literature.[ ¹¹ , ¹⁴ ] For instance, the ortho‐methyl‐substituted analogs of 1 and 2 (1′ and 2′) showed experimental (computed) $t_{1/2}$ values of 74 (33) days and 9 (19) h, ^[76] respectively. ^[11] In that case, the computational results were obtained with PBE0‐D3 (similar ones were obtained with M06‐2x) and concerned the inversion pathway, as it was found that rotation was unfavorable. Our computations for the unsubstituted 1 and 2, carried out with the ωB97X‐D functional, lead to $t_{1/2}$ values of 321 and 89 days, respectively, for the same inversion pathway. Although these cannot be directly compared with the aforementioned results for 1′ and 2′ (74 days and 9 h), such significant difference suggests that ωB97X‐D overestimates$t_{1/2}$ (see Figure S2.2 in the Supporting Information). When using PBE0+D3BJ, the resulting$t_{1/2}$ values for 1 and 2 are 43 and 3 days, much closer to the values reported for 1′ and 2′. The significant difference in $t_{1/2}$ among functionals results from a change of only approximately 2 kcal mol⁻¹ in the evaluation of${\Delta G}^{\ne }$ , which highlights the difficulty of predicting $t_{1/2}$ values accurately. However, both functionals retrieve the same relative $t_{1/2}$ between 1 and 2, which suggests that the trends are correct. This point is further confirmed by the results contained in section S2 (in the Supporting Information). Therefore, for the main discussion, we prioritized the results with ωB97X‐D for the sake of its better description of the photochemistry of azo‐dyes.[ ³⁰ , ⁶⁸ , ⁶⁹ ]

Interestingly, the rotational pathway is in some cases much faster than inversion (see Table S6.2 in the Supporting Information). The greatest difference between pathways is found for the acyclic azoheteroarenes, with $t_{1/2}$ on the order of 104 and 4 min for 1 and 2, respectively (compared with 321 and 89 days for inversion). These are much smaller than the experimental $t_{1/2}$ values reported in similar N‐containing heteroarenes, even considering the computational error. It is therefore unlikely than the rotation pathway is actually accessible under experimental conditions, at least not in all compounds, in line with the interpretation in recent literature reports.[ ¹¹ , ¹⁴ ] A possible explanation could be drawn from the thiazole‐based heteroarenes reported by Velasco and co‐workers. ^[77] These systems are able to undergo a rapid thermal isomerization under the ns timescale, and with a dependence on the solvent polarity, as expected for systems following the rotation mechanism. It is possible that these sulfur‐containing heteroarenes increase the rate of (S₀→T₁→S₀) intersystem crossing (associated with the rotational pathway) by virtue of the larger spin‐orbit coupling of the heavy atom, making the non‐adiabatic rotation pathway competitive to the inversion one. However, such possibility can be discarded when considering the heavy‐atom‐free arylazoindazoles of Otten and co‐workers, ^[78] which according to DFT computations of the energy barrier and activation entropy, show a preference for the rotation mechanism. Another possibility is that either the functional, or the environment (i.e., gas phase), might be misrepresenting the rotational pathway. To test this possibility, we have recomputed the inversion and rotation pathways of the main series by using the hybrid PBE0‐D3BJ functional and the meta‐GGA M06L functional, and obtained the same picture as with ωB97X‐D (see section S2 in the Supporting Information). The incorporation of water or dichloromethane solvent using the PCM implicit model also does not change the picture provided by any of the investigated functionals. Therefore, it remains an open question as to why most heteroarenes explore the inversion mechanism for thermal isomerization while having a rotational transition state lower in energy, as described by our and previous ^[44] computations.

Photochemistry of short‐ and long‐bridged derivatives

To evaluate the impact of the bridge on the photochemistry of the azoheteroarene derivatives, we have studied compounds 2113 and 1127. These are examples of short‐ and long‐bridge derivatives, respectively. We have selected these specific compounds because both feature the E‐isomer as the most stable one. That is an advantage for practical reasons and in long‐bridge derivatives, the E‐isomer has brighter transitions at Franck–Condon (FC) than the Z‐isomer (see Tables S5.1 and S5.2 in the Supporting Information for nπ* and ππ* state energies and oscillator strength), and also for the sake of comparison, because recent literature has dealt with the E‐to‐Z photoisomerization of 1 and 2, ^[62] providing an excellent opportunity to compare the photochemistry of bridged versus non‐bridged azoheteroarenes. Moreover, using a compound with a shorter bridge than 2113 would have implied the study of the Z‐to‐E isomerization, which is expected to be less affected by a bridge. ^[26] To study the photoisomerization of 2113 and 1127, we have used the same computational protocol as in ref. [62]. That is, we performed non‐adiabatic molecular dynamics simulations (NAMD) based on the fewest‐switches surface hopping method. ^[79] Swarms of 25 trajectories were initiated at both the S₁ (nπ*) and S₂ (ππ*) states for 1127 and 2113, which are located at 433/268 nm and 449/300 nm, respectively, at the Franck–Condon geometry (the evolution of the nπ* and ππ* bands with the bridge length can be found in section S5 in the Supporting Information, revealing a significant increase of band separation for short‐bridged derivatives). The trajectories are then propagated until an S₁–S₀ energy gap below 0.1 eV is reached (see Computational Details). At this point, it is assumed that population transfer to the ground state will occur, leading to either of the two minima (E or Z).

The mechanism of photoisomerization in both AB and azoheteroarenes is determined by the character of the S₁/S₀ conical intersection (CoIn), which is reached during the trajectory. The main CoIns are associated with the rotation (CoIn_A) and inversion (CoIn_B) motions.[ ⁷⁷ , ⁸⁰ , ⁸¹ , ⁸² ] CoIn_A and CoIn_B are indeed the extremes of a crossing seam, ^[62] with the former (latter) at the low (high) energy end, as in AB.[ ⁴⁶ , ⁸³ ] Unsubstituted compounds 1 and 2 feature a similar distribution of CoIn_A‐ and CoIn_B‐like structures within the crossing seam, which indicates that both rotation and inversion pathways are accessible. ^[62] Such scenario is completely different in bridged azoheteroarenes; we observe in Figure 3 a pronounced preference of both 1127 and 2113 towards the rotation pathway. One reason is that the E‐isomer minima of both compounds already show a non‐planar CNNC angle, so the initial structures are indeed closer to the CoIn_A‐like region of the crossing seam than in acyclic heteroarenes. This has been previously identified as a driving force towards a fast photoisomerization in bridged AB. ^[26] Another reason is that the opening of the CNN angles associated with the inversion pathway is energetically too unfavorable, presumably owing to the steric constrains: the trajectories of 2113 barely explore CNN angles above 140° (see Figure S5.2 in the Supporting Information), which is where the inversion‐like CoIn appear in 1 and 2. ^[62] The longer bridge in 1127 alleviates the steric hindrance, so this region is increasingly explored along the trajectories (see Figure S5.2 in the Supporting Information), and thus the distribution of CoIn extends more towards inversion (see Figure 3).

Figure 3.

Space of CNN and CNNC angles featured by the relevant geometries in all trajectories of (left) 1, from ref. [62], (middle) 2113, and (right) 1127 (the structure of the E‐isomer minima is also shown). The CNNC angle is evaluated as the deviation from planarity, with 0° corresponding to the E‐isomer, and 90° corresponding to CNNC either +90 or −90°. In color, the geometries that reached an S₁/S₀ CoIn before the time limit (1 ps). The color code indicates trajectories initiated at S₁ (red) and S₂ (green). In dark gray, all geometries at which a hopping between S₁ and S₂ occurred. These results are extracted from NAMD trajectories at the ωB97X‐D/6‐31G(d) level.

The photoisomerization kinetics are significantly faster for the bridged azoheteroarenes 2113 and 1127 than for the acyclic parent compounds (1 and 2, Table 1). ^[62] That is mainly assessed from the time required to reach a CoIn in our trajectories ($t_{\mathrm{C}\mathrm{o}\mathrm{I}\mathrm{n}}$ ), and also with $t_{\mathrm{S}1}$ and$t_{\mathrm{S}2}$ , described as the time spent in S₁ and S₂ states, respectively. In unsubstituted azoheteroarenes, the S₂/S₁ decay is ultrafast (100–200 fs), whereas the overall time to reach an S₁/S₀ CoIn after irradiation is approximately 500 fs, with small differences depending on the compound and on the excitation energy. ^[62] In the bridged heteroarenes 2113 and 1127, the photoisomerization is significantly faster. In the case of 2113, all 25 trajectories initiated at S₁ and S₂ reach an S₁/S₀ CoIn at an average $t_{\mathrm{C}\mathrm{o}\mathrm{I}\mathrm{n}}$ of 27 and 165 fs, respectively. In both cases, the S₁ PES leads very efficiently towards a CoIn, with very short residence times in S₁ ($t_{\mathrm{S}1}$ ) of 27 and 37 fs. Thus, the longer $t_{\mathrm{C}\mathrm{o}\mathrm{I}\mathrm{n}}$ associated with the S₂ excitation is exclusively due to the extra S₂→S₁ relaxation step, the timescale of which ($t_{\mathrm{S}2}=128$  fs) is indeed very similar to the non‐bridge compound ($t_{\mathrm{S}2}=113$  fs). ^[62] That is because the S₂→S₁ relaxation occurs at geometries close to the E‐isomer minima, and thus it does not require significant molecular motion that could be affected by the steric hindrance caused by the bridge. The kinetics of 1127, with a longer bridge than 2113 (n=7 vs. 3), lies between those of 1 and 2113, in terms of both the S₂→S₁ and S₁→S₀ relaxation times (compare $t_{\mathrm{S}1}$ and$t_{\mathrm{S}2}$ , respectively). In contrast to 2113, excitation to the ππ* state (S₂) leads to a shorter $t_{\mathrm{S}1}$ than under direct excitation to S₁. That is also the case of the acyclic 1 and 2, and is due to warmer molecules having access to a broader region of the crossing seam (see Figure S5.2 in the Supporting Information), thus reaching a CoIn faster. It is, thus, only in the case of the short‐bridged 2113 that both S₁ and S₂ excitations lead to photoisomerization in the same timescale.

Table 1.

Comparison of the photoisomerization kinetics of compounds 2113 and 1127, with a short and a long alkyl bridge, respectively, and the unsubstituted compounds 2 and 1, studied in ref. [62]. It shows the (top) ratio of trajectories reaching a CoIn before the time limit (1 ps), and (below) the characteristic times described in the main text. See Table S5.3 (in the Supporting Information) for an assessment of the error associated with these values.

	Initial	Compound
	state	2113	2	1127	1
R	S1	1.0	1.0	1.0	0.84
	S2	1.0	0.96	0.96	0.56
$t_{\mathrm{C}\mathrm{o}\mathrm{I}\mathrm{n}}$	S1	27	330	282	419
	S2	165	373	386	530
$t_{\mathrm{S}1}$	S1	27	330	282	419
	S2	37	260	160	250
$t_{\mathrm{S}2}$	S1	0	0	0	0
	S2	128	113	226	280

Conclusion

We have evaluated the thermal stability and the thermal relaxation half‐life times ($t_{1/2}$ ) of phenyl‐azoheteroarene photoswitches based on 3‐pz (1) and 2‐im (2), in which the two rings are connected through an alkyl bridge. We have explored bridges of varying length, and anchored at different positions on the aromatic rings. We obtained wide range of half‐life times that span 15 orders of magnitude (in the inversion pathway only), from the microsecond to the year timescale. This supports the use of bridges to tune the thermal stability of azoheteroarenes, as proposed in the literature for other families of photoswitches.[ ²² , ²⁵ , ²⁶ ] Our results support the general trend observed in experiments that bridges tend to reduce$t_{1/2}$ . However, we show that it is possible to recover, or even increase, the half‐life times of acyclic compounds, by using long bridges. Moreover, although short bridges reverse the E/Z thermal stability, a window of bridge lengths exists for which the regular stability can be preserved. This behavior is the result of the variable impact of strain on the relative stability of the TS and the E‐ and Z‐minima.

The impact of the bridge on the photoisomerization kinetics has been studied by using surface‐hopping molecular dynamics on two systems representing extreme cases. A 2‐imidazole heteroarene with a 3C‐bridge attached in ortho positions (2113) features a regular E/Z stability, one of the shortest$t_{1/2}$ (ca. 10 ms), and it undergoes the E‐to‐Z photoisomerization ten times faster than the acyclic parent compound, under both S₁ and S₂ excitation. In turn, a 3‐pyrazole derivative with a long 7C‐bridge attached in ortho (Ph) and meta (het) positions (1127) features a regular E/Z stability, the longest computed $t_{1/2}$ (ca. 47 years), and a comparatively fast E‐to‐Z photoisomerization. In both cases, the photoisomerization proceeds through the rotational pathway, which is associated with a higher efficiency (better quantum yields), as reported in other constrained azo‐dyes. ^[25]

Overall, we unravel how alkyl bridges modify the relative E/Z thermal stability of two azoheteroarene families, the associated half‐life times (through the TS energies), and the photoisomerization pathway and kinetics.

Dataset

A dataset is available at Zenodo with all minimum‐energy and the non‐adiabatic molecular dynamics trajectories (https://doi.org/10.5281/zenodo.4043290).

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

S. Vela, A. Scheidegger, R. Fabregat, C. Corminboeuf, Chem. Eur. J. 2021, 27, 419.