MICRODOSIMETRIC UNDERSTANDING OF DOSE RESPONSE AND RELATIVE EFFICIENCY OF THERMOLUMINESCENCE DETECTORS

Abstract

LiF:Mg,Ti detectors show relative efficiency η for heavy charged particles significantly lower than one. It was for a long time not recognised that η varies also for electron energies and, as a consequence for photons. For LiF:Mg,Cu,P detectors measured photon energy response was named ‘anomalous’ because it differed significantly from the ratio of photon absorption coefficients. The decrease of η was explained as a microdosimetric effect due to local saturation of trapping centres around the electron track. For TLD-100 it was noticed by Horowitz that the measured photon energy response disagrees with the ratio of absorption coefficient by about 10%. It was demonstrated that a fraction of the TL signal in LiF:Mg,Ti is generated in the supralinear dose–response range, due to the high local doses generated by photon-induced tracks. Prediction of TL efficiency is particularly important in space dosimetry and in dosimetry of therapeutic beams like protons or carbon ions.

INTRODUCTION

Lithium fluoride thermoluminescence (TL) detectors are broadly applied in radiation dosimetry due to their numerous advantages such as good tissue equivalence, millimetre dimensions and broad linear dose response⁽¹⁾. It is well known in radiation physics that energy lost by ionising radiation depends not only on radiation type and energy but also on the atomic composition of the target. The first approach to assess response of TL detectors for photons is to calculate mass energy absorption coefficient for the detector material and to normalise it to the corresponding coefficient for air⁽²⁾. Some 40 years ago the newly developed high sensitive LiF:Mg,Cu,P, with practically the same atomic composition as commonly used LiF:Mg,Ti was found to demonstrate significantly different dosimetric properties. LiF:Mg,Cu,P showed much lower TL efficiency for densely ionising alpha particles relative to photons, saturation of response without supralinearity and, what was the biggest surprise, quite different photon energy response⁽³⁾. This photon energy response of LiF:Mg,Cu,P was named ‘anomalous’ because it differed significantly from the ratio of photon mass energy absorption coefficients of LiF and air. In particular, the response for X-rays of energies between 80 keV and 120 keV to ¹³⁷Cs γ-rays was lower by about 20%, which was not observed for LiF:Mg,Ti.

It became clear that the response of LiF:Mg,Cu,P and LiF:Mg,Ti detectors could not be explained just by studying radiation interaction with lithium fluoride. Therefore microdosimetric models of radiation action have been applied to understand the complicated pattern of the measured responses^(4,5). It was found that these phenomenological models, based on analysis of the distribution of energy deposited in nanometre size targets were able to correlate dose, linear energy transfer (LET) and photon energy response of TL detectors, even without a full understanding of underlying physical phenomena⁽⁶⁾. These correlations were observed not only for LiF detectors, but for the broad range of luminescent detectors which showed sublinear or supralinear dose response.

The understanding of TL detector response is particularly needed for measurement in the complicated, mixed radiation fields such as they are present in space. The extremely broad energy range of cosmic-rays and the secondary radiation produced within a spacecraft makes the interpretation of TL detector response challenging. Therefore, for preparation of measurement in space, intensive experimental activity was performed on high energy accelerators to measure relative TL efficiency for the most abundant ions in the cosmic-ray spectrum. Such data are also valuable for verification of models of TL radiation response. Therefore, in this paper, we present a broad set of experimental data on the relative TL efficiency of lithium fluoride detectors and present how microdosimetric models are helpful in understanding and predicting the response of these detectors in different radiation fields.

In this paper, all analysed experimental data will be presented for TL lithium fluoride detectors, mostly for MTS-N (LiF:Mg,Ti) and MCP-N (LiF:Mg,Cu.P) developed at the Institute of Nuclear Physics Kraków, Poland and produced in form of sintered pellets. However, most of the conclusions drawn from the analysis remain valid for all types of TL detectors.

DEFINITIONS

Dose response of TL detectors, R_i (D) for the i-th radiation modality relates the observed TL signal to absorbed dose D. Dose response is frequently normalised to dose and presented in a form of linearity index, f(D). Linearity index describes the departure of the detector’s response from linearity at the dose level D₀ used for calibration.

(1)

Relative detector efficiency, η_i(E), is defined as a detector response per unit dose R_Eⁱ(D) normalised to the response of the unit dose of reference radiation, typically ¹³⁷Cs or ⁶⁰Co gamma rays.

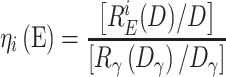(2)

D_γ and D must be at low-dose region to assure that the response is still at the linear part of the dose response.

In individual dosimetry, the response of dosemeters to photon radiation is frequently normalised to air kerma because air-filled ionisation chambers are used to determine exposure in radiation fields used for calibration. Therefore relative photon energy response S′(E) is expressed as detector response R normalised per unit air kerma K_air. S′(E) can be expressed as the product of relative detector’s efficiency η(E) and the ratio of mass energy absorption coefficients for the detector material and the air μ’(E) = [[μ_en/ρ]_LiF/[μ_en/ρ]_air]_E/[[μ_en/ρ]_LiF/[μ_en/ρ]_air]_γ

(3)

These general definitions presented above are used not only for the integrated TL signal typically used in dosimetry but also for describing response of individual peaks of the glow curve.

RELATIVE TL EFFICIENCY OF LiF DETECTORS FOR IONS, η

The dependence of TL efficiency on ionisation density was known already in the 1960s, starting probably from the work of Wingate et al. presented at the first Conference on Luminescent Dosimetry⁽⁷⁾. Since that time numerous papers on this subject were published, most of them concerning LiF:Mg,Ti material. The early results of these studies were reviewed by Horowitz^(1,8,9). In the mid-1990s, a heavy-ion accelerator (HIMAC) at the National Institute of Radiological Sciences in Chiba (Japan), capable of accelerating ions up to xenon to energies up to 800 MeV/nucleon, was put into operation and shortly after applied to the TL efficiency studies⁽¹⁰⁾. In 2002, the project ICCHIBAN (InterComparison of Cosmic rays with Heavy-Ion Beams at NIRS), based on the HIMAC, was initiated⁽¹¹⁾. During the next years, within subsequent ICCHIBAN sessions as well as many other projects, numerous research teams investigated TL detectors at HIMAC, producing a vast amount of data. At the same time, experimental capabilities were also increased by a rise of the proton (and carbon ion in a smaller number) radiotherapy facilities all over the world. All this together has enabled a collection of a huge amount of good quality experimental data on TL efficiency to ions. Some of these data were partly summarised by Berger and Hajek⁽¹²⁾ and Bilski et al.⁽¹³⁾.

The present review aims at collecting a possibly complete set of reliable data produced during the last about 20 years. Earlier data were generally not included, with a few exceptions from the 1990s. Tables 1 and 2 describe the origin of the datasets which were exploited in the present study. Only the results of research groups which published data for several ion species were included. These were the following: IFJ PAN (Poland), ATI (Austria), DLR (Germany), GSI (Germany), UNAM (Mexico) and SCK-CEN (Belgium). In total 318 datapoints were included for LiF:Mg,Ti and 137 datapoints for LiF:Mg,Cu,P. All the data concern the main dosimetric peak of the TL glow curves.

Table 1.

Description of LiF:Mg,Ti TL efficiency datasets included in the review.

Research group	Studied ions	TLD types	References
IFJ PAN	H, He, C, Ne, N, O, Si, Ar, Kr, Xe	MTS-N, MTS-7	(14–19)
ATI	He, C, Ne, O, Si, Ar, Kr, Xe	TLD-700, TLD-600	(12, 16, 20)
DLR	He, C, Ne, O, Si, Ar, Kr, Xe	TLD-700, TLD-600	(12, 16)
GSI	H, He, C, B, Li, Ni, Sb, Xe	TLD-700	(21)
UNAM	H, He, C, O, Ne	TLD-100	(22, 23)
SCK-CEN	H, He, C	MTS-7, MTS-6	(24)

Table 2.

Description of LiF:Mg,Cu,P TL efficiency datasets included in the review.

Research group	Studied ions	TLD types	References
IFJ PAN	H, He, C, Ne, N, O, Si, Ar, Kr, Xe	MCP-N, MCP-7	(14–19, 25)
ATI	He, C, Ne, O, Si, Ar, Kr, Xe	TLD-700H	(12, 20, 26)
DLR	He, C, Ne, O, Si, Ar, Kr, Xe	TLD-700H, TLD-600H	(12, 16, 27)
SCK-CEN	H, He, C	MCP-7, MCP-6	(24)

Figure 1 presents all collected efficiency data for LiF:Mg,Ti. Three apparent observations result from this plot: (1) efficiency generally decreases with increasing LET, (2) efficiency is not a unique function of LET and (3) TL efficiency exceeds unity for protons and He ions of low-LET. The most interesting is possibly the last of these observations, as the occurrence of such overresponse for low-LET ions was not obvious in the past. The datapoints show some scattering, what however was to be expected, taken into account large variation of the used TLD batches, processed by each laboratory in a somewhat different way. One should also note, that the efficiency data are based on different methods of TL glow-curve quantification (peak height, region-of-interest integral and deconvolution), which may have some impact on the results. It can be noticed, that for He (c.a. 2 keV/μm), C (c.a. 11 keV/μm) and Fe (c.a. 400 keV/μm), there are groups of the efficiency values largely dispersed for almost one value of LET. These data correspond to the primary ion beams at HIMAC, which were the most frequently exploited during the conducted experiments.

Figure 1.

Relative TL efficiency of LiF:Mg,Ti for different ion species vs. LET in water (all collected data).

Figure 2 presents the relative efficiency for these selected ion species, for which datapoints were available over a wide range of LET values. The origin of the particular data (a research group) is also indicated. The datapoints for light-ions: H, He, C, O and Ne, follow unique trend lines, which decrease steeply with increasing LET. These trend lines were approximated by purely empirical functions, which formulas are given in Table 3. In the case of the heavier ions (Z ≥ 14) the datapoints seem to follow a different, less steeply decreasing trend.

Figure 2.

Relative TL efficiency of LiF:Mg,Ti for selected ion species. Solid lines represent empirical fits (see Table 3).

Table 3.

The formulas used for fitting dependence of LiF:Mg,Ti efficiency on LET for various ions.

Ion	Equation	LET range
H	(1+0.037L2–0.0023L4–4.4×10−5 L6 exp(0.289–0.158ln2(L)	L∈(0.4, 2.9) keV/μm L∈(2.9, 50) keV/μm
He	1.11/(1+6(L/35)2)0.75	L∈(2, 170) keV/μm
C	0.58exp(−L/37.8)+0.56exp(−L/200)	L∈(10, 900) keV/μm
O	0.48exp(−L/40)+0.56exp(−L/300)	L∈(20, 1000) keV/μm
Ne	0.66exp(−(L-50)/300)-0.06	L∈(30, 900) keV/μm
Z ≥ 14	0.0025exp(−(L-553)/120)+10exp(−(L-553)/216000)-9.595	L∈(55, 3000) keV/μm

Table 4.

The formulas used for fitting dependence of LiF:Mg,Cu,P efficiency on LET for various ions.

Ion	Equation	LET range
H	exp(−0.058–0.084L1.5)	L∈(0.4, 4.5) keV/μm
He	1/(0.96+0.15 L)	L∈(2, 200) keV/μm
C	0.53exp(−L/61.7)+0.042	L∈(10, 300) keV/μm
Z ≥ 14	0.254+0.9ln(L)/L	L∈(40, 1400) keV/μm

Figures 3 and 4 show analogous TL efficiency data for LiF:Mg,Cu,P material. In that case, the number of available datapoints is smaller and the majority of them were obtained by IFJ PAN. They are however supported by a number of results from other groups, being generally in agreement. The relative TL efficiency of LiF:Mg,Cu,P is always lower than that of LiF:Mg,Ti. The general trend of decreasing efficiency with increasing LET is similar to LiF:Mg,Ti, with this difference that no datapoints exceed the unity. On the other hand, quite interesting are the data for heavy ions (Z ≥ 14), which show an almost constant value of relative efficiency of about 0.3 for a wide range of LET extending from 55 keV/μm to c.a. 1000 keV/μm. This is still less than in the case of LiF:Mg,Ti, which however shows a significant decrease in the efficiency (from about 0.59 to 0.38) over the same LET range.

Figure 3.

Relative TL efficiency of LiF:Mg,Cu,P for different ion species vs. LET in water (all collected data). Solid lines represent empirical fits (see Table 4).

Figure 4.

Relative TL efficiency of LiF:Mg,Cu,P vs. LET in water, with indication of origin of the datasets.

DOSE RESPONSE OF LITHIUM FLUORIDE DETECTORS FOR PHOTONS

Consistent experimental data on dose response of TL detectors are less frequent in literature. This is partly because it is difficult to perform irradiation with doses varying over several orders of magnitude using a single radiation source due to the unacceptable growing irradiation time. In addition, with increasing dose, the glow curves evolve and the relevant observables must be precisely defined, e.g. the amplitude of the deconvoluted peak or the integrated main dosimetric peak. Also TL readers have to be adopted to measure the dose varying over several ranges of magnitude. This can be done by installing additional filters or diaphragms to reduce the light intensity reaching the photomultiplier (PM) tube. It is also known that detector batch variability influences TL glow curves at high doses.

In Figure 5 linearity index f(D) for three different experiments with LiF:Mg,Ti detectors (TLD-100 and MTS-N), irradiated with Co-60 γ-rays is presented. f(D) of the main dosimetric peak of LiF:Mg,Ti is equal 1 until approximately 1 Gy and is reaching the maximum of 3–5 at about 200–700 Gy. For even higher doses TL signal saturates which leads to a systematic decrease of f(D) vs. dose. In all experiments, f(D) was calculated for the main dosimetric peak. Despite differences between different authors, three regions of dose response can be distinguished: linear, supralinear and saturated dose response.

Figure 5.

Dose response of LiF;Mg,Ti detectors normalised do linearity index f(D) after doses of Co-60 γ-rays. Adopted from publications of Majborn et al.⁽²⁸⁾, Horowitz et al.⁽²⁹⁾ and Bilski⁽³⁰⁾.

Another interesting finding, which has a tremendous impact for understanding radiation action on TLDs is the reduction of the f(D) maximum with decreasing photon energy, as demonstrated by results published by Horowitz⁽²⁹⁾: f_max(D)=4 for Co-60, f_max(D) =2.3 for 50 kVp X-rays and f_max(D) = 1.7 for 20 kVp X-rays.

The glow curve of LiF:Mg,Ti is very complex and is composed on many individual peaks. The detailed response of particular peaks in the glow curve was studied e.g. by Massillon et al.⁽³¹⁾ and Bilski et al.⁽³²⁾. When only peaks 4 and 5 are taken into account the supralinearity onset starts for doses between 1 Gy and 5 Gy. Much earlier supralinearity onset is observed for high-temperature peaks (6a-9) which starts at about 50–200 mGy. The f(D) reached the maximum value of 3.6 ± 0.3 for peak 5 and up to 207 for the high-temperature part of the glow curve.

The LiF:Mg,Cu,P glow curve is relatively simple and the shape of the main dosimetric peak, composed mainly from the peak 4, remains practically unchanged up to saturation of response at about 1000 Gy (see Figure 6). The high sensitive LiF:Mg,Cu,P emits at low doses ~25 times more light per unit absorbed dose as compared to LiF:Mg,T. This ratio decreases at doses of hundreds Gy because the response of LiF:Mg,Cu,P is sublinear i.e. saturates exponentially with dose without supralinearity. A fascinating feature of MCP-N detectors is the presence of high-temperature peaks which enables to measure doses up to 1 MGy⁽³³⁾. For doses of tens and hundreds of kGy the main dosimetric peak disappears and the new peak structure is observed. The structure is gradually shifted to higher temperatures with increasing dose.

Figure 6.

Linearity index for MCP-N detectors after exposure of ¹³⁷Cs or ⁶⁰Co γ-rays. The solid line corresponds to dose response described by the formula f(D) = const (1-exp(−D/D₀))/D, where D₀=233 Gy.

PHOTON ENERGY RESPONSE OF LiF DETECTORS

Relative photon energy response is expected to follow the ratio of mass energy absorption coefficients for LiF and air. As it was shown by Horowitz⁽¹⁾ some 35 years ago the measured response of TLD−100 is about 10% higher for X-rays in the energy range between 20 keV and about 250 keV photons. The compilation of response of MTS-N detectors for narrow X-rays beams collected over a decade in several experiments at Main Office of Measurements in Poland (GUM), KfK Karlsruhe, Korean Energy Atomic Research Institute KAERI and CIEMT (Madrid) is shown in Figure 7. Results collected for the same detector type show a ±5% dispersion for intermediate X-ray energies. This dispersion is less visible for photon energy response of MCP-N which shows a characteristic minimum at about 100 keV named an ‘anomalous photon energy response' (see Figure 8).

Figure 7.

Relative photon energy response of MTS-N detectors after exposure of γ-rays and narrow beams of X-rays.

Figure 8.

Relative photon energy response of MCP-N detectors after exposure of MCP-N detectors in different calibration laboratories (GUM- Główny Urząd Miar, Warsaw, CIEMAT –Madrid, KfK Karlsruhe) using γ-rays and narrow beams of X-rays.

MICRODOSIMETRIC MODELLING OF THE RESPONSE OF LiF DETECTORS

Microdosimetry describes the fluctuation of energy deposition of ionising radiation at micrometre and nanometre size targets. At the microscopic level, ionising particles interacting in the volume produce a non-uniform, stochastic pattern of energy deposition. The energy imparted to the volume in a single event, ε, is a stochastic quantity because it depends on the current configuration of the track and the target volume. The energy imparted normalised to the mass of the volume is called specific energy, z, and lineal energy, y when normalised to the mean chord length of the volume. In microdosimetry, frequency and dose distributions z and y are considered. f₁(z) and d₁(z) are frequency and dose distributions, where subscript 1 stays for a single event. Dose distribution d₁(z) specifies fraction of dose delivered to the target with the given value of z whereas frequency distribution f₁(z) quantifies fraction of events delivered with the specific energy z. The mean of the frequency distribution of specific energy is defined as:

(4)

the mean dose distribution d₁(z) is equal to

(5)

Microdosimetric models of radiation action, developed primarily for the analysis of the response of biological cells, bacteria and viruses, were successfully adapted for studying response of lithium fluoride TLDs^(5,34–36). The response of MCP-N detectors was found similar to a sublinear dose response of viruses, and the supralinear response of MTS-N detectors was quantified by linear–quadratic model well-describing survival of biological cells. Similarly like in biological cells, TL phenomena in LiF take place at the distances much <1 μm and are clearly related to a track structure.

What do we expect from microdosimetric analysis? The real gain from the application of phenomenological models is the understanding relationship between dose and energy (LET) response for different radiation modalities. Even if the mechanisms of the TL phenomenon are not fully understood and mathematically described, the models allow to connect apparently different phenomena and to predict the response for dose range and radiation modalities not available for calibration.

Microdosimetric one–hit detector model for calculation of the response of MCP-N detectors

In the one-hit detector model, it is assumed that the target is affected by the single energy deposition event called hit. In the population of targets, radiation produces hits independently of each other. It leads to the exponential relationship between the dose (fluence) and the non-hit (surviving) targets. If energy is imparted to the target there is a finite probability 1-exp(−αz) that the effect will take place, where α is a saturation parameter. Then the dose response R_i(D) for the i-th radiation modality is equal:

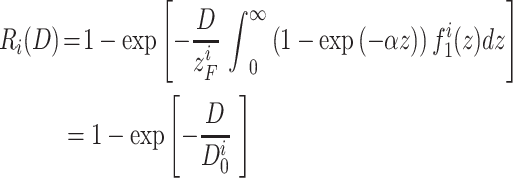(6)

where 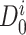is called the characteristic dose. Then, relative TL efficiency can be calculated as:

(7)

The microdosimetric one hit detector model has two free parameters: saturation parameter α and the target diameter, d, which is hidden in f₁(z) distribution. These two parameters were derived for MCP-N detectors by fitting Equation 3 to the measured dose response for ¹³⁷Cs γ-rays and Equation 4 to a few data for TL efficiency of MCP for α- and β- particles. It yielded α = 0.0091 Gy⁻¹ and d = 60 nm in water (24 nm in LiF). With these only two parameters it was possible to predict response for many other radiation modalities.

The biggest success of the one-hit detector model was the explanation of the anomalous photon energy response of MCP-N detectors (see Figure 9). Stopping power of electrons decreases with increasing energy and less densely ionising electron track leads to lower value of and in consequence to lower relative TL efficiency. Almost 10 keV photons predominately interact by the photoelectric effect, emitting secondary electron of energy reduced only by the binding energy on the K shell. When photon energy grows the photoelectric electron energy is also growing, stopping power decreasing and the corresponding η increasing. This simple picture changes for photon energies exceeding about 40 keV, where the competing Compton scattering starts to be more visible. At this moment not only high energy photoelectrons but also low energy Compton electrons appear, which again lead to an increase of 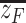, a decrease of η and appearing of a local minimum around 80 keV. For even higher energy photons producing more energetic Compton electrons, η is growing again. In summary, the anomalous photon energy response is the result of the extreme sensitivity of LiF:Mg,Cu,P for tiny changes of ionisation density for secondary electron spectra produced in LiF by X-rays. At the microscopic level it corresponds to local saturation of trapping centres around the electron track. This significant dependence of η on ionisation density is related to the very fast sublinear saturation of dose response, characterised by the characteristic dose 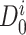= 233 Gy for ¹³⁷Cs γ-rays. A sensitive target is easily activated by the radiation hit and the energy deposited by the second hit is simply lost. This leads to the sublinear dose response.

Figure 9.

Relative photon energy response of MCP-N (LiF:Mg,Cu,P) detectors [4]. The solid line represents the result of model calculation. The local minimum of response at about 100 keV corresponds to local minimum of relative TL efficiency η_cal for secondary electrons produced by photons of the given energy.

Photon energy response of MTS-N (LiF:Mg,Ti)

Relative photon energy response of LiF:Mg,Ti detectors is, in the first approximation, following well the ratio of mass energy absorption coefficients. This supports the thesis that relative TL efficiency η of LiF:Mg,Ti is fairly independent of electron energy. Horowitz⁽¹⁾ in early 80’s pointed out that surprisingly the measured response exceeds this theoretical value by 10%, which was later confirmed in more recent measurements (see Figure 7). It was demonstrated that the enhanced photon energy response was related to the supralinear dose response of LiF: Mg,Ti for photons (see Figure 5) and could be numerically explained by a microdosimetric analysis⁽³⁷⁾.

When 10 keV electron is crossing 2.5 g/cm³ LiF it loses energy with the rate of about 1.79 eV/nm. For a 20 nm LiF spherical target the maximum energy deposit is then 71.6 eV which leads to specific energy, z = (71.6 eV/8.4 10⁻²⁰ kg) = 137 Gy. For some fraction of slower electrons produced by Compton scattering, the local dose in the target (specific energy) will be even higher. For so high doses the response of LiF:Mg,Ti is supralinear and the locally produced TL signal enhanced. The dose response of MTS-N detectors for ¹³⁷Cs γ-rays was then fitted with the function⁽⁵⁾:

R(D) = A(1- exp(− αD))+(1-A)(1-exp(− βD²))

where A = 0.362 ± 0.015, α = 7.3 × 10⁻⁴ ± 0.4 × 10⁻⁴ Gy⁻¹ and β = 3.92 × 10⁻⁶ ± 0.24 × 10⁻⁶ Gy⁻².

In Figure 10 the measured values of η  ⁽³⁷⁾ are compared with the model calculations.

Figure 10.

Relative TL efficiency of MTS-N detectors after narrow filtered beams of X-rays. Squares represent our experimental results, solid line model calculation for d = 20 nm. Different colours correspond to experiments with two batches of MTS-N detectors.

It is worth to point out that high local dose in LiF targets is produced not by the multiply events during high dose irradiation and interactions between tracks. In the low-dose region, for doses of a few mGy, electron tracks are (on average) so separated that probability of a multi-hit in the target is close to zero. Supralinearity results from the high doses deposited in the nanometre size targets by a fraction of secondary electrons with low energies i.e. with relatively high stopping power.

Microdosimetric d(z) model

A similar approach to analyse the response of LiF detectors was proposed by Parisi et al.⁽³⁵⁾. He studied relative TL efficiency of LiF:Mg,Ti and LiF:Mg,Cu,P detectors after irradiation with 10 different ions from protons to ¹³²Xe. Similarly as in the previous models, he did not assume any particular mechanisms of TL processes in LiF. The only assumption was that the relative TL efficiency was dependent on energy deposited in the sensitive targets.

One of the approaches to calculate the response of TLDs to heavy charged particle (HCP) is to calibrate microscopic distribution of energy deposition produced by this HCP using the experimentally derived dose response R(D) for photons. In the microdosimetric d(z) model microscopic distribution of energy deposition may be derived by calculation of microdosimetric distribution. This distribution is next folded with a response function in term of specific energy r(z) of the detector.

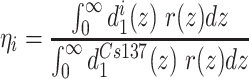(8)

In the work of Parisi⁽³⁵⁾ dose distribution d₁ⁱ(z) was calculated using the radiation transport code PHITS. It was assumed, similarly as in the previous model, that the response function r(z) can be represented by the measured dose response R(D). For LiF:Mg,Ti and for LiF:Mg,Cu,P the corresponding measured dose responses were taken into account in calculations. It was justified because for high macroscopic dose a large number of events take place in a sensitive target volume. In that case, the average value of is close to the one of the macroscopic absorbed dose D. The only free model parameter is the target diameter, which is also hidden in the d₁(z) microdosimetric distribution. A big success of the model is that with a single free parameter (d_LiF = 40 nm) it is possible to calculate relative TL efficiency for a broad range of ions and energies and both for LiF:Mg,Cu, P and LiF:Mg,Ti. The agreement between calculation and experiment is really remarkable for both detector types. The fact that a single parameter worked well for two very different TL materials is really surprising because the mechanism of TL in both phosphors is different in many aspects⁽³⁸⁾. ‘Engineering is the art of being approximately right rather than exactly wrong’ responded the author of the model⁽³⁹⁾. Even if we do not fully understand the underlying mechanisms the model works well and has strong predictive power.

It was a significant contribution of microdosimetry to explain the response of LiF:Mg,Ti and LiF:Mg,Cu,P detectors. The decrease of efficiency for detectors with sublinear dose response and increase with the supralinear was found as a general rule, applicable for a response of known TL detectors. For dose response, energy response (LET response), relative TL efficiency and photon energy response the same mechanisms are responsible. The supralinearity goes together with enhanced relative TL efficiency and slightly enhanced photon energy response. Fast dose saturation with no supralinearity implicates decreased TL efficiency, higher dependence on LET and possible reduction of photon energy response. These models work also well for other detectors like Al₂O₃, CaF₂:Tm or alanine.

Marco Moscowitch was one of the first researchers who contributed to the devolvement of large scale individual dosimetry systems based on LiF:Mg, Cu,P⁽⁴⁰⁾. He perfectly understood the relationship between different observed properties of the high sensitive lithium fluoride:

‘The decreased TL efficiency of LiF:Mg,Cu,P at the lower photon energies is a result of local saturation (decrease) of the TL efficiency in microscopic volumes along the tracks of the secondary electrons. This local microdosimetric saturation, in turn, is a result of the lack of supralinearity and early saturation in the dose response curve of LiF(MCP). The dose response curve of LiF(MCP) is linear–sub-linear rather than linear–supralinear–sub-linear.’

It was our privilege to know Marco Moscovitch and to profit from his research. We are proud to have a chance to publish this paper to memorise his great achievements in the field of TL dosimetry.