Calibration-free B0 correction of EPI data using structured low-rank matrix recovery

Abstract

We introduce a structured low-rank algorithm for the calibration-free compensation of field inhomogeneity artifacts in Echo Planar Images (EPI). We combine the measurements from two fully-sampled EPI acquisitions to reformulate the field inhomogeneity compensation problem as a recovery of an image time series from highly undersampled k-space measurements; the temporal profile at each pixel is assumed to follow a single exponential model. We exploit this exponential behavior at every pixel, along with the spatial smoothness of the exponential parameters to derive a 3D annihilation relation in the Fourier domain. This relation translates to a low rank property on a structured multi-fold Toeplitz matrix, whose entries correspond to the measured k-space samples. We introduce a fast two-step algorithm for the completion of the Toeplitz matrix from the available samples. In the first step, we estimate the null space vectors of the Toeplitz matrix using only its fully-sampled rows. The null-space is then used to estimate the signal subspace, which facilitates the efficient recovery of the time series of images. We finally demonstrate the proposed approach on spherical MR phantom data and invivo datasets and show that the artifacts are significantly reduced. The proposed approach could potentially be used to compensate for time varying field-map variations in dynamic applications such as functional MRI.

I. INTRODUCTION

Echo Planar Imaging (EPI) is a fast image acquisition scheme for acquiring Fourier data in a single shot. Its capability to provide high temporal resolution makes it a popular choice in many dynamic imaging studies, including imaging of the BOLD contrast in functional MRI (f-MRI) [1], [2] and temperature monitoring during ablation therapy [3]. EPI acquisitions are also widely used to reduce the scan time in MR imaging applications including diffusion MRI and parameter mapping [4]. In recent years, there has been a push towards achieving higher spatial and temporal resolution in many of these applications. However, the long read-out associated with EPI makes it particularly susceptible to off-resonance related geometric distortion artifacts. Magnetic field (B0) inhomogeneities are inevitable in MRI and arise due to the imperfections in the magnet, improper shimming of gradient coils and the difference in magnetic susceptibility between air, tissue, and bone; the distortions are primarily around air-tissue interfaces in the sinus and air canal regions.

Numerous methods have been proposed to reduce the B0 distortions in EPI images [5]–[18]. Broadly, they can be classified as calibration-based or calibration-free algorithms. In calibration-based methods, a field map is estimated prior to the EPI scan [19], which is then used in the recovery of a distortion-free image. The reconstruction algorithms range from computationally efficient conjugate phase methods [7]–[12] to more sophisticated and computationally expensive model based reconstruction methods [13]–[15]. The main challenge with calibration based methods is the mismatch between the estimated and the actual field map, which manifests as distortions in the EPI images. This discrepancy occurs due to patient motion, scanner drift and field inhomogeneity differences due to physiological changes such as respiration. To overcome these issues, calibration-less methods which jointly estimate the field map and the distortion-free image from the acquired data have been proposed [16], [17]. An alternative strategy is image space correction using registration [20], which can work with magnitude images acquired with two different sampling trajectories. The main challenge with the above calibrationless methods is the non-convex nature of the optimization algorithms, which translates to high computational complexity and risk of local minima.

In this paper, we propose a fast calibration-free structured low-rank framework for the compensation of field inhomogeneity artifacts in EPI. We combine the information from two EPI acquisitions, whose read-outs differ in echo-time (TE) by a few milli-seconds. We note that such datasets can be acquired in the interleaved mode in f-MRI applications, which allows for the compensation of dynamic variations in the fieldmap. Using the time segmentation approach [9], we transform the EPI field inhomogeneity compensation problem to the recovery of an image time series from highly undersampled measurements. Upon recovery, the distortion-free image just corresponds to the first image of the series. The temporal intensity profile of each pixel in the time series is assumed to decay exponentially with a frequency and damping constant, which is dependent on the fieldmap and $T_2^{*}$ value at that pixel. We also assume that the exponential parameters vary smoothly across space, which allows us to exploit the smooth nature of fieldmap variations. The above assumptions imply that the k − t space samples of the image time series are annihilated by convolutions with several finite impulse response filters; the filter taps are dependent on the exponential parameters. The convolution between the signal and the filter can be compactly represented as the product of a multi-fold Toeplitz matrix, formed from the Fourier samples, with a vector of filter coefficients. The annihilation relations imply that the above Toeplitz matrix has several linearly independent null-space vectors and hence is low-rank [21], [22]. Note that several entries of the above matrix are unknown since the corresponding signal samples are not measured. We propose to exploit the low rank property of this matrix to complete its missing entries, and hence recover the image series.

The direct implementation of the structured low-rank matrix recovery algorithm requires the evaluation and storage of this large multifold Toeplitz matrix. Since the number of entries of this matrix is considerably higher than the number of signal samples, this approach will result in a computationally expensive algorithm. Instead, we introduce a fast two-step approach to solve this problem. In the first step, we form a sub-matrix of the above Toeplitz matrix by selecting the fully sampled rows, and estimate the null-space from it. Note that this submatrix is an order of magnitude smaller than the original Toeplitz matrix, and hence the first step has low memory demand and is computationally efficient. These null-space vectors are then used to recover the missing entries of the original Toeplitz matrix in the second step. Specifically, we are seeking a matrix that is orthogonal to the estimated null-space vectors, while satisfying data-consistency. To reduce the computational complexity of the second subproblem, we estimate the signal subspace by compactly representing the signal using an exponential signal model. This facilitates the easy estimation of the signal from its measurements. Specifically, this approach reduces the number of effective unknowns to be solved and results in a very fast and efficient algorithm. It also eliminates the need to store the entries of the Toeplitz matrix. We demonstrate the effectiveness of the proposed approach by performing simulations on a numerical brain phantom and also applying it on an ACR spherical MR phantom and two human subject data.

The proposed field inhomogeneity compensation scheme is an addition to the growing family of structured low-rank methods for continuous domain compressed sensing [21],[23]–[27], parallel MRI [28], [29], as well as calibration-free correction of multishot EPI data [30], correction of Nyquist ghost artifacts in EPI [31]–[33] and trajectory correction in radial acquisitions [34]. Despite the conceptual similarities between the proposed work and [17], there are a few fundamental differences. In [17], field map compensation is done on every column of the image independently using prony’s method; additional sorting steps are introduced to ensure a smoothly varying intensity and phase values. This is suboptimal, especially when the noise level is high or when the field map is highly non smooth, in which case additional interpolation steps are required to replace the intensity values in the discontinuous regions.

II. PROBLEM SETUP

A. Model of signal acquisition in EPI

We model the acquired EPI signal as [35]:

$$s(k(t))=\int \underset{\rho (r,t)}{\underbrace{{\rho }_0(r)e^{-\gamma (r)t}}}{e}^{-j2\pi k(t)\cdot r}dr+\eta (t),$$ (1)

where k(t) is the k-space location sampled at time t and s(k(t)) is the corresponding measurement. ρ₀(r) denotes the transverse magnetization of the object and η represents zero mean white Gaussian noise. The term γ(r) is a complex quantity that captures the field inhomogeneity induced distortion:

$$\gamma (r)=R_2^{*}(r)+j\omega (r).$$ (2)

Here $R_2^{*}(\text{r})$ and ω(r) are the relaxation and off-resonance effects, respectively, at the spatial location r. Note that if γ(r) = 0, the relation in (1) simplifies to a simple Fourier transform between the object ρ₀(r) and its measurments s(k(t)).

Since (1) contains the field distortion γ(r), it is no longer a Fourier integral and cannot be efficiently computed using the fast Fourier transform (FFT). Hence we adopt the time segmentation approach which enables the use of FFTs, thus resulting in reduced computational complexity. Specifically, we divide the acquisition window into a number of time segments and assume that the temporal evolution of the field inhomogeneity is constant in each of the segments. This is a fairly safe assumption when the duration of each time segment is short. For simplicity, we assume that the spatial support of each time segment be of dimension N × N and each segment contains only k lines of kspace. Assume that the time taken to acquire one line of kspace be ΔT and let the time between two segments be T = kΔT. Using this, the measurements at t_n = nT; $n=1,2,\dots \frac{N}{k}$, are given by:

$$\begin{gathered} b_n=\int \underset{{\rho }_n(r)}{\underbrace{{\rho }_0(r)e^{-\gamma (r)nT}}}{e}^{-j2\pi k\cdot r}dr+{\eta }_n \\ ={\mathcal{A}}_n\left({\rho }_n\right)+{\eta }_n \end{gathered}$$ (3)

Here ρ_n is the image corresponding to the time instant t_n = nT, while b_n is its Fourier measurement. The operator ${\mathcal{A}}_n$ is a linear acquisition operator corresponding to the n^th segment, which represents a fast Fourier transform, followed by multiplication by a sampling mask of the n^th segment. See Fig. 1 a) for an illustration of the time segmentation approach. Since the temporal evolution of e^−γ(r)t can be safely ignored during the duration T, the magnitude of the images ρ_n(r) can be assumed to have no geometric distortion. However, due to relaxation effects the magnitude image ρ_n(r) is given by ${\rho }_0{e}^{-R_2^{*}(r)nT}$; the first image, ρ₁(r), is least affected by $R_2^{*}$. Since b_n corresponds to only a small fraction of the k-space measurements of ρ_n, the direct recovery of ρ_n(r); $n=1,2,\dots \frac{N}{k}$ from b_n is challenging.

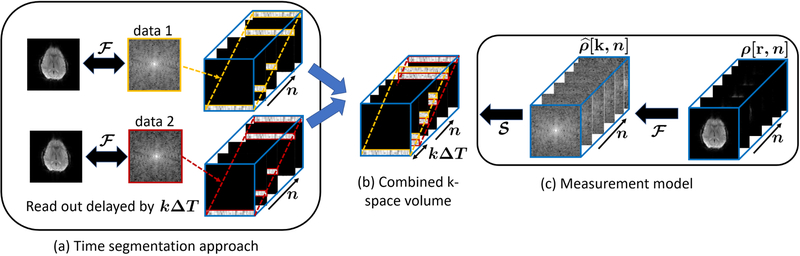
Fig. 1.

Illustration of the time segmented approach and the measurement model: (a) The data acquired from the two EPI acquisitions and their corresponding uncorrected ifft reconstructions are shown. A time segmentation approach is adopted such that the acquisition window of the two datasets is divided into a number of segments. (b) By combining the time segmented volumes of both the datasets, a k-space volume with many missing entries is formed. Data from the two EPI acquisitions lie on the yellow and red oblique planes respectively. (c) The operators $\mathcal{F}$ and $\mathcal{S}$ are defined. The data $\widehat{\rho }$ can be under-sampled using the operator $\mathcal{S}$ to obtain the volume shown in (b).

B. Reformulation as recovery from undersampled data

We consider the joint estimation of the distortion (field inhomogeneity and relaxation) map and the distortion-free image from the given set of Fourier measurements. This translates to estimating two complex unknowns, corresponding to ρ_n(r) and γ(r) at every pixel location. By a simple degrees of freedom argument, we can deduce that we need atleast two complex measurements at every location r to estimate all of the unknown parameters. For this purpose, we acquire two sets of EPI data such that the readout of the second dataset is delayed by mΔT, $m\in \mathbb{Z}$. The Fourier measurements corresponding to the two EPI acquisitions are shown to lie on the yellow and red oblique planes respectively in Fig. 1(a).

Let ${\text{b}}_n^{(1)}$ and ${\text{b}}_n^{(2)}$ represent the under-sampled Fourier measurements corresponding to the two acquisitions. We can express them using the linear acquisition operator ${\mathcal{A}}_n$, defined in (3), as

$$\begin{gathered} b_n^{(1)}={\mathcal{A}}_n\left({\rho }_n\right);n=1,2,\dots \frac{N}{k} \\ {b}_{n-\frac{m}{k}}^{(2)}={\mathcal{A}}_{n-\frac{m}{k}}\left({\rho }_n\right);n=\frac{m}{k}+1,\dots M \end{gathered}$$ (4)

where $M:=\frac{N}{k}+\frac{m}{k}$. We have assumed that the two EPI datasets have been time-segmented into $\frac{N}{k}$ segments and each segment contains exactly k lines. For example, when N = 64 and m, k = 4, the time segmented volume contains 16 segments or frames. When m = k, we can observe that the phase evolution present in the second segment of ${\text{b}}_n^{(1)}$ and first segment of ${\text{b}}_n^{(2)}$ will be the same, the phase evolution present in the third segment of ${\text{b}}_n^{(1)}$ and second segment of ${\text{b}}_n^{(2)}$ will be the same and so on. We combine the measurements from both the acquisitions and express them compactly:

$$\text{b\hspace{0.17em}}=\mathcal{A}(\rho )+\eta$$ (5)

where ρ = [ρ₁, ρ₂, … ρ_M] is the time series of images, $\mathcal{A}$ is a Fourier under-sampling operator and η represents zero mean white Gaussian noise. The formation of the combined k-space volume corresponding to the image series ρ, for the case m = k, is illustrated in Fig. 1 (b). For an illustration of the measurement model refer Fig. 1 (c).

From Fig. 1 (b), we also note that all but the first and last frame of the time-segmented volume consists of two blocks of kspace data, while only one block is sampled in the first and the last frame. Hence by recovering the Fourier samples of the volume, in particular the first frame, we can obtain the distortion-free image. Thus by adopting the time segmentation approach, we have been able to transform the inhomogeneity correction problem into a problem of recovering an image series from highly under-sampled and structured Fourier measurements. We propose a two step algorithm to recover the Fourier samples corresponding to the entire volume, and thus solve the field inhomogeneity compensation problem.

C. Annihilation and structured low-rank properties

We model the signal ρ at every pixel location r as a single decaying exponential:

$$\rho [\mathbf{r},n]=\alpha (\mathbf{r})\beta {(\mathbf{r})}^n$$ (6)

where $\alpha (\text{r})\in ℂ$ are the amplitudes and β(r) is a spatially varying exponential function (exponential parameter) dependent on the underlying physiology. In this work, β(r) = e^−γ(r)T is an exponential parameter dependent on the relaxation and off-resonance effects at a spatial location r. T is the time between two image segments.

Since the signal in (6) is a single decaying exponential, at each pixel location it can be annihilated by a two tap FIR filter[36]:

$$\sum _{l=0}^1\rho [\mathbf{\text{r}},l]d[\mathbf{\text{r}},n-l]=0,\forall \mathbf{\text{r}}.$$ (7)

where (7) represents a 1-D convolution between the signal ρ[r, n] and the two tap filter d[r, n]. Here d[r, n] is a FIR filter whose filter coefficients at every spatial location r are given by [1, −β(r)] [36] and n is the signal index along the temporal dimension. In practice, the relaxation and off-resonance effects due to field inhomogeneity depend on the structure of the underlying physiology and hence can be assumed to vary smoothly across the spatial locations. This means that the filter coefficients, which depend on the exponential parameters, can be assumed to be smooth functions of the spatial variable r. Taking the 2D Fourier transform along the spatial dimension r in (7), we obtain the following 3-D annihilation relation:

$$\widehat{\rho }[k,n]\otimes \widehat{d}[k,n]=0.$$ (8)

where $\rho [r,n]\stackrel{{\mathcal{F}}_{2}D}{\leftrightarrow }\widehat{\rho }[k,n]$ and $d[r,n]\stackrel{{\mathcal{F}}_{2}D}{\leftrightarrow }\widehat{d}[k,n]$ are the 2-D Fourier coefficients of ρ[r, n] and d[r, n] respectively, while ⊗ denotes 3-D convolution. Since the inhomogeneity map is smooth, we assume $\widehat{d}[k,n]$ to be a bandlimited 3-D FIR filter; its spatial bandwidth controls the smoothness of the parameters, while its bandwidth along the temporal dimension is dependent on the number of exponentials in the signal model, which is two in this case. The single exponential model considered in this paper is a special case of the model considered in [21]. When the filter dimensions are overestimated, there will be multiple filters d₁, .., d_P that annihilate the signal and hence satisfy (8) [21], [23]. Expressing these annihilation relations in compact matrix notation, we obtain

$$\mathcal{T}(\widehat{\rho })\left[\widehat{d_1},\dots ,\widehat{{\text{d}}_P}\right]=0$$ (9)

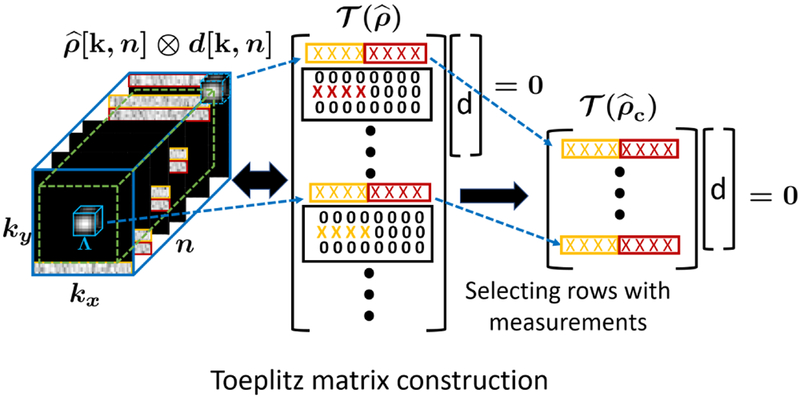
where $\mathcal{T}$ is a linear operator that maps a 3-D dataset $\widehat{\rho }$ into a Toeplitz matrix $\mathcal{T}(\widehat{\rho })\in {ℂ}^{m\times s}$. Here m refers to the number of valid convolutions between $\widehat{\rho }[k,n]$ and $\widehat{d}[k,n]$, which is represented by the green cuboid in Fig. 2, and s = |Λ| is the product of the dimensions of the filter. Similarly, each ${\widehat{\text{d}}}_i$; i = 1,2,…p, represents the vectorized 3-D filter d_i[k, n]. From (9), we can see that the Toeplitz matrix $\mathcal{T}(\widehat{\rho })$ has a large null space and hence has a low rank structure.

Fig. 2.

Illustration of the construction of the matrices $\mathcal{T}(\widehat{\rho })$ and $\mathcal{T}\left({\widehat{\rho }}_c\right)$ from the combined k-space volume $\widehat{\rho }$: The 3D convolution between a filter, with support Λ, and $\widehat{\rho }$ results in a large Toeplitz matrix $\mathcal{T}(\widehat{\rho })$ with many rows filled with zeros; the valid convolutions are defined inside the green cuboid. The rows of $\mathcal{T}(\widehat{\rho })$ correspond to cuboid shaped neighborhoods of the Fourier samples. A smaller Toeplitz matrix $\mathcal{T}\left({\widehat{\rho }}_c\right)$ is constructed from $\mathcal{T}(\widehat{\rho })$ by selecting only fully sampled rows.

III. PROPOSED TWO-STEP ALGORITHM

We propose to exploit the low-rank property of the Toeplitz matrix to recover the signal from highly undersampled measurements. However, the direct implementation of a structured low-rank matrix recovery algorithm, similar to [23] requires the evaluation and storage of $\mathcal{T}(\widehat{\rho })$. This will be a computationally expensive operation, especially in the EPI setting where the kspace volume to be recovered is quite large. Instead, we propose a fast two step approach to solve the problem. In the first step, we construct a sub-matrix of the Toeplitz matrix $\mathcal{T}(\widehat{\rho })$ by selecting only the fully sampled rows, and estimating the null-space from it. Note that this submatrix is an order of magnitude smaller than the original Toeplitz matrix, and hence the first step has low memory demand and is computationally efficient. The estimated null space vectors are then used to recover the missing entries of the full matrix in the second step. Specifically, we seek a matrix that is orthogonal to the estimated null-space vectors, while satisfying data-consistency. To accelerate the second step, we adopt a synthesis exponential signal model, which aids in the realization of a fast and memory efficient algorithm.

A. Step 1: Estimation of the null space

We propose to estimate the null-space of the low-rank multi-fold Toeplitz matrix $\mathcal{T}(\widehat{\rho })$ from the observed samples. Specifically, we construct a sub-matrix of $\mathcal{T}(\widehat{\rho })$, denoted by $\mathcal{T}\left({\widehat{\rho }}_c\right)$, by selecting rows that are fully sampled. Since the rows of $\mathcal{T}\left({\widehat{\rho }}_c\right)$ are the subset of the set of rows of the larger Toeplitz matrix $\mathcal{T}(\widehat{\rho })$, both the matrices have a common right null space. This is facilitated by using a small filter, which is sufficient to represent the smooth field inhomogeneity map. The estimate of the null-space will be less sensitive to noise, when the number of rows in $\mathcal{T}\left({\widehat{\rho }}_c\right)$ is high. When data from multiple channels are available, Toeplitz matrices corresponding to each coil are formed and they are concatenated vertically to form the matrix $\mathcal{T}\left({\widehat{\rho }}_c\right)$. Furthermore, to improve noise robustness, we consider additional shifts of the filter on the data lying on the oblique planes, that will provide additional rows and null space relations. See Fig. (2) for the construction of the Toeplitz matrices $\mathcal{T}(\widehat{\rho })$ and $\mathcal{T}\left({\widehat{\rho }}_c\right)$.

We adopt an eigen decomposition approach to estimate the null space of $\mathcal{T}\left({\widehat{\rho }}_c\right)$. Let the gram matrix be given by $R={\left[\mathcal{T}\left({\widehat{\rho }}_c\right)\right]}^{*}\left[\mathcal{T}\left({\widehat{\rho }}_c\right)\right]$. The eigen decomposition of R is given by VΛV*, where V ∈ C^L×L is an orthogonal matrix containing the eigen vectors v⁽ⁱ⁾ and Λ is a diagonal matrix containing the eigen values λ⁽ⁱ⁾. We use the matrix V to form the null space in the following way:

$$\text{D\hspace{0.17em}}=\text{\hspace{0.17em}VQ}$$ (10)

where Q is a diagonal matrix with the i^th diagonal entry given by ${\lambda }_i^{-\frac{q}{2}}$; q is a small number between 0 and 0.5 Since the eigen values are small for null space vector, more weight is given to them. Hence this strategy eliminates the need for a threshold on the eigen values to determine the null space.

B. Step 2: Null space aware recovery of distortion-free image

One the null-space matricx D is estimated from $\mathcal{T}\left({\widehat{\rho }}_c\right)$. we use it to recover the entire kspace volume from the under-sampled Fourier measurements. We formulate the recovery of k-space volume $\widehat{\rho }$ from the measurements b as the following constrained least squares problem in the Fourier domain:

$$\underset{\widehat{\rho }}{\text{min}}\Vert \mathbf{\text{S}}\widehat{\rho }-\text{\hspace{0.17em}b}{\Vert }_2^2\text{ such that }\mathcal{T}(\widehat{\rho })\mathbf{\text{D\hspace{0.17em}}}=0$$ (11)

Where $\mathcal{T}(\widehat{\rho })$ is a multi-fold Toeplitz matrix formed from the Fourier samples $\widehat{\rho }$, D is the null space matrix computed in (10) and S is a sampling matrix.

IV. ACCELERATING NULLSPACE AWARE RECOVERY USING SIGNAL SUBSPACE ESTIMATION

We exploit the structure of the nullspace, or equivalently the columns of D, to realize a fast algorithm to solve (11). Note that by computing the 2-D inverse Fourier transform of the columns of D, we obtain spatial filters $d_i[r,n]\stackrel{{\mathcal{F}}_{2}D}{\leftrightarrow }{\widehat{d}}_i[k,n]$ with two taps along time. From (7), we known that the 1-D convolution between these filters and the x−t signal ρ[r, n] is zero. Using the coefficients of the filter, we can form a matrix D_s(r) at a spatial location r in the following way:

$$D_{\text{s}}(\text{r})=\left[\begin{array}{lll}{d}_1[r,0]\hfill & \dots \hfill & d_L[r,0]\hfill \\ d_1[r,1]\hfill & \dots \hfill & d_L[r,1]\hfill \end{array}\right]$$ (12)

We observe from (6) that if ρ[r, n] is composed of a single exponential, it can be annihilated by a unique two-tap filter as shown in (7). This implies that the columns of the matrix D_s(r) will be linearly dependent, whenever ρ[r, n] ≠ 0. However, at spatial location r with no signal (i.e, ρ[r, n] = 0.), the matrix D_s(r) will be full rank and there is no unique filter d_i[r, n] satisfying (7) Since the 1-D filters d_i[r, n] differ only in the background regions with zero signal, we propose to choose a single filter $\widehat{d}[k,n]$ that resides in the null-space of $\mathcal{T}(\widehat{\rho })$ and simplify (11) to

$$\underset{\widehat{\rho }}{\text{min}}\Vert \mathbf{\text{S}}\widehat{\rho }-\text{\hspace{0.17em}b}{\Vert }_2^2\text{ such that }\mathcal{T}(\widehat{\rho })\widehat{d}=0$$ (13)

where $\widehat{\text{d}}$ represents the vectorized 3-D filter $\widehat{d}[k,n]$. This approach is equivalent to assuming that all spatial locations (irrespective of background or foreground) satisfy the single exponential model (6).

Once $\widehat{\text{d}}$ is identified, we can estimate the exponential parameters β(r) from d[r, n] by computing the (zero-padded) inverse Fourier transform of the the filter coefficients $\widehat{d}[k,n]$, followed by normalization. Expressing mathematically, we obtain $\mu (r)=F*P_{\text{Λ}}^{*}\widehat{d}$, which consists of two frames and has the form [1, − β^k]; 1 represents a matrix of ones. $P_{\text{Λ}}^{*}$ represents zero padding operation outside the filter support Λ and F* is the inverse discrete Fourier transform (iDFT) matrix. Once β is estimated, we can re-express (13) efficiently as

$$\underset{\rho }{\text{min}}\Vert \mathcal{A}(\rho )-\text{\hspace{0.17em}b}{\Vert }_2^2\text{ such that }\rho [\mathbf{r},n]=\alpha (\mathbf{r})\beta {(\mathbf{r})}^n,$$ (14)

Here, $\mathcal{A}$ represents the Fourier under-sampling operator, α(r) is the inhomogeneity corrected image and β(r) = e^−γ(r)T is the exponential parameter. The problem (14) is equivalent to

$${\alpha }^{*}=\arg \underset{\alpha }{\text{min}}\Vert \mathcal{A}\left(\alpha (r)\beta {(r)}^n\right)-\mathbf{\text{b}}{\Vert }_2^2+ϵ\Vert \alpha {\Vert }_2^2$$ (15)

when the regularization parameter ∊ = 0. Note that this least squares problem can be efficiently solved without the evaluation and storage of the Toeplitz matrix $\mathcal{T}(\widehat{\rho })$. To solve (15), we just need a few iterations of the CG algorithm. When data from multiple channels are available, we solve (15) for each coil independently. The final solution α is obtained from a square root of sum-of-squares (sos) of each coil solution.

We observe that choosing an arbitrary vector $\widehat{\text{d}}$ from the matrix D can result in noise amplification in the back-ground regions. Hence, we introduce two strategies with slightly different assumptions to estimate an appropriate null space vector for which the noise amplification is minimal. The first approach aims to find a null space vector, which corresponds to the smoothest exponential parameter β. The second approach aims to exploit the low rank property of the Toeplitz matrix and combines information from all the null space vectors to estimate the exponential parameter β.

A. Smoothness based estimation of the nullspace vector

We estimate a vector in the nullspace that yields exponential parameters that are spatially smooth. We formulate the recovery of this vector as the following regularized optimization problem in the Fourier domain:

$$\underset{\widehat{\text{d}}}{\text{min}}\Vert \mathcal{T}\left({\widehat{\rho }}_c\right)\widehat{\text{d}}{\Vert }_2^2+{\mu }_0\Vert \text{C}\widehat{\text{d}}{\Vert }^2$$ (16)

where C is a diagonal matrix with entries $\sqrt{\left(k_x^2+k_y^2\right)}$; (k_x, k_y) are the kspace coordinates corresponding to the filter coefficients and μ₀ is a regularizing parameter. The regularizer in (16) has an equivalent form in the image domain:

$$\Vert \text{C}\widehat{\text{d}}{\Vert }^2=\Vert \nabla d{\Vert }^2$$ (17)

where $d[r,n]\stackrel{{\mathcal{F}}_{2}D}{\leftrightarrow }\widehat{d}[k,n]$ is the 3-D polynomial corresponding to the Fourier coefficients $\widehat{d}[k,n]$ and ∇ is the gradient operator. To solve (16), we take its gradient with respect to $\widehat{\text{d}}$ and set it to zero. This gives us the following equation:

$$\left[\underset{\text{G}}{\underbrace{{\left[\mathcal{T}\left({\widehat{\rho }}_c\right)\right]}^{*}\left[\mathcal{T}\left({\widehat{\rho }}_c\right)\right]+{\mu }_0{C}^{*}\mathbf{\text{C}}}}\right]\widehat{\text{d}}=0$$ (18)

The solution to (18) is the eigen vector corresponding to the minimum eigen value of the matrix G. From the estimated vector $\widehat{\text{d}}$, we can estimate the corresponding 3D function as

$$\mu (\text{r})={\mathbf{\text{F}}}^{*}{\mathbf{\text{P}}}_{\text{Λ}}^{*}\widehat{\text{d}}$$ (19)

where μ(r) = [μ⁽¹⁾ (r), μ⁽²⁾(r)]. To estimate the inhomogeneity map β, we normalize the polynomial μ such that its frames are given by $\left[1,{\overline{\mu }}^{(2)}\right]$; the map corresponding to it is given by:

$$\beta (\text{r})={\left(-{\overline{\mu }}^{(2)}(\text{r})\right)}^{\frac{1}{k}}$$ (20)

where $k\in \mathbb{Z}$ and kΔT is the delay in the readout of the second EPI dataset. The main benefit of this scheme is that the vector $\widehat{\text{d}}$ can be estimated using a single eigen decomposition of the G matrix and hence is computationally efficient.

The above approach provides a single null-space filter, assuming the field map to be smooth. It is also robust to noise and other sources of errors. A concern with this approach is its potential degradation in cases with abrupt field map variations at the air tissue interfaces. We will now discuss an alternate approach that does not rely on smoothness assumptions.

B. Null space vector estimation without smoothness assumptions (Low rank approach)

When the measurements are corrupted by noise, the estimation of the null space vectors and hence β will not be very accurate. In such cases, we propose to denoise the measurements prior to the null space estimation step. We formulate the denoising of the k-space data as the following Schatten-p norm minimization:

$${\widehat{\rho }}_c^{\star }=\arg \underset{{\widehat{\rho }}_c}{\text{min}}\Vert {\widehat{\rho }}_c-\text{b}{\Vert }_2^2+{\gamma }_0\Vert \mathcal{T}\left({\widehat{\rho }}_c\right){\Vert }_p$$ (21)

where γ₀ is a regularization parameter, $\mathcal{T}\left({\widehat{\rho }}_c\right)$ is the sub-matrix formed from the Toeplitz matrix $\mathcal{T}(\widehat{\rho })$. ∥X∥_p is the Schatten-p defined as $\Vert X{\Vert }_p:=\frac{1}{p}Tr\left[{\left(X^{H}X\right)}^{\frac{p}{2}}\right]=\frac{1}{p}\sum {}_i{\sigma }_i^p$, where σ_i are the singular values of X.

We employ the iterative reweighted least-squares (IRLS) based algorithm recently proposed in [21] to solve (21). The IRLS based scheme alternates between the solution to the quadratic subproblem

$${\widehat{\rho }}_c=\arg \underset{{\widehat{\rho }}_c}{\text{min}}\Vert {\widehat{\rho }}_c-\text{b}{\Vert }_2^2+{\gamma }_0\Vert \mathcal{T}\left({\widehat{\rho }}_c\right)\sqrt{W}{\Vert }_F^2,$$ (22)

and the update of the weight matrix W:

$$W={\left[\underset{R}{\underbrace{{\left[\mathcal{T}\left({\widehat{\rho }}_c\right)\right]}^{*}\left[\mathcal{T}\left({\widehat{\rho }}_c\right)\right]}}+ϵI\right]}^{\frac{p}{2}-1}$$ (23)

Here ∊ is added to stabilize the inverse. Note that (22) seeks a signal $\widehat{{\rho }_c}$ such that the projection of $\mathcal{T}\left({\widehat{\rho }}_c\right)$ onto its null-space $\sqrt{W}$ is as small as possible. However, the matrix $\sqrt{W}$ has a similar structure as the null space matrix D, which is computed in (10). Specifically, the columns of $\sqrt{W}$ correspond to the weighted eigen vectors of the gram matrix R; the weights being inversely proportional to the eigen values [21]. This means that more weight is given to the null space vectors, thus eliminating the need for a threshold on the eigen values to determine the null space.

Now, we propose to estimate the null space vector from the matrix $\sqrt{W}$. Recall from Sec. IV that we expect a unique annihilating filter in the regions where the signal is non-zero. Once the nullspace matrix $\sqrt{W}$ is obtained, we can extract the spatial filters d_i[r, n] by computing the zero-padded IFFT of its columns. At each spatial location r, we can form the matrix D_s (r) ∈ C^2×L as shown in (12) and compute its rank. We expect the rank of D_s(r) = 1 in foreground regions, which results in a unique null-space vector. Similarly, the rank of D_s(r) = 2 in background regions, where the signal is zero. In the first case, the maximum eigen vector of the matrix D_s(r) can be chosen, and the exponential parameters can be estimated from it as described in (20). When the rank of D_s(r) = 2, there is no unique null space vector and hence we arbitrarily set it to a small value.

V. EXPERIMENTS AND RESULTS

We validate the proposed approach using simulations performed on a numerical brain phantom, and MRI experiments performed on phantom and human data. MRI experiments were performed on a GE 3T scanner with 32-channel head coil using a gradient-echo EPI (GRE-EPI) acquisition. Data from the spherical phantom and two healthy volunteers were acquired using standard shim settings. The scan parameters used for the phantom and the human experiments were as follows: FOV = 25.6 mm, matrix size = 64 × 64, slice thickness = 3.6 mm, TR = 3100 ms with number of slices = 40 and the minimum TE = 30 ms. For the above GRE-EPI, the time taken to acquire one k-space line, ΔT, was 0.636 ms. For each experiment, we acquired two sets of GRE-EPI data such that the readout of the second data set was delayed by 4ΔT. In order to compare the proposed reconstructions to a reference image, we collected a four-shot GRE-EPI data and a high spatial resolution structural data.

For the MRI experiments and the numerical phantom simulations, while solving the least squares problem (15) we formed the time-segmented k-space volume by assuming one line of k-space per time segment (k = 1). This resulted in a total of sixty eight time frames (M = 68). The regularization parameters for the proposed low rank and smoothness approaches were chosen empirically. For the phantom and invivo experiments, we had to denoise the kspace data prior to the estimation of inhomogeneity map. We noticed that for the low rank approach, this was able to get rid of some pixelation artifacts in the final inhomogeneity corrected image. However, the denoising step did not have much effect on the estimate of the map and the final reconstruction for the proposed smoothness approach.

A. Comparison with an iterative based smoothness approach [16]:

We compare the reconstructions from the proposed smoothness and low rank methods to those obtained from an iterative approach [16] on a numerical brain phantom. The joint recovery of the inhomogeneity corrected image ρ₀, field map ω and $R_2^{*}$ map can be formulated as the following optimization problem:

$$\underset{{\rho }_0,\omega ,R_2^{*}}{\text{min}}\Vert E\left({\rho }_0\right)-\text{\hspace{0.17em}b}{\Vert }_F^2+{\lambda }_1\Vert H\omega {\Vert }_2^2+{\lambda }_2\Vert H{R}_2^{*}{\Vert }_2^2+{\lambda }_3\Vert {\rho }_0{\Vert }_2^2$$ (24)

where E captures the signal model, H is the finite difference matrix, which is used to penalize the roughness of the fieldmap and the $R_2^{*}$ map respectively and λ₁, λ₂ and λ₃ are the regularization parameters. The objective function in (24) is very similar to the one in [16]. In [16], rectangular basis functions were used to model the object, which resulted in a different data consistency term. They also ignored the effects due to $R_2^{*}$. To solve (24), we employ an alternating minimization algorithm, which cycles between the updates of the image ρ₀, ω and $R_2^{*}$. We employ a gradient descent algorithm to solve the field map and $R_2^{*}$ map sub-problems. Using these updates, we update ρ₀ by solving the least squares problem in (15).

B. Simulation:

We demonstrate the proposed method in correcting the artifacts due to inhomogeneities on a numerical brain phantom [37]. For this purpose, we introduced intensity losses and geometric distortion artifacts on the brain phantom, shown in Fig. 3 (b), using the fieldmap and $R_2^{*}$ map shown in Fig. 3 (f) and 3 (j) respectively. For generating the artifacts, we created two sets of image series, such that the temporal profile at every pixel was a single exponential signal. We generated the Fourier data corresponding to the image series and combined them to form the kspace volume using equations (4) and (5) respectively. The readout of the Fourier data corresponding to the second image series was delayed by 4ΔT; ΔT := 0.636 ms. The kspace volume generated was very similar to the one shown in Fig.1 (b). One of the distorted (ifft) reconstructions is shown in Fig. 3 (a).

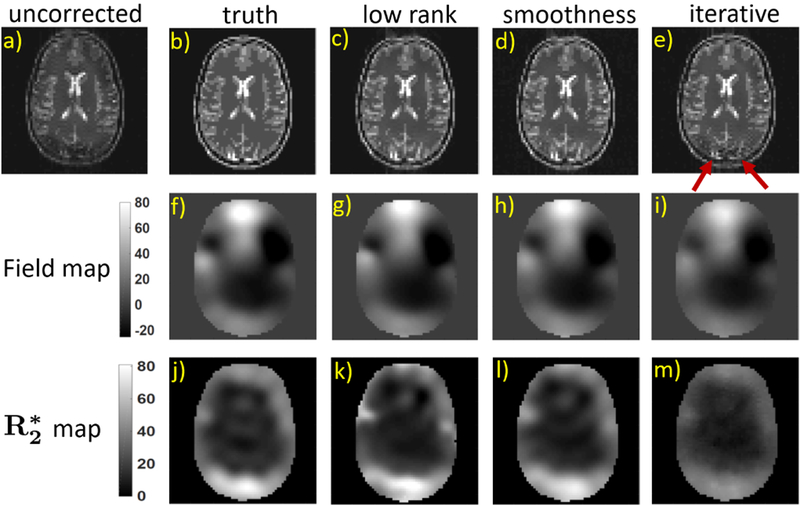
Fig. 3.

Comparison of the proposed smoothness and low rank approaches with the iterative reconstruction scheme on the correction of inhomogeneity artifacts on a numerical brain phantom: The simulated image with artifacts due to field inhomogeneity is shown in a) and the proposed reconstructions in (c) and (d) are compared with the reconstruction from the iterative method, which is shown in (e). We observe some artifacts in the iterative reconstruction, which are pointed by the red arrows. The estimated maps from the proposed and iterative approaches are compared with the true maps in the second and third row. The scales of both the field map and the $R_2^{*}$ maps are displayed in Hz and s⁻¹ respectively.

In Fig. 3, we compare the reconstructions and the maps from the proposed low rank and smoothness methods with the iterative approach [16]. We used a filter of dimensions 11 × 11 × 2 for the proposed methods. For the iterative approach, we set the number of overall iterations to 1500. To get reasonable results, we set the number of gradient descent (gd) iterations to 100 and 200 for the field map and $R_2^{*}$ sub-problems respectively. We observe that the geometric distortion artifacts have been reduced to a great extent in the reconstructions corresponding to both the proposed and iterative approaches. From the second and third rows of Fig. 3, we also observe that the the field maps from the proposed and the iterative methods closely match the ground truth field map. However the $R_2^{*}$ map from the iterative approach has a lot more errors than the ones obtained using the proposed approaches. This results in some artifacts as pointed by the red arrows in the image. We compare the computation times of different methods in table I. We observe that the run times of the proposed smoothness and low rank approaches are 0.22 s and 41.7 s respectively, while the iterative approach is extremely slow with a run time of 5645 s. Note that the increased run time of the low rank approach is due to the additional IRLS based optimization step (21) for denoising. The computation times of different methods were recorded on a high performance computing (hpc) server with twenty four core Xeon processor.

TABLE I.

Computation time of different methods.

Method	time (s)
Uncorrected (ifft)	0.0023
Smoothness	0.22
Low rank	41.7 40.9 (denoising) + 0.8
Iterative	5645

C. Phantom experiment:

The effect of the magnetic field inhomogeneities leading to image distortions can be clearly appreciated in the spherical phantom data in Fig. 4. For instance, the lines in the uncorrected image appear as curves. We compare a few reconstructed slices of the proposed methods to the uncorrected single-shot and four-shot data in A) in Fig. 4. These artifacts are greatly reduced in the reconstructions from the proposed methods and the image quality is quite close to that of the four shot reconstructions. In B), we compare the reconstructions and the field map of the proposed methods, corresponding to the slice in the green box, to those corresponding to a high spatial resolution structural scan. We observe that the performance of the proposed methods are similar and the reconstructions are closer to the reference than the single shot ifft reconstruction. For the proposed approaches, a small filter of dimension 5×5×2 was used to recover this slice.

Fig. 4.

Demonstrating the proposed methods on correcting the inhomogeneity artifacts on spherical MR phantom: In A), the reconstruced slices from the proposed approaches are displayed inside the blue box. A few reconstructed slices corresponding to the single and multi-shot ifft reconstructions are displayed in the first and fourth row respectively. The slices inside the green box in A) are compared to a high spatial resolution image in B). The proposed field maps in (vi) and (vii) are also compared to a reference map in (viii) and the scale is in Hz. We observe that the reconstructions from the proposed approaches are similar and are able to correct the inhomogeneity artifacts.

D. Invivo experiments:

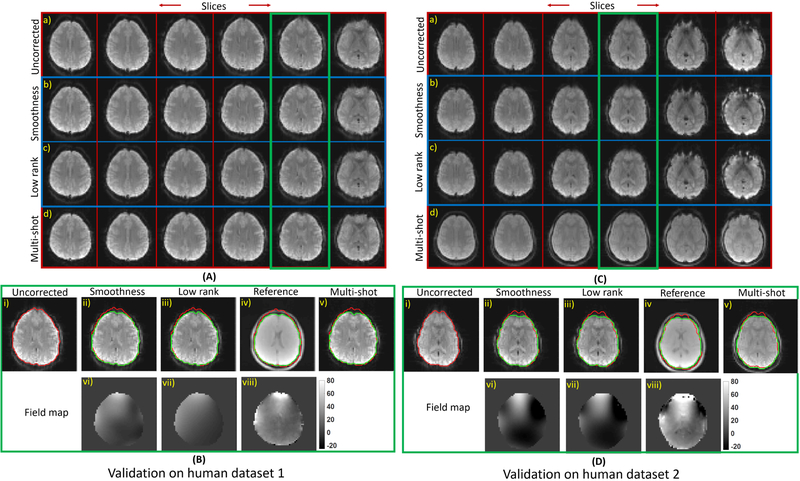
We also validate the proposed algorithms on two invivo datasets. For both the datasets, we compare a few reconstructed slices of the proposed approaches to the uncorrected single and four shot ifft reconstructions in A) and C) in Fig. 5 respectively. We observe that the severity of the artifacts are quite different for both datasets and the proposed algorithms are able to correct them effectively. Note that there are some differences between the proposed and the multi-shot reconstructions for invivo dataset 2 and this is due to the shorter echo time of the multi-shot data. In B) and D) of Fig. 5, the field map and the reconstructions from the proposed methods, corresponding to the slice in green box, are compared to those corresponding to a high spatial resolution reference scan. We observe that the proposed approaches perform similarly and provide improved reconstructions with minimal artifacts, when compared to the single-shot ifft reconstruction. In the case of low rank approach, we used a filter of size 7×7×2 to recover the slice corresponding to both the datasets, while the filter size used by the smoothness approach was 5×5×2 for invivo dataset 1 and 7×7×2 for invivo dataset 2.

Fig. 5.

Demonstrating the proposed methods on correcting the inhomogeneity artifacts on two invivo datasets: Corresponding to the invivo datasets 1 and 2, the reconstruced slices from the proposed approaches are displayed inside the blue box in A) and C). A few reconstructed slices corresponding to the single and multi-shot ifft reconstructions of both the datasets are displayed in the first and fourth row respectively in A) and C). The slices in the green box in A) and C) are displayed alongside high spatial resolution structural scans in B) and D) respectively. The field maps from proposed methods are compared to reference maps in the second row in B) and D). We observe that the proposed approaches perform similarly in correcting the inhomogeneity artifacts in both the invivo datasets. Specifically, the improvements in the reconstruction offered by the proposed approaches can be clearly appreciated using the red contour.

VI. DISCUSSION AND CONCLUSION

We introduced a two step structured low-rank algorithm for the calibration-free compensation of field inhomogeneity artifacts in Echo Planar Images (EPI). We introduced approximations which enabled a fast and efficient algorithm. The validations on spherical MR phantom and the invivo data demonstrated the potential of the proposed approaches. Specifically, the inhomogeneity artifacts and intensity losses were significantly reduced in the reconstructions from the proposed methods, compared to the uncorrected single-shot ifft reconstruction. The proposed reconstructions were very similar to a high resolution structural scan and a four shot EPI IFFT reconstruction, which were used as references in our experiments.

The validations on the MR phantom and invivo data also show that the single null space filter, and hence the exponential parameter, estimated from smoothness and low rank approaches are very similar, thus resulting in similar reconstructions. However, we observe that the smoothness based method is more robust to noise, compared to the low rank approach and does not require denoising of the measurements prior to the estimation of the null space. Specifically for the low rank approach, the denoising step was able to get rid of some pixelation artifacts in the inhomogeneity corrected image. The need for low-rank optimization (21) for denoising makes it more computationally expensive than the smoothness based approach. Specifically, the run times for the smoothness and low rank approaches were 0.22 s and 41.7 s respectively. The increased run time of the low rank approach was due to the denoising step which took 40.9 s.

Our numerical simulations on the brain phantom in Fig. 3 show that the proposed schemes can provide similar or improved reconstructions compared to the iterative approach [16]. The main benefit of the proposed schemes is the significantly reduced computation time, which makes it applicable to practical dynamic imaging problems. The comparisons with the iterative scheme were omitted for the MR phantom and invivo experiments due to its long computation time.

The proposed approach relies on two EPI acquisitions, where the read-out of the second acquisition is delayed by a few milliseconds. Such acquisitions can be acquired in an interleaved fashion. Thus, the proposed method can be applied in dynamic applications such as functional MRI, where it has the potential to compensate time varying field-map variations. We plan to investigate such applications in the future.