Machine learning predictive model for severe COVID-19

Abstract

To develop a modified predictive model for severe COVID-19 in people infected with Sars-Cov-2. We developed the predictive model for severe patients of COVID-19 based on the clinical date from the Tumor Center of Union Hospital affiliated with Tongji Medical College, China. A total of 151 cases from Jan. 26 to Mar. 20, 2020, were included. Then we followed 5 steps to predict and evaluate the model: data preprocessing, data splitting, feature selection, model building, prevention of overfitting, and Evaluation, and combined with artificial neural network algorithms. We processed the results in the 5 steps. In feature selection, ALB showed a strong negative correlation (r = 0.771, P < 0.001) whereas GLB (r = 0.661, P < 0.001) and BUN (r = 0.714, P < 0.001) showed a strong positive correlation with severity of COVID-19. TensorFlow was subsequently applied to develop a neural network model. The model achieved good prediction performance, with an area under the curve value of 0.953(0.889–0.982). Our results showed its outstanding performance in prediction. GLB and BUN may be two risk factors for severe COVID-19. Our findings could be of great benefit in the future treatment of patients with COVID-19 and will help to improve the quality of care in the long term. This model has great significance to rationalize early clinical interventions and improve the cure rate.

1. Introduction

In 2019, an outbreak of very contagious pneumonia began in Wuhan, China. The disease and the virus causing the disease were named coronavirus disease 2019 (COVID-19) and severe acute respiratory syndrome coronavirus two (SARS-COV-2), respectively. Mild COVID-19 has a self-limiting course with a low mortality rate, and patients with mild symptoms are reported to recover after one week. On the other hand, severe cases are reported to experience progressive respiratory failure due to alveolar damage from the virus, which may lead to death. Proinflammatory responses play a role in the pathogenesis of severe COVID-19. In vitro experiments have shown that delayed release of cytokines and chemokines occurs in respiratory epithelial cells, dendritic cells, and macrophages during the early stages of SARS-CoV2 infection. Later, the cells secrete low levels of antiviral factors, such as interferons, and high levels of proinflammatory cytokines, such as interleukin (IL)-1β, IL-6, and tumor necrosis factor, and chemokines, such as C-C motif chemokine ligand (CCL)-2, CCL-3, and CCL-5.(Law et al., 2005; Cheung et al., 2005; Lau et al., 2013) The rapid increase in cytokines and chemokines attracts inflammatory cells, such as neutrophils and monocytes, resulting in excessive infiltration of inflammatory cells into the lung tissue, leading to lung injury. Serum cytokine and chemokine levels are significantly higher in patients with severe COVID-19 compared with those with mild and moderate COVID-19.(Yang et al., 2020) Elevated serum cytokine and chemokine levels in COVID-19 patients are associated with a high number of neutrophils and monocytes in the lung tissues and peripheral blood, suggesting that these cells may play a role in lung pathology.(Yang et al., 2020) Onset COVID-19 is usually concealed and it is difficult to predict severe COVID-19, despite knowing its causes. While studies have reported ways of predicting COVID-19, these have mostly explored the linear relationship between each feature and COVID-19 severity to identify independent risk factors. However, some of the factors related to the severity of COVID-19 are nonlinear. Classical linear prediction methods do not take nonlinear phenomena into account. Therefore, a heuristic methodology for the epidemic forecast could help to resolve this problem, and we set sights on the artificial neural network (ANN). An artificial neural network can integrate the linear and nonlinear relationships of each feature to obtain prediction results, adding to the credibility of the forecast results. Since years, Artificial neural network has been widely applied in medical studies. Because the hidden neurons are unnecessary for linearity, the input and output are not required to be linearly related either. This approach could make the prediction more flexible.(Borzouei et al., 2020) If the selected input variables are sufficient and representative, and there is neither a closed correlation between them, the network could reveal their complex relationship and show the advantages in extrapolation. This view has been supported by Schonenberger, et al. (Schonenberger et al., 2020) Furthermore, this methodology has been applied to the prediction of the SARS epidemic by Bai and Jin (2005) (Yanping Bai, 2005). A highlighted characteristic of the neural network is training, this study has proved its strong associative and rational ability under large and non-linear conditions in the theoretical and practical aspects. Due to 4 ways of controlling the capacity, the network can prevent overfitting, which is one of the typical problems that the linear regression model has faced.(Konaté, 2019) In conclusion, this method is opted for in this study.

Our study aimed to introduce a neural network predictive model to predict the severity of COVID-19 using the results from routine examinations. A neural network is a simplified model of how the human brain processes information. There are typically three parts in a neural network: an input layer, with units representing the input fields; one or more hidden layers; and an output layer, with a unit or units representing the target field(s). The units are connected with varying connection strengths (or weights). Input data are presented to the first layer, and values are propagated from each neuron to each neuron in the next layer. Eventually, a result is delivered from the output layer. Finally, we built the predictive model and the model achieved good prediction performance, with area under the curve (AUC) values of 0.953 (0.889–0.982).

2. Materials and methods

2.1. Patient and public involvement

Data were collected from the Tumor Center of Union Hospital affiliated with Tongji Medical College of Huazhong University of Science and Technology, Hubei, China. All participants gave verbal consent to take part in the study.

2.2. Data collected

Data from consecutive patients with COVID-19 were collected between January 26, 2020, and March 20, 2020. Data were obtained at admission (Table 1 ). Inclusion criteria were patients with a confirmed diagnosis of SARS-COV-2 infection (according to Diagnosis and Treatment Protocol for Novel Coronavirus Pneumonia Version 7(Chin. Med. J., 2020)). Exclusion criteria were patients with existing severe or critical COVID-19 at the time of admission. A detailed description of the criteria is described in Table 2 .

Table 1.

Data collected.

Data type	Parameter
Quantitative	Age, RBCs, Hb, WBCs, TP, ALB, GLB, CREA, BUN, mycoplasma IgM, mycoplasma IgG, chlamydial IgM
Categorical	Patient condition (mild cases, moderate cases, severe cases, and critical cases), sex, diabetes, diabetes with complications, acquired immune deficiency syndrome, cancer, history of lung disease, solitary patchy foci, multiple patchy foci, solitary ground-glass opacity, multiple ground-glass opacity, diffuse interstitial change, solitary interstitial change, solitary pulmonary consolidation, multiple pulmonary consolidations, solitary infiltrate, multiple infiltrates, chronic kidney diseases (>3 months)
Ordinal	Hypertension classification†, cardiac functional grading (according to New York Heart Association functional classification)

ALB, albumin; BUN, blood urea nitrogen; GLB, globulin; CREA, creatinine; Hb, hemoglobin; IgG, immunoglobulin G; IgM, immunoglobulin M; RBCs, red blood cells; TP, total protein; WBCs, white blood cells.

^†Measured according to the 2017 edition of American College of Cardiology/American Heart Association guidelines for hypertension.

Table 2.

Criteria for assessing COVID-19 severity.

Severity	Criteria
Mild	Minimal symptoms without pulmonary involvement in chest imaging studies
Moderate	Fever and/or respiratory symptoms; multiple limited patchy shadows and interstitial changes in chest imaging
Severe	Dyspnea with a respiratory rate > 30 breaths per minute; resting oxygen saturation < 95% or arterial blood oxygen partial pressure/oxygen concentration ≤ 300 mmHg (1 mmHg = 0.133 kPa); multilobular disease or lesion progression >50% within 48 h; SOFA ≥2 points; pneumothorax and/or other
Critically ill	Respiratory failure requiring mechanical ventilation; septic shock; additional organ failure

SOFA, sequential organ failure assessment.

2.3. Software used

① Scikit-learn: Scikit-learn is a software machine learning library for the Python programming language. It has a powerful data preprocessing function (https://scikit-learn.org/stable/).

② TensorFlow: TensorFlow is a framework for data stream-oriented programming, which is widely used in machine learning (https://github.com/tensorflow/tensorflow).

③ Scipy.stats: Scipy.stats contains a large number of probability distributions as well as a growing library of statistical functions. (https://docs.scipy.org/doc/scipy/reference/stats.html).

2.4. Study design

The study consisted of the following phases:

2.4.1. Data preprocessing

Cases with missing and invalid values were deleted. Next, data were normalized using the median normalization, and the qualitative variable was coded as dummy variables to eliminate their effect on the model (using scikit-learn package in Python software).

2.4.2. Data splitting

The data set was randomly split into three parts:training set，verification set，and test set. For the training set and verification set, the split ratio was 9:1 (ten-fold cross-validation).

2.4.3. Feature selection

Pearson correlation coefficient was used to analyze correlations of quantitative data, and Kendall correlation coefficients were used to analyze the correlations of qualitative data. Statistically significant (P < 0.05) features were extracted as the input for the neural network model (using the Scipy.stats package in Python software).

2.4.4. Model building

The training set was used for training and tuning the parameters, the validation set was for preventing the overfitting problem, and the test set was used to evaluate the performance (using the TensorFlow package in Python software). Four parameters need to be set in modeling: learning rate, epochs, the number of nodes, and the number of layers in the hidden layer. We describe the approaches of adjustment parameters in detail below.

2.4.4.1. Learning rate

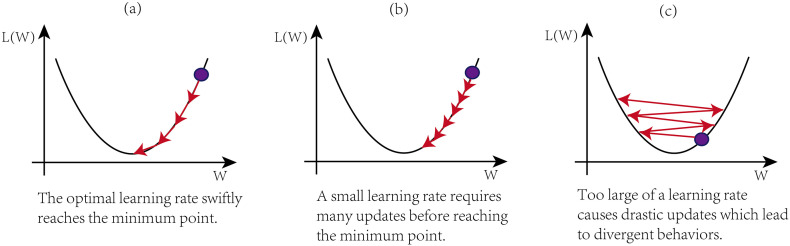
The learning rate is a hyperparameter that deter-mines how much the model should change concerning the error each time the model parameters are updated. It is important to tune the learning rate properly because a too small learning rate, as shown in Fig. 1(a), may result in a very long and very slow training process that may get stuck, whereas a too-large learning rate value, as shown in Fig. 1(c), may result in diverging away from the optimal point rather than converging towards it.

Fig. 1.

The impact of learning rate on the model performance.

However, there is currently no algorithm to obtain the optimal value of the learning rate. The learning rate can be determined through experiments.(Konar et al., 2020) Experiments have shown that starting the learning rate from 0.1 gives a relatively good performance, we used the same method in this study. If setting the learning rate to 0.1 does not give good accuracy then we choose another constant number based on experiments again, options are 0.01, 0.001, 0.0001, 0.00001.

2.4.4.2. Epochs

For the number of epochs, the residual error decreases with an increase in the number of epochs and finally tended to be stable, but it needs a much longer training time. To find the optimal quantity of epochs, we recorded the residual error (cross-entropy) of each epoch. When the residual error tends to stabilize, the optimal quantity of epochs was determined.

2.4.4.3. The number of nodes and layers in the hidden layer

Kolmogorov's theorem stating that any continuous function defined on an n-dimensional cube can be represented by sums and superpositions of continuous functions of one variable. Hecht-Nielsen imported this theorem later in neurocomputing by proving that any continuous function can be represented by a neural network that has only one hidden layer with exactly 2n + 1 nodes, where n is the number of input nodes.(Nielsen, 1987) But Hecht-Nielsen stated that the 2n + 1 rule is not for all classes of activation functions. Therefore, Kurkova suggested that two hidden layers should be used to compensate for lost efficiency when using regular activation functions.(Kurkova, 1992) So we used two hidden layers (each layer consists of 2n + 1 nodes) in this study.

2.4.5. Prevention of overfitting

The 10-fold internal cross-validation was used to prevent overfitting of the data. In the 10-fold cross-validation, the original sample was randomly partitioned into 10 equal-sized subsamples. Of the 10 subsamples, a single subsample was retained as the validation data for testing the model, and the remaining nine subsamples were used as training data. The cross-validation process was then repeated 10 times, using each of the 10 subsamples once as the validation data. An average of the 10 results was then taken to produce a single estimation.(Victor et al., 2012) The 10-fold cross-validation tested the model's ability to predict new data that was not used in the estimation of flag problems, such as overfitting. This method was effective in preventing overfitting.

2.4.6. Evaluation indexes of the model

The performance of the model was evaluated using receiver operating characteristics (ROC) curve analysis(Feinstein, 2001) and AUC.

3. Results

3.1. Data preprocessing

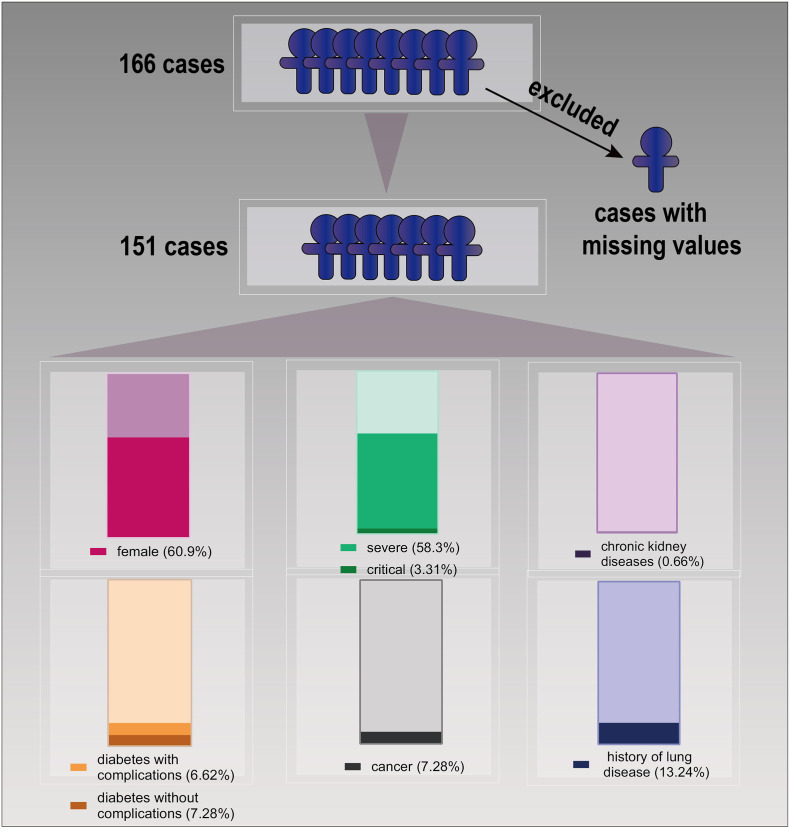
A total of 166 cases were included in the study, although 15 cases were excluded due to missing data. The remaining 151 COVID-19 patients comprised 59 males and 92 females with a mean age of 62.4 ± 16.12 (range 18–96) years. There were 58 mild and moderate cases, 88 severe cases, five critical cases (age 84, 84, 69, 65, and 34 years), one case of chronic kidney disease, 21 cases of diabetes (10 with complications), none were human immunodeficiency virus-infected, 11 patients had a history of cancer, and 20 had a history of lung disease (Fig. 2 ).

Fig. 2.

Data preprocessing.

3.2. Feature selection

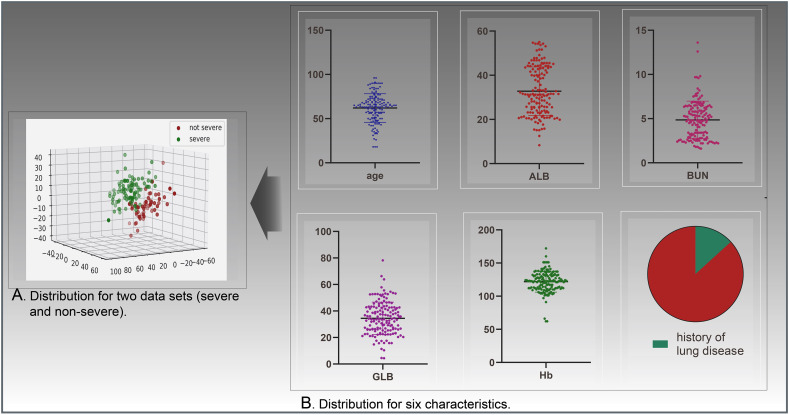
The feature set of the present study consisted of 33 features. After feature selection, six eligible features were used for modeling: a history of lung disease, age, hemoglobin (Hb), albumin (ALB), globulin (GLB), and blood urea nitrogen (BUN) (Table 3 ). The data distribution of these features is illustrated in Fig. 3 . For the correlation analysis, a correlation coefficient P ≥ 0.8 was considered a very strong correlation, P = 0.60–0.79 was strong, P = 0.4–0.59 was moderate, P = 0.20–0.39 a weak correlation, and P ≤ 0.19 was negligible. In the present study, ALB showed a strong negative correlation (r = 0.771, P < 0.001) whereas GLB (r = 0.661, P < 0.001) and BUN (r = 0.714, P < 0.001) showed a strong positive correlation with severity of COVID-19. Furthermore, age showed a weak positive correlation (r = 0.266, P < 0.001), Hb showed a weak negative correlation (r = −0.231, P = 0.021), and history of lung disease shows a negligible positive correlation (r = 0.137, P = 0.011) with severity of COVID-19.

Table 3.

Correlation analysis.

	Features	Correlation coefficient	P-value	Significance level
Kendall correlation coefficient	Sex	−0.031	0.754
	Hypertension classification	−0.011	0.722
	Chronic kidney diseases	0.123	0.200
	Cardiac functional grading	0.107	0.052
	Diabetes	−0.124	0.875
	AIDS	–	–
	Cancer	0.091	0.072
	History of lung disease	0.137	0.011	<0.05
	Solitary patchy foci	−0.058	0.141
	Multiple patchy foci	−0.032	0.717
	Solitary ground-glass opacity	0.076	0.954
	Multiple ground-glass opacity	0.033	0.231
	Solitary interstitial change	0.064	0.132
	Diffuse interstitial change	0.026	0.223
	Solitary pulmonary consolidation	−0.040	0.852
	Multiple pulmonary consolidations	0.160	0.162
	Solitary infiltrate	−0.136	0.149
	Multiple infiltrates	−0.136	0.472
Pearson correlation coefficient	Age	0.266	0.007	<0.05
	WBC	0.145	0.153
	RBC	−0.111	0.272
	Hb	−0.231	0.021	<0.05
	TP	−0.075	0.459
	ALB	−0.771	0.000	<0.05
	GLB	0.661	0.000	<0.05
	CREA	0.069	0.497
	BUN	0.714	0.000	<0.05
	Mycoplasma immunoglobulin M	−0.069	0.496
	Mycoplasma immunoglobulin G	−0.138	0.171
	Chlamydial immunoglobulin M	−0.107	0.291
	Chlamydial immunoglobulin G	−0.137	0.177

AIDS, acquired immunodeficiency syndrome’ ALB, albumin; BUN, blood urea nitrogen; GLB, globulin; CREA, creatinine; Hb, hemoglobin; RBCs, red blood cells; TP, total protein; WBCs, white blood cells.

Fig. 3.

Data distribution.

3.3. Model building

The total data were divided into a training set (99 cases) and a verification set (11 cases) and a test set (41 cases).

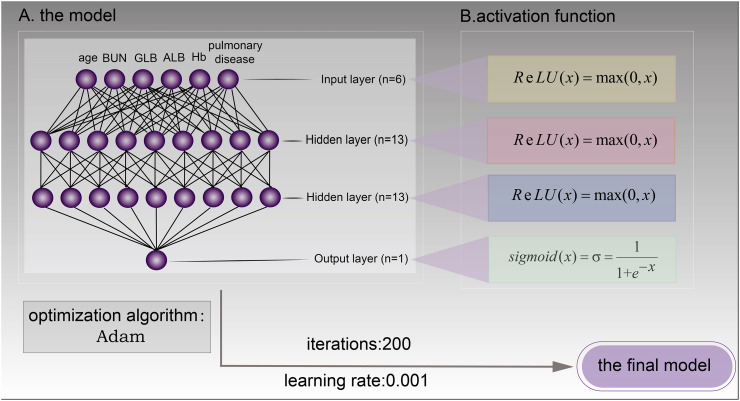
① The number of nodes in the hidden layer: According to the results of data pre-processing, the number of nodes in the input layer is six. So the number of nodes in the hidden layer is thirteen.

② Learning rate: In this study, the optimal value of the learning rate is 0.001 through experiments.

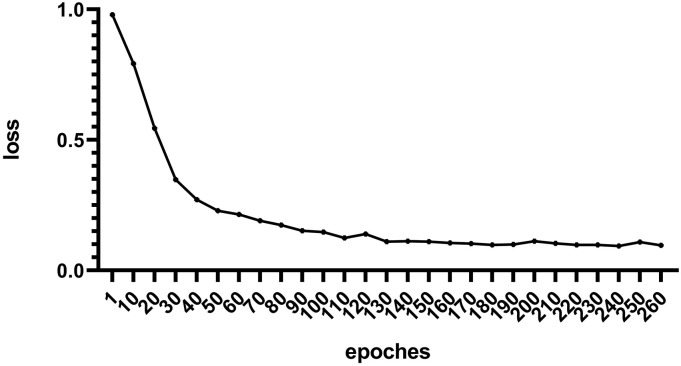
③ Epochs: The residual error tends to stabilize in 200, as shown in (Fig. 4 ). So the number of epochs was set to 200.

Fig. 4.

Changes in residual error.

After adjusting for parameters, the final predictive model made up an input layer (six units), two hidden layers (13 units), and an output layer (one unit: severe COVID-19 or non-severe COVID-19). Hidden layer nodes use the ReLU (rectified linear unit) activation function (Eq. a), the output node uses the Sigmoid activation function (Eq. b), and the cost function was minimized using the adaptive moment estimation method (Fig. 5 ).

$$R\mathrm{e}\mathit{LU}\left(x\right)=max\left(0,x\right)$$ (1)

$$\mathit{sigmoid}\left(x\right)=\mathrm{\sigma }=\frac{1}{1+e^{-x}}$$ (2)

ADAM, adaptive moment; ReLU, rectified linear unit.

Fig. 5.

The final model.

3.4. Evaluation of the model

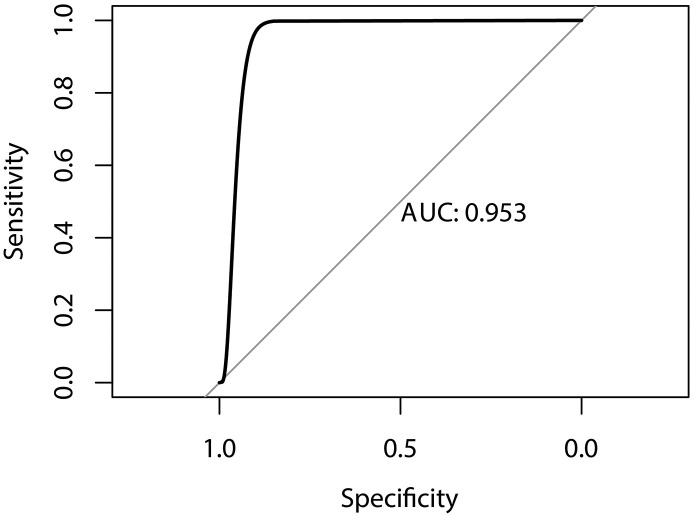
In verification set，the results of 10-fold cross-validation: 0.999, 0.998, 0.997, 0.894, 0.916, 0.960, 0,986, 0.999, 0.940, 0.999. Mean value was 0.969. In test set, the F1-Score reaches 96.4%, the AUC of the model was 0.953(0.889–0.982)(Fig. 6 ), the Specificity and sensitivity values of this model were selected at 85.7% and 100%, respectively. Results showed a good prediction of the model.

Fig. 6.

ROC curve of our model.

4. Discussion

The present study included a total of 151 cases. At the data preprocessing stage, 33 features among all cases were subjected to relatedness analyses, and six features were extracted for modeling (P < 0.05). Our results show that the AUC of the model was 0.953 (0.889–0.982), and the model had a perfect fit and accuracy. Our study aimed to predict the severity of COVID-19 using the results from routine examinations. Routine laboratory variables are extremely meaningful as they are readily accessible at the initial diagnosis, which helps early prediction.

Correlation analysis revealed that age showed a weak positive correlation (r = 0.266, P < 0.001), ALB showed a strong negative correlation (r = −0.771, P < 0.001), and GLB (r = 0.661, P < 0.001) and BUN (r = 0.714, P < 0.001) showed a strong positive correlation with severity of COVID-19, whereas Hb showed a weak negative correlation (r = −0.231, P = 0.021) and history of lung disease showed a negligible positive correlation (r = 0.137, P = 0.011).

Previous studies have reported that age is a risk factor for severe COVID-19.(Cheung et al., 2005; Ramtohul et al., 2020; Nawar et al., 2020) Fei Zhou et al. analyzed 191 patients with severe COVID-19 requiring hospitalization. In this cohort, patients had a median age of 56.0 years.(Zhou et al., 2020) ALB is an acidic, hydrophilic, and highly stable globular protein that is synthesized specifically in the liver. Our study showed that decreased ALB levels were a risk factor. Several studies have shown a negative correlation between ALB and the severity of COVID-19,(Lau et al., 2013) which parallels the findings of the present study. A meta-analysis of 90 cohort studies that evaluated hypoalbuminemia as a prognostic biomarker in acutely ill patients showed that each 10-g/L decrease in serum albumin concentration was associated with a 137% increase in odds of death, 89% increase in morbidity, and 71% increase in the length of hospital stay. Thus, there is a clear association between albumin level and severity of the insult Based on the existing literature, we speculated three reasons for this phenomenon. First, low albumin levels can influence pharmacokinetics. Albumin transports multiple endogenous and exogenous substances; therefore, changes in albumin concentration during critical illness can have potentially marked effects on drug delivery and efficacy in a systematic review, Ulldemolins et al. reported that protein binding of antibacterials was frequently decreased in critically ill patients with hypoalbuminemia, notably with increased volume of distribution and drug clearance. These changes could result in suboptimal treatment. Second, low albumin levels can change the acid-base balance in the human body. The balance of acidic to basic residues on albumin makes it a weak acid in physiological concentrations, and a decrease in albumin concentration increases the anion gap. This massively increases bicarbonate concentration. Third, low albumin levels could affect endothelial cell function since albumin is a crucial part of the endothelial surface layer. However, experiments in isolated organs have shown that the endothelial surface layer appears to function well until the albumin concentration falls to values as low as 10 g/L. Hence, the major insult when the vascular barrier fails to function due to severe acute illness is likely not the low albumin level, but the breakdown of the molecular structure of the endothelial glycocalyx due to hypervolemia or ischemia/reperfusion injury and other forms of systemic inflammation.(Chappell et al., 2009) However, these are only speculations, and definitive conclusions cannot be drawn. Therefore, it remains unclear whether the effect of hypoalbuminemia on the outcome is a cause and effect relationship or whether hypoalbuminemia is a marker of serious disease.

ALB (r = −0.771) and GLB (r = 0.661) showed similar relevant intensity in our study, and an increase in GLB may be a risk factor for COVID-19 severity. GLB and ALB are commonly used as markers for assessing patient hepatic function, and low levels of ALB and high levels of GLB could indicate impaired liver function.(Jawahar et al., 2020) Thus, the deterioration of COVID-19 patients maybe is correlated with damage to liver function. Furthermore, it is also important to consider the impact of BUN on the severity of COVID-19. Elevated BUN is a key indicator of kidney malfunction. This seems to indicate that renal impairment may result in the deterioration of COVID-19. This speculation is consistent with our statements concerning ALB. The antioxidant and anti-inflammatory effects of ALB properties can mediate renoprotective effects.(Iglesias et al., 1999) However, it is worth noting that the present study only included one case with chronic kidney disease. This means that BUN had likely already resulted in a harmful impact on patients with COVID-19 before BUN reached the level of renal damage. Studies have indicated basic disease as a risk factor for COVID-19 exacerbation.(Dantzer et al., 2020; Montoya-Barthelemy et al., 2020; Nowak-Wegrzyn et al., 2020; Hwee et al., 2020; Schultz and Wolf, 2020) On the other hand, our results showed that the correlation between basic diseases and the severity of COVID-19 was not significant. May be due to a low number of cases with the basic disease in our cohort.

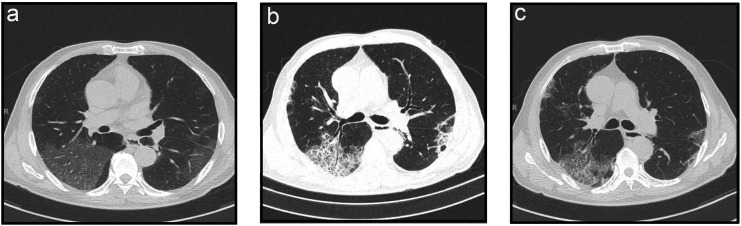
An independent analysis of various imaging manifestations of COVID-19 was performed in the present study. Our results showed a very weak (r < 0.2) correlation between imaging manifestations and severe COVID-19. This may be because predicting severe COVID-19 needs to observe dynamic changes of imaging manifestations (Fig. 7 ) rather than a single imaging manifestation.(Guan et al., 2020; Lee et al., 2020)

Fig. 7.

Imaging manifestations of severe COVID-19 (a) before treatment, (b) during treatment, and (c) after treatment.

Artificial neural network technology, which is widely implemented in various fields of science, was used in the establishment of our model.(Jaganathan et al., 2019; Pan et al., 2019; Stokes et al., 2020; Zeiser et al., 2020) This model has good accuracy as long as there is a suitable parameter adjustment. Thus, the neural network model is extremely useful for complex diseases. This test result has shown its outstanding performance in prediction, with an area under the curve value of 0.953 (0.889–0.982). It could be utilized to monitor the training and predicting process. This has further significance for the rationalization of clinical interventions. And the scientific findings in this study could be of great benefit in the future treatment of patients with COVID-19 and will help to improve the quality of care in the long term.

Whereas our model showed good results in the test set, there are several other limitations to our study. First, although we examined our model in an internal population, we did not validate it in an external population, and its generalizability needs to be confirmed. Second, the data of our study was not comprehensive enough. Yong Gao et al. reported that IL-6 and D-dimer were closely connected with the occurrence of severe COVID-19 in adult patients.(Gao et al., 2020) Hongyi Zhang et al. reported that patients with severe COVID-19 had a significant reduction in granulocytes compared with patients with mild COVID-19.(Zheng et al., 2020) We did not collect information on these factors. Third, the verification of our model using prospective testing with a larger sample size is warranted. Our sample size was relatively small and we are currently collecting recent data from a larger sample size to validate further and improve the current models. Fourth, the operational process of the artificial neural network model is complicated, as the neural activity of the human brain. Therefore, there is currently no quantitative indicator that can express the relevance between predictors and forecast results in the artificial neural network model. This is a limitation of this study, as well as difficulties with machine learning.(Gao et al., 2020; Zheng et al., 2020)

CRediT authorship contribution statement

Jianhong Kang: Conceptualization, Writing- Original draft preparation, revision, Methodology. Ting Chen: Software, Writing- Original draft preparation, Visualization. Honghe Luo: revise, Proofreading, Supervision. Yifeng-Luo: revise, Proofreading, Professional technical support. Guipeng-Du: Collecting data.

Declaration of Competing Interest

The authors declared that they have no conflicts of interest in this work.