Mechanics of Bacterial Interaction and Death on Nanopatterned Surfaces

Abstract

Nanopatterned surfaces are believed to kill bacteria through physical deformation, a mechanism that has immense potential against biochemical resistance. Because of its elusive nature, this mechanism is mostly understood through biophysical modeling. Problematically, accurate descriptions of the contact mechanics and various boundary conditions involved in the bacteria-nanopattern interaction remain to be seen. This may underpin conflicting predictions, found throughout the literature, regarding two important aspects of the mechanism—that is, its critical action site and relationship with geometry. Herein, a robust computational analysis of bacteria-nanopattern interaction is performed using a three-dimensional finite element modeling that incorporates relevant continuum mechanical properties, multilayered envelope structure, and adhesion interaction conditions. The model is applied to more accurately study the elusory mechanism and its enhancement via nanopattern geometry. Additionally, micrographs of bacteria adhered on a nanopatterned cicada wing are examined to further inform and verify the major modeling predictions. Together, the results indicate that nanopatterned surfaces do not kill bacteria predominantly by rupture in between protruding pillars as previously thought. Instead, nondevelopable deformation about pillar tips is more likely to create a critical site at the pillar apex, which delivers significant in-plane strains and may locally rupture and penetrate the cell. The computational analysis also demonstrates that envelope deformation is increased by adhesion to nanopatterns with smaller pillar radii and spacing. These results further progress understanding of the mechanism of nanopatterned surfaces and help guide their design for enhanced bactericidal efficiency.

Significance

Nanopatterned surfaces show immense potential; however, their mechanism has not yet been well resolved. This work challenges the prevailing dogma that bacteria are killed in the region between pillars, which has been the dominant view on the mechanism since the discovery of antibacterial nanopatterned surfaces over half a decade ago. Instead, it is clearly demonstrated that critical envelope strains consistent with rupture readily occur at the pillar tips, which locally perturb and may penetrate the cell. In addition, recommendations are given on how to increase envelope strain and concomitant killing efficiency through geometric design, which remains poorly understood and is needed to optimize nanopatterned surfaces.

Introduction

Bacteria have a well-demonstrated proficiency for outsmarting biochemical attacks. This is most apparent in the case of antibiotics, which have seen dwindling effectiveness due to a myriad of individual-level and biofilm-specific mechanisms such as production of hydrolyzing enzymes, overexpression of efflux, and formation of persister phenotypes (1). Similarly, evidence has emerged of alcohol-based disinfectants becoming increasingly ineffective against certain human pathogens with longstanding clinical presence (2). These trends have spurred interest in nonbiochemical killing actions that can circumvent the existing resistance mechanism and may be more robust to evolved resistance (3).

Nanopatterned surfaces seem to elicit such a killing action. This killing action, discovered on cicada wings (4), is believed to be predominantly physical, as evidenced by its ability to span vast biological and chemical diversities. For instance, nanopatterned surfaces can inactivate a range of biologically diverse cells, including bacteria of both Gram types (5), superbugs (6), viruses (7), and, problematically, human cells (8). Also, the mechanism can be incorporated into a variety of chemically diverse, natural and synthetic materials such as insect cuticle (4,9), polymer (10,11), titanium (12,13), stainless steel (14) aluminum (6,7), and silicon wafer (15,16). Common to all these observations is the inclusion of a nonplanar topography composed of nondevelopable nanoscale surface features. Accordingly, nanopatterned surfaces are believed to kill bacteria by adhesion to these protruding features that physically deform the cell envelope via contact, possibly to the point of rupture (4). Consistent with this mechanism, indications of envelope damage can be seen in postmortem micrographs of nanopattern-treated bacteria, which often show turgor loss (deflation) and cytoplasm leakage (9,10,17). Also, as expected for such a mechanism, killing efficiency has been found to be mediated by physical or mechanical parameters such as envelope stiffness (18,19), envelope extensibility (20,21), pattern geometry (10,22), and adhesion strength (23,24), adding further support.

Given that directly characterizing the deformation is not possible because of the size and dynamic nature of the interaction, present understanding of the mechanism is informed by biophysical modeling. Modeling is also best suited to elucidate nanopattern geometry for enhanced killing efficiency, which remains elusive to experimental investigation because of the difficulties of selective and systematic variation of diameter, spacing, and height (10,22,25,26). That being said, accurate biophysical analysis remains to be seen. Previous attempts to model the deformation have been marred by use of misrepresentative loads (26,27), a priori shape assumptions (25), monolayer envelope models (18), and plane strain simplifications of a nondevelopable, three-dimensional problem (28). Although these points of difference may initially seem trivial, they have a direct bearing on the deformation mechanics and therefore underpin predictions about the critical action site and geometry enhancement of the physical mechanism. This is quite evident, for example, with the popular “biophysical model” by Pogodin and others (18), whose predictions of envelope rupture between pillars seem to conflict with commonly seen pillar penetration (11,28, 29, 30, 31). This incompatibility reflects the challenge of mathematically analyzing the bacteria-nanopattern problem, which requires careful consideration of contact mechanics and boundary conditions.

To address this, this work analyses the mechanics of adhesion-driven envelope deformation by computational methods, namely three-dimensional finite element analysis using Abaqus/Standard (Dassault Systèmes Simulia, Johnston, RI). Going beyond previous efforts, realistic properties and multilayered structure are incorporated into a continuum model of a Gram-negative envelope that is brought into contact with a nanopattern using loads and boundary conditions that mimic adhesion. The model is used to study the magnitude and location of critical strains induced in the envelope as a result of adhering to a cicada-like nanopattern. This is supported by analysis of micrographs of dead bacteria on a nanopatterned cicada wing surface. The computational analysis is also extended to study different pattern geometries by selectively varying pillar radius, spacing, and height, thus informing upon the enhanced design of nanopatterned surfaces.

Materials and Methods

Finite element method

Geometry

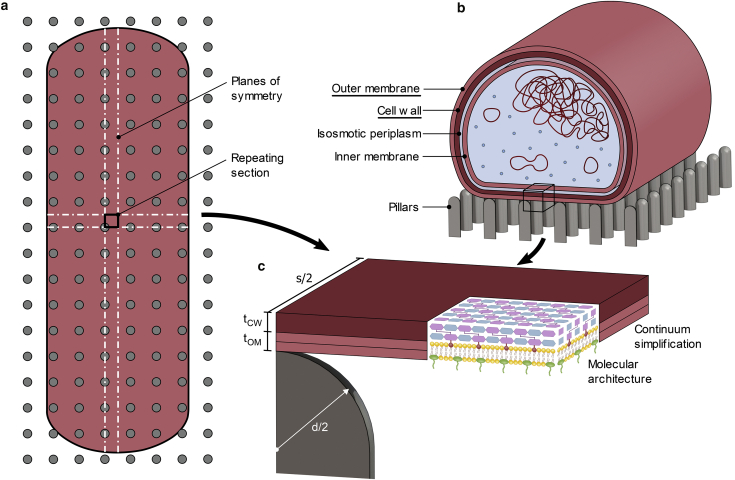
The model considered a Gram-negative bacterium interacting with a square array of spherically capped, cylindrical pillars. Several observations were used to reduce the problem, which was otherwise quite convoluted because of the number of pillars and cellular components appearing on the global scale (Fig. 1). Firstly, the curvature and global shape change of the cell were ignored as previously because of the pillars being over a magnitude smaller than the bacteria (18,32). Because the curvature was negligible, the interaction at each pillar appeared as a repeating event, both in terms of loading and geometry. Hence, it was only necessary to model one representative section with symmetry constraints at the boundaries (Fig. 1, a and c). Additionally, only cellular components that appeared at, or were directly coupled to, the outermost surface of the bacteria were included in the model. This is due to the nature of the intermolecular forces believed to drive the nanopattern interaction that are finite ranged and thus only engage components in proximity to the contact interface. For a Gram-negative bacterium, this includes the outer membrane and cell wall, which are covalently linked by very abundant lipoproteins that facilitate stress transfer (33, 34, 35). The next closest component—the inner membrane—is separated by an isosmotic fluid periplasm, making it distant from the other layers and non-load-bearing (36). Accordingly, the bacterium was reduced to only an outer membrane and a cell wall (Fig. 1, b and c).

Figure 1.

Reducing the bacteria-nanopattern problem. (a) Shown is an accurately scaled top view of a typically sized (1 × 3 μm), rod-shaped bacterium on a nanopattern (d = 60 nm, s = 180 nm). (b) Shown is the central cross section of a Gram-negative bacterium. Load-bearing components are underlined. (c) Shown is the representative section used to model the bacteria-nanopattern problem with continuum smearing of the molecular architecture. To see this figure in color, go online.

To model the interaction of these components with a nanopillar, a continuum approach was utilized (Fig. 1 c). Though the outer membrane and cell wall have been well resolved, the size of the model (10³–10⁴ nm²) and timescale of adhesion (10–100 s) are considered too big for atomistic study (4,37). Moreover, this problem involves interactions and contact conditions between structures and components that are challenging to enforce atomistically (38,39). Therefore, the cell wall and outer membrane were represented as three-dimensional continuum layers. These layers were defined by a thickness (t_CW and t_OM, respectively) and a lateral dimension (s/2) that was controlled—through symmetry boundary conditions—by the center-to-center spacing between pillars (s). Pillars were defined by a diameter (d) or radius (r) and height (h). Initial diameter, spacing, and height were set at 60, 180, and 200 nm, respectively, to mimic the nanopattern found on the wings of the Psaltoda claripennis cicada. Subsequently, dimensions were parametrically varied. Pillar diameter was adjusted between 20 and 180 nm, with the lower bound approaching the maximal resolution of current nanofabrication techniques (30,40). Dimensionless center-to-center spacing (s/d) and height were varied between 2–4 and 100–300 nm, respectively.

Material models

By implementing a continuum approach, commonly reported continuum properties such as area compressibility (K_A) and Young’s modulus (E) could be invoked to accurately describe the mechanical behavior of the cell wall and outer membrane. Characteristic of biological materials, moduli of these cellular components have large scattering. To account for this, three different envelope configurations were evaluated, covering the softest to the stiffest reported values (Table 1).

Table 1.

Constitutive Models for Gram-Negative Envelope

Part	Material Model	Parameter	Selection			Estimate	Reference
			Soft	Intermediate	Stiff
Outer membrane	isotropic neo-Hookean	C10	1.61 MPa	4.83 MPa	8.05 MPa	KA = 50–250 mN/m	(33,41, 42, 43)
		D1	0.018 MPa−1	0.006 MPa−1	0.004 MPa−1	vOM = 0.485	(44)
		tOM	4 nm (2 nm per leaflet)			3–5 nm	(43,45)
Cell wall	orthotropic elastic	E1 (=EG)	25 MPa	50 MPa	75 MPa	25–75 MPa	(46, 47, 48)
		E2, E3 (=EP)	10 MPa	20 MPa	30 MPa	10–30 MPa	(48, 49, 50)
		v12, v13,v23, v32 (=vGP)	0.35			0.32–0.67	(47,51)
		v21, v31 (=vPG)	0.14			0.01–0.23	(47,51)
		G12, G13 (=GGP)	5.3 MPa	10.5 MPa	15.8 MPa	3.55–17.95 MPa	(Supporting Materials and Methods, Section A)
		G23 (=GP)	3.7 MPa	7.4 MPa	11.1 MPa	3.7–11.1 MPa
		tCW	4 nm			2–6 nm	(46,50,52)

An isotopic neo-Hookean material was used to model the constitutive response of the outer membrane, which stems from hydrophobic and van der Waal’s forces opposing the separation of lipids. This hyperelastic model is frequently applied to cell membranes (53,54) and is particularly relevant for bacterial membranes, which are known to be strain softening (33,55). The material model was informed by previous micropipette aspiration and molecular dynamics studies on bacterial membranes and mimetic lipid systems (33,41, 42, 43, 44, 45). Reported estimates of area compressibility (K_A), Poisson’s ratio (v), and thickness (t_OM) from a range of these studies are shown in Table 1. These values were used to calculate relevant neo-Hookean parameters (C₁₀, D₁) (Supporting Materials and Methods, Section A). Evidently, the outer membrane has significant mechanical stiffness, rivaling that of the cell wall; hence, both will participate roughly equally in load bearing (34,56).

The cell wall was modeled as a linear orthotropic material. Though peptidoglycan is thought to be a strain-stiffening biopolymer, an approximately linear response has been observed in many cases, even to rupture (46,50,57). Hence, linearity is a good first approximation. Orthotropy was included to account for the directional differences in the stiffness of peptidoglycan, which are at least a factor of 2 (58). This effect stems from the ordered molecular architecture of peptidoglycan, in which rigid glycan strands (_G) and flexible peptides stems (_P) are covalently cross-linked in a roughly orthogonal fashion (47,52,59). A range for the in-plane Young’s moduli (E₁ = E_G and E₂ = E_P) and Poisson’s ratios (v₁₂ = v_GP and v₂₁ = v_PG) was established by taking values directly from previous studies (Table 1) that include force spectroscopy (46), optical trapping (50), microfluidic bending (49), finite element modeling (48), and atomistic simulation (47,51). The remaining parameters—namely the shear moduli (G) and out-of-plane Young’s modulus (E₃) and Poisson’s ratios (v₁₃, v₃₁, v₂₃, and v₃₂)—were either approximated or inferred (Supporting Materials and Methods, Section A). For instance, the transverse isotropy of the peptidoglycan network was utilized to reduce the number of unknowns and to infer in-plane properties from corresponding out-of-plane properties. Shear moduli, on the other hand, were approximated using empirically derived formulas and tensor rotation demonstrated previously for analogous, cellular, orthotropic materials (60). In either case, the approximated and inferred properties did not have a significant impact on results. This is most likely due to the nature of the deformation and the small thickness of the cell wall, which emphasize the in-plane Young’s moduli. The thickness value (t_CW) used in this study represents roughly two layers of peptidoglycan in the cell wall, which can be between one to three layers thick (2–6 nm) depending on the Gram-negative species (46,47).

Lastly, the pillar was modeled as an infinitely stiff (rigid) material. In some cases, bending of nanopattern features is observed (61). This, however, occurs only in features with low flexural rigidity and only at the cell periphery, where adhesion forces have an angled line of action. It is not seen for features that fall under the projected area of the cell, which represent a larger proportion of the contact points. Also, it has not been observed for nanopatterns made of highly stiff materials such as titanium (13) and titanium oxide (30) even when utilizing geometrically slender features. Therefore, rigid pillars are well representative.

Interactions

Interactions were applied to define contact relationships between the various components in a manner that was biophysically relevant. There were three such interactions representing surface adhesion, between the pillar and outer leaflet, hydrophobic effects, between the membrane leaflets, and lipoprotein linkages, between the cell wall and inner leaflet (Table 2).

Table 2.

Interactions Involved in the Adhesion of a Bacterial Envelope to a Nanopattern

Interaction	Contact Surface		Type	Constraint Method	Contact Properties
	Master	Slave			Normal	Tangential
Surface adhesion	pillar	outer leaflet	surface-to-surface contact	penalty and finite sliding	hard (no separation)	rough (μ = ∞)
Hydrophobic effect	outer leaflet	inner leaflet	surface-to-surface contact	penalty and finite sliding	hard (no separation)	frictionless (μ = 0)
Lipoprotein linkage	inner leaflet	cell wall	tie constraint	surface-to-surface discretization	no relative motion

Surface adhesion was modeled as a hard pressure overclosure, with no separation and rough friction. This dictated that points on the outer leaflet were firmly stuck to the pillar upon contact. Although it is known that contact only becomes irreversible after some time, the underlying bond strengthening process unfolds at a rate faster than that at which the bacteria conforms to the nanopattern (4,62). Hence, rough friction most correctly describes adhesion. A similar surface-to-surface contact, albeit with no friction, was used for the interaction between membrane leaflets. Thus, the leaflets were allowed to slide over one another but not to separate. This mimics the hydrophobic forces that hold the leaflets together and oppose only deformation modes that threaten to expose the hydrophobic core. Intermonolayer friction was totally omitted because it scales with relative velocity, which is negligible on the timescale of adhesion (63). Lastly, a tie constraint was used to fuse the inner membrane leaflet to the cell wall, restricting their relative motion. In reality, these envelope components are tightly coupled through covalent lipoprotein linkages that facilitate stress transfer (33,36). Although these are discrete, their very high abundance on the surface of the cell (over 10⁶ instances) (64) can be reasonably approximated as a continuous tie constraint. All interaction properties were enforced with more lenient formulations (penalty constraint and surface-to-surface discretization) to ease the convergence. Also, use of the more general finite sliding formulation was required.

Elements and mesh

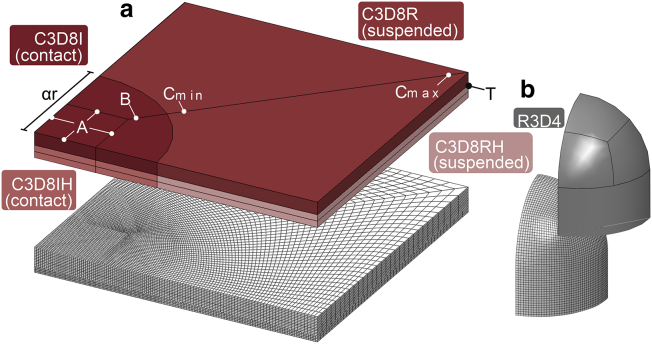
Element selection and mesh generation were optimized to the region-specific deformation modes incurred by the envelope. More specifically, although the entire envelope was observed to stretch, albeit nonuniformly, the region in contact with the pillar also incurred bending. Bending requires specific elements and mesh refinement to circumvent hourglass and locking phenomena (65). To allow for this, the envelope was partitioned into an O-grid-like pattern, separating contacting and suspended regions by a relative radius (αr), which is a scalar multiple of the pillar radius (r) (Fig. 2).

Figure 2.

Element selection and mesh generation. (a) Envelope components are partitioned to enable use of mesh refinement and bending-specific elements in contact regions. (b) Shown is the partitioning of the pillar to create a smooth spherical mesh with hex elements. To see this figure in color, go online.

Contact regions were modeled with first-order, incompatible mode elements (C3D8I) because of their accuracy in bending and efficient elimination of spurious modes via added degrees of freedom and full integration scheme (65). Suspended regions, which remained approximately parallel, were assigned less-expensive, first-order, reduced integration elements (C3D8R) to optimize computational efficiency. For the outer membrane, which is near incompressible, hybrid formulation (C3D8IH and C3D8RH) was added to avoid volumetric locking (65). Rigid elements (R3D4) were used for the pillar. All parts were meshed with hex elements because of their higher rate of convergence. The hex mesh was generated by a structured mesh approach using local seeds along partitioned edges (A, B, and C) as well as through the thickness (T) (Fig. 2). The local seeds were controlled to create gradual refinement of the mesh toward the contact region with smooth transitions. Mesh quality was verified using shape metrics. Mesh sensitivity was evaluated to ensure element size was sufficiently small for a converged result (Supporting Materials and Methods, Section B).

Loading and analysis

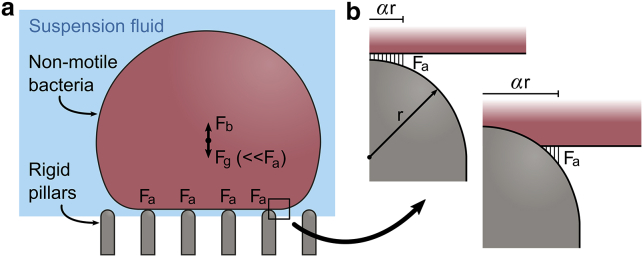
For a cell atop a nanopattern, intermolecular adhesion forces are the dominant external force acting in the direction of contact (Fig. 3 a). Though the cell also experiences weight, its effects are insignificant relative to adhesion forces and the strain limits of the envelope (Supporting Materials and Methods, Section C). Accordingly, loading was applied to mimic the more critical adhesion forces, which act in an evolving “bond front” because of their finite range (Fig. 3 b; (66)). To capture this, several simulations were run in which a downward pressure load was applied to the bottommost face of the outer leaflet over an area bounded by a relative radius (αr) that was increased incrementally (α = 0.3: 0.1: 2). For each load area, plots of envelope strain energy (U) and adhesion area (A) were generated from the relevant strain energy (ALLSE) and contact area (CAREA) history outputs. The plots were used to calculate the maximal converged strain energy accumulation rate (dU/dA) by fitting a high order polynomial and applying a numerical differentiation scheme between iterations (Supporting Materials and Methods, Section D). This rate was used to infer the work of adhesion (W), which is equivalent at equilibrium (i.e., W = dU/dA). In other words, adhesion will continue to propagate until the strain work done on the envelope to achieve an incremental increase in the contact area equals the corresponding energy released by adhesion (67). By these means, the work of adhesion required to induce a certain level of deformation was estimated.

Figure 3.

Free body diagram of an idealized, nonflagellated bacteria atop an array of rigid nanopillars. (a) The only significant force driving contact is from adhesion (F_a), whereas other physical forces such as weight (F_g) and buoyancy (F_b) are comparatively insignificant (F_a ≫ F_g ∼ F_b). (b) Shown is the propagating bond front of finite-ranged intermolecular adhesion forces. To see this figure in color, go online.

Monitored outputs and locations

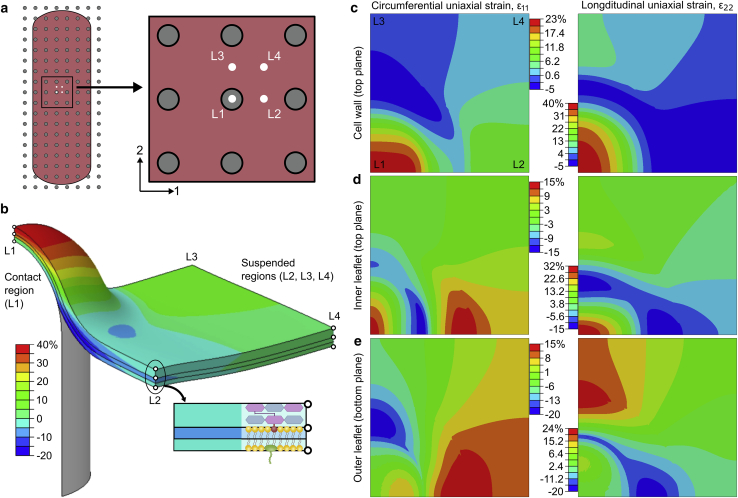
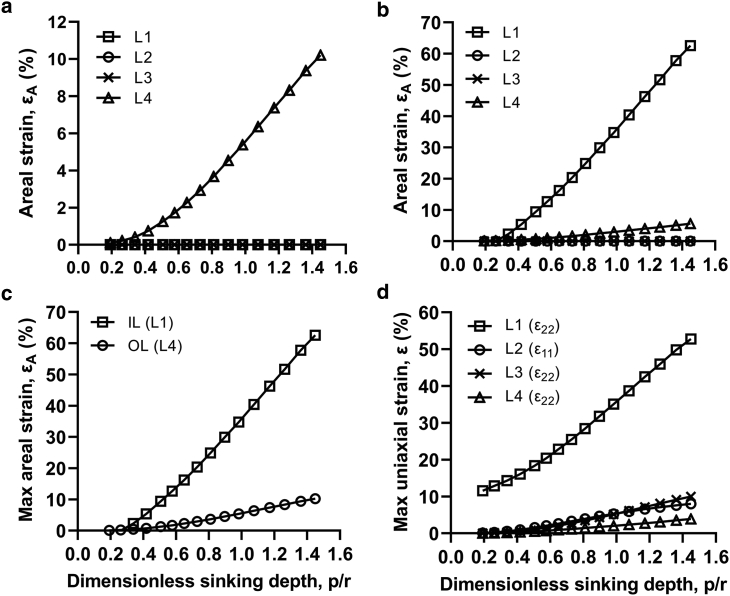
For each load application area, the adhered area, sinking depth, and strain conditions corresponding to the maximal equilibrium position were recorded. Adhered area was retrieved from the contact area history output. Sinking depth (p) was measured as the distance from the apex of the pillar tip to the lowest point on the envelope. In-plane uniaxial strains, both circumferential (ε₁₁) and longitudinal (ε₂₂), were probed from the output database. These were then used to also calculate in-plane areal strains (ε_A = (1 + ε₁₁) (1 + ε₂₂) − 1). Both types of strains were monitored at several potentially critical locations (Fig. 4, a and b) to capture the envelope’s highly nonuniform deformation. These locations included the pillar apex (L1), the midpoints between two nearest pillars (L2 and L3), and the midpoint between an array of pillars (L4). Classification based on contact (L1) and suspended regions (L2, L3, and L4) was also used to coincide with the popular “biophysical model” by Pogodin and others (18). For the inner and outer membrane leaflets, values were probed from the top and bottom planes, respectively, corresponding to the position of the hydrophilic headgroups. For the cell wall, maximal values appearing at the top plane were probed (Fig. 4 b).

Figure 4.

Probe locations to monitor the nonuniform deformation of the envelope. (a) Shown is the top view of the four locations that include the pillar apex (L1), the circumferential and longitudinal midpoints between two nearest pillars (L2 and L3), and the midpoint between an array of pillars (L4). (b) Shown is a contour plot of longitudinal uniaxial strain (ε₂₂) for an adhered envelope. Probe locations are shown and categorized into contact (L1) and suspended regions (L2, L3, and L4). At each location, in-plane uniaxial strains are probed at three points through the thickness, representing each of the three layers. For the inner and outer leaflets, the points correspond to the position of hydrophilic headgroups (top and bottom planes, respectively). For the cell wall, the maximal through-thickness value is probed, which is found at the top plane. (c–e) Shown are the contour plots of the circumferential (ε₁₁) and longitudinal (ε₂₂) uniaxial strain for each envelope layer. All contour plots are for the soft envelope configuration with an adhesion energy, dimensionless sinking depth, pillar diameter, and center-to-center spacing of 21 mJ/m² and 1.36, 60, and 180 nm, respectively. To see this figure in color, go online.

The monitored strains were also used to assess physical damage to the envelope via comparison with extensibility limits. Based on previously reported values, the extensibility limit of the cell wall and membrane leaflets was taken to be between 18 < ε₂₂ < 65% (57,68,69) and 5 < ε_A < 35% (70,71), respectively. Different strain-based failure criteria have been used for the two cell components because of their different molecular architectures and, relatedly, failure mechanisms. For the cell wall, rupture occurs by uniaxial strain, in particular along its longitudinal axis (ε₂₂), which corresponds to the weaker peptide cross-links (57,72). For the membrane leaflets, rupture occurs by area increase between hydrophilic headgroups, which opens unstable pores (73,74). In this case, areal strain (ε_A) is more critical than uniaxial strain (71).

Bacterial studies

Sample preparation

Bacterial interaction with a nanopatterned was also studied experimentally using wings of the P. claripennis cicada. Dried, unmounted cicadas were purchased online (http://www.insectfarm.com.au). Wings were detached and cut into square samples (∼10 × 10 mm) for testing. The samples were immobilized onto glass coverslips using small pieces of strategically placed double-sided tape to enable removal when required.

Bacterial attachment

A rod-shaped, Gram-negative strain, namely Pseudomonas aeruginosa (ATCC 27853) from the American Type Culture Collection (ATCC), was used for the bacterial interaction studies. Before the experiment, bacterial cultures were refreshed on nutrient agar plates (Oxoid, Hampshire, UK). The bacterial cells were grown in 5 mL of sterile nutrient broth at 37°C with overnight shaking at 180 rpm in an orbital shaker. The bacterial cells were then harvested during the logarithmic phase of growth and the bacterial suspensions adjusted to an OD600 (optical density at 600 nm) of 0.20 in phosphate-buffered saline solution as described elsewhere (7). The three wings were immersed in 400 μL of bacterial suspension in triplicate in a sterile, 48-well polystyrene plate. The surfaces were incubated for 4 h at room temperature in an orbital shaker at 80 rpm. After incubation, bacteria-adhered surfaces were characterized using fluorescent microscopy to assess viability and scanning electron microscopy to visualize morphology.

Fluorescent microscopy

Viability of adherent P. aeruginosa was determined by staining the cells with the LIVE/DEAD BacLight Bacterial Viability kit (Molecular Probes, Invitrogen, Carlsbad, CA). The BacLight kit (Molecular Probes, Invitrogen) contains 3.3 mM SYTO 9 and 20 mM propidium iodide. Cells were stained for 15 min and imaged for live (green) and dead cells (red), respectively, after a 4-h incubation. Fluorescent microscopy was performed using an inverted Nikon Eclipse TI-S microscope (Tokyo, Japan). The 40× objective used was a CFI Plan Fluor ELWD ADM 40× (Nikon) with a numerical aperture of 0.6 and working distance of 3.6–2.8 mm, PH2. Ten images of at least three independent replicates were obtained.

Scanning electron microscopy

For visualization by scanning electron microscopy (SEM), the bacterial suspension was removed from the well plates, and bacterial cells were fixed on the wing samples using 3% glutaraldehyde (C₅H₈O₂). Fixed samples were then washed in a 0.1-M cacodylate buffer and 1% OsO₄ followed by dehydration in a graded ethanol series (from 50 to 100%) and drying with hexamethyldisiloxane (C₆H₁₉NSi₂). Dried samples were then gold coated and mounted. To visualize the underlying deformation and sinking of the bacteria, samples were mounted at a very large incline (∼80°); hence, images were captured from almost front on, not top down. Two scanning electron microscopes were utilized, one with stage-tilt capabilities (JEOL JSM-7001F; Tokyo, Japan) and another with an in-lens detector, albeit fixed stage (Tescan MIRA3; TESCAN ORSAY HOLDING, Brno, Czech Republic). Both were operated at 5–10 keV with a working distance between 5 and 7 mm.

Results and Discussion

Critical action site

Identifying the critical location of envelope deformation is needed to better understand the mechanism of nanopatterned surfaces. This is particularly important given the incompatibility of the longstanding “biophysical model” with commonly observed tip penetration (11,28, 29, 30, 31). To this effect, Fig. 5 shows the evolution of in-plane strains with sinking depth in each envelope layer at each location of interest on a cicada-like nanopattern (d = 60nm, s = 180nm). The nonuniformity of the strain distribution can be inferred from the differing strain levels at each location (Fig. 5) and is easily apparent in contour plots of in-plane uniaxial strain (Fig. 4, b–e).

Figure 5.

Evolution of in-plane tensile strains with dimensionless sinking depth (p/r) at contact (L1) and suspended (L2, L3, and L4) regions. (a) Shown are the areal strains within the outer leaflet. (b) Shown are the areal strains within the inner leaflet. (c) Shown is the comparison of the maximal areal strains in the inner and outer leaflets of the bilayer membrane. (d) Shown is the maximal uniaxial strain in the cell wall. Data are for the soft envelope configuration with a pillar diameter and pattern spacing of 60 and 180 nm, respectively.

Accordingly, one or more of these locations was critical for the envelope. Interestingly, however, the critical location of each of the layers did not always coincide. For instance, the outer leaflet of the bilayer membrane experienced maximal areal strain in the suspended region at the center of an array of pillars (L4) (Fig. 5 a). Other locations on the outer leaflet either did not experience strain (L1) or experienced tensile strain that was mostly uniaxial (L2 and L3) and, thus, was less critical (71). Conversely, the inner leaflet had its maximal areal (and uniaxial) strain clearly at the pillar apex (L1) (Fig. 5 b). Moreover, this strain was much higher than that occurring anywhere in the outer leaflet (Fig. 5 c). This implied that any stretch-induced pore formation and possible rupture of the bilayer would always first initiate within the inner leaflet at the pillar apex. Similarly, in the cell wall, strains at the pillar apex were significantly larger than at any other location (Fig. 5 d). Taking these results together, the critical location for both the cell wall and membrane—and thus the envelope overall—was in the contact region precisely at the apex of the pillar tip (L1).

The criticality of the contact region was also confirmed by micrographs of bacteria adhered to the nanopattern of the cicada wing surface (Fig. 6). These showed the bacterial envelopes to be compromised at the pillars, whereas regions of the envelope suspended between pillars remained seemingly intact. This could be identified by pillar tips penetrating through the envelope, which corresponded to either partial (Fig. 6 a) or total (Fig. 6, b–e) loss of turgor. Moreover, clear penetration seemed to occur shortly after the envelope had sunk below the pillar tip. This is indicated by circular outlines in Fig. 6 that highlight examples of penetration in which the envelope had sunk to reveal the full spherical dome of the pillar (p/r ≥ ∼1). Where the sinking depth was insufficient (p/r < ∼1), there was only perturbation, not penetration, as highlighted by rectangular outlines. This differential deformation could be due to a number of factors, such as the dynamic nature of adhesion and the inhomogeneous surface properties of the bacteria. Most importantly, however, these observations implied that the contact region was critical and that the tip of the pillar delivered high levels of mechanical deformation to the envelope, reinforcing the modeling predictions.

Figure 6.

Gram-negative Pseudemonas aeruginosa adhered to the wing nanopattern of the P. claripennis cicada. (a) Shown is a penetrated cell retaining some shape and turgor. (b–e) Shown are penetrated cells with total loss of turgor. (f) Shown are cells with some turgor loss but no clear signs of penetration, only perturbation. Circular and rectangular outlines are used to highlight penetration and perturbation, respectively. Scale bars, 200 nm.

Although these findings contradict the prevailing dogma that envelope rupture occurs in the suspended region (18), the criticality of the contact region is not at all surprising. This is due to the nature of the shape change in the contact region, where the envelope is seen to wrap the pillar (Fig. 6, rectangular outlines). In doing so, it transforms from an approximately flat plane into a three-dimensional, nondevelopable surface. This type of nondevelopable transformation is notoriously difficult to withstand physically because of double curvature known to generate large tensile membrane strains, in addition to bending strains, at high deflections and rotations, as demonstrated within the model (75,76). This explains why the suspended region, which remains relatively flat, experiences comparatively lower deformation than the contact region and why penetration, not interstitial tearing, is observed. Consistent with this reasoning and these findings, observations of tip penetration have also been reported previously on a variety of nanopatterned surfaces. Cicada pillars, gecko spinules (28), dragonfly rods (9), titania wires (30), and black silicon spikes (29), to name a few, have all been seen to penetrate bacterial cells. Additionally, physical penetration is one of the well-established toxicity mechanisms of carbon nanotubes and graphene materials, which can have characteristic dimensions similar to nanopillars (77). For instance, even the thicker multiwalled variants of carbon nanotubes (d = 50 nm) can kill cells in this way (78). Accordingly, penetration is likely a common physical mechanism among nanoscale materials.

On an additional note, though the outer leaflet did not see comparatively high strains (Fig. 5 c), it is worthwhile not to dismiss its deformation behavior. Importantly, this was the only layer in the envelope that behaved as predicted by the “biophysical model” of Pogodin and others (18), having its maximal uniaxial and areal strains in the suspended region (Figs. 4 e and 5 a). Unlike other layers, the outer leaflet directly contacts the pillar and sticks to its surface as a result of bond strengthening and subsequent irreversible adhesion, which was modeled by rough friction (62,79). The effect is that deformation in the contact region is arrested and instead redistributed to the suspended region. Unsurprisingly, an effectively similar condition is found in the case of the “biophysical model,” which requires adhesion or “negative adsorption” for stretching to be higher in the suspended region. Although some level of surface adhesion or sticking is indeed relevant, its impact is easily overestimated if the envelope is simplified as a single layer with small or negligible thickness. This is demonstrated by the outer leaflet, which can be considered a numerical analog to the analytical solution by Pogodin and others (18) because both represent the adhesion of a single monolayer. However, such simplifications are not accurate for either Gram-negative or Gram-positive cells, which have multiple load-bearing layers and significant thickness, respectively. As shown in this simulation, when the envelope is more accurately modeled as a multilayered structure, the impact of sticking is minimized, and the criticality of the suspended region disappears. Instead, the contact region and pillar apex are revealed to be critical action sites for the envelope, in better agreement with these experimental observations.

Feasibility of adhesion-driven death

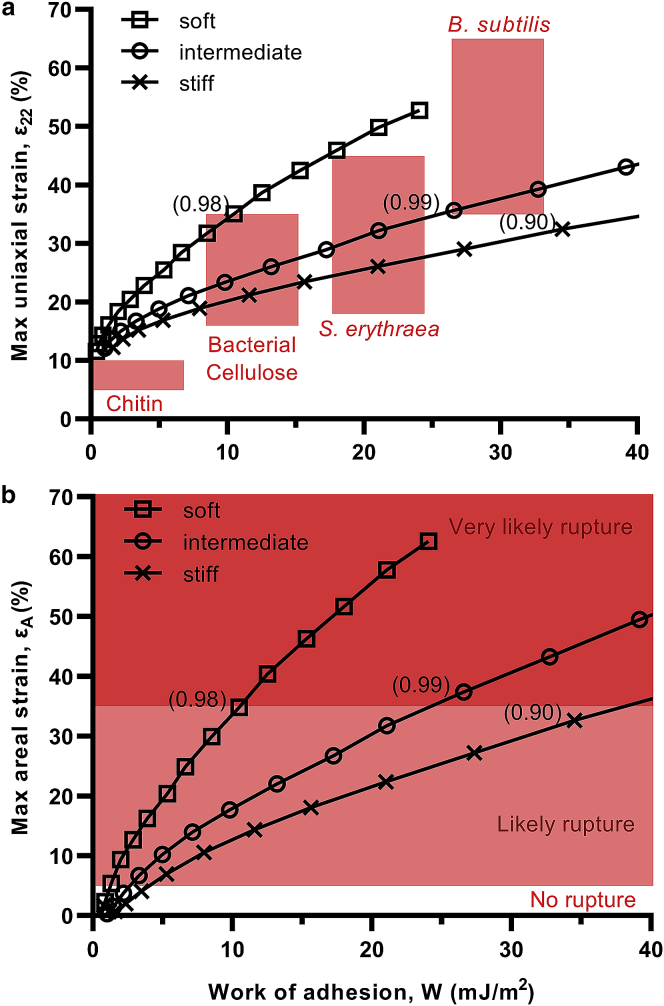
Citing the “biophysical model” by Pogidin and others (18), it is most commonly explained that deformation is driven by passive adhesion forces and that these forces eventually cause death by rupture (24,29). Problematically, the strength of adhesion forces or bacterial envelopes has not been quantitatively considered. Hence, it remains unclear whether adhesion can induce the levels of deformation commonly observed on nanopatterned surfaces and whether this deformation is sufficient to kill the cell. This has left room for speculations, of varying validity and parsimony, about other forces potentially implicated in nanopattern bactericidal activity (9,17,26). To provide quantitative insight, Fig. 7 demonstrates the estimated work of adhesion for the deformation of three different Gram-negative envelopes of varying reported stiffness on a cicada-like nanopattern.

Figure 7.

Work of adhesion required to deform Gram-negative bacteria. (a) Shown is the assessment of the cell wall deformation by the maximal uniaxial strain in longitudinal direction (ε₂₂), probed at pillar apex. (b) Shown is the assessment of the outer membrane deformation by maximal areal strain (ε_A), probed at pillar apex. Bracketed values indicate corresponding dimensionless sinking depth (p/r). Data are for pillar diameter and pattern spacing of 60 and 180 nm, respectively. To see this figure in color, go online.

To give further meaning to the results, the calculated strains were contextualized with relevant adhesion strengths and envelope extensibilities. As seen in Fig. 7 a, the cell wall of Saccharopolyspora erythraea and Bacillus subtilis has been found to rupture at longitudinal uniaxial strains between 18–45% (57,68) and 35–65% (69,80), respectively. Similarly, cellulose and chitin–the plant and fungal analogs of peptidoglycan—are known to rupture between 16–35% (81,82) and 5–10% (83), respectively. As for phospholipid membranes, their areal extensibility is a dynamical property that depends on loading rate (84) and strained area (70). Accordingly, small (∼10² nm²) mimetic lipid systems strained at fast rates (∼10² mN/m) (as in molecular dynamics simulations) rupture between areal strains of 35–100% (70,85), whereas large areas loaded quasistatically (as in micropipette aspiration experiments) rupture between 2 and 5% (86). In nanopattern interaction, loading is delivered quasistatically through adhesion, and the strained area will at most be localized around the pillar tip (∼10³–10⁴ nm²). Accordingly, a plausible critical range at intermediate strains (5–35%) can be defined, and strains reported from molecular dynamics (>35%) can be considered an absolute upper limit (Fig. 7 b). For adhesion strength, the van der Waals component can be estimated from the Hamaker constant for bacterial interfaces in aqueous media (typically between 1–10 × 10⁻²¹ J), giving 1–10 mJ/m² at molecular contact (87, 88, 89). When additional acid-base interactions are considered, the adhesion strength can be as high as 20–30 mJ/m² (90,91), depending on the specific physicochemical properties of the bacteria, interaction medium, and substrate.

Based on these values, it is apparent that intrinsic adhesion forces can, in some cases, drive rupture of the envelope. This is most easily appreciated in the case of the soft envelope configuration, which incurred rupture-associated longitudinal and areal strains of 35% in the cell wall and outer membrane, respectively, even at a modest adhesion strength of 10 mJ/m² (Fig. 7 a). Furthermore, at this adhesion strength, the sinking depth of the envelope was at a level consistent with rupture observed in micrographs (p/r ∼ 1), as described previously. A similar argument can also be made for the intermediate stiffness envelope, which required 27 mJ/m² to achieve similar strains and sinking depth, also reasonably within upper reported values for bacterial adhesion. The stiffest envelope, however, did not reach depths seen in micrographs for rupture within 40 mJ/m², which is uncharacteristically high for bacterial adhesion. Accordingly, all but one of the envelope configurations strongly support adhesion-driven rupture.

The apparent resistance of one of the Gram-negative envelope configurations could quite simply be due to overestimations of mechanical properties and failure criteria. For instance, some previous experimental studies (49,50), have neglected the additional and comparable stiffness of the outer membrane; hence, their reported cell wall stiffness may be overstated up to a factor of 2. Similarly, the cited rupture strains are taken from previous experiments existing only for Gram-positive peptidoglycan, which is inherently stronger than its Gram-negative counterpart because of increased cross-linking (52). It is also possible that the requirement of total rupture for death may be an overstatement. Envelope stress and strain below rupture-inducing levels, concomitant with lower sinking depths (p/r < 1) and adhesion energies, may cause other nonrupture modes of death. For instance, without penetrating through the envelope, it is possible that stretching caused by adhesion is sufficient to sustain several large—otherwise transient—pores, causing osmotic imbalance and subsequent death (77,92). Additionally, prolonged perturbation and envelope stress may trigger a biochemical cascade of protein, DNA, and oxidative damage as seen in the so-called “wrapping” mechanism of carbon nanotubes and graphene materials, which does not require explicit penetration (93,94). Penetration and wrapping mechanisms of these carbon-based nanoscale materials are also believed to be driven by intermolecular adhesion forces, predominantly van der Waals (93) and electrostatic (95). These additional mechanical—or mechanically triggered modes—may explain the occurrence of nonvisibly penetrated cells on the cicada wing surface (Fig. 6 f), which were also presumably compromised based on the overwhelming proportion of dead cells in fluorescence microscopy images (Fig. S4). In light of these possible overestimations and less-pronounced death modes, the numerical results overall reaffirm adhesion-driven deformation and death, as originally posited by Pogodin and others (18).

Effects of geometry

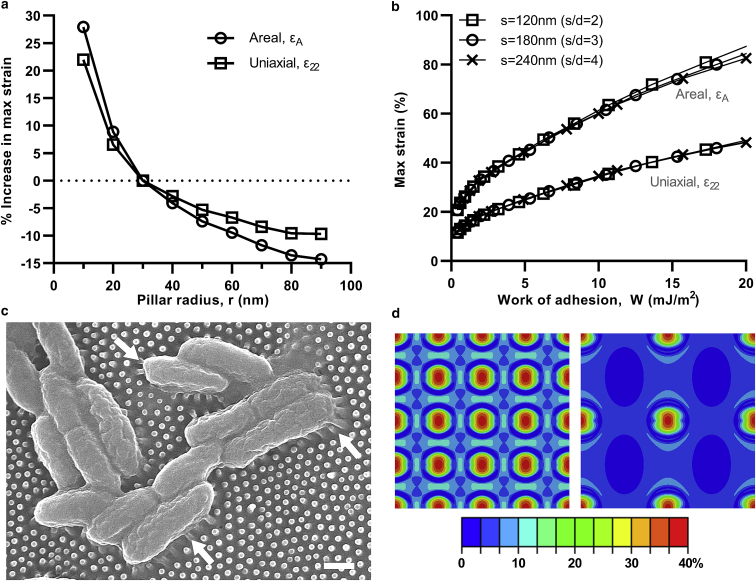
The level of deformation and death induced through adhesion is expected to depend on the geometry of the nanopattern. Although this notion seems relatively intuitive, the effects of even broad geometric parameters such as radius, spacing, and height are still not systematically understood (10,22). To provide clearer insight, Fig. 8 demonstrates the impact of pillar radius and spacing on the maximal uniaxial and areal strain in the envelope. For all geometries studied, maximums of uniaxial and areal strain in the cell wall and outer membrane appeared consistently at the pillar apex. Also, the global maximum for the envelope was at the pillar apex in the cell wall.

Figure 8.

Impact of individual geometric parameters. (a) Shown is the percentage increase in the maximal uniaxial and areal strain due to pillar radius at an adhesion energy, dimensionless spacing, and pillar height of 10 mJ/m² and 3 and 200 nm, respectively. (b) Shown is the effect of dimensionless spacing on the maximal areal and uniaxial strain at a pillar radius and height of 30 and 200 nm, respectively. (c) Shown is the bending of cicada wing pillars at the periphery P. aeruginosa cells, highlighted with arrows. Scale bar, 500 nm. (d) Given are top-view contour plots of the maximal uniaxial strain for spacing of 120 nm (left) and 240 nm (right) at an adhesion energy, pillar radius, and pillar height of 20 mJ/m² and 30 and 200 nm, respectively. All data shown are for the soft envelope configuration. To see this figure in color, go online.

Decreasing radius and spacing increased the maximal uniaxial and areal strain in the envelope. For radius (Fig. 8 a), the effect was quite pronounced. At an adhesion energy of 10 mJ/m², decreasing radius from 30 to 10 nm increased maximal envelope strain by ∼25%, whereas increasing radius from 30 to 90 nm produced a reduction of ∼10–15%. Spacing, on the other hand, had a less-significant impact on the maximal strain (Fig. 8 b). Its effects only appeared at higher adhesion energies and sinking depths. Plots of maximal uniaxial and areal strain for all three spacings (120, 180, and 240 nm) were coincident up to ∼10 mJ/m², indicating that there was effectively no variation in maximal envelope strain. At 20 mJ/m², however, some deviation could be observed, most noticeably in terms of maximal areal strain, which increased by 5% with a reduction in spacing from 240 to 120 nm.

The trend with radius is in good agreement with previous literature. Increased killing efficiency against bacteria with thinner or sharper pillars is a common experimental observation (10,13,96). For instance, investigating the bactericidal performance of three cicada species against Gram-negative bacteria, Kelleher and others (22) found that the species with the smallest radius produced the highest killing efficiency. Similarly, Michalska and others (29) also demonstrated that sharper tipped black silicon pillars were more effective than blunt counterparts against a range of Gram-negative and Gram-positive bacteria. In both studies, however, changes to pillar radius were coupled to height and spacing; hence, conclusions on the impact of any parameters individually have so far been limited. In combination with this modeling, however, the role of radius is more convincing. Its impact can be straightforwardly interpreted as a stress concentration, which intensifies stress and strain in the contact region because of the reduced contact area. More accurately, however, the effect of radius is due to the curvature (1/r), which is proportional to the membrane and bending strains produced by the nondevelopable transformation of the envelope in the contact region (75). Accordingly, refining the pillar tip radius can be recommended to enhance bactericidal efficiency.

Comparatively, the role of spacing is not so straightforward. Sensitivity to spacing in this study can be attributed to stress distributions overlapping and compounding as neighboring pillars are brought closer, thus increasing the maximal strain in the envelope. This effect, however, is weak in comparison with the radius because the critical deformation and maximal strain occur at the pillar apex. Interestingly, however, some other theoretical studies have reported a strong spacing sensitivity with a contradictory trend. In their respective analytical and finite element models, Xue and others (27) and Mirzaali and others (26) demonstrated that larger spacing increased the maximal deformation of the envelope. Both models, however, considered the weight of the cell to be the driving force behind the interaction. Not only is weight a trivial load (Supporting Materials and Methods, Section C), but it is also conceptually misrepresentative. Weight, or any other “constant” load, will always produce a straightforward sensitivity to spacing resulting from the distribution of that load over a given number of pillars or contact points. This is similar to how a bed of nails becomes injurious once the nails are distantly separated. The case of bacteria on a nanopattern, however, is a very different scenario. Interaction forces develop individually at each pillar. This phenomenon can be observed in micrographs, specifically at the periphery of cells, where pillars are “pulled” into contact (Fig. 8 c). Accordingly, reducing spacing should not adversely affect maximal stress and strain and should only enhance it, as demonstrated presently. Spacing also has another important role, distinct from maximal strain—that is, controlling the number of contact points. Although there is only a small (at most 5%) increase in maximal strain by reducing spacing from 240 to 120 nm, the pillar density and number of contact points increase by a factor of 4 (Fig. 8 d). Having increased contact points enables more envelope damage to be delivered over the cell. It also increases the chances of a localized tip rupture, given that bacteria are known to have mechanical properties and adhesive biopolymer concentrations varying spatially across their surface (91,97). These results indicate that spacing can be safely reduced to increase the number of contact points without detriment to the maximal stress and strain, unlike suggested previously. Importantly, this recommendation is more consistent with experimental trends. Across several studies involving black silicon (16,96), polymer (10), and insect wings (22,23), more closely spaced pillars have exhibited enhanced killing efficiency, though direct conclusions were again precluded by simultaneous changes to the radius and height. More recently, however, a study by an electron-beam-induced deposition clearly demonstrated enhanced killing efficiency against Gram-positive bacteria resulting from selective spacing reduction (98). Taking these experimental observations together with this modeling, it can be strongly recommended that reducing spacing increases killing efficiency.

Effects of height were not explicitly shown. Beyond the value needed to allow sufficient sinking (h/r > ∼1), height was totally inconsequential to the deformation of the envelope. In contrast, an interest in height has been popular in the literature, tracing back to early reports of increased killing efficiency correlated to higher pillar “aspect ratios” (22,29). Several possible explanations can be offered for these observations. For example, some authors have suggested that height may have an effect indirectly via adhesion energy (23). As shown by the surface element integration technique, pillars can drastically reduce the repulsive interaction energy barrier commonly seen in bacterial adhesion by separating the cell from the bulk of the underlying substrate (99). However, these effects should only be present for pillar heights within the range of intermolecular forces (at the very most 50 nm), whereas pillars are typically much taller (100–1000 nm). This is consistent with a recent study that found similar adhesion forces for pillars between 220 and 420 nm tall, with the same diameter and spacing (61). It has also been postulated that taller pillars may be more bactericidal because of their reduced flexural rigidity, which causes increased deflection under equivalent interaction forces (17,61). According to this theory, elastic strain energy stored in the pillars through deflection may lead to increased envelope stretching. Problematically, modeling of the direct link between the pillar deflection and the resulting envelope stress and strain is totally absent. Moreover, it can be argued that this link is not convincing. For one, the deflection of pillars—which typically bend toward the cell (Fig. 8 c)—would effectively reduce the distance the envelope must stretch to come into contact. More importantly, the intermolecular forces that cause pillar bending are not removed upon contact; therefore, the bent pillars would not exert their stored “springback” energy upon the envelope, as has been suggested (61). And lastly, bent pillars tend to be confined to the cell periphery. Though having boundary conditions that are poorly defined, this region of the envelope is evidently less constrained and therefore presumably less critical. Also, overall, the significance of bent pillars is questionable because proportionally, more contact points occur underneath the projected area of the cell where the pillars remain upright (Fig. 6 b). Accordingly, height-modulated killing efficiency is not strongly explained by the existing deflection theory. A final explanation is that changes to pillar height have often been accompanied by changes to radius, which is overlooked when descriptions of “aspect ratio” are used (22,29). The variable efficiency in these studies may have been solely due to the reduction in radius and not related to height whatsoever. Albeit relatively unexciting, this suggestion bodes well with this research, which finds that smaller radii pillars significantly enhance envelope stress and strain, whereas pillar height has no such effect. With no clear role of height from a theoretical perspective, including this work, radius and spacing are more effective design parameters for enhancing killing efficiency.

Mechanism updates and perspectives

Combining the various aspects of this work, an updated mechanism for bactericidal activity on nanopatterned surfaces can be put forth. Accordingly, nanopatterned surfaces kill bacteria by eliciting significant deformation through contact, which is driven by intermolecular adhesion forces acting locally between the pillars and the bacteria. This deformation may occasional death in a number of ways, ranging from relatively inconspicuous DNA, oxidative, or protein damage to highly pronounced physical rupture. In either case, deformation is critical at the pillar apex because of the nondevelopable shape transformation of the envelope around the pillar tips that induces significant in-plane strains. When these strains exceed the tensile limits of the cell wall and outer membrane, a tip-localized rupture occurs and presents itself in a manner resembling penetration, with pillars protruding through the cell. The killing efficiency for such a mechanism can be enhanced by reduction to pillar radius and spacing, which intensify the maximal strain and increase the frequency of perturbation points, respectively.

This tip-localized mechanism is expected to dominate a significant proportion of cell-nanopattern interactions. For instance, based on the geometries studied, all nanopatterned surfaces having a dimensionless spacing ratio greater than 2 will kill Gram-negative bacteria predominantly in this way. This range captures a large population of previously reported bactericidal nanopatterns, both natural—such as cicada wings (22) and gecko skin (11)—and synthetic—such as those fabricated by reactive ion etching (29,100), electron beam lithography (13), and nanoimprint lithography (10). Also, a tip-localized mechanism seems more compatible with the killing effect of certain disordered nanostructures with variable heights, such as dragonfly wings (9) and hydrothermally synthesized nanowires (30,31). Because of their nonuniformity, these create only a few discrete contact points that are unlikely to cause significant interstitial stretching. As for different cell types, this mechanism is plausible but ultimately requires further investigation. Gram-positive and eukaryotic cells have distinctly different physical structures that would significantly impact the deformation mechanics. Gram-positive bacteria, for instance, do not contain an outer membrane and instead have cell walls up to 80 nm thick. Their cell walls are also under a high, non-negligible initial strain because of the significant turgor pressure. For eukaryotic cells, the outer membrane is attached to and supported by a cytoskeleton that pervades through the cell. In this case, a model of isolated layers may not be sufficiently accurate. That being said, certain trends from this study do seem to align with the behavior of these cells on nanopatterned surfaces, both of which have reported instances of enhanced resistance (19,20,30). For Gram-positive cells, their occasional resistance to nanopatterned surfaces can be explained straightforwardly by cell wall thickness, which has the effect of increasing envelope stiffness. Similarly, the occasional ressitance of eukaryotic cells could be due in part to the inclusion of cholesterol in their lipid membrane, which increases both stiffness and extensibility—relative to the pure phospholipid membranes found in bacteria—by at least a factor of 2–3 (74). As shown in Fig. 7, increased stiffness and extensibility limits would indeed lead to greater survivability. Also, both cells become susceptible when subjected to nanopatterns with very small radii (8), as has been suggested in Fig. 8. Although the mechanism is indeed compatible with these trends, studies with more appropriate cell models are ultimately required before their failure mode can be confidently elucidated.

Conclusions

Valuable insights to the mechanism of nanopatterned surfaces lie behind accurate descriptions of contact and interaction mechanics. This has been demonstrated in this work through computational modeling of bacteria-nanopattern adhesion with carefully considered multilayer structure, interaction properties, and boundary conditions. By this approach, improved understanding of the critical action site and geometric enhancement of nanopatterned surfaces has been derived. It is now understood that nondevelopable deformation about pillar tips can produce critical strains at the pillar apex, which may locally rupture and penetrate through the bacteria. Bactericidal activity by this effect can be enhanced through reduction to pillar radius and spacing, which increase the magnitude of maximal strains and the frequency of perturbation points, respectively. These findings can immediately help toward the design of nanopatterned surfaces with enhanced bactericidal efficiency and may offer a starting point for cytocompatibility studies in the future. Nanopatterned surfaces exhibiting both properties are ultimately needed to progress this promising technology through the development pipeline.

Author Contributions

All authors made significant scientific contributions to the reported work. A.V. conceptualized and designed the research, performed computational modeling and microscopy, analyzed the data, prepared the figures and tables, and wrote the manuscript. J.H. performed the microscopy and reviewed the manuscript. Z.L. and P.K.D.V.Y. provided the ongoing technical and high-level expertise to all aspects and reviewed the manuscript.

Editor: Markus Deserno.