Using Queue Theory and Load-Leveling Principles to Identify a Simple Metric for Resource Planning in a Pediatric Emergency Department

Abstract

Increased waiting time in pediatric emergency departments is a well-recognized and complex problem in a resource-limited US health care system. Efforts to reduce emergency department wait times include modeling arrival rates, acuity, process flow, and human resource requirements. The aim of this study was to investigate queue theory and load-leveling principles to model arrival rates and to identify a simple metric for assisting with determination of optimal physical space and human resource requirements. We discovered that pediatric emergency department arrival rates vary based on time of day, day of the week, and month of the year in a predictable pattern and that the hourly change in pediatric emergency department waiting room census may be useful as a simple metric to identify target times for shifting resources to better match supply and demand at no additional cost.

Introduction

Long waiting time for patients in emergency departments (EDs) is a well-recognized international phenomenon.^1-3 Increased waiting is associated with decreased patient^4-8 and staff⁹ satisfaction, higher left without being seen (LWBS) rates,^10,11 and suboptimal outcomes.^12-14 Basic supply and demand calculations suggest that wait times can be ameliorated or eliminated by increasing the capacity of health care services (ie, build more ED rooms and hire more providers); however, these interventions are oftentimes neither financially feasible nor sustainable.^15,16 The United States is listed as having the highest inflation-adjusted per capita spending on health care among the World’s countries¹⁷ but is ranked 37th in health care quality by the World Health Organization.¹⁸ These data would suggest that there is room for improvement in the US health care system, even in the absence of increased expenditure. Historically, emergency department wait times are blamed on the randomness of patient arrival times; however, a variety of forecasting models have demonstrated reasonable success in predicting the effects of calendar and environmental variables and the need for admission.^19-22 We chose to investigate the predictability of arrival rates to our pediatric emergency department (PED) and apply queue theory and load-leveling principles to determine if there are recognizable patterns in demand that can be utilized to level service supply at no additional cost.

Methods

Study Setting and Population

This retrospective review selected children (<18 years of age) who were seen at the PED at the University of Florida, a large academic, research, and tertiary referral center, between July 2011 and October 2018. The PED is open 24 hours, 365 days per year, and serves an annual census of ~25 000 patients. The PED was staffed with one attending emergency physician at all times and 1 to 5 physicians in training (ie, residents). Patients arriving to the PED are sequentially registered, triaged, roomed, seen by a front-line provider, and, if required, seen or discussed with a PED attending physician. Residents and attendings see patients 24 hours a day. There is often, but not always, a quick care general pediatrician who sees low acuity patients from 5 pm to 11 pm daily. We defined “front-line provider” as a resident or quick care general pediatrician. Once the evaluation is complete, the patient is assigned a disposition of discharged home, admitted, transferred to another facility, or other (eg, deceased). The PED currently has a goal of a total time in the PED (door to departure) of <3.5 hours.

Ethical Approval and Informed Consent

The institutional review board of the University of Florida waived the need for ethics approval and the need to obtain consent for the collection, analysis, and publication of the retrospectively obtained and anonymized data for this non-interventional study.

Study Protocol

The first objective of this study was to assess the variation in historical patient arrival data from the University of Florida PED. Data were collected retrospectively on patient arrival times, acuity, length of stay, and door-to-provider wait times for all patients entering the PED between July 2011 and October 2018. Statistical analysis was performed to identify patterns and consistency of arrival rates, PED census, and waiting-to-be-seen census based on time of day, day of the week, and month of the year. Patient flow in the PED was quantified by measuring the number of patients within the PED for each hour of a 24-hour day and patients waiting to be seen by a provider. We assumed that arrivals occurred according to a time-homogenous Poisson process with a constant rate. Patients were classified as waiting or in-process (ie, within a PED examination room) until a disposition was assigned.

Standard deviation (SD) and coefficient of variation (COV) were determined for continuous variables. SD generally increases or decreases proportionally as the mean increases or decreases.²³ Division of SD by the mean yields COV, a unitless value that allows comparison of variability estimates regardless of the magnitude of the mean.

Application of Queue Theory

Queue theory can be applied to health care service processes by using mathematical models with specific assumptions about the probabilistic nature of the number of arrivals into a system in a given time frame, the number and type of “servers,” and the structure of the service process.¹⁶ One commonly used queueing model is the M/M/s or Erlang delay model. This model assumes a single queue with an unlimited waiting area that feeds into s identical servers and makes 2 so-called “Markovian” (M/M) assumptions: (1) customers arrive according to a Poisson process with a constant rate and (2) the service duration has an exponential distribution. A Poisson process expresses the probability of a given number of events occurring in a fixed interval of time if these events occur with a known constant rate and independently of the time since the last event.²⁴ An advantage of using the M/M/s model is that it requires only 3 parameters: an average arrival rate, λ; an average service duration, 1/µ; and the number of servers, s. With this model, one can predict the probability of remaining within established performance measures. In our case, we chose the requirement that 80% of patients have wait times <1 hour before seeing a medical provider. We defined “wait time” as the delay from the time of patient registration to the time at which a provider was available to treat that patient.

A variation of the M/M/s model applies priority to certain patients based on acuity of illness (eg, nonurgent, urgent, or emergent). Our hospital uses the Emergency Severity Index (ESI) triage system with a 1 to 5 scale, and it is recognized that higher acuity patients often require longer service times.²⁵ However, since we assumed a Poisson distribution of patient arrivals for all acuity levels in a similar fashion to total arrival rates, we did not feel it was necessary to apply a priority model to our trial design.

Because arrival rates were found to vary significantly based on time of day, we, like others, felt that a single daily model would lack precision.¹⁶ Instead, we chose to use a series of 24 M/M/s models for each day to determine how to vary staffing to meet changing demand on an hourly basis.

We chose to use number of front-line providers as our “server” variable (ie, the s in the M/M/s model) but recognize that s can represent a variety of entities. For example, we could have chosen s to represent number of PED rooms or number of PED nurses instead of the number of PED medical providers. In our PED, we have access to flexible-use patient rooms and additional PED nursing can be shifted from other work areas when PED demand increases and we rarely found physical space or nurse availability to be a rate-limiting step. The PED was staffed with one attending emergency physician separated into 3 shifts (day, evening, and night), and a variable number of front-line providers (a fast-track pediatrician and physician residents). Resident physicians are required to check out all patients to the PED attending while fast-track pediatricians are not. Infrequently, emergency attendings would see patients without the involvement of a resident but this circumstance was not felt to be common enough to significantly affect our model results.

Determination of ΔP_w

The M/M/s model depends on several assumptions about a service process and targets a specific performance goal. Although we found the M/M/s queue theory model to be enlightening, we sought to identify a simple metric to determine the degree of supply-demand matching. Our aim was to identify a solution that would not require additional resources, but instead, would leverage existing resources to produce a desirable outcome (ie, load leveling). We calculated the change in the number of patients waiting for each hour-long timeframe (ΔP_w). For example, an increase in waiting room census of 3 to 4 patients from 9 am to 10 am would be represented as (ΔP_w = 4 − 3 = 1 at 10 am). We hypothesized that an increasing PED waiting room census in a given hour timeframe, or a positive value for ΔP_w, represented a process bottleneck and that since PED waiting census was stable over a 24-hour time frame (ie, it did not infinitely increase), there must be times of both over- and under-capacity. The ΔP_w was calculated for each hour of a 24-hour day to determine at what times the PED throughput, on average for the given hour, failed to meet demand. We further postulated that ΔP_w would demonstrate positive correlation with arrival rates and negative correlation with increased PED staffing.

Statistical Analysis

Data specifying hourly volumes of patients waiting and in-process, along with arrivals and tracked time to discharge were retrieved from the University of Florida Integrated Data Repository. All data management and analyses were conducted using SAS 9.4. Data were cleaned to remove wait times in minutes that were negative, time to MD exceeded the total time to discharge that was deemed an error, or extreme values determined to be implausible (time to MD >500 minutes). Data for arrivals, volumes, and wait times were aggregated to hourly averages overall, by day of the week and month. Means and SDs were plotted to describe hourly trends, as were coefficients of variation for each metric.

Results

There were 174 985 PED arrivals between July 2011 and October 2018. The dispositions of these patients were discharged 135 948 (77.69%), admitted 33 769 (19.3%), ED to ED transfer 1441 (0.82%), LWBS 2914 (1.67%), and other 913 (0.52%). The acuities of these patients were as follows: ESI-1, 577 (0.33%); ESI-2, 25 187 (14.39%); ESI-3, 94 623 (54.07%); ESI-4, 51 606 (29.49%); ESI-5, 1497 (0.86%); not listed 1495 (0.85%). During the study timeframe, the PED population was 8.57% Hispanic, 35.66% African American, 51.48% White, and 46.81% female. About 15% of patients arrived via ambulance. The admission rate for patients seen by a provider was 19.3%.

Our review of PED arrivals, total patient volume (non-waiting), patients waiting, and patient wait times during the study time frame demonstrated significant variation based on time of day, day of the week, and month of the year. Each of these variables demonstrated a similar diurnal pattern (Figures 1 and 2), with peak activity occurring in the evening hours (eg, 6 pm to 9 pm) and diminished activity occurring in the early morning (eg, 2 am to 8 am). The mean arrival rates by hour of day ranged from 1.43 patients (SD ± 0.70) at 5 am and 4.70 patients (SD ± 2.26) at 7 pm. The mean total patient volume of the PED ranged from 2.80 (SD ± 2.22) at 7 am to 11.89 (SD ± 3.43) at 9 pm.

Figure 1.

Hourly Patient Flow in Shands Pediatric ED: Patient Volume and Arrivals by Hour of Day (July 2011 – October 2018).

Figure 2.

Hourly Patient Flow in Shands Pediatric ED: Patients Waiting and Wait Time by Hour of Day (July 2011 – October 2018).

The mean number of patients waiting in the PED ranged from 1.10 (SD ± 1.13) at 5 am to 7.33 (SD ± 3.65) at 8 pm (Figure 2). The mean wait times by hour ranged from 18.49 (SD ± 23.20) minutes at 7 am to 54.94 (SD ± 53.93) minutes at 10 pm.

Hourly mean PED waiting room census varied by month of the year, with higher means in the winter months (November, December, and January) and lower mean values over the summer months (May, June, and July; Figure 3).

Figure 3.

Hourly Mean +/- STD Patients Waiting in Shands Pediatric ED by Month (July 2011 – October 2018).

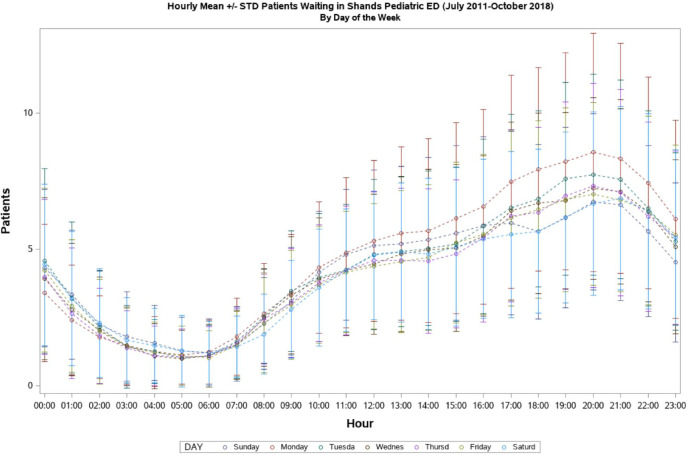
Hourly mean PED waiting room census varied by day of the week, with higher means on Monday and Tuesday, and lower mean values over the weekend (Saturday, Sunday; Figure 4).

Figure 4.

Hourly Mean +/- STD Patients Waiting in Shands Pediatric ED by Day of Week (July 2011 – October 2018).

To determine to what degree variation in PED waiting room census may have been affected by increased variation in mean arrival rates, a COV was calculated for arrivals based on hour of the day. COV of patient arrivals by hour was fairly consistent with a range over 24 hours ranging from 48 to 59 (Figure 5).

Figure 5.

Hourly Coefficient of Variation by Hour of Day: Arrivals.

Pediatric emergency department wait time by hour of the day demonstrated a consistently higher COV than did the hourly number of arrivals; however, the COV was fairly consistent over a 24-hour day with a range between 98 and 124 (Figure 6).

Figure 6.

Hourly Coefficient of Variation by Hour of Day: Wait Time.

Mean number of PED patients waiting ranged between 1.117 at 5 am and 7.331 at 8 pm and values generally increased between 6 am and 8 pm (positive values for ΔP_w) and decreased between 9 pm and 5 am (negative values for ΔP_w; Table 1).

Table 1.

Mean Number of PED Patients Waiting and ΔP_w by Hour of the Day, July 2011 to October 2018.

	Hour of day
	0:00	1:00	2:00	3:00	4:00	5:00	6:00	7:00	8:00	9:00	10:00	11:00
Mean # of patients waiting	4.123	2.928	2.041	1.52	1.273	1.117	1.132	1.551	2.369	3.152	3.917	4.397
ΔPw	−1.22	−1.2	−0.89	−0.52	−0.25	−0.16	0.015	0.419	0.818	0.783	0.765	0.48
	Hour of day
	12:00	13:00	14:00	15:00	16:00	17:00	18:00	19:00	20:00	21:00	22:00	23:00
Mean # of patients waiting	4.783	4.938	5.021	5.305	5.732	6.331	6.513	6.962	7.331	7.203	6.429	5.343
ΔPw	0.386	0.155	0.083	0.284	0.427	0.599	0.182	0.449	0.369	−0.13	−0.77	−1.09

Abbreviations: PED, pediatric emergency department; ΔP_w, change in the number of patients waiting.

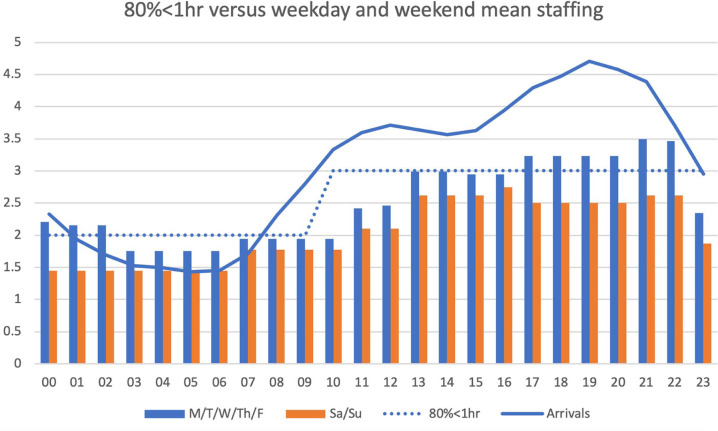
The mean number of PED arrivals ranged between 1.433 at 5 am and 4.704 at 7 pm. Mean number of PED front-line staff ranged between 1.75 and 3.5 on weekdays and between 1.45 and 2.75 on weekends. Using a series of queue theory M/M/s models (80% <1 hour) with the requirement that 80% of patients have wait times <1 hour before seeing a medical provider, the estimated minimum number of front-line providers required was 2 between midnight and 9 am, and 3 between 10 am and 11 pm (Figure 7).

Figure 7.

Queue theory M/M/s model (80% patients evaluated in less than 1 hour), mean staffing levels (weekdays and weekends), and arrivals by hour of day.

Discussion

The time a child spends waiting to be seen by a medical provider in the PED is wasted, adding no value to the health care service. The primary driver of increased PED waiting time is an imbalance between the demand for services and supply of physical space and/or human resources needed to provide those services. There has been extensive review on methodology for predicting demand and adjusting capacity to optimize the efficiency of the PED visit.^26-28 Queueing theory provides one method of predicting staff requirements with mathematical models that aim to identify the minimum number of servers (in our case, medical providers) required to meet a specific service target during a specified timeframe.^29-33 These methods can provide information on process bottlenecks that can be specifically targeted to leverage the impact of process improvement interventions. Nonetheless, predictive models are limited by the variability of the measure they aim to predict.²³ That is, variables with a large COV cannot be predicted with accuracy. Our data demonstrate that PED arrival rates vary over relatively small ranges with a COV that is not significantly different for each hour of a 24-hour day. This supports the argument that patient arrival rates to the PED are random but predictable. Recognizing these diurnal trends may allow for shifting of resources from low-demand periods to high-demand periods without additional cost.

Our data demonstrate that PED arrival rates vary based on time of day, day of the week, and month of the year in a highly predictable pattern. We recognized that increased volume of arrivals yielded predictable increases (and decreases) in PED waiting times. This phenomenon can be predicted using complex modeling; however, we identified a simple fluid marker of PED capacity-demand matching that is useful for resource management planning: change in PED waiting room census (ΔP_w). We considered a positive ΔP_w to be a marker of developing process bottleneck and felt it useful to categorize the source of this bottleneck as either provider-related, nurse-related, or space-related. Equally important, however, was recognizing that a negative ΔP_w represented a time period when PED capacity exceeded demand. We propose that shifting resources from the negative ΔP_w time periods to the times with positive ΔP_w could potentially improve the match between capacity and demand.

By definition, the number of persons entering a queue that is neither lengthening nor shortening must equal the number of persons leaving. On short time scales (eg, hours), process bottlenecks are buffered by increased wait times or increased LWBS rates. On larger time scales (eg, days) changes in arrival rates are accommodated by changes in capacity (eg, number of staff, number of available rooms, process refinement). Demand can be temporarily increased by marketing or decreased by diversion of patients to other facilities. In a stable PED process, the rate of patients entering the PED must equal the rate of patients exiting the PED (including all disposition types) on average. In the absence of ever-increasing wait times or LWBS rates, capacity is meeting demand (on average) but process resources are not necessarily optimally distributed. Recognizing patterns of demand and capacity presents an opportunity to move resources from times of low need to times of high need (ie, load-leveling).

In review of our PED, we noted that waiting room census consistently increased between 6 am and 8 pm and decreased between 9 pm and 5 am. We interpret these results to mean that the 6 am and 8 pm represents a process bottleneck with regard to the transition from the PED waiting area to a PED room. This bottleneck may be the result of inadequacy of available PED rooms, nursing or staff, number of providers, or may represent a combination of factors. Based on a superficial review of our data and facilities and interviews with key staff, it was determined that this process bottleneck was most likely the result of an inadequate number of front-line providers during these hours. This problem could easily be fixed by adding staff for the “understaffed” hours; however, it was our intention to identify cost-neutral solutions. With this reasoning, it was determined that the 9 pm and 5 am time period was, relatively speaking, overstaffed, and that shifting resources from the overstaffed time period to the understaffed time period would result in overall load leveling of PED capacity. We further propose that this strategy would be effective regardless of the source of the process bottleneck as long as minimum thresholds are not exceeded (eg, there cannot be <1 front-line provider). We believe that these data demonstrate an area of opportunity for ED throughput process improvement in a cost-neutral fashion and that this load-leveling strategy could be used in other health care processes as well.

This study was limited by its retrospective nature and did not consider the effects of special cause variation and outliers. We recognize the complexity of operations in a large academic, research, and tertiary referral center combined with a resident teaching program. Our assumptions for the M/M/s queueing model require estimation of average provider service time per patient, which must include the times of all activities including direct patient care, review of X-rays and laboratory tests, phone calls, charting, and speaking with other providers or consults. We also recognize that there may be unintended consequences of creating a highly efficient ED, including encouraging the inappropriate use of emergency services in lieu of nonemergent outpatient clinics. It is our hope that equal quality improvement efforts in the outpatient clinics will mitigate this undesirable side effect. Prospective trials will be needed to further measure the effects of our methods.

In conclusion, our data demonstrate that PED arrival rates are random but predictable and that load-leveling analysis, queue theory, and determination of hourly ΔP_w can be used to identify potential target times for shifting resources to better match supply and demand at no additional cost.