Analysis and prediction of COVID-19 epidemic in South Africa

Abstract

The coronavirus disease-2019 (COVID-19) has been spreading rapidly in South Africa (SA) since its first case on 5 March 2020. In total, 674,339 confirmed cases and 16,734 mortality cases were reported by 30 September 2020, and this pandemic has made severe impacts on economy and life. In this paper, analysis and long-term prediction of the epidemic dynamics of SA are made, which could assist the government and public in assessing the past Infection Prevention and Control Measures and designing the future ones to contain the epidemic more effectively. A Susceptible–Infectious–Recovered model is adopted to analyse epidemic dynamics. The model parameters are estimated over different phases with the SA data. They indicate variations in the transmissibility of COVID-19 under different phases and thus reveal weakness of the past Infection Prevention and Control Measures in SA. The model also shows that transient behaviours of the daily growth rate and the cumulative removal rate exhibit periodic oscillations. Such dynamics indicates that the underlying signals are not stationary and conventional linear and nonlinear models would fail for long-term prediction. Therefore, a large class of mappings with rich functions and operations is chosen as the model class and the evolutionary algorithm is utilized to obtain the optimal model for long term prediction. The resulting models on the daily growth rate, the cumulative removal rate and the cumulative mortality rate predict that the peak and inflection point will occur on November 4, 2020 and October 15, 2020, respectively; the virus shall cease spreading on April 28, 2021; and the ultimate numbers of the COVID-19 cases and mortality cases will be 785,529 and 17,072, respectively. The approach is also benchmarked against other methods and shows better accuracy of long-term prediction.

1. Introduction

The first case of COVID-19 was reported in Wuhan, China in December 2019. Then, COVID-19 spread nearly all over the world rapidly. In eight months, more than 16 million people of 213 countries were infected, where 645k people lost their lives unfortunately. This indicates the strong human transmission and some distinguishing biological features of COVID-19 with respect to other epidemics. The effective Infection Prevention and Control Measures (IPCMs) are urgently needed. To this end, modelling this epidemic is necessary. The dynamical behaviour of the COVID-19 spreading was analysed [1], [2], [3], [4], [5], [6], [7], [8], which focused on the cases in China [1], [2], [3], Japan [4], South Korea [5], Iran [6], Italy [7] and India [8]. The effectiveness of IPCMs was evaluated [9], [10], [11], [12]. Among these, the effectiveness of the quarantine of Wuhan was assessed by calculating the contact rate of latent individuals with the SEIR model [9]. The conclusion is that the quarantine and isolation effectively reduced the potential peak number of COVID-19 infections and successfully delayed the date of peak infection. Similarly, the impact of the disease control measures in Wuhan was studied [10], with the non-constant transmission rates with a modified SEIR model. In addition, two simple approaches to data analysis were adopted to evaluate the influence of the intervention measures [11], [12]. Specifically, the second derivative of the function of the cumulatively diagnosed cases was calculated [11] to show the effect of the massive interventions in China, and a stochastic model that predicts the cumulative number of the laboratory-confirmed patients was introduced [12] to simulate the evolution process of the epidemic under intervention measures. It is noted that their estimation of the transmission parameter was made under many assumptions on the model of epidemiology, e.g., the number of exposed cases in the incubation period. Further, the asymptomatic and infected cases of incubation result in inaccuracy in the reported daily number of confirmed cases. Therefore, the aforementioned approaches to evaluating the epidemic situation are over simplified and not accurate, as shown by the recent data of the epidemic.

Since the COVID-19 continues to spread around the world, it is necessary to model the dynamics of COVID-19 to predict its future trend. The existing epidemic models can be divided into two categories, i.e., the first-principle model [13], [14], [15], [16], [17] and the data-driven model [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29]. The first-principle model is able to clearly show how and why an input has an effect on the output. Building such a model necessitates some specific knowledge that is however difficult to acquire. For example, to predict the status of one person via an epidemic model in a network, we have to know the statuses of those who have contacted him/her, and determine the probability with it the person is infected by them. In addition, the interventions from the human, e.g., precautions from individuals, isolation of suspect cases, and development of ascertainment infections, need to be explicitly specified in advance. Otherwise, the prediction may be far away from the true case [20].

The data-driven modelling is sometimes preferable, which builds the relationship between the system inputs and outputs without explicit domain knowledge. An exponential model was obtained with the number of the daily cumulative cases at the early phase of the outbreak in China and gives the basic reproduction number [21]. Similarly, another data-driven model was developed [22], which is matched with the mean and standard deviations of the number of the reported daily cumulative cases on the Diamond Princess cruise ship with a gamma distribution and gives also the basic reproduction number. The end time and the total numbers of the infectious cases and the mortality cases of COVID-19 in China were predicted by different types of data-driven models, i.e., the logistic model, the Bertalanffy model and the Gompertz model [23]. The social media search indices (SMSIs) were taken into consideration, which were fitted by the data of the confirmed cases via a model of subset selection [24]. In Castorina [25], a generalized Gompertz law was found to predict the maximum number of the infected individuals in China, Singapore, South Korea and Italy. In Li [26], the Gaussian distribution theory was utilized to analyse and predict the transmission of COVID-19. Besides, prediction algorithms were also provided [27], [28] based on machine learning. Among them, the epidemic trend of COVID-19 in India was predicted by a model that is trained by the data of China [27]. The risk category of the country was assessed [28] by shallow long short-term memory (LSTM) networks.

In South Africa (SA), the first case was confirmed on March 5, 2020. After that, COVID-19 has been rapidly spreading throughout SA. At present, the number of the cumulative infectious cases (CICs) still keeps increasing. In total, 674,339 confirmed cases and 16734 mortality cases in total were reported by 30 September 2020. This pandemic has thus given South Africans with huge health risks. To refrain it, a series of domestic containment measures have been carried out by the SA government. These however cause other social impacts. For example, the Gross Domestic Product (GDP) of SA is expected to sink by 7.1% this year, based on the World Bank. To our best knowledge, the studies of the COVID-19 epidemic in SA are rarely seen in the literature.

This paper presents analysis and long-term prediction of the epidemic dynamics of SA, which could assist the government and public in assessing the past IPCMs and designing the future ones to contain the epidemic more effectively and contribute the global study of the virus as the unique case of African people in the world population. A Susceptible–Infectious–Recovered model is adopted to analyse epidemic dynamics. The model parameters are estimated over different phases with the SA data. They indicate variations in the transmissibility of COVID-19 under different phases and thus reveal weakness of the past IPCMs in SA. For long-term prediction, it is noted that the data-driven modelling is well developed with wide applications, but its success depends on prior knowledge of the system to be modelled, which enables selection of the model structures and use of big data. However, COVID-19 is a new type of epidemic with high transmissibility and unknown pathogenicity with no past experience and data, Our analysis model shows that transient behaviours of the daily growth rate (DGR) and the cumulative removal rate (CRR) exhibit persistent rise mixed with periodic oscillations. Such dynamics indicates that the underlying signals are not stationary and conventional linear and nonlinear models would fail for long term prediction. Therefore, a large class of mappings with rich functions and operations is chosen as the model class and the evolutionary algorithm is utilized to obtain the optimal model for long term prediction. The resulting models on the DGR, the CRR and the cumulative mortality rate (CMR) predict that the peak and inflection point will occur on 4 November 2020 and 15 October 2020, respectively; the virus shall cease spreading on April 28, 2021; and the ultimate numbers of the COVID-19 cases and mortality cases will be 785,529 and 17,072, respectively. The approach is also benchmarked against other methods and shows better accuracy of long-term prediction.

The rest of the paper is organized as follows. Section 2 introduces SA with the epidemic and data descriptions. The epidemic analysis and long-term prediction are presented in Sections 3, 4 , respectively. The conclusions are drawn in Section 5.

2. South Africa and COVID-19 epidemic

SA is located in the southernmost region of Africa, with a long coastline that stretches more than 2500 km along the South Atlantic and the Indian Oceans. With a total area of 1,221,037 km², SA is the 24th largest country in the world. The interior of SA consists of a vast, in most places almost flat, plateau with an altitude of between 1000 m and 2100 m, with a generally temperate climate. It is to the north by the neighbouring countries of Namibia, Botswana, and Zimbabwe and to the east and northeast by Mozambique and Eswatini, and surrounds the enclaved country of Lesotho [30].

According to the Worldometer elaboration of the latest United Nations data in 2020, the population of SA is estimated at 59,308,690, which ranks 25th in the world. SA is a nation of diverse origins, cultures, languages, and religions, with 79.2% of Black Africans, 8.9% of Whites, 8.9% of Colours, 2.5% of Asians, and 0.5% of unspecified people [31].

SA is a developing country with a mixed economy. In 2019, its GDP was worth 350 billion US dollars, ranking 42th in the world. It has been being burdened by a relatively high rate of crime, poverty, and unemployment, and is also ranked in the top ten countries in the world for income inequality. In 2015, 71% of net wealth were held by 10 percent richest of the population, whereas 60% of the poorest held only 7% of the net wealth with the Gini coefficient of 0.63 [32].

The health system of SA comprises the public sector and the private sector. The public health services are divided into primary, secondary and tertiary through health facilities that are located in and managed by the provincial departments of health. The health care system of SA owns more than 400 public hospitals and 200 private hospitals, and consumes about 8.8% of the GDP in this country. Nonetheless, the vacancy rates for doctors and nurses are estimated at 56% and 46%, respectively. Moreover, 84% of the population depends on the public healthcare system, which is the preferred government health provision within a primary health care approach. However, only 21% of doctors work in it [33]. In addition, SA has an estimated seven million people living with HIV, more than any other country in the world [34]. Thus, the health care in SA is beset with chronic human resource shortages and limited resources.

The COVID-19 spread to nearly all the countries after it broke out in Wuhan, China in December 2019. The first known patient of COVID-19 in SA was confirmed, a 38-year-old male citizen infected during travel to Italy, on March 5, 2020. After that, a series of IPCMs were introduced in succession by the National Institute for Communicable Diseases (NICD) of SA, e.g., contacts tracing and isolation by the Emergency Operating Centre (EOC), travel restrictions since 18 March, 2020, closure of schools and universities since 18 March, 2020, and a 500 billion rand stimulus spending plan. Besides, to prevent and control COVID-19 in SA, a national-wide lockdown was conducted by the government on March 26, 2020. It was initially with the most restrictive level of 5, and then relaxed to the level of 4 on May 1, 2020; for example, the railway station was reopen. The lockdown was further relaxed to the level of 3 on June 1, 2020, until now. Nonetheless, COVID-19 spreads throughout SA rapidly, and the number of daily new case (DNC) creates a record high of 13,944 on July 24, 2020, which further weakens the health care system of SA. As a result of the long-term lockdown, a series of economic and social problems were brought, such as an increase in domestic violence and intimate partner violence, the geopolitical dysfunctions. Especially, the exchange rate between Rand and Dollar was depreciated at an all-time low on April 5, 2020. The effective IPCMs are urgently needed. For reference, an exact model contributes to revealing the epidemic features and forecasting its trend, e.g., the inflection point, the peak, and the final size of infectious and death.

Our study is on SA and uses the COVID-19 data from Worldometer [35]. Specifically, the data consists of the CICs, the active cases (ACs) and the cumulative mortality cases (CMCs) and covers the days from March 5, 2020 to September 20, 2020. The data is divided into four sections according to the level of lockdown as shown in Table 1. The total population in 2020 is 59,308,690 [36]. The cases are plotted in Fig. 1, which shows the epidemic becomes increasingly severe in SA. Our study compare SA with China. The data for China is from the National Health Committee of China [37]. It covers the days from January 22, 2020 to April 18, 2020, including a 62-day period of lockdown from January 24, 2020 to March 25, 2020. The data is divided into four sections as well and is shown in Table 2. Note that the length of each phase is the same as that of SA. Since the COVID-19 spread in China was mainly confined in Hubei province before April 2020, the population size of Hubei province is used and 59,270,000 from the Institute of National Statistics of China (INSC) [38].

Table 1.

Transmission coefficients of COVID-19 in SA.

Lockdown level	Time period	$\hat{\beta }$	$\widehat{R_0}$	Drop rate
0	2020.03.05–2020.03.26	0.3993	5.5901
5	2020.03.27–2020.04.30	0.2231	3.124	44.1155%
4	2020.05.01–2020.05.31	0.1854	2.5958	16.9078%
3	2020.06.01–2020.06.20	0.1726	2.4167	6.8996%

Fig. 1.

Incidence data of SA.

Table 2.

Transmission coefficients of COVID-19 in China.

State	Time period	$\hat{\beta }$	$\widehat{R_0}$	Drop rate
Non-lockdown	2019.12.17–2020.1.23	0.2448	3.4266
Lockdown	2020.01.24–2020.02.27	0.2289	3.2041	6.4933%
Lockdown	2020.02.28–2020.03.29	0.1629	2.2809	28.813%
Lockdown	2020.03.30–2020.04.18	0.1325	1.8545	18.6944%

3. Epidemic analysis

Let $x\left(i\right)$ be the number of CICs at the $i$th day, $i=1,2,\dots ,N$, and define the number of DNCs and DGR as $d\left(i\right)=x\left(i\right)-x(i-1)$, $X\left(i\right)=(x\left(i\right)-x(i-1))/x(i-1)$, $i=2,3,\dots ,N$, respectively. Let $y\left(i\right)$ be the number of the cumulative cured cases at the $i$th day, $i=1,2,\dots ,N$, and define the cumulative cure rate (CCR) as $Y\left(i\right)=y\left(i\right)/x\left(i\right)$, $i=1,2,\dots ,N$. Let $z\left(i\right)$ be the number of the CMCs at the $i$th day, $i=1,2,\dots ,N$, and define the CMR as $Z\left(i\right)=z\left(i\right)/x\left(i\right)$, $i=1,2,\dots ,N$. Let $W\left(i\right)=y\left(i\right)+z\left(i\right)$, $i=1,2,\dots ,N$, be the number of cumulative removed cases (CRCs) at the $i$th day, $i=1,2,\dots ,N$, and define the CRR as $w\left(i\right)=W\left(i\right)/x\left(i\right)$, $i=1,2,\dots ,N$. Let $I\left(i\right)=x\left(i\right)-y\left(i\right)-z\left(i\right)$, $i=1,2,\dots ,N$, be the number of ACs at the $i$th day, $i=1,2,\dots ,N$.

With the SA and China data, we calculate their DGR, CCR and CMR. To show the effect of lockdown, these rates from the lockdown date are plotted in Fig. 2, Obviously, during the level-5 lockdown, the DGR and CCR were decreasing and increasing, respectively. The mortality rate keeps low and stable. However, with the level of lockdown relaxed to 4 on May 1, 2020, the DGR presents a tendency of small-amplitude oscillation. Fortunately, the CCR trends up. For comparison, consider China data. Assume that the COVID-19 outbreaks in China on December 17, 2019 [39]. It is observed that the DGR of China fell to 0.05453% on the 44th day after lockdown and went zero in end, whereas, the DGR of SA has been keeping oscillating. Moreover, the CCR in China is much higher than that in SA in the middle and later stages. Specifically, on the 86th day of lockdown, the CCR in China was 93.1432%, yet only 54.3002% in SA. Besides, the CMR in China is slightly higher than that in SA basically.

Fig. 2.

COVID-19 trends in SA and China.

Now we analyse the epidemic spreading of COVID-19 with modelling. The popular Susceptible–Infectious–Removed (SIR) model [40] is adopted in this paper. Consider a closed set of population, that is, the population in a given region does not change over the time horizon of study. Denote $P$ and $S$ as the numbers of total population and susceptible population, respectively. The SIR model consists of the following three equations:

$$\frac{dS\left(t\right)}{dt}=-\frac{\beta I\left(t\right)S\left(t\right)}{P},$$ (1)

$$\frac{dI\left(t\right)}{dt}=\frac{\beta I\left(t\right)S\left(t\right)}{P}-\gamma I\left(t\right),$$ (2)

$$\frac{dW\left(t\right)}{dt}=\gamma I\left(t\right),$$ (3)

where $\beta$ denotes the effective contact rate, and $\gamma$ represents the removal rate that is the inverse of the expectation of infection duration for COVID-19. Here, the reason for choosing $\gamma$ as $\frac{1}{14}$ is given as follows. On the one hand, the WHO indicates that the recovery time of people with mild symptoms for COVID-19 is about two weeks [41]. On the other hand, the mild case (including the asymptomatic case) accounts for $96.79\text{\%}\sim 99.49\text{\%}$ of the total infectious cases in SA [42].

In the initial phase of the epidemic, the infectious population accounts for a small fraction of the total population, and thus $S\approx P$. Substituting $S=P$ in (2) yields

$$\frac{dI\left(t\right)}{dt}=(\beta -\gamma )I\left(t\right),$$ (4)

whose solution is given by

$$I\left(t\right)=I\left(0\right)\times e^{(\beta -\gamma )t}.$$ (5)

$\beta$ is estimated by the least square method as

$$\hat{\beta }=\underset{\beta }{min}\sum _{t=n_1}^{n_2}{\left(\hat{I}\left(t\right)-I\left(t\right)\right)}^2,$$ (6)

where $\hat{I}\left(t\right)$ is prediction from (5), $I\left(t\right)$ is the recorded number; $n_1$ and $n_2$ respectively denote the first and last days in a phase, e.g., during the lockdown of level 4 in SA. $\beta$ in SIR indicates the transmission rate of an epidemic.

To measure the capacity of epidemic spreading, the basic reproduction number, $R_0$, which denotes the average number of secondary infections produced by an infected host in a completely susceptible population [43], is introduced as follows

$$R_0=\frac{\beta }{\gamma }.$$ (7)

To obtain $R_0$ for COVID-19 in different phases, the incidence data of SA is divided into four sections according to the levels of the lockdown. The initial conditions in (1)–(3) are set based on the population of SA as $S\left(0\right)=$59,308,689, $I\left(0\right)=1$ and $W\left(0\right)=0$, respectively. $\hat{\beta }$ is obtained based on (6). $R_0$ is calculated from (7) as $\widehat{R_0}=\frac{\hat{\beta }}{\gamma }$. By using the package of scipy.optimize.curve_fit in Python, the result is given in Table 1. It indicates that although $\widehat{R_0}$ is decreasing during lockdown in SA, its drop rate, $(\widehat{R_0}\left(T_{k-1}\right)-\widehat{R_0}\left(T_k\right))/\widehat{R_0}\left(T_{k-1}\right)$, is also gradually decreasing, where $T_k$ denotes the time period of the level-$k$ lockdown.

The same analysis is carried out on China case, where $S\left(0\right)=$ 59,269,999, $I\left(0\right)=1$ and $W\left(0\right)=0$. $\hat{\beta }$ and $\widehat{R_0}$ are given in Table 2, which shows that the drop rate of $\widehat{R_0}$ in China is higher than that in SA in the middle and later periods of lockdown.

Note that $R_0$ is obtained under the assumption that everyone is susceptible. If only a part of people is the susceptible host, the effective reproduction number, $R\left(t\right)$, is defined [44] as

$$R\left(t\right)=\frac{S\left(t\right)}{P\left(t\right)}\times R_0.$$ (8)

Note that $S\left(t\right)$ is unknown. It follows [44] that

$$d\left(t\right)=e^{\gamma \times (R\left(t\right)-1)}\times d(t-1).$$ (9)

This is the AR(1) model. $d\left(t\right)$ is a series of observations and available. Thus, it is desirable to make a robust estimation of $R\left(t\right)$ with $d\left(t\right)$, for which the Bayesian estimation is probably best. The prior distributions for $R\left(t\right)$ and $d\left(t\right)$ are assumed and the posterior distribution for the autoregressive parameter $R\left(t\right)$ is then calculated by Bayes${}^{\prime }$ theorem. The mean of $R\left(t\right)$ is obtained on such a distribution and taken as the estimate for $R\left(t\right)$. By successive applications of this at each $t$ with a rolling window [44], a recursive estimation scheme, which uses the observations up to $t$, is constructed using the posterior distribution for $R\left(t\right)$, as the prior in the next estimation step at time $t+1$, leading to an update scheme. The resulting probability distribution for $R\left(t\right)$ includes information on all observations up to time $t$, and contrasts with the “instantaneous” $R\left(t\right)$ used in (9), which only considers the data at $t$ and $t-1$. Thus, it is a robust estimator of the effective reproduction number assumed to be constant for the whole epidemic up to time $t$. Any changes in $R\left(t\right)$ over time result from the assimilation of each new data point, leading to an updated estimate of $R\left(t\right)$.

Applying the above approach to our data, $R\left(t\right)$ is plotted in Fig. 3, which shows that the epidemic of COVID-19 in SA is not stable and that $R\left(t\right)$ is with a trend of slightly growing in the middle and later periods of the lockdown. However, Fig. 4 shows $R\left(t\right)<1$ after the 34th day of lockdown, which means that COVID-19 in China is under control and will be extinguished. Therefore, the IPCMs in China work better than that in SA.

Fig. 3.

Estimation of $R_e$ for SA.

Fig. 4.

Estimation of $R_e$ for China.

It is found from above analysis that although $R_0$ in SA decreased over the time sections, it still reaches up to 2.4167. This means COVID-19 is still prevailing in SA. The values of DGR and $R\left(t\right)$ show upward trends with oscillations in the middle and later periods of lockdown, indicating that a large number of virus carriers, e.g., latent patients and asymptomatic carriers, fail to be traced and that the speed of early detection is not high. It is found by comparison that China is with a higher CCR and obtains better effects of IPCMs. Therefore, while the lockdown in SA has positive effects on suppression of COVID-19, it is still not fully under control and with high risks of a rebound in the middle and later periods. This means that the containment measures should be enhanced; for example all close contacts should be promptly traced and effectively quarantined.

The SIR model was also applied to long-term epidemic prediction in China and South Korea [2], [17], [20]. The recent data shows, however, that the prediction of the approaches [2], [20] is not accurate. We attempt to predict the epidemic trend in SA. The recent data in SA, however, reveals that the prediction accuracy is not satisfactory with SIR to be shown in Section 4.

4. Forecasting

The long-term forecasting of COVID-19 in many countries has been well studied. Among these, the work for China has received considerable attention, including the exponential model [21], the logistic model [23] and the Gompertz model [25]. To our best knowledge, however, no work on the long-term forecasting of the COVID-19 in SA is reported to date in the literature.

Notably, the epidemic curves of COVID-19 in China and SA exhibit quite different features. Specifically, the epidemic in China is more stable with a convergent tendency. However, the same does not hold for SA. Therefore, it is more challenging in forecasting the epidemic trend of COVID-19 in SA. Through the analysis of the incidence data in SA from March 5, 2020, to August 31, 2020, it is found that the DGR, which is related to the DNCs and CICs, shows a tendency of periodic oscillation. In addition, the CRR, which is the sum of CMR and CCR, tends to rise, while the CMR basically keeps flat. As seen, the epidemic dynamics of DGR, CRR and CMR are nonlinear and different from each other. The evolution algorithm [45] has the great capability of learning the unknown dynamics of a nonlinear coupled system and no need to specify the model structure a priori, which is however required by the existing long-term forecasting methods, thus it is adopted to train models for DGR, CRR and CMR for epidemic prediction in SA.

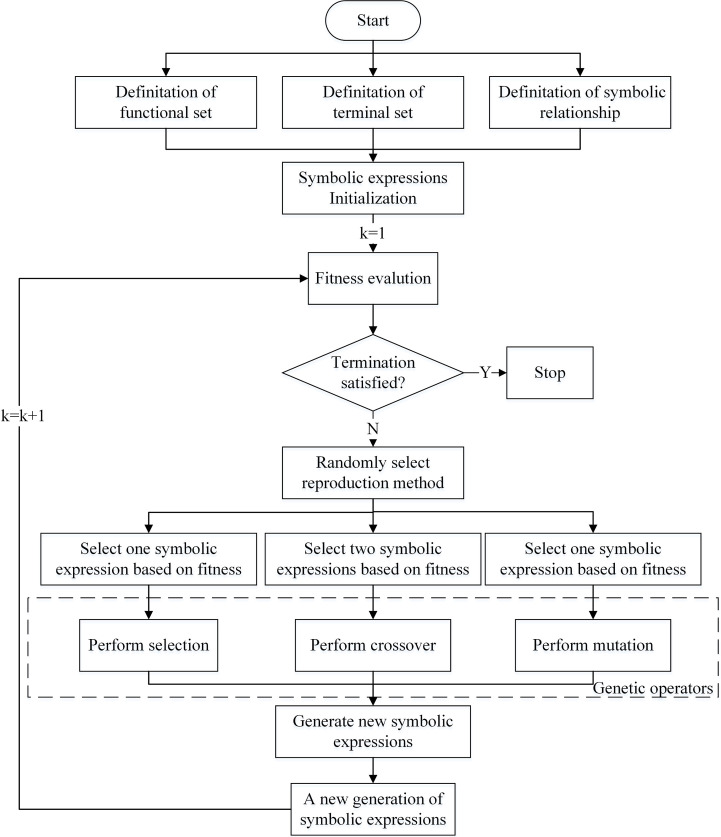
The flowchart of modelling is shown in Fig. 5 and explained as follows. Given a time series, $u\left(i\right)$, $i=1,2,\dots ,N$, we want to build a model, $f\left(i\right)$, to make the prediction, $\hat{u}\left(i\right)=f\left(i\right)$, as close to $u\left(i\right)$ as possible. The mapping, $f$, is taken from a set of functions with free parameters. The optimal one, $f^{\ast }$, is found by maximizing a chosen fitness function. A function set, ${\Omega }_f$, is chosen [46], [47] as

$${\Omega }_f=\{+,-,\ast ,/,-,\wedge ,sin\left(\right),cos\left(\right),tan\left(\right),exp\left(\right),log\left(\right),\mathrm{factorial}\left(\right),\sqrt{\left(\right)},log\left(\right),\mathrm{gauss}\left(\right),tanh\left(\right),\mathrm{floor}\left(\right),\mathrm{ceil}\left(\right),\mathrm{round}\left(\right),\mathrm{abs}\left(\right),sinh\left(\right),cosh\left(\right),\mathrm{asin}\left(\right),\mathrm{acos}\left(\right),\mathrm{atan}\left(\right),\mathrm{atan2},\mathrm{asinh}\left(\right),\mathrm{acosh}\left(\right),\mathrm{atanh}\left(\right)\}.$$

Algorithm $1$ outlines the overall process of modelling. The initial generation of population, $f^0=\{f_1^0,f_2^0,\dots ,f_q^0\}$, is randomly created. By iteratively performing genetic operators, i.e., selection, crossover and mutation, a series of new generations of population, $f^k$, $k=1,2,\dots$, is produced. The optimal one, $f^{\ast }$, is obtained [48] as

$$f^{\ast }=\underset{f^k}{max}\left\{r^2\right\},$$

where

$$r^2=1-\sum _{i=m_1}^{m_2}\frac{{\left(u\left(i\right)-f^k\left(i\right)\right)}^2}{{\left(u\left(i\right)-\overline{u}\left(i\right)\right)}^2},$$

where $f^k\left(i\right)$, $i\in [m_1,m_2]$, is the predicted value on the $i$th day, and $\overline{u}\left(i\right)=\frac{1}{m_2-m_1+1}{\sum }_{i=m_1}^{m_2}u\left(i\right)$ is the mean of $u\left(i\right)$. Output $u\left(i\right)$, $i=m_1,m_1+1,\dots ,m_2$, is used to train the above model.

Fig. 5.

Flowchart of modelling.

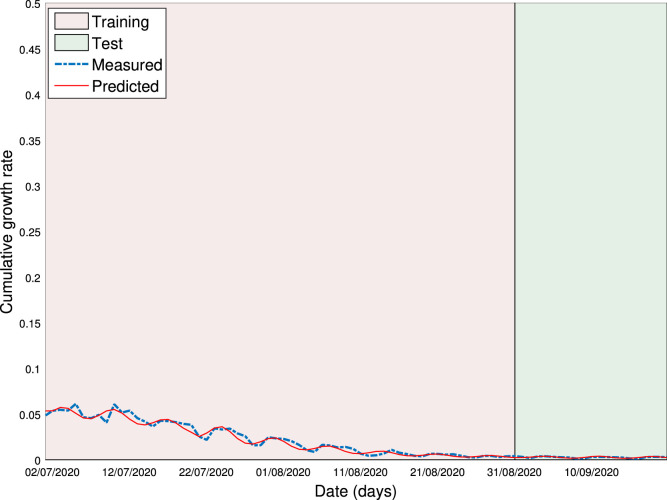
Now we apply the above model to the SA data. Consider DGR with $m_1=119$ and $m_2=180$ for training. By using the software of Eureqa [49], the optimal prediction model of DGR is obtained with $r^2=0.997$ and

$$f_X^{\ast }=0.96^{i-119}\times exp(-\left((1.7109718740005+0.915052571455619\times tanh(0.000400767440371075\times {(i-119)}^2)-0.0120437904816557\times (i-119)-0.0263440613969856\times sin(6.03655745282247+0.899692679789361\times (i-119))\times \lfloor (1.57031206300012+0.0214894750987405\times (i-119))\rfloor \times \mathrm{atan2}(i-119.899692679789361,\lceil (1.7109718740005/(i-119)-0.5)\rceil )){}^2\right)).$$ (10)

This model is used to make prediction, i.e., substitute $i=181,182,\dots ,200$ to (10) to obtain $X\left(i\right)$. It is depicted in Fig. 6. The CICs or DNCs in general gains more attention, because the long-term prediction of CICs or DNCs reveals when the epidemic stops spreading. CIC and DNC are found, respectively, from DGR as

$$x\left(i\right)=x(i-1)\times (1+X(i-1)),i=181,182,\dots ,420,$$

$$d\left(i\right)=x\left(i\right)-x(i-1),i=181,182,\dots ,420.$$

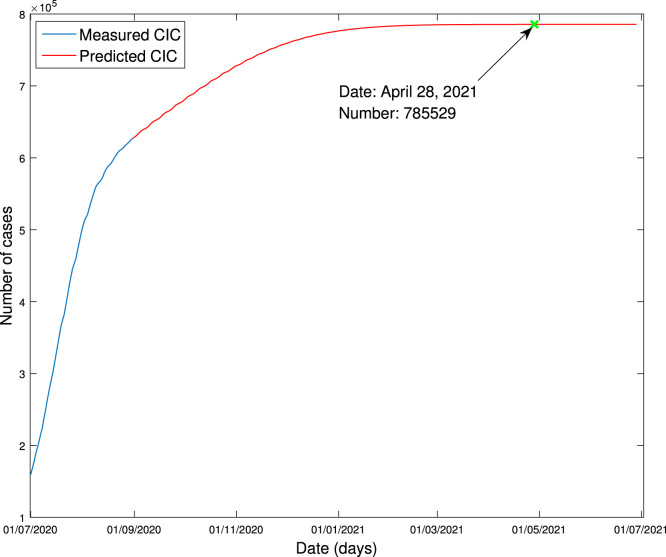
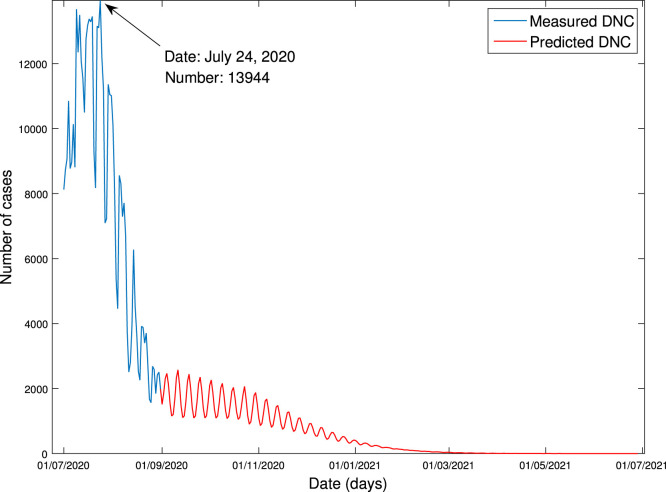
They are exhibited in Fig. 7, Fig. 8, respectively. It is seen from Fig. 7 that CIC stops increasing on April 28, 2021, and the amount of the COVID-19 cases is expected to be around 785,529. It is seen from Fig. 8 that the peak of DNC is expected to be 13,944, occurring on July 24, 2020.

Fig. 6.

Modelling of daily growth rate.

Fig. 7.

Forecasting of cumulative infectious cases.

Fig. 8.

Forecasting of daily new cases.

Consider now CRR. Our simulation gives $r^2=0.997$ and the optimal prediction model as

$$f_w^{\ast }=\frac{2}{\pi }\times \mathrm{atan}(1.005^{i-7}\times \mathrm{atan2}(i-7+3.58344312241981\times cos(0.180642079027816\times (i-7)),60.8845419842163+0.13429637454712\times (i-7)+|i-75.2844145431054|\times cos(0.0523522020801796\times (i-7)+\mathrm{atan2}(cos(i-6.355998362951549),0.13429637454712\times (i-7)))){}^2).$$ (11)

This model is used to make prediction for $w\left(i\right)$, which is depicted in Fig. 9.

Fig. 9.

Modelling of cumulative removal rate.

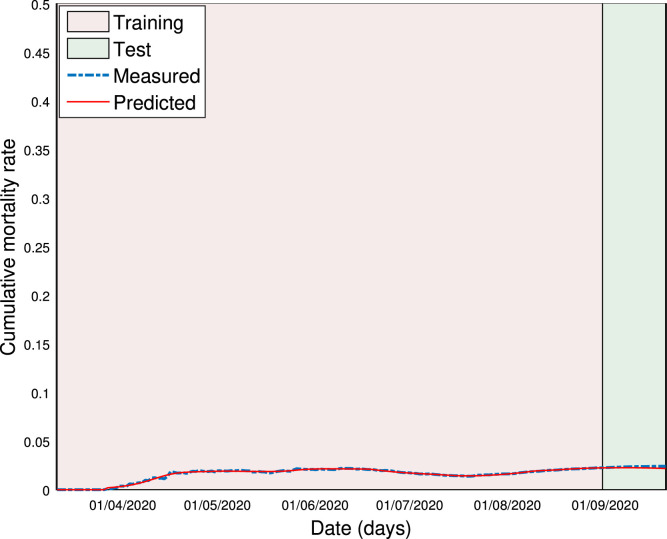
Consider CMR with the same procedure as above. The optimal prediction model is found with $r^2=0.997$ and

$$f_Z^{\ast }=\frac{1}{\left|H\left(i\right)\right|},$$

where

$$H\left(i\right)=log(cosh(50.0179251655876+(0.0149857496976635\times (i-7)){}^{-4.69976682036215}+3.43657143039247\times sin(4.93733980670225+0.139102002005918\times (i-7))+sin(0.300255825306365\times (i-7))+sinh(sin(exp(-(3.43657143039247\times sin(4.93733980670225+0.139102002005918\times (i-7))){}^2)-50.6215493185659\times (i-7))))).$$ (12)

This model is used to make prediction for $Z\left(i\right)$, which is depicted in Fig. 10. To predict when the epidemic ends, CRC and AC are calculated into the future, respectively, by

$$W\left(i\right)=w\left(i\right)\times x\left(i\right),i=181,182,\dots ,$$

$$I\left(i\right)=x\left(i\right)-W\left(i\right),i=181,182,\dots .$$

They are plotted in Fig. 11. It is observed that the predicted AC would be less than 10,000 after August 18, 2021. We treat the rising inflection point as the point at which the curvature of the ACs changes of sign. It is predicted that the peak and inflection point of the number of the ACs will occur on November 4, 2020 and October 15, 2020, respectively. Besides, we predict the ultimate number of the CMCs caused by COVID-19 in SA via the forecasted CMR and CIC. The result is 17072.

Fig. 10.

Forecasting of cumulative mortality rate.

Fig. 11.

Forecasting of cumulative removal cases and active cases.

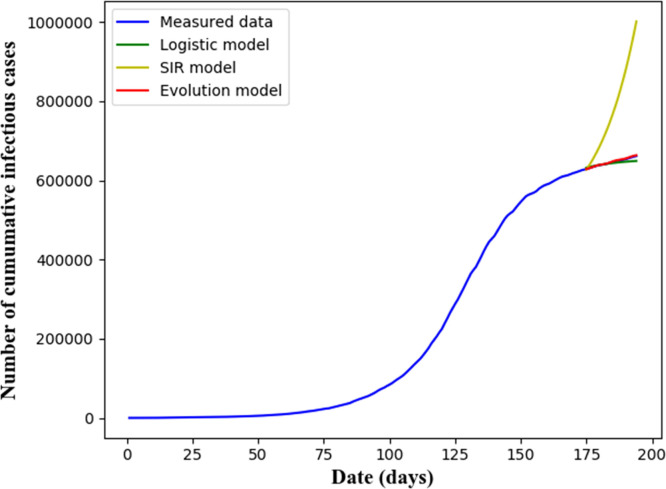
We compare our models with popular ones in the literature. To this end, the prediction models of the SIR [40] and the Logistic growth [23] are chosen. They predict CICs and ACs which are also obtained from our models. Denote by $R$ the root mean square error, which together with the coefficient of determination, $r^2$, is used to assess the prediction accuracy. Specifically, $R_1$ and $r_1$ correspond to the number of CICs, and $R_2$ and $r_2$ correspond to the number of ACs. The results are provided in Table 3. The predicted epidemic curves of CICs and ACs are plotted in Fig. 12, Fig. 13, respectively. It is seen that our approach is with a lower $R$ and a higher $r^2$, indicating our approach with a higher prediction accuracy.

Table 3.

Prediction on SA case.

Model	$R_1$	$r_1^2$	$R_2$	$r_2^2$
SIR model	168605.7152	−310.0851	103922.2234	−954.8337
Logistic model	5446.8394	0.6753	71873.2667	−456.1937
Evolution model	1381.9596	0.9791	3337.2853	0.0143

Fig. 12.

Prediction of cumulative infectious cases.

Fig. 13.

Prediction of active cases.

5. Conclusions

In this paper, a Susceptible–Infectious–Recovered model is adopted to analyse epidemic dynamics. The model parameters are estimated over different phases with the SA data. They indicate variations in the transmissibility of COVID-19 under different phases and thus reveal weakness of the past IPCMs in SA. Furthermore, a novel model is developed to forecast the long-term epidemic trend of COVID-19 in SA. The model class is wide and the evolution algorithm learns the optimal one iteratively from a random initial model, which does not requires prior knowledge of the underlying system and data properties. The so-trained model shows: (1) the peak and inflection point would occur on November 4, 2020 and October 15, 2020, respectively; (2) the epidemic shall be basically under control in April 28, 2021; and (3) the ultimate number of the COVID-19 cases could be 785,529, in which there would be 17,072 people losing their lives. Using historical incidence data of SA, the experimental result illustrates the effectiveness of our approach, and the comparative experimental result shows a higher prediction accuracy of our approach than the others.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.