Memory Reactivation during Learning Simultaneously Promotes Dentate Gyrus/CA_2,3 Pattern Differentiation and CA₁ Memory Integration

Abstract

Events that overlap with previous experience may trigger reactivation of existing memories. However, such reactivation may have different representational consequences within the hippocampal circuit. Computational theories of hippocampal function suggest that dentate gyrus and CA_2,3 (DG/CA_2,3) are biased to differentiate highly similar memories, whereas CA₁ may integrate related events by representing them with overlapping neural codes. Here, we tested whether the formation of differentiated or integrated representations in hippocampal subfields depends on the strength of memory reactivation during learning. Human participants of both sexes learned associations (AB pairs, either face-shape or scene-shape), and then underwent fMRI scanning while they encoded overlapping associations (BC shape-object pairs). Both before and after learning, participants were also scanned while viewing indirectly related elements of the overlapping memories (A and C images) in isolation. We used multivariate pattern analyses to measure reactivation of initial pair memories (A items) during overlapping pair (BC) learning, as well as learning-related representational change for indirectly related memory elements in hippocampal subfields. When prior memories were strongly reactivated during overlapping pair encoding, DG/CA_2,3 and subiculum representations for indirectly related images (A and C) became less similar, consistent with pattern differentiation. Simultaneously, memory reactivation during new learning promoted integration in CA₁, where representations for indirectly related memory elements became more similar after learning. Furthermore, memory reactivation and subiculum representation predicted faster and more accurate inference (AC) decisions. These data show that reactivation of related memories during new learning leads to dissociable coding strategies in hippocampal subfields, in line with computational theories.

SIGNIFICANCE STATEMENT The flexibility of episodic memory allows us to remember both the details that differentiate similar events and the commonalities among them. Here, we tested how reactivation of past experience during new learning promotes formation of neural representations that might serve these two memory functions. We found that memory reactivation during learning promoted formation of differentiated representations for overlapping memories in the dentate gyrus/CA_2,3 and subiculum subfields of the hippocampus, while simultaneously leading to the formation of integrated representations of related events in subfield CA₁. Furthermore, memory reactivation and subiculum representation predicted success when inferring indirect relationships among events. These findings indicate that memory reactivation is an important learning signal that influences how overlapping events are represented within the hippocampal circuit.

Introduction

The hippocampus is composed of multiple subfields that contribute to memory processing and representation. Computational models propose that the anatomic properties of dentate gyrus and CA_2,3 (DG/CA_2,3) make these subfields ideal for pattern separation, or the automatic orthogonalization of highly similar cortical inputs though sparse firing (Marr, 1971; Schapiro et al., 2017). In contrast, the characteristics of CA₁ have been proposed to mediate memory integration, or the formation of overlapping representations that code the common features across related episodes (Eichenbaum et al., 1999; Schlichting and Preston, 2015; Schapiro et al., 2017). Electrophysiological research evinces such representational dissociations among subfields: DG/CA_2,3 ensembles elicit distinct firing patterns with only small changes in the perceptual features of an environment, whereas CA₁ activity patterns change gradually as environments become perceptually distinct (Leutgeb et al., 2004, 2007). Parallel work in humans has shown that changes in DG/CA_2,3 activation distinguish between highly similar object images or objects that share a similar context, whereas CA₁ responses do not (Bakker et al., 2008; Lacy et al., 2011; Dimsdale-Zucker et al., 2018). Subiculum, the output structure of the hippocampal circuit (O'Mara et al., 2001), may contribute to both pattern differentiation (Potvin et al., 2009) and integration (Schapiro et al., 2012).

However, such prior work has not considered how memory reactivation drives dissociable representational strategies within hippocampus, allowing representation learning to go beyond a simple transformation between external sensory input and memory output. Classic computational learning models propose that memory representations should adjust to predict likely outcomes in response to environmental cues, with integration occurring when stimuli predict the same outcome and differentiation when stimuli predict distinct outcomes (Rumelhart et al., 1986). However, recent fMRI findings indicate that differentiation can also occur when stimuli share a common association or outcome (Schlichting et al., 2015; Favila et al., 2016; Zeithamova et al., 2018). In those studies, hippocampal representations were more distinct for stimuli that shared a common outcome than stimuli with different outcomes. Such differentiation cannot be explained in terms of automatic separation of external input through sparse coding in DG/CA_2,3; rather, a recent theoretical perspective proposes that memory reactivation may account for how hippocampal representations change in the face of event overlap (Ritvo et al., 2019).

According to this theory, optimal learning reduces competition among memories through either differentiation or integration (Ritvo et al., 2019). Although sensory overlap in the environment is certainly one factor that might drive formation of optimal representations that reduce ambiguity (Leutgeb et al., 2004, 2007; Lacy et al., 2011; Yassa and Stark, 2011), what may be more essential is how overlapping sensory input drives reactivation of competing memories. Reactivated memories may be the “target” of learning more so than the sensory features that elicited reactivation. Thus, in the present study, we went beyond considering perceptual similarity as the sole driver of hippocampal representations and tested whether the reactivation of related memories in cortex during learning results in dissociable subfield coding. We hypothesized that memory reactivation would be modulated by event similarity across learning (Vieweg et al., 2015) and may thus be the key factor mediating the degree of representational overlap observed for similar events in hippocampal subfields (Ritvo et al., 2019). We also hypothesized that integration and differentiation would not be mutually exclusive outcomes in response to memory reactivation, but that reactivation would instead lead to the simultaneous formation of complementary differentiated and integrated representations in DG/CA_2,3 and CA₁.

To test these predictions, we parametrically manipulated perceptual similarity between overlapping events in an associative inference task (Fig. 1). Participants studied initial pairs and were scanned using high-resolution fMRI while learning overlapping pairs. We tested memory for the learned pairs and inferred knowledge of the indirect relationships across pairs, with inference performance serving as a behavioral index of integration (Shohamy and Wagner, 2008; Zeithamova et al., 2012). Critically, we quantified how memory reactivation during overlapping event learning impacted hippocampal subfield representation.

Figure 1.

Experimental design. A, Schematic of the behavioral task. Participants were first exposed to individually presented pictures (faces, scenes, and novel objects) that would later become indirectly related through associative learning (A and C items). Then, participants learned to associate initial pairs (face-shape or scene-shape AB associations) and were scanned while learning overlapping pairs (shape-object BC associations). Participants were scanned again in a postexposure phase while they viewed the same items from preexposure (A and C items). Participants then completed an across-episode inference task. Finally, participants completed a localizer task in which they viewed individually presented faces, scenes, objects, and shapes in a blocked design. B, Visual similarity manipulation. The similarity of the shared B item across pairs was parametrically manipulated. In this example, the top shape would have been seen in the initial AB pairs, whereas the bottom row represents the different shape morphs that could be seen when learning the overlapping BC pairs. The linking B item presented during overlapping pair learning could either be an exact match to the B item presented during initial (AB) pair learning, a high similarity or low similarity morph, or new (i.e., nonoverlapping) item. C, Subjective similarity of shape stimuli used for B linking items. An independent sample of participants rated visual similarity between parent shapes and shape morphs presented side by side using a 5 point Likert scale (1 = not at all similar, 5 = very similar). *p < 0.05 (paired t tests). Error bars indicate ± SEM.

Materials and Methods

Participants

Thirty-two right-handed individuals (15 females, aged 18-31 years, mean = 21.5 years) participated after giving informed consent in accordance with a protocol approved by the Institutional Review Board at the University of Texas at Austin. Participants received $25/h in compensation. Data from 6 participants were excluded from the analyses: 2 participants because of excessive head motion, 1 participant who withdrew from the experiment, 2 participants who had incomplete scanning sessions (the postexposure and/or localizer phases were not scanned), and 1 participant for image artifacts in the functional scans that precluded analysis of the preexposure and localizer phases. The remaining participants (n = 26, 14 females) were included in the analyses. We determined our final sample size based on related studies that used similar paradigms and analytical approaches (Zeithamova et al., 2012; Schlichting et al., 2015; Dimsdale-Zucker et al., 2018). Furthermore, this sample size gave us an estimated statistical power of >0.99 to detect an effect of visual similarity on across-episode inference accuracy based on pilot data from a separate group of participants (n = 30, 22 females, aged 18-22 years, mean = 18.9 years; repeated-measures ANOVA resulting in partial η squared (η²) = 0.280).

Stimuli

Stimuli were 58 unfamiliar faces (half male, half female, all white), 58 unfamiliar scenes (half natural, half manmade), 671 black shapes generated in MATLAB (for more information, see Visual similarity manipulation during new encoding), and 74 novel objects (Hsu et al., 2014; Schlichting et al., 2015). A subset of the stimuli was organized into 32 triads consisting of three items (A, B, C) that were used in the associative inference task (Fig. 1A). The A items consisted of faces (16) evenly split by gender, and scenes (16) evenly split by natural and manmade; all B items were shapes (56); all C items were novel objects (32). Another subset of stimuli (42 faces, 42 scenes, 42 objects, and 42 shapes) were used in the localizer task and were not seen during the associative inference task. Assignment of stimuli to the triads and localizer task was randomized across participants. Stimuli were presented using Psychtoolbox in MATLAB (Brainard, 1997; Pelli, 1997; Kleiner et al., 2007).

Task procedure

Initial pair (AB) learning

Participants learned the initial pairs (AB) across four study-test blocks. During the study phase, each of the 32 initial pairs was presented for 3.5 s with a 0.5 s intertrial interval (ITI). The A item (face or scene) was always presented on the left, and the B item (shape) was always presented on the right. After studying all of the pairs, participants were tested using a 3-alternative forced choice test. Participants were cued with the A item on the top of the screen and had to choose between the appropriate B item and two foils. The foils were shapes from other triads, such that participants could not base their decision on the familiarity of the shapes. Participants had 10 s to respond on each trial. After the participant's response, corrective feedback was provided at the end of each trial for 1 s. Test trials were separated by 0.5 s ITI. Anatomical images were collected during this phase.

Visual similarity manipulation during new encoding

To examine how the similarity of event elements affects memory reactivation and behavior, the visual similarity of the linking element (the shape, or B item) in the associative inference task was parametrically manipulated (Fig. 1B). We manipulated visual similarity based on prior work showing that hippocampal subfield responses are modulated by visual feature overlap among events (Leutgeb et al., 2004, 2007; Bakker et al., 2008; Lacy et al., 2011). There was a total of four conditions: exact match, high similarity, low similarity, and new. In the exact match condition, participants saw the exact same linking B shape when learning the initial pairs (AB) and overlapping pairs (BC). In the high and low similarity conditions, each shape seen in the overlapping pairs was a parametric morph of a shape from one of the initial pairs. “Parent” shapes were generated by taking 16 points distributed along the perimeter of a circle, randomly translating each point, and then connecting adjacent points to create edges using spline interpolation. The shapes in the high and low similarity conditions were generated by taking two parent shapes and averaging the coordinates of corresponding vertices using different weights. The high similarity shapes were weighted 80% to one parent shape and 20% to the other parent, while the low similarity shapes were weighted 70% to one parent and 30% to the other. In the new condition, participants saw a new shape paired with a novel object, making these pairs nonoverlapping with the initial pairs. The new pairs thus served as a baseline for associative learning. Each participant studied eight triads per visual similarity condition.

Differences in subjective similarity between the high and low similarity items were confirmed in an independent sample of 9 participants (8 females, aged 18-22 years, mean = 19.4 years). Participants in this sample rated visual similarity between parent shapes and shape morphs presented side by side using a 5 point Likert scale (1 = not at all similar, 5 = very similar) across 180 trials. Exact matches were rated as more similar than high similarity morphs (t₍₈₎ = 6.255, p < 0.001, Cohen's d = 2.085), high similarity morphs were rated as more similar than low similarity morphs (t₍₈₎ = 9.312, p < 0.001, d = 3.104), and low similarity morphs were rated as more similar than new items (t₍₈₎ = 10.021, p < 0.001, d = 3.340). One caveat to quantifying subjective similarity using this approach is that the comparison does not involve a memory component. It is possible that, if we inserted a delay between the presentation of two shapes, the observed subjective similarity function (Fig. 1C) may have differed; for instance, the subjective similarity differences between the high and low similarity conditions might have been less pronounced. While this measurement caveat might influence interpretation of the subjective similarity judgments themselves, it has less impact on interpretation of our central behavioral and neural analyses. We observe differences in memory performance and reactivation between the similarity conditions (including the high and low conditions) that indicate the four similarity conditions differentially impacted processing (see Results). Furthermore, our neural analyses assessing learning-related representational change focus on the high similarity condition only and do not rely on comparisons to the other similarity conditions (see Exposure of individual items before and after learning).

Overlapping pair (BC) learning

After participants learned the initial pairs, they were scanned while learning the overlapping pairs. This phase again consisted of four study-test blocks. During the study phase, the 32 pairs were presented using an event-related design, with pairs presented for 3.5 s followed by 8.5 s ITI of fixation. The C item (object) was always presented on the left, and the B item (shape) was always presented on the right. After each study phase, participants were tested on the BC pairs using a 3-alternative forced choice test, which was not scanned. Participants were cued with the C item on the top of the screen and had to choose between the appropriate B item and two foils. Feedback was not given during this phase. Participants had 10 s to respond on each test trial, and trials were separated by 0.5 s ITI.

Exposure of individual items before and after learning

Before learning the initial pairs and after learning the overlapping pairs, participants were exposed to individually presented A and C items (faces, scenes, and objects) from the high similarity condition. These exposure phases were limited to a single visual similarity condition to maximize the number of presentations for each stimulus and improve estimation of task-related activation patterns (see Estimation of individual stimulus patterns before and after learning). Using a single similarity condition also allowed us to control for the effects of visual similarity when calculating representational change. The high visual similarity condition was used because prior work in humans has shown that highly visually similar stimuli elicit differential responses in DG/CA_2,3 and CA₁ (Lacy et al., 2011).

In each exposure run, participants were scanned while items were presented for 1 s with a 3 s ITI. While each item was on the screen, participants completed a change-detection task by indicating via button press whether a superimposed black cross changed color to green or blue 100-200 ms after stimulus onset (Kriegeskorte et al., 2008; Schlichting et al., 2015). There were four repetitions of each item per run, and a total of four runs each in the preexposure and postexposure phases. Trials were pseudorandomized such that items within a triad were presented with at least two interleaved items from other triads. Additionally, 20% of trials were null (i.e., there was no object or change detection task) to improve item-level activation estimation in the analysis; these null trials were placed randomly between item presentation trials. Trial order and timing were identical in the preexposure and postexposure phases. Accuracy on the change detection task was monitored to ensure that participants were paying attention to the task but was not considered further.

There was also a nonscanned preexposure phase for items from the exact match, low similarity, and new conditions that occurred before the first scanned preexposure run. The purpose of this phase was to equate familiarity of the A and C items in the exact match, low similarity, and new conditions to items in the high similarity condition before pair learning. The nonscanned exposure was similar to the scanned exposure phases, except the ITI was 0.5 s and there were no null trials.

Associative inference (AC) test

Following the postexposure phase, participants were given a surprise test on the indirect relationships between the A and C items that shared a common associate (B). The inference test was performed inside the scanner but was not scanned. In this phase, participants were cued with the C item (object) and could choose between A items of the same category (i.e., three faces or three scenes). On face trials, participants were instructed to choose the person who would most likely own the cued object. On scene trials, they were instructed to choose the location in which they would most likely find the cued object. Critically, at no point were participants explicitly instructed about the visual similarity manipulation or the overlap across learning. Participants were given 10 s to respond. No feedback was given.

Localizer

After the inference test, participants were scanned in a localizer task. In this task, participants viewed a series of stimuli from the four stimulus categories used in the experiment: faces, scenes, shapes, and objects. Stimuli were presented in a blocked design, with each block consisting of eight images presented for 2.5 s each with 0.5 s ITI. During each stimulus block, participants completed a one-back memory task in which they had to detect a repeated stimulus. There was one repeated stimulus in each block. Accuracy on the one-back task was monitored to ensure that participants were paying attention to the task but was not considered further. Blocks were separated by 8 s of fixation. Participants completed three runs of the localizer task, with two blocks per stimulus type per run.

fMRI data collection and preprocessing

Data were collected with a 3T Siemens Skyra. There was a total of 15 functional scans (TR = 2000 ms, TE = 30 ms, flip angle = 73°, 1.7 mm isotropic voxels, EPI, multiband acceleration factor = 3) across the preexposure, overlapping pair study, postexposure, and localizer phases. Three field maps (TR = 589 ms, TE = 5 ms/7.46 ms, 1.5 × 1.5 × 2 mm voxels, flip angle = 5°) were collected to correct for distortions in the magnetic field: one immediately before the preexposure phase to correct the preexposure scans, one before the overlapping pair study phase to correct the study and postexposure scans, and one before the localizer phase to correct the localizer scans. A T1-weighted 3D MPRAGE volume was collected (TR = 1900 ms, TE = 2.43 ms, flip angle = 9°, 1 mm isotropic voxels) to facilitate alignment and normalization of the functional data to an anatomic template. Two coronal T2-weighted structural scans, aligned perpendicular to the hippocampal long axis, were collected (TR = 13,150 ms, TE = 82 ms, 0.4 mm × 0.4 mm in-plane, 1.5 mm through-plane) and then averaged for subfield segmentation.

Functional and anatomic images were preprocessed using FMRIB Software Library version 5.0.9 (FSL: http://fsl.fmrib.ox.ac.uk/fsl/) and Advanced Normalization Tools (ANTS) version 2.1 (Avants et al., 2011). Functional scans were motion-corrected using MCFLIRT in FSL and then registered to the final overlapping pair study run using affine transformations in ANTS. Nonbrain structures were removed from the functional scans and MPRAGE using BET in FSL. Additional data processing was conducted using FEAT (FMRI Expert Analysis Tool) version 6.00, part of FSL. The following prestatistics processing was applied to all functional images; coregistration with the MPRAGE and field map-based EPI unwarping using FUGUE (Jenkinson, 2003); grand-mean intensity normalization of the entire 4D dataset by a single multiplicative factor; high-pass temporal filtering (Gaussian-weighted least-squares straight line fitting, with σ = 64 s). Spatial smoothing using a Gaussian kernel of FWHM 4 mm was applied to the overlapping pair learning and localizer scans.

ROIs

Anatomical ROIs included whole-brain gray matter for the reactivation analysis and hippocampal subfields for the neural coding analysis. A whole-brain gray matter mask was created for each participant in native space using FAST (Zhang et al., 2001), part of FSL, with the MPRAGE. Gray matter masks were then moved into functional resolution using linear transformations in ANTS. Within hippocampus, activation patterns in subfields CA₁, a combined DG/CA_2,3 region, and subiculum were analyzed. Hippocampal subfields were identified in the head and body of the hippocampus in native space by reverse normalizing masks from an open source template with segmented subfields (Schlichting et al., 2019) to the average T2 coronal image of each participant using nonlinear SyN transformations in ANTS. This procedure has been shown to provide results comparable to manual tracing (Schlichting et al., 2019). Masks were then inspected and edited manually for each participant to remove voxels outside the hippocampus and ensure accurate segmentation based on established protocols (West and Gundersen, 1990; Duvernoy, 1998; Mai et al., 2007). Finally, the subfield masks were transformed to the space of the functional scans by first registering the average coronal image to the MPRAGE using linear transformations and then applying the previously calculated transform to functional space.

Quantification and statistical analysis

Decoding memory reactivation during overlapping event learning

To measure reactivation of encoding patterns related to the initial pairs during overlapping pair learning, we used a pattern classification analysis in PyMVPA (Hanke et al., 2009). If participants reactivated related information (i.e., A face and scene items from AB pairs) when learning overlapping pairs (BC shape-object pairs), then a pattern classifier trained on the localizer data should be sensitive to the category of information (either face or scene) that is being reactivated (Polyn et al., 2005; Kuhl et al., 2011; Zeithamova et al., 2012). Thus, we trained the pattern classifier with data from the localizer phase and then applied the classifier to the overlapping pair learning phase. We operationalized memory reactivation as classifier evidence for the category of the A items (i.e., face or scene) from the initial AB pairs related to the overlapping BC pairs.

We measured memory reactivation using a multistep procedure. First, we ran a whole-brain searchlight (Kriegeskorte et al., 2006) to identify regions where information about A items was reinstated during overlapping pair learning. In each searchlight sphere (radius = 3 voxels, volume = 123 voxels), a linear support vector machine was trained to differentiate neural patterns from the localizer phase associated with faces, scenes, objects, and shapes. To account for hemodynamic lag, each functional image was labeled by taking the trial labels and time-shifting them forward by 4 s (two TRs). The trained classifier was then applied to neural patterns from the overlapping pair learning phase, which was also time-shifted by 4 s. Trial-level reactivation estimates were extracted by taking classifier evidence for the category associated with the A item of each triad (e.g., classifier evidence for faces for face-shape-object triads) for the two TRs corresponding to the presentation of each pair. Classifier evidence values were sorted into two sets: a reactivation set and baseline set. The reactivation set contained classifier evidence values from the exact match, high similarity, and low similarity trials. The baseline set contained face and scene evidence values from trials in the new condition. Because shape-object pairs in the new condition did not overlap with any of the previously learned pairs, they should not elicit reactivation of face or scene memories. The final reactivation index was calculated in each sphere by taking the difference between the average evidence for the reactivation set and the average of the baseline set.

To test the significance of this reactivation index, we compared the actual reactivation index to a null distribution in each searchlight sphere. The null distribution was created over 1000 iterations by shuffling classifier evidence values across the reactivation and baseline sets and then recalculating the reactivation index every iteration. The center voxel of each searchlight sphere reported the proportion of the null distribution with reactivation indices greater than or equal to the observed reactivation index (i.e., p value). To identify reactivation regions across participants, individual participant searchlight maps were normalized to a group template for significance testing. The p value images were converted to z-statistic images and then warped to the MNI 152 anatomic template (resampled to the resolution of the functional scans, 1.7 mm isotropic voxels) using nonlinear SyN transformations in ANTS. Voxelwise, nonparametric permutation testing was done using Randomise in FSL over 5000 iterations (Winkler et al., 2014). Significant clusters were identified by applying a voxel threshold of p < 0.01 (uncorrected) and a cluster threshold of p < 0.05. Thresholds were calculated using the AFNI (Cox, 1996) function 3dClustSim with smoothness estimates derived from the study phase using 3dFWHMx based on the spatial AutoCorrelation Function. Cluster extent was determined using two-sided thresholding with second-nearest neighbor clustering.

To confirm that the reactivation measure was not driven by a single stimulus category, we further interrogated searchlight clusters to test whether reactivation varied with stimulus category (face or scene) of the A item in a post hoc analysis. The significant clusters identified in the reactivation searchlight analysis were converted to binary masks and reverse-normalized into native space using ANTS. Then, the reactivation analysis was repeated in each functional ROI for every participant. We used repeated-measures ANOVA with region and stimulus category as factors to assess whether reactivation in each region differed as a function of stimulus category.

While our initial searchlight analysis localized regions in which reactivation occurred above baseline, we also ran an independent searchlight to identify regions where reactivation strength varied with visual similarity. This searchlight used a similar approach to the analysis measuring overall reactivation, but with an additional level that compared classifier evidence for reactivation between the exact match condition and the other similarity conditions (i.e., the high similarity condition and low similarity condition combined). The effect of similarity was calculated in each sphere by taking the difference between the average evidence for the exact match condition and the average evidence for the high and low similarity conditions combined. This difference was then compared with a null distribution in each searchlight sphere, which was created over 1000 iterations by shuffling classifier evidence values across the exact match and similarity morph conditions. Normalization to the group template, statistical testing, and cluster correction were identical to the searchlight identifying reactivation above baseline.

Estimation of individual stimulus patterns before and after learning

We derived estimates of neural activation patterns elicited by each of the A (faces, scenes) and C (novel 3D objects) stimuli from the preexposure and postexposure phases using a GLM with a least squares–separate approach (Mumford et al., 2012) in the native space of each participant. Each of the 16 objects from the scanned exposure phases (i.e., the eight A items and eight C items from the high similarity condition) were modeled iteratively in each run of the preexposure and postexposure phases separately (Schlichting et al., 2015).

Object presentations were modeled as a 1 s event, and the regressor for each object included all four repetitions within a scanning run. Each of the 16 object regressors was convolved with the canonical double Γ HRF. Temporal filtering was then applied. The GLMs included additional confound regressors: motion parameters, their temporal derivatives, framewise displacement, and DVARS (Power et al., 2012; Schlichting and Preston, 2014; Schlichting et al., 2015). Additional motion regressors were added for time points during which head motion exceeded both 0.5 mm for framewise displacement and 0.5% change in BOLD signal for DVARS (Power et al., 2012). Beta images were generated for each A and C item for every preexposure and postexposure run, totaling 128 statistics images per participant.

Quantifying learning-related changes in hippocampal subfield neural similarity

Pattern differentiation and memory integration in hippocampus were indexed using a representational similarity analysis (Kriegeskorte et al., 2008) implemented in PyMVPA (Hanke et al., 2009). Searchlights were run separately within anatomically defined DG/CA_2,3, CA₁, and subiculum in the native space of each participant. Within each searchlight sphere (radius = 2 voxels, volume = 33 voxels) (Schapiro et al., 2012), similarity matrices were generated by calculating the pairwise Pearson's correlation values for the 128 statistics images corresponding to the A and C items in the preexposure and postexposure runs, transformed to Fisher's z. Then, change in pattern similarity due to learning was measured by subtracting the preexposure similarity values from the postexposure similarity values in corresponding cells.

After the change in pattern similarity (hereafter referred to as Δ) was calculated, Δ values were sorted depending on whether the value was for a within-triad comparison or an across-triad comparison. These two sets of values allowed us to determine how representational change was influenced by event overlap due to learning (within-triad comparison set) relative to a baseline that simply reflected repeated exposure without event overlap (across-triad comparison set). Importantly, only Δ values that reflected across-run correlations were used to reduce bias that could be introduced from autocorrelation in the BOLD signal (Mumford et al., 2012).

To assess the effect of reactivation during learning on representational change, the within-triad Δ values were further subdivided based on the strength of memory reactivation during learning of the overlapping pairs. For each participant, reactivation strength was calculated for every triad by taking the mean reactivation index across the network of regions identified in the reactivation searchlight analysis (see Fig. 3A), averaged across study blocks. Triads were then divided into stronger reactivation triads and weaker reactivation triads using a median split on the average reactivation values. Thus, within-triad Δ comparisons were further sorted into a stronger reactivation within-triad Δ set and a weaker reactivation within-triad Δ set in each searchlight sphere. Finally, all Δ sets were averaged to create three summary values: average within-triad similarity change for stronger reactivation triads (Δ_{Within stronger}), average within-triad similarity change for weaker reactivation triads (Δ_{Within weaker}), and average across-triad similarity change (Δ_Across). We compared these summary values to determine whether neural coding varied as a function of reactivation strength.

Figure 3.

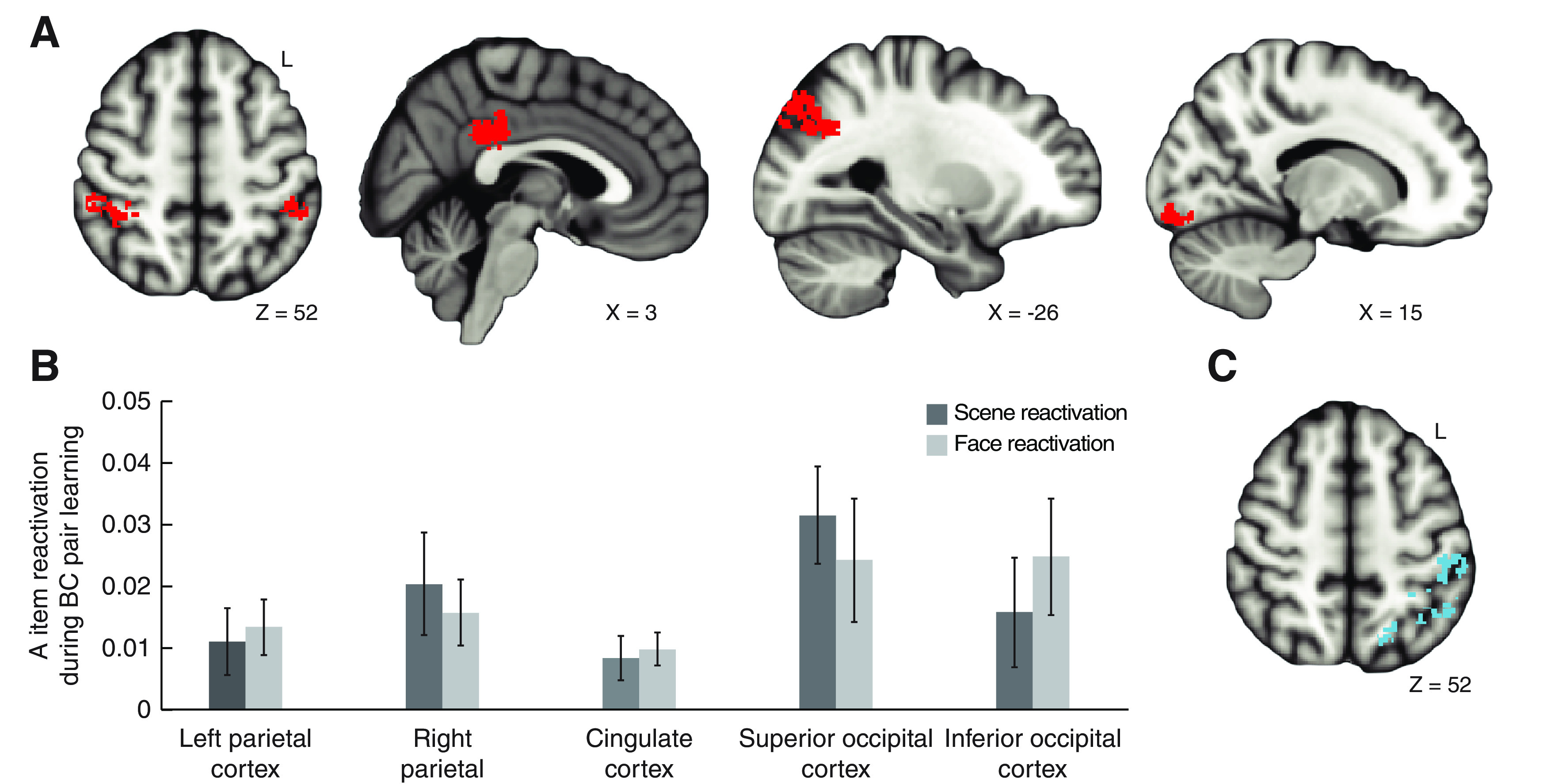
Memory reactivation during overlapping pair learning. A, Results of the searchlight analysis identifying regions where classifier evidence for A item reactivation exceeded baseline (i.e., evidence during new, nonoverlapping pairs) when participants were learning the overlapping BC pairs. B, Evidence for reactivation of A items as a function of stimulus category (face and scene) during overlapping pair learning for each of the regions identified in A. Error bars indicate ± SEM. C, Results of the searchlight analysis identifying regions where classifier evidence for A item reactivation varied with visual similarity of the linking B item (exact match > high and low similarity). One cluster in left parietal cortex overlapped with the cluster identified in the searchlight analysis comparing reactivation to baseline (A, leftmost image); the other cluster extended into occipital cortex. All searchlight clusters are displayed on the 1 mm MNI 152 anatomic template.

Neural coding was assessed using four searchlight contrasts (Schlichting et al., 2015) (see Fig. 4B). Two analyses identified hippocampal voxels for which there was memory integration or differentiation across all triads, regardless of reactivation strength. Integration_Overall was calculated as (Δ_{Within stronger} – Δ_Across) + (Δ_{Within weaker} – Δ_Across), reflecting greater within-triad than across-triad similarity after learning across all degrees of reactivation. Differentiation_Overall was calculated as (Δ_Across – Δ_{Within stronger}) + (Δ_Across – Δ_{Within weaker}), reflecting lesser within-triad than across-triad similarity across all degrees of reactivation. Two additional analyses identified voxels for which neural coding varied as a function of reactivation strength (Integration_Reactivation and Differentiation_Reactivation). The Integration_Reactivation searchlight identified voxels for which integration occurred to a greater extent for stronger reactivation triads. Integration_Reactivation was calculated as (Δ_{Within stronger} – Δ_{Within weaker}). In contrast, the Differentation_Reactivation searchlight identified voxels for which differentiation occurred to a greater extent for stronger reactivation triads. Differentiation_Reactivation was calculated as (Δ_{Within weaker} – Δ_{Within stronger}).

Figure 4.

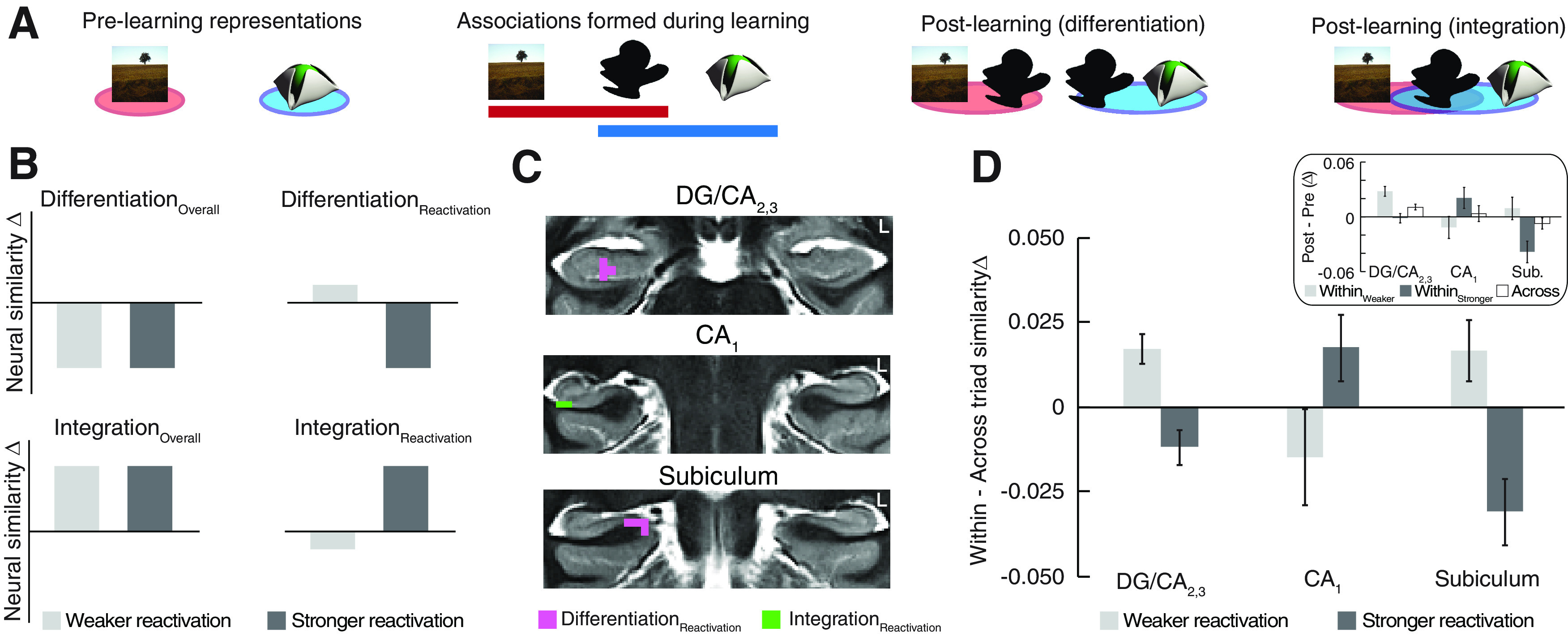
Assessing learning-related representational change as a function of memory reactivation during learning. A, Predictions for memory formation through associative learning. Before learning, individual A and C items in the preexposure phase do not share any relationships. After learning, the representations of A and C items may shift as a function of their shared relationships with B items. We tested for two neural outcomes; in the case of differentiation, the neural patterns for indirectly related A and C items are predicted to be less similar in the postexposure phase relative to the prelearning representations. In contrast, for memory integration, the neural similarity of indirectly related A and C items is predicted to increase from prelearning to postlearning, reflecting the formation of overlapping neural codes linking elements experienced across events. B, Four searchlight contrasts were used to determine whether memory representation in hippocampal subfields varied with memory reactivation strength during learning. Two of the searchlights identified regions in which differentiation or integration occurred across all degrees of reactivation strength. Another set of searchlights identified regions in which neural coding varied as a function of reactivation. C, Learning-related representational change in hippocampus. Subregions of DG/CA_2,3 and subiculum showed differentiation of the indirectly related elements of overlapping memories, but only when reactivation was stronger during learning. In contrast, a subregion of CA₁ showed evidence of memory integration, but again only when reactivation was stronger during overlapping pair learning. Hippocampal regions are depicted on an open source high-resolution group T2 template created for hippocampal subfield analyses (Schlichting et al., 2019). D, Neural similarity change in the clusters identified in the searchlight analysis (C) after reverse normalization to native space, confirming the predicted pattern of results from B. Inset, The same data separately for the within-triad and across-triad similarity measures before calculating the difference scores. Because this analysis is based on voxels identified in the searchlight analysis, it is not fully independent. Error bars indicate ± SEM.

The significance of each of these calculations was determined by comparing the computed similarity change values to a null distribution in each searchlight sphere. The null distribution was created over 1000 iterations by shuffling cells across the Δ_{Within stronger}, Δ_{Within weaker}, and Δ_Across sets and then recalculating the statistic of interest for each iteration. The center voxel of each searchlight sphere reported the proportion of the null distribution with values greater than or equal to the observed similarity change (i.e., p value). Significant clusters were identified using the same method as the reactivation searchlights, except the z-statistic images were warped to a functional-resolution hippocampal template rather than the resampled MNI template for the group-level analysis. Normalized searchlight maps were then masked by each anatomic hippocampal subfield template before cluster correction to ensure clusters were exclusive to each hippocampal subfield.

Post hoc analyses further interrogated the direction of representational change observed in each subfield identified from this searchlight analysis. An important caveat to these post hoc analyses is that they are not completely unbiased because they compare sets of voxels preselected to exhibit specific effects based on the searchlight contrasts. Thus, our follow-up analyses did not directly compare the Δ_Within values for the stronger and weaker reactivation items. Our post hoc analyses instead focused on the magnitude of Δ_Across values to test whether there were global shifts in neural similarity across the preexposure and postexposure phases, in addition to comparing Δ_Within values to Δ_Across values to quantify the degree of learning-related integration and differentiation.

For these post hoc analyses, similarity change in DG/CA_2,3, CA₁, and subiculum was calculated for each participant in native space. The searchlight clusters identified by the group searchlight analyses were converted into masks and reverse-normalized into each participant's native space using nonlinear transformations in ANTS. For each participant, the native space clusters were then dilated with FSL using a 3 × 3 × 3 mm box as a kernel. To ensure that clusters were still restricted to their respective subfield when converted to participant native space, each cluster was masked using anatomic subfield masks defined for each individual participant. One participant had a CA₁ cluster in native space without a sufficient number of voxels for representational similarity analysis (<10 voxels) and was excluded from subsequent analysis of this subfield. For the remaining participants, we computed the average similarity change within each cluster separately for triads associated with stronger reactivation during learning, those associated with weaker reactivation during learning, and the across-triad baseline.

Quantifying the relationship between neural measures and behavior

The relationship between behavior and our neural measures of reactivation and representational change was assessed using a Linear Ballistic Accumulator (LBA) model to fit performance on the inference test (Morton et al., 2020). For each participant and subfield (CA₁, DG/CA_2,3, and subiculum), we calculated the z score of similarity change between A and C items from prelearning to postlearning (Δ) for each triad. We also calculated the z score of A item reactivation across triads for each participant. We then used the LBA model to fit behavioral responses and response times during the AC inference test, using similarity change and reactivation as predictors of variability between triads. We used a multilevel Bayesian approach to estimate mean slope parameters reflecting the relationship between the neural measures and AC inference performance. Positive slopes for the Δ measures indicate larger similarity values between A and C items after learning are associated with faster and more accurate inference. Positive slopes for the reactivation measure indicate that greater reactivation is associated with faster and more accurate inference.

Model definition

The LBA model (Brown and Heathcote, 2008) assumes that, on each trial, the starting point k of each accumulator is drawn randomly from a uniform distribution on the interval [0, A]. Each accumulator then follows a line with a slope of d until it reaches the response threshold b. On each trial, the slope d of accumulator i is drawn from a normal distribution with mean v_i and SD s (here, fixed at 1). The time for an accumulator to reach the threshold is (b − k)/d. We modeled the three-alternative forced-choice inference tests using three accumulators with mean drift rates v₁ (for the correct response) and v₂ (for the other two responses).

As derived in the initial description of the LBA model (Brown and Heathcote, 2008), the probability density function (PDF) for accumulator i at time t is as follows:

$$f_i(t)=\frac{1}{A}\left[-v_i\Phi \left(\frac{b-A-t{v}_i}{ts}\right)+s\varphi \left(\frac{b-A-t{v}_i}{ts}\right)+v_i\Phi \left(\frac{b-t{v}_i}{ts}\right)-s\varphi \left(\frac{b-t{v}_i}{ts}\right)\right]$$

Where ϕ and Φ are the probability density function and cumulative distribution functions, respectively, of the standard normal distribution. The cumulative distribution function (CDF) for accumulator i at time t is as follows:

$$F_i(t)=1+\frac{b-A-t{v}_i}{A}\Phi \left(\frac{b-A-t{v}_i}{ts}\right)-\frac{b-t{v}_i}{A}\Phi \left(\frac{b-t{v}_i}{ts}\right)+\frac{ts}{A}\varphi \left(\frac{b-A-t{v}_i}{ts}\right)-\frac{ts}{A}\varphi \left(\frac{b-t{v}_i}{ts}\right)$$

The PDF for accumulator i hitting the threshold first, at time t, is the probability of accumulator i finishing at time t, conditional on the other accumulators not having finished yet as follows:

$${\text{PDF}}_i\text{(}t\text{)}=f_i(t){\displaystyle \prod _{j\ne i}(1-F_{j(t)})}$$

Because drift rate d is drawn from a normal distribution, there is some probability of no accumulators finishing. Following prior work (Brown and Heathcote, 2008; Annis et al., 2017), we conditionalized on the probability of at least one accumulator having a positive drift rate as follows:

$$P(\text{resp})=1-{\displaystyle \prod _{i=1}^N\varphi \left(-\frac{v_i}{s}\right)}$$

Nondecision time (e.g., time to perceive the test stimuli) was modeled as a fixed time interval τ. The probability of a correct response at time t was as follows:

$$P(\text{correct,}t)=\frac{{\text{PDF}}_{\text{1}}(t-\tau )}{P(\text{resp})}$$

The probability of an incorrect response at time t was as follows:

$$P(\text{incorrect,}t)=\frac{{\text{2PDF}}_{\text{2}}(t-\tau )}{P(\text{resp})}$$

The model was implemented in Python 3.7 using PsiReact 0.2 (Morton et al., 2020). We used Bayesian sampling to estimate parameters, using the No U-Turn Sampler (NUTS) implemented in pyMC 3.9.2. We fixed s = 1 and b = 8 to improve stability of parameter estimates. An intercept drift rate parameter β_0,i for correct responses was estimated for each participant i. We also estimated the drift rate of incorrect responses v_2,i for each participant. We used the within-participant z score of similarity change for each subfield (e.g., z_CA1,ij) and reactivation estimates (z_React,ij) to predict the drift rate on each trial j. Trial-level variability in drift rate was modeled as a linear combination of the similarity change and reactivation z scores. The correct item drift rate v_1,ij for participant i, trial j was as follows:

$$v_{\text{1,}ij}\text{=}{\beta }_{\text{0,}i}\text{+}{\beta }_{\text{CA1,}i}{z}_{\text{CA1,}ij}\text{+}{\beta }_{\text{DG/CA2,3,}i}{z}_{\text{DG/CA2,3,}ij}\text{+}{\beta }_{\text{Subiculum,}i}{\text{z}}_{\text{Subiculum,ij}}\text{+}{\beta }_{\text{React,}i}{\text{z}}_{\text{React,ij}}$$

The slope parameters (e.g., β_CA1,i) were estimated for each participant i. To improve robustness of estimates for the individual participant parameters, we defined them as being drawn from a group-level normal distribution. The prior distributions for parameters were as follows:

$${\beta }_{\text{0,}i}\text{∼ Normal(0,4)}$$

$${\beta }_{\text{CA1,i}}\text{∼ Normal(}{\mu }_{\text{CA1}}\text{,}{\sigma }_{\text{CA1}}\text{)}$$

$${\beta }_{\text{DG/CA2,3,i}}\text{∼ Normal(}{\mu }_{\text{DG/CA2,3}}\text{,}{\sigma }_{\text{DG/CA2,3}}\text{)}$$

$${\beta }_{\text{Subiculum,i}}\text{∼ Normal(}{\mu }_{\text{Subiculum}}\text{,}{\sigma }_{\text{Subiculum}}\text{)}$$

$${\beta }_{\text{React,i}}\text{∼ Normal(}{\mu }_{\text{React}}\text{,}{\sigma }_{\text{React}}\text{)}$$

$$v_{\text{2,}i}\mathrm{\sim \; Normal(}{\mu }_{\text{2}}\text{,}{\sigma }_{\text{2}}\text{)}$$

$$\tau \text{∼ Unif(0,2)}$$

$$\text{A∼Unif(0,8)}$$

Prior distributions for group-level parameters were as follows:

$${\mu }_{\text{CA1}}\text{,}{\mu }_{\text{DG/CA2,3}}\text{,}{\mu }_{\text{Subiculum}}\text{,}{\mu }_{\text{React}}\text{,}{\mu }_2\text{∼ Normal(0,4)}$$

$${\sigma }_{\text{CA1}}\text{,}{\sigma }_{\text{DG/CA2,3}}\text{,}{\sigma }_{\text{Subiculum}}\text{,}{\sigma }_{\text{React}}\text{,}{\sigma }_{\text{2}}\mathrm{\sim \; Gamma(1}\mathrm{.5,0}\text{.75)}$$

For each of four chains, there was a tuning phase of 1000 iterations with a target acceptance rate of 0.99, followed by 5000 samples. Convergence was assessed using bulk effective sample size and rank-normalized split potential scale reduction statistic $R^{^}$ (Vehtari et al., 2017). We assessed the fit of the model by calculating mean posterior parameters for each trial as well as simulating responses and response times. We simulated 50 replications of each trial to obtain a robust estimate of model performance. Finally, we calculated the 95% high-density interval (HDI) for each of the group-level mean parameters (e.g., μ_CA1 for CA₁) to determine whether they were different from zero, indicating a relationship between similarity change or reactivation and AC inference performance.

Results

Behavioral performance

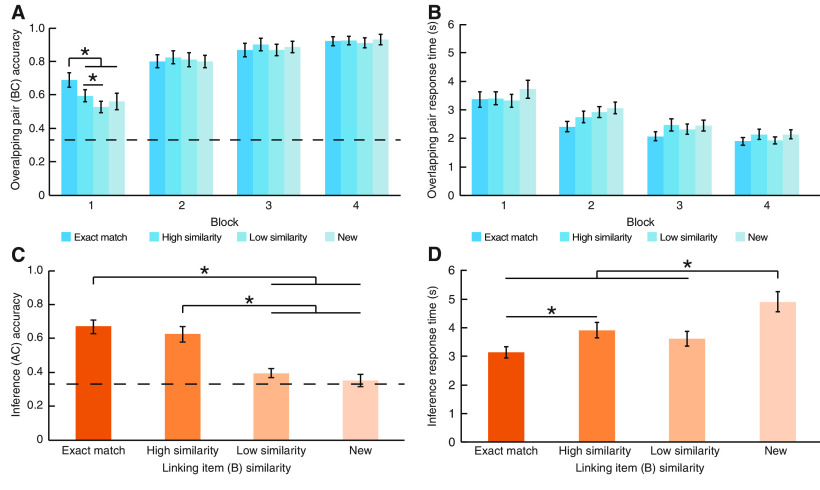
By the end of the initial pair (AB) learning phase, participants had formed strong memories of the face-shape and scene-shape pairs. All participants were above chance on the final test (mean proportion correct = 0.91, SD = 0.01) and were therefore included in subsequent analyses. Memory for the overlapping (BC) shape-object pairs was influenced by the visual similarity of the linking item across learning (Fig. 2A,B). A repeated-measures ANOVA with the within-subjects factors of overlapping pair block (1, 2, 3, 4) and visual similarity (exact match, high similarity, low similarity, new) revealed that visual similarity modulated memory accuracy (main effect of block, F_(3,75) = 79.93, p < 0.001, η² = 0.762; block × visual similarity interaction, F_(9,225) = 2.88, p = 0.003, η² = 0.103) and response time (main effect of similarity on correct trials, F_(3,72) = 5.14, p = 0.003, η² = 0.176). For the first learning block of overlapping pairs, performance was superior (Fig. 2A) when the linking item (B) was an exact match to the initially learned pairs (AB) relative to all other conditions. There was an effect of visual similarity in the first test block (effect of visual similarity in the first run, F_(3,75) = 6.901, p < 0.001, η² = 0.216) but not in subsequent runs (F values ≤ 0.479, all p ≥ 0.698, all η² ≤ 0.019). In the first run, post hoc paired t tests revealed that accuracy was highest for pairs with an exact match relative to all other pairs (compared with high similarity: t₍₂₅₎ = 3.33, p = 0.003, d = 0.654; low similarity: t₍₂₅₎ = 4.52, p < 0.001, d = 0.894; new: t₍₂₅₎ = 2.74, p = 0.011, d = 0.539). Performance was greater for high similarity pairs than low similarity pairs (t₍₂₅₎ = 2.306, p = 0.03, d = 0.459). There was no difference in performance between the high similarity and new pairs (t₍₂₅₎ = 0.87, p = 0.394, d = 0.172) or the low similarity and new pairs (t₍₂₅₎ = 0.76, p = 0.452, d = 0.151). When collapsed across block, pairs with exact matches had the fastest response time (Fig. 2B) on correct trials (compared with all other conditions, t values ≥ 2.206, all p < 0.05, all d ≥ 0.445). Response time did not differ between the high similarity, low similarity, or new pairs (all t values ≤ 1.748, all p > 0.05, all d ≤ 0.348).

Figure 2.

Behavioral performance. A, Overlapping pair (BC) test accuracy and (B) response time (correct trials only) by learning block for each similarity condition. C, Across-episode (AC) inference accuracy and (D) response time (correct trials only) for each similarity condition. *p < 0.05 (paired t tests). Error bars indicate ± SEM. Dotted lines indicate chance performance on the 3-alternative forced choice tests.

Visual similarity of the linking item also influenced a cross-episode inference accuracy (F_(3,75) = 26.61, p < 0.001, η² = 0.516). Participants were more likely to infer a relationship among indirectly related memory elements (AC) when the linking item (B) was an exact match or highly similar across overlapping pairs (Fig. 2C). Inference performance did not differ between exact match and high similarity triads (t₍₂₅₎ = 1.20, p = 0.24, d = 0.230), but performance for exact match triads was superior to both low similarity triads (t₍₂₅₎ = 6.82, p < 0.001, d = 1.327) and new triads (t₍₂₅₎ = 6.61, p < 0.001, d = 1.286). Likewise, performance for high similarity triads exceeded low similarity triads (t₍₂₅₎ = 5.05, p < 0.001, d = 0.987) and new triads (t₍₂₅₎ = 5.38, p < 0.001, d = 1.055). Follow with performance (Inference performance did not differ between the low similarity and new triads (t₍₂₅₎ = 1.17, p = 0.254, d = 0.224). However, performance for low similarity triads was reliably better than chance (t₍₂₅₎ = 2.22, p = 0.04, d = 0.435), whereas performance for new triads was not (t₍₂₅₎ = 0.47, p = 0.64, d = 0.093).

Inference decisions were also faster for the exact match and high similarity conditions relative to the new condition (F_(3,72) = 11.79, p < 0.001, η² = 0.329), with inferences for the exact match condition being fastest overall (Fig. 2D). Response time was faster for exact match triads relative to high similarity conditions (t₍₂₅₎ = 3.41, p = 0.002, d = 0.669) and new triads (t₍₂₄₎ = 5.00, p < 0.001, d = 0.999), but no different from low similarity triads (t₍₂₅₎ = 1.64, p = 0.114, d = 0.321). Response time was faster for high similarity triads compared with new triads (t₍₂₄₎ = 2.93, p = 0.007, d = 0.585), but did not differ from low similarity triads (t₍₂₅₎ = 1.11, p = 0.28, d = 0.217). Low similarity triads were faster than new triads (t₍₂₄₎ = 3.86, p = 0.001, d = 0.773). Together, these findings show that associative memory and a cross-episode inference, two processes that are thought to be supported by hippocampal subfields (Schapiro et al., 2017), are influenced by the perceptual similarity of shared event elements, with facilitated performance with higher levels of a cross-episode similarity.

Reactivation of overlapping memories during learning

To test how cortical memory reactivation during overlapping pair learning impacts hippocampal subfield representations, we first used a searchlight analysis to identify where information about the initial pairs was reactivated in cortex during learning. Within each searchlight sphere, a pattern classifier was trained on data from a localizer phase and then applied to the overlapping pair study phase (Zeithamova et al., 2012). The searchlight identified regions in which classifier evidence for the target category of the related item (face or scene A items from the initial pairs) exceeded a baseline index of classifier evidence for the same category derived from the new (or nonoverlapping) trials. We found evidence that related memories were reactivated when learning the overlapping pairs in posterior cingulate cortex, occipital cortex, and parietal cortex (Fig. 3A).

Importantly, there were no differences in reactivation strength as a function of A item category (face, scene) across regions identified in the searchlight analysis (Fig. 3B). A repeated-measures ANOVA with the within-subjects factors of region (left parietal, right parietal, cingulate, superior occipital, inferior occipital) and stimulus category (face, scene) demonstrated that reactivation varied across regions (main effect of region, F_(4,100) = 2.84, p = 0.028, η² = 0.102) but did not differ by stimulus category (main effect of category, F_(1,25) = 0.002, p = 0.967, η² = 0; category × region interaction, F_(4,100) = 0.375, p = 0.826, η² = 0.015). Thus, our results were not driven by a single stimulus category and reflect memory reactivation rather than the engagement of category-specific processing regions.

We further tested whether visual similarity of the shared B item across learning influenced the strength of memory reactivation for the A items. We predicted that memory reactivation during learning would be stronger for pairs linked by a more visually similar item. Using a similar approach to the previous analysis, a separate searchlight analyses identified regions where classifier evidence for the related A item was greater for the exact match condition than the high and low similarity conditions. Consistent with our hypothesis, we found that the similarity of event components modulated the strength of memory reactivation in left parietal cortex and occipital cortex (Fig. 3C).

Memory reactivation impacts neural coding in hippocampal subfields

To test our hypothesis that reactivation of related memories during new encoding would lead to dissociable representation of overlapping memories in DG/CA_2,3 and CA₁, we quantified hippocampal subfield coding as a function of memory reactivation strength during learning. Both before and after learning the pairs, participants were scanned while viewing individual images of the A and C items from overlapping pairs in the high similarity condition (Fig. 1A). We indexed differentiation and integration by measuring learning-related changes in pattern similarity for indirectly related A and C items from the same triad (Schlichting et al., 2015). Similarity changes within the same triad were compared with a baseline of similarity changes between items in different triads. We measured differentiation by testing for a decrease in pattern similarity between A and C items after learning (Fig. 4A). In contrast, integration would be marked by increased pattern similarity among indirectly related A and C items, reflecting formation of overlapping codes for related memories (Fig. 4A).

To assess the impact of memory reactivation during learning on neural coding of indirectly related memory elements, we calculated representational change for triads based on the strength of reactivation across overlapping learning trials. For each participant, we sorted overlapping pairs into those associated with stronger and weaker reactivation of the corresponding initial pair, based on a median split of averaged reactivation indices across all clusters identified in the reactivation searchlight (Fig. 3A). We then compared neural coding between indirectly related A and C items associated with different levels of reactivation. Critically, all analyses assessing representational change in hippocampal subfields were based on data from high similarity triads only. This approach holds the visual similarity of the linking item constant, providing a critical test of whether memory reactivation mediates representational change above and beyond alterations of the physical environment.

We ran four searchlight analyses within individual hippocampal subfields to test for the effects of reactivation on learning-related representational change for indirectly related memory elements (Fig. 4B). First, we used two searchlight analyses to identify hippocampal regions that showed differentiation or integration of A and C items regardless of the degree of memory reactivation during overlapping pair learning (Differentiation_Overall and Integration_Overall, respectively) and observed no significant effects within hippocampus. Instead, we predicted that the representational similarity of indirectly related items in hippocampal subfields would depend on the strength of memory reactivation during learning of the overlapping pairs. To test this hypothesis, we ran two additional searchlight analyses that looked for an interaction between learning-related representational change and memory reactivation; these searchlights isolated hippocampal regions showing either differentiation or integration on trials with stronger reactivation during overlapping pair learning (Differentiation_Reactivation and Integration_Reactivation).

We found that stronger reactivation of initial pair memories during learning of the overlapping pairs had different consequences on the direction of representational change observed in hippocampal subfields. When initial (A) memories were strongly reactivated during overlapping (BC) pair learning, DG/CA_2,3 pattern similarity decreased between A and C items from prelearning to postlearning (Fig. 4C,D; Differentiation_Reactivation). Subiculum exhibited the same pattern as DG/CA_2,3, with stronger reactivation leading to decreased pattern similarity for A and C items. In contrast, CA₁ showed an opposing pattern of representational change when memory reactivation was stronger, with increased similarity among A and C items after learning (Fig. 4C,D; Integration_Reactivation). These findings suggest that representation of overlapping memories within hippocampal subfields is contingent on memory reactivation during learning, with the same conditions leading to dissociable representational codes within DG/CA_2,3, CA₁, and subiculum.

Finally, we performed a series of post hoc analyses on each hippocampal subfield identified in the searchlight analysis to further understand how reactivation modulated coding in each region. We first quantified whether there were any global shifts in neural similarity simply as a function of learning by calculating the across-triad Δ for unrelated A and C items (i.e., the across-triad baseline). Across-triad Δ was not significantly different from zero in CA₁ (t₍₂₄₎ = 0.383, p = 0.705, d = 0.077) or subiculum (t₍₂₅₎ = 1.233, p = 0.229, d = 0.242), but was greater than zero for DG/CA_2,3 (t₍₂₅₎ = 3.431, p = 0.002, d = 0.673). These results demonstrate the importance of comparing similarity change for related events to a baseline, as even unrelated items may change in similarity after learning.

Next, we compared the within-triad Δ for triads associated with strong reactivation to the across-triad Δ baseline as a validation of our searchlight results (Fig. 4D). As mentioned previously, a caveat to this analysis is that the results are potentially biased by selecting voxels identified in the neural coding searchlight analysis. Consistent with the predicted patterns of the searchlight contrasts (Fig. 4B), we found evidence for differentiation, whereby neural similarity change for triads associated with strong reactivation was less than the across-triad baseline in DG/CA_2,3 (t₍₂₅₎ = 2.298, p = 0.030, d = 0.451) and subiculum (t₍₂₅₎ = 3.158, p = 0.004, d = 0.619). Within CA₁, we showed a trend for integration with greater similarity within triads associated with stronger reactivation after learning relative to the across-triad baseline (t₍₂₄₎ = 1.766, p = 0.090, d = 0.353). Together, these post hoc analyses support the outcome of the searchlight analysis and show that representation of overlapping events in subfields is influenced by the reactivation of related memories during learning.

As an exploratory analysis, we also quantified within-triad Δ for triads associated with weaker reactivation during learning. We found evidence for integration in DG/CA_2,3 (t₍₂₅₎ = 3.709, p = 0.001, d = 0.727) and a trend in subiculum (t₍₂₅₎ = 1.849, p = 0.076, d = 0.363), wherein Δ for triads associated with weaker reactivation was greater than that observed for the across-triad baseline. This result suggests that representational shifts in DG/CA_2,3 may vary as a function of the level of competition, which may be different when memories are strongly or weakly reactivated. No differences from baseline were observed for triads associated with weaker reactivation in CA₁ (t₍₂₄₎ = 1.062, p = 0.299, d = 0.212).

Memory integration supports inference decisions

We used a Bayesian multilevel model to examine the relationship between similarity change after learning (i.e., integration or differentiation) and performance on the AC inference test. We also examined the relationship between reactivation of related memories during learning and inference performance. One participant was excluded from this analysis because of an insufficient number of voxels in CA₁ (<10 voxels). We used an LBA model to simultaneously model inference accuracy and response times. We used Bayesian sampling with the model to estimate the slope of relationships between inference performance and triad-level variability in similarity change and memory reactivation. We first assessed whether the Bayesian sampling was converged. There were no divergences during sampling; for each parameter in the model, [Rhat] was <1.00102 and the effective sample size was at least 5225. These results indicate that the sampling successfully converged, and there were sufficient samples to estimate each parameter.

We used mean posterior parameters to simulate model responses and found that there was a good fit to the observed accuracy (Fig. 5A) and response times (Fig. 5B) on the inference test, with the exception of a small number of trials with very long response times. The mean slope parameters for learning-related change (Fig. 5C) were positive for subiculum (95% HDI = [0.043, 0.477], d = 1.37) and memory reactivation (HDI = [0.005, 0.437], d = 1.51). The slope parameters for CA₁ (HDI = [−0.189, 0.244], d = 0.15) and DG/CA_2,3 (HDI = [−0.393, 0.102], d = 0.50) were not different from zero. The 95% HDIs for the other model parameters were as follows: A = [2.059, 5.601], τ = [0.00,009, 0.515], μ₂ = [0.130, 0.812], σ₂ = [0.191, 0.831], σ_CA1 = [0.004, 0.458], σ_DG/CA2,3 = [0.010, 0.577], σ_Subiculum = [0.002, 0.408], and σ_React = [0.0002, 0.327]. These results indicate that greater memory reactivation during learning and greater AC similarity after learning in subiculum predict faster and more accurate inference at the level of individual trials.

Figure 5.

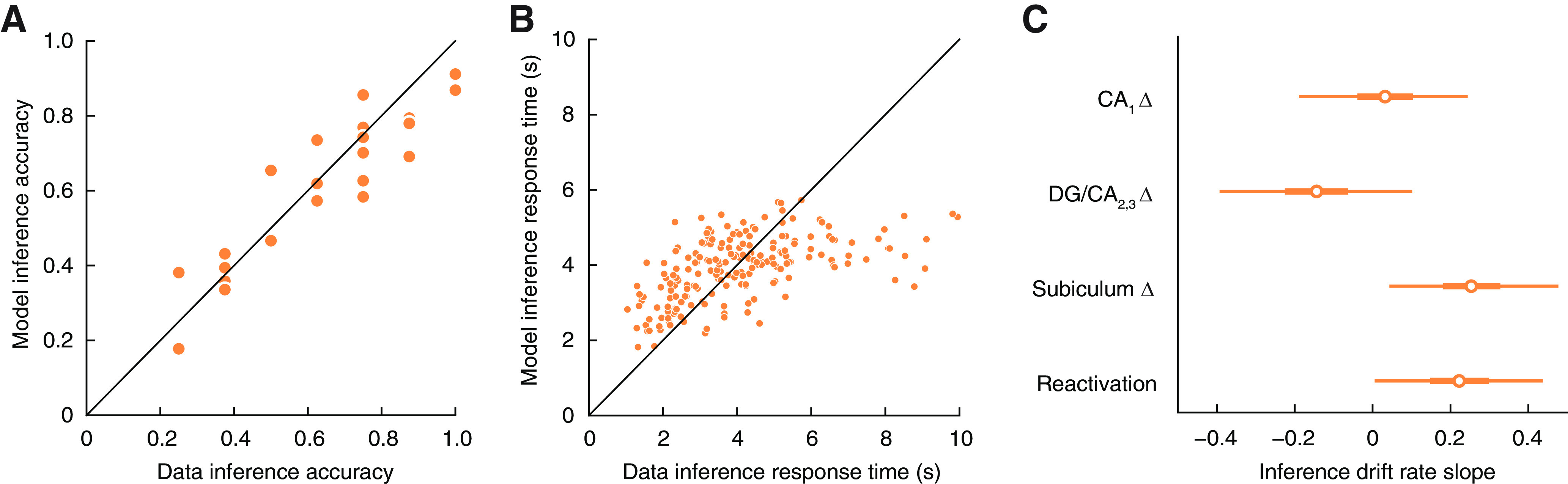
Results of the multilevel response time model used to examine relationships between neural measures and AC inference performance. A, Fit of response time model to accuracy on individual AC inference trials. B, Fit of response time model to trial-level inference response times. C, We examined whether reactivation of related memories during BC study or neural similarity change (Δ) in hippocampal subfields after learning predicted trial-level variability in AC inference performance (i.e., the slope of the drift rate from the model). Negative values indicate a decrease in the neural measures predicted faster and more accurate inference, whereas positive values indicate an increase in the neural measures predicted better inference. Reactivation of related memories and representational change within subiculum predicted improved AC inference performance. Bars represent 95% HDIs of posterior parameter estimates.

Discussion

Our results indicate that reactivated memories guide how representations of related events are organized within the hippocampal circuit. Reactivation of prior memories during encoding of new, overlapping events predicted across-episode inference performance and had different consequences for representation in hippocampal subfields; strong reactivation led to differentiation of overlapping memories within DG/CA_2,3 and subiculum, while simultaneously promoting integration of those same memories in CA₁. Prior work has focused on explaining hippocampal subfield coding in terms of a transfer function through which changes in environmental cues lead to differential neural output (Leutgeb et al., 2004, 2007; Lacy et al., 2011; Yassa and Stark, 2011). Here, we show that changes in perceptual input are not the only factor determining representation learning within hippocampal subfields. Rather, our data indicate that hippocampal subfield coding is further driven by the degree to which a new experience triggers reactivation of related episodes. Our results thus extend prior findings to show, at a representational level, that cortical memory reactivation drives dissociations in hippocampal subfield coding in the face of competition between highly similar memories.

Prior work on hippocampal representation has primarily conceptualized subfield coding as an automatic process in response to environmental changes, wherein sensory inputs are assumed to be the main driver of hippocampal responses. For instance, early electrophysiological studies in rodents measured how place field responses in hippocampal subfields remapped as animals navigated environments with gradually changing perceptual features (Guzowski et al., 2004; Lee et al., 2004; Leutgeb et al., 2004, 2007; Vazdarjanova and Guzowski, 2004). Such work revealed that small changes in environmental features led to dramatic changes in DG and CA₃ responses, reflecting orthogonalization of input patterns. In contrast, CA₁ responses changed gradually, scaling linearly with the amount of perceptual change between environments; for environments that were more perceptualy similar, CA₁ activity showed a greater overlap in responding. Prior work in humans took a similar approach, presenting participants with pairs of highly similar visual images (e.g., pictures of two different apples) and measuring the magnitude of hippocampal subfield responses to both images (Bakker et al., 2008; Lacy et al., 2011). In those studies, DG/CA_2,3 showed a novelty response for both highly similar images, suggesting separate coding of the two images. CA₁ and subiculum responses to the second, highly similar image from a pair, however, were suppressed relative to the presentation of the first pair member, suggesting similar representation of the paired images.

While past animal and human work has revealed important dissociations between hippocampal subfield processing, our findings build on that work to show that hippocampal representation learning is not simply a passive process, but instead is actively influenced by memory reactivation (Hulbert and Norman, 2015; Kim et al., 2017; Ritvo et al., 2019). We show that hippocampal subfield dissociations are most apparent when past memories are strongly reactivated, producing a competitive learning state that promotes differentiation in DG/CA_2,3 and subiculum, simultaneously with integration in CA₁. Our data thus indicate the need to quantify both the perceptual similarity among events and how overlapping perceptual features trigger memory reactivation to fully account for how dissociable representations emerge within the hippocampal circuit. One interesting aspect of the prior human work described above is that dissociations among subfields depended on the nature of the task being performed (Kirwan and Stark, 2007; Bakker et al., 2008; Lacy et al., 2011). When the critical experimental manipulation (i.e., the visual similarity among items) was incidental to the task participants performed, dissociations between subfields were observed (Bakker et al., 2008; Lacy et al., 2011). However, when the same stimuli and presentation procedures were combined with an intentional task focus, dissociations were less apparent (Kirwan and Stark, 2007). The mechanistic source of these divergent findings has yet to be revealed. By quantifying memory reactivation during tasks with an intentional or incidental focus, further insights might be gained about how task goals influence the dynamics of how memory competition impacts neural representation (Richter et al., 2016).

Our findings may be conceptualized in terms of supervised and unsupervised models of learning, which each focus on different learning targets. Whereas supervised learning is directed by matching representations to sensory cues observed directly in the environment, unsupervised learning adjusts representations to reduce competition between a current experience and reactivated memory representations triggered by the new event (Ritvo et al., 2019) through integration or differentiation. While learning likely reflects a balance between supervised and unsupervised mechanisms, our findings indicate that reactivated memories are an important facet of how dissociable coding strategies emerge across hippocampal subfields.

To date, only one other study in humans has used multivariate representational analyses to quantify a dissociation between hippocampal subfields, specifically when individuals retrieved information about shared or distinct spatial contexts (Dimsdale-Zucker et al., 2018). That study showed that items learned within the same spatial context elicited overlapping activation patterns in CA₁ and differentiated patterns in DG/CA_2,3 during retrieval relative to items that did not share contextual information. The present findings differ from that study in several key ways. First, the prior study measured subfield codes during memory retrieval, while our work reveals the active learning processes that drive formation of dissociable subfield representations. Specifically, that prior study did not quantify how reactivation of similar memories, either during learning or retrieval, related to hippocampal subfield coding. Here, we show a dissociation in hippocampal subfield coding as a result of memory reactivation. Furthermore, we show that neural codes formed by hippocampal subregions not only support simple recognition (Dimsdale-Zucker et al., 2018) or spatial memory (Leutgeb et al., 2004, 2007), but also inference about the relationships among memories (see also Schlichting et al., 2014). Inference decisions were faster and more accurate with increasing similarity among indirectly items after learning in subiculum, indicating how overlapping codes promote knowledge extraction beyond direct experience.

Our finding that subiculum representations track inference decisions may reflect that subiculum is the output structure of the hippocampal circuit (O'Mara et al., 2001), which plays a key role in recollection (Viskontas et al., 2009; Lindberg et al., 2017). While subiculum showed evidence of learning-related differentiation for overlapping pairs overall, our modeling data indicate that representational change in subiculum reflects a continuum of responses. Increased integration (which can also be thought of as less differentiation) promoted faster and more accurate inference. Our results suggest that, when memories are more integrated (or less differentiated), inference is facilitated by retrieving a stored connection between indirectly related items (Shohamy and Wagner, 2008; Schlichting et al., 2014); in contrast, differentiation might slow inference between two separate traces that would need to be retrieved and recombined at test (Koster et al., 2018).

Like subiculum, DG/CA_2,3 exhibited learning-related differentiation of indirectly related memory elements when memory reactivation was stronger during encoding. However, it should be noted that DG/CA_2,3 differentiation of overlapping memory elements was only observed relative to the unrelated, across-triad baseline; there was no change in similarity from prelearning to postlearning for the indirectly related items on their own (Fig. 4D, inset). This finding is consistent with prior work showing hippocampal differentiation for related relative to unrelated events after learning (Favila et al., 2016; Dimsdale-Zucker et al., 2018), while also controlling for baseline changes in similarity that occur over time. Moreover, DG/CA_2,3 showed evidence for memory integration when memory reactivation was weaker during learning, suggesting the potential for more nuanced representational dynamics in this region. For instance, memory competition elicited by reactivation may have a nonmonotonic relationship to representational change in DG/CA_2,3 (Ritvo et al., 2019). Stronger reactivation may promote active differentiation; weaker or intermediate levels of reactivation may lead to integration; and no reactivation may produce nonoverlapping representations that are separated via passive orthogonalization. This complex coding strategy could explain why DG/CA_2,3 shows evidence of differentiated (Kim et al., 2017) and integrated (Schapiro et al., 2012) representations under different circumstances. Alternatively, our results may reflect the use of a combined DG/CA_2,3 region, the components of which are thought to exhibit different transfer functions between environmental cues and resulting memory representations (Yassa and Stark, 2011). The observed pattern of results indicates that quantifying memory reactivation along with representational change is necessary to fully understand how memory competition impacts representation learning in DG/CA_2,3.

In conclusion, our empirical findings support a recently proposed computational model of the hippocampal circuit (Schapiro et al., 2017); simulations from this model suggest that CA₁ may represent relationships across events, whereas DG and CA₃ representations may emphasize differences between similar episodes. Our findings align with these computational predictions, with CA₁ forming integrated representations for similar memories, while DG/CA_2,3 and subiculum differentiate those same experiences. Additionally, we show that hippocampal representations support novel inference, facilitating the discovery of unobserved relationships between distinct but related experiences. The present work further shows that hippocampal subfield dissociations are not a simple function of sensory input, but result from memory-based competition during learning. Together, the present study advances our understanding of how prior knowledge shapes how new events are represented within the hippocampal circuit, providing an empirical test of key predictions of computational models of hippocampal memory function.