Abstract
Background
Nutrition is not a treatment for COVID-19, but it is a modifiable contributor to the development of chronic disease, which is highly associated with COVID-19 severe illness and deaths. A well-balanced diet and healthy patterns of eating strengthen the immune system, improve immunometabolism, and reduce the risk of chronic disease and infectious diseases.
Objective
This study aims to assess the effect of diet, nutrition, obesity, and their implications for COVID-19 mortality among 188 countries by using new statistical marginalized two-part models.
Methods
We globally evaluated the distribution of diet and nutrition at the national level while considering the variations between different World Health Organization regions. The effects of food supply categories and obesity on (as well as associations with) the number of deaths and the number of recoveries were reported globally by estimating coefficients and conducting color maps.
Results
The findings show that a 1% increase in supplementation of pulses reduced the odds of having a zero death by 4-fold (OR 4.12, 95% CI 11.97-1.42). In addition, a 1% increase in supplementation of animal products and meat increased the odds of having a zero death by 1.076-fold (OR 1.076, 95% CI 1.01-1.15) and 1.13-fold (OR 1.13, 95% CI 1.0-1.28), respectively. Tree nuts reduced the odds of having a zero death, and vegetables increased the number of deaths. Globally, the results also showed that populations (countries) who consume more eggs, cereals excluding beer, spices, and stimulants had the greatest impact on the recovery of patients with COVID-19. In addition, populations that consume more meat, vegetal products, sugar and sweeteners, sugar crops, animal fats, and animal products were associated with more death and less recoveries in patients. The effect of consuming sugar products on mortality was considerable, and obesity has affected increased death rates and reduced recovery rates.
Conclusions
Although there are differences in dietary patterns, overall, unbalanced diets are a health threat across the world and not only affect death rates but also the quality of life. To achieve the best results in preventing nutrition-related pandemic diseases, strategies and policies should fully recognize the essential role of both diet and obesity in determining good nutrition and optimal health. Policies and programs must address the need for change at the individual level and make modifications in society and the environment to make healthier choices accessible and preferable.
Keywords: COVID-19, diet, nutrition, obesity, marginalized two-part model, semicontinuous data
Introduction
Transmission of COVID-19 began in Wuhan, Hubei Province, China on December 31, 2019 [1,2]. According to the latest World Health Organization (WHO) report on July 3, 2020, there were 11,188,120 confirmed cases and 528,431 deaths worldwide, with 1505 total cases and 69.3 deaths per 1 million population [3]. The WHO named it a global pandemic because of the rapid outbreak of the disease worldwide [4,5].
The COVID-19 epidemic started during winter in areas of the world where the consumption of wildlife is not uncommon. Coronavirus is one of the viruses causing the common cold, a disease that has never had a cure nor any effective prevention or vaccine. However, there are relatively consistent data suggesting that the risk of contracting the common cold is high under inadequate sleep, psychosocial or physical stress including exposure to cold temperatures, inadequate nutrition, and any condition that compromises the body’s immune system [6].
A high percentage of COVID-19 deaths worldwide are associated with one or more chronic conditions. It is also evident that older people are at a higher risk for severe illness with this pandemic [7,8]. Nutrition is not a treatment for COVID-19, but it is a modifiable contributor to the development of chronic disease, which is highly associated with COVID-19 severe illness and deaths [9]. A well-balanced diet and healthy patterns of eating strengthens the immune system, improves immunometabolism, and reduces the risk of chronic disease and infectious diseases [10,11]. Furthermore, nutrition may have a positive or negative impact on COVID-19, as it may be a way to support people at higher risk for the disease (ie, older people and people with pre-existing conditions of noncommunicable diseases) [12].
It is clear in these challenging times that optimizing nutrition is important, not only for ourselves but also for every patient that goes through their own period of treatment. Every health system should be aware of the benefits of healthy eating and be able to provide sound nutritional guidance to their patients, especially those with chronic disease. Having knowledge about nutritional interventions that may help prevent chronic conditions and their associated risks is now more important than ever [13].
On the other hand, being overweight or obese are interpreted as excessive fat [14] accumulation and represent a risk to health [15]. Most of the world’s populations live in countries where being overweight or obese kill more people than being underweight. However, does it cause a decrease in the immune system or severity of COVID-19? Is it dangerous toward getting an infection and the mortality of COVID-19?
This study aims to assess the effect of diet, nutrition, and obesity on COVID-19 mortality among 188 countries by using new statistical marginalized two-part (mTP) models. Hence, we globally evaluated the distribution of diet and nutrition on the national level while considering the variation between different regions. The effects of food supply categories and obesities on (as well as associations with) the number of deaths and the number of recoveries is reported worldwide by estimating coefficients and conducting color maps.
Methods
Overview
This section starts with a short description of the data set and information on relevant sources. In the following section, we introduce the conventional two-part (TP) regression model and the proposed mTP regression model for semicontinuous data. For the continuous part, we considered two flexible distributions including log-normal (LN) and beta prime (BP). We also described their properties to assess the overall impact of covariates on the marginal mean and demonstrated that the proposed model outperforms the conventional model. Finally, the proposed mTP model was applied to the healthy diet data set on fat quantity and protein to investigate the effects of nutrition categories and obesity on the number of deaths and recoveries in 100 cases of COVID-19.
Dietary, Obesity, and COVID-19 Data
Food supply data is some of the most important data in both Food and Agriculture Organization (FAO)/WHO STAT [16]. In fact, this data is the basis for estimations of global and national undernourishment assessment when it is combined with parameters and other data sets. In addition, both businesses and governments use this data for economic analysis and policy setting, and the academic community also uses this data.
In this data set, we combined data of different types of food, world population obesity and undernourished rates, and the global COVID-19 cases count from around the world (188 countries) to learn more about how a healthy eating style could help combat COVID-19. In addition, from the data set, we can gather information regarding diet patterns from countries with lower COVID-19 infection rates and adjust our own diet accordingly. The spread of the disease, deaths, recoveries, and their different distributions are shown in Figure 1, which can be evaluated according to the WHO regions.
Figure 1.
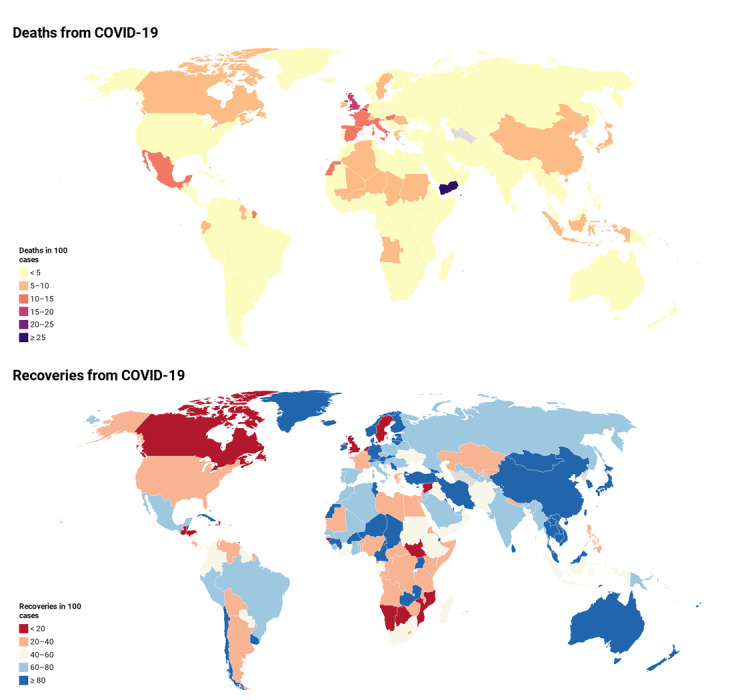
World map related to the number of deaths (top) and the number of recoveries (bottom) in 100 cases of COVID-19 as of July 3, 2020.
From the data sets, accessible as Google sheets in GitHub [17], we have used fat quantity and protein for different categories of food (all calculated as percentage of total intake amount). We have also added on the obesity rate (in percentage) for comparison. The end of the data sets also included the most up-to-date confirmed infections, deaths, recoveries, and active cases (also in percentage of current population for each country). In this study, response variables were the deaths in 100 cases and the recoveries in 100 cases that were continuously (ranged 0 to 100) measured for 188 countries [18].
To synchronize results relative to interregional variations, data sets were grouped according to WHO regions (Multimedia Appendix 1), and a mTP analysis of deaths and recoveries was conducted using a random effects (regions cluster) model. Supply food data description is described in Multimedia Appendix 2. Both fat quantity and protein data sets, including 23 categories, were obtained from the FAO database [19] and were used to show the specific types of food that belong to each category for assessing influential effects of the fat quantity and protein supply.
Semicontinuous response variables such as mortality indexes are typically characterized by the presence of zeros and positive continuous outcomes that are often right skewed. In this paper, we propose a class of models for positive and zero responses by means of a zero-augmented mixed regression model. Under this class, we are particularly interested in studying positive responses whose distribution accommodates skewness. At the same time, responses can be zero, and therefore, we justified the use of a zero-augmented mixture model.
Marginalized Two-Part Models for Semicontinuous Data
Conventional Two-Part Model
We began with a review of the conventional TP model presented in Cragg [20], Manning et al [21], Duan et al [22], and elsewhere. Let Yij be a semicontinuous variable for the i-th (i=1,2, ..., n) subject at cluster j (j=1,2, ..., ni). For nonnegative data (Yij≥0) consisting of independent observations that clustered in the j-th level, the generic form of the conventional TP model can be written as:
where πij = Pr(Yij>0), 1(.) is the indicator function, and g(yij|yij>0) is any density function applicable to the positive values of Yij, although the LN density is often chosen. This model is parameterized following equations (2) and (3) relevant to zero and nonzero components, respectively:
where Zij is a 1 × q covariate (used as an explanatory variable) vector, α is a q × 1 regression coefficient vector, and b1i is the cluster-level random effect in the zero component. The location parameter μij is modeled in the second part of the TP model assuming a log link:
where Xij is a 1 × p covariate vector, β is a p × 1 regression coefficient vector, and b2i is again the cluster-level random effect in the nonzero component. The error term εij is assumed to be normally distributed as N(0,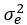 
). Note that this TP mixed model can be extended to include additional random effects. For illustration purposes and simplicity, we restricted attention here to the TP mixed models with two levels; extensions to multilevel models are straightforward.
When fitting this model to independent responses, the binary and conditionally continuous components of the likelihood are separable, and therefore, these two parts are fit separately. The binary component is often modeled using logistic regression, and the continuous component can be fit using standard regression models such as the BP [23], LN [24], gamma [25,26], and long-skew normal [27].
The marginal mean and variance of Yij from a TP model can be derived as follows:
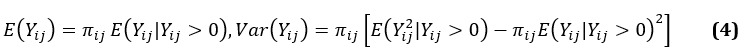
When LN is assumed in the continuous part, the marginal mean is:
E(Yij) = νij = πij exp{μij + σ2 ⁄ 2} (5)
Marginalized Two-Part Model
To obtain interpretable covariate effects on the marginal (unconditional) mean, we proposed the following mTP model that parameterizes the covariate effects directly in terms of the marginal mean, νi=E(Yi), on the original (ie, untransformed) data scale. The mTP model specifies the linear predictors:
where b1i represents the random effect that accounts for the within-subject correlation pertaining to the clustered measures in the zero part, b1i ~ N(0,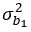 
).
where b2i represents the random effect that accounts for the within-subject correlation pertaining to the clustered measures in the continuous part, b2i ~ N(0,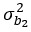 
).
The two random effect intercepts b1i and b2i in the two processes of zero and nonzero are assumed to be independent and uncorrelated.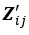 
is the vector of covariates for the i-th subject measured at the j-th cluster for the binary part, and 
is the vector of covariates for the i-th subject measured at the j-th cluster used for the continuous part. The two parts might have common covariates or completely different ones. α is the vector of model coefficients corresponding to the binary part, and β is the vector of coefficients corresponding to the continuous part, conditional on the values being nonzero. The model can be easily extended to include higher-order random effects.
Marginalized Two-Part Log-Normal Model
When modeling semicontinuous data, the continuous component is most frequently modeled using a LN distribution. The generic form of the marginalized two-part log-normal (mTP LN) model for independent responses can be written as in equation (1), with g(yij|yij>0), taking the LN density function LN(.; μ, σ2) with mean μ and variance σ2 on the log scale. The marginal mean and variance of Yij are:
E(Yij) = νij = πijexp(μij + σ2 ⁄ 2) (8)
Var(Yij) = πijexp(2μij + σ2)[exp(σ2) – πij] (9)
The likelihood (L), parameterized in terms of πij and μij, is:
where ϕ(b1ij, b2ij) represents the bivariate normal distribution for the random effects with a mean vector of zeros and variance-covariance matrix 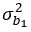and 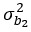for zero and nonzero parts, respectively.
To use this LN likelihood framework, the marginal mean in equation (8) can be rearranged to solve for μij, yielding:
Noting that:
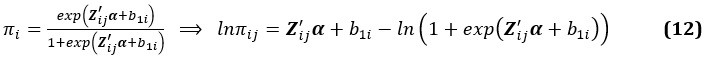
and:
Marginalized Two-Part Beta Prime Model
The BP distribution [28,29] is also known as inverted beta distribution or beta distribution of the second kind, often the model of choice for fitting semicontinuous data where the response variable is measured continuously on the positive real line (Y>0) because of the flexibility it provides in terms of the variety of shapes it can accommodate. The probability density function of a BP distributed random variable Y parameterized in terms of its mean μ and a precision parameter ϕ is given by:
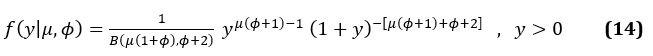
where, B denotes the beta function μ>0, ϕ>0, E(Y) = μ, and Var(Y) = (μ(1 + μ)) / ϕ.
To obtain interpretable covariate effects on the marginal mean, we proposed the following mTP model that parameterizes the covariate effects directly in terms of the marginal mean, νij = E(Yij), on the original (ie, untransformed) data scale. The mTP model with random (cluster) effects Z1ij and Z2ij for the zero and the continuous components, respectively, specifies the linear predictors:
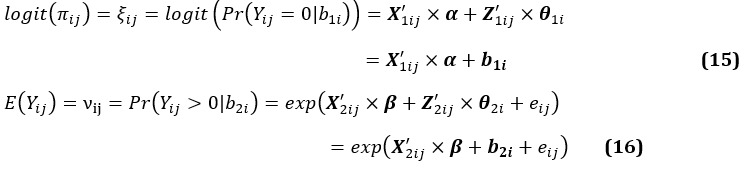
where,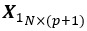 
and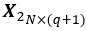 
have full rank p and q for the zero and the continuous components, respectively; α(p+1)×1 and β(q+1)×1 are the corresponding vectors of the regression coefficients. As seen in equations (15) and (16), the mixing probability and mean of the component of the continuous parts are linked to the independent variables through logit and logarithmic link functions. The vectors b1=(b11, b12, ..., b1m)' and b2=(b21, b22, ..., b2m)' denote random effects of the third level in the components of logistic and continuous, respectively. For simplicity of interpretation and mathematical calculations, the random effects (b1, b2) were assumed to be joint normally distributed with mean zero and variances 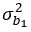and 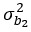, respectively [30,31]. The errors term eij ~ N(0, 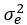) was also assumed to be of normal distribution and independent of the random effects.
Let ψij = I(yij>0) denote the indicator of Yij being nonzero. The general form of the likelihood function for the i-th subject can be described as follows:
where the log-likelihood for the binary part is:
and the log-likelihood for the continuous part is:
with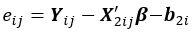 
, which can be implemented in the SAS NLMIXED procedure by quasi-Newton optimization with adaptive Gaussian quadrature techniques [32]. With the conventional model, the likelihood and score equations can be separated into two independent components: one for the binary part and one for the continuous part. In contrast, note that the score equations for the mTP model are not separable, and thus, the binary and continuous parts are fit simultaneously. Model-based asymptotic standard errors are computed using Fisher information matrix, Ι(α, β, σ), as:
with the maximum likelihood estimates substituted for α, β, and σ.
Results
In this section, the proposed mTP model was applied to the healthy diet data set on fat and protein to investigate the effects of supplementation categories on the number of deaths per 100 cases and recoveries per 100 cases of COVID-19. The estimations of mTP BP and mTP LN related to deaths and recoveries are shown in Tables 1 and 2, respectively. In these tables, variances (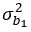 and 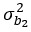) show the variety of responses among level 2 (ie, the WHO regions) related to each part of the zero and nonzero (ie, positive) components. Tables 1 and 2 show that almost all categories have the same effect on the number of deaths and recoveries in 100 cases. The number of deaths per 100 cases, number of recoveries per 100 cases, and the obesity rates until July 3, 2020, for all countries and split by the WHO regions is shown in Multimedia Appendix 3. Deaths are more common in Western and Southwest Europe (eg, Belgium, the United Kingdom, France, Italy, Hungary, Netherlands, and Spain), North America (eg, Mexico, Bahamas, Canada, Barbados, Belize, and the United States), and North Africa (eg, Western Sahara, Chad, Algeria, and Niger). The highest number of deaths occurred in Yemen (26.62 deaths per 100 cases), which could be due to the crises caused by the war and the poor health conditions in this country in the last years. Frequently, it seems that the northern regions of the world appear to have had more deaths, which may be due to temperature differences between the two hemispheres.
Table 1.
Results of marginalized two-part BP and LN model in predicting number of deaths per 100 cases and considering the cluster effect of World Health Organization regions in the fat data set.
| Fat (categories) | Fat quantity | Protein | |||||||
| Zero component | Nonzero component | Zero component | Nonzero component | ||||||
| Coefficient (α) |
|
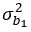
Coefficient (β) |
|
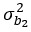
Coefficient (α) |
|
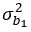
Coefficient (β) |
|
||
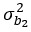
| Alcoholic beverages | |||||||||
| BPa | —b | — | –7.0449 | 0.1145 | 1.3670 | 0.4907 | 0.04707 | 0.1286 | |
| LNc | — | — | –6.4512 | 0.1165 | 1.3752 | 0.4814 | 0.04918 | 0.1189 | |
| Animal products | |||||||||
| BP | 0.0401 | 0.7457 | –0.0028 | 0.1539 | 0.0736 d | 0.6212 | 0.0105 | 0.1236 | |
| LN | 0.0405 | 0.6543 | –0.0031 | 0.1495 | 0.0812 | 0.5965 | 0.0108 | 0.1209 | |
| Animal fats | |||||||||
| BP | 0.1505 | 0.6458 | 0.0009 | 0.1223 | 7.6487 | 0.3055 | 0.3259 | 0.1212 | |
| LN | 0.1489 | 0.6147 | 0.0009 | 0.1239 | 7.5461 | 0.2891 | 0.3319 | 0.1801 | |
| Aquatic products other | |||||||||
| BP | 4.3474 | 0.7746 | –13.9857 | 0.1123 | 30.9618 | 0.4060 | –0.7270 | 0.1201 | |
| LN | 4.5421 | 0.7469 | –10.2576 | 0.1127 | 29.1456 | 0.3995 | –0.7345 | 0.1193 | |
| Cereals excluding beer | |||||||||
| BP | –0.0839 | 0.6195 | –0.0218 | 0.1485 | –0.0548 | 0.4994 | –0.0171 | 0.1163 | |
| LN | –0.0956 | 0.6015 | –0.0221 | 0.1399 | –0.0551 | 0.4861 | –0.0170 | 0.1123 | |
| Eggs | |||||||||
| BP | 0.3217 | 0.6155 | –0.1291 | 0.1391 | 0.3993 | 0.4487 | –0.0466 | 0.1297 | |
| LN | 0.3514 | 0.5412 | –0.1299 | 0.1381 | 0.4125 | 0.4912 | –0.0481 | 0.1183 | |
| Fish seafood | |||||||||
| BP | –0.0556 | 0.6000 | 0.0383 | 0.1903 | 0.0542 | 0.4220 | 0.0305 | 01318 | |
| LN | –0.0598 | 0.5816 | 0.0401 | 0.1849 | 0.0556 | 0.4001 | 0.0351 | 0.1301 | |
| Fruits excluding wine | |||||||||
| BP | –0.4420 | 0.6323 | 0.0933 | 0.1633 | –0.4744 | 0.5036 | 0.0783 | 0.1176 | |
| LN | –0.4511 | 0.5971 | 0.0931 | 0.1617 | –0.4598 | 0.5121 | 0.0803 | 0.1165 | |
| Meat | |||||||||
| BP | 0.0394 | 0.7340 | 0.0008 | 0.1699 | 0.1246 | 0.4690 | 0.0256 | 0.1174 | |
| LN | 0.0391 | 0.7300 | 0.0008 | 0.1684 | 0.1268 | 0.4581 | 0.0221 | 0.1173 | |
| Miscellaneous | |||||||||
| BP | 2.9863 | 0.6822 | 2.0655 | 0.0994 | 0.0900 | 0.6768 | –0.0090 | 0.1336 | |
| LN | 2.5531 | 0.5836 | 2.1510 | 0.0991 | 0.0912 | 0.6154 | –0.0061 | 0.1136 | |
| Milk excluding butter | |||||||||
| BP | 0.0589 | 0.6160 | –0.0139 | 0.1667 | 0.5456 | 0.4718 | 0.0561 | 0.1259 | |
| LN | 0.0512 | 0.6013 | –0.0142 | 0.1561 | 0.5537 | 0.4316 | 0.0560 | 0.1241 | |
| Offals | |||||||||
| BP | 0.0196 | 0.6429 | –0.1844 | 0.1022 | –0.0526 | 0.4808 | 0.0704 | 0.1227 | |
| LN | 0.0197 | 0.6129 | –0.1798 | 0.1124 | –0.0541 | 0.4493 | 0.0713 | 0.1201 | |
| Oilcrops | |||||||||
| BP | –0.2833 | 0.5580 | 0.0179 | 0.1876 | –0.1453 | 0.5600 | 0.0090 | 0.1245 | |
| LN | –0.2891 | 0.5137 | 0.0184 | 0.1773 | –0.1457 | 0.5413 | 0.0094 | 0.1239 | |
| Pulses | |||||||||
| BP | –1.4170 | 0.1944 | 0.1150 | 0.1434 | –0.1583 | 0.4308 | 0.1496 | 0.1290 | |
| LN | –1.4242 | 0.1832 | 0.1159 | 0.1400 | –0.1581 | 0.4311 | 0.1499 | 0.1289 | |
| Spices | |||||||||
| BP | –0.5889 | 0.4622 | 0.0476 | 0.1907 | –0.0916 | 0.4309 | –0.0561 | 0.1161 | |
| LN | –0.5887 | 0.4604 | 0.0467 | 0.1891 | –0.0914 | 0.4312 | –0.0551 | 0.1163 | |
| Starchy roots | |||||||||
| BP | –0.9187 | 0.5559 | –0.3262 | 0.1637 | 0.3208 | 0.4513 | –0.0469 | 0.1246 | |
| LN | –0.9188 | 0.5412 | –0.3301 | 0.1621 | 0.3208 | 0.4511 | –0.0461 | 0.1212 | |
| Stimulants | |||||||||
| BP | 0.6042 | 0.6715 | –0.0287 | 0.1704 | 0.3476 | 0.4530 | –2.4158 | 0.1227 | |
| LN | 0.6101 | 0.6712 | –0.0288 | 0.1698 | 0.3479 | 0.4530 | –2.4129 | 0.1201 | |
| Sugar crops | |||||||||
| BP | –13.0537 | 0.5727 | –6.2283 | 0.1063 | 5.7548 | 0.4394 | 1.4861 | 0.1217 | |
| LN | –12.5132 | 0.5624 | –6.3120 | 0.1059 | 5.5431 | 0.4329 | 1.4869 | 0.1214 | |
| Sugar sweeteners | |||||||||
| BP | –0.8040 | 0.6104 | 10.2992 | 0.2136 | 1.7184 | 0.4899 | 0.5042 | 0.1328 | |
| LN | –0.8042 | 0.6112 | 9.4532 | 0.2013 | 1.7204 | 0.4782 | 0.5100 | 0.1236 | |
| Tree nuts | |||||||||
| BP | 0.3739 | 0.6207 | 0.1138 | 0.2178 | –0.0736 | 0.6211 | –0.0105 | 0.1236 | |
| LN | 0.3721 | 0.6211 | 0.1142 | 0.2017 | –0.0740 | 0.6127 | –0.0104 | 0.1221 | |
| Vegetal products | |||||||||
| BP | –0.0401 | 0.8313 | 0.0028 | 0.1485 | 39.1538 | 0.5764 | 2.8053 | 0.1327 | |
| LN | –0.0413 | 0.8219 | 0.0027 | 0.1449 | 27.1870 | 0.4365 | 2.8101 | 0.1254 | |
| Vegetable oils | |||||||||
| BP | –0.0008 | 0.6667 | 0.0025 | 0.1663 | 0.0228 | 0.4442 | –0.0376 | 0.1228 | |
| LN | –0.0012 | 0.6120 | 0.0024 | 0.1659 | 0.0224 | 0.4318 | –0.0354 | 0.1224 | |
| Vegetables | |||||||||
| BP | –0.5748 | 0.6205 | –0.4784 | 0.1099 | 1.3637 | 0.3991 | 0.7713 | 0.1050 | |
| LN | –0.5739 | 0.5945 | –0.4754 | 0.1098 | 1.3641 | 0.3981 | 0.7716 | 0.1002 | |
| Obesity | |||||||||
| BP | 0.0228 | 0.5954 | 0.0054 | 0.1716 | 0.0228 | 0.4798 | 0.0054 | 0.1261 | |
| LN | 0.0212 | 0.5871 | 0.0057 | 0.1624 | 0.0227 | 0.4821 | 0.0034 | 0.1178 | |
aBP: beta prime.
bEmpty cells related to unestimated or nonconverged values.
cLN: log-normal.
dItalics indicate statistical significance at the .05 significance level.
Table 2.
Results of marginalized two-part BP and LN model in predicting number of deaths in 100 cases and considering the cluster effect of World Health Organization regions in the protein data set.
| Protein (categories) | Fat quantity | Protein | |||||||
| Zero component | Nonzero component | Zero component | Nonzero component | ||||||
| Coefficient (α) |
|
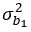
Coefficient (β) |
|
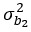
Coefficient (α) |
|
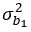
Coefficient (β) |
|
||
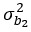
| Alcoholic beverages | |||||||||
| BPa | 0.3934 | —b | –3.3321 | 0.0053 | –0.5040 | — | 0.3291 | 0.0241 | |
| LNc | 0.3941 | 0.6541 | –3.3520 | 0.0051 | -0.5139 | — | 0.3301 | 0.0240 | |
| Animal products | |||||||||
| BP | –0.0518 | — | –0.0030 | 5.0390 | –0.0377 | — | –0.0036 | — | |
| LN | –0.0520 | — | –0.0031 | 5.0011 | –0.0378 | — | –0.0035 | — | |
| Animal fats | |||||||||
| BP | –0.1417 | 0.6458 | 0.0037 | 0.1223 | –4.3929 d | 0.6854 | –0.1882 | 0.0291 | |
| LN | –0.1419 | 0.5454 | 0.0039 | 0.1221 | –4.3821 | 0.6855 | –0.1881 | 0.0297 | |
| Aquatic products other | |||||||||
| BP | 0.1026 | 0.7746 | 0.0998 | 0.1123 | 13.6501 | 0.6543 | –0.1588 | 0.0102 | |
| LN | 0.9817 | 0.7751 | 0.0981 | 0.1123 | 11.5479 | 0.6571 | –0.1581 | 0.0115 | |
| Cereals excluding beer | |||||||||
| BP | 0.2108 | 0.6195 | 0.0201 | 0.1485 | 0.0935 | 0.5987 | 0.0070 | — | |
| LN | 0.2107 | 0.5981 | 0.0200 | 0.1498 | 0.0992 | 0.4564 | 0.0074 | 0.0120 | |
| Eggs | |||||||||
| BP | 1.0198 | 0.6155 | 0.0585 | 0.1391 | 0.3015 | 0.7154 | 0.0971 | 1.0199 | |
| LN | 1.0211 | 0.6154 | 0.0594 | 0.1384 | 0.3101 | 0.6245 | 0.0954 | 0.8745 | |
| Fish seafood | |||||||||
| BP | 2.1882 | 0.6000 | –0.0587 | 0.1903 | 0.3784 | 0.6542 | –0.0109 | 2.0553 | |
| LN | 2.1452 | 0.6124 | –0.0591 | 0.1914 | 0.3781 | 0.6549 | –0.0117 | 2.4923 | |
| Fruits excluding wine | |||||||||
| BP | 3.5529 | 0.6323 | 0.0049 | 0.1633 | 0.5023 | 0.6980 | –0.0284 | 0.3869 | |
| LN | 3.5504 | 0.6341 | 0.0051 | 0.1601 | 0.5001 | 0.7401 | –0.0294 | 0.3881 | |
| Meat | |||||||||
| BP | –0.0020 | 0.7340 | –0.0081 | 0.1699 | –0.0720 | 0.7012 | –0.0050 | 2.8965 | |
| LN | –0.0019 | 0.7341 | –0.0078 | 0.1692 | –0.0711 | 0.6984 | –0.0050 | 2.8457 | |
| Miscellaneous | |||||||||
| BP | 8.988 | 0.6822 | –0.1517 | 0.0994 | –0.1208 | 0.6503 | –0.0057 | 1.8106 | |
| LN | 7.5415 | 0.6824 | –0.1540 | 0.0982 | –0.1235 | 0.6511 | –0.0064 | 1.8001 | |
| Milk excluding butter | |||||||||
| BP | –0.1359 | 0.6160 | –0.0020 | 0.1667 | –0.3806 | 0.4562 | 0.0398 | 0.4047 | |
| LN | –0.1314 | 0.5912 | –0.0080 | 0.1724 | –0.3817 | 0.4575 | 0.0410 | 0.4521 | |
| Offals | |||||||||
| BP | –3.0231 | 0.6429 | –0.1611 | 0.1022 | –0.1169 | 0.6985 | 0.0301 | — | |
| LN | –3.0024 | 0.6540 | –0.1617 | 0.1512 | –0.1141 | 0.7211 | 0.0341 | — | |
| Oilcrops | |||||||||
| BP | 0.0091 | 0.5580 | 0.0070 | 0.1876 | –0.1958 | 0.5913 | –0.0269 | 1.2942 | |
| LN | 0.0084 | 0.5557 | 0.0072 | 0.1868 | –0.1954 | 0.5914 | –0.0264 | 1.3125 | |
| Pulses | |||||||||
| BP | –1.6086 | 0.1944 | –0.3639 | 0.1434 | 4.1312 | 0.2456 | –0.2215 | 0.0303 | |
| LN | –1.5401 | 0.1984 | –0.3578 | 0.1545 | 4.0128 | 0.2541 | –0.2211 | 0.0311 | |
| Spices | |||||||||
| BP | 3.1903 | 0.4622 | –0.2388 | 0.1907 | 0.0560 | 0.5441 | 0.0208 | 0.6601 | |
| LN | 3.1912 | 0.4684 | –0.2491 | 0.1912 | 0.0541 | 0.5237 | 0.0214 | 0.6641 | |
| Starchy roots | |||||||||
| BP | 0.4714 | 0.5559 | 0.0997 | 0.1637 | –0.2431 | 0.6003 | 0.1089 | 0.0603 | |
| LN | 0.4787 | 0.5651 | 0.0984 | 0.1746 | –0.2433 | 0.6210 | 0.1146 | 0.0701 | |
| Stimulants | |||||||||
| BP | 0.5780 | 0.6715 | 0.1503 | 0.1704 | –0.0752 | 0.6439 | 2.1776 | 0.0100 | |
| LN | 0.5417 | 0.6871 | 0.1511 | 0.1724 | –0.754 | 0.7431 | 2.1290 | 0.0150 | |
| Sugar crops | |||||||||
| BP | 0.3393 | 0.5727 | 0.9821 | 0.1063 | 0.3819 | 0.5589 | –4.7273 | 0.1670 | |
| LN | 0.3365 | 0.5821 | 0.9807 | 0.1163 | 0.3814 | 0.5613 | –4.7198 | 0.1687 | |
| Sugar sweeteners | |||||||||
| BP | 1.3970 | 0.6104 | –9.6769 | 0.2136 | 0.5242 | 0.6987 | –0.4085 | 0.2326 | |
| LN | 1.4121 | 0.6255 | –9.5421 | 0.2166 | 0.5420 | 0.6999 | –0.4142 | 0.2401 | |
| Tree nuts | |||||||||
| BP | 0.2521 | 0.6207 | –0.1732 | 0.2178 | 0.0378 | 0.7432 | 0.0036 | 2.8525 | |
| LN | 0.2515 | 0.6210 | –0.1732 | 0.2245 | 0.0412 | 0.7421 | 0.0065 | 3.1450 | |
| Vegetal products | |||||||||
| BP | 0.0517 | 0.8313 | 0.0030 | 0.1485 | –18.9397 | 0.7823 | 0.7848 | 0.0053 | |
| LN | 0.0521 | 0.8214 | 0.0024 | 0.1521 | –15.2981 | 0.7888 | 0.6954 | 0.0055 | |
| Vegetable oils | |||||||||
| BP | 0.0081 | 0.6667 | –0.0007 | 0.1663 | 0.4467 | 0.5968 | –0.0039 | 2.4944 | |
| LN | 0.0043 | 0.6821 | –0.0014 | 0.1681 | 0.4428 | 0.5960 | –0.0041 | 2.4912 | |
| Vegetables | |||||||||
| BP | 2.7153 | 0.6205 | –0.1959 | 0.1099 | 1.6107 | 0.5935 | 0.1003 | 0.0184 | |
| LN | 2.7154 | 0.6650 | –0.1991 | 0.1124 | 1.5459 | 0.6520 | 0.1000 | 0.0156 | |
| Obesity | |||||||||
| BP | 0.0042 | 0.5954 | –0.0009 | 0.1716 | 0.0042 | 0.4986 | –0.0009 | 4.1135 | |
| LN | 0.0041 | 0.5954 | –0.0005 | 0.1712 | 0.0041 | 0.5101 | –0.0009 | 4.1232 | |
aBP: beta prime.
bEmpty cells related to unestimated or nonconverged values.
cLN: log-normal.
dItalics indicate statistical significance at the .05 significance level.
According to the results of Table 1, except pulses in fat quantity and animal products, meat, tree nuts, and vegetables in the protein data set, all categories had no significant effect on the number of deaths. A 1% increase in supplementation of pulses reduced the odds of having a zero death by 4-fold (1 / exp(–1.417) = 4.1251). In addition, a 1% increase in supplementation of animal products and meat increased the odds of having a zero death by 1.076-fold (exp(0.0736) = 1.076) and 1.133-fold (exp(0.0736) = 1.133), respectively. Tree nuts reduced the odds of having a zero death, and vegetables increased the number of deaths.
Continuously, except animal fats, sugar sweeteners, and tree nuts in fat quantity, and animal fats and sugar crops in the protein data, all categories had no significant effect on the number of recoveries (Table 2). The effect of consuming sugar products on mortality was considerable. Every 1% increment in sugar sweeteners decreased the number of recoveries by 98.17% (–9.68, 95% CI –12.6440 to –6.7098). Tree nuts in fat quantity also reduced the number of recoveries by 16.9% (–0.1732, 95% CI –0.3157 to –0.3070). In the protein data, sugar crops reduced the number of recoveries by 99.11% (1 – exp(–4.7273) = 0.9911). The world map related to sugar and sweetener supply is shown in Figure 2. Based on the results of the proposed model and estimates of the effects of sugar, our prediction for the coming days is that the countries of the Americas, with more sugar product intake, will probably face more deaths.
Figure 2.
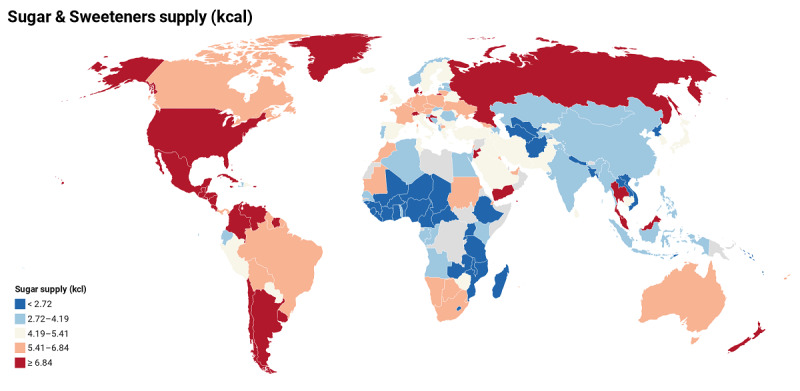
World map related to sugar and sweeteners supply (kcal).
For further evaluation, we calculated correlations between categories (plus obesity rate) with the number of deaths (Figure 3 A and C) and the number of recoveries (Figure 3 B and D) by using the bivariate Pearson correlation. Results of the correlations showed that, in the protein data, countries that consumed more spices, tree nuts, cereals, aquatic products, stimulants, vegetable oils, oil crops, pulses, fruit (wine), and alcoholic beverage (in order) had fewer deaths from COVID-19, and conversely, countries that consumed more meat, vegetables, vegetal products, sugar and sweeteners, animal products, animal fats, sugar crops, milk, fish, offals, miscellaneous, eggs, and starchy roots (in order) had more deaths from COVID-19. In the fat quantity data, countries that consumed more sugar and sweeteners, miscellaneous, tree nuts, meat, animal products, animal fats, offals, and fish had more deaths from COVID-19. Finally, same as the mTP model results, obesity has affected increased death rates and reduced recovery rates in all correlation analyses (Figures 3 and 4).
Figure 3.
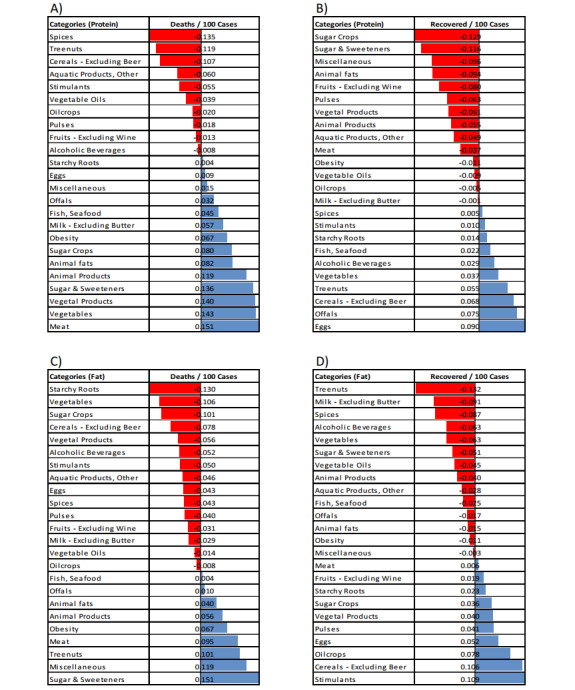
Bivariate Pearson correlation between nutrition categories (plus obesity) and the number of deaths (A and C) and the number of recoveries (B and D) in 100 cases of COVID-19.
Figure 4.
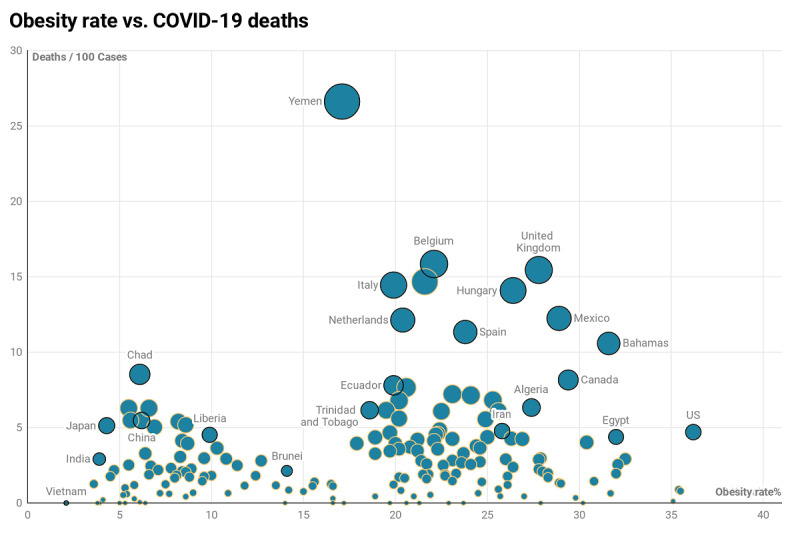
Scatterplot of obesity rate versus deaths per 100 cases of COVID-19 by country. The circle’s size is related to the number of deaths per 100 cases.
Discussion
Principal Results
In this study, we proposed a mTP regression model for clustered semicontinuous diet and nutrition data. This model allows investigators to obtain covariate effects on the marginal mean of the outcome (eg, deaths and recoveries). It also has an unconditional interpretation of the covariate effect on the marginal mean. Our proposed mTP model had satisfactory performance in the diet and nutrition data analysis.
Findings of this study show that populations (countries) who consume more eggs, cereals excluding beer, spices, and stimulants had the greatest impact on the recovery of patients with COVID-19. In addition, populations that consumed more meat, vegetal products, sugar and sweeteners, sugar crops, animal fats, and animal products were associated with more deaths and less recoveries in patients. The effect of consuming sugar products on mortality was considerable. In addition, obesity has affected increased death rates and reduced recovery rates.
Comparison With Prior Work
Healthy diets and physical activity are key to good nutrition and necessary for a long and healthy life and prevention of chronic disease [33]. Eating nutrition dense foods and balancing energy intake with necessary physical activity to maintain a healthy weight is essential at all stages of life. Unbalanced consumption of foods high in energy (sugar, starch, and fat) and low in essential nutrition contributes to energy excess, being overweight, and being obese. The amount of energy consumed in relation to physical activity and the quality of food are key determinants of nutrition-related chronic disease [11]. In a review study from January 2020, Zhang and Liu [13] reviewed the importance of some nutrition interventions (vitamins, minerals, immunoenhancers) in infectious and respiratory diseases. The authors suggested that the nutritional status of each patient who was infected should be evaluated before the administration of general treatments, and the current children’s RNA‐virus vaccines, including the influenza vaccine, should be used for people who are not infected and health care workers. Moreover, the results of their review showed that all the potential interventions (nutritional or immunoenhancers) should be implemented to control COVID‐19 if the infection is uncontrollable [13]. Our results also confirm these associations by introducing influential diet categories, including sugar and sweeteners, animal products, animal fats, sugar crops, miscellaneous, and tree nuts as more important risk factors for death or slowing of recovery in patients with COVID-19.
Recent studies point to obesity as a critical risk factor for being hospitalized or dying from COVID-19 [34-36]. Indeed, a high prevalence of obesity has been observed in patients with COVID-19, requiring invasive mechanical ventilation [37], a robust proxy of SARS-CoV-2 severity. In patients younger than 60 years, those with obesity were at almost double the risk of being admitted to critical care when compared with patients of a normal weight [38]. Results from this study confirm previous findings on the risk of obesity and add that obesity slows down patients’ recovery and treatment.
People need to eat fewer prepared foods and more complex plant-based foods [11]. Although there are differences in dietary patterns, overall, unbalanced diets are a health threat across the world and do not just affect death rates but also the quality of life. To achieve best results in preventing nutrition-related pandemic diseases, strategies and policies should fully recognize the essential role of both diet and obesity in determining good nutrition and optimal health. Policies and programs must address the need for change at the individual level as well as the modifications in society and the environment to make healthier choices accessible and preferable.
Study Limitations
We have some limitation in using the nutrition data sets. The study is based on observational data, and inevitably with 188 countries included, there were variations in how the data were collected. This study included 23 dietary attributes; some that are of interest to health such as saturated and monounsaturated fatty acids and free sugars across the diet (not just those in drinks) were not included in the analysis. The study also did not take into account lifestyle factors, such as smoking and physical activity, that can have a significant impact on the risk of the disease outcomes used in the study.
Finally, we remind all our readers to take care of themselves during this pandemic, follow the guidelines of the Centers for Disease Control and Prevention [39], and eat healthy foods with sufficient amounts of fruits and vegetables as previously discussed.
Conclusions
Good nutrition is important before, during, and after an infection. The findings of this study show that populations who consume more eggs, cereals excluding beer, spices, and stimulants had the greatest impact on the recovery of patients with COVID-19. In addition, populations that consumed more meat, vegetal products, sugar and sweeteners, sugar crops, animal fats, and animal products were associated with more deaths and less recoveries in patients. The effect of consuming sugar products on mortality is considerable. In addition, obesity has affected increased death rates and reduced recovery rates. Although there are differences in dietary patterns, overall, unbalanced diets are a health threat across the world and affect not only death rates but also the quality of life. To achieve best results in preventing nutrition-related pandemic diseases, strategies and policies should fully recognize the essential role of both diet and obesity in determining good nutrition and optimal health. Policies and programs must address the need for change at the individual level as well as the modifications in society and the environment to make healthier choices accessible and preferable.
Acknowledgments
This study was adapted from a PhD thesis by Naser Kamyari (No. 9804253260) at Hamadan University of Medical Sciences. The authors are grateful to Dr Maryam Seyedtabib for providing the data for this paper.
Abbreviations
- BP
beta prime
- FAO
Food and Agriculture Organization
- LN
log-normal
- mTP
marginalized two-part
- TP
two-part
- WHO
World Health Organization
Appendix
Geographical distribution of the six World Health Organization regions and member states for each region (alphabetical order).
The specific types of food that belong to each category for the fat quantity and protein data sets.
Number of deaths per 100 cases, number of recoveries per 100 cases, and obesity rates until July 3, 2020, by countries and split by World Health Organization regions.
Footnotes
Conflicts of Interest: None declared.
References
- 1.Zhan C, Tse CK, Fu Y, Lai Z, Zhang H. Modeling and prediction of the 2019 coronavirus disease spreading in China incorporating human migration data. PLoS One. 2020;15(10):e0241171. doi: 10.1371/journal.pone.0241171. https://dx.plos.org/10.1371/journal.pone.0241171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Shen C, Chen A, Luo C, Zhang J, Feng B, Liao W. Using reports of symptoms and diagnoses on social media to predict COVID-19 case counts in mainland China: observational infoveillance study. J Med Internet Res. 2020 May 28;22(5):e19421. doi: 10.2196/19421. https://www.jmir.org/2020/5/e19421/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Coronavirus disease (COVID-19) situation report – 165. World Health Organization. 2020. Jul 03, [2021-01-19]. https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200703-covid-19-sitrep-165.pdf?sfvrsn=b27a772e_6.
- 4.Epidemiology Working Group for NCIP Epidemic Response, Chinese Center for Disease Control and Prevention [The epidemiological characteristics of an outbreak of 2019 novel coronavirus diseases (COVID-19) in China] Zhonghua Liu Xing Bing Xue Za Zhi. 2020 Feb 10;41(2):145–151. doi: 10.3760/cma.j.issn.0254-6450.2020.02.003. [DOI] [PubMed] [Google Scholar]
- 5.Xu C, Zhang X, Wang Y. Mapping of health literacy and social panic via web search data during the COVID-19 public health emergency: infodemiological study. J Med Internet Res. 2020 Jul 02;22(7):e18831. doi: 10.2196/18831. https://www.jmir.org/2020/7/e18831/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kalantar-Zadeh K, Moore LW. Impact of nutrition and diet on COVID-19 infection and implications for kidney health and kidney disease management. J Ren Nutr. 2020 May;30(3):179–181. doi: 10.1053/j.jrn.2020.03.006. http://europepmc.org/abstract/MED/32291198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Osama T, Pankhania B, Majeed A. Protecting older people from COVID-19: should the United Kingdom start at age 60? J R Soc Med. 2020 May;113(5):169–170. doi: 10.1177/0141076820921107. https://journals.sagepub.com/doi/10.1177/0141076820921107?url_ver=Z39.88-2003&rfr_id=ori:rid:crossref.org&rfr_dat=cr_pub%3dpubmed. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Li J, Chen Z, Nie Y, Ma Y, Guo Q, Dai X. Identification of symptoms prognostic of COVID-19 severity: multivariate data analysis of a case series in Henan Province. J Med Internet Res. 2020 Jun 30;22(6):e19636. doi: 10.2196/19636. https://www.jmir.org/2020/6/e19636/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Butler MJ, Barrientos RM. The impact of nutrition on COVID-19 susceptibility and long-term consequences. Brain Behav Immun. 2020 Jul;87:53–54. doi: 10.1016/j.bbi.2020.04.040. http://europepmc.org/abstract/MED/32311498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Caccialanza R, Laviano A, Lobascio F, Montagna E, Bruno R, Ludovisi S, Corsico AG, Di Sabatino A, Belliato M, Calvi M, Iacona I, Grugnetti G, Bonadeo E, Muzzi A, Cereda E. Early nutritional supplementation in non-critically ill patients hospitalized for the 2019 novel coronavirus disease (COVID-19): rationale and feasibility of a shared pragmatic protocol. Nutrition. 2020 Jun;74:110835. doi: 10.1016/j.nut.2020.110835. http://europepmc.org/abstract/MED/32280058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.GBD 2017 Diet Collaborators Health effects of dietary risks in 195 countries, 1990-2017: a systematic analysis for the Global Burden of Disease Study 2017. Lancet. 2019 May 11;393(10184):1958–1972. doi: 10.1016/S0140-6736(19)30041-8. https://linkinghub.elsevier.com/retrieve/pii/S0140-6736(19)30041-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Muscogiuri G, Barrea L, Savastano S, Colao A. Nutritional recommendations for CoVID-19 quarantine. Eur J Clin Nutr. 2020 Jun;74(6):850–851. doi: 10.1038/s41430-020-0635-2. http://europepmc.org/abstract/MED/32286533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhang L, Liu Y. Potential interventions for novel coronavirus in China: a systematic review. J Med Virol. 2020 May;92(5):479–490. doi: 10.1002/jmv.25707. http://europepmc.org/abstract/MED/32052466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Garvey WT. Clinical definition of overweight and obesity. In: Gonzalez-Campoy JM, Hurley DL, Garvey WT, editors. Bariatric Endocrinology: Evaluation and Management of Adiposity, Adiposopathy and Related Diseases. Cham: Springer; 2019. pp. 121–143. [Google Scholar]
- 15.Bansal S, Zilberman D. Role of health care expenditure in countering adverse effects of obesity on health: evidence from global data. 2018 International Association of Agricultural Economists (IAAE) Conference; July 28-August 2, 2018; Vancouver, BC. 2018. [DOI] [Google Scholar]
- 16.Leclercq C, Allemand P, Balcerzak A, Branca F, Sousa RF, Lartey A, Lipp M, Quadros VP, Verger P. FAO/WHO GIFT (Global Individual Food Consumption Data Tool): a global repository for harmonised individual quantitative food consumption studies. Proc Nutr Soc. 2019 Nov;78(4):484–495. doi: 10.1017/S0029665119000491. [DOI] [PubMed] [Google Scholar]
- 17.COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University. GitHub. 2020. [2021-01-19]. https://github.com/CSSEGISandData/COVID-19.
- 18.Reported cases and deaths by country, territory, or conveyance. Worldometer. [2020-07-03]. https://www.worldometers.info/coronavirus/#countries.
- 19.FAOSTAT: FAO statistical database. Food and Agriculture Organization of the United Nations. 2016. [2021-01-19]. http://www.fao.org/faostat/en/#home.
- 20.Cragg JG. Some statistical models for limited dependent variables with application to the demand for durable goods. Econometrica. 1971 Sep;39(5):829. doi: 10.2307/1909582. [DOI] [Google Scholar]
- 21.Manning WG. A two-part model of the demand for medical care : preliminary results from the Health Insurance Study. In: van der Gaag J, Perlman M, editors. Health, Economics, and Health Economics: Proceedings of the World Congress on Health Economics, Leiden, The Netherlands, September 1980. Amsterdam: North-Holland Publishing Company; 1981. pp. 103–123. [Google Scholar]
- 22.Duan N, Manning WG, Morris CN, Newhouse JP. A comparison of alternative models for the demand for medical care. J Business Econ Statistics. 1983 Apr;1(2):115. doi: 10.2307/1391852. [DOI] [Google Scholar]
- 23.Bourguignon M, Santos-Neto M, de Castro M. A new regression model for positive data. arXiv. Preprint posted online April 20, 2018. [Google Scholar]
- 24.Smith VA, Preisser JS, Neelon B, Maciejewski ML. A marginalized two-part model for semicontinuous data. Stat Med. 2014 Dec 10;33(28):4891–903. doi: 10.1002/sim.6263. [DOI] [PubMed] [Google Scholar]
- 25.Nieto-Barajas LE, Bandyopadhyay D. A zero-inflated spatial gamma process model with applications to disease mapping. J Agricultural Biol Environ Statistics. 2013 Feb 7;18(2):137–158. doi: 10.1007/s13253-013-0128-z. [DOI] [Google Scholar]
- 26.Voronca DC, Gebregziabher M, Durkalski VL, Liu L, Egede LE. Marginalized two part models for generalized gamma family of distributions. arXiv. Preprint posted online November 18, 2015. [Google Scholar]
- 27.Chai HS, Bailey KR. Use of log-skew-normal distribution in analysis of continuous data with a discrete component at zero. Stat Med. 2008 Aug 15;27(18):3643–55. doi: 10.1002/sim.3210. http://europepmc.org/abstract/MED/18186536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Keeping ES. Introduction to Statistical Inference. North Chelmsford, MA: Courier Corporation; 1995. [Google Scholar]
- 29.McDonald JB. Some generalized functions for the size distribution of income. In: Chotikapanich D, editor. Modeling Income Distributions and Lorenz Curves. New York, NY: Springer; 2008. pp. 37–55. [Google Scholar]
- 30.Li X, Hedeker D. A three-level mixed-effects location scale model with an application to ecological momentary assessment data. Stat Med. 2012 Nov 20;31(26):3192–210. doi: 10.1002/sim.5393. http://europepmc.org/abstract/MED/22865663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Liu L, Ma J, Johnson B. A multi-level two-part random effects model, with application to an alcohol-dependence study. Stat Med. 2008 Aug 15;27(18):3528–39. doi: 10.1002/sim.3205. [DOI] [PubMed] [Google Scholar]
- 32.Tooze J, Grunwald G, Jones R. Analysis of repeated measures data with clumping at zero. Stat Methods Med Res. 2002 Aug;11(4):341–55. doi: 10.1191/0962280202sm291ra. [DOI] [PubMed] [Google Scholar]
- 33.Ng R, Sutradhar R, Yao Z, Wodchis W, Rosella L. Smoking, drinking, diet and physical activity-modifiable lifestyle risk factors and their associations with age to first chronic disease. Int J Epidemiol. 2020 Feb 01;49(1):113–130. doi: 10.1093/ije/dyz078. http://europepmc.org/abstract/MED/31329872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Dietz W, Santos-Burgoa C. Obesity and its implications for COVID-19 mortality. Obesity (Silver Spring) 2020 Jun;28(6):1005. doi: 10.1002/oby.22818. [DOI] [PubMed] [Google Scholar]
- 35.Finer N, Garnett SP, Bruun JM. COVID-19 and obesity. Clin Obes. 2020 Jun;10(3):e12365. doi: 10.1111/cob.12365. http://europepmc.org/abstract/MED/32342637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kassir R. Risk of COVID-19 for patients with obesity. Obes Rev. 2020 Jun;21(6):e13034. doi: 10.1111/obr.13034. http://europepmc.org/abstract/MED/32281287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Simonnet A, Chetboun M, Poissy J, Raverdy V, Noulette J, Duhamel A, Labreuche J, Mathieu D, Pattou F, Jourdain M, LICORN and the Lille COVID-19 and Obesity study group High prevalence of obesity in severe acute respiratory syndrome coronavirus-2 (SARS-CoV-2) requiring invasive mechanical ventilation. Obesity (Silver Spring) 2020 Jul;28(7):1195–1199. doi: 10.1002/oby.22831. http://europepmc.org/abstract/MED/32271993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lighter J, Phillips M, Hochman S, Sterling S, Johnson D, Francois F, Stachel A. Obesity in patients younger than 60 years is a risk factor for COVID-19 hospital admission. Clin Infect Dis. 2020 Jul 28;71(15):896–897. doi: 10.1093/cid/ciaa415. http://europepmc.org/abstract/MED/32271368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Centers for Disease Control and Prevention. [2020-03-28]. https://www.cdc.gov/coronavirus/2019-ncov/prevent-getting-sick/prevention.html?CDC_%20AA_refVal5https%3A%2F%202Fwww.cdc.gov%2Fcoronavirus%2F2019-ncov%%202Fprepare%2Fprevention.html.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Geographical distribution of the six World Health Organization regions and member states for each region (alphabetical order).
The specific types of food that belong to each category for the fat quantity and protein data sets.
Number of deaths per 100 cases, number of recoveries per 100 cases, and obesity rates until July 3, 2020, by countries and split by World Health Organization regions.