Investigation of potential aerosol transmission and infectivity of SARS-CoV-2 through central ventilation systems

Abstract

The COVID-19 pandemic has raised concern of viral spread within buildings. Although near-field transmission and infectious spread within individual rooms are well studied, the impact of aerosolized spread of SARS-CoV-2 via air handling systems within multiroom buildings remains unexplored. This study evaluates the concentrations and probabilities of infection for both building interior and exterior exposure sources using a well-mixed model in a multiroom building served by a central air handling system (without packaged terminal air conditioning). In particular, we compare the influence of filtration, air change rates, and the fraction of outdoor air. When the air supplied to the rooms comprises both outdoor air and recirculated air, we find filtration lowers the concentration and probability of infection the most in connected rooms. We find that increasing the air change rate removes virus from the source room faster but also increases the rate of exposure in connected rooms. Therefore, slower air change rates reduce infectivity in connected rooms at shorter durations. We further find that increasing the fraction of virus-free outdoor air is helpful, unless outdoor air is infective in which case pathogen exposure inside persists for hours after a short-term release. Increasing the outdoor air to 33% or the filter to MERV-13 decreases the infectivity in the connected rooms by 19% or 93% respectively, relative to a MERV-8 filter with 9% outdoor air based on 100 quanta/h of 5 μm droplets, a breathing rate of 0.48 m³/h, and the building dimensions and air handling system considered.

Graphical abstract

1. Introduction

As central heating, ventilation, and air-conditioning (HVAC) systems become ubiquitous across the globe, buildings, especially public and commercial buildings, are not only essential to many community and economic activities but may also play a key role in disease transmission within communities. The recent COVID-19 pandemic has highlighted the role of the indoor environment in viral spread. Most of the documented spread of the disease has occurred within buildings, and a majority of the “superspreader” events where multiple individuals have been infected occurred at least partially in buildings [1,2]. Until recently, it was believed that HVAC systems with their filters may fully protect occupants from viral spread and that increasing filtration effectiveness, increasing the outdoor air fraction, and increasing the number of air changes per hour offered protection [3]. However, a recent peer reviewed study by de Man et al. [4], found that 81% of residents and 50% of health care workers (using surgical masks) became infected in one ward in contrast to the other six wards in the same facility that had no COVID-19 cases. The authors attributed the spread in the ward with infections to the ventilation system, which had recently been remodeled with carbon dioxide sensors that added outdoor air only when the levels were elevated (>1000 ppm) to save energy, in contrast to the other wards that had older HVAC systems that supplied a regular rate of outdoor air through the supply ducts. These findings, coupled with mounting evidence of airborne spread of SARS-CoV-2 [5,6], raise serious questions about the extent to which the virus may spread to connected rooms through HVAC systems—questions to be evaluated quantitatively in this article. Can virus spread significantly through the central air handling system? How much does filtration reduce the risk of virus spreading between rooms connected by an air handling unit? Are higher air change rates inherently more protective of spaces connected by air handling systems? Does increasing the outdoor air fraction always reduce the probability of infection? Without adequate knowledge of the relative effectiveness of these building interventions in reducing aerosol transmission, building managers and operators face difficult choices of how to maintain safe, comfortable, and efficient buildings.

Several studies have explored the aerosol spread of SARS-CoV-2 or other respiratory diseases within buildings. Morawska et al. [7], reviewed engineering controls to minimize the indoor spread of COVID-19, primarily focused on single room analyses, similar to a prior review of bio-aerosol spread by Qian and Zheng [8]. Their primary multiroom recommendation, without quantitative argument, was that air recirculation should be avoided, which is ideal from an infectivity perspective but not always possible (e.g., HVAC system are not designed to handle and most cannot sustain introduction of 100% outdoor air during particularly hot/humid or cold outdoor conditions). In general, models of aerosolized pathogen spread throughout buildings divide into those that account for local concentration gradients, typically using computational fluid dynamics codes (e.g., Ref. [9] for recirculation flows within elevators, classrooms, and supermarkets using a single room formulation inclusive of obstacles), and those that neglect concentration gradients and use well-mixed models [10]. Thus far, most models of virus spread generally, and SARS-CoV-2 specifically, use well-mixed models. For example, Yang and Marr [11] predicted the evolving size distribution as a function of time for influenza A viruses in a well-mixed room to find that increased air change rates reduce the concentration of the virus within a well-mixed space faster. Additionally, Noakes and Sleigh [12] and Emmerich et al. [13], evaluated the spread in a hospital of nosocomial bacterial infections including tuberculosis. Although single room models of infectious spread are well studied, the impact of aerosolized spread of SARS-CoV-2 via air handling systems in multiroom buildings remains relatively unexplored. Here we use a multiroom model to evaluate SARS-CoV-2 infectivity adapting the well-known Wells-Riley model. This model is based on a standard well-mixed model of a single space originally with a continuous release of infective dose or quanta [[14], [15], [16], [17]], though our extension accounts for transients. A Poisson distribution is then used to link the release rate of viral dose to the probability of becoming ill.

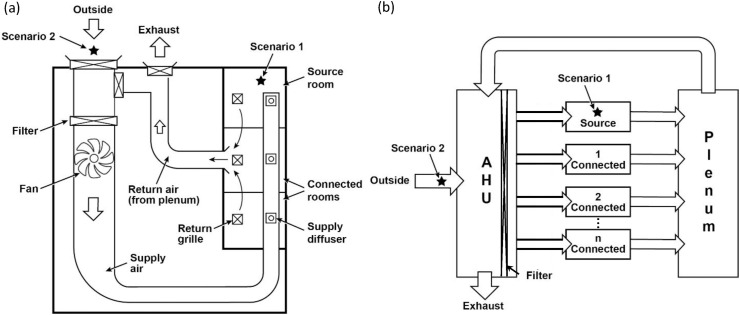
In the remainder of this article, we evaluate the aerosolized viral spread across a small multiple room building with rooms connected solely through a central air handling system (see Fig. 1 a). After explicitly deriving the equations and describing the parameters, we evaluate the influence of filtration, air change rates, and the fraction of outdoor air on the probability of infection using the well-known well-mixed modeling approach for a multiroom building. Parameters in the model were selected to be quantitatively specific to SARS-CoV-2, but the insights are general.

Fig. 1.

Essential elements of a central air handling system (a) in a generic small building (b) with their process flow representation. The two scenarios considered include a virus containing particle source that was either internal (Scenario 1) or external (Scenario 2) to the building (from a source room or outdoor air, respectively). The virus spreads to the connected rooms via a centrally connected plenum and air handling unit (AHU).

2. Theory and calculation

In this section, we use conservation of mass to derive equations that relate the concentration of an aerosolized virus across a connected multiroom building (i.e., see Fig. 1). We investigate two contaminant source locations—indoor (Scenario 1) and outdoor (Scenario 2). When the source location is within one room termed a source room, our model includes connected rooms (e.g., two or more per Fig. 1), a common plenum, and an air handling system that receives internal exposure. When the exposure occurs from sources external to the building (i.e., in front of the outdoor air intake), our model includes connected rooms, a common plenum, and an air handling system that receives the external source. The air handling system mixes outdoor air with air from the return plenum and delivers that air through a minimum efficiency reporting value (MERV) rated filter to the individual rooms. A well-mixed approximation (although not appropriate for some buildings and room configurations not considered here) is used where the concentration within each room may be assumed to be spatially uniform (gradients in concentration remain negligible or vanish much faster than the concentrations within the rooms). Equations are written out explicitly below to clarify assumptions.

We begin with the source room. Species conservation of momentum [18] requires

$$\frac{\partial c}{\partial t}=-\nabla \cdot \mathit{N}+R_V.$$ (1)

where c is the local concentration, t is time, N is the flux vector, and R _V is a bulk source term. Integration over a room volume V and application of the divergence theorem returns

$$\underset{V}{\int }\frac{\partial c}{\partial t}dV=\underset{A}{\int }-\mathit{n}\cdot \mathit{N}dA+\underset{V}{\int }{R}_{V}dV,$$ (2)

where n is the outward pointing normal vector and A is a surface area along the boundary of the room. Application across one inlet (a supply) and two outlets (one for a return and one for a small, perhaps negligible gap under the door) with deposition on the floor finds

$$\frac{dCV}{dt}=A_i{N}_i-A_o{N}_o-A_d{N}_d-A_s{N}_s+\underset{V}{\int }{R}_{generation}dV+\underset{V}{\int }{R}_{decay}dV,$$ (3)

where C is the volume average concentration, N without bolding is a positive flux magnitude averaged across the area, A, each with subscript i, o, d, and s indicating the inlet supply, outlet return, door (assumed shut hereafter), and settling, respectively. Inward leaks of virus laden air are not included in this formulation. Outward leaks (where present) are included in this formulation and are lumped into the term for the door, yet both outward leaks and flow through the door (where shut) are taken to be small in these simulations. Any leaks are small if the product of area and flux for the leaks are substantially smaller than the product of area and flux for inlet supply or outlet return. The bulk source term accounts for both release or generation within a space, R _generation, and for viral decay, R _decay, which is treated as first order based on experimental findings of Schuit et al., [19]. The volume of the room is constant, fluxes in and out of a space may be expressed as a concentration times a velocity (in the absence of significant diffusion, electrostatic forces, or thermophoretic phenomena), and the bulk source term is divided into a transient source term (e.g., coughing, sneezing, singing, laughing, talking, breathing, etc.) and a viral decay term so that

$$V\frac{dC}{dt}=A_i{v}_i{C}_i-A_o{v}_o{C}_o-A_d{v}_d{C}_d-A_s{v}_s{C}_s+V{\dot{C}}_{generation}-V{k}_{decay}C,$$ (4)

where C represents volumetric or area-wise averaged concentration, the over dot indicates a rate, and k _decay is a first-order rate constant that represents viral decay by either biophysical/biochemical or photonic means. Now we impose the well-mixed approximation so that the outlet concentrations through the return (and under the door) are the same as in the bulk volume. Because the concentration is uniform within the room, the concentration that determines the flux to the floor is also uniform so that

$$\frac{dC}{dt}=\frac{A_i{v}_i}{V}{C}_i-\frac{A_o{v}_o+A_d{v}_d}{V}C-\frac{A_s{v}_s}{V}C+{\dot{C}}_{generation}-k_{decay}C.$$ (5)

In keeping with Yang and Marr [11]; we recognize that the number of air changes (given in air changes per hour or ACH) is the product of all entering (or all leaving) areas and velocities divided by the volume of the room so that we may define λ = (A _o v _o + A _d v _d)/V = A _i v _i/V. Then

$$\frac{dC}{dt}=\lambda C_i-\lambda C-\frac{v_s}{H}C+{\dot{C}}_{generation}-k_{decay}C,$$ (6)

where H = A _s/V is vertical height of the room (not the height at which the particles are released). Grouping then returns

$$\frac{dC}{dt}=\lambda C_i+{\dot{C}}_{generation}-\left(\lambda +\frac{v_s}{H}+k_{decay}\right)C.$$ (7)

this form concurs with that of Yang and Marr [11] for a single room in the absence of inlet and generation terms. In their case, they begin with an initial well-mixed concentration of C _o (instead of a pulse as given below) and integrate to find

$$C=C_{o}Exp\left[-\left(\lambda +\frac{v_s}{H}+k_{decay}\right)t\right].$$ (8)

For a given air change rate, a decay rate constant, and settling velocity (as a function of particle size), this expression can be used to adjust the particle size distribution as a function of time within a single room. Our analysis includes the first two terms on the right of Eq. (7) neglected in prior analyses but needed to describe multiple rooms.

We now consider a small building where the rooms are connected and the common plenum (that collects air from the rooms and returns it to the air handling unit) is well mixed. The room in which the viral source or dose is generated is termed the “source room” below, and its concentration is labeled as C _source in Eq. (7) with a generation term included (either as shown in Eq. (23b) or as an initial condition). Eq. (7) also describes the temporal evolution of the virus concentration in a connected room, labeled C _connected, when the generation term is zeroed. When the common plenum is well mixed, multiple connected rooms are considered to be identical, so that their concentrations may be represented by a single expression.

We now address the functional form of the plenum and the air handling unit (AHU). The plenum between the ceiling and the roof extends to AHU ducting. The first portion of the AHU starts at the ducting from the plenum and extends to the filter including the exhaust and outside air intake; this portion of the AHU is labeled pre meaning prefilter below. A second portion within the AHU extends from the downstream side of the filter to the source and connected rooms; this portion of the AHU is labeled post meaning postfilter below. In each physical volume, settling and viral decay are incorporated. Application of Eq. (2) to a plenum with multiple inlets (one from a source room and the rest from connected rooms starting at the return grilles) and one outlet (common return to the AHU, which starts at the ducting from the plenum) finds

$$\frac{d{C}_{plenum}{V}_{plenum}}{dt}=A_{source}{N}_{source}+\sum A_{connected}{N}_{connected}-A_{pre}{N}_{pre}-A_s{N}_s+\underset{V}{\int }{R}_{V}dV.$$ (9)

The volume of the plenum is constant, and fluxes in and out of a space may be expressed as a concentration times a velocity as above, and the well-mixed approximation is imposed so that the outlet concentration to the AHU is the same as in the bulk volume of the plenum. Following the same steps as above,

$$\frac{d{C}_{plenum}}{dt}=f_Q{\lambda }_p{C}_{source}+\left(1-f_Q\right){\lambda }_p{C}_{connected}-\left({\lambda }_p+\frac{v_s}{H_p}+k_{decay}\right)C_{plenum},$$ (10)

where f _Q is the fraction of the flow that comes from source room versus the other connected rooms, and where λ _p and H _p are the air change rates in the plenum and the typical entry height of particles in the plenum. Application of Eq. (2) to the prefilter portion of the AHU with two inlets (plenum return and outdoor air intake) and two outlets (to the exhaust and to the filter) finds

$$\frac{d{C}_{pre}{V}_{pre}}{dt}=A_{plenum}{N}_{plenum}+A_{OA}{N}_{OA}-A_{prefilter}{N}_{prefilter}-A_{ex}{N}_{ex}-A_s{N}_s+\underset{V}{\int }{R}_{V}dV,$$ (11)

where OA stands for outdoor air, ex stands for the exhaust, and prefilter stands for the upstream face of the filter. The physical volume of the AHU (i.e., the physical dimensions of the ductwork and other parts of the AHU) is constant, and fluxes in and out of a space may be expressed as a concentration times a velocity in the absence of significant diffusion, and we impose the well-mixed approximation so that the outlet concentrations to the exhaust and filter are the same as in the bulk of its physical volume. Because the concentration is uniform within the prefiltered portion of the AHU, the concentration that determines the settling flux to the floor is also uniform so that in the absence of generation within the plenum itself

$$\frac{d{C}_{pre}}{dt}={\lambda }_{pre}{C}_{plenum}+f_{OA}{\lambda }_{pre}{C}_{OA}-\left(\left(1+f_{OA}\right){\lambda }_{pre}+\frac{v_s}{H_{pre}}+k_{decay}\right)C_{pre},$$ (12)

where f _OA is the fraction of the outdoor air that is added to the flow (i.e., the outdoor air volumetric flow rate, which is equivalent to the exhaust volumetric flow rate, is the fraction of outdoor air multiplied by the volumetric flow rate entering from the plenum), and where λ _pre and H _pre are the air change rates in and height of the prefiltered portion of the AHU, respectively. The outdoor air added is exactly balanced by the building air exhausted to the outside in order to maintain constant pressure. Further application of Eq. (2) to the portion of AHU downstream of the filter with one inlet (from the filter) and multiple outlets (to the source room and connected rooms) finds

$$\frac{d{C}_{post}{V}_{post}}{dt}=A_{postfilter}{N}_{postfilter}-A_{source}{N}_{source}-\sum A_{connected}{N}_{connected}-A_s{N}_s+\underset{V}{\int }{R}_{V}dV,$$ (13)

where the subscript postfilter indicates the downstream face of the filter. The physical volume of the filtered portion of the AHU is constant, and fluxes in and out of a space may be expressed as a concentration times a velocity in the absence of significant diffusion, and we impose the well-mixed approximation so that the outlet concentrations through the AHU are the same as in the bulk of its physical volume. Because the concentration is uniform within the room, the concentration that determines the flux to the floor is also uniform so that in the absence of generation within the plenum itself

$$\frac{d{C}_{post}}{dt}={\lambda }_{post}\left(1-\epsilon \right)C_{pre}-\left({\lambda }_{post}+\frac{v_s}{H_{post}}+k_{decay}\right)C_{post},$$ (14)

because C _postfilter=(1-ε)C _pre, where λ _post and H _post are the air change rates in and height of the postfilter portion of the AHU, respectively, and the filter has an efficiency of ε (i.e., ε = 0.75 for a MERV-8 filter, see Fig. 5 of [20]). This analysis does not include other mechanisms of virus loss in the ducts (e.g., thermophoresis, turbophoresis, dehumidification, etc.).

Together our multiroom model becomes

$$\begin{array}{l}\frac{d{C}_{source}}{dt}=\lambda C_{post}+{\dot{C}}_{generation}-\left(\lambda +\frac{v_s}{H}+k_{decay}\right)C_{source},\\ \frac{d{C}_{connected}}{dt}=\lambda C_{post}-\left(\lambda +\frac{v_s}{H}+k_{decay}\right)C_{connected},\\ \frac{d{C}_{plenum}}{dt}=f_Q{\lambda }_p{C}_{source}+\left(1-f_Q\right){\lambda }_p{C}_{connected}-\left({\lambda }_p+\frac{v_s}{H_p}+k_{decay}\right)C_{plenum},\\ \frac{d{C}_{pre}}{dt}={\lambda }_{pre}{C}_{plenum}-\left(\left(1+f_{OA}\right){\lambda }_{pre}+\frac{v_s}{H_{pre}}+k_{decay}\right)C_{pre}\\ \frac{d{C}_{post}}{dt}=\left(1-\epsilon \right){\lambda }_{post}{C}_{pre}-\left({\lambda }_{post}+\frac{v_s}{H_{post}}+k_{decay}\right)C_{post},\end{array}$$ (15)

because C _i in Eq. (7) becomes C _post, and C _OA = 0 in this scenario. The initial conditions may be constructed so that all of concentrations are zero at the initial time, and concentration is driven by the generation term in the first of these. This contrasts with the approach of Yang and Marr [11] who used a nonzero initial condition in the source room, their only room, but forced the generation term to vanish.

We further consider the scenario where outdoor air containing virus enters a building via an outdoor air intake. Here

$$\begin{array}{l}\frac{d{C}_{connected}}{dt}=\lambda C_{post}-\left(\lambda +\frac{v_s}{H}+k_{decay}\right)C_{connected},\\ \frac{d{C}_{plenum}}{dt}={\lambda }_p{C}_{connected}-\left({\lambda }_p+\frac{v_s}{H_p}+k_{decay}\right)C_{plenum},\\ \frac{d{C}_{pre}}{dt}={\lambda }_{pre}{C}_{plenum}+f_{OA}{\lambda }_{pre}{C}_{OA}-\left(\left(1+f_{OA}\right){\lambda }_{pre}+\frac{v_s}{H_{pre}}+k_{decay}\right)C_{pre}\\ \frac{d{C}_{post}}{dt}=\left(1-\epsilon \right){\lambda }_{post}{C}_{pre}-\left({\lambda }_{post}+\frac{v_s}{H_{post}}+k_{decay}\right)C_{post},\end{array}$$ (16)

where all rooms are now connected because the source is external to the building. The initial conditions require zero concentrations in all spaces with the driving force as the second term on the right of the third equation.

For completion, these equations require a settling velocity. As a first-order approximation, the Stokesian settling velocity, v _s, is

$$v_s=\frac{{\rho }_d-{\rho }_f}{18{\mu }_f}g{d}^2,$$ (17)

where ρ _d is the density of the droplet, ρ _f is the density of the fluid, g is the gravitation constant, d is the diameter of the droplet, and μ _f is the dynamic viscosity of the fluid. Setting v _s = f _significant H _i(λ _i + k _decay), determines the diameter at which the settling velocity becomes significant as

$$d=\sqrt{\frac{18{\mu }_f{H}_i{f}_{significant}\left({\lambda }_i+k_{decay}\right)}{g\left({\rho }_d-{\rho }_f\right)}},$$ (18)

where f _significant is the factor at which significance begins (e.g., f _significant = 10% when v _s/H _i is 10% of λ _i + k _decay).

The analysis above specifies a well-mixed concentration in each space. However, the units of concentration have not been specified (options include moles, mass, droplets, virions, or even quanta (i.e., infectious dose) each per unit volume; all are valid interpretations of these equations). If C with its location subscript has units of quanta per unit volume, then the risk follows directly from the Wells-Riley approach, in which the cumulative probability of infection, P, is given by

$$P=1-e^{-\mu },$$ (19)

where μ is the average number of quanta breathed by a susceptible person, meaning someone who could become infected [21]. Rudnick and Milton [14] relate the average number of quanta (one quantum gives a 63% probability of inducing infection) breathed to the average quantum concentration, where this average is generalized as

$$\mu =p\underset{t_1}{\overset{t_2}{\int }}{C}_{i}dt,$$ (20)

where C _i is any of the concentrations in any of these rooms, p is the volumetric breathing rate, and t ₁ and t ₂ are the starting and ending times of exposure (where t ₂>t ₁ ≥ 0). This implementation does not include masks. The community's public health risk may be estimated with a replication number as

$$R_o=\left(n-1\right)P=\left(n-1\right)\left(1-Exp\left[-p\underset{t_1}{\overset{t_2}{\int }}{C}_{i}dt\right]\right),$$ (21)

where n is the number of people in the space (including the one shedding virus). Analysis below sets t ₁ = 0 h.

The Wells-Riley equation as typically constructed requires that air flow rates, the emission rate, and the infectious agent concentrations to be at steady state [14]. This contrasts with the dynamic analysis here. The difference is important because quanta provided in the literature correspond to steady emission rates. A connection may be forged by integrating the quanta rate over time and dividing by the relevant volume. For exposure within the building, the initial concentration is then

$$C_{total}=\frac{1}{V_{source}}\underset{0}{\overset{5\min }{\int }}qdt,$$ (22)

where q is the quanta emission rate and V _source is the volume of the source room to represent a 5 min emission or exposure (e.g., the duration of a coughing bout or other exposure from coughing, sneezing, singing, laughing talking, breathing, etc.), assuming spread throughout the room is instantaneous. This exposure time corresponds to a duration of release of virus from an infected individual, after which the individual departs from the space or stops shedding virus. Similarly, for a contaminated outdoor air source,

$$C_{total,OA}=\frac{1}{V_{pre}}\underset{0}{\overset{5\min }{\int }}qdt,$$ (23a)

where C _total,OA is the total outdoor air concentration and V _pre is the volume of the prefiltered portion of the AHU. Because Eqs. (15), (16) are linear, they may be scaled by any non-zero scalar, here C _total and C _total,OA, respectively. When scaling Eq. (15) on C _total, the generation term requires special attention. During emission, the generation term may be written as q/V _source and zero otherwise so that we may write

$$\frac{{\dot{C}}_{generation}}{C_{total}}=\frac{\left(q/V_{source}\right)G\left(t\right)}{\underset{0}{\overset{5\min }{\int }}\frac{q}{V_{source}}dt}=\frac{1}{5\min }G\left(t\right),$$ (23b)

where q and V _source are constants and G is a smooth top hat function that ranges between 0 and 1 as

$$G=\sum _i\left(\frac{1}{1+Exp\left[-30000/\min \left(t-0.1\min \right)\right]}-\frac{1}{1+Exp\left[-30000/\min \left(t-5.1\min \right)\right]}\right)$$ (24)

to represent the same 5 min emission, assuming spread throughout the room is instantaneous. For an external source, C _OA is taken as C _total,OA multiplied by G. When scaled on C _total,OA

$$\frac{C_{OA}}{C_{total,OA}}=\frac{\left(\underset{0}{\overset{5\min }{\int }}\frac{q}{V_{pre}}dt\right)G\left(t\right)}{\underset{0}{\overset{5\min }{\int }}\frac{q}{V_{pre}}dt}=G\left(t\right).$$ (25)

Table 1 shows the parameters used in the simulation. These equations were solved in Mathematica (Wolfram Research, Champaign, IL).

Table 1.

Parameters used in simulation.

Baseline Parameter	Variable	Baseline Value	Range Evaluated
Settling Velocity (5 μm)a	vs	2.7 m/h
Air Change Rate (Source and Connected Rooms)	λ	6 ACH	1.8–12 ACH
Room Height	H	8 ft
Fraction from Source Room to Plenum	fQ	1/3	1/3–1/30
Air Change Rate (in Plenum)b	λp	72 ACH	22–144 ACH
Plenum Height	Hp	2 ft
Fraction Outdoor Air	fOA	9%	0–33%
Air Change Rate (in prefilter portion of AHU)b	λpre	36.9 ACH	11–74 ACH
Height of Prefilter portion of AHU	Hpre	2 ft
Air Change Rate (in postfilter portion of AHU)b	λpost	61.4 ACH	18–123 ACH
Height of postfilter portion of AHU	Hpost	2 ft
Infectious Dosec	q	100 quanta/h	10–300 quanta/h
Receptor Breathing Rated	p	8 L/min = 0.48 m3/h
Single-pass Filtratione	ε	0.75	0–98%
Virus Decay Ratef	kdecay	0.008/min = 0.48/h
Volume of the Source Roomg	Vsource	512 ft3
Physical Volume of the AHU	Vpre	250 ft3

^aFrom Eq. (17) with ρ_d = 1000 kg/m³, ρ_f = 1 kg/m³, g = 9.8 m/s², and μ_f = 1.81×10⁻⁵ Pa s.

^bFor three rooms (one of which is the source), a plenum volume of 128 ft³, a prefilter AHU physical volume of 250 ft³ including ducts from the plenum to the AHU, and a post filter AHU physical volume of 150 ft³ including ducting to rooms.

^cThis translates into a dose concentration of 0.57 quanta/m³ in the source room and 1.18 quanta/m³ for outdoor exposure via the AHU; see Section 3.5.

^dRudnick and Milton [14].

^eFig. 5 of Dols et al. [20], for MERV-8 at 5 μm.

^fSchuit et al., [19].

^gRelated to square footage by V_source/H; same as the connected rooms.

Five microns was chosen as the nominal virus containing particle size, because it is the boundary between coarse and fine infective aerosols as described by Milton and colleagues [31]. Filtration efficiency may decrease by more than 10% when the virus containing particle size is <2 μm and the droplet settling rate may decrease the virus removal rate by more than 10% relative to when the virus containing particle size is >130 μm (Eq. (18) with μ _f = 1.8^.10⁻⁵ Pa s, f _significant = 10%, g = 9.8 m/s², ρ _d = 1000 kg/m³ and ρ _f = 1 kg/m³), though larger particles may not be swept into the plenum. All of these sizes are substantially larger than a naked virus but represent the sizes of respiratory droplets that encapsulate virus [31].

3. Results and discussion

The objective of this article is to evaluate the concentrations and probabilities of infection of SARS-CoV-2 for both building interior and exterior exposure sources using a well-mixed model in a multiroom building connected via a central air handling system. We present two scenarios: (1) exposure from a source within one of the rooms of a building and (2) exposure from a source external to the building that enters through the air intake of an air handling unit. Specifically, we explore the influence of filtration, air change rates, and outdoor air in ten cases on the probability of infection. The analysis does not include the effect of individual masks (which vary in efficacy with corresponding costs and benefits, [22]). For the remainder of this article, Table 2 gives the cases used to evaluate the influence of filtration, air change rates, and outdoor air fraction on the temporal evolution of the droplet concentration and the probability of infection.

Table 2.

Cases considered.

Number	Case	Room ACH	Filter (Efficiency)a	Outdoor Airb
1	Baseline (code compliant)	6	MERV 8 (75%)	9%
2	No filtration	6	No Filter (0%)	9%
3	High filtration	6	MERV 11 (94%)	9%
4	Extra high filtration	6	MERV 13 (98%)	9%
5	Extra low airflow rate	1.8	MERV 8 (75%)	29%
6	Low airflow rate	3	MERV 8 (75%)	17%
7	High airflow rate	12	MERV 8 (75%)	4%
8	No outdoor air	6	MERV 8 (75%)	0%
9	Less outdoor air	6	MERV 8 (75%)	6%
10	More outdoor air	6	MERV 8 (75%)	33%

^aSingle pass efficiency (Fig. 5 of [20]).

^bValues for experimental test facility in Fig. 1 (a) assuming one person per each of the three rooms. Variations for Cases 5–7 set to keep the volumetric flow rate of outside air constant.

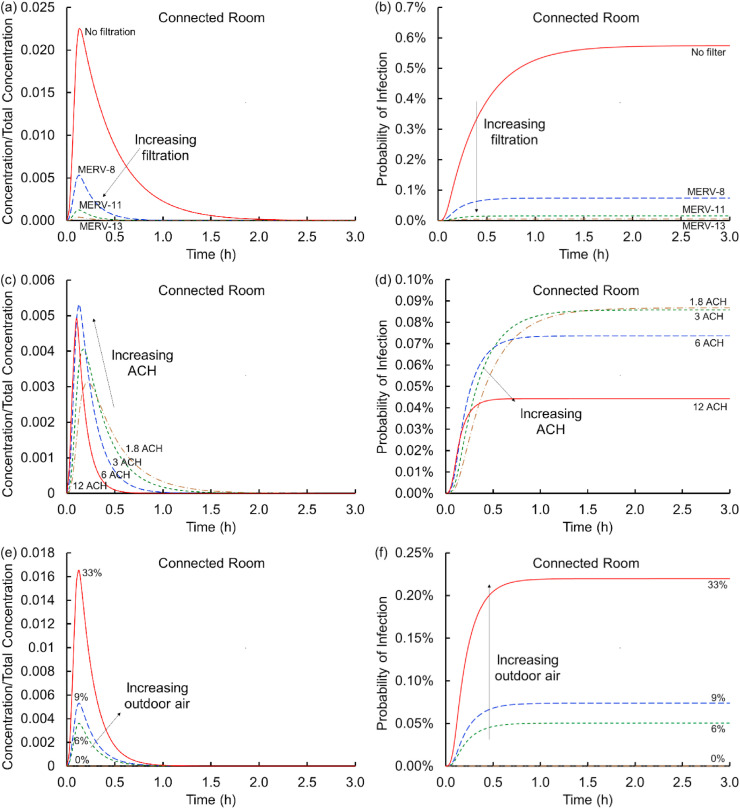
3.1. Influence of filtration

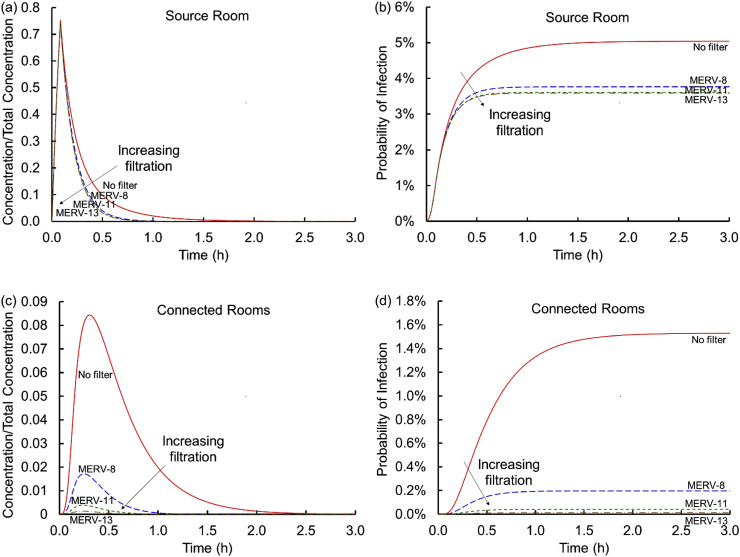
Air handlers recirculate air and mix it with outdoor air creating an interplay between the fraction of outdoor air and level of filtration, which affects viral transmission only when some air is recirculated (if all air is from outdoors and outdoor air is virus free, filtration does not affect respiratory droplet transmission). Fig. 2 shows the influence of filtration. Fig. 2 (a) shows that in the absence of filtration, the concentration in the source room rises sharply and then gradually decreases as the air containing the virus encapsulating particles mixes with the virus-free air in the remainder of the spaces (e.g., connected rooms, plenum, and AHU), outdoor air exchange continues, particles land on floors, and viral decay reduces concentrations further. In the connected rooms (Fig. 2 (c)), the concentration is initially zero but rises as infective particles enter via the air handling unit. With filtration, the peak concentration in the connected rooms and the duration of that exposure decrease substantially. For example, a MERV-8 filter decreases the peak virus concentration in connected rooms by a factor of five, and for a MERV-13 filter the decrease is over an order of magnitude. The shape of the curve does not vary significantly as the MERV rating increases, but reducing the peak reduces the time for potentially meaningful concentrations to be present. Similarly shaped curves were observed by Emmerich et al., [13]; who predicted the spread of Mycobacterium tuberculosis in health care facility bathrooms. Because filters do not remove 100% of the particles, some of the virus returns back into the source room, especially when the MERV rating is lower. This modestly extends the time it takes for the concentration to drop below preferred levels.

Fig. 2.

Concentrations scaled on the total virus concentration shed, C_total, (a and c) and cumulative probabilities of infection (b and d) versus time for the source (a and b) and connected (c and d) rooms across the four conditions of no filter and MERV-8, MERV-11, and MERV-13 filters (Scenario 1 Cases 1–4).

Fig. 2 (b) and (d) translates these curves into cumulative probabilities of infection by integrating the exposures over time, multiplying by a breathing rate, and exponentiating the product per an assumed Poisson distribution of Wells-Riley. The cumulative probability starts at time zero and only increases over time. In contrast to the concentration curves which, because they are normalized, may represent any suitable concentration units (e.g., particles/volume, moles/volume, mass/volume, droplets/volume, virions/volume, or even quanta or infectious dose), infectivity here is based only on dose measured as quanta. Fig. 2 (b) and (d) shows that, in the absence of effective filtration, the probability of infection rises sharply in the source room with a somewhat lower probability of infection in the connected rooms. With filtration, the probability of infection in the source room is attenuated by a percent or two. In the connected rooms, filtration with a MERV-8 filter lowers the risk by almost an order of magnitude and a MERV-13 filter further lowers the risk of infection by another order of magnitude. Even so, there is still a risk of only one in ~7300 with a MERV-13 filter in the connected room, the lowest probability of infection for any of the cases considered here.

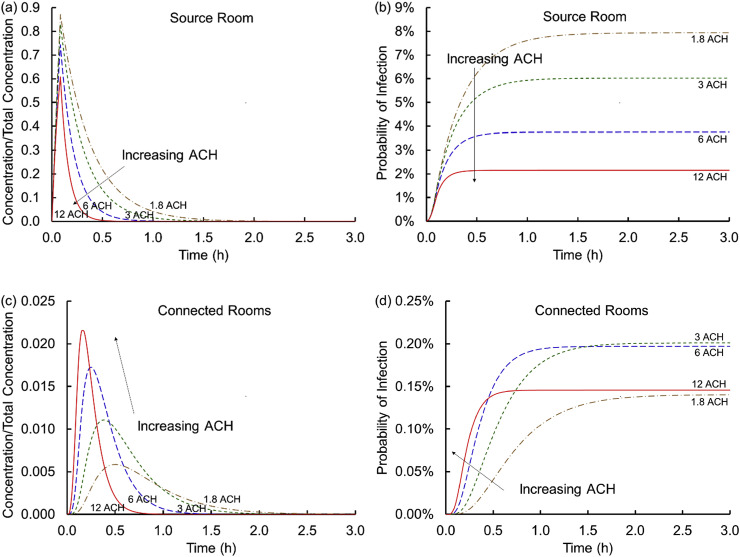
3.2. Influence of air change

Fig. 3 (a) and (c) evaluates the influence of the air change rate on the temporal evolution of the virus containing particle concentration. Fig. 3 (a) shows that higher air change rates substantially decrease the concentration in the source room. If that room has single occupancy, then this is a relatively unimportant effect because the virus shedding individual does not infect others in the source room. If the room has an occupancy level greater than one (consider multiple occupants in an office) then increasing the ACH would be an important means of minimizing exposure (in the absence of an enhanced near-field concentration (e.g., the downstream exposure in a Guangzhou restaurant [5,6]), not addressed by a well-mixed model). These results are unsurprising given the multiple reports of this effect in the literature for a single room [11]. However, this is not the end of the story in connected multiroom buildings. As the virus containing particles are removed from the source room they proceed through the plenum and the AHU to the connected rooms. As the ACH increases, the peak concentration in the connected rooms rises because more of the flow from the source room transports into the connected rooms, but this concentration persists in these connected rooms for shorter time periods. This result suggests that shorter exposures at lower ACH may be preferential relative to higher ACH.

Fig. 3.

Concentrations scaled on the total virus concentration shed, C_total, (a and c) and cumulative probabilities of infection (b and d) versus time for the source (a and b) and connected (c and d) rooms for air change rates of 1.8, 3, 6, and 12 ACH (Scenario 1 Cases 1 and 5–7).

Fig. 3 (b) and (d) translates these observations for air change rates to cumulative probabilities of infection. In the source room increasing the air flow rate substantially decreases the probability of infection as suggested above. With low air change rates, the probability of infection even with a MERV-8 filter is ~8%, suggesting that the combination of filtration with meaningful flow rates is important. At the highest air change rate considered (12 ACH) the probability of infection drops to ~2% in the source room. In the connected rooms, short time exposures (~15–30 min) present the highest probability of infection for the largest air change rates. This is because higher air change transports infective dose into the connected rooms much more quickly leading to short term infectivity risks about an order of magnitude higher at higher air change rates than at lower air change rates. At longer exposure times, the baseline (Case 8) condition is surprisingly among the highest risk of infection, indicating that the lowest air flow rate is not the worst among these cases (the exact order of the curves at long times depends in part on the parameters selected, the building dimensions and air handling system considered). This finding that code conditions or higher air change rates might not reduce risk of exposure in downstream rooms is an important finding of this analysis. In the absence of viral degradation (via k _decay), the 1.8 ACH curve would achieve a somewhat higher steady state than the 12 ACH curve indicating a distinction between biological and non-biological contaminant spread. These are not insights that may be obtained without multiroom coupling between connected spaces but follow directly from standard and well-established approaches in building science and epidemiology.

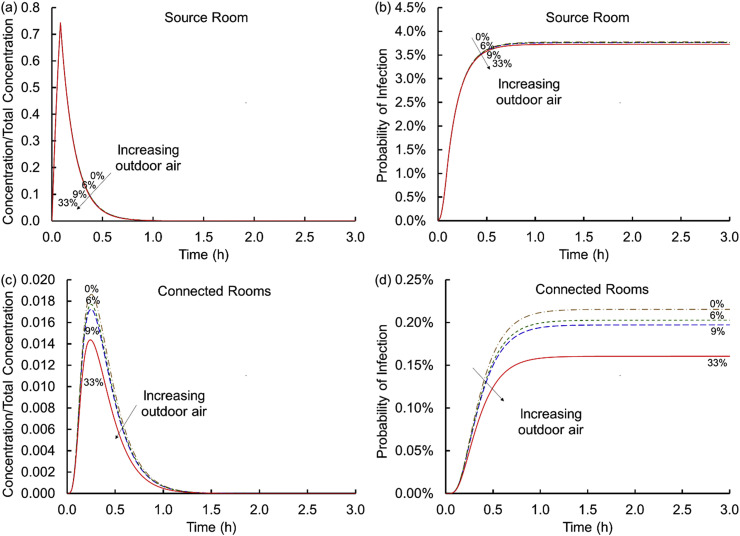
3.3. Influence of outdoor air fraction

Fig. 4 (a) and (c) shows the effect of varying the amount of virus-free outdoor air supplied to the AHU. Increasing the amount of outdoor air decreases the peak concentration in the connected rooms. The decrease is meaningful and is less than a factor of two from the case with no outdoor air (Case 8) to 33% outdoor air (Case 10), which is smaller than the difference between MERV-8 and MERV-11 filters suggesting that increasing filtration efficiency may be more effective than increasing outdoor air fraction. Please note in Fig. 3 that increasing the ACH while decreasing the outdoor air fraction holds the volumetric flow rate approximately constant in contrast to Fig. 4 that holds ACH constant with increasing fraction and volumetric flow rate of outdoor air. Fig. 4 (b) and (d) shows the risk of infection as a function of the percent of outdoor air added. In the source room, the outdoor air intake makes very little difference, which is remarkably different from the single room analyses in large measure because outdoor air enters through the HVAC system instead of entering directly. However, in the connected rooms, increased amounts of outdoor air lower the infection probability by less than a factor of two for conditions considered.

Fig. 4.

Concentrations scaled on the total virus concentration shed, C_total, (a and c) and cumulative probabilities of infection (b and d) versus time for the source (a and b) and connected (c and d) rooms for virus-free outdoor air fractions of 0, 6, 9, and 33% (Scenario 1 Cases 1 and 8–10).

3.4. Influence of virus-laden outdoor air

Next, we evaluate the scenario where outdoor air provides a concentration of virus into the AHU that then spreads throughout the remainder of the building. This scenario is important because outdoor air is not always virus-free and outdoor spread from building to building has been tied to SARS-CoV-1 spread [23,24]. Indeed, the exhaust from most buildings is not filtered and virus from a neighboring building's exhaust and relief vents, open windows, or from sewer gasses may be drawn into the AHU. Schuit et al. [19], show that high-intensity simulated sunlight, typical of a summer day, drives rapid decay of SARS-CoV-2, decreasing this risk. During the other seasons, the light intensity and heat are lower permitting the virus to persist longer outdoors. In this second scenario all rooms are identical and connected. The exposure lasts for 5 min as before (short compared to hours of impact), after which the outdoor air is again assumed to be virus-free. Outdoor concentrations may vary substantially; the intake concentration is set to the same dose rate as the indoor release to permit comparison between source scenarios.

Fig. 5 (a) and (b) shows that, as above, no filtration results in the highest concentration in the rooms for the longest duration (similar to the internal exposure scenario). Indeed, the highest probabilities of infection occur in the absence of filtration. As the MERV rating increases, the probability of infection decreases because the infectious dose in the outdoor air goes through a filter prior to entering the connected rooms. This would suggest that removing or incorrectly installing the filter is undesirable. Fig. 5 (c) and (d) compares the influence of the air change rates. The peak concentration generally decreases and is delayed as the air change rate decreases. When integrated, the cumulative probability of infection rises most quickly for the highest air change rates but asymptotes to modest steady states in contrast to the lowest air change rates that accumulate risk more slowly but asymptote to higher cumulative probabilities. Fig. 5 (e) and (f) shows the influence of outdoor air. Because the pathogen comes from outdoors, increasing the outdoor air intake fraction leads to more dose, so that the highest outdoor air fraction leads to the highest probability of infectivity. In this scenario, no outdoor air introduction to the AHU would be preferential.

Fig. 5.

Concentrations scaled on the total outdoor air concentration of virus, C_total,OA, (a, c and e) and cumulative probabilities of infection (b, d, and f) versus time for (a and b) no filter and MERV-8, MERV-11, and MERV-13 filters (Scenario 2 Cases 1–4); (c and d) air change rates of 1.8, 3, 6, and 12 ACH (Scenario 2 Cases 1 and 5–7); outdoor air fractions of 0, 6, 9, and 33% (Scenario 2 Cases 1 and 8–10). For an outdoor virus source, all rooms are connected rooms.

These findings contrast with those where exposure occurred in the source room; there increased outdoor air was considered helpful and lowered the exposure in connected rooms.

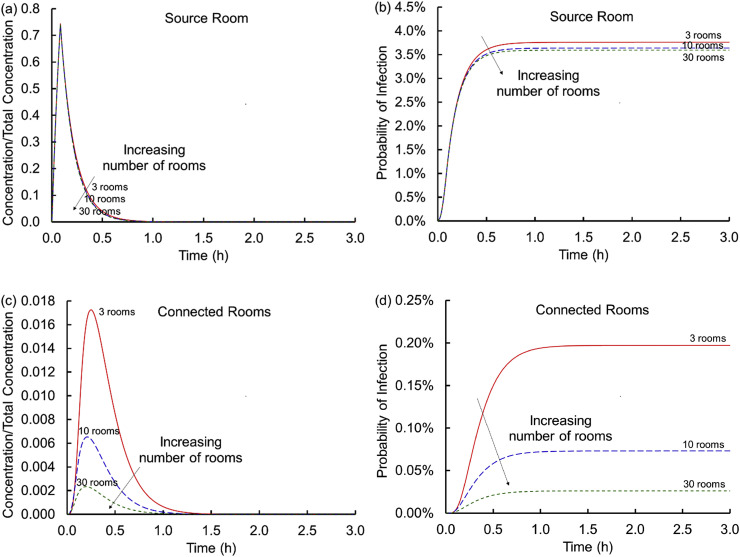
3.5. Dose and number of rooms

Each of the results above held the number of rooms and the infectious dose constant as ventilation strategies vary. For the internal source scenario, Fig. 6 shows that as the number of rooms increases the concentration within the connected rooms decreases. The effect is marginal in the source room. Therefore, the conditions evaluated are somewhat “conservative” because they may over predict the risk of infection for larger buildings (e.g., larger office suites). However, with larger buildings, the potential for more than one infectious person shedding virus increases.

Fig. 6.

Concentrations scaled on the total virus concentration, C_total, shed (a and c) and cumulative probabilities of infection (b and d) versus time for the source (a and b) and connected (c and d) rooms for 3, 10 and 30 rooms (Scenario 1 Case 1 varying f_Q and corresponding supply flow rates through the AHU).

Fig. 7 shows that the probability of infection via the Wells-Riley approach in both types of rooms increases as the infectious dose measured in quanta increases. Quanta is a unit of infectious dose that may or may not correspond to a specific droplet size, size distribution, or viral load. Indeed, the relationship between droplet concentrations and infective dose has at times for various diseases been contentious and confusing [25]. Dai and Zhao [26] estimate the infective dose for SARS-CoV-2 to be 14–48 quanta/h. Zemouri et al. [27], estimated intermediate risk for SARS-CoV-1 to be ~29 quanta/h (with a range of 11.4–295.5 quanta/h for low to high risk, respectively). Miller et al. [28], estimated an infectious dose of 970 quanta/h for the superspreading Skagit Valley choir practice. Buonanno et al. [29], suggest that typical quanta rates are in the range of 1–100 quanta/h and that lower doses presented (10 quanta/h) may be more representative of passive breathing, while the highest dose may be representative of singing or exercise (e.g., 300 quanta/h).1 Our analysis elsewhere in this article assumes an emission rate of 100 quanta/h, recognizing that it is likely lower in many cases but could be higher and may depend on the disease state of the individuals shedding the virus and likely changes across the course of the disease and from person to person.

Fig. 7.

Cumulative probabilities of infection versus time for the source (a) and connected (b) rooms for q = 10, 30, 100, and 300 quanta/h (Scenario 1 Case 1).

The Wells-Riley approach in its original formulation required steady flows and steady concentration; here the flows are steady (no active control) but the concentrations are dynamic [15]. Rudnick and Milton [14] provide a pathway to connect dynamic concentrations from a steady source with infective doses. We extend that approach to dynamic sources that never achieve a steady state.

3.6. Implications

Each of these probabilities of infection are based on the parameters given in Table 1, which were selected for short term exposure (5 min) to a moderately high infective dose of SARS-CoV-2. They are not a worst-case scenario (higher infectivity doses are possible), and infective doses likely vary significantly across individuals and as a function of disease progression. Whether these probabilities of infection are large or small depends on personal and community risk tolerances. For example, an individual may determine that some risk is acceptable as they balance competing individual health, social, and economic needs, or, alternatively, only fully minimized risk may be acceptable to protect a vulnerable person. Furthermore, a community may accept risk by balancing viral spread against access to health care (“flattening the curve”) while maintaining some economic activity in the process, or, alternatively, a community may seek to eradicate viral spread in the spirit of a cordon sanitaire. Each of these involves different risk tolerances, the balancing of which across a population remains outside the scope of this quantitative analysis. Similarly, each of these scenarios and cases has distinct implications for building energy usage, occupants' comfort, and HVAC equipment maintenance. For example, higher air filtration (i.e., higher MERV rating) uses more fan energy and may impede HVAC system performance if the fan does not have power to overcome resistance or too much pressure is built up. More outdoor air intake increases energy use during the heating or cooling seasons. If the HVAC systems are not sized to handle a high percentage of outdoor air, occupants’ thermal comfort will have to be compromised when the temperature setpoints cannot be met. Moreover, if outdoor air quality is in a poor condition, other risks may be introduced by bringing in more outdoor air, especially when unfiltered (such as opening the windows). Additional labor or material costs will likely be incurred to mitigate these other risks or side effects. For some, additional costs may be acceptable, while to others, the increased cost would be prohibitive. While a quantitative analysis of associated costs is also outside the scope of this article, this quantitative analysis may be helpful to decision makers.

Finally, we recognize that well-mixed models, while insightful for modeling the transport and fate of aerosolized materials across rooms, do not account for spatial variations of virus-containing particles within the breathing zones. For example, individuals in the direct pathway of a cough or sneeze may experience substantially higher concentrations. Similarly, individuals in the direct pathway of air coming from supply vents may breathe elevated droplet/particle concentrations compared to the well-mixed average. This is important because some recent and well-intentioned guidance suggests building managers should substantially increase the flow rate throughout the building, which may disadvantage some individuals downstream of virus emitters in rooms that are not well mixed.

4. Conclusion

In summary, we evaluated concentrations and probabilities of infection for both internal and external exposure sources using a well-mixed model in a building with a central HVAC system. The presented results indicate meaningful exposure via the ventilation system in support of our hypothesis.

Our findings for the select cases and exposure considered here (see Table 1, Table 2) at long times (hours of breathing) for the connected rooms are:

• •For typical levels of recirculation, filtration is most effective in lowering the aerosol concentration and probability of infection via HVAC systems as filters block the path of viral aerosols. For example, MERV-8 filters reduce the risk of infection from 1.5% (no filter) to 0.2% in the connected rooms. In theory, higher filtration level(s) result in higher level(s) of protection. However, the risks of infection are all relatively small beyond MERV-8 (e.g., 0.04% and 0.01% risks of infection for MERV-11 and MERV-13, respectively).
• •Outdoor air is the second most effective measure to reduce the aerosol transmission via the HVAC system. When the fraction of outdoor air is increased from 0% to 33%, the risk is decreased from 0.22% to 0.16%. Given its significant impact on energy use and thermal comfort in the heating- or cooling-dominated climate zones, ventilation should be increased with thoughtfully.
• •Increasing the air change rate should also be considered with caution because it may increase the rate of viral aerosol spread via HVAC systems. In our study, when the ACH is increased from 1.8 to 12, the time to the peak concentration of virus in the connected rooms decreases from 30 min to 11 min.

We acknowledge that buildings are heterogeneous, and it is nearly impossible to prescribe a set of effective measures without knowing the building location, layout, HVAC system type and vintage. Nevertheless, our study provides a foundational analysis using a generic building system, assuming typical settings and infectivity levels.

Author contributions

All authors participated in the planning and manuscript preparation and have approved the final article. LFP and TIS performed the quantitative calculations. NW and LFP secured funding.

Funding sources

Research was supported by the DOE Office of Science through the National Virtual Biotechnology Laboratory (NVBL), a consortium of DOE national laboratories focused on response to COVID-19, with funding provided by the Coronavirus CARES Act. This work was performed at Pacific Northwest National Laboratory under contract DE-AC05-76RL01830. No funding source governed the design, data collection and interpretation of this article.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix.

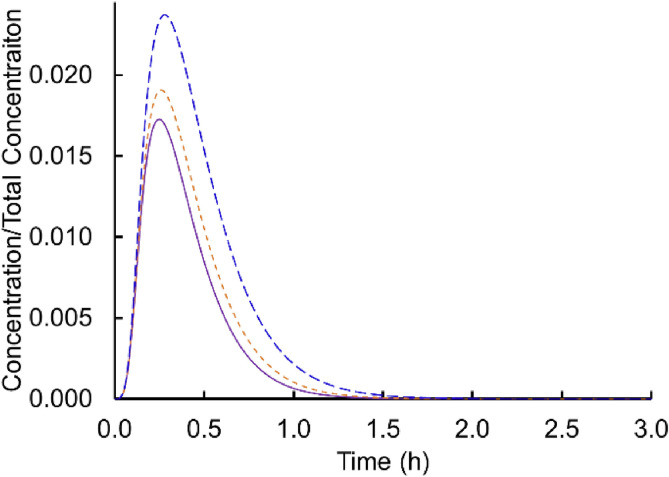
In the main body of the text, calculations include both viral decay and settling. To provide a sense for the relative importance of these terms, Fig. A.1 shows the concentration profiles with both viral decay and settling, without viral decay but with settling, and with viral decay but without settling for the baseline condition (Case 1 Scenario 1 in Table 2). The figure suggests that both effects are distinctive for the connected rooms, and that neglecting either settling or viral decay overestimates the concentrations and by extension probability of infectivity.

Fig. A.1.

Concentrations scaled on the total virus concentration shed, C_total, for the baseline condition with both viral decay and settling included (solid), without viral decay but with settling (short dash), and with viral decay but without settling (long dash).